Patient-based estimation of organ dose for a population of 58 adult patients across 13 protocol categories

Abstract

Purpose:

This study aimed to provide a comprehensive patient-specific organ dose estimation across a multiplicity of computed tomography (CT) examination protocols.

Methods:

A validated Monte Carlo program was employed to model a common CT system (LightSpeed VCT, GE Healthcare). The organ and effective doses were estimated from 13 commonly used body and neurological CT examination. The dose estimation was performed on 58 adult computational extended cardiac-torso phantoms (35 male, 23 female, mean age 51.5 years, mean weight 80.2 kg). The organ dose normalized by CTDI_vol (h factor) and effective dose normalized by the dose length product (DLP) (k factor) were calculated from the results. A mathematical model was derived for the correlation between the h and k factors with the patient size across the protocols. Based on this mathematical model, a dose estimation iPhone operating system application was designed and developed to be used as a tool to estimate dose to the patients for a variety of routinely used CT examinations.

Results:

The organ dose results across all the protocols showed an exponential decrease with patient body size. The correlation was generally strong for the organs which were fully or partially located inside the scan coverage (Pearson sample correlation coefficient (r) of 0.49). The correlation was weaker for organs outside the scan coverage for which distance between the organ and the irradiation area was a stronger predictor of dose to the organ. For body protocols, the effective dose before and after normalization by DLP decreased exponentially with increasing patient's body diameter (r > 0.85). The exponential relationship between effective dose and patient's body diameter was significantly weaker for neurological protocols (r < 0.41), where the trunk length was a slightly stronger predictor of effective dose (0.15 < r < 0.46).

Conclusions:

While the most accurate estimation of a patient dose requires specific modeling of the patient anatomy, a first order approximation of organ and effective doses from routine CT scan protocols can be reasonably estimated using size specific factors. Estimation accuracy is generally poor for organ outside the scan range and for neurological protocols. The dose calculator designed in this study can be used to conveniently estimate and report the dose values for a patient across a multiplicity of CT scan protocols.

I. INTRODUCTION

Remarkable technological developments in computed tomography (CT) in the last four decades, especially after the introduction of helical CT technology in the late 1980s,¹ have made CT an essential medical diagnostic tool. CT usage in the United States has been growing by 10%–15% every year.^2,3 The average effective dose per person in the United States has nearly doubled in the last three decades mostly due to an increase in the number of CT examinations performed.^4,5 As a result, radiation dose from CT has become a subject of public attention. The number of publications focusing on radiation dose in x-ray CT has risen considerably in the last 12 years.^6–8 There is a need to more accurately estimate the radiation dose and associated risks to patients undergoing CT examination.

In clinical practice, the volume CT dose index (CTDI_vol) and the dose length product (DLP) are currently the only measures of radiation dose displayed by the scanner manufacturers. Since CTDI_vol and DLP are computed based on standard-size cylindrical phantoms (16- and 32-cm phantoms, respectively), they do not provide dose information reflective of individual patients.^4,9–12 The concept of size-specific dose estimates (SSDE) has been recently proposed to address this limitation,¹³ but fell short of providing estimation of organ dose.¹⁴ Several studies have aimed to estimate organ doses using Monte Carlo methods,^4,15–17 leading to organ dose databases^9,18,19 and CT dose software packages such as ImpactDose,²⁰ ImPACT CTDosimetry,²⁰ CTDOSE (CT-Dose 2010),²¹ and VirtualDose.⁹ However, most of these approaches have been based on oversimplified stylized phantoms or a small number of adult phantoms.^9,10

The purpose of this study was to compute patient-specific organ doses and effective dose conversion factors for a representative collection of routinely used CT protocols across a large number (58) of adult patient phantoms. Based on the findings, the work included the development of an iPhone operating system (iOS) application as a convenient calculator for providing reasonable estimation of organ and effective doses for adult patients undergoing CT examination.

II. MATERIAL AND METHODS

II.A. Patients and computer models

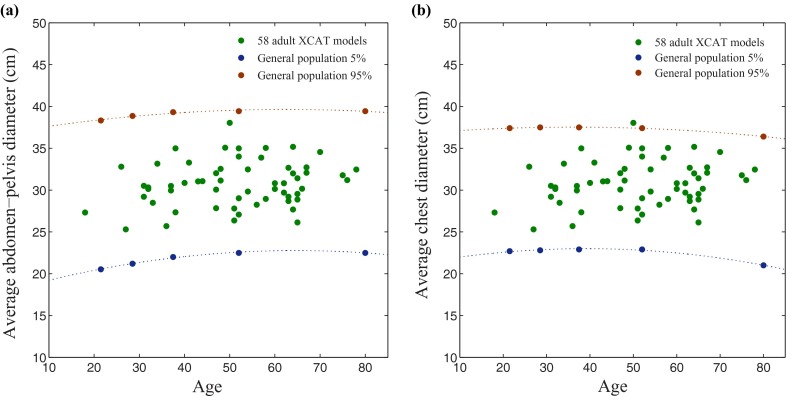
The study included 58 adult patients with mean age of 51.5 years (age range, 18–78) and mean weight of 80.2 kg (weight range, 52–117); including 35 male patients (age range, 18–78 years; weight range, 60–117 kg) and 23 female patients (age range, 27–75 years; weight range, 52–106 kg). The population was selected from the patients who underwent a standard chest-abdomen-pelvis CT examination using an IRB approved protocol. The variability in patient size among the patient population studied matched that of the general population (Fig. 1).²² The high resolution chest-abdomen-pelvis CT data were used as a basis to create a whole-body computational model from each patient.²³ Applying the semi-automatic software IMAGESEGMENT developed in our laboratory, the large organs and anatomical structures (lungs, heart, liver, kidneys, stomach, backbone, rib cage, gallbladder, spleen) within the CT images were segmented and modeled.²³ The obtained segmented images were converted to three-dimensional nonuniform rational basis spline (NURBS) surfaces using a NURBS-based 3D modeling software (Rhinceros, McNeel North America, Seattle, WA).²³ Remaining organs, not easily segmented or visible in the scan coverage, as well as head, neck, arms, and legs, were added by morphing organs from an existing extended cardiac-torso (XCAT) model developed from visible human data to fit the framework defined by segmented organs.^23–25 The organ volumes were further scaled and matched to predictions based on the patient's height, weight, and gender. The predictions were based on autopsy studies.²⁶ Tissue composition of each organ and structure in the models was defined based on the elemental composition and mass density information tabulated in the CIRS manual.²⁷

FIG. 1.

Variability in size among the patient models. The individual data points represent the average diameter of (a) abdomen-pelvis and (b) chest for 58 individual models, while lines represent the various (5% and 95%) percentiles according to general population-based studies (PeopleSize 2008, Open Ergonomics, UK).

II.B. CT protocols

Thirteen CT examination protocol groups, consisting of ten body categories and three neurological categories were selected based on existing protocols in use at our institution (Table I). All ten body categories shared the same set of scan parameters of tube voltage of 120 kVp, pitch of 1.375, beam collimation of 40 mm, and large body scan field-of-view per our routine clinical procedure. The scan parameters used for neurological categories were tube voltage of 120 kVp, pitch of 1, beam collimation of 20 mm, and head scan field-of-view per our routine clinical procedures. All 13 protocols and the associated scan parameters were explicitly modeled in the Monte Carlo simulation.

TABLE I.

CT examination categories investigated in this study and the associated starting and ending anatomical landmarks of scan coverage.

		Simulated scan coverage
	Examination category	Start (1 cm above)	End (1 cm below)
	Chest-abdomen-pelvis	Lung apex	Inferior ischium
	Chest	Lung apex	Lung base
	Abdomen-pelvis	Superior liver	Inferior ischium
	Abdomen	Superior liver	Superior iliac crest
Body	Pelvis	Superior iliac crest	Inferior ischium
	Adrenals	Superior adrenals	Inferior adrenals
	Liver	Superior liver	Inferior liver
	Kidneys	Superior kidney	Inferior kidney
	Liver-to-kidney	Superior liver	Inferior kidney
	Kidneys-to-bladder	Superior kidney	Inferior bladder
	Head	Vertex of skull	Scalp bottom
Neurological	Neck	C1	C7
	Head-and-neck	Vertex of skull	C7

II.C. Radiation dose estimation

In this study, the Monte Carlo simulation package (PENELOPE, version 2006, Universitat de Barcelona, Spain) was implemented to simulate the CT examinations.²⁸ The organ dose for each patient was calculated by running the MC code based on the geometry of a common 64-slice CT system (GE Light-Speed VCT system) including helical and axial modes and the bowtie filters.^29,30 The simulation was previously validated in both cylindrical and anthropomorphic phantoms to agree with measurements within 1%–11% on average and 5%–17% maximum.²⁹

For a given protocol, the pertinent starting and ending points of scan for each patient model were computed. For helical scans (body protocols) the over-ranging length (required for data interpolation in helical reconstruction) was estimated to be 6.40 cm.¹¹ The total scan length for each examination was determined by adding the total image coverage to the over-ranging length.

To simulate each CT scan, 80 × 10⁶ photons were initiated and tracked through each patient's phantom, resulting in relative errors within 1%–4%. The dose to the organs was tallied from the deposited energy by the photons in each individual organ as a whole (as opposed to in individual voxels). The secondary electrons were assumed to be absorbed locally once they were generated. As the dose data were binned into (large) organs, the simplifying assumption regarding secondary particle absorption would not impact the results. The collision kerma estimator used can be categorized as a track-length estimator which keeps track of photon fluence track-length.³¹ Dose to the red bone marrow which was not explicitly modeled was estimated by tallying the volume-averaged photon fluence spectrum at each skeletal site and using the fluence-to-dose conversion coefficients of monoenergetic photons in cancellous bone of skeleton.^32,33 A single active marrow dose was then calculated as its skeletal average using the age-dependent fractional distribution of active marrow tabulated in ICRP 89.³⁴

A given organ can appear in different locations with respect to the scan coverage in different patients. This location was categorized as being completely “inside,” “on the periphery,” or completely “outside” of the scan region for each patient. An average likelihood, $P_{\mathrm{scan}}$, was computed for each organ-protocol combination using

$$P_{\mathrm{scan}}=\left(\frac{N_{\mathrm{in}}·1+N_{\mathrm{per}}·\frac{1}{2}+N_{\mathrm{out}}·0}{N_{\mathrm{total}}}\right)·100\%,$$ (1)

where N_in, N_per, and N_out are the number of patients in which that given organ is located inside, on the periphery, or outside of the scan, respectively, and N_total is the total number of the patients. In the dose analysis in this study, if the probability of an organ for being inside the scan field of view was less than 25%, the organ was considered to be outside the scan. If the probability was between 25% and 75%, the organ was considered to be on the periphery of the scan protocol. If the probability was greater than 75%, the organ was considered to be inside the scan protocol.

The estimated absorbed organ dose values were then weighted by the tissue weighting factors and summed to obtain the effective dose as

$$E={\sum }_T{w}_T{H}_T,$$ (2)

where H_T is the dose to organ T and w_T is the tissue weighting factor defined by ICRP publication 103.³⁷ Dose to gonads was approximated as dose to testes or ovaries separately, thus computing effective dose as a patient specific construct. Breast dose was included in the calculation of effective dose for all the phantoms. The “remainder” tissues mean dose of each gender was calculated as the remainder dose.

The estimated organ values for each patient across the CT examination categories were normalized by CTDI_vol to calculate the so-called h factor. The CTDI_vol was estimated from the technical reference manual of the GE LightSpeed VCT scanner using the tables of CTDI₁₀₀ and technique adjustment factors. The DLP was calculated using the corresponding CTDI_vol and total scan length for each examination protocols as

$$\mathrm{DLP}={\mathrm{CTDI}}_{\mathrm{vol}}\times {\mathrm{scan}\mathrm{length}}_{\mathrm{total}},$$ (3)

where the total scan length (scan length_total) included the over-ranging distance. The DLP and CTDI_vol calculated in the way shown, agreed with those from patients’ dosimetry reports to within 5%. The CTDI_vol per tube current values used for the body and neurological CT protocols, 6.23 and 21 mGy/100 mAs, respectively, were estimated based on 32- and 16-cm-diameter CTDI phantoms.

III. RESULTS

III.A. Organ dose

Figure 2 provides a summary of the geometry of the various protocols and the organs receiving dose in the protocols with respect to their location and the scan area. In general, as expected key organs are within the scan coverage in their associated anatomical categories. But that is not always the case, particularly for small organs.

FIG. 2.

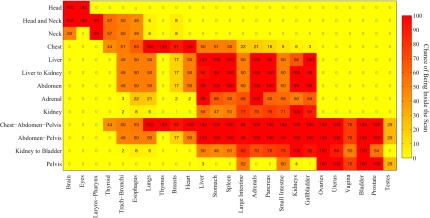
Probability that a given organ on the x-axis in a given CT examination category on the y-axis is inside, on the periphery, or outside the scan coverage over the population of patients.

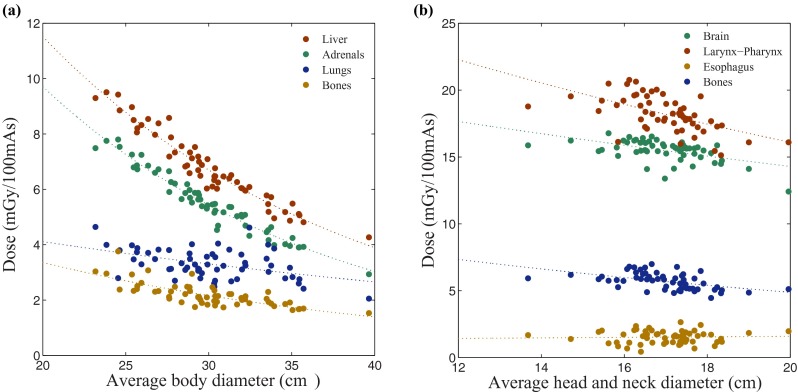
The dose results acquired from all 13 CT scanning protocol categories generally showed an exponential relationship with patient's body size for organs fully or partially irradiated. The organ dose (in mGy per 100 mAs) before (H_T) and after (h) normalization by CTDI_vol decreased exponentially with increasing average diameter of the patient's body within the scan field of view (SFOV) corresponding to each CT examination (Fig. 3) as

$$H_T\left(d_{\mathrm{avg}}\right)=\exp \left({\alpha }_T{d}_{\mathrm{avg}}+{\beta }_T\right),$$ (4a)

$$h\left(d_{\mathrm{avg}}\right)=\exp \left({\alpha }_h{d}_{\mathrm{avg}}+{\beta }_h\right),$$ (4b)

where d_avg is the average diameter of the cross sections of the patient's body within the scan coverage and α_T, β_T, α_h, and β_h are the fitting parameters. The average diameter was calculated for each patient model as

$$d_{\mathrm{avg}}=2\sqrt{\frac{V}{\pi l},}$$ (5)

FIG. 3.

Organ dose plotted against average diameter of patient's body inside the scan coverage. Dose to the organs which are fully or partially irradiated in (a) liver scan; liver (as a large organ inside), adrenals (as a small organ inside), lungs (as an organ on the periphery), and bone (as a distributed organ), and (b) head-and-neck scan; brain (as a large organ inside), larynx and pharynx (as small organs inside), esophagus (as an organ on the periphery), and bone (as a distributed organ).

where V and l are the total volume and length of the scan coverage, respectively.

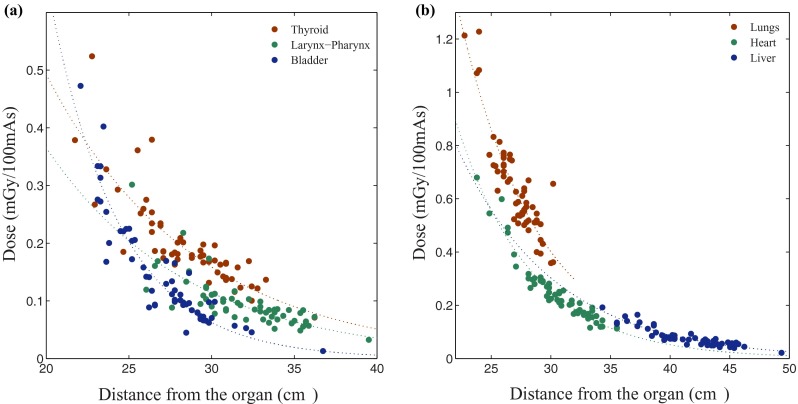
The dose results obtained from body categories for the organs fully or partially inside the scan coverage showed that the correlation between patient size (d_avg) and dose to individual organs was strongly dependent on the size and location of the organ. The correlation was generally strong for large organs that were entirely located inside the corresponding scan coverage (r > 0.88); however, it was generally weaker for small organs inside the scan coverage (r > 0.68), for the ones on the periphery (r > 0.49), and for the distributed organs (r > 0.63) [Fig. 3(a)]. The small organs that did not follow this pattern, i.e., the organs inside the scan coverage for which r < 0.68, were the breasts in chest and chest-abdomen-pelvis categories. The organs on the periphery that did not follow this pattern, i.e., the organs that were partially irradiated but had r < 0.49 were the trachea-bronchi in liver, liver-to-kidney, adrenals, and kidney-to-bladder scans; the esophagus in liver and liver-to-kidney; the testes in abdomen-pelvis and pelvis; and finally the gallbladder in adrenals scan. The dose for the organs outside the scan coverage showed weaker correlation with patient size (d_avg) but strong correlation with the distance between the center of the organ and the center of the scan region. The organ dose (in mGy per 100 mAs) normalized by CTDI_vol (h factor) decreased exponentially with increasing distance from the center of the scan region for each CT examination to the center of each organ outside the scan coverage [Fig. 4(a)] as

$$h\left(D\right)=\exp \left({\alpha }_{\mathrm{hout}}D+{\beta }_{\mathrm{hout}}\right),$$ (6)

where D is the distance from the center of the scan region to the center of the organ outside the scan coverage and α_hout and β_hout are the fitting parameters.

FIG. 4.

Organ dose plotted against distance between the center of the scan and the center of the organ. Dose to the organs which are outside the scan region in (a) liver scan; thyroid, larynx and pharynx, and bladder, and (b) head-and-neck scan; lungs, heart, and liver.

The dose results obtained from neurological protocols for the organs fully or partially inside the scan coverage showed a relatively weak correlation with patient size (d_avg) and dose to individual organs. Some organs showed no correlation between organ dose and patient size, mainly small organs such as the eyes, thyroid, trachea-bronchi, and esophagus. However, the correlation was generally stronger for large organs, such as the brain and larynx-pharynx, that were located entirely inside the corresponding scan coverage (r > 0.53), and for the distributed organs (bone, red bone marrow, and skin) (r > 0.45) [Fig. 3(b)]. For the organs outside the scan coverage, the organ dose strongly correlated with the distance between the center of the scan region and the center of the organ (r > 0.75) [Fig. 4(b)]. The organs outside the scan coverage that did not follow this pattern (r < 0.75) were ovaries, uterus, vagina, bladder, prostate, and testes for all the neurological scans; and eyes for neck category. Since CTDI_vol was constant for a given protocol, the same held true after the organ dose was normalized by CTDI_vol. For each protocol-organ combination, the fitting parameters (α_h, β_h,α_out, and β_out), root-mean-square of residuals, and mean value of h factor are reported in Table II.

TABLE II.

Fitting parameters (α, β), root-mean-square from the residual, and the mean value for h factor for each protocol-organ combination. The fitting parameters (α, β) and RMSE for h factor for the organs completely or partially inside the scan coverage in bold and for the organs outside the scan coverage in italic are shown here. [See the complete table in the supplementary material (Ref. 47)].

	(a) Chest and liver protocols
	Chest				Liver
Organ	Alpha	Beta	RMSEa	Meanb	Alpha	Beta	RMSE	Mean
Marrow	−0.06	0.90	0.03	0.375 ± 0.067	−0.05	−0.02	0.02	0.241 ± 0.045
Bones	−0.05	1.15	0.05	0.625 ± 0.103	−0.04	0.26	0.04	0.351 ± 0.067
Skin	−0.04	−0.02	0.02	0.251 ± 0.036	−0.02	−0.97	0.02	0.188 ± 0.022
Brain	−0.06	−2.25	0.00	0.016 ± 0.004	−0.11	−1.53	0.00	0.001 ± 0.000
Eyes	−0.09	−1.47	0.00	0.014 ± 0.004	−0.12	−1.30	0.00	0.001 ± 0.001
Larynx-pharynx	−0.03	0.27	0.17	0.484 ± 0.166	−0.12	−0.51	0.00	0.016 ± 0.007
Thyroid	−0.05	1.63	0.18	1.100 ± 0.229	−0.11	−0.27	0.01	0.032 ± 0.012
Trachea-bronchi	−0.06	2.03	0.11	1.236 ± 0.224	−0.01	−0.83	0.06	0.288 ± 0.063
Esophagus	−0.07	2.06	0.09	1.074 ± 0.209	−0.02	−0.32	0.06	0.438 ± 0.069
Lungs	−0.06	1.92	0.06	1.270 ± 0.197	−0.02	0.02	0.08	0.532 ± 0.085
Thymus	−0.05	1.97	0.12	1.384 ± 0.232	−0.11	0.46	0.07	0.212 ± 0.080
Breasts	−0.04	1.28	0.16	1.123 ± 0.196	−0.15	1.02	0.13	0.294 ± 0.198
Heart	−0.06	2.12	0.08	1.335 ± 0.228	−0.04	1.05	0.11	0.887 ± 0.164
Liver	−0.06	1.68	0.12	0.846 ± 0.179	−0.05	1.70	0.05	1.091 ± 0.204
Stomach	−0.06	1.59	0.14	0.908 ± 0.189	−0.06	1.82	0.07	1.110 ± 0.224
Spleen	−0.07	1.93	0.15	0.863 ± 0.214	−0.05	1.50	0.06	1.036 ± 0.181
Large Intestine	−0.04	−0.73	0.05	0.146 ± 0.055	−0.05	1.17	0.08	0.634 ± 0.142
Adrenals	−0.11	1.02	0.19	0.577 ± 0.211	−0.06	1.61	0.04	0.886 ± 0.178
Pancreas	−0.02	−0.17	0.20	0.562 ± 0.201	−0.07	1.94	0.04	1.007 ± 0.223
Small Intestine	−0.04	−0.7	0.06	0.157 ± 0.063	−0.06	1.63	0.13	0.800 ± 0.214
Kidneys	−0.18	2.21	0.13	0.296 ± 0.162	−0.07	1.93	0.07	0.957 ± 0.224
Gallbladder	−0.12	1.28	0.27	0.452 ± 0.314	−0.05	1.79	0.13	1.180 ± 0.248
Ovaries	−0.12	−0.83	0.00	0.005 ± 0.002	−0.26	2.86	0.01	0.054 ± 0.038
Uterus	−0.10	−1.66	0.00	0.004 ± 0.001	−0.25	3.02	0.01	0.043 ± 0.029
Vagina	−0.11	−1.61	0.00	0.002 ± 0.001	−0.26	3.27	0.00	0.014 ± 0.009
Bladder	−0.14	−0.24	0.00	0.002 ± 0.001	−0.24	2.45	0.01	0.023 ± 0.015
Prostate	−0.14	−0.23	0.00	0.001 ± 0.001	−0.23	2.43	0.00	0.012 ± 0.009
Testes	−0.10	−3.06	0.00	0.000 ± 0.000	−0.15	−0.55	0.00	0.002 ± 0.001
	(b) Liver-to-kidney and abdomen protocols
	L-to-K				Abdomen
Organ	Alpha	Beta	RMSE	Mean	Alpha	Beta	RMSE	Mean
Marrow	−0.03	−0.38	0.02	0.256 ± 0.038	−0.04	−0.06	0.03	0.292 ± 0.049
Bones	−0.03	−0.10	0.05	0.373 ± 0.062	−0.04	0.23	0.05	0.426 ± 0.074
Skin	−0.01	−1.31	0.02	0.203 ± 0.018	−0.01	−1.07	0.02	0.225 ± 0.022
Brain	−0.13	−0.85	0.00	0.001 ± 0.000	−0.13	−0.35	0.00	0.001 ± 0.000
Eyes	−0.14	−0.20	0.00	0.001 ± 0.001	−0.16	0.97	0.00	0.001 ± 0.001
Larynx- pharynx	−0.14	0.23	0.00	0.016 ± 0.007	−0.15	0.90	0.00	0.016 ± 0.007
Thyroid	−0.13	0.35	0.01	0.032 ± 0.013	−0.14	0.84	0.01	0.031 ± 0.012
Trachea-bronchi	−0.01	−0.82	0.06	0.288 ± 0.063	−0.02	−0.74	0.05	0.284 ± 0.055
Esophagus	−0.02	−0.31	0.07	0.440 ± 0.070	−0.02	−0.27	0.06	0.436 ± 0.070
Lungs	−0.02	0.02	0.08	0.533 ± 0.085	−0.02	0.08	0.07	0.528 ± 0.079
Thymus	−0.10	0.37	0.07	0.212 ± 0.080	−0.10	0.43	0.05	0.205 ± 0.056
Breasts	−0.21	2.18	0.13	0.295 ± 0.198	−0.25	3.12	0.13	0.284 ± 0.187
Heart	−0.04	1.05	0.11	0.889 ± 0.165	−0.04	1.07	0.11	0.885 ± 0.162
Liver	−0.05	1.64	0.05	1.099 ± 0.198	−0.05	1.64	0.05	1.106 ± 0.202
Stomach	−0.06	1.78	0.07	1.119 ± 0.221	−0.06	1.77	0.07	1.127 ± 0.224
Spleen	−0.05	1.45	0.06	1.044 ± 0.176	−0.05	1.44	0.06	1.051 ± 0.178
Large intestine	−0.03	0.58	0.10	0.714 ± 0.127	−0.04	1.03	0.12	0.855 ± 0.166
Adrenals	−0.05	1.52	0.03	0.902 ± 0.170	−0.05	1.51	0.04	0.914 ± 0.172
Pancreas	−0.06	1.84	0.04	1.025 ± 0.214	−0.06	1.84	0.04	1.042 ± 0.218
Small intestine	−0.04	1.02	0.13	0.900 ± 0.175	−0.05	1.42	0.12	1.057 ± 0.206
Kidneys	−0.06	1.70	0.05	1.005 ± 0.200	−0.06	1.69	0.04	1.031 ± 0.201
Gallbladder	−0.05	1.69	0.13	1.195 ± 0.241	−0.05	1.71	0.13	1.215 ± 0.247
Ovaries	−0.19	1.40	0.01	0.060 ± 0.020	−0.20	1.89	0.02	0.110 ± 0.037
Uterus	−0.16	0.86	0.01	0.048 ± 0.017	−0.18	1.56	0.02	0.089 ± 0.033
Vagina	−0.20	1.73	0.00	0.016 ± 0.006	−0.14	0.30	0.00	0.028 ± 0.008
Bladder	−0.16	0.62	0.01	0.031 ± 0.012	−0.17	1.27	0.02	0.057 ± 0.022
Prostate	−0.15	0.22	0.00	0.019 ± 0.007	−0.16	1.03	0.01	0.034 ± 0.014
Testes	−0.09	−2.63	0.00	0.003 ± 0.001	−0.10	−1.87	0.00	0.005 ± 0.002

^aRoot-mean-square of the residuals (RMSE) represents the average discrepancy between the h factor values predicted by using the fitting function and the h factor values calculated for individual patient. It has the same unit as h factor or organ dose.

^bMean represents the average value of the h-factor calculated for individual organs across all the patients. It has the same unit as h factor or organ dose.

III.B. Effective dose

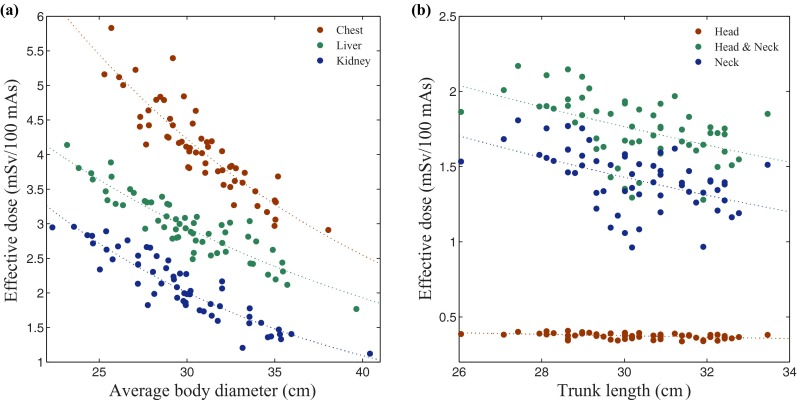
For all body protocols, the correlation between the effective dose before and after normalization by DLP (in mSv per 100 mAs and mSv per mGy-cm, respectively) and patient size (averaged diameter of the patient's body inside the scan coverage) could be well described by an exponential fit [Fig. 5(a)]. The effective dose decreased exponentially with the patient size as

$$E\left(d_{\mathrm{avg}}\right)=\exp \left({\alpha }_E{d}_{\mathrm{avg}}+{\beta }_E\right),$$ (7a)

$$k\left(d_{\mathrm{avg}}\right)=\exp \left({\alpha }_k{d}_{\mathrm{avg}}+{\beta }_k\right),$$ (7b)

where k denotes effective dose normalized by DLP. The exponential correlation for the body protocols was strong (r > 0.87), but weaker for the neurological protocols (r < 0.41). For neurological protocols, effective dose was slightly more strongly correlated with the measured trunk length of the patient than with the patient diameter. More specifically, the r value of the correlation of effective dose with diameter for protocol head, neck, and head-and-neck were 0.41, 0.15, and 0.18 which improved to 0.46, 0.48, and 0.48, respectively, when trunk length was used as the correlation factor. The estimated effective dose after normalization by DLP (“k factor”) (in mSv per mGy-cm) decreased exponentially with increasing length of trunk [Fig. 5(b)] as

$$k\left(L_{\mathrm{trunk}}\right)=\exp \left({\alpha }_{kl}{L}_{\mathrm{trunk}}+{\beta }_{kl}\right),$$ (8)

where L_trunk is the measured trunk's length and α_kl and β_kl are the fitting curve parameters. The fitting parameters (α_k, β_k, α_kl, and β_kl), root-mean-square of residuals, and mean value of the k factor are reported in Table III.

FIG. 5.

Effective dose for body and neurological CT examination categories. Effective doses are plotted against (a) average patient's body diameter for the body scan categories; chest, liver, and kidney, and (b) patient's trunk length for neurological scan categories; head, neck, head-and-neck.

TABLE III.

Fitting parameters (α, β) and root mean square from the residual for k factor for each CT examination category. The fitting parameters (α, β), RMSE, and the mean value for k factor for the body CT examination categories in bold and for the neurological categories in italic are shown here.

	k factor
Protocol	Alpha	Beta	RMSEa	Meanb
Head	−0.02	−6.25	0.0013	0.0011 ± 0.0001
Head-and-neck	−0.04	−4.65	0.0004	0.0028 ± 0.0004
Neck	−0.05	−3.98	0.0006	0.0044 ± 0.0007
Chest	−0.04	−2.52	0.0014	0.0211 ± 0.0028
Liver	−0.05	−2.57	0.0018	0.0195 ± 0.0035
Liver-to-kidney	−0.05	−2.37	0.0014	0.0187 ± 0.0037
Abdomen	−0.05	−2.49	0.0013	0.0177 ± 0.0034
Adrenal	−0.06	−1.98	0.0016	0.0212 ± 0.0047
Kidney	−0.07	−2.10	0.0018	0.0174 ± 0.0044
CAP	−0.05	−2.56	0.0007	0.0157 ± 0.0025
Abdomen-pelvis	−0.05	−2.64	0.0009	0.0144 ± 0.0026
Kidney-to-bladder	−0.07	−2.35	0.0017	0.0135 ± 0.0033
Pelvis	−0.06	−2.86	0.0009	0.0101 ± 0.0020

^aRoot-mean-square of the residuals (RMSE) represents the average discrepancy between the k factor values predicted by using the fitting function and the k factor values calculated from the organ dose values of individual patients. It has the same unit as k factor or effective dose.

^bMean represents the average value of the k factor calculated for individual patients. It has the same unit as k factor or effective dose.

IV. DISCUSSION

As summarized in the Introduction, CTDI_vol, DLP, and even SSDE, do not represent the structure of patient dose in terms of organ dose definitions. In this work, we estimated organ dose conversion coefficients via a validated Monte Carlo program with our library of patient-specific computer models developed from clinical CT images.^29,30 It has been shown that normalizing the organ dose by CTDI_vol as a value that accounts for the differences between scanners makes the organ dose results largely scanner-independent (error <8%).³⁶ Similarly when the effective dose is normalized by DLP to calculate k factor, the dependence on the scanner model is minimized (<10%).^37,38 Taking these facts into account, although in this study a specific scanner model (GE Light-Speed VCT system) was simulated, the results can be generalized to other CT scanner models.

Using the dose results from a large library of retrospectively chosen patients from our clinical operation such that they represent a wide range of body types and age groups of adult males and females, enabled accurate estimation of organ and effective doses. Most importantly, due to the fact that the CTDI_vol-normalized organ dose (h factor) and DLP-normalized effective dose (k factor) results are largely scanner-independent, they can be further applied to other CT systems with reasonable accuracy [<10% (Refs. 36,37,39) and 15% according to our calculations]. k factors may also be applied to tube current modulated scan with some discrepancy (<8%).³⁹ However, these numbers are averaged across the entire population. For a given patient, this discrepancy can indeed be as large as 25%, consistent with our earlier report.⁴⁰ This is due to the fact that when the individual discrepancies are averaged across the population, the case variability reduces the differences. These results indicate that as a first order approximation, as approached in this study, we can generalize across scanners. However, true patient specific organ dose calculations need to take the exact scanner into account. Furthermore, more work is needed to enable organ dose estimation with tube current modulation.

One of the challenges in organ dosimetry for the individual patients is that the organs appear in different places in different patients. In order to compute the probability of a given organ appearing in a scan coverage with higher precision compared to previous studies, we have included a larger population of patients in this study. To demonstrate this higher precision, consider an example from Fig. 2, examining testes in pelvis scan. For three male patients studied by Li et al., testes were reported as organs totally inside pelvis scan,¹² while our study of 35 male patients shows that in 20 patients the testes were partially irradiated and in 15 patients the testes were totally outside the scan coverage. Applying Eq. (1) indicated that if we have a representative population of patients undergoing a pelvis scan, the probability of the testes to be inside the scan is only 29%. As such, while approximation can be made to generalize organ doses across patient, the actual dose for a specific patient can only be most accurately estimated with full knowledge of patient and scan geometry.

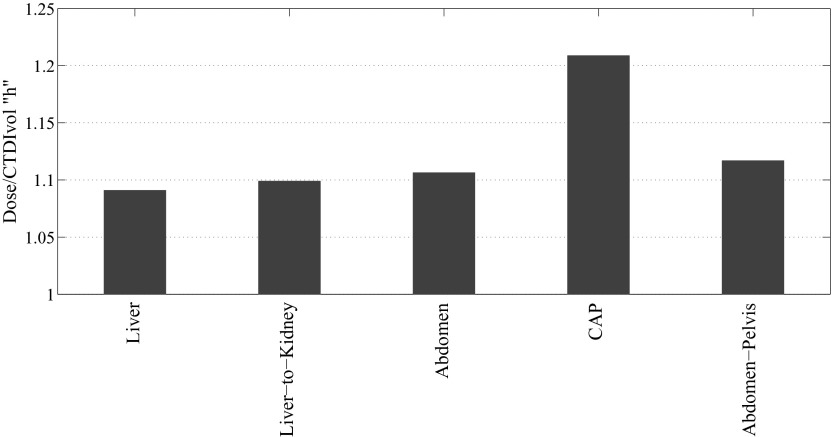
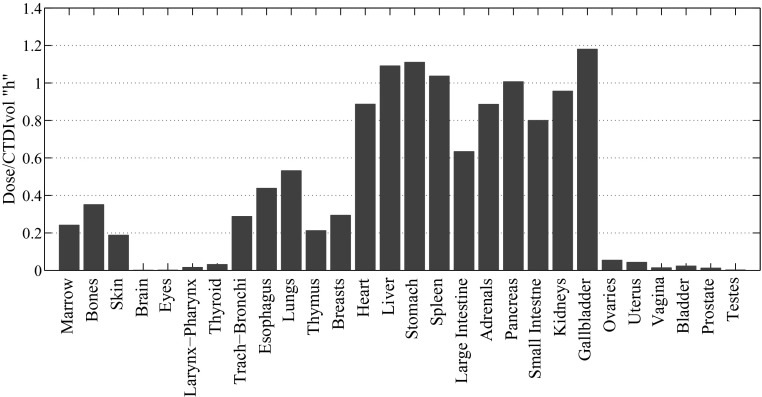
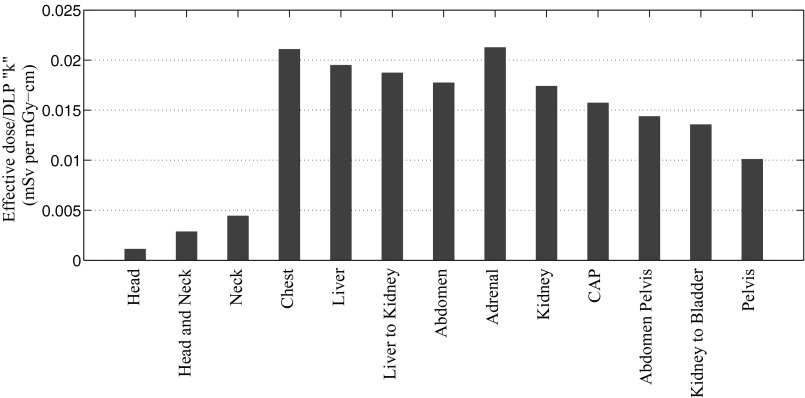
Our study showed that for a fully irradiated organ, organ dose normalized by CTDI_vol averaged over all the patients varied only slightly across different CT examination categories. For instance, the coefficient of variation (COV) of average h factor estimated for the liver across five examination categories of liver, liver-to-kidney, abdomen, abdomen-pelvis, and chest-abdomen-pelvis examination categories was 4.3% (Fig. 6). For these organs, the dose differences between different CT examination categories seem to be primarily based on the difference caused by the scattered radiation, which was directly related to the scan length, hence the highest h factor for chest-abdomen-pelvis protocol. Contrary to the slight difference between the dose received by the same organ over different categories, the dose to the organs in the same protocol, varied significantly. For instance, for liver scan, the coefficient of variation of h factor across organs averaged over all the patients was 97% (Fig. 7). This was primarily due to the variabilities in the location and size of the organs with respect to the scan region. The study further showed that the averaged k factor over all the patients varied significantly across different CT examination categories with a COV of 51% (Fig. 8). This can be understood from the definition of the effective dose and the different numbers of the radiosensitive organs exposed in different CT scans.

FIG. 6.

Comparison of dose to the liver after normalization by CTDI_vol (h factor) across five different protocols.

FIG. 7.

Comparison of organ doses after normalization by CTDI_vol (h factor) in liver scan.

FIG. 8.

Comparison of effective dose after normalization by DLP (k factor) (mSv per mGy-cm).

In this study, the organ dose results were normalized by CTDI_vol based on prior arts. However a rationale can be made that this normalization is better to be done in terms of the DLP⁴¹ as to better account for scattered dose. We have conducted a parallel study (not detailed here) that showed that a normalization by DLP provides a slight improvement over that by the CTDI_vol (typical Pearson r increase of less than 5%). We believe that this small level of improvement relates to the fact that, by and large, the scan length of the patients were in the same order of magnitude as that of the CTDI phantom measurements. Thus, the h factor being the organ dose normalized by the CTDI_vol would have the same general level of fluctuation even if it is normalized by the DLP. Given the small magnitude of improvement, we maintained the prior methodology of normalizing organ dose by the CTDI_vol. However, the concept needs to be revisited for protocols with shorter scan length.

Our study of dose to 58 adult patients undergoing different CT examinations showed that dose (normalized by tube current-time product) to the organs that are fully or partially irradiated decreased exponentially with patient size (average diameter of the patient's body inside the scan coverage) (Fig. 3). The exponential fit to the data was applied based on underlying physics of x-ray interaction as demonstrated by others.⁴² This exponential relationship is further consistent with the correlation between mean section dose and water phantom radius described by Huda et al.⁴³ and also the correlation between the dose and average chest diameter reported for the pediatric patients by Li et al.¹¹

For the organs outside the scan coverage, the organ dose strongly correlated with the distance of the organ from the scan region rather than average diameter of the body inside the scan (Fig. 4). This can be explained simply by the fact that the dose distributed to the organs outside the scan region is primarily from scattered radiation. The absorption is exponentially related to the distance from the center of the scan region to the center of the organ outside the scan, i.e., larynx-pharynx, thyroid, and bladder in liver scan, and the liver, lungs, heart in head-and-neck scan (Fig. 4).

The study further showed that, for the body protocols, the effective dose before and after normalization by DLP strongly correlated with the average diameter of the patient's body inside the scan coverage [Fig. 5(a)]. This can be explained by the fact that the most of the radiosensitive organs with majority of tissue weighting factors [defined by ICRP publication 103 (Ref. 35)] are directly exposed. For example, in liver scan, majority of the radiosensitive organs (shown with probability value larger than 25% in Fig. 2) with total tissue weighting factors of 0.65 are located within the scan coverage. Consequently, most of the contribution of the effective dose is due to the attenuation of the primary beams, which is related to the average diameter of the patient body inside the scan coverage.

In contrast to the k factor for the body CT examinations, the k factor estimated for the neurological CT examinations were weakly correlated with the average diameter of the patient. This can be explained by the fact that only a minority of the radiosensitive organs are located inside the neurological scan regions. For example, in head-and-neck scans, only a small number of radiosensitive organs (brain, eyes, larynx-pharynx, thyroid, trachea-bronchi, and esophagus with total weighting factor of 0.12) are located inside the scan coverage. Most contributions to effective dose are from the organs outside the scan region, exposed to scattered particles along the body axis. As a result, the effective dose is more related to the distance from the radiosensitive organs outside the scan length than the average diameter of the patient's body inside the scan region.

In our study, patient's diameter was measured as an average across the scan range. However, an adaptive thresholding algorithm can be applied to determine the patient's diameter from the scout images.⁴⁴ The same can be applied to trunk length. Organ distances, alternatively, can be assumed based on average anatomical geometry or assessed using a method implemented based on scout images, though either requires robust clinical implementation.⁴⁴ Meanwhile, it would be possible to physically measure the patient habitus prior to exam to assess an estimate of the imparted dose.

This work not only has extended the validity of the method by Turner et al., it has also suggested a new method of dose calculation for organs outside the scan coverage. Including a larger number (13) of CT examinations and the largest population of anthropomorphic phantoms among the CT studies are important distinguishing components of this work. Moreover, although the dose to the organs outside the scan coverage is not strongly correlated to the patient's size (body diameter) a strong correlation was found between the dose and the distance-from-the-organ [Figs. 4(a) and 4(b)] as a robust alternate prediction tool.

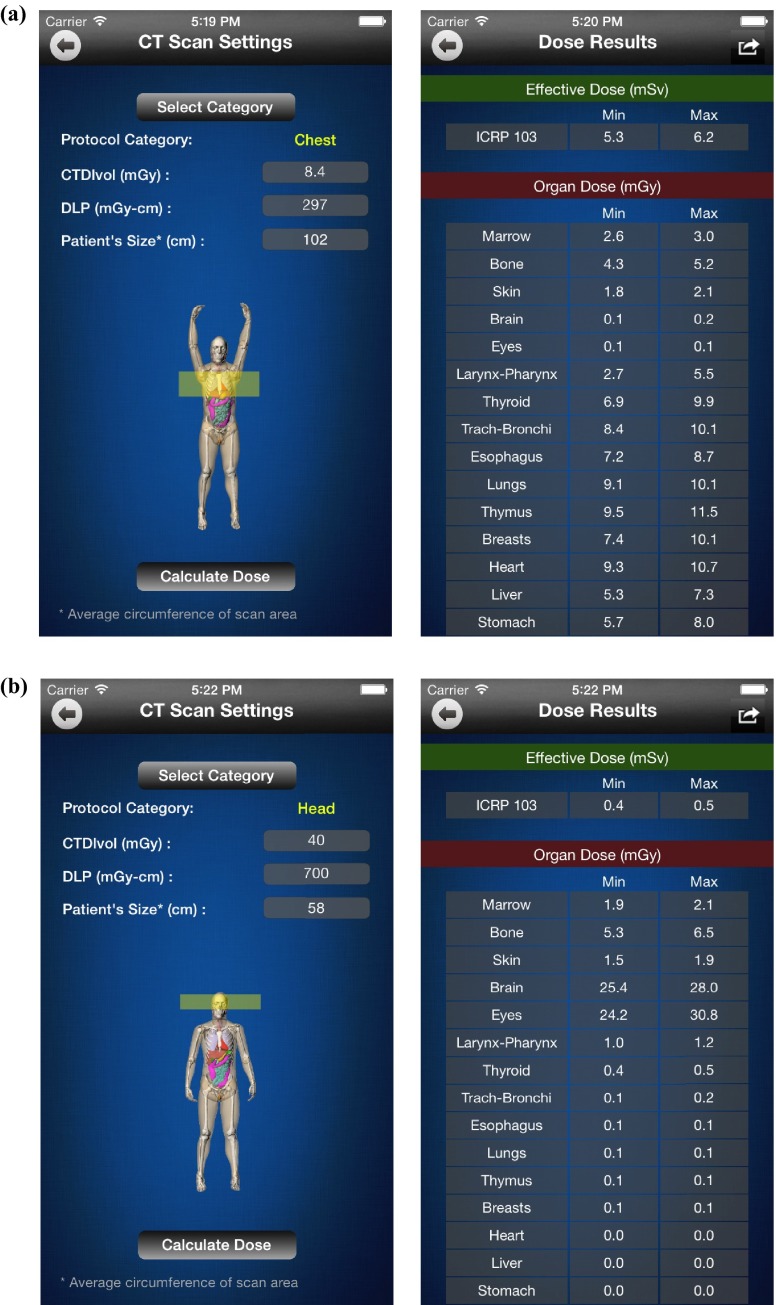
A novel application of this dose estimation technique is an application for the iPhone that radiologists can use to quickly estimate the approximate dose that their patients will receive for a given CT examination (Fig. 9). The dose estimation iOS app was scripted in Objective-C to apply the dose results from Monte Carlo simulations to predict the dose to the patients for the modeled CT examinations. The software, using the fitting parameters (Tables II and III), computes the estimated effective and organ doses as H_organ = h(S) × CTDI_vol and E = k(d) × DLP, where h and k are functions of size (S and d) derived in Secs. III.A [Eq. (4b)] and III.B [Eq. (7b)], respectively; and CTDI_vol and DLP are specified by the user. Depending on organ's location category (as either inside-periphery or outside with respect to the scan area), S is either average diameter simply derived from average circumference C $\left(\mathrm{i}.\mathrm{e}.,d_{\mathrm{avg}}=\frac{C}{\pi }\right)$ of the patient's body within the scan coverage specified by the user, or average distance D_avg from the center of the scan region to the center of the organ outside the scan coverage, respectively. The variable d is either the average diameter (d_avg) for body or trunk length (L_trunk) for neurological protocols. In this way, the software applies the fitting parameters for the specified scan from our library of CT examination-organ combinations to predict the organ and effective doses for the specific patient.

FIG. 9.

Screen captures of the Dose Calculator iPhone app showing a male adult patient XCAT phantom in interactive rendering mode undergoing (a) chest and (b) head scans. The user first selects the CT examination category from a scrolling list view of 13 CT examination categories. Based on the selected category, the starting and ending point location of the scan is shown in a transparent yellow box. CTDI_vol, DLP, and the patient's size (average circumference of the patient's body inside the scan coverage) are further specified by the user. Based on the inputs, by pushing the “Calculate Doses” button, the effective (according to the ICRP Publication 103) and organ doses are displayed on the “Dose Results” screen. Dose values included correspond to the spread of the data in our database and reflect mean ± root mean square from the residual (RMSE) in the computed data specific to the patient size.

One limitation of our study was that only one CT scanner system (LightSpeed VCT, GE Healthcare) was modeled. Although, the dose values may differ from one scanner model to the other, normalizing the dose by CTDI_vol and DLP has shown to provide reasonably consistent results across different CT scanners.³⁶ Our study of different CT examination protocols was also limited by the lack of scan parameter diversity (i.e., the same tube potential, beam collimation, and pitch size were used for body and neurological protocols). There might be some dependency on scan parameters that were not examined in this study. However, it could be assumed those parameters are already reflected in the CTDI_vol figure; therefore, the difference in the results may not be significant (<10%).¹¹ The other limitation was that this study was based on the fixed-tube-current examination, i.e., the tube-current-modulation was not explicitly modeled in our simulation. The other potential source of error could be importing the morphed and scaled organs from original XCAT phantoms as surrogate of indistinct organs, a step in creating the new XCAT models. However, the error should be negligible as the radiation dose does not vary notably across the patient's cross section. The other limitation is that no practical method was suggested for predicting the dose values to the organs totally outside the scan regions, i.e., the organs shown in Fig. 2 with value less than 25%. No strong correlation was discovered between the organ dose and practically measurable patient geometry for organs with fitting parameters given in italic in Table II. However, we suggested a robust correlation between the dose and the distance from the scan region to the organ as a prediction tool for estimating the dose to such organs. The mean values and range of error to these dose values are provided in Table II. Finally, the use of effective dose for characterizing radiation burden to individual patients is not consistent with the definition of effective dose as a generic metric of radiation protection.

ICRP publication 103 (Ref. 35) defines effective dose based on a hermaphrodite reference. However, our methodology represents the wide use of effective dose to assess CT imaging doses for individual patients to make the dose comparable to that for background exposure or that from other imaging modalities.^45,46 In the absence of any single metric of radiation burden, effective dose is currently the only alternative. More complete metrics such as risk index¹¹ have been suggested that can provide a more reflective characterization, but a definitive alternative awaits consensus and professional endorsement of the scientific community.

V. CONCLUSION

The effective and organ doses received by patients for a range of different CT scan protocols can be estimated using Monte Carlo simulations. The appropriate exponential model that describes the correlation between the radiation dose and the patient size can be used to quickly estimate the organ and effective doses for different patients. This exponential model can further be integrated into a user-friendly calculator.