Abstract
Purpose:
The buildup of noncalcified plaques (NCPs) that are vulnerable to rupture in coronary arteries is a risk for myocardial infarction. Interpretation of coronary CT angiography (cCTA) to search for NCP is a challenging task for radiologists due to the low CT number of NCP, the large number of coronary arteries, and multiple phase CT acquisition. The authors conducted a preliminary study to develop machine learning method for automated detection of NCPs in cCTA.
Methods:
With IRB approval, a data set of 83 ECG-gated contrast enhanced cCTA scans with 120 NCPs was collected retrospectively from patient files. A multiscale coronary artery response and rolling balloon region growing (MSCAR-RBG) method was applied to each cCTA volume to extract the coronary arterial trees. Each extracted vessel was reformatted to a straightened volume composed of cCTA slices perpendicular to the vessel centerline. A topological soft-gradient (TSG) detection method was developed to prescreen for NCP candidates by analyzing the 2D topological features of the radial gradient field surface along the vessel wall. The NCP candidates were then characterized by a luminal analysis that used 3D geometric features to quantify the shape information and gray-level features to evaluate the density of the NCP candidates. With machine learning techniques, useful features were identified and combined into an NCP score to differentiate true NCPs from false positives (FPs). To evaluate the effectiveness of the image analysis methods, the authors performed tenfold cross-validation with the available data set. Receiver operating characteristic (ROC) analysis was used to assess the classification performance of individual features and the NCP score. The overall detection performance was estimated by free response ROC (FROC) analysis.
Results:
With our TSG prescreening method, a prescreening sensitivity of 92.5% (111/120) was achieved with a total of 1181 FPs (14.2 FPs/scan). On average, six features were selected during the tenfold cross-validation training. The average area under the ROC curve (AUC) value for training was 0.87 ± 0.01 and the AUC value for validation was 0.85 ± 0.01. Using the NCP score, FROC analysis of the validation set showed that the FP rates were reduced to 3.16, 1.90, and 1.39 FPs/scan at sensitivities of 90%, 80%, and 70%, respectively.
Conclusions:
The topological soft-gradient prescreening method in combination with the luminal analysis for FP reduction was effective for detection of NCPs in cCTA, including NCPs causing positive or negative vessel remodeling. The accuracy of vessel segmentation, tracking, and centerline identification has a strong impact on NCP detection. Studies are underway to further improve these techniques and reduce the FPs of the CADe system.
Keywords: coronary CT angiography (cCTA), noncalcified plaque, computer-aided detection
I. INTRODUCTION
Over 16 × 106 Americans have coronary heart disease and the prevalence of myocardial infarction approaches 8 × 106.1 Over 445 000 Americans die of coronary heart disease and over 151 000 die of myocardial infarction each year. Acute MI is often caused by rupture of coronary atherosclerotic plaques. In a study of the prevalence of atherosclerosis in patients with fatal stroke,2 it was found that coronary plaques, coronary stenoses, and myocardial infarction were highly prevalent in patients who died from a stroke regardless of etiology.
Plaque composition is an important factor in determining the risk for plaque rupture. Noncalcified plaques (NCP) are lipid-rich and more vulnerable to rupture than calcified plaques. NCPs are more difficult to visualize by radiologists because their CT numbers of NCP are low and soft plaque buildup may not significantly narrow the lumen. Conventional angiography and stress tests fail to provide a complete picture of plaque accumulation. ECG triggering contrast-enhanced coronary CT angiography (cCTA) with multi-detector row CT is a noninvasive diagnostic tool that can directly capture 3D images of a beating heart using a CT scanner. cCTA can identify the early stages of vulnerable plaque buildup even before the stenosis caused by the plaque can be visualized on conventional angiography images.3 However, the interpretation of cCTA (Ref. 4) is a demanding task even for experienced radiologists because of the large volume of data and the many vessel segments that need to be analyzed. Studies using 64-slice cCTA showed that the segment-based detection sensitivity ranged from 82% to 95%, specificity from 95% to 97% for >50% stenosis in >1.5 mm vessels.5–9 However, the reported sensitivities of NCP of <50% occlusion can be as low as about 35%–50%.10–12
Computerized analysis is essential for diagnostic accuracy for cCTA. The American Heart Association recommends that a workstation that allows for interactive manipulation and post-processing of the acquired data set is crucial. Most advanced clinical workstations provide functions to semiautomatically find a centerline between two points specified by the user.13 Automatic segmentation techniques in combination with user interactive correction are used for calcium scoring, which has been widely used to assess the risk of coronary artery disease. Arnoldi et al.14 reported that a computer-aided detection (CADe) system for detection of stenosis of ≥50% occlusion on four major coronary arteries (left main, left anterior descending, left circumflex, and right coronary artery) achieved 74% sensitivity with an average 0.56 false positives (FPs) per patient on 59 patients who underwent both cCTA and cardiac catheterization. However, there are no NCP analysis tools available in current clinical workstations. Such tools may be able to provide more comprehensive quantitative information about the patient's plaque burden and to monitor the response to therapy for patients undergoing medical treatment.14,15
The development of plaques in a coronary artery can cause arterial remodeling. Vessel remodeling is related to the progression and regression of atherosclerotic diseases. Positive remodeling (arterial expansion) may be a characteristic of early, unstable lesions, allowing considerable plaque accumulation despite normal luminal size. Negative remodeling (arterial shrinkage) and fibrotic changes may be associated with more stable plaques. Detection of NCP of positive remodeling is more challenging because the vessel lumen may not be narrowed and the contrast of NCPs is low relative to the surrounding tissue. In this study, we investigated the feasibility of our topological soft-gradient (TSG) detection method for prescreening followed by luminal analysis for FP reduction in a CADe system that is designed to assist radiologists in detection of NCPs in cCTAs including both positive and negative remodeling.
II. MATERIALS AND METHODS
II.A. Data set
Institutional Review Board approval was obtained before collection of patient data. We retrospectively collected a data set of 83 cCTA studies from files of 83 patients from 2005 to 2011. Eligible cases are those diagnosed with coronary artery disease and having at least one NCP in the cCTA study. The contrast-enhanced cCTA scans were acquired with ECG-gating using GE 64-slice scanners (LightSpeed VCT or Discovery CT750 HD) at 100–120 kVp and 340–790 mA in our department. Forty-seven of the 83 cCTA studies were acquired with retrospective ECG gating and the remaining 36 studies were acquired with prospective ECG gating. Both the acquisition and reconstruction protocols were those set up for cCTA in our cardiothoracic imaging division during the period of time the clinical exams were performed. For the prospective gating cCTA studies, adaptive statistical iterative reconstruction algorithm from GE was used, which further reduced dose in the acquisition of cCTA images. The effective dose was, on average, 23.3 ± 1.9 mSv for the studies with retrospective gating in comparison to 4.0 ± 1.9 mSv for those with prospective gating. The reconstructed cCTA volumes have a slice interval of 0.625 mm and in-plane pixel size of 0.391 or 0.488 mm, which were interpolated to isotropic voxel sizes of 0.130 mm or 0.162 mm, respectively, upon input to the CADe system for processing.
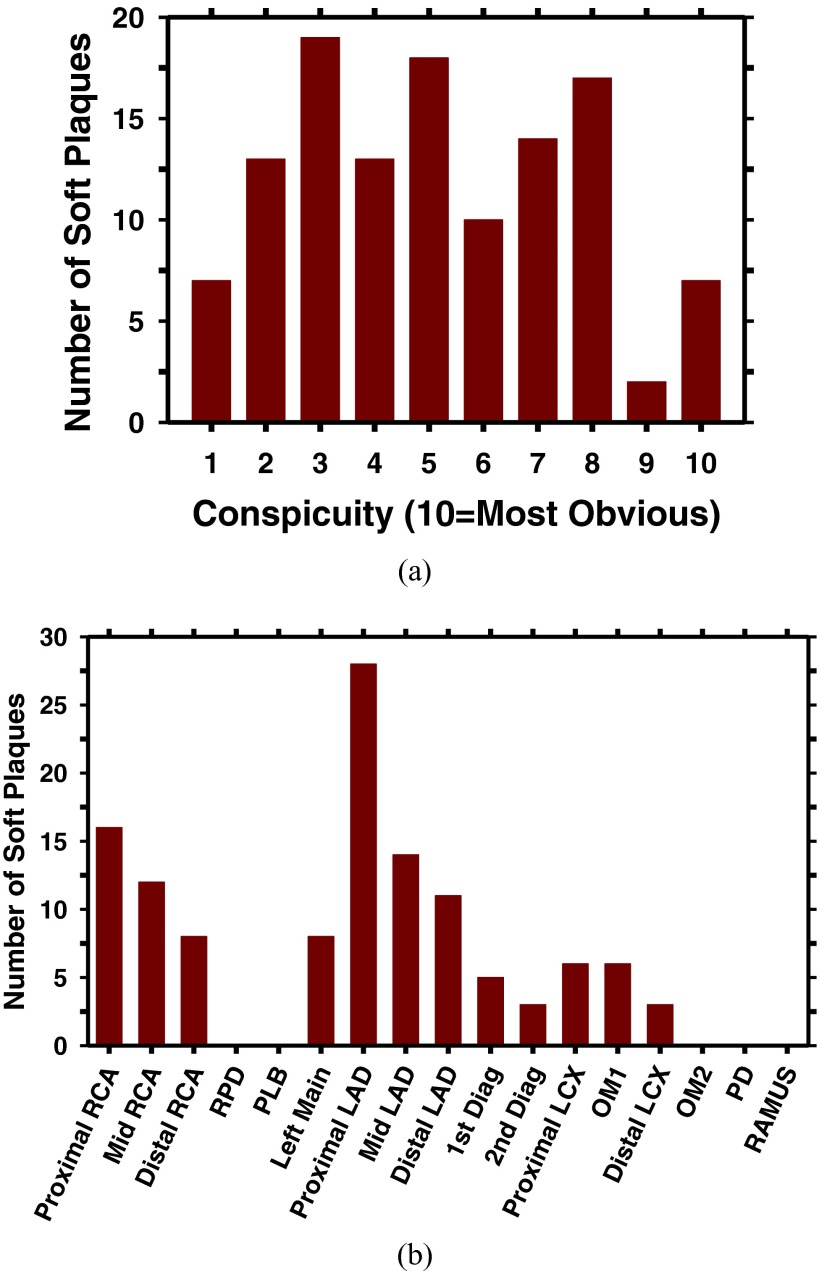
Each case was first read independently by two cardiothoracic radiologists. A single reconstructed phase (70% or 75%) for each scan, in which more major coronary arterial segments are relatively stationary, was selected and read by both radiologists. During the reading, the radiologist manually marked the location of each plaque with a 3D bounding box in the cCTA volume and traced the plaque longitudinally along the coronary vessel using an in-house developed graphical user-interface. The radiologists followed the 17-segment model of coronary arteries to label the locations of the NCPs. The 17 major coronary arterial segments16 that are considered clinically significant include (1) proximal RCA, (2) mid RCA, (3) distal RCA, (4) right posterior descending artery, (5) left main, (6) proximal left anterior descending (LAD), (7) mid LAD, (8) distal LAD, (9) first diagonal, (10) second diagonal, (11) proximal left circumflex (LCX), (12) first obtuse marginal, (13) distal LCX, (14) second obtuse marginal, (15) posterior descending, (16) posterior lateral branch, and (17) ramus intermedius. A GE Advantage workstation was available for the radiologist to read the cCTA images with the clinical visualization software. The radiologist also reviewed the clinical report of the cCTA exam as a reference for double checking the presence or absence of soft plaques. In addition to the location of the NCP, the radiologist provided the conspicuity rating of the NCP on a ten-point scale (10: most obvious) and the confidence level of the marked location having an NCP on a ten-point scale (10: highest confidence). In this study, only coronary arterial segments with diameters greater than about 2 mm were considered for NCP detection because plaques in very small coronary arteries are less significant clinically and also difficult to determine its presence. For any NCP location that did not agree in the two independent readings, the location would be reread by the radiologists. If there was still disagreement, an independent expert radiologist would serve as the adjudicator to decide whether the location had an NCP. With this process, a total of 120 NCPs were identified in the 83 cCTA volumes. The distributions of the conspicuity ratings and locations of the NCPs in the data set are shown in Fig. 1. Four of the 120 NCPs in our data set extended over two arterial segments, which were counted as one target but each of the arterial segments received a count in the location histogram in Fig. 1. The radiologist-marked NCP locations along the arteries were used as reference standard for evaluation of the CADe system.
FIG. 1.
(a) Distribution of conspicuity ratings of 120 NCPs in our data set. The conspicuity of the NCPs was rated by experienced cardiothoracic radiologists on a 10-point scale (10 = most obvious); (b) Bar chart of locations of NCPs in our data set. Four of the 120 NCPs spread over two arterial segments. RPD: right posterior descending artery; LAD: proximal left anterior descending; LCX: proximal left circumflex; OM1: first obtuse marginal; OM2: second obtuse marginal; PD: posterior descending; PLB: posterior lateral branch; RAMUS: ramus intermedius.
II.B. Detection of NCP by computer vision and machine learning techniques
II.B.1. Definition and reformation of search space
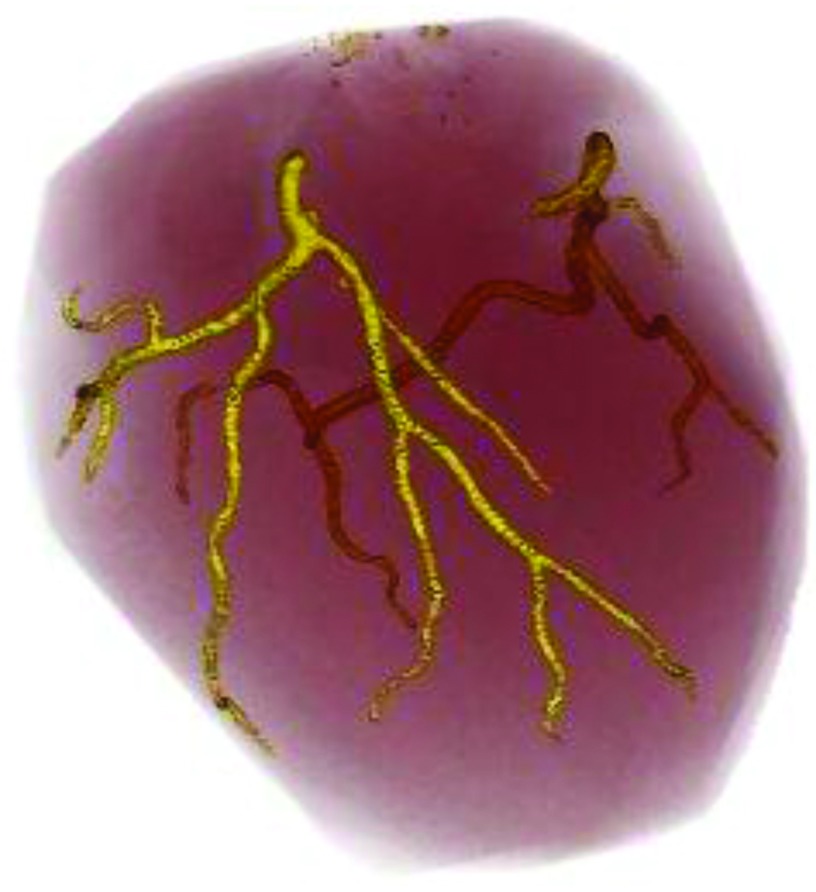
NCP results from a buildup of atherosclerotic deposits within the walls of coronary arteries and is prone to rupture without warning. Our computerized detection scheme is established upon the analysis of coronary artery walls. We first used a previously developed multiscale coronary artery response-rolling balloon region growing (MSCAR-RBG) method17 to extract the coronary artery trees. Figure 2 showed an example of the segmented and tracked arterial trees from a cCTA volume.
FIG. 2.
An example of coronary arterial trees extracted by our MSCAR-RBG method. The left coronary arterial tree is shown in the front and the right coronary arterial tree is in the back.
Our current MSCAR-RBG method does not have perfect performance. In a separate study,18 we evaluated its performance with 62 cCTA volumes using radiologists’ manually tracked coronary arterial segments following the 17-segment model16 as reference standard. We found that the MSCAR-RBG method correctly tracked 86.2% of the coronary arterial segments with 55 false vessels in the 62 cCTA volumes. For the current study, we evaluated the FP detections of NCPs in the segmented vessels rather than those in the false vessels. Therefore, the false segments were manually eliminated in the current data set of cCTA scans and only the true coronary arteries were processed in the detection stages.
Coronary arteries are relatively small tubular structures in the heart region. The centerline is determined during segmentation and tracking. For the subsequent plaque detection, an optimal path finding algorithm19 traced each vessel along its centerline from the seed point to the end of the vessel based on Dijkstra's algorithm20 and labeled them as a vessel for further analysis. Note that these vessel labels were different from the arterial segments in the clinical 17-segment model, and the coronary arteries closer to the seed point would be a part of the optimal paths for other downstream vessels multiple times. The NCPs in the repeatedly traced segments might therefore be detected multiple times but they would be merged at the later stage of the detection algorithm, as described later.
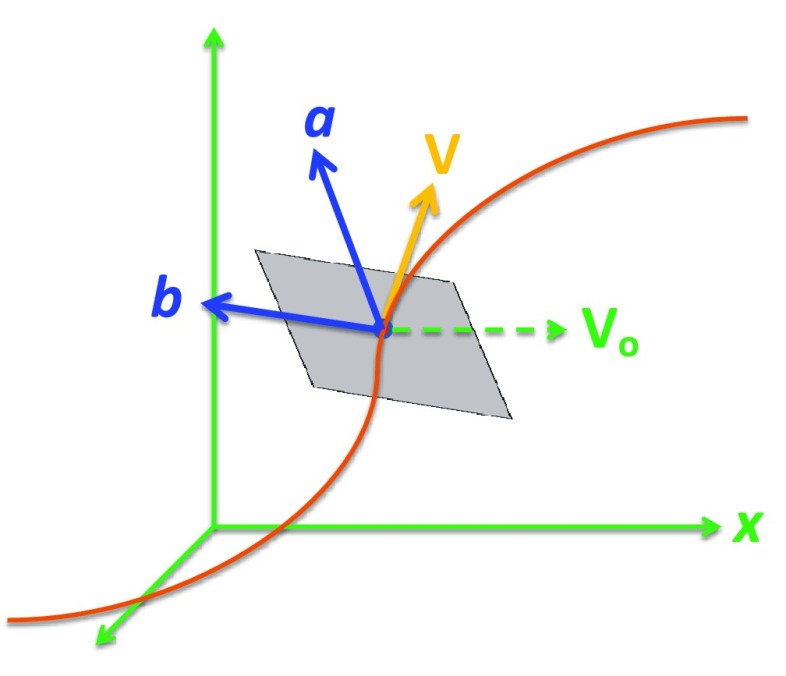
We applied curved planar reformation (CPR) to each vessel traced by the optimal path finding algorithm. The entire length of each coronary vessel was transformed to a single volume by resampling the cCTA volume in planar cross sections perpendicular to the vessel centerline. The CPR simplifies the analysis of the lumen, wall, diameter variation and surrounding tissues by reformatting the originally curved planes and volume into a rectangular volume. The cross section of the volume was chosen to be 81 × 81 voxels and the length of the volume was determined by the length of the tracked vessel except that it was cutoff when the vessel diameter was reduced to smaller than about 2 mm. The spatial position and shape of the vessel centerline determined which parts of the 3D space were transformed. As the coordinate system of a plane cannot be uniquely defined by a single vector tangential to the vessel centerline, a reference vector was defined. Figure 3 illustrates the definition of the cross-sectional plane relative to a stationary reference frame. We defined the reference vector to be parallel to the x-axis of the reference frame and used the right-hand rule to define the direction of the cross product of two vectors. Given a vector that was tangential to the vessel centerline at point p, the cross-sectional plane centered at p was defined by the vectors and as
FIG. 3.
Illustration of the determination of the vectors and that defined the cross-sectional plane.
The voxel values on the cross-sectional plane were obtained by interpolation from the original cCTA volume.
II.B.2. Prescreening of NCP candidates
In order to prescreen the candidates of NCPs, we first used anisotropic diffusion method21 to reduce the voxel value variation, which is commonly encountered due to factors such as image noise, motion, and numerical sampling in reconstruction, while preserving edges. Since plaque buildup occurred on the vessel wall, we transformed the coordinate system of the CPR volume from Cartesian to cylindrical, where the vessel centerline was set to be the cylindrical axis, to facilitate analysis of the vessel wall. In the cylindrical coordinate system, an in-slice horizontal gradient along any radius from the cylindrical axis towards the vessel periphery was calculated and the location of maximum radial gradient was detected as the initial vessel wall or the radius of the vessel lumen. Assuming the cross section of a vessel is round, the radii around the cross section were averaged to reduce the estimation error. A one-dimensional median filter was further applied to the average radius profile along the vessel to reduce noise and define the location of the vessel wall.
We developed a TSG detection method for prescreening of NCP candidates along the vessel wall in the CPR volume22 Fig. 4 showed a schematic diagram of our prescreening method. In the TSG method, the gradient along the radial direction from the vessel centerline to the wall on a reformatted slice was defined as the difference between the average CT value at half radius from the vessel center to the wall and the average CT value from the wall to a distance of half radius outside the vessel. The radial gradient was calculated at all wall locations which were then transformed to a 2D topological surface characterizing the radial gradient field on the vessel wall. The radial gradient field topology on this surface was treated as a 2D image and analyzed to identify regions of interest with soft gradients as follows. For each voxel along the vessel centerline, a running window of 1.1-mm in length centered at the voxel was defined and mapped to the TSG surface for histogram analysis. The histogram of the calculated radial gradient values in the window was generated. The upper boundary of the lowest quartile on the histogram was treated as the soft gradient value at the corresponding voxel along the vessel centerline. The voxel-by-voxel soft gradients determined along the vessel centerline formed the soft gradient profile, which was then searched to identify local minima. Each local minimum was labeled as an NCP candidate and a 2-mm vessel segment centered at the candidate was defined as the region of interest (ROI) for luminal analysis.
FIG. 4.
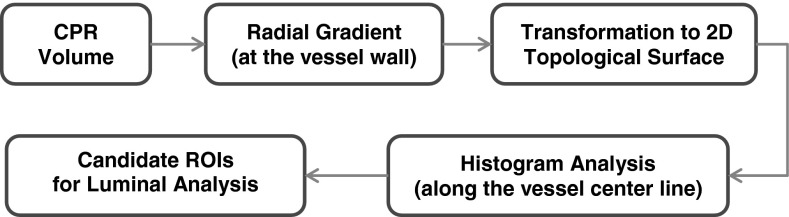
Diagram of the TSG detection method for prescreening of NCP candidates.
II.B.3. Luminal analysis
A quantitative luminal analysis was designed for FP reduction. The luminal analysis used 3D geometric features to quantify the shape information and gray-level features to evaluate the density of the NCP candidates.
In the geometric analysis, a measure of the degree of stenosis, referred to as radius differential, was calculated as the first derivative of the radius profile along the straightened vessel. In addition, the straightened volume underwent two transformations at each voxel: volumetric shape indexing (VSI) and gradient direction mapping. In general, VSI used differential geometry to capture the intuitive notion of local (in a small neighborhood) shape of a surface. We used the definition by Dorai and Jain23 in which VSI at a point is defined as
| (1) |
where k1 and k2 are the principal curvatures of the surface, with k1 ⩾ k2. The principal curvatures measure the maximum and minimum bending of a regular surface at each point. Given the Gaussian curvature K and mean curvature H, the following quadratic equation can be written,
| (2) |
the solutions of which yield the principal curvatures:
| (3) |
| (4) |
The VSI provides a continuous gradation between convex and concave curvatures therefore it can differentiate the subtle shape variations.
The second transformation, gradient direction mapping, is designed to characterize the local direction of the gradient vectors at a given point. Without loss of generality, one can assume that a straightened vessel in cCTA can be adequately modeled as a bright cylinder in a dark background and the gray level of its cross section is gradually decreasing from the center to the edge of the cylinder. According to the above assumptions, the gradient field in the vessel is homogeneous with the radial gradient vectors pointing to the central axis of the cylinder while inhomogeneity occurs at the locations of NCPs. A quantitative measure of gradient direction mapping (GDM) at a point is defined as
| (5) |
where is the gradient vector and is the vector from the given point to the central axis of the cylinder.
Four features that described the statistical characteristics in the local region were calculated for each NCP candidate in the two transformed volumes to obtain eight geometric features and in the CPR volume to obtain four gray level features. Let si denote the ROI of the ith NCP candidate (a 2-mm-long vessel segment centered at the NCP candidate location, defined in Sec. II B 2). A histogram was generated from each of the three volumes with VSI, GDM, or gray level values. Let Xj be the value of the jth bin of a given histogram in the ROI, H(si), the following four features were calculated to characterize the statistics of the ROI:
| (6) |
| (7) |
| (8) |
| (9) |
where Pj was the probability of a voxel having the value of Xj in the ROI si, which was estimated from the histogram normalized by the total number of voxels in si.
In addition, we designed an asymmetry features in measuring the asymmetric spatial location of the NCP candidates relative to the vessel centerline. Let {Ii} represent the set of voxels in the 30o sector subtended at the vessel centerline and is 2-mm-long centered at the ith candidate along the vessel while be the set of voxels in the sector at the 180o symmetric location of {Ii}with the vessel centerline as the axis of symmetry. The asymmetry measure (A) was defined as
| (10) |
where μ and σ2 were the mean and variance of CT values in the corresponding set.
In total, we extracted 14 feature descriptors including nine geometric features, four gray-level features, and one asymmetry features to quantify the differences between NCPs and FPs. To evaluate the performance of our computer-vision methods, we applied tenfold cross-validation resampling with a linear discriminant classifier in which useful features were selected and linearly combined into an NCP discriminant score to differentiate true NCPs from FPs. Denote the full data set as T, and the ten randomly partitioned and disjoint subsets by case as Tv, (v = 1, 2, …, 10), for the vth cross-validation fold, the training and validation subsets were given by Tt = T − Tv and Tv, respectively. We considered a two-class supervised machine learning problem where a set of n training samples was available in the training subset Tt. Here, x is the 14-dimensional feature vector, and y ∈ [0, 1] is the class label (0: false and 1: true NCP). Assuming that the class conditional distributions are multivariate normal distributions with mean vector mo and m1, respectively, and identical covariance matrix Σ, the optimal discriminant function is given by
| (11) |
with
| (12) |
| (13) |
where Pi is the class prior of class i. During training, we considered supervised learning in settings where there were many irrelevant features and only a small subset of the features was sufficient to differentiate the two classes (Sahiner et al.24). Therefore, stepwise feature selection with simplex optimization24 was used to reduce the number of features and prevent overfitting. In each fold, to maintain the independence of the validation subset, feature selection was performed only in the training subset. The selected feature subset was used as input predictor variables to formulate the discriminant function in that fold. The trained discriminant function was applied to the validation subset to generate the discriminant scores for the NCP candidates. Since the discriminant function [Eq. (11)] represented the corresponding maximum likelihood estimates of the targeted classes using training sets that were drawn from the same population, the tenfold validation results could be combined into a full set in the test evaluation. Receiver operating characteristic (ROC) analysis25 was used to assess the classification performance of the NCP discriminant scores for the full validation set. The ROC analysis was also used to study the discriminatory ability of the individual features.
To evaluate the overall detection performance, a free response receiver operating characteristic (FROC) curve was generated by varying the decision threshold on the NCP discriminant score. At a given threshold, an NCP candidate with discriminant score above the threshold was scored as a true positive (TP) if it was located in the radiologist's manually marked plaque segment. Otherwise, it would be scored as FP. As discussed above, the upstream vessels are traced multiple times by the optimal path finding algorithm, the straightened vessels have overlapping segments in which an NCP may be detected multiple times. For the purposes of scoring and output of the CADe marks, all true and false NCP candidate locations were transformed to the coordinate system of the original cCTA volume and the NCP candidates marking the same location were combined and counted only once. The FROC curve was obtained as the fraction of TPs relative to the total number of reference NCPs in the data set plotted as a function of the number of FPs per cCTA volume.
III. RESULTS
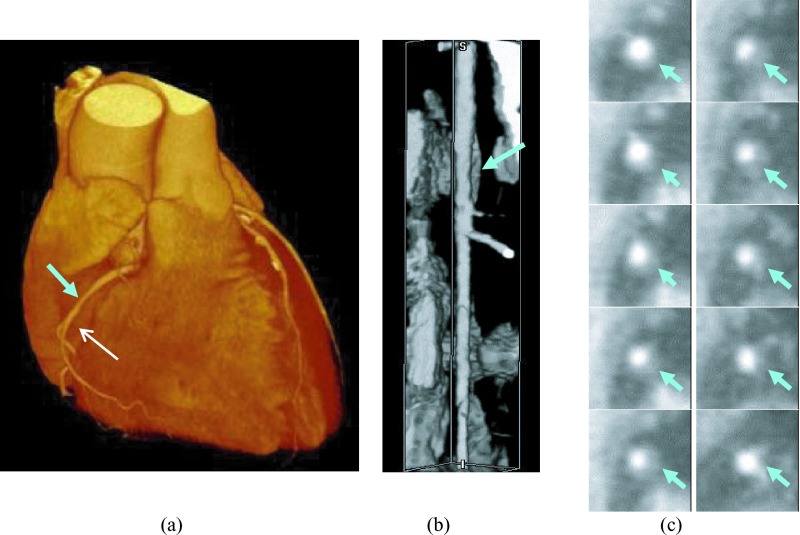
Figure 2 showed an example of coronary arterial trees extracted by our MSCAR-RBG method. The MSCAR-RBG algorithm tracked and segmented 166 coronary arterial trees from the 83 cCTA volumes (LCA and RCA trees in each case). After manual elimination of false positives and tracing by the optimal path finding algorithm, a total of 729 vessels were extracted and used for the detection of NCPs. Six of the 120 NCPs were located in coronary arteries that failed to be segmented and they were counted as false negatives in estimation of sensitivity. Figure 5 showed an example of a straightened coronary artery segment by CPR and cross sectional planes intersecting an NCP.
FIG. 5.
An example of vessel straightening by our implementation of the curved planar reformation method. (a) 3D volume rendering of the heart with the NCP location identified by the cyan arrow (b) volume rendering of the straightened coronary artery segment corresponding to the vessel indicated by the white arrow in (a). The NCP (cyan arrow) caused positive remodeling of the vessel wall; (c) cross sectional images of the NCP from up to down in the reformatted volume with the NCP locations identified by a cyan arrow. The slices were arranged from up to down as: left column: slice 1–5 and right column: slice 6–10 (the slice numbers are relative).
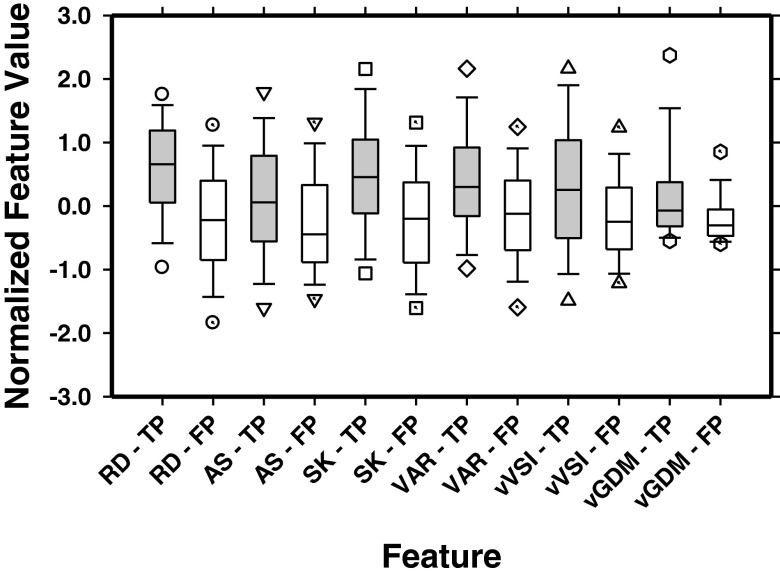
The discriminatory ability of the individual features evaluated as the area under the ROC curve (AUC) ranged from 0.59 to 0.76. In each fold of the tenfold cross-validation training of the NCP discriminant function, the stepwise selection procedure selected the most effective subset of features from the available feature pool. Because of the difference in a fraction of the samples of each training set, the stepwise procedure could select a slightly different subset of features in each fold. On average, six features were selected in the ten training folds. The most often selected features in the ten folds included the radius differential, asymmetry, skewness of gray levels in the CPR volume, variance of gray levels in the CPR volume, variance of VSI, and variance of gradient direction mapping. These features may be considered to be the most robust features within the original feature set for the current classification task. Figure 6 compared the box plots of these six features in differentiating the NCPs from FPs.
FIG. 6.
Box plots of the six most often selected features for the true NCPs (TP) and FPs with the end of whiskers representing the 5th and 95th percentile. RD: radius differential, AS: asymmetry, SK: skewness of gray levels in CPR volume, VAR: variance of gray levels in CPR volume, vVSI: variance of VSI, vGDM: variance of gradient direction mapping.
In each fold, the discriminant function combined the features selected in that fold with the learned weights, the average AUC value for the training sets in the ten folds was 0.87 ± 0.01. The discriminant scores of the validation subsets in the ten folds were combined into a full validation set for ROC analysis and the AUC value was 0.85 ± 0.01.
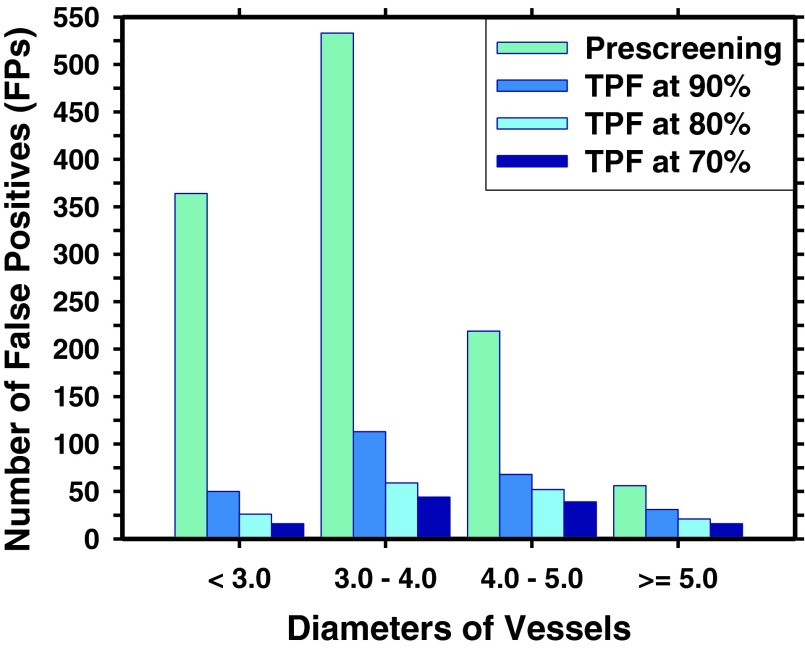
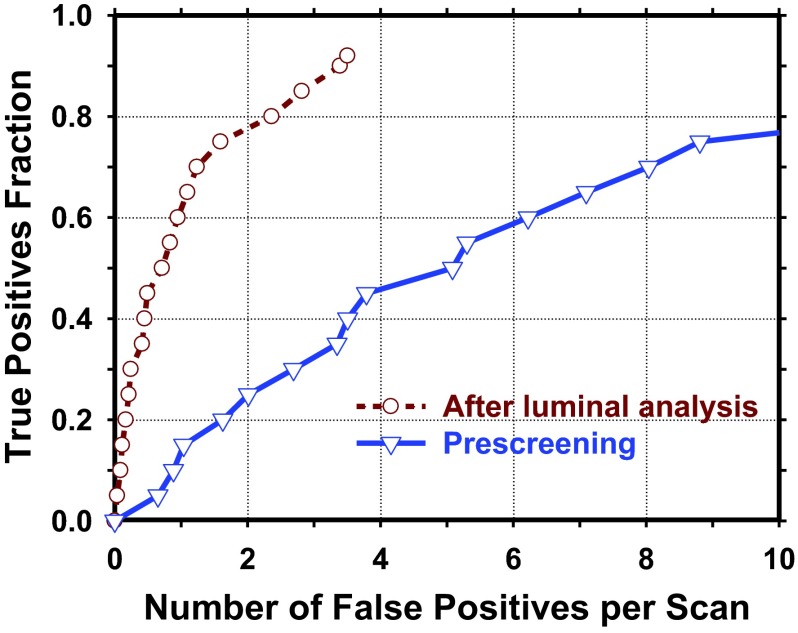
With our TSG prescreening method, a prescreening sensitivity of 92.5% (111/120) was achieved with a total of 1181 FPs (14.2 FPs/scan). Figure 7 illustrated the distribution of the FPs detected in coronary arteries of various diameters. Using the luminal analysis and the NCP discriminant score, the test result from tenfold cross validation showed a reduction of the FP rates to 3.16, 1.90, and 1.39 FPs/scan at sensitivities of 90%, 80%, and 70%, respectively. Figure 8 showed the FROC curve of the overall detection performance in the validation set. Figure 9 compared the performances of our CADe system for detections of NCPs when the retrospective gating cases (47 cases) and the perspective gating cCTA cases (36 cases) in the validation set were used to generate the FROC curves separately.
FIG. 7.
The relationship between FPs and diameters of vessels where FPs are located. With luminal analysis, 1181 FPs from prescreening was reduced to 262, 158, and 115 FPs at the corresponding true positive fraction (TPF) of 90%, 80%, and 70%, respectively.
FIG. 8.
FROC curve at prescreening and the FROC curve of the validation set from tenfold cross validation after luminal analysis.
FIG. 9.
Comparison of the performances of our CADe system for detections of NCPs when the retrospective gating cases (47 cases) and the perspective gating cCTA cases (36 cases) in the validation set were used to generate the FROC curves separately.
IV. DISCUSSIONS
NCP detection in cCTA is challenging because of their subtle CT number differences from the surrounding tissues and the large number of coronary arteries. Computer-aided detection may be useful for assisting radiologists in NCP detection in cCTA. In this study, we developed a new topological soft-gradient prescreening method based on a transformation of the radial gradient field on the coronary arterial wall to a 2D topological surface. Our NCP detection approach was designed to detect both positive and negative vessel remodeling. In addition, we developed a luminal analysis for characterization of NCPs. Two image transformations were designed to facilitate the statistical analysis of geometric and gray level characteristics of the NCP candidates. A number of quantitative measures were extracted as the input predictor variables for a linear discriminant classifier to differentiate NCPs from FPs. The output score from the linear discriminant has good discriminatory ability for NCP but further improvement is needed.
A number of factors in cCTA, including the small-size coronary arteries, the noise and limited spatial resolution of CT, and the low contrast of the fatty plaques, affect the visibility of the borders between the vessel lumen, the NCP, and the arterial wall and thus the detectability of NCPs by radiologists or CADe systems. In this study, we reformatted the coronary artery by CPR to facilitate vessel narrowing detection and feature analysis in the cross-sectional planes and designed a topological soft gradient transformation to analyze the radial gradients on the object surface for prescreening of NCP candidates. We performed feature analysis in 2-mm vessel segments at the candidate locations. Feature extraction from NCPs in cCTA volume is challenging because some feature measures such as those from texture analysis models may not be reliable in objects with few voxels. To evaluate the characteristics of the target objects, we developed a luminal analysis in which 3D geometric features were extracted to quantify the shape information and gray-level features to assess the density of the NCP candidates. In our current system, we used an anisotropic diffusion filter to reduce the noise and preserve the edge information. A sharpening filter26 may be potentially useful for enhancing edges and facilitating detection. We will investigate the tradeoffs between edge enhancement and noise for different techniques in future studies.
Reliable tracking of coronary arterial trees is a critical step for successful automated NCP detection. Our current CADe system is not fully automatic due to the fact that we used manually placed seed points at the origins of the LCA and RCA trees to initialize vessel tracking by the MSCAR-RBG method. In addition, since the purpose of the current study is to evaluate the topological soft-gradient prescreening method in combination with the luminal analysis, independent of the performance of the coronary artery segmentation and tracking stage, we excluded the FPs from vessel tracking to avoid the confounding effects of other factors. An automated seed detection method is under development. Further work is underway to improve the vessel segmentation and tracking techniques and to automatically exclude false vessels in order to fully automate the CADe system.
The accuracy of the vessel centerline has a strong impact on the quality of the CPR volume and the vessel and the detection of NCP candidates in the reformatted volume. Noise and jaggedness of the centerline will lead to jaggedness in the straightened artery and erroneous variations of the vessel radius along the centerline. Since the prescreening of NCP candidates depends on estimation of the vessel wall location and to a certain extent the variations in the vessel radius, erroneous variations in the radius would cause false positives and false negatives. Many factors can cause jaggedness and errors in the centerline, including poor vessel contrast in the original cCTA volume, noise, presence of calcified plaques, blurring and partial volume effects on small vessels, sharp turns, and bifurcation of the vessel. Further improvement in vessel centerline localization is essential to improve the smoothness and continuity of the CPR volume.
The image data used in this study was acquired with ECG gating and reconstructed at multiple phases. We selected one phase for NCP detection. Our CADe method can be affected by the image quality of the selected cCTA phase. In our data set, 15 out of 120 NCPs were rated as poor image quality by radiologist (12 as excellent, 64 as good, and 29 as adequate) due to factors such as low contrast filling, noisy background, or blurring by cardiac motion. We are developing automated methods for registration of coronary arterial trees from multiple phases27 and selection of the phase of best image quality for each arterial segment for NCP detection. The incorporation of the automated vessel segment selection method will likely alleviate some of the problems and improve the accuracy of NCP detection.
To our knowledge, at present there is no simple answer to the question of how high the sensitivity and specificity of a CADe system should be in order for it to be clinically useful. The acceptability of a CADe system in a given application depends on many factors such as the radiologists’ experience and accuracy on the specific disease which the CADe application is designed for, whether the overall performance improves when radiologist uses CADe in his/her clinical practice, and even the subjective preference of the individual radiologists (for example, some radiologists prefer high sensitivity even at the cost of lower specificity whereas others prefer the opposite, as demonstrated by the wide range of operating points in the ROC space in a study of the variability in radiologists’ interpretation of mammograms.28 The performance required of a CADe system (or similarly, where the operating point of radiologists should be to maximize clinical utility) is a complicated issue involving many factors such as the tradeoffs among overdiagnosis, delayed diagnosis, health care costs and morbidity for work-up, which in turn, are disease dependent. These issues are far beyond the scope of our work. Automated NCP detection is still in the early stage. The current study demonstrates the feasibility of our approach to NCP detection and the various steps that need refinement. We will continue to improve the performance of our CADe system and conduct an observer ROC study to compare radiologists’ detection accuracy with and without CADe to assess its potential usefulness in the future.
V. CONCLUSION
This study indicated the feasibility of our topological soft-gradient prescreening method in combination with the luminal analysis for detection of NCPs in cCTA, including NCPs causing positive or negative vessel remodeling. The accuracy of vessel segmentation, tracking, and centerline identification has a strong impact on the accuracy of NCP detection. Further studies are needed to improve these techniques and reduce the false positives of the CADe system.
ACKNOWLEDGMENTS
This work is supported by USPHS grant R01HL106545. The content of this paper does not necessarily reflect the position of the funding agencies and no official endorsement of any equipment and product of any companies mentioned should be inferred.
REFERENCES
- 1.Lloyd-Jones D.et al. , “Heart disease and stroke statistics–2009 update: A report from the American heart association statistics committee and stroke statistics subcommittee,” Circulation 119, e21–e181 (2009). 10.1161/CIRCULATIONAHA.108.191261 [DOI] [PubMed] [Google Scholar]
- 2.Gongora-Rivera F., Labreuche J., Jaramillo A., Steg P. G., Hauw J.-J., and Amarenco P., “Autopsy prevalence of coronary atherosclerosis in patients with fatal stroke,” Stroke 38, 1203–1210 (2007). 10.1161/01.STR.0000260091.13729.96 [DOI] [PubMed] [Google Scholar]
- 3.Schoenhagen P., White R. D., Nissen S. E., and Tuzcu E. M., “Coronary imaging: angiography shows the stenosis, but IVUS, CT, and MRI show the plaque,” Cleveland Clin. J. Med. 70, 713–719 (2003). 10.3949/ccjm.70.8.713 [DOI] [PubMed] [Google Scholar]
- 4.Budoff M.et al. , “Diagnostic performance of 64-multidetector row coronary computed tomographic angiography for evaluation of coronary artery stenosis in individuals without known coronary artery disease: Results from the prospective multicenter ACCURACY (Assessment by Coronary Computed Tomographic Angiography of Individuals Undergoing Invasive Coronary Angiography) trial,” J. Am. Coll. Cardiol. 52, 1724–1732 (2008). 10.1016/j.jacc.2008.07.031 [DOI] [PubMed] [Google Scholar]
- 5.Fine J. J., Hopkins C. B., Ruff N., and Newton F. C., “Comparison of accuracy of 64-slice cardiovascular computed tomography with coronary angiography in patients with suspected coronary artery disease,” Am. J. Cardiol. 97, 173–174 (2006). 10.1016/j.amjcard.2005.08.021 [DOI] [PubMed] [Google Scholar]
- 6.Ropers D., Rixe J., Anders K., Kuttner A., Baum U., Bautz W., Daniel W. G., and Achenbach S., “Usefulness of multidetector row spiral computed tomography with 64-x 0.6-mm collimation and 330-ms rotation for the noninvasive detection of significant coronary artery stenoses,” Am. J. Cardiol. 97, 343–348 (2006). 10.1016/j.amjcard.2005.08.050 [DOI] [PubMed] [Google Scholar]
- 7.Nikolaou K., Knez A., Rist C., Wintersperger B. J., Leber A., Johnson T., Reiser M. F., and Becker C. R., “Accuracy of 64-MDCT in the diagnosis of ischemic heart disease,” Am. J. Roentgenol. 187, 111–117 (2006). 10.2214/AJR.05.1697 [DOI] [PubMed] [Google Scholar]
- 8.Raff G. L., Gallagher M. J., O’Neill W. W., and Goldstein J. A., “Diagnostic accuracy of noninvasive coronary angiography using 64-slice spiral computed tomography,” J. Am. Coll. Cardiol. 46, 552–557 (2005). 10.1016/j.jacc.2005.05.056 [DOI] [PubMed] [Google Scholar]
- 9.Schroeder S., Kopp A. F., Baumbach A., Meisner C., Kuettner A., Georg C., Ohnesorge B., Herdeg C., Claussen C. D., and Karsch K. R., “Noninvasive detection and evaluation of atherosclerotic coronary plaques with multislice computed tomography,” J. Am. Coll. Cardiol. 37, 1430–1435 (2001). 10.1016/S0735-1097(01)01115-9 [DOI] [PubMed] [Google Scholar]
- 10.Busch S., Johnson T. R. C., Nikolaou K., von Ziegler F., Knez A., Reiser M. F., and Becker C. R., “Visual and automatic grading of coronary artery stenoses with 64-slice CT angiography in reference to invasive angiography,” Eur. J. Radiol. 17, 1445–1451 (2007). 10.1007/s00330-006-0512-y [DOI] [PubMed] [Google Scholar]
- 11.Achenbach S.et al. , “Detection of calcified and noncalcified coronary atherosclerotic plaque by contrast-enhanced, submillimeter multidetector spiral computed tomography: A segment-based comparison with intravascular ultrasound,” Circulation 109, 14–17 (2004). 10.1161/01.CIR.0000111517.69230.0F [DOI] [PubMed] [Google Scholar]
- 12.Leber A. W.et al. , “Quantification of obstructive and nonobstructive coronary lesions by 64-slice computed tomography - A comparative study with quantitative coronary angiography and intravascular ultrasound,” J. Am. Coll. Cardiol. 46, 147–154 (2005). 10.1016/j.jacc.2005.03.071 [DOI] [PubMed] [Google Scholar]
- 13.Ohnesorge B. M., Flohr T. G., Becker C. R., Knez A., and Reiser M. F., Multi-Slice and Dual-Source CT in Cardiac Imaging: Principles - Indications - Outlook (Springer-Verlag, Berlin, Germany, 2007). [Google Scholar]
- 14.Arnoldi E., Gebregziabher M., Schoepf U. J., Goldenberg R., Ramos-Duran L., Zwerner P. L., Nikolaou K., Reiser M. F., Costello P., and Thilo C., “Automated computer-aided stenosis detection at coronary CT angiography: Initial experience,” Eur. J. Radiol. 20, 1160–1167 (2010). 10.1007/s00330-009-1644-7 [DOI] [PubMed] [Google Scholar]
- 15.Schoenhagen P., Barreto M., and Halliburton S. S., “Quantitative plaque characterization with coronary CT angiography (CTA): Current challenges and future application in atherosclerosis trials and clinical risk assessment,” Int. J. Cardiovasc. Imaging 24, 313–316 (2008). 10.1007/s10554-007-9284-y [DOI] [PubMed] [Google Scholar]
- 16.Austen W. G., Edwards J. E., Frye R. L., Gensini G. G., Gott V. L., Griffith L. S., McGoon D. C., Murphy M. L., and Roe B. B., “A reporting system on patients evaluated for coronary artery disease. Report of the Ad Hoc Committee for Grading of Coronary Artery Disease, Council on Cardiovascular Surgery, American Heart Association,” Circulation 51, 5–40 (1975). 10.1161/01.CIR.51.4.5 [DOI] [PubMed] [Google Scholar]
- 17.Zhou C., Chan H.-P., Chughtai A., Patel S., Hadjiiski L. M., Wei J., and Kazerooni E. A., “Automated coronary artery tree extraction in coronary CT angiography using a multiscale enhancement and dynamic balloon tracking (MSCAR-DBT) method,” Comput. Med. Imaging Graphics 36, 1–10 (2012). 10.1016/j.compmedimag.2011.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou C., Chan H.-P., Chughtai A., Kuriakose J., Agarwal P., Kazerooni E. A., Hadjiiski L. M., Patel S., and Wei J., “Computerized analysis of coronary artery disease: Performance evaluation of segmentation and tracking of coronary arteries in CT angiograms (CTA),” Med. Phys. (submitted). [DOI] [PMC free article] [PubMed]
- 19.Zhou C., Chan H.-P., Kuriakose J. W., Chughtai A., Wei J., Hadjiiski L. M., Guo Y., Patel S., and Kazerooni E. A., “Pulmonary vessel segmentation utilizing curved planar reformation and optimal path finding (CROP) in computed tomographic pulmonary angiography (CTPA) for CAD applications,” Proc. SPIE 8315, 83150N (2012). 10.1117/12.912446 [DOI] [Google Scholar]
- 20.Dijkstra E. W., “A note on two problems in connexion with graphs,” Numer. Math. 1, 269–271 (1959). 10.1007/BF01386390 [DOI] [Google Scholar]
- 21.Perona P. and Malik J., “Scale-space and edge detection using anisotropic diffusion,” IEEE Trans. Pattern Anal. Mach. Intell. 12, 629–639 (1990). 10.1109/34.56205 [DOI] [Google Scholar]
- 22.Wei J., Zhou C., Chan H.-P., Chughtai A., Patel S., Agarwal P., Kuriakose J., Hadjiiski L. M., and Kazerooni E. A., “Computerized detection of non-calcified plaques in coronary CT angiography: Topological soft-gradient detection method for plaque prescreening,” Proc. SPIE 8670, 867016 (2013). 10.1117/12.2008047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dorai C. and Jain A. K., “COSMOS - A representation scheme for 3D free-form objects,” IEEE Trans. Pattern Anal. Mach. Intell. 19, 1115–1130 (1997). 10.1109/34.625113 [DOI] [Google Scholar]
- 24.Sahiner B., Chan H. P., Petrick N., Wagner R. F., and Hadjiiski L. M., “Feature selection and classifier performance in computer-aided diagnosis: The effect of finite sample size,” Med. Phys. 27, 1509–1522 (2000). 10.1118/1.599017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Metz C. E., “ROC methodology in radiologic imaging,” Invest. Radiol. 21, 720–733 (1986). 10.1097/00004424-198609000-00009 [DOI] [PubMed] [Google Scholar]
- 26.Saba O. I., Hoffman E. A., and Reinhardt J. M., “Maximizing quantitative accuracy of lung airway lumen and wall measures obtained from X-ray CT imaing,” J. Appl. Physiol. 95, 1063–1075 (2003). 10.1152/japplphysiol.00962.2002 [DOI] [PubMed] [Google Scholar]
- 27.Hadjiiski L., Zhou C., Chan H.-P., Chughtai A., Agarwal P., Kuriakose J., Patel S., Wei J., and Kazerooni E. A., “Automated registration of coronary arterial trees from multiple phases in coronary CT angiography (cCTA),” Proc. SPIE 8670, 86703M (2013). 10.117/12.2008058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Elmore J. G.et al. , “Variability in interpretive performance at screening mammography and radiologists’ characteristics associated with accuracy,” Radiology 253, 641–651 (2009). 10.1148/radiol.2533082308 [DOI] [PMC free article] [PubMed] [Google Scholar]