Abstract
Purpose:
Using the graphical processing units (GPU) hardware technology, an extremely fast Monte Carlo (MC) code ARCHERRT is developed for radiation dose calculations in radiation therapy. This paper describes the detailed software development and testing for three clinical TomoTherapy® cases: the prostate, lung, and head & neck.
Methods:
To obtain clinically relevant dose distributions, phase space files (PSFs) created from optimized radiation therapy treatment plan fluence maps were used as the input to ARCHERRT. Patient-specific phantoms were constructed from patient CT images. Batch simulations were employed to facilitate the time-consuming task of loading large PSFs, and to improve the estimation of statistical uncertainty. Furthermore, two different Woodcock tracking algorithms were implemented and their relative performance was compared. The dose curves of an Elekta accelerator PSF incident on a homogeneous water phantom were benchmarked against DOSXYZnrc. For each of the treatment cases, dose volume histograms and isodose maps were produced from ARCHERRT and the general-purpose code, GEANT4. The gamma index analysis was performed to evaluate the similarity of voxel doses obtained from these two codes. The hardware accelerators used in this study are one NVIDIA K20 GPU, one NVIDIA K40 GPU, and six NVIDIA M2090 GPUs. In addition, to make a fairer comparison of the CPU and GPU performance, a multithreaded CPU code was developed using OpenMP and tested on an Intel E5-2620 CPU.
Results:
For the water phantom, the depth dose curve and dose profiles from ARCHERRT agree well with DOSXYZnrc. For clinical cases, results from ARCHERRT are compared with those from GEANT4 and good agreement is observed. Gamma index test is performed for voxels whose dose is greater than 10% of maximum dose. For 2%/2mm criteria, the passing rates for the prostate, lung case, and head & neck cases are 99.7%, 98.5%, and 97.2%, respectively. Due to specific architecture of GPU, modified Woodcock tracking algorithm performed inferior to the original one. ARCHERRT achieves a fast speed for PSF-based dose calculations. With a single M2090 card, the simulations cost about 60, 50, 80 s for three cases, respectively, with the 1% statistical error in the PTV. Using the latest K40 card, the simulations are 1.7–1.8 times faster. More impressively, six M2090 cards could finish the simulations in 8.9–13.4 s. For comparison, the same simulations on Intel E5-2620 (12 hyperthreading) cost about 500–800 s.
Conclusions:
ARCHERRT was developed successfully to perform fast and accurate MC dose calculation for radiotherapy using PSFs and patient CT phantoms.
Keywords: Key words: radiation therapy, Monte Carlo, GPU, dose calculation, software
I. INTRODUCTION
Intensity modulated radiation therapy (IMRT) is designed to deliver superior dose conformity and uniformity when compared to traditional three-dimensional conformal therapy.1 However, few treatment planning systems (TPS) employ sophisticated dose calculation algorithms such as Monte Carlo (MC) method. Approximate algorithms used in many TPSs, including convolution/superposition method, are known to be fast but only approximately correct in cases when the treatment site involves complex and heterogeneous tissue structures.2,3 MC and grid-based Boltzmann solver (GBBS) are two methods that can handle tissue heterogeneity in three-dimensional objects and will yield accurate radiation dose distributions in the human body for a range of medical physics applications.4 Among these two methods, GBBS is much less popular than MC. To date, MC methods remain the gold standard of radiation dose calculation. Although a few commercial TPSs adopt MC methods, computation speeds of current MC methods still prevent a widespread use for dose calculations in radiation therapy. With advancements in the ability to monitor inter- and/or intra-fraction variation of patient anatomy during the treatment, radiation oncology clinics are exploring adaptive radiation therapy (ART) and real-time replanning—modalities that require the integration of accurate and fast dose calculation approaches.5–7 It is clear that new methods of accelerating Monte Carlo calculations will play an important role in future radiation oncology research.
A review of the history of Monte Carlo methods suggests that vectorization schemes were proposed and proven by Brown and Martin in 1980s as a revolutionary way to accelerate MC calculations.8 However, little advance has been made in the recent decades in adopting MC methods as a clinical dose computation and treatment planning tool. It is well known that MC algorithms are ideally suited for parallel computing and certain MC algorithms are considered as “embarrassingly parallelizable.” Now we may have arrived at a tipping point in research, with recent development of heterogeneous high-performance computing hardware and software designs. The new “hardware accelerator” technologies—the general-purpose Graphical Processing Units (GPU) by NVIDIA and AMD and the Xeon Phi coprocessors by Intel—have high energy-efficiency and arithmetic-throughput. The compute-intensive, but parallelizable algorithms for particle tracking can now be offloaded to hardware accelerators and be concurrently executed by hundreds or thousands of threads. Such hardware-based acceleration methods have become secure and affordable parallel computing platforms for high performance computing.9 With extensive thread-level parallelism and impressive energy efficiency, such hardware accelerators are essential in the so-called exascale computers that will arrive near the end of this decade.10 In fact, on the Top-500 list as of June 2013, 4 out of the 10 most powerful supercomputers in the world had adopted either the NVIDIA GPUs or Intel coprocessors.11
Accelerators such as GPUs have been used in medical physics MC dose calculations.12–16 Zhou et al. implemented Monte Carlo convolution/superposition (MCCS) on GPU platform to perform dose calculation of conventional IMRT.17 Despite of what their paper title had implied, their method did not involve MC based radiation transport. Jia et al. developed a GPU MC code based on DPM and achieved 5.0–6.6 speedup factors.18 Hissoiny et al. developed another code GPUMCD, in which the MC implementation is tailored for GPU, and reported 900 times speedup over EGSnrc.13 Jia et al. later improved their code and observed the speedup of 69.1–87.2.12 Jahnke et al. ported part of GEANT4 functions to GPU and reported a speedup factor of 6400.14 Jia et al. also came up with a GPU based MC code for patient-specific CT/CBCT imaging dose calculation and reported that it was 76.6 times faster than EGSnrc.19 Hissoiny et al. reported a GPU based brachytherapy dose calculation tool using a precalculated phase space file (PSF) as input and achieved ∼2 s speed for a preoptimized plan.20 However, electron transport was absent from their MC code and they did not consider external beam radiotherapy. Townson et al. reported a GPU dose calculation engine for IMRT,21 in which they used “phase-space-let” method to calculate dose distribution from a patient-independent PSF. Townson et al. only considered a tongue treatment case and did not analyze performance in terms of full phantom dose distribution and dose volume histograms (DVHs).
Although the idea of using GPUs to accelerate MC calculations is no longer new today, the methods are far from being mature. In fact, several challenges can be readily identified in the current research: (1) Considerable software development is needed to truly optimize algorithms in new hardware/software environments. (2) There is little or no effort to understand the underlying challenges presented. (3) Comparison against traditional CPU-based methods lacks fairness, leading to false performance rating for GPUs. (4) Clinical benefits have not been systematically evaluated. (5) There is an uncertainty about the GPUs future as a parallel computing technology because Intel Xeon Phi coprocessors were adopted in the world's #1 supercomputer (the Tianhe-2) in 2013 and NVIDIA on longer dominates the market place.
To address some of the challenges mentioned above, we have been developing a testbed under the framework called ARCHER (Accelerated Radiation-transport Computations in Heterogeneous EnviRonments). ARCHER is envisioned as a suite of GPU-based and Xeon Phi-based MC codes for diverse applications including X-ray CT imaging dose calculations,16 nuclear reactor analysis,22 and medical oriented electron-photon coupled transport.23 One study under ARCHER framework compares the performance of multithread CPU, GPU, and Xeon Phi coprocessor in the application of CT dose evaluation. The Xeon Phi programming models involved are offload OpenMP, Cilk (a C language extension for multithreaded parallel computing),24 and hybrid MPI/OpenMP. This paper describes the development of ARCHERRT for external bean radiation therapy based on GPU and multicore CPU.
The novelty of this paper: (1) it focuses on GPU-based tomotherapy dose calculations and evaluates three clinical cases in terms of dose contours, DVHs, and gamma analysis. (2) It reports for the first time the evaluation of the “heterogeneous architecture” involving a host CPU and different GPUs as “devices” including NVIDIA M2090 (six cards), K20, and K40 cards, thus providing valuable insight into emerging computer hardware technologies. (3) To achieve a fair comparison, this study develops the MC code for both the CPU and GPU platforms using the multithreaded CPU code in OpenMP to maximize the use of CPU computing power. (4) It implements a variance reduction technique on GPU and discusses the efficiency discrepancies on different hardwares.
The structure of the paper is as follows: Section II describes the MC modeling of ARCHERRT and other software development details. Section III demonstrates the dosimetric and timing results of our code, compared with established MC codes. Section IV delivers some useful discussions and Sec. V concludes this paper.
II. METHODS
II.A. Hardware specification
Two heterogeneous systems are used for testing and running ARCHERRT. The first is a generic desktop with Intel Xeon E5-2620 CPU (6 cores 2.0 GHz) and 8 GB RAM, hosting one GPU card. The second is a specialized GPU workstation, consisting of an Intel Xeon 5650 CPU with 16 GB memory and multiple PCI-E slots which host as many as six GPUs concurrently. The GPU cards employed in this study are as follow: six Fermi-based NVIDIA M2090 GPUs, each with 512 streaming processors (SP), 1.33 TeraFlOPS floating point capability and 6 GB global memory; one Kepler-based NVIDIA K20 GPU, with 2496 SPs, 3.52 TeraFlOPS floating point capability, and 5 GB global memory; one state-of-art Kepler-based NVIDIA K40 GPU, with 2880 SPs, 4.2 TeraFlOPS floating point capability, and 12 GB global memory. Figure 1 shows the system with 6 M2090 cards. It resembles a slice of the RPI's Blue Gene supercomputer or the Oak Ridge National Lab's Titan supercomputer.
FIG. 1.
The specialized GPU workstation used in this study, consisting of one Intel Xeon 5650 CPU and 6 NVIDIA M2090 GPUs.
II.B. Software design for GPU and multithread CPU codes
ARCHERRT GPU code is developed using NVIDIA CUDA C.25 The code has two major parts: host code that runs on the CPU and the device code (also called kernel) that runs on the GPU. The general code structure follows a typical CUDA execution pattern: first the host code is executed to read in data and transfer data from host memory to device memory. Then the kernel code is called by the host code and it is executed on the GPU in parallel with multiple threads.
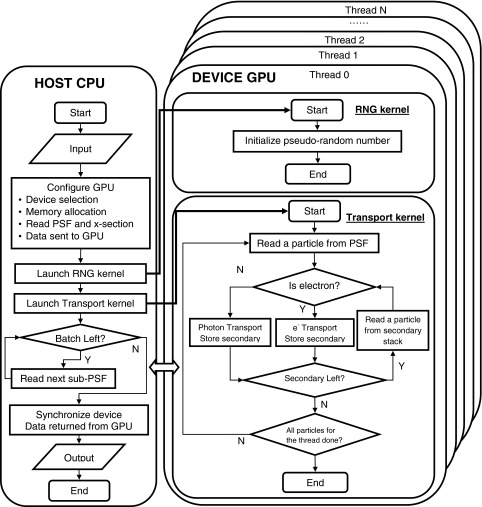
The overall workflow of ARCHERRT is shown in Fig. 2. As will be discussed in Sec. II D, batch simulation is employed. The PSF, which contains the source information, is partitioned into smaller part (sub-PSF). The host code first reads in cross section data, CT phantom, the first batch of sub-PSF, and stores them in the host memory. Then it allocates device memory on the GPU and copies data needed for transport to the device. Afterward, a pseudorandom number (PRN) kernel initiates a unique random number stream for each thread to make sure simulations in different threads are statistically uncorrelated. In this study we employed the CURAND library provided by NVIDIA for generating high quality PRNs with fast speed. After the PRN initiation, the transport kernel is invoked and executed by a large number of threads in parallel with each thread in charge of a number (e.g., 400) of particles. The number of threads is determined by the total number of particles to simulate. As will be described in Sec. II D, once the kernel is launched, the CPU begins to read sub-PSF for the next batch. This implementation enables concurrent execution of both particle transport and reading PSF, thus the total execution time is reduced. After each batch simulation, the results are sent back to host side; after all batches are completed, the dose results are processed and batch statistical uncertainties are evaluated. For simulation with multiple GPUs, the CPU reads all sub-PSFs and then copies the data to different GPU and launch kernel on each GPU. Since the memory copy and kernel launch are asynchronized (returned immediately), all the GPUs start working virtually at the same time.
FIG. 2.
Flowchart of ARCHERRT GPU code. The left panel describes the work for CPU which is the host and the right panel describes the work for GPU which is the device. Device cannot interact with outer world directly and can only send/receive data to/from host. Host and device communicate via PCI-E bus. Host first reads data and sends them to device; after simulation, device sends results back to host. Pseudorandom number (PRN) kernel is used to initiate the PRN streams. Transport kernel handles the MC simulation of particles. Batch simulation is employed. After all batches are done, the host synchronizes all thread on the device and processes and outputs results.
Inside the transport kernel, shown in Fig. 2, all the secondary particles created in each thread are stored in preallocated array in the device global memory; after primary particle transport, secondary particles in the stack are fetched and transported in the same way as primary particles. Each thread is in charge of all secondary particle generated in that thread. The next primary particle is not started until the secondary stack is emptied. During the simulation, radiation energy deposited in each step is added directly to the global counter in the device memory. To avoid race conditions resulting from multiple threads attempting to write to the same tally, the CUDA atomic operation is used.25 In this mode, writing operations by different threads are serialized and the correct radiation dose summation is guaranteed.
GPU uses different memory types and appropriate handling is essential for achieving the best performance. Registers are on-chip local memory that is private to each thread. Shared memory is also on-chip but can be shared by a block of threads. These two kinds of on-chip memory are fast to access but their sizes are very limited. There is a large off-chip global memory (up to 12 GB) accessible to all the threads. Compared with registers and shared memory, global memory has much larger access latency. As a static allocated read-only memory, constant memory features relatively high access speed and it is suitable for storing constant variables. However, due to its limited size (64 kB on Fermi architecture), in ARCHERRT only some scientific constants such as the electron rest mass and value of π are stored in constant memory, while other data including cross sections, distribution tables and parameters needed for transport are still stored in the global memory. In addition, the dose counters for each voxel as well as the secondary particle stack for each thread also reside on the global memory. For fast access, we used registers to store temporary variables in threads. Shared memory is not used in our code.
As found in our previous work,23 single precision arithmetic provides adequate accuracy for our medical application and was adopted in our code. Moreover, fast-math compiler option was enabled to achieve higher speed of floating point operations. This choice bears no measureable error in the results.
To fairly compare the performance of GPU and CPU, we wrote multithreaded CPU code using OpenMP. With Intel's hyperthreading technique, our 6-core CPU can support as many as 12 threads running concurrently. In the OpenMP CPU code, the input data (PSFs and cross sections) and the dose tallies are shared by all threads. Atomic directive is used for tally function to avoid race condition.
II.C. Electron-photon coupled transport
II.C.1. Photon transport
The main physics models implemented in ARCHERRT were similar to production MC codes, including MCNP, EGSnrc, GEANT4, PENELOPE, and DPM.26–30 For photon transport, we considered photoelectric effect, Compton scattering, and pair production. Rayleigh scattering is disregarded in this study because it has negligible impact on dose distribution for photon energy range used for radiotherapy.30 Compton scattering is sampled according to the Klein-Nishina cross section, assuming electrons are free and at rest before scattering. Binding effect and Doppler broadening, which are important for photon energies below 100 keV,27 are excluded in ARCHERRT. Everett et al.'s method is used to obtain the direction and angle of the scattered photon.31 The photoelectric effect is modeled by ignoring electron shell structure and binding energy. A secondary electron is produced isotropically with the same energy of the incident photon. For pair production, the electron and positron are assumed to split the incident photon energy using a uniformly distributed random number. The angular distributions of electron-positron pair are calculated using the method employed by the PENELOPE code (Sec. 2.4.1.1).28 No triplet production is modeled in our code due to trivial probability of the interaction. The photon cross section used in ARCHERRT is from NIST XCOM.32
II.C.2. Electron transport
An electron undergoes a large number of interactions with media, making the analog event-by-event simulation unfeasible.28 Meanwhile, the angular deflection and energy loss in each electron interaction is relatively small; thus, a mixed “condensed history” method can be used to model the transport. ARCHERRT employs the so called class-II condensed history method.33 In this method, interactions with an energy loss greater than a preset value (hard collision) are simulated explicitly; below that preset value, the energy loss is treated with continuously slowing down approximation (CSDA).33
The hard inelastic collision is sampled according to the Møller cross section,27 and the binding energy of a scattered electron is ignored here since the hard interaction threshold (∼200 keV) is typically much larger than the binding energy of the electron (several keV). Because the primary and scattered electrons are indistinguishable, the electron with a higher energy is considered primary, i.e., an electron can lose no more than half of its kinetic energy in scattering. The hard bremsstrahlung interaction is modeled by the method described in Sec. 3.3.4 of the PENELOPE manual.28 In such hard bremsstrahlung, an electron can lose up to its total kinetic energy. Occurrence of Møller scattering and hard bremsstrahlung is controlled by corresponding mean free path (MFP). The effect of a large number of elastic interactions within a given pathlength is modeled according to the Goudsmit and Saunderson (GS) multiple scattering theory.34,35 In particular, the scattering angle is sampled using the method described by Sempau et al.,30 which is a modification of Kawrakow and Bielajew's method.36 The electron step length for multiple scattering is calculated according to the energy of the electron, and is not restricted by the voxel boundaries.30 This implementation enables an electron to travel through more than one voxel in a single step, thus speeding up the MC simulations. The soft energy loss is handled by the CSDA using the restricted stopping power. If there is no hard interaction inside a voxel, the energy loss is calculated for the trajectory length from boundary to boundary. If there is an interaction in the current voxel, the trajectory length for energy loss is from boundary to interaction site instead. Electron stopping power data are adopted from ICRU Report No. 37.37 In addition, positrons are simulated as electrons, except they annihilate after losing all their energy, leading to two photons, each with energy of 0.511 MeV.26
An electron or a photon is transported in ARCHERRT until its energy falls below a cutoff energy. At this point, the particle is killed immediately and its remaining energy is deposited locally. The cutoff energies of electron and photon are set to be 200 keV and 10 keV, respectively, in this study.
II.D. Helical tomotherapy and phase-space file implementation
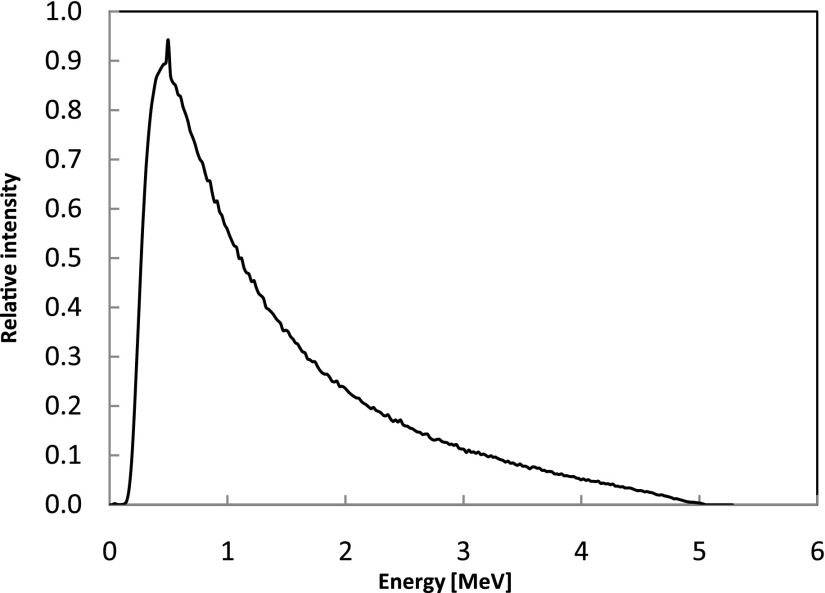
Helical tomotherapy is a sophisticated IMRT delivery modality developed at the University of Wisconsin-Madison (UW) and commercialized by TomoTherapy®, which is now owned and distributed by Accuray Inc (Sunnyvale, CA). The Hi-Art TomoTherapy® system utilizes a unique mechanical structure that resembles a helical CT scanner. Different from the traditional IMRT, the treatment head in a Tomotherapy® system is mounted on a slip ring gantry and can rotate continuously around the isocenter. During the treatment, the head rotates continuously while the couch is translated concurrently, delivering the dose in a helical manner. Zhao et al.38 and Sterpin et al.39 have performed MC simulations of helical tomotherapy using the general purpose codes EGSnrc and PENELOPE, respectively. In this study, we adopted Sterpin et al.'s method to generate the patient dependent PSFs. The PSFs of finished treatment plans are used to calculate 3D dose distributions in patient CT geometries. The PSF was generated by MC modeling of a SIEMENS accelerator head—which is used in a TomoTherapy® system—with nominal energy of 5.3 MeV and utilizes a fast technique for transporting photons through the patient-specific multi-leaf collimators (MLCs).39 For the details of the patient-specific PSF generation, the readers are referred to Ref. 38. All particles defined in the PSFs lie on a cylindrical surface formed by the gantry rotation and couch translation—such that these particles can be used in the next-stage MC simulations involving patient-specific parameters of the treatment plan. Contaminant electrons are not included in PSFs because a previous study had showed that the electron contamination from a helical tomotherapy system could be ignored without introducing measurable error.40 After benchmarking the code, three clinical cases are considered: a prostate case, a lung case, and a head & neck case. The energy spectrum of the PSF particles in prostate case is shown in Fig. 3, where the average photon energy is 1.45 MeV.
FIG. 3.
Energy spectrum of the PSF photons used in the prostate case, with the average energy of 1.45 MeV and the maximum energy of ∼5.3 MeV. Spectra for other treatment cases (not shown) are similar.
For the prostate plan, a PSF size is 6.4 GB, which is too large to easily load into the GPU global memory (i.e., the largest memory pool in GPU). To circumvent this problem, the entire PSF file is partitioned into smaller pieces and simulated in batches. Typically, the batch number is set to be 10, reducing the sub-PSF to a more manageable size of 640 MB. The ARCHERRT code works as follows: the CPU reads the first sub-PSF and copies the data to the GPU global memory. The GPU kernel is then launched asynchronously to perform the MC calculations. The CPU reads in the next sub-PSF immediately after the first kernel is launched. In this way, the simulation and PSF reading are performed concurrently, thus enhancing the code execution efficiency. For the prostate case, the PSF contains about 200 million photons; for the lung case, the PSF contains about 54 million photons; and for the head & neck case, the PSF contains 160 million photons. Each PSF is recycled to achieve the desired statistical error, 1% in the PTV.
II.E. Patient CT phantom
The CT dataset is converted into mass density and material composition using the Hounsfield unit (HU)-to-density conversion curve provided by the TomoTherapy® TPS. Using a commercial treatment planning system at UW–Madison, the conversion is calibrated in accordance with recommendations by Verhaegen and Devic.41 In these simulations, four materials, each having densities specified by the HU, are used for the patient phantom: water, dry air, compact bone (defined by ICRU), and lung (defined by ICRP). Although the code is capable of more materials, these four materials provide enough accuracy for the MC investigation.42
The prostate phantom consists of 260 × 256 × 108 voxels, with a voxel size of 0.1875 × 0.1875 × 0.3 cm3. Organs at risk (OARs) include the bladder, rectum, and “ring” around PTV. The lung phantom consists of 256 × 256 × 160 voxels, with a voxel size of 0.195×0.195× 0.2 cm3. OARs include the left lung, right lung, and spinal cord. The head & neck phantom consists of 256 × 256 × 127 voxels, with a voxel size of 0.195 × 0. 195 × 0.25 cm3. OARs include the brainstem, left parotid, right parotid, and spinal cord.
ARCHERRT is designed to handle the MC particle transport inside a voxelized CT patient phantom. From the source to the phantom, particles are transported using a direct raytracing method without MC simulation.
II.F. Statistical error evaluation
MC transport methods provide the most accurate results for dose calculation by harvesting the power of a large number of stochastic trials. The uncertainty in the final result is mainly from statistical errors which must be assessed accurately. The statistical error for an estimated mean value of a quantity x can be calculated using Eq. (1):
| (1) |
where N is the total number of histories simulated, xi is the score of the ith history, is the mean value of all xi, and is the variance of . According to Eq. (1), one needs to track and on the fly. In our case, x is the dose of a certain voxel. In a primary particle history, there are many energy deposition events. Calculating can be done by accumulating the energy deposition in the voxel from all particle histories. For , on the other hand, per-history energy deposition is calculated one history at a time. Obviously, computing dose using this conventional approach for every voxel in the phantom is a lengthy and slow simulation process. In ARCHERRT, different threads may deposit doses to the same voxel concurrently. Thus, one cannot tell which part of the voxel dose is incurred by a particular thread. One may attempt to solve the problem by assigning each thread an independent set of voxel tallies. However, there are millions of voxel tallies and thousands of threads while the GPU memories are limited to several GBs. For this reason, the batch statistics error estimation method43 is employed in ARCHERRT to avoid issues with the conventional direct error estimation defined in Eq. (1). The calculation of in Eq. (1) is no longer needed; instead, only for each batch is required. The equation to calculate statistical error is similar to Eq. (1), with N now being the number of batches and xi being from the ith batch simulation. Generally, a larger batch number will yield a more accurate estimation of the statistics error. If the batch number equals the number of histories simulated, the batch estimation reduces to the direct estimation. In our study, we use 10 batches—a number previously reported for the EGS code system.43 When simulating with multiple GPUs, the batch number can be larger. An important point for batch error estimations is to minimize the correlation between batch particles. Partitioning the PSF by areas of the phase space plane may result in biased error estimations. In our study, a sub-PSF is sampled in an interlaced manner from the original PSF to minimize correlations between sub-PSFs.
II.G. Woodcock tracking and variance reduction
The efficiency, ε, is defined to assess the performance of the MC code by Eq. (2):27
| (2) |
where s and T are the statistical error and simulation time, respectively. Any method that reduces the variance of tallies with a fixed number of particle histories can be called a variance reduction technique. Note that the variance reduction implementation may cost additional simulation time and decrease the efficiency.
The Woodcock ray-tracing technique,44 also known as fictitious interaction method, is a variance reduction technique that eliminates frequent boundary checking for photon transport in heterogeneous geometries. The technique works as follows: The maximum cross section μm(E) of the whole geometry for each energy E is calculated before the transport. For each voxel with cross section μ(E), a “fictitious cross section,” μm(E)-μ(E), is added so that all voxels have the same μm(E). The fictitious cross section corresponds to the “fictitious interaction.” The fictitious interaction is treated the same as a real interaction such as Compton scattering. The difference is, when the fictitious interaction is sampled, the code does nothing to the particle and the simulation continues. By doing this, the heterogeneous phantom becomes a homogeneous phantom and the code does not need to stop to check the voxel boundaries. Once the interaction occurs, the interaction type (Compton scattering, pair production, photoelectric effect, or fictitious interaction) is sampled according to corresponding the local cross sections. In the case of a fictitious interaction, the phase space of photon remains unchanged and previous process is repeated. The Woodcock technique avoids time-consuming boundary detection and boundary crossing operations, thereby increasing the simulation efficiency in highly heterogeneous media. The Woodcock tracking method works most efficiently in situations involving MeV photons traversing water-equivalent materials—i.e., where the value of μ(E) is comparable with μm(E) and the probability of factious interactions is small.
A modified Woodcock technique is also implemented in ARCHERRT as an additional variance reduction method to achieve higher efficiency.45 In this method, once a photon undergoes an interaction (whether fictitious or real), it is split into two photons. One is forced to undergo a real interaction (Compton scattering, pair production, or photoelectric absorption). To keep the scoring results unbiased, the weight of the photon (and all its secondary particles) is multiplied by the factor μ(E)/μm(E). The other photon remains unchanged (fictitious interaction) with the weight multiplied by the factor (1 − μ(E)/μm(E)). The Russian roulette technique is used for scattered Compton photons and fictitious interaction photons with the survival rate of μ(E)/μm(E) and (1 − μ(E)/μm(E)), respectively. This treatment increases the secondary electron generation and reduces the variance of tally for the same number of primary particles simulated. A comparison of the efficiency gains produced by the original Woodcock method and modified Woodcock method is provided in Sec. III C.
II.H. Performance evaluation
Before simulating the PSF dose distribution in a patient CT phantom, the code was first tested with a homogeneous water phantom. The PSF for testing was from a 6 MV Elekta PRECISE linear accelerator.46 The source-to-surface distance was set to 90 cm. The phantom was a 30 cm cube with a voxel size of 0. 5 × 0. 5 × 0.5 cm3. The depth dose and lateral dose profiles at 2, 5, and 10 cm from ARCHERRT were compared with those from DOSXYZnrc.
For clinical case simulations, the results of ARCHERRT were compared to those from the GEANT4 code. To achieve less than 1% statistical uncertainty, the prostate PSF was recycled 2 times while lung PSF and head & neck PSF were recycled 9 times and 5 times, respectively. For all MC simulations, voxel doses were normalized in such a way that the median dose at PTV equaled the prescribed dose—60 Gy for the lung case and 70 Gy for both the prostate and head & neck cases. DVHs were employed to represent dose statistics in different structures. Isodose maps were generated to compare the dose distributions from the GEANT4 and ARCHERRT. A gamma index test was used to examine the overall dosimetric accuracy of ARCHERRT.
The efficiency defined in Eq. (2) can be used when only a single tally is desired. For our three-dimensional dose distribution, a measure of the “average” uncertainty s2 is used,42 which is defined as
| (3) |
where Di is voxel dose, sDi is the standard deviation of Di calculated per Eq. (1), and n is the number of voxels with dose greater than 50% of the maximum dose.
Combining Eqs. (2) and (3), one can calculate the efficiency of a 3D dose simulation. The efficiency of the original Woodcock technique and modified Woodcock method with splitting and Russian roulette (see Sec. II H) are evaluated and compared.
III. RESULTS
III.A. Dosimetric results
Dosimetric results from different hardwares agree with each other within 0.5% difference. Here, we only discuss results obtained from NVIDIA M2090 card. The relative depth dose and lateral dose profile curves using the 6 MV Elekta PRECISE PSF for a water phantom are shown in Fig. 4. Doses are normalized to the maximum dose in each case. The estimated standard deviations are less than 0.3% of the maximum dose. It can be observed that the results from ARCHERRT agree well with those from DOSXYZnrc.47
FIG. 4.
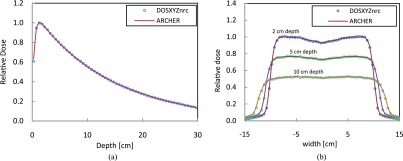
Depth dose and dose profile curves from ARCHERRT (circles) and DOSXYZnrc (solid line). Statistical uncertainty is less than 0.3% of dose maximum. (a) Depth dose along central axis, (b) lateral dose profiles at depth of 2, 5, and 10 cm.
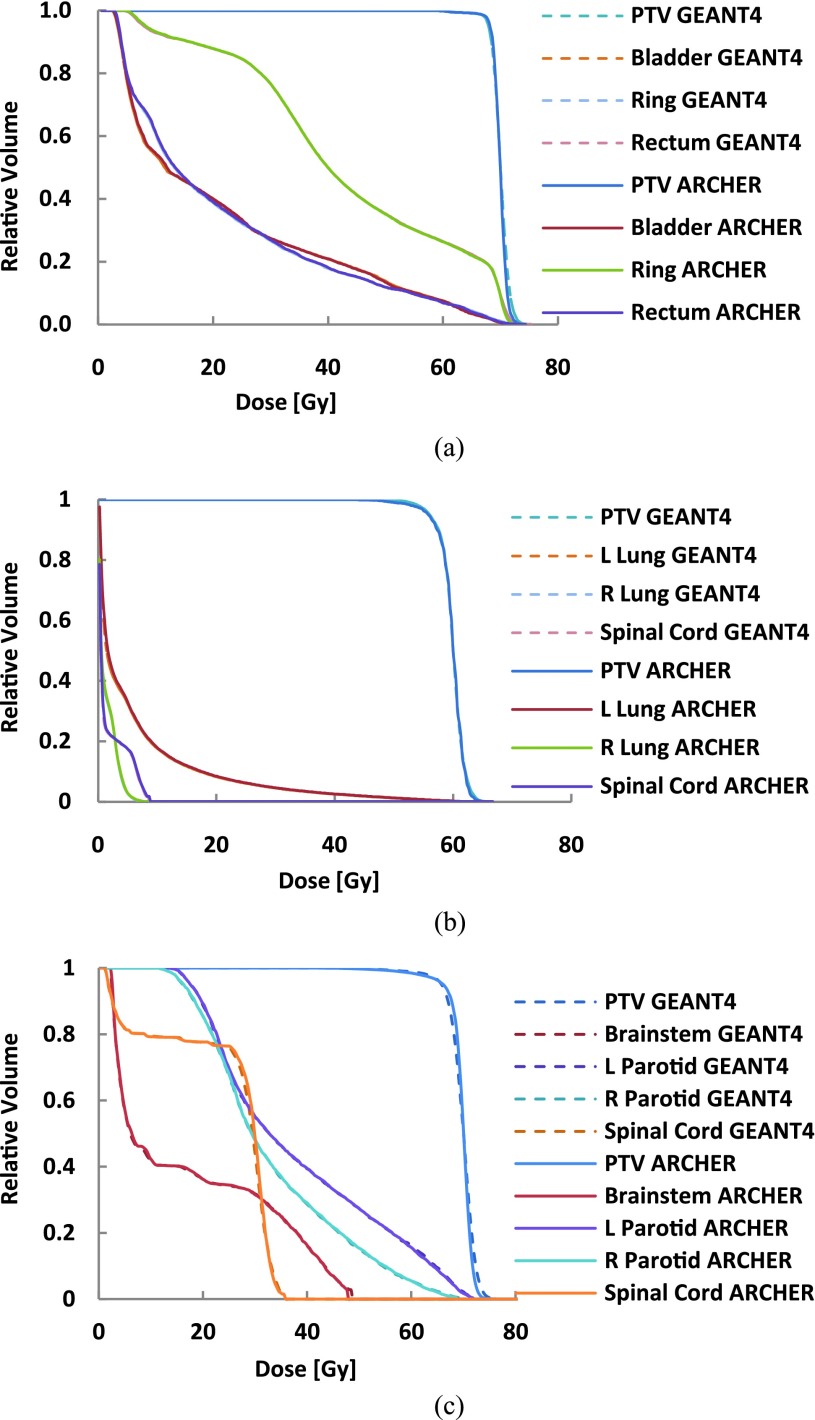
For the voxel doses in the PTV, relative statistical error (1 σ) is kept to be about 1% for all clinical cases considered in this study. The comparisons of GEANT4 and ARCHERRT for clinical cases are provided in Fig. 5. Figure 5(a) shows the DVHs for the prostate case, including PTV, the bladder, rectum, and ring area. The lung and head & neck DVHs are displayed in Figs. 5(b) and 5(c), respectively. It can be seen that these two MC codes agree with each other, for the cases studied, except for the fall-off tail of the PTV curve for the lung and head & neck. Such slight dose differences, as shown in Fig. 5, are partially caused by the heterogeneity in these two cases, but are considered to be insignificant in treatment planning.
FIG. 5.
DVH comparisons between GEANT4 and ARCHERRT. (a) The prostate case; (b) the lung case; (c) the head & neck case. General agreement between the two MC codes is evident for all three cases and the heterogeneity is the cause of minor discrepancies near the fall-off tails of the PTV curves.
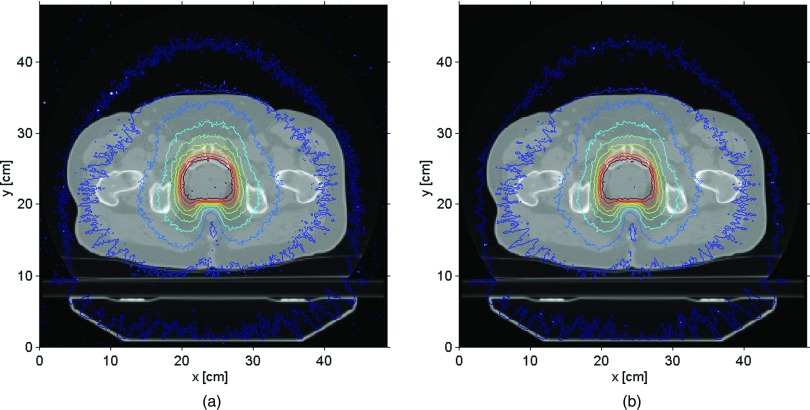
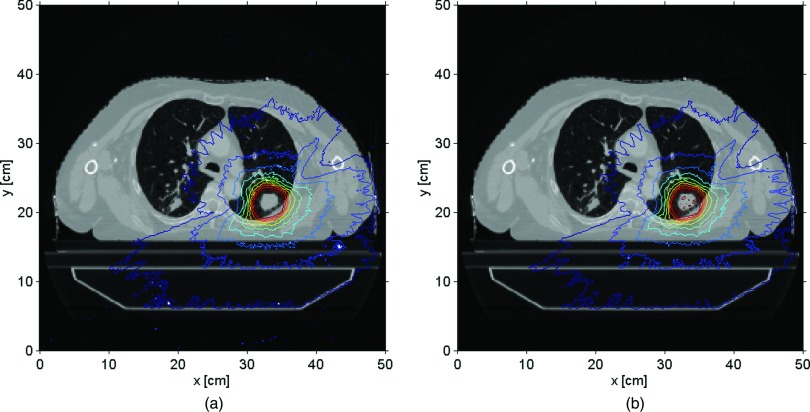
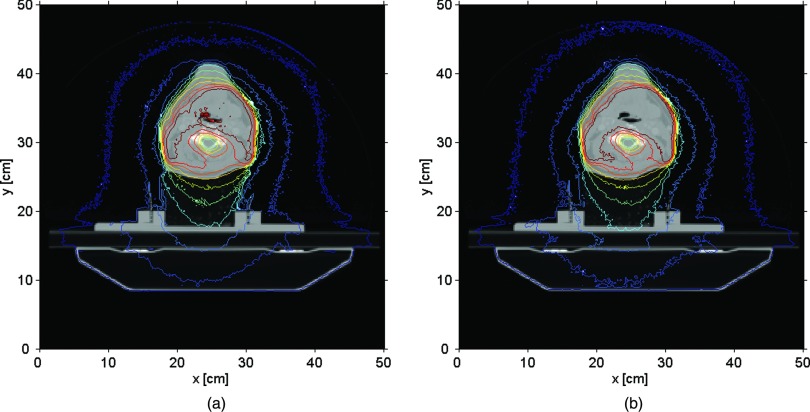
A different way to compare the two codes involved the isodose maps for the same treatment sites. Figures 6(a) and 6(b) show the prostate isodose maps obtained from ARCHERRT and GEANT4, respectively. Similar comparisons for the lung and the head & neck cases are given subsequently in Figs. 7 and 8. From these visual inspections, it was clear that ARCHERRT and GEANT4 agree well for all three cases, although less conformity is observable for regions in the head & neck case where heterogeneity is present. A gamma index test was performed for those voxels that are dosimetrically important, i.e., having a dose greater than 10% of the maximum dose. For gamma test criteria of 2% of dose tolerance and 2 mm of distance tolerance, it was found that the passing rate was 99.7%, 98.5%, and 97.2% for the prostate, lung, and head & neck cases, respectively. Since GEANT4 is a well-tested code and is currently used for treatment verification at UW-Madison, these benchmark results suggest that the accuracy of ARCHERRT is satisfactory for the cases tested here.
FIG. 6.
Prostate isodose maps on one transverse slice. (a) ARCHERRT. (b) GEANT4. The similarity of the contour lines from two MC codes is obvious showing the satisfactory accuracy in dose calculations by ARCHERRT.
FIG. 7.
Lung isodose maps on one transverse slice. (a) ARCHERRT. (b) GEANT4. The similarity of the contour lines from two MC codes is obvious showing the satisfactory accuracy in dose calculations by ARCHERRT.
FIG. 8.
Head & neck isodose maps on one transverse slice. (a) ARCHERRT. (b) GEANT4. Although larger discrepancies are observed, the overall agreement of the contour lines from two MC codes is satisfactory for one of the most complicated case (head & neck) in radiation therapy.
III.B. Timing studies
For fast MC simulations using PSF as source input, it is found that reading PSF from the hard drive costs a large fraction of code execution time. For instance, on a desktop mounted with single M2090 card, as introduced in Sec. II A, reading a binary prostate PSF of 6.4 GB to the CPU memory takes about 40 s. On the other hand, using the batch simulation explained before, file reading works concurrently with kernel execution, thus avoiding explicit file read time. With this improvement, the GPU MC transport time for simulating 600 million particles is found to be only about 63 s for the prostate case. Additional processes, such as reading the CT dataset, account for about 9 s, making the total MC execution time 72 s. For the lung case, the GPU MC transport time for 530 million particles was found to be 50 s and the total execution time was 58 s. For the head & neck case, the GPU transport time for 800 million particles was found to be 80 s and the total execution time was 89 s. Table I summarizes the timing results for one M2090 GPU card.
TABLE I.
ARCHERRT execution times for clinical cases on single M2090 card.
| Reading phantom, | Total | |||
|---|---|---|---|---|
| Clinical | No. of particles | Transport | first sub-PSF | execution |
| cases | (million) | time (s) | and misc (s) | time (s) |
| Prostate | 600 | 63.4 | 9 | 72 |
| Lung | 530 | 49.8 | 8 | 58 |
| Head & neck | 800 | 79.1 | 9 | 89 |
For multithreaded CPU code, the MC transport times on Intel E5-2620 (12 hyperthreads) are 614 s, 507 s, and 798 s for three cases. Single M2090 GPU is 10.2–11.5 times faster than multithread E5-2620 CPU.
Different MC simulation times for different hardware are listed in Table II. One may find that the simulation time is not proportional to the floating point capability of a GPU card. The main reason is that ARCHERRT is not FLOPS bound and more time is spent on the memory access than arithmetic calculation. The increase of FLOPS does elicit performance enhancement albeit nonlinearly. Nevertheless, K20 and K40 cards still achieved on the average 1.5 and 1.8 times, respectively, speedup over M2090.
TABLE II.
ARCHERRT MC transport times using different CPU and GPU cards.
| Intel E5-2620 | |||||
|---|---|---|---|---|---|
| Clinical | No. of particles | (12 threads) | M2090 GPU | K20 GPU | K40 GPU |
| cases | (million) | time (s) | time (s) | time (s) | time (s) |
| Prostate | 600 | 729 | 63.4 | 44.7 | 36.0 |
| Lung | 530 | 507 | 49.8 | 35.6 | 29.9 |
| Head & neck | 800 | 876 | 79.1 | 59.4 | 44.2 |
In addition, ARCHERRT was also tested with six M2090 cards (the second system described in Sec. II A). Harvesting the power of enterprise Solid State Drive (SSD), we were able to squeeze the PSF reading time from 12–38 to only 2–5 s. The execution timing information is shown in Table III. The simulation time ranges remarkably from 8.9 to 13.4 s, nearly a real-time performance in the clinical practice. Compared with single M2090 results, it is almost linear scale up from one to six GPU cards. However, as indicated in previous work,23 to provide the best GPU performance involving multiple cards, a minimum workload is needed to achieve reasonable scale up factor.
TABLE III.
ARCHERRT execution times using six M2090 cards.
| Clinical | GPU time | Reading PSF | Reading phantom | Total execution |
|---|---|---|---|---|
| cases | (s) | time (s) | and misc (s) | time (s) |
| Prostate | 10.9 | 4.8 | ∼4 | ∼20 |
| Lung | 8.9 | 1.6 | ∼3 | ∼15 |
| Head& neck | 13.4 | 3.9 | ∼5 | ∼23 |
In contrast, the use of GEANT4 in clinical treatment verification at UW-Madison generally requires 500 CPU-hours to finish the same simulation task. Obviously, the inherent parallel computing power brought forth in the GPU hardware has made the ARCHERRT an extremely fast MC code. There are two additional reasons why GEANT4 is much slower than ARCHERRT. First, as a general-purpose MC code, GEANT4 has complicated code structures that can handle a variety of application scenarios. In comparison, ARCHERRT is specifically designed for radiation therapy dose calculations. Second, GEANT4 employs more detailed physics models than ARCHERRT does, including binding effect, Doppler broadening, and X-ray fluorescence. ARCHERRT uses simpler physics models that are justified for radiotherapy application, which greatly enhances the simulation speed without sacrificing the accuracy.
III.C. Efficiency of variance reduction
In an initial attempt to improve the simulation efficiency, we implemented a modified Woodcock algorithm. The performance of this modification was compared with the original algorithms. Table IV presents the results for this efficiency comparison. Interestingly, our results differ from those in the literature for CPU-based methods,45 with the finding that the modified Woodcock method achieved less efficiency than the original implementation. We believe this is partially caused by the fact that splitting and Russian roulette require more writing and reading operation of the global memory of GPU. Accessing global memory is relatively expensive, introducing execution penalty for the modified Woodcock algorithm in GPU.
TABLE IV.
Efficiency of two Woodcock algorithms. s2, T, and ε are from Eq. (2), s2 are calculated via Eq. (3). The first column data are for modified Woodcock algorithm, with PSF being used once. The second column data are for original Woodcock algorithm, with PSF being used once. The third column data are for original Woodcock algorithm, with PSF being used 3 times (2× recycles) for prostate case and 10 times (9× recycles) for lung case.
| Modified | Original | |||
|---|---|---|---|---|
| Woodcock | Woodcock | Original | ||
| (no recycle) | (no recycle) | Woodcock | ||
| Prostate | s2 | 7.56 × 10−4 | 2.20 × 10−3 | 7.72 × 10−4 |
| T (s) | 144.2 | 22 | 63 | |
| ε(s−1) | 9.17 | 20.7 | 20.6 | |
| Lung | s2 | 1.25 × 10−3 | 9.61 × 10−3 | 9.87 × 10−4 |
| T (s) | 54.8 | 6.23 | 50.2 | |
| ε(s−1) | 14.6 | 16.7 | 20.2 |
IV. DISCUSSION
IV.A. GPU execution characteristics and comparison of CPU and different GPUs
The GPU is a highly parallel computational tool with hundreds of streaming processors. Although the so-called thread divergence prevents the peak performance to be achieved, the GPU can still dynamically allocate threads to minimize processor idle time. For example, if a thread stalls to wait for global memory access, another ready thread is switched in immediately. Therefore, the GPU works the best when a large number of threads are occupied. This finding can be further illustrated in the previous Table IV where, for the original Woodcock algorithm, the efficiency of the simulations without particle recycling (16.7 s−1) is lower than that of the simulation with 9× recycling (20.2 s−1). The main reason is that without recycling, there are only 5 million particles in each batch. Such number of particles is insufficient to saturate the GPU to achieve it peak performance.
Compared with Intel E5-2620 CPU, NVIDIA M2090 GPU achieved 10.2–11.5 speedup. While some other GPU related studies reported much more attractive speedup (near 100) over CPU, most of them simply compared GPU code with single-threaded CPU code. Since current prevailing CPUs usually consist of multiple cores, employing only single core not only wastes CPU's computational capability but also makes the comparison biased. Therefore, in our study, we make full use of our 6-core E5-2620 CPU with 12 hyperthreads, providing a fairer comparison. In addition, as shown in Sec. III B, K40 GPU has 1.7–1.8 speedup over M2090, although the former has about 3 times higher FLOPS than the latter. It suggests that except for floating point capability, the memory access latency is another key factor that impacts the overall performance of ARCHER GPU code.
IV.B. Comparison with previous work
Compared with previous work on GPU-based fast MC dose calculation,12–14,18–20 this study does better job on “fair comparison.” Instead of comparing GPU code with serial CPU code, this study makes multithreaded CPU code and conducts a fairer comparison of GPU and CPU. In addition, this work is one of the first to investigate “heterogeneous architecture” involving a host CPU and different GPUs as devices. Among previous studies, at least two of them involved the IMRT dose calculation. Jahnke et al. developed GMC based on GEANT4 and tested it on a mediastinum IMRT case with unspecified phantom size.14 The simulation of 240 million particles costs 349 s, which is much slower than ARCHERRT. Meanwhile, the 2%/2mm gamma test pass rate of 91.74% is worse than ARCHERRT. Townson et al. developed GPU based MC dose calculation tool for traditional IMRT using a PSF source.21 They performed a 7-field IMRT treatment simulation of a tongue tumor treatment. The phantom consisted of 154 × 90 × 109 voxels with a voxel size of 0.3 × 0.3 × 0.3 cm3. The overall phantom size was smaller with lower resolution in the Townson's simulation, than all of the phantoms used in this investigation. Townson's investigation required 50 s to simulate 500 million 6 MV photons, achieving less than 1% statistical uncertainty near isocenter. In comparison, ARCHERRT requires 60 s to simulate 600 million 6 MV photons, achieving the same precision in the PTV. For the Townson investigation, an NVIDIA GTX 580 card was used. Although it is not designed for general purpose scientific computing, it has higher single precision FLOPs relative to M2090 card. Thus, the overall speed of our TomoTherapy® simulation is comparable with or faster than Townson's work in traditional IMRT. In addition, for the first time, we report the use of six M2090 cards to finish a full plan dose calculation in about 10 s. Furthermore, our study provides DVHs and whole phantom isomaps for three common clinical cases. Finally, Townson used a so-called phase-space-let (PSL) method together with fluence map to achieve patient independent PSF dose calculation for traditional IMRT. However, those implementations do not work for HT due to different machine structure and treatment protocol. In on-going work, we are adopting patient independent PSFs for the simulation using Sterpin's method.39
IV.C. Meaning of ARCHER in context of trends of CPU and accelerator development
From the inception of microprocessor in 1970s, the clock rate of the CPU kept increasing, bringing growing computational power, until early 2000s. During that time, the majority of personal and business computers was equipped with single core CPUs. The enhancement of computing power was achieved by increasing the clock rate as well as the number of transistors on chip. In 2000s, the clock rate had reached several GHz. Further increase of clock rate not only reduces energy efficiency but also introduces cooling difficulties. Therefore, the development of CPU has turned to multicore, with moderate clock rate (typically 1–2 GHz). At the same time, hardware accelerators have been emerging quickly. NVIDIA and AMD provided general purpose GPU (GPGPU), which has hundreds of streaming cores. Intel invented Xeon Phi, a coprocessor consisting of more than 60 cores. In addition, Intel is said to apply knights landing architecture to future CPU production, which means the future CPU may change from multicore to many-core, similar to Xeon Phi coprocessor. These companies are competing for the incoming exascale computing era. While it is still not clear who will win the contest eventually, the consensus has formed that the parallel computing is no doubt the trend of future computing paradigm. In this context, the work of ARCHER provides a testbed for different hardwares in terms of radiation transport application. The significance of our study is to establish a scalable Monte Carlo software framework on different developing platforms, so that as the hardware architecture is upgraded at a steady pace—with increased memory bandwidth, memory size, number of cores, etc.—we will be able to, in a timely manner, fine-tune the code, re-evaluate the performance, and find out which platform benefits us most.
V. CONCLUSIONS
We have successfully developed and applied ARCHERRT, a GPU-based fast and accurate dose calculation engine for radiotherapy. It was benchmarked against DOSXYZnrc for 6 MV Elekta PRECISE PSF dose distributions in a water phantom. Three clinical TomoTherapy® treatment plans of the prostate, the lung, and the head & neck were studied to further benchmark against GEANT4 which was used in clinical treatment verification in UW-Madison to show the clinical utility. ARCHERRT was tested on different hardware including multithreaded Intel E5-2620 CPU, NVIDIA K20, K40, and up to six M2090 GPU cards.
For all cases, gamma tests were performed and the dosimetric accuracy of ARCHERRT was demonstrated. The total ARCHERRT execution times for three cases one M2090 were found to be about 60–80 s. The simulation time is reduced by a factor of ∼1.8 using the latest K40 GPU card. Using six M2090 cards, the simulation of full clinical plan can be completed in about 10 s. In comparison, 12-hyper-threaded E5-2620 CPU takes 507–876 s and GEANT4 takes hundreds of CPU hours for same simulation. These results suggest that ARCHERRT is capable of performing swift yet accurate MC dose calculations for the TomoTherapy® treatment cases. Although we report in this paper only application for the helical tomotherapy, ARCHERRT can be readily used for other radiotherapy modalities including RapidArc (Varian Medical Systems, Palo Alto, CA) and VMAT (Elekta, Stockholm, Sweden). Currently, ARCHERRT accepts patient-specific PSFs, and on-going work is carried on to adopt patient-independent PSFs.
ACKNOWLEDGMENTS
The GPU programming tools were developed using funding from the National Institute of Biomedical Imaging and Bioengineering (Grant No. R01EB015478). Discussions with Dr. Josep Sempau and Dr. Christopher D. Carothers are appreciated.
REFERENCES
- 1.Bortfeld T., “IMRT: A review and preview,” Phys. Med. Biol. 51, R363–R379 (2006). 10.1088/0031-9155/51/13/R21 [DOI] [PubMed] [Google Scholar]
- 2.Fogliata A., Vanetti E., Albers D., Brink C., Clivio A., Knöös T., Nicolini G., and Cozzi L., “On the dosimetric behaviour of photon dose calculation algorithms in the presence of simple geometric heterogeneities: Comparison with Monte Carlo calculations,” Phys. Med. Biol. 52, 1363–1385 (2007). 10.1088/0031-9155/52/5/011 [DOI] [PubMed] [Google Scholar]
- 3.Sterpin E., Tomsej M., Smedt B. D., Reynaert N., and Vynckier S., “Monte Carlo evaluation of the AAA treatment planning algorithm in a heterogeneous multilayer phantom and IMRT clinical treatments for an Elekta SL25 linear accelerator,” Med. Phys. 34, 1665–1677 (2007). 10.1118/1.2727314 [DOI] [PubMed] [Google Scholar]
- 4.Rogers D. W., “Fifty years of Monte Carlo simulations for medical physics,” Phys. Med. Biol. 51, R287–R301 (2006). 10.1088/0031-9155/51/13/R17 [DOI] [PubMed] [Google Scholar]
- 5.Yan D., Vicini F., Wong J., and Martinez A., “Adaptive radiation therapy,” Phys. Med. Biol. 42(1), 123–132 (1997). 10.1088/0031-9155/42/1/008 [DOI] [PubMed] [Google Scholar]
- 6.Hansen E. K., Mk M. K. B., Quivey J. M., Weinberg V., and Xia P., “Repeat CT imaging and replanning during the course of IMRT for head-and-neck cancer,” Int. J. Radiat. Oncol., Biol., Phys. 64(2), 355–362 (2006). 10.1016/j.ijrobp.2005.07.957 [DOI] [PubMed] [Google Scholar]
- 7.Dawson L. A. and Jaffray D. A., “Advances in image-guided radiation therapy,” J. Clin. Oncol. 25(8), 938–946 (2007). 10.1200/JCO.2006.09.9515 [DOI] [PubMed] [Google Scholar]
- 8.Martin W. R. and Brown F. B., “Status of vectorized Monte Carlo for particle transport analysis,” Int. J. High Performance Comput. Appl. 1(2), 11–32 (1987). 10.1177/109434208700100203 [DOI] [Google Scholar]
- 9.Pratx G. and Xing L., “GPU computing in medical physics: A review,” Med. Phys. 38, 2685–2697 (2011). 10.1118/1.3578605 [DOI] [PubMed] [Google Scholar]
- 10.Shalf J., Dosanjh S., and Morrison J., in High Performance Computing for Computational Science–VECPAR, 2010 (Springer, 2011), pp. 1–25 [Google Scholar]
- 11. Top500.org, “Top 500 List - June 2013,” http://www.top500.org/list/2012/11/, accessed on Dec 12 2013
- 12.Jia X., Gu X., Graves Y., Folkerts M., and Jiang S. B., “GPU-based fast Monte Carlo simulation for radiotherapy dose calculation,” Phys. Med. Biol. 56, 7017–7031 (2011). 10.1088/0031-9155/56/22/002 [DOI] [PubMed] [Google Scholar]
- 13.Hissoiny S. and Ozell B., “GPUMCD: A new GPU-oriented Monte Carlo dose calculation platform,” Med. Phys. 38, 754–764 (2011). 10.1118/1.3539725 [DOI] [PubMed] [Google Scholar]
- 14.Jahnke L., Fleckenstein J., Wenz F., and Hesser J., “GMC: A GPU implementation of a Monte Carlo dose calculation based on Geant4,” Phys. Med. Biol. 57, 1217–1229 (2012). 10.1088/0031-9155/57/5/1217 [DOI] [PubMed] [Google Scholar]
- 15.Su L., Liu T., Ding A., and Xu X. G., “A GPU/CUDA based Monte Carlo code for proton transport: Preliminary results of proton depth dose in water,” Med. Phys. 39(6), 3945 (2012). 10.1118/1.4736101 [DOI] [Google Scholar]
- 16.Liu T., Ding A., and Xu X. G., “GPU-based Monte Carlo methods for accelerating radiographic and CT imaging dose calculations: Feasibility and scalability,” Med. Phys. 39(6), 3876 (2012). 10.1118/1.4735826 [DOI] [Google Scholar]
- 17.Zhou B., Yu C. X., Chen D. Z., and Hu X. S., “GPU-accelerated Monte Carlo convolution/superposition implementation for dose calculation,” Med. Phys. 37(11), 5593–5603 (2010). 10.1118/1.3490083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jia X., Gu X., Sempau J., Choi D., Majumdar A., and Jiang S. B., “Development of a GPU-based Monte Carlo dose calculation code for coupled electron–photon transport,” Phys. Med. Biol. 55(11), 3077–3086 (2010). 10.1088/0031-9155/55/11/006 [DOI] [PubMed] [Google Scholar]
- 19.Jia X., Yan H., Gu X., and Jiang S. B., “Fast Monte Carlo simulation for patient-specific CT/CBCT imaging dose calculation,” Phys. Med. Biol. 57(3), 577–590 (2012). 10.1088/0031-9155/57/3/577 [DOI] [PubMed] [Google Scholar]
- 20.Hissoiny S., D’amours M., Ozell B., Despres P., and Beaulieu L., “Sub-second high dose rate brachytherapy Monte Carlo dose calculations with bGPUMCD,” Med. Phys. 39(7), 4559–4567 (2012). 10.1118/1.4730500 [DOI] [PubMed] [Google Scholar]
- 21.Townson R., Jia X., Tian Z., Zavgorodni Y. J. G. S., and Jiang S. B., “GPU-based Monte Carlo radiotherapy dose calculation using phase-space sources,” Phys. Med. Biol. 58, 4341–4356 (2013). 10.1088/0031-9155/58/12/4341 [DOI] [PubMed] [Google Scholar]
- 22.Liu T., Ding A., Ji W., Xu X. G., Carothers C., and Brown F. B., “A Monte Carlo neutron transport code for eigenvalue calculations on a dual-GPU system and CUDA environment,” in Proceedings of International Topical Meeting on Advances in Reactor Physics, Knoxville, Tennessee (PHYSOR, 2012). [Google Scholar]
- 23.Su L., Du X., Liu T., and Xu X. G., “Monte Carlo electron-photon transport using GPUs as an accelerator: Results for a water-aluminum-water phantom,” in Proceedings of the International Conference on Mathematics and Computational Methods Applied to Nuclear Science & Engineering, Sun Valley, ID (M&C, 2013). [Google Scholar]
- 24.Kim W. and Voss M., “Multicore desktop programming with intel threading building blocks,” IEEE Software 28(1), 23–31 (2011). 10.1109/MS.2011.12 [DOI] [Google Scholar]
- 25. NVIDIA, “Cuda C programming guide,” http://docs.nvidia.com/cuda/cuda-c-programming-guide/, accessed on 12 Dec 2013.
- 26.Brown F. B., “MCNP–A General Monte Carlo N-Particle Transport Code, Version 5,” Los Alamos National Laboratory, Oak Ridge, TN, 2003.
- 27.Kawrakow I. and Rogers D. W. O., “The EGSnrc code system: Monte Carlo simulation of electron and photon transport,” NRCC Report No. PIRS-701, 2011.
- 28.Salvat F., Fernandez-Varea J. M., and Sempau J., “PENELOPE-2006: A code system for Monte Carlo simulation of electron and photon transport,” OECD Nuclear Energy Agency, 2006.
- 29.Agostinelli S., Allison J., Amako K. E., Apostolakis J., Araujo H., Arce P., Asai M., Axen D., Banerjee S., and Barrand G., “GEANT4—A simulation toolkit,” Nucl. Instrum. Methods, Phys. Res. A 506(3), 250–303 (2003). 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
- 30.Sempau J., Wilderman S. J., and Bielajew A. F., “DPM, a fast, accurate Monte Carlo code optimized for photon and electron radiotherapy treatment planning dose calculations,” Phys. Med. Biol. 45, 2263–2291 (2000). 10.1088/0031-9155/45/8/315 [DOI] [PubMed] [Google Scholar]
- 31.Everett C., Cashwell E. D., and Turner G., “A new method of sampling the Klein–Nishina probability distribution for all incident photon energies above 1 keV,” Los Alamos Scientific Lab, 1971.
- 32.Berger M. J., Hubbell J. H., Seltzer S. M., Coursey J. S., and Zucker D. S., “XCOM: Photon cross sections database,” Physics Laboratory, National Institute of Standards and Technology, 1999.
- 33.Berger M. J., in Methods in Computational Physics, edited by Alder B., Fernbach S., and Rotenberg M. (Academic, New York, 1963), Vol. 1, pp. 135–215 [Google Scholar]
- 34.Goudsmit S. A. and Saunderson J. L., “Multiple scattering of electrons,” Phys. Rev. 57, 24–29 (1940). 10.1103/PhysRev.57.24 [DOI] [Google Scholar]
- 35.Goudsmit S. A. and Saunderson J. L., “Multiple scattering of electrons. II,” Phys. Rev. 58, 36–42 (1940). 10.1103/PhysRev.58.36 [DOI] [Google Scholar]
- 36.Kawrakow I. and Bielajew A. F., “On the representation of electron multiple elastic-scattering distributions for Monte Carlo calculations,” Nucl. Instrum. Methods, Phys. Res. B 134(3), 325–336 (1998). 10.1016/S0168-583X(97)00723-4 [DOI] [Google Scholar]
- 37.International Commission on Radiation Units and Measurements, “Stopping powers for electrons and positions,” ICRU Report No. 37, 1984.
- 38.Zhao Y.-L., Mackenzie M., Kirkby C., and Fallone B. G., “Monte Carlo calculation of helical tomotherapy dose delivery,” Med. Phys. 35, 3491–3500 (2008). 10.1118/1.2948409 [DOI] [PubMed] [Google Scholar]
- 39.Sterpin E., Salvat F., Cravens R., Ruchala K., Olivera G. H., and Vynckier S., “Monte Carlo simulation of helical tomotherapy with PENELOPE,” Phys. Med. Biol. 53, 2161–2180 (2008). 10.1088/0031-9155/53/8/011 [DOI] [PubMed] [Google Scholar]
- 40.Sterpin E., Salvat F., Oliverac G. H., and Vynckier S., “Analytical model of the binary multileaf collimator of Tomotherapy for Monte Carlo simulations,” J. Phys.: Conf. Ser. 102, 012022–012029 (2008). 10.1088/1742-6596/102/1/012022 [DOI] [Google Scholar]
- 41.Verhaegen F. and Devic S., “Sensitivity study for CT image use in Monte Carlo treatment planning,” Phys. Med. Biol. 50, 937–946 (2005). 10.1088/0031-9155/50/5/016 [DOI] [PubMed] [Google Scholar]
- 42.Kawrakow I. and Walters B. R. B., “Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc,” Med. Phys. 33, 3046–3056 (2006). 10.1118/1.2219778 [DOI] [PubMed] [Google Scholar]
- 43.Walters B. R. B., Kawrakow I., and Rogers D. W. O., “History by history statistical estimators in the BEAM code system,” Med. Phys. 29, 2745–2752 (2002). 10.1118/1.1517611 [DOI] [PubMed] [Google Scholar]
- 44.Woodcock E., Murphy T., Hemmings P., and Longworth S., “Techniques used in the GEM code for Monte Carlo neutronics calculations in reactors and other systems of complex geometry,” Argonne National Laboratories Report No. ANL-7050, 1965.
- 45.Kawrakow I. and Fippel M., “Investigation of variance reduction techniques for Monte Carlo photon dose calculation using XVMC,” Phys. Med. Biol. 45, 2163–2183 (2000). 10.1088/0031-9155/45/8/308 [DOI] [PubMed] [Google Scholar]
- 46. IAEA, “Phase-space database for external beam radiotherapy,” http://www-nds.iaea.org/phsp/phsp.htmlx, accessed on 12 Dec 2013.
- 47.Walters B., Kawrakow I., and Rogers D. W. O., “DOSXYZnrc users manual,” NRCC Report No. PIRS-794revB, 2011.