iMatch2: Compound identification using retention index for analysis of gas chromatography–mass spectrometry data

Abstract

We developed a method, iMatch2, for compound identification using retention indices (RI) in NIST11 library. Three-way ANOVA test and Kruskal–Wallis test respectively demonstrate that column class and temperature program type defined by the NIST library are the most dominant factors affecting the magnitude of retention index while the retention index data type does not cause significant difference. The developed linear regression transformation for merging retention indices with different data types, but the same column class and temperature program type, reduces the standard deviation of retention index up to 8%, compared to the simple union approach used in the original iMatch. As for outlier detection methods to remove retention indices having large difference with the remaining data of the same compound, Tietjen–Moore test and generalized extreme studentized deviate test are the strictest methods, while methods such as Dixon’s test, Thompson tau approach, and Grubbs’ test are more conservative. To improve the accuracy of retention index window, a concept of compound specific retention index window is introduced for compounds with a large number of retention indices in the NIST11 library, while the retention index window is calculated from empirical distributions for the compounds with a small number of retention indices. Analysis of the experimental data of a mixture of compound standards and the metabolite extract from mouse liver show significant improvement of retention index quality in the NIST11 library and the new data analysis methods.

1. Introduction

Compound identification in analysis of gas chromatography–mass spectrometry (GC–MS) data is currently achieved by mass spectrum matching. Multiple mass spectral similarity measures have been proposed, including composite similarity [1], wavelet transform-based composite measure [2], mixture partial and semi-partial correlation [3]. Some efforts have been also devoted to find the optimal weight factors to improve the identification accuracy [4,5]. The performance of mass spectral matching can be affected by many factors such as the reference spectral library, spectral similarity measure and the weight factors [4,5]. Furthermore, the mass spectrum matching-based compound identification cannot differentiate the isomers from each other. For example, Lee et al. [6] reported that the mass spectra of four farnesol isomers have very similar mass spectra, while the retention indices of them are different from each other with high confidence interval. For these reasons, retention indices have been used for high accuracy compound identification [7–11]. Smith et al. [9] suggested compound identification using combined spectral similarity measure and retention index deviation. Schauer et al. [10] created a platform for mass spectral and retention time index libraries for metabolite identification. Babushok et al. [11] comprehensively evaluated the retention indices for 505 frequently reported plant essential oil components using a large retention index database. AMDIS software also provided an application to use retention index database with mass spectrum for identification [1]. A software package iMatch was introduced for compound identification using retention index to filter the potential false-positive identifications generated by mass spectrum matching [12].

The main objective of this work was to improve the performance of iMatch by introducing a new retention index window and updating the retention index library to the NIST/EPA/NIH Mass Spectral Library 2011 (NIST11). The retention index window refers to the range of true retention index of a compound with a certain confidence level. A suite of methods were developed for detecting and removing the outliers of the retention indices of the same compound, transforming retention indices acquired in one experimental condition (i.e., data type defined in the NIST11 library) to the values in the other condition, and calculating empirical distribution. These newly developed methods have been implemented as a software package iMatch2 using MATLAB 2010b (The Math-works, Natick, MA, USA). We further compared the performance of the aforementioned analysis procedures with that of iMatch.

2. Materials and methods

2.1. Materials for experimental

2.1.1. Mixture of compound standards

A mixture of analytes was created by the combination of two commercially available mixtures, a mixture of 76 compounds each at 1000 μg/mL (Cat. no. 31850, 8270 MegaMix, Restek Corp., Bellefonte, PA) and a mixture of C₇–C₄₀ n-alkanes each at 1000 mg/mL (Cat. no. 49452-U, Sigma–Aldrich Corp., St. Louis, MO). These two mixtures were mixed in a ratio of 1:1.

2.1.2. Metabolite extract from mouse liver

Mouse liver tissue was weighed and homogenized for 2 min after adding water at a ratio of 100 mg liver tissue/mL water. The homogenized sample was then stored at −80 °C until use. A 100 μL aliquot of the homogenized liver sample and 400 μL methanol were mixed and vortexed for 1 min followed by centrifugation at room temperature for 10 min at 15000 rpm. 400 μL of the supernatant was aspirated into a plastic tube and dried by N₂ flow. The metabolites extracts were then dissolved in 40 μL ethoxyamine hydrochloride solution (30 mg/mL) and vigorously vortex-mixed for 1 min. The methoxymation and derivatization were prepared just before GC × GC–TOF MS analysis.

All samples were analyzed on a LECO Pegasus 4D GC × GC–TOF MS instrument equipped with an electron ionization (EI) ion source (LECO, St. Joseph, MI). A 30 m × 0.25 mm ¹d_c × 0.25 μm ¹d_f, Rxi-5 ms GC capillary column (95% dimethylpolysiloxane/5% diphenyl, Restek Corp., Bellefonte, PA) was used as the primary column and a 1.2 m × 0.10 mm ²d_c × 0.10 μm ²d_f, BPX-50 GC capillary column (50% phenylpolysilphenylene-siloxane, SGE Incorporated, Austin, TX) was used as the second column. The primary column temperature was programmed with an initial temperature of 60 °C for 0.5 min and then ramped at a temperature gradient of 7 °C/min to 315 °C. The second column temperature program was set to an initial temperature of 65 °C for 0.5 min and then also ramped at the same temperature gradient employed in the first column to 320 °C accordingly. The thermal modulator was set to +20 °C related to the secondary oven and a modulation time of 5 s was used. Details of derivatizing the liver samples, the instrument analysis, and spectral deconvolution are identical to our previous work [13].

2.2. The retention index library

The latest version of NIST/EPA/NIH Mass Spectral Library 2011 (NIST11) has four types of retention index, Kováts, linear, normal alkane and Lee retention index. To normalize retention time using homologous n-alkane series as the retention references, the Kováts retention index I_K [14] was defined for isothermal experimental condition while the linear retention index I_L [15] was defined for ramped temperature condition, as follows:

$$I_K(S)=100n+100\left(\frac{log(t_{R(S)}^{\prime })-log(t_{R(n)}^{\prime })}{log(t_{R(n+1)}^{\prime })-log(t_{R(n)}^{\prime })}\right)$$ (1)

$$I_L(S)=100n+100\left(\frac{log(t_{R(S)})-log(t_{R(n)})}{\text{log(}{t}_{R(n+1)})-log(t_{R(n)})}\right)$$ (2)

where I_K(S) is the Kovátz retention index for compound S, I_L(S) is linear retention index, t_R is retention time, $t_R^{\prime }$ stands for the adjusted retention time, and t_R(n), t_R(n+1) are the retention times of two adjacent alkane series beside the compound S.

The Lee retention index was defined by using polycyclic aromatic hydrocarbons (PAHs) as retention references instead of n-alkane series [16]. The type of normal alkane indices in NIST11 library corresponds to cases when authors did not indicate a definition used to derive RI value.

NIST11 contains 346,757 literature-reported retention indices for 70,838 compounds. Compared with the 2008 version of NIST retention index library, the data collection procedure of NIST11 was well conducted by quality controls [17–19] and the number of retention indices recorded in the NIST11 library is increased by 122,719. Tables 1 and S-1 show the numbers of retention index in the NIST11 library corresponding to column types (i.e., capillary and packed, respectively). A total of 318,909 retention indices were acquired on capillary columns, while only 26,765 values were acquired on packed columns. Therefore, the retention index on the packed columns is not discussed in this work. In case of capillary column, even though Lee retention index [16] is an alternative retention index for the Kováts retention index [14] and is highly correlated with boiling point, the size of the Lee retention indices reported in the NIST11 library is very small, which is about 1.8% as shown in Table 1. It is not accurate to estimate a retention index window from the Lee retention indices for the purpose of compound identification. As a result, we ignore the Lee retention index in this study.

Table 1.

Retention indices acquired on capillary columns in the NIST11 library categorized by column class, program type and data type defined by the NIST library.

Column type		Capillary
Column class	Data type	Program type
		Isothermal	Ramp	Complex	Grand total
Semi-standard non-polar	Kovats RI	10,678	5846	1180	17,704
	Lee RI	91	4410	793	5294
	Linear RI		41,736	20,257	61,993
	Normal alkane RI	1629	38,712	15,767	56,108
	Sub-total	12,398	90,704	37,997	141,099
Standard non-polar	Kovats RI	18,145	6202	1154	25,501
	Lee RI	33	361		394
	Linear RI	14	19,259	1907	21,180
	Normal alkane RI	3018	39,077	8273	50,368
	Sub-total	21,210	64,899	11,334	97,443
Standard polar	Kovats RI	9581	2844	215	12,640
	Lee RI		26		26
	Linear RI		20,750	4551	25,301
	Normal alkane RI	1244	29,815	11,341	42,400
	Sub-total	10,825	53,435	16,107	80,367
Grand total		44,433	209,038	65,438	318,909

2.3. Methods for removing outliers

Outliers are defined as data that are statistically inconsistent with the rest of the data. We considered six outlier detection methods to find outliers of retention indices of the same compound, which are Thompson tau methods with mean and median [20], Dixon’s test [21], Grubbs’ test [22], Tietjen–Moore (TM) test [23], and generalized extreme studentized deviate (ESD) test [24]. TM test and ESD methods were designed to detect multiple outliers at once, while the other outlier detection methods were developed for detection of single outlier at a time. The advantage of ESD test against TM test is to automatically determine the number of outliers. To determine the k outliers for TM test, we choose the largest k₀ to reject null hypothesis H₀ (there are no outliers in the data) corresponding to TM statistic E_k, k = 1, …, 10. For the other four methods, the outlier detection test is repeated several times until the null hypothesis is accepted.

To investigate the relative performance of each method, we define the ratio of empirical standard deviation and the relative ratio of the number of outliers as follows:

$${RS}_c=\frac{\mathit{Std}({\widehat{\mathbf{x}}}_c)}{\mathit{Std}({\mathbf{x}}_c)},c\in C$$ (3)

$${RN}_c=\frac{\#({\mathbf{x}}_c)-\#({\widehat{\mathbf{x}}}_c)}{\#({\mathbf{x}}_c)},c\in C$$ (4)

where x_c, x̂_c are sets of retention indices of a compound c before and after outlier removal, respectively, C is a collection of compounds, and #(x) is the number of retention indices. If standard deviation of a compound is much reduced after outlier removal, RS_c is close to zero. On the contrary, RS_c is exactly one if there is no outlier. Eq. (4) shows the relative ratio of difference between before and after outlier removal. If a compound is identified as having a lot of outliers, then RN_c is close to one. Otherwise, it is close to zero.

2.4. Transformation of retention index values

The data type does not introduce large variation to the magnitude of retention index. Therefore, iMatch merged all retention indices regardless of their data types as long as they were acquired using the same column class and temperature program type [12]. In this study, we developed a linear regression approach to transfer retention index values from one data type to another, instead of simply merging all retention indices. The purpose of developing a transition function is to further minimize the variation of retention index values between data types. For example, assuming that a compound c_j has multiple normal alkane retention index values on a standard non-polar column with isothermal program condition, we then can convert these normal alkane retention indices of this compound into Kováts retention indices for this compound via a transition function. The linear regression function is created by using the retention indices of all compounds that have a large number of normal alkane retention indices on standard non-polar column with isothermal program type. The normal alkane retention indices are used as an explanatory variable while the Kováts retention indices as a dependent variable. The converted Kováts retention indices are then merged with other existing Kováts retention index value(s) of compound c_j for further analysis.

Consider a set of multiple observations of data type D_i for compound c_j under the experimental conditions defined by column class and temperature program type

$$x_j=\{x_{j,1},\dots ,x_{j,p}\}$$ (5)

where x_j,k is the kth retention index of compound c_j in the NIST11 library, p is the total number of observations. Let a set be defined as follow:

$$S^{D_i}=\{\begin{array}{cccccc}\mathrm{a}& \text{compound}& c_j\mid \#({\mathbf{x}}_j)\ge m,x_{j,k}& \text{corresponding}& \text{to}& D_i\end{array}\}$$ (6)

where D_i is the ith data type, m is a threshold of the number of observations of each compound c_j, S^D_i is a collection of D_i retention index values of all compounds.

A small number of retention index observations of a compound are inaccurate for the estimation of regression coefficients. In this study, we set a threshold of m ≥ 10 observations for the linear regression. If the number of common observations in two data type D₁ and D₂ is less than 10, we simply merge the two data types of retention indices into one new set for the compound c_j, the same as in iMatch [12]. That is the linear regression function is y = f(x) = x if # (S^D₁ ∩ S^D₂) < 10. The final set of retention index for a compound c_j is $\stackrel{\sim }{\mathbf{x}}=\left\{x_{j,1}^{D_1},\dots ,x_{j,n_1}^{D_1},x_{j,1}^{D_2},\dots ,x_{j,n_2}^{D_2}\right\}$.

If # (S^D₁ ∩ S^D₂) ≥10, we set the following procedure:

1. Calculate ${\mu }_j^1=E({\mathrm{x}}_j^{D_1})=(1/n_1){\sum }_{i=1}^{n_1}{x}_{j,i}^{D_1}$ and ${\mu }_j^2=E({\mathrm{x}}_j^{D_2})=(1/n_1){\sum }_{i=1}^{n_2}{x}_{j,i}^{D_2}$ for a compound c_j, j = 1, …, n.

2. Generate two vector for linear regression as follows:

   $$X=\left[\begin{array}{c}{\mu }_1^1\\ ⋮\\ {\mu }_j^1\\ ⋮\\ {\mu }_n^1\end{array}\right]\text{and}Y=\left[\begin{array}{c}{\mu }_1^2\\ ⋮\\ {\mu }_j^2\\ ⋮\\ {\mu }_j^2\end{array}\right]$$
3. Estimate linear regression

   $$f(x):=\widehat{y}={\widehat{\beta }}_0+{\widehat{\beta }}_{1}x$$

   For estimating coefficients of the linear regression, ordinary least squares method is used [25].

4. Make a new data set for the compound c_j

   $$\stackrel{\sim }{\mathbf{x}}=\{f(x_{j,1}^{D_1}),\dots ,f(x_{j,n_1}^{D_1}),x_{j,1}^{D_2},\dots ,x_{j,n_2}^{D_2}\}$$

In our previous study [12], the data type effect on the retention index was ignored and all retention index values were simply merged to form a union of these values. In order to evaluate the performance of the linear regression transformation-based union and the simple union approach, the relative change of standard deviation of the retention index after merging is defined as follows:

$$P_c=\frac{\mathit{Std}({\mathbf{x}}_{s,c})-\mathit{Std}({\mathbf{x}}_{t,c})}{\mathit{Std}({\mathbf{x}}_{s,c})},c\in C$$ (7)

where x_s,c, x_t,c are merged observations of a compound c ∈ C corresponding to simple union and linear transformation-based union, respectively. If a compound has a positive value of P_c, then the standard deviation of merging based on linear transformation is smaller than the simple union. Otherwise, simple merge has smaller standard deviation.

2.5. Determining compounds with large retention index variation

Some compounds in the NIST11 library have large retention index variations because the NIST library was compiled from multiple sources with a large diversity of experimental conditions. Several retention index clusters can be even observed for some compounds. The diversity of the experimental conditions including temperature conditions, stationary phase, type of data treatment used, erroneous identification, etc. contributed to the retention index variations. The very large retention index variations greatly affect the accuracy of the iMatch2 software. It is necessary to recognize these compounds and classify them as a special dataset. If any compound is identified as one of these compounds by mass spectrum matching, that compound is considered as having correct retention index value regardless the deviation between the experimental retention index and the reference value. For this case, the mass spectrum matching is the only approach for compound identification, and therefore, it may be necessary for increase the minimum threshold of spectrum similarity score for an accurate compound identification.

We apply standard error instead of standard deviation to assess the deviation of the retention index values for each compound as follows,

$$S=\sqrt{\frac{1}{n}\sum {(x_i-\overline{x})}^2}\text{and}SE=\frac{S}{\sqrt{n}}$$ (8)

where S is standard deviation, SE is standard error, n is the number of retention index values, x_i is the ith retention index value and x̄ is the mean of all retention indices of the compound of interest. One advantage of standard error is that it reflects the number of retention indices for a compound in the NIST11 library. For example, if two compounds have the same standard deviation, but different number of observations in the NIST11 library, the compound with a large number of retention indices has a small standard error. To determine whether a compound having large standard error, we use 90% quantile corresponding to the nine experimental conditions defined by the three column classes and three temperature program types, respectively. In addition, we also consider a compound having large retention index variation, if the standard deviation of its retention index values is more than twice of the average of standard deviation of all compounds under a given experimental condition.

2.6. Calculation of retention index window

To calculate the retention index window for a given compound in each of the nine experimental conditions defined by column class (three category values) and temperature program type (three category values) in the NIST11 library, all compounds are categorized into two groups based on the size of retention index values of the compound in each experimental condition, by setting the threshold of the size of retention index values to 10. The first group contains compounds that each has at least 10 retention index values. The other group contains compounds that each has less than 10 retention index values.

2.6.1. Compound specific probability function

For each compound with at least 10 retention index values under a specific experimental condition, a range of retention index values with less than a probability cutoff (confidence level) α can be defined as follows:

$$Pr(a\le X\le b)=\alpha$$ (9)

where X is a random variable representing retention index and Pr(·) is a probability density function of X. As following notation of Eq. (9), the range of retention index from a to b is the retention index window. Under the assumption that retention index of a corresponding compound is normally distributed with a mean of μ and a standard deviation of σ, the probability of retention index belonging to interval (μ − z_(1−α)/2 · σ, μ + z_{(1− α)/2} · σ) is α. For the interval of each compound, we use maximum likelihood estimator for θ = (μ, σ²) as follows:

$$\widehat{\theta }=(\widehat{\mu },{\widehat{\sigma }}^2)=\left(\frac{1}{n}\sum x_i,\frac{1}{n}\sum {(x_i-\widehat{\mu })}^2\right)$$ (10)

where x_i, i = 1, …, n_c is retention indices of a compound.

An alternative approach is to use a percentile-based retention index window, where the distribution of the retention indices of a compound does not need to follow the normal distribution. The user can choose 90%, 95%, and 99% percentile intervals.

2.6.2. Empirical distribution function

For the group of compounds that each has less than 10 retention index values, an empirical distribution function of absolute retention index deviation is used to determine a variation window for all compounds in the group. The absolute deviation of a compound c_i is defined as follows,

$${\text{AbsDev}}_i=\left\{\mid x_{i,1}-{\overline{\mathbf{x}}}_i\mid ,\dots ,\mid x_{i,n}-{\overline{\mathbf{x}}}_i\mid :{\overline{\mathbf{x}}}_i=\frac{1}{n}\sum x_i\right\}$$ (11)

where x_i,k is the kth retention index value of compound c_i, and x̄_i is the mean of the retention indices of compound c_i. Instead of mean value, we can use median value m(·) as follows,

$${\text{AbsDev}}_i=\left\{\mid x_{i,1}-m({\mathbf{x}}_i)\mid ,\dots ,\mid x_{i,n}-m({\mathbf{x}}_i)\mid :m({\mathbf{x}}_i)=\mathit{median}(x_i)\right\}$$ (12)

Most compounds in the NIST11 library have single retention index value and therefore, result in having a value of zero for the absolute deviation. These compounds are excluded for the calculation of the empirical distribution function.

3. Results and discussion

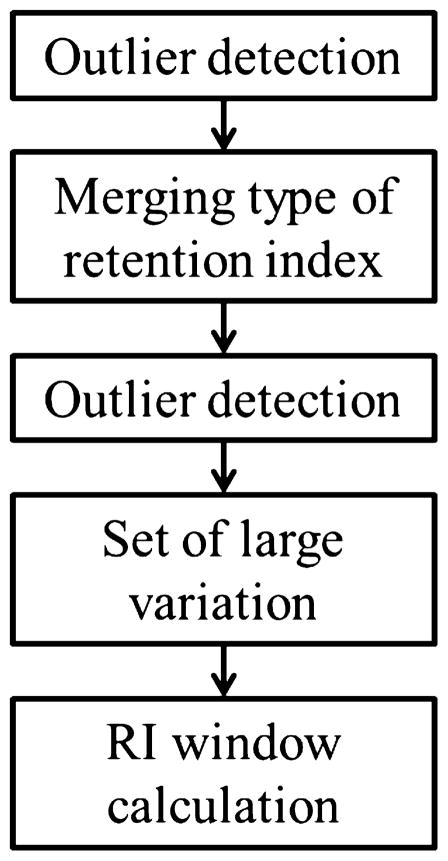
Fig. 1 depicts the workflow of the proposed data procedure for constructing retention index window. We first analyze the retention index data in the NIST11 library to understand the retention index distribution of each compound that has multiple observations, i.e., retention index values. Multiple outlier detection methods are then employed to detect and remove the outliers for each compound. To increase the population of retention index values, a linear regression-based transformation method is developed to calculate the retention index value of a compound under one data type from its value acquired under another data type, provided that all retention index values were acquired using the same column class and temperature program type. After classifying the compounds with extremely large retention index deviations, the remaining compounds are categorized into two groups according to the number of observations for each compound, where the threshold was set as ≥10 observations. The retention index window for the first group is derived for each compound based on the distribution of its retention index values. The retention index window for the second group is derived from an empirical distribution function constructed using the absolute retention index deviation of all compounds in the group.

Fig. 1.

Workflow of processing retention index data in the NIST11 library for development of iMatch2 algorithms.

3.1. Analysis of the NIST11 retention index library

The retention indices in the NIST11 library were extracted from literature reports, and therefore most compounds have multiple retention index values acquired among laboratories for experimental conditions. It is important to understand the distribution of these retention indices in order to use them for compound identification. We applied Kolmogorov–Smirnov test (KS-test) to assess whether the retention indices for a given compound follows normal distribution. Figure S-1 in the Supplementary Material shows that the p-value of KS-test is dependent on the sample size, i.e., the number of retention index values. It is interesting that the retention index distribution does not follow the normal distribution with the increase of sample size. To the compounds with small sample size, such as ≤50 observations, majority of the compounds have normal distributions while a small fraction does not.

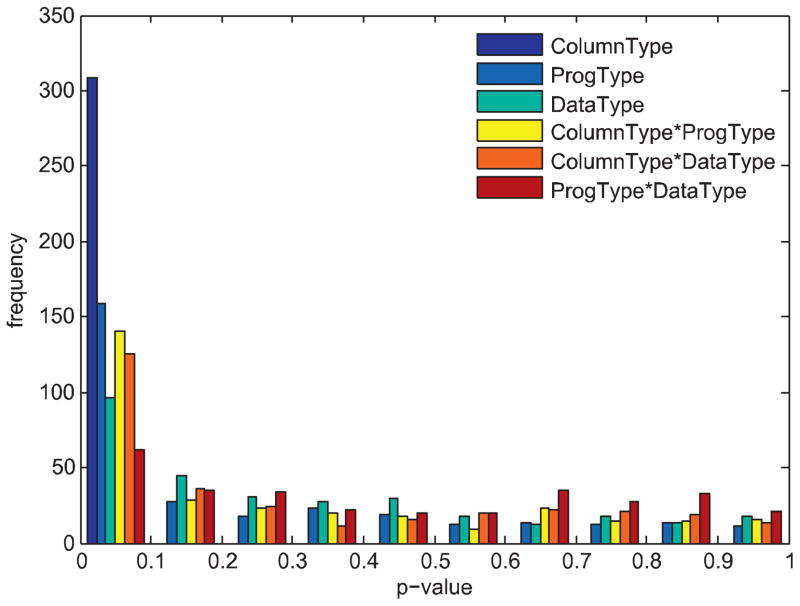
NIST library categorized the experimental conditions into column class, temperature program type, data type, etc. In order to see the statistical effect of these three NIST categorized factors on the retention index, three-way ANOVA tests were performed. Fig. 2 depicts the p-value histogram of the three-way ANOVA corresponding to column class, temperature program type and data type with their pair-wise interaction effects. The top five smallest p-values are column class < temperature program type < interaction between column class and temperature program type < interaction between column class and data type < data type, with median p-values of 9.9 × 10⁻²⁸⁸, 0.094, 0.15, 0.16, and 0.25, respectively. Therefore, the column class is the most important factor which affects the mean difference of the retention index, followed by temperature program type. The data type is the least significant effect on the mean difference of retention index (median p-value = 0.25).

Fig. 2.

Histogram of p-values of three-way ANOVA test in analysis of the compound retention indices corresponding to three experimental factors including column class, temperature program type and data type, and the effect of their pair-wise interactions.

Based on our previous study using the NIST08 library [12], all data under different categories of data type, i.e., Kováts, linear, and normal alkane, can be merged if these data were acquired using the same column class and temperature program type. To make sure that this is still true in the NIST11 library, the Kruskal–Wallis test (KW-test) was also employed to all nine experimental conditions defined by column class and temperature program type. Table S-2 in Supplementary Material lists the test results, indicating that NIST11 library has the same trend as the NIST08 library. The percentage of compounds that have significantly different retention index values among the data type ranges from 12.5% (polar column and isothermal condition) to 34.8% (non-polar and complex condition). In general, complex program type generates more percentage of significant cases than other temperature conditions. The results of both the three-way ANOVA and the KW-test demonstrate that the data type does not cause significant difference in retention index and can be therefore ignored, which agrees with our previous study using NIST08 library [12].

3.2. Construction of retention index window

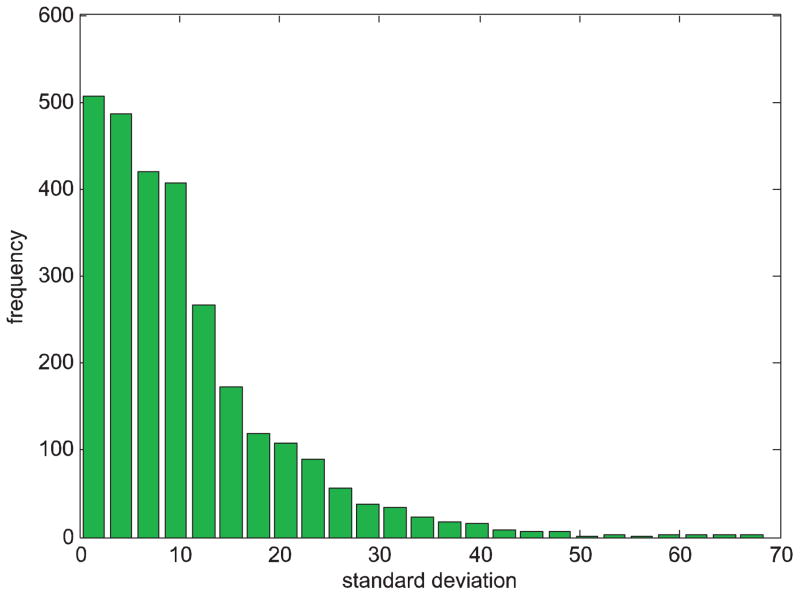
It is believed that the variation of Kováts indices is about 5–10 iu (index unit) on standard non-polar column and 10–25 iu on standard polar phases [26]. Fig. 3 shows that the retention index variations of some compounds in the NIST11 library are very large. To recognize the retention indices with large variations, we first analyzed the performance of six outlier detection methods, including Thompson tau methods with mean and median, Dixon’s test, Grubbs’ test, Tietjen–Moore (TM) test, and generalized extreme studentized deviate (ESD) test, for removal of outlier retention indices.

Fig. 3.

Histogram of standard deviation of retention indices in the NIST11 library. The retention indices of each compound are extracted from the NIST11 library with conditions of capillary semi non-polar column, ramp condition and linear retention index. The standard deviation of retention indices of each compound is calculated if the compound has multiple retention indices. The histogram depicts the distribution of the standard deviation of all compounds.

We employed the standard deviation after removing outliers as an indirect measure to evaluate the performance of the outlier detection methods. A small standard deviation is considered as a better result. In general, the standard deviation decreases with the increase of the number of outliers detected by each method. A strict outlier detection method does not always have a good performance because the true observations with marginal values may be considered as outliers.

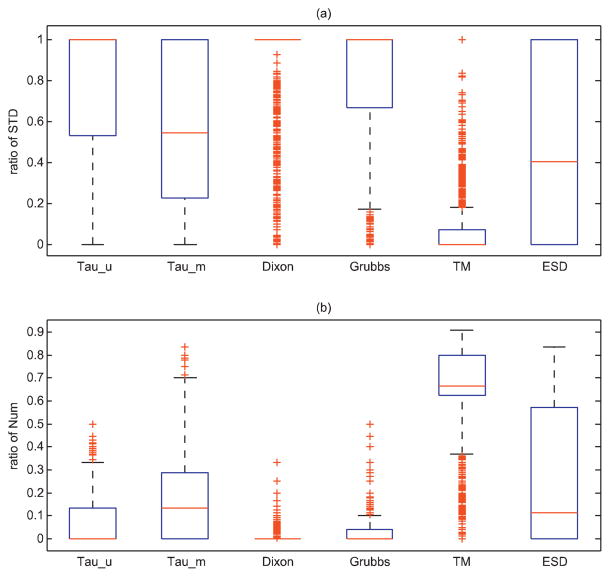
Fig. 4 shows the boxplot of RS_c and RN_c defined in Eqs. (3) and (4) for linear retention index with semi non-polar and ramp program type. The TM test method has the smallest value of standard deviation (average of RS_c = 13.8%) and detected the largest number of outliers (average of RN_c = 0.621). The Dixon’s test has the largest standard deviation (average of RS_c = 83.9%), but detected the smallest number of outliers (average of RN_c = 0.0416). The TM test and ESD test that find multiple outliers out simultaneously are stricter than the methods sequentially removing outliers such as Dixon’s test and Grubbs’ test. The median-based Thompson tau approach is also a stricter outlier detection method than mean-based approach. Based on this analysis, we choose the Grubbs’ test as the method for outlier removing.

Fig. 4.

Performance of six outlier detection methods. (A) Boxplot of the ratio of standard deviation defined in Eq. (3). (B) The relative ratio of the number of outliers defined in Eq. (4). The testing data are compounds with linear retention index acquired under the condition of using capillary semi non-polar and ramp program type.

As for the merging different types of retention index data, the accuracy of the linear regression transformation-based method was compared with the simple union approach implemented in iMatch [12]. Table 2 lists the P_c value defined in Eq. (7) calculated after outlier removal using six different outlier detection methods. The relative change of standard deviation P_c increased by 0.1–8.0% across all experimental conditions if the outlier detection method was Thompson tau methods with mean and median, Dixon’s test, or Grubbs’ test. In case that The TM test or ESD test was used for outlier detection, the P_c values in some of experimental cases does not change and P_c = −0.1% in only one experimental condition of ramp program type and non-polar column. A positive P_c value means that the linear regression transformation-based merging method proposed in this study has a better performance than the simple union approach used in iMatch [12]. Furthermore, the regression coefficients for all experimental conditions are close to one (R² >0.98), indicating that the data points of two different types of retention index are well explained by a linear relationship as shown in Supplementary Table S-3. Overall, the linear regression transformation-based union method performs better than the previously proposed simple union method.

Table 2.

Medians of relative standard deviation difference of retention indices between two merging methods, linear regression transformation-based merging and simple union method. A positive value indicates that standard deviation using the linear regression transformation-based merging is smaller than that of using the simple union method. The τ_u and τ_m refer to Thompson tau based on mean and median, respectively.

		τu (%)	τm (%)	Dixon (%)	Grubbs (%)	TM (%)	ESD (%)
Isothermal	Non-polar	0.4	0.8	0.7	0.7	0.0	1.0
	Semi non-polar	0.7	0.9	0.5	0.6	0.0	0.4
	Polar	8.0	7.8	7.7	7.7	0.0	10.0
Ramp	Non-polar	0.2	0.1	0.2	0.1	0.0	−0.1
	Semi non-polar	0.5	0.4	0.4	0.4	0.2	0.5
	Polar	0.5	0.4	0.4	0.4	0.3	0.3
Complex	Non-polar	0.6	0.5	0.6	0.5	0.0	0.7
	Semi non-polar	0.4	0.5	0.4	0.4	0.1	0.4
	Polar	0.5	0.5	0.4	0.4	0.0	0.2

For determining compounds with large retention index variation, Supplementary Figure S-2 shows that the standard error-based approach is likely to preserve a compound having large number of retention index observations than standard deviation-based approach, if the two compounds have the same standard deviation with different sample size. For this reason, we chose standard error to obtain higher confidence on retention index window. We classified a compound with an extremely large deviation which is determined by standard error greater than a threshold of quantile value of 0.9. Supplementary Excel File 1 lists all of the compounds categorized as compounds with extremely large retention index values in the NIST11 library. A compound whose standard deviation of its retention index values is more than twice of the average of standard deviation of all compounds under a given experimental condition is also included in the Supplementary Excel File 1.

After separating a set of compounds having large deviation, we further divide the remaining compounds into two groups based on the number of retention index values under each experimental condition. Supplementary Figure S-3 shows that the histograms of the standard deviations of retention indices of compounds with at least 10 observations for nine experimental conditions. The smallest and the largest median of standard deviation of retention index are 3.6 and 15.6 iu in the semi non-polar column with isothermal program type and the polar column with ramp conditions, respectively. A small standard deviation can provide a small compound-specific retention index window for the identification of that compound with high confidence. In order to categorize compounds into two groups by a threshold of the number of retention index observations, we considered the trade-off between the accuracy of estimating retention index distribution and the number of compounds in each group. Supplementary Table S-4 shows the number of compounds in the group with large observations is dependent on the value of threshold. We choose 10 observations of retention index as the threshold to group compounds.

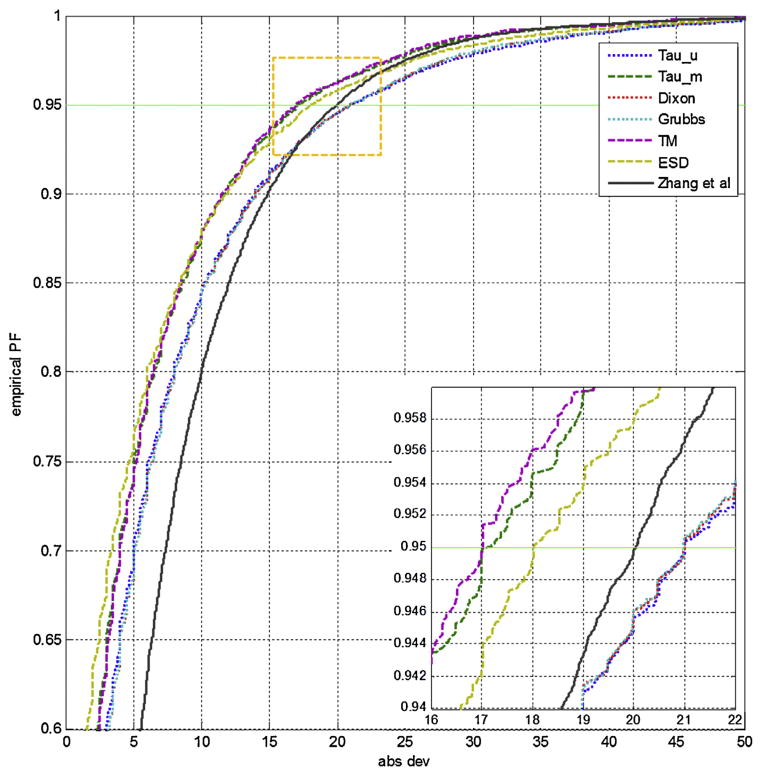
As for the group containing compounds with less than 10 retention index observations, Fig. 5 depicts the empirical distributions of retention index on non-polar column with ramp program type. Here, we compare empirical distributions generated using the six outlier detection methods and the distribution generated using the outlier detection method implemented in iMatch [12]. Overall, all the empirical distributions constructed by different outlier detection methods have the same trend, and the difference among the absolute retention index deviations decreases with the increase of confidence interval. The empirical distributions using the Dixon’s and Grubbs’ tests are more similar to each other, while the distributions of using Thompson tau with median method, the TM test and the ESD test are similar. As shown in Fig. 5, the retention index window, i.e., the absolute retention index deviation, calculated using the iMatch method with the same confidence level is larger than the windows calculated by ESD test, TM test, and Thompson tau with median. However, as for conservative methods such as Dixon’s, Grubbs’ and Thompson tau with mean tests, the retention index window is dependent on the confidence level; when the confidence level is less than 0.95, conservative methods have larger window than window of iMatch. Otherwise, the windows of those conservative methods are smaller than iMatch’s window. Comparing with iMatch, most empirical distribution curves (seven cases out of nine experimental conditions) are shifted left as shown in Supplementary Figures S-4 to S-6. Therefore, the size of retention index windows calculated by iMatch2 is smaller than the windows by iMatch at the same confidence level, except the cases of semi non-polar with both ramp and complex temperature conditions. As a result, we expect that new version of retention index window more accurate.

Fig. 5.

Comparison of seven empirical distributions (ED) corresponding to six outlier detection methods. The retention indices were acquired on standard non-polar column with ramp program type. The right bottom insert is a portion of the ED highlighted in yellow box. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.3. Performance comparison

All instrument data were first processed using the LECO’s instrument control software ChromaTOF. For compound identification, the threshold of spectral similarity was set as ≥600 for an EI mass spectrum to be assigned to a compound. In general, the selection of optimal value as the threshold of spectral similarity score is sample complexity dependent. A large value of similarity threshold induces a high rate of true-positive rate, but also generates a high false-negative rate of identifications [27,28].

3.3.1. Analysis of the mixture of compound standards

A total of 111 chromatographic peaks were identified with a spectral similarity ≥600. Of these 111 peaks, 62 peaks were assigned to 57 compound standards of the MegaMix, and 24 peaks to the n-alkanes. The remaining 25 chromatographic peaks were identified as compounds that do not belong to the mixture. The average of peak area of the detected MegaMix compounds, n-alkanes, and unexpected compounds are 484,002, 491,306, and 230,967, respectively, indicating that the chromatographic peaks of the unexpected compounds have small peak area.

Table 3 summarizes the analysis results of the mixture by iMatch2 and iMatch, corresponding to four confidence intervals of 0.999, 0.995, 0.990, and 0.950. At the confidence level of 0.990, iMatch2 preserved all the MegaMix compounds identified by mass spectrum matching, while iMatch discarded three of them, including “Phenol, 2-methyl, 4,6-dinitro-”, “Benzene, 1-bromo-4-phenoxy-”, and “Hexanedioic acid, bis(2-ethylhexyl) ester”. The absolute retention index difference between the experimental retention indices and the corresponding iMatch calculated retention indices of these three compounds from the NIST08 library are 33.8, 47.5 and 34.1 iu, respectively. Since three absolute retention index differences are larger than the retention index window ΔI = 33.1 iu calculated by iMatch, the identification of these compounds were filtered out as false identifications. The retention index differences of these three peaks calculated by iMatch2 using the NIST11 library are 2.1, 35.5 and 34.1 iu, respectively. Compared to the corresponding value calculated using iMatch, the retention index calculated by iMatch2 has smaller difference from experimental retention indices. A small value of retention index difference calculated by iMatch2 indicates the improvement of the quality of retention index data in the NIST11 library and the improvement of the data processing methods in iMatch2. Table S-5 in Supplementary Material shows compounds with different results analyzed by iMatch and iMatch2.

Table 3.

Analysis results of the mixture of compound standards using iMatch and iMatch2 at four confidence intervals.

		# of compounds (peaks)
		0.999		0.995		0.990		0.950
		iMatch	iMatch2	iMatch	iMatch2	iMatch	iMatch2	iMatch	iMatch2
Retention index window (iu)		59.1	56. 1	39.6	46.9	33.1	42.1	19.1	25.9
Preserved	MegaMix	57	57	56	57	54	57	51	54
	n-Alkane	24	24	24	24	24	24	24	24
	Unexpected	3	3	3	3	3	3	3	3
Discarded	MegaMix			1		3		6	2
	n-Alkane
	Unexpected	3	3	3	3	3	3	3	3

3.3.2. Analysis of the mouse liver extract

A total of 406 compounds corresponding to 746 chromatographic peaks were identified from the liver sample. By setting the confidence level ≤0.990, 361 and 357 compounds corresponding to 636 and 527 chromatographic peaks were respectively preserved by iMatch2 and iMatch. A total of 18 compounds have difference analysis results by using iMatch2 and iMatch, of which two compounds were derivatized while the remaining 16 compounds were not derivatized. iMatch2 preserved 16 of the 18 compounds while iMatch preserved 8 compounds. Compounds “Acetophenone” and “Heptane, 2,2,4,6,6-pentamethyl-” are removed by iMatch2. Each of these two compounds has a large number of retention index values in the NIST11 library. Therefore the compound specific retention index window was individually calculated at confidence level of 0.990 from the NIST11 library, where the individual retention index windows for these two compounds are 14.0 and 17.7 iu, respectively. Although the difference between experimental retention index and estimated retention index by iMatch2 are relatively smaller (24.5 and 22.4 iu, respectively) than the retention index window calculated by the empirical distribution function of Eq. (12), those compounds’ peaks are filtered out as false identifications by iMatch2, due to larger variations than their individual retention index windows (14.0 and 17.7 iu).

It is very common that multiple chromatographic peaks are assigned to the same compound due to the spectral similarity and/or variations introduced during spectrum deconvolution. Many factors contribute to this, including that the observed compound is absent from the library, library entry is inaccurate, low spectrum similarity (≥600) induces a certain rate of inaccurate identifications, etc. For example, a total of 20 chromatographic peaks were assigned to compound “Phosphoric acid, tris(tert-butyldimethylsilyl) ester” by mass spectrum matching. iMatch2 removed 15 of the 20 assignments as false identifications due to a large retention index difference, while iMatch kept all peaks because this compound was categorized as a compound with large standard deviation in its retention index. In another case, iMatch2 categorized compound “Butanedioic acid, 2-[(tert-butyldimethylsilyl)oxy]-, bis(tert-butyldimethylsilyl) ester” as a compound with large standard deviation in its retention index. Two chromatographic peaks assigned to this compound were both preserved after retention index matching, but one assignment was filtered out by iMatch. The reason is that retention indices of these compounds in the NIST11 library are updated. Supplementary Table S-6 shows an example of database change as updating compound retention indices in the NIST11 library compared to the NIST08 library. Because of this update (adding two new retention indices with a large standard deviation of 41.01 iu), this compound is now classified by iMatch2 as a compound with large standard deviation under semi non-polar and ramp temperature condition.

We further compared the performance of iMatch2 with literature-reported results [19] for analysis of frequently reported compounds in plant essential oils, by considering standard deviation of retention indices for the same compound that has more than 10 RIs under each column class and temperature program condition, respectively. It should be noted that we separately treated the nine groups of retention index corresponding to experimental conditions defined by column class and temperature program condition, while Babushok et al. [19] used three groups determined by column class. The Supplementary Table S-7 summarizes the number of compounds with standard deviation calculated from our method smaller than that from the Babushok approach [19], as well as the number of opposite case. In ramp and complex temperature conditions, more compounds have smaller standard deviation from our approach than the Babushok approach. The standard deviation of 315 compounds calculated using iMatch2 is smaller than that of Babushok approach, while the standard deviation of 105 compounds calculated using iMatch2 is larger than that of the Babushok approach. Supplementary Figure S-7 depicts that mean difference between the two approaches according to column class. Majority of retention indices calculated from these two approaches have a retention index difference of ±5 iu, while a relatively large retention index difference present in the polar column.

The previous literatures [9–11] suggested approaches help compound identification using retention index information. Also the AMDIS software (NIST) provides a tool of retention index filtering in conjunction with mass spectrum matching for compound identification. The main advantage of our approach is to automatically determine the retention index window or confidence interval with pre-determined confidence level based on retention index distributions, while users have to choose (most likely based on experience) a retention index window size for both the Smith and AMDIS approaches [1,8]. Like the Babushok approach [11], our approach is built based on the largest and latest version of retention index database. However, iMatch2 constructs the retention index window respectively from the distribution of retention index deviation and linear regression-based merging retention index data types, resulting in increased statistical power and decreased standard deviation.

4. Conclusions

We developed a suite of methods to improve the accuracy of compound identification using retention indices in the NIST11 library. The newly developed methods have been implemented as a software package iMatch2 using MATLAB. The three-way ANOVA test demonstrates that column class remains as the most dominant factor to retention index followed by temperature program type. The results of both the three-way ANOVA and the KW-test show that the data type does not cause significant difference in retention index and therefore can be merged, which agrees with our previous study using NIST08 library. In the merging process, a linear regression transformation-based approach is proposed, resulting in reduction of standard deviation of retention index up to 8%. As for outlier detection methods, TM test and ESD test are the strictest methods, while methods iteratively removing outliers such as Dixon’s test, Thompson tau approach, and Grubbs’ test are conservative. Interestingly, in the Thompson tau approach, median-based method is stricter than when removing outliers based on mean. To improve accuracy of retention index window, the concept of compound specific retention window was introduced to compounds with large number of observations greater than a threshold. On the contrary, the retention index window is calculated from the curves of empirical distributions for the compounds having a small number of observations. Analysis of the experimental data of a mixture of standard compounds and the metabolites extract form mouse liver show the significant improvement of NIST11 library and the new data analysis methods.

Appendix A. Supplementary data

Supplementary material related to this article can be found, in the online version, at http://dx.doi.org/10.1016/j.chroma.2014.02.049.