Modeling Confidence Judgments, Response Times, and Multiple Choices in Decision Making: Recognition Memory and Motion Discrimination

Abstract

Confidence in judgments is a fundamental aspect of decision making, and tasks that collect confidence judgments are an instantiation of multiple-choice decision making. We present a model for confidence judgments in recognition memory tasks that uses a multiple-choice diffusion decision process with separate accumulators of evidence for the different confidence choices. The accumulator that first reaches its decision boundary determines which choice is made. Five algorithms for accumulating evidence were compared, and one of them produced proportions of responses for each of the choices and full response time distributions for each choice that closely matched empirical data. With this algorithm, an increase in the evidence in one accumulator is accompanied by a decrease in the others so that the total amount of evidence in the system is constant. Application of the model to the data from an earlier experiment (Ratcliff, McKoon, & Tindall, 1994) uncovered a relationship between the shapes of z-transformed receiver operating characteristics and the behavior of response time distributions. Both are explained in the model by the behavior of the decision boundaries. For generality, we also applied the decision model to a 3-choice motion discrimination task and found it accounted for data better than a competing class of models. The confidence model presents a coherent account of confidence judgments and response time that cannot be explained with currently popular signal detection theory analyses or dual-process models of recognition.

Understanding human decision making is integral to progress in many fields, notably psychology, neuroscience, and neuroeconomics. Major advances in understanding how simple decisions are made have been achieved when theoretical approaches deal jointly with choice proportions and response times (RTs). When both dependent variables are considered, some classes of models are falsified and others are left with no direct empirical support.

Up to now, decision models have most often focused on tasks with only two alternatives (Busemeyer & Townsend, 1992; Laming, 1968; Link, 1975; Ratcliff, 1978; Ratcliff & McKoon, 2008; Ratcliff, Thapar, & McKoon, 2010; Ratcliff, Van Zandt, & McKoon, 1999; Usher & McClelland, 2001; Wagenmakers, 2009). However, there is growing interest in tasks with multiple alternatives (Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Leite & Ratcliff, 2010; McMillen & Holmes, 2006; Milosavljevic, Malmaud, Huth, Koch, & Rangel, 2010; Niwa & Ditterich, 2008; Roe, Busemeyer, & Townsend, 2001; Usher & McClelland, 2004; Usher, Olami, & Mc-Clelland, 2002), and a number of algorithms have been proposed to describe how such decisions are made. The most promoted are based on random walk or diffusion processes that gradually accumulate noisy evidence toward decision boundaries. Each of the possible choices is represented by its own accumulator and has its own boundary, and a choice is made when the amount of evidence in one of the accumulators reaches its boundary. The algorithms differ in whether evidence for one alternative is evidence against the others, whether there is inhibition among accumulators, whether there is decay in the amount of evidence in the accumulators, whether the stopping rule is absolute or relative, and whether the evidence in an accumulator can fall below zero.

Confidence judgments provide a compelling application for multiple-choice decision algorithms because they require one of several choices, where the choices range from a high level of confidence to a low level. The confidence with which decisions are made and the time taken to make them are fundamental components of decision making. Confidence has been examined with brain-imaging techniques (e.g., Curran, 2004; Fleming, Weil, Nagy, Dolan, & Rees, 2010; Rolls, Grabenhorst, & Deco, 2010), and it has become a focus in the neurophysiological domain where analogs of confidence have been investigated in animal studies (Kepecs, Uchida, Zariwala, & Mainen, 2008; Kiani & Shadlen, 2009).

Confidence judgments have also played a prominent role in claims about memory. There has been considerable debate about whether recognizing a previously-presented item involves one cognitive process or two separate ones, and researchers have attempted to resolve this debate with signal detection theory (SDT) analyses of confidence-judgment data. However, as we show below, SDT analyses are inadequate and misleading because only the proportions of choices for each level of confidence are considered, not their RTs. For this reason, SDT can no longer be used to model how information is represented in memory for recognition tasks or how information is retrieved. Instead, a model must incorporate both the proportions of responses for each of the different levels of confidence and their RTs, and show how they arise from a common underlying decision process. One consequence of joint consideration of proportions and RTs is that findings that have been taken to support dual processes can be explained by a single process.

In a study prior to this one, Ratcliff and Starns (2009) developed a model designed to explain how information in memory is translated to confidence choices. In their paradigm, subjects decided whether test words had or had not appeared in a previously studied list and pressed one of six response keys corresponding to high-confidence “old,” medium-confidence “old,” low-confidence “old,” low-confidence “new,” medium-confidence “new,” and high-confidence “new”. In the model (RTCON for Response-Time Confidence), there was an accumulator for each of the choices, with a diffusion process for each accumulator. The accumulator that reached its boundary first determined which choice was made and the time taken to make that choice. The model accounted well for the proportions of responses for each choice and the RTs of the responses.

However, we have since examined data sets that show qualitatively different patterns of results. Subjects in Ratcliff and Starns’s (2009) experiments were encouraged to make fast decisions and they were trained to press all of the confidence keys quickly. The resulting RT distributions were flat across confidence categories in that the fastest RTs (the leading edges of the RT distributions) were about the same across the six levels of confidence. In this article, we model data from Experiment 5 in Ratcliff, McKoon, and Tindall (1994). These subjects experienced less severe time pressure than those in Ratcliff and Starns, and they showed a large range of differences among individuals in the patterns of choice proportions and RT distributions. Some subjects’ responses were faster for lower-confidence choices than higher-confidence choices and some slower. In both cases, the differences primarily took the form of shifts in the RT distributions, with increased spread, but with no discernible changes in shape. The leading-edges (i.e., the fastest responses) moved by as much as about 500 ms for some subjects. These shifts in the RT distributions as a function of confidence cannot be accommodated by RTCON and several other decision models (as described later). Shifts like these were also found in the three-choice motion-discrimination paradigm used for the second experiment described in this article.

RTCON also cannot accommodate a second feature of Ratcliff et al.’s (1994) data (a feature presented below for the first time): The shapes of z-ROC functions matched the profiles of the RT distributions. z-ROC functions are generated from confidence judgments. Hit and false alarm rates are computed for the highest confidence category, then computed for the two highest categories combined, and so on, and z-ROC functions plot the z-transforms of these hit rates and false alarm rates. In Ratcliff et al.’s study, U-shaped z-ROC functions were obtained when lower-confidence judgments were faster than higher-confidence judgments, and inverted U-shaped z-ROC functions were obtained when higher-confidence responses were faster than lower-confidence responses (this held when the number of observations in the confidence categories were not less than about 2%—see the Appendix). Like the shifts in RT distributions, RTCON cannot accommodate these regularities in the relation between RT distributions and z-ROC functions.

To model the data from Ratcliff et al. (1994), we developed a new model (we call it RTCON2) that kept three key assumptions from RTCON. First, the information from memory that is available to the decision process—that is, the strength of the match between a test item and a representation in memory—is not a single value, but rather a distribution across the strength dimension. For example, a well-remembered item might have maximal strength for a “high-confidence old” response and also some degree of strength for a “medium-confidence old” response. Second, the strength dimension is divided into regions, with each region corresponding to one of the possible confidence choices. For each choice, the area of the distribution that falls in its region determines the rate at which evidence is accumulated in its accumulator. Third, each accumulator has its own boundary, so more evidence can be required for some accumulators to reach their boundaries than others.

For the decision algorithm from RTCON, it was assumed that evidence is accumulated independently in each accumulator, that the amount of evidence in an accumulator decays with time, and that the amount of evidence in an accumulator cannot fall below zero. For RTCON2, it is assumed that if the amount of evidence in one accumulator is incremented, then the others are decremented such that the total size of the decrements equals the increment. It is also assumed that there is no decay with time and that the amount of evidence can fall below zero. We combine these assumptions into the “constant summed evidence” algorithm. As we show below, RTCON2 accommodates Ratcliff et al.’s (1994) data: the shapes of the RT distributions, the large shifts in leading edges across confidence categories, and the relationship between RTs and the shapes of z-ROC functions constructed from the proportions of responses in each category. We also tested three other decision algorithms, but none were successful.

The assumptions that memory strength is distributed and that areas under the distribution determine rates of accumulation of evidence are not common, but precedents do exist. In psychology, these assumptions have been used in explaining data from letter-matching and word-matching paradigms (e.g., does the letter string ABCDE match the string ABDCE?; Gomez, Ratcliff, & Perea, 2008; Ratcliff, 1981), and they have been used in a model of attention (Logan, 1996). In neuroscience, a neuron that responds maximally to one stimulus also responds, to a lesser extent, to other similar stimuli. For example, the response of a neural population to a specific motion direction has a peak for neurons tuned to that direction and falls off for nearby neurons that are tuned to slightly different directions (Beck et al., 2008; Cowell, Bussey, & Saksida, 2006; Jazayeri & Movshon, 2006). The summed activity of the neural population would correspond to the area under the strength distribution for confidence judgments.

Signal Detection Theory and Dual-Process Accounts of Memory

RTCON2 speaks directly to the claims that have been made about whether recognition of previously-studied items involves one cognitive process or two separate ones. For dual-process theories, the processes are often labeled “familiarity” and “recollection” (e.g., Yonelinas, 1994, 1997; see also Squire, Wixted, & Clark, 2007; Wixted, 2007). It has been claimed that these two processes occur in different areas of the brain (Chua, Schacter, Rand-Giovannetti, & Sperling, 2006; Eichenbaum, Yonelinas, & Ranganath, 2007; Henson, Rugg, Shallice, & Dolan, 2000; Kim & Cabeza, 2007; Kirwan, Wixted, & Squire, 2008; Moritz, Glascher, Sommer, Buchel, & Braus, 2006; Rissman, Greely, & Wagner, 2010; and reviews in Cabeza, Ciaramelli, Olson, & Moscovitch, 2008), that they occur at different points in the time course of processing (Curran, 2004; Rugg & Curran, 2007), and that they can be separately affected by memory disorders (e.g., Yonelinas, 2002).

Typically, SDT analyses of confidence-judgment data have been used to support single-process or dual-process theories. However, when SDT is applied to a single condition in an experiment, it cannot be falsified because it transforms two numbers, the hit rate and the false alarm rate, into two other numbers, d′ and the criterion. It also cannot be falsified by the shapes of z-ROC functions generated from confidence judgments. The standard assumption is that distributions of memory strength are normal, and so z-ROC functions must be linear (e.g., Macmillan & Creelman, 1991). However, if the distributions are not normal, z-ROC functions can be non-linear. Moreover, distributions other than normal can produce linear z-ROC functions (Banks, 1970; Lockhart & Murdock, 1970). In addition to problems with falsifiability, SDT does not explain how decisions unfold over time and so cannot explain RTs. We show that jointly modeling proportions and RTs explains data previously taken to support dual processes with a model using a single decision process. Consideration of RTs also addresses the question of why the z-ROC functions have different shapes for different subjects (Malmberg & Xu, 2006; Ratcliff et al., 1994). These limitations, it should be noted, do not detract from SDT’s practical utility in separating discriminability from bias.

As mentioned above, in examining the data from Ratcliff et al. (1994), we found a systematic relationship between the behavior of RT distributions and the shapes of z-ROC functions constructed from the proportions of choices for each of the confidence levels. To anticipate the analyses below, when responses are faster for lower-confidence choices, z-ROC functions are slightly U-shaped, whereas when responses are faster for higher-confidence choices, z-ROC functions are either roughly linear or inverted U-shaped. Neither single- nor dual-process signal detection models can explain this relationship; it can only be explained by a more complete approach that accommodates the time course of decision processes.

The most important difference between SDT analyses and the RTCON models is that in the latter, the evidence from memory in favor of a choice does not map directly to responses. Instead, decision processes transform the strength of the match between a test item and memory to a confidence judgment. Whether a particular choice is made depends not only on the amount of evidence in favor of it but also the criteria that separate the relevant dimension into regions and the boundaries on the accumulators. Depending on the confidence criteria, the decision boundaries, and combinations of them, the confidence choice for a particular test item and its RT do not necessarily reflect its mean value of strength. For example, a large value of mean strength could be associated with a high boundary, which would lead to fewer high-confidence responses and longer RTs for them.

Empirical Data

In the sections below, we describe the decision algorithms we considered and the RTCON2 model, and apply the model to the data from Ratcliff et al. (1994). We then test the generality of the successful decision algorithm, the constant summed evidence algorithm, in a new experiment.

For Ratcliff et al.’s (1994) experiment, the choices were levels of confidence about memory. For the new experiment, the task was a three-choice motion discrimination task (Niwa & Ditterich, 2008). On each trial, there was a display of dots, with some of the dots moving in the same direction as each other and others moving randomly. Subjects were asked to choose whether the dots moving together were moving downward to the left, downward to the right, or straight up vertically. The probabilities of the three directions were manipulated such that one direction occurred with a higher probability than the other two. These data provided convergent evidence for the constant summed evidence algorithm. Just as this algorithm provided the best account of leading-edge shifts across confidence levels for Ratcliff et al.’s (1994) data, it also provided the best account of leading-edge shifts for the low-probability directions in the motion discrimination task.

Decision-Making Algorithms

We tested five decision algorithms, each specifying a different way in which processing might proceed. It has been argued that it is difficult or even impossible to discriminate among such algorithms on the basis of behavioral data (Ditterich, 2010), but here we show that behavioral data can, in fact, discriminate among some classes of algorithms.

The successful algorithm was the constant summed evidence algorithm. On each time step Δt during the decision process, one of the accumulators is selected at random. This accumulator gets an increment to its accumulated evidence (Δx) that is determined by the amount of evidence in its region of the strength distribution (“drift rate,” v) plus a noise term to represent variability in processing. In our implementation of this algorithm, the non-chosen accumulators (N − 1) are each decremented such that the sum of the decrements is equal to the increment in the chosen accumulator. The expression for the increment in the chosen accumulator is

$$\mathrm{\Delta }{x}_i={av}_i\mathrm{\Delta }t+\mathrm{\sigma }{\mathrm{\eta }}_i\sqrt{\mathrm{\Delta }t}$$ (1a)

and the expression for the decrement in each of the other accumulators is

$$\begin{array}{l}\mathrm{\Delta }{x}_j=-\left(\frac{1}{N-1}\right)\left({av}_i\mathrm{\Delta }t+\mathrm{\sigma }{\mathrm{\eta }}_i\sqrt{\mathrm{\Delta }t}\right)\\ =-\left(\frac{1}{N-1}\right)\mathrm{\Delta }{x}_i\mathit{for}j\ne i\end{array}$$ (1b)

where a scales the area under the strength distribution to drift rate, σ is the standard deviation (SD) in within-trial variability in the accumulation process (the square root of the diffusion coefficient), and η is a normally-distributed random variable with mean zero and SD 1. Note that, because of noise, on any time step, evidence can take a negative value; if this occurs, the evidence in the chosen accumulator decreases rather than increases and the sum of the evidence in the other accumulators increases. Note also that, again because of noise, evidence in some accumulators can fall below zero. However, because this is a linear algorithm, a constant could be added to the amounts of evidence and decision boundaries with no change in any predictions.

The constant summed evidence algorithm is a variant on a scheme proposed by Audley and Pike (1965) and has more recently been termed feedforward inhibition by Shadlen and Newsome (2001; see also Bogacz et al., 2006; Ditterich, 2006; Niwa & Ditterich, 2008). A related input normalization scheme has been used in decision field theory by Roe et al. (2001). The algorithm can also be viewed as a generalization of the diffusion model for two-choice decisions (Ratcliff, 1978; Ratcliff & McKoon, 2008; Shadlen & Newsome, 2001).

One of the other algorithms we examined was the linear independent accumulators algorithm. It is the same as the constant summed evidence algorithm in that evidence is accumulated independently in each accumulator, but there is no decrement to the other accumulators. That is, on each time step the selected accumulator moves up without the other accumulators moving down, so the summed evidence across all accumulators does not remain at zero.

The other three algorithms have been termed “neurally plausible,” because at each time step, the evidence decays by some fractional amount, and the amount of evidence in an accumulator cannot fall below zero (i.e., “neural firing rates” cannot be negative). One was the leaky competing accumulator algorithm (LCA; Usher & McClelland, 2001). On each time step, one accumulator is randomly chosen and the amount of evidence added to it is the increment specified by Equation 2. There is decay of evidence in the accumulator that depends on the amount of evidence already in it (−kx), and there is inhibition from the other accumulators that is a function of the summed evidence in them (−βΣx):

$$\mathrm{\Delta }{x}_i=a\left(v_i-{kx}_i-\sum _{j\ne i}\mathrm{\beta }{x}_j\right)\mathrm{\Delta }t+\mathrm{\sigma }{\mathrm{\eta }}_i\sqrt{\mathrm{\Delta }t}$$ (2)

Another was the independent accumulators with decay algorithm used by Ratcliff and Starns (2009, RTCON; see also Bogacz & Gurney, 2007; Ratcliff et al., 2007). The equation for updates is the same as for the LCA algorithm except that the inhibition term (−βΣx) from Equation 2 is removed. The third algorithm was the same as the independent accumulators with decay algorithm but with a different decision rule, the “max. versus next” rule (Ditterich, 2010; McMillen & Holmes, 2006; Ratcliff & McKoon, 1997). This algorithm has been argued to be optimal or approximately optimal for multiple-choice decisions (Draglia, Tartakovsky, & Veeravalli, 1999). In our version of this algorithm, the accumulator with the highest amount of evidence wins when the evidence in it exceeds the next highest amount of evidence by a criterial amount.

The RTCON2 Model

The assumptions for RTCON2 are that memory strength is distributed across a dimension of strength, that the strength dimension is divided by criteria into confidence categories, that the areas between and outside the criteria determine drift rates, and that each confidence category has its own decision boundary. Choices and RTs are determined by the constant summed evidence algorithm.

The parameters of the model can be illustrated with the design of the experiment from Ratcliff et al. (1994). There were six conditions in the experiment that varied in difficulty, and subjects were asked to choose among six confidence categories. The mean of the strength distribution is different for each of the conditions, with one of them fixed at zero, giving five parameters. Across trials, the means are drawn from normal distributions with a different SD for each condition (analogous to variability in memory strength in SDT), giving six parameters. There are five confidence criteria to divide the strength continuum into six regions for each response on the confidence scale, and this gives another five parameters. These 16 parameters make up the parameters that describe memory strength and how it is divided across confidence categories.

There are 11 parameters for the decision process. One is a scaling parameter that converts area in the strength distribution to drift rate. Another is the amount of time taken up by processes other than the decision process (e.g., stimulus encoding, memory access, response execution), which has mean RT of T_er ms. A third is the variability in nondecision time across trials, assumed to be a uniform distribution with range s_t ms. There are six decision boundaries (b), one for each of the accumulators (one for each of the six confidence choices). The boundaries vary across trials with a uniform distribution with range s_b, the same s_b for all the boundaries. Finally, the within-trial variability in the accumulation process is σ, which is the square root of the diffusion coefficient.

The assumption that the strength of a test item is distributed across the strength dimension helps constrain the number of model parameters. It also explains why one confidence category can have a relatively higher proportion of responses than another across all the conditions of an experiment; if two of the criteria were widely separated, the areas for all conditions would be large, and hence all the drift rates would be large, compared with the case in which the criteria had a small separation. The confidence criteria are fixed across all the experimental conditions (because conditions are randomly intermixed within a test list), so changes in the drift rates for the six confidence levels are determined only by differences in the mean and SD of memory evidence distributions. Thus, given the confidence criteria, two parameters for each condition give the six areas for the six confidence categories. Thus, for six conditions of the experiment, 12 memory parameters and five confidence criteria are needed instead of 36 independent parameters.

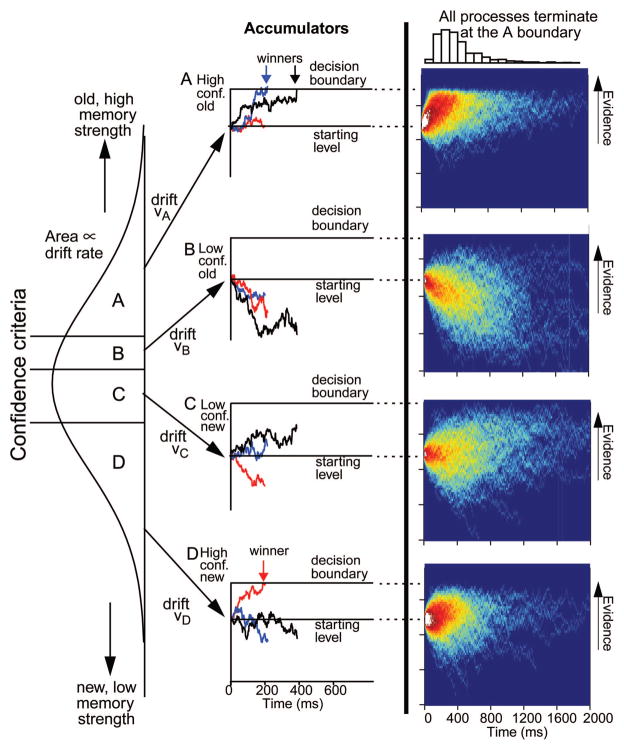
Figure 1 illustrates the model with four confidence categories—A, B, C, and D—and their accumulators (the four panels under “Accumulators”). Accumulation paths for three example trials are shown in blue, black, and red. The noise in the accumulation processes means that the times at which winning accumulators reach their boundaries vary and that the category with the largest drift rate may not be the winner. For the blue processes, Category A wins fairly quickly and for the black processes it wins more slowly. The differences in winning times lead to a right-skewed RT distribution. For the red processes, Category D is the winner. The patterns of subjects’ decision boundaries can vary substantially. Some subjects might be biased toward a high-confidence “old” response (Category A in the example) and so set the “A” decision boundary lower than the boundaries for the other categories, some might be biased against high-confidence responses, and so on.

Figure 1.

The left-hand vertical distribution represents memory strength or perceptual strength (depending on the task). Three confidence criteria divide the distribution into four areas—A, B, C, and D—and the sizes of the areas determine the drift rates for the four accumulators, as shown by the arrows. The middle column shows paths of evidence accumulation in the accumulators, the red paths for one test item, the black for another, and the blue for another. The right hand column shows heat maps for 2,000 simulated decision processes for the constant summed evidence model when the top process wins. The histogram on the top plot shows the distribution of finishing times. The top and bottom processes have low decision boundaries (b₁ andb₂ in Table 1), and the middle two plots have higher criteria (b₃ and b₆ in Table 1). The mean of the memory evidence distribution was 0.0, and the other model parameters were those from the averages of the fits shown in Table 1. conf. = confidence.

The right-hand column of Figure 1 shows four plots of evidence accumulation processes, all terminating at the A boundary, each with 2,000 simulated trials, with red for a high density of paths and dark blue for a low density. For the A and D processes, the decision boundary is set relatively low, and for the B and C processes, it is set higher. Because it takes more time to reach the boundaries for the B and C processes, the paths are more diffuse than for the A process. For the B process, with a small value of drift rate, the paths tend to decline as the paths for the winning accumulator (A) move to their boundary. For the C process, with a moderate value of drift rate, the paths tend to remain in the middle of the range. For all four plots, the density decreases with time as processes terminate (as A processes hit the A boundary).

Predictions from RTCON2

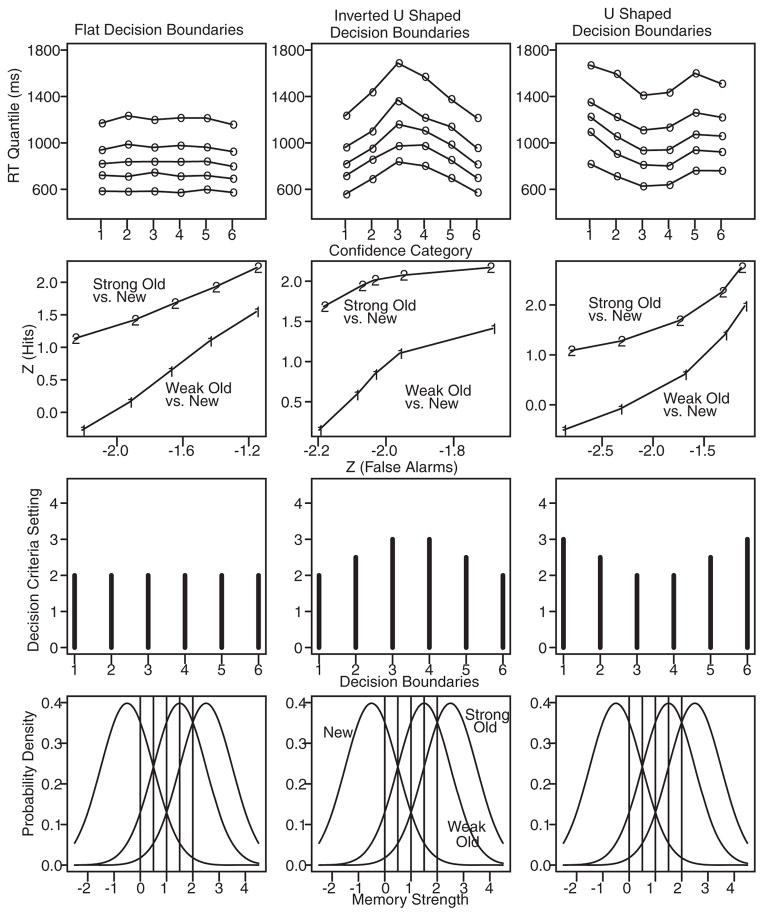
We simulated data for an experiment with six confidence categories and three conditions that varied in the means of their strength distributions (e.g., new items, old items with short study times, and old items with long study times). We repeated the simulations for each of three settings of the boundaries on the accumulators: In one case, the boundaries were the same for all the accumulators; in the second case, they were inverted U-shaped with higher boundaries for the middle accumulators (those for low-confidence responses); and in the third case, they were U-shaped with higher boundaries for the right- and left-most accumulators. Figure 2, third row, shows these three settings. The strengths of the distributions from memory and the placements of the confidence criteria are shown in the bottom panel, the same strengths and criteria for all three. Given the strength distributions, the confidence criteria, and the decision boundaries, the proportions of responses in each confidence category and their RTs were generated. (The other parameters of the model were set to the mean values in the fits to Experiment 1 below.).

Figure 2.

Data were simulated for three conditions of a recognition memory experiment: new items (mean strength = −0.5), weak old items (mean strength = 1.5), and strong old items (mean strength = 2.5). The bottom row of the figure shows their distributions of strength (for these simulations, across-trial variability in memory strength was small at .05 for all items) and five confidence criteria. The second-from-bottom row shows the decision criteria that were used to simulate data: equal criteria for each confidence category, inverted U-shaped, and U-shaped. The top row shows the .1, .3, .5, .7, and .9 quantile response times (RTs) for one condition, strong old items. The second-from-top row shows z-ROC functions derived from the weak old and new item conditions and from the strong old and new item conditions. Nondecision time was 323 ms, within-trial variability was .09, the scaling parameter a was .035, across-trial variability in boundaries was 1.13, and the range in nondecision time was 108 ms.

The top panel of Figure 2 shows the distributions of RTs produced by the simulations for new items. The distributions for the other conditions were similar. For each of the confidence categories, the figure shows the .1, .3, .5, .7, and .9 quantiles of its RT distribution. (The .7 quantile, e.g., is the time by which .7 of the trials have terminated.) The important result is that the relative positions of the RT quantiles follow the decision boundaries: flat when the boundaries are flat (left-most panel), inverted U-shaped when the boundaries are inverted U-shaped (middle panel), and U-shaped when the boundaries are U-shaped (right-most panel).

With inverted U-shaped or U-shaped boundaries, the whole RT distribution shifts from choices that are made with higher probabilities to choices that are made with lower probabilities. RTCON2 shows this behavior because more evidence is needed for a decision when a boundary is relatively high and so the probability of it winning is lower. Of the algorithms we tested, only the constant summed evidence algorithm could produce shifts like these.

The simulations show that the shapes of z-ROC functions are not diagnostic of single- versus dual-process models. To demonstrate this, the proportions of responses produced by the simulations for each confidence category were used to generate the z-ROC functions shown in the second row of Figure 2. The functions follow the decision boundaries: linear when the boundaries are the same for each category and inverted U-shaped and U-shaped when the boundaries are inverted U-shaped and U-shaped, respectively. Thus, the U-shaped z-ROC function that has been said to be diagnostic for dual-process models can be produced by a single process (other z-ROC shapes are possible; see the other experiments in Ratcliff et al., 1994).

For the results shown in Figure 2, the proportions of responses in each confidence category were not close to zero. When the proportion of responses in one or more categories is close to zero (e.g., less than 1% of the total number of observations for all conditions), the patterns of the z-ROC function shapes may not follow the decision boundaries (this is true for the data analyzed below for Subjects 1 and 11). This issue is examined with additional simulations in the Appendix.

The conclusion to be drawn from the simulations is that performance—the proportions of responses in the confidence categories, the z-ROC functions generated from them, and the distributions of RTs—comes from memory strength and decision processes jointly, not memory strength alone. The model explains the empirical relationship between z-ROC shapes and the behaviors of RT distributions and it explains why the shapes of z-ROC functions must be interpreted in the context of the behavior of RT distributions.

The components of the model that are most important in predicting the locations of RT distributions and the shapes of z-ROC functions are the values of memory strength and the relative heights of the boundaries. The positions of the confidence criteria play only a small role. If the confidence criteria are moved, points on the z-ROC functions move around, but the shapes of the z-ROC functions do not change and neither do the relative positions of the RT distributions.

Fitting the RTCON2 Model to Data

Because we have no exact solutions for this model, we used simulation to generate predicted values from the model. For simulation of the process given by Equation 1, we used the simple Euler’s method with 1-ms steps (cf. Brown, Ratcliff, & Smith, 2006; Usher & McClelland, 2001). Updates were asynchronous: In each millisecond, one accumulator was chosen randomly, and the evidence in it was incremented or decremented according to Equations 1 or 2. With synchronous updates, in which all accumulators are updated in each one millisecond step, the model predictions and parameters were similar as for the asynchronous update version except for the parameters for within-trial variability and the scaling from area to drift rate (because six increments were taken per millisecond). Also, the computer program implementing the model ran 4 or 5 times slower than the program with one asynchronous update per millisecond.

For the experiment from Ratcliff et al. (1994) that is analyzed below, there were six confidence categories and six conditions that differed in difficulty (described later). Response proportions and .1, .3, .5, .7, and .9 RT quantiles were generated for each confidence category for each condition using 20,000 iterations of the decision process for each condition. For each evaluation of the model, a chi-square statistic was computed over the observed data and expected model-based frequencies. This was done by using the observed quantiles to produce the cumulative proportions between the quantiles and hence the frequencies by multiplying by the number of observations. These are computed for each of the four bins between quantiles and the two bins outside the extreme quantiles, for the six confidence categories (for details, see Ratcliff & Starns, 2009; Ratcliff & Tuerlinckx, 2002). When the number of observations was less than eight, we used a single value computed from observed and expected proportions in the chi-square calculation. This occurred for nine out of 396 bins (the product of six conditions, six levels of confidence, and 11 subjects). The chi-square value was computed from (O − E)²/E; it is asymptotically equivalent to Wilks’s likelihood ratio G-square (see Ratcliff & Smith, 2004). We computed G-square values for the parameters and found the G-squares tracked the chi-squares (correlation .98) and were similar to the chi-square values. With six confidence categories and six bins per category, there are 36 degrees of freedom, but one is lost because they must sum to the total number of observations. With six levels of difficulty, the total number of degrees of freedom was 210 (6 × 35).

An iterative simplex minimization routine was used to find parameter values that produced the smallest value of chi-square. The initial values were obtained after trial and error fitting. The simplex fitting process was restarted seven times with starting values from the prior fit. This process is not guaranteed to produce the best fit, but it shows the model can fit at least this well.

Recognition Memory: Experiment 5 From Ratcliff et al. (1994)

Ratcliff et al. (1994, Experiment 5) tested recognition memory for 11 subjects, with 7 to 11 one-hr sessions per subject. Subjects studied pairs of words and then were tested on memory for single words. The six confidence categories ranged from “very sure old” to “very sure new.” Subjects used a different finger for each confidence key and were asked to keep their fingers on the keys throughout the test lists. The 6 conditions were strongly-encoded old items (studied for 5 s per pair), weakly-encoded old items (studied for 1.5 s per pair), and new items, and for each of these conditions, the words occurred in English with high- or low-frequency. In the experiment, for some lists of pairs, the study time was the same for all the pairs. For other lists, pairs with short and long study times were mixed together. For the analyses here, we collapsed over list types so that all the strong old items were combined and all the weak old items were combined. Ratcliff et al. reported only response proportions, but here both proportions and RTs are analyzed. The details of the experiment are described fully in Ratcliff et al. (1994).

The paradigm used by Ratcliff et al. (1994) is common in memory research (e.g., Egan, 1958; Hautus, Macmillan, & Rotello, 2008; Heathcote, 2003; Murdock & Dufty, 1972; Ratcliff, Sheu, & Gronlund, 1992). However, it is less common in research on perception where a confidence judgment is often made after a two-choice judgment (Baranski & Petrusic, 1998; Vickers, 1979, and reviews of earlier work therein). Pleskac and Busemeyer (2010) and Van Zandt (2000) have proposed models for this task, but we have not applied RTCON2 to it. It could be that combining such a model with RTCON2 would constrain the parameters of both. Whether this could be done is a question for further research.

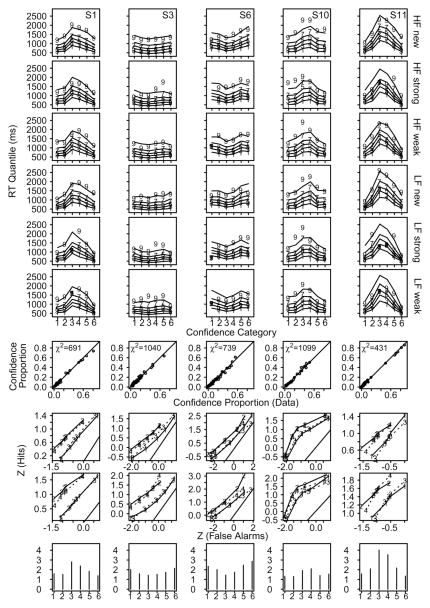
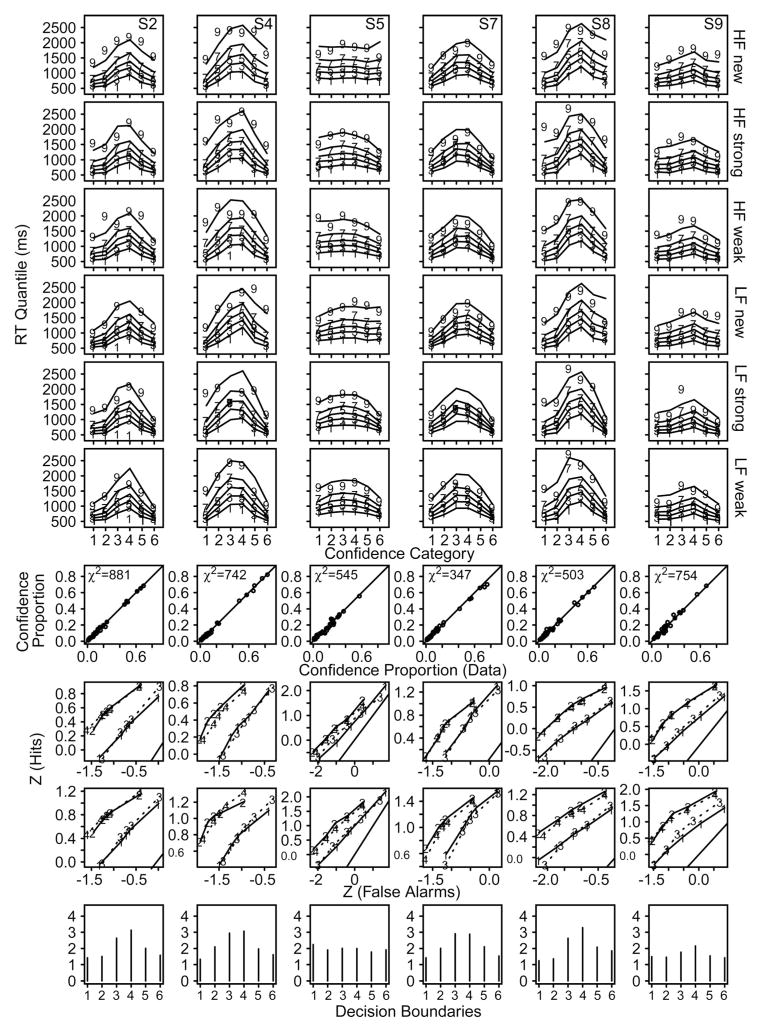
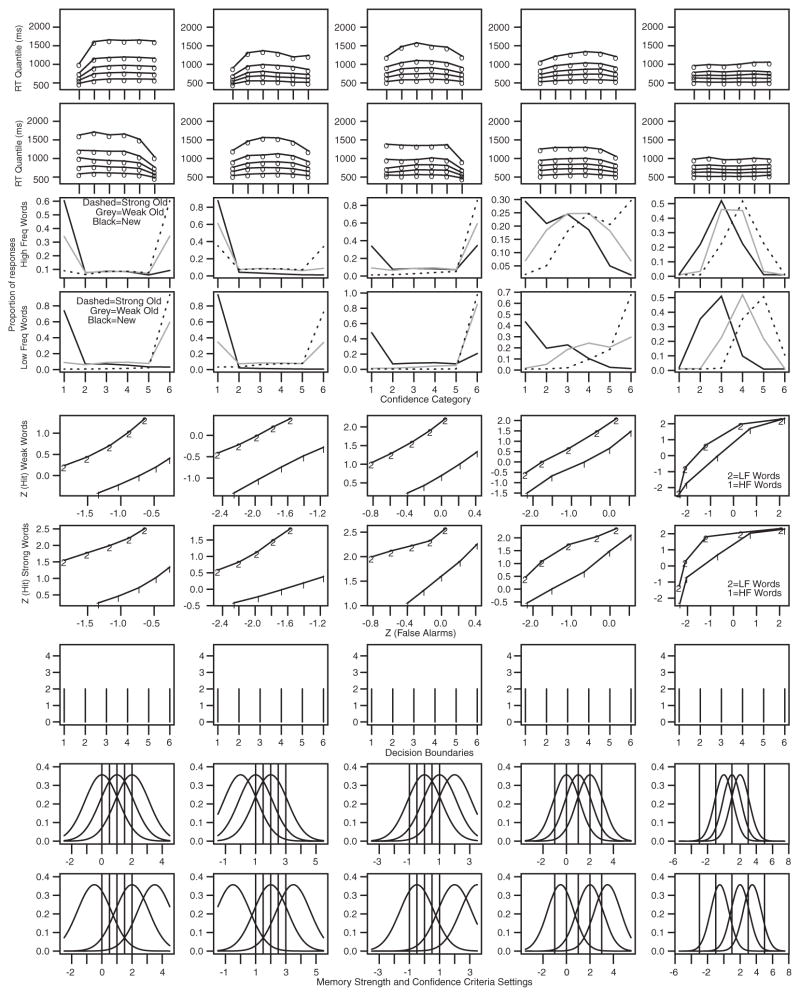
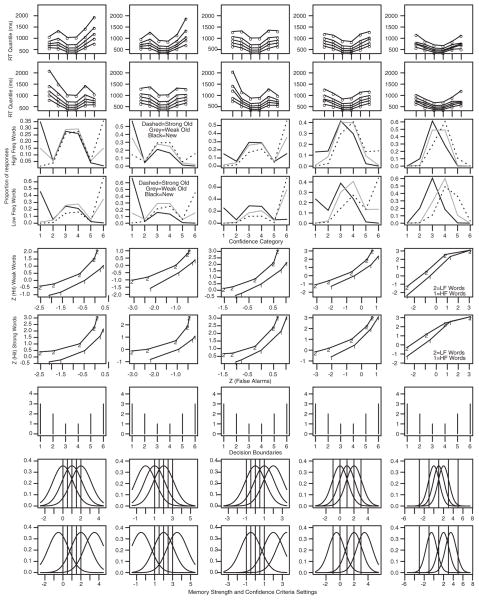
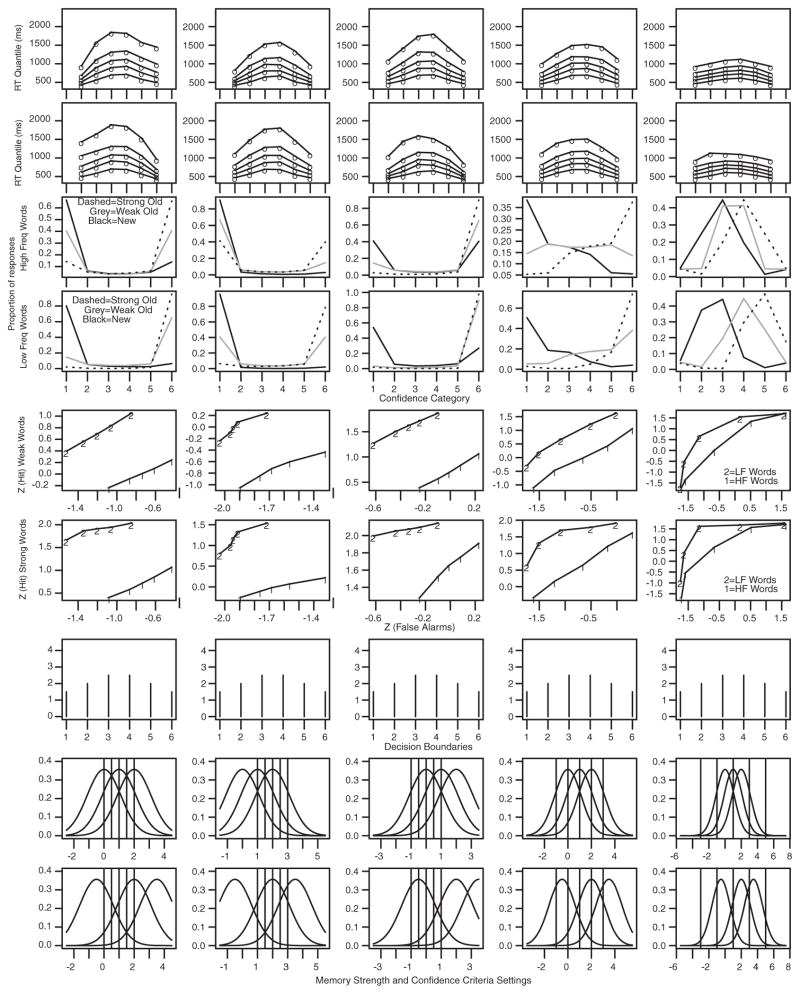
There were 11 subjects in the experiment, with between 7 and 11 one-hr sessions per subject. Nine of the subjects showed shifts in their whole RT distributions. For seven of them, RTs were longer for the low-confidence categories than the high-confidence categories; for the other two, the pattern was the opposite. For the remaining two subjects, RTs were about the same across the categories. We fit the RTCON2 model to the data for each individual subject as described above. Figure 3 displays results for the five subjects who showed maximum variation in the shape of their z-ROC functions, and Figure 4 shows the other six subjects. For each subject, the top six rows of the figure show the RT quantiles for the six confidence categories for the six conditions. The numbers are the data and the lines joining them are the predictions generated from the model using the best-fitting values of the parameters. The right-skewed RT distributions (smaller separation between the .1 and .3 quantiles than between the .7 and .9 quantiles) produced by the model generally match the right-skewed RT distributions produced by the subjects. This is strong confirmation of the model because RT distributions provide an extremely stringent test (Ratcliff & McKoon, 2008; Ratcliff & Murdock, 1976; Ratcliff & Tuerlinckx, 2002).

Figure 3.

Plots of model fits and data for 5 subjects showing the largest differences in z-ROC shape from Experiment 5 in Ratcliff et al. (1994). The top six rows show response time (RT) quantiles as a function of confidence for high-frequency (HF) new words, HF strong old words, HF weak old words, low-frequency (LF) new words, LF strong old words, and LF weak old words. The 1, 3, 5, 7, 9 symbols are the .1, .3, .5, .7, and .9 quantile RTs from the data, and the lines are the model predictions. The seventh row shows a plot of empirical against predicted response proportions (for the six confidence conditions and six experimental conditions). The eighth row shows empirical and predicted z-ROC functions for weak and strong LF words (data are “1” for weak and “2” for strong, and model predictions are “3” and “4”). The ninth row shows empirical and predicted z-ROC functions for weak and strong HF words. The tenth row shows the decision boundaries for the best fit to the data.

Figure 4.

The same plots as for Figure 3 for the other six subjects from Ratcliff et al. (1994). RT = response time; HF = high-frequency; LF = low-frequency.

The model also fit response proportions well: The seventh row shows the proportions in each confidence category for each condition, with data on the x-axis and model predictions on the y-axis. All the points fall close to the line with slope 1.0 (the diagonal black line). The eight and ninth rows show that the model fits z-ROC functions well. In the eighth row, z-transforms of response proportions are plotted against each other: Old high-frequency words presented for 1 s are plotted against new high-frequency words (data the solid line with “1” symbols, model fits the dashed line with “3” symbols), and old low-frequency words presented for 1 s are plotted against new low-frequency words (data the solid line with “2” symbols, model fits the dashed line with “4” symbols). The ninth row shows the same plots for words studied for 5 s. The tenth row shows decision boundaries. The values of the model parameters averaged over subjects are shown in Table 1.

Table 1.

Model Parameters

Model and parameters	Parameter symbol
	Ter	st	a	σ	sb
Confidence model	384	76	0.038	0.093	0.78
Three-choice model	392	155	0.066	0.120	1.04
Decision boundaries	b1	b2	b3	b4	b5	b6
Confidence model	1.64	1.71	2.41	2.53	1.92	1.75
Three-choice model	1.46	1.48	2.26
Confidence criteria	c1	c2	c3	c4	c5
Confidence model	−0.96	−0.06	0.67	1.56	2.44
Memory strength means	μhfN	μhfS	μhfW	μlfN	μlfS	μlfW
Confidence model	0.00	2.20	1.81	0.68	3.04	2.37
Memory strength standard deviations	shfN	shfS	shfW	slfN	slfS	slfW
Confidence model	0.85	1.19	1.29	0.92	1.58	1.90
Three-choice model drift rates	v1	v2	v3
40:10:10	0.56	0.20	0.24
30:20:10/40:30:10	0.46	0.34	0.20
10:10:30	0.20	0.21	0.59

Note. T_er is the mean nondecision time, s_t is the range in nondecision time, a is the scaling factor that multiplies drift rate, σ is the standard deviation in within trial variability, s_b is the range in variability in the decision boundaries, and b₁–b₆ are decision bounds. For the three-choice model, b₃ is higher than b₁ and b₂ because it is correct for a low proportion of the trials. For the confidence model, c₁–c₅ are confidence criteria from the division between high confidence new and medium confidence new to the division between medium confidence old and high confidence old, hf represents high frequency, lf represents low frequency, N represents new, W represents weak studied items (1.5 s per pair), and S represents strong studied items (5 s per pair). For the three-choice model, across trial standard deviation in drift rate for the largest drift rate was .042.

Conclusions

The data from this experiment show large differences among individuals. RTCON2 captures these differences, showing the relations among memory strength, confidence categories, and decision boundaries, and how different combinations of them can produce the same or different z-ROC functions and the same or different RT profiles. Subjects 1, 5, 8, 9, and 11 had inverted U-shaped decision boundaries, roughly linear z-ROC functions, and inverted U-shaped RT-quantile plots; Subjects 3 and 6 had U-shaped boundaries, U-shaped z-ROC functions, and U-shaped RT-quantile plots; and Subjects 4, 7, and 10 had inverted U-shaped boundaries, inverted U-shaped z-ROC functions, and inverted U-shaped RT-quantile plots. All of these patterns are produced by RTCON2 from a single source of information from memory, including the U-shaped z-ROC functions (Subjects 3 and 6) that have been claimed to require two sources.

These data and the fit of the model to them show that SDT can no longer be used to interpret z-ROC functions. In SDT analyses, z-ROC functions are determined by the strengths of test items in memory. Strength is mapped to accuracy and accuracy to z-ROC functions. This simple interpretation of z-ROC functions as direct reflections of strength is not tenable because the shapes of z-ROC functions covary with RTs. SDT assigns all variability in processing to variability in memory strength, while RTCON2 includes variability in memory strength, within-trial variability in the decision process, variability in decision boundaries, and variability in nondecision time. If a SDT representation were mapped to RTs by assuming a direct relationship between strength and RTs, errors and RT distribution shapes would be mis-predicted (Ratcliff et al., 1999, Figure 15). It might be feasible to combine a SDT representation with a diffusion decision process such that both accuracy and RTs could be predicted, but then the simple relationship between SDT and z-ROC functions would no longer hold.

In standard SDT, if the strength distributions are normal, the slope of the z-ROC is the ratio of new item to old item SDs (Ratcliff et al., 1992). In RTCON2, the slope of the z-ROC function usually differs from the ratio of SDs (see also Ratcliff & Starns, 2009). In fitting the model to the data, we found that for high-frequency words, the ratio of new-to-old item SDs was .69, but the slope was .79, and for low-frequency words, the ratio was .53 and the slope was .71. The z-ROC slope is nearer 1 than the SD ratio because the decision process introduces sources of variability in addition to variability in memory evidence, and adding the same amount of variability to two distributions with unequal SDs produces distributions with SDs more nearly the same. (In one respect, the results with RTCON2 are similar to those for SDT, specifically that the SDs for old items were larger than the SDs for new items; e.g., Egan, 1958; Ratcliff et al., 1992.)

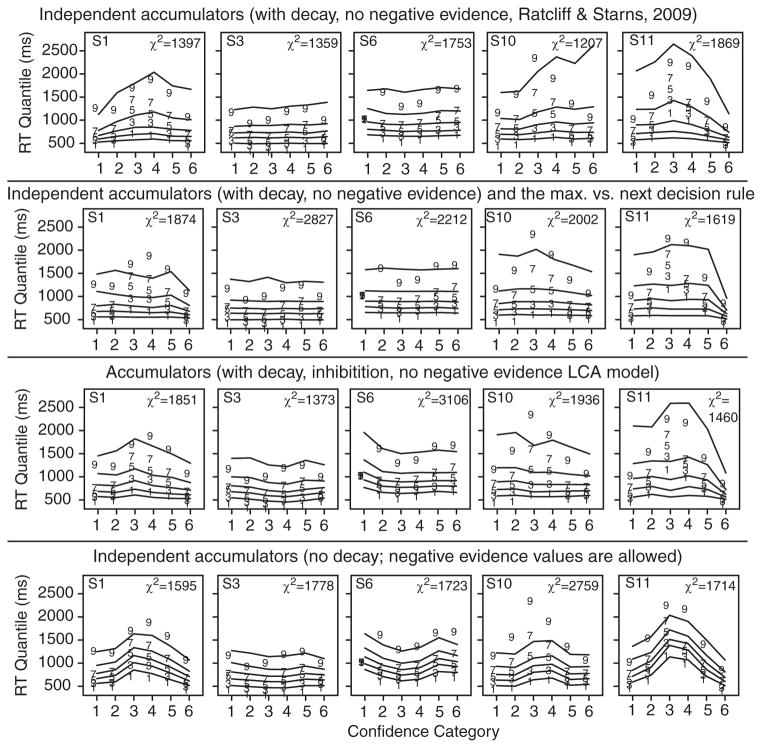
Other Decision Algorithms

First, we examined the linear independent accumulators algorithm in which only one accumulator is incremented at a time and the others are not altered. All of the other assumptions were the same as those for RTCON2. This algorithm can produce bowed RT-quantile functions with shifts in the leading edges like those in the data (see Figure 5). However, it misses the tails of the RT distributions; on average, the predicted .9 quantile RT is 226 ms shorter than the data. In contrast, RTCON2 predicts a .9 quantile RT only 6 ms longer than the data.

Figure 5.

For the data in the third row of Figure 3, the plots show response time (RT) quantiles for new low-frequency words generated from the best-fitting parameters for these algorithms: independent accumulators with decay, max. versus next, leaky competing accumulator algorithm (LCA), and the independent accumulators with no decay, respectively.

The LCA, the independent accumulators with decay, and the max. versus next algorithms were combined with the assumptions of RTCON2 in the same way as for the linear independent accumulators algorithm. The resulting three models fit RT distributions poorly (see Figure 4) because they could not capture leading-edge shifts (especially for Subjects 1, 10, and 11 as well as Subjects 4, 7, and 8, which are not shown). In contrast to their failure to fit RT distributions, the models did produce adequate fits to response proportions.

With these latter three algorithms, evidence in an accumulator decays on each time step. This is the reason they predict almost flat .1 quantiles across the categories. For low values of drift rate, the only way evidence in an accumulator can reach its boundary is if within-trial variability gives several large increments in a row. If they are not successive, each single increment is subject to decay back to zero and its advantage is lost. With low values of drift rate, such a run of large increments can occur at any time in the decision process (early or late). This means that, over many simulated trials, all of the accumulators will have some trials with a run of large increments early which in turn means that the predicted shortest RTs for all of them will differ by relatively small amounts, as in Figure 5. However, simply removing decay from these algorithms does not solve the problem. It produces RT distributions with right tails that are too short, as for the linear independent accumulators model (see also the models in Ratcliff & Smith, 2004).

In contrast to the three algorithms with decay, for the linear independent accumulator and constant summed evidence algorithms, when an accumulator gets a large increment, that advantage does not decay away. This means that more gradual approaches to the boundaries can occur because several large increments can be separated from each other in time, or a number of moderately large increments can allow a low-probability accumulator to win. Also, because there is no decay, larger increments from noise are not as critical to allowing a low-probability accumulator to win (because increments separated in time can add) and this explains why the SD of the within-trial noise for the linear algorithms is estimated to be about half the value of the three algorithms with decay.

Chi-square goodness of fit

In the chi-square (quantile-based) measure, not only do the response proportions have to be divided among the six confidence categories, they also have to be divided among the quantile bins. This provides quite stringent constraints on a model because a single set of decision boundaries and a single set of confidence criteria must produce these divisions, and do so consistently across the conditions of an experiment. This speaks to the regularity in the data that the model captures: For example, if a low confidence condition has a high quantile for low frequency new words, it has a high quantile for high frequency old words also.

The mean chi-square for RTCON2 (with 27 parameters) was 706 with 183 degrees of freedom with a critical value of 216; that is, the mean chi-square value is about 3.3 times the critical value. This is in line with the fits in Ratcliff and Starns (2009) and shows a misfit that is only modest given the large amounts of data (see the discussion in Ratcliff & Starns, 2009, p. 74).

The linear independent accumulators model (with 27 parameters) fit the data reasonably well qualitatively, capturing the bow in the .1 quantile RTs, but the mean chi-square was 1,811, and the model missed the tails of the distributions as described above. This model and RTCON2 have the same number of free parameters and so using an alternative goodness of fit metric, the Bayesian information criterion (BIC), does not affect the relative goodness of fit of the two models. BIC indicates a better fit for the model with more parameters if the difference in G-square between this model and a model with fewer parameters is larger than Mln(N), where M is the difference in the number of parameters between the two models, and N is the sample size. BIC indicates a better fit for the model with fewer parameters if the G-square difference is less than Mln(N).

The original RTCON model (with 28 parameters) had a mean chi-square of 1,842. For the LCA model (with 29 parameters), the mean chi-square was 1,652, and for the max. versus next algorithm (with 24 model parameters), the chi-square was 2,525. Our implementation of the max. versus next model had three parameters less than the constant summed evidence model. The difference between the BIC complexity penalty for the two models is 27 and 26 for Subjects 1–7 and 8–11, respectively. The difference in G-square is much larger than this value, so BIC also prefers the constant summed evidence algorithm over the max. versus next algorithm.

It is important to distinguish between how well an algorithm fits the data qualitatively and how good its chi-square value is. Figure 5 shows that the LCA model and the RTCON (Ratcliff & Starns, 2009) model miss the experimental data qualitatively but that the independent linear accumulator model captures the qualitative trends quite well. However, the better qualitative fit of the independent accumulator model is not reflected in chi-square values, which are better for the LCA model than the independent accumulator model. The reason the chi-square values for the LCA and RTCON models are not a great deal larger given the qualitative misses is that there are very few observations in the intermediate-and low-confidence categories for the subjects that have pronounced inverted U-shaped quantile functions (for which the models miss the data). This produces relatively small contributions to the chi-square despite the large qualitative misses.

To illustrate the consequences of mispredictions with low numbers of observations, we used the number of observations for Subject 11. There were on average 21 observations per condition for the each of the two lowest-confidence categories (248 observations for the two-lowest confidence categories for the six experimental conditions out of a total of 6,214 observations). We took 21 counts and randomly placed them in six bins with probability 1., .2, .2, .2, .2, and .1 (the proportions outside and between the .1, .3, .5, .7, and .9 quantiles) and computed chi-square values (the mean is 5). Then we moved all the counts from the first bin (.1 proportion) to the last bin, the counts from the second to the fifth, and the counts from the third to the fourth. This would correspond to a shift in the RT distribution such that all the counts between the lower quantiles moved out of the lower three bins to the higher three bins. The mean change in the chi-square value was about 30 (for 1,000 simulations with 21 observations randomly divided among the six bins with expected proportions 1., .2, .2, .2, .2, and .1). Multiplying this by 12 to mimic 12 conditions (the two lowest-confidence categories by six experimental conditions) adds 360 to the chi-square value. If half the subjects showed this shift in the distribution relative to the predictions (see Figures 3 and 4), the increment to chi-square would be about 180, which is about 10% of the average chi-square value for the LCA algorithm (and about one fifth of the difference between the chi-squares for RTCON2 and LCA). Thus, the large qualitative misses in the shifts of the RT distributions between the data and the LCA, RTCON, max. versus next algorithms show up in only modest increases in chi-square. We believe that such qualitative misses are more important in evaluating models than numerical goodness of fit measures, although both are useful.

Variants of the Constant Summed Evidence Algorithm

The assumption that evidence for one confidence category is evidence against all the others may be too extreme. For example, we might not want evidence for a high-confidence old category to be evidence against the medium- and low-confidence old categories, but only evidence against the new categories. We implemented this scheme by assuming that when there was an increase in evidence in one of the “old” accumulators, there were decreases only in the “new” accumulators (each by 1/3 the amount as the selected accumulator), not the other “old” accumulators. This variant produced about the same quality of fit to the data as the RTCON2 model with about the same model parameters. The goodness of fit value was lower than for RTCON2 (χ² = 676), but this was not consistent across subjects: Chi-square was lower for this model relative to RTCON2 for five of the 11 subjects.

There are other variants that are also reasonable. For example, if an accumulator in one category is incremented, the accumulators for other members of the category (e.g., “old”) might be incremented by half or some proportion of that increment and the accumulators in the other category (e.g., “new”) would be decremented by one third of the total increment. Such a scheme would be similar in tenor to the friends and enemies behavior of McClelland and Rumelhart’s (1981) interactive activation model. This analogy with the interactive activation model suggests that a variant of this scheme might be applicable to tasks in which subjects are asked to name a word. In naming, one might want some similar words to be incremented, some similar and some less similar words to be decremented, but distant words not to be affected (e.g., Ratcliff & McKoon, 1997).

Motion Discrimination

One of the key results from applying RTCON2 to the data from Ratcliff et al. (1994) is that the RT distributions for low-probability choices were shifted relative to high-probability choices. The shift in the leading edges of the distributions (the .1 quantiles) was as large as several hundred ms for some of the subjects. To generalize application of the constant summed evidence algorithm, and also further test the LCA algorithm, we sought to produce the same kinds of RT shifts in a quite different paradigm.

On each trial, a circular field of dots was displayed. Some proportion of the dots moved together downward to the left, some proportion moved downward to the right, and some proportion moved straight up vertically. Subjects were asked to choose for which direction the proportion of the dots that moved was the largest, pressing one of three buttons. The stimuli and their presentation followed Niwa and Ditterich (2008). On each trial, one of the directions had the strongest motion, and we manipulated the proportion of trials so that one direction was correct much less frequently than the other two. The question was whether the RT distribution for the low-probability choice would be shifted relative to the high-probability choices.

The proportions of moving dots for the three directions were assumed to map to the rates of accumulation of evidence (drift rates) in three accumulators, one for each direction. The drift rates were assumed to add to 1 (e.g., Usher & McClelland, 2001) for both the constant summed evidence and LCA algorithms. Otherwise, the assumptions about the algorithms were the same as those given above. The LCA algorithm was tested as a representative of the algorithms that incorporate decay of evidence in the accumulators.

Method

Stimuli

The dots were displayed on a computer monitor that was 17 in. (43.18 cm) on the diagonal with 640 × 480 pixel resolution. Each dot was 2 pixels (0.1 degree) on a side. Five dots were initially placed randomly within a circular disk that was in the center of the screen, 5 degrees in diameter. If a coherent move placed a dot outside of the disk, then the dot was placed back into the disk on the opposite edge. The screen was updated at a rate of 60 Hz, making the dots per square degree per second equal 5/ (2.5 × 2.5 × 3.14159)/.0166 = 15.34 (5 dots in 2.5-degree radius disk at 16.6 ms per screen).

The five dots were assigned to four populations, depending on the coherence proportions for the conditions. Three populations moved coherently in three directions 120 degrees apart and the fourth population moved randomly. Each population moved coherently every third screen. Population 1 and the random population moved in the same frame, followed by Population 2 on the next frame, and Population 3 on the third frame. Dots were randomly assigned to one of the three populations every third screen (so some dots remained in the same population and moved consistently for a few frames, but others switched to a different population). Coherent dots moved at a rate of 5 degrees of visual angle per second. If, for example, a coherent dot moved once every three screens, then it took 20 screens at 60 screens per second to move 5 degrees. At normal viewing distance, 5 degrees is 100 pixels (20 pixels per degree), so dots moving coherently move 100/20 = 5 pixels per screen.

Subjects

The subjects were 12 undergraduate students recruited from the Ohio State University population by advertisement. They each participated in four or five sessions and were paid $15 per session. Each session was about 50 min long. They were instructed to respond with the “b,” “n,” or “m” dots for the lower left, up, or lower right choices, respectively, with one finger for each key.

Procedure

There were two experimental manipulations. One was that one direction (C) occurred with a much lower probability than the other two directions (A and B) over the experiment. To accomplish this, over trials, A was the strongest direction 4/9 times, B was strongest 4/9 times, and C was strongest 1/9 times. Subjects were reminded at the beginning of each block which direction was the low probability one. This low probability direction was the same throughout all the sessions for a given subject and which of the three directions was the low probability one was counterbalanced over subjects.

The second manipulation was the strength of motion, that is, the coherence of the motion, for the three directions. Coherence was defined as the proportion of dots moving coherently in a direction. For the first six subjects, there were five conditions: the proportions for the three directions (A, B, and C) were 40:10:10, 10:40: 10, 30:20:10, 20:30:10, and half as many trials as for those four conditions with coherences 10:10:30. For the other six subjects, conditions were the same except that 30:20:10 and 20:30:10 were replaced by 40:30:10 and 30:40:10.

Individual differences were larger than differences averaged over subjects between the 30:20:10 and 40:30:10 conditions and the patterns of results were the same, so we grouped the two sets of conditions into one for modeling and data analysis. This produced three conditions for modeling.

There were 10 blocks of 108 trials per session. On each trial, the stimulus was displayed until the subject made a response. Then, if the response was longer than 1,500 ms, the message “too slow” was displayed for 300 ms. If the response was shorter than 250 ms, “too fast” was displayed for 300 ms. In all cases, there was a 500-ms delay before the next stimulus was displayed.

Three-Choice Models

For the constant summed evidence algorithm, it was assumed that there are three accumulators and that when one is incremented, the others are each decremented by half the increment. Three drift rates were used for each experimental condition, one for each accumulator, and these add to 1 so that there are two independent parameters. Many of the parameters are the same as for RTCON2: nondecision time, the range in nondecision time, a scaling parameter multiplied by drift rates to map them into accumulation rates, a parameter representing within-trial variability, three boundary settings for the three choices, and variability in the decision boundaries. The means of these parameters are shown in Table 1.

Adding across trial-variability to drift rates is not straightforward. Random variability in the drift rates for the three accumulators would not allow the drift rates to add to a constant, and if drift rates were to be positive, variability should decrease as drift rates approach zero. To implement across-trial variability, we decided to add a normally distributed random number (which could be positive or negative) to the accumulator with the largest drift rate. Half this random number was subtracted from the other two accumulators.

The LCA algorithm that we implemented to represent versions of the algorithms with decay was identical to the constant summed evidence model just described except that the decision mechanism was that given by Equation 2.

Results

The data from each session were examined separately for each subject. If a subject’s performance for the first session was similar to performance for the others (in both mean RTs and accuracy), then the data for the first session and the following three sessions were combined; there was no fifth session. If a subject’s performance in the first session was different from performance in the following three (usually slower and less accurate), then a fifth session was added and the last four sessions were combined. Responses with RTs less than 300 ms and greater than 2,000 ms were eliminated from analyses. This was less than 0.6% of the data.

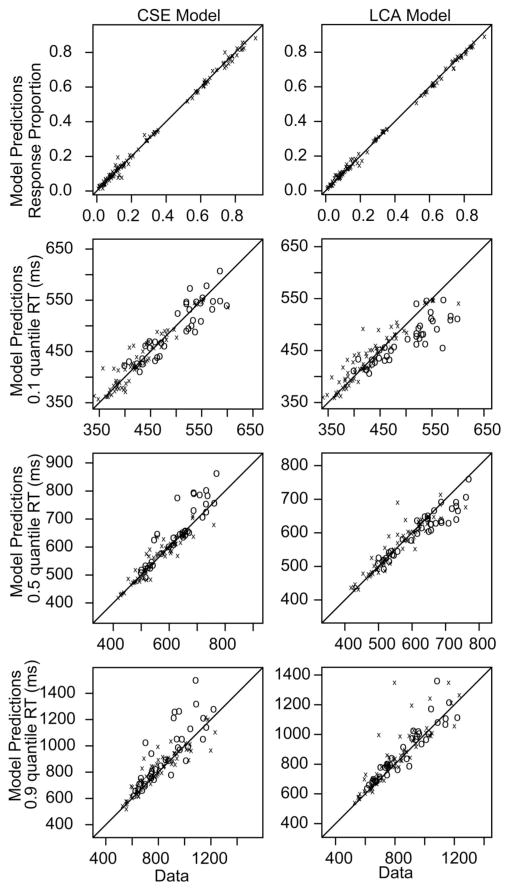
The data for each subject were fit individually using the same fitting routines as were used for RTCON2 for Experiment 1. For both experiments, Figure 6 shows plots of the model predictions versus the data for response proportions, and the .1, .5, and .9 quantile RTs for each subject and each condition of the experiment. The circles are for responses for the low-probability conditions, and the xs are for the other conditions.

Figure 6.

Fits of the multiple-choice model for response proportion, and the .1, .5, and .9 quantile response times (RTs) for the constant summed evidence model (first column) and the leaky competing accumulator algorithm (LCA) model (second column). The circles are for the conditions with the lower proportion of responses, and the xs are for the higher proportion conditions. CSE = constant summed evidence.

Just as for the recognition memory experiment above, some of the RT distributions showed large shifts. The fastest responses for the high-probability conditions were mostly between 350 and 500 ms, whereas the fastest for the low-probability conditions were mostly between 400 and 600 ms. For the constant summed evidence model, the only large misses were those for the median and the .9 quantile RTs (the eight circles furthest above the diagonal). These misses were all for errors from the low-probability conditions (conditions for which accuracy was less than .05). For the LCA model, there were underestimates of the shifts in the .1 quantile RTs for the low-probability conditions in all except five out of 36 cases. This is similar to the results for Experiment 1: The LCA algorithm does not account for large shifts in RT distributions between low- and high-probability conditions.

The parameters for the constant summed evidence model are shown in Table 1. The parameters that are in common with RTCON2 are in the same range, with the exception of the parameter that scales drift rate to accumulation rate. The drift rates show that when there is one dominant direction, the drift rate for that is almost 3 times higher than for the other two directions, but when there are two directions that both have strong motion, the drift rates differ less from each other.

The chi-square value for the constant summed evidence model was 101.0, and the chi-square for the LCA model was 122.9 (the BIC penalty for two additional parameters for the LCA relative to the constant summed evidence model is about 17). The chi-square value for the LCA model is 191.2 if across trial variability in drift is removed. The critical value was 54.6 with 39 degrees of freedom, so the mean chi-square for the constant summed evidence model is a little less than twice the critical value. The misfits are modest given the large number of observations and large number of conditions (see discussion in Ratcliff & Starns, 2009, p. 74).

General Discussion

Our understanding of how simple decisions are made has been advanced when model-based approaches have dealt jointly with choice proportions and RTs (e.g., Hanes & Schall, 1996; Ratcliff & McKoon, 2008; Roe et al., 2001; Usher & McClelland, 2001; Wagenmakers, 2009). Confidence judgments about memory have usually been interpreted with SDT, but SDT cannot explain RTs. Arguments for dual-process models have depended on the specific shapes of z-ROC functions, but RTCON2 shows that those shapes can be produced by a single-process model (see also Ratcliff, Van Zandt, & McKoon, 1995).

RTCON2 offers insights into the architecture of the interactions between decision making and memory. Because the information retrieved from memory is a distribution over strength, not a single value, it produces evidence not just for one confidence category, but for all of them, to different degrees. This means that memory strength cannot be mapped directly to responses. Instead, decision processes act on the distributions of strength that retrieval processes produce and set confidence criteria along the strength dimension. Some confidence categories may cover only a narrow range of strength values and others a wider range. Decision processes also set the boundaries that determine the amounts of evidence required to make a decision; the boundaries may be higher for some categories than others. Depending on the confidence criteria, the boundaries, and combinations of them, the confidence choice for a particular test item and its RT do not necessarily reflect the mean of an item’s strength distribution.

With the constant summed evidence algorithm, the assumption that memory produces a distribution over strength, and the assumption that criteria divide the distribution into confidence categories, RTCON2 explains choice proportions, the shapes of z-ROC functions, the shifts in the locations and spreads of RT distributions across conditions, and relationships between the shapes of z-ROC functions and RT distributions, and it does so for individual subjects. The shapes of z-ROC functions for individual subjects (linear, U-shaped, or inverted U-shaped) follow the shapes of their RT distributions, which in turn are determined by the decision boundaries for the confidence categories (unless the choice proportions are extremely small; see the Appendix). The model has 16 memory-related parameters, the same number as would be needed for SDT to fit choice proportions, and 11 parameters for the decision process (six of them decision boundaries). Together, these 27 parameters allow the model to fit the 210 degrees of freedom in the data from Ratcliff et al.’s (1994) experiment. If SDT were fit to the choice proportions, its 16 parameters would fit only 30 degrees of freedom.

Currently, there are no memory models that allow retrieval processes to produce distributions of memory strength that could be used to drive RTCON2, although there have been some proposals for integrating memory models and sequential-sampling decision models (Donkin & Nosofsky, 2012; Malmberg, 2008; Nosofsky, Little, Donkin, & Fific, 2011). If such a model were developed, it could be combined with a decision algorithm such as the ones examined here. The question would be whether the values of memory strength produced by the model could, when combined with a decision algorithm, give the correct proportions of responses and their RTs.

With the three-choice motion discrimination task, we generalized the result that RT distributions shift when the probability of a response to a choice is small compared to when it is larger. We manipulated the choices so that one of them was correct on a low proportion of trials and the other two were correct on higher proportions of trials. The data showed a shift in the RT distribution for the low-probability choice relative to the higher-probability choices. This shift was accommodated well with the assumptions that there were three accumulators, one for each choice, and that the accumulators were incremented according to the constant summed evidence algorithm. This is a modest generalization of the algorithm, but it does suggest that its applicability is not limited to confidence decisions about memory.

Signal Detection Theory and the Single-Process Versus Dual-Process Controversy

The distinction between RTCON2, based on choice proportions and RTs, and SDT, based only on choice proportions, merits further discussion. In RTCON2, for each type of test item (e.g., strongly-encoded old items), the mean of its strength distribution varies from trial to trial. This suggests that RTCON2 could be used to update SDT to handle the time course of decision making and so give SDT the ability to handle RT distributions. However, as we pointed out above, doing this would produce quite different estimates of the means and SDs of the strength distributions than would SDT alone. This is because in RTCON2, there are several sources of across-trial variability whereas in SDT, there is across-trial variability only in memory strength. This contrast is one reason that SDT by itself cannot be used to describe how information is retrieved from memory or how information is represented in memory.

In most applications of SDT, the slope of a z-ROC function is the ratio of the SD of the strength distribution for new items to the SD of the distribution for old items. This means that for SDT, the slope of the z-ROC function can only be understood in terms of the SDs of those distributions. In contrast, in RTCON2, the slope of the z-ROC is not directly tied to the strength distributions.

In a dual-process framework, the slope and shape of the z-ROC function provide a way to estimate the relative contributions of recollection and familiarity to decisions. Recollection contributes high-accuracy responses at the high-confidence old end of the ROC function, and so makes the function non-linear. The greater the proportion of recollection responses, the more U-shaped is the function. U-shaped z-ROC functions have been claimed as support for dual-process models in many applications, including studies of the effects of clinical neuropsychological conditions on recognition memory and studies of the patterns of brain activity that are observed with imaging techniques during recognition. However, the findings here show that U-shaped functions are not diagnostic. To put this point in a different way, the U shapes of z-ROC functions may have nothing to do with the relative contributions of two memory processes.

Ratcliff and Starns (2009; also Van Zandt, 2000) provided another example of a situation in which decision processes can change z-ROC slope even when memory strength is constant. In their study, subjects showed a bias to repeat the response made on the previous trial, and z-ROC slope was higher following “old” responses than following “new” responses. Fits of the RTCON model showed that changing decision boundaries accounted for changes in the response proportions along with changes in the z-ROC slope, with higher slopes when the boundaries were higher for “old” responses and lower slopes when they were higher for “new” responses. Strength of encoding of an item should not be affected by the previous response. In a similar way, inducing response biases by changing the proportion of old items in a test list or by changing the reward structure for responses affects the slopes of z-ROC functions formed from confidence judgments (Mueller & Weidemann, 2008; Van Zandt, 2000). Still another example of decision processes changing z-ROC properties when memory strength is constant is provided by experiments in which speed/accuracy tradeoffs are manipulated, for example, when subjects are given instructions that stress speed over accuracy or accuracy over speed. Speed/accuracy tradeoffs are also an issue when performance is compared across populations, for example, college students, elderly adults, amnesic patients, and children.

Comparisons of Algorithms

We considered four algorithms in addition to the constant summed evidence algorithm: a linear independent accumulator algorithm, the LCA, an independent accumulator algorithm with decay, and a max. versus next algorithm. None of these could accommodate the recognition memory data or the motion discrimination data. The linear independent accumulator algorithm could account for shifts in the RT distributions between high- and low-probability conditions but underestimated the tails of the distributions. The three algorithms with decay could not account for the shifts in the RT distributions. As described earlier, these failures come about because several large noise increments in a row are needed to boost a low-probability alternative over the decision boundary. Large increments from noise can occur both early and late in processing, which means that, on average, the earliest occur at close to the same time across conditions.

It has been argued that behavioral data cannot discriminate among algorithms such as those considered here (e.g., Ditterich, 2010), but very few data sets have been produced to decisively test among multiple-choice models. Those that have been produced (e.g., Leite & Ratcliff, 2010; Niwa & Ditterich, 2008) come from paradigms in which subjects discriminated among different stimuli rather than among different levels of confidence. In these studies, typically, the probabilities of the response choices were not manipulated and this might account for the relatively small differences in the locations and spreads of the RT distributions. When we manipulated probabilities in the Motion Discrimination experiment, we found RT distribution shifts. It was this manipulation that distinguished the constant summed evidence algorithm from the other algorithms (similar conclusions were obtained with two-choice data in Starns, Ratcliff, & McKoon, 2012).

Conclusion

Theories of memory must specify how the evidence supplied by a memory system is translated into overt decisions. For decades, this role has been played by SDT. Although SDT has guided volumes of research across all of psychology, it fails to explain basic decision-making phenomena: the time subjects take to make decisions and the relationship between time and response proportions. The model presented here does just that. In addition, the model demonstrates a previously unknown relationship, that z-ROC shapes reflect the patterns of RT data. Both single- and dual-process models for recognition memory ignore RT as a dependent variable. Hence, we argue, the single- versus dual-process debate can be advanced only by a fundamentally new approach that encompasses RTs as well as response proportions.

We anticipate that the decision algorithm in RTCON2 can be applied to many domains in addition to recognition memory. We are currently using it to investigate other kinds of memory tasks (e.g., associative recognition, source memory) and perceptual tasks, and the model can be applied to issues in the neuropsychology of memory, neuroeconomics, and the neurophysiology of decision making. Switching from models that account only for response proportions to models that also account for RTs will strongly impact many current theories. The notion of confidence runs through numerous real-life decision-making tasks and through much research on memory and decision making. Thus, research into confidence, and more generally multiple-choice decision making, requires a serious consideration of the combination of RT and response proportion data, and this should begin sooner rather than later.

Appendix. Simulations of the Constant Summed Evidence Model

Figures A1, A2, and A3 present simulated data for a range of conditions in a design that mimics that of the experiment in the body of the article. The discussion below is in terms of the experimental factors. There were six kinds of test words, strong and weak study words and new words and each of these is crossed with high and low word frequency in English. The mean strength for the high-frequency words was for new words, 0.0, for weak old words, 1.0, and for strong old words, 2.0; and for low frequency words, they were for new words, −0.5, for weak old words, 2.0, and for strong old words, 3.5. The other parameters were set at values like those for a typical subject (e.g., Table 1). These were T_er = 323, s_t = 108, a = .035, and σ = .092. Across-trial standard deviation in memory strength was set to be small, at 0.05. In each of the three figures, the pattern of decision boundaries across confidence categories was different: For Figure A1, decision boundaries were equal; for Figure A2, they were U-shaped; and for Figure A3, they were inverted U-shaped. In the simulations corresponding to the five columns in each figure, we changed the locations of the confidence criteria (the same way in each figure). The top two rows show response time (RT) quantile plots as a function of confidence. The next two rows show the proportions of responses in the different confidence categories. The next two rows show the z-ROC functions for the two classes of old items against new items. The next row shows decision boundary settings. The last two rows show the distributions of within-trial strength (SD = 1) for high- and low-frequency words, respectively. Along with the distributions are shown the confidence criteria, which are different for the different columns. As we move from the left to right columns, the criteria are narrow (0, 0.5, 1, 1.5, and 2), then move right by one unit, then left from the settings from column 1 by one unit, then spread out in the next two columns (in the fourth column they are −1, 0, 1, 2, and 3, and if the fifth column they are −3, −1, 1, 3, and 5). As the boundaries spread out, the proportion of responses in the extreme confidence categories decreases, and the proportions in the lower confidence categories increase.

In Figure A1 (third and fourth rows), the response proportions are near zero for the middle categories in the first three columns and are close to zero in the extreme categories in the fifth column. The z-ROC functions move from almost U-shaped in the first three columns to inverted U-shaped in the last column. In Figure A2 with U-shaped decision boundaries, the first four columns have few conditions with near zero counts, and the z-ROC functions are U-shaped and follow the decision boundary shape. In the fifth column, the extreme confidence categories have almost zero counts in them, and the z-ROC function shape moves to have a small inverted U-shape. In Figure A3 with inverted U-shaped decision boundaries across confidence categories, in the first three columns, there are near zero counts in the middle categories, and the functions are linear or slightly inverted U-shaped. In the last two columns, there are more counts in the middle categories, and the functions become inverted U-shaped and follow the decision boundary shape.

These results show that the z-ROC function shape follows decision boundary shape across confidence categories when there are observations in each confidence category. If there are very few observations (less than 1 or 2%), then the shapes of the z-ROC function and decision bounds across confidence categories can be different, as shown in Figures A1–A3.

Figure A1.

Simulated data from the model with confidence criteria changing across columns. The top two rows are representative response time (RT) quantiles for new low-frequency words (top row) and strong old low-frequency words (second row). The third and fourth rows show response proportions for weak and strong old items and new items for high- and low-frequency words. The fifth and sixth rows show z-ROC functions for strong and weak high- and low-frequency words. The seventh row shows decision boundaries. The eighth row shows distributions of memory strength for new high-frequency words, weak old high-frequency words, and strong old high-frequency words. From the left to the right columns, the confidence criteria are narrow (set at 0, 0.5, 1, 1.5, and 2), move right by 1 unit, move left by one unit from those in column 1, and then spread out (−1, 0, 1, 2, and 3), and then spread out again (−3, −1, 1, 3, and 5). Freq = frequency; LF = low frequency; HF = high frequency.

Figure A2.

The same plots as for Figure A1 except with U-shaped decision boundaries across confidence categories. RT = response time; Freq = frequency; LF = low frequency; HF = high frequency.

Figure A3.

The same plots as for Figure A1 except with inverted U-shaped decision boundaries across confidence categories. RT = response time; Freq = frequency; LF = low frequency; HF = high frequency.