Abstract
We report the first application of wavelet-based denoising (noise removal) methods to time-domain box-car fluorescence lifetime imaging microscopy (FLIM) images and compare the results to novel total variation (TV) denoising methods. Methods were tested first on artificial images and then applied to low-light live-cell images. Relative to undenoised images, TV methods could improve lifetime precision up to 10-fold in artificial images, while preserving the overall accuracy of lifetime and amplitude values of a single-exponential decay model and improving local lifetime fitting in live-cell images. Wavelet-based methods were at least 4-fold faster than TV methods, but could introduce significant inaccuracies in recovered lifetime values. The denoising methods discussed can potentially enhance a variety of FLIM applications, including live-cell, in vivo animal, or endoscopic imaging studies, especially under challenging imaging conditions such as low-light or fast video-rate imaging.
Keywords: Time-gated fluorescence lifetime imaging microscopy, precision improvement, image denoising, wavelet analysis, total variation
1. Introduction
Fluorescence lifetime imaging and fluorescence lifetime imaging microscopy (FLIM) are useful molecular imaging techniques for pre-clinical and clinical studies in living cells, tissues, small animals, and endoscopic samples, with fluorescence lifetime providing image contrast [1-10]. Fluorescence lifetime can be employed as an optical sensor to indicate micro-environmental conditions such as oxygen levels, the state of endogenous / exogenous fluorophores, and Förster resonance energy transfer in live cells [11-18].
The interest in biological FLIM is increasing, as commercial FLIM modules become available for confocal and multi-photon microscopes. However, low fluorescence signals from biological samples can be a challenge, causing poor lifetime precision. For endogenous fluorophores, low signals could result from low concentrations and / or unfavorable optical properties. For exogenous fluorophores, low signals could result from low concentrations desired to minimize the effects on sample physiology and / or low transfer efficiency. To increase measured fluorescence signals from biological samples, high-intensity light sources such as lasers can be used in FLIM, but this may cause unexpected cell responses and sample damage / ablation [19, 20], and may also cause fluorophore photobleaching.
Image “denoising” (noise removal) [21, 22] has great potential to improve FLIM precision. Wavelet analysis is a commonly used method that has been used for restoring fluorescence microscopy images [23, 24] and for denoising frequency-domain confocal and full-field FLIM images [25, 26]. Other image denoising methods include total variation (TV) denoising, Tikonov denoising, Gaussian smoothing [27], non-parametric regression method [28], and multiframe SURE-LET (Stein's unbiased risk estimate-linear expansion of thresholds) denoising [29]. Among these techniques, TV denoising has been reported to improve FLIM precision [30]. In this study, we report the first application of wavelet-based denoising methods to time-domain FLIM, and compare them with previously developed TV denoising methods [30, 31]. This is a new research area that, to our knowledge, has not yet been explored before, potentially aiding a variety of emerging in vivo and clinical applications.
2. Methods
2.1 Time-gated FLIM system and live-cell sample preparation
We designed and characterized a novel wide-field, time-domain box-car FLIM system for picosecond time-resolved biological imaging [32, 33]. A pulsed (repetition rate = 1-20 Hz) nitrogen laser (337.1 nm, GL-3300, Photon Technology International, Lawrenceville, NJ) pumping a dye laser (GL-301, Photon Technology International, Lawrenceville, NJ) for UV-visible-NIR excitation offers a significantly less expensive, wide-field, and potentially portable alternative to multi-photon excitation for sub-nanosecond FLIM imaging of biological samples [33]. After a sample was illuminated by an excitation pulse, the fluorescence emission was recorded at different gate delays. The time interval between the starting points of two consecutive gates was denoted by “dt”. At each gate delay, the emission intensities were integrated during a gate width (denoted by “g”) controlled by the intensifier of an intensified charge-coupled device (ICCD) camera (microchannel size = ~10 μm, Picostar HR, LaVision, Germany). The gain of the ICCD is controllable and the gate width settings can vary from 200 ps to 10 ms for high-speed imaging applications [34]. The large temporal dynamic range (750 ps – 1 μs), the 50 ps lifetime discrimination, and the spatial resolution of less than 1.4 μm of the system make it suitable for studying many endogenous and exogenous fluorophores that may transit through cells [35-37]. To create fluorescence lifetime maps rapidly, a four-gate protocol, based on single-exponential fluorescence decay, with an analytical least squares lifetime determination algorithm was used on a pixel-by-pixel basis. It is more precise than a two-gate protocol while still being easy to implement [38-40]. The fitting was implemented without any weighting and no particular form of variance distribution (such as Poisson distribution) was assumed. This is because, as mentioned later in Section 2.2, there was a combination of noise distributions in our real images and this kind of noise distribution was taken into consideration in the denoising process. The analytical solution can be derived by first linearizing the overdetermined system in log domain and then solving the normal equations, (XTX)a = XTy, where a is the system parameters we are interested in, with X and y as the independent and dependent variables, respectively:
| (1) |
where τp is the lifetime of pixel p, Ii,p is the intensity of pixel p in image i, ti is the gate delay of image i, and N is the number of images, which is four. All sums are over i. This method is generally inefficient in terms of signal detection as compared to time-correlated single photon counting (TCSPC) or even frequency-domain methods, since a large percentage of the signal is simply discarded. However, it enables much faster and sometimes video-rate image recording (only four intensity values are needed for each pixel) and also very rapid lifetime determination due to the ability to evaluate all pixels simultaneously using the analytical solution (Eq. (1)).
HCT-116 live cells (purchased from ATCC, CCL-247™) were cultured with modified McCoy's 5a medium under 5% CO2 incubation. After removing the culture media and washing 3 times using phosphate buffered saline (PBS), cells at 80% confluence were incubated with 1 μM of the acetoxymethyl (AM) ester derivative of BCECF (2′,7′-bis-(2-carboxyethyl)-5-(and-6)-carboxyfluorescein, a widely used fluorescent indicator for intracellular pH) (Invitrogen, CA) in PBS at 37°C for 1 hr for cell staining. The laser excitation wavelength was 434 nm and the fluorescence emission was collected at 480 ± 20 nm with a 40x, 1.3 NA objective. Five images were averaged for each gate in the FLIM imaging of the samples with dt = 1 ns and g = 0.2 ns.
2.2 Total variation denoising
The f-weighted TV (FWTV) model was described previously [30, 31, 41-43]. It has been demonstrated to have some advantages over other previously developed TV models, which are mostly based on the commonly known Rudin-Osher-Fatemi (ROF) model [44]. The FWTV model keeps the major advantage of TV denoising models, which are edge-preserving, but was specifically developed to remove Poisson noise, an inevitable form of noise occurring in image acquisition with photon counting devices, while still having high flexibility to be easily adapted for removing non-Poisson noise (described below). In our previous studies, we have demonstrated how the FWTV model can be used in time-gated FLIM and time-correlated single photon counting FLIM to improve lifetime precision [30, 31, 41-43].
The FWTV model has the following mathematical form:
| (2) |
where E denotes the energy, through minimization of which denoising was performed, Ω denotes the signal domain, λ is the fidelity coefficient, u represents the processed image, f represents the input or noise-corrupted image, and the variables x and y represent the spatial location of the pixels. The values of λ were determined by the “discrepancy rule” [45], which requires the fidelity term (the second term on the right hand side of Eq. (2)) evaluated with f and the final u to be the same as that evaluated with f and the estimated original image without noise corruption [41]. Eq. (2) was designed for removing Poisson noise, since the data variance due to noise (the denominator of the integrand in the fidelity term, or, the “weighting”) is equal to the intensity, f, which is a characteristic of Poisson noise.
To minimize the defined energy, E, and to implement denoising, the gradient descent of E, with respect to time, t, along the direction of u was used with iterations to achieve the final stable, denoised u. Here, the “time” is just a dimension along the iterations towards the stable u and does not involve real time. Mathematically, u evolves from f (the input of u) through iterations, and in this process the measurement f is selectively smoothed to a denoised state: the smoothing occurs only in the direction perpendicular to, but not in parallel with, local intensity gradient. This process, therefore, preserves the edges of objects delineated by intensity contrast.
Further modification of FWTV for removing non-Poisson noise (such as a combination of different forms of noise at low photon counts in real imaging systems) has been demonstrated to be quantitatively accurate when applied to FLIM [41]. In the modified FWTV, f in the weighting of FWTV was replaced with Gf, where G represented the ratio of the signal variance to the mean intensity counts and was a function of local mean intensity of the image [41]. This modified FWTV was also used here to denoise live-cell FLIM images.
2.3 Wavelet-based denoising
A wavelet is a waveform of effectively limited duration with an average value of zero. A wavelet transform is to describe a function by using wavelets, which can be scaled and translated (shifted). For example, the continuous wavelet transform (CWT) is defined as an integral over the dimension of the signal (a continuous, square-integrable function) multiplied by scaled, shifted versions of the wavelet function. The results of the CWT are the wavelet coefficients, which are a function of scale and position.
In this study, the first wavelet-based denoising method was based on Discrete Wavelet Transform (DWT). In DWT, the concept is to choose only a subset of scales and positions for the calculations of wavelet coefficients. Only scales and positions based on powers of two (the dyadic scales and positions) are chosen. To use DWT for image denoising, the resulting wavelet coefficients from DWT decomposition are thresholded before the image is reconstructed. The thresholding can be performed with either “hard thresholding”, which sets the coefficients that are less than or equal to the threshold to zero, or “soft thresholding”, where, in additional to hard thresholding, the threshold value is subtracted from all the coefficients with their values greater than the threshold. An efficient way to implement DWT is to use filters. This was developed in 1988 by Mallat [46]. In this case, each level of filtering produces approximation coefficients and detail coefficients, followed by a “decimation” process, which retains only even indexed elements. The approximation coefficients can then be further filtered into the next level of decomposition, and thresholding can be applied to the detail coefficients for denoising.
The second wavelet-based denoising method was based on Stationary Wavelet Transform (SWT). SWT was developed to remove the disadvantage of DWT being not time-invariant, meaning that when the input signal is translated, the DWT transform is not translated accordingly. SWT solves this problem by averaging some slightly different DWT, called epsilon-decimated DWT [47]. Epsilon-decimated DWT is generated by the decimation that chooses either even or odd indexed elements instead of choosing only even indexed elements, following DWT. This choice is involved in each level of decomposition.
DWT and SWT image denoising was implemented with four levels of decomposition and soft-thresholding, which makes smooth transitions between the values above and below the threshold, using Matlab's Wavelet Toolbox version 4.4. The default threshold determination method (universal thresholding s (log(n))1/2, with n being the number of pixels in the image and s being the median absolute value of the detail wavelet coefficients divided by 0.6745) was not used due to the fact that s would be zero and hence no denoising would be performed for our artificial images (possibly because there are many zero-intensity background pixels, described in Section 2.4) corrupted by Poisson noise. Therefore, mean absolute value divided by 0.6745 was used as s in the expression s (log(n))1/2. Global thresholding (meaning the same threshold value is used for all decomposition levels) was used for all four levels of detail coefficients of each gate, but the threshold values were determined separately for different gates. Fixed threshold values of 100 and 500 were also used in SWT denoising for comparison. These values are comparable to and enclose the “appropriate” values (see below). The wavelet biorthogonal 3.7 (bior 3.7) was chosen, not only because it is a commonly used wavelet but also because it has been demonstrated to perform well in frequency-domain FLIM for background subtraction and denoising [26].
A more sophisticated wavelet-based algorithm [48, 49] employed in this study (denoted as “Poisson Wavelet” below) is a Bayesian approach to Poisson intensity estimation based on the translation invariant hereditary unnormalized Haar wavelet transform. This type of wavelet allows a simple formulation for Poisson data. Translation invariant Haar estimation for Poisson data includes thresholding decisions based not only on the magnitude of the coefficients, but also on the coefficients of the node's descendants. Image estimation based on this method is near minimax optimal reconstruction techniques for photon-limited images. It reduces artifacts by averaging over all possible shifts of the underlying partition. Previous studies improved the robustness of this technique by including a hereditary constraint in the thresholding rule: a coefficient can only be thresholded if all its descendants are also thresholded [49].
Poisson Wavelet image denoising was implemented by using the Matlab function provided on the web-site of Dr. Rebecca Willett's laboratory at Duke University. The penalty values (similar to the threshold values used in DWT and SWT) were determined using the default approach of log(summation of the values of all the pixels)/2.
The threshold values used in DWT (and SWT with “varying threshold”, see Section 3.1.2) were 458.50 ± 1.87, 319.86 ± 1.42, 224.46± 0.97, 159.04 ± 0.63 (number of trials = 20) for the first, second, third, and fourth gates, respectively. These values were not fixed and had distributions, because in each Monte Carlo simulation (Section 2.5), noise was randomly generated based on Poisson distribution. The penalty values used in Poisson Wavelet were 8.56 ± 0.079×10-3, 8.35 ± 0.093×10-3, 8.14 ± 0.17×10-3, 7.94 ± 0.18×10-3 (number of trials = 20) for the first, second, third, and fourth gates, respectively.
2.4 Artificial images
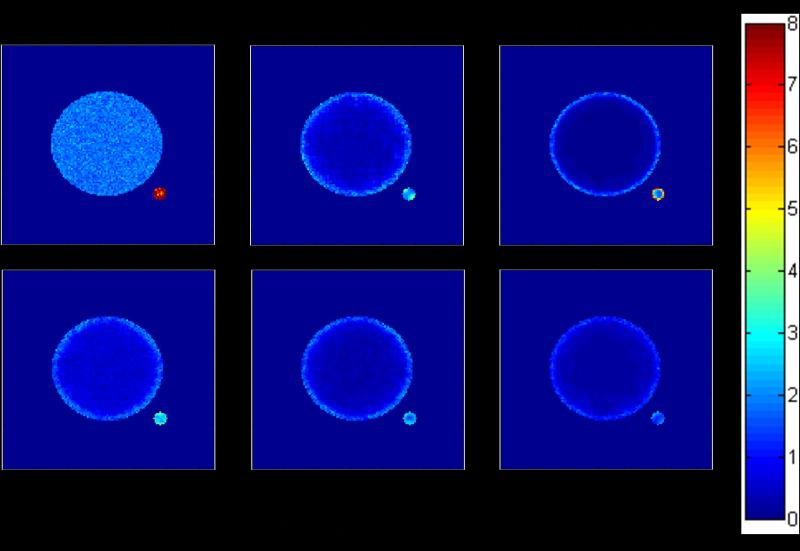
Artificial images with predetermined parameters were employed to evaluate fluorescence lifetime determination accuracy and precision after denoising. The fluorescence decay model was single-exponential with the intensity profile I(t) = α exp (-t/τ), where τ is fluorescence lifetime and α is a pre-exponential term, or amplitude. Geometry that we may encounter with live-cell FLIM was mimicked. It consisted of “the ring” (the large open circle shown in the upper-right panel of Figure 1) with τ = 5 ns and α = 1000, “the inner circle” (the centered solid circle inside the ring) with τ = 10 ns and α = 1000, and “the satellite” (the small dot to the bottom right of the inner circle and the ring) with τ = 10 ns and α = 50. The image size was 128 pixels × 128 pixels. Note that total photon counts (ατ) here were kept relatively high, making the relative standard deviation (Section 2.5) low, for better characterizations of the denoising methods with minimized possible bias of Poisson distribution at low photon counts. A combination of different forms of noise including Poisson noise at low photon counts will be considered in live-cell images (Section 3.2). As an example of the geometry mentioned here, a cell may have some fluorophores inside it with higher lifetime and others interacting in its membrane with lower lifetime, while in another smaller cell or organism the same fluorophores at lower concentration are present. The optimal gating scheme was determined to be g = 16 ns and dt = 4 ns [41]. It was an optimal gating scheme for a certain lifetime range in which the above setting was covered.
Figure 1.
RSD (Relative Standard Deviation, in %), indicating the precision, of the lifetime map constructed with the undenoised and denoised artificial images using several different denoising methods. The precision improvement was method- and geometry-dependent. The ring was the most difficult to denoise. SWT with threshold = 500 generally had the best precision but it suffered from severe inaccuracy (see Figure 2 and Table 1).
2.5 Evaluation of accuracy and precision
To assess accuracy and precision, Monte Carlo (MC) simulations were used, along with the artificial images (Section 2.4), to construct the lifetime distribution determined from Poisson-noise-corrupted intensity images, either with or without denoising. First, the single-exponential decay model I(t) (Section 2.4), the correct values of lifetime τ and pre-exponential term α, gate width g, and time interval dt between two consecutive gates were used to simulate the noise-free time-gated fluorescence intensity images. Then, Poisson noise was added to each pixel in each image, and denoising was applied to each image. The lifetime values retrieved from the denoised images using Eq. (1) were recorded in each iteration to build up a histogram for each pixel over a number of iterations of noise addition, denoising, and lifetime determination. The number of simulations was 20 in each denoised or undenoised case. The mean and standard deviation (std.) of the lifetime distribution were used for the evaluation of accuracy and precision with RSD [relative standard deviation, in %, defined as (std. / mean) × 100, also known as coefficient of variation] and RME {relative mean error, in %, defined as [(mean – correct value) / correct value] × 100}. In the undenoised case (see Section 3), the step of “denoising” was omitted.
3. Results and discussion
3.1 Artificial images
3.1.1 A comparison of DWT, Poisson Wavelet, and FWTV
FWTV has previously been tested on the artificial images (Section 5.2 in [41]). The results demonstrate that after FWTV denoising, the precision of lifetime determination was improved for all three objects (the RSD values were 0.14%, 1.43%, and 4.76% for the inner circle, the ring, and the satellite, respectively), while the accuracy was preserved (the RME values of all three objects were within 1% from zero).
Figure 1 and Table 1 show that precision improvement was method- and geometry-dependent. FWTV and Poisson Wavelet performed approximately equally well, with the ring being most difficult to denoise. In the undenoised image, the satellite had a much higher RSD value due to its much lower total photon counts. After denoising with the three methods (DWT, Poisson Wavelet, and FWTV [41]), all the three objects had lowered RSD and the precision improvement was most significant in the inner circle. However, DWT had the smallest improvement (averaged RSD = 0.64%) and FWTV the greatest (averaged RSD = 0.14% [41], precision improvement > 10-fold when compared with the undenoised value of 1.80%), while Poisson Wavelet had slightly smaller improvement (averaged RSD = 0.23%) than FWTV. The ring was most difficult to denoise for all the three methods, probably due to the fact that it had an edge-rich geometry. Still, FWTV produced the lowest RSD and improved the precision by about 1.3-fold [41]. Interestingly, for the satellite, DWT produced the best precision, but it caused inaccuracy (described below).
Table 1.
Averaged RME and RSD (%), over the pixels in each of the three objects (the inner circle, the ring, and the satellite) in the undenoised and denoised artificial images using several different denoising methods.
| Undenoised |
DWT |
Poisson Wavelet |
||||
|---|---|---|---|---|---|---|
| RSD | RME | RSD | RME | RSD | RME | |
| Inner circle | 1.80 | 0.035 | 0.64 | −0.12 | 0.23 | 0.0028 |
| Ring | 1.91 | −0.020 | 1.75 | 6.34 | 1.64 | −0.0054 |
| Satellite | 7.90 | 0.031 | 2.49 | −11.89 | 4.35 | 0.33 |
| SWT threshold = 100 |
SWT varying threshold |
SWT threshold = 500 |
||||
|---|---|---|---|---|---|---|
| RSD | RME | RSD | RME | RSD | RME | |
| Inner circle | 0.74 | −0.16 | 0.52 | −0.12 | 0.39 | −0.74 |
| Ring | 1.62 | 3.24 | 1.57 | 5.80 | 1.15 | 19.24 |
| Satellite | 2.99 | −9.19 | 2.23 | 0.62 | 1.64 | −11.10 |
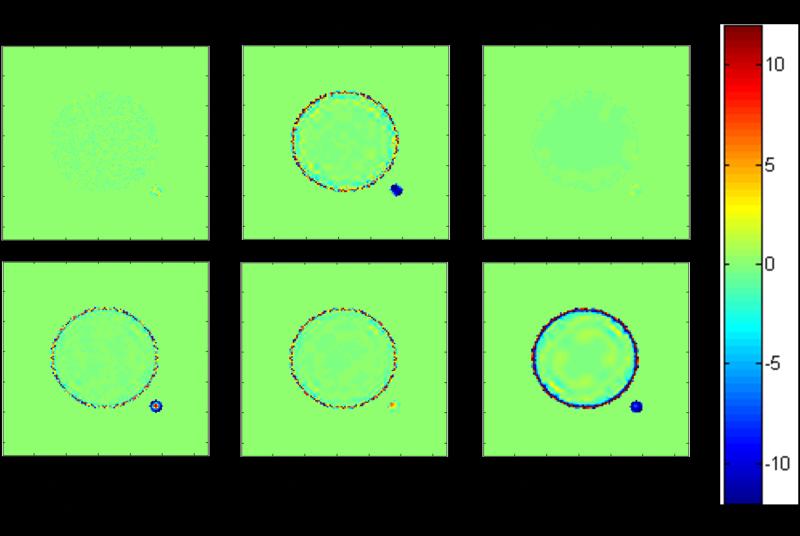
Figure 2 and Table 1 show that both FWTV [41] and Poisson Wavelet preserved the accuracy of lifetime determination after denoising, with Poisson Wavelet performing slightly better especially for the satellite. In this case, the undenoised image and its RME values served as the accuracy standard, since the noise was defined by Poisson random distribution. In other words, these RME values are not exactly zero simply due to randomness. Compared to the undenoised case, if denoising causes RME values to become farther away from zero (possibly due to unsuitable assumption of noise distribution), this is an evidence of producing a bias and making lifetime determination inaccurate. Our goal is therefore to find the denoising methods that can improve the precision to the best degree without causing inaccuracy.
Figure 2.
RME (Relative Mean Error, in %), indicating the accuracy, of the lifetime map constructed with the undenoised and denoised artificial images using several different denoising methods. FWTV [41] and Poisson Wavelet performed equally well and preserved the accuracy of lifetime determination after denoising.
On the other hand, DWT denoising suffered from severe inaccuracy for the ring (averaged RME > 6%) and the satellite (averaged RME < -10%) and even for the inner circle (negative RME on the edge but positive RME off-edge).
3.1.2 A comparison of SWT with different threshold values
With SWT, the RSD values for all the three objects decreased with increasing threshold values from 100 to varying values (between 100 and 500) to 500, because higher threshold caused greater smoothing and removed more noise. However, only SWT with varying threshold had both the inner circle and satellite accurate (absolute values of averaged RME < 1%), although the RME of the ring was still high (5.80%), and higher than that from SWT with threshold = 100. Also, SWT with varying threshold was better than DWT in terms of both precision and accuracy, especially for the accuracy of the satellite.
3.1.3 Overall performance of FLIM denoising methods
Overall, although DWT and SWT under current settings improved precision, they mostly suffered from severe inaccuracies. SWT with varying threshold could still be a good choice except that edge-rich objects such as the ring would have inaccurate lifetime values. Poisson Wavelet and FWTV appeared to be better choices for both improved precision and good accuracy. As for the running times for each 128 × 128 image, wavelet-based methods were faster (DWT, Poisson Wavelet, and SWT had running times ~0.1 sec, ~0.2 sec, and ~0.6 sec, respectively) compared to FWTV (~2.4 sec), making Poisson Wavelet the best choice. However, as will be demonstrated in the next section, our FWTV could be further modified (Section 2.2) to remove non-Poisson distributed noise with good accuracy.
Another key point to make is that, after denoising, the edge of each object may become less definite or blurred due to intensity diffusion. Therefore, it is important to check if denoising causes any bias for segmentation after different types of denoising. This has been indirectly investigated with our artificial images and is presented in Figures 1, 2, and Table 1. When evaluating the accuracy and precision of lifetime determination of the three different objects (the inner circle, the ring, and the satellite), the same pixels were used for the mask for a certain object after different kinds of denoising (or no denoising). In other words, any denoising that caused the object shape / size to slightly change could introduce a bias in the averaged lifetime value, since in this case the mask for that object could not exactly cover the entire object and / or included pixels in the background or in another object. On the other hand, further segmentation analysis will be considered as one of our future directions (Section 3.3).
3.2 Denoising live-cell FLIM images
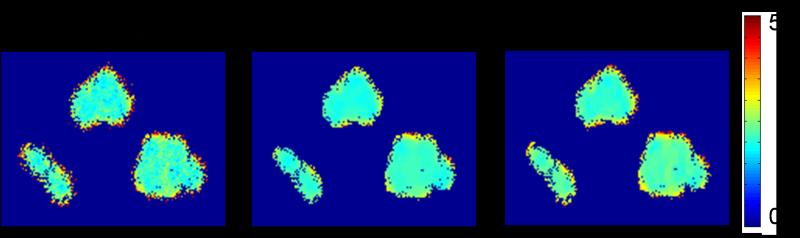
Poisson Wavelet and a modified FWTV were used to denoise the gated fluorescence intensity images from our FLIM system before lifetime map construction. DWT and SWT were not used since they suffered from severe inaccuracies (Section 3.1). FWTV was modified because real imaging systems, especially at low photon counts, have forms of noise other than Poisson distribution. The total photon counts were around 600, which was in the appropriate range (approximately 102 - 104) for the use of denoising for FLIM precision improvement [30]. Both denoising methods could reduce the uncertainties, as shown in Figure 3. However, the lifetime values were different when averaged, and were compared with the averaged undenoised lifetime value, which should remain almost constant pre- and post-denoising, due to the randomness of the uncertainties. Table 2 clearly demonstrates that the modified FWTV could better preserve the overall τ and α values (< 3.5% changes) while still improving local lifetime fitting with averaged R2 increase = ~1.5% and averaged χ2 decrease = ~20%. This is due to the fact that the flexibility and modification of our FWTV rendered it the capability of removing a combination of different forms of noise that occur in real imaging systems. In addition, the accurate denoising results of the modified FWTV illustrated here are also consistent with our previous real-image denoising results [30, 31, 41-43].
Figure 3.
The lifetime maps (in ns) of HCT-116 live cells stained with BCECF. Each map was constructed from four gated intensity images that were either undenoised or denoised with one of the two methods: Poisson Wavelet and modified FWTV. Both denoising methods could reduce the uncertainties compared to the undenoised image. However, the lifetime values within the cell regions denoised with the two methods were different.
Table 2.
The averaged lifetime values (τ, in ns), pre-exponential terms (α), R-squared values (R2) and Chi-squared values (χ2) over the non-zero pixels in the live-cell lifetime images shown in Figure 3, and their % changes compared to the undenoised image.
| Undenoised | Poisson Wavelet | Modified FWTV | |
|---|---|---|---|
| τ | 2.38 | 2.08 | 2.30 |
| % τ change | 0 | −12.61 | −3.32 |
| α | 190 | 183 | 186 |
| % α change | 0 | −3.68 | −2.11 |
| R 2 | 0.93 | 0.96 | 0.94 |
| % R2 change | 0 | 2.91 | 1.51 |
| χ 2 | 1.20 | 0.79 | 0.95 |
| % χ change | 0 | −34.31 | −20.33 |
3.3 Future improvements
Future improvements of the current algorithms include local thresholding (different threshold values can be used for different decomposition levels) and more sophisticated approaches to threshold determination in DWT, SWT, and other wavelet-based methods for FLIM use. Newly developed methods for wavelet-based denoising of Poisson-corrupted images [50] will be further considered in the future. Also, high-speed FWTV may be developed by improving the code efficiency and adopting advanced algorithms [51, 52]. In addition, precision and accuracy evaluation of multi-exponential decay lifetime determination is also an important issue and will be investigated in combination with FLIM image denoising. Finally, since precise and accurate noise removal can enhance other image processing techniques including deconvolution (with 3D image slicing) / deblurring [53], segmentation, and object tracking, the combination of denoising and these techniques could be employed for FLIM use, as well.
As a key future direction, we understand that segmentation analysis following denoising is an important issue. However, advanced segmentation methods need to be applied to the images for this kind of analysis, and this will inevitably introduce more uncertainties since the results will definitely depend on the choice of segmentation method. In this work, therefore, we focused more on preserving the accuracy of the lifetime determination while enhancing the precision, leaving segmentation analysis as one of our major future directions following this work.
4. Conclusions
In this study, TV-based and wavelet-based image denoising methods were characterized and compared for individual strengths and weaknesses with artificial images and live-cell images acquired from a gated time-domain FLIM system. With artificial images, FWTV and Poisson Wavelet performed almost equally well (precision improvement up to 10-fold, depending on the geometry of objects) and better than DWT and SWT in terms of mostly accuracy and partially precision, with wavelet-based methods running faster. For live-cell images, the modified FWTV better preserved the overall τ and α values (< 3.5% changes compared to the undenoised image) while still improving local lifetime fitting (averaged R2 increase = ~1.5% and averaged χ2 decrease = ~20%). The methods proposed here can enhance both the precision and the accuracy of FLIM, especially under challenging imaging conditions, such as low-light or fast video-rate imaging. This approach should aid current and rapidly emerging FLIM applications, including live-cell, in vivo animal, or endoscopic imaging, and is potentially applicable to other biomedical imaging systems.
Acknowledgements
This work was supported in part by National Institutes of Health grant R01-CA-114542 (to M.-A.M.).
ACRONYMS
- CWT
Continuous Wavelet Transform
- DWT
Discrete Wavelet Transform
- FLIM
Florescence Lifetime Imaging Microscopy
- FWTV
f-weighted Total Variation
- RME
Relative Mean Error
- RSD
Relative Standard Deviation
- SWT
Stationary Wavelet Transform
- TV
Total Variation
Biography
 Ching-Wei Chang received his Ph.D. degree in biomedical engineering from the University of Michigan, Ann Arbor, in 2009. Currently, he is a postdoctoral research fellow at the University of California, Berkeley. His research interests include image processing (denoising, segmentation, and object tracking) and the application of advanced optical methods (FRET, FLIM, 2-photon laser ablation) to cell biology.
Ching-Wei Chang received his Ph.D. degree in biomedical engineering from the University of Michigan, Ann Arbor, in 2009. Currently, he is a postdoctoral research fellow at the University of California, Berkeley. His research interests include image processing (denoising, segmentation, and object tracking) and the application of advanced optical methods (FRET, FLIM, 2-photon laser ablation) to cell biology.
 Mary-Ann Mycek is an Associate Professor of Biomedical Engineering at the University of Michigan. She received her Ph.D. in Physics from U.C. Berkeley, where she specialized in condensed matter physics and optical spectroscopy, before pursuing postdoctoral training in laser medicine at Harvard Medical School. Her translational research program in Biomedical Optics includes basic (pre-clinical), applied (clinical), and computational research toward quantitative, noninvasive, optical sensing and imaging in cells and tissues.
Mary-Ann Mycek is an Associate Professor of Biomedical Engineering at the University of Michigan. She received her Ph.D. in Physics from U.C. Berkeley, where she specialized in condensed matter physics and optical spectroscopy, before pursuing postdoctoral training in laser medicine at Harvard Medical School. Her translational research program in Biomedical Optics includes basic (pre-clinical), applied (clinical), and computational research toward quantitative, noninvasive, optical sensing and imaging in cells and tissues.
References
- 1.Bloch S, Lesage F, McIntosh L, Gandjbakhche A, Liang KX, Achilefu S. Journal of Biomedical Optics. 2005;10:054003. doi: 10.1117/1.2070148. [DOI] [PubMed] [Google Scholar]
- 2.Pelet S, Previte MJR, Kim D, Kim KH, Su TTJ, So PTC. Microscopy Research and Technique. 2006;69:861–874. doi: 10.1002/jemt.20361. [DOI] [PubMed] [Google Scholar]
- 3.Schweitzer D, Schenke S, Hammer M, Schweitzer F, Jentsch S, Birckner E, Becker W, Bergmann A. Microscopy Research and Technique. 2007;70:410–419. doi: 10.1002/jemt.20427. [DOI] [PubMed] [Google Scholar]
- 4.Elson DS, Munro I, Requejo-Isidro J, McGinty J, Dunsby C, Galletly N, Stamp GW, Neil MAA, Lever MJ, Kellett PA, Dymoke-Bradshaw A, Hares J, French PMW. New Journal of Physics. 2004;6:1–13. [Google Scholar]
- 5.Munro I, McGinty J, Galletly N, Requejo-Isidro J, Lanigan PMP, Elson DS, Dunsby C, Neil MA, Lever MJ, Stamp GW, French PM. Journal of Biomedical Optics. 2005;10:051403. doi: 10.1117/1.2102807. [DOI] [PubMed] [Google Scholar]
- 6.Siegel J, Elson DS, Webb SED, Lee KCB, Vlanclas A, Gambaruto GL, Leveque-Fort S, Lever MJ, Tadrous PJ, Stamp GWH, Wallace AL, Sandison A, Watson TF, Alvarez F, French PMW. Applied Optics. 2003;42:2995–3004. doi: 10.1364/ao.42.002995. [DOI] [PubMed] [Google Scholar]
- 7.Berezin MY, Akers WJ, Guo K, Fischer GM, Daltrozzo E, Zumbusch A, Achilefu S. Biophys J. 2009;97:L22–4. doi: 10.1016/j.bpj.2009.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Goiffon RJ, Akers WJ, Berezin MY, Lee H, Achilefu S. J Biomed Opt. 2009;14:020501. doi: 10.1117/1.3095800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nothdurft RE, Patwardhan SV, Akers W, Ye Y, Achilefu S, Culver JP. J Biomed Opt. 2009;14:024004. doi: 10.1117/1.3086607. [DOI] [PubMed] [Google Scholar]
- 10.Schweitzer D, Quick S, Schenke S, Klemm M, Gehlert S, Hammer M, Jentsch S, Fischer J. Ophthalmologe. 2009;106:714–22. doi: 10.1007/s00347-009-1975-4. [DOI] [PubMed] [Google Scholar]
- 11.Chang CW, Sud D, Mycek MA. Methods Cell Biol. 2007;81:495–524. doi: 10.1016/S0091-679X(06)81024-1. [DOI] [PubMed] [Google Scholar]
- 12.Sud D, Mehta G, Mehta K, Linderman J, Takayama S, Mycek MA. Journal of Biomedical Optics. 2006;11:050504. doi: 10.1117/1.2355665. [DOI] [PubMed] [Google Scholar]
- 13.Sud D, Mycek MA. Journal of Biomedical Optics. 2009;14:020506. doi: 10.1117/1.3116714. [DOI] [PubMed] [Google Scholar]
- 14.Sud D, Zhong W, Beer DG, Mycek MA. Optics Express. 2006;14:4412–4426. doi: 10.1364/oe.14.004412. [DOI] [PubMed] [Google Scholar]
- 15.Chang CW, Wu M, Merajver SD, Mycek MA. Journal of Biomedical Optics. 2009;14:060502. doi: 10.1117/1.3257254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chang CW, Mycek MA. Reviews in Fluorescence. 2012;2010:173–198. [Google Scholar]
- 17.Pelet S, Previte MJ, So PT. J Biomed Opt. 2006;11:34017. doi: 10.1117/1.2203664. [DOI] [PubMed] [Google Scholar]
- 18.Barber PR, Ameer-Beg SM, Pathmananthan S, Rowley M, Coolen AC. Biomed Opt Express. 2010;1:1148–1158. doi: 10.1364/BOE.1.001148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Konig K, Becker TW, Fischer P, Riemann I, Halbhuber KJ. Opt Lett. 1999;24:113–5. doi: 10.1364/ol.24.000113. [DOI] [PubMed] [Google Scholar]
- 20.Rau KR, Guerra A, Vogel A, Venugopalan V. Applied Physics Letters. 2004;84:2940–2942. [Google Scholar]
- 21.Guo LW, Au OC, Ma MY, Liang ZQ. Journal of Signal Processing Systems for Signal Image and Video Technology. 2010;60:273–290. [Google Scholar]
- 22.Guo LW, Au OC, Ma MY, Wong PHW. Ieee Transactions on Circuits and Systems for Video Technology. 2010;20:236–249. [Google Scholar]
- 23.Vonesch C. Ph.D. thesis, École Polytechnique Fédérale De Lausanne. 2009. [Google Scholar]
- 24.Vonesch C, Unser M. IEEE Trans Image Process. 2009;18:509–23. doi: 10.1109/TIP.2008.2008073. [DOI] [PubMed] [Google Scholar]
- 25.Spring BQ, Clegg RM. Journal of Microscopy-Oxford. 2009;235:221–237. doi: 10.1111/j.1365-2818.2009.03212.x. [DOI] [PubMed] [Google Scholar]
- 26.Buranachai C, Kamiyama D, Chiba A, Williams BD, Clegg RM. Journal of Fluorescence. 2008;18:929–942. doi: 10.1007/s10895-008-0332-3. [DOI] [PubMed] [Google Scholar]
- 27.Buades A, Coll B, Morel JM. Multiscale Modeling & Simulation. 2005;4:490–530. [Google Scholar]
- 28.Boulanger J, Sibarita JB, Kervrann C, Bouthemy P. 2008 Ieee International Symposium on Biomedical Imaging: From Nano to Macro. 2008;1-4:748–751. [Google Scholar]
- 29.Delpretti S, Luisier F, Ramani S, Blu T, Unser M. 2008 Ieee International Symposium on Biomedical Imaging: From Nano to Macro. 2008;1-4:149–152. [Google Scholar]
- 30.Chang CW, Mycek MA. Optics Express. 2010;18:8688–8696. doi: 10.1364/OE.18.008688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chang CW, Mycek MA. Proc. SPIE. 2009;7370:7370091–7370096. [Google Scholar]
- 32.Zhong W, Wu M, Chang CW, Merrick KA, Merajver SD, Mycek MA. Optics Express. 2007;15:18220–18235. doi: 10.1364/oe.15.018220. [DOI] [PubMed] [Google Scholar]
- 33.Urayama P, Zhong W, Beamish JA, Minn FK, Sloboda RD, Dragnev KH, Dmitrovsky E, Mycek MA. Applied Physics B-Lasers and Optics. 2003;76:483–496. [Google Scholar]
- 34.Xu Z, Raghavan M, Hall TL, Chang CW, Mycek MA, Fowlkes JB, Cain CA. Ieee Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2007;54:2091–2101. doi: 10.1109/TUFFC.2007.504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Urayama PK, Beamish JA, Minn FK, Hamon EA, Mycek M-A. Conference on Lasers and Electro-Optics. Optical Society of America; Washington D.C.: 2002. A UV fluorescence lifetime imaging microscope to probe endogenous cellular fluorescence. [Google Scholar]
- 36.Urayama PK, Mycek MA. Fluorescence lifetime imaging microscopy of endogenous biological fluorescence. In: Mycek MA, Pogue BW, editors. Handbook of Biomedical Fluorescence. Marcel Dekker, Inc.; New York: 2003. [Google Scholar]
- 37.Zhong W, Urayama P, Mycek M-A. Journal of Physics D: Applied Physics. 2003;36:1689–1695. [Google Scholar]
- 38.Bugiel I, König K, Wabnitz H. Lasers in the Life Sciences. 1989;3:47–53. [Google Scholar]
- 39.Wang XF, Uchida T, Coleman DM, Minami S. Applied Spectroscopy. 1991;45:360–366. [Google Scholar]
- 40.Sharman KK, Periasamy A, Ashworth H, Demas JN, Snow NH. Analytical Chemistry. 1999;71:947–952. doi: 10.1021/ac981050d. [DOI] [PubMed] [Google Scholar]
- 41.Chang CW. Ph.D. thesis. University of Michigan; 2009. http://deepblue.lib.umich.edu/bitstream/2027.42/63765/1/chingwei_1.pdf. [Google Scholar]
- 42.Chang CW, Mycek MA. Proc. SPIE. 2010;7570:757007. [Google Scholar]
- 43.Chang CW, Mycek MA. Journal of Biomedical Optics. 2010;15:056013. doi: 10.1117/1.3494566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rudin LI, Osher S, Fatemi E. Physica D. 1992;60:259–268. [Google Scholar]
- 45.Le T, Chartrand R, Asaki TJ. Journal of Mathematical Imaging and Vision. 2007;27:257–263. [Google Scholar]
- 46.Mallat S. IEEE Pattern Anal. and Machine Intell. 1989;11:674–693. [Google Scholar]
- 47.Coifman RR, Donoho DL. Lecture Notes in Statistics. 1995;103:125–150. [Google Scholar]
- 48.Rodrigues I, Sanches J, Bioucas-Dias J. 2008 15th IEEE International Conference on Image Processing. 2008;1-5:1756–1759. [Google Scholar]
- 49.Willett RM, Nowak RD. 2004 2nd IEEE International Symposium on Biomedical Imaging: Macro to Nano. 2004;1 and 2:1192–1195. [Google Scholar]
- 50.Luisier F, Vonesch C, Blu T, Unser M. Signal Processing. 2010;90:415–427. [Google Scholar]
- 51.Chambolle A. Energy Minimization Methods in Computer Vision and Pattern Recognition. Proceedings. 2005;3757:136–152. [Google Scholar]
- 52.Figueiredo MAT, Dias JB, Oliveira JP, Nowak RD. Proceedings International Conference on Image Processing. 2006;1-7:2633–2636. [Google Scholar]
- 53.Rooms F, Philips W, Lidke DS. J Microsc. 2005;218:22–36. doi: 10.1111/j.1365-2818.2005.01455.x. [DOI] [PubMed] [Google Scholar]