Integration of Network Topological and Connectivity Properties for Neuroimaging Classification

Abstract

Rapid advances in neuroimaging techniques have provided an efficient and noninvasive way for exploring the structural and functional connectivity of the human brain. Quantitative measurement of abnormality of brain connectivity in patients with neurodegenerative diseases, such as mild cognitive impairment (MCI) and Alzheimer’s disease (AD), have also been widely reported, especially at a group level. Recently, machine learning techniques have been applied to the study of AD and MCI, i.e., to identify the individuals with AD/MCI from the healthy controls (HCs). However, most existing methods focus on using only a single property of a connectivity network, although multiple network properties, such as local connectivity and global topological properties, can potentially be used. In this paper, by employing multikernel based approach, we propose a novel connectivity based framework to integrate multiple properties of connectivity network for improving the classification performance. Specifically, two different types of kernels (i.e., vector-based kernel and graph kernel) are used to quantify two different yet complementary properties of the network, i.e., local connectivity and global topological properties. Then, multikernel learning (MKL) technique is adopted to fuse these heterogeneous kernels for neuroimaging classification. We test the performance of our proposed method on two different data sets. First, we test it on the functional connectivity networks of 12 MCI and 25 HC subjects. The results show that our method achieves significant performance improvement over those using only one type of network property. Specifically, our method achieves a classification accuracy of 91.9%, which is 10.8% better than those by single network-property-based methods. Then, we test our method for gender classification on a large set of functional connectivity networks with 133 infants scanned at birth, 1 year, and 2 years, also demonstrating very promising results.

I. INTRODUCTION

ALZHEIMER’S disease (AD) is the most common type of dementia, accounting for 60%–80% of age-related dementia cases. It is predicted that the number of affected people will double in the next 20 years, and 1 in 85 people will be affected by 2050 [1]. Since the AD-specific brain changes begin years before the patient becomes symptomatic, early clinical diagnosis becomes a challenging task. Accordingly, there have been a lot of studies focusing on possible identification of such changes at the early stage, i.e., mild cognitive impairment (MCI), by leveraging neuroimaging data [2], [3]. Recently, machine learning and pattern classification approaches have been widely used to identify AD and MCI at an individual level [4]–[8], rather than at a group level, i.e., only the comparison between different clinical groups. Most of these works focused on using regions-of-interest (ROIs) or voxel-wise features extracted from single imaging modality or multiple imaging modalities, e.g., magnetic resonance imaging (MRI) or/and fluorodeoxyglucose positron emission tomography (FDG-PET).

In the literature, it has been shown that many neurological and psychiatric disorders can be categorized as dysconnectivity/hyperconnectivity syndromes, which are commonly associated with the disrupted synchronization or the abnormal integration of different brain regions [9], [10]. Rapid advances in neuroimaging techniques have provided an efficient and noninvasive way for studying the structural and functional connectivity of human brain [11]. Functional connectivity, which is referred to as the functional association pattern among brain regions, provides a view to understand the relationship between the activities in certain brain regions and the specific mental functions, and thus could provide an insight into the pathophysiological mechanism in neurodegenerative diseases, such as MCI and AD.

Several groups have investigated the connectivity of brain networks in neurodegenerative diseases (e.g., MCI and AD) by using group analysis, where abnormal connectivities are found in a series of brain networks, including default-mode network (DMN) [12] and other resting-state networks (RSNs) [13]. These findings indicate that AD/MCI is associated with a large-scale highly connected functional network, rather than a single isolated region [14]. For instance, “small-world” properties (characterized by high local clustering and short path length) have been reported to be disrupted in functional brain network of AD and MCI patients [15].

On the other hand, connectivity network based methods have also been applied to accurately identify individuals with AD and MCI from the healthy controls (HCs) [8], [16]–[22]. For example, some researchers used local measures (e.g., local clustering coefficients and the weights between nodes) of connectivity network to identify AD/MCI patients [8], [16], [23]. However, to the best of our knowledge, most of the existing approaches use only a single type of network property for AD and MCI classification, although multiple network properties, including local connectivity and global topological properties, can potentially be used. Intuitively, effective integration of these multiple network properties may further improve the classification performance.

Accordingly, in this paper, we present a new connectivity network based classification framework to accurately identify individuals with MCI from the HCs. The key to our approach involves the use of kernel-based method to quantify and integrate multiple properties of connectivity network. Specifically, for each brain connectivity network, we first construct two different types of kernels: a vector-based kernel corresponding to the conventional local network property (e.g., local clustering coefficients) and a graph kernel corresponding to the global topological property of the network, and then we effectively integrate them for classification. Our method provides a new perspective to apply different yet complementary properties of the connectivity network for improving brain disease classification.

II. MATERIALS AND METHOD

A. Data Acquisition

Subjects used in the current study were recruited by the Duke-UNC Brain Imaging and Analysis Center (BIAC), Durham, North Carolina, USA. There are totally 37 participants, including 12 MCI patients and 25 HCs. Demographic information of the participants is shown in Table I. Informed consent was obtained from all participants, and the experimental protocols were approved by the institutional ethics board. All recruited subjects were diagnosed by expert consensus panels. A 3.0-T GE Signa EXCITE scanner was used to acquire resting-state functional MRI (fMRI) volumes. The fMRI volumes of each participant were acquired with the following parameters: TR/TE = 2000/32 ms, flip angle = 77°, acquisition matrix = 64 × 64, FOV = 256 × 256 mm², voxel resolution = 4 × 4 × 4 mm³, 34 slices, 150 volumes, and voxel thickness = 4 mm. During scanning, all subjects were instructed to keep their eyes open and stare at a fixation cross in the middle of the screen, which lasted for 5 min.

TABLE I.

Characters of the Participants in the Current Study

Group	MCI	HC
No. of subjects (male/female)	6/6	9/16
Age (mean ± SD)	75.0 ± 8.0	72.9 ± 7.9
Years of education (mean ± SD)	18.0 ± 4.1	15.8 ± 2.4
MMSE (mean ± SD)	28.5 ± 1.5	29.3 ± 1.1

Note: MMSE = Mini-Mental State Examination.

B. Method

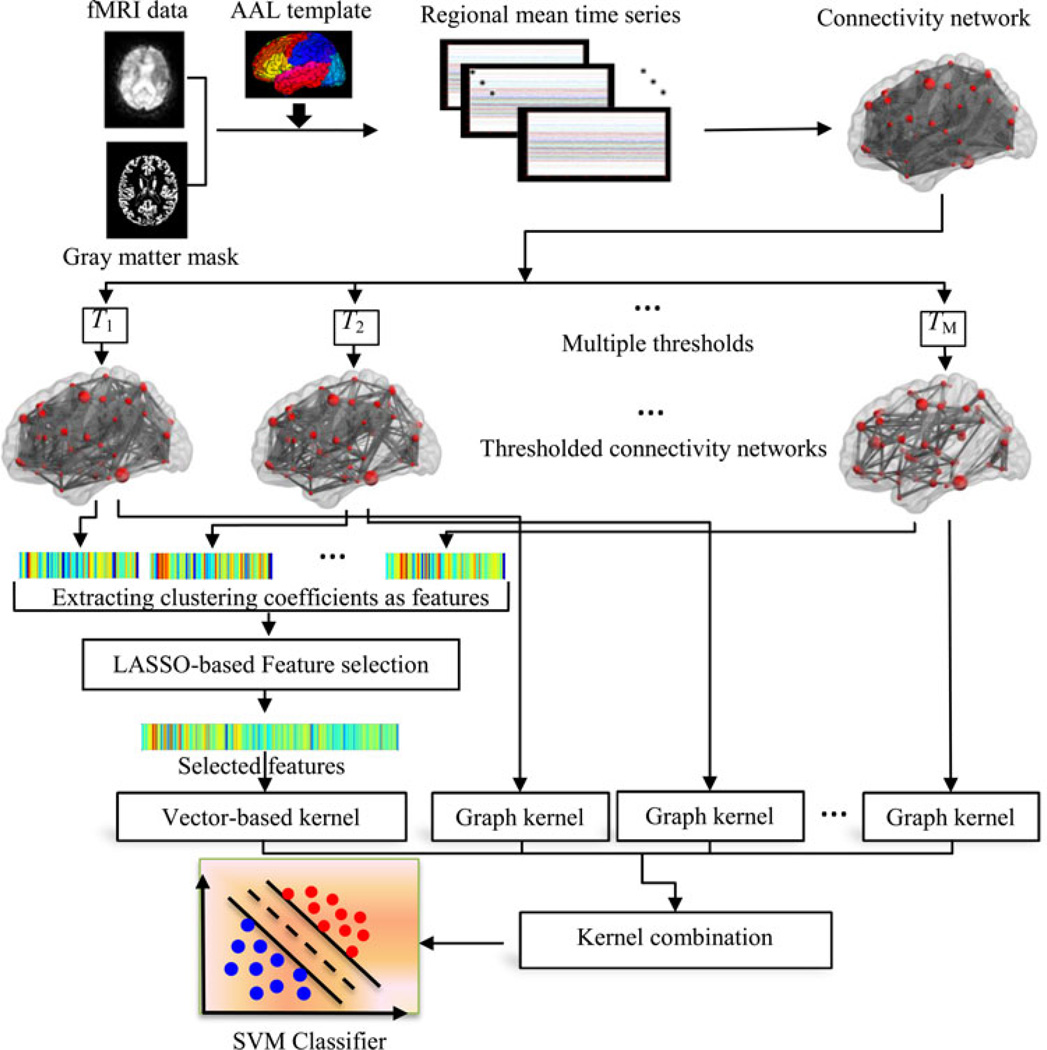
It has been reported that the connectivity patterns/properties of the brains with AD/MCI differ from those of the normal brains [13], [24]. Thus, these properties may serve as potential biomarkers for disease diagnosis. In this paper, we propose a new method for integrating multiple properties of a connectivity network to improve the disease diagnosis performance. Fig. 1 illustrates the framework of our proposed method. Specifically, for each subject, a functional connectivity network is first constructed from the respective fMRI data. In order to remove weak or potentially insignificant connections and also to reflect multiple levels of topological properties of the original functional connectivity network, multiple pre-defined values are used to separately threshold the functional connectivity network. Then, two different types of kernels, i.e., a vector-based kernel and a graph kernel, are respectively computed to quantify two different yet complementary network properties, i.e., local clustering and global topological properties. Finally, the multikernel support vector machine (SVM) is adopted to fuse these two heterogeneous kernels for distinguishing the individuals with MCI from the HCs. Different from the previous multimodality-based integrating methods [6], [7], which combine the same type of kernels from multiple data sources, in this study, we combine different types of kernels from different properties of the same connectivity network. The core of our proposed method is summarized below and will be discussed comprehensively in the subsequent sections:

1. Extraction of multilevel topological properties of connectivity network using multiple thresholds;

2. Measurement of topological similarity using graph kernel;

3. Feature selection using the least absolution shrinkage and selection operator (LASSO) method;

4. Integration of different yet complementary network properties using a multikernel SVM.

Fig. 1.

Proposed classification framework.

1) Image Processing and Network Construction

The preprocessing step of the fMRI images, which includes slice timing correction and head-motion correction, was performed using the Statistical Parametric Mapping software package (SPM8, available at http://www.fil.ion.ucl.ac.uk.spm). Specifically, the first 10 acquired fMRI images of each subject were discarded to ensure magnetization equilibrium. The remaining 140 images were first corrected for the acquisition time delay among different slices before they were realigned to the first volume of the remaining images for head motion correction. Since the regions of ventricles and white matter (WM) contain a relatively high proportion of noise caused by the cardiac and respiratory cycles [25], we utilized only the blood oxygenation level dependent (BOLD) signals extracted from gray matter (GM) tissue to construct the functional connectivity network. Accordingly, we first segmented the T1-weighted MR image of each subject into GM, WM, and cerebrospinal fluid (CSF). GM tissue of each subject was then used to mask the corresponding fMRI images to eliminate the possible effects from CSF and WM.

The first scan of the remaining fMRI scans was co-registered to the T1-weighted MR image of the same subject. The estimated transformation was then applied to all other fMRI scans of the same subject. The aligned fMRI scans were further parcellated into 90 ROIs by warping the Automated Anatomical Labeling (AAL) [26] template to the subject space using a deformable registration method [27]. Finally, for each subject, the mean time series of each ROI was computed by averaging the fMRI time series over all voxels in that particular ROI.

In the current study, the mean time series of each ROI was band-pass filtered within in frequency interval [0.025 ≤ f ≤ 0.100 Hz], since the fMRI dynamics of neuronal activities are most salient within this frequency interval. It has been reported in [28] that the frequency band of (0.027–0.073 Hz) demonstrated significantly higher test-retest reliability than other frequency bands. Also, it provides a reasonable tradeoff between avoiding the physiological noise associated with higher frequency oscillations [29] and the measurement error associated with estimation of very low frequency correlations from the limited time series [30].

Finally, by using pairwise Pearson correlation coefficient, a functional connectivity network was constructed with the nodes of network corresponding to the ROIs and the weights of edges corresponding to the Pearson correlation coefficients between a pair of ROIs. Fisher’s r-to-z transformation was applied on the elements of the functional connectivity network (matrix) to improve the normality of the correlation coefficients. Moreover, we removed all negative correlations from the obtained connectivity networks to extract the meaningful network measures.

2) Kernel-Based Method

Kernel-based method offers a very general framework for performing pattern analysis (e.g., classification and clustering) on different types of data. The main idea of kernel-based method is to implicitly perform a mapping from the input space to a high dimensional feature space, where the input data are more likely to be linearly separable than in the original lower dimensional space. Informally, a kernel is defined as a function of two subjects that quantifies their similarity. Specifically, given two subjects x and x′, the kernel can be defined as

$$k(x,x\prime )=\langle \mathrm{\Phi }(x),\mathrm{\Phi }(x\prime )\rangle$$ (1)

where Φ is a mapping function that maps data from the input space to the feature space. Once given a kernel function, many kernel-based learning algorithms, such as SVM, can be used to perform pattern analysis.

The definition/selection of the kernel depends on specific data type and the domain knowledge concerning the patterns (i.e., training subjects). There are several kernel functions which have been successfully used in the literature, such as the linear kernel and Gaussian radial basis function (RBF) kernel. In the following, we will introduce the topology-based graph kernel, which will be used in our proposed method.

a) Topology-Based Graph Kernel

Kernel can also be defined on complex data types, e.g., graph in the connectivity network. The respective kernel is called graph kernel, which maps the graph data from the original graph space to the feature space and further measures the similarity between two graphs by comparing their topological structures [31]. Thus, graph kernel bridges the gap between graph-structured data and many kernel-based learning algorithms, with successful applications in computer vision [32] and bioinformatics [33].

Many methods have been proposed to construct the graph kernel. In this study, the graph kernel proposed in [31], called Weisfeiler–Lehman subtree kernel, is used to measure the topological similarity between paired connectivity networks. It has been shown that this type of graph kernel can effectively capture the topological information from graphs and achieve better performance than the state-of-the-art graph kernels [31].

Before giving the definition of graph kernel, some basic terms are first introduced. Here, a graph is composed of a finite set of nodes and edges. The graph which has a label associated with each node is called the labeled graph. A subtree is a restricted form of a graph, where one node is called the root and each node has a path to the root (i.e., any two nodes are connected by exactly one simple path with no recurring nodes). Subtree pattern extends the notion of subtree by allowing repetitions of nodes. However, these same nodes are treated as distinct nodes.

Shervashidze et al. proposed a subtree-pattern-based method to construct the graph kernel [31]. The core concept of their graph kernel comes from the Weisfeiler–Lehman test of isomorphism. For a pair of graphs G and G′, the basic process of the 1-dimensional Weisfeiler–Lehman test is as follows: if these two graphs are unlabeled, i.e., vertices of the graph have not been assigned with labels, every vertex in each graph is first labeled with the number of edges that are connected to that vertex. Then, at each subsequent step (or iteration), the label of each node is simultaneously updated based on its previous label and the labels of its neighbors. For example, for each node, we augment its label by the sorted set of node labels of its neighboring nodes, and compress these augmented labels into a new shorter label. This process is iterated until the node label sets ofG and G′ differ, or the number of iteration reaches a predefined maximum value h.

Given two graphs G and G′, let L_i = {l_i1, l_i2,…, l_i|li|} (i = 0, 1,…, h) be the set of letters that occur as node labels in G or G′ at the end of the ith iteration of the Weisfeiler–Lehman test of isomorphism. Here, L₀ denotes the set of the initial labels of graph G or G′. Assume all L_i are pairwise disjointed. Without loss of generality, assume every L_i is ordered, and then the Weisfeiler–Lehman subtree kernel on two graphs G and G′ with h iterations is defined as [31]:

$$k(G,G\prime )=\langle \mathrm{\Phi }(G),\mathrm{\Phi }(G\prime )\rangle$$ (2)

where

$$\mathrm{\Phi }(G)=({\rho }_0(G,l_{01}),\dots ,{\rho }_0(G,l_{0|L_0|}),\dots ,{\rho }_h(G,l_{h1}),\dots ,{\rho }_h(G,l_{h|L_h|}))$$

and

$$\mathrm{\Phi }(G\prime )=({\rho }_0(G\prime ,l_{01}),\dots ,{\rho }_0(G\prime ,l_{0|L_0|}),\dots ,{\rho }_h(G\prime ,l_{h1}),\dots ,{\rho }_h(G\prime ,l_{h|L_h|}))$$

with ρ_i (G, l_ij) and ρ_i (G′, l_ij) are the numbers of occurrences of the letter l_ij in G and G′, respectively. It has been proven that this kernel is positive definite [31]. It is worth noting that each compressed label denotes a subtree pattern. According to this definition, the graph kernel embeds the local and global graph topological information into kernel.

b) Multikernel Support Vector Machine

Recent studies on multikernel learning (MKL) have shown that the integration of multiple kernels not only increases the classification accuracy but also enhances the interpretability of the results [34]. Several recent studies in neuroimaging have also shown that multikernel combination provides a powerful tool for systematically aggregating different imaging modalities into a single learned model [6]–[8]. Generally, kernel integration is achieved through a linear combination of multiple kernels

$$k(x,x\prime )=\sum _m{\beta }_m{k}_m(x,x\prime )$$ (3)

where k_m (x, x′) is a basic kernel built for subjects x and x′, and β_m is a nonnegative weighting parameter with Σ_m β_m = 1.

In the current study, we adopt our previously developed multikernel SVM method [7], [8], [35] to combine multiple kernels. Different from the existing MKL methods [34] that jointly optimize the weighting parameters β_m together with other SVM parameters, in our multikernel SVM, the optimal weighting parameters β_m are determined via grid search on the training data. Once the optimal weighting parameters β_m are obtained, the multikernel SVM can be naturally embedded into the conventional single-kernel SVM framework to classify the MCI patients from HCs. On the other hand, since the vector-based kernel and the graph kernel are two different types of kernels, a normalization step must be performed individually as in (4), before combining them using the multikernel SVM.

$$\tilde{k}(x,x\prime )=k(x,x\prime )/\sqrt{k(x,x)k(x\prime ,x\prime ).}$$ (4)

3) Multiple Properties of Connectivity Network

In functional connectivity networks, the connectivity describes frequency-dependent correlation between spatially distinct brain regions. Some weak and potentially insignificant connections for identifying patients from controls could obscure the network topology, when considered together with strong and important connections. Thus, it may be important to discard these connections by using a thresholding approach. Moreover, the thresholded networks are often simpler to characterize and thus have more easily defined models for statistical comparison [36]. However, the thresholds are often arbitrarily determined [13], [15], [37], and the optimal threshold can only be determined after exploring the network properties over a broad range of plausible thresholds. On the other hand, the network with different thresholds may represent different level of topological properties, and these properties may be complementary to each other in improving the classification performance. Therefore, in the current study, a multiple-threshold method is adopted to reflect the multiple levels of network properties. Specifically, given a threshold T_m (m = 1,…, M), the connectivity network (matrix) G = [τ_ijn×n is thresholded as

$${\tau }_{ij}^m=\{\begin{array}{cc}0,\hfill & \text{if}{\tau }_{ij}<T_m\hfill \\ {\tau }_{ij},\hfill & \text{otherwise}\hfill \end{array}$$ (5)

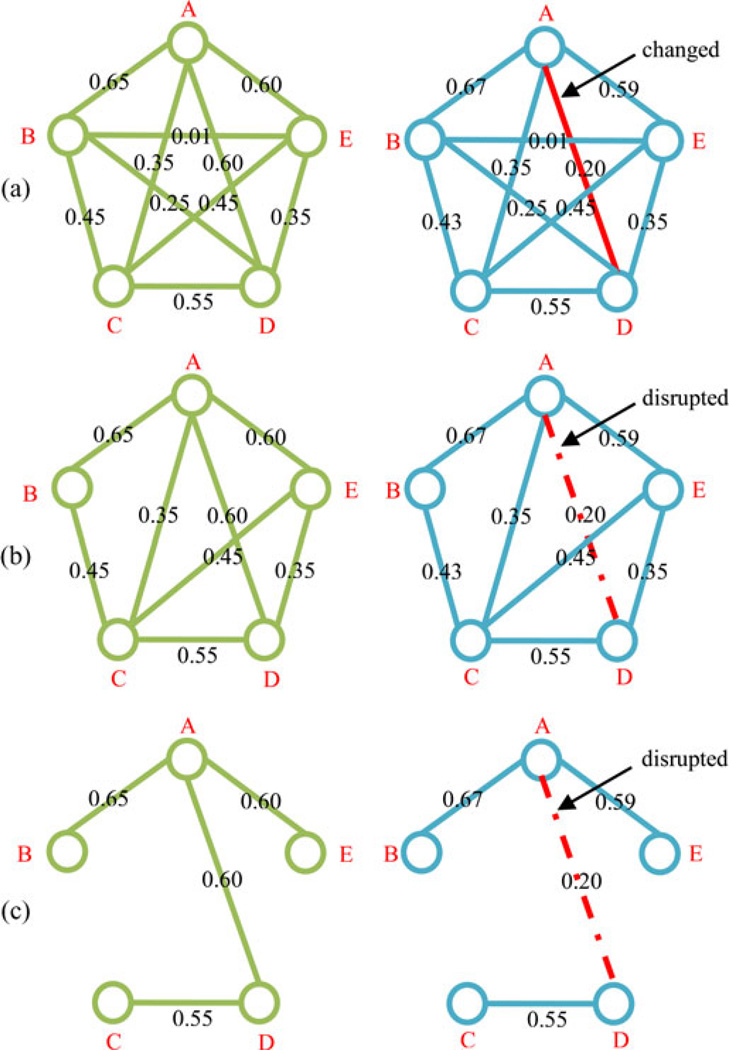
where τ_ij denotes the connection weight between the ith and jth network-nodes/ROIs. Fig. 2 gives an example of our multiple-threshold method. Here, the original connectivity networks in Fig. 2(a) are fully connected, with no differences between MCI and HC in the topological structures. However, when these networks are thresholded with the value T = 0.3 and T = 0.5 respectively, significant differences can be observed between MCI and HC, where the weak connections (e.g., the connection between nodes B and E) and the nonsignificant connections (e.g., the connection between nodes B and D) have been removed, as shown in Fig. 2(b) or (c). Moreover, the topological structures with different thresholds are obviously different for each healthy subject (or MCI subject).

Fig. 2.

Examples of multiple-thresholded connectivity networks. (a) Original functional connectivity networks, (b) thresholded connectivity networks with T = 0.3, and (c) thresholded connectivity networks with T = 0.5. Here, A, B, C, D, and E represent five different nodes/ROIs; value on each edge denotes the connection weight between a pair of ROIs. The connectivity between nodes A and D on a patient with MCI (right) has been changed, compared to a HC (left).

As a local network property, local clustering reflects the prevalence of clustered connectivity around individual network nodes (or brain regions). Numerous studies have shown that the local clustering of functional connectivity network has been disrupted in the AD and MCI patients at a group comparison level [13], [38]. In this study, the local weighted clustering coefficients are extracted from each thresholded connectivity network as [11], [39]

$$c_p^m=\frac{2{\sum }_{i,j}{({\tau }_{pi}^m{\tau }_{ij}^m{\tau }_{jp}^m)}^{1/3}}{d_p^m(d_p^m-1)}$$ (6)

where $d_p^m$ is the number of neighboring nodes around the node p. The coefficients of n nodes ${\mathit{x}}^m={[c_p^m]}_{p=1,\dots ,n}$ compose a feature vector representing the local clustering property of the thresholded connectivity network G^m. We then concatenate the feature vectors of all the thresholed connectivity networks to form a single large vector x = [(x¹)^T…(x^m)^T…(x^M)^T]^T. Features extracted from all thresholded connectivity networks potentially include many irrelevant and redundant features for classification. Therefore, LASSO-based feature selection (see next section) is performed in our method to filter out those features. Finally, vector-based kernel is computed, based on the selected features, to measure the similarity of two connectivity networks using local clustering property.

Another important network property is the topological structure of the whole connectivity network, which characterizes the entire network. It has been widely reported that the topological properties of the whole brain network have been changed for AD and MCI [15], [40]. Since the connectivity network is a form of graph, where the ROIs and the connectivities between ROIs correspond, respectively, to the nodes and edges, it is natural to apply graph kernel to our data. In this study, the Weisfeiler–Lehman subtree kernel [31] discussed in the previous subsection will be constructed on each thresholded connectivity network across different subjects to measure the similarity of topological structures, as shown in Fig. 1. It is noteworthy that graph kernel only preserves the local and global structural information of connectivity networks, while it does not consider the weight information (i.e., connectivity strength) of edges, which can be captured by vector-based kernel through extraction of features based on the local clustering property of connectivity networks.

4) LASSO-Based Feature Selection

Feature selection, which can be considered as the biomarker identification for AD and MCI, attempts to remove as many irrelevant and/or redundant features as possible and at the same time to select a feature subset for effective classification. Different from the other feature selection methods, LASSO [41] can achieve feature selection by minimizing a penalized objective function, which trends to assign zero weight to most irrelevant and redundant features. It has been shown that LASSO is particularly effective for the cases where there are many irrelevant features while only a few training samples [42].

The loss function of LASSO is defined as

$$\underset{w,b}{\text{min}}\frac{1}{2}\sum _i^N{(y_i-w^T{\mathbf{x}}_i-b)}^2+\mathrm{\lambda }\Vert w{\Vert }_1$$ (7)

where x_i represents a feature vector extracted from all thresholded connectivity networks on the i-th subject, y_i is the corresponding class label, w denotes the regression coefficients for the feature vector, b is the intercept, and N is the number of training subjects. The L₁-norm regularizer ‖w‖₁ typically leads to a sparse solution in the feature space, i.e., the regression coefficients for most irrelevant or redundant features are shrunk to zero. The features with nonzero coefficients will be selected and used for constructing the vector-based kernel. λ > 0 is a regularization parameter, which balances between the complexity of the model and the goodness-of-fit. The optimal λ value is determined using cross-validation on the training data.

5) Implementation Details

To evaluate the performance of different methods, a leave-one-out (LOO) cross-validation strategy is adopted to enhance the generalization power of the classifier and to avoid the over-fitting on small sample dataset. Specifically, for all subjects, one is left out for testing, and the remaining are used for training. This entire process is repeated for each subject. The classifier training of standard SVM is implemented using LIBSVM library [43] with default parameter values (i.e., C = 1). In our experiment, five thresholded connectivity networks are obtained using five different values, i.e., T = [0.2 0.3 0.38 0.4 0.45] with 0.38 as the average value of connectivity strength between all nodes/ROIs across all training subjects. The corresponding connection densities (i.e., the fraction of present connections to the possible connections) of these thresholds are located in the interval of [40% 75%]. It is reported in [44] that the connection density interval of [25% 75%] provides significantly better classification performance. A total of 450 (5*90) features (i.e., local clustering coefficients) are extracted from all thresholded connectivity networks for each subject. Moreover, we adopt the method used in [7] to normalize each extracted feature. At the feature selection step, the SLEP package [45] is used to solve the LASSO regression, with the regularization parameter λ (λ ∈ [0 1]) learned from the training subjects by using another LOO cross-validation. In addition, the linear kernel is adopted in our experiment as the vector-based kernel. Also, the optimal weighting parameter β_m for each kernel is learned similarly based on the training subjects via another LOO cross-validation through a grid search using the range from 0 to 1 at a step size of 0.1.

III. RESULTS

A. Classification Performance

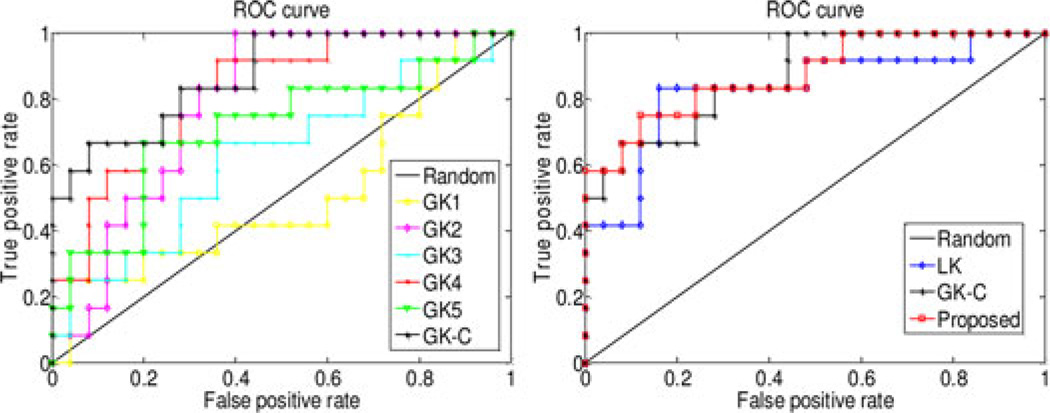
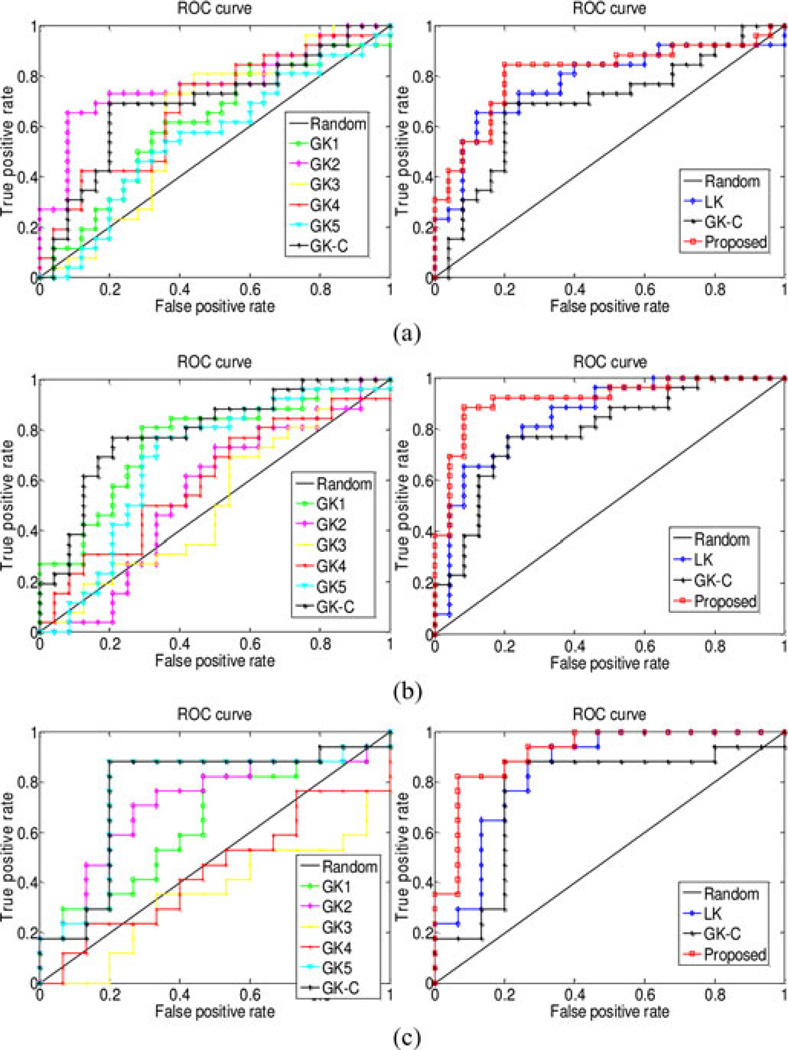
The classification performance is evaluated based on classification accuracy and the area under receiver operating characteristic (ROC) curve (AUC), respectively. Besides, to avoid the inflated performance estimates on imbalanced datasets, we also compute the balanced accuracy of classification, which can be defined as average accuracy obtained on either class (i.e., the arithmetic mean of sensitivity and specificity). In our experiments, we compare our proposed method based on multinetwork properties with those using only single network property. Specifically, in the linear-kernel-based method (denoted as LK), we first perform LASSO for feature selection on the obtained 450 (5*90) features (i.e., local clustering coefficients extracted from five thresholded connectivity networks) and then compute the linear kernel based on those selected features. On the other hand, for the graph kernel based methods, five graph kernels are constructed on the five thresholded connectivity networks, denoted as GK1, GK2, GK3, GK4, and GK5, respectively. These five graph kernels, which correspond to five different levels of topological properties of connectivity network, are combined and denoted as GK-C. All experiments are performed using LOO cross-validation. The classification performances for different methods are summarized in Table II. Fig. 3 plots the ROC curves for these methods.

TABLE II.

Classification Performance of Different Methods

method	Accuracy (%)	Balanced accuracy (%)	AUC
LK	81.1	79.5	0.84
GK1	73.0	60.5	0.51
GK2	73.0	64.8	0.79
GK3	70.3	58.5	0.63
GK4	73.0	60.5	0.83
GK5	75.7	64.7	0.71
GK-C	81.1	75.2	0.87
Proposed	91.9	89.7	0.87

Fig. 3.

ROC curves of different methods on MCI classification. Left: using single graph kernel and mixed kernel of all graph kernels; right: using single linear kernel, mixed kernel of all graph kernels, and combination of both linear kernel and graph kernels.

As can be seen from Table II and Fig. 3, our proposed method achieves the best performance (w.r.t. both classification accuracy and AUC), by combining both the vector-based kernel and the graph kernels from multinetwork properties of connectivity network. Specifically, our method yields a classification accuracy of 91.9% and a balanced accuracy of 89.7%, which are at least 10.8% and 10.2% improvements, respectively, over other compared methods. Also, our method achieves an AUC of 0.87, indicating excellent diagnostic power. These results indicate that different properties of connectivity network (i.e., local clustering features and global topological properties) contain complementary information and thus can be integrated for further improving the classification performance. Table III gives the combination weights of six kernels at each LOO cross-validation. On the other hand, both Table II and Fig. 3 show that: 1) GK-C significantly outperforms other single-graph-kernel based methods (i.e., GK1, GK2, GK3, GK4, and GK5), which implies that the topological information conveyed by multiple thresholded networks is complementary to each other and thus can lead to performance improvement if integrated together; 2) LK outperforms other single-graph-kernel based methods, and in most cases the weight value of β₀ in Table III is larger than other weights, indicating that the local network property (i.e., local clustering) is more important than the topological property of the whole connectivity network for classification.

TABLE III.

Combination of Weights for Six Kernels in Each Loo Cross-Validation

LOO	β0(LK)	β1(GKl)	β2(GK2)	β3(GK3)	β4(GK4)	β5 (GK5)
1	0.5	0.1	0.4	0.0	0.0	0.0
2	0.8	0.1	0.0	0.0	0.1	0.0
3	0.9	0.1	0.0	0.0	0.0	0.0
4	0.7	0.0	0.1	0.0	0.2	0.0
5	1.0	0.0	0.0	0.0	0.0	0.0
6	0.9	0.1	0.0	0.0	0.0	0.0
7	0.9	0.0	0.0	0.1	0.0	0.0
8	0.4	0.0	0.1	0.0	0.5	0.0
9	0.3	0.1	0.0	0.1	0.2	0.3
10	0.9	0.0	0.1	0.0	0.0	0.0
11	1.0	0.0	0.0	0.0	0.0	0.0
12	0.6	0.1	0.1	0.0	0.0	0.2
13	0.3	0.1	0.6	0.0	0.0	0.0
14	0.9	0.0	0.0	0.1	0.0	0.0
15	0.9	0.0	0.0	0.0	0.1	0.0
16	0.5	0.1	0.4	0.0	0.0	0.0
17	1.0	0.0	0.0	0.0	0.0	0.0
18	0.5	0.0	0.0	0.2	0.3	0.0
19	0.7	0.1	0.0	0.0	0.0	0.2
20	0.4	0.0	0.1	0.0	0.5	0.0
21	0.3	0.1	0.3	0.0	0.0	0.3
22	0.3	0.1	0.5	0.0	0.0	0.1
23	0.5	0.0	0.0	0.0	0.5	0.0
24	0.5	0.1	0.4	0.0	0.0	0.0
25	0.3	0.3	0.4	0.0	0.0	0.0
26	1.0	0.0	0.0	0.0	0.0	0.0
27	1.0	0.0	0.0	0.0	0.0	0.0
28	1.0	0.0	0.0	0.0	0.0	0.0
29	0.8	0.0	0.0	0.0	0.0	0.2
30	0.3	0.1	0.5	0.0	0.0	0.1
31	0.5	0.1	0.4	0.0	0.0	0.0
32	0.4	0.1	0.0	0.0	0.5	0.0
33	0.8	0.0	0.1	0.1	0.0	0.0
34	0.4	0.2	0.4	0.0	0.0	0.0
35	1.0	0.0	0.0	0.0	0.0	0.0
36	0.7	0.0	0.2	0.0	0.1	0.0
37	0.6	0.1	0.3	0.0	0.0	0.0

Furthermore, we performed an additional experiment by comparing our MKL-based method with a baseline scheme, i.e., assigning a uniform weight to all kernels, including vector-kernel and graph-kernels. This method achieves a classification accuracy of 86.5%, which is inferior to our proposed MKL-based method as shown in Table II. This result implies that different types of kernels contribute differently and thus should be integrated adaptively for achieving better classification performance.

Finally, instead of using LASSO-based feature selection method, we also employed other feature selection method, i.e., statistical t-test, to evaluate the classification performance of our proposed framework. Specifically, those features with their p-values lower than a given threshold are selected for subsequent kernel construction and classification. The classification results are summarized in Table IV, where our proposed method also achieves much better performance.

TABLE IV.

Classification Performance of Two Different Methods, in the Case of Using the t-Test-Based Feature Selection, Instead of Using Lasso-Based Feature Selection

Method	Accuracy (%)	Balanced accuracy (%)	AUC
LK	78.4	77.5	0.76
Proposed	86.5	83.5	0.81

B. Effect of Regularization Parameter λ

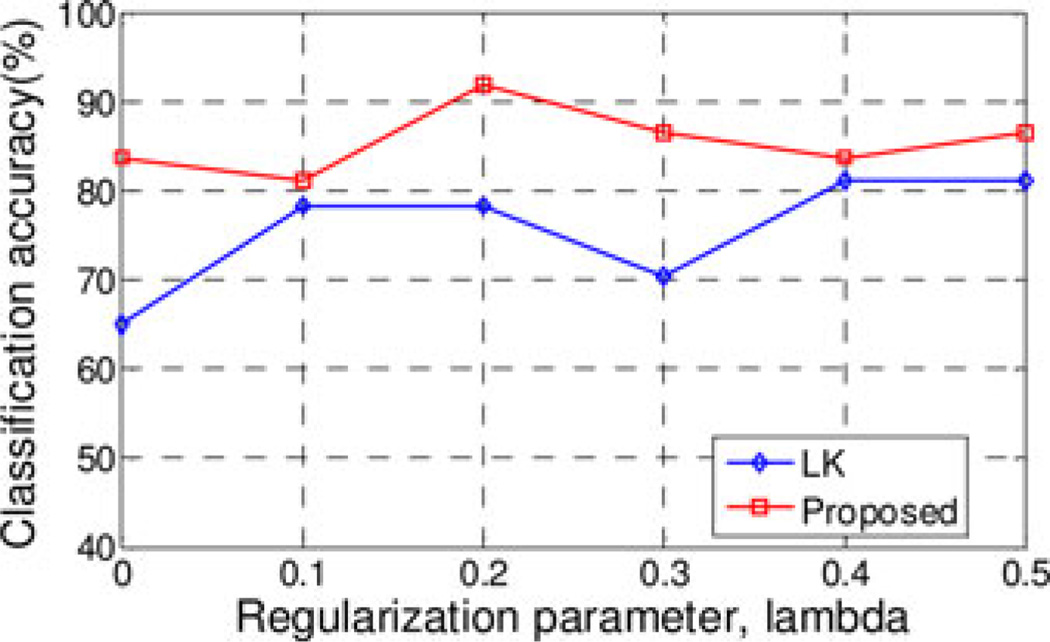
Regularization parameter λ of LASSO balances between the complexity of the model and the goodness-of-fit. Larger λ value means fewer features are preserved for classification and vice versa. Specially, classification performance of the vector-kernel-based method often deteriorates when too large or too small λ values are used. However, our proposed method takes into account multiple network properties by combining vector-based kernel and graph kernel, and thus improves the final classification performance. In this experiment, we investigate the influences of λ value on the classification accuracy of our proposed method. The classification accuracies with different λ values are plotted in Fig. 4. Here, the λ values used are [0.0, 0.1, 0.2, 0.3, 0.4, 0.5]. It is worth noting that, when λ = 0, no feature selection step is performed, i.e., all features extracted from the thresholded connectivity networks are used for the linear kernel construction and classification.

Fig. 4.

Performance w.r.t. the selection of λ value.

As can be seen from Fig. 4, our proposed method consistently performs better than LK method for all λ values. Specifically, our method yields relatively high classification accuracies (i.e., more than 80%) for all λ values, showing its robustness to the regularization parameter. Particularly, with no feature selection step (i.e., λ = 0), our method achieves a classification accuracy of 83.8%, which is still higher than the LK method. This again validates the advantage of our multinetwork properties based method (i.e., using both the local clustering features and global topological properties) over the conventional single-network-property based methods (i.e., using only the local clustering features).

C. Most Discriminant Brain Regions

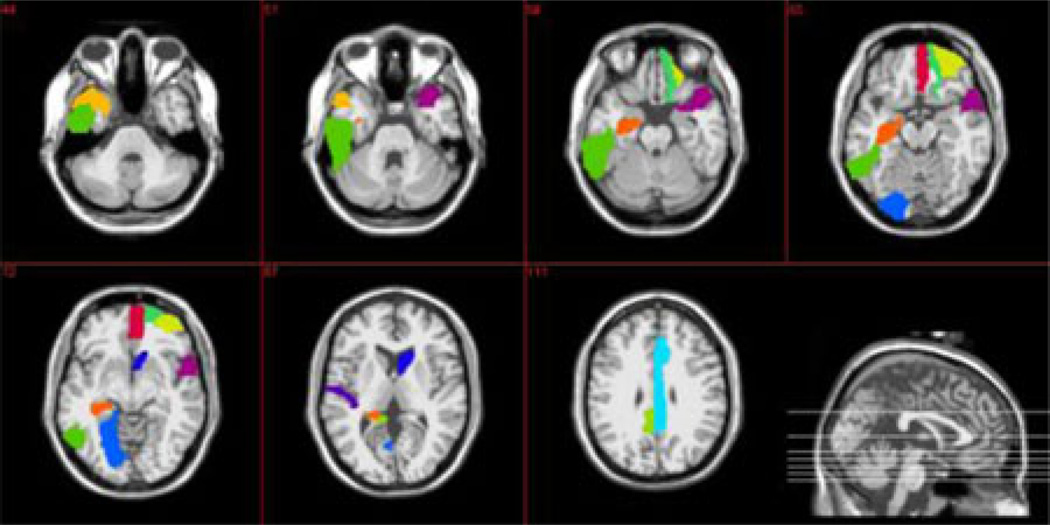
Besides reporting the classification performance measured with classification accuracy and AUC, another important issue is to investigate which features (i.e., brain regions or ROIs) are selected for brain disease classification and interpretation. To this end, for each (local clustering) feature, we count its selection frequency by LASSO method in all LOO cross-validations, and then select those features with top selection frequency as the most important features. For each selected important feature, t-test is performed on all subjects to evaluate its discriminative power for identifying patients from normal controls. Table V lists the top 12 brain regions that are selected based on the local clustering property. These regions include temporal pole, orbitofrontal cortex, heschl gyrus, hippocampus, middle, and posterior cingulate gyri. These identified regions are consistent with previous findings.

TABLE V.

Top 12 ROIs that are Selected Based on the Local Clustering Property

Selected ROIs (features)	Thresholded connectivity network	Number of occurrence	p-value
Left temporal pole (middle)	T2	37	0.035
Right caudate	T1	37	0.0154
Right temporal pole (superior)	T3,T5	37,17	0.0329, 0.3246
Right orbitofrontal cortex (superior)	T2	36	0.0068
Right orbitofrontal cortex (medial)	T1,T4	36,36	0.0044, 0.0243
Left heschl gyrus	T2	36	0.0111
Right orbitofrontal cortex (middle)	T2	34	0.4219
Left posterior cingulate gyrus	T2	33	0.0462
Left hippocampus	T1	32	0.0338
Left lingual gyrus	T2	32	0.7901
Right middle cingulate gyrus	T2	15	0.4484
Left inferior temporal	T2	15	0.0465

As can be seen from Table V, most features have relatively small p-values, showing good discriminative power between patients and controls. Table V also shows that the selected features are from multiple thresholded connectivity networks, validating our assumption that different thresholded connectivity networks contain complementary information which is useful for improving classification performance. Finally, for visual inspection, in Fig. 5, we show those selected ROIs listed in Table V.

Fig. 5.

Top 12 selected ROIs based on LASSO feature selection.

On the other hand, to further evaluate the discriminative power of different ROIs, we also characterize the top brain regions (i.e., ROIs) based on their global topological property. Let R = {R₁, R₂,…, R_n} be the set of ROIs. For each ROI R_p a sub-network can be built according to the connectivity between R_p and the remaining ROIs R_q (q = 1 2,…, n, q ≠ p) on the m-th thresholded connectivity network, and the graph kernel $k_m^p(G_m^i,G_m^j)$ between the samples G_i and G_j on the corresponding sub-network is computed using the method introduced in the previous section. Then, the group difference of ROI R_p on the m-th thresholded connectivity network can be defined as follows:

$$d_m(p)=\frac{1}{n_1{n}_2}\sum _{i\in L^{+},j\in L^{-}}{k}_m^p(G_m^i,G_m^j)$$ (8)

where L⁺ is the index set of patients, and L⁻ is the index set of normal controls, with number of subjects of n₁ and n₂ respectively. According to the definition in Eq. (8), the group difference d_m (p) represents the discriminative power of ROI R_p between patients and normal controls on them-th thresholded connectivity network. Then, for each thresholded connectivity network, we rank the ROIs according to their group differences and select also the top 12 ROIs with the highest group difference. Table VI gives the top selected ROIs based on the global topological property, which include orbitofrontal cortex, rectus gyrus, posterior cingulate gyrus, parahippocampal gyrus, amygdale, and temporal pole. These finding are consistent to previous AD/MCI studies. For instance, it has been reported that the functional connectivity between posterior cingulate cortex and other regions is significantly reduced in MCI patients [46]–[48]. Also, it is worth noting that most of ROIs selected based on the global topological property are identical to those selected based on the local clustering.

TABLE VI.

Top Selected ROIS Based on the Global Topological Property

T1	T2	T3
Left rectus gyrus	Right temporal pole (superior)	Right temporal pole (superior)
Left temporal pole (middle)	Left rectus gyrus	Left temporal pole (middle)
Left paraHippocampal gyrus	Left paraHippocampal gyrus	Left rectus gyrus
Right temporal pole (superior)	Left temporal pole (middle)	Left paraHippocampal gyrus
Right temporal pole (middle)	Right temporal pole (middle)	Left temporal pole (superior)
Left amygdala	Left amygdala	Right temporal pole (middle)
Left pallidum	Left pallidum	Left amygdala
Right amygdala	Right paraHippocampal gyrus	Left pallidum
Right paraHippocampal gyrus	Left temporal pole (superior)	Right paraHippocampal gyrus
Right rectus gyrus	Right amygdala	Right rectus gyrus
Left temporal pole (superior)	Right rectus gyrus	Right amygdala
Right posterior cingulate gyrus	Right posterior cingulate gyrus	Left olfactory
T4	T5	All
Right temporal pole (superior)	Right temporal pole (superior)	Left olfactory
Left paraHippocampal gyrus	Left paraHippocampal gyrus	Left orbitofrontal cortex (medial)
Left temporal pole (middle)	Left temporal pole (middle)	Right orbitofrontal cortex (medial)
Left rectus gyrus	Left temporal pole (superior)	Left rectus gyrus
Right temporal pole (middle)	Left rectus gyrus	Right rectus gyrus
Left temporal pole (superior)	Left pallidum	Right posterior cingulate gyrus
Left pallidum	Right temporal pole (middle)	Left paraHippocampal gyrus
Left amygdala	Left amygdala	Right paraHippocampal gyrus
Right paraHippocampal gyrus	Right paraHippocampal gyrus	Left amygdala
Right rectus gyrus	Right rectus gyrus	Right amygdala
Right amygdala	Right amygdala	Left pallidum
Right orbitofrontal cortex (medial)	Left orbitofrontal cortex (medial)	Left temporal pole (superior)
		Right temporal pole (superior)
		Left temporal pole (middle)
		Right temporal pole (middle)

D. Results on Infant Gender Classification

To further investigate the efficacy of our proposed method, we evaluate it on a larger dataset for gender classification of 133 infants with ages ranged from 0 to 2. The participants include 51 neonates (26 males, 25 females), 50 one-year-old (26 males, 24 females) infants, and 32 two-year-old (17 males, 15 females) infants.

1) Data Acquisition, Postprocessing, and Connectivity Network Construction

The detailed descriptions of data acquisition and postprocessing can be found in [49]. In short, all images were acquired using a 3 T head-only MR scanner. A 3D magnetization prepared rapid gradient echo (MP-RAGE) sequence was used for providing anatomical images to co-register among subjects, and the time series images were acquired by using a T2-weighted echo planar imaging (EPI) sequence. The preprocessing step of the fMRI images included the exclusion of voxels outside of the brain, time shifting, motion correction, spatial smoothing (6-mm full width at half maximum Gaussian kernel), linear trend removal, and low pass filtering (< 0.08 Hz). For within-group registration, longitudinal T1 MR images from one subject scanned at 3 weeks, 1 year, and 2 years were selected as templates for the corresponding age groups, and then an intensity-based HAMMER nonlinear registration [27] was performed to warp each individual subject onto its age-matched template space. Registration between each age group template (from the longitudinal data set) and the MNI space was then done using 4D HAMMER registration. The rationale for using a longitudinal dataset as templates was to achieve higher registration accuracy through the use of 4D HAMMER registration, which takes into account the longitudinal correlation information. Subsequently, the transformation fields from the 4D HAMMER registration were employed to warp the automatic labeling template (AAL) template (90 ROIs) covering the cerebral cortex, defined in [26] based on adult sulcal pattern, to each individual age group template space, achieving an age-specific ROI map. The corresponding connectivity networks (i.e., correlation matrices) were derived based on this age-specific map for all three age groups. The mean time course of each ROI was separately extracted from each individual subject and used to construct a connectivity network using the Pearson correlation coefficients between a pair of ROIs. Fisher’s r-to-z transformed was used to improve the normality of the correlation coefficients.

2) Experimental Results

In this experiment, we adopt the same setting as the experiments on MCI dataset, except using different sets of thresholds T = [0.0 0.1 0.2 0.3 0.4]. Note that, for each age group, the average value of connectivity strength between all ROIs across all training subjects is located in the interval of [0.25 0.35], with the corresponding connection densities of these thresholds located in the interval of [25% 75%]. Table VII gives the classification performances, and Fig. 6 plots the ROC curves of different methods. As we can see from Table VII and Fig. 6, our proposed method consistently achieves better classification performance compared with other methods for all age groups. The classification performance for the neonate group is relatively poor due to the possible incomplete connectivity network and/or larger imaging noise [49]. Table VIII lists the top 12 selected brain regions, which includes amygdala, parietal gyrus, temporal pole, superior frontal region, and lingual gyrus, in line with previous studies [50]–[55]. Moreover, some ROIs, i.e., amygdala, posterior cingulate gyrus, and inferior temporal gyrus, have been selected for all age groups.

TABLE VII.

Performance of Different Methods on Infant Gender Classification

Method	Accuracy (%)			Balanced accuracy (%)			AUC
	age 0	age 1	age 2	age 0	age 1	age 2	age 0	age 1	age 2
LK	68.6	80.0	78.1	68.5	80.0	77.8	0.78	0.85	0.85
GK1	56 9	70 0	68.8	56.8	70.0	67.8	0.61	0.75	0.64
GK2	74.5	60.0	71.9	74.6	59.9	72.0	0.77	0.55	0.71
GK3	68.6	54.0	43.8	68.5	53.7	43.1	0.62	0.52	0.35
GK4	66.7	60.0	50.0	66.6	59.8	50.2	0.68	0.60	0.45
GK5	60.8	68.0	81.3	60.8	67.6	81.2	0.55	0.68	0.76
GK-C	76.5	80.0	84.4	76.5	80.0	84.1	0.69	0.79	0.76
Proposed	80.4	92.0	87.5	80.4	92.0	87.8	0.81	0.92	0.92

Fig. 6.

ROC curves of different methods on infant gender classification. Left: using single graph kernel and mixed kernel of all graph kernels; right: using single linear kernel, mixed kernel of all graph kernels and the combination of both linear kernel and graph kernels. (a) age 0, (b) age 1, and (c) age 2.

TABLE VIII.

Top 12 Selected ROIS for Infant Gender Classification

age 0	age 1	age 2
Left, Middle frontal gyrus	Right, Inferior frontal gyrus (triangular)	Right, Precentral gyrus
Left, Inferior frontal gyrus (opercular)	Right, Olfactory	Left, Middle cingulate gyrus
Right, Rolandic operculum	Right, Superior frontal gyrus (media)	Right, Posterior cingulate gyrus
Right, Posterior cingulate gyrus	Right, Posterior cingulate gyrus	Left, Amygdala
Left, Hippocampus	Right, Amygdala	Right, Amygdala
Right, Amygdala	Right, Superior occipital gyrus	Right, Lingual gyrus
Left, Lingual gyrus	Right, Middle occipital gyrus	Right, Superior occipital gyrus
Right, Inferior occipital gyrus	Right, Paracentral lobule	Left, Inferior occipital gyrus
Right, Superior parietal gyrus	Left, Thalamus	Left, Fusiform gyrus
Left, Paracentral lobule	Right, Thalamus	Right, Superior parietal gyrus
Left, Thalamus	Left, Inferior temporal	Left, Caudate
Left, Inferior temporal	Right, Inferior temporal	Left, Inferior temporal

IV. DISCUSSION

This paper presents a new connectivity-network-based classification framework that integrates multiple network properties (i.e., the local clustering and global topology) through MKL method for automatic brain disease classification. We evaluated our proposed method on two applications, i.e., identifying MCI subjects from normal controls, and classifying the infant gender. The experimental results show that our proposed method can significantly improve the classification performance over state-of-the-art methods on the connectivity-network-based classification.

Integration of multiple modalities of data (e.g., MRI, PET imaging biomarkers, and nonimaging biological biomarkers) has been recently studied for AD/MCI classification. On the other hand, multiple types of properties can also be extracted from a single modality of data for improving the classification performance. For example, for a single connectivity network, both local clustering property and the global topological property, which are complementary to each other, can be extracted and integrated to improve the disease classification accuracy, even without using information from other modalities. This has been validated in our study of identifying MCI patients from normal controls.

Many studies have suggested that the diseased brains (such as with AD/MCI) differ from the normal brains in connectivity patterns, reflected in various network properties such as local clustering [37], [38] and the topological properties of whole network [13], [15], [40]. In our method, two different types of kernels were used to quantify these two different network properties. Specifically, a vector-based kernel was calculated on the feature vectors (i.e., with local weighted clustering coefficients) to measure the similarity of local clustering of the connectivity networks. Here, feature selection (i.e., with LASSO) is first used to remove the irrelevant features for classification. The selected brain regions during feature selection were found to be consistent with the conventional group comparison studies, which include temporal pole [56], orbitofrontal cortex [57], [58], heschl gyrus [37], hippocampus [38], [47], [59], and posterior cingulate gyrus [46], [47], [60], etc.

On the other hand, graph kernel was used to capture and characterize the topological property of the whole connectivity networks [31]. Here, graph-kernel-based group analysis was performed to rank the discrimination power of each ROI, and the result shows that the most discriminative ROIs were in line with previous studies, which include orbitofrontal cortex [57], [58], rectus gyrus [16], posterior cingulate gyrus [46]–[48], [60], parahippocampal gyrus [61], [62], amygdala [60], and temporal pole [56], etc. Finally, it is worth noting that most of the selected ROIs based on these two properties (i.e., local clustering and global topology) are consistent due to the same underlying pathology in AD/MCI.

In AD/MCI studies, threshold-based method has been used for exploring topological properties of functional connectivity network [13], [15], [37], [44]. However, there is no golden standard to select a single threshold, and thus network properties are often explored over a range of plausible threshold. For example, Zanin et al. in [44] proposed to determine the best threshold by exploring the classification performance on the whole range of applicable threshold. Supekar et al. [13] adopted thresholds ranged from 0.01 to 0.99 with an increment of 0.01 to explore the “small-world” properties of functional connectivity networks in AD. In our method, multiple thresholds were adopted to reflect multiple levels of topological properties of network. Compared with the single threshold based methods, our method has the following advantages: 1) avoiding testing over a range of thresholds to find the optimal one; 2) taking advantage of the complementary topological properties of different thresholded networks. Moreover, it is worth noting that, by using the multiple-kernel learning technique, our method can automatically determine the optimal network property or combination of network properties of multiple thresholded networks for classification.

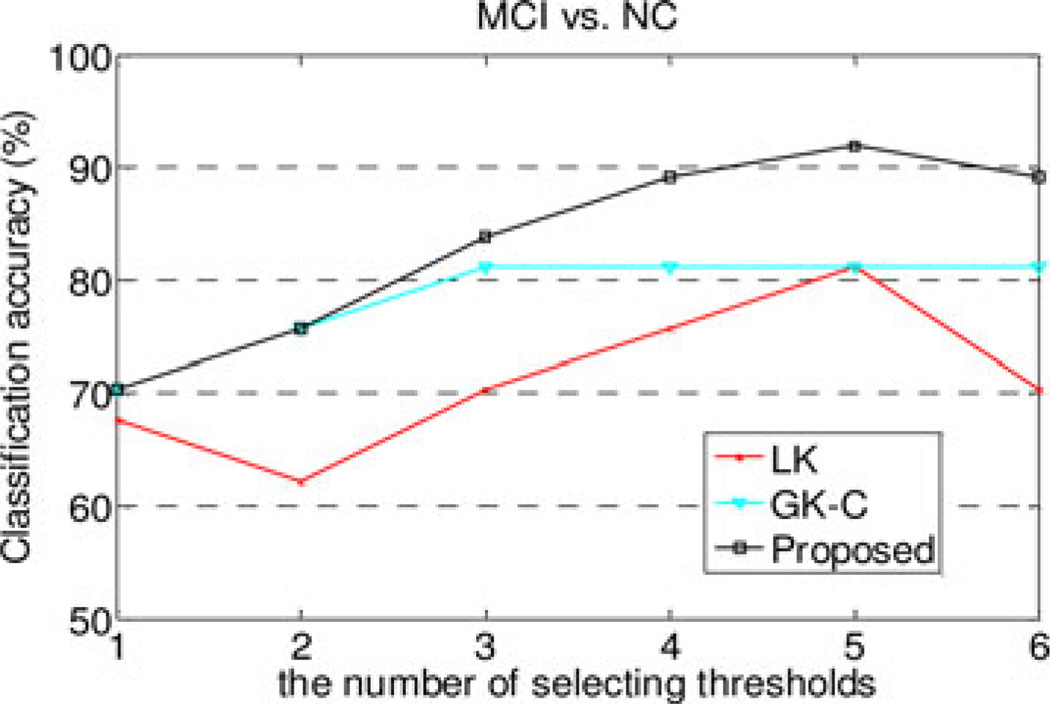
To investigate the effect of the number of thresholds on final classification performance, we performed an additional experiment on MCI dataset with six different groups of thresholds, i.e., T¹ = [0.38], T² = [0.38 0.4], T³ = [0.3 0.38 0.4], T⁴ = [0.3, 0.38 0.4 0.45], T⁵ = [0.2 0.3 0.38 0.4 0.45], and T⁶ = [0.2 0.3 0.38 0.4 0.45 0.6]. The classification accuracies using different numbers of thresholds are plotted in Fig. 7. As can be seen in Fig. 7, our proposed method consistently outperforms other comparison methods for all groups of thresholds. On the other hand, our method achieves the best performance when using five thresholds, and the use of more than five thresholds does not further improve its classification performance. This may be because the use of more thresholds leads to more features and thus more challenging to select the discriminative features for the LK method; this may cause the LK method (i.e., vector-kernel based) to perform poorly and finally affect the performance of our proposed method which combines both vector-kernel and graph-kernels.

Fig. 7.

Performance w.r.t. the number of selecting thresholds.

A. Limitations

The current study is limited by the following factors. First, in our study, we use only the topological information of the whole connectivity network for classification, while intuitively selecting the disease-related sub-networks from the whole network may further improve the classification performance. Full investigation on this issue will be our future work. Second, the network construction is a very important step and different network construction methods may exhibit different properties. Our current study does not analyze the impact of these differences on classification performance. Third, there are many imaging modalities that have been used for AD or MCI classification, and simultaneous integration of different imaging modalities and different network properties of each modality may further improve the classification performance, which will be explored in the future. Finally, our current study is limited by the small number of MCI subjects, which may reduce its generalization ability on MCI classification. Thus, in the future work, we plan to apply the proposed method on larger MCI dataset.

V. CONCLUSION

In summary, we have presented a new connectivity network based classification framework to fuse multiple properties of connectivity networks for classification. In the proposed framework, multiple thresholds were first applied on functional connectivity network to reflect multiple levels of network properties. Then, two different types of kernels (i.e., vector-based kernel and graph kernel) were used to quantify two different yet complementary network properties, and an MKL technique was further adopted to fuse these heterogeneous kernels. Experimental results show that our proposed method not only can significantly improve the performance of classification, but also can potentially detect the ROIs that are sensitive to disease pathology. In the future work, we will investigate how to select the disease-related sub-networks from whole network for further improving the classification performance and also for better interpretation of the pathology of disease.

Biographies

Biao Jie received the B.S. degree in computer science from Fuyang Normal College, Fuyang, China, in 2001, and the M.S. degree in computer science from the Yunnan Normal University, Yunnan, China, in 2006. He is currently working toward the Ph.D. degree in the Department of Computer Science, Nanjing University of Aeronautics and Astronautics, Nanjing, China.

His current research interests include machine learning and medical image analysis.

Daoqiang Zhang received the B.Sc. and Ph.D. degrees in computer science from Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 1999 and 2004, respectively.

He is currently a Professor in the Department of Computer Science and Engineering, Nanjing University of Aeronautics and Astronautics. His current research interests include machine learning, pattern recognition, and biomedical image analysis. In these areas, he has authored or coauthored more than 100 technical papers in the refereed international journals and conference proceedings.

Dr. Zhang was nominated for the National Excellent Doctoral Dissertation Award of China in 2006, won the best paper award at the 9th Pacific Rim International Conference on Artificial Intelligence (PRICAI’06), and was the winner of the best paper award honorable mention of Pattern Recognition Journal 2007. He is currently an Editorial Board Member for the Computational Intelligence and Neuroscience Journal and a Program Committee Member for several international conferences. He is a member of the Machine Learning Society of the Chinese Association of Artificial Intelligence (CAAI) and the Artificial Intelligence and Pattern Recognition Society of the China Computer Federation (CCF).

Wei Gao received the B.S. and M.S. degrees from Tianjin University, Tianjin, China, in 2004 and 2006, and the Ph.D. degree from the University of North Carolina at Chapel Hill in 2010.

He is currently an Assistant Professor in the Department of Radiology and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill. His current research interests include MRI studies of early brain development and normal/abnormal adult brain functioning with a focus on connectivity-based network-level analysis.

Qian Wang received the B.S. and M.S. degrees from Shanghai Jiao Tong University, Shanghai, China, in 2006 and 2009, respectively. He is currently working toward the Ph.D. degree in the Department of Computer Science, the University of North Carolina at Chapel Hill.

He is with the Image Display, Enhancement, and Analysis Research Laboratory, Department of Radiology and BRIC, the University of North Carolina at Chapel Hill. His current research interests include medical image registration, segmentation, machine learning, and fMRI analysis.

Chong-Yaw Wee received the Ph.D. degree in electrical engineering from the University of Malaya, Malaysia, in 2007.

Since 2010, he has been a Postdoctoral Research Associate at the Biomedical Research Imaging Center, University of North Carolina at Chapel Hill. His current research interests include machine learning, neurodegenerative and neurodevelopment disorders, and multimodal multivariate neuroimaging classification.

Dinggang Shen (M’00–SM’07) received the Ph.D. degree in electronic communication from Shanghai Jiao Tong University, China, in 1995.

He is a Professor of Radiology, Biomedical Research Imaging Center (BRIC), Computer Science, and Biomedical Engineering in the University of North Carolina at Chapel Hill (UNC-CH). He is currently directing the Center for Image Informatics, the Image Display, Enhancement, and Analysis (IDEA) Lab, Department of Radiology, and also the Medical Image Analysis Core in the BRIC. He was a tenure-track Assistant Professor in the University of Pennsylvanian (UPenn) and a Faculty Member in the Johns Hopkins University. His current research interests include medical image analysis, computer vision, and pattern recognition. He has authored or coauthored more than 450 papers in the international journals and conference proceedings. He is as an Editorial Board Member for four international journals.

Dr. Shen is with the Board of Directors, the Medical Image Computing and Computer Assisted Intervention (MICCAI) Society.