Abstract
Pediatric manual wheelchair users (MWU) require high joint demands on their upper extremity (UE) during wheelchair mobility, leading them to be at risk of developing pain and pathology. Studies have examined UE biomechanics during wheelchair mobility in the adult population; however, current methods for evaluating UE joint dynamics of pediatric MWU are limited. An inverse dynamics model is proposed to characterize three-dimensional UE joint kinematics and kinetics during pediatric wheelchair mobility using a SmartWheel instrumented handrim system. The bilateral model comprises thorax, clavicle, scapula, upper arm, forearm, and hand segments and includes the sternoclavicular, acromioclavicular, glenohumeral, elbow and wrist joints. A single 17 year-old male with a C7 spinal cord injury (SCI) was evaluated while propelling his wheelchair across a 15-meter walkway. The subject exhibited wrist extension angles up to 60°, large elbow ranges of motion and peak glenohumeral joint forces up to 10% body weight. Statistically significant asymmetry of the wrist, elbow, glenohumeral and acromioclavicular joints was detected by the model. As demonstrated, the custom bilateral UE pediatric model may provide considerable quantitative insight into UE joint dynamics to improve wheelchair prescription, training, rehabilitation and long-term care of children with orthopaedic disabilities. Further research is warranted to evaluate pediatric wheelchair mobility in a larger population of children with SCI to investigate correlations to pain, function and transitional changes to adulthood.
Keywords: Biomechanics, manual wheelchair, pediatric, upper extremity, inverse dynamics
I. INTRODUCTION
A 2012 Americans with Disabilities Report states that about 3.7 million people in the United States of America (USA) use a wheelchair, with about 124,000 wheelchair users under the age of 21 and 67,000 under the age of 15 (Brault, 2012). Additionally, 90% of wheelchair users in the USA are manual wheelchair users (MWU) and among children under the age of 18, the wheelchair is the most used assistive mobility device (Kaye, 2000).
It has been reported that adults experience approximately a 4.2–6.6 Nm mean net shoulder moment, with peak moments between 6.7 and 10.3 Nm (van Drongelen et al., 2011). Specifically maximum shoulder flexion moments have been reported at 5.7 Nm and 7.9 Nm during wheelchair propulsion at speeds of 3km/h and 4km/h, respectively (Gil-Agudo et al., 2010a). As the upper extremities (UEs) are not constructed for high magnitude or high frequency force demands, overuse injuries such as carpal tunnel syndrome, shoulder impingement and UE pain are commonly developed (Crane, 2007; Veeger et al., 1998) and were reported in 50% of MWU with spinal cord injury (SCI) (Boninger et al., 2005). These secondary problems have been associated with increased loading at extremes of joint excursions (Corfman et al., 2003). Due to increased life expectancy and continual wheelchair usage, these injuries may reduce or severely limit independent function and quality of life (Crane, 2007).
These issues may be of even greater concern in the pediatric population of long-term wheelchair users. Due to pediatric growth and maturation, simple scaling of adult body segment parameters is not appropriate (Jensen, 1989). While studies have examined wheelchair mobility in the adult population (Mercer et al., 2006; Gil-Agudo et al., 2010b), current biomechanical models for pediatric wheelchair mobility are limited by non-standard kinematic models (Bednarczyk et al., 1995, Wu, et al., 2005). We propose a pediatric UE model for biomechanical analysis of wheelchair mobility in children and adolescents with orthopaedic disabilities, such as spinal cord injury. Previous models from our group lay the groundwork for pediatric assistive mobility modeling (Slavens et al., 2009; Konop et al., 2009).
Studies have shown that assuming symmetry between left-hand and right-hand sides, when assessing wheelchair propulsion, may result in errors (Boninger et al., 2002). While the clinical implications of asymmetry are still unclear, asymmetrical propulsion may be a contributing factor to the development of pain and pathology (Hurd et al., 2008). Characterizing bilateral UE joint dynamics during wheelchair propulsion will provide insight to motion and loading patterns. Investigation of bilateral peak joint dynamics may help identify potentially injurious risk factors. Better knowledge of UE joint dynamics during wheelchair mobility may improve our understanding of the onset and propagation of UE pathologies. Additionally, this work may be applied to identify biomechanical risk factors of pain and pathology for long-term wheelchair users. This may guide clinicians and engineers to improvements in wheelchair prescription, design, training and transitional and long-term care. Thereby, pain and pathology onset may be slowed or prevented, and quality of life restored.
II. Methods
A. Kinematic Model
The bilateral UE model comprises 11 segments, including the thorax, clavicles, scapulae, upper arms, forearms and hands. The joints of interest are three degree-of-freedom wrist, glenohumeral (GH) and acromioclavicular (AC) joints; and two-degree-of-freedom sternoclavicular (SC) and elbow joints. To define the segments, twenty-seven passive reflective markers are placed on the subject (Figure 1). Additionally, the wheelchair was modeled as one rigid body segment using four markers. Joint axes were embedded at the joint centers, which are calculated using subject specific anthropometric data. A Z-X-Y Euler sequence is used to determine the joint angles of the distal segment with respect to the proximal segment for the thorax and the GH, elbow and wrist joints. A Y-X-Z Euler sequence is used for AC joint (scapula with respect to the clavicle) and SC joint (clavicle with respect to the sternum) angle determination. All rotation sequences follow ISB recommendations (Wu et al., 2005). Matlab (MathWorks, Inc., Natick, MA) was used for model development.
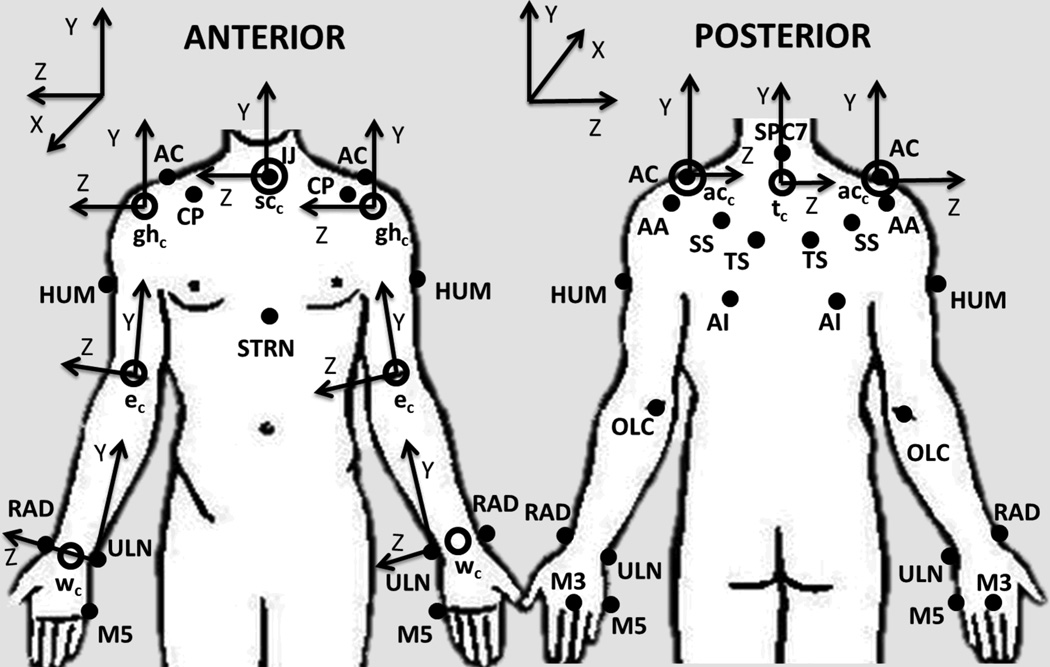
Figure 1.
Upper extremity model marker set: suprasternal notch (IJ), xiphoid process (STRN), spinous process at C7 (C7), acromioclavicular joint (AC), inferior angle (AI), trigonum spine (TS), scapular spine (SS), acromial angle (AA), coracoid process (CP), humerus (HUM), olecranon (OLC), radial styloid (RAD), ulnar styloid (ULN), third and fifth metacarpals (M3 and M5). Joint centers: wrist joint center (wc), elbow joint center (ec), glenohumeral joint center (ghc), acromioclavicular joint center (acc), sternoclavicular joint center (scc) and thorax center (tc) are represented by the open circles. Following ISB recommendations, definition of axes of rotation follow right-hand rule and the Z-axis points laterally towards the subject’s right side, the X-axis points anteriorly, and the Y-axis points superiorly (Wu et al., 2005).
B. Model Features
Previous, validated UE models for the evaluation of pediatric assisted mobility, created by our group (Slavens et al 2011a; Slavens et al 2011b; Slavens et al 2010; Slavens et al 2009; Konop et al., 2009) served as the foundation for the development of this model. The model incorporated ISB recommendations for segment design (Wu et al., 2005) as well as custom features specific to pediatric wheelchair mobility. To avoid possible marker contact with the wheelchair during propulsion, a single marker was placed on the olecranon, a method previously validated (Hingtgen et al., 2006). The marker set used to describe the thorax was refined to closely reflect the pediatric model described by Nguyen and Baker to reduce the influence of shoulder girdle movement on thoracic kinematic measurements (Nguyen et al., 2004). To provide a comprehensive description of shoulder girdle dynamics, scapula and clavicle segments were included in this model. ISB recommended modeling methods were closely followed (Wu et al., 2005), except that, in order to accommodate a child’s smaller size, a single marker on the suprasternal notch was used in place of dual SC joint markers for clavicle segment definition, after research showed a minimal effect on the results (van der Helm and Pronk, 1995). A regression method was applied for determining GH joint center locations that used the positions of five markers on the scapula (Meskers et al., 1998). This method was chosen because of its ease of implementation with this model, its general acceptance and its increased accuracy over more simplistic methods, such as using shoulder circumference (Campbell et al., 2009). A marker tracking method was utilized for the scapula markers to reduce the effects of skin motion artifact as well as possible marker-wheelchair interaction (Senk and Cheze, 2010). Body segment parameters were calculated by equations specifically developed for the pediatric population (Jensen, 1989; Yeadon and Morlock, 1989).
C. Kinematic Model: Joint Centers
The joint center positions were located at the origins for each segment’s local coordinate system, except for the scapulae and forearms, whose origins were the acromial angles (AA) and ulnar styloids (ULN), respectively (Wu et al., 2005). All joints were assumed to have fixed centers of rotation.
D. Kinematic Model: Segment Coordinate Systems
Segment coordinate systems (SCS) were determined for each segment. The joint angles were determined by the relative motion between two adjacent SCS, distal relative to proximal. The SCS follow the right-hand rule with the Z-axis as the flexion/extension axis; the X-axis as the abduction/adduction axis; and the Y-axis as the internal/external rotation axis. Equations presented in Table 1 define the right-hand side.
Table 1.
Segment coordinate system definitions for the right-hand side; Variables representing marker locations are defined as: m̅i, where i represents the marker: suprasternal notch (IJ), xiphoid process (STRN), spinous process at C7 (SPC7), acromioclavicular joint (AC), inferior angle (AI), trigonum spine (TS), scapular spine (SS), acromial angle (AA), coracoid process (CP), humerus (HUM), olecranon (OLC), radial styloid (RAD), ulnar styloid (ULN), third and fifth metacarpals (M3 and M5). The joint center locations include: the thorax (t̅c), the glenohumeral joint (), the elbow joint (ēc), the wrist joint (w̅c) and the third metacarpal joint (). Additionally, a temporary point (p̅t), was used during the calculation of the thorax segment y-axis. The left-hand side was similarly defined.
| Segment | X-axis () | Y-axis () | Z-axis () | |||
|---|---|---|---|---|---|---|
| Thorax (t̅) | t̅z = t̅x × t̅y | |||||
| Clavicle (c̅) | c̅x = t̅y × c̅z | c̅y = c̅z × c̅x | ||||
| Scapula (s̅) | s̅y = s̅z × s̅x | |||||
| Upper Arm () | ||||||
| Forearm (f̅) | f̅z = f̅x × f̅y | |||||
| Hand (h̅) | h̅z = h̅x × h̅y |
E. Kinetic Model: Body Segment Parameters
The mass and segment center of mass location of the hands, forearms and upper arms, were calculated using polynomial regression equations (Jensen, 1989). These equations were developed for subjects between the ages of four and twenty and use the subject’s age (in years) as the independent variable (Jensen, 1989). Segment inertias for each subject were calculated using equations developed by Yeadon and Morlock that require multiple measurements of each segment (Yeadon and Morlock, 1989).
F. Kinetic Model: Newton – Euler Equations
The SmartWheel, a validated, commercially available product, (Out-Front, Mesa, AZ, USA), enabled kinetic data to be recorded during wheelchair propulsion. The SmartWheel utilizes voltage changes in six strain gauges placed on specialized wheel spokes and 12 calibration constants to calculate the three forces and three moments as applied by the user to the wheelchair handrim. The SmartWheel has a selectable sampling frequency between 30 and 240 Hz with a 12 bit digital sample resolution and a 300 foot indoor communication range (SmartWheel User’s Guide, 2009). The kinetic handrim data was used in Newton-Euler equations of motion to determine the forces and moments at each UE joint of interest through the inverse dynamics method (Zatsiorsky, 2002). The resulting equations calculated the forces and moments of each joint in all three planes of motion (Table 2).
Table 2.
Joint force and moment calculations. The following variables were used: Ḣ: rate of change of angular momentum, ā: acceleration of center of mass (COM), F̅: force, M̅: moment, r̅: moment arm from COM to distal and proximal joint, and ḡ: gravity (9.81m/s2). Subscripts denote the following: SW: SmartWheel, H: hand, W: wrist, F: forearm, E: elbow, UA: upper arm, or GH: glenohumeral.
| Joint | Force | Moment |
|---|---|---|
| Wrist | F̅W = massH(āH + ḡ) − F̅SW | M̅W = ḢH − M̅SW + r̅DisH × F̅SW − r̅ProxH × F̅W |
| Elbow | F̅E = massF(āF + ḡ) − F̅Wrist | M̅E = ḢF − M̅Wrist + r̅DisF × F̅Wrist − r̅ProxF × F̅E |
| Glenohumeral | F̅GH = massUA(āUA + ḡ) − F̅Elbow | M̅GH = ḢUA − M̅Elbow + r̅DisUA × F̅Elbow − r̅ProxUA × F̅GH |
G. Patient Evaluation Protocol
The biomechanical model was implemented at Shriners Hospitals for Children – Chicago for analysis of pediatric mobility in MWU. The protocol was IRB approved and informed consent was obtained prior to evaluation. A 17 year-old male, with a C7, ASIA level B, SCI propelled his wheelchair along a 15-meter walkway at a self-selected speed for multiple trials. Due to his SCI level, the subject’s hands were not able to grasp the handrims and friction cuffs were worn to facilitate wheelchair mobility. Adequate rest was provided between trials. A SmartWheel System was used unilaterally to collect right-hand (dominant) force and moment data at the hand-handrim interface at 240 Hz. The SmartWheel software triggered simultaneous bilateral kinematic data collection at 120 Hz using a 14-camera Vicon MX motion capture system. The thorax, wrist, elbow, GH, AC and SC joint kinematics and wrist, elbow and GH joint moments were determined in all three planes of motion. Wrist, elbow and GH joint kinetics were determined along all three axes: mediolateral, anteroposterior and inferosuperior. The kinetic data was re-sampled to 120 Hz and then all data was normalized to 100% stroke cycle and processed every 1%. The stroke cycle was defined to include both the push and recovery phases, with 0% representing the onset of a moment about the axle. Matlab and Excel (Microsoft, Redmond, WA) were used for data processing. Paired t-tests, 30 total, were conducted to determine angular asymmetry between left-hand side and right-hand side kinematic data.
III. RESULTS
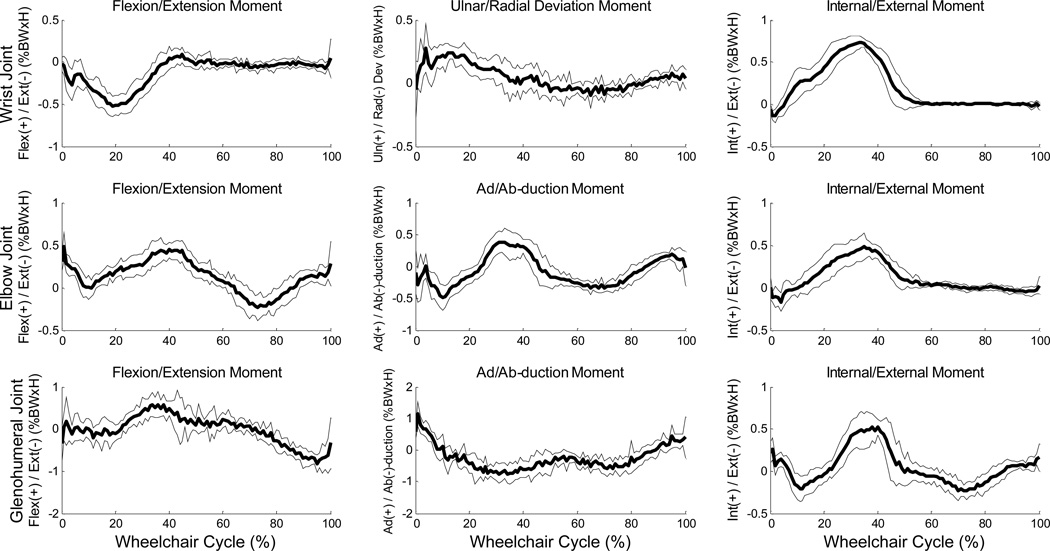
Mean (+/− one standard deviation) joint angle curves in each plane of motion were characterized over the wheelchair stroke cycle for all UE joints (Figures 2–3). The subject’s transition from push phase to recovery phase occurred on average at 52% stroke cycle. Additionally, the kinematic peaks from each of the 10 stroke cycles and their locations of occurrence during the stroke cycle were averaged, as well as joint ranges of motion (ROMs), for each joint during the stroke cycle (Tables 3–4). Of note, the large average(stdev) peak wrist extension values were −60°(6.8°) on the dominant side and −56°(2.8°) on the non-dominant side (Table 5) and dominant side elbow ranges of motion were 47°(1.9°) in the sagittal plane and 76°(8.2°) in the transverse plane. Additionally, for the wrist, elbow and GH joints, the joint force curves and joint moment curves of each stroke cycle were averaged together (Figures 4–5). The GH joint experienced the highest forces with an average peak force of 9.6 %BW (1.7%BW) superiorly directed and 8.4 %BW (1.5%BW) laterally directed. The mean kinetic peaks and their locations of occurrence during the stroke cycle were computed (Table 6). Note that the averaged peak dynamics from each trial may not align with the point-to-point joint dynamics average as the individual peaks do not all occur at the same point in the wheelchair stroke cycle. Interestingly, many of the average peak joint angles, forces and moments occurred at similar times as one another. For example, on average, the mean peak wrist extension occurred at 24% stroke cycle, mean peak elbow flexion at 26%, mean peak GH superior force at 20%, mean peak wrist extension moment at 22% and mean peak elbow flexion moment at 21% stroke cycle, indicating certain times within the stroke cycle may put the individual at greater risk than others, and needs to be further investigated.
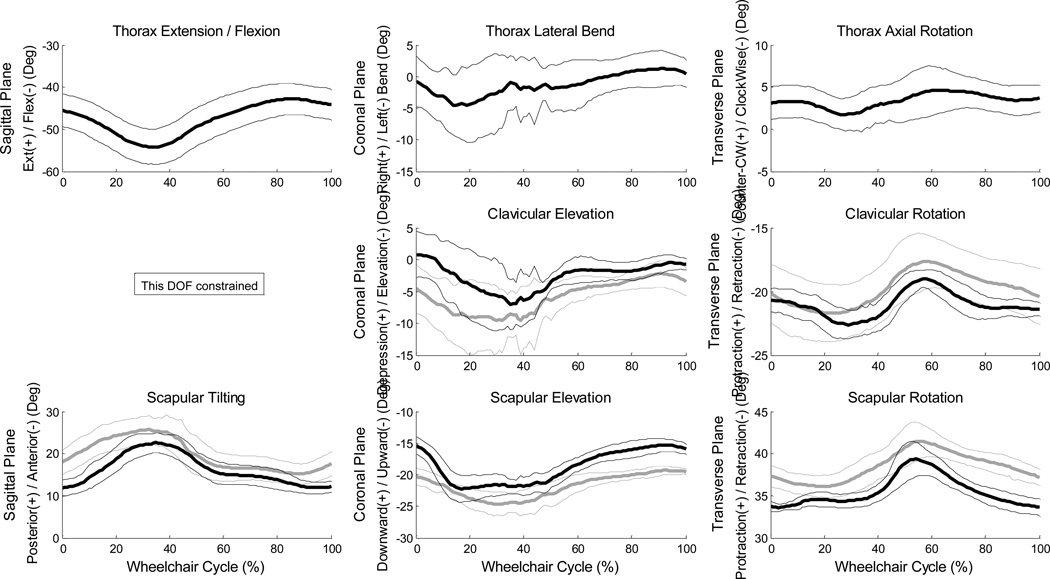
Figure 2.
Ensemble average joint kinematic data for 10 stroke cycles of the thorax, sternoclavicular and acromioclavicular joints. Mean (bold) and +/− one standard deviation joint kinematics of the thorax: top row, the sternoclavicular (SC) joint: middle row, and the acromioclavicular (AC) joint: bottom row. (left side: grey, right side: black)
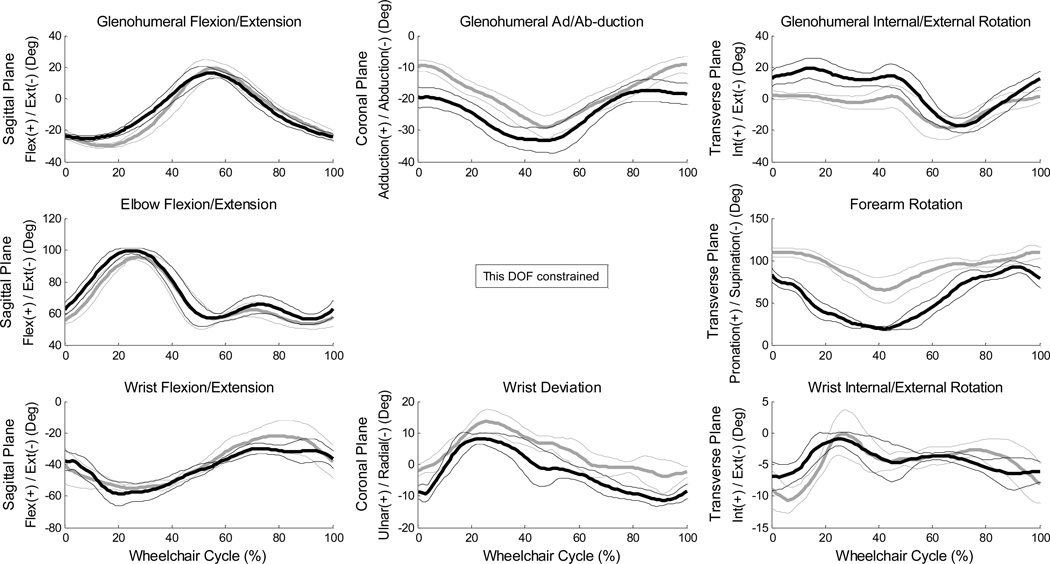
Figure 3.
Ensemble average joint kinematic data for 10 stroke cycles of the glenohumeral, elbow and wrist joints. Mean (bold) and +/− one standard deviation joint kinematics of the glenohumeral (GH) joint: top row, the elbow joint: middle row, and the wrist joint: bottom row. (left side: grey, right side: black)
Table 3.
Mean peak glenohumeral, elbow and wrist joint angles, ranges of motion and standard deviations for 10 stroke cycles. The sagittal plane is described by flexion (+)/extension (−). The coronal plane of the glenohumeral (GH) joint is represented by adduction (+)/ abduction (−); the coronal plane of the elbow is constrained; the coronal plane of the wrist is represented by ulnar deviation (+)/radial deviation (−). The transverse plane is described by internal rotation (+)/external rotation (−) for the GH and wrist, and pronation (+)/ supination (−) for the elbow.
| Dominant Side (Right) | Non-Dominant Side (Left) | ||||||
|---|---|---|---|---|---|---|---|
| Plane | Joint | Max Angle (deg) (Stdev) |
Min Angle (deg) (Stdev) |
ROM (deg) (Stdev) |
Max Angle (deg) (Stdev) |
Min Angle (deg) (Stdev) |
ROM (deg) (Stdev) |
| Sagittal | GH | 17.9 (2.1) | −25.6 (1.5) | 43.4 (2.2) | 20.7 (3.9) | −30.6 (1.1) | 51.3 (3.6) |
| Elbow | 100.0 (2.0) | 53.8 (1.8) | 46.8 (1.9) | 96.2 (1.8) | 51.2 (1.5) | 45.0 (1.7) | |
| Wrist | −27.4 (4.2) | −60.2 (6.8) | 32.8 (6.2) | −20.2 (8.9) | −56.3 (2.8) | 36.0 (9.2) | |
| Coronal | GH | −16.4 (3.1) | −34.8 (3.8) | 18.4 (3.3) | −8.2 (2.1) | −30.2 (2.4) | 22.0 (2.6) |
| Wrist | 8.9 (1.6) | −12.5 (1.3) | 21.4 (2.2) | 14.4 (3.4) | −6.2 (4.0) | 20.6 (3.8) | |
| Transverse | GH | 21.8 (6.9) | −18.3 (5.0) | 40.1 (9.3) | 7.3 (2.7) | −19.7 (6.8) | 26.9 (7.2) |
| Elbow | 94.6 (6.5) | 18.2 (3.0) | 76.3 (8.2) | 113.8 (7.4) | 60.6 (12.9) | 53.2 (12.2) | |
| Wrist | −0.4 (1.2) | −8.5 (2.3) | 8.0 (2.3) | 1.4 (2.7) | −11.3 (1.6) | 12.7 (3.0) | |
Table 4.
Mean peak thorax, sternoclavicular and acromioclavicular joint angles, ranges of motion and standard deviations for 10 stroke cycles. The sagittal plane of the thorax is described by flexion (+)/extension (−); the sagittal plane of the sternoclavicular (SC) joint is constrained; and the sagittal plane of the acromioclavicular (AC) joint is described by posterior (+) and anterior (−) tilt. The coronal plane of the thorax is represented by right lateral bend(+)/ left lateral bend (−); the coronal plane of the SC joint is represented as depression (+) and elevation (−); the coronal plane of the AC joint is described as downward (+) and upward (−). The transverse plane is described by counter-clockwise axial rotation(+)/clockwise axial rotation(−) for the thorax, and protraction (+)/ retraction (−) for the SC and AC joints.
| Dominant Side (Right) | Non-Dominant Side (Left) | ||||||
|---|---|---|---|---|---|---|---|
| Plane | Joint | Max Angle (deg) (Stdev) |
Min Angle (deg) (Stdev) |
ROM (deg) (Stdev) |
Max Angle (deg) (Stdev) |
Min Angle (deg) (Stdev) |
ROM (deg) (Stdev) |
| Sagittal | Thorax | −42.6 (3.7) | −54.3 (4.2) | 11.7 (1.7) | N/A | N/A | N/A |
| AC | 23.2 (2.3) | 11.0 (1.6) | 12.2 (2.1) | 26.1 (3.6) | 14.6 (2.1) | 11.5 (2.0) | |
| Coronal | Thorax | 2.6 (2.2) | −7.0 (5.8) | 9.6 (5.5) | N/A | N/A | N/A |
| SC | 2.3 (4.1) | −8.6 (2.0) | 11.0 (5.2) | −1.8 (1.8) | −11.6 (6.1) | 9.9 (6.0) | |
| AC | −14.8 (1.3) | −23.2 (1.5) | 8.4 (1.6) | −19.1 (0.6) | −25.2 (1.9) | 6.1 (1.5) | |
| Transverse | Thorax | 6.0 (1.7) | 0.9 (2.1) | 5.1 (1.9) | N/A | N/A | N/A |
| SC | −18.7 (0.9) | −23.0 (1.0) | 4.3 (1.0) | −17.3 (2.0) | −22.1 (2.3) | 4.8 (1.1) | |
| AC | 40 (1.7) | 33.1 (0.8) | 6.9 (1.5) | 42.0 (1.8) | 36.0 (1.2) | 6.1 (1.1) | |
Table 5.
Peak wrist extension angles for each of the 10 stroke cycles, along with the mean and standard deviation (stdev), for the dominant and non-dominant sides.
| Peak Wrist Extension Angle (deg) | ||
|---|---|---|
| Stroke | Dominant | Non-Dominant |
| 1 | −57.51 | −56.22 |
| 2 | −51.90 | −50.41 |
| 3 | −70.94 | −56.54 |
| 4 | −60.79 | −56.85 |
| 5 | −65.38 | −61.08 |
| 6 | −68.54 | −58.12 |
| 7 | −57.27 | −57.66 |
| 8 | −63.53 | −53.46 |
| 9 | −51.88 | −56.32 |
| 10 | −54.29 | −55.87 |
| Mean | −60.20 | −56.25 |
| Stdev | 6.77 | 2.81 |
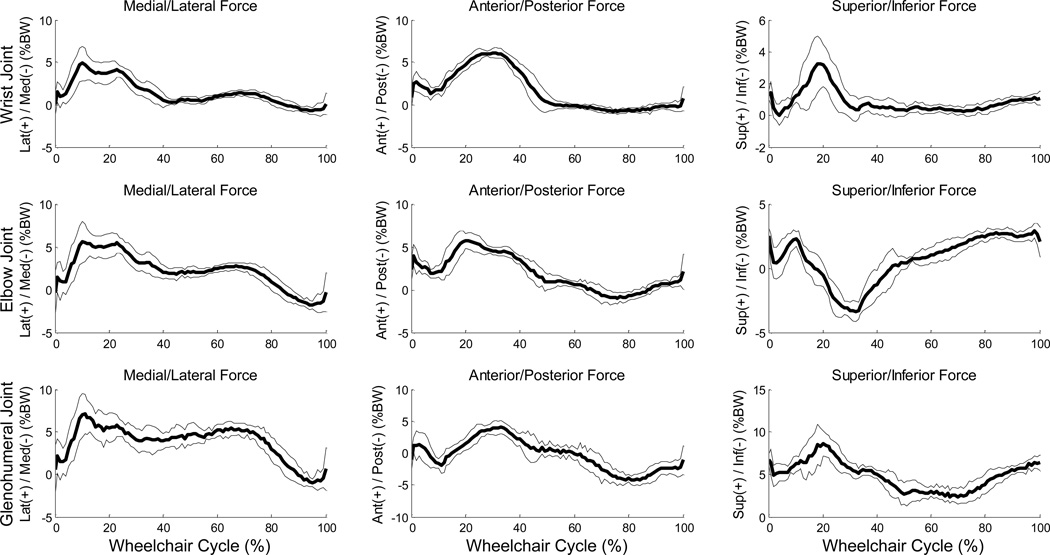
Figure 4.
Ensemble average joint force data for 10 stroke cycles of the glenohumeral, elbow and wrist joints. Mean (bold) and +/− one standard deviation joint forces of the wrist joint: top row, elbow joint: middle row, and the glenohumeral (GH) joint: bottom row of the subject’s right-hand side.
Figure 5.
Ensemble average joint moment data for 10 stroke cycles of the glenohumeral, elbow and wrist joints. Mean (bold) and +/− one standard deviation joint moments of the wrist joint: top row, elbow joint: middle row, and the glenohumeral (GH) joint: bottom row of the subject’s right-hand side.
Table 6.
Mean peak force along all three axes for the wrist, elbow and glenohumeral joints. Force is presented as a percentage of the subject’s body weight (%BW), along with standard deviation (SD).
| Joint | Magnitude of Lateral (+) / Medial (−) Joint Forces | ||||
| Max Force (%BW) | % Cycle Timing | Min Force (%BW) | % Cycle Timing | Force Range (%BW) | |
| Wrist | 5.9 (1.1) | 14.2% (4.9) | −1.0 (0.3) | 95.7% (4.7) | 6.9 (1.2) |
| Elbow | 7.0 (1.0) | 14.8% (4.6) | −2.2 (0.6) | 96.4% (5.2) | 9.2 (1.2) |
| Glenohumeral | 8.4 (1.5) | 19.1% (14.3) | −1.6 (0.5) | 96.5% (4.0) | 10.1 (1.5) |
| Magnitude of Anterior (+) / Posterior (−) Joint Forces | |||||
| Max Force (%BW) | % Cycle Timing | Min Force (%BW) | % Cycle Timing | Force Range (%BW) | |
| Wrist | 6.6 (0.4) | 30.1% (4.8) | −1.1 (0.3) | 81.9% (8.4) | 7.7 (0.4) |
| Elbow | 6.3 (1.1) | 22.0% (8.3) | −1.5 (0.5) | 76.9% (4.4) | 7.7 (1.1) |
| Glenohumeral | 4.8 (0.7) | 24.0% (13.9) | −5.2 (0.7) | 83.6% (7.9) | 10.0 (0.8) |
| Magnitude of Superior (+) / Inferior (−) Joint Forces | |||||
| Max Force (%BW) | % Cycle Timing | Min Force (%BW) | % Cycle Timing | Force Range (%BW) | |
| Wrist | 3.8 (1.5) | 19.8% (3.6) | −0.6 (0.3) | 21.8% (18.1) | 4.5 (1.7) |
| Elbow | 3.3 (0.4) | 92.2% (8.8) | −3.8 (0.5) | 31.8% (3.7) | 7.1 (0.6) |
| Glenohumeral | 9.6 (1.7) | 20.1% (3.5) | 1.4 (0.6) | 61.5% (10.1) | 8.1 (1.8) |
Paired t-tests were conducted to assess angular asymmetry (Table 7). The transverse plane exhibited the most asymmetrical parameters, followed by the sagittal and coronal planes. The most clinically important joint angle peaks, defined as those with asymmetry exhibited in all three planes of motion, were maximum wrist and GH angles and maximum and minimum elbow and AC angles (Table 7).
Table 7.
Mean angular values (standard deviation) of the parameters in which the paired t-test found significant differences (p<0.05) between the dominant side (right) and non-dominant side (left) in all three planes of motion.
| Sagittal Plane | Coronal Plane | Transverse Plane | ||||
|---|---|---|---|---|---|---|
| Parameter | Dominant | Non-Dominant | Dominant | Non-Dominant | Dominant | Non-Dominant |
| Maximum Wrist Angle | −27.4° (4.2°) | −20.2° (8.9°) | 8.9° (1.6°) | 14.4° (3.4°) | −0.4° (1.2°) | 1.4° (2.7°) |
| Maximum Elbow Angle | 100.0° (2.0°) | 96.2° (1.8°) | N/A | N/A | 94.6° (6.5°) | 113.8° (7.4°) |
| Minimum Elbow Angle | 53.8° (1.8°) | 51.2° (1.5°) | N/A | N/A | 18.2° (3.0°) | 60.6° (12.9°) |
| Maximum GH Angle | 17.9° (2.1°) | 20.7° (3.9°) | −16.4° (3.0°) | −8.2° (2.1°) | 21.8° (6.9°) | 7.3° (2.7°) |
| Maximum AC Angle | 23.2° (2.3°) | 26.1° (3.6°) | −14.8° (1.3°) | −19.1° (0.6°) | 40.0° (1.7°) | 42.0° (1.8°) |
| Minimum AC Angle | 11.0° (1.6°) | 14.6° (2.1°) | −23.2° (1.5°) | 25.2° (1.9°) | 33.6° (1.2°) | 36.0° (1.2°) |
IV. Discussion
The custom pediatric UE biomechanical model successfully quantified 3-D joint kinematics and kinetics in an adolescent MWU with SCI. The model outputs are within the expected range based on data from other pediatric inverse dynamics models that have been extensively validated (Slavens et al., 2011b; Slavens et al., 2010; Slavens et al., 2009; Konop et al., 2009). The model demonstrated high wrist extension angles and high elbow joint ranges of motion in all three planes of motion and large joint forces tri-axially at the GH joint. The similar timing of occurrence of the peak angular positions and peak forces highlights a heightened concern regarding increased joint demands during manual wheelchair propulsion in the developing joints of pediatric users.
Studies have shown asymmetrical propulsion patterns, kinetics and pain in adult MWUs, though the clinical implications are still unclear (Boninger et al., 2002; Fay et al., 2004; Hurd et al., 2008). Therefore, assuming symmetry between left and right side data, may lead to errors (Boninger et al., 2002). This model enabled identification of differences between the dominant and non-dominant sides of pediatric MWU, and multiple asymmetrical parameters were found to be statistically significant.
It is expected that the proposed model will improve our understanding of the complex shoulder dynamics due to the inclusion of anatomically relevant shoulder girdle segments and subject specific segment parameters for the pediatric population. New methods for joint center locations are implemented to further increase angular, and thus kinetic, data accuracy (Campbell, 2009). Additionally, the kinetic data provides greater quantitative information available for assessment of UE joint demand effects, such as those resulting from limb dominance, anthropometry, pathology, and maneuvering demands.
This exploratory single case study has demonstrated the utility of the model to identify asymmetry, motion and loading patterns and peak joint dynamics during pediatric wheelchair mobility. Further investigation of the correlation among joint demands, pediatric pathologies, pain, and overuse injuries is warranted to assess the biomechanical changes during growth, transition to adulthood, and use of other wheelchair and mobility systems. This model may provide insights into the biomechanics of pediatric manual wheelchair mobility which may ultimately lead to reductions in UE pain and pathology. We hope this quantitative methodology will assist clinicians in therapeutic planning and rehabilitation of pediatric wheelchair users.
Acknowledgment
We acknowledge the Orthopaedic and Rehabilitation Engineering Center (OREC) and Shriners Hospitals for Children, Chicago, for their support. Special thanks to Philip Voglewede, Joseph Krzak, Adam Graf and Kathy Reiners for their assistance and knowledge. The contents of this work were developed under a grant from the Department of Education, NIDRR grant number H133E100007. However, the contents of this work do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.
References
- Bednarczyk JH, Sanderson DJ. Limitations of kinematics in the assessment of wheelchair propulsion in adults and children with spinal cord injury. Physical therapy. 1995;75:281–289. doi: 10.1093/ptj/75.4.281. [DOI] [PubMed] [Google Scholar]
- Boninger ML, Souza AL, Cooper Ra, Fitzgerald SG, Koontz AM, Fay BT. Propulsion patterns and pushrim biomechanics in manual wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 2002;83:718–723. doi: 10.1053/apmr.2002.32455. [DOI] [PubMed] [Google Scholar]
- Boninger ML, Koontz AM, Sisto SA, Dyson-Hudson TA, Chang M, Price R, Cooper RA. Pushrim biomechanics and injury prevention in spinal cord injury: Recommendations based on CULP-SCI investigations. Journal of Rehabilitation Research and Development. 2005;42:9–20. doi: 10.1682/jrrd.2004.08.0103. [DOI] [PubMed] [Google Scholar]
- Brault MW. Current Population Reports. Washington, DC: US Census Bureau; 2012. Americans with disabilities: 2010; pp. 70–131. [Google Scholar]
- Campbell aC, Lloyd DG, Alderson Ja, Elliott BC. MRI development and validation of two new predictive methods of glenohumeral joint centre location identification and comparison with established techniques. Journal of biomechanics. 2009;42:1527–1532. doi: 10.1016/j.jbiomech.2009.03.039. [DOI] [PubMed] [Google Scholar]
- Corfman TA, Cooper RA, Boninger ML, Koontz AM, Fitzgerald SG. Range of Motion and stroke frequency differences between manual wheelchair propulsion and pushrim-activated power-assisted wheelchair propulsion. The Journal of Spinal Cord Medicine. 2003;26:135–140. doi: 10.1080/10790268.2003.11753673. [DOI] [PubMed] [Google Scholar]
- Crane B. Adaptive seating in management of neuromuscular and musculoskeletal impairment. In: Lusardi MM, Nielsen CC, editors. Orthotics and Prosthetics in Rehabilitation. St. Louis, MO: Elsevier Inc.; 2007. pp. 489–516. [Google Scholar]
- Fay BT, Boninger ML, Fitzgerald SG, Souza AL, Cooper RA, Koontz AM. Manual wheelchair pushrim dynamics in people with multiple sclerosis. Archives of Physical Medicine and Rehabilitation. 2004;85:935–942. doi: 10.1016/j.apmr.2003.08.093. [DOI] [PubMed] [Google Scholar]
- Gil-Agudo A, Del Ama-Espinosa A, Pérez-Rizo E, Pérez-Nombela S, Crespo-Ruiz B. Shoulder joint kinetics during wheelchair propulsion on a treadmill at two different speeds in spinal cord injury patients. Spinal cord. 2010a;48:290–296. doi: 10.1038/sc.2009.126. [DOI] [PubMed] [Google Scholar]
- Gil-Agudo A, Del Ama-Espinosa A, Pérez-Rizo E, Pérez-Nombela S, Pablo Rodríguez-Rodríguez L. Upper limb joint kinetics during manual wheelchair propulsion in patients with different levels of spinal cord injury. Journal of biomechanics. 2010b;43:2508–2515. doi: 10.1016/j.jbiomech.2010.05.021. [DOI] [PubMed] [Google Scholar]
- Hingtgen B, McGuire JR, Wang M, Harris GF. An upper extremity kinematic model for evaluation of hemiparetic stroke. Journal of biomechanics. 2006;39:681–688. doi: 10.1016/j.jbiomech.2005.01.008. [DOI] [PubMed] [Google Scholar]
- Hurd WJ, Morrow MM, Kaufman KR, An K-N. Biomechanic evaluation of upper-extremity symmetry during manual wheelchair propulsion over varied terrain. Archives of physical medicine and rehabilitation. 2008;89:1996–2002. doi: 10.1016/j.apmr.2008.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen RK. Changes in segment inertia proportions between 4 and 20 years. Journal of Biomechanics. 1989;22:529–536. doi: 10.1016/0021-9290(89)90004-3. [DOI] [PubMed] [Google Scholar]
- Kaye HS, Kang T, Laplante MP. Disability Statistics Report. Washington, DC: US Department of Education, National Institute on Disability and Rehabilitation Research; 2000. Mobility Device Use in the United States; pp. 1–60. [Google Scholar]
- Konop KA, Strifling KMB, Wang M, Cao K, Schwab JP, Eastwood D, Jackson S, Ackman JD, Harris GF. A biomechanical analysis of upper extremity kinetics in children with cerebral palsy using anterior and posterior walkers. Gait & Posture. 2009;30:364–369. doi: 10.1016/j.gaitpost.2009.06.012. [DOI] [PubMed] [Google Scholar]
- Mercer JL, Boninger M, Koontz A, Ren D, Dyson-Hudson T, Cooper R. Shoulder joint kinetics and pathology in manual wheelchair users. Clinical biomechanics (Bristol, Avon) 2006;21:781–789. doi: 10.1016/j.clinbiomech.2006.04.010. [DOI] [PubMed] [Google Scholar]
- Meskers CG, Van der Helm FC, Rozendaal La, Rozing PM. In vivo estimation of the glenohumeral joint rotation center from scapular bony landmarks by linear regression. Journal of biomechanics. 1998;31:93–96. doi: 10.1016/s0021-9290(97)00101-2. [DOI] [PubMed] [Google Scholar]
- Nguyen TC, Baker R. Two methods of calculating thorax kinematics in children with myelomeningocele. Clinical biomechanics (Bristol, Avon) 2004;19:1060–1065. doi: 10.1016/j.clinbiomech.2004.07.004. [DOI] [PubMed] [Google Scholar]
- Šenk M, Chèze L. A new method for motion capture of the scapula using an optoelectronic tracking device: a feasibility study. Computer methods in biomechanics and biomedical engineering. 2010;13:397–401. doi: 10.1080/10255840903263945. [DOI] [PubMed] [Google Scholar]
- Slavens B, Sturm P, Bajournaite R, Harris GF. Upper extremity dynamics during Lofstrand crutch-assisted gait in children with myelomeningocele. Gait & posture. 2009;30:511–517. doi: 10.1016/j.gaitpost.2009.07.125. [DOI] [PubMed] [Google Scholar]
- Slavens B, Sturm PF, Harris GF. Upper extremity inverse dynamics model for crutch-assisted gait assessment. Journal of biomechanics. 2010;43:2026–2031. doi: 10.1016/j.jbiomech.2010.03.026. [DOI] [PubMed] [Google Scholar]
- Slavens B, Graf A, Krzak J, Vogel L, Harris GF. Upper Extremity Wheelchair Kinematics in Children with Spinal Cord Injury; Conference Proceedings IEEE Engineering in Medicine and Biology Society; 2011a. pp. 8158–8161. [DOI] [PubMed] [Google Scholar]
- Slavens B, Bhagchandani N, Wang M, Smith Pa, Harris GF. An upper extremity inverse dynamics model for pediatric Lofstrand crutch-assisted gait. Journal of biomechanics. 2011b;44:2162–2167. doi: 10.1016/j.jbiomech.2011.05.012. [DOI] [PubMed] [Google Scholar]
- SmartWheel User’s Guide 2010. Three Rivers. Mesa, AZ: 2009. p. 61. [Google Scholar]
- Van der Helm FCT, Pronk GM. Three-Dimensional Recording and Description of Motions of the Shoulder Mechanism. Journal of Biomechanical Engineering. 1995;117:27–40. doi: 10.1115/1.2792267. [DOI] [PubMed] [Google Scholar]
- Van Drongelen S, Van der Woude LHV, Veeger HEJ. Load on the shoulder complex during wheelchair propulsion and weight relief lifting. Clinical biomechanics (Bristol, Avon) 2011;26:452–457. doi: 10.1016/j.clinbiomech.2011.01.006. [DOI] [PubMed] [Google Scholar]
- Veeger HEJ, Meershoek LS, Van der Woude LHV, Langenhoff JM. Wrist motion in handrim wheelchair propulsion. Journal of rehabilitation research and development. 1998;35:305–313. [PubMed] [Google Scholar]
- Wu G, Van der Helm FCT, Veeger HEJD, Makhsous M, Van Roy P, Anglin C, Nagels J, Karduna AR, McQuade KJ, Wang X, Werner FW, Buchholz B. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion - Part II: shoulder, elbow, wrist and hand. Journal of Biomechanics. 2005;38:981–992. doi: 10.1016/j.jbiomech.2004.05.042. [DOI] [PubMed] [Google Scholar]
- Yeadon MR, Morlock M. The appropriate use of regression equations for the estimation of segmental inertia parameters. Journal of Biomechanics. 1989;22:683–689. doi: 10.1016/0021-9290(89)90018-3. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM. Kinetics of Human Motion. Champaign, IL: Human Kinetics; 2002. [Google Scholar]