Abstract
Purpose
: A method is presented for generating simulated low-dose cone-beam CT (CBCT) preview images from which patient- and task-specific minimum-dose protocols can be confidently selected prospectively in clinical scenarios involving repeat scans.
Methods
: In clinical scenarios involving a series of CBCT images, the low-dose preview (LDP) method operates upon the first scan to create a projection dataset that accurately simulates the effects of dose reduction in subsequent scans by injecting noise of proper magnitude and correlation, including both quantum and electronic readout noise as important components of image noise in flat-panel detector CBCT. Experiments were conducted to validate the LDP method in both a head phantom and a cadaveric torso by performing CBCT acquisitions spanning a wide dose range (head: 0.8–13.2 mGy, body: 0.8–12.4 mGy) with a prototype mobile C-arm system. After injecting correlated noise to simulate dose reduction, the projections were reconstructed using both conventional filtered backprojection (FBP) and an iterative, model-based image reconstruction method (MBIR). The LDP images were then compared to real CBCT images in terms of noise magnitude, noise-power spectrum (NPS), spatial resolution, contrast, and artifacts.
Results
: For both FBP and MBIR, the LDP images exhibited accurate levels of spatial resolution and contrast that were unaffected by the correlated noise injection, as expected. Furthermore, the LDP image noise magnitude and NPS were in strong agreement with real CBCT images acquired at the corresponding, reduced dose level across the entire dose range considered. The noise magnitude agreed within 7% for both the head phantom and cadaveric torso, and the NPS showed a similar level of agreement up to the Nyquist frequency. Therefore, the LDP images were highly representative of real image quality across a broad range of dose and reconstruction methods. On the other hand, naïve injection ofuncorrelated noise resulted in strong underestimation of the true noise, which would lead to overly optimistic predictions of dose reduction.
Conclusions
: Correlated noise injection is essential to accurate simulation of CBCT image quality at reduced dose. With the proposed LDP method, the user can prospectively select patient-specific, minimum-dose protocols (viz., acquisition technique and reconstruction method) suitable to a particular imaging task and to the user's own observer preferences for CBCT scans following the first acquisition. The method could provide dose reduction in common clinical scenarios involving multiple CBCT scans, such as image-guided surgery and radiotherapy.
Keywords: cone-beam CT, dose reduction, protocol optimization, quantum noise, electronic noise, image quality, iterative reconstruction
I. INTRODUCTION
Cone-beam CT (CBCT) is finding increased application in areas such as image-guided surgery (IGS), image-guided radiation therapy (IGRT), and interventional radiology.1–9 In many of these applications, repeat CBCT scans are often acquired. For example, in IGS, an initial CBCT may be used for patient setup and registration of preoperative planning information, while subsequent CBCTs may be used for visualizing surgical progress, detection of complications, and/or verifying the surgical product. Additionally, in IGRT, patients may receive a CBCT scan at each treatment fraction. In accordance with efforts to reduce radiation dose to the patient (and in some cases to the clinicians, as with IGS),10–12 each CBCT should be acquired at the minimum dose such that a particular imaging task(s) can still be reliably performed. For scenarios in which multiple CBCTs of a patient are acquired, ensuring that each scan is conducted at the minimum dose sufficient for a given imaging task is especially important in reducing the total accumulated dose, since a fractional dose reduction per scan is multiplicative with the number of scans. Of course, lower dose techniques generally produce higher noise images, and selection of the minimum-dose protocol for a particular patient is challenging—usually guided simply by a coarse technique chart in which scan protocols are simply stratified by patient body habitus. The ability to confidently select low-dose protocols sufficient for a given imaging task and patient is therefore a challenge, and perhaps even more so for nonlinear model-based image reconstruction (MBIR) methods for which complex dose-noise-resolution tradeoffs may defy a simple predictive model.
One method to aid in selecting a patient- and task-specific protocol (i.e., acquisition technique, image reconstruction method, and image processing/postprocessing parameters) is to provide a “low-dose preview” (LDP) of the image quality that can be expected for a CBCT image acquired at reduced dose. Such simulated dose reduction methods allow the user to visualize image quality at reduced dose, followed by confident selection of minimum-dose protocols sufficient for the imaging task. The methods have been developed and validated for diagnostic CT and successfully used to establish low-dose CT protocols—both in creating optimal technique charts from retrospective studies (“How low could we have gone?”) and in prospectively determining protocols for individual patients (“How low can we go next time?”). An early method proposed by Mayo et al. demonstrated that by injecting noise into raw CT data to simulate dose reduction, the reconstructed CT images were indistinguishable from real low-dose images.13 Subsequent studies used simulated dose reduction to demonstrate the potential for low-dose protocols in applications such as pediatric abdominal CT,14 CT colonography,15 chest CT,16 and chest radiography.17 More recently, simulated dose reduction methods have utilized more advanced models of noise beyond just quantum noise, such as inclusion of electronic noise,18,19 that led to accurate reproduction of not only image noise magnitude but also noise power spectra.20–23 Other extensions of simulated dose reduction include using dual energy scans to allow simulated changes in tube voltage24 or using an image-based approach that does not assume availability of projection data (but does not allow for different reconstruction methods/parameters).25–27 Common to these methods is the assumption of spatially uncorrelated noise in the projection data, which may be a fair assumption for detectors employed in multidetector CT scanners. However, correlated noise is an important consideration for flat-panel detectors (FPDs) that are typically used in CBCT—for example, scintillator blur is known to introduce spatial correlation in the quantum noise, and electronic noise can be an important source of noise at very low dose levels.28–30 Therefore, previous methods for low-dose simulation in CT cannot be directly extended to CBCT based on indirect-detection FPDs since they do not include the effect of correlated noise (quantum or electronic noise).
We propose a new LDP method for FPD-based CBCT that seeks to inject both quantum noise and electronics noise in a manner that is accurate in terms of both the magnitude and correlation of noise exhibited at lower dose. The LDP images operate upon the initial CBCT of the patient (i.e., the first CBCT in a series of subsequent images, as in IGS or fractionated IGRT) to generate simulated low-dose projection data that are in turn reconstructed by whatever algorithm and postprocessing methods are available in the imaging system. In using the observer's own preferences to select the minimum-dose protocol for a particular imaging task, this approach to prospective protocol selection is independent of models of observer performance; moreover, by operating on the actual projection data from the initial CBCT scan, it is patient-specific and applicable to advanced image reconstruction and processing methods (including MBIR and possible proprietary artifact correction or postprocessing methods incorporated by a particular system). An accurate LDP method can also be used retrospectively to perform population-wide protocol optimization based on patient-specific attributes (e.g., patient size, gender) and imaging task (e.g., bone, soft-tissue visualization), ultimately providing minimum-dose CBCT technique charts. This paper therefore establishes a method for generating realistic LDP images and validates the method quantitatively to assess the similarity between preview and real CBCT images acquired at lower dose for different reconstruction methods.
II. METHODS
Figure 1 illustrates the LDP methodology and general workflow for selecting the minimum-dose protocol for subsequent CBCT scans in a manner that is patient-specific and accounts for the imaging task, the reconstruction algorithm (including artifact correction and postprocessing methods therein), and user preferences in perceived image quality.
FIG. 1.
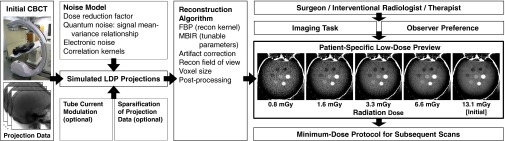
Overview of LDP workflow. The first CBCT (denoted here as initial) is acquired as part of the normal clinical workflow and provides the projection data for creating the LDP images. The LDP creates accurate CBCT simulation images at any level of dose reduction (and for any choice of available reconstruction algorithm and parameters therein) from which to select minimum-dose CBCT protocols for subsequent scans.
II.A. Theoretical basis for noise simulation
II.A.1. Model for projection image noise magnitude and correlation
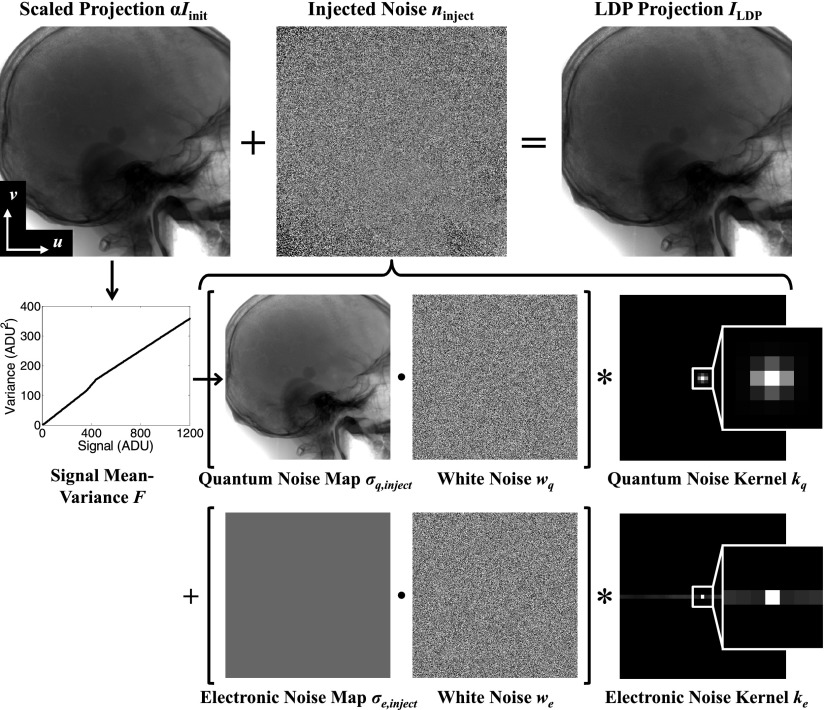
The proposed LDP method modifies the projections from the initial CBCT in a manner that simulates tube output (given by the tube current-time product, units of mAs) reduction. When the tube output is reduced by a factor of α < 1 (i.e., exposure of the low-dose technique relative to that of the initial technique), the mean signal is reduced in proportion to α, and the signal-to-noise ratio (SNR) is also reduced. Simulation of LDP projections ILDP from initial projections Iinit therefore comprises two main steps: (1) scaling the detected signal, and (2) injecting noise ninject into the projection. The overall relationship is expressed as
| (1) |
where (u, v) is the pixel position. Scaling the initial projections ensures that the patient position, spatial resolution, x-ray energy, beam hardening, and scatter-to-primary ratio are preserved, while the addition of noise simulates tube output reduction but does not affect these other properties. Note that the first step of scaling the initial projections by α assumes detector linearity (a reasonable assumption for a well-calibrated detector) and image acquisition at the same x-ray energy (tube voltage (kVp) and filtration).
Accurate estimation of the injected noise ninject requires a model for both the magnitude and correlation of the quantum and electronic noise. From Eq. (1), the variance in the LDP projection is related to that in the initial projection and the injected variance by
| (2) |
As illustrated in Fig. 2, the notation I(.) denotes a projection image, n(.) denotes a zero-mean noise realization, and σ(.) denotes a noise map (alternatively σ2(.) a variance map). In Eq. (2), therefore, dose reduction is seen to scale the initial variance by α2, and the injected noise is assumed to be independent of σinit. The system-specific signal-to-variance relationship is determined by a simple calibration detailed below. Each term in Eq. (2) represents the sum of two main sources of noise in x-ray imaging—quantum and electronic—which are assumed to be independent. For example, the first two terms of Eq. (2) can be written as a sum of quantum and electronic noise (subscripts q and e, respectively):
After substituting Eq. (3) into Eq. (2) and rearranging terms, the injected variance can be written:
| (4) |
This suggests that the injected noise can also be represented by two components, which are defined to be the quantum and electronic injected variance:
| (5a) |
| (5b) |
The two components comprise the total injected variance:
| (6) |
as in Eq. (4). The method for evaluating the injected quantum noise [Eq. (5a)] and injected electronic noise [Eq. (5b)] is explained in the following sections.
FIG. 2.
Flowchart illustration of the process for simulating low-dose projections. The noise injected to the projection data accounts for both the magnitude and correlation of both the quantum and electronic noise components at an arbitrary level of dose reduction (fraction α) compared to the initial CBCT.
II.A.1.a. Quantum noise
The variance associated with quantum noise increases approximately linearly with the mean signal.31 More generally, however, the relationship can be characterized by a function F, where
| (7) |
and is the mean signal in the projection. In practice, the mean projections are unavailable from a single scan, so the projections of the initial scan Iinit are used as a surrogate for (and αIinit as a surrogate for ). The injected quantum variance is then related to the initial projections using the approximation:
| (8) |
which generalizes Eq. (5a) to include a potentially nonlinear relationship between and . Since Iinit is an unbiased (albeit noisy) estimate of and F is locally well-approximated as a linear transform, the approximation yields an estimate of that is also unbiased (albeit noisy). In this work, the approximation is applied for a high-quality initial scan, and further investigation is needed to verify the ability of a low-dose initial scan to approximate the injected quantum variance and may require using recently developed methods by Zabic et al.23
II.A.1.b. Electronic noise
A basic model for electronic noise assumes that it is spatially invariant and independent of the signal magnitude, with variance σe2. Therefore, the electronic variance of Eq. (5b) simplifies to
| (9) |
which is uniform across the projection.
II.A.1.c. Noise correlations
In addition to the magnitude of the injected noise, the correlations in the noise are an important consideration for CBCT not previously considered in similar methods developed for low-dose CT simulation. Correlations in quantum noise originate primarily from the scintillator blur in (indirect-detection) FPDs, while correlations in electronic noise may originate from line noise, crosstalk, etc. in the readout electronics of the detector. These correlations are represented by convolution kernels kq and ke for quantum and electronic noise, respectively, which are also assumed to be spatially invariant and independent of exposure. When convolved with white (uncorrelated) noise, these kernels introduce noise correlation to match that found in the projection data. Therefore, while multiplying the standard deviation map σq,inject by white noise iid (independent and identically distributed) would produce uncorrelated noise of the desired magnitude for injection, the appropriate degree of correlation can be introduced by convolving the resulting product with the kernel kq, as in
| (10a) |
where · denotes the Hadamard (element-wise) product and * denotes 2D convolution. Because the standard deviation map σq, inject(u, v) is derived from the initial projection Iinit(u, v), which includes scintillator blur, the standard deviation map exhibits a degree of unavoidable blur that could contribute to errors in the magnitude of the injected noise nq, inject(u, v); however, the error associated with blur in the noise map is shown to be minor in results reported below. The injected noise exhibits an accurate degree of correlation due to the element-wise product with white noise (which produces spatially uncorrelated noise) followed by convolution with the noise kernel. Note that the kernels kq and ke have unit norm so that the magnitude of the injected variance is unchanged even after the correlations are introduced. Similarly, for the electronic noise:
| (10b) |
with white noise we independent of wq. Although the effect of each stage in the imaging chain is not directly modeled (e.g., the conversion of x-rays to optical photons, which typically follows a non-Poisson distribution characterized by the Swank factor), the first- and second-moments of the true distribution in the detected signal can be well-approximated by a Gaussian distribution.32 While this approximation is expected to break down at very low signal, it is seen to provide a reasonable model over a fairly broad exposure range, as shown below.
Collecting terms, Eq. (1) can be expanded to a closed form for generating LDP projections:
| (11) |
as illustrated in Fig. 2 for an anthropomorphic head phantom.
II.A.2. System calibration
The model presented above involves four key characteristics—namely, F, σe2, kq, and ke—that can be determined by a calibration measured from projections of a simple phantom. To decouple the quantum and electronic noise contributions of the total noise, projections at two exposure levels are required. For exposure levels ξ = {A, B}, the noise in a projection is found from the difference of two successive projections in the same position (denoted Iξ, 1 and Iξ, 2, where 1 and 2 index the two projections with independent noise realizations) and normalized by :
| (12) |
The noise kernels are most easily related to the autocorrelation Rξ(i, j) of the projection noise, which is computed using the definition:
| (13) |
where Nu × Nv is the size of a region-of-interest (ROI) within which the noise is determined, and ⋆ represents the cross-correlation operation. Note that Rξ can also be written as the sum of its components:
| (14a) |
| (14b) |
where Rq, ξ and Re represent the quantum and electronic noise contributions to the autocorrelation, respectively, and mξ is the mean value of Iξ in the ROI. We assume that Rq, ξ increases in proportion to exposure and is characterized by a constant slope η (which is in fact the slope of F when F is modeled by a linear relationship), while Re is independent of exposure. The tilde denotes an autocorrelation function normalized by the variance, such as:
| (15) |
After computing Rξ for both exposure levels, and Re can be solved through a set of linear equations. For example, Re is solved by extrapolating the exposure to zero, using:
| (16) |
While in some systems Re could be measured directly from dark-field projections (detector readout in the absence of x-ray exposure), the projections would be zero-mean with electronic noise producing an equal number of positive and negative analog-to-digital units (ADU). In the system used in experiments below, all values were clipped at 0 ADU by the manufacturer (presumably so that an unsigned 16-bit integer data format could be used), so the electronic noise could not be accurately characterized without a positive mean signal to ensure recorded values above 0 ADU—hence the use of two nonzero exposure levels and extrapolation to zero exposure.
The autocorrelation functions can then be related to the convolution kernels. Once (and ) are determined by the calibration, the corresponding kernels kq (and ke) can be estimated such that they satisfy:
| (17) |
In the results below, the kernels were determined by using the fminunc function in Matlab (MathWorks, Natick, MA) to minimize the mean squared error between and kq ⋆ kq as follows:
| (18) |
where each kq(i, j) was a free parameter within a small region about i = j = 0 that depended on the spatial extent of Rq and was set to 0 elsewhere to better condition the estimation. Alternatively, Fourier methods for estimating and applying the noise kernels could be considered but must be careful to keep the simulated noise real-valued. As noted above, to preserve the magnitude of the variance while introducing the correlations, the norm of kq (and ke) must equal 1, which is satisfied since:
| (19) |
The electronic variance is given by σe2 = Re(0, 0), and the signal mean-variance relationship F can be determined by first sorting and binning the values in the average projection . The variance of nξ for the pixels in each bin was plotted against the mean for the pixels in each bin, after subtracting the electronic noise variance σe2 so that only the quantum variance remains. A linear fit approximating F can then be applied to the sample points derived from the binned data.
II.B. Experimental methods
The proposed LDP method was experimentally tested using a prototype mobile C-arm (modified Powermobil, Siemens Healthcare, Erlangen, Germany; see Fig. 1) capable of CBCT. A computer-controlled motorized drive provided continuous rotation of the C-arm over a ∼178° orbit while collecting 198 projections, and the source-axis distance (SAD) of 60 cm and source-detector distance (SDD) of 120 cm provided a ∼15 × 15 × 15 cm3 volumetric field of view (FOV). A previously developed geometric calibration phantom was used to measure the source-detector position of each projection relative to the C-arm isocenter, which was represented as projection matrices.33–35 The x-ray source was operated in pulsed-fluoroscopic mode, with the tube potential fixed at 100 kVp while the tube output of the scan was varied from 20–320 mAs in the head and 30–480 mAs in the body.
The C-arm was equipped with a Varian PaxScan 3030+ FPD (Varian Medical Systems, Palo Alto, CA) operated by the system manufacturer in 2 × 2 binning mode (768 × 768 effective pixels at 388 μm pitch) and in dual-gain mode to increase the signal dynamic range. For each projection, a high-gain image was recorded to provide a larger dynamic range for low signal values, while a low-gain image was recorded to prevent saturation of high signal values. The dual-gain measurements were then corrected for detector dark current offset and combined into a 16-bit unsigned integer ADU value per pixel,36 with a minimum signal value of zero enforced. These corrected and combined projections were the input to the LDP calibration and validation. Due to the different gains, the signal-variance relationship F was composed of two distinct regions as seen in Fig. 2—a low-signal, high-gain region and a high-signal, low-gain region. Based on the empirical measurements of F, it was found that the low-signal region ranged from [0, 360] ADU, while the high-signal region ranged from [440, 216−1] ADU. Therefore, in approximating F with a linear relationship, separate linear fits were applied to the two regions. A linear interpolation was applied between the fitted values at 360 and 440 ADU to provide a piecewise-linear fit to F that ensures continuity and an increasing relationship.
Radiation dose was previously measured and reported in the head and body,9,37 using a 0.6 cm3 Farmer ionization chamber (Accu-Pro, RadCal, Monrovia, CA). The head dose was measured in an acrylic 16 cm diameter cylindrical CTDI phantom, and good linearity was observed between specified tube output (mAs) and measured dose, with a conversion of 0.041 mGy/mAs at 100 kVp. The dose in the abdomen was measured in an oblate abdominal phantom (QRM GmbH, Erlangen, Germany) and found to be 0.026 mGy/mAs at 100 kVp.
II.B.1. Calibration and assessment of LDP in head imaging
The accuracy of the LDP method was first evaluated for head imaging. Calibration measurements for F, σe, kq, and ke were obtained with the 16 cm acrylic cylinder wrapped in an 8 mm thick PVC layer (simulating the skull) scanned twice each at settings of 100 kVp, {20, 40, 80, 160, and 320} mAs.
Following calibration, quantitative analysis of LDP accuracy was performed in an anthropomorphic head phantom comprising a human skull encased in Rando tissue-equivalent plastic with seven 12.7 mm diameter plastic spheres embedded within the interior of the cranium with contrast ranging from ∼40 to 900 HU (The Phantom Laboratory, Greenwich, NY; see Fig. 1). The head phantom was scanned twice, each at the same techniques as the calibration phantom. The 320 mAs technique was used as the “initial” CBCT, and LDP projections were formed at 20, 40, 80, and 160 mAs. The reconstructed LDP images were then compared with real images at the same techniques. As detailed below, the two sets of scans (and preview images) at each technique allowed determination of image noise from the difference images of two iid realizations.
II.B.2. Calibration and assessment of LDP in body imaging
Since body imaging involves increased attenuation and scatter compared to head imaging (with possible effects on F and kq), a separate calibration was performed for body imaging using the oblate abdominal QRM phantom. A second oblate thoracic phantom (QRM GmbH, Erlangen, Germany) was placed immediately superior to the abdomen phantom, and an acrylic 32 cm CTDI body phantom was placed immediately inferior to provide fairly realistic scatter from outside the imaging volume. The imaging techniques were 100 kVp, {30, 60, 120, 240, and 480} mAs, each acquired twice.
After calibration with the abdominal phantom, studies were conducted using a fresh, unfixed cadaveric torso presenting realistic bone, soft-tissue structures, and fine-detail gas pockets in the bowel. The same imaging techniques as the body calibration were acquired for the cadaver, with the 480 mAs scan used as the “initial” CBCT, and the remaining scans used for comparison between LDP and real images.
II.C. Image reconstruction
In addition to conventional filtered backprojection (FBP) reconstruction, we applied the penalized-likelihood (PL) framework as a representative selection of the much broader class of MBIR algorithms such as total-variation (TV) minimization,38 penalized weighted least-squares,39 compressed sensing,40 and tight-frame regularization.41 The LDP and real CBCT projections were both reconstructed using FBP and PL. Note that the purpose of the work was not to make a direct comparison between FBP and PL, although such comparisons could potentially be facilitated with accurate LDP methods that eliminate the need for scans at multiple dose levels. Rather, the goal was to assess whether the LDP noise injection in projections is sufficiently accurate to produce realistic images in either reconstruction method. Therefore, for both reconstruction algorithms, the LDP and real projections were reconstructed in the same manner so that any differences in the reconstructed images originate from the accuracy of the proposed LDP method and its underlying assumptions rather than the reconstruction algorithm. While both FBP and PL offer reconstruction parameters that may be freely tuned (for example, trading off spatial resolution and image noise), for simplicity only one set of parameters was selected that was representative of each reconstruction algorithm.
All images were reconstructed with isotropic 0.6 × 0.6 × 0.6 mm3 voxels using Matlab, which interfaced with custom external libraries for the computationally intensive 3D forward and backprojectors. The projectors were implemented in CUDA for GPU acceleration (GTX 680, nVidia, Santa Clara, CA) and utilized the separable footprints with trapezoid functions (SF-TT) method for projecting voxels onto the detector plane.42,43 While other projection methods could have been used, SF-TT was shown by Long et al. to be more accurate than other methods, such as the distance-driven method or Siddon's method.43–45
II.C.1. Cone-beam filtered backprojection (FBP)
Cone-beam FBP reconstruction was performed with a modified Feldkamp-Davis-Kress (FDK) algorithm applied to the line integrals l = −log(I/I0), where I is a projection (preview or real) and I0 is the flood-field projection.46 A minimum value of I = I0e−8 was enforced (i.e., the line integrals were capped at 8, corresponding to ∼40 cm water taken as a reasonable estimate of object diameter for the abdomen) to avoid streak artifacts from photon starvation. Although clipping the values like this may introduce a bias in the line integrals, the method was applied to both the preview and real projections, which provided a consistent comparison between the two. The lateral edge values were extended beyond the detector edge (in the u-direction) as a form of basic truncation correction, and a Hann window with cutoff frequency fc = 0.4 × fNyquist was applied to the ramp filter. No scatter or beam-hardening corrections were applied to either the preview or real reconstructions, although the LDP process is compatible with various artifact correction or postprocessing methods that might be applied, since it uses the projection data directly.
II.C.2. Penalized likelihood (PL) iterative reconstruction
The penalized likelihood method combines a data consistency term with image regularization to form the reconstructed image. The data consistency term utilizes a statistical model of the projections I to construct the log-likelihood function L(μ; I) for image μ, while image regularization penalizes the image roughness R(μ) with strength β. The reconstructed image is then the solution to the following optimization problem:
| (20) |
which seeks to maximize the likelihood function while penalizing image roughness (e.g., noise). In order to apply a statistical model to the data, the projection measurements I and flood-field air scan I0 were first normalized by the effective detector gain η0, so that
| (21) |
where
| (22) |
Then a basic Poisson statistical model was applied, with
| (23) |
where A is the forward-projection operator. Although we have already shown that the true statistics are neither independent (due to spatial correlations) nor Poisson distributed (due to the various detector gain stages and additive electronic noise), this model provides a basic form of statistical weighting of the measurements that is commonly applied in practice. The log-likelihood function (ignoring constant terms) is then
| (24) |
The image regularization reduces image noise in a manner that generally trades off spatial resolution with image noise (though in a different manner than FBP). Regularization was applied to a first-order neighborhood of each voxel, with unity weights wjk and penalty function ψ applied to the difference of neighboring voxels:
| (25) |
Rather than a basic quadratic penalty function , an edge-preserving penalty is often adopted to provide lower noise images while maintaining edge information. In results reported below, the Huber penalty function
| (26) |
was used, which provides a greater degree of edge-preservation for smaller δ at the potential expense of blotchy image texture.
The PL reconstructions were initialized by the corresponding FBP reconstructions and iteratively solved with the ordered subset, separable quadratic surrogates (OS-SQS) technique, which allowed for all voxels to be updated simultaneously per iteration.47,48 The primary computational burden lay with the forward- and back-projection operations per iteration, which were accelerated by GPU implementation of the projectors. The OS-SQS algorithm was run for 200 iterations with 11 subsets, and the selected PL reconstruction parameters were δ = 10−3 mm−1 and β numerically equivalent to the tube output (e.g., β = 20 for the 20 mAs scan), which coincidentally served as a convenient selection of β (as opposed to a formal relationship) that also took into account the need for larger β with higher I0. These values of δ and β served as a fairly general-purpose selection that avoided patchy image noise and preserved spatial resolution. Alternative parameter selection—for example, specifically to enhance soft-tissue imaging performance37—is possible and completely compatible the LDP process.
II.D. Assessment of image quality and accuracy of LDP images
The accuracy of the LDP was quantitatively assessed by comparison of spatial resolution, image contrast, and image noise characteristics of the LDP and real low-dose images. Since neither the injection of noise (for the LDP images) nor the reduction of exposure (for the real images) was expected to affect the spatial resolution or absolute contrast, these two metrics provided a “sanity check” to ensure that the LDP algorithm did not have unexpected adverse effects on image quality, and emphasis of the analysis was on the accuracy of the LDP image noise magnitude and correlation.
II.D.1. Spatial resolution
The spatial resolution was assessed by measuring the edge spread function (ESF) of the high-contrast sphere (3 o'clock position, Fig. 1) in the anthropomorphic head phantom. The sphere was divided into 12 nonoverlapping 30° conical sections whose apices were at the center of the sphere and axes lay in the axial plane, and an error function (erf) was fit to the edge. The derivative of the erf (a Gaussian) yielded the line spread function (LSF) characterized by its full-width at half-maximum (FWHM). The difference in measured FWHM between the LDP and real CBCT images for all 12 conical sections and for both realizations at each dose level provided 24 measurements for evaluating the preservation of spatial resolution.
II.D.2. Image contrast
The seven spheres embedded in the anthropomorphic head phantom provided varying contrast levels (ranging from ∼40 to 900 HU) that were compared between the preview and real images. For each reconstructed image, the contrast of each sphere was determined by subtracting the average attenuation within the sphere (20 voxel diameter ROI) from the average attenuation adjacent to the sphere (also a 20 voxel diameter ROI). Agreement was assessed by examining the difference in contrast between the LDP and real images for all seven spheres and in both realizations at each dose level. Although the images were reconstructed with units of mm−1, the image contrast (and noise) were converted to HU by an approximate factor of 5 × 104 HU/mm−1 determined from CBCT images of known materials (e.g., water) in comparable head and body phantom configurations.
II.D.3. Image noise
Since CBCT images were acquired twice at each dose level, subtraction of two reconstructions at each tube output level was used to measure image noise (after normalization by ). The noise magnitude was first assessed by measuring the standard deviation within an ROI. In the anthropomorphic head phantom, the standard deviation was measured in a 51 × 51 voxel ROI at the center of the axial plane for the 31 central slices and averaged. In the cadaveric torso, the standard deviation was measured in a 51 × 51 voxel ROI centered on the right kidney (i.e., within a reasonably homogeneous region of soft-tissue) in the coronal plane and averaged across 31 coronal slices centered on the kidney.
Accurate reproduction of noise texture in the reconstructed LDP images was also assessed by computing the noise-power spectrum (NPS).49–51 Both axial-plane and longitudinal (z-) direction NPS were considered, since detector correlations were expected to affect both. In the head phantom, the 2D NPS was computed in the axial plane and averaged in the longitudinal direction for the 51 × 51 voxel ROIs in the 31 axial slices at the center of the volume. A radial average of the 2D NPS was performed to reduce statistical error in the NPS estimate. In the cadaver, the 1D NPS was computed in the longitudinal (z-) direction and averaged in the other directions for the 51 × 51 voxel ROIs in the 31 coronal slices centered on the kidney. It was assumed that within these small ROIs, the properties were locally stationary such that the computed NPS were representative of the local noise texture. Additionally, the ROIs avoided high-contrast edges so as to avoid the nonlinear behavior of the PL edge-preserving penalty.
Finally, as a basis of comparison to naïve simulation of noise without proper accounting of correlation, LDP projections were created by injecting white noise rather than correlated noise (i.e., using kq = ke = δ2, a 2D discrete impulse function). The injected noise therefore possessed the correct magnitude but was not spatially correlated. The resulting LDP images were similarly assessed in terms of the NPS, hypothesizing that the reconstructed image NPS would be lower when injecting white noise due to the effect of the reconstruction process.
III. RESULTS
III.A. Calibration phantom empirical results
III.A.1. Signal-variance mapping
Figure 3(a) illustrates a single projection of the 16 cm acrylic cylinder from the 1.6 mGy (100 kVp, 40 mAs) acquisition, and the difference of two such projections [Fig. 3(b)] yields a noise realization (after normalization by ). Figure 3(c) shows the variance in the difference image plotted against the mean signal in the projection. Two linear regions can be observed for this FPD (which employs a dual-gain readout mode)—a high-gain region from 0 to ∼360 ADU and a low-gain region above ∼440 ADU. Within each region, a linear fit described the signal-variance relationship well (R2 > 0.99). A seemingly nonmonotonic relationship was observed in the transition between the two regions. We believe the transition region corresponds to signal overlap between the two gain modes, and the behavior of the variance-signal relationship here could be due to a slightly suboptimal combination (from a noise perspective) of dual-gain readout by the system manufacturer. Because the observed effect covered only a small fraction of the detector dynamic range, for simplicity, the transition region was approximated by a linear interpolation between the low-gain and high-gain linear fits that might be better generalized to other detectors, and the mismatch in projection variance within this narrow region was expected to have a small effect overall. The y-intercept is near 0, since the measured electronic variance σe2 = 4.47 ADU2 was subtracted out prior to fitting.
FIG. 3.

Calibration of the (potentially nonlinear) signal-variance relationship. For head imaging, a 16 cm acrylic cylinder served as a simple calibration phantom. (a) Single projection of the cylinder from the 1.6 mGy (100 kVp, 40 mAs) acquisition, with grayscale pixel values in ADU. (b) A noise realization computed from the difference image of two projections (normalized by ), displayed in ADU. (c) Signal mean-variance relationship for a head-sized object and the 1.6 mGy technique. The points represent the measurements, and the lines represent linear fits in the high-gain [0, 360] ADU and low-gain [440, 216−1] regions, with a linear interpolation in the transition region between [360, 440] ADU.
III.A.2. Noise correlation kernels
Noise autocorrelation functions were computed as in Eq. (13) using projections of the calibration phantom from the 100 kVp, 20 and 40 mAs scans. As illustrated in Fig. 4, the major portion of quantum noise correlation was contained within the central 5 × 5 region of , with an autocorrelation coefficient of up to 0.22 for neighboring pixels and falling to zero outside the central 5 × 5 region. A slight asymmetry in the u- and v-directions was observed, with stronger correlations in the u-direction. Although commonly assumed to be uncorrelated, Re was found to exhibit correlation across v = 0, the direction of detector readout lines, with an autocorrelation coefficient of up to 0.08 for pixels along the same readout line.
FIG. 4.
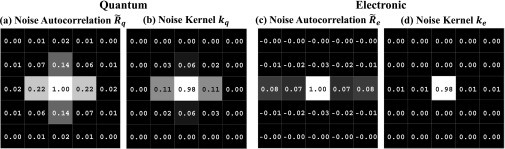
Central 5 × 5 region of the measured noise autocorrelation (a) and (c) from the calibration phantom. The noise kernels (b) kq and (d) ke estimated from the respective autocorrelation functions.
Due to the generally ill-conditioned nature of estimating kq as a free parameter consistent with as in Eq. (18), only the central 3 × 3 region of kq was allowed to vary, with a value of 0 enforced elsewhere. For estimating ke, only the elements along v = 0 were allowed to vary from zero, which captured most of the correlated behavior of electronic noise. More advanced models for estimating ke could also account for the small amounts of negative correlation observed along v = ±1. The resulting noise kernels (Fig. 4) were used in the LDP of the anthropomorphic head phantom.
III.B. Anthropomorphic head phantom
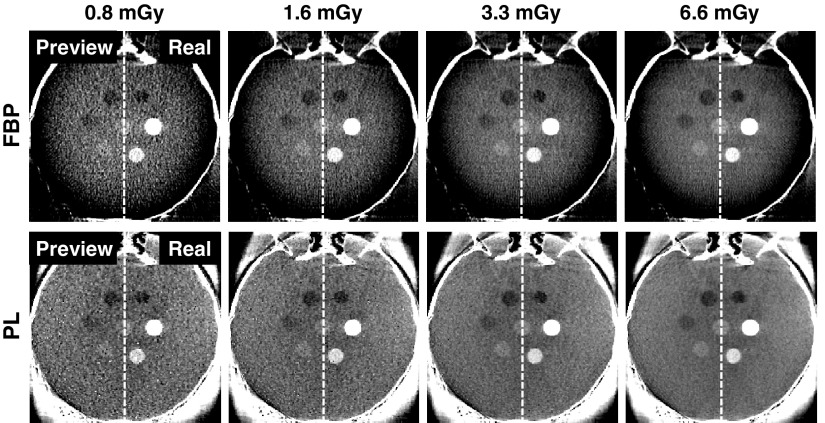
LDP reconstructions are shown in Fig. 5, computed from an initial CBCT acquired at 320 mAs (13.1 mGy). In each case, the LDP image is shown split side-by-side with a real CBCT image acquired at the reduced-dose technique (20, 40, 80, and 160 mAs, corresponding to 0.8, 1.6, 3.3, and 6.6 mGy, respectively). The LDP and real images agree qualitatively, demonstrating realistic image quality, including the increased noise at lower dose and the effect of reconstruction algorithm (FBP or PL). For example, FBP has streak artifacts from the incomplete orbit and reduced image intensity at the edge of the circular FOV, while PL mitigates these artifacts. Additionally, with the selected PL parameters, the PL images exhibit lower noise and visibly different noise texture than the corresponding FBP images. Such characteristics are readily appreciated in viewing the LDP images and could be difficult to appreciate otherwise, illustrating how the LDP process could guide low-dose protocol selection in a manner that includes nonlinear artifacts and complex characteristics of the reconstruction method.
FIG. 5.
Side-by-side split comparison between LDP and real CBCT images acquired at dose reduced from that of the initial image (13.1 mGy). In each case, the left half shows the LDP, and the right half is a real CBCT acquired at the stated low-dose technique. (Top row) FBP reconstructions and (bottom row) PL reconstructions. The image quality and noise characteristics demonstrate qualitative agreement, with LDP images realistically depicting the increase in noise at lower dose and a distinct difference in noise texture observed between reconstruction methods. Images are displayed on a [0.015, 0.023] mm−1 grayscale window.
As shown in Fig. 6(a), the difference in spatial resolution measured between the LDP and real CBCT images showed an agreement within 10 ± 37 μm (mean ± std) for FBP and 9 ± 62 μm for PL across all dose levels. Additionally, the image contrast [Fig. 6(b)] exhibited agreement within −0.09 ± 2.00 HU for FBP and 0.50 ± 1.28 HU for PL across all dose levels. These findings demonstrate that the LDP process of scaling projections and injecting noise does not alter the spatial resolution or image contrast, as expected. On the other hand, the image noise increases at lower dose as shown in Fig. 6(c), showing agreement within 2.9% for FBP and 6.4% for PL. A power-law curve fit (y = axb + c) was applied to the measured noise at the five dose levels and plotted up to the 13.1 mGy dose of the initial CBCT. The LDP and real CBCT curve fits overlap almost identically, with PL presenting lower noise than FBP for this particular set of reconstruction parameters (which are not meant to serve as a direct comparison between PL and FBP).
FIG. 6.
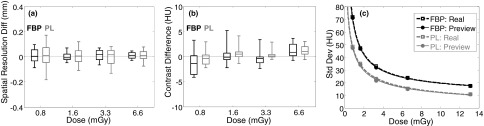
Quantitative comparison between LDP and real CBCT images for FBP (black) and PL (gray) reconstructions across all dose levels. (a) Difference in measured spatial resolution (mm). (b) Difference in measured contrast (HU) of spheres in the head phantom. (c) Comparison of measured image noise (HU). Each metric demonstrates strong agreement between LDP and real CBCT images.
The local NPS of 3D image reconstructions demonstrate strong agreement when detector correlations are correctly modeled, as shown in Fig. 7 for the 1.6 mGy case. The noise exhibits similar levels of magnitude and texture between the LDP and real CBCT images and illustrates the difference in noise characteristics between the FBP and PL reconstructions. The 2D axial NPS side-by-side split-comparison exhibits the expected Hermitian symmetry, while again illustrating the difference in noise magnitude and texture between FBP and PL reconstructions. The enhanced lobes along the fx-axis result from the asymmetry of the object (i.e., the head phantom exhibits a larger path length in the anterior-posterior (y-) direction).
FIG. 7.
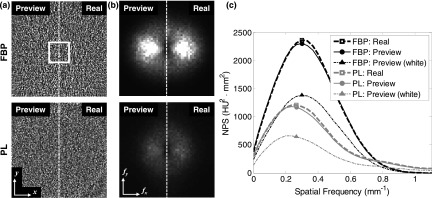
Comparison of reconstructed image NPS measured in LDP and real CBCT images at 1.6 mGy. (a) Difference image in the axial plane for (top) FBP and (bottom) PL reconstructions, showing qualitatively good agreement in the magnitude and noise between LDP and real images. The white square in (a) marks the position of the 3D ROI for computing the local NPS. Display window [−80, 80] HU. (b) Axial NPS shown in split side-by-side comparison of LDP and real CBCT. Display window [0, 3200] HU2 mm2. (c) Radially averaged axial NPS. The NPS of LDP and real CBCT images are in close agreement, whereas preview images simulated using a naïve injection of white noise underestimates the NPS by almost a factor of 2.
The radially averaged NPS plot [Fig. 7(c)] demonstrates strong agreement between the LDP and real CBCT noise, with the NPS for LDP peaking at a slightly lower value by 2.5% for FBP and 3.1% for PL. However, preview images simulated with a naïve white noise injection exhibit substantially lower noise-power and do not realistically portray the image noise at reduced dose. The peak of the NPS with naïve white noise injection is lower by 41.5% for FBP and 46.5% for PL, and the shape of the curve (and therefore, the noise texture) also differs from the real image NPS. While the injected white noise contains an equal amount of noise-power at all frequencies, the injected correlated noise was formed by convolution with noise kernels that boosts the noise-power at lower frequencies (particularly kq, which has a low-pass characteristic typical of an indirect-detection FPD) while reducing the injected noise power at higher frequencies in a manner that conserves the injected noise magnitude (since ‖kq‖ = ‖ke‖ = 1). Because image reconstruction effectively acts as a bandpass filter in the axial plane (i.e., ramp filter with Hann window and backprojection in FBP, or image regularization in PL), the boosted lower-frequency noise-power of the injected correlated noise is evident by the higher main lobe of the reconstructed image NPS.
III.C. Cadaver abdomen
Following a similar phantom calibration process as detailed for the head calibration but instead using the QRM body phantom, LDP images for the cadaver were produced as shown in Fig. 8. The split comparison shows qualitatively good agreement between the LDP and real CBCT images in features such as the fine-detail, high-contrast vertebrae, the contrast of soft-tissue structures, and the increase in image noise at lower dose. The LDP images could enable a clinician to confidently select a patient-specific, minimum-dose protocol in a manner that directly considers the imaging task (as well as the observer's preferences)—for example, in selecting a protocol sufficient for high-contrast bone detail, PL at 0.8 mGy. Numerous other considerations could (and should) be incorporated in technique selection as well—e.g., although PL improves overall image quality, FBP may be preferred for reasons of speed in fast, repeat scans sufficient for high-contrast visualization. On the other hand, for visualization of the kidney, liver, muscle, and surrounding fat, LDP would enable the user to determine a minimum-dose technique and reconstruction algorithm sufficient for imaging of low-contrast soft tissues—e.g., PL at 3.1 mGy.
FIG. 8.
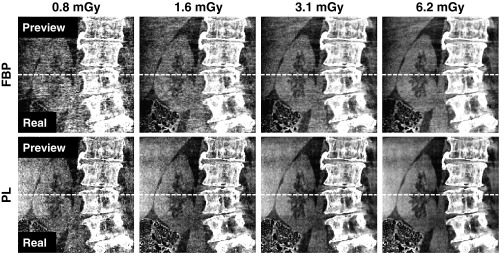
Comparison of LDP and real CBCT images in a coronal slice of the cadaveric torso. The top half of each image is from the LDP, and the bottom half is from a real CBCT acquisition at each technique. The differences in image quality in (top row) FBP and (bottom row) PL reconstructions at different dose levels is well-depicted by LDP. Display window [0.016, 0.022] mm−1.
As shown in Fig. 9(a), difference images (coronal slices) in 3D reconstructions of the cadaver images at 1.6 mGy show the noise to be strongly correlated and nonstationary. For example, PL exhibits noise that is highly dependent on the object, and edge-preservation of high contrast structures such as bone-tissue or air-tissue interfaces causes larger differences at these edges in the difference image. The ROI in the soft tissue (kidney) therefore provides more homogeneous noise characteristics for standard deviation and NPS analysis. The agreement in standard deviation between LDP and real CBCT images was within 6.7% for FBP and 1.1% for PL across all dose levels [Fig. 9(b)]. For the longitudinal NPS at 1.6 mGy [Fig. 9(c)], LDP exhibited peak noise-power at a spatial frequency that was just 3.7% lower for FBP and 4.7% higher for PL, likely within experimental error. On the other hand, simulation of low-dose images with a naïve injection of white noise yields NPS peaking at a frequency 40.6% lower for FBP and 44.7% lower for PL and grossly underestimating the total noise magnitude. Here again, the correlations in the quantum noise boost the lower frequencies in the injected noise, and a white noise model leads to inaccurate noise estimates that could cause one to underestimate the effect of low-dose protocols on image noise.
FIG. 9.
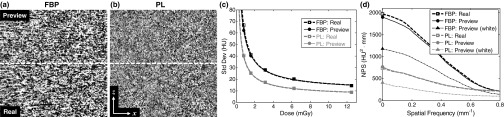
Comparison of LDP and real CBCT image noise in the torso cadaver. Difference images (coronal slice, 1.6 mGy, display window [−50, 50] HU) for (a) FBP and (b) PL reconstructions, with the LDP in the top half and real CBCT in the bottom half. (c) Image noise evaluated in a ROI in the kidney as a function of dose. (d) Longitudinal NPS (1.6 mGy) shows close agreement in the LDP and real CBCT noise, whereas a naïve white noise injection underestimates the NPS.
IV. DISCUSSION AND CONCLUSIONS
The LDP method was found to accurately depict CBCT image quality for scan techniques of lower dose than an initial reference, including faithful reproduction of spatial resolution, contrast, noise, and NPS characteristics. Although the results showed comparisons at specific dose levels, reconstruction methods, and smoothing/regularization parameters, the LDP method is general in that it operates directly on the initial reference projections data; therefore, the dose reduction factor (α ≤ 1) can be freely adjusted, and any reconstruction method and smoothing/regularization parameter selection can be applied. The correlated noise injection accounts for both quantum and electronic noise sources, as well as their spatial correlation, which in turn affects the reconstructed image NPS. Without accounting for these spatial correlations, the preview image would not exhibit the correct noise texture and, more importantly, tends to underestimate the real image noise magnitude. For quantum noise, the scintillator blur induces noise correlations to the first-order neighborhood of a pixel (resulting in a 3 × 3 kernel) for the FPD considered in this work, and the electronic noise possessed a small correlated component along the entire readout line. In the results reported here, the same dose reduction factor α was applied to all projections of a scan, but the LDP method can similarly allow for tube current modulation by applying different α ≤ 1 to each projection according to the desired modulation. Additionally, LDP could be used to simulate dose reduction via sparse projection acquisition by discarding a subset of the projections.
The calibration procedure involving a simple head or body cylinder could be applied to other CBCT systems as well and performed as a part of the overall routine system calibration. Our results suggest that the calibration is fairly robust to object size when the calibration object is of similar size and attenuation to the actual subject—e.g., a 16 cm acrylic cylinder for head imaging or a simple abdomen phantom for body imaging. Future work could include assessment across a broader range in patient size and C-arm FOV positioning to assess overall robustness to calibration in routine clinical use. Additionally, the signal mean-variance relationship, electronic noise, and noise kernels may not be spatially invariant, as assumed in this work, with possible nonstationarity arising from nonuniform FPD response, the heel effect, or use of a bowtie filter. These may require the noise characteristics to be measured locally rather than using a global characterization.
The proposed method is well-suited to clinical scenarios involving repeat CBCT scanning (e.g., fractionated IGRT) and requires an initial reference CBCT obtained at nominal dose. In many contexts, however, the patient may have a preoperative (or diagnostic) CT available prior to treatment. Therefore, the ability to compute a LDP from an initial CT image would allow even the initial CBCT to be previewed and acquired at lower dose. There are, of course, several additional challenges with such a CT-to-CBCT LDP approach that are not a factor in the CBCT-to-CBCT LDP method reported above, including matching spatial resolution, x-ray energy and filtration, beam hardening, and scatter. Nonetheless, the noise model developed in this work enters in the same manner as described above in a CT-to-CBCT LDP. An additional useful feature of LDP to be investigated in future work is the virtual insertion of interventional devices, since such devices (e.g., a deep-brain stimulation electrode or transpedicle spine screws) may be introduced during a procedure and result in degraded image quality. The LDP could therefore allow the user to anticipate the change in image quality arising from the device (e.g., photon starvation) and select the optimal protocol based on images with realistic artifact and noise. One possible approach—analogous to the initialization step in the known-component reconstruction method of Stayman et al.52—would be to allow the user to virtually place the interventional device in its anticipated location in the image, followed by forward-projecting the device and modifying the projections so that the affected rays are attenuated and increased in noise.
Finally, the correlated noise injection for simulating LDP projections only requires a small computational effort to generate a noise realization. Therefore, generating the LDP images is more likely constrained by image reconstruction time (although a single axial slice may suffice for visualization and low-dose technique selection), and ideally the LDP projections would be reconstructed using the same process as the real CBCT. In surgery, the timescale between CBCT acquisitions at specific milestones in the operation may range from ∼10 to 60 min (depending on the procedure and workflow), and in IGRT timescales of one day between fractions would allow for a potentially large menu of LDP images to be computed at various levels of dose reduction, reconstruction techniques, and reconstruction parameters. The use of LDP should nonetheless be well-integrated into the workflow to avoid excess manual intervention and prevent user error—for example, the image menu could be constrained to a fixed number of images within a predetermined dose range that avoids unreasonably low dose protocols while still encouraging dose reduction. The patient-specific LDP images would then enable a number of new capabilities in prospective dose reduction—including task-specific and observer-specific selection of minimum-dose protocols. Additionally, the use of LDP in retrospective studies would be equally valuable for setting general guidelines (e.g., CBCT technique charts) based on attributes such as patient size and imaging task, as well as for training purposes for new users of CBCT systems. Therefore, the new LDP method can be a powerful tool to both prospective and retrospective approaches by providing accurate visualization of the impact of low-dose protocols and (advanced) reconstruction methods on CBCT image quality.
ACKNOWLEDGMENTS
This research is supported by a 2013 AAPM Research Seed Funding grant, NIH fellowship F32EB017571, and academic-industry partnership with Siemens Healthcare (XP Division, Erlangen, Germany). The authors would like to thank Ronn Wade (University of Maryland Anatomy Board) for assistance with cadaver specimens, Joshua Levy (The Phantom Laboratory, Greenwich, NY) for assistance with phantom development and construction, and Dr. Jonathan Lewin and Laurie Pipitone (Department of Radiology, Johns Hopkins University) for support and research infrastructure.
REFERENCES
- 1.Fahrig R., Fox A. J., Lownie S., and Holdsworth D. W., “Use of a C-arm system to generate true three-dimensional computed rotational angiograms: Preliminary in vitro and in vivo results,” Am. J. Neuroradiol. 18(8), 1507–1514 (1997). [PMC free article] [PubMed] [Google Scholar]
- 2.Jaffray D. A., Siewerdsen J. H., Wong J. W., and Martinez A. A., “Flat-panel cone-beam computed tomography for image-guided radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53(5), 1337–1349 (2002). 10.1016/S0360-3016(02)02884-5 [DOI] [PubMed] [Google Scholar]
- 3.Siewerdsen J. H.et al. , “Volume CT with a flat-panel detector on a mobile, isocentric C-arm: Pre-clinical investigation in guidance of minimally invasive surgery,” Med. Phys. 32(1), 241–254 (2005). 10.1118/1.1836331 [DOI] [PubMed] [Google Scholar]
- 4.Daly M. J., Siewerdsen J. H., Moseley D. J., Jaffray D. A., and Irish J. C., “Intraoperative cone-beam CT for guidance of head and neck surgery: Assessment of dose and image quality using a C-arm prototype,” Med. Phys. 33, 3767–3780 (2006). 10.1118/1.2349687 [DOI] [PubMed] [Google Scholar]
- 5.Chen G.-H., “Design and development of C-arm based cone-beam CT for image-guided interventions: Initial results,” Proc. SPIE 6142, 614210–1 614210–12 (2006). 10.1117/12.653197 [DOI] [Google Scholar]
- 6.Wallace M. J., Kuo M. D., Glaiberman C., Binkert C. A., Orth R. C., and Soulez G., “Three-dimensional C-arm cone-beam CT: Applications in the interventional suite,” J. Vasc. Interv. Radiol. 19(6), 799–813 (2008). 10.1016/j.jvir.2008.02.018 [DOI] [PubMed] [Google Scholar]
- 7.Orth R. C., Wallace M. J., and Kuo M. D., “C-arm cone-beam CT: General principles and technical considerations for use in interventional radiology,” J. Vasc. Interv. Radiol. 19(6), 814–820 (2008). 10.1016/j.jvir.2008.02.002 [DOI] [PubMed] [Google Scholar]
- 8.Miracle A. C. and Mukherji S. K., “Conebeam CT of the head and neck, part 2: Clinical applications,” Am. J. Neuroradiol. 30(7), 1285–1292 (2009). 10.3174/ajnr.A1654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schafer S.et al. , “Mobile C-arm cone-beam CT for guidance of spine surgery: Image quality, radiation dose, and integration with interventional guidance,” Med. Phys. 38, 4563 (2011). 10.1118/1.3597566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Strauss K. J. and Kaste S. C., “The ALARA (as low as reasonably achievable) concept in pediatric interventional and fluoroscopic imaging: Striving to keep radiation doses as low as possible during fluoroscopy of pediatric patients: A white paper executive summary,” Radiology 240(3), 621–622 (2006). 10.1148/radiol.2403060698 [DOI] [PubMed] [Google Scholar]
- 11.Tsiklakis K., Donta C., Gavala S., Karayianni K., Kamenopoulou V., and Hourdakis C. J., “Dose reduction in maxillofacial imaging using low dose cone beam CT,” Eur. J. Radiol. 56(3), 413–7 (2005). 10.1016/j.ejrad.2005.05.011 [DOI] [PubMed] [Google Scholar]
- 12.Wang J., Li T., Liang Z., and Xing L., “Dose reduction for kilovotage cone-beam computed tomography in radiation therapy,” Phys. Med. Biol. 53(11), 2897 (2008). 10.1088/0031-9155/53/11/009 [DOI] [PubMed] [Google Scholar]
- 13.Mayo J. R.et al. , “Simulated dose reduction in conventional chest CT: Validation study,” Radiology 202(2), 453–457 (1997). [DOI] [PubMed] [Google Scholar]
- 14.Frush D. P.et al. , “Computer-simulated radiation dose reduction for abdominal multidetector CT of pediatric patients,” Am. J. Roentgenol. 179(5), 1107–1113 (2002). 10.2214/ajr.179.5.1791107 [DOI] [PubMed] [Google Scholar]
- 15.van Gelder R. E.et al. , “CT colonography at different radiation dose levels: Feasibility of dose reduction,” Radiology 224(1), 25–33 (2002). 10.1148/radiol.2241011126 [DOI] [PubMed] [Google Scholar]
- 16.Hanai K.et al. , “Computer-simulation technique for low dose computed tomographic screening,” J. Comput. Assist. Tomogr. 30(6), 955–961 (2006). 10.1097/01.rct.0000230011.16468.0e [DOI] [PubMed] [Google Scholar]
- 17.Veldkamp W. J. H., Kroft L. J. M., van Delft J. P. A., and Geleijns J., “A technique for simulating the effect of dose reduction on image quality in digital chest radiography,” J. Digit. Imag. 22(2), 114–25 (2009). 10.1007/s10278-008-9104-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Massoumzadeh P., Don S., Hildebolt C. F., Bae K. T., and Whiting B. R., “Validation of CT dose-reduction simulation,” Med. Phys. 36(1), 174 (2009). 10.1118/1.3031114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Benson T. M. and De Man B. K. B., “Synthetic CT noise emulation in the raw data domain,” in 2010 IEEE Nuclear Science Symposium Conference Record (NSS/MIC) (IEEE, Piscataway, NJ, 2010), pp. 3169–3171 [Google Scholar]
- 20.Joemai R. M. S., Geleijns J., and Veldkamp W. J. H., “Development and validation of a low dose simulator for computed tomography,” Eur. Radiol. 20(4), 958–66 (2010). 10.1007/s00330-009-1617-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Söderberg M., Gunnarsson M., and Nilsson M., “Simulated dose reduction by adding artificial noise to measured raw data: A validation study,” Radiat. Prot. Dosim. 139(1–3), 71–77 (2010). 10.1093/rpd/ncq027 [DOI] [PubMed] [Google Scholar]
- 22.Yu L., Shiung M., Jondal D., and McCollough C. H., “Development and validation of a practical lower-dose-simulation tool for optimizing computed tomography scan protocols,” J. Comput. Assist. Tomogr. 36(4), 477–87 (2012). 10.1097/RCT.0b013e318258e891 [DOI] [PubMed] [Google Scholar]
- 23.Žabić S., Wang Q., Morton T., and Brown K. M., “A low dose simulation tool for CT systems with energy integrating detectors,” Med. Phys. 40(3), 031102 (14pp.) (2013). 10.1118/1.4789628 [DOI] [PubMed] [Google Scholar]
- 24.Wang A. S. and Pelc N. J., “Synthetic CT: Simulating arbitrary single and dual energy protocols from a dual energy scan,” Med. Phys. 38(10), 5551–5562 (2011). 10.1118/1.3633895 [DOI] [PubMed] [Google Scholar]
- 25.Britten A. J., “The addition of computer simulated noise to investigate radiation dose and image quality in images with spatial correlation of statistical noise: An example application to X-ray CT of the brain,” Br. J. Radiol. 77(916), 323–328 (2004). 10.1259/bjr/78576048 [DOI] [PubMed] [Google Scholar]
- 26.Wang A. S., Feng C., and Pelc N. J., “Image-based synthetic CT: Simulating arbitrary low dose single and dual energy protocols from dual energy images,” Proc. SPIE 8313, 83131G–1 83131G–7 (2012). 10.1117/12.912163 [DOI] [Google Scholar]
- 27.Won Kim C. and Kim J. H., “Realistic simulation of reduced-dose CT with noise modeling and sinogram synthesis using DICOM CT images,” Med. Phys. 41(1), 011901 (16pp.) (2014). 10.1118/1.4830431 [DOI] [PubMed] [Google Scholar]
- 28.Siewerdsen J. H., Antonuk L. E., El-Mohri Y., Yorkston J., Huang W., and Cunningham I. A., “Signal, noise power spectrum, and detective quantum efficiency of indirect-detection flat-panel imagers for diagnostic radiology,” Med. Phys. 25(5), 614–628 (1998). 10.1118/1.598243 [DOI] [PubMed] [Google Scholar]
- 29.Tward D. J. and Siewerdsen J. H., “Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT,” Med. Phys. 35(12), 5510–5529 (2008). 10.1118/1.3002414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tu S.-J., Shaw C. C., and Chen L., “Noise simulation in cone beam CT imaging with parallel computing,” Phys. Med. Biol. 51(5), 1283–1297 (2006). 10.1088/0031-9155/51/5/017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Macovski A., Medical Imaging Systems (Prentice-Hall, 1983). [Google Scholar]
- 32.Barrett H. H. and Myers K. J., Foundations of Image Science (Wiley-Interscience, Hoboken, NJ, 2003). [Google Scholar]
- 33.Navab N.et al. , “Dynamic geometrical calibration for 3D cerebral angiography,” Proc. SPIE 2708, 361–370 (1996). 10.1117/12.237798 [DOI] [Google Scholar]
- 34.Galigekere R. R., Wiesent K., and Holdsworth D. W., “Cone-beam reprojection using projection-matrices,” IEEE Trans. Med. Imaging 22(10), 1202–1214 (2003). 10.1109/TMI.2003.817787 [DOI] [PubMed] [Google Scholar]
- 35.Daly M. J., Siewerdsen J. H., Cho Y. B., Jaffray D. A., and Irish J. C., “Geometric calibration of a mobile C-arm for intraoperative cone-beam CT,” Med. Phys. 35, 2124 (2008). 10.1118/1.2907563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schmidgunst C., Ritter D., and Lang E., “Calibration model of a dual gain flat panel detector for 2D and 3D x-ray imaging,” Med. Phys. 34, 3649–3664 (2007). 10.1118/1.2760024 [DOI] [PubMed] [Google Scholar]
- 37.Wang A. S.et al. , “Soft-tissue imaging with C-arm cone-beam CT using statistical reconstruction,” Phys. Med. Biol. 59(4), 1005–1029 (2014). 10.1088/0031-9155/59/4/1005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sidky E. Y. and Pan X., “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Phys. Med. Biol. 53(17), 4777–4807 (2008). 10.1088/0031-9155/53/17/021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wang Jing, Li Tianfang, Lu Hongbing, and Liang Zhengrong, “Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography,” IEEE Trans. Med. Imaging 25(10), 1272–1283 (2006). 10.1109/TMI.2006.882141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tang J., Nett B. E., and Chen G.-H., “Performance comparison between total variation (TV)-based compressed sensing and statistical iterative reconstruction algorithms,” Phys. Med. Biol. 54(19), 5781–5804 (2009). 10.1088/0031-9155/54/19/008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jia X., Dong B., Lou Y., and Jiang S. B., “GPU-based iterative cone-beam CT reconstruction using tight frame regularization,” Phys. Med. Biol. 56(13), 3787 (2011). 10.1088/0031-9155/56/13/004 [DOI] [PubMed] [Google Scholar]
- 42.Wu M. and Fessler J. A., “GPU acceleration of 3D forward and backward projection using separable footprints for X-ray CT image reconstruction,” in Proceedings of Fully 3D Image Reconstruction (Fully 3D, Potsdam, Germany, 2011), pp. 56–59 [Google Scholar]
- 43.Long Y., Fessler J. A., and Balter J. M., “3D forward and back-projection for X-ray CT using separable footprints,” IEEE Trans. Med. Imaging 29(11), 1839–1850 (2010). 10.1109/TMI.2010.2050898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.De Man B. and Basu S., “Distance-driven projection and backprojection in three dimensions,” Phys. Med. Biol. 49(11), 2463–2475 (2004). 10.1088/0031-9155/49/11/024 [DOI] [PubMed] [Google Scholar]
- 45.Siddon R. L., “Prism representation: A 3D ray-tracing algorithm for radiotherapy applications,” Phys. Med. Biol. 30(8), 817–824 (1985). 10.1088/0031-9155/30/8/005 [DOI] [PubMed] [Google Scholar]
- 46.Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” JOSA A 1(6), 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- 47.Erdogan H. and Fessler J. A., “Ordered subsets algorithms for transmission tomography,” Phys. Med. Biol. 44(11), 2835–2851 (1999). 10.1088/0031-9155/44/11/311 [DOI] [PubMed] [Google Scholar]
- 48.Erdogan H. and Fessler J. A., “Monotonic algorithms for transmission tomography,” IEEE Trans. Med. Imaging 18(9), 801–814 (1999). 10.1109/42.802758 [DOI] [PubMed] [Google Scholar]
- 49.Riederer S. J., Pelc N. J., and Chesler D. A., “The noise power spectrum in computed X-ray tomography,” Phys. Med. Biol. 23(3), 446–454 (1978). 10.1088/0031-9155/23/3/008 [DOI] [PubMed] [Google Scholar]
- 50.Kijewski M. F. and Judy P. F., “The noise power spectrum of CT images,” Phys. Med. Biol. 32(5), 565–575 (1987). 10.1088/0031-9155/32/5/003 [DOI] [PubMed] [Google Scholar]
- 51.Siewerdsen J. H., Cunningham I. A., and Jaffray D. A., “A framework for noise-power spectrum analysis of multidimensional images,” Med. Phys. 29(11), 2655–2671 (2002). 10.1118/1.1513158 [DOI] [PubMed] [Google Scholar]
- 52.Stayman J. W., Otake Y., Prince J. L., Khanna A. J., and Siewerdsen J. H., “Model-based tomographic reconstruction of objects containing known components,” IEEE Trans. Med. Imaging 31(10), 1837–1848 (2012). 10.1109/TMI.2012.2199763 [DOI] [PMC free article] [PubMed] [Google Scholar]