Joint Analysis for Integrating Two Related Studies of Different Data Types and Different Study Designs Using Hierarchical Modeling Approaches

Abstract

Background

A chronic disease such as asthma is the result of a complex sequence of biological interactions involving multiple genes and pathways in response to a multitude of environmental exposures. However, methods to model jointly all factors are still evolving. Some of the current challenges include how to integrate knowledge from different data types and different disciplines, as well as how to utilize relevant external information such as gene annotation to identify novel disease genes and gene-environment interactions.

Methods

Using a Bayesian hierarchical modeling framework, we developed two alternative methods for joint analysis of an epidemiologic study of a disease endpoint and an experimental study of intermediate phenotypes, while incorporating external information.

Results

Our simulation studies demonstrated superior performance of the proposed hierarchical models compared to separate analysis with the standard single-level regression modeling approach. The combined analyses of the Southern California Children's Health Study and challenge study data suggest that these joint analytical methods detected more significant genetic main and gene-environment interaction effects than the conventional analysis.

Conclusion

The proposed prior framework is very flexible and can be generalized for an integrative analysis of diverse sources of relevant biological data.

Introduction

Identifying causal susceptibility alleles for complex diseases poses many challenges. These include the multigenic nature of the disease, difficulties in assessing individual exposures, and complex interactions with environmental factors. Current analytical approaches have limitations, and analytical challenges are formidable for aggregating the findings from a wide variety of data types. Although prior knowledge about gene functions, protein interactions, and disease pathways have been used in various hierarchical modeling approaches for a single study [1-11], they have not been previously incorporated into joint modeling of related studies with different designs. Hence, an integrated statistical framework would enhance our ability to identify causal susceptibility alleles for complex diseases.

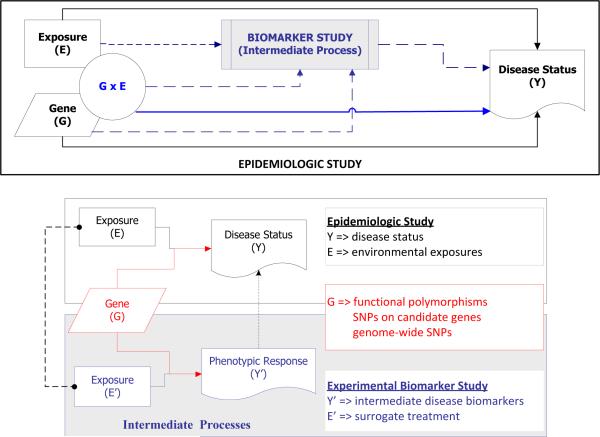
Our proposed models are motivated by, and later illustrated with, an example of two related studies: an observational epidemiologic study and an experimental challenge study. The first is the Southern California Children's Health Study (CHS), an observational epidemiologic cohort study designed to assess the risk of respiratory disorders such as asthma attributable to the genetic effects G, long-term exposure to air pollution E, and gene-environment G × E interactions in over 11,000 school children from Southern California [12,13]. In this study, the environmental exposure to major oxidants and pro-oxidants in ambient air such as particulates (PM₁₀ or PM_2.5) were routinely monitored at the selected communities. Several papers have reported on the associations of children's asthma with genetic variants, ambient air pollution, and other exposures [13-23]. The other is a single-blind, randomized, placebo-controlled crossover study conducted in a group of 70 allergen-sensitive subjects from polluted areas in Southern California. The goal of this experimental biomarker study was to simultaneously characterize the effects of G, diesel exhaust particles (DEPs) T and their interactions on multiple phenotypic measurements of intermediate biological processes involved in asthma occurrence. Specifically, all participants underwent four intranasal challenges at least 6 weeks apart with cat allergen plus placebo, DEPs plus placebo, cat allergen plus DEPs, or pure placebo, in random order. The phenotypic responses measured after each challenge included the levels of 13 cytokine and chemokine markers (i.e. IFNgamma, TNFalpha, IL-1b, IL-4, IL-5, IL-8, MCP-1, MCP-3, MIP-1a, IP-10, RANTES, EOTAXIN, GM-CSF), allergen-specific IgE and IgG-4 levels, histamine concentration, allergic symptom score (e.g. occurrences of sneezing, runny nose, and nasal itching), and counts of four cell types (i.e. eosinophils, macrophages, lymphocytes, neutrophils). DEPs are a standardized experimental exposure comprising varying sizes of particulate matter [24] and can serve as surrogates for air pollution to assess phenotypic responses [25]. The details regarding demographics of study participants, challenge procedures, and the protocols for phenotypic measurements will be described elsewhere [H. E. Volk, personal communication].

In this example, the treatment (T) being examined in the biomarker challenge study is viewed as a surrogate for the exposure (E) being studied in the epidemiologic CHS study. The treatment-induced responses measured in the biomarker challenge study may reflect intermediate steps in a biological pathway leading to disease occurrence being observed in the epidemiologic CHS study. Hence, the CHS and the challenge study together offer an opportunity to investigate the interactions between genetic variation and exposure to particulates on the risk of allergic airway disease through joint modeling of effects attributable to differential responses of immune phenotypes. We hypothesized that an integrative analysis of the epidemiologic and biomarker studies could improve power for discovering the disease-susceptibility loci and/or for identifying genes that influence the disease risk through interactions with environmental determinants. The design of a biomarker study could involve an independent set of disease-susceptible subjects or a subset of subjects sampled from a large-scale longitudinal study of multiple endpoints. However, our approach is applicable to any such combination of biologically related studies under the assumption that these studies are estimating similar patterns of effects. For example, CHS investigators are currently conducting toxicological assays of the biological effectiveness of particulate pollution samples collected at the homes of a subset of individuals from this same epidemiological study for use in joint analysis; other examples might include the use of expression quantitative trait locus (eQTL) or metabolomics measurements on the same genes or metabolites being studied in an epidemiologic study.

Using a Bayesian hierarchical modeling framework, biological annotation of gene functions, disease mechanisms, and pathways can be incorporated into a flexible regression model for the prior distribution and then combined with the genetic association data to form a posterior distribution. The dependency among selected variables can be structured in a hierarchical manner to reflect the strength of the disease associations in the statistical analyses [7,26,27]. For example, a second-level of a hierarchical model can inform the regression coefficients from the first-level model by borrowing strength from other estimates to which they are similar with respect to the characteristics pre-specified in a prior covariate matrix. The implementation of Markov-chain Monte Carlo (MCMC) methods in the BUGS software has enabled estimation of posterior distributions from complex Bayesian models. Hence, Bayesian methods provide a coherent analytical framework for computing measures of effect by combining the evidence across studies.

Methods

Analysis Models

We propose two alternative approaches for linking the analyses of related studies within a Bayesian hierarchical modeling framework. The first approach incorporates the measurements of the experimental biomarker study directly into the main analysis of G and G × E interactions for the epidemiologic study through a second-level univariate linear model (HM1 approach), whereas the second approach analyzes the epidemiologic and the biomarker studies jointly, using a multivariate model for the second level (HM2 approach). Both methods can incorporate external information through prior covariates in the second-level model.

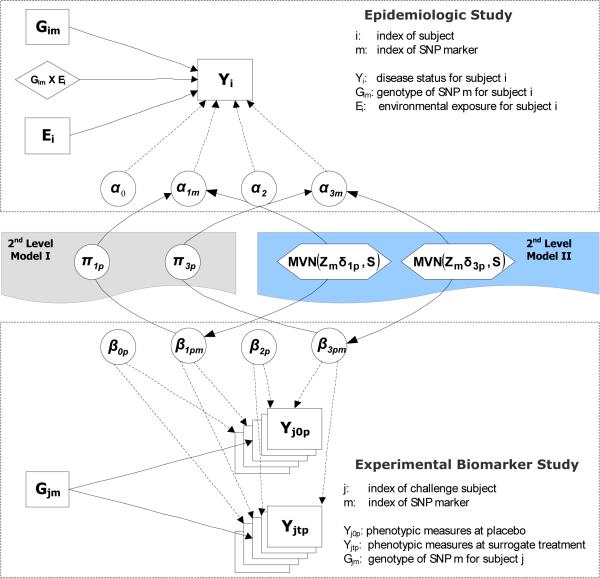
Let G_im denote the genotype of SNP marker m for subject i from the epidemiologic study and G_jm the corresponding genotype for subject j from the biomarker study. In the first-level of the hierarchical model, a logistic regression model and a linear regression model are applied to fit the epidemiologic data and biomarker data for M SNPs separately as follows:

For the epidemiologic study,

$$\mathbf{logit}\mathbf{Pr}(Y_i=1\mid G_{im},E_i)={\alpha }_0+\sum _{m=1}^M{\alpha }_{1m}{G}_{im}+{\alpha }_2{E}_i+\sum _{m=1}^M{\alpha }_{3m}{G}_{im}\times E_i.........$$ [1]

where Y denotes a disease status, G is a coded genotype, E is a binary exposure indicator, α1, α2 and α3 are the corresponding regression coefficients for main effects of genetic and environmental factors, and their interaction effect, respectively.

For the biomarker study,

$${\mu }_{\mathbf{tp}}\equiv \mathbf{E}(Y_{jtp}\mid G_{jm},T)={\beta }_{0p}+\sum _{m=1}^M{\beta }_{1mp}{G}_{jm}+{\beta }_{2p}T+\sum _{m=1}^M{\beta }_{3mp}{G}_{jm}\times T+R_j......$$ [2]

where Y denotes P-dimensional normal phenotypic responses, G is a coded genotype, T is a treatment indicator, β1, β2, and β3 are the corresponding regression coefficients (the differences in mean measurements) for the main effects of the genetic factors and the treatment, and their interaction, respectively. The within-subject correlation (before and after the treatment) is modeled as a random effect: $R_{j}iidN(0,{\sigma }_R^2)$.

The combined analysis of the two datasets can be performed by linking the first-level regression coefficients for the main G effects (α_1m ~ β_1pm) and G × E interactive effects (α_3m ~ β_3pm) through a second-level of the hierarchical model in two alternative ways (Figure 1).

Fig. 1.

Conceptual framework linking the experimental biomarker study to the epidemiologic study using hierarchical modeling approaches

In one form, the findings of the biomarker data serve as covariates informing the corresponding estimates of the epidemiologic data using a univariate linear model (2^nd Level Model I). Specifically, for each SNP maker m, we treat the P regression coefficients for the main G effects or G × E interactive effects (β_1pm or β_3pm) from the first-level model of the biomarker data as predictors in a regression model for the corresponding parameter estimates of the epidemiologic data (α_1m or α_3m). In its simplest form, we do not include any external information:

$$\text{Model}\mathrm{HM}1\mathrm{a}:{\alpha }_m=N\left(\sum _{p=1}^P{\pi }_p{\beta }_{mp},{\sigma }^2\right)$$

To incorporate external information, we regress both sets of coefficients α_m and β_mp on a vector of prior covariates Z_m for each gene m, as well as on each other:

$$\text{Model}\mathrm{HM}1\mathrm{b}:{\alpha }_m\sim N\left(\sum _{p=1}^P{\pi }_p^{\prime }{\beta }_{mp}+Z_m\delta ,{\sigma }^{\prime 2}\right){\beta }_{mp}\sim N(\varphi Z_m,{\tau }^2)$$

where δ and φ denote vectors of second-level prior coefficients for Z; σ² and τ² are the variances of the residuals from the fitted second-level linear models.

Alternatively, treating the shared biological relationships underlying disease etiology among the epidemiologic and biomarker studies symmetrically, a multivariate linear model can be applied to simultaneously fit the first-level regression coefficients from both datasets (2^nd Level Model II). As with the HM1 approach, we describe two variants, HM2a with only a vector of intercepts and HM2b incorporating prior covariates. But rather than regressing the αs on the βs, their relationships are described by a covariance matrix S:

$$\text{Model}\mathrm{HM}2\mathrm{a}:\underset{\sim m}{\lambda }\equiv \left({\alpha }_m,{\left[{\beta }_{mp}\right]}_{p=1\mathsf{K}P}\right)\sim MV{N}_{p+1}\left(\underset{\sim m}{\mu },S^{\prime }\right)$$

where [β_mp] denotes a m-by-p matrix of the first-level regression coefficients, βs.

$$\text{Model}\mathrm{HM}2\mathrm{b}:{\lambda }_{qm}\equiv ({\alpha }_m,{\beta }_{mp})\sim MV{N}_{p+1,m}(Z_m,\underset{\sim }{\delta },S)$$

where S denotes the prior similarity matrix representing the connection among the first-level regression coefficients of the form:

$$\left[\begin{array}{ccccc}\hfill {\sigma }_{\alpha }^2\hfill & \hfill {\rho }_{\alpha \beta }{\sigma }_{\alpha }{\sigma }_{\beta }\hfill & \hfill {\rho }_{\alpha \beta }{\sigma }_{\alpha }{\sigma }_{\beta }\hfill & \hfill {\rho }_{\alpha \beta }{\sigma }_{\alpha }{\sigma }_{\beta }\hfill & \hfill {\rho }_{\alpha \beta }{\sigma }_{\alpha }{\sigma }_{\beta }\hfill \\ \hfill {\rho }_{\alpha \beta }{\sigma }_{\alpha }{\sigma }_{\beta }\hfill & \hfill {\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill \\ \hfill {\rho }_{\alpha \beta }\sigma {\alpha }^{\sigma }\beta \hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill \\ \hfill {\rho }_{\alpha \beta }{\sigma }_{\alpha }{\sigma }_{\beta }\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill \\ \hfill {\rho }_{\alpha \beta }{\sigma }_{\alpha }{\sigma }_{\beta }\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\rho }_{\beta }{\sigma }_{\beta }^2\hfill & \hfill {\sigma }_{\beta }^2\hfill \end{array}\right]$$

Since fitting the HM2 model requires a high dimensional integral that is not easy to compute, we used Markov chain Monte Carlo (MCMC) techniques as implemented in WinBUGS for fitting all four hierarchical models. In the Bayesian paradigm, model parameters are treated as random variables that are characterized by prior distributions. For both HM1 and HM2 approaches, we specified vague prior information (i.e. normal distributions with mean 0 and variance 10) for the second-level coefficients and inverse gamma distributions for the precision of the residuals of the hierarchical models. Given all prior distributions and fully-specified conditional probabilistic model (i.e. the distribution of the parameter of interest given all other quantities in the model), the MCMC method uses an iterative procedure, sampling from each of the full conditional distributions in turn. After the algorithm has reached equilibrium, subsequent parameter values are generated from the joint posterior distribution.

Simulation Studies

We simulated paired datasets for a typical epidemiologic study and an experimental biomarker study. For a specific parameter choice (described in Table 1), we fixed the baseline disease risk and exposure prevalence in the simulation of the epidemiologic data. Genetic and environmental factors were assumed to be independent. Disease status was assigned using Equation [1] and subjects were simulated until the target numbers of cases and controls were generated. In the simulation of the P = 10 phenotypic biomarkers, we assumed 5 were relevant to the disease outcome and 5 not. We further assumed that the P phenotypic measurements were multivariate normally distributed, Y_jtp ~ MVN(μ_tp, R) with means given by Equation [2]. The correlation matrix R used randomly-generated ρs from a uniform distribution between 0.3 and 0.8 among the 5 disease-related phenotypes and between 0 and 0.1 for the 5 disease irrelevant phenotypes, subject to the constraint that the entire R matrix be positive definite. The parameter settings for the disease model were identical for the paired datasets. We adopted a dominant coding of the genes and assumed Hardy-Weinberg and linkage equilibrium.

Table 1.

Calculated Power for Standard Logistic Regression and Hierarchical Modeling (HM) Approaches

HM Model	Parameter Values Set in Simulations	Standard Approach		HM Approach
		Main G Effect	G × E Interaction	Main G Effect	G × E Interaction
HM1a	ORg-e=1.5; ORg=1.5	0.797	0.472	0.900	0.522
	ORg-e=2.0; ORg=1.5	0.789	0.587	0.903	0.684
HM1b	Prior highly informative; ORg-e=2.0, ORg=1.5	0.775	0.603	0.926	0.771
	Prior moderately informative; ORg-e=2.0, ORg=1.5			0.889	0.730
	Prior slightly informative; ORg-e=2.0, ORg=1.5			0.871	0.687
	Prior not informative; ORg-e=2.0, ORg=1.5			0.861	0.682
HM2a	Intercept only; ORg-e=2.0, ORg=1.5	0.683	0.559	0.701	0.399
HM2b	Prior highly informative; ORg-e=2.0, ORg=1.5			0.949	0.946
	Prior moderately informative; ORg-e=2.0, ORg=1.5			0.844	0.811
	Prior slightly informative; ORg-e=2.0, ORg=1.5			0.771	0.673
	Prior not informative; ORg-e=2.0, ORg=1.5			0.780	0.605

Note: For G and G × E terms under a two-sided alternative, respectively, using the standard logistic regression (first-level model only) and four hierarchical modeling approaches, power was calculated as average over the proportions of the disease susceptibility loci (of 20 markers, n=10 pre-specified risk alleles) detected significant in 100 replicates.

The parameter values for the second-level of the hierarchical models were chosen to yield identical settings for the first-level regression coefficients from the epidemiologic data (α_1m, α₂, and α_3m) as well as for the biomarker data (β_1mp, β_2p, and β_3mp). The dependences between the first-level model coefficients corresponding G and G × E terms (β₁ versus α₁ and β₃ versus α₃) were specified differently according to the respective second-level model properties (see the online supplement for details). The construction of the second-stage prior covariate matrix Z is illustrated in Supplement Table 3. The true covariate matrix Z was used in the simulation of paired datasets for HM1b and HM2b approaches. For analysis, we used various mis-specified Z matrices, defined by a true positive rate (TPR, the probability of correct designation of risk alleles) and a true negative rate (TNR, the probability of correct designation of null alleles). We varied the TPR and TNR to simulate four scenarios: highly informative (95%), prior moderately informative (75%), prior slightly informative (60%), and uninformative (50%). For example, given a true covariate matrix Z, 25% of risk alleles were mis-specified as null alleles under the scenario of prior moderately informative. The HM1b and HM2b models were fitted using the four mis-specified prior covariate matrices.

Datasets were replicated 100 times for each of the proposed hierarchical modeling approaches. For each of the 100 replications, the paired datasets were jointly analyzed with the four hierarchical modeling approaches using the WinBUGS software (http://www.mrcbsu.cam.ac.uk/bugs/). In order to compare the testing performance to ordinary regression methods, we computed the posterior probability of the model parameters being greater than zero. For each of the 15 combinations of datasets and models, the power and type I errors were examined for G and G × E interaction under various scenarios. For computing the type I error, both the epidemiologic and biomarker datasets were simulated assuming no disease association (e.g. odds ratios = 1.0 for G and G × E terms in epidemiologic study). Here, the type I error was defined as the proportion of null markers for which the posterior credibility intervals excluded zero. For assessing statistical power, 10 out of 20 typed SNP markers were chosen as disease-associated markers with expected values of odds ratios for the main G effects and G × E interactions set to 1.5 and 2.0, respectively, in the simulated epidemiologic data. Power was defined as the proportion of the true G or G × E estimates whose posterior credibility intervals excluded zero. The joint posterior distributions for hierarchical model parameters generated by the MCMC algorithm were also summarized using posterior means, posterior medians, posterior variances and 95% credible intervals (CI). The results were compared with those obtained from the conventional logistic or linear regression methods (first-level model only).

Two independent chains were run for assessing convergence, where each chain was randomly initialized. The trace plots of posterior estimates generated at each iteration for the first-level and second-level model parameters indicated adequate mixing and convergence from fitting each of four hierarchical models. In the simulation, the number of iterations was set to 2000 with 1000 burn-in. Across the 100 replications, the posterior estimates were similar to their simulated parameter values (data not shown).

Application to the Children Health Study and the Biomarker Challenge Study

For genetic association datasets from the CHS and the biomarker challenge study, we focused on a set of functional polymorphisms in candidate genes for which strong links of the main genetic effects and/or the joint effects with environmental modifiers on asthma risk have been reported in previous CHS publications [28-39]. Genes inducible by oxidative stress (glutathione S-transferase [GST] superfamily) [28,31] or involved in neutrophilic inflammation (catalase [CAT], myleoperoxidase [MPO], epoxide hydrolase [EPHX1], adrenergic receptor gene [ADRB2], intercellular adhesion molecule-1 [ICAM-1], transforming growth factor [TGFB1], or tumor necrosis factor [TNFA]) [29,30,32,34-38] have previously been shown to adversely influence lung function growth or were associated with an increased risk of asthma occurrence.

For the application of the proposed hierarchical modeling approaches, the analyses were restricted to a subset of 2937 children with complete genotypes from the CHS cohorts A to D and 65 challenge study subjects for whom the genotyping have been conducted. For each marker locus, genotype and allele frequencies were stratified by ethnicity. Hardy-Weinberg equilibrium of allele distributions was tested overall and then separately by disease status. The dominant genetic model was used to assess the association of the variant allele with asthma outcome, with the exception of TGFB1, for which previous literature has suggested a recessive model.

For the first-level of the hierarchical model for the CHS, physician-diagnosed asthma at study entry was fitted with all genetic markers, community-level particulate matter (PM_2.5), and all two-way G × E interactions (the product term of these two variables) along with other covariates using the logistic regression given by Equation [1]. Exposure was classified as high or low level of ambient PM_2.5 based on the median of the central site annual average levels for each community, as in previously reported analyses [38]. The following covariates were included in the model: age, gender, self-reported ethnicity, family income, health insurance status, parental education, family history of asthma, atopy, in utero exposure to maternal smoking, and exposure to second-hand smoke. All variables were categorized as described elsewhere [35,38].

For the challenge study, fourteen phenotypic outcomes (i.e. IL-4, IL-5, GM-CSF, Eotaxin, RANTES, MIP1a, MCP-1, IP-10, lymphocytes, IFN-γ, Histamine, IgE, IL-8, eosinophils) were included in the analysis in order to avoid colinearity and overfitting. Measurements below the limit of detection were assigned to the lower limit of detection for the respective assay in the analyses. A rank-based transformation was performed on all phenotypes and these rank scores were then converted to standard normal deviates. The first-level model used a mixed-effect linear regression of individual quantitative phenotype on genotypes for each challenge subject, DEP treatment, and all the possible interactions of the two variables in the form of Equation [2].

The second level of the hierarchical models used either the univarate (HM1) or multivariate (HM2) linear form to link the parameter estimates corresponding to G and G × E terms from the above first-level models. For the HM1b and HM2b models, biological information about the SNP markers was obtained from the Ingenuity Pathway Analysis tool (IPA, Ingenuity Systems, Inc.). Supplement Table 4 shows the Z matrix with 16 rows corresponding to first-level genetic factors (ADRB2, CAT, CC16, EPHX1, GPX1, GSTM1, GSTM3, GSTP1, HO1, ICAM-1, MMP9, NOS3, NQO1, PPARR, TGFB, TNFA) and 15 columns corresponding to asthma outcome being studied in the CHS (1^st column) plus the annotated phenotypes being measured in the challenge study (columns 2 to 15). A binary indicator was coded 1 if the biological connectivity between genotypes (in a row) to phenotypes (in a column) was present and 0 otherwise. The biological connectivity can be protein–protein interactions (PPIs) or transcriptional regulations that are retrieved based on literature-annotated functional relationships and algorithmically built in the IPA.

All statistical analyses were conducted using R version 2.10 (http://www.r-project.org/) and the WinBUGS program (http://www.mrc-bsu.cam.ac.uk/bugs/), which implements an MCMC sampler. Priors, numbers of iterations, and convergence diagnostics were implemented as described previously for the simulations.

Results

Simulation Results

The type I error rates computed for G and G × E terms were 5.5% and 5.4%, respectively, for the standard logistic regression. The corresponding values were 3.6% and 4.3% for the HM1a procedure. For various scenarios, the type I error rates ranged from 0.033 to 0.037 for the G term and from 0.033 to 0.039 for G × E term by using the HM1b procedure. For the HM2b approach, they were smaller than 1.7% and 5.2% using identical datasets simulated with null G and G × E effects, respectively.

Table 2 summarizes the calculated power for G and G × E effects on disease risk under a two-sided alternative using the standard logistic regression and each of the four hierarchical models. For assessing the statistical power using the HM1a testing procedure, two scenarios were simulated by varying the strength of G × E interaction while fixing the OR for the main effect of G to 1.5. For 20% prevalence of the exposure and relatively common variants (frequency = 20%), HM1a was more powerful than the standard approach for detecting the main genetic effect at an OR of 1.5; the standard approach had 80% power, while HM1a had 90% power regardless of the size of the G × E effects. In the presence of a true relationship between the simulated epidemiologic and biomarker datasets, the HM1a procedure increased power for G × E interactions from 47.2% to 52.2% and from 58.7% to 68.4% for interaction RRs of 1.5 and 2.0 respectively.

Table 2.

Design of Second-level Prior Covariate Z Matrix

Column (phenotype)		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Row (Genetic Loci)		Asthma	IL4	IL5	GMCSF	EOTAXIN	RANTES	MIP1A	MCP1	IP10	MCP3	IFNG	HIST	IGE	IL8	IL1B
1	ADRB2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	CAT	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0
3	CC16	1	1	1	0	1	0	0	0	0	0	1	0	0	0	0
4	EPHX1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5	GPX1	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0
6	GSTM1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
7	GSTM3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
8	GSTP1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
9	HO1	1	0	0	0	0	0	0	1	0	0	0	0	0	1	1
10	ICAM-1	1	0	0	0	0	1	0	0	0	0	1	0	0	0	1
11	MMP9	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1
12	NOS3	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0
13	NQO1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
14	PPARR	0	0	0	0	0	1	0	1	1	0	0	0	0	1	0
15	TGFB	1	1	0	1	1	1	1	0	1	1	1	1	1	1	1
16	TNFA	1	1	1	1	1	1	1	1	1	1	1	0	0	1	1

The performance of the HM1b and HM2b approaches was evaluated across a range of TPR and TNR in the prior Z matrix. Overall, the performance was better by any of these two procedures than the standard approach. The power for detecting the main effect of G increased from 77.5% with the standard approach to 87.1%, 88.9 %, and 92.6% with the HM1b approach for slightly, moderately, and highly informative prior covariates. The corresponding values of power for detecting G × E interactions increased from 60.3% for the standard approach to 68.7%, 73.0% and 77.1% for increasingly informative priors. When compared to the standard logistic regression approach (68.3% for main G effects and 55.9% for G × E interactions), the power for the HM2b model ranged from 77.1% to 94.9% for detecting main G signals and from 67.3% to 94.6% for detecting G × E interactions. For the non-informative prior, the calculated power was in general the smallest for both G and G × E effects. In contrast, for the HM2a approach, the model performance was comparable to the standard logistic regression procedure for detecting main G effects but gained no power for detecting G × E interactions.

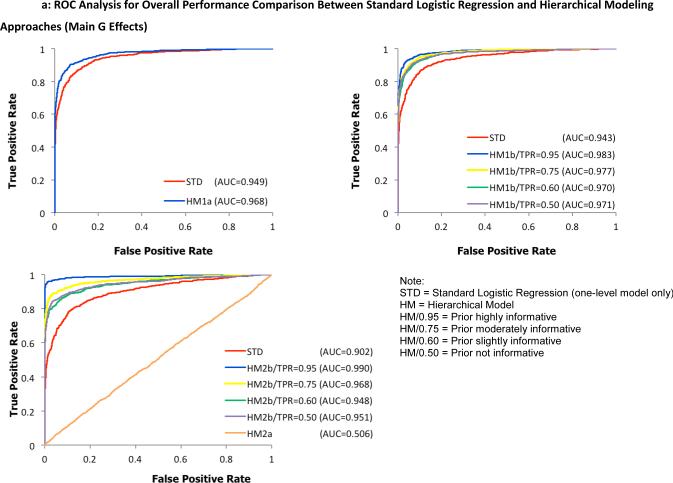
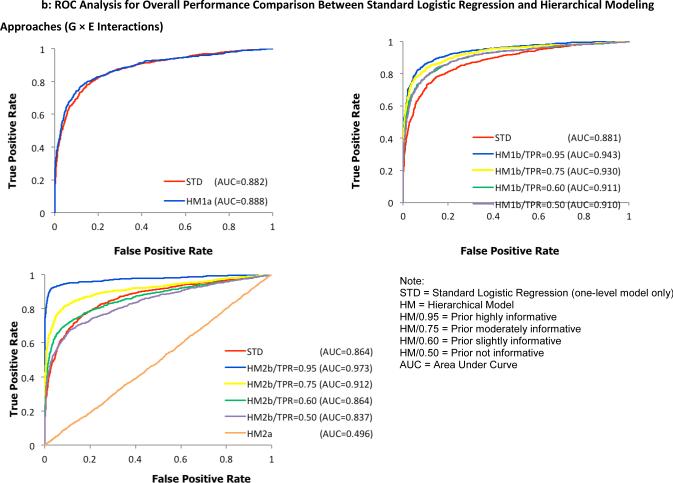
To examine the overall performance of the four hierarchical modeling approaches compared to the standard logistic regression method, receiver operating characteristic (ROC) curves were plotted separately for detecting G effects in Figure 2 and G × E interactions in Figure 3. Here, a test statistic was computed as a ratio of the average to the standard deviation of first-level model parameters α₁ and α₃ for individual SNPs, taken across all 100 replicates. For the hierarchical models, the ratio of posterior means and posterior standard deviations from the WinBUGS output were used to compute the test statistic. Second, the values were ranked in a descending order to construct discrimination thresholds. The true positive rate (power) was computed as the fraction of pre-specified risk alleles found significantly above each threshold of the test statistic while the false positive rate (type I error rate) was calculated as the fraction of designated null alleles with the test statistic above the same threshold. Hence, the ROC graphs visually depict the performance of the statistical models being compared. For example, the bigger the area under the curve, the better the model performs. Under a more stringent threshold (upper left part of the curve with higher power and lower type I error rate), any of the joint hierarchical models with the exception of HM2a showed an improved performance over the traditional logistic regression method across all simulated scenarios. Using identical parameter settings for the first-level models, models with informative priors outperformed the less informative models.

Fig. 2.

ROC analysis for overall performance comparison between the standard logistic regression method and proposed hierarchical modeling approaches (A: HM1a, B: HM1b, C: HM2) for the identification of main G effects

Fig. 3.

ROC analysis for overall performance comparison between the standard logistic regression method and proposed hierarchical modeling approaches (A: HM1a, B: HM1b, C: HM2) for the identification of G × E interactions

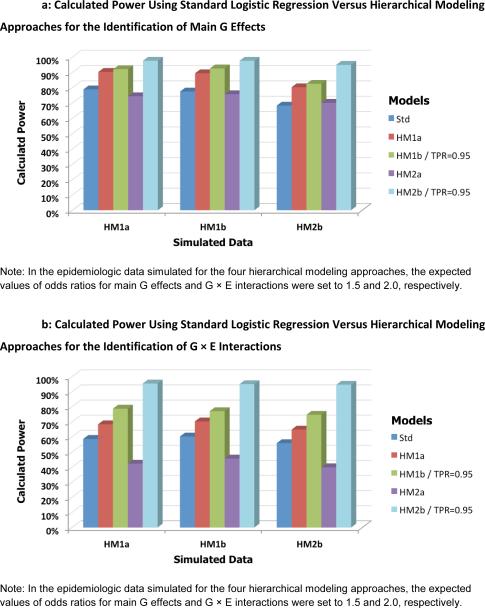
Next to assess the between-model performance with respect to the second-level model specification, each of the 3 separate datasets (simulated under scenarios for HM1a, HM1b and HM2b) was fitted individually with the standard logistic regression method (one-level model only) and the 4 proposed hierarchical models (HM1a, HM1b, HM2a and HM2b). Figure 4 shows the calculated power averaged over 100 replications for detecting G (Fig. 4A) and G × E effects (Fig. 4B) for various combinations of three simulation models and five testing procedures. Compared to the standard one-level logistic regression approach, the trend in power was very similar for each hierarchical model regardless of the simulation model used. For all three simulation models, the power for detecting the main effects of G increased from 74.9% with the standard approach to 86.7%, 89.0%, and 96.7% on average for HM1a, HM1b and HM2b with highly informative prior, respectively. The corresponding values for detecting G × E interactions were from 58.3% to 67.9%, 76.9% and 95.0%. In addition, power was consistently better for the multivariate than for the univariate model, and better when adding external information to either model.

Fig. 4.

Calculated power using standard logistic regression versus hierarchical modeling approaches for the identification of main G effects (A) and G × E interactions (B). Each bar represents the estimated power for various combinations of simulation parameters and testing procedures.

Application Results

Tables 3a and 3b present the posterior estimates of odds ratios (ORs) and corresponding 95% credible intervals (CIs) that were computed for the association of each genetic marker with asthma from the hierarchical modeling approaches for the main genetic effect and G × E interactions, respectively. For comparison, the respective maximum likelihood estimates of ORs and 95% confidence intervals (CIs) obtained from the multivariate logistic regression model are also shown. The HM1a and HM2a approaches were applied to assess the potential of hierarchical modeling with no external information. As seen in previous publications, there was no evidence from model HM2a for any disease association. The prevalence of asthma was not significantly different between communities with low to high levels of PM_2.5 for any of the models.

Table 3a.

Comparisons of Results from the Logistic Regression and Proposed Hierarchical Modeling Approaches – Main G Effects

SNP (Gene)	Loaistic Regression		HM1a		HM1b		HM2a		HM2b
	OR (95% CI)	Wald P	OR (95% CI)	Posterior P	OR (95% CI)	Posterior P	OR (95% CI)	Posterior P	OR (95% CI)	Posterior P
ADRB2	1.00 (0.73, 1.38)	0.988	1.00 (0.73, 1.33)	0.457	1.04 (0.80, 1.33)	0.41	1.06 (0.92, 1.22)	0.225	1.06 (0.92, 1.22)	0.211
CAT	0.58 (0.41, 0.82)	0.002	0.63 (0.45, 0.84)	<0.001	0.64 (0.46, 0.85)	0.001	0.93 (0.79, 1.06)	0.135	0.76 (0.63, 0.89)	<0.001
CC16	1.66 (1.21, 2.27)	0.002	1.55 (1.16, 2.05)	0.002	1.59 (1.18, 2.11)	0.003	1.12 (0.97, 1.29)	0.057	1.41 (1.17, 1.69)	<0.001
EPHX1	1.31 (0.95, 1.81)	0.098	1.30 (0.95, 1.71)	0.05	1.25 (0.93, 1.64)	0.071	1.02 (0.89, 1.16)	0.406	1.03 (0.89, 1.18)	0.378
GPX1	1.15 (0.85, 1.57)	0.362	1.18 (0.87, 1.57)	0.164	1.15 (0.87, 1.50)	0.181	1.01 (0.89, 1.15)	0.457	1.02 (0.89, 1.18)	0.386
GSTM1	0.90 (0.66, 1.24)	0.529	0.93 (0.69, 1.24)	0.298	0.91 (0.68, 1.19)	0.253	1.00 (0.87, 1.15)	0.501	0.86 (0.73, 1.01)	0.032
GSTM3	1.15 (0.82, 1.61)	0.423	1.16 (0.82, 1.57)	0.193	1.07 (0.80, 1.43)	0.365	0.96 (0.83, 1.09)	0.244	0.95 (0.83, 1.09)	0.215
GSTP1	1.28 (0.93, 1.76)	0.127	1.27 (0.94, 1.70)	0.062	1.23 (0.93, 1.62)	0.078	1.05 (0.92, 1.20)	0.265	1.04 (0.91, 1.19)	0.312
HO1	0.75 (0.54, 1.04)	0.088	0.81 (0.58, 1.08)	0.075	0.74 (0.55, 0.98)	0.017	0.99 (0.86, 1.15)	0.429	0.82 (0.70, 0.97)	0.008
ICAM-1	1.01 (0.70, 1.46)	0.949	1.01 (0.70, 1.39)	0.51	1.07 (0.74, 1.46)	0.365	1.01 (0.87, 1.17)	0.453	1.24 (1.03, 1.47)	0.008
MMP9	0.81 (0.60, 1.11)	0.192	0.86 (0.63, 1.14)	0.144	0.88 (0.66, 1.16)	0.181	0.99 (0.86, 1.11)	0.405	1.12 (0.94, 1.31)	0.102
NOS3	1.00 (0.73, 1.37)	0.999	0.99 (0.72, 1.32)	0.453	1.02 (0.76, 1.35)	0.473	1.04 (0.91, 1.19)	0.325	1.04 (0.91, 1.19)	0.287
NQO1	0.60 (0.43, 0.84)	0.003	0.66 (0.48, 0.90)	0.004	0.67 (0.49, 0.89)	0.002	0.94 (0.82, 1.08)	0.178	0.77 (0.65, 0.90)	0.002
PPARR	1.36 (0.94, 1.98)	0.107	1.36 (0.93, 1.91)	0.064	1.27 (0.90, 1.74)	0.087	1.06 (0.92, 1.24)	0.206	1.05 (0.89, 1.24)	0.279
TGFβ1	1.05 (0.77, 1.44)	0.74	1.07 (0.80, 1.38)	0.344	1.10 (0.81, 1.45)	0.287	0.99 (0.86, 1.13)	0.414	1.22 (1.02, 1.44)	0.013
TNFA	1.47 (1.05, 2.07)	0.027	1.40 (1.00, 1.88)	0.025	1.48 (1.07, 1.98)	0.007	1.03 (0.88, 1.18)	0.372	1.28 (1.08, 1.53)	0.002

Note: For the standard one-level logistic regression analysis, maximum likelihood estimates of odds ratios (ORs), 95% confidence intervals (CIs), and p value of Wald significant testing were reported in this summary table.

Note: For each of the four hierarchical modeling approaches, posterior estimates of odds ratios (ORs), 95% credible intervals (CIs), and p value were reported in this summary table.

Note: Statisitcal significant findings (two-sided p values less than 5%) were highlighted in red.

Table 3b.

Comparisons of Results from the Logistic Regression and Proposed Hierarchical Modeling Approaches – G × E Interactions

SNP (Gene)	Loaistic Regression		HM1a		HM1b		HM2a		HM2b
	OR (95% CI)	Wald P	OR (95% CI)	Posterior P	OR (95% CI)	Posterior P	OR (95% CI)	Posterior P	OR (95% CI)	Posterior P
ADRB2	1.15 (0.73, 1.81)	0.555	1.22 (0.79, 1.79)	0.205	1.11 (0.76, 1.59)	0.333	1.04 (0.85, 1.27)	0.368	1.03 (0.84, 1.28)	0.399
CAT	1.92 (1.18, 3.11)	0.008	1.76 (1.12, 2.64)	0.006	1.72 (1.10, 2.61)	0.01	1.06 (0.88, 1.29)	0.312	1.37 (1.08, 1.77)	0.005
CC16	0.65 (0.42, 1.02)	0.06	0.75 (0.48, 1.09)	0.064	0.72 (0.47, 1.05)	0.047	1.00 (0.82, 1.22)	0.505	0.78 (0.61, 0.98)	0.017
EPHX1	0.96 (0.61, 1.51)	0.848	0.97 (0.63, 1.45)	0.4	1.03 (0.69, 1.48)	0.478	1.07 (0.89, 1.30)	0.276	1.08 (0.86, 1.33)	0.263
GPX1	0.86 (0.55, 1.34)	0.503	0.88 (0.55, 1.31)	0.251	0.89 (0.59, 1.25)	0.242	0.96 (0.79, 1.17)	0.331	0.96 (0.77, 1.17)	0.349
GSTM1	0.95 (0.60, 1.48)	0.805	0.93 (0.60, 1.37)	0.331	0.92 (0.62, 1.40)	0.304	1.07 (0.85, 1.31)	0.286	1.01 (0.79, 1.31)	0.509
GSTM3	0.65 (0.40, 1.06)	0.086	0.67 (0.42, 1.04)	0.037	0.77 (0.48, 1.12)	0.088	0.92 (0.74, 1.10)	0.172	0.92 (0.73, 1.13)	0.205
GSTP1	0.85 (0.54, 1.33)	0.478	0.90 (0.58, 1.33)	0.273	0.93 (0.62, 1.32)	0.312	1.04 (0.85, 1.26)	0.372	1.06 (0.87, 1.29)	0.288
HO1	1.36 (0.86, 2.16)	0.193	1.30 (0.84, 1.96)	0.138	1.46 (0.96, 2.13)	0.04	1.06 (0.88, 1.27)	0.289	1.33 (1.06, 1.67)	0.007
ICAM-1	0.83 (0.48, 1.44)	0.505	0.88 (0.50, 1.44)	0.26	0.80 (0.48, 1.27)	0.156	0.96 (0.78, 1.15)	0.313	0.76 (0.58, 0.96)	0.01
MMP9	1.58 (1.01, 2.46)	0.045	1.47 (0.95, 2.20)	0.044	1.50 (0.99, 2.16)	0.027	1.10 (0.92, 1.34)	0.167	1.27 (1.00, 1.58)	0.025
NOS3	1.13 (0.73, 1.76)	0.581	1.19 (0.76, 1.80)	0.231	1.14 (0.76, 1.64)	0.284	0.98 (0.79, 1.18)	0.417	0.98 (0.80, 1.19)	0.377
NQO1	1.76 (1.11, 2.78)	0.015	1.61 (1.05, 2.44)	0.016	1.56 (1.06, 2.27)	0.013	1.03 (0.86, 1.27)	0.408	1.29 (1.03, 1.62)	0.016
PPARR	0.64 (0.37, 1.10)	0.104	0.68 (0.39, 1.13)	0.06	0.74 (0.45, 1.11)	0.078	0.96 (0.79, 1.18)	0.329	0.96 (0.76, 1.19)	0.342
TGFβ1	1.10 (0.70, 1.73)	0.665	1.12 (0.74, 1.66)	0.324	1.08 (0.70, 1.61)	0.389	1.05 (0.86, 1.29)	0.328	0.87 (0.68, 1.12)	0.123
TNFA	0.61 (0.37, 1.01)	0.055	0.69 (0.43, 1.04)	0.036	0.63 (0.40, 0.97)	0.019	0.97 (0.79, 1.16)	0.377	0.76 (0.58, 0.95)	0.01

Note: For the standard one-level logistic regression analysis, maximum likelihood estimates of odds ratios (ORs), 95% confidence intervals (CIs), and p value of Wald significant testing were reported in this summary table.

Note: For each of the four hierarchical modeling approaches, posterior estimates of odds ratios (ORs), 95% credible intervals (CIs), and p value were reported in this summary table.

Note: Statisitcal significant findings (two-sided p values less than 5%) were highlighted in red.

For the main effect of each genetic variant, CAT, CC16, NQO1, and TNFA were statistically significantly associated with asthma in the conventional logistic regression; these findings were also supported by HM1a, HM1b, and HM2b. Interactions between environmental exposure to PM_2.5 and three genes of CAT, MMP9, and NQO1 were statistically significant by both the conventional analysis and the hierarchical models. The main effects and modifying effects for HO1 and ICAM-1 were statistically significant in hierarchical model HM2b, but their association with disease was not supported by the conventional logistic regression approach. The homozygous TT genotype in the promoter region of TGFB1 has been previously reported to be associated with an increased risk in asthma [34], but this adverse effect was only found in the hierarchical modeling (HM2b). On the other hand, the estimates of the interaction effects for TNFA appeared to be more consistent across the different hierarchical models.

In general, the risk estimates from the conventional regression model were slightly higher compared to those derived from the hierarchical model, but the corresponding 95% credible intervals from the hierarchical modeling were tighter; TNFA had an OR of 1.47 (95% CI: 1.05-2.07) for asthma in the conventional regression model, whereas the hierarchical models yielded more precise estimates of 1.40 (95% CI: 1.00-1.88), 1.48 (95% CI: 1.07-1.98), and 1.28 (95% CI: 1.08-1.53) for HM1a, HM1b and HM2b respectively. From the challenge dataset fitted with HM1a, there was very little shrinkage toward the overall mean for the posterior estimates of main genetic effects and their interactions with DEP treatment. In contrast, for HM1b and HM2b, the posterior distributions of the first-level model parameters tended to be shrunk away from the maximum likelihood estimates towards their prior predictions from the second-level model.

Discussion

Measurements of intermediate phenotypes contributing to the disease process in a biomarker study can help discover novel genetic effects and decipher G × E interactions in an epidemiologic study. Under the Bayesian hierarchical modeling framework, joint analysis for integrating related epidemiologic and biomarker studies can be performed by relating their first-level regression coefficients via a second-stage univariate (HM1) or multivariate (HM2) linear model, with or without incorporating external information (the “a” or “b” versions) into a shared prior Z matrix. Hence, our proposed hierarchical modeling approaches are very flexible to accommodate either biomarker measurements from a biologically connected study or relevant annotation information as priors for joint modeling.

Our simulation studies demonstrated greater power for the proposed hierarchical models compared to separate analysis with the standard single-level regression modeling approach, while protecting the Type I error rate. Furthermore, incorporating external information into a shared prior and adopting a multivariate linear approach for the second-level modeling yielded the most power for detection of both the main genetic effects and the G × E interactions. Even under scenarios of no disease association for any phenotypic biomarker, when compared to the traditional regression method, HM1a showed a similar performance while HM1b and HM2b had superior performance if the second-stage prior Z matrix was highly informative (Supplement Table 5). The combined analyses of the CHS and challenge study data suggest that these joint analytical methods detected more significant genetic effects and G × E interactions than the conventional analysis. Moreover, HM1b and HM2b can be substantially more powerful than their “a” counterparts by incorporating an informative prior Z matrix into the second-level hierarchy. For example, the protective effect of HO1 was found only by HM1b and HM2b, but not by the conventional regression analysis and model HM2b was able to identify a positive association of ICAM-1 with asthma risk. Note that HO1 and ICAM-1 were specified as asthma-related genes in the Z matrix. The biological implications of these findings were discussed previously [32,40]. Conversely, in the absence of external biological information, HM2a provided no improved performance compared to the conventional analysis for testing the significance of G and G × E terms. Lastly, the single-marker assessment and recessive genetic coding were used in the conventional regression methods from the previous reports [34], which may explain the false-negative finding of TGFB1 shown in our results with the standard logistic regression approach.

Current analytical approaches for genetic studies range from simple methods like data preprocessing and dimension reduction followed by traditional parametric regression, to various feature selection and more sophisticated data mining techniques, including Multifactor Dimensionality Reduction (MDR) [41], tree-based Random Forests [42], and supervised Support Vector Machines [43-45]. However, such approaches have not been generalized to joint assessment of related studies of different data types and study designs. Gene set methods [46-48] and network-based methods [49-55] were recently developed as a complement to traditional regression methods for using biological knowledge about gene functions, protein interactions, and pathways. However, these post-processing approaches are used only for biological interpretation of the final results. Meta-analysis is a well-established and validated statistical approach for pooling evidence across multiple independent studies of the same phenotype and comparable designs, weighing them by the confidence in the study-specific results and the degree of heterogeneity in the study population. This method is aimed at increased chances of finding true positives among the false positives [56-60] has a loosely related goal to we are presenting here, in that case to evaluate the causality of a relationship between an intermediate phenotype and disease, using a gene as an instrumental variable. However, these approaches aim to use assumptions of the biological mechanisms to combine gene-biomarker and gene-disease estimates to obtain an unconfounded biomarker-disease estimate. In contrast, we are focused on letting the gene-biomarker and gene-disease estimates simply borrow information from each other without the strict assumptions required for valid inference from instrumental variable analysis. Hence, our joint modeling approaches can be potentially useful as we move towards more integrative analysis of biological and genetic data in future applications.

Spurred by recent advances in high-throughput technologies, accumulation of research data concerning the genetic basis of common diseases is rapidly increasing in speed and complexity. The hierarchical modeling framework proposed here not only performs better than the conventional regression methods but is also scalable to meet future needs. First, the proposed joint analytic approaches can be extended to analyze diverse sources of relevant biological data. For example, different kinds of phenotypic, genotypic, and genomic data from separate studies can be linked hierarchically and the distribution of observed associations can be estimated jointly. Second, instead of assuming an independent prior for the first-level regression coefficients, one can extend these models to incorporate functional relatedness such as gene-gene interactions within a pathway. In this regard, similar rules built into protein network methods [52-54] can be applied to model the network properties and represent the connection path between genes under generalized hierarchical modeling framework. Although this idea is still at an early stage of development, Thomas et al. have proposed a conceptual form to tackle this problem [10].

There are several limitations with the proposed methods. First, the construction of the second-stage prior Z matrix is limited to functionally annotated disease-gene families and therefore more likely to be available for better characterized genes. Second, crude values of 0 or 1 in the Z matrix may not reflect the true differences between genetic factors and needs to be further refined as additional biological information becomes available. Large-scale GWAS have evolved rapidly and become a standard method for disease gene discovery. In principle, the proposed hierarchical modeling approaches can enrich the overall GWAS signals by borrowing strength from similarities among SNPs. In particular, the probability of specific SNPs being true positives derived from external studies or relevant biology can be incorporated into prior covariates, leading to an increased power for detecting significant associations relative to SNPs without prior evidence. However, there are additional limitations to consider in applications of these models to GWAS data. Specifying an informative second-stage Z matrix for SNPs can be difficult given the limited annotation available for most genomic regions. The implementation of a fully Bayesian hierarchical modeling approach for integrative analysis in GWAS is computationally prohibitive, although penalized likelihood [1] or empirical Bayes [8] implementations may be feasible. For a run on a 64-bit Windows server with 24 GB RAM and 2.83 GHz CPU, the model fitting may take up to a week for HM1 and a month for HM2 for a study size of >2,000 subjects, >100 SNPs, and >20 Phenotypic markers. Hence, extensions of our proposed models to GWAS are beyond the scope of this paper.

In conclusion, the prior framework is very flexible, allowing substantive and heterogeneous information to be incorporated into the analysis. Such statistical approaches provide a potentially valuable path to further integrate several disciplines. We have illustrated the hierarchical modeling principles first using simulation, and then on the candidate gene association data from the CHS and biomarker challenge study for joint assessment of the main G and G × E interactive effects on asthma risk. Although these methods have computational limitations, this approach can be scalable and unified with other biology-driven methods into one analytical framework.