Channel Selection Methods for the P300 Speller

Abstract

The P300 Speller brain-computer interface (BCI) allows a user to communicate without muscle activity by reading electrical signals on the scalp via electroencephalogram. Modern BCI systems use multiple electrodes (“channels”) to collect data, which has been shown to improve speller accuracy; however, system cost and setup time can increase substantially with the number of channels in use, so it is in the user’s interest to use a channel set of modest size. This constraint increases the importance of using an effective channel set, but current systems typically utilize the same channel montage for each user. We examine the effect of active channel selection for individuals on speller performance, using generalized standard feature-selection methods, and present a new channel selection method, termed Jumpwise Regression, that extends the Stepwise Linear Discriminant Analysis classifier. Simulating the selections of each method on real P300 Speller data, we obtain results demonstrating that active channel selection can improve speller accuracy for most users relative to a standard channel set, with particular benefit for users who experience low performance using the standard set. Of the methods tested, Jumpwise Regression offers accuracy gains similar to the best-performing feature-selection methods, and is robust enough for online use.

1. Introduction

Brain-Computer Interface (BCI) systems are designed to analyze real-time data associated with a human user’s brain activity and translate it into computer output. The clearest current motivation for BCI development is to extend a means for communication and control to people with neurological diseases, such as amyotrophic lateral sclerosis (ALS) or spinal-cord injury, who have lost motor ability (“locked-in” patients). However, state-of-the-art BCI systems for such individuals are still expensive and limited in speed and accuracy, and setup for home use is nontrivial; most systems remain in the experimental stage and are primarily used in a laboratory environment (Vaughan et al., 2006).

One BCI that has been successfully deployed to users with ALS (Sellers and Donchin, 2006) is the P300 Speller, first developed by Farwell and Donchin (1988). This system combines measurements of electroencephalogram (EEG) signals on the user’s scalp, a software signal processor, an online classifier, and presentation of stimuli that evoke a P300 event-related potential (ERP), in order to sequentially choose items from a list (e.g. the letters in a word, or commands such as “Page Down” or “Escape”).

The original P300 Speller, as conceived by Farwell and Donchin, employed only a single electrode (one “channel” of information). The use of additional channels was discovered to improve classification performance, and most if not all modern P300 Speller systems include data from multiple recording sites (e.g. Krusienski et al. 2006, Schalk et al. 2004, Sellers and Donchin 2006). However, larger channel sets require more complicated electrode caps and more amplifier channels, which can greatly increase the cost of a system: implementing a 32-channel system rather than an 8-channel system can raise the system cost by tens of thousands of dollars. This cost can be prohibitive to home users. Further, each channel must be calibrated individually for proper placement and impedance before each spelling session, adding to setup time and user discomfort. As a result, clinically relevant systems are limited to using a subset of all possible electrode locations. The selection of these channel locations impacts system performance: one sensitivity analysis concluded that identifying an appropriate channel set for an individual was more important than factors such as feature space, pre-processing hyperparameters, and classifier choice (Krusienski et al., 2008). In addition to empirical demonstrations of the benefit of channel selection (Cecotti et al., 2011, Krusienski et al., 2008, Rakotomamonjy and Guigue, 2008, Schröder et al., 2005), principled reasons for selecting channel sets on a per-subject basis include the difficulty of outpatient calibration of electrode caps by nonclinical aides (such that electrodes that might have been useful do not yield as much information), as well as several neurological motivations, including variation in brain structure and response across subjects arising from their unique cortical folds, and the plasticity of the brain over time, particularly as it adapts to a new system. Disease progression may also impact the optimal set of electrodes. Furthermore, BCI deployment for home use has proven much more challenging than deployment in the laboratory environment (Kübler et al., 2001, Sellers and Donchin, 2006, Sellers et al., 2006); it is possible that the subject-independent channel sets that are effective for healthy subjects do not generalize to other populations. As a practical note, it is anticipated that in order for users to obtain both a performance benefit from selecting channels from an extensive set and the cost and setup savings of employing a system with a small subset of those channels, a channel selection calibration session could first be conducted in a laboratory environment to determine the optimal subset, which would then be the only channels set up for home use.

Although channel selection has been investigated for other BCI paradigms, such as recursive channel elimination for motor imagery tasks (Lal et al., 2004) and mutual information maximization for cognitive load classification (Lan et al., 2007), examples of per-subject channel selection for the P300 Speller or even time-domain data are more limited. Rakotomamonjy and Guigue (2008) use a channel selection procedure built in to the training of a support vector machine classifier. As such, the method is not modularized to the extent that it could be easily combined with another classifier and compared to other methods. Jin et al. (2010) reported success using Particle Swarm Optimization (PSO) and Bayesian Linear Discriminant Analysis (BLDA) to select channels in a system that spelled Chinese characters. However, PSO can be a computationally-intensive technique, which may limit its effectiveness in the clinical or home setting, where setup time is an important aspect of system usability. Finally, Cecotti et al. (2011) demonstrated a state-of-the-art active channel selection method that improved P300 Speller classification performance, comprised of a sequential reverse selection with a cost function determined by the signal-to-signal-plus-noise ratio (SSNR) after spatial filtering. Due to its relatively low computational time, incorporation of spatial filtering, and effectiveness, this method is included in this study for comparison. Since its use of one-directional sequential selection could leave the method vulnerable to nesting effects, in which the early removal of channels with redundant information hampers performance later in the process, further comparison of standard and new feature selection techniques for the P300 Speller channel selection problem is worth considering. In the current study, the Stepwise Linear Discriminant Analysis (SWLDA) classifier is used due to its support among the literature (e.g. Farwell and Donchin 1988, Krusienski et al. 2008, Sellers and Donchin 2006); however, the proposed methods for channel selection could be used in conjunction with other classifiers or could be similarly included into a classifier training phase.

Each channel of EEG data contributes a number of time-samples (features) for classification decisions; channel selection can be viewed as a feature selection problem, with the additional constraint that only entire channels of features may be selected for inclusion or exclusion. Feature selection is commonly performed in machine learning problems with high dimensionality (many features) under the assumption that it is possible to discard some features at a low cost (for example, if the features are irrelevant or redundant). Feature selection reduces data storage and computational requirements by discarding unnecessary dimensions, reduces classifier training time by training on less-complex data, and guards against classifier over-fitting by reducing the effect of the “curse of dimensionality.” (See Guyon and Elisseefi 2003 for an excellent introduction to feature selection.) Methods for feature selection fall into two categories: wrapper methods, which determine feature subsets’ value by measuring their performance with the chosen classifier; and filter methods, which choose subsets of features independently of the classifier. Wrapper methods observe a “search space” of possible combinations of features, assigning each combination a value based on the classifier’s performance; these methods are appealing for their empiricism and simplicity, but can suffer high computation requirements due to the need to repeatedly train and test the classifier (Guyon and Elisseefi, 2003). Filter methods can be faster, but require a performance metric independent of classification performance. These categories remain when generalizing features to channels, and approaches from both categories are explored here: a heuristic filter method, Maximum Signal-to-Noise Ratio Selection (Max-SNR); the wrapper methods Sequential Forward Selection (SFS) and k-Forward-m-Reverse Selection (KFMR); and a new filter method, Jumpwise Selection (JS). The performance of each method is compared to baseline results obtained with the standard eight-channel montage determined in Krusienski et al. (2008), which provides a compromise of reasonably high accuracy and modest system cost by requiring only an eight-electrode system. For comparison to a current adaptive channel selection algorithm, the results obtained with the montage chosen by the sequential reverse method of Cecotti et al. (2011) are included as well.

2. Methods

2.1. Subjects and Equipment

A total of 18 healthy subjects were recruited at East Tennessee State University, gave informed consent, and received course credit in return for participation in this study. Data was collected with subjects using both the Row/Column paradigm (Farwell and Donchin, 1988) and with the experimental “Checker-board” paradigm (Townsend et al., 2010), but only the row/column data are used for the analysis in this study. Data collection protocols and human subject use were approved by the ETSU Institutional Review Board (IRB). Subsequent data analysis was approved by both the ETSU IRB and the Duke University IRB.

EEG data was collected from a right mastoid-referenced 32-channel cap (by Electro-Cap; montage shown in Figure 1). The signal was digitized at 256 Hz and bandpass-filtered to [0.5 Hz, 30 Hz] by two 16-channel g.tec g.USBamp amplifiers. Data collection and stimulus presentation was performed by the BCI2000 open-source software suite (Schalk et al., 2004). Before the session, the impedance of each channel was reduced below 10kΩ.

Figure 1.

Location of channels used in study (relative distances are not to scale). Set corresponds to the International 10–20 electrode placement (Sharbrough et al., 1991); darkened locations compose the subset defined in Krusienski et al. (2008) and used as a baseline comparison.

2.2. The P300 Speller

2.2.1. Paradigm

The P300 component of an evoked response is an event-related potential that can be elicited via the “oddball” paradigm, in which the subject searches for a target stimulus presented infrequently and unpredictably; the potential begins approximately 300 ms after the target appears (see Polich, 2007). Although the P300 is not consciously generated by the user, it can still be used for communication by allowing the user to consciously decide which of a set of random, repeating stimuli contains the target. The system then assumes that the stimulus that elicited the strongest P300 component is the target.

In this implementation, each participant sat in a comfortable chair, approximately 1 m from a computer screen displaying a 9 × 8 matrix of characters (including the letters of the alphabet, the digits 0–9, and various control characters; see Figure 2). The user was instructed to spell a preselected word or number. As the user concentrated on each character, the system flashed each individual row and column (i.e. intensified their brightness) in a random order for 62.5 ms, then paused for 62.5 ms; the process of flashing each row and column was repeated five times per character spelled. The system then paused for 3.5 s, and continued to the next character.

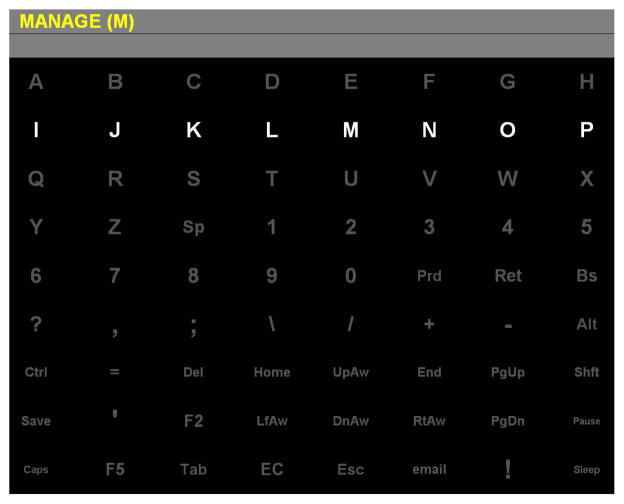
Figure 2.

P300 Speller matrix with example word to be spelled (“MANAGE”). At this moment, the subject is attending to flashes of the letter “M”; the row containing this character is currently illuminated. In “test” mode, after each row and column has flashed five times, the P300 Speller will select a character and display it in the row underneath the target word.

Data was collected in two phases. First, EEG data from 38 character selections (comprising five words) were collected following the above procedures for a training phase, in which subjects received no feedback about their spelling performances. The training data was then analyzed in MATLAB to calculate a subject-specific linear classifier. Then, users spelled the same five words again in an online testing phase, during which the system provided real-time feedback by displaying the selected character (i.e. the character at the intersection of the highest-scoring row and highest-scoring column). In the testing phase, row and column data were averaged while spelling to increase the signal-to-noise ratio.

2.2.2. Pre-processing

Raw EEG data is pre-processed for classification in order to eliminate or condense redundant features and increase the P300 signal-to-noise ratio. The method used in this study follows Krusienski et al. (2008): for each 800ms window after a row or column flash, the time-series data for each channel is moving-averaged and decimated to 17 Hz (i.e., each feature is the average of $\frac{1}{17\text{Hz}}=58.8\text{ms}$ of data); then the selected channels’ responses are concatenated. This forms the feature vector x_i (for the i^th flash); the truth value y_i = {0, 1} records whether flash i illuminated the target character (and can be expected to contain a P300).

2.2.3. Classification

Predicting y_i from the associated x_i is the binary classification problem, which we approach using Stepwise Linear Discriminant Analysis (SWLDA). In Krusienski et al. (2006), a comparison of five classifiers on P300 Speller data, the SWLDA method exhibited competitive classification performance and was cited for built-in feature selection. SWLDA is one of the methods used in Farwell and Donchin’s original P300 Speller, as well as in successful systems for ALS patients (Sellers and Donchin, 2006), and is used as a baseline classifier for evaluation of other system parameters (Krusienski et al., 2008).

SWLDA trains a linear discriminant using stepwise regression: linear discriminants have been found to perform favorably for BCI due to their simplicity, robustness, and resistance to over-training (Garrett et al., 2003, Krusienski et al., 2006, Muller et al., 2003), and stepwise regression performs both linear regression and feature selection simultaneously. The algorithm may be summarized as: starting with an empty set of features in a linear regression model, alternate between (1) adding the most-informative unused feature to the subset of selected features; and (2) measuring the individual relevance of every feature in the regression subset and sequentially removing those that fall below a user-defined threshold. “Most-informative” is judged by partial correlation with response, and “relevance” is judged by p-values obtained via the partial F-test. Per Krusienski et al. (2006), the algorithm was trained using p-to-enter of 0.10 and p-to-remove of 0.15 for this study. A full description of the stepwise regression algorithm may be found in Draper and Smith (1981). The feature selection performed therein guards against over-training while still selecting features that offer independent discriminative information.

2.3. Channel Selection

2.3.1. Performance Assessment

Channel selection can be viewed as an optimization problem: choose the optimal subset of channels from the full set available. Since the ultimate goal of the P300 Speller is to select characters from the screen, optimal in this case means “that which maximizes the percentage of correctly-chosen characters.”

However, the relatively low speed of the P300 Speller means that training data is limited: in this case the data used to compare the following channel-selection techniques consist of 38 characters per subject. This is a very low-resolution (“blocky”) scoring space for comparing performance. Compounding this problem, wrapper methods that use the score directly to select features (such as SFS and KFMR, discussed below) must compare improvements on the order of 0–5 characters per channel added. This problem is circumvented by using the Area Under Receiver Operating Characteristic score, which is based on each flash rather than each spelled character; each 38-character training dataset includes over 4000 flashes. A Receiver Operating Characteristic (ROC) is a curve that describes the discriminative ability of a binary classifier (see Hanley and McNeil, 1982); it may be estimated by applying the classifier to a set of test data and measuring the overlap between target and non-target classifier scores. In order to turn an estimated ROC into a scalar suitable for scoring channel selection, the area underneath the ROC (AUC) is computed. Information is lost in this calculation, but it is generally true that an increase in AUC represents an increase in discriminative ability (see Hanley and McNeil, 1982). Since the P300 Speller’s classification task is to differentiate response-to-target data from response-to-non-target data, this discriminative ability is what drives the P300 Speller’s performance, and AUC is an appropriate measure to use for channel-selection algorithm scoring.

AUC and accuracy scores for each channel selection method are calculated in the manner channel selection would be implemented practically: for each subject, all 32 channels of the five training runs of data are analyzed by the channel selection algorithm, which returns an eight-channel subset; then, SWLDA is trained on those channels of the training data; the resulting linear classifier is applied to the selected channels of the five testing runs; and the scores of the testing runs are analyzed as above to form an ROC, from which AUC is calculated. Character runs include five sequences each. Note that, following the goal of finding the most useful small subset of electrodes, each algorithm is constrained to select exactly eight channels. This also facilitates the performance comparison to the “standard set” described in Krusienski et al. (2008): {F_z, C_z, P_z, O_z, P₃, P₄, PO₇, PO₈}.

2.3.2. Maximum Signal-to-Noise Ratio

A simple baseline method to select channels heuristically can be constructed by making a set of assumptions:

• The channels that are the most helpful for identifying responses to targets are the channels with the strongest P300 response.

• Since the P300 is a relatively large deflection in potential, recordings in which it is present will register a relatively large change in signal energy between target responses and non-target responses.

• This energy difference corresponds to the strength of the P300 response, so the highest-performing channel set will be the set with the largest ratio of average energy between targets and non-targets.

Calculating the energy of a feature vector $E({\mathit{x}}_i)={\Vert {\mathit{x}}_i\Vert }_2^2$, this is equivalent to selecting the channels that display the highest signal-to-noise ratio (SNR), if we define “signal” to mean “target response” and “noise” to mean “non-target response”. Two versions of this method are used: one in which the energy of the full [0ms, 800ms] window is calculated, and one in which energy is calculated only for the window [300ms, 600ms], as this generally encompasses the majority of the P300 component for this task.

2.3.3. Sequential Forward Search

Instead of following a heuristic that relies on assumptions about a channel subset’s performance, an algorithm can simply evaluate the performance of the subsets in which it is interested, and choose the best one (a “wrapper” method). Unfortunately, there are $\left(\begin{array}{c}32\\ 8\end{array}\right)\approx {10}^7$ eight-channel subsets of a 32-channel EEG cap, so a bounded search must be performed. Sequential Forward Selection (SFS) is an intuitive and widely-used feature-selection method in this vein, cited in Muller et al. (2004). Due to its simplicity and monotonic performance increase with channel set size, it is performed here as the baseline active channel selection method. It can be summarized as:

1. Begin with an empty currentSubset. While currentSubset has fewer than 8 members:

   1. For all j unusedChannels not in currentSubset:

      1. augmentedSubset ← currentSubset + unusedChannel_i∈j.

      2. Evaluate the performance of augmentedSubset.

   2. Select the unusedChannel whose augmentedSubset performance was highest.

   3. currentSubset ← currentSubset + selectedChannel.

SFS repeatedly adds channels to the subset, at each step selecting the channel that yields the highest performance increase. However, this performance must be evaluated before encountering the testing data. This is accomplished via 10-fold cross-validation: a classifier is trained on $\frac{9}{10}$ of the training data, then applied to the remaining $\frac{1}{10}$ of the training data; the process is repeated until all data has been tested, and an ROC is constructed from the entire set of resulting scores.

2.3.4. Sequential Reverse Selection

The converse method to SFS, Sequential Reverse Selection (SRS), begins with the full set of channels and sequentially removes the least helpful. However, SRS requires more iterations to reach eight channels, and each iteration must analyze more data than an SFS iteration; as a result, standard SRS (with cross-validated AUC as its cost function) requires over three days of computation for a single subject and was not evaluated for this study.

However, as noted earlier, Cecotti et al. (2011) found that SRS selected channel sets that exhibited improved spelling accuracy, when using a different cost function that is based on the signal-to-signal-plus-noise ratio (SSNR). Modeling the signal as a sum of superimposed delay-locked target and nontarget flash responses allows the SSNR to be calculated directly using singular value decomposition, and this is much cheaper computationally than cross-validated classifier training. Additionally, the use of spatial filtering was found to improve classification accuracy in the case of low training data in Rivet et al. (2009), and was incorporated into the SRS experiment in Cecotti et al. (2011). This method is applied to the data in this study as well, with and without spatial filtering, for comparison.

2.3.5. k-Forward, m-Reverse Search

SFS suffers from a “nesting effect” (see Pudil et al., 1994): once added, channels remain in the subset, even if the information they contributed is fully duplicated by later channels (i.e., there is a risk of adding broadly informative but specifically mediocre channels). To adjust for this, k-Forward, m-Reverse Selection was considered (KFMRS, sometimes known as “plus-l minus-r” selection). Referring to the previous definitions of SFS and SRS, the algorithm can be summarized as:

1. Begin with an empty currentSubset. While currentSubset has fewer than 8 members:

   1. Add k members to currentSubset using SFS.

   2. Remove m members from currentSubset using SRS.

Efficiency can be somewhat improved by maintaining a library of channel subsets for which performance has already been calculated, and the next step forward or backward. With KFMR comes added computational cost relative to SFS, as well as two parameters k and m (with m < k) that must be set. A high value of k implies that the algorithm may have to begin the SRS phase with a high number of channels in the current subset (a high number of channels takes much longer to analyze, as cross-validation and SWLDA training both require more time with increased feature dimensionality). However, a low value of k may prevent the algorithm from discovering mutually complementary channels. To investigate both possibilities, the (k, m) pairs (3, 1) and (16, 8) were evaluated.

2.3.6. Jumpwise Regression for Channel Selection

Cross-validating with SWLDA over many channel sets is computationally intense and likely infeasible in a clinical or home environment. This motivates the design of an algorithm that utilizes information in the data to choose channels in one process (a filter method, per Lal et al. 2004). Ideally this method would use a statistically-sound principle rather than a heuristic like SNR.

In fact, this task is similar to the feature selection performed in training; this similarity inspired the algorithm considered here titled “Jumpwise Regression”, a stepwise regression-inspired method that operates on groups of features, taking “jumps” instead of “steps”. Instead of adding one feature and then testing each feature in the regression for continued relevance, Jumpwise Regression adds a channel’s worth of features, and then tests each channel’s-worth-of-features in the regression model for continued relevance. The statistical relevance tests are identical to stepwise regression, as the partial F-test makes no specific claims on the difference in size of regression models and sub-models. However, Jumpwise must add features differently: stepwise regression selects the next feature to add by choosing the feature with the highest partial correlation with the response, controlling for features already in the model, but partial correlation does not have a scalar analogue for multidimensional data. Instead, Jumpwise selects the next channel to add in the same way channels are removed: each channel is temporarily added to the current model in turn, and the channel judged most relevant by the partial f-test is selected. (MATLAB code for Jumpwise Regression is electronically available by request.) In this study, p-to-enter is set at 0.10, and p-to-remove is set at 0.15. (Note that there is no natural way to force Jumpwise Selection to choose more channels than it deems statistically relevant, besides re-running it with a looser relevance test; at these p-values, Jumpwise Selection chose eight channels for every subject, which was the maximum number allowable as discussed above.)

1. Begin with an empty currentSubset. While currentSubset has fewer than 8 members:

   1. For all unusedChannels not in currentSubset:

      1. Perform a partial f-test of the model containing {all features of currentSubset and the features of unusedChannel_i} against {the features in currentSubset alone}.

   2. If the lowest p-value of the above f-tests is less than p-to-enter, add the corresponding channel to currentSubset; else, quit the algorithm.

   3. For all selectedChannels in currentSubset:

      1. Perform a partial f-test of the model containing {all features of currentSubset} against {all features of currentSubset except those belonging to selectedChannel_i}.

   4. If the highest p-value of the above f-tests is greater than p-to-remove, remove the corresponding channel from currentSubset and repeat (c); else, go to (a).

3. Results

3.1. Performance

Figures 3, 4, and 5 display the AUC and percent-correct performance obtained for each subject, using classifiers trained on the respective channel subsets selected by each method; the corresponding ROCs are displayed in Figure 7. The baseline for comparison is the standard subset, plotted in each figure and sorted from high AUC score to low. The average performance over all subjects is compared in Table 1.

Figure 3.

AUC (area under receiver operating characteristic) and Percent Correct scores for the subsets chosen by full- and short-windowed Max-SNR methods on each subject’s data. (Different methods are offset by a slight margin on the x-axis so that identical scores may be viewed.) AUC is a general measure of classifier discriminability, and Percent Correct measures the direct accuracy of the simulated output. Scores are sorted by each subject’s AUC score using the “standard” subset defined in Krusienski et al. (2008). In nearly every case, the subset selected by Max-SNR yields lower accuracy than the standard subset.

Figure 4.

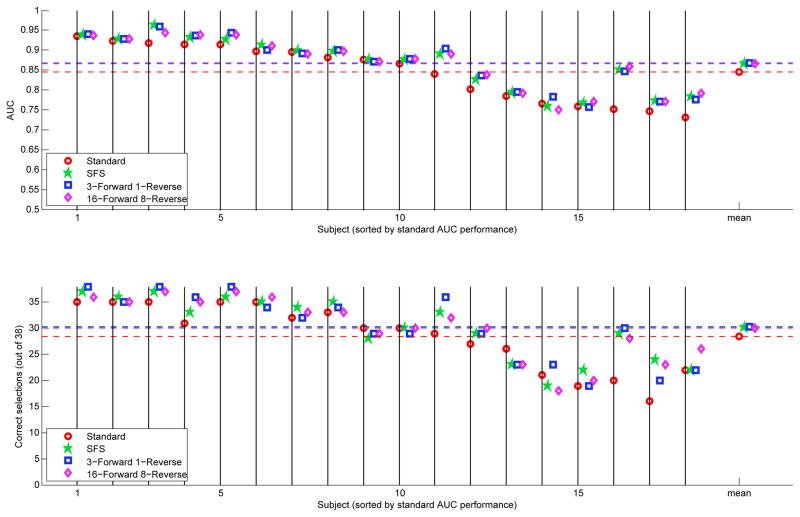
AUC and Percent Correct scores for the subsets chosen by sequential selection methods. In contrast to Max-SNR, the mean accuracy obtained with the selected subsets increases relative to the standard subset. Further, many subjects at the lower end of the spectrum see a large increase in accuracy with channel selection. Subsets selected by SFS obtain performance similar to subsets selected by KFMR.

Figure 5.

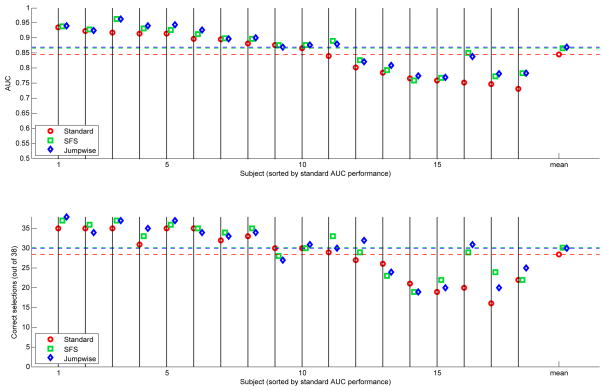
AUC and Percent Correct scores for the subsets chosen by Jumpwise Selection. The mean accuracy of subsets selected by Jumpwise Selection is significantly higher than the accuracy of the standard set. The increase is similar in scale to that obtained by SFS, including the large gains for subjects with previously low accuracy. However, Jumpwise requires only one minute to compute, in contrast to the one hour required by SFS.

Figure 7.

Comparison of receiver operating characteristics obtained by SWLDA on each subject’s training data, using the respective channel subsets obtained by each investigated method. Several subjects obtain considerably superior ROCs with actively-selected subsets than with the standard set described in Krusienski et al. (2008).

Table 1.

Results of each method. Subjects’ scores are calculated individually; the average over subjects is presented here. Computation time was calculated by training each algorithm on 38 characters of data in MATLAB on a quad-core CPU with 4GB RAM. Significance test for AUC differences is the clustered AUC comparison test of Obuchowski (see Obuchowski, 1997); for percent-correct, the proportion difference test is used. In each case, scores from the subsets obtained by a new method are compared to the scores of the standard set. Both SNR methods choose subsets that average a decrease in performance relative to the standard set, whereas the other methods choose subsets that result in an average increase in performance, using either scoring metric.

Method	Mean Time	Mean AUC	p	Mean Acc.	p
(Standard set)	-	0.844	-	74.7%	-
Full-window SNR	5 sec	0.750	-	45.3%	-
Short-window SNR	5 sec	0.756	-	48.1%	-
Seq. Reverse Search (SSNR)	90 sec	0.8407	-	72.2%	-
Seq. Rev. (SSNR), Sp. Filt.	90 sec	0.8303	-	68.3%	-
Seq. Forward Search	1 hour	0.866	< 0.0001	79.2%	0.048
3-Forward, 1-Reverse	1.5 hour	0.868	0.00076	79.7%	0.028
16-Forward, 8-Reverse	7.5 hour	0.866	0.00021	79.1%	0.054
Jumpwise Selection	90 sec	0.869	< 0.0001	79.1%	0.054

As can be noted from Figure 3, the channel subsets chosen by the heuristic method, Maximum SNR, yield poorer performance than the standard channel subset for nearly every subject. Their mean percent-correct scores are below 50%, making the Speller unusable (since incorrectly-spelled letters must be followed by a correctly-spelled backspace character, on average, to be usable). No clear pattern exists differentiating performance by SNR channel sets chosen with the full window versus the shortened window. The mean computational time to run SNR on five training runs is 5.0 seconds.

There are many possible reasons for the poor performance of the Max-SNR algorithm. For example, channels 17 and 18 are selected for nearly every subject: these channels correspond to electrodes directly above the eyebrows, which see large potential deflections any time the subject’s eyes or surrounding facial musculature move. If subjects’ eyes are more likely to move when they see their target than when they see a non-target, their target response may have higher variance but retain no difference in mean from the non-target response, making these features worthless to a linear classifier. However, excluding these channels from consideration and using Maximum SNR was also performed, and still did not result in an increase in average accuracy. Similarly, other areas of the scalp could see an energy difference due to responses that are not stable in the time domain. Thus, energy-based metrics for channel selection do not appear effective.

As shown in Figure 4, SFS selects channel subsets that outperform the standard set for most subjects (p < 0.0001, Obuchowski clustered-AUC test Obuchowski (see 1997)); several subjects see large increases in performance relative to the standard subset (particularly subjects with lower standard-subset scores) and of the few that see a performance decrease, it is by a narrow margin relative to the gains. The average of the SFS scores also demonstrates an improvement over the average of the standard-subset scores. The mean computational time required for SFS to select channels for one subject-session is approximately one hour. This set of improvements indicates that effective channel selection can indeed reliably outperform the standard channel subset. However, the time required for the algorithm is infeasible in a clinical or home setting.

The results shown in Figure 4 for KFMR are very similar to the SFS results, although different channels are chosen. The difference in performance relative to the performance with the standard set is also statistically significant (p = 0.00076 for (3,1)-KFMR and p = 0.00021 for (16,8)-KFMR, Obuchowski clustered-AUC test). Improvements for the majority of subjects appear in both parameterizations of KFMRS. However, the mean time required to run (3, 1)-KFMRS was 1.5 hours, and the time required to run (16, 8)-KFMRS was 7.5 hours. Considering the limited improvement over SFS, the increased computational time cannot be justified, and still remains outside the selection computation duration acceptable for practicable use.

The results shown in Figure 5 compare Jumpwise Selection to SFS, as a representative of the wrapper methods, and the standard set. Again, a statistically-significant increase in performance is observed over the standard subset (p < 0.0001, Obuchowski clustered-AUC test). Further, the improvement of mean AUC is very close to the improvements found with SFS and KFMR, with similar results for poor default performers for whom some large performance boosts are observed. However, the computation required by Jumpwise is approximately 90 seconds: a 40x increase in speed relative to SFS, and easily fast enough to compute between training and testing runs.

Figure 6 compares the performance obtained by SFS and Jumpwise to the SRS-SSNR method utilized by Cecotti et al. (2011). No clear pattern exists for the SRS-SSNR scores: some subjects obtained substantial improvements (see the 3^rd, 11^th, and 16^th subjects’ AUC scores), while others obtained lower scores (8^th, 9^th, 12^th), and two subjects obtained dramatic decreases compared to the standard subset (14^th and 15^th). Regardless of whether spatial filtering is applied, the mean scores for Jumpwise are significantly higher than the mean scores for SRS-SSNR (p = 0.027 and p = 0.0026 with and without spatial filtering, Obuchowski clustered-AUC test). Spatial filtering does not appear to aid performance; however, the performance benefits from spatial filtering in Rivet et al. (2009) were primarily seen in cases with far less training data than this study (2–5 training characters rather than 38). Although SRS-SSNR requires approximately the same amount of time as Jumpwise Selection to choose a subset, its wide variance in observed scores may make it a less reliable channel selection algorithm; further studies in an online test could help determine whether this is the case.

Figure 6.

AUC and Percent Correct scores for the subsets chosen by the Sequential Reverse Seach using signal-to-signal-plus-noise ratio, per Cecotti et al. (2011). Although several subjects observe comparable or better performance using the SRS-SSNR method, two subjects are left with nearly unusable channel sets. On average, SFS and Jumpwise Selection both outperform the SRS method.

3.2. Channels Selected

The consistency of the subsets selected by the effective methods was also considered: if a method improved accuracy by selecting the same (non-standard) subset for all subjects, for example, active channel selection could be avoided by simply replacing the standard subset from Krusienski et al. (2008) with the new subset. Figure 8 displays the number of times each channel was selected by each method, compiling that method’s selections for all subjects. In fact, no method selected even a single channel for more than 15 of 18 subjects, and among the effective methods, nearly every channel was selected at least once. Channels in the standard subset are shown in red in the figure; as expected, many are selected often, implying that the standard subset does provide predictive power. However, most standard-subset channels were still selected for fewer than half of the subjects tested. Also note that channels numbered higher than 24 refer to occipital locations, where over half the standard-subset channels are clustered; these channels were often selected by the effective methods, suggesting that the standard subset is clustered in an area with valuable discriminative information, but that optimal sites differ from user to user. This can be easily seen in the topographical heat map of Jumpwise-selected channels in Figure 8. The subsets selected by each method for three representative subjects are displayed in Figure 9: the effective methods tend to share more channels with each other than with the standard subset. By contrast, the Maximum SNR methods selected very few of the same channels as the standard subset or the effective methods’ selected subsets, with the exception of Subject 11—the only user for whom the Maximum SNR subset obtained accuracy similar to the other methods’ subsets. Figure 10 displays the mean ERP for each subject on three representative channels. Little consistency in waveform can be seen from subject to subject, demonstrating that active channel selection is not matching waveforms to a pattern but rather determining whether the channel is most beneficial to the user.

Figure 8.

Histogram representing how many times each channel was selected by each method across all subjects; the channels in the standard subset are shown in red. Channel positions on the scalp are shown in Figure 1. The maximal value, 18, would be attained only if the method chose this channel for every subject; notably, no method did so for any channel. The effective methods (SFS, KFMR, and Jumpwise) selected the channels in the standard set more often than the Maximum SNR methods, but most were still selected for fewer than half of subjects. Instead, the effective methods selected nearly every channel for at least one subject. The Jumpwise Selection histogram is also displayed as a topographical heat map, in which more popular channels are colored darker than less popular channels. Rather than following the exact layout of the standard channels, popular channels are distributed throughout the occipital region.

Figure 9.

Channel subsets chosen by each method for three representative subjects. Subjects 3, 11, and 16 (as sorted by AUC score in Figure 5) represent users who observe good, average, and poor performance, respectively, with the standard channel subset. Often, the effective methods (SFS, KFMR, and Jumpwise) include only a few of the standard channels, although those methods frequently selected many of the same channels. The Maximum SNR methods selected very different subsets than the standard set or the effective methods, with the exception of Subject 11 (the only subject to observe improved performance with the SNR subsets). Two methods very rarely selected identical subsets for a given dataset.

Figure 10.

Each subject’s average ERP response over all trials on three representative channels: a “popular” channel, PO₈, which Jumpwise selected for 14 of 18 subjects; a “common” channel, P₇, selected for 8 subjects; and an “unpopular” channel, F₇, selected for only one subject. ERP waveform is plotted in blue if Jumpwise selected the channel for that subject. Wide variation is seen across subjects, even for popular channels: active channel selection finds helpful channels for a user rather than matching waveforms to a particular pattern.

4. Discussion

The motivation for this investigation was to enhance the practicality of the P300 Speller using active channel selection, which offers the potential to improve spelling accuracy and correct for potential implementation errors or neural changes in the user, while still utilizing a channel subset of modest size. The obtained results are consistent with the literature (Krusienski et al., 2008, Schröder et al., 2005) in demonstrating that channel selection can have a dramatic effect on P300 Speller usability—poor channel sets, such as those selected by Max-SNR, can make the system unusable, whereas other channel sets, such as those selected by sequential methods and Jumpwise, can increase system accuracy relative to a standard channel subset with statistical significance. However, the ultimate goal of a channel selection algorithm is to enhance the practicality of the system; computation time, therefore, is quite important. Since the sequential methods examined here required far too much computation to be implemented during system setup, their usefulness is limited; further, although more sophisticated and computationally intensive sequential selection methods exist, such as the Sequential Forward Floating Search method described in Pudil et al. (1994), their investigation is not motivated by these results. Of the methods tested, Jumpwise Selection combines the performance improvements of the sequential methods with practical computation requirements that may be put into practice for data collection and home use. While not presented here, these results were replicated using Dataset II of the BCI Competition III, demonstrating that these results are not unique to the 18-subject dataset analyzed here.

Most notable is the dramatic improvement observed in several subjects’ sessions that began with low default-set scores. It is easy to see that channel-selected scores are strongly correlated with standard-set scores, implying that the driving factor in score variation is not channel subset. However, this pattern is interrupted by at least four of the poorer performers, suggesting that, for these subjects, poor response near the standard channels may be (a) a primary reason their scores are lower than average, and (b) correctable with these methods. This may be an important consideration for transitioning P300 Spellers for use with populations with disabilities. For example, Sellers and Donchin (2006) observed lower average P300 Speller performance from subjects with ALS, compared to healthy subjects. Therefore, benefits to users in this range of performance may be important.

Additionally, the ability of Jumpwise Selection to choose effective channel subsets suggests that it may have the capacity to counteract poor electrode-cap placement, a risk of home use, by selecting other channels that still contain discriminative information. However, since the data for this study were collected under careful laboratory conditions, this hypothesis cannot be tested using the current dataset.

We have thus presented a new method for channel selection that is based on the SWLDA classifier, is fast enough to deploy for home and clinical use, obtains state-of-the-art performance compared to existing approaches, and may make the P300 Speller a far more effective system for certain subjects, while maintaining or improving performance relative to the standard subset for others. Further, several avenues for investigation into P300 Speller channel selection remain inviting. Although the eight-channel limit demonstrates that these channel-selection methods can select higher-performance channel sets than the standard set, the amount of additional performance “purchased” by adding an electrode may be valuable information to users. Thus, one measure of interest might be AUC scores of Jumpwise Selection and SFS as the number of desired channels steps through a wide range. Also, longitudinal results that examine selected-subset consistency for a single user over time are of interest: considerable implementation effort could be saved if a subset of channels need only be determined once per subject.

• Active electrode (“channel”) selection leads to higher average P300 Speller classification performance compared to a standard channel set of similar size

• Jumpwise Regression is capable of selecting an effective electrode subset at runtime

• Some experimental subjects see large gains in accuracy with channel selection