Comparative analysis of discrete and continuous absorption weighting estimators used in Monte Carlo simulations of radiative transport in turbid media

Abstract

We examine the relative error of Monte Carlo simulations of radiative transport that employ two commonly used estimators that account for absorption differently, either discretely, at interaction points, or continuously, between interaction points. We provide a rigorous derivation of these discrete and continuous absorption weighting estimators within a stochastic model that we show to be equivalent to an analytic model, based on the radiative transport equation (RTE). We establish that both absorption weighting estimators are unbiased and, therefore, converge to the solution of the RTE. An analysis of spatially resolved reflectance predictions provided by these two estimators reveals no advantage to either in cases of highly scattering and highly anisotropic media. However, for moderate to highly absorbing media or isotropically scattering media, the discrete estimator provides smaller errors at proximal source locations while the continuous estimator provides smaller errors at distal locations. The origin of these differing variance characteristics can be understood through examination of the distribution of exiting photon weights.

1. INTRODUCTION

Monte Carlo (MC) simulations provide transport-rigorous solutions to the radiative transport equation (RTE) used to model light propagation in turbid media. MC simulations have become the de facto “gold standard” technique to provide benchmark RTE solutions, since the simulations are relatively easy to formulate and run. Moreover, MC simulations can be readily applied to a variety of geometries, boundary conditions, and optical properties. For these reasons, many groups have developed MC codes to provide predictions of reflectance, internal radiance, and transmittance for various systems [1–10]. Nevertheless, MC simulations represent a stochastic, as opposed to deterministic, solution method and the solutions obtained have an associated uncertainty based on the variation in the tallied photon weights obtained for a given number of trials. A key objective in any MC simulation method is to devise an approach that provides estimates that are unbiased with the smallest variance for a given number of trials.

In MC simulations of radiative transport, each trial represents the launch, propagation, and possible detection of a single photon. In these trials, the simulation must account for optical absorption associated with the photon propagation. The simplest scheme to accomplish this is the analog method. In this method, at each interaction location, the photon can be absorbed and terminated with probability μ_a/μ_t, or continue propagating with probability μ_s/μ_t, where μ_t = (μ_a + μ_s) is the total attenuation coefficient and μ_a and μ_s are the absorption and scattering coefficients, respectively. While analog MC simulations are fully consistent with both the RTE and the “physics” of photon propagation, absorption, and scattering, they often insufficiently sample the medium and can lead to estimates with very high variance [11]. As a result, investigators have developed alternate schemes to treat photon absorption that provide RTE solution estimates with lower variance. One approach to accomplishing this is the use of “absorption weighting” techniques. In these techniques, the unit photon weight is reduced during propagation to take values between 0 and 1. Such an approach requires modification of the random walk process to ensure that the resulting RTE predictions are unbiased.

The two most common absorption weighting techniques are discrete and continuous absorption weighting (CAW). In discrete absorption weighting (DAW), a fraction μ_a/μ_t of the existing photon weight is deposited at each interaction location and the photon propagation continues with a new weight corresponding to the residual fraction μ_s/μ_t of the prior weight. In CAW, photon absorption is modeled by distributing the weight of the photon continuously along the photon path length l between interaction locations according to Beer's Law: exp(−μ_al).

It is often assumed that CAW is more effective than DAW in terms of minimizing variance because CAW is based on photon path lengths, whereas, DAW is based on collision points. For example, in optically thin regions, where photons often pass through, but rarely collide within, CAW can produce smaller variance than DAW because CAW estimates contribute to the measurement prediction more often. However, each physical system being modeled is unique and intuition alone cannot be used to guide which estimator to use. In fact, we know of no pair of estimators for which one always provides better estimates than the other. One objective of this work is to expose the relative shortcomings of CAW and DAW in terms of providing accurate spatially resolved reflectance predictions.

Other groups have begun to examine and identify the circumstances that lead to the advantageous use of CAW versus DAW for predictions of reflectance, internal radiance, and transmittance [12,13]. Wong et al. compare the performance of CAW and DAW methods in providing reflectance predictions for slabs of various thickness. They perform a numerical analysis of the statistical error of each method within homogeneous slab systems with isotropic scattering. Their results show that DAW provides smaller errors than CAW for slabs with small albedo μ_s/μ_t < 0.5, and vice versa, when μ_s/μ_t > 0.5. For radially resolved reflectance, they discuss the improved precision of DAW at proximal source locations and CAW at distal source locations. They further estimate the cross over source–detector separation ρ, where both methods provide equivalent errors to be ρ = 10/τ, where τ is the optical thickness of the slab. Sassaroli et al. provide the first exposition on the statistical equivalence of four methods, including DAW and CAW, using probability theory arguments. They provide numerical results for 1 mm thick slabs with isotropic scattering, and compare time-resolved reflectance estimates of the methods. In terms of computational time, they found that, in most of the systems analyzed, CAW is superior to DAW.

Here, we advance the current understanding of these absorption weighting methods by exposing their formulation within the context of the RTE. This formulation provides a framework that can be used to verify whether an alternate photon propagation scheme provides a stochastic model that is consistent with the RTE. Within this context, the goals of our analysis of DAW and CAW techniques are twofold. First, we establish that MC simulations that utilize either CAW or DAW techniques provide unbiased, transport-rigorous solutions to the RTE. Second, we provide a comparative analysis of the variance provided by CAW and DAW MC predictions for spatially resolved diffuse reflectance. We use this analysis to provide guidelines, with supporting rationale, for a preference of CAW over DAW (or vice versa) for specific sets of optical properties and source–detector separations. Finally, we provide quantitative comparisons in terms of computational efficiency that consider the computational cost required to perform the simulations.

2. THEORY

In this section, we formulate both analytic and probability models of radiative transport and establish their equivalence. This equivalence ensures that stochastic estimates obtained from a MC simulation designed in accordance with the probability model provide solutions fully consistent with the RTE. This establishes a rigorous framework within which the mean value and variance of MC-based radiative transport predictions can be evaluated and assessed in terms of the effects of analog, CAW, or DAW schemes that may be employed within the MC simulation.

A. Analytic RTE Model

The RTE for the photon radiance is traditionally expressed in terms of an integro-differential equation. Here, we limit our consideration to the time-independent case at a single wavelength where it takes the form

$$\omega \cdot \nabla \Phi (\mathbf{r},\omega )+{\mu }_t\left(\mathbf{r}\right)\Phi (\mathbf{r},\omega )=\int {\int }_{\Gamma }{\mu }_s\left(\mathbf{r}\right)f(\mathbf{r};{\omega }^{\prime }\to \omega )\Phi (\mathbf{r},{\omega }^{\prime })\mathrm{d}{\omega }^{\prime }+Q(\mathbf{r},\omega ),$$ (1)

where Φ is the photon radiance as a function of position r and photon propagation direction ω, f is the single-scattering phase function, Q is the photon source and Γ = D × S² is the phase space, where D is a convex, bounded subset of R³, D ⊂ R³, and S² is the unit sphere. The radiance Φ is the photon rate impinging at position r propagating in direction ω, per unit area and solid angle.

To establish equivalence between the analytic RTE and the probabilistic models for photon transport, it is advantageous to express the RTE solution using terms that specify the photon source, propagation, interaction probabilities, and possible detection, as these are the essential steps that constitute the generation of photon biographies within a MC simulation. To accomplish this, we use the method of characteristics to reformulate the RTE as an integral equation [14]:

$$\Psi =\mathcal{K}\Psi +S,$$ (2)

where Ψ = μ_tΦ is the collision density, $\mathcal{K}$ is an integral operator

$$\mathcal{K}\Psi (\mathbf{r},\omega )={\int }_{\Gamma }K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]\Psi ({\mathbf{r}}^{\prime },{\omega }^{\prime })\mathrm{d}{\mathbf{r}}^{\prime }\mathrm{d}{\omega }^{\prime },$$ (3)

and S represents the density of first collisions experienced by photons launched from the source Q(r,ω)

$$S(\mathbf{r},\omega )={\int }_{D}T({\mathbf{r}}^{\prime }\to \mathbf{r},\omega )Q(\mathbf{r},\omega )\mathrm{d}{\mathbf{r}}^{\prime },$$ (4)

where

$$T({\mathbf{r}}^{\prime }\to \mathbf{r},\omega )={\mu }_t\left({\mathbf{r}}^{\prime }\right)\exp \left\{-{\int }_0^{\omega \cdot (\mathbf{r}-{\mathbf{r}}^{\prime })}{\mu }_t({\mathbf{r}}^{\prime }+s\omega )\mathrm{d}s\right\}.$$ (5)

The kernel K consists of a product of a collision kernel C(r′, ω′ → ω) and a transport kernel T(r′ → r, ω) . The collision kernel C describes the probability of interaction at r′ and, in the case of scattering interactions, the change of photon propagation direction. The transport kernel T describes the change in photon position due to transport between collisions. Thus, the kernel K can be written as:

$$K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]=C({\mathbf{r}}^{\prime },{\omega }^{\prime }\to \omega )T({\mathbf{r}}^{\prime }\to \mathbf{r},\omega ).$$ (6)

The collision kernel C(r′, ω′ → ω) has the form

$$C({\mathbf{r}}^{\prime },{\omega }^{\prime }\to \omega )=\frac{{\mu }_s\left({\mathbf{r}}^{\prime }\right)}{{\mu }_t\left({\mathbf{r}}^{\prime }\right)}f({\mathbf{r}}^{\prime },{\omega }^{\prime }\to \omega ),$$ (7)

where μ_s(r′)/μ_t(r′) describes the probability of scattering at position r′ and f describes the angular redirection of the photon produced by a scattering interaction. The kernel K can then be written as

$$K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]=f(\mathbf{r},{\omega }^{\prime }\to \omega ){\mu }_s\left({\mathbf{r}}^{\prime }\right)\times \exp \left\{-{\int }_0^{\omega \cdot (\mathbf{r}-{\mathbf{r}}^{\prime })}{\mu }_t({\mathbf{r}}^{\prime }+s\omega )\mathrm{d}s\right\}.$$ (8)

The integral form of the RTE [Eq. (2)] is useful for two reasons. First, a representation of the solution Ψ as a convergent infinite series can be shown. Equation (2) can be rewritten as

$$\Psi ={(I-\mathcal{K})}^{-1}S,$$ (9)

$$=(I+\mathcal{K}+{\mathcal{K}}^2+{\mathcal{K}}^3+\cdots )S.$$ (10)

Convergence of this infinite series, known as the Neumann series, is guaranteed if the operator $\mathcal{K}$ is norm-reducing, i.e.,

$${\Vert \mathcal{K}\Vert }_1<1,$$ (11)

where || · ||₁ is the ${\mathcal{L}}_1$ norm [15–18]. The series written out fully is

$$\Psi (\mathbf{r},\omega )=S(\mathbf{r},\omega )+{\int }_{\Gamma }K[({\mathbf{r}}_1,{\omega }_1)\to (\mathbf{r},\omega )]S({\mathbf{r}}_1,{\omega }_1)\mathrm{d}{\mathbf{r}}_1\mathrm{d}{\omega }_1+{\int }_{\Gamma }K[({\mathbf{r}}_2,{\omega }_2)\to (\mathbf{r},\omega )]\times {\int }_{\Gamma }K[({\mathbf{r}}_1,{\omega }_1)\to ({\mathbf{r}}_2,{\omega }_2)]\times S({\mathbf{r}}_1,{\omega }_1)\mathrm{d}{\mathbf{r}}_1\mathrm{d}{\omega }_1\mathrm{d}{\mathbf{r}}_2\mathrm{d}{\omega }_2+\cdots ,$$ (12)

$$=\sum _{k=1}^{\infty }{\int }_{\Gamma }\cdots {\int }_{\Gamma }S({\mathbf{r}}_1,{\omega }_1)K[({\mathbf{r}}_1,{\omega }_1)\to ({\mathbf{r}}_2,{\omega }_2)]\cdots \times K[({\mathbf{r}}_{k-1},{\omega }_{k-1})\to ({\mathbf{r}}_k,{\omega }_k)]\times \mathrm{d}{\mathbf{r}}_1\mathrm{d}{\omega }_1\cdots \mathrm{d}{\mathbf{r}}_k\mathrm{d}{\omega }_k.$$ (13)

Examination of the right hand side of Eq. (12) shows that the collision density Ψ(r,ω) is represented as a sum of contributions from disjoint sets of photons. The first term represents those photons that arrive at (r, ω) directly from the source. The second term represents those photons that arrive at (r, ω following a single scattering event at location r₁. The third term represents those photons that arrive at (r, ω) after experiencing only two scattering events at r₁ and r₂. Continuation of this series to include contributions from photons undergoing any number of scattering events provides the complete RTE solution.

The second reason the integral form of the RTE is useful is that existence and uniqueness of the RTE solution can be demonstrated if the condition given in Eq. (11) is satisfied. This requirement is mandatory for the formation of the MC probability model, as it ensures that the photon population will experience enough absorption or loss at boundaries so that there is zero probability that photon trajectories will experience an infinite number of collisions.

To use this RTE solution to compute a physical measurement I, such as reflectance, transmittance, fluence or radiance, we integrate the product of a known detector function g and the collision density Ψ to arrive at

$$I={\int }_{\Gamma }g(\mathbf{r},\omega )\Psi (\mathbf{r},\omega )\mathrm{d}\mathbf{r}\mathrm{d}\omega ,$$ (14)

$$={\int }_{\Gamma }g(\mathbf{r},\omega )S(\mathbf{r},\omega )\mathrm{d}\mathbf{r}\mathrm{d}\omega +{\int }_{\Gamma }g(\mathbf{r},\omega )K[({\mathbf{r}}_1,{\omega }_1)\to (\mathbf{r},\omega )]S({\mathbf{r}}_1,{\omega }_1)\times \mathrm{d}{\mathbf{r}}_1\mathrm{d}{\omega }_1\mathrm{d}\mathbf{r}\mathrm{d}\omega +\cdots ,$$ (15)

where g is a detector function that specifies how the detector tallies photons within the system. Note that Eq. (15) is the integral of the product of g with the terms of the Neumann series [Eq. (12)]. Convergence of Eq. (15) is guaranteed by Eq. (11), which ensures ${\mathcal{L}}_1$ convergence of the Neumann series [15–18]. For example, reflectance in space–angle bins Δr × Δω is obtained by a detector function that takes the form [19]

$$g(\mathbf{r},\omega )=\frac{\mid \mathbf{n}\cdot \omega \mid }{\Delta \mathbf{r}\Delta \omega }\chi (\mathbf{r},\omega ),$$ (16)

where χ is a characteristic function defined by

$$\chi (\mathbf{r},\omega )=\{\begin{array}{cc}1\hfill & (\mathbf{r},\omega )\in [\Delta \mathbf{r}\times \Delta \omega ]\hfill \\ 0\hfill & (\mathbf{r},\omega )\notin [\Delta \mathbf{r}\times \Delta \omega ].\hfill \end{array}\phantom{\}}$$ (17)

B. Probability RTE Model

A probability model for MC simulations of radiative transport requires a representation of the random walk process, which includes specification of the photon's initial state, transport, and termination either via absorption or exit. The construction of photon random walks is determined by a set of functions {p¹(P₁), p(P_i → P_i+1), p(P_k)}, where p¹(P₁) is the density function the first collision state P₁, p(P_i → P_i+1) describes transition probability density from one state P_i to the next P_i+1 prior to termination, and p(P_k) is the probability of termination in state P_k after k collisions. These functions satisfy

$$p^1\left(P_1\right)\ge 0,$$ (18)

$$p(P_i\to P_{i+1})\ge 0,$$ (19)

$$p\left(P_i\right)=1-{\int }_{\Gamma }p(P_i-P_{i+1})\mathrm{d}{P}_{i+1}.$$ (20)

The first two conditions require that the probability density functions that define the first collision state p¹, and p(P_i → P_i+1), to be non-negative. The last equation states that the probability of terminating at state P_i is equal to 1 minus the sum of all possible scattering events leaving this state. For example, if the probability of scattering from state P_i is 0, then the probability of termination at this state is 1. Note also that, in Eq. (18), the probability density of first collisions must be normalized, such that ∫_Γ p¹ (P₁)dP₁ = 1.

We describe each random walk using a collection of states β = (P₁, P₂..., P_k , where P₁ = (r₁, ω₁) represents the first photon collision in the medium, P₂,..., P_k−1 are subsequent states that the photon experiences upon transport through the medium, and state P_k represents photon termination either by absorption or escape from the phase space Γ. Each state is defined by the photon location, propagation direction, and weight. The sample space $\mathcal{B}$ consists of all random walks depicting photon movement through the medium. The probability measure ν describes the probability density of the (infinite) set of all random walks $\beta \in \mathcal{B}$.

To complete the probability model, these probability density functions that specify the random walk process must be augmented with detector functions that characterize the measurements of interest. The detector function is an estimator, a random variable that maps the random walks to a measurement of interest. The “classical” terminal estimator is defined on a single random walk β = (P₁, P₂,..., P_k) by [15]:

$${\xi }_T\left(\beta \right)=\frac{S\left(P_1\right)}{p^1\left(P_1\right)}w(P_1\to P_2)\cdots w(P_{k-1}\to P_k)\frac{g\left(P_k\right)}{p\left(P_k\right)},$$ (21)

where

$$w(P_i\to P_{i+1})=\{\begin{array}{cc}\frac{K(P_i\to P_{i+1})}{p(P_i\to P_{i+1})}\hfill & \text{if}p(P_i\to P_{i+1})\ne 0\hfill \\ 0\hfill & \text{if}p(P_i\to P_{i+1})=0.\hfill \end{array}\phantom{\}}$$ (22)

We can interpret Eq. (21) as a product of weight factors the first of which, S(P₁)/p¹(P₁), is acquired at the first collision point, subsequent weight factors K(P_i → P_i+1)/p(P_i → P_i+1) that are acquired as the photon propagates through the medium, and a final weight factor g(P_k)/p(P_k) that is acquired when the random walk β is detected at P_k. Note that, when an analog simulation is used, all weight factors are 1 and the terminal estimator reduces to a binomial estimator [20] that tallies 1 upon detection and 0 otherwise. This random variable provides an unbiased estimator of I = ∫_ΓgΨ when it has a finite expected value E[ξ] < ∞ [15].

C. Equivalence of Analytic and Probability Models

To ensure that the probability model produces correct estimates of the desired measurement, we must demonstrate equivalence between the probability and the analytic RTE models. As described in the Introduction, DAW and CAW modify the photon weight to take a value between 0 and 1. To allow this, the random walk process is also modified so that the resulting predictions are unbiased. For this purpose, the random walk process, based on Eqs. (18)–(22), is generalized to one that accommodates nonunit weights. This provides a model that enables the formulation of both DAW and CAW estimators. The more general random walk process is specified by the functions

$$p^1\left(P_1\right)=\frac{S\left(P_1\right)}{{\int }_{\Gamma }S\left(P_1\right)\mathrm{d}{P}_1},$$ (23)

$$p(P_i\to P_{i+1})=\frac{K(P_i\to P_{i+1})}{1-p\left(P_i\right)},$$ (24)

$$p\left(P_i\right)=1-{\int }_{\Gamma }K(P_i\to P_{i+1})\mathrm{d}{P}_{i+1},$$ (25)

and weight factors

$$w(P_i\to P_{i+1})=\frac{K(P_i\to P_{i+1})}{p(P_i\to P_{i+1})}.$$ (26)

These equations are based on the key assumption that the operator $\mathcal{K}$ is norm-reducing [Eq. (11)].

For example, to form a DAW estimator, photon termination due to absorption is forbidden, therefore p(P_k) = 0, and the probability of transitioning from state P_i to P_i+1 becomes

$$p(P_i\to P_{i+1})=\frac{K(P_i\to P_{i+1})}{{\int }_{\Gamma }K(P_i\to P_{i+1})\mathrm{d}{P}_{i+1}},$$ (27)

$$=\frac{K(P_i\to P_{i+1})}{{\mu }_s\left(P_i\right)∕{\mu }_t\left(P_i\right)},$$ (28)

where the denominator is determined by integrating Eq. (8). The details of this derivation are given in Appendix A. The full set of equations that define the DAW random walk process is then

$$p^1\left(P\right)=\frac{S\left(P_1\right)}{{\int }_{\Gamma }S\left(P_1\right)\mathrm{d}{P}_1},$$ (29)

$$p(P_i\to P_{i+1})=\frac{K(P_i\to P_{i+1})}{{\mu }_s\left(P_i\right)∕{\mu }_t\left(P_i\right)},$$ (30)

$$p\left(P_k\right)=0.$$ (31)

This derivation assumes a transport kernel that sampled intercollision distances from the probability density function μ_t exp(−μ_tl), based on the total attenuation shown in Eq. (8). These equations show that, since termination of the photon due to absorption is forbidden, the photon weight is reduced discretely by μ_s(P_i)/μ_t(P_i) at collision points P_i to account for absorption.

In CAW, photon termination due to absorption is also not allowed and, instead, the photon weight is reduced continuously along the photon path. In this case, the transport kernel is modified to select intercollision distances sampled from the probability density function μ_s exp(−μ_sl), based on the scattering coefficient. The probability of transitioning from state P_i to P_i1 becomes

$$p(P_i\to P_{i+1})=\frac{K(P_i\to P_{i+1})}{{\int }_{\Gamma }K(P_i\to P_{i+1})\mathrm{d}{P}_{i+1}},$$ (32)

$$=\frac{K(P_i\to P_{i+1})}{\exp \left\{-{\int }_{P_i}^{P_{i+1}}{\mu }_a\left(s\right)\mathrm{d}s\right\}},$$ (33)

where the denominator is determined by integrating a refactored Eq. (8) with a transport kernel based on μ_s. The integral from P_i to P_i+1 accounts for varying μ_a along that track. The details of this derivation are given in Appendix B. The complete set of equations that define the CAW random walk process is

$$p^1\left(P_1\right)=\frac{S\left(P_1\right)}{{\int }_{\Gamma }S\left(P_1\right)\mathrm{d}{P}_1},$$ (34)

$$p(P_i\to P_{i+1})=\frac{K(P_i\to P_{i+1})}{\exp \left\{-{\int }_{P_i}^{P_{i+1}}{\mu }_a\left(s\right)\mathrm{d}s\right\}},$$ (35)

$$p\left(P_k\right)=0.$$ (36)

The fact that the termination probability due to absorption is zero in both DAW and CAW [p(P_k = 0] precludes the use of a “classical” terminal estimator [Eq. (21)], because the final factor g(P_k)/p(P_k) would have a zero denominator. Moreover, reflectance measurements require the placement of a detector on the media boundary ∂Γ rather than within the media, which requires a mechanism for the capture of photons as they exit Γ. For both of these reasons, the tally of reflectance requires a “modified” terminal estimator. Using the general random walk process constructed above, {p¹(P₁), p(P_i → P_i+1), p(P_k)}, a modified terminal estimator is defined on a single random β = (P₁, P₂,..., P_k) by

$${\xi }_{\mathrm{MT}}\left(\beta \right)=\frac{S\left(P_1\right)}{p^1\left(P_1\right)}w(P_1\to P_2)\cdots w(P_{k-1}\to P_k)\times w(P_k\to P_k^{\left(1\right)})g\left(P_k^{\left(1\right)}\right),$$ (37)

where

$$w(Q\to P)=\{\begin{array}{cc}\frac{K(P_i\to P_{i+1})}{p(P_i\to P_{i+1})}\hfill & \text{if}p(P_i\to P_{i+1})\ne 0\hfill \\ 0\hfill & \text{if}p(P_i\to P_{i+1})=0.\hfill \end{array}\phantom{\}}$$ (38)

In Eq. (37), $g\left(P_k^{\left(1\right)}\right)$ is the detector function given by Eq. (16) and $P_k^{\left(1\right)}$ is the pseudo-collision that occurs at the boundary crossing after the last true collision P_k inside Γ. A pseudo-collision is a nonphysical collision that is used at points that lie on ∂Γ at the location where the photon exited Γ. In Appendix C, we show that this modified terminal estimator provides an unbiased estimate of I.

The DAW estimator for reflectance is then formed by substituting Eqs. (29)–(31) and (16) into Eq. (37):

$${\xi }_{\mathrm{DAW}}=\{\begin{array}{cc}\prod _{i=1}^k\frac{{\mu }_s\left(P_i\right)}{{\mu }_t\left(P_i\right)}\hfill & \text{if the photon crosses}{S}_{r\times {\omega }_{\mathrm{NA}}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},$$ (39)

where S_r×ωNA is the space–angle bin that accounts for the area and numerical aperture (NA) of the detector. This estimator is unbiased, and so E[ξ_DAW] = ∫ ξ_DAWdν_DAW = I, where ν_DAW is the measure defined by the DAW random walk process [Eqs. (29)–(31)]. In homogeneous media, this estimator reduces to

$${\xi }_{\mathrm{DAW}}={({\mu }_s∕{\mu }_t)}^k,$$ (40)

where k is the total number of collisions experienced by the photon in the medium.

The CAW estimator is obtained by substituting Eqs. (4), (34)–(36) and (16) into Eq. (37):

$${\xi }_{\mathrm{CAW}}=\{\begin{array}{cc}\exp \left\{-{\int }_Q^{P_1}{\mu }_a\left(s\right)\mathrm{d}s-\sum _{i=1}^{k-1}{\int }_{P_i}^{P_{i+1}}{\mu }_a\left(s\right)\mathrm{d}s-{\int }_{P_k}^{P_k^{\left(1\right)}}{\mu }_a\left(s\right)\mathrm{d}s\right\}\hfill & \text{if the photon crosses}{S}_{r\times {\omega }_{\mathrm{NA}}}\text{at}{P}_k^{\left(1\right)}\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (41)

This estimator is also unbiased, and so E[ξ_CAW] = ∫ ξ_CAWdν_CAW = I, where ν_CAW is the measure defined by the CAW random walk process [Eq. (34)–(36)]. In homogeneous media, this estimator reduces to

$${\xi }_{\mathrm{CAW}}=\exp (-{\mu }_{a}L),$$ (42)

where $L={\int }_Q^{P_1}\mathrm{d}s+{\sum }_{i=1}^{k-1}{\int }_{P_i}^{P_{i+1}}\mathrm{d}s+{\int }_{P_k}^{P_k^{\left(1\right)}}\mathrm{d}s$ is the total photon path length from source Q to exiting the medium at pseudo-collision $P_k^{\left(1\right)}$.

Defining the random walk process in terms of K and S of the transport equation thus defines a probability measure ν on the space $\mathcal{B}$ of all random walks that is consistent with the RTE. This provides the equivalence between the analytic and probability models:

$$\begin{array}{ccc}\hfill \text{Analytic Model}\hfill & \hfill \leftrightarrow \hfill & \hfill \text{Probability Model}\hfill \\ \hfill I={\int }_{\Gamma }g\left(P\right)\Psi \left(P\right)\mathrm{d}P\hfill & \hfill \hfill & \hfill I={\int }_{\mathcal{B}}\xi \left(\beta \right)\mathrm{d}\nu \left(\beta \right).\hfill \end{array}$$ (43)

3. NUMERICAL RESULTS AND ANALYSIS: SPATIALLY RESOLVED REFLECTANCE USING DAW OR CAW

Using the derived estimators for DAW and CAW, we examine spatially resolved reflectance in homogeneous, semi-infinite media. The geometry employed considers a narrow collimated beam incident on the medium surface with refractive index n = 1.4. Fifty million photons are launched in each simulation. The scattering angle at each interaction point is sampled from the Henyey–Greenstein phase function [21]. The NA of the detector is fully open. Russian roulette was not employed. All of these assumptions were invoked within a single MC code, which modified the track length sampling and associated photon weights based on whether the simulation employed DAW or CAW.

We analyzed media with ratios of reduced scattering to absorption coefficients ${\mu }_s^{\prime }∕{\mu }_a=100$, 10, 1 and anisotropy values of g = 0.9, 0. We held $l^{\ast }=1∕({\mu }_a+{\mu }_s^{\prime })=0.99$ fixed. Table 1 displays the optical properties we investigated.

To assess the error of each MC reflectance prediction, we evaluate the tallied variance. The N-sample variance is determined using

$$\mathrm{Var}\left[\xi \right]=\frac{1}{(N-1)}\{\mathrm{E}\left[{\xi }^2\right]-{\left(\mathrm{E}\left[\xi \right]\right)}^2\},$$ (44)

where N is the number of photons launched, E[ξ] is the expected value or mean, and E[ξ²] is the second moment of estimator. The square root of the variance is the standard deviation

$$\sigma =\sqrt{\mathrm{Var}\left[\xi \right]},$$ (45)

which defines a 1σ confidence interval for each mean estimate. By the Central Limit Theorem [22], we expect that, as N goes to infinity, there is a 68% chance that the true result lies in the range E[ξ] ± 1σ. The relative error is then

$$R=\frac{\sigma }{\mathrm{E}\left[\xi \right]},$$ (46)

which indicates the quality of each mean estimate and is proportional to $1∕\sqrt{N}$. A relative error <0.05 is a guideline for assessing the quality of the estimated mean prediction to be “generally reliable” [11].

We examine two metrics to evaluate the relative performance of DAW and CAW. The first is the relative difference in the mean reflectance values

$$\Delta \mathrm{Mean}=\frac{\mathrm{E}\left[{\xi }_{\mathrm{DAW}}\right]-\mathrm{E}\left[{\xi }_{\mathrm{CAW}}\right]}{\mathrm{E}\left[{\xi }_{\mathrm{CAW}}\right]}.$$ (47)

We also evaluated 1σ confidence interval about this difference by using the standard deviations for DAW and CAW [Eq. (45)] [23]. Since the mean reflectance values for DAW and CAW are statistically equivalent, we expect ΔMean to be smaller than the 1σ confidence interval 68% of the time.

The second metric is the difference in the relative error

$$\Delta R=R_{\mathrm{DAW}}-R_{\mathrm{CAW}}.$$ (48)

This metric allows us to evaluate which estimator provides the smallest relative error. Moreover, comparison of this metric to the intrinsic relative error indicates the significance of the advantage.

A. Relative Error Analysis for Anisotropically Scattering Media

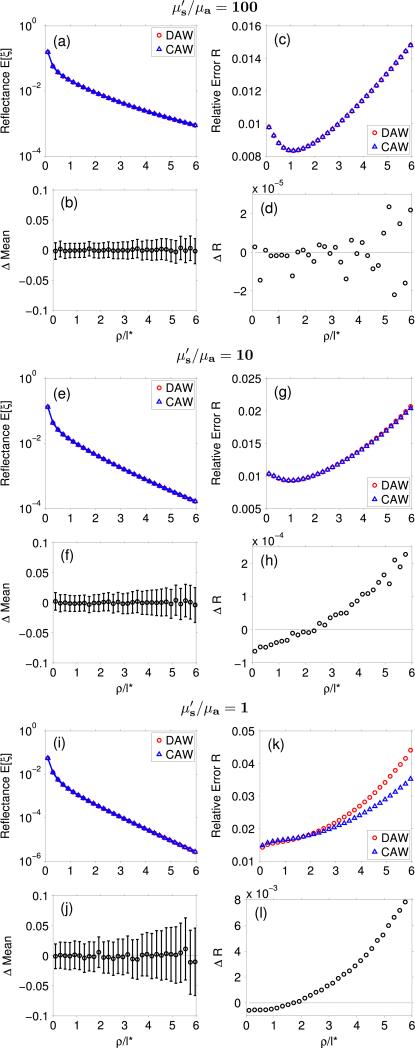
We first examine the case of anisotropic scattering with g = 0.9, due to its relevance to biological tissue and the resulting disparate spatial scales for the single scattering length l_s = 1/μ_s and the isotropic scattering length $1∕{\mu }_s^{\prime }$. Figure 1(a) displays spatially resolved reflectance predictions E[ξ] provided by DAW and CAW estimators for ${\mu }_s^{\prime }∕{\mu }_a=100$, and Fig. 1(b) shows the relative difference of these results ΔMean [Eq. (47)]. In these results, the source–detector separation ρ is normalized by the transport mean free path l^* . The two estimators provide mean results that agree within 0.36%, which is well below the 1σ error bars (maximum value 2%) for the span ρ ∈[0–6]l^* . This agreement is consistent with the fact that both estimators are unbiased and thus, their expected values are identical. Figure 1(c) displays the relative error R [Eq. (46)] using DAW and CAW estimators and Fig. 1(d) shows the difference of these results ΔR [Eq. (48)]. In Fig. 1(d), positive values represent cases where CAW provides the smaller error, whereas negative difference values represent cases where DAW provides the smaller error. The fact that the ΔR plot has no systematic pattern with respect to ρ and is always much smaller than the relative error values shown in Fig. 1(c), demonstrates that there is no clear advantage to either CAW or DAW estimators in this case.

Fig. 1.

Plots of [(a), (e), (i)] spatially resolved reflectance, [(b), (f), (j)] ΔMean with 1σ error bars, [(c), (g), (k)] relative error, and [(d), (h), (l)] ΔR for increased absorption ${\mu }_s^{\prime }∕{\mu }_a=100$, 10, 1 and g=0.9.

We apply the same analysis to a more highly absorbing system, ${\mu }_s^{\prime }∕{\mu }_a=10$. Figures 1(e) and 1(f) display the reflectance and ΔMean results, respectively, for the two estimators, and show that the mean predictions agree to within 0.44%, again well below the 1σ maximum value of 3%. Figures 1(g) and 1(h) display the relative error and ΔR results, respectively, and show that DAW provides smaller relative error than CAW for $\rho \lesssim 2.4l^{\ast }$, whereas, for $\rho \gtrsim 2.4l^{\ast }$ CAW provides the smaller relative error and this difference increases for increasing ρ. The ΔR values are less than 2% of the intrinsic relative error estimates and, therefore, not significant.

Finally, we examine a system with ${\mu }_s^{\prime }∕{\mu }_a=1$. Figures 1(i) and 1(j) display the reflectance and ΔMean results, respectively, and show that the mean predictions agree to within 1.1%, with 1σ maximum value of 6%. Figures 1(k) and 1(l) display the relative error and ΔR, and these are qualitatively similar to the ${\mu }_s^{\prime }∕{\mu }_a=10$ case above in that DAW provides smaller relative error than CAW for $\rho \lesssim 1.6l^{\ast }$; then, beyond 1.6l^* , CAW provides the smaller relative error and this advantage increases as ρ increases. However, here the difference in relative errors between DAW and CAW becomes significant as it is comparable to the relative error estimates themselves. The relative error provided by DAW proximal to the source is 4% smaller than CAW, whereas, near ρ/l^* = 6 the relative error provided by CAW is 25% smaller than DAW.

There are some trends to note in this set of results. First, in the relative difference plots of the reflectance shown in Figs. 1(b), 1(f), and 1(j), the 1σ error bars increase as the source–detector separation increases. This is because as ρ increases, both the number of photons exiting the detector decreases and the exiting weight fluctuates more due to a wider variation of path lengths from source to detector. Note that, as ${\mu }_s^{\prime }∕{\mu }_a$ decreases, the error bars also increase, which is due to the variation in the path lengths and number of collisions the photon experiences prior to detection. Second, in the relative error difference plots shown in Figs. 1(d), 1(h), and 1(l), as ${\mu }_s^{\prime }∕{\mu }_a$ decreases, the results change from a noisy straight line, which indicates no preference to DAW or CAW to monotonically increasing plots that cross 0 somewhere between ρ = [1–2]l^*, and shows the advantage of using DAW for small source–detector separations $(\rho \lesssim 2l^{\ast })$ as well as the advantage of using CAW for large source–detector separations $(\rho \gtrsim 2l^{\ast })$. In addition, the magnitude of the relative error differences at ρ = 0 and ρ = 6l^* grows as ${\mu }_s^{\prime }∕{\mu }_a$ decreases. We will examine this trend further in Subsection 3.C.

B. Relative Error Analysis for Isotropically Scattering Media

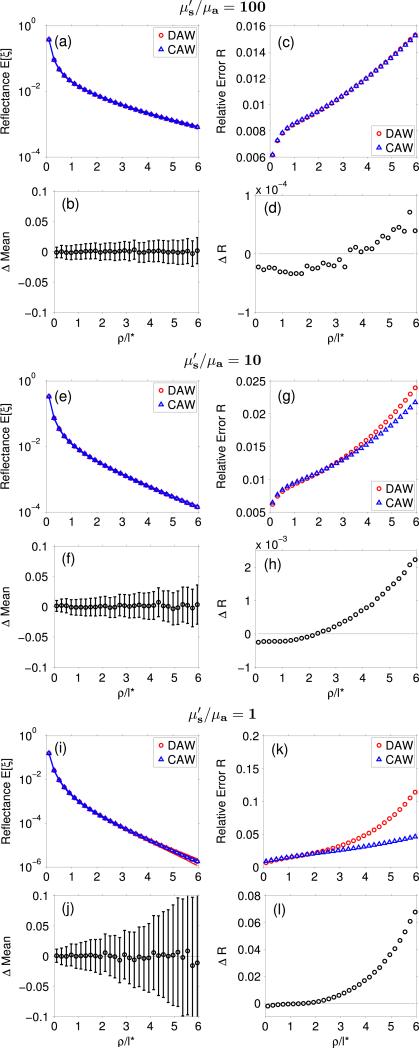
We next examine the relative performance of DAW and CAW in media with isotropic scattering. This case is important, as it considers systems in which the single scattering and isotropic scattering lengths are equal. For the highly scattering system, ${\mu }_s^{\prime }∕{\mu }_a=100$, Figs. 2(a) and 2(b) display the reflectance predictions and ΔMean results, respectively, and show that the two estimators provide mean results that agree within 0.33% (with a maximum 1σ error bar value of 2%), and is similar to the g = 0.9 case. Figures 2(c) and 2(d) display the relative error and the ΔR results, respectively, for the two estimators, and show that DAW provides smaller relative error proximal to the source for $\rho \lesssim 3.5l^{\ast }$ , whereas CAW provides smaller relative error for $\rho \gtrsim 3.5l^{\ast }$. This display of a distinct advantage for DAW at proximal source locations and for CAW at distal locations was not seen in the case of ${\mu }_s^{\prime }∕{\mu }_a=100$ with g = 0.9, shown in Fig 1(d). Note also that the relative error differences are about 2× larger as compared to the g = 0.9 case. However, the differences are small compared to the intrinsic relative error estimates.

Fig. 2.

Plots of [(a), (e), (i)] spatially resolved reflectance, [(b), (f), (j)] ΔMean with 1σ error bars, [(c), (g), (k)] relative error, and [(d), (h), (l)] ΔR for increased absorption ${\mu }_s^{\prime }∕{\mu }_a=100$, 10, 1 and g=0.

For the more highly absorbing system, ${\mu }_s^{\prime }∕{\mu }_a=10$, Figs. 2(e) and 2(f) display the reflectance and the ΔMean results, respectively, for the two estimators and show that the means agree to within 0.73% (maximum error bar value 3%), almost 2× larger than the g = 0.9 case. Figures 2(g) and 2(h) display the relative error and the ΔR results, respectively, and show that DAW provides smaller relative error than CAW for $\rho \lesssim 2.3l^{\ast }$, whereas, for $\rho \gtrsim 2.3l^{\ast }$, CAW provides the smaller relative error, and its advantage increases as ρ increases. Comparison of the relative error differences with the g = 0.9 case reveals a roughly 10× increase in the relative error difference while the overall trend of a DAW advantage at $\rho \lesssim 2l^{\ast }$ and CAW advantage at $\rho \gtrsim 2l^{\ast }$ is preserved.

For the highest absorbing system, ${\mu }_s^{\prime }∕{\mu }_a=1$, Figs. 2(i) and 2(j) display the reflectance predictions and the ΔMean results, respectively, and show that the means agree to within 0.85% (maximum error bar value 12%). Figures 2(k) and 2(l) display the relative error and ΔR results, respectively, and show that DAW provides smaller relative error than CAW for $\rho \lesssim 1.6l^{\ast }$. Then, for $\rho \gtrsim 1.6l^{\ast }$, CAW provides the smaller relative error, and its advantage again increases as ρ increases. Comparison with the g = 0.9 case reveals a 10× increase in the relative error differences between DAW and CAW for g = 0. However, the overall advantage of DAW for $\rho \lesssim 1.6l^{\ast }$ and CAW for $\rho \gtrsim 1.6l^{\ast }$, is preserved. Here, when absorption is comparable to scattering, the differences in relative errors between DAW and CAW are significant. Proximal to the source, the relative error provided by DAW is 24% smaller than CAW; whereas, at ρ/l^* = 6, the relative error provided by CAW is 146% smaller than DAW.

C. Analysis of Photon Weights

Our results show that for highly scattering systems ${\mu }_s^{\prime }∕{\mu }_a=100$ with g = 0.9, there is no significant advantage in applying either DAW or CAW estimator. However, as absorption increases to ${\mu }_s^{\prime }∕{\mu }_a=10$, 1 or for isotropically scattering systems, DAW provides smaller relative error for source– detector separations proximal to the source for $\rho \lesssim 2l^{\ast }$, whereas CAW provides smaller relative error for $\rho \gtrsim 2l^{\ast }$. These findings are consistent with those of Wong and co-workers [12].

To investigate the origin of these differences between DAW and CAW estimates, we examine the distribution of detected photon weights at proximal and distal detector locations. Recall that for highly scattering media with ${\mu }_s^{\prime }∕{\mu }_a=100$ and g = 0.9, the relative error for both estimators was comparable. Because the relative error is the standard deviation divided by the mean, a smaller relative error can only be achieved by a smaller variance, since the mean estimates provided by DAW and CAW are equivalent. Figure 3(a) shows the photon weight distribution for a detector most proximal to the source ρ ∈ [0–0.2]l^*. One hundred equally spaced weight bins were used to generate these results. The weight distribution is not normalized by the surface area of the detector bin and, therefore, displays the raw photon weights modified only by specular reflection and the absorption method employed. The photon weights span 0–0.9722 where the value A = 0.9722 originates from a photon weight reduced solely by specular reflection. These results show that the majority of photons exit the medium with weights very close to this maximum value. These photons experienced very few collisions and traveled very small distances in the medium. The silhouette of the distribution of photon weights resulting from DAW and CAW simulations is similar, indicating little difference between the detected photon weights at this proximal position. Figure 3(b) shows the photon weight count for a detector positioned distal from the source ρ ∈ [5.8–6]l^* . Again, the silhouettes of the photon weight distribution produced by the two estimators are similar, indicating little difference between the relative errors for this distal detector. Both these findings are consistent with the relative error difference results shown in Fig. 1(d).

Fig 3.

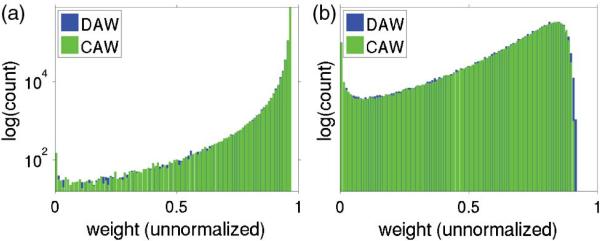
Plots of the photon weight count for (a) ρ ∈ [0–0.2]l^* and (b) ρ ∈ [5.8–6]l^* for high scattering media ${\mu }_s^{\prime }∕{\mu }_0=100$ and g = 0.9.

This situation changes when absorption is increased to ${\mu }_s^{\prime }∕{\mu }_a=10$ and scattering is isotropic. In Fig. 2(h), we observe a crossover of the relative error difference from smaller errors provided by DAW at $\rho \lesssim 2l^{\ast }$ to smaller errors provided by CAW at $\rho \gtrsim 2l^{\ast }$. Figures 4(a) and 4(b) show the photon weight distributions at proximal ρ ∈ [0–0.2]l^* and distal ρ ∈ [5.8–6]l^* locations, respectively. In both of these plots, we now see two important differences in the weight distributions for DAW and CAW. First, we see that the range of detected weights is substantially different depending on the absorption weighting method used, and provides an indication for the variance of the estimator. Second, we see that the weight distribution provided by DAW is not continuous, but notably quantized, due to the fixed weight reduction produced by the number of collisions, which assumes only integer values. Although this was the case also when ${\mu }_s^{\prime }∕{\mu }_a=100$, the effect is more notable as absorption increases. As absorption is increased further, and becomes comparable to the reduced scattering coefficient, the differences become even more stark, as seen in Fig. 5. The advantage of DAW proximal to the source arises from the smaller bandwidth of the photon weight distribution as compared with CAW, shown in Fig. 5(a) for ${\mu }_s^{\prime }∕{\mu }_a=1$ and g = 0. This is most noticeable at the larger photon weights. Here, we see the CAW results are characterized by a relatively smooth weight distribution, spanning 0 to a maximum weight of 0.9722. By contrast, the DAW weight distribution displays prominent discrete spikes with a maximum weight of 0.4861. The dramatic reduction in the maximum DAW photon weight arises because photon detection requires at least one collision and results in a photon weight reduction due to one collision combined with specular reflection: W = A · (μ_s/μ_t) = 0.4861. In contrast, the maximum CAW photon weight is based on the total path length, which can be very small. For the data shown here, the photon path lengths were as small as 4.01 × 10⁻⁷ mm, which produces a negligible weight reduction. The discrete nature of the DAW estimator reduces the bandwidth of the photon weight distribution, leading to smaller variance and relative error compared with CAW, and provides an advantage over the continuous nature of CAW for these results.

Fig. 4.

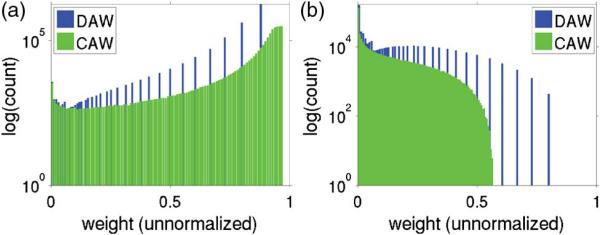
Plots of the photon weight count for (a) ρ ∈ [0–0.2]l^* and (b) ρ ∈ [5.8–6]l^* for moderate absorbing media ${\mu }_s^{\prime }∕{\mu }_a=10$ and g = 0.

Fig. 5.

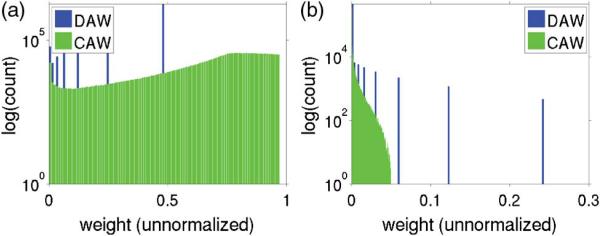
Plots of the photon weight count for (a) ρ ∈ [0–0.2]l^* and (b) ρ ∈ [5.8–6]l^* for high absorbing media ${\mu }_s^{\prime }∕{\mu }_a=1$ and g = 0.

Figure 5(b) shows the photon weight distribution for ρ ∈ [5.8–6]l^* . Here, the span of photon weights produced by the DAW simulations is distinctly greater than CAW. Again, the discrepancy occurs near the maximum weight of the detected photon. For a given detector location, there is a lower limit of the minimum path length of any photon exiting the detector, due to the geometry. The maximum CAW weight is governed by the minimum path length between source and detector, which must be ≥5.8 mm and, for the CAW data shown here, the minimum path length experienced by a photon is 5.89 mm. Thus, the largest detected photon weight is W = A · exp(−0.5051 × 5.89) = 0.05, and this limits the variance of this estimator. However, in DAW, there is a finite probability that a photon can be detected after just 1 collision. For the DAW data shown here, as few as 2 collisions were experienced by the detected photons, producing a maximum weight of W = A · (μ_s/μ_t)² = 0.243 and gives rise to the larger variance of DAW compared with CAW. These results show that at larger ρ, the path length-based CAW estimator provides an advantage over the collision-based DAW estimator. Qualitatively similar results are produced for the photon weight histograms of all other sets of optical properties that exhibit this cross over from smaller relative errors for DAW near the source to smaller relative errors for CAW far from the source (results not shown).

D. Computational Efficiency

Our discussion so far has focused on the comparison of relative errors. However, in terms of practical usage, it is important to consider the relative computational efficiency of these DAW and CAW MC simulations. The computational efficiency of determining the value of a random variable ξ is defined as the product

$$\mathrm{Eff}\left[\xi \right]={\left[R^{2}T\right]}^{-1},$$ (49)

where R is the relative error of ξ [Eq. (46)] and T is the computer run time [11]. Table 2 displays the computational efficiency and its components for proximal ρ ∈ [0–0.2]l^* and distal ρ ∈ [5.8–6]l^* detection. The values with an asterisk (*) indicate the estimator that provided the larger efficiency.

For the highly scattering media ${\mu }_s^{\prime }∕{\mu }_s=100$ with g = 0.9, we found no advantage to DAW or CAW with respect to relative error. This is because there is no significant difference between the intercollision distances used in DAW (1/μ_t = 0.1 mm) and CAW (1/μ_s = 0.1 mm). However, CAW took 3.6% longer than DAW to simulate the same number photons (Intel Xeon CPU 2.67GHz), because the path length calculation required in CAW is more costly. Therefore, in terms of efficiency, DAW provides a slight advantage at both proximal and distal detectors.

As absorption is increased to ${\mu }_s^{\prime }∕{\mu }_s=10$, CAW provides a slight advantage for both proximal and distal detectors, due to a greater reduction in CAW run times. The slight edge DAW provides over CAW in terms of relative error at the proximal detector does not compensate for the longer DAW run times. As absorption is increased further to ${\mu }_s^{\prime }∕{\mu }_s=1$, the run times are now 28% smaller for CAW compared to DAW. This is because the intercollision distances for CAW (1/μ_s = 1.97 mm) are significantly larger than that for DAW (1/μ_t = 0.99 mm). The larger number of collisions in DAW simulations outweighs the cost of the path length calculations required for CAW. For isotropic scattering g = 0, we see a similar trend, in which DAW provides an advantage in terms of computational speed over CAW for highly scattering media, but as absorption is increased, CAW simulations become more computationally efficient.

Note that our analysis is limited to homogeneous media. For spatially heterogeneous media, the time required for CAW simulations will dramatically increase, especially if the characteristic spatial scale of the heterogeneities have dimensions smaller than 1/μ_s. This is because the partial path lengths created when intercollision tracks straddle media interfaces will need to be calculated. In comparison, DAW relies only on the position of collision points and the time required for DAW simulations will not increase substantially.

4. CONCLUSIONS

In conclusion, we have presented the theoretical formulation for the commonly used DAW and CAW absorption weighting techniques used in MC simulations. We have proved that both methods produce equivalent mean values. This theory provides a framework to evaluate if potential new MC estimators or weighting schemes are fully consistent with the RTE and provide unbiased results.

We compare the performance of each estimator in predictions of spatially resolved reflectance in terms of relative error. This shows no strong advantage to either estimator in highly scattering media with forward-peaked scattering g = 0.9. However, for moderately to highly absorbing media with g = 0.9, or in all media with isotropic scattering, DAW provides better predictions at locations proximal to the source $\rho \lesssim 2l^{\ast }$ and CAW provides better predictions at distal locations $\rho \gtrsim 2l^{\ast }$. This is explained by examination of the detected photon weight distributions, which give key insight into the variance characteristics of these methods.

Our comparative analysis of computational efficiency reveals that DAW provides a slight advantage over CAW for highly scattering media for all source–detector separations. However, when absorption is increased, CAW provides larger computational efficiency over DAW. These conclusions are shown for both highly anisotropic and isotropic media.

Table 1.

List of Optical Properties Studied

${\mu }_s^{\prime }∕{\mu }_a$	g	μa [/mm]	μs [/mm]	${\mu }_s^{\prime }$ [/mm]	μ s/ μ t
100	0.9	0.01	10.0	1.0	1.0
10	0.9	0.092	9.182	0.9182	0.99
1	0.9	0.5051	5.051	0.5051	0.91
100	0.0	0.01	1.0	1.0	0.99
10	0.0	0.092	0.9182	0.9182	0.91
1	0.0	0.5051	0.5051	0.5051	0.5

Table 2.

Calculated Efficiencies for Reflectance Predictions at Proximal and Distal Source Locations^a

			T [h]		R		Eff[ξ]
${\mu }_s^{\prime }∕{\mu }_a$	g	ρ [mm]	DAW	CAW	DAW	CAW	DAW	CAW
100	0.9	[0—0.2]	28	29	0.0098	0.0098	372*	359
100	0.9	[5.8—6]	28	29	0.0148	0.0148	163*	157
10	0.9	[0—0.2]	26.7	26	0.0103	0.0104	353	356*
10	0.9	[5.8—6]	26.7	26	0.0207	0.0204	87	92*
1	0.9	[0—0.2]	19	13.7	0.0143	0.0148	257	333*
1	0.9	[5.8—6]	19	13.7	0.0441	0.0352	27	59*
100	0.0	[0—0.2]	2.8	2.9	0.0061	0.0062	9598*	8971
100	0.0	[5.8—6]	2.8	2.9	0.0153	0.0153	1525*	1473
10	0.0	[0—0.2]	2.9	2.5	0.0062	0.0064	8971	9766*
10	0.0	[5.8—6]	2.9	2.5	0.0240	0.0217	598	849*
1	0.0	[0—0.2]	3.6	1.5	0.0066	0.0087	6377	8808*
1	0.0	[5.8—6]	3.6	1.5	0.1141	0.0463	21	311*

^aProximal (ρ ε [0—0.2] mm) and distal (ρ ε [5.8—6] mm), where ${\mu }_s^{\prime }∕{\mu }_a=100,10,1$ and g = 0.9, 0. Efficiency values with an asterisk (*) indicate the larger value when comparing DAW with CAW.

APPENDIX A: DERIVATION OF THE INTERCOLLISION WEIGHTS FOR DAW

We derive the density function p(P_i → P_i+1), which specifies the photon de-weighting between two collisions for DAW, shown in Eq. (30). The denominator of the general equation for p(P_i → P_i+1) [Eq. (24)] can be written as

$$1-p\left(P_i\right)=1-\left[1-{\int }_{\Gamma }K(P_i\to P_{i+1})\mathrm{d}{P}_{i+1}\right],$$ (A1)

$$={\int }_{\Gamma }K(P_i\to P_{i+1})\mathrm{d}{P}_{i+1}.$$ (A2)

Confining our consideration to homogeneous media, the transport kernel Eq. (8) can be written as

$$K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]=f({\mathbf{r}}^{\prime };{\omega }^{\prime }\to \omega ){\mu }_s\left({\mathbf{r}}^{\prime }\right)\exp \{-{\mu }_t\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}.$$ (A3)

For DAW, we rewrite Eq. (A3) as

$$K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]=f({\mathbf{r}}^{\prime };{\omega }^{\prime }\to \omega )\frac{{\mu }_s\left({\mathbf{r}}^{\prime }\right)}{{\mu }_t\left({\mathbf{r}}^{\prime }\right)}\times \left[{\mu }_t\left({\mathbf{r}}^{\prime }\right)\exp \{-{\mu }_t\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\right].$$ (A4)

Note that the last factor in square brackets is the “transport” portion T of kernel K. The rest of the right hand side is the “collision” portion C. Integrating K with respect to drdω means that T is integrated with respect to dr and C is integrated with respect to dω. Thus, integration produces

$${\int }_{\Gamma }K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]\mathrm{d}\mathbf{r}\mathrm{d}\omega ={\int }_{\Gamma }f({\mathbf{r}}^{\prime };{\omega }^{\prime }\to \omega )\frac{{\mu }_s\left({\mathbf{r}}^{\prime }\right)}{{\mu }_t\left({\mathbf{r}}^{\prime }\right)}\times {\mu }_t\left({\mathbf{r}}^{\prime }\right)\exp \{-{\mu }_t\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\mathrm{d}\mathbf{r}\mathrm{d}\omega ,$$ (A5)

$$=\left[{\int }_{S^2}f({\mathbf{r}}^{\prime };{\omega }^{\prime }\to \omega )\mathrm{d}\omega \right]\left[\frac{{\mu }_s\left({\mathbf{r}}^{\prime }\right)}{{\mu }_t\left({\mathbf{r}}^{\prime }\right)}\right]\times \left[{\int }_D{\mu }_t\left({\mathbf{r}}^{\prime }\right)\exp \{-{\mu }_t\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\mathrm{d}\mathbf{r}\right],$$ (A6)

$$=1\cdot \frac{{\mu }_s\left({\mathbf{r}}^{\prime }\right)}{{\mu }_t\left({\mathbf{r}}^{\prime }\right)}\cdot 1,$$ A7)

and justifies the denominator in Eq. (30).

APPENDIX B: DERIVATION OF THE INTERCOLLISION WEIGHTS FOR CAW

Here, we derive the density function p(P_i → P_i+1) for CAW, shown in Eq. (35). For CAW, we rewrite Eq. (A3) as

$$K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]=f({\mathbf{r}}^{\prime };{\omega }^{\prime }\to \omega )\exp \{-{\mu }_a\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\times \left[{\mu }_s\left({\mathbf{r}}^{\prime }\right)\exp \{-{\mu }_s\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\right].$$ (B1)

The first portion represents the collision kernel C while the last factor in square brackets is the transport kernel T. Integrating this produces

$${\int }_{\Gamma }K[({\mathbf{r}}^{\prime },{\omega }^{\prime })\to (\mathbf{r},\omega )]\mathrm{d}\mathbf{r}\mathrm{d}\omega ={\int }_{\Gamma }f({\mathbf{r}}^{\prime };{\omega }^{\prime }\to \omega )\exp \{-{\mu }_a\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\times {\mu }_s\left({\mathbf{r}}^{\prime }\right)\exp \{-{\mu }_s\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\mathrm{d}\mathbf{r}\mathrm{d}\omega ,$$ (B2)

$$=\left[{\int }_{S^2}f({\mathbf{r}}^{\prime };{\omega }^{\prime }\to \omega )\mathrm{d}\omega \right]\exp \{-{\mu }_a\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\times \left[{\int }_D{\mu }_s\left({\mathbf{r}}^{\prime }\right)\exp \{-{\mu }_s\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\mathrm{d}\mathbf{r}\right],$$ (B3)

$$=1\cdot \exp \{-{\mu }_a\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid \}\cdot 1,$$ (B4)

and justifies the denominator in Eq. (35).

APPENDIX C: PROOF THAT MODIFIED TERMINAL ESTIMATOR IS UNBIASED

Here, we prove that the modified terminal estimator, defined by Eq. (37), is an unbiased estimator for reflectance. Recall that, for reflectance, the random walk includes a pseudo-collision $P_k^{\left(1\right)}$ at the point of exiting the medium boundary, i.e., the boundary of Γ, after the final true internal collision P_k. Taking the expectation of the estimator produces:

$$\mathrm{E}\left[{\xi }_T\left(\beta \right)\right]=\sum _{\beta }P\left(\beta \right){\xi }_T\left(\beta \right),$$ (C1)

$$=\sum _{k=1}^{\infty }{\int }_{\Gamma }\cdot {\int }_{\Gamma }\frac{S\left(P_1\right)K(P_1\to P_2)}{p^1\left(P_1\right)p(P_1\to P_2)}\cdots \frac{K(P_{k-1}\to P_k)}{p(P_{k-1}\to P_k)}\times \frac{K(P_k\to P_k^{\left(1\right)})}{p(P_k\to P_k^{\left(1\right)})}g\left(P_k^{\left(1\right)}\right)\times p^1\left(P_1\right)p(P_1\to P_2)\cdots p(P_{k-1}\to P_k)p(P_k\to P_k^{\left(1\right)})\times \mathrm{d}{P}_1\mathrm{d}{P}_2\cdots \mathrm{d}{P}_k\mathrm{d}{P}_k^{\left(1\right)},$$ (C2)

$$=\sum _{k=1}^{\infty }{\int }_{\Gamma }\cdots {\int }_{\Gamma }S\left(P_1\right)K(P_1\to P_2)\cdots K(P_{k-1}\to P_k)\times K(P_k\to P_k^{\left(1\right)})g\left(P_k^{\left(1\right)}\right)\mathrm{d}{P}_1\mathrm{d}{P}_2\cdots \mathrm{d}{P}_k\mathrm{d}{P}_k^{\left(1\right)},$$ (C3)

$$={\int }_{\Gamma }\Psi \left(P\right)g\left(P\right)\mathrm{d}P=I,$$ (C4)

where the last step uses Eq. (12). This proves that this estimator is unbiased.