Contributions of Executive Function and Spatial Skills to Preschool Mathematics Achievement

Abstract

Early mathematics achievement is highly predictive of later mathematics performance. Here we investigate the influence of executive function (EF) and spatial skills, two generalizable skills often overlooked in mathematics curricula, on mathematics performance in preschoolers. Children (N = 44) of varying socio-economic status (SES) levels were assessed at age three on a new assessment of spatial skill (Test of Spatial Assembly, TOSA) and a vocabulary measure (the PPVT-4). The same children were tested at age four on the Beery Test of Visual-Motor Integration (VMI), as well as measures of EF, and mathematics. The TOSA was created specifically as an assessment for 3-year-olds, allowing the investigation of links between spatial, EF, and mathematical skills earlier than previously possible. Results of a hierarchical regression indicate that EF and spatial skills predict 70% of the variance in mathematics performance without an explicit math test, EF is an important predictor of math performance as prior research suggested, and spatial skills uniquely predict 27% of the variance in mathematics skills. Additional research is needed to understand if EF is truly malleable and whether EF and spatial skills may be leveraged to support early mathematics skills, especially for lower-SES children who are already falling behind in these skill areas by ages 3 and 4. These findings indicate that both skills are part of an important foundation for mathematics performance and may represent pathways for improving school readiness for mathematics.

Early mathematics achievement is highly predictive of later mathematics skill (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; Duncan et al., 2007; Jordan, Glutting, & Ramineni, 2010; Morgan, Farkas, & Qiong Wu, 2009). However, with a few notable exceptions (Clements & Sarama, 2011; Gunderson, Ramirez, Beilock, & Levine, 2012; Wai, Lubinski, & Benbow, 2009; Webb, Lubinski, & Benbow, 2007), previous investigations of early mathematics skill focus solely on number recognition, cardinality, counting, and number magnitude. Likewise, many mathematics curricula for preschoolers focus exclusively on building these skills. Although they are important (e.g., Jordan, Kaplan, Ramineni, & Locuniak, 2009), a growing body of research demonstrates that other abilities, not traditionally viewed as “mathematics skills,” such as spatial (Grissmer et al., 2013; Gunderson et al., 2012; Verdine et al., in press) and executive function skills (Blair & Razza, 2007; Clark, Pritchard, & Woodward, 2010; Espy et al., 2004; Geary, 2005; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Geary, Hoard, Nugent, & Byrd-Craven, 2008; Kroesbergen, Van Luit, Van Lieshout, Van Loosbroek, & Van de Rijt, 2009; Monette, Bigras, & Guay, 2011), make significant contributions to young learners overall mathematics performance. Just how these skills together are related to mathematical achievement is not entirely clear, especially the extent to which spatial skills influence mathematics performance once you take into account that some executive function (EF) skills are required to successfully complete most mathematics and spatial tests. Here we focus on evaluating the contribution that EF and spatial skills make to the prediction of mathematics skill in preschoolers of diverse social class.

Executive Function and Mathematics

Executive function refers to higher-order cognitive abilities used in planning, information processing, and problem solving for goal-directed behaviors in novel or challenging settings (Beck, Schaefer, Pang, & Carlson, 2011; Bierman, Nix, Greenberg, Blair, & Domitrovich, 2008; Blair, 2010). Components of EF which may be important in mathematics include set-shifting, inhibition, cognitive flexibility, working memory, planning, and updating (Blair & Razza, 2007; Herbers et al., 2011; Miyake, 2000). Rather than enter the theoretical debate about which specific skills constitute EF and can be isolated from one another, here we opted to assess two areas of EF with established histories. Although not a complete list of EF skills, these generally agreed upon components of EF –inhibition and cognitive flexibility– would appear to have applications in the mathematical domain.

Children from low-SES backgrounds often perform below their middle-income peers on measures of EF (Blair, 2010) and the relationship between EF and early mathematics performance appears to be influenced, at least in part, by experiential factors associated with SES (Aunola et al., 2004; Diamond, 2011; Riggs, Jahromi, Razza, Dillworth-Bart, & Mueller, 2006). Some research suggests that these skills can be improved with targeted intervention (Barnett et al., 2008; Bierman et al., 2008; Diamond, Barnett, Thomas, & Munro, 2007) and adaptive training (Holmes, Gathercole, & Dunning, 2009), but positive effects are not always found (e.g., Farran, Wilson, Lipsey, & Turner, 2012) and the extent to which effects last or generalize beyond the trained stimuli is hotly debated (Melby-Lervåg & Hulme, 2013; Egeland, Aarlien, & Saunes, 2013). Regardless of the ability to train EF, however, there is little debate over whether these skills are generally useful in academic settings or for mathematics. Regardless, EF skills are only part of a broader skill set that impacts mathematics achievement.

Geometric, Spatial, and Mathematics Skills

Clements and Sarama (2011) posit that, at its core, mathematics involves spatial thinking. That is, spatial skills support the process of representing, analyzing, and drawing inferences from relations between objects. This definition, and the spatial assessments used in this research, are intended to capture a broad range of related skills including those used for specific manipulations of spatial information (e.g., mental rotation) and likely captures other spatial skills which support spatial thinking more broadly (e.g., visuospatial working memory; Alloway, Gathercole, & Pickering, 2006). Research supports a strong association between spatial and mathematics skills (Ansari et al., 2003; Geary & Burlingham-Dubree, 1989; Gunderson et al., 2012; Mix & Cheng, 2012). Likewise, spatial skills are important for school readiness in mathematics (Common Core State Standards Initiative, 2010) and a number of organizations now suggest that children be introduced to spatial and geometric concepts in preschool (e.g., NCTM, 2006).

A major motivation for building these skills early is that geometric and spatial skills appear to serve as a necessary foundation for some aspects of mathematical learning (Mix & Cheng, 2012). In fact, new research suggests that spatial skills contribute to children’s learning of the number line, specifically, their ability to array numerals on the line based on relative quantity (Gunderson et al., 2012). Having a mental representation of the number line is closely related to a child’s general number knowledge performance. For example, to apprehend that numbers farther down the number line are bigger than those at the beginning, children have to spatially represent this ordering of numbers and the quantities associated with each number. Those children who develop mental representations earlier can build on this knowledge base to learn other mathematical concepts (Mix & Cheng, 2012).

While Gunderson and colleagues analyzed the relationship between spatial skills and linearity, a study by Verdine and colleagues (2012; in press) found a relationship between skill at replicating 2-D geometric puzzles and block constructions and later mathematics skills. Success on such activities may require conceptual understanding of part/whole relationships, units, and counting, all likely important for understanding analogous relationships in mathematics problem solving tasks. For example, the block constructions used block units of varying lengths that could be counted and placed according to the pips that held them together. And replicating a design requires part/whole understanding. While these examples suggest a few additional ways spatial skills may promote understanding of foundational mathematics principles, limited research has analyzed these associations longitudinally and in young children (Mix & Cheng, 2012). However, unlike EF, there appears to be relatively little debate that spatial skills are malleable under various circumstances (Uttal et al., 2013).

The Present Study

This study sought primarily to: 1) determine the contribution of spatial skills and EF to early mathematics achievement and 2) assess the unique contribution of spatial skills over and above EF when predicting early mathematics performance, while also 3) characterizing the influence of the level of mothers’ education on early spatial, EF, and mathematics skills. It was of particular importance to test whether spatial skill offered any additional benefits over and above those delivered by EF because the relationship between EF and mathematics is so strong that this association may eclipse the contributions of spatial skills to mathematics performance. Further, many spatial tasks require EF skills to achieve success. Therefore, removing variance explained by executive function from predictions linking spatial skills to mathematics will help clarify the extent to which the link between these skills is related to other factors.

Although research has explored the relationship between EF and mathematics in preschool (e.g., Clark et al., 2010), no previous work has considered how the contribution of spatial skills influences this dynamic, possibly because most spatial assessments start at age 4. To assess spatial skills in 3-year-olds, the Test of Spatial Assembly (TOSA; Farmer et al., 2013; Verdine et al., in press) was used. The TOSA is a non-verbal task intended to minimize the influence of language skills, thereby reducing the influence of a variable known to be related to SES (Hart & Risley, 2003). Children were also given two measures of EF (cognitive flexibility and inhibition), a spatial task, and a test of mathematical skill at age four. This line-up of tasks afforded a look at the link between spatial skill at age 3 and mathematics skills one year later, prior to ages investigated in existing research. Further, we investigated the influence of EF and vocabulary on this relationship, allowing us to assess the unique contribution of very early spatial skills to later mathematical skills.

Methods

Participants

Participants were recruited from preschool and Head Start facilities in two northeastern states. Forty-four children (22 girls, 22 boys) were assessed at two time-points: an initial assessment in Year 1 between the ages of 38-48 months (M = 43.5; SD = 2.37), and in Year 2 between 52-62 months (M = 57.1; SD = 2.54). All children were native English speakers. Participants were recruited to capture varied socio-economic status (SES) backgrounds helping to ensure a representative sample that captured the breadth of children’s skills in the tested domains.

Procedures

Children were tested individually in a quiet room seated across the table from an experimenter. Measures were administered in a random order during three or four sessions lasting approximately 30 minutes, adjusted to accommodate children’s engagement. Age three assessments included the TOSA and the Peabody Picture Vocabulary Test (PPVT). Age four assessments included the Flexible Item Selection Task (FIST), the Tap Test, the Beery Test of Visual-Motor Integration (VMI), and the Wechsler Individual Achievement Test (WIAT): Math Problem Solving subtest.

Measures

Gender and Socio-economic status (SES)

In the reported analyses, males were coded as 1 and females as 0. The highest level of education achieved by each mother whose child participated was reported via a short questionnaire and coded on a 5-point scale ranging from some HS to a graduate degree (see Table 1). This variable was used for the SES variable in the regression analyses. Mothers’ education level was further coded to create SES groups (Hoff, 2013), allowing analysis by t-test, with those obtaining a bachelors or graduate degree in the higher-SES category (lower-SES = 20; higher-SES = 24). In one case this information was not reported and the child was placed in the lower-SES group because they attended a Head Start.

Table 1.

Demographics characteristics of the sample

		Gender		Mothers’ Highest Level of Education*
	N	Male	Female	Some High School	High School Diploma or GED	Trade School	Bachelor’s Degree	Graduate Degree
Lower- SES	20	10	10	3	11	5	0	0
Higher- SES	24	12	12	0	0	0	8	16
Total	44	22	22	3	11	5	8	16

^*The parent of one participant who was enrolled in a Head Start did not report their education level and was characterized as a lower-SES participant, but was not included in these data columns.

Test of Spatial Assembly (TOSA)

The TOSA is a spatial assembly task, comprised of two-dimensional and three-dimensional trials, which was used to assess early geometric and spatial reasoning. This measure was chosen because few appropriate spatial tasks exist for 3-year-old children. The WISC Block Design subtest, for example, is a popular test but 3-year-olds pass only a limited number of items, which reduces the variability in scores dramatically. Having a longer and more varied test, including both 2-D and 3-D trials, was expected to produce more overall variability for the sample and yet more stable results for individuals, especially important when assessing such young children.

The 2-D trials of the TOSA require participants to recreate a picture of a design using foam cut-outs of geometric shapes. The 3-D trials required children to recreate a model made of colored plastic Mega Blocks® using a matching set of blocks. Each test included six test trials for a total of twelve (see Figures 1 and 2 for the test items). Because the scores for each portion of the test are on a different scale, overall TOSA scores were generated by calculating z-scores for the 2-D and 3-D trials (scoring procedures below) and averaging them. Performance on the TOSA requires problem solving that taps a variety of spatial skills such as orienting objects properly, composing individual objects into a group (i.e., part/whole), and determining the location of objects relative to one another (i.e., behind, above, underneath). Cronbach’s alpha was .802 for all trials that made up the TOSA. This was calculated based on the total scores for each test trial prior to adding the trials together and z-scoring each portion of the test.

Figure 1.

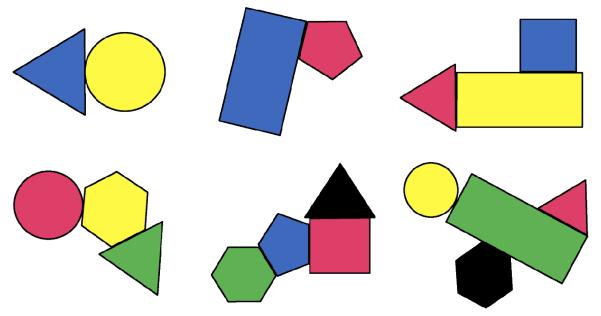
2-D TOSA Target Models. Each item was an image affixed to the top of a white board and children had to copy the model using matching foam shapes that were magnetized.

Figure 2.

3-D TOSA Target Models. Each item was made of blocks ranging in length from one unit (2 pips × 2 pips; pips are the knobs which lock the pieces together; measuring 32 mm long × 32 mm in width × 24 mm in height) to three units (2 pips × 6 pips; 32 × 96 × 24). Items 1 and 2 (top left) were at ceiling and not included in the total score for the 3-D portion of the test.

2-D trial procedure

Each stimulus was a picture of the target design on a laminated 9.53 cm x 6.67 cm card affixed to the top of a magnetic white board (21.59 cm x 27.94 cm). Accompanying each board were two to four magnetized and colored foam shape pieces approximately three mm thick, matching those depicted in each picture. The foam shapes ranged in size from 2.22 cm to 4.76 cm (M = 3.15 cm in length). A black line was drawn across the magnetic boards below the design picture to create a working space and the foam shapes were arranged randomly at the bottom of that space.

Trial order was fixed starting with the training trial and proceeding as in Figure 1. For the practice trial, the experimenter pointed to the shape pieces and indicated that they were “going to try to make my pieces look just like this [pointing to picture of stimulus design].” They then placed the pieces in a way that did not match the picture. After confirming twice that the child could identify a non-matching design, the experimenter then placed the shapes in the correct formation, and corroborated the match with the child. The experimenter then reset the pieces to the bottom of the board and instructed the participant to “make [his or her] pieces look just like the picture.” All participants correctly performed the task on the first try.

For the six test trials the experimenter presented the child with each target configuration and set of pieces (organized randomly) and asked the child to “make your pieces look just like this.” Target designs were always visible throughout their respective trials and no feedback was given. The task was untimed, and the participant indicated completion of each design. If the child stopped working, the experimenter would ask if they were done and either proceed to the next design or allow more time. After the test the experimenter took photographs of the constructions for later coding by trained researchers, including independent coding for reliability.

2-D trial scoring

The coding system results in an overall score for 2-D spatial assembly skill. Each component piece in a design was scored except for the base piece because it was used as a reference piece. The base piece was either the largest of all component pieces, the piece connected to the greatest number of component pieces, or both. For item 1, the triangle was assigned as the base since the component pieces are equally sized. Each component piece was scored on each of the following three dimensions:

1) Adjacent pieces

If a component piece was placed next to its correct neighboring piece (within 1 cm) a point was awarded. This dimension was not scored for Designs 1 and 2 because there were only two pieces in each design.

2) Horizontal and vertical direction

Could children correctly place the component pieces either above or below or to the left or the right of the base piece? An x, y axis drawn on a transparency was placed over the center of the base piece and aligned with the sides of the whiteboard. Each component piece received a score of 1 if at least 50% of its volume was within the same quadrant as its correct location in the target model.

3) Relative position

Using a transparent overlay with outlines showing the correct locations of the pieces, coders tried arranging the overlay in every possible rotation for which the base piece could be matched. They penciled in a total point value for each possible rotation, awarding 1 point for each component shape that was within 1 cm of the correct location indicated by the overlay. The orientation of the overlay that yielded the most points provided the final score for relative position.

Points from the coding dimensions for each component piece were summed (total possible = 35) and z-scored for each participant. To ensure inter-rater reliability, 20% of the participants were scored by more than one coder, with coders matching on 96% of the data points.

3-D trial procedure (following Verdine et al., in press)

The 3-D trials were identical to the 2-D trials except that: a) they involved constructions using Mega Blocks® (see Figure 2); and b) the models were glued together constructions rather than a drawing. Differences between the tasks permitted us to assess a wider range of spatial skills. For example, the 2-D trials have a clearly delineated orientation, allowing us to assess the spatial orientation of participants’ copies. Likewise, the 2-D trials do not feature component pieces that overlap or models with vertical levels like the 3-D trials, creating more complex inter-piece relationships and the possibility of both vertical and horizontal translational errors. Also, 2-D trials do not require children to make use of pips on the surface of the blocks that may invoke counting. Coding for the 3-D trials, like for 2-D trials, was done using photographs of each construction taken after the testing sessions.

3-D trial scoring

Test constructions were each given an overall score based on two coding steps. The first step rated accuracy relative to a central piece in the design (i.e., the base -the biggest piece or the piece that had the most other pieces attached). A point for vertical location was awarded if a component block was on the correct level of the design compared with the base. Rotation was scored by determining if a piece’s axis was oriented correctly with respect to the long axis of the base piece (parallel or perpendicular to it). If, for example, the long axes of the component and base pieces were perpendicular in the model and children copied this orientation, they received a point. A translation point was awarded if a component piece was placed over the correct pips in relation to the base piece. Reliability coding for the first scoring step was done for 20% of the sample with 96% agreement.

The second scoring step focused on the more complex constructions with multiple component pieces (designs 3-6), giving credit for maintaining accuracy on the relationships between pairs of component pieces, as opposed to component pieces in relation to the base piece in the previous step. Component pieces were coded in pairs, or dyads, ignoring the base piece. Designs 3 and 4 each contained 1 dyad, design 5 contained 2 dyads, and design 6, 3 dyads. The larger of the two pieces from each dyad was designated as the ground piece and this was used as the reference piece rather than the base. Percent agreement was 97%. Scores for both 3-D coding steps from items 3-6 were added together (total possible = 41) and z-scored to create scores for the 3-D trials, which were then averaged with 2-D trial z-scores.

Peabody Picture Vocabulary Test (PPVT)

The PPVT is a flipbook-style standardized test of vocabulary knowledge in which children select a picture displaying a target word, said aloud by an experimenter, out of four options displayed on a page (Dunn & Dunn, 2007). Testing on the PPVT followed the standardized procedures in the manual. The PPVT is included as a measure to control for the extent to which language ability is a driving force behind the expected relations between spatial, EF, and mathematical abilities. It was not expected that the PPVT would be a strong predictor of mathematics once the other variables were included in the models. Only the TOSA and the PPVT were given at age 3; the rest of the measures were given to the same children at age 4. The mean percentile score for the PPVT, the only complete standardized test given, was 71.9 with a standard deviation of 27.1 percentile points (see Table 2). This indicates that the sample scored above average compared to the norming sample as a group. The sample also had quite a lot of variability, as would be expected from a mixed-SES sample.

Table 2.

Descriptive statistics for the measures used in both years of the study

		Mean	Std. Dev.	Max	Min	Percentiles
						75th	50th	25th
Year 1 – Age 3	TOSA	0.12	1.01	2.49	−1.69	0.66	0.16	−0.59
	PPVT Raw	71.50	20.29	131.00	35.00	84.25	70.50	57.00
	PPVT Percentile	71.89	27.09	99.90	16.00	95.25	78.00	53.75
Year 2 – Age 4	FIST	24.70	3.96	30.00	14.00	28.00	25.00	22.00
	Tap Test	11.82	4.68	16.00	0.00	15.75	13.00	10.00
	VMI	11.23	3.09	20.00	1.00	13.00	11.00	9.25
	WIAT	19.09	5.21	30.00	9.00	23.75	18.00	15.25

Notes: TOSA = Test of Spatial Assembly (average of z-scores from 2-D and 3-D portions of the test); PPVT = Peabody Picture Vocabulary Test; FIST = Flexible Item Selection Task; VMI = Beery Test of Visual-Motor Integration; WIAT = Wechsler Individual Achievement Test– Math Problem Solving subtest.

Beery Test of Visual-Motor Integration (VMI)

Testing followed the administration manual and consists of increasingly difficult forms that children are asked to draw. Children earn 1 point for each form they complete correctly with the sum of points used as the score for the test. Testing is stopped after three consecutive incorrect drawings. The VMI measures children’s skill in accurately perceiving and copying simple forms by drawing them. As the name suggests, it is a measure of participants’ ability to integrate their visual-spatial and motor abilities. Previous studies suggest that similar tasks relate strongly to early mathematics skills (Cameron et al., 2012; Sortor & Kulp, 2003) and this measure was included as a way to further investigate how figure copying tasks relate to mathematics and other spatial skills in young children.

Executive function

In the Tap Test (Diamond & Taylor, 1996), children are told to tap twice with a wooden dowel when the experimenter taps once, but to tap once when the experimenter taps twice. This task assesses children’s inhibitory control by requiring them to respond differently than the experimenter, while simultaneously remembering the correct response in the face of an opposing stimulus. Children are given two practice trials followed by 16 test trials with 8 one-tap and 8 two-tap trials (Diamond & Taylor, 1996) for a total possible score of 16.

To assess the role of cognitive flexibility in EF, the Flexible Item Selection Task (FIST; Jacques & Zelazo, 2001) was used. Children are presented with pictures of three items that vary by two or three dimensions (i.e., shape, size, color). In the pretest, children are given a demonstration trial and then two practice trials where they are asked to identify two objects that are alike in one way (e.g., color) and two objects that are alike in another way (e.g., size). After practice they are given 15 test trials with points awarded for each set of objects they correctly pair (total possible = 30).

Early mathematics knowledge

Early mathematics skill was assessed at age four using the Math Problem Solving subtest from the Wechsler Individual Achievement Test–third edition (WIAT; Wechsler, 2009). The WIAT Math Problem Solving subtest consists of 72 items and was administered as stated in the testing manual. Testing began with item one and continued until four consecutive test items were answered wrong. Children in the 75^th percentile answered a mean of 23.75 questions correctly on the WIAT. Test items 1 through 23 can be characterized as assessing overall number knowledge skills including counting, number identification, number magnitude, as well as children’s understanding of number words such as “more, “less”, “equal”, “second”. For example, one item had participants point to the picture with the “most” balloons while 4 pictures of hands holding balloons were displayed. Another item had children count the number of red wagons on a page. The Math Problem Solving subtest has an internal reliability of .93 for preschoolers.

Results

See Table 2 for descriptive statistics on all measures. No gender differences were found in preliminary analyses and all reported analyses collapse across gender. Independent samples t-tests comparing SES groups were conducted on the WIAT, FIST, Tap Test, VMI, TOSA, PPVT raw scores, and PPVT percentile scores to address our third aim of characterizing the influence of SES on early spatial, EF, and mathematical skills. Children in the higher-SES group demonstrated significantly better performance on all the measures except the Tap Test (see Table 3), which had a similar trend (p = .056). PPVT percentile scores are presented in Tables 2 and 3 for easy comparison to an external sample. PPVT raw scores are used for the remainder of the analyses because scores for the other tests were not standardized. The choice of score type for the PPVT had little effect on the outcome of these analyses.

Table 3.

Results of t-tests comparing performance from lower-SES children to higher-SES children

	Higher SES		Lower SES
Variable	M	SD	M	SD	t	p	Effect Size*
WIAT: Math Problem Solving	22.29	4.29	15.25	3.26	6.03	<.001	1.79
Flexible Item Selection Task	26.13	3.58	23.00	3.78	2.81	.007	0.84
Tap Test	13.04	4.22	10.35	4.88	1.96	.056	0.58
Beery Test of Visual- Motor Integration	12.63	2.65	9.55	2.76	3.76	.001	1.12
Test of Spatial Assembly	0.71	0.91	−0.59	0.59	5.52	<.001	1.63
PPVT Raw Scores	82.09	16.05	58.68	17.49	4.52	<.001	1.36
PPVT Percentile Scores	88.55	9.65	51.72	27.81	5.51	<.001	1.81

Notes: WIAT = Wechsler Individual Achievement Test; PPVT = Peabody Picture Vocabulary Test.

^*Effect sizes calculated using Hedges g.

Bivariate correlations were analyzed between predictive variables and the dependent variable (WIAT) showing positive, sizeable correlations with the EF (FIST r = .60; p <.001; Tap Test r = .58, p <.001) and spatial measures (VMI r = .67, p <.001; TOSA r = .71, p <.001). See Table 4 for the full matrix. Partial correlations between the WIAT and each of the spatial and EF independent variables (TOSA, VMI, Tap Test, and FIST), controlling for the other three independent variables, continued to show positive, mid-level correlations for the TOSA (r = .43; p = .005), VMI (r = .43; p = .005), and Tap Test (r = .40; p = .010) and a marginal correlation for the FIST (r = .27; p = .093).

Table 4.

Correlations between measures taken in both years of the study

Variable	1	2	3	4	5	6	7	8
1. WIAT: Math  Problem Solving	--
2. Flexible Item  Selection Task	.601***	--
3. Tap Test	.577***	.511***	--
4. Beery Test of Visual-  Motor Integration	.673***	.286	.343*	--
5. Test of Spatial  Assembly	.714***	.526***	.289	.597***	--
6. PPVT Raw Scores	.654***	.437**	.415**	.659***	.444**	--
7. Socio-economic  Status	.699***	.482**	.356*	.473**	.635***	.545***	--
8. Gender	−.141	.076	−.147	−.074	.021	−.191	.008	--

Notes: WIAT = Wechsler Individual Achievement Test; PPVT = Peabody Picture Vocabulary Test.

^*p < .05;

^**p < .01;

^***p < .001

Regression analyses were conducted to determine the contribution of spatial skills and EF to early mathematics performance as well as exploring the extent to which spatial skills predict early mathematics achievement over and above EF alone. In preliminary models, age at testing in the first year when children were 3 and the time between testing sessions, were entered as the initial predictors with the PPVT and mothers’ education. However, these age variables were removed because, by design, they had low variability (age at year 1 testing: M = 43.52 months, SD = 2.33; time between testing: M = 13.6, SD = 1.17) and were not significant predictors.

PPVT raw scores were entered in the first step of our initial model to remove the variability associated with vocabulary skill. Mothers’ education, our measure of SES, was also included in the first step because SES is a variable that is traditionally controlled for in studies for which it is an independent variable. However, due to the expected inter-relationships between some of the independent variables, including SES likely represent an example of over-controlling (see Newcombe, 2003). There is strong evidence that many SES effects are linked to experiential factors (Burchinal, Nelson, Carlson, & Brooks-Gunn, 2008; Hart & Risley, 2003). Thus, SES should explain much of the variability in mathematics skills including the portion of variance in mathematics skills that are explained by spatial skills and including it in the regressions may significantly underestimate the extent to which spatial skills influence mathematical performance. Nonetheless, the initial model we report does contain mothers’ education, but it is removed from the subsequent regressions.

Following the theoretical basis for our analysis, the FIST and Tap Test were entered in step 2 and the VMI and TOSA in step 3 of the initial regression (see Table 5). In the overall model, when the other variables are entered, SES was a significant predictor (std. = 0.276, t = 2.45, p = .020) but the PPVT was not (std. = 0.137, t = 1.23, p = .226). This first step accounted for 61% of the variability in mathematics skills (adj. R² = 0.612, F(2, 38) = 32.57, p = <.001). The Tap Test was a significant predictor in the overall model (std. = 0.234, t = 2.37, p = .023), but contrary to our expectations the FIST was not (std. = 0.013, t = 0.11, p = .912). The TOSA was a significant predictor in the final model (std. = 0.284, t = 2.40, p = .022) and the VMI was a marginal predictor (std. = 0.216, t = 1.84, p = .075). Overall this initial model accounts for about 76% of the variability in age 4 mathematics scores (adj. R² = .762, F(6, 34) = 22.33, p = <.001), with the EF measures entered in step 2 accounting for 6.5% of the variability in mathematics scores after entry of the PPVT and mothers’ education ( adj. R² = .065, F(2, 36) = 4.83, p = .014), and with spatial skills (the TOSA and VMI) uniquely accounting for 8.5% of the variability after all other variables were entered ( adj. R² = .085, F(2, 34) = 7.40, p = .002).

Table 5.

Results of hierarchical multiple regression models for predicting scores on the Math Problem Solving subtest of the WIAT

		Unstandardized Coefficients		Standardized Coefficients
Model 1 (Initial)	Variable	β	SE	β	t	p	Partial r	F	df	sig.† ΔF	adj. R2	Δ adj. R2
	Constant	4.467	3.983		1.122	.270
Step 1								32.57*	2, 38	<.001	.612	.612
	PPVT	0.036	0.029	0.137	1.233	.226	.207
	SES††	1.039	0.425	0.276	2.448	.020	.387
Step 2								21.98*	4, 36	.014	.677	.065
	FIST	0.017	0.157	0.013	0.111	.912	.019
	Tap Test	0.256	0.108	0.234	2.374	.023	.377
Step 3								22.33*	6, 34	.002	.762	.085
	VMI	0.422	0.230	0.216	1.837	.075	.301
	TOSA	1.546	0.644	0.284	2.401	.022	.381
Model 2
	Constant	3.503	4.144		0.85	.404
Step 1								29.88*	1, 40	<.001	.413	.413
	PPVT	0.050	0.030	0.193	1.69	.100	.270
Step 2								19.45*	3, 38	.001	.575	.162
	FIST	0.142	0.157	0.105	0.90	.372	.149
	Tap Test	0.258	0.115	0.235	2.24	.031	.350
Step 3								22.47*	5, 36	<.001	.724	.149
	VMI	0.465	0.244	0.239	1.91	.064	.303
	TOSA	1.889	0.602	0.360	3.14	.003	.464
Model 3 (Final)
	Constant	3.11	3.88	-	.802	.427	-
Step 1								17.41*	2, 41	<.001	.433	.433
	FIST	0.249	0.145	0.189	1.72	.093	.266
	Tap Test	0.301	0.112	0.270	2.70	.010	.397
Step 2								26.61*	4, 39	<.001	.704	.271
	VMI	0.539	0.181	0.320	2.98	.005	.430
	TOSA	1.779	0.605	0.346	2.94	.005	.426

^*Notes: F value significant at p<.001 level.

^†“sig ΔF” is the p-value of the change in F for a given step of the regression.

^††the SES variable used is mothers’ education level

To understand the influence of the PPVT on the other steps of the regression and determine if PPVT is a significant predictor in the final model if mothers’ education was removed we performed a second regression, identical to the first, except only PPVT was entered in the first step. In this overall model, the PPVT was again not a significant predictor (std. = 0.193, t = 1.69, p = .100), although when entered alone in the first step it accounts for 41% of the variability in mathematics skills (adj. R² = 0.413, F(1, 40) = 29.88, p = <.001). The Tap Test was a significant predictor in the overall model (std. = 0.235, t = 2.24, p = .031), but again the FIST was not (std. = 0.105, t = 0.90, p = .372). The TOSA was the strongest predictor (std. = 0.360, t = 3.14, p = .003) and the VMI was a marginal predictor (std. = 0.239, t = 1.91, p = .064). Overall this initial model accounts for about 72% of the variability in age 4 mathematics scores (adj. R² = .724, F(5, 36) = 22.47, p = <.001), with the EF measures entered in step 2 accounting for 16% of the variability in mathematics scores after entry of the PPVT ( adj. R² = .162, F(2, 38) = 8.58, p = .001), and with spatial skills (the TOSA and VMI) uniquely accounting for about 15% of the variability after all other variables were entered ( adj. R² = .149, F(2, 36) = 11.25 p = <.001). To understand the influence of the PPVT on the other steps of the regression, and because it was not a significant predictor in this overall model, we removed the PPVT from the final model reported below. This removal also makes the final model more parsimonious and reduces the potential for overfitting the data, making the model more likely to replicate in future research.

In the final model (Table 5), the FIST and Tap Test were added in the first step of the regression. These variables significantly accounted for 43% of the variance in total WIAT raw scores (adj. R² = .433, F(2, 41) =17.41, p = <.001). Again, the Tap Test (std. = .270, t = 2.70, p = .010) was a significant predictor in the overall model, but the FIST was still not (std. = .189, t = 1.72, p = .093) despite a larger standardized beta weight than the preliminary model and a p-value closer to statistical significance. To determine the unique contribution of spatial skills, the TOSA and VMI scores were then entered in the second step of the regression, and significantly added to the variance accounted for on the WIAT ( adj. R² = .271, F(2, 39) = 19.82, p = <.001), with the overall model accounting for 70% of the variance in age 4 mathematics scores. The TOSA remained a strong predictor (std. = .346, t = 2.94, p = .005). However, it is interesting to note that in this model, which did not remove variability explained by the PPVT, the standardized beta weight for the VMI becomes much larger (std. = .320, t = 2.98, p = .005), increasing by 0.104 in comparison to the initial model. This effect is likely due to the large correlation between the VMI and the PPVT, an indication that the VMI is also tapping verbal ability or has a relatively strong association with general intelligence compared to the TOSA. As the last step was significant in both the initial and final models, we reject the null hypothesis that spatial skills do not predict early mathematics achievement over and above EF alone.

Discussion

The present study investigated the contributions of EF and spatial knowledge to children’s early mathematics performance. Despite the fact that mathematics curricula for young children have narrowed their focus to children’s knowledge of number and number operations (Clements & Sarama, 2011), hints in the literature suggested that both EF (Espy et al., 2004; Mazzocco & Kover, 2007) and spatial skill (Ansari et al., 2003; Rasmussen & Bisanz, 2005) might play a foundational role in children’s success in the mathematics arena. A significant relationship between EF and children’s early mathematics skills was found, consistent with previous research (Blair & Razza, 2007; Bull & Espy, 2006; Bull, Espy, & Wiebe, 2008; Kroesbergen, Van de Rijt, & Van Luit, 2007). Thus, our sample and measures are appropriate to test the unique relationship between spatial skills and mathematics.

To further evaluate the relationship between spatial skills and mathematics, we explored children’s performance using a new spatial task designed to assess their skill in copying models of 2- and 3-dimensional structures (Verdine et al., 2012; in press). The partial correlations between spatial skills and mathematics (TOSA r = .43; VMI r = .43, p’s < .01) indicate that, even when effects of other variables are removed, spatial skills are an important predictor of general mathematics performance. The reported hierarchical regression models result in similar conclusions, with EF and spatial skills in the final model accounting for over 70% of the variance in children’s early mathematics performance without the use of an overt number knowledge measure. It is also important to note the large unique contribution of spatial skills, which explained 27.1% of the variability in mathematics performance after EF was added to the model and 14.9% even in the second model that also included the PPVT. The most conservative interpretation that controls for both PPVT and SES, which we have argued over-controls the model, still shows that the spatial measures uniquely explain 8.5% of the variability in mathematics. Also of note is that the TOSA, despite being given a year prior to the VMI, is as strong a spatial predictor of mathematics as the VMI which was given contemporaneously with the WIAT. Previous research had not investigated the combined contribution of these skills to preschoolers’ mathematics performance and whether spatial skills offer anything beyond EF in predicting mathematics performance. The strong association between spatial skill and overall mathematics performance, spanning a year’s time, indicates an important role for spatial skills in mathematics achievement beyond other generalizable skills like vocabulary and EF.

Recent research demonstrates that early spatial skills are malleable (Levine, Ratliff, Huttenlocher, & Cannon, 2012; Pruden, Levine, & Huttenlocher, 2011; Uttal et al., 2013). A study by Grissmer and colleagues (2013) tested EF and motor skill performance in kindergarteners (ages 4 and 5). Their results were similar to these: children with higher EF and motor skills also showed stronger overall performance in areas of reading and mathematics. The assessment of “motor skills” was conducted using a series of building and drawing tasks. While these tasks do tap a child’s motor capabilities, the act of building a bridge with blocks also necessitates shape sensitivity and spatial knowledge. Figure copying tasks, similar to the Beery Test of Visual-Motor Integration (VMI) that we also used, require both visual-spatial skills and motor coordination. Therefore, what Grissmer and colleagues typify primarily as “motor skills”, also rely on a significant amount of what we refer to here as “spatial skills.” More research will be needed to definitively determine the specific skills that drive the relationship between figure-copying tasks and mathematics, but prior investigations with older children (Sortor & Kulp, 2003) suggest that it is not the motor component that is of primary importance.

While the results of the present study indicate that skills beyond standard number knowledge are associated with stronger mathematics achievement, many preschool programs do not provide any instruction targeting the development of spatial or EF skills. In fact, more often, early mathematics instruction focuses exclusively on mathematics-specific skills like number knowledge (Clements & Sarama, 2011). However, our findings suggest that time spent practicing overlooked skills like EF and spatial skills might pay dividends in preparing children to succeed in mathematics.

The SES differences reported here, with lower-SES children already falling behind in spatial skills by age 3 and EF skills by age 4, suggests a need to implement preschool training in these skill areas, particularly for disadvantaged youth. However, for instruction in these skills to be adopted within the classroom, research must firmly establish whether these skills are malleable (up for debate with regard to EF) and teachers must be given training and afforded the instructional time necessary. This, in turn, requires stakeholders to recognize that as long as standardized tests, which assess only subject-specific knowledge, drive classroom instruction, generalizable skills like EF and spatial knowledge are unlikely to hold a position of priority.

Limitations

One limitation of this study is the relatively small sample size, precluding a more in depth look at individual differences within the sample. However, this limitation is at least partially offset by a strength of this study, which is that the sample is from a varied SES background and likely more representative of the overall population. Future research should focus on the specific mechanisms by which SES influences the relationship between early spatial, EF, and mathematics skills in an effort to determine the most promising means for intervention.

Conclusion

As teachers and researchers better understand the long-term outcomes associated with mathematics achievement in school and opportunities in STEM fields (science, technology, engineering, and mathematics), appreciation of the importance of high-quality mathematics instruction for younger students increases (Lubinski, 2010). For those young students who struggle with mathematics early in schooling, providing appropriate supports is crucial for preventing a cycle of failure. Without strategic intervention, students are unlikely to “catch up” to their peers and more likely to continue to miss opportunities to learn key skills because of weak foundational knowledge (Jordan et al., 2009). Nevertheless, it is also important to remember that mathematics knowledge is more than a single set of skills and includes more than the obvious elements of number knowledge. Because spatial skills can be altered (Uttal et al., 2013), and our data show a relationship between spatial and mathematics skills, it may be possible to improve mathematical skills by enhancing spatial and geometric skills. This conclusion receives support from research showing mathematics improvements in kindergartners from interventions using spatial activities (Grissmer et al., 2013). When we acknowledge the interrelated and interdependent nature of learning (Diamond, 2007), it appears that it is the combination of generalizable skills like EF and spatial skills with mathematics-specific skills that impact children’s ability to solve mathematical problems.

Highlights.

• Assessed preschool spatial ability, executive function (EF), vocabulary, and math.

• Generalizable spatial and EF skills play an important role in math ability.

• EF skills predicted 43% of the variance in math scores.

• Spatial skills account for an additional 27% of the variability in math scores.

• Early math instruction should focus on foundational skills beyond number knowledge.