Quantifying Cardiometabolic Risk Using Modifiable Non–Self-Reported Risk Factors

Abstract

Background

Sensitive general cardiometabolic risk assessment tools of modifiable risk factors would be helpful and practical in a range of primary prevention interventions or for preventive health maintenance.

Purpose

To develop and validate a cumulative general cardiometabolic risk score that focuses on non–self-reported modifiable risk factors such as glycosylated hemoglobin (HbA1c) and BMI so as to be sensitive to small changes across a span of major modifiable risk factors, which may not individually cross clinical cut off points for risk categories.

Methods

We prospectively followed 2,359 cardiovascular disease (CVD)-free subjects from the Framingham offspring cohort over a 14–year follow-up. Baseline (fifth offspring examination cycle) included HbA1c and cholesterol measurements. Gender–specific Cox proportional hazards models were considered to evaluate the effects of non–self-reported modifiable risk factors (blood pressure, total cholesterol, high–density lipoprotein cholesterol, smoking, BMI, and HbA1c) on general CVD risk. We constructed 10–year general cardiometabolic risk score functions and evaluated its predictive performance in 2012–2013.

Results

HbA1c was significantly related to general CVD risk. The proposed cardiometabolic general CVD risk model showed good predictive performance as determined by cross-validated discrimination (male C-index=0.703, 95% CI=0.668, 0.734; female C-index=0.762, 95% CI=0.726, 0.801) and calibration (lack-of-fit χ²=9.05 [p=0.338] and 12.54 [p=0.128] for men and women, respectively).

Conclusions

This study presents a risk factor algorithm that provides a convenient and informative way to quantify cardiometabolic risk based on modifiable risk factors that can motivate an individual’s commitment to prevention and intervention.

Introduction

Cardiovascular disease (CVD), accounting for more than one third of total deaths in the U.S.,¹ has constantly necessitated the development of powerful predictive models for the “modifiable” probability of future CVD events, especially with cardiovascular prevention strategies rapidly shifting toward modifiable behavioral interventions, such as direct interventions modifying diet or exercise to reduce risk.² Related but slightly varying Framingham CVD risk score models assign weights to major CVD risk factors such as age, gender, total cholesterol, low–density lipoprotein (LDL) cholesterol, high–density lipoprotein (HDL) cholesterol, smoking status, blood pressure, and diabetes status.^3–8

General assessment of modifiable cardiometabolic risk would be most helpful and practical in a range of primary prevention interventions (e.g., to quantify intervention efficacy) or for preventive health maintenance.^9,10 To address the need for a practical general CVD risk assessment tool, D’Agostino et al.⁶ developed a model (hereafter D’Agostino model) assessing risk of developing any major atherosclerotic CVD event. We added BMI and glycosylated hemoglobin (HbA1c) to extend the function of their model by incorporating variables that can reflect change and relies less on self-reported measures prone to bias in community samples.^11–13

The aim of this study is to develop and evaluate a cumulative general cardiometabolic risk score that focuses on non–self-reported modifiable risk factors such as HbA1c and BMI in order to be sensitive to small changes across a span of modifiable risk factors, which may not individually cross clinical cut off points for risk categories. Recognizing the important role of metabolic function and diabetes in overall cardiometabolic disease development, the proposed risk model includes the evaluation of HbA1c, a time-integrated marker of average blood glucose concentration that is increasingly used for management and screening of diabetes,¹⁴ on general CVD risk prediction. Elevated levels of cardiometabolic biomarkers are associated with increased risk of CVD and premature mortality.^15–18 Additionally, HbA1c is highly associated with the risk of complications compared to single or episodic measures of glucose levels.^19,20

Operationally, the proposed general cardiometabolic risk model will keep continuous risk factor measures as such to maximize their contribution to risk assessment. The rationale is that intervention and behavioral change strategies in community settings may produce small but persistent changes across risk factors, which may yield large population health effects.²¹ In these cases, small changes in the distribution of risk factors can have substantial effects on overall population health patterns.

Methods

Study Population

Study participants were selected from the Framingham offspring study, a community–based prospective study of general CVD risk factors.^22,23 Time to general CVD was defined using standard Framingham heart study criteria for general CVD: diagnosed conditions that fall into coronary heart disease (coronary death, myocardial infarction, coronary insufficiency, and angina), cerebrovascular events (including transient ischemic attack, ischemic stroke, and hemorrhagic stroke), peripheral artery disease (intermittent claudication), and diagnosed heart failure.^24,25 Permission to analyze the Framingham offspring database was obtained from the National Heart, Lung, and Blood Institute according to a research proposal approved by our IRB. Baseline was the fifth examination cycle (January 1991–June 1995), where HbA1c measurements were collected for 2,359 subjects. Participants free of general CVD at baseline with no missing observations on any modifiable risk factors were considered (see Appendix). Participants with diabetes were included if they did not have a general CVD event before baseline. The median follow-up time for a total of 2,359 subjects free of general CVD at baseline was 14.25 years (SD=3.5 years). A total of 342 general CVD events were observed during the follow-up period.

Evaluation of Modifiable Risk Factors

At each exam, Framingham participants underwent a physical examination and BMI was calculated based on standardized measurements of height and weight. Fasting blood samples were also collected from participants during each exam. Ethylenediaminetetraacetic acid (EDTA) plasma from these samples was used to obtain participants’ total and HDL cholesterol levels via the Abell–Kendall technique and the Lipid Research Clinics Program protocol, respectively.^3,26 These samples were also assayed to measure plasma HbA1c, insulin, and lipid levels. Glucose and insulin levels were also measured through use of a 75–g oral glucose tolerance test for participants who were not previously known to have diabetes.^27–29 Systolic and diastolic blood pressure were obtained using the average of two separate readings taken by a physician at least 5 minutes apart.³⁰ Smoking status was defined as smoking cigarettes regularly in the last year before the examination with categories of yes, no, and unknown.

Statistical Analyses

Descriptive statistics for all continuous (mean and SD) and categorical (relative frequencies) study variables were calculated. We evaluated Framingham general CVD risk through gender–specific Cox proportional hazards models.³¹ The covariates included in the gender–specific Cox model include baseline age, BMI, smoking, systolic blood pressure, total cholesterol, HDL cholesterol, and HbA1c. A summary of the similarities and differences between the D’Agostino and proposed risk models is described in Table 1. Diastolic blood pressure was excluded from our model because of its strong collinearity with systolic blood pressure. Model diagnostics, including nonlinearity checks³² and testing of proportional hazards assumptions,³³ were performed to ensure proper functional form of risk factors and validity of the proportional hazard assumptions.

Table 1.

Risk factors of the D’Agostino et al.⁶ and proposed risk scores

D’Agostino risk score	Proposed risk score
Blood pressure	Blood pressure
log(systolic blood pressure), if treated (self-report)	Systolic blood pressure  No self-report
log(systolic blood pressure) if not treated (self-report)
Smoking in previous year (yes/no)	Smoking in previous year (yes/no)
Diabetes (any of below)	Diabetes
Blood glucose ≥126 mg/dL	Measured HbA1c levels (%)
Use of insulin medication (self-report)	No self-report
Use of oral hypoglycemic medication (self-report)
log(total cholesterol, mg/dL)	Total cholesterol, mg/dL
log(HDL cholesterol, mg/dL)	HDL cholesterol, mg/dL
	BMI, kg/m2
log(Age)	Age
STRATA: Gender	Strata: Gender

HbA1C, glycosylated hemoglobin; HDL, high-density lipoprotein

Evaluation of Model Performance

We considered three metrics to evaluate the performance of the risk prediction model: discrimination, calibration, and reclassification. Discrimination quantifies the ability of the proposed prediction model to correctly distinguish between subjects who experienced CVD events and those who did not. For Cox models, the typical measure of discrimination is the C-index.^34,35 A completely random prediction would yield a C-index of 0.5 and a perfect predictive model would yield a C-index of 1.0. We obtained the C-index for the proposed model and the D’Agostino general CVD risk model applied to this specific Framingham offspring sample. Additionally, we estimated the C-index for the proposed model exchanging HbA1c with self–reported diabetes diagnosis to assess the change in predictive performance. To avoid overestimation of the predictive ability^36,37 of the models, we estimated a 10–fold cross-validated (CV) C-index and obtained its 95% CI using 10,000 bootstrap replicates.^38,39

Calibration quantifies how the predicted outcome for each individual patient agrees with the actual outcome.⁴⁰ We constructed ten equally sized groups based on their estimated risk score, ranging from low risk to high risk. For each subgroup, we computed the average model–based risk probabilities and observed risk probabilities using the Kaplan–Meier estimate of the decile. A model is well calibrated if the observed and predicted survival probabilities do not differ among subgroups. We summarized calibration statistics based on a modified Hosmer–Lemeshow χ² statistic with nine degrees of freedom.⁴¹

A reclassification analysis was performed to evaluate the ability of HbA1c to reclassify risk using 10–year risk categories defined as low (<6%), intermediate (6% to <20%) or high (≥20%). We assessed the number of reclassified participants and estimated the net reclassification improvement (NRI).⁴² For discrimination, calibration, and reclassification measures, we compared the proposed cardiometabolic model with HbA1c to the proposed model replacing HbA1c with self–reported diabetes status and D’Agostino general CVD risk model. We performed a gender–specific Cox regression using the variables in the D’Agostino model applied to the offspring data to estimate parameter and baseline hazard estimates for the D’Agostino model. From these parameter and baseline hazard estimates, we calculated risk functions to estimate 10–year general CVD risk for use in discrimination and calibration analyses. Similar 10–year general CVD risk was estimated for the proposed cardiometabolic risk models. Analyses were performed in 2012–2013 using R, version 2.15.1. Type I error was set to 5%.

Results

Baseline Characteristics

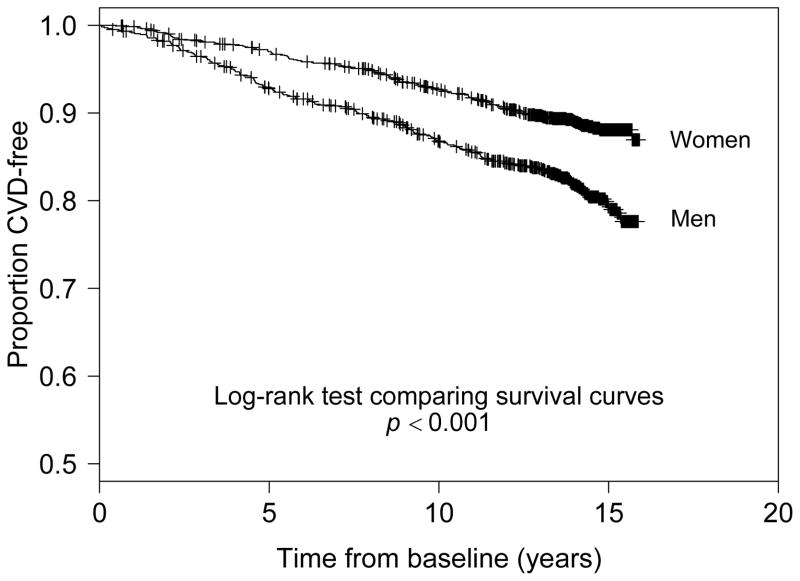
A total of 2,359 subjects free of general CVD at baseline were assessed over 14 years of follow-up. The mean (SD) age of the offspring study participants at baseline was 54.3 (9.7) years. The gender–specific subject characteristics at baseline are reported in Table 2. About 19% of male and female participants smoked regularly at baseline. Mean BMI at baseline for men was 28.8 kg/m² and 26.6 kg/m² for women. Mean HbA1c was similar for men (5.42%) and women (5.37%) at baseline. Average total and HDL cholesterol levels were higher in women whereas mean systolic blood pressure was higher in men. During follow-up, men experienced the highest general CVD cumulative incidence at 18.7% and women had a lower cumulative incidence of general CVD at 11.1%. Figure 1 shows the Kaplan–Meier survival curve of general CVD stratified by gender. An increased risk of general CVD appeared 2–3 years after baseline, after which there was a clear widening of survival curves between gender groups throughout the follow-up period (p<0.001).

Table 2.

Baseline characteristics of offspring Framingham cohort participants at exam 5

Risk factor	Men (n=1,047)	Women (n=1,312)
BMI (kg/m2)	28.2 (4.3)	26.6 (5.4)
Age (years)	54.5 (9.9)	54.2 (9.8)
Smoked regularly in past year	19.1%	18.5%
Systolic blood pressure	128.3 (16.7)	123.3 (20.0)
Diastolic blood pressure	76.8 (9.7)	72.2 (10.0)
Total cholesterol, mg/dL	200.9 (34.0)	206.6 (38.3)
HDL cholesterol, mg/dL	43.8 (11.5)	56.4 (15.4)
HbA1c (%)	5.42 (1.01)	5.37 (0.85)
CVD during follow-up	18.7%	11.1%

For continuous risk factors, the top number denotes the sample mean and the bottom its corresponding standard deviation.

Categorical risk factors are summarized by percentages.

CVD, cardiovascular disease; HbA1C, glycosylated hemoglobin; HDL, high-density lipoprotein

Figure 1.

Kaplan–Meier survival plots of time (years) to hard CVD outcome for age –gender strata categories.

Note: “+” denotes censoring.

CVD, cardiovascular disease

Proposed Cardiometabolic Risk Model

Multivariable gender–specific Cox model hazard ratios (HRs) for the proposed cardiometabolic risk model are presented in Table 3. Men had a 23% increased risk of general CVD for every percentage increase in HbA1c (HR=1.23; 95% CI=1.11, 1.36, p<0.0001). For women, a percentage increase in HbA1c led to a 14% higher general CVD risk (HR=1.146; 95% CI=1.00, 1.32, p=0.053).

Table 3.

Gender–specific Cox regression hazard ratios of general cardiovascular disease for the D’Agostino et al.⁶ and proposed models

	Men
	D’Agostino et al. (2008) model			Cardiometabolic model (proposed)
Risk factors	HR	95% CI	p-value	HR	95% CI	p-value
Total cholesterol	2.302	0.948, 5.591	0.065	1.003	0.999, 1.007	0.163
HDL cholesterol	0.618	0.350, 1.093	0.098	0.989	0.976, 1.003	0.122
Age	26.235	9.684, 71.073	<0.0001	1.063	1.045, 1.082	<0.0001
Smoking	1.431	0.992, 2.065	0.055	1.353	0.939, 1.949	0.105
SBP				1.008	1.000, 1.016	0.059
If treated	3.513	1.118, 11.040	0.032
If not treated	3.327	1.047, 10.571	0.042
Diabetes	1.981	1.279, 3.066	0.002
HbA1c				1.231	1.114, 1.361	<0.0001
BMI				1.033	0.997, 1.070	0.070
Women
Total cholesterol	2.168	0.833, 5.636	0.113	1.004	1.000, 1.008	0.069
HDL cholesterol	0.331	0.180, 0.608	<0.001	0.979	0.967, 0.992	0.001
Age	38.860	11.512, 131.2	<0.0001	1.069	1.048, 1.091	<0.0001
Smoking	1.888	1.267, 2.815	0.002	1.948	1.316, 2.883	0.0008
SBP				1.012	1.003, 1.020	0.006
If treated	5.476	1.688, 17.767	0.005
If not treated	5.182	1.559, 17.216	0.007
Diabetes	1.666	0.899, 3.090	0.105
HbA1c				1.146	0.999, 1.315	0.053
BMI				1.022	0.991, 1.054	0.163

The HR provides an estimate of the relative risk of cardiovascular disease between two groups or for a one-unit increase in continuous risk factors.

All continuous factors for the D’Agostino et al.⁶ model were log transformed.

HbA1c, glycosylated hemoglobin; HDL, high-density lipoprotein; HR, hazard ratio of general cardiovascular disease; SBP, systolic blood pressure

For men and women, smoking led to a 35% and 95% increase in general CVD risk, respectively. Additionally, an increase in BMI was marginally associated with an increased risk of general CVD. HDL cholesterol was significantly associated with general CVD risk for female participants (HR=0.979, 95% CI=0.967, 0.992) as well as systolic blood pressure (HR=1.012, 95% CI= 1.003, 1.020). Nonlinearity checks showed that a linear functional form for all continuous risk factors was appropriate and proportional hazards testing suggested the assumption was appropriate (results not shown).

Comparison of Risk Factors Between Models

We compared the HRs of the risk factors between the proposed risk score and the gender–specific D’Agostino risk score (Table 3). Presence of diabetes led to a doubling of general CVD risk for men (p=0.002). Systolic blood pressure was positively related to CVD risk in both men and women. For both models, age was highly associated with general CVD risk.

Evaluation of the Model: Discrimination

Model performance evaluated by discrimination is presented in Table 4. Discrimination (10–fold CV C-index⁴³) achieved by the D’Agostino risk model on the offspring sample was 0.687 for men and 0.748 for women. The CV C-index of the proposed cardiometabolic risk score with HbA1c was 0.703 for men and 0.762 for women. When HbA1c was replaced with self–reported diabetes diagnosis in the proposed model, the CV C-index decreased to 0.690 for men and 0.757 for women. The difference in C-index between the proposed cardiometabolic model with HbA1c versus diabetes self-report was not statistically significant (men=0.0131, 95% CI= −0.0006, 0.0187; women=0.0047, 95% CI= −0.0078, 0.0055).

Table 4.

Evaluation of model performance for the D’Agostino et al.⁶ and proposed cardiometabolic models

Men (n =1,047)
	D’Agostino et al. (2008) model	Cardiometabolic model (with diabetes diagnosis self-report)	Proposed cardiometabolic model (with HbA1c)
Discrimination
C-index	0.706	0.704	0.715
CV C-index	0.687	0.690	0.703
95% CI for CV C-index	0.652, 0.730	0.659, 0.734	0.668, 0.742
Calibration
χ2	5.016	8.912	9.051
p-value for χ2	0.755	0.349	0.338
Women (n=1,312)
Discrimination
C-index	0.772	0.771	0.773
CV C-index	0.748	0.757	0.762
95% CI for CV C-index	0.714, 0.791	0.724, 0.799	0.726, 0.801
CALIBRATION
χ2	3.1026	12.674	12.547
p-value for χ2	0.9277	0.1235	0.1284

C-index and CV C-index denote the estimated probability that the prediction model assigns a higher cardiometabolic risk to subjects that develop CVD compared to those who do not develop CVD.

Calibration quantifies how the predicted outcome for each individual patient agrees with the actual outcome; p-values >0.05 suggest good fit.

CV, cross-validated; CVD, cardiovascular disease

Evaluation of the Model: Calibration

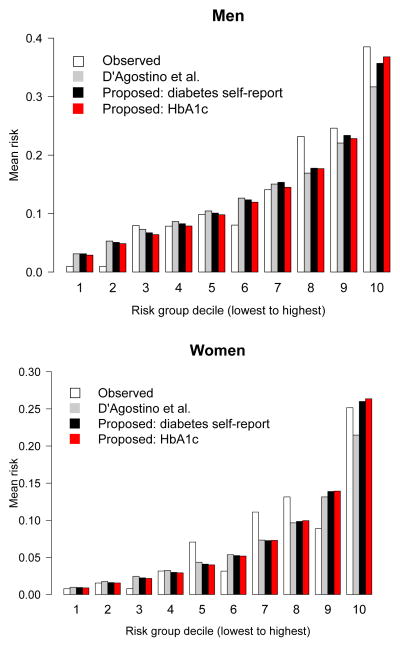
Figure 2 shows the calibration plot comparing predicted deciles of general CVD risk and observed risk for the D’Agostino model and proposed cardiometabolic risk models. Overall, the models demonstrate good calibration across all risk deciles. The calibration χ² statistics for the two models are presented in Table 4. The goodness-of-fit χ² statistic was lowest in the D’Agostino model (men, χ²=5.02; women, χ² =3.10). The p-values for lack of fit were >0.05 for the all models, suggesting proper model fit.

Figure 2.

Calibration plot comparing agreement between observed, D’Agostino et al.⁶ model, proposed model with self-reported diabetes status, and proposed model with HbA1c instead of self–reported diabetes status for 10–year predictions for general CVD risk.

Ten groups (equal number of subjects per group) were categorized using proposed risk scores that range from low risk to high risk. Kaplan–Meier estimates were used for observed bars. Men (top panel) and women (bottom panel).

CVD, cardiovascular disease; HbA1c, glycosylated hemoglobin

Comparison of Cardiometabolic Risk Score in Subjects With and Without a Self–Reported Diabetes Diagnosis

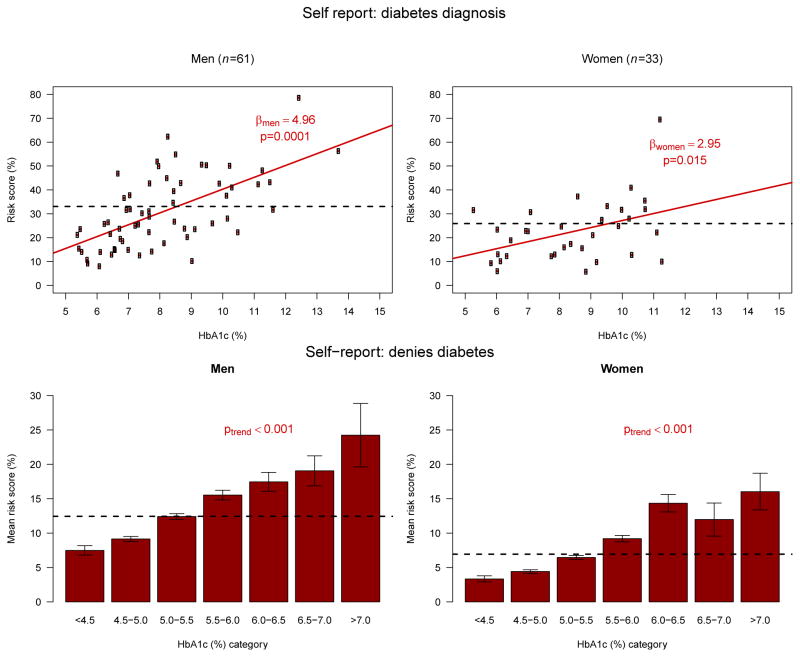
Figure 3 plots the estimated risk scores of the proposed model against HbA1c values for subjects with self–reported diabetes diagnosis (top panels). There was a significant dose–response relationship between HbA1c levels, with lower HbA1c values conferring less risk than the average risk score using the self–reported diabetes model, and higher HbA1c values conferring greater risk than the average risk score using the self–reported diabetes model, in both men and women. Additionally, for subjects who did not report a diabetes diagnosis (Figure 3, bottom panels), we observed a similar and significant trend.

Figure 3.

Comparison of cardiometabolic models with self–reported diabetes diagnosis versus Hba1c.

From a subset of responders who self-reported diabetes diagnosis (n=94), the average risk scores from the self–reported diabetes model stratified by gender is plotted as a black horizontal line for each group. For those with self–reported diabetes diagnosis (A, men; B, women), there is a significant dose–response relationship between HbA1c levels, with lower HbA1c values conferring less risk than the average, and higher HbA1c values conferring greater risk than the average. Bottom panels (C, D) present mean and SE of risk scores for each category of HbA1c. For those who deny a diabetes diagnosis (C, men; D, women), there is a significant dose-response relationship between HbA1c levels, with lower HbA1c values conferring less risk than the average, and higher HbA1c values conferring greater risk than the average.

HbA1c, glycosylated hemoglobin

Reclassification results for 10–year CVD risk are presented in Table 5. For ten subjects who experienced CVD events, classification using HbA1c in lieu of diabetes self-report improved, and for another ten it became worse with a net reclassification proportion of 0.00 (p=1.00). The net gain in reclassification proportion for subjects who did not experience an event was 0.013, with 65 subjects reclassified down and 38 reclassified up (p=0.008). The NRI was estimated as 0.013 and was not statistically significant (p=0.522).

Table 5.

Reclassification of 10–year cardiometabolic risk among people who experienced a CVD event and those who did not

	Proposed cardiometabolic model with HbA1c
Proposed model with diabetes self-report	<6%	6% to <20%	≥20%	Total
Participants who experience a CVD event
<6%	22 (88.0)	3 (12.0)	0 (0.0)	25
6% to <20%	5 (4.2)	108 (90.0)	7 (5.8)	120
≥20%	0 (0.0)	5 (6.0)	79 (94.0)	84
Total	27	116	86	229
Participants who do not experience a CVD event
<6%	940 (97.6)	23 (2.4)	0 (0.0)	963
6% to <20%	36 (4.0)	858 (94.4)	15 (1.6)	909
≥20%	0 (0.0)	29 (12.9)	196 (87.1)	225
Total	976	910	211	2097

Columns and rows refer to categories of 10–year predicted risk.

Table is restricted to events occurring during the first 10 years of follow-up.

CVD, cardiovascular disease; HbA1c, glycosylated hemoglobin

Discussion

The Framingham risk score model is a widely used, practical model to evaluate CVD risk.⁶ We developed a general cardiometabolic risk score that is sensitive to modifiable and measurable non–self-reported risk factors that can be changed in an intervention. Focusing on modifiable risk factors such as HbA1c and BMI allows researchers and practitioners to better evaluate small changes in important risks and then communicate general cardiometabolic risk to individuals who may be involved in community–level primary prevention interventions. Small changes across multiple risk factors can substantially impact overall population patterns of health.⁴⁴ We hope that this will serve to motivate an individual’s commitment to recommended behavioral changes or interventions that reduce risk. This innovative statistical and analytic tool utilizes new biomarkers and measures to optimize CVD or other risk prediction models. Of note, the use of HbA1c provides significantly better discriminatory power than self–reported diabetes diagnosis, and has a significant dose–response relationship with CVD risk even in those who deny a diabetes diagnosis. However, reducing HbA1c via medications may not reduce or even increase CVD risk.⁴⁵ Behavioral risk reduction (eg. through diet and exercise) can lower HbA1c,⁴⁶ which we and others find is associated with CVD risk.⁴⁷

This study has several major strengths. The proposed prediction model expands the global CVD functions of the D’Agostino model, where Hba1c, now diagnostic for prediabetes and diabetes,^48,49 is collected with BMI. Advances in cardiometabolic biomarkers have produced an abundance of data, providing a unique opportunity to study cardiometabolic risk in populations of individuals studied in a fuller context (e.g., workplace and home), and enhanced socioecologic validity (e.g., representative rather than convenience samples).

The use of the offspring cohort to develop the model allows us to generalize the risk score to a more general U.S. adult population that is typically found in intervention and primary care settings. We also demonstrated through discrimination analyses that inclusion of HbA1c and BMI leads to predictive performance that is in the same range of the D’Agostino model and of C-indexes from other Framingham risk scores.^50,51 With calibration models, we showed that the generalized cardiometabolic model has good agreement between predicted and observed outcomes. Again, our goal here was not to improve on the excellent predictive ability of the earlier scales, but rather to introduce the ability to monitor small changes in important non–self-reported modifiable risk factors such as HbA1c.

This study has limitations. The study was restricted to Framingham offspring subjects with HbA1c at exam 5, which produced a smaller sample size with potentially more confounded data in the Framingham offspring cohort than the sample used in previous Framingham models, somewhat limiting generalizability. As a result, multiple risk factors in the both gender–specific risk models analyzed in this study, such as self–reported smoking status, did not show statistically significant relationships with general CVD risk as previous studies have shown.⁶ The lack of significance may be due to not having enough Framingham data in the analysis, or inherent self–report measure limitations, and may underestimate the true relationship between the risk factors and general CVD risk. The direction of the associations of the risk factors and general CVD risk are in line with previous published studies.^3,6 Our emphasis is on cardiometabolic risk prediction. Often, measures of association do not meaningfully describe the ability of the variable to classify subjects.⁵² Future studies using measured risk factors (e.g., cotinine levels to assess smoking status and high–sensitivity C-reactive protein^53–55) may identify models that are more predictive than those using self-reported measures. Unfortunately, we were limited by risk factors collected at Framingham offspring cohort exam 5, which did not include some risk factors such as C-reactive protein. The Framingham cohort is also predominantly white, which limits our generalizability to non-white cohorts. A possible solution to extend this work to non-white groups would be to consider adapting the probabilities to the demographics of the study population through recalibration.⁵⁶ Future work should assess the impact of measurement error using self-reported measures, including diabetes, on estimates of association. Future studies should estimate predictive performance of the proposed model on an independent, more diverse population, and incorporate assessment of all risk factors, including health behaviors.

In conclusion, the study presents an algorithm that quantifies general CVD risk based on modifiable risk factors, including HbA1c and BMI, which can motivate an individual’s commitment to prevention and intervention. This model could be utilized in settings where measured biomarkers are already being collected: primary prevention efforts in communities and worksites, health outcomes research that use electronic medical records and administrative data, assessments in prediabetic patients, and primary care settings (e.g. managing patient care through annual check-ups). As preventive care in the U.S. and in other countries advances toward promising interventions, we hope that both medicine and public health will incorporate quantitative, modifiable risk factors into common practice.