Blind prediction performance of RosettaAntibody 3.0: Grafting, relaxation, kinematic loop modeling, and full CDR optimization

Abstract

Antibody Modeling Assessment II (AMA-II) provided an opportunity to benchmark RosettaAntibody on a set of eleven unpublished antibody structures. RosettaAntibody produced accurate, physically realistic models, with all framework regions and 42 of the 55 non-H3 CDR loops predicted to under an Ångström. The performance is notable when modeling H3 on a homology framework, where RosettaAntibody produced the best model among all participants for four of the eleven targets, two of which were predicted with sub-Ångström accuracy. To improve RosettaAntibody, we pursued the causes of model errors. The most common limitation was template unavailability, underscoring the need for more antibody structures and/or better de novo loop methods. In some cases, better templates could have been found by considering residues outside of the CDRs. De novo CDR H3 modeling remains challenging at long loop lengths, but constraining the C-terminal end of H3 to a kinked conformation allows near-native conformations to be sampled more frequently. We also found that incorrect V_L–V_H orientations caused models with low H3 RMSDs to score poorly, suggesting that correct V_L–V_H orientations will improve discrimination between near-native and incorrect conformations. These observations will guide the future development of RosettaAntibody.

INTRODUCTION

Antibodies are vital immunological molecules, protecting their hosts by binding to their infectious targets, antigens, and triggering a directed immune response. In addition to their biological role, antibodies serve as protein therapeutics.^{1, 2} Advances in computational protein modeling and a growing understanding of the sequence-structure relationship in antibodies have fueled development of methods to engineer improved affinity,^3–6 stability⁷ and solubility.^7–12

Antibody structure prediction typically focuses on modeling the variable fragment (F_V), which is composed of the N-terminal domains from the heavy and light chains (V_H, V_L). The F_V contains the antigen-binding site,¹³ composed of the six complementarity determining region (CDR) loops (L1-L3, H1-H3) that are responsible for antigen recognition and binding. While the structure of the V_L and V_H domains is highly conserved, the CDR loops, especially CDR H3, vary considerably both in terms of sequence and structure, prompting many studies, both computational and experimental, focused on CDR loops^14–27 and their interactions with antigens.^28–37 Several antibody prediction methods are available as servers on the web.^38–40

In 2011 the first Antibody Modeling Assessment (AMA-I) was conducted, wherein some of these servers and commercial software tools were benchmarked against nine newly determined antibody crystal structures.⁴¹ Templated regions were predicted to about 1 Å RMSD, and CDR H3 loops were predicted to about 3 Å RMSD. Since that time, efforts in the antibody structure prediction field have included updated databases,⁴² additional examination of the V_L–V_H orientation,⁴³ reassessment of canonical loop clusters,²⁶ designs of antibodies for thermal resistance⁸ and non-canonical residue antigen crosslinking.⁴⁴ In addition, progress has been made in ab initio loop modeling.^45–48 In response to these developments, a second antibody modeling assessment was organized this year.

In this report, we discuss the performance of RosettaAntibody implemented in the Rosetta 3 framework⁴⁹ when blindly predicting the structure of eleven unpublished antibody crystal structures as a part of Antibody Modeling Assessment II (AMA-II). This experiment is the second blind test of several antibody-modeling methods and the first test of an updated Rosetta-based antibody modeling method still under active development. The eleven targets provided to us represent a diverse set of antibodies, including a rabbit antibody (Ab01), a human antibody with a λ light chain (Ab05), antibodies derived from phage display libraries (Ab03 and Ab05) and CDR H3 loops ranging from 8 – 14 residues in length (Kabat/Chothia definition). Modeling these targets enabled us both to test new methods and to incorporate the results from AMA-I into our workflow. In addition to our overall performance, we discuss sampling and scoring issues that can guide future improvements to RosettaAntibody.

METHODS

Target Sequences

The target dataset consisted of the sequences for 11 unpublished antibody F_V structures crystallized in the free state with a maximum resolution of 2.8 Å comprising 6 mouse antibodies, 4 human antibodies and 1 rabbit antibody.

Construction and relaxation of the crude F_V models

We used a new Python script for the first step of antibody modeling to build a crude F_V model and relax it to remove grafting anomalies. The script inputs light and heavy chain sequences and calls BLAST for the template selections and several Rosetta applications for the template grafting and refinement. Then, we assessed the model geometry and torsion angles by MolProbity. If the MolProbity score⁵⁰ for the model was poor, the problematic templates were removed from the database and the process repeated. This process produced a Chothia-numbered intermediate structure and a constraint file for CDR H3 loop de novo modeling.

Kinematic loop modeling and simultaneous V_L–V_H optimization

After the initial model was refined, the CDR H3 loop was modeled de novo while simultaneously refining the V_L–V_H orientation using the Rosetta docking algorithm⁵¹ (stage 1). Next-generation KIC (NGK)⁴⁷ without two-body Ramachandran sampling and legacy KIC⁴⁶ were used to sample CDR H3 loop conformations. The conventional sequence-based classification rules²³ predicted all targets other than Ab07 to have a kinked CDR H3 loop. The sequence of the Ab07 is featureless, and since the majority of antibodies have a kinked CDR H3 conformation, it was also presumed to adopt a kinked conformation. The kink prediction is incorporated into the sampling routine by restricting the pseudodihedral angle of the four consecutive Cα atoms of residues H100X, H101, H102 and H103 to −10° to 70°, a range consistent with the kink.¹⁶

CDR H3 loop modeling on a crystal framework

For stage 2, we were given the crystal structures for the targets with the CDR H3 loop coordinates removed. After repacking the side chains, we ran NGK with two-body Ramachandran sampling as well as legacy KIC without any constraints for 7 targets (Ab04/05/06/07/09/10/11), and legacy KIC with the kink constraint for 3 targets (Ab02/Ab03/Ab08). Given the rapid turnaround required for this challenge, the protocols for each target were chosen based on the estimated computational time required and available resources. For Ab05/Ab06/Ab10, however, the kinked conformations were rarely sampled in the unconstrained simulations, so we employed legacy KIC with the kink constraint as described above.

CDR loop definitions

RosettaAntibody uses the Chothia numbering scheme.¹⁸ CDRs L1-L3, H2 and H3 follow the Kabat definitions (L1: L24-L34, L2: L50-56, L3: L89-L97, H2: H50-H65, H3: 95-102), while CDR H1 is defined as residues H26-H34. FRL and FRH are defined as the whole VL and VH domains except for the CDR loops.

V_L–V_H packing angle calculation

The V_L–V_H packing angle, α, is calculated using a Rosetta implementation of the protocol described in Abhinandan and Martin,⁵² which defines the packing angle as a pseudo-torsion angle between four non-atomic points at the V_L–V_H interface. These points are identified using two pairs of conserved β-strands at the V_L–V_H interface, one pair located in the V_L framework (L35-L38, L85-L88), the other in the V_H framework (H36-H39, H89-H92). For each β-strand pair, C_α coordinates were extracted, and the centroid and best-fit line (first principal component) of the coordinate set were identified. Points 2 and 3 in the pseudo-torsion calculation are defined as the V_L centroid and V_H centroid, respectively, while points 1 and 4 are defined as points along the V_L and V_H best-fit lines, respectively, that lie to the same side of the centroid as the CDRs.

RMSD calculation

As reported in AMA-I,⁴¹ all RMSDs for model assessment were calculated over the backbone atoms (C, C_α, N, O). The RMSDs of CDR-H and L are computed after superposing the corresponding FR, while the RMSDs used to assess domain orientation are defined as the RMSD of FRH and FRL after superposing FRL or FRH, respectively. The RMSD of template availability was examined based on the CDRs in the Chothia definition, which excludes structurally conserved regions from our CDR definitions. All RMSDs were computed using the McLachlan algorithm⁵³ as implemented in the ProFit software.⁵⁴ All antibody models generated by RosettaAntibody 3.0 are available upon request or on the web (http://www.Abmodeling.com).

MolProbity

We used MolProbity version 3.⁵⁰ To ensure fair comparisons between crystal structures and models, all hydrogen atoms are removed from the models before calculating MolProbity scores.

Algorithm Availability

All methods used for this work are included in the Rosetta biomolecular modeling suite, distributed freely for academics and non-profits through the Rosetta Commons (http://www.rosettacommons.org). Along with compiled Rosetta executables, there are pre-and post-processing scripts and tools. The initial template grafting and refinement is driven by a master python script as follows:

     ./antibody.py --light-chain <L.fasta> --heavy-chain <H.fasta>

This script generates several PDB files and a constraint file called cter_constraint, which is for the kink constraint. The grafted.relaxed.pdb is recommended to use in the H3 modeling step below. The script is included in the latest Rosetta release (Rosetta/tools/antibody/antibody.py),

The H3 modeling jobs above can be run using the Rosetta command. For NGK with kink constraint, the command line is:

     ./antibody_H3.macosclangrelease
          -s ./grafted.relax.pdb -antibody::remodel perturb_kic
          -antibody::snugfit true -antibody::refine refine_kic
          -antibody::cter_insert false -antibody::flank_residue_min true
          -antibody::bad_nter false -antibody::h3_filter true
          -antibody::h3_filter_tolerance 20
          -antibody:constrain_cter -antibody:constrain_vlvh_qq
          -constraints:cst_file ./cter_constraint
          -ex1 -ex2 -extrachi_cutoff 0
          -kic_bump_overlap_factor 0.36
          -corrections:score:use_bicubic_interpolation false
          -loops:legacy_kic false -loops:kic_min_after_repack true
          -loops:kic_omega_sampling -loops:allow_omega_move true
          -loops:ramp_fa_rep -loops:ramp_rama -loops:outer_cycles 5
          -run:multiple_processes_writing_to_one_directory
          -nstruct 2000

For legacy KIC with the kink constraint, the command line is:

     ./antibody_H3.macosclangrelease
          -s grafted.relaxed.pdb -antibody:remodel perturb_kic
          -antibody:snugfit true -antibody:refine refine_kic
          -antibody:flank_residue_min true -antibody:bad_nter false
          -antibody:h3_filter false -antibody:cter_insert false
          -ex1 -ex2
          -constraints:cst_file ./cter_constraint
          -nstruct 2000

These flags are compatible with the public Rosetta release 2013-wk48 (3-Dec-2013).

RESULTS

The basis of our approach used for AMA-II is the original RosettaAntibody algorithm described by Sivasubramanian et al. in 2009,⁵⁵ with each component revisited and updated. Briefly, RosettaAntibody uses templates from other antibody structures for the framework regions (FRs) and non-H3 CDR loops.⁵⁶ Because CDR H3 does not form canonical conformations, it is modeled de novo while optimizing the V_L–V_H orientation and minimizing CDR loop torsions. In this paper, we analyze successes and shortcomings at each step of the process, starting with template selection, then de novo CDR H3 modeling on both a homology and a crystal framework, and finally V_L–V_H orientation.

Template based modeling is accurate… except when it’s not

RosettaAntibody begins by searching curated databases containing sequences of structural components (FRL, FRH, L1-3, H1-3) from high-quality antibody crystal structures (resolution ≤ 2.8 Å; CDR C_α B-factors ≤ 50) in the Protein Data Bank (PDB)^{57, 58} as of June 2012. Templates are selected by BLAST⁵⁹ bit-score. A template for the initial V_L–V_H orientation is similarly identified by using an overall sequence similarity to a complete F_V. The template structures are then assembled into a crude model and refined in Rosetta. The templates for each structural component are listed in the Table I.

Table I.

PDB accession codes of the source of the template used for each antibody structural component.

Target	FRL	FRH	L1	L2	L3	H1	H2	H3	light_heavy
Ab01	2hwz	1mvu	3ghb	2aj3	2otu	3s34	2ojz	1uz6	1dql
Ab02	1mvu	3cvi	3o2d	3t65	3o2d	2ok0	1ktr	1p7k	3q3g
Ab03	3eo9	3qot	1rzg	3ncj	1yqv	3nps	3qot	1fgn	2cmr
Ab04	1ncc	2jel	1ztx	1h8n	1kb5	1nlb	2jel	1uz6	1ztx
Ab05	1aqk	3njc	4d9l	3c2a	1rzf	2b1h	3ncj	1uz6	2xwt
Ab06	3uc0	3kdm	1vge	3idg	1vge	3s34	2hrp	1dql	3bn9
Ab07	2xqy	1ft8	2vl5	3phq	2aab	3rvv	1hq4	1uj3	1f58
Ab08	2ap2	1q0x	1mvu	3t65	1mvu	2q76	1d5i	3phq	1mvu
Ab09	3eo9	3njc	1hez	3ncj	3qot	2h32	2xwt	3qot	3nab
Ab10	3t65	1e4x	3qot	3t65	3oz9	1kb5	1ktr	2xzq	3o2d
Ab11	1yy8	3cvi	1yy8	2ih3	1bm3	3cvi	1igj	1s3k	2oz4

FRL and FRH, light and heavy variable domain framework templates; L1…H3, complementarity determining loops L1 through H3 templates; light_heavy; template for initial FRL-FRH orientation.

Table II shows RMSDs of the templates for each submitted model. Excluding the rabbit Ab01, the average backbone RMSDs of the L1, L2, L3, H1 and H2 CDR loops were 0.61 ± 0.27 Å, 0.48 ± 0.12 Å, 1.02 ± 0.54 Å, 1.00 ± 0.63 Å, and 0.99 ± 0.64 Å, respectively. All of our submitted models have sub-Ångström FRL and FRH regions relative to the crystal structure including Ab01. So as in previous works,^{14, 18, 26, 60} the CDRs, other than H3, form canonical conformations, which, when identified correctly, provide high-quality backbone atom coordinates for the loop. In this assessment, 42 of the 55 non-H3 CDR loops submitted were predicted to sub-Ångström accuracy.

Table II.

RMSD of heavy and light variable domain framework regions (FRH/FRL) and non-H3 CDR loops (L1…H2) for all submitted models in stage 1.

Target	Model	FRL	FRH	L1	L2	L3	H1	H2	FRL-frh	FRH-frl
Ab01	1 2 3	0.43 0.44 0.44	0.72 0.72 0.72	3.27 3.28 3.27	0.44 0.44 0.42	4.13 4.17 4.38	0.69 0.72 0.70	1.82 1.85 1.99	2.08 2.14 1.86	2.09 2.33 1.88
Ab02	1 2 3	0.33 0.33 0.33	0.72 0.72 0.71	0.66 0.59 0.56	0.44 0.45 0.43	1.10 1.12 1.08	0.86 0.94 0.83	1.04 1.16 0.99	2.28 1.93 2.31	1.99 1.90 1.77
Ab03	1 2 3	0.37 0.37 0.37	0.51 0.50 0.51	0.36 0.36 0.37	0.46 0.47 0.45	1.32 1.28 1.32	2.58 2.63 2.59	2.24 2.04 2.05	2.89 2.89 1.34	1.93 1.93 1.49
Ab04	1 2 3	0.63 0.63 0.63	1.10 1.10 1.10	0.58 0.58 0.58	0.81 0.66 0.84	1.00 1.03 0.97	0.71 0.73 0.78	0.24 0.24 0.24	1.46 2.19 1.59	1.37 2.14 1.89
Ab05	1 2 3	0.67 0.67 0.67	0.29 0.29 0.28	1.16 1.15 1.20	0.51 0.52 0.47	2.17 2.21 2.13	0.92 1.13 0.96	0.71 0.89 0.67	1.95 1.55 1.70	1.50 1.75 1.82
Ab06	1 2 3	0.47 0.47 0.47	0.50 0.50 0.50	0.32 0.34 0.32	0.46 0.44 0.46	0.71 0.72 0.84	1.09 1.05 1.05	0.51 0.58 0.51	1.32 1.66 1.53	1.32 1.33 1.49
Ab07	1 2 3	0.31 0.31 0.31	0.50 0.51 0.51	0.82 0.78 0.82	0.36 0.37 0.37	0.64 0.60 0.64	0.46 0.50 0.44	0.37 0.52 0.57	1.25 2.01 1.96	0.84 0.88 1.36
Ab08	1 2 3	0.52 0.52 0.52	0.46 0.46 0.45	0.80 0.90 0.84	0.55 0.55 0.57	0.58 0.59 0.61	0.55 0.47 0.46	0.89 1.01 0.84	2.27 0.82 1.54	3.28 0.90 2.99
Ab09	1 2 3	0.34 0.34 0.34	0.27 0.26 0.26	0.35 0.36 0.36	0.44 0.41 0.41	0.42 0.41 0.36	0.37 0.37 0.34	0.38 0.48 0.78	1.18 0.81 1.07	0.99 0.78 0.96
Ab10	1 2 3	0.42 0.42 0.42	1.02 1.02 1.02	0.71 0.68 0.76	0.38 0.42 0.37	1.70 1.70 1.69	1.36 1.43 1.65	0.96 1.00 1.31	1.55 1.56 1.05	1.44 0.84 0.55
Ab11	1 2 3	0.42 0.42 0.42	0.56 0.56 0.56	0.39 0.38 0.37	0.42 0.43 0.32	0.62 0.55 0.59	1.04 0.85 0.89	1.99 2.23 2.17	1.41 1.56 1.39	0.95 0.95 1.29
Ab01-11	All average	0.45 ± 0.11	0.60 ± 0.26	0.85 ± 0.82	0.47 ± 0.11	1.31 ± 1.07	0.97 ± 0.61	1.07 ± 0.66	1.70 ± 0.51	1.54 ± 0.62
Ab02-11	All average	0.45 ± 0.12	0.59 ± 0.27	0.61 ± 0.27	0.48 ± 0.12	1.02 ± 0.54	1.00 ± 0.63	0.99 ± 0.64	1.67 ± 0.52	1.49 ± 0.62

The model FRL and FRH were superposed onto the corresponding crystallographic framework before computing the RMSD, while CDR loop RMSDs were computed after superposing the FR (i.e. to compute the RMSD of CDR L1-3, the model FRL was superposed onto the crystallographic FRL, and FRHs were superposed before computing the and the RMSDs for H1 and H2). In order to measure the effect of V_L–V_H orientation, the RMSD of each framework was computed after superposing the other framework (i.e. the RMSD of FRL was computed after superposing FRH). These values are annotated as FRL-frh and FRH-frl where the FR written in lowercase is the FR that was superposed. All RMSDs are reported in Å.

We examined the validity of our hypothesis of choosing templates based on BLAST bit score by investigating the causes of modeling errors in the 13 non-H3 loops that were not predicted accurately Figure 1 shows the RMSD of all possible candidate templates to the crystal loop structure for three representative loops. Figure 1A shows the successful case of the CDR L1 loop for Ab06; there are many accurate (low RMSD) loop templates in the database, and those with the highest sequence identity or BLAST bit score are accurate. In this case our models were based upon the 1vge template and, after all refinements, resulted in loop RMSDs of 0.71 – 0.84 Å.

Figure 1. CDR loop template selection.

Scatterplot of the RMSD vs. sequence identity (SID) for (A) a typical success case (Ab06-L1) where a sub-Ångström template is selected; (B) a case where a good template is in the database but RosettaAntibody does not select it (Ab11-H2); and (C) a case where there are no templates in our structural database with an RMSD ≤ 1.0 Å of the target, which results in a modeling failure (Ab03-H1). Dashed line at RMSD = 1.0 Å for reference. The superposition of the models on the crystal structure (D) shows the result of this modeling failure.

Figure 1B shows accuracies of all template candidates for CDR loop H2 in Ab11. In this case, many low-RMSD templates were available, but the algorithm chose a template from 1igi that was less accurate. Four cases in total exhibited this failure mode (Ab03-L3, Ab10-L3, Ab06-H1, Ab11-H2), missing potential sub-Ångström templates. These failures suggest that incorporating other environmental effects into template selection may be necessary. The structural determinants of the canonical CDR conformations includes some residues in the framework regions,^{15, 26} and the identity of these residues has a species dependence. This information has been used to guide the humanization of antibodies⁶¹ and would likely be useful in building a more sophisticated template selection scheme.

Figure 1C shows a third example, namely the CDR H1 loop of Ab03. In this case, there are no near-native templates in the structural database, even though there are three templates with an exact loop sequence match. Five failure cases in total suffer from lack of accurate (sub-Ångström) templates (Ab01-L1/L3/H2, Ab03-H1, and Ab05-L3). Unsurprisingly, three of these five loops are in the rabbit antibody and have uncommon loop lengths (Ab01-L1, L3, and H2). The other targets in this category, Ab03 and Ab05, are human antibodies derived from phage display libraries, suggesting that phage display may yield structures that depart from those in biologically derived antibodies. Ab01, the rabbit antibody, requires separate discussion. During the challenge, only 1 rabbit antibody (4HBC) was available in the PDB, and we used it for templates for the frameworks (FRL, FRH), the CDRs that matched in length (L2, H1, H2) and the initial V_L–V_H orientation. However, the RMSD values are much higher than the other targets. Thus, more rabbit antibody crystal structures are needed for more diverse templates, or we must recognize challenging, non-template loops and resort to de novo loop building.

Ab03 CDR H1 has templates with excellent sequence identity (100%; 3NPS/3QOT/1RZI) but incorrect structures (Figure 1D). Based on the BLAST bit-score, we choose 3NPS, which is a complex of a human antibody and a membrane-type serine protease with some contacts between the H1 and the antigen. Although the unbound-state antibody is not available in the current PDB, the H1 can be classified into a known canonical conformation, and it is typical that the backbone of the H1 conformation is not influenced by the contact with the antigen. In the case of the human germline antibody 3QOT, the B-factors of the H1 region are high, but it still forms the same canonical conformation as 3NPS. 1RZI is a crystal structure of anti-HIV human antibody, which contains eight unique F_Vs in the asymmetric unit. We included only the first heavy and light chains in the file (B and A) during the database construction process, resulting in a candidate template with 2.7 Å RMSD (Figure 1D). The H1 loop of chain L, which was not included in our database, is closer to the target with 2.3 Å RMSD, indicating that structural differences between different F_Vs. in the asymmetric unit can be significant. Thus, if all asymmetric unit chains were included in our database, it would have been possible to identify a better loop template. Further, H1 conformations both with (2CMR, 1.3 Å RMSD) and without a helical region are present in the database with 90% sequence identity to Ab03-H1, indicating that canonical conformations are heavily influenced by the local environment and highlighting the difficulty of selecting the best template for this target.

Ab05 has a λ light chain, which is underrepresented in the PDB (i.e. 61 of 415 light chains in our curated non-redundant database). Although there are 56 templates of 11-residue CDR L3 loops available in the database, the highest sequence identity is only 55% (2J6E; RMSD 1.7 Å), and no template is structurally similar to the CDR L3 loop of Ab05.

The remaining four poorly predicted non-H3 CDR loops (Ab02-L3, Ab03-H2, Ab05-L1, Ab10-H1) have low-RMSD templates in the database which our protocol can select correctly, but minimization of the loop perturbed the coordinates to an incorrect conformation. As discussed in the previous antibody modeling assessment,⁴¹ relaxation to improve the physical realism of a model can destroy the accuracy originally present in a crystallographically-derived template. In fact, an antibody modeling server, PIGS, often generates better non-H3 CDR backbones, but several steric clashes and bad geometries are observed as reflected in poor MolProbity score.⁴¹

In summary, three scenarios led to failures in CDR template selection: 1) no availability of low-RMSD templates, (six cases); 2) inability to identify the best template (four cases); and 3) perturbation of the template away from the native structure by energy minimization and refinement (three cases). Fortunately these scenarios were relatively rare, and 42 of the submitted non-H3 CDR loops were predicted correctly (i.e. backbone RMSD ≤ 1.0 Å).

Template refinement improves physical realism of models

In the first Antibody Modeling Assessment,⁴¹ some Rosetta antibody structures suffered from poor MolProbity scores. MolProbity tests structure files for reasonable backbone torsion angles and clashes.⁵⁰ We determined that some of these issues arose from uncommon template backbone angles and odd torsion angles at the graft points. To improve these ratings and make the RosettaAntibody models more physically realistic, we tested new relaxation methods after the template grafting and before the CDR refinement steps.

The new template refinement steps are as follows. After grafting the selected template structures, the bond angles and bond lengths are set to standard values⁶² to alleviate artifacts at the graft points. The model is refined by running side-chain repack and minimization cycles, where we gradually increase the weight of the repulsive component of the Lennard-Jones potential and enforce all-atom constraint to prevent large distortions from the original templates.⁶³ Figure 2 shows the improvement in geometry as assessed by MolProbity scores. Initial models after grafting have clashes and strained backbone dihedral angles, but the refinement process results in models with geometries that score well within the range of the crystal structures.

Figure 2. MolProbity scores of model quality at various stages.

Scores for each target are plotted 1) after the initial grafting; 2) after relaxation using the Rosetta force field; and 3) for the final model. The crystal structure score is shown for reference. Hydrogen atoms were omitted. Overall, MolProbity scores improve throughout refinement, ending up within the range of the crystal structures.

β-sandwich assembly is accurate for antibodies with a near-average packing angle

The accuracy of the β-sandwich assembly process can be assessed by superposing the model and crystal FRH domains and examining the RMSD of the FRL domains. This RMSD is sub-Ångström for five out of the eleven targets (Ab07, Ab08, Ab09, Ab10, Ab11).

All five of the correctly-predicted targets have a V_L–V_H packing angle,⁵² α (see Methods), within one standard deviation of the mean packing angle of antibodies in the PDB (−52.3° ± 3.9°). Among the six targets without a sub-Angström model, three (Ab01, Ab02, and Ab05) have packing angles further than one standard deviation from the PDB average: −46.6°, −56.8° and −47.2°, respectively. The initial orientation of these three targets was taken from 1DQL (α = −50.7°), 3G3G (α = −49.9°), and 2XWT (α = −52.4°), respectively; each of these initial orientations was closer to the PDB average than to the target packing angle. Similarly, our final models for these three targets have packing angles ranging from −49° to −52°, also closer to the PDB average packing angle than to the target.

Figure 3A shows the RMSD for each structural component when a particular alignment is performed for Ab09, a typical success case. The non-H3 CDR loops and the self-aligned frameworks show little variation between models because these regions are not explicitly sampled after they are grafted. Figure 3B shows the top-scoring models superimposed on the crystal structure, showing the variation is localized to the H3 loop.

Figure 3. Examples of convergent (A, B) and divergent (C, D) modeling attempts.

RMSDs are plotted for each structural component (top line along horizontal axis) when a particular alignment (bottom line along horizontal axis) is performed. (A) Ab09; (C) Ab08. When CDR H3 and the V_L–V_H orientation varies between models, top-scoring models diverge (C). The top-scoring models superimposed on the crystal structure are shown for Ab09 (B) and Ab08 (D). Figures generated in UCSF Chimera.⁷⁵

In contrast, for Ab08, the top scoring models diverge (Figure 3C), and the FRL RMSDs when superposing FRH are 3.28 Å, 0.90 Å and 2.99 Å for the three submitted models. Although 1MVU (α = −53.0°) was used for the initial orientation of Ab08 (α_xtal = −49.0°), the submitted models have packing angles ranging from −49° to −55°. Figure 3D shows the top scoring structures superposed on the crystal structure (white), showing that models 1 and 3 have a significantly different V_L–V_H orientation than the crystal. In this view it is clear these models would be difficult to use for additional simulations such as docking because the variation within the antigen binding site may prevent important atomic interactions from forming. Comparison of the hydrogen bonds of the H3 loop of the threse models and the native structure reveals a possible explanation of the discrepancy (Figure 4). In the native structure there are two notable hydrogen bonds involving the H3 loop: 1) the side chain of the Ser H100A points back toward the V_H domain and forms a hydrogen bond with the backbone of the Tyr H98 within the H3 loop; and 2) the backbone of the Gly H99 forms a hydrogen bond with the side chain of the Trp L50 in the L2 loop. Conversely in the submitted models, the Ser H100A points toward the V_L domain, and in models 1 and 3, it forms a hydrogen bond with the backbone of Trp L50. In model 2, Ser H100A forms a hydrogen bond with the side chain of Trp L50. As a result, the V_L domain in models 1 and 3 is tilted back compared to the native structure, resulting in the increased RMSDs.

Figure 4. Non-native contacts arising from errors in V_L–V_H orientation lead to scoring complications.

The crystal structure for Ab08 (white) forms a hydrogen bond between H99 Gly and the side chain of L50 Trp. However, two of the submitted models have an incorrect V_L–V_H orientation that is incompatible with this hydrogen bond and instead allows the side chain of Ser H100A to form a hydrogen bond with the backbone N of Trp L50. These non-native hydrogen bonds cause these structures to score favorably. Figure generated in UCSF Chimera.⁷⁵

These issues can be classified into sampling and scoring problems. Sampling problems can occur both in the initial orientation template selection as well as in de novo H3 modeling, while scoring problems arise from favorable scores of non-native interactions with the CDR H3 loop. These observations suggest a relationship between H3 conformation and the packing angle, which is discussed further below.

New loop modeling methods and constraints for CDR H3 prediction

The classic RosettaAntibody algorithm performs de novo CDR H3 modeling by inserting small fragments of residues from known structures followed by loop closure using the cyclic coordinate descent (CCD)^{64, 65} algorithm. Recently, new loop prediction algorithms have shown promising results. We updated RosettaAntibody to take advantage of two of these new methods: Kinematic Closure (KIC)⁴⁶ and next-generation KIC (NGK).⁴⁷ KIC randomly perturbs several loop angles and then solves for the remaining six torsions of three ‘pivot’ residues to close the loop using a fast analytical formulation. NGK improved the KIC approach by incorporating annealing via ramping of van der Waals energy and Ramachandran potential weights, including neighbor-dependent Ramachandran propensities⁶⁶ and ω angle sampling.⁶⁷ Unfortunately the large neighbor-dependent Ramachandran propensity arrays exceeded the memory available on our standard supercomputing nodes, so we disabled this feature.

When building H3 on a homology framework (AMA-II stage 1), we used KIC and NGK in conjunction with a constraint to favor kinked^{16, 23} C-terminal conformations. For CDR H3 conformations on the crystal environment (AMA-II stage 2), we used NGK and KIC with and without kink constraints. We first summarize the results of modeling short H3 loops (8–10 residues) on a crystal framework, long H3 loops (11–14 residues) on a crystal framework, and then H3 loops on a homology framework.

Modeling short H3 loops (8–10 residues) is moderately accurate (Ab03/04/05/07/09/11)

We were able to build a model of all short CDR H3 loops with an RMSD < 2.0 Å for all targets except Ab11. Among the submitted models, the average loop RMSDs were 1.66 ± 0.96 Å and 1.58 ± 0.97 Å for the top-ranked and lowest-RMSD models, respectively (Table III).

Table II.

H3 RMSDs for top ranked and lowest RMSD models in stages I and II. All RMSDs reported in Å.

Target	H3 length	Best scored (I)	Best RMSD (I)	Best scored (II)	Best RMSD (II)
Ab02	11	3.52	2.35	2.85	1.42
Ab03	8	2.48	2.31	1.82	1.36
Ab04	8	1.62	1.62	1.20	1.17
Ab05	8	3.02	2.92	1.86	1.86
Ab06	14	3.90	3.88	3.77	3.70
Ab07	8	1.27	1.27	0.68	0.68
Ab08	11	2.88	2.79	3.33	2.03
Ab09	10	1.75	0.92	1.02	1.02
Ab10	11	2.21	1.68	1.13	1.13
Ab11	10	3.30	0.91	3.39	3.39
Short H3s	8–10	2.24 ± 0.82	1.66 ± 0.81	1.66 ± 0.96	1.58 ± 0.97
Long H3s	11–14	3.13 ± 0.74	2.68 ± 0.92	2.77 ± 1.16	2.07 ± 1.15

Long H3 loops (11–14 residues) benefit from constraints (Ab02/06/08/10)

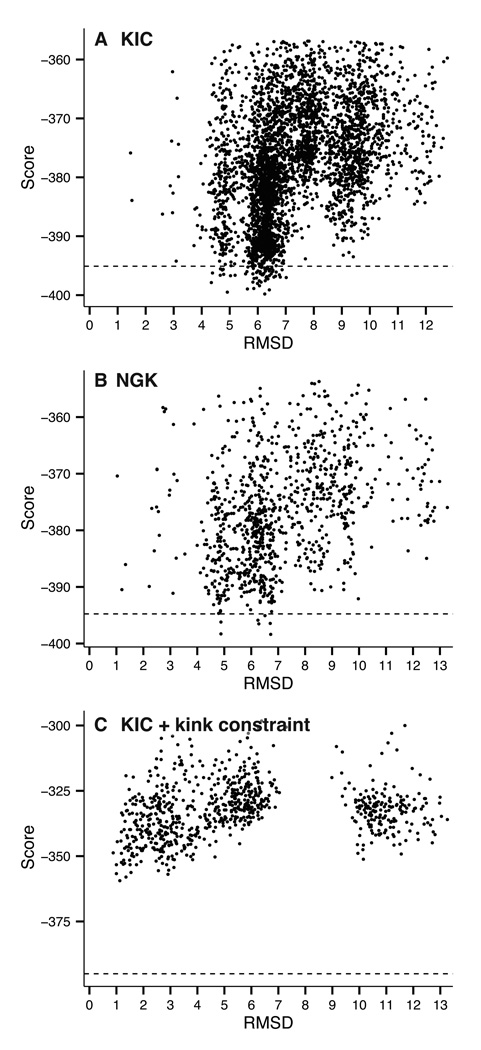
For long CDR H3 loops built on the crystal frameworks, the lowest RMSD models have RMSDs of 2.07 ± 1.15 Å (Table III). For insight, we examine the loop sampling and scoring through a plot of candidate structure score vs. distance from the native structure. Figure 5 compares a) unconstrained KIC, b) unconstrained NGK, and c) KIC using a kink constraint for Ab10 (11-residue CDR H3 loop). Although unconstrained KIC samples a couple conformations as low as 2 Å, those models score worse than other structures with RMSD ~5.0 Å (Figure 5A). NGK samples more near-native conformations than unconstrained KIC, but some non-native structures still score better (Figure 5B). Enforcing the kink constraint drastically alters the results, with the best scoring model having an H3 RMSD of 1.1 Å (Figure 5C).

Figure 5.

Score vs. RMSD plots for unconstrained de novo modeling the CDR H3 loop of Ab10 (A) shows that near-native conformations of CDR H3 are rarely sampled. Utilizing next-generation KIC (B) results in more near-native conformations sampled, but lowest scoring models are still far from the native structure. Including a constraint to prefer the C-terminal kink of the H3 loop (C) greatly improves the result.

When using the kink constraint, the lowest-scoring structure scores approximately 40 units higher than the lowest-scoring structures when using unconstrained KIC or NGK (Figure 5), suggesting that our choice of constraints is preventing formation of the lower-scoring near-native loop structures. Further, the constrained algorithm created a cluster of structures with RMSDs between 10 and 13 Å (Figure 5C) that satisfy the constraints with a kink rotated into a conformation inconsistent with antibodies. Therefore, predictions might be further improved by a more precise constraint defining the kink.

CDR H3 prediction on a homology framework can produce models with sub-Ångström accuracy

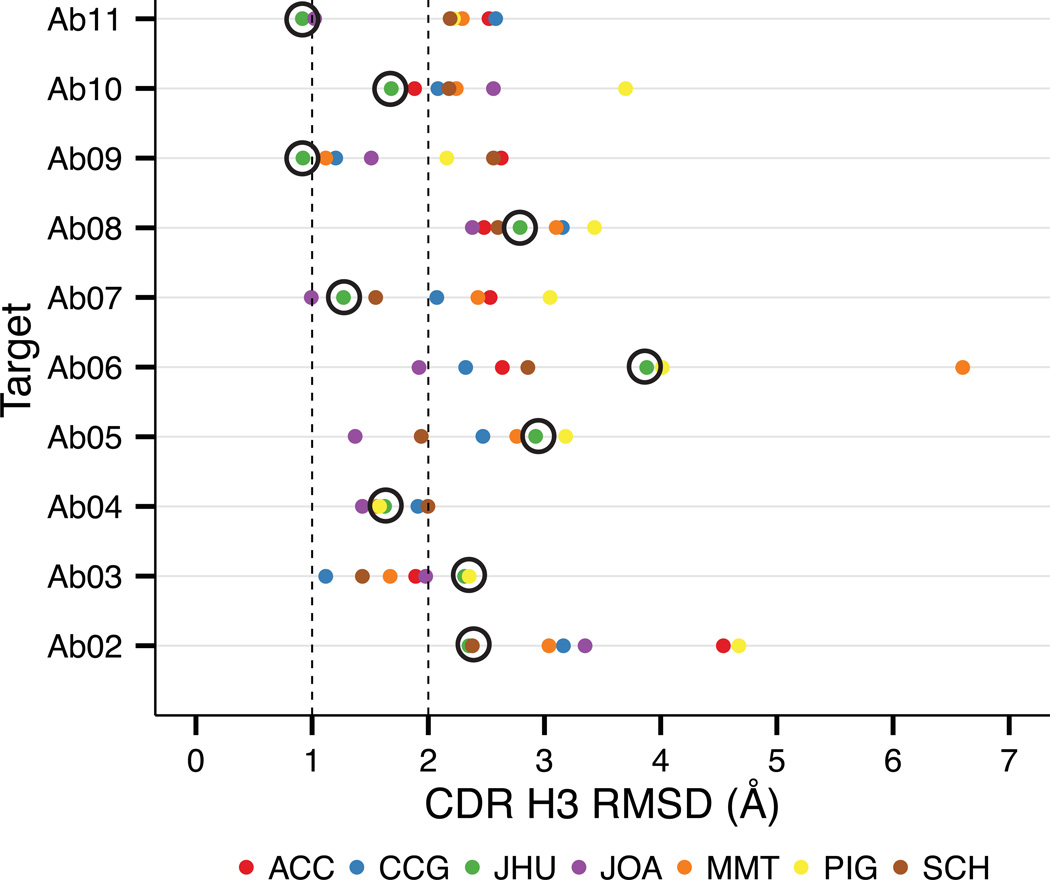
Figure 6 shows the RMSD of the closest-to-native model submitted by each group in stage 1 of the challenge for Ab02–Ab11. Our lab contributed the lowest-RMSD models for four targets (Ab02, Ab09, Ab10, Ab11), two of which have sub-Ångström RMSDs (Ab09, Ab11). For short (7–10 residue) CDR H3 loops, the average RMSD of the best submitted H3 model is 1.66 ± 0.81 Å, while for long (11–14 residue) H3 loops the average H3 RMSD of the lowest RMSD model is 2.68 ± 0.92 Å.

Figure 6. Modeling CDR H3 RMSD on a homology framework.

The lowest-RMSD model for targets Ab02-Ab11 from each participant in AMA-II stage I reveals the progress that has been made toward accurately modeling CDR H3. For four targets (Ab02, Ab09, Ab10, Ab11), RosettaAntibody (green plots, circled) produced the best CDR H3 models, two of which are sub-Ångström (Ab09, Ab11). Chemical Computing Group (blue plots) produced the best model for Ab03, and the collaboration between Astellas and Osaka University (purple plots) produced the best models for the remaining five targets.

Even on a homology framework, RosettaAntibody built models of 4 of 6 short CDR H3 loops with an RMSD < 2.0 Å. For the two failures (Ab03 and Ab05), near-native H3 conformations were sampled (1.6 Å and 0.5 Å, respectively) but scored poorly, so they were not submitted. Retrospective analysis revealed that the poor scores of the models with near-native H3 conformations are due to the lack of low-RMSD templates for non-H3 CDRs (Ab03-H1-2, Ab05-L3) as discussed above. These failures in particular highlight the importance of accurately predicting all of the CDR conformations in order to model H3 successfully.

Effect of V_L–V_H orientation on CDR H3 modeling

Even when the packing angle significantly deviates from the crystal structure, near-native CDR H3 conformations were sampled (e.g. candidate structures for Ab04 deviate from the crystal packing angle by as much as ~10° yet still maintain an H3 RMSD of ~1.0 Å). However, these structures do not score as low as those with a near-native packing angle and a sub-Angström H3 RMSD. When such a decoy is produced, as it is for Ab05, the near-native decoys can clearly be distinguished from those with deviating packing angles. This suggests that important inter-chain atomic contacts are not present in the latter models and that correctly identifying the V_L–V_H orientation is a critical factor for model ranking.

DISCUSSION AND CONCLUSIONS

Computational antibody structure prediction algorithms have the potential to dramatically alter the development of new antibody products, including therapeutics. The performance of RosettaAntibody in AMA-II demonstrates the progress made toward predicting atomically accurate models solely from a query sequence. This community-wide challenge provided us with the opportunity to test our knowledge of antibody sequences and structures with newly developed RosettaAntibody components and related methods of Rosetta 3.

An important lesson learned is the degree to which template availability is still a limiting factor. Attempting to predict Ab01, a rabbit antibody, resulted in abject failure due to the dearth of appropriate templates for the CDR loops and the fact that these algorithms require templates. Both phage display antibodies, Ab03 and Ab05, also proved difficult due to template availability. Ab05 prediction was complicated by the paucity of templates for λ light chains. In humans the populations of κ and λ light chains are almost equivalent, but κ antibodies are more abundant in the PDB since murine antibodies dominate the PDB and mice have predominantly κ light chains. λ light chains can have a longer CDR L3 loop than κ light chains,⁶⁸ and thus accurately predicting the L3 loop may prove to be a bottleneck for predicting and designing many human antibodies.⁶⁹

Analysis of failures where RosettaAntibody did not select the best template in the database revealed that more sophisticated search criteria may need to be developed that include residues outside the target loop and use of all templates from crystal structures with multiple copies in an asymmetric unit. Additionally, some templates retain high MolProbity scores after refinement, indicating that a priori filtering of bad templates may improve model quality. Finally, in cases where templates are clearly not adequate (such as species not represented in the antibody database), de novo modeling might be used.

The scoring function used can also cause some systematic problems as evidenced by situations where energy minimization of the template caused deviations from the target crystal coordinates. This can result in an inaccurate model of non-H3 CDR loops even when the best template structure in the database is selected, and these deviations can lead to inaccuracies in the H3 modeling steps. Other sources of error in the H3 modeling stage stem from the infrequent sampling of the native-like conformations and, in some cases, the inability of the Rosetta score function to effectively discriminate native-like conformations from incorrect ones. Using a constraint to penalize non-kinked conformations results in significantly better sampling, and we are pursuing alternate kink constraint formulations.

The difficulty of CDR H3 loop prediction is demonstrated by Ab06, which has the longest H3 loop (14 residues; Kabat/Chothia definition) in the challenge set. Even when building the loop in the crystal environment, near-native models are sampled rarely. The difficulty of predicting long CDR H3 loops is problematic when considering that the average human CDR H3 length is 12 residues (Kabat/Chothia definition). The conformational space accessible by the large number of degrees of freedom in long loops remains the central challenge for de novo loop prediction for CDR H3 modeling. Accurately modeling the non-H3 CDR loops is critical to create the environment in which to model H3, so we believe that continuing to improve our template-based modeling efforts is a necessary aspect of H3 modeling. These improvements may involve incorporating multiple templates, as well as metadata for each template to provide genetic information such as germline genes, species, and length and conformations of the other CDR loops in the parent structure.

Although incorrect V_L–V_H orientations do not preclude sampling of near-native CDR H3 conformations, the packing angle affects the score of the model such that the correct loop conformation cannot be recognized. Our current method for selecting an initial homology template for V_L–V_H orientation does not fare well when the native packing angle is far from the PDB average, nor is the packing angle adequately corrected during modeling. New approaches may require multiple V_L–V_H templates to capture a wider range of orientations, a packing angle constraint during modeling to direct orientation sampling, better V_L–V_H orientation predictions from sequence, or the development of statistical filters for the V_L–V_H interface.

A major weak point with RosettaAntibody models generated for AMA-I was their poor MolProbity scores. By relaxing the structures after grafting the templates in AMA-II, we were able to build models with MolProbity scores within the range of the crystal structures of the targets in the assessment. Because the differing target sequences, length of H3 loops and the number of models considered in AMA-I and AMA-II, it is difficult to directly gauge the difference of H3 modeling accuracy between AMA-I and AMA-II. However, there is a trend toward improvement in H3 accuracy. In AMA-I, the average RMSD of the medium-long H3 (10–12 residue loops, 8 targets) was 3.3 ± 1.3 Å whereas that of the rank 1 models in the AMA-II (10–11 residue loops, 5 targets) is 2.7 ± 0.8 Å. Notably, when considering the lowest 3 scored models in AMA-II, the average H3 RMSD decreases to 1.7 Å ± 0.8, highlighting the importance of using multiple models for further applications such as computational protein-protein docking^{70, 71}, design² and drug discovery.^{72, 73}

The object-oriented design in Rosetta 3 was critical during the challenge as it enabled us to quickly incorporate new modeling routines into RosettaAntibody. The continued interest in antibodies and rapidly increasing number of antibody crystal structures in the PDB contributes to the improvement of the method. RosettaAntibody 3 is available through the web server ROSIE (http://rosie.rosettacommons.org/).⁷⁴