Abstract
It has long been known that processes occurring within a species may impact the interactions between species. For example, since competitive ability is sensitive to parameters including reproductive rate, carrying capacity and competition efficiency, the outcome of interspecific competition may be influenced by any process that alters these attributes. While several such scenarios have been discussed, the influence of selfish genetic elements within one species on competition between species has not received theoretical treatment. We show that, with strong competition, sex-ratio meiotic drive systems can result in a significant shift in community composition because the effective birth rate in the population may be increased by a female-biased sex-ratio. Using empirical data we attempt to estimate the magnitude of this effect in several Drosophila species. We infer that meiotic drive elements, selfish genetic elements within species, can provide a substantial competitive advantage to that species within a community.
Keywords: sex-ratio meiotic drive, interspecific competition, genetic conflict, species interaction
Organisms must adapt to both their external environment (climate change, parasites, competitors) as well as their internal genomic environment (transposable elements, selfish chromosomes, cytoplasmic elements). While examples of adaptation to the external environment are well known, the importance of the internal genomic environment on evolutionary processes has only recently been appreciated (reviewed in Werren 2011). Ecological interactions between species and biological processes occurring within species are, however, not necessarily independent. In fact, Levin (1970) noted that any factor that influences population dynamics in one species may also have an effect on species interactions.
Sex-ratio meiotic drive systems involve a selfish sex-chromosome that is over-represented in the gametes of males. In most cases, the X chromosome harbors the sex-ratio distorter that disables or kills sperm carrying the Y chromosome. Since the phenotype requires both chromosomes, it occurs only in the heterogametic sex (usually males). These systems are widespread in Drosophila, but are also found in other Diptera, plants and mammals (Jaenike 2001). Drivers may lead to population extinction (Hamilton 1967), but are also found at stable equilibrium due either to fitness costs in females or fertility disadvantages in males (Carvalho and Vaz 1999, Taylor and Jaenike 2002). Several other evolutionary consequences of sex-ratio meiotic drive systems have been noted, including reproductive isolation (reviewed in McDermott and Noor 2010), sex-chromosome evolution (Kosielska et al. 2010) and changes in polyandry (Price et al. 2008).
James and Jaenike (1990) suggested that sex-ratio meiotic drive may provide some advantage in interspecific competition because a female-biased sex-ratio might increase the reproductive potential of a species with a sex-ratio meiotic drive system. While the influence of a female-biased sex-ratio may provide some immediate advantage in interspecific competition, the full dynamics of a sex-ratio drive system are complex. This is because, for the sex-ratio allele to be at equilibrium, there must be some cost to the sex-ratio distorter and such costs could decrease the reproductive capacity of that species.
Here we bring together a population genetic model for sex-ratio meiotic drive with Shorrocks’ (1979) competition model to determine the impact of the sex-ratio meiotic drive system on interspecific competition. This allows us to find parameter space that allows for species coexistence, the proportion of the total community that belongs to the species with sex-ratio meiotic drive and the conditions that lead to the extirpation of the species without drive. Finally, we use data available from sex-ratio meiotic drive systems to predict the impact of these systems on competition in natural communities.
Methods
We have taken two approaches to integrate a continuous-time interspecific competition model and a discrete-time sex-ratio meiotic drive population genetic model. First, we calculated the equilibria and invasion criteria for each model separately then used these solutions to find equilibria and invasion criteria for the combined sex-ratio meiotic drive and competition model. This approach is appropriate given a scenario where a sex-ratio meiotic drive system comes to equilibrium then two species begin to compete. However, we also created a continuous time model that contains both competition and sex-ratio meiotic drive. The equilibria are identical, though the integrated model allows us to consider the impact of more parameters (e.g. a genotype-specific mortality rate in the species with sex-ratio meiotic drive). For the sake of clarity of presentation, we therefore present the two models separately in the text and provide the integrated model in the appendix.
Competition is modeled using the Shorrocks et al. (1979) modification of the standard Lotka-Volterra model, incorporating both a patchy, ephemeral resource and a density-independent death rate. This model was designed for arthropods (Drosophila in particular), and is therefore likely appropriate for many of the species known to harbor sex-ratio meiotic drive systems. Average reproductive rate is assumed to depend on the number of females available. It is also assumed that males are not limiting (i.e. that when sex-ratios are skewed toward females, the remaining males are able to fertilize all available eggs) and that there is no paternal parental investment. In our model, resource usage is equal for individuals of each sex. Finally, we assume that greater density leads to more intense competition, which is more likely true in specialist than generalist species. Taken together, and all else being equal, the above means that a species with a female-biased sex-ratio has a higher per capita reproductive rate than one with an equal sex-ratio, and therefore has an advantage in interspecific competition. It should be noted that, while we chose the Shorrocks model because we feel it is appropriate for most insects, our analysis does not work with a standard Lotka-Volterra model since the equilibria do not depend on r.
Sex-ratios are skewed by SR meiotic drive, but driving X chromosomes that find themselves at polymorphic equilibrium have an associated cost either in females, males or both. This means that, while the skewed sex-ratio may provide a competitive advantage because of an excess of females, the mean fitness of a population is compromised by the SR meiotic drive system. In the context of competition, there is a tradeoff between the benefit from the skewed sex-ratio and the cost to average fitness from the segregating driving X chromosome. While several analytical solutions exist for SR meiotic drive equilibrium (Edwards 1961, Clark 1987, Hall 2004), none are quite appropriate for the present purpose, because they do not allow us to calculate genotype frequencies and sex-ratio at equilibrium. We first solve the system of recursions similar to those presented by Edwards (1961) for the genotype frequencies, which allows us to proceed with the interspecific competition problem. This population genetic model accounts for both the transmission bias that the driver enjoys and the cost of being a carrier of the driver (male or female), and therefore allows us to track the frequency of the driver across generations. It is important to make a distinction here between average female reproductive rate and population per capita reproductive rate. Only the latter is affected by the population sex ratio.
Combining the interspecific competition model with the sex-ratio meiotic drive model allows us to determine the parameter space in which a sex-ratio meiotic drive system provides an advantage in interspecific competition. While this may seem like an unorthodox approach, we recover the same equilibrium frequencies when a single continuous time model incorporating both competition and sex-ratio meiotic drive is employed. This combined approach is, however, less intuitive so we present the overall model that combines competition and sex-ratio meiotic drive post hoc and relegate the truly integrated model to the appendix.
Mathematical results were obtained by hand and using Mathematica 8.0 (Wolfram Research Inc., Champaign, IL).
Results
Sex-ratio meiotic drive model
We utilize a sex-ratio meiotic drive model where all costs associated with the driving X chromosome are assumed to be fertility costs (no viability cost). This model is very close to one developed by Edwards (1961), who assumed all costs were viability costs. Consider a driving X chromosome denoted XSR that carries an associated fertility cost in females and males but results in a skewed sex-ratio in the offspring of male carriers. If u, v, w, x and y are the genotype frequencies of XX, XXSR, XSRXSR, XY and XSRY respectively, the system is described by the following set of recursions:
| (1.1) |
| (1.2) |
| (1.3) |
| (1.4) |
| (1.5) |
where T = 2(u + faν + fbw)(x + fcy), terms fa, fb, and fc are the relative fertility fitness values (with possible values from zero, meaning sterile, to one) for heterozygous females, homozygous females and males carrying the driver respectively, and t is the strength of drive ranging from ½ to 1 (see also Table S1). Note, that the system is identical to that of Edwards (1961) if the population is censused as zygotes, however the solutions are different because for our purposes, the frequencies of each genotype and sex-ratio at equilibrium are necessary to describe the full dynamics of the system. The equilibria of interest (where the driving X is stably polymorphic) are
| (2.1) |
| (2.2) |
| (2.3) |
| (2.4) |
| (2.5) |
| (2.6) |
where is the sex-ratio at equilibrium and D = 4(fa − 1 + 2fct(fa − fb))[fa (1 + fc)(1 + 2fct) − 2(fc + 2fbfct)]. The equilibrium is stable if fa(1 + 2fct) > max[2,4fbfct] (as in Edwards 1961).
The model presented above allows fitness costs in heterozygous females to be any value. To simplify the analysis, we focus on recessive fitness costs (fa=1) and address the case later. In addition to providing for a simpler analysis, the assumption of recessive fitness cost is supported by empirical data and additive fitness costs lead to such a narrow range of parameter space with the driver segregating that it seems much less likely to occur in nature. To determine the effect of the sex-ratio meiotic drive system on average reproductive rate, we must know the average per capita female fertility relative to a system without drive, as well the increased fertility due to the greater equilibrium sex-ratio. With recessive costs in females, this is
| (3) |
For sex-ratio meiotic drive to increase the average reproductive rate of the population must be greater than 1. Solving for t shows that this only occurs when t > 1/(2fc), the exact same conditions necessary for the driver to spread in the first place.
Shorrock’s competition on a divided ephemeral resource model
We begin with a standard model without regard to the sex-ratio problem. The Shorrocks model is an extension of a standard Lotka-Volterra (LV) model with two added components. First, the model assumes density-dependent birth rates, but density-independent death rates. This seems reasonable for insect species, especially if we consider birth to be emergence as adults (Shorrocks and Begon 1975). The second deviation from the LV model is that competition is reduced by θij, which measures the proportion of species j that species i encounters (Shorrocks et al. 1979). This gives us the following system of equations for two competing species:
| (4.1) |
| (4.2) |
where Ni is the population size of species i, ri is the per capita birth rate of species i, Ki is the carrying capacity, αij is the effect of competition from species j on species i, and mi is the density-independent mortality rate. Shorrocks et al. (1979) showed that species could coexist stably if and . Rearranging we find that species 2 excludes species 1 if
| (5.1) |
and species 1 excludes species 2 if
| (5.2) |
Given parameters allowing for coexistence, the proportion of the community that is species 1 is
| (6) |
Though equations are presented to allow both α and θ to differ in the two species, numerical results will assume they are equal and competition is symmetrical. Furthermore, since α and θ always appear as the product of the two of them, we simplify the analysis by presenting αθ as a single term, with the understanding that, for example, αθ=0.5 could mean very strong competition (α=1.0) and a moderate degree of patchiness (θ=0.5), weaker competition (α=0.5) and a almost complete species overlap (θ=1.0), or any combination in between whose product is equal to 0.5.
Shorrocks’ model with general sex-ratio distortion
If the sex-ratio in one species is skewed toward females, assuming sperm does not become limiting, the reproductive output per capita is greater in that species compared to the same species with a 50:50 sex-ratio. For now, we make no assumption about the nature of that sex-ratio skew or any associated costs. Since we now need to consider separate sexes, the system in 4 (above) is rewritten as
| (7.1) |
| (7.2) |
| (7.3) |
| (7.4) |
where πf1is the proportion females in species 1, and the subscripts after Ni denote sex. Above we assume that mortality rates and competition coefficients are equal in males and females. We assume that species 2 maintains 50% females so 7.3 and 7.4 are equivalent. Species 1 is now excluded if (a la equation 5.1) and species 1 excludes species 2 if (a la equation 5.2). Given two species can coexist, the proportion of the community that is species 1 is
| (8) |
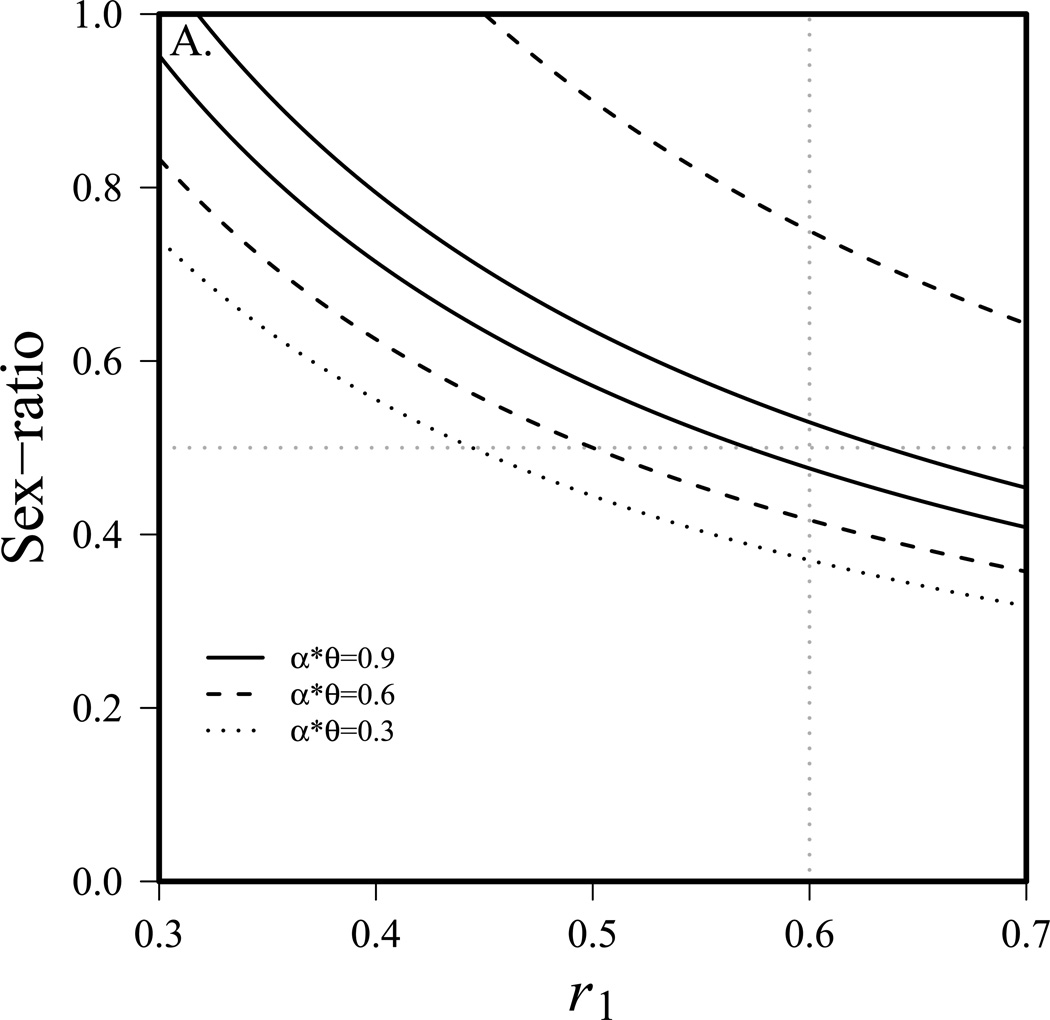
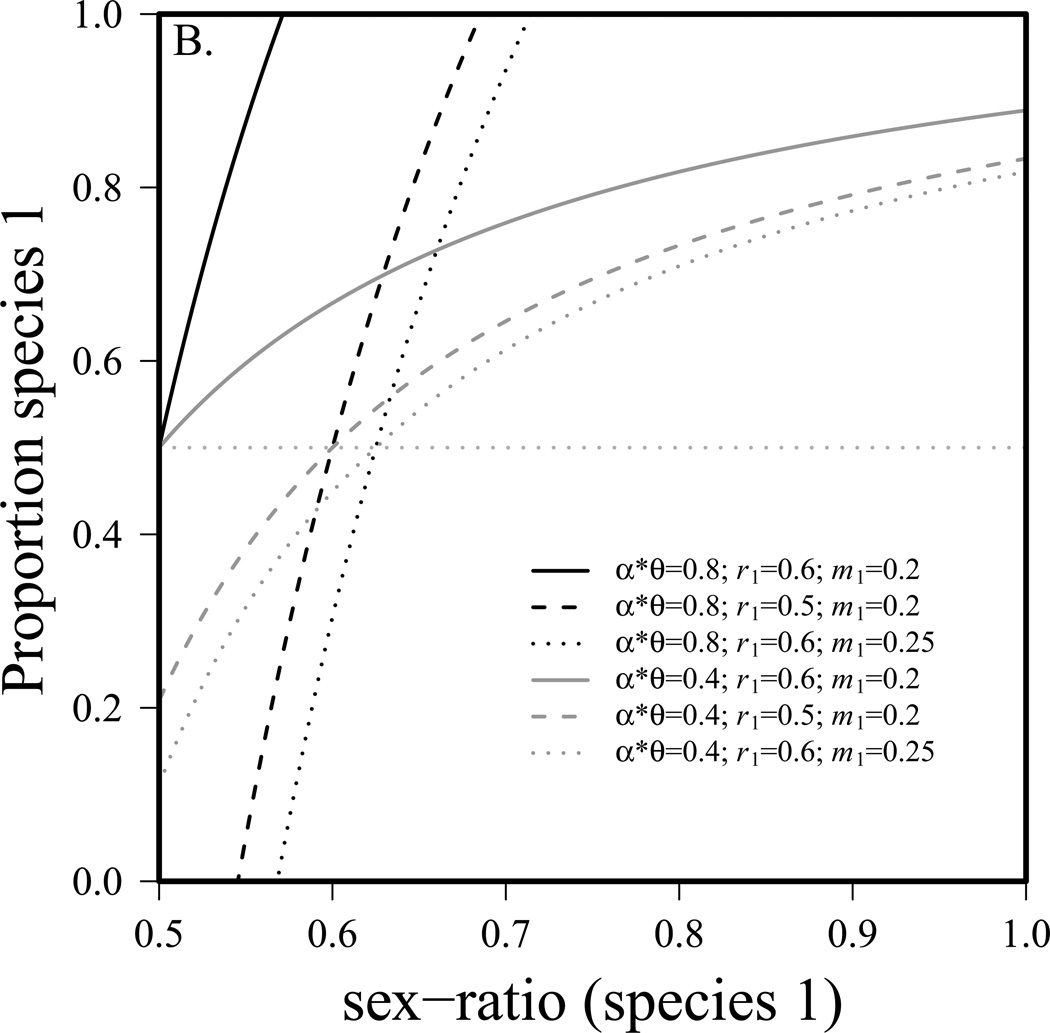
Figure 1a shows the range of parameter values allowing for coexistence of the two species. Below the lower line, species 1 is excluded by species 2. Above the upper line, species 1 excludes species 2 (note that for weaker competition there is no upper line since species 1 cannot exclude species 2 with these parameters). From figure 1a, it is evident that as competition (αθ) increases, the parameter space allowing for coexistence shrinks, as expected. The figure also illustrates that even with a considerable disadvantage in per capita birth rate (r), a skewed sex-ratio can still allow species 1 to exclude species 2. For example, with strong competition (αθ = 0.9), and a 10% birth rate disadvantage (r1=0.54, r2=0.6), species 1 can still exclude species 2 if the sex-ratio is greater than 0.58. Note that when competition is weak, species 2 cannot be excluded with parameters employed and thus there is no upper dotted line. Figure 1b shows the proportion of the community that is species 1 (with sex-ratio) as the sex-ratio and other parameters are allowed to vary. As in figure 1a, it is evident that conditions of stronger competition (black lines) have a narrower range allowing for coexistence than do conditions with weaker competition (gray lines). Figure 1b also illustrates that a species with a female-biased sex-ratio can withstand considerable insults to its fertility or mortality and still be the predominant species in the community.
Figure 1.
General sex-ratio effect on competition, a) conditions allowing for coexistence of two species. Species 1 excludes species 2 above upper line, species 2 excludes species 1 below lower line. Gray dotted lines indicate 50% female (horizontal) and r1=r2 (vertical). Competition is symmetrical (α12θ12 = α21θ21), K1=K2=10000, r2=0.6, m1=m2=0.2. b) proportion of the community that is species 1 (with sex-ratio skew) at equilibrium under strong and weak competition. The gray horizontal line indicates that species are present in equal proportions. Competition is symmetrical (α12θ12 = α21θ21), K1=K2=10000, r1=r2=0.6, m1=m2=0.2 unless noted on figure.
Above we assumed no mechanism of sex-ratio distortion and therefore any costs associated with this distortion are not taken into account. Having shown the general effect of skewed sex-ratio on competition, we now address the case of sex-ratio meiotic drive.
Shorrocks’ model with sex-ratio meiotic drive
In addition to a skewed sex-ratio at equilibrium, most sex-ratio meiotic drive chromosomes are assumed to carry some cost in males, females or both. We assume (see above) that the costs that matter in terms of competition are fertility costs in females – we still assume that sperm is not limiting, understanding that this may break down as sex-ratios become very skewed toward females. For now, we also assume that the two species are geographically isolated and the sex-ratio system comes to equilibrium in species 1, then the two species are allowed to come into contact. This allows us to keep the continuous competition model and the discrete sex-ratio model separate. Later we attempt to combine the two.
Females of species 1 now produce offspring at a rate of compared to the same species without a sex-ratio system. Their offspring are female and male. Modifying equation 7, we get
| (9.1) |
| (9.2) |
| (9.3) |
| (9.4) |
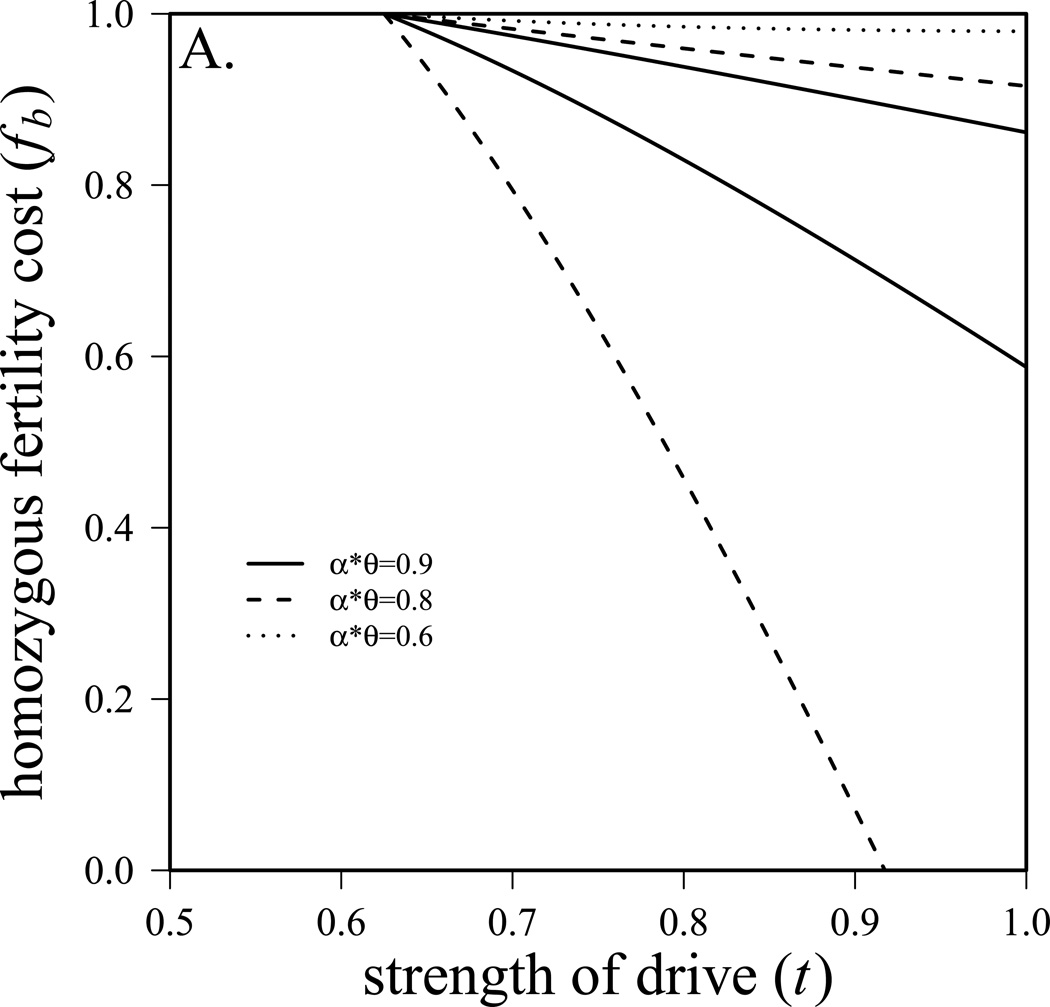
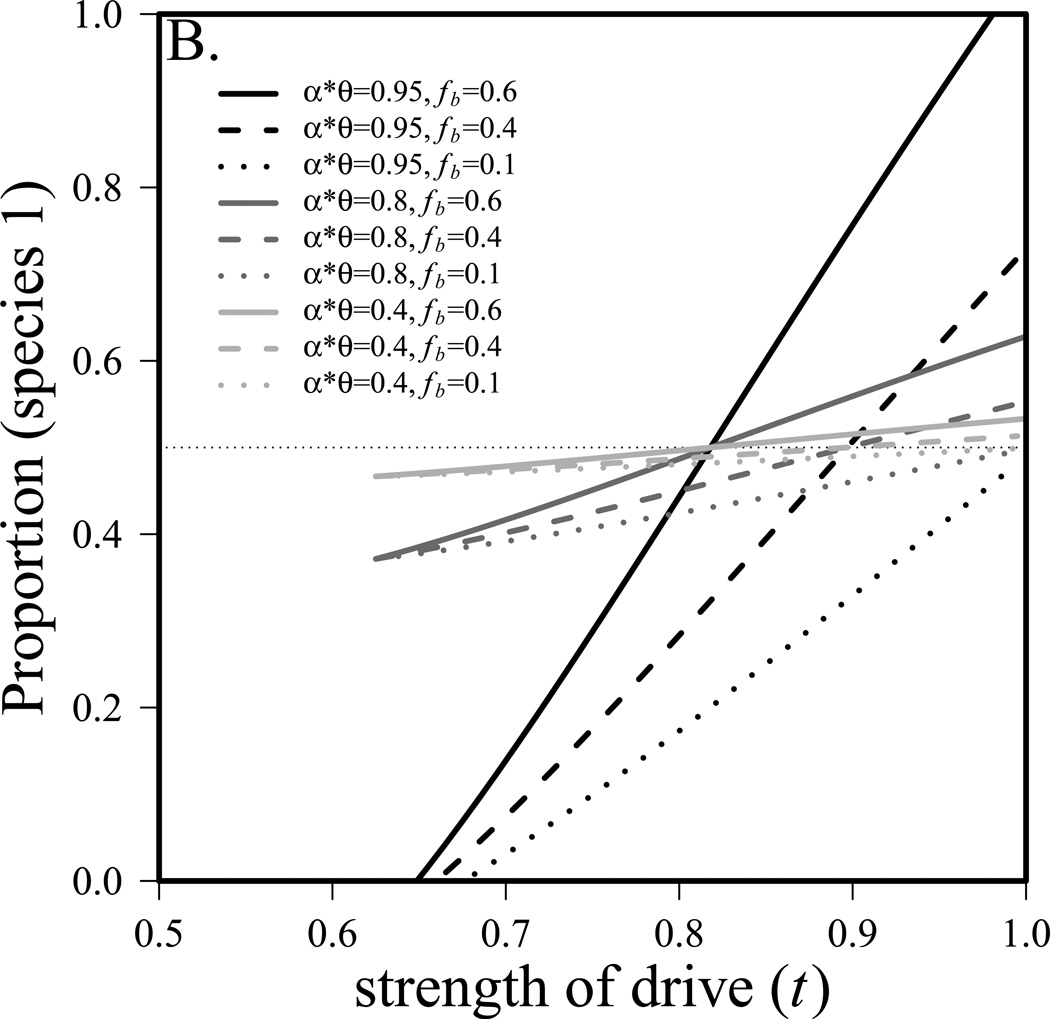
Solutions to this set of equations are analogous to those from equation 7 (Supplemental equation S1). The conditions for coexistence of the two species (found by setting equation S1.1 and S1.3 equal to 0 and solving for fb) are also analogous to the general case, but are now much less elegant (Equation S2). Figure 2a shows these conditions graphically. Like figure 1a, it is evident that stronger competition allows for narrower parameter space leading to coexistence. Well-studied drivers are generally strong (t>0.9, Jaenike 2001), making it more likely that species can coexist. In figure 2a, we assume that r1 is two-thirds of r2 so species 1 is at a considerable disadvantage in the absence of drive. The system in equation 9 also allows us to determine the proportion of the community that is species 1 ((N1f + N1m)/(N1f + N1m + N2f + N2m)), which is presented in figure 2b. Note again, that with strong competition, changes in the strength of drive (t) can have a significant impact on interspecific competition. For example, if αθ = 0.95, and fertility fitness in homozygous females is moderate (f3=0.6), then species 1 makes up 14% of the community with t=0.7 and excludes species 2 when t=0.99. Again, it is important to note that most known drivers have t>0.9 where competitive advantages are greatest.
Figure 2.
The influence of sex-ratio meiotic drive on interspecific competition. a) conditions for coexistence of two species if species 1 harbors a sex-ratio meiotic drive system. Above the upper line species 2 is excluded, below the lower line species 1 is excluded. r1=0.4, r2=0.6, m1=m2=0.1, K1=K2=10,000, fa=1, fb=0.6, fc=0.8. Note that with weaker competition (αθ = 0.6), species 1 cannot exclude species 2. b) the proportion of the community that is species 1 (with sex-ratio meiotic drive system). r1=0.54, r2=0.6, m1=m2=0.1, K1=K2=10,000, fa=1, fc=0.8.
In graphical results presented thus far we have assumed that fertility costs in females are recessive. Dominant fertility costs in females are impossible since the conditions for stability of the drive system cannot be met. If we assume that fertility costs in females are additive , the parameter space allowing for stable polymorphism of the driver is much smaller. Supplemental figure S1 is analogous to figure 2b, but assuming additive fitness effects. It is evident from the figure that a driver with additive cost is much less likely to be segregating in a species to begin with and therefore is less likely to impact interspecific competition. Furthermore, a driver that is segregating and has additive costs on females might bring a cost in interspecific competition, depending on the parameters. For example, a strong driver (t>0.9), with a relatively week fitness cost in homozygous females (f=0.6) leads to a competitive disadvantage if fitness costs are additive in heterozygous females.
A sex-ratio system arises in an established community
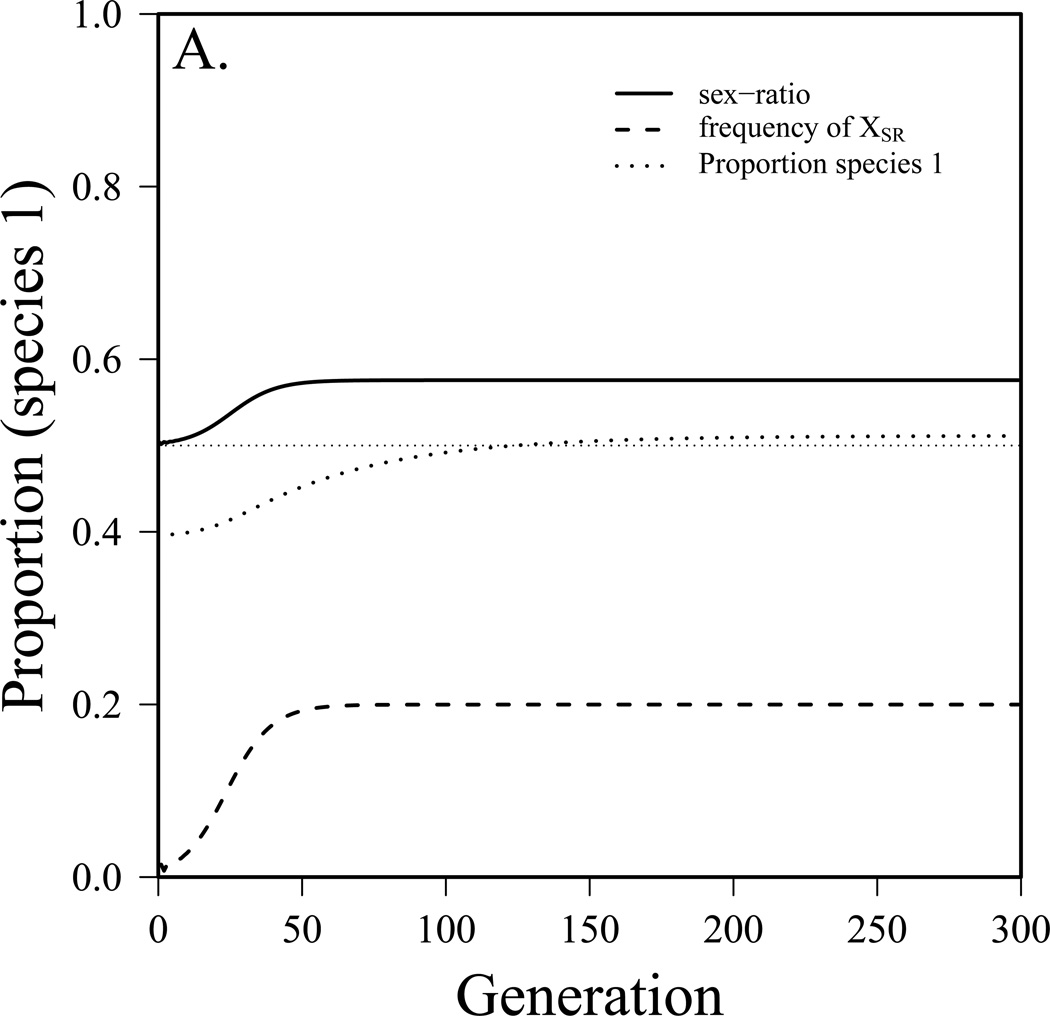
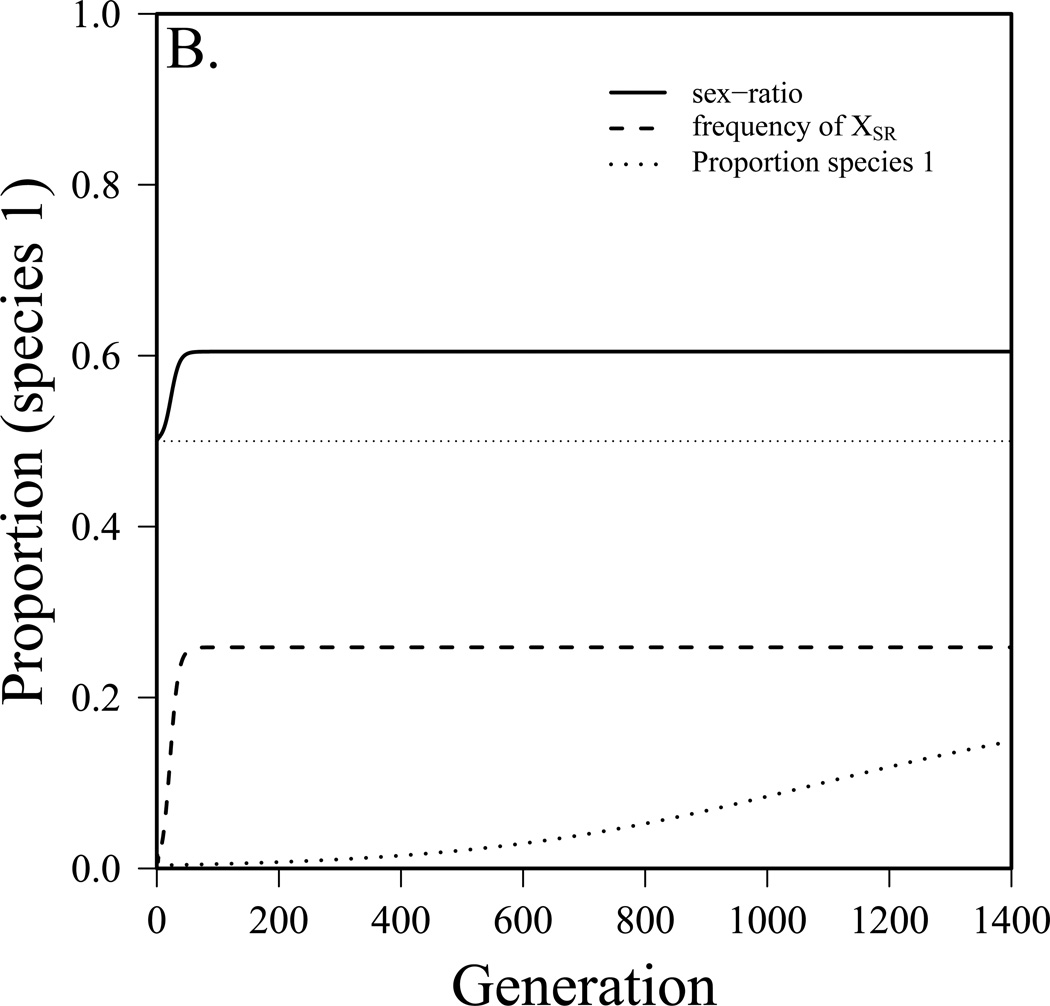
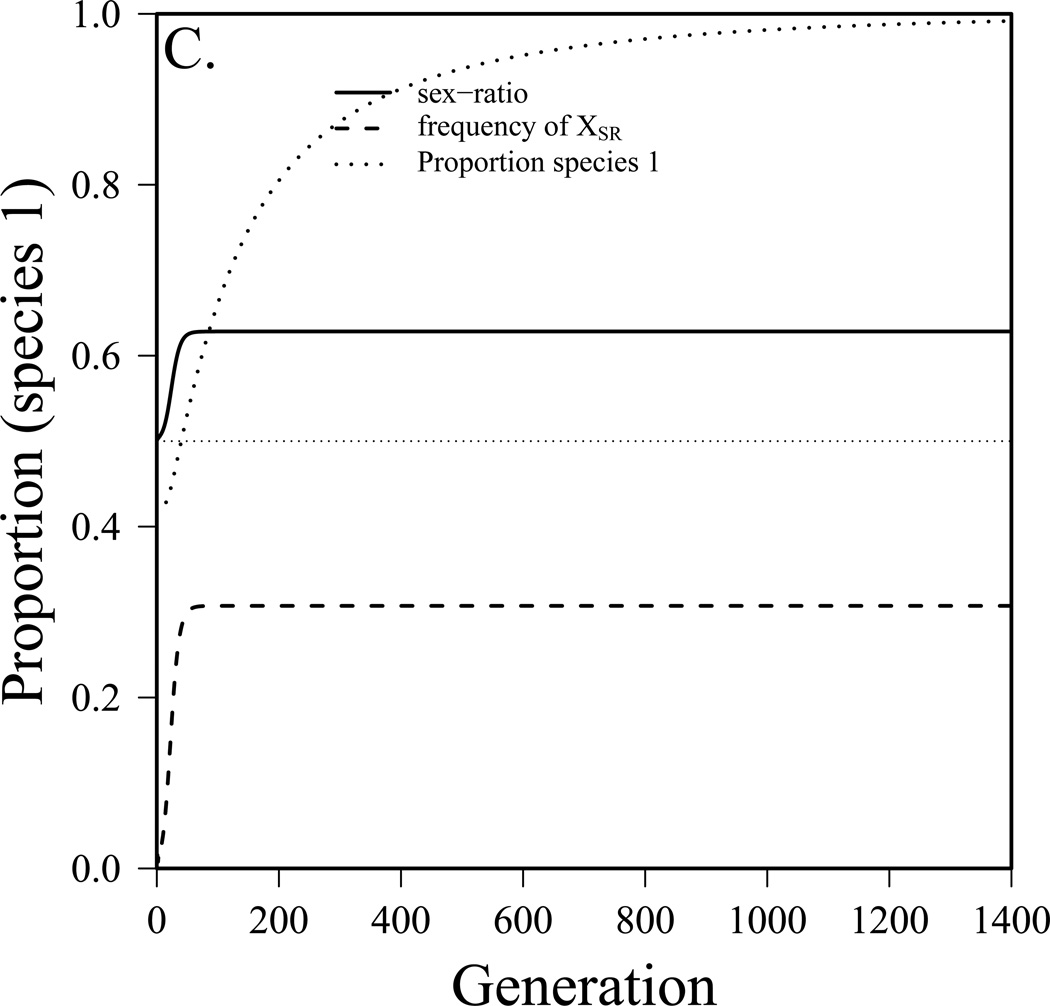
To this point we have assumed that the sex-ratio system came to equilibrium prior to competition between species. It is also interesting to explore the dynamics of interspecific competition as a sex-ratio system becomes established in one of the two species. To do this, we employ the combined model (see appendix equation S3) and start with the driving X-chromosome rare (single copy) and the numbers of species 1 and species 2 what they would be at equilibrium without drive. Figure 3 presents three simulated scenarios. In figure 3a, species 1 goes from 40% of the community to 51%, the driver reaches an equilibrium frequency (in males) of 20% and the sex-ratio is 0.58. In figure 3b, species 1 had been excluded previously due to a combination of a lower birth rate and very strong competition. After the driver reaches equilibrium (26% frequency, 60% female sex-ratio), species 1 makes up 20% of the community. In figure 3c, prior to the spread of the driver the two species were similar, though species 2 had a slight advantage. After the driver reaches equilibrium (frequency in males = 31%, sex-ratio = 63% female), species 1 is able to exclude species 2. In this case, r1 went from 0.59 to effectively 0.69 because of the driver. While the parameter values used in figure 3 were chosen to illustrate these three scenarios, those for drive do not fall far outside the range of values observed in wild Drosophila populations (see below). While competition is more difficult to measure, it is likely to be quite strong in some Drosophila species (Shorrocks et al. 1979, Jaenike and James 1991). For example, Shorrocks (1979) measured the overlap component (θ) to be between 0.75 and 1 for several fungus-feeding Drosophila species measured and somewhat less for domestic Drosophila. Jaenike and James (1991) found the strength of interspecific competition to be of the same general magnitude as intraspecific competition in fungus-feeding Drosophila. In laboratory studies, competition between Drosophila species was found to be most intense during larval stages (Merrell 1950, Barker and Podger 1970). Finally, Wallace (1974) found that increasing density of heterospecifics lead to a greater reduction in offspring production than the same increase in density of conspecifics in some species pairs, again indicating interspecific competition on par with intraspecific competition.
Figure 3.
The dynamics of interspecific competition as a sex-ratio meiotic drive system becomes established in species 1. m1=m2=0.1, K1=K2=10,000, fa=1, r2=0.6. a) Coexistence before and after spread, but species 1 becomes dominant (r1=0.55, αθ = 0.8, fb=0.2, fc=0.75, t=0.98), b) species 1 was excluded before, after is dominant (r1=0.5, αθ = 0.95, fb=0.3, fc=0.8, t=0.98), c) coexistence before, species 2 excluded after (r1=0.59, αθ = 0.95, fb=0.4, fc=0.8, t=0.99).
Though the combined model is more cumbersome, it does allow us to assign different mortalities to each genotype in the sex-ratio model. In the recessive case, whether fitness costs are fertility or viability does not have a qualitative effect on our result. For example, imagine a strong driver (t=0.98) with r1=r2=0.6, K1=K2=10000, symmetrical competition with αθ = 0.8, and all mi=0.1, with no fitness costs in heterozygous females or males carrying the driver. If homozygous females are sterile, then the equilibrium frequency of the driver is 0.25, the sex-ratio is 0.62 and species 1 is 61.5% of the community. If homozygous females are semi-inviable (mw=1), then the equilibrium frequency of the driver is 0.27, the sex-ratio is 0.61 and species 1 is 62.6% of the community. Note that this does allow homozygous females to exist for one unit of time before they die.
It makes good sense that the integrated model yields the same result as when the two models are taken separately and combined. Since we assume that competition does not influence sex-ratio (K, α and θ don’t depend on genotype), if mortality rates are equal between genotypes, the equilibrium should be the same.
Discussion
Sex-ratio meiotic drive systems may have several evolutionary consequences. Above we show that it may also have a pronounced ecological impact by imparting a competitive advantage on the species harboring drive. In a general sense, assuming no cost of the skewed sex-ratio, species with a female-biased sex ratio may enjoy a substantial competitive advantage. With moderate levels of competition and bias in sex-ratio, the species with biased sex-ratio becomes more prominent (~60–70% of the community).
Several studies have shown that females might bias sex-ratios toward daughters in response to interspecific competition (Dickman 1988 and references therein). It is important to note here that the competitive advantage from sex-ratio meiotic drive does not lead to selection for skewed sex-ratio. Within the population, the Fisherian principle still applies: the autosomes are selected to increase the frequency of the rare sex, given equal parental investment, and this would occur even if it were to reduce the interspecific competitiveness of the species.
Above we assumed that sex-ratios do not become so skewed that males and/or sperm become limiting. This seems reasonable given the known cases of sex-ratio meiotic drive where sex-ratios are not expected to exceed 70% (see table 1). For example, if the sex-ratio is 2/3 female, each male mates twice as often as each female, which they are probably happy to do. If sex-ratios become excessively skewed toward females, sperm would become limiting and population extinction is a real possibility. When our assumption that sperm is not limiting is violated, average per capita reproductive output likely decreases, reducing competitive advantage. In fact, in this case, competition would likely hasten a population’s decline.
Table 1.
Parameters from known SR systems and their predicted effects on competition
| Species | t | fa | fb | fc | πf | Freq. (♂) | Adj. | Proportion (α*θ=0.5/0.9) |
Host | Source |
|---|---|---|---|---|---|---|---|---|---|---|
| D. affinis | 0.98 | 1 | 0.3 | 0.59 | 0.53 | 0.10 | 1.05 | 0.52/0.61 | Sap flux** | Unckless (unpublished) |
| D. pseudoobscura* | 0.99 | 0.93 | 0.34 | 0.7 | 0.55 | 0.15 | 1.06 | 0.52/0.64 | Sap flux** | Curtsinger and Feldman 1980 |
| D. neotestacea | 0.99 | 1 | 0.12 | 0.8 | 0.59 | 0.21 | 1.11 | 0.59/0.73 | Fungus | James and Jaenike 1990 |
| D. recens | 0.98 | 1 | 0 | 0.57 | 0.51 | 0.05 | 1.03 | 0.51/0.56 | Fungus | Jaenike 1996 |
| D. quinaria | 0.98 | 1 | 0.44 | 0.54 | 0.51 | 0.05 | 1.03 | 0.51/0.56 | Fungus | Jaenike 1996 |
(Values in italics are inferred using the fertility model presented above,
fertility and viability costs are collapsed into fertility costs,
best guess, but not confirmed, Adj. is the adjustment to r due to the sex-ratio system)
Additionally we assume that the sex-ratio system influences competition only through fertility fitness (r). In principle, any competition parameter could be affected by the presence of a driving X-chromosome. For example, if males and females utilize resources differently, a skewed sex-ratio might also alter the carrying capacity of the population. Additionally, drivers might carry viability costs (reviewed in Jaenike 2001), which may in turn influence the equilibrium of the sex-ratio system and the competitive balance between species. In the latter case, we have explored the differences between fertility and viability costs and their influence on the population genetics of sex-ratio are real, but not large. The same is true for viability costs in interspecific competition, especially if we assume costs are recessive in females and the driver is at low frequency.
Cases of sex-ratio meiotic drive are well-studied in Drosophila, but the suite of parameters necessary to estimate the reproductive advantage gained by drive are usually only partially known. Furthermore, little is known about competition between related Drosophila, except in the mushroom feeding group where competition can be quite intense (James and Jaenike 1991, Grimaldi and Jaenike 1984). Shorrocks et al. (1979) showed that overlap between closely related species could also be quite high (in some cases approaching 1). Taken together, this suggests that competition between Drosophila species is likely to be intense.
The known parameters for SR systems in Drosophila are presented in Table 1, approximating unknown parameters based on knowledge from other Drosophila sex-ratio systems. All parameters from the competition model are assumed to be equal in the focal species and its competitor. The impact of the sex-ratio system on interspecific competition is predicted to be greatest in those species with the largest skew in sex-ratio, but cost also plays an important role. D. neotestacea harbors a sex-ratio chromosome at a relatively high frequency (0.20), this leads to a modest advantage with weak competition (59% of the community), but a much larger advantage with greater competition. The magnitude of competitive advantage declines with both equilibrium sex-ratio and frequency of the sex-ratio X chromosome in males. In fact, although the fertility parameters used in these estimates varied widely, the relationship between the proportion of the community that is species 1 and equilibrium sex-ratio and male frequency appears nearly linear over the known range of values (supplemental figure S2). This suggests that the relationship is driven almost completely by the sex-ratio and that the fertility costs play a minor role in determining the outcome of competition. This makes sense since we are assuming that fertility costs are recessive (or nearly recessive) and that equilibrium frequencies are low enough that homozygous females are rare. Note that this linear relationship breaks down as the equilibrium sex-ratio approaches 50% female.
A competitive advantage enjoyed by species with female-biased sex-ratio is also consistent with species distributions in at least one case. The frequency of the sex-ratio phenotype in male D. affinis increases with decreasing latitude (Unckless unpublished), as does the proportion of the community D. affinis comprises (Miller 1958). Of course, to speculate that this relationship is causal is premature without much more data.
Several mechanisms of sex-ratio distortion (due to local mate competition, cytoplasmic male sterility in plants, etc.) may result in a competitive advantage for a species. Cytoplasmic male-killers such as Spiroplasma and Wolbachia, could provide this sort of advantage, but the sex-ratio is skewed by killing embryos (just decreasing the number of males), not manipulating gamete composition (increasing the number of females and decreasing the number of males) so the effect is likely small and sometimes negative. Wolbachia can also act as a feminizer in which case an infected species might gain a competitive advantage.
Conversely, interspecific competition likely would have an effect on male-killing dynamics within species. As competition increases (larger αθ), the probability that two conspecific females lay eggs in the same resource increases. If daughters benefit from male-killing by avoiding competition with their brothers, this benefit is diluted if they also have to share resources with another species. The male-killing benefit would therefore decrease and the equilibrium infection frequency would be lower.
It is now clear that intragenomic conflict can influence several aspects of species evolution. Here we show that sex-ratio meiotic drive can also influence ecological relationships between species by providing a reproductive advantage due to an excess of females. It is also possible the skewed sex-ratio produced by such system may have other ecological consequences, such as transmission dynamics of sex-specific parasites or predator-prey dynamics if predation rates are sex-specific.
Supplementary Material
Acknowledgements
We thank John Jaenike, Hidetoshi Inamine and Tim Connallon for thoughtful discussion and useful comments on previous versions of the manuscript. We also thank reviewers for comments and suggestions. This work was supported by NIH grant R01-GM064590 to AGC and to NIH grant F32-HD071703 to RLU.
Contributor Information
Robert L. Unckless, Email: rlu1@cornell.edu.
Andrew G. Clark, Email: ac347@cornell.edu.
References
- Barker JSF, Podger RN. Interspecific Competition Between Drosophila melangaster and Drosophila simulans: Effects of Larval Density on Viability, Developmental Period and Adult Body Weight. Ecology. 1970;50:170–189. [Google Scholar]
- Carvalho AB, Vaz SC. Are Drosophila SR drive chromosomes always balanced? Heredity. 1999;83:221–228. doi: 10.1038/sj.hdy.6886100. [DOI] [PubMed] [Google Scholar]
- Clark AG. Natural selection and Y-linked polymorphism. Genetics. 1987;115:569–577. doi: 10.1093/genetics/115.3.569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickman CR. Sex-ratio variation in response to interspecific competition. The American Naturalist. 1988;132:289–297. [Google Scholar]
- Curstinger JW, Feldman MW. Experimental and theoretical analysis of the “sex-ratio” polymorphism in Drosophila pseudoobscura. Genetics. 1980;94:445–466. doi: 10.1093/genetics/94.2.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards AWF. The population genetics of the sex ratio in Drosophila pseudoobscura. Heredity. 1961;16:291–304. [Google Scholar]
- Grimaldi D, Jaenike J. Competition in natural populations of mycophagous Drosophila. Ecology. 1984;65:1113–1120. [Google Scholar]
- Hall DW. Meiotic drive and sex chromosome cycling. Evolution. 2004;58:925–931. doi: 10.1111/j.0014-3820.2004.tb00426.x. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Extraodinary sex-ratios. Science. 1967;156:477–388. doi: 10.1126/science.156.3774.477. [DOI] [PubMed] [Google Scholar]
- James AC, Jaenike J. "Sex ratio" meiotic drive in Drosophila testacea. Genetics. 1990;126:651–656. doi: 10.1093/genetics/126.3.651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaenike J, James AC. Aggregation and the coexistence of mycophagous Drosophila. Journal of Animal Ecology. 1991;60:913–928. [Google Scholar]
- Jaenike J. Sex-chromosome meiotic drive. Annual Review of Ecology and Systematics. 2001;32:25–49. [Google Scholar]
- Kozielska M, Weissing FJ, Beukeboom LW, Pen I. Segregation distortion and the evolution of sex-determining mechanisms. Heredity. 2010;104:100–112. doi: 10.1038/hdy.2009.104. [DOI] [PubMed] [Google Scholar]
- Levin S. Community equilibria and stability, and an extension of the competitive exclusion principle. Am. Nat. 1970;104:413–423. [Google Scholar]
- McDermott SR, Noor MAF. The role of meiotic drive in hybrid male sterility. Philosophical Transactions of the Royal Society of London Series B. 2010;365:1265–1272. doi: 10.1098/rstb.2009.0264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merrell DJ. Interspecific Competition between Drosophila funebris and Drosophila melanogaster. The American Naturalist. 1950;85:159–169. [Google Scholar]
- Miller DD. Geographical distributions of the American Drosophila affinis subgroup species. American Midlands Naturalist. 1958;60:52–70. [Google Scholar]
- Price TAR, Hodgson DJ, Lewis Z, Hurst GDD, Wedell N. Selfish genetic element promotes polyandry in a fly. Science. 2008;322:1241–1243. doi: 10.1126/science.1163766. [DOI] [PubMed] [Google Scholar]
- Shorrocks B, Atkinson W, Charlesworth P. Competition on a divided and ephemeral resource. Journal of Animal Ecology. 1979;48:899–908. [Google Scholar]
- Taylor JE, Jaenike J. Sperm competition and the dynamics of X chromosome drive: Stability and extinction. Genetics. 2002;160:1721–1731. doi: 10.1093/genetics/160.4.1721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace B. Ecology. 1974;55:227–244. [Google Scholar]
- Werren JH. Selfish genetic elements, genetic conflict and evolutionary innovation. PNAS. 2011;108:10863–10870. doi: 10.1073/pnas.1102343108. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.