Abstract
Working memory (WM) is positively correlated with socioeconomic status (SES). It is not clear, however, if SES predicts the rate of WM development over time nor whether SES effects are specific to family rather than neighborhood SES. A community sample of children (n = 316) enrolled between ages 10 and 13 completed four annual assessments of WM. Lower parental education, but not neighborhood disadvantage, was associated with worse WM performance. Neither measure of SES was associated with the rate of developmental change. Consequently the SES disparity in WM is not a developmental lag which narrows nor an accumulating effect that becomes more pronounced. Rather, the relation between family SES and WM originates earlier in childhood and is stable though adolescence.
Working memory refers to the active, short-term maintenance and manipulation of information, generally in the service of guiding behavior, and is dependent on the prefrontal cortex (Baddeley, 2003; Best & Miller, 2010). Working memory becomes differentiated from single, overarching executive control processes by middle childhood and exhibits improvement through childhood and adolescence as the prefrontal cortex develops (Best & Miller, 2010; Lee, Bull, & Ho, in press). In the past decade the question of how social contexts, such as socioeconomic status, influence working memory performance and development has emerged as an increasing area of focus to explain individual differences in working memory development.
This question also has considerable applied relevance. Working memory is a strong candidate mediator explaining the graded association between socioeconomic status (SES) and disparities in achievement, health and psychopathology (Adler et al., 1994; Bradley & Corwyn, 2002; Brooks-Gunn & Duncan, 1997; Sirin, 2005). It is not surprising, given its function of holding and integrating information, that working memory plays a critical role in a wide array of cognitive abilities (Kimberg & Farah, 1993), mathematical skills (Alloway & Alloway, 2010; Bull, Espy, & Wiebe, 2008) and reading comprehension (Alloway & Alloway, 2010; Daneman & Merikle, 1996), and thus is an important foundational ability for cognitive development and achievement. Additionally, working memory has also been associated with depression (Snyder, 2013), health behaviors such as nutrition and physical activity (Riggs, Chou, Spruijt-Metz, & Pentz, 2010), alcohol use (Houben, Wiers, & Jansen, 2011) and sexual debut (Khurana et al., 2012). Consequently, working memory is a plausible mediator that may account, at least in part, for a wide-range of SES-related disparities.
SES can be measured by various indices such as family income, parental education, and neighborhood characteristics (Krieger, Williams, & Moss, 1997). It is generally correlated with child and family stress and parenting behavior (Bradley & Corwyn, 2002; Conger & Donnellan, 2007; Evans, 2004), factors which would be expected to impact the development of neurocognitive systems including working memory (Bernier, Carlson, Deschenes, & Matte-Gagne, 2012; Blair, 2010;), and indeed many research groups have found a positive relation between childhood SES and working memory measured at different ages. For example, lower-SES preschool and early elementary school children perform worse on working memory tasks (Noble, McCandliss, & Farah, 2007), and on composite or latent measures of executive function (Blair et al., 2011; Hughes, Ensor, Wilson, & Graham, 2010; Noble, Norman, & Farah, 2005; Wiebe et al., 2011). In middle childhood, SES effects have been observed in WM tasks including digit span, spatial working memory, and an object 2-back (Farah et al., 2006; Sarsour et al., 2011). SES effects on working memory are apparent through adolescence: Evans and Schamberg (2009) found that duration of poverty was inversely related to spatial working memory at age 17, while Waber (2007) found SES effects on tests of spatial working memory and digit span in a group of children aged 6–17 years.
The present analysis was undertaken to address two basic questions about the association between SES and the development of working memory. First, what is the trajectory of SES disparities in working memory development? In contrast to other aspects of executive function, working memory development continues without leveling off through the end of adolescence (Best & Miller, 2010), suggesting that it may remain sensitive to ongoing experiential effects throughout this period. Does the SES disparity in working memory widen, as the effects of experience accumulate, further disadvantaging lower SES individuals? Does it hold steady, reflecting early emerging differences but similar developmental processes across time? Or does the SES disparity in working memory gradually resolve as children mature into adolescence and young adulthood, perhaps because it represents a delay for low SES children along a common developmental path? In addition to addressing basic questions concerning the developmental plasticity of working memory, understanding when SES effects emerge and how they change over time provides critical guidance for identifying the mechanisms underlying these differences. Identification of such mechanisms can then provide additional targets for prevention programs aimed at reducing disparities in academic and cognitive functioning.
Findings that SES predicts working memory in adults (Lee, Kawachi, Berkman, & Grodstein, 2003) might appear to demonstrate the persistence of SES effects on working memory. However, unlike the effects of childhood SES, these effects can be explained by the mechanism of “social selection,” a downward drift in SES for individuals with lower working memory (Conger & Donnellan, 2007). In addition, the absence of common measures of working memory and SES across child and adult studies precludes knowing whether disparities increase, decrease or hold constant in the transition from childhood to adulthood.
Evans and Schamberg’s (2009) finding that the duration of poverty predicts working memory is consistent with a progressive widening of SES disparities over development, as disadvantage accumulates and compounds. However, this may not be due to the effects of poverty on developmental trajectories of working memory. Instead, it may be due to the repeated, additive effects of continuous exposure to poverty, and thus not indicative of early SES-related disparities that widen over time. To our knowledge no study has examined SES effects on working memory longitudinally through adolescence. In addition, despite prospective evidence that SES predicts executive function overall in young children (Blair et al., 2011), there is little prospective evidence demonstrating the specific association between childhood SES and later working memory performance. For these reasons we analyzed data from a longitudinal study of executive function development spanning the ages of 10–17 years old.
The second question addressed here concerns the more specific aspects of SES related to working memory development, and in particular whether previously reported effects of family-level SES are independent and unique from other aspects of SES, such as neighborhood disadvantage. From a theoretical perspective, neurocognitive development may emerge via a dynamic interaction between individuals and their social contexts (e.g Bronfenbrenner & Morris, 1998), including neighborhoods, which may become increasingly important as children and adolescents age and engage in more direct interaction with their wider social contexts and institutions. Such a developmental perspective is consistent with the public health and sociological literatures, which posit that neighborhood factors reflect unique components of socioeconomic experience that have different associations with health and behavior beyond the effects of income and education (Diez-Roux & Mair, 2010; Krieger et al., 1997). In addition, relations between neighborhood SES and neurocognitive or health outcomes may be mediated by mechanisms that are both overlapping with and unique from family-level SES. Among the hypothesized unique causes for neighborhood effects, compared to family-level effects, include housing quality, the built environment, environmental exposures, peer effects, collective social support and efficacy, neighborhood resources, and violence exposure (Diez-Roux & Mair, 2010; Leventhal & Brooks-Gunn, 2000). Acute violence exposure has been linked to performance decrements on tasks of attention (Sharkey, Tirado-Strayer, Papachristos, & Raver, 2012), while lead exposure has been linked to lower working memory performance (Chiodo, Jacobson, & Jacobson, 2004), indicating that such mechanisms are plausible. Consequently, the specificity of SES effects has considerable consequences for the theoretical propositions concerning underlying mechanisms as well as for the nature of policy or programmatic interventions that may be recommended to address disparities. Nevertheless, despite an emerging literature on neighborhood SES and cognitive function in general, and verbal ability in particular (Sampson, Sharkey, & Raudenbush, 2008; Wight et al., 2006), neighborhood SES has yet to be investigated with respect to working memory.
To address the two questions just described, we analyzed data from a community-based cohort of children enrolled between the ages of 10 and 13 and followed for five years. This data set was ideally suited to the study of working memory because the annual assessment included four different tests of working memory that were found to load on a common factor. Our goal was to determine whether either neighborhood disadvantage, family SES, indexed by parental education, or both, predicted the working memory factor at the study outset, and whether disparity observed in this measure grew, held steady or narrowed through the end of adolescence.
Method
Sample and Study Procedures
The current study sample is derived from a 5-year accelerated longitudinal study of executive function, risk behaviors, and impulsivity. Participants between the ages of 10 and 13 were recruited from urban public and parochial schools. The current analysis employs the final four years of data for tasks of working memory, due to change in the assessment battery after the first year of assessment. Testing occurred in the school setting, research center testing rooms, and community libraries. Working memory tasks were administered using E-Prime 1.0 (Psychology Software Tools, Pittsburgh, PA) on touch-screen laptops. Complete testing sessions lasted up to two hours, with a break to reduce fatigue and maintain interest. Parental consent and youth assent were obtained, and youth were reimbursed for their time and travel. The study was approved by the Institutional Review Board of the Children’s Hospital of Philadelphia.
Through the 5th annual assessment 87% of the original sample was retained (n = 335 from a possible 387), indicative of minimal attrition. The distribution of those who completed the final assessment did not differ from those who did not in terms of age at study entry (p = .73), gender (p = .66), African-American racial identity (p = .09), Hispanic or Latino ethnicity (p = .79), whether the primary caregiver is the mother (p = .14), whether or not a secondary caregiver was present (p = .27). In addition there were no differences in performance on any working memory task administered prior to the final year of assessment (all p > .09), indicating no differential attrition by working memory performance. There were no differences between those who completed the final assessment and those who did not with respect to parental education (p = .95) or neighborhood rates of poverty (p = .11), receipt of public assistance (p = .23), or population under 18 (p = .17). However, those who remained in the study came from neighborhoods with higher rates of unemployment (p = .03), African-American populations (p = .005), and female-only households (p = .02), indicating that adolescents living with greater neighborhood disadvantage were more likely to remain in the study until completion.
Participants were omitted from analysis if they reported regular medication use for Attention Deficit Hyperactivity Disorder or a diagnosis of depression, bipolar disorder, or obsessive-compulsive disorder at the time of the first assessment (n = 31). In addition, 38 participants were omitted from analyses because a sibling or household member was also in the study, due to concerns regarding non-independence and because our independent variables of interest would be identical across household members. Members of the dyad with the most complete data were retained in this analysis or, if there was no difference between household members, the first enrollee was retained. In addition, participants who withdrew or did not provide demographic information prior to the first assessment were omitted (n = 2). Sample characteristics for those included in the analysis (n = 316) are reported in Table 1.
Table 1.
Sample Characteristics
| Variable | n (%) |
|---|---|
| Gender | |
| Male | 145 (45.9) |
| Female | 171 (54.1) |
| Race and Ethnicity | |
| White | 193 (61.1) |
| African-American | 82 (25.9) |
| Asian or Pacific Islander | 31 (9.8) |
| American Indian | 1 (0.3) |
| Mixed | 9 (2.8) |
| Hispanic or Latino | 26 (8.2) |
| Primary Caregiver | |
| Mother | 270 (85.4) |
| Father | 36 (11.4) |
| Family member, Not Parent | 7 (2.3) |
| Other | 3 (0.9) |
| Secondary Caregiver | |
| Present | 254 (80.4) |
| Mother | 31 (9.8) |
| Father | 189 (59.8) |
| Family member, Not Parent | 31 (9.8) |
| Other | 4 (1.3) |
(n = 316)
Measurement of parental education and neighborhood disadvantage
Parents completed a demographic questionnaire in a telephone interview during the first study year that included questions regarding the child’s grade in school, medical history, family composition, and caregiver education. As a secondary caregiver was reported for 80.4% of the children included in this analysis, average parental education, measured in years, was employed to ensure that data reflected the education of both parents without raising concerns due to multicollinearity. Table 2 outlines the distribution of parental education for the primary and secondary caregivers as well as the average.
Table 2.
Parental Education, Years
| Average* | Primary Caregiver |
Secondary Caregiver |
|
|---|---|---|---|
| Summary Statistics | |||
| Mean (SD) | 13.9 (2.3) | 14.0 (2.6) | 13.9 (2.7) |
| Range (Min-Max) | 6.0 – 20.5 | 3.0 - 25.0 | 5.0 – 22.0 |
| Interquartile Range | 12.0 – 16.0 | 12.0 – 16.0 | 12.0 – 16.0 |
| Distribution [Number (%)] | |||
| Less than 12 years | 27 (8.5) | 23 (7.3) | 18 (5.7) |
| 12 years | 75 (23.7) | 93 (29.4) | 100 (31.6) |
| 12 – 16 years | 134 (42.4) | 91 (28.8) | 49 (15.5) |
| 16 years | 40 (12.7) | 73 (23.1) | 53 (16.8) |
| > 16 years | 40 (12.7) | 36 (11.4) | 32 (10.1) |
(n = 316)
Average of primary and secondary caregivers, if present
Based on earlier work on neighborhood effects (Sampson et al., 2008), we employed a measure of concentrated disadvantage based on the United States (U.S.) census tract for the child’s home address during the first study year. Five measures were employed from the 2000 U.S. Census: percentage of individuals below the poverty line, unemployed, and receiving public assistance, as well as the density of children under the age of 18 and female-headed households with no spouse present. Principal components analysis confirmed a single factor of concentrated disadvantage that explained 79.1% of the variance in these measures. Factor loadings, presented in Table 3, were used to create a regression-weighted factor score for concentrated disadvantage for each participant. Loadings were similar to those derived from the Chicago study (Sampson et al., 2008), and thus similarly reflect disadvantage in urban neighborhoods. Prior literature had used such a factor to create a categorical variable for exposure to disadvantage, based on the bottom quartile of scores in a sample of neighborhoods, stratified by race and SES. However, as such a sampling procedure was not employed in the design of this study, we employed a continuous measure of disadvantage: the natural logarithm of derived factor scores transformed because the distribution of factor scores was positively skewed.
Table 3.
Neighborhood Characteristics and Concentrated Disadvantage Factor Loadings (n = 316)
| Neighborhood Measure* | M (SD) | Range (Min- Max) |
Inter-Quartile Range |
Factor Loading |
Rates for U.S. |
|---|---|---|---|---|---|
| Below Poverty | 13.3 (11.3) | 0.7 – 55.2 | 5.7 – 16.6 | 0.95 | 12.4 |
| Unemployed | 7.2 (5.4) | 0.0 – 35.7 | 3.7 – 8.6 | 0.92 | 5.7 |
| Public Assistance | 5.4 (5.6) | 0.0 – 31.9 | 1.8 – 6.4 | 0.93 | 3.4 |
| Under 18 | 22.5 (6.1) | 7.6 – 43.7 | 17.8 – 25.9 | 0.71 | 25.7 |
| Female-only household | 24.6 (14.7) | 4.1 – 72.1 | 14.5 – 31.5 | 0.91 | 18.0 |
Expressed as percentage in the census tract
Working Memory Tasks and Factor Construction
Digit Span Backwards
The digit span subtest from the Wechsler Intelligence Scale for Children–Fourth Edition (WISC-IV) (Wechsler, 2003) taxes auditory working memory, with participants immediately repeating sequences of digits of increasing length in both forward and reverse order. In functional imaging studies, this task reliably activates lateral prefrontal cortex (Owen, 2000). The WISC Digit Span Backwards raw score was used as the dependent variable in analyses, as it requires manipulation in addition to maintenance of information. No performance levels greater than 3 SD below the mean were identified and thus all observations were included.
Corsi Block Tapping
In this non-verbal variant of Digit Span task (Milner, 1971), participants view a set of identical blocks that are spatially dispersed. Blocks are individually illuminated in a random sequence, for 500 msec each, and participants are asked to tap each box in the reverse order. Sequence length begins at 3 blocks and proceeds through 9, in sets of 3. The task is discontinued when participants fail 2 or more trials per level. The total correct score was used in analyses. Performance on this task is dependent on right prefrontal brain regions (Owen, 2000; Van Asselen et al., 2006). No performance levels greater than 3 SD below the mean were identified and thus all observations were included.
Spatial Working Memory
This computerized task requires the subject to search for hidden tokens one at a time within sets of four, six, or eight randomly positioned boxes. Tokens are hidden only once in each box. Working memory skills are tapped as the subject, while searching, must hold in working memory the locations already checked and, as tokens are found, they must remember and update the information about the locations of the found tokens (Luciana et al., 2005). The between-search errors score was employed in analyses, due to its higher requirements for continual updating of representations. Lesion studies of patient populations as well as functional imaging studies demonstrate the important of the prefrontal cortex (PFC), particularly the dorsolateral PFC, in performance on this task (Van Asselen et al., 2006). Observations greater than 3SD from the mean were excluded from the analysis due to concerns that extreme values were indicative of poor task understanding or non-compliance, leading to the exclusion of 1.3% or fewer of the observations at each session.
Object Two-Back
This computerized task requires participants to monitor the serial presentation of irregularly shaped polygons, and to press the space bar when they observe a repetition of the stimulus that appeared 2 stimuli previously (Postle, D’Esposito, & Corkin, 2005). Participant must continually update their working memory in order to compare the current shape to the shape presented 2 trials back and inhibit attention to representations of earlier polygons. The total correct response score was employed in analyses. Imaging studies find lateral prefrontal activation with this task (Owen, McMillan, Laird, & Bullmore, 2005). Observations greater than 3SD from the mean were excluded from the analysis due to concerns that extreme values were indicative of poor task understanding or non-compliance, leading to the exclusion of a maximum of 6.3% of observations at each wave.
Working Memory Factor
Table 4 reports mean task performance by session of assessment for each individual task. Table 5 shows bivariate correlations among participant scores on each working memory task, averaged across assessments, as well as correlations with parental education and concentrated disadvantage. All working memory tasks were significantly correlated with each other. These correlations largely held when examining the correlations by session or by age of assessment as well (data not shown). Confirmatory factor analysis conducted with average performance across sessions on each of these four tasks specified a single factor and fit the data well, χ2 (2) = 5.02, p = .07, comparative fit index (CFI) = .99, Tucker-Lewis Index (TLI) = .96, root-mean square error of approximation (RMSEA) = .07, Akaike information criterion (AIC) = 6639.34, Bayesian information criterion (BIC) = 6683.946. Loadings from this analysis were used to create a single working memory factor score. To create a composite that remains sensitive to developmental change, participant’s scores on each task at each session were centered on the grand mean for that task across the study.
Table 4.
Average performance on working memory tasks during each session of data collection.
| Session 2 | Session 3 | Session 4 | Session 5 | |
|---|---|---|---|---|
| Age (Years) | 12.6 (0.9) | 13.5 (0.9) | 14.4 (0.9) | 15.7 (0.9) |
| Corsi Block Tapping Total Correct |
6.1 (3.1) | 6.5 (3.1) | 6.8 (3.2) | 8.1 (3.1) |
| Digit Span Backwards, Total (Raw) |
7.3 (1.8) | 7.7 (1.8) | 7.8 (2.0) | 8.3 (2.0) |
| Object 2-back Total Correct |
75.7 (8.4) | 78.3 (7.0) | 79.0 (6.9) | 82.2 (5.2) |
| Spatial Working Memory Between Errors |
26.6 (17.2) | 23.6 (16.9) | 22.4 (16.5) | 15.6 (12.7) |
Performance expressed as mean with standard deviation in parentheses
Note. Data from Session 1 was omitted due to a change in the assessment battery between Sessions 1 and 2.
Table 5.
Intercorrelation among average performance levels on working memory tasks and indicators of socioeconomic status
| Measure | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1. Corsi Block Tapping | - | |||||
| 2. Digit Span Backwards | .40*** | - | ||||
| 3. Spatial Working Memory, Errors | −.53*** | −.33*** | - | |||
| 4. Object 2-Back | .39*** | .27*** | −.48*** | - | ||
| 5. Parental education, average | .19** | .23*** | −.21*** | .18** | - | |
| 6. Neighborhood concentrated disadvantage | −.10 | .00 | .06 | −.10 | −.26*** | - |
Note. Sample size ranges from 305 to 316, employing pairwise deletion.
p < .05
p < .01
p < .001
To examine if this factor was invariant across SES levels, multiple group confirmatory factor analysis was conducted for both parental education and concentrated neighborhood disadvantage, following Brown (2006), to examine invariance in both factor loadings and intercepts. For this analysis, conducted in Mplus version 7 (Muthén & Muthén, 1998), groups were created using a median split to create equal subsamples of high and low parental education and concentrated disadvantage, respectively. For parental education, a model assuming equal form across groups but allowing differences in factor loadings and intercepts fit the data well, χ2 (7) = 9.92, p = .19, CFI = .986, TLI = .977, RMSEA = .052, AIC = 6629.35, BIC = 6707.41. In addition, a subsequent model assuming equal form, factor loadings and intercepts across groups fit the data well, χ2 (10) = 14.34, p = .16, CFI = .98, TLI = .976, RMSEA = .053, AIC = 6627.77, BIC = 6694.67. Both the chi-squared difference test (p = .22) and the criteria for non-invariance recommended by Chen (2007) for this sample size, based on change in CFI and RMSEA, suggest there no significant differences across groups, indicative of strong invariance. For concentrated disadvantage, the model assuming equal form across groups but allowing differences in factor loadings and intercepts also fit the data well: χ2 (7) = 8.15, p = .32, CFI = .995, TLI = .991, RMSEA = .033, AIC = 6654.55, BIC = 6732.61. A subsequent model assuming equal form, factor loadings and intercepts across groups of concentrated also fit the data well, χ2 (10) = 8.99, p = .53, CFI = 1.00, TLI = 1.005, RMSEA = .00, AIC = 6649.39, BIC = 6716.30. As with parental education, both the chi-squared difference test (p = .84) and the CFI and RMSEA criteria recommended by Chen (2007) suggest there no significant differences across groups for concentrated disadvantage, indicative of strong invariance. These findings are consistent with prior literature demonstrating factorial invariance and a lack of differential item functioning for executive function and working memory across SES levels (e.g. Wiebe et al., 2011).
In addition, to examine longitudinal invariance we fit a series of three models following the guidelines of Widaman, Ferrer, and Conger (2010). The first model, assuming configural invariance across time but not invariance in loadings and intercepts, fit the data well, χ2 (74) = 66.54, p = .72, CFI = 1.0, TLI = 1.009, RMSEA = .00, AIC = 13032.73, BIC = 13322.66. Second, a model assuming equal factor loadings for each indicator across waves, or a weak factorial invariance model, also fit the data well, χ2 (83) = 89.84, p = .28, CFI = 0.995, TLI = 0.993, RMSEA = .16, AIC = 13038.02, BIC = 13294.50. Lastly, a strong factorial invariance model, with constraints placed for equal factor loadings and intercepts for each indicator across time, also fit the data well without showing signs of strain, χ2 (92) = 110.66, p = .09, CFI = 0.986, TLI = 0.982, RMSEA = .26, AIC = 13040.84, BIC = 13263.87. Although sequential comparison of these models using the chi square difference test indicates that both the weak (p = .01) and strong (p = .01) factorial invariance models are worse fitting models, it is likely this test is overpowered (Chou, Bentler, & Pentz, 1998; Hu & Bentler, 1999). Evaluating the models sequentially for non-invariance using the criteria recommended by Chen (2007) for this sample size, based on change in CFI and RMSEA, suggest there are no significant differences between models and thus there is evidence for strong longitudinal invariance in the working memory factor.
Analysis Plan
A total of 304 participants with 1,104 total observations were included in the analysis, including only observations from assessment sessions in which there was complete data to create the working memory composite. The large majority of participants (231, 76.0%) contributed data from all four study sessions, while 42, 23, and 8 participants had 3, 2, and 1 observations included in analyses, respectively. Descriptive analyses were performed with PASW 18.0 (IBM: New York, NY).
Our primary analytic strategy was longitudinal growth-curve modeling using hierarchical linear models (Singer & Willett, 2003), permitting the examination of the effects of parental education and concentrated disadvantage on both early working memory performance as well as the trajectory of change through adolescence. In this approach, a Level-1 model represents the individual change in working memory performance across time and includes random components (intercept and slope) that are permitted to vary across individuals. Level-2 models are estimated in which the variance in intercept and change parameters at Level-1 is predicted by time-invariant, person-level predictors to identify systematic, between-subject variance in both the level of working memory performance and the rate of change. To ease interpretation, the value of time was centered on the earliest age of study enrollment, 10 years old, such that effects on the intercept are interpreted as effects on performance at age 10 (Verbeke & Molenberghs, 2000). Two independent variables at Level-2 were examined: (1) average parental education, and (2) concentrated disadvantage in the child’s neighborhood. Analyses were conducted in HLM6 (Raudenbush, Bryk, & Congdon, 2004) using full maximum likelihood estimation for hypothesis-testing concerning fixed effects. Level-2 variables were grand-mean centered and estimates of fixed effects were obtained with robust standard errors.
Results
Socioeconomic Status: Sample characteristics
Descriptive statistics for parental education are presented in Table 2. Average parental education for families was 13.9 (SD = 2.3), and ranged from 6 years to 20.5 years. For individual caregivers, 7.3 percent of participants had a primary caregiver with less than a high school education while 29.4% had a high school education. Of secondary caregivers, those of 5.7% of participants had no high school degree while 31.6% had a high school education. Primary and secondary caregiver education were correlated (r = .56, p < .001).
Table 3 presents the characteristics of children’s neighborhoods. Children lived in 144 unique census tracts in which, on average, 13.3% (SD = 13.3) of individuals were below the poverty line, with a range from 0.7% to 55.2%. Neighborhood unemployment averaged 7.2% (SD = 5.4), while 5.4% (SD = 5.4) of neighborhood residents were receiving public assistance. One-sample t-tests indicate that the current sample had higher rates of unemployment, t(315) = 5.02 p < .001, percentages female-headed households with no spouse, t(315) = 8.04, p < .001, and rates of enrollment in public assistance, t(315) = 6.41, p < .001, than the U.S. as a whole. There were no differences between the current sample and the U.S. with respect to the percentage of families below the poverty line, t(315) = 1.43, p = .15, however the current sample had lower rates of children under 18, t(315) = −9.20, p < .001. Average parental education and concentrated disadvantage were correlated (r = −0.26, p < .001), such that lower parental education was related to higher levels of neighborhood disadvantage.
Working Memory: Unconditional Model of Growth
The best fitting growth model was determined by sequentially adding fixed linear, quadratic and cubic effects of age at Level 1, selecting the best model by means of likelihood ratio tests between the models’ deviance statistics (Singer & Willett, 2003). Subsequently the best random effects model was selected by sequentially adding random effects and comparing model deviance statistics, using restricted maximum likelihood model estimation. This resulted in the following Level-1 model:
WMti = π0i + π1i (Age)ti + π2i(Age2)ti + εti
In this model, the outcome is working memory, and π0i represents the intercept, π1i represents the linear effect of age and π2i represents the quadratic effect of age. This model contained a random intercept (σ02 = 15.9, SE = 4.0, p < .001), random linear slope (σ12 = 2.2, SE = 0.8, p = .009), and random quadratic slope (σ22 = 0.02, SE = 0.01, p = .056). The fixed effects of linear (B = 1.1, p < .001) and quadratic (B = −0.04, p = .04) age were significant. Consequently, the unconditional model of working memory change over time indicated that working memory performance increased with age but the rate of increase decreased through adolescence, as performance leveled off.
Working Memory: Predictors of Intercept and Growth
Average parental education and concentrated neighborhood disadvantage were then added as predictors at Level 2 of all random effects for which significant or trend-level (p < .10) variation existed, because of concerns regarding possible overestimation of p-values for random effect terms (Altham, 1984):
π0i = β00 + β01 (Parental Education)i + β02(Concentrated Disadvantage)i + ζ0i
π1i = β10 + β11 (Parental Education)i + β12(Concentrated Disadvantage)i + ζ1i
π2i = β20 + β21 (Parental Education)i + β22(Concentrated Disadvantage)i + ζ2i
Subsequently, we included the covariates gender, African-American racial identity, Hispanic or Latino ethnicity, whether the primary caregiver is the mother, whether or not a secondary caregiver was present, and the interaction between parental education and concentrated disadvantage individually to this basic model in all Level 2 equations. Covariates that were significant at a trend level of p < .10 were then entered into a final prediction model.
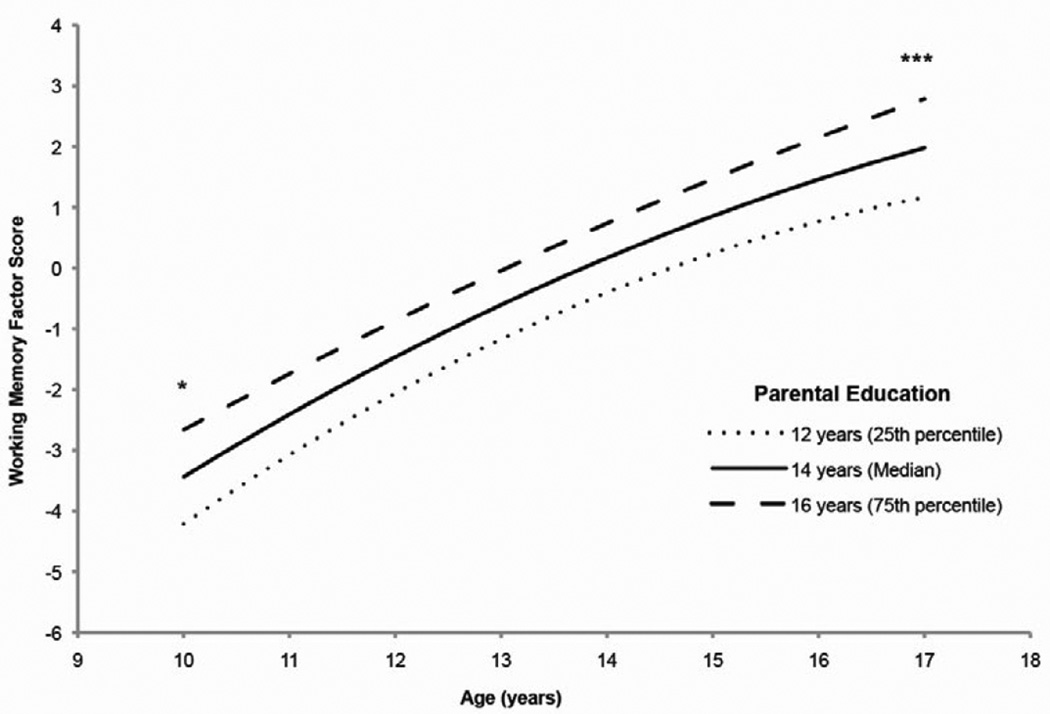
In the final model, as illustrated in Figure 1 and Table 6, the effect of parental education on the intercept for the working memory factor was significant and positive (B = 0.38 SE = 0.16, p = .02, reffect = .13). Higher parental education predicted better performance on the working memory factor, evident at the earliest age of study enrollment. In contrast, concentrated neighborhood disadvantage did not predict differences in the intercept (B = −1.44 SE = 0.91, p = .11, reffect = .09). African-American racial identity also predicted a lower intercept, indicative of worse performance (B = −0.70, SE = 0.34, p = .04, reffect = .12), while Hispanic or Latino identity did not predict differences in the intercept (B = 0.32, SE = 0.52, p = .54, reffect = .04). Neither gender, having a maternal primary caregiver, secondary caregiver presence, or the interaction between parental education and disadvantage met criteria for inclusion in the final model as predictors of the intercept..
Figure 1.
Model-based graph of working memory performance by age at different levels of parental education.
Note: Given the accelerated longitudinal design, each participant provided a maximum of four longitudinal assessments to this model.
* p < .05 ** p < .01 *** p < .001
Table 6.
Multilevel model predicting the development of working memory: Estimates of fixed (top) and random (bottom) effects
| Parameter | Working Memory Factor | ||
|---|---|---|---|
| Fixed Effects | |||
| B | p | reffect | |
| Initial Status, π0i | |||
| Intercept | −3.45 | < .001 | .44 |
| Parental Education | 0.38 | .02 | .13 |
| Concentrated Disadvantage | −1.44 | .11 | .09 |
| African-American | −0.70 | .04 | .12 |
| Hispanic or Latino | 0.32 | .54 | .04 |
| Age, π1i | |||
| Intercept | 1.08 | <.001 | .32 |
| Parental Education | −0.06 | .45 | .04 |
| Concentrated Disadvantage | 0.66 | .10 | .10 |
| Age-squared, π2i | |||
| Intercept | −0.04 | .03 | .13 |
| Parental Education | 0.01 | .30 | .06 |
| Concentrated Disadvantage | −0.06 | .17 | .08 |
| Random Effects | |||
| Estimate | SE | ||
| Level 1 | |||
| Within-person, σε2 | 1.85 | 0.12 | |
| Level 2 | |||
| Initial Status, σ02 | 14.10 | 3.85 | |
| Age, σ12 | 2.16 | 0.82 | |
| Age-squared, σ22 | 0.02 | 0.01 | |
| Covariance, σ01 | −4.72 | 1.74 | |
| Covariance, σ02 | 0.44 | 0.19 | |
| Covariance, σ12 | −0.20 | 0.09 | |
| Rε2 | 0.42 | ||
| R02 | 0.12 | ||
| R12 | 0.04 | ||
| R22 | 0.07 | ||
| Deviance | 4553.33 | ||
To place the magnitude of parental education effects in context, it is useful to compare the size of the effect of parental education on the intercept to working memory growth over time in the unconditional growth model, including both linear and quadratic factors to account for the decrease in the rate of change across childhood and adolescence. In particular, the difference between having parents with 12 years of education (high school degree) compared to 16 years of education (completed college) is equivalent to the performance difference between children 10 years of age and those 11 years, 5.5 months of age. Similarly, the difference between having parents who on average did not complete high school compared to those whose parents have a professional degree (estimated comparison of 11 years of education to 19 years) is equivalent to the performance difference between children 10 years of age and those who are 13 years, 1.5 months. Given the quadratic effects of time, such equivalent age comparisons would be even larger towards the end of adolescence.
Concerning developmental changes in SES disparity, neither parental education nor concentrated neighborhood disadvantage predicted differences in linear or quadratic change (all p ≥ 0.1) in the working memory factor. Neither gender, African-American racial identity, Hispanic or Latino identity, having a maternal primary caregiver, secondary caregiver presence, or the interaction between parental education and disadvantage met criteria for inclusion in the final model as predictors of linear or quadratic change. Finally, effects of parental education (B = 0.41, SE = 0.07, p < .001, reffect = .31) and African-American racial identity (B = −0.70, SE = 0.34, p = .04, reffect = .12) remained significant and in the same direction at 17 years old, indicating persistent effects of parental education and racial identity on working memory performance. Thus, while the four annual assessments of working memory showed continued improvement, there was no SES difference in the growth rate of working memory and no detectable tendency for SES disparities to grow or diminish.
Discussion
In an accelerated longitudinal study in a community sample of youth, we found that lower parental education, but not concentrated neighborhood disadvantage, predicted small to moderate decrements in working memory performance that were apparent at the earliest age of study enrollment, age 10, and persisted without change through the end of adolescence. This suggests that the relation between parental education and working memory emerges earlier in childhood, and provides prospective evidence for an association between parental education in childhood and working memory at the end of adolescence. As working memory is a core cognitive ability associated with achievement, intelligence, health behavior, affective control, and psychopathology this finding is relevant to understanding socioeconomic gradients across multiple outcomes.
Most prior research on SES and working memory, as reviewed earlier, has focused on young children, and none has investigated the trajectory of SES disparities through later childhood and adolescence. SES disparities might ultimately diminish, remain constant, or grow. If the disparities consist partly or wholly of developmental delays, then they would narrow as lower SES children “catch up” with their higher SES counterparts. Alternatively, if the disparities result from accumulating effects of disadvantage (cf. Evans & Schamberg, 2009), then they would “snowball” and widen over time. The current findings indicate that parental education effects emerge before the age of 10, and that parental education does not influence the rate of working memory development through adolescence, providing no evidence of differences in underlying developmental processes in middle childhood and adolescence.
The implications of constant effects of parental education on working memory across time are twofold. First, they indicate that SES-related disparities observed in late adolescence and adulthood (Evans & Schamberg, 2009; Lee et al., 2003; Waber et al., 2007) are not explained by social selection (Conger & Donnellan, 2007), in which those with lower working memory drift down the socioeconomic ladder as they enter the world of higher education or work. Instead, it is more consistent with either social causation, in which SES causes lower working memory performance, or the effects of passive gene-environment correlation.
Second, by identifying the timing and specificity of such effects, these finding imply that any putative causal mechanisms are likely to be operating in the family environment in early and middle childhood, before the ages studied here. This is consistent with many other findings of SES-related differences in cognition and achievement by preschool or kindergarten (Duncan, Morris, & Rodrigues, 2011; Sirin, 2005), and indicative of the possibility that differences in working memory emerge even younger in childhood than established in the current study. Moreover, this suggests that mediators related primarily to the neighborhood (Diez-Roux & Mair, 2010; Leventhal & Brooks-Gunn, 2000) are less likely to underlie SES effects on working memory.
Consequently, the most plausible causal factors at work in creating SES disparities in working memory are those in the early childhood family environment. Among the most strongly supported candidate mediators in this epoch are parental warmth, sensitivity and emotional functioning, cumulative and chronic stress, and the quality of the home environment (Blair, 2010; Hackman, Farah, & Meaney, 2010). Others have suggested that differences in language development or the linguistic environment may account for differences in executive function (Noble et al., 2005; Sheridan, Sarsour, Jutte, D’Esposito, & Boyce, 2012). There is support for many of these potential mediators, particularly with respect to the development of executive function more broadly. Studies have found evidence for a relation between executive function performance and parental scaffolding (Bernier, et al, 2012; Hammond, Muller, Carpendale, Bibok, & Lieberman-Finestone, 2012), learning resources at home (Clark et al., in press), and stress (Blair, 2010). There is mixed evidence about which factors mediate SES effects, as there is some evidence that parenting practices and cortisol (Blair et al., 2011), the home environment (Sarsour et al., 2011), and allostatic load (Evans and Schamberg (2009) mediate the effects of SES on executive function. However, candidate mediators tend to be correlated with each other as well as SES (Bradley & Corwyn, 2002; Evans, 2004), which raises a methodological challenge, as no mediation analyses have simultaneously compared pathways via parenting, the home environment, and stress or allostatic load within the same model to determine if they are truly specific. Consequently, what mediates the effects of parental education in this study remains an open question.
The absence of a neighborhood effect on working memory, like any null result, must be interpreted with caution. This is especially true given that the SES measures of this study were collected only once, at study outset, and neighborhood SES may be less stable than parental education (Krieger et al., 1997). If neighborhood SES in infancy or early childhood were associated with working memory, the present study might fail to detect neighborhood effects. Moreover, the number of participants in each census tract was too small to treat individuals as nested within the neighborhood as a higher level of organization.
In addition, the effects of parental education were observed across a diverse gradient of parental education levels. If SES effects were primarily driven by more extreme disadvantage, rather than a gradient across SES levels, neighborhood disadvantage would be more likely to predict working memory difference given that on balance the distribution of this measure in the current sample captures more variance at lower SES levels than the measure of parental education. Consequently, the absence of neighborhood effects suggests that more extreme disadvantage is not driving the observed effects. This is consistent with considerable evidence in the domains of both achievement as well as health that SES-related disparities are best explained as gradients or graded associations across diverse ranges of SES rather than by absolute thresholds, such as poverty (Adler et al., 1994; Sirin, 2005), with some evidence that disparities between middle- and upper-SES families may be increasing in magnitude, particularly with respect to achievement (Reardon, 2011). Consequently, the graded effect of parental education across a diverse sample suggests that working memory differences are potential mechanisms underlying the SES gradients observed in health and achievement. It should be noted that, given the distribution of participants’ SES levels, the current study likely had insufficient power to detect SES effects on trajectories of development if effects were primarily due to extremely low-SES. Nevertheless, the absence of such effects across a diverse gradient that includes a broad range of SES levels suggests that, even if such effects were present due to extremely low-SES, they would not be the likely mechanisms underlying the full gradient of SES-related disparities.
However, it should be noted that the stability of SES disparities in working memory does not imply the immutability of these disparities. Interventions designed to strengthen working memory clearly operate by environmental mechanisms and may be effective years after the end of a hypothesized period of early childhood sensitivity (Klingberg, 2010). There are likely to be many paths to improved working memory; training games may not work by strengthening working memory in the same ways that felicitous early childhood experiences do. Consequently, interventions designed to improve working memory remain a plausible approach to reduce these disparities.
In sum, we conducted the first prospective study of the relation between SES and working memory development from childhood through the end of adolescence. Parental education was positively associated with working memory performance, and the SES disparity held constant over the age range examined, suggestive of similar developmental processes across levels of parental education. In contrast, concentrated neighborhood disadvantage was not associated with working memory performance. These results suggest that family SES effects on working memory remain stable from childhood through adolescence and thus SES effects present in late adolescence and early adulthood have their roots in childhood and remain stable across time. Future research, employing both prospective meditational and intervention approaches, is thus warranted to determine the degree to which differences in working memory account for disparities in achievement, health, and psychopathology across development.
Acknowledgments
This research and preparation of this manuscript was supported by NIH grant numbers R01DA018913, R01DA033996, R01HD055689, and T32 MH018269. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.
References
- Adler NE, Boyce T, Chesney MA, Cohen S, Folkman S, Kahn RL, Syme SL. Socioeconomic status and health: The challenge of the gradient. American Psychologist. 1994;49:15–24. doi: 10.1037//0003-066x.49.1.15. [DOI] [PubMed] [Google Scholar]
- Alloway TP, Alloway RG. Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology. 2010;106:20–29. doi: 10.1016/j.jecp.2009.11.003. [DOI] [PubMed] [Google Scholar]
- Altham PME. Improving the precision of estimation by fitting a model. Journal of the Royal Statistical Society, Series B. 1984;46:118–119. [Google Scholar]
- Baddeley A. Working Memory: Looking Back and Looking Forward. Nature Reviews Neuroscience. 2003;4:829–839. doi: 10.1038/nrn1201. [DOI] [PubMed] [Google Scholar]
- Bernier A, Carlson SM, Deschenes M, Matte-Gagne C. Social factors in the development of early executive functioning: a closer look at the caregiving environment. Developmental Science. 2012;15:12–24. doi: 10.1111/j.1467-7687.2011.01093.x. [DOI] [PubMed] [Google Scholar]
- Best JR, Miller PH. A developmental perspective on executive function. Child Development. 2010;81:1641–1660. doi: 10.1111/j.1467-8624.2010.01499.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair C. Stress and the development of self-regulation in context. Child Development Perspectives. 2010;4:181–188. doi: 10.1111/j.1750-8606.2010.00145.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair C, Granger DA, Willoughby M, Mills-Koonce R, Cox M, Greenberg MT, Family Life Project I. Salivary cortisol mediates effects of poverty and parenting on executive functions in early childhood. Child Development. 2011;82:1970–1984. doi: 10.1111/j.1467-8624.2011.01643.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley RH, Corwyn RF. Socioeconomic status and child development. Annual Review of Psychology. 2002;53:371–399. doi: 10.1146/annurev.psych.53.100901.135233. [DOI] [PubMed] [Google Scholar]
- Bronfenbrenner U, Morris PA. The ecology of developmental processes. In: Lerner RM, editor. Theoretical Models of Human Development. 5th ed. Vol. 1. New York: Wiley; 1998. pp. 993–1028. [Google Scholar]
- Brooks-Gunn J, Duncan GJ. The effects of poverty on children. The Future of Children. 1997;7:55–71. [PubMed] [Google Scholar]
- Brown TA. Confirmatory factor analysis for applied research. New York: Guilford Press; 2006. [Google Scholar]
- Bull R, Espy KA, Wiebe SA. Short-term memory, working memory, and executive functioning in preschoolers: Longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology. 2008;33:205–228. doi: 10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen FF. Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling. 2007;14:464–504. [Google Scholar]
- Chiodo LM, Jacobson SW, Jacobson JL. Neurodevelopmental effects of postnatal lead exposure at very low levels. Neurotoxicology and Teratology. 2004;26:359–371. doi: 10.1016/j.ntt.2004.01.010. [DOI] [PubMed] [Google Scholar]
- Chou C-P, Bentler PM, Pentz MA. Comparisons of two statistical approaches to study growth curves: The multilevel model and the latent curve analysis. Structural Equation Modeling. 1998;5:247–266. [Google Scholar]
- Clark CAC, Sheffield TD, Chevalier N, Nelson JM, Wiebe SA, Espy KA. Charting longitudinal trajectories of executive control with the Shape School. Developmental Psychology. doi: 10.1037/a0030578. (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conger RD, Donnellan MB. An interactionist perspective on the socioeconomic context of human development. Annual Review of Psychology. 2007;58:175–199. doi: 10.1146/annurev.psych.58.110405.085551. [DOI] [PubMed] [Google Scholar]
- Daneman M, Merikle PM. Working memory and language comprehension: A meta-analysis. Psychonomic Bulletin & Review. 1996;3:422–433. doi: 10.3758/BF03214546. [DOI] [PubMed] [Google Scholar]
- Diez-Roux AV, Mair C. Neighborhoods and Health. Annals of the New York Academy of Sciences. 2010;1186:125–145. doi: 10.1111/j.1749-6632.2009.05333.x. [DOI] [PubMed] [Google Scholar]
- Duncan GJ, Morris PA, Rodrigues C. Does money really matter? Estimating impacts of family income on young children’s achievement with data from random-assignment experiments. Developmental Psychology. 2011;47:1263–1279. doi: 10.1037/a0023875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans GW. The environment of childhood poverty. American Psychologist. 2004;59:77–92. doi: 10.1037/0003-066X.59.2.77. [DOI] [PubMed] [Google Scholar]
- Evans GW, Schamberg MA. Childhood poverty, chronic stress, and adult working memory. Proceedings of the National Academy of Sciences. 2009;106:6545–6549. doi: 10.1073/pnas.0811910106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farah MJ, Shera DM, Savage JH, Betancourt L, Giannetta JM, Brodsky NL, Hurt H. Childhood poverty: Specific associations with neurocognitive development. Brain Research. 2006;1110:166–174. doi: 10.1016/j.brainres.2006.06.072. [DOI] [PubMed] [Google Scholar]
- Hackman DA, Farah MJ, Meaney MJ. Socioeconomic status and the brain: mechanistic insights from human and animal research. Nature Reviews Neuroscience. 2010;11:651–659. doi: 10.1038/nrn2897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammond SI, Muller U, Carpendale JIM, Bibok MB, Lieberman-Finestone DP. The effects of parental scaffolding on preschoolers’ executive function. Developmental Psychology. 2012;48:271–281. doi: 10.1037/a0025519. [DOI] [PubMed] [Google Scholar]
- Houben K, Wiers RW, Jansen A. Getting a grip on drinking behavior: Training working memory to reduce alcohol abuse. Psychological Science. 2011;22:968–975. doi: 10.1177/0956797611412392. [DOI] [PubMed] [Google Scholar]
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
- Hughes C, Ensor R, Wilson A, Graham A. Tracking executive function across the transition to school: A latent variable approach. Developmental Neuropsychology. 2010;35:20–36. doi: 10.1080/87565640903325691. [DOI] [PubMed] [Google Scholar]
- Khurana A, Romer D, Betancourt LM, Brodsky NL, Giannetta JM, Hurt H. Early adolescent sexual debut: The mediating role of working memory ability, sensation seeking, and impulsivity. Developmental Psychology. 2012;48:1416–1428. doi: 10.1037/a0027491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimberg DY, Farah MJ. A unified account of cognitive impairments following frontal lobe damage: The role of working memory in complex, organized behavior. Journal of Experimental Psychology: General. 1993;122:411–428. doi: 10.1037//0096-3445.122.4.411. [DOI] [PubMed] [Google Scholar]
- Klingberg T. Training and plasticity of working memory. Trends in Cognitive Sciences. 2010;14:317–324. doi: 10.1016/j.tics.2010.05.002. [DOI] [PubMed] [Google Scholar]
- Krieger N, Williams DR, Moss NE. Measuring social class in U.S. public health research: Concepts, methodologies, and guidelines. Annual Review of Public Health. 1997;18:341–378. doi: 10.1146/annurev.publhealth.18.1.341. [DOI] [PubMed] [Google Scholar]
- Lee K, Bull R, Ho RMH. Developmental changes in executive functioning. Child Development. doi: 10.1111/cdev.12096. (in press). [DOI] [PubMed] [Google Scholar]
- Lee S, Kawachi I, Berkman LF, Grodstein F. Education, other socioeconomic indicators, and cognitive function. American Journal of Epidemiology. 2003;157:712–720. doi: 10.1093/aje/kwg042. [DOI] [PubMed] [Google Scholar]
- Leventhal T, Brooks-Gunn J. The neighborhoods they live in: The effects of neighborhood residence on child and adolescent outcomes. Psychological Bulletin. 2000;126:309–337. doi: 10.1037/0033-2909.126.2.309. [DOI] [PubMed] [Google Scholar]
- Luciana M, Conklin HM, Hooper CJ, Yarger RS. The Development of Nonverbal Working Memory and Executive Control Processes in Adolescents. Child Development. 2005;76:697–712. doi: 10.1111/j.1467-8624.2005.00872.x. [DOI] [PubMed] [Google Scholar]
- Milner B. Interhemispheric differences in the localization of psychological processes in man. British Medical Bulletin. 1971;27:272–277. doi: 10.1093/oxfordjournals.bmb.a070866. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén Bengt O. Mplus User’s Guide. Seventh Edition. Los Angeles, CA: Muthén & Muthén; 1998. [Google Scholar]
- Noble KG, McCandliss BD, Farah MJ. Socioeconomic gradients predict individual differences in neurocognitive abilities. Developmental Science. 2007;10:464–480. doi: 10.1111/j.1467-7687.2007.00600.x. [DOI] [PubMed] [Google Scholar]
- Noble KG, Norman MF, Farah MJ. Neurocognitive correlates of socioeconomic status in kindergarten children. Developmental Science. 2005;8:74–87. doi: 10.1111/j.1467-7687.2005.00394.x. [DOI] [PubMed] [Google Scholar]
- Owen AM. The role of the lateral frontal cortex in mnemonic processing: the contribution of functional neuroimaging. Experimental Brain Research. 2000;133:33–43. doi: 10.1007/s002210000398. [DOI] [PubMed] [Google Scholar]
- Owen AM, McMillan KM, Laird AR, Bullmore E. N-Back working memory paradigm: A meta-analysis of normative functional neuroimaging studies. Human Brain Mapping. 2005;25:46–59. doi: 10.1002/hbm.20131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postle BR, D’Esposito M, Corkin S. Effects of verbal and nonverbal interference on spatial and object visual working memory. Memory & Cognition. 2005;33:203–212. doi: 10.3758/bf03195309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raudenbush SW, Bryk AS, Congdon RT. HLM 6 for Windows (Version 6.08) Lincolnwood, IL: Scientific Software International, Inc.; 2004. [Google Scholar]
- Reardon SF. The widening academic achievement gap between the rich and the poor: New evidence and possible explanations. In: Murnane RJ, Duncan GJ, editors. Whither Opportunity? Rising Inequality and the Uncertain Life Chances of Low-Income Children. New York: Russell Sage Foundation Press; 2011. pp. 91–115. [Google Scholar]
- Riggs NR, Chou C-P, Spruijt-Metz D, Pentz MA. Executive cognitive function as a correlate and predictor of child food intake and physical activity. Child Neuropsychology. 2010;16:279–292. doi: 10.1080/09297041003601488. [DOI] [PubMed] [Google Scholar]
- Sampson RJ, Sharkey P, Raudenbush SW. Durable effects of concentrated disadvantage on verbal ability among African-American children. Proceedings of the National Academy of Sciences. 2008;105:845–852. doi: 10.1073/pnas.0710189104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarsour K, Sheridan M, Jutte D, Nuru-Jeter A, Hinsh S, Boyce WT. Family socioeconomic status and child executive functions: The roles of language, home environment, and single parenthood. Journal of the International Neuropsychological Society. 2011;17:120–132. doi: 10.1017/S1355617710001335. [DOI] [PubMed] [Google Scholar]
- Sharkey PT, Tirado-Strayer N, Papachristos AV, Raver CC. The effect of local violence on children’s attention and impusle control. American Journal of Public Health. 2012;102:2287–2293. doi: 10.2105/AJPH.2012.300789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheridan MA, Sarsour K, Jutte D, D’Esposito M, Boyce WT. The impact of social disparity on prefrontal function in childhood. PLoS One. 2012;7 doi: 10.1371/journal.pone.0035744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer JD, Willett JB. Applied longitudinal data analysis: Modeling change and event occurrence. New York: Oxford University Press; 2003. [Google Scholar]
- Sirin SR. Socioeconomic Status and Academic Achievement: A Meta-Analytic Review of Research. Review of Educational Research. 2005;75:417–453. [Google Scholar]
- Snyder HR. Major depressive disorder is associated with broad impairments on neuropsychological measures of executive function: A meta-analysis and review. Psychological Bulletin. 2013;139:81–132. doi: 10.1037/a0028727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Asselen M, Kessels RPC, Neggers SFW, Kappelle LJ, Frijns CJM, Postma A. Brain areas involved in spatial working memory. Neuropsychologia. 2006;44:1185–1194. doi: 10.1016/j.neuropsychologia.2005.10.005. [DOI] [PubMed] [Google Scholar]
- Verbeke G, Molenberghs G. Linear mixed models for longitudinal data. New York: Springer-Verlag; 2000. [Google Scholar]
- Waber DP, de Moor C, Forbes PW, Almli CR, Botteron KN, Leonard G, Rumsey J. The NIH MRI study of normal brain development: Performance of a population based sample of healthy children aged 6 to 18 years on a neuropsychological battery. Journal of the International Neuropsychological Society. 2007;13:729–746. doi: 10.1017/S1355617707070841. [DOI] [PubMed] [Google Scholar]
- Wechsler D. The Wechsler Intelligence Scale for Children - Fourth Edition. San Antonio, TX: The Psychological Corporation; 2003. [Google Scholar]
- Widaman KF, Ferrer E, Conger RD. Factorial invariance within longitudinal structural equation models: Measuring the same construct across time. Child Development Perspectives. 2010;4:10–18. doi: 10.1111/j.1750-8606.2009.00110.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiebe SA, Sheffield T, Nelson JM, Clark CAC, Chevalier N, Espy KA. The structure of executive function in 3-year-olds. Journal of Experimental Child Psychology. 2011;108:436–452. doi: 10.1016/j.jecp.2010.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wight RG, Aneshensel CS, Miller-Martinez D, Botticello AL, Cummings JR, Karlamangla AS, Seeman TE. Urban neighborhood context, educational attainment, and cognitive function among older adults. American Journal of Epidemiology. 2006;163:1071–1078. doi: 10.1093/aje/kwj176. [DOI] [PubMed] [Google Scholar]