Percutaneous inner-ear access via an image-guided industrial robot system

Abstract

Image-guided robots have been widely used for bone shaping and percutaneous access to interventional sites. However, due to high-accuracy requirements and proximity to sensitive nerves and brain tissues, the adoption of robots in inner-ear surgery has been slower. In this paper the authors present their recent work towards developing two image-guided industrial robot systems for accessing challenging inner-ear targets. Features of the systems include optical tracking of the robot base and tool relative to the patient and Kalman filter-based data fusion of redundant sensory information (from encoders and optical tracking systems) for enhanced patient safety. The approach enables control of differential robot positions rather than absolute positions, permitting simplified calibration procedures and reducing the reliance of the system on robot calibration in order to ensure overall accuracy. Lastly, the authors present the results of two phantom validation experiments simulating the use of image-guided robots in inner-ear surgeries such as cochlear implantation and petrous apex access.

1 INTRODUCTION

The surgical robot systems existing today can be classified in many ways. One kind of classification is based on the manner in which the user interacts with the robot, leading to two main categories –surgical assistant systems and surgical computer aided design/computer aided manufacturing (CAD/ CAM) systems [1, 2]. Surgical assistant robots are either teleoperated devices that mimic the surgeon’s motions in real-time or cooperative devices manipulating the instrument simultaneously by both robot and surgeon. In contrast, surgical CAD/CAM systems are characterized by a high degree of autonomy. They typically take as inputs certain prespecified coordinates, trajectories, or surfaces (e.g. based on preoperative planning), and then utilize a robot to transfer these actions into the operating room with accuracy and a high degree of automation.

An example of a teleoperated system is the widely-known da Vinci^® Surgical System of Intuitive Surgical, Inc. (Sunnyvale, CA, USA). It was designed for cardiologic interventions and is nowadays very successfully used for radical prostatectomy. The DLR MiroSurge system is another example of tele-manipulated minimally invasive surgery [3]. The system implements three kinematically redundant torque controlled DLR MIRO robots [4, 5]. The actuated instruments are equipped with miniaturized force/torque sensors enabling haptic feedback.

The cooperative robotic system modiCAS® for total hip replacement surgery is presented in reference [6]. It uses optical tracking for guidance of the robotic arm, and a force/torque sensor mounted at the end effector, allowing for intuitive interaction. Further cooperative systems include the robotic system developed by Xia et al. [7]. It integrates a StealthStation® (Medtronic Inc., Minneapolis, MN) navigation system, a neuromate® (Renishaw plc, Gloucestershire, United Kingdom) robotic arm with a force/torque sensor, and the 3D Slicer [8] visualization software to allow the tool to be cooperatively controlled. This approach is similar to the former Acrobot system, which also employs cooperative control [9, 10]. A very recent cooperative robotic system is the Kinemedic [11], which is capable of impedance control in both Cartesian space and joint space, and was designed for biopsy and drilling pilot holes for pedicle screw placement.

The robot systems described in this paper belong to the Surgical CAD/CAM type, as many of the robots in the advent of robotic surgery. The system described in reference [12] led to the first commercial surgical robot, the Robodoc® system (Curexo Technology Corp., Fremont, CA). Initial versions of the Robodoc® developed by Taylor et al. [12] used rigid registration and pre-planned tool paths to produce precise implant pockets in knee and hip replacement procedures. Since the pioneering Robodoc®, robotic bone drilling and milling systems have been developed for a number of other surgical applications, including joint replacements, skull-base procedures, and spine surgeries. In addition to the robot itself, these systems include some or all of the following: (1) methods for image acquisition, segmentation, and human definition of surgical objectives based on images and/or computer models, (2) automated and/or interactive preoperative planning of tool trajectories, (3) real-time tool tracking during drilling or milling, and (4) post-surgical quality control analysis. While these general tasks remain the same, the specifics of hardware and software employed can vary significantly across different systems.

In most of the systems mentioned above, ‘virtual fixtures’ [13, 14] can be employed to guide tools or enforce ‘no-fly zones’, constraining the surgeon’s motion to safe areas while allowing him or her to maintain control of manipulation. Advantages of this method with respect to automated cutting/drilling as implemented, for example, by Robodoc® and the systems described in this paper, among others, include the ability of the surgeon to maintain a level of shared control during the procedure. However, it is unlikely that cooperative control will enable the surgery to be accomplished as rapidly or repeatably as a fully automated robotic solution.

In this paper the authors describe their recent results in creating an image-guided robot system for drilling and milling procedures in the skull, which is an evolution of a prior system described in reference [15]. The enhanced system proposed here (Fig. 1) was also replicated at Vanderbilt University to create a mirror system, using a similar robot and the same system architecture and control strategies. Commercially available industrial robots are used to create a surgical CAD/CAM system that shares many aspects with the previous CAD/CAM robots described above, but addresses new and highly challenging applications, namely percutaneous access to inner-ear structures such as the cochlea and the petrous apex. Features of the system include optical tracking of the robot base and tool relative to the patient and Kalman filter-based data fusion of redundant sensor information (from encoders and optical tracking system) for enhanced accuracy and patient safety. Control is implemented based on differential robot positions rather than absolute positions, which simplifies necessary calibration procedures and reduces the dependence of the overall system accuracy on calibration accuracy.

Fig 1.

The robotic system at Hannover with the KUKA KR 3, the ARTtrack2, and the mounting device

This paper is organized as follows. The challenging clinical requirements due to the new inner-ear applications are discussed in section 2. Section 3 describes the image-guided robot system designed to meet these requirements. Section 4 deals with image guidance, planning, and registration aspects. In section 5 the details of vision-based control, filtering, and data fusion are given. Section 6 describes initial experiments and their results in phantom studies representing targeting of inner-ear structures. The results are discussed in section 7, and a conclusion is given in section 8.

2 CLINICAL REQUIREMENTS OF A CAD/CAM ROBOT FOR INNER EAR SURGERY

There are a number of possible locations in the inner ear where percutaneous access from the lateral skull is potentially useful. Two examples (among many possible surgical targets) that have been studied in depth to date are the cochlea and the petrous apex [16, 17].

2.1 Cochlear implantation

Cochlear implants can restore hearing to deaf patients. The implantation surgery involves inserting an electrode into the cochlea and connecting it to a receiver implanted under the skin. The challenging aspect of the surgery is accessing the cochlea, which is embedded at a depth of approximately 35 mm in the temporal bone. Accessing the cochlea requires passing between two bone-embedded nerves – the facial nerve, which if violated will cause paralysis to the ipsilateral side of the patient’s face, and the chorda tympani, which if violated will result in less sensitivity to the ipsilateral tongue tip. The space between these nerves is approximately 2 mm. Thus, standard manual procedure involves a mastoidectomy procedure, where the bone of the skull behind the ear is gradually shaved down using a drill to permit access to the cochlea between the nerves. During the mastoidectomy, the surgeon must expose other important anatomical structures embedded in the temporal bone, including the sigmoid sinus, carotid artery, and labyrinth. It is, thus, highly desirable to reduce reliance on human hand–eye coordination in this procedure. A single-channel approach where a hole is drilled percutaneously directly to the cochlea would reduce invasiveness and the time the patient must remain under anesthesia [16, 18–21].

2.2 Petrous apex access

The petrous apex is the most medial portion of the temporal bone and lies in close proximity to the cochlea, carotid artery, facial nerve, and internal jugular vein. The number of reported cases of petrous apex lesions are increasing with advancement in imaging technology [22–24] of which 90 per cent are inflammatory/cystic lesions [25]. Surgical access to the petrous apex involves providing a drainage channel that avoids critical structures. An optimal surgical approach would be to provide the drainage channel via a single drill pass from the lateral cortex of the mastoid to the petrous apex, avoiding critical structures. For this approach, accuracy on the order of 1 mm or less is required. The feasibility of such a ‘minimally invasive approach’ to the petrous apex has been reported in vitro using customized, microstereotactic frames [17].

3 SYSTEM DESCRIPTION

To create this CAD/CAM surgical robot system for inner-ear procedures, three main hardware components are necessary: a positioning system (e.g. industrial robot), a tracking system (e.g. optical tracker), and a control workstation for processing the data and controlling the robot (see Fig. 1). To adapt for any relative motion between the patient and robot base that may occur during surgery, three locations are tracked: robot base, tool frame, and patient itself (Fig. 2).

Fig 2.

The robotic system implemented at Vanderbilt with the fiducial markers on the robot end effector, the robot base, and simulated patient shown

3.1 Robots

Instead of retrofitting existing surgical robots (e.g. the Robodoc®), standard industrial robots are utilized in the proposed applications. This is mainly due to the lack of open programming interfaces of commercially available surgical robotic systems. Those are a prerequisite for developing new surgical applications in an academic area. Furthermore, standard industrial robots offer high precision and stiffness at relatively low costs.

Serial robots possess excellent repeatability (this is the specification always quoted by manufacturers), but their absolute positioning accuracy is generally lower because any small modelling errors in their kinematics (e.g. dimensional tolerances in fabrication) have more impact on absolute motions than on small differential motions. While it is possible to calibrate a robot system to enhance accuracy, it was decided instead to track the tool centre point (TCP) and implement control in the task space using differential motion commands to the robot based on external optical navigation data. Using this framework, there is no need to solve the inverse kinematics problem with high accuracy. Instead, the control computer computes a new position and orientation (relative to the current position and orientation of the robot) and transmits this to the robot control box. The control box then handles low-level control for moving the robot from its current configuration to the new desired configuration.

Two similar systems have been constructed, one at Leibniz Universität Hannover and one at Vanderbilt University, which are nearly identical in terms of system architecture, control, and registration. The two systems differ in terms of the properties of robots and the optical tracking hardware used. Both employ standard six-degrees-of-freedom (DoF) off-the-shelf industrial robots. The Hannover system implements a KUKA KR 3 (KUKA Roboter GmbH, Augsburg, Germany), while the Vanderbilt system uses a Mitsubishi RV-3S (Mitsubishi Electric Europe B.V., Ratingen, Germany). Each robot has a maximum workspace radius of about 650 mm, can easily be mounted on a tabletop or cart for transportation, and possesses a maximum payload of 3 kg as well as excellent repeatability (KR 3: 0.05 mm; RV-3S: 0.02 mm).

In both systems, an external control computer interfaces the robot control box using an Ethernet connection. To enable real-time control over the Ethernet, the control box of the KR 3 was upgraded with KUKA’s Remote Sensor Interface (RSI) and the Ethernet Remote Sensor Interface (Kuka.Ethernet KRL XML), while the RV-3S contains a built-in application (CRn-500). Consequently, robot motion can be dynamically adjusted externally by a computer and all relevant robot data (e.g. the current pose and encoder values) can be read over the same link. Data are exchanged via the TCP/IP protocol in a 12 ms cycle (KUKA KR 3) and via UPD/IP in a 40 ms cycle (Mitsubishi RV-3S). To ensure safety, the robot control boxes are set to expect periodic handshake signals from the external control computer. The communication will be shut down and robot motion will be stopped if the expected handshake signal is not received within a given time period.

3.2 Optical tracking

Optical tracking is used to measure the poses of several coordinate frames of the set-up, as described above. The Hannover system employs an ARTtrack2 (Advanced Realtime Tracking GmbH, Weilheim, Germany) and the Vanderbilt system uses a Polaris Spectra® (NDI Inc., Waterloo, Ontario, Canada). Using optical markers placed accordingly to a known geometry, the position and orientation of the associated coordinate frame can be measured. The position of a marker in the tracking area can be determined with a remaining root mean squared (r.m.s.) error of less than 0.25 mm (Polaris Spectra®). For the ARTtrack2 no comparable value can be given, due to the customized assembly of the system.

The data derived from the cameras contain the translation (x, y, z) and the orientation represented in unit quaternion format q₀, q_x, q_y, q_z [26]. For example, the pose of the TCP coordinate frame is given with respect to the optical tracking system coordinate frame by

$${{}_{(\text{cam})}\mathit{x}}_{\text{tcp}}={\left[\begin{array}{ccccccc}x,& y,& z,& q_0,& q_x,& q_y,& q_x\end{array}\right]}^{\mathrm{T}}$$ (1)

Given this information, one can easily convert equation (1) to the corresponding homogeneous transformation ^camT_tcp (see references [27] and [28]). Thereafter, an object pose can be transformed from one coordinate frame (e.g. the TCP frame) into the optical tracking frame by

$${{}_{(\text{cam})}\mathit{x}}_{\text{obj}}={{}^{\text{cam}}\mathbf{T}}_{\text{tcp}(\text{tcp})}{\mathit{x}}_{\text{obj}}$$ (2)

The Polaris Spectra® is connected to the computer via a modified serial interface as USB is usually not supported in real-time environments. The ARTtrack2 interfaces using the UDP protocol via Ethernet. Because of hardware and interface limitations the measurement rate for both optical tracking systems was set to 25 Hz. Additionally, the systems have a time lag of two working cycles due to the internal signal processing. Since measurement values contain significant noise, filtering is important and is discussed in sections 5.2 and 5.3. A major drawback of optical tracking systems is the so-called line-of-sight problem, i.e. a direct line of sight between cameras and tracking markers must always be maintained. Thus, to ensure safety in the event of short occlusions, the system shuts down and no movement of the robot will occur. Possible solutions exploiting data fusion are presented in reference [29]. However, they were not incorporated into the experimental set-ups described in this paper.

3.3 Control workstation

The external control computers used in both the Hannover and Vanderbilt systems are standard PCs (Pentium IV-class) running a Linux operating system. Real-time control was implemented via the RTAI extension [30]. Using the rapid prototyping development environment MATLAB® /Simulink® (The MathWorks Inc., Natick, MA, USA), a library for accessing optical tracking systems, robots, and other peripherals was established, called mediLAB. Using the model-based development environment, even an inexperienced user without deep real-time programming knowledge can rapidly create a control circuit model. By building the model using the integrated Real Time Workshop, a real-time capable C program is generated, which is to be compiled into a real-time compatible executable file. This allows for a convenient development process.

4 IMAGE GUIDANCE, PLANNING, AND REGISTRATION

The three main components (patient, robot, and optical tracking system) of the image guided system (IGS), described in detail in section 3, are shown in Fig. 3. There are several different coordinate frames of the system, which can be considered embedded in each component. The coordinate frame (CF)_cam is associated with the optical tracking system. Therefore, the poses of the reference marker frames attached rigidly to the robot base (CF)_rob, the tool (CF)_tool, which is mounted on the robot end effector (EE), and the patient (CF)_pat are measured in the optical tracking system, (CF)_cam, and processed to get the homogeneous transformations ^camT_tool, ^camT_rob, and ^camT_pat.

Fig 3.

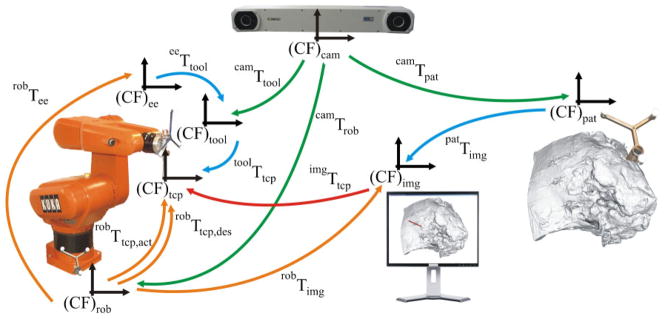
The components and transformations used in our IGS system. Pictured are the three main components of the system, namely the patient, robot, and optical tracking system, as well as their spatial relationships

The transformation ^eeT_tool between the end effector and the tool reference marker frame as well as^toolT_tcp between the tool and the tool centre point, which is located at the manipulated surgical instrument tip, can be determined by a calibration procedure (see section 4.3). The transformation between the image space and the physical space ^patT_img can be computed by performing the registration (see section 4.2) between these two spaces. The transformations ^eeT_tool, ^toolT_tcp, and patT_img are considered to be constant during the robot operation.

4.1 Planning and trajectory executing

As described in section 2, percutaneous access to inner-ear targets requires high accuracy and must use trajectories that achieve the desired target while avoiding sensitive structures (e.g. nerves embedded in the bone of the skull). To plan a trajectory for percutaneous inner-ear access only, two coordinates in the image data set are required, the entry point on the skull _(img)x_e and the target point at the end of the drill canal _(img)x_t. The direct line between these points defines the trajectory.

It is also crucial to maximize the distances between the drill and all adjacent critical anatomical structures. To assist the surgeon with selecting the optimal drill trajectory, a path planner can be used to compute statistically optimal trajectories and then display them for approval (or modification) by the surgeon [31, 32]. In the phantom experiments included in section 6, desired target and entry positions within the phantom were selected manually by the experimenters.

To generate sequential pose values _(img)x_{tcp, des} of the TCP in the image coordinate frame along the pre-planned trajectory, a human machine interface (HMI) device (i.e. Logitech Marblemouse) was used. This device allows the human user (e.g. the surgeon) to manually control the insertion of the drill along the preplanned trajectory, providing a level of shared control. Since the orientation of the drill around the drill axis is arbitrary, the robot was programmed to keep the optical tracking fiducial mounted to its EE aimed towards the optical tracker, as good as possible.

4.2 Registration

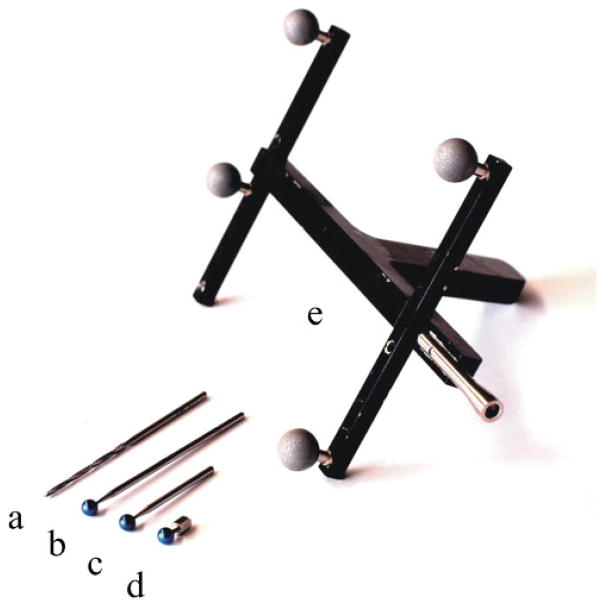
The transformation between the image space and the physical space ^patT_img is derived by performing a point-based registration process with artificial landmarks. In these experiments, embedded metal spheres as well as embedded bone anchors with attached spheres were used for this purpose. These spheres were detected in computer tomography (CT) images with subpixel accuracy using an automatic segmentation algorithm [33]. To determine their location in optical tracker space, a tracked, calibrated pointer with a detent at its tip was used to identify their locations precisely (see Figs 4(d) and (e)).

Fig 4.

(a) Surgical drill, (b) and (c) calibration drills, (d) spherical bone anchor, and (e) calibrated pointer tool

The patient reference adapter pose _(cam)x_pat and the anchor positions _(cam)p_{anchor, i} are measured at the same time, with the adapter’s pose converted to the corresponding homogenous transformation ^camT_pat. Therefore, the position of the landmarks can be transformed into the patient coordinate frame by

$${{}_{(\text{pat})}\mathit{p}}_{\text{anchor},\mathrm{i}}={({{}^{\text{cam}}\mathbf{T}}_{\text{pat}})}^{-1}{{}_{(\text{cam})}\mathit{p}}_{\text{anchor},\mathrm{i}}$$ (3)

After measuring all landmarks with respect to the patient coordinate frame, a homogeneous transformation ^imgT_pat can be calculated using the standard point-based rigid registration algorithm [34]. It minimizes the squared distances of the registration error

$$e=\sum _{i=1}^N{\Vert {{}_{(\text{img})}\mathit{p}}_{\text{anchor},\mathrm{i}}-{{}^{\text{img}}\mathbf{T}}_{\text{pat}(\text{pat})}{\mathit{p}}_{\text{anchor},\mathrm{i}}\Vert }_2^2$$ (4)

of N anchor points by using a singular value decomposition. Since the desired drill trajectory is planned relative to these anchors in image space, the drill trajectory is now known with respect to the physical patient space.

4.3 Calibration

Calibration is used to determine two fixed transformations that relate the various frames associated with the drill (see Fig. 5). The robot tool frame is defined as the coordinate frame of the optical tracking fiducial attached to the drill. The position and orientation of this tool frame with respect to the physical drill tip (the TCP as referred to throughout this paper) is ^toolT_tcp. The other relevant transformation is the transformation from the tool frame to the robot’s internally defined EE frame ^eeT_tool, which lies at the intersection of its revolute wrist joints and is used to command the differential movements described in section 3.1.

Fig 5.

Detailed view of the tool mounted at the robot end effector. It depicts the positions of the end effector, tool, and TCP coordinate frame

To determine ^eeT_tool a calibration movement is employed. The robot is programmed to perform known rotations of its EE frame, while optical tracking data are recorded. From these two synchronized data sets, ^eeT_tool is estimated using least squares.

In order to calculate the transformation ^toolT_tcp, the Hannover system uses two calibration bits with different lengths and titanium balls of 5 mm attached at their tips (see Figs 4(b) and (c)). Each bit is inserted subsequently in the drill holder and the position of the titanium balls are measured by the optical tracking system with respect to the tool marker frame using the calibrated pointer tool (Fig. 4(e)). With the help of the measured points, ^toolT_tcp can easily be calculated by taking the difference in length of the surgical drill (Fig. 4(a)) compared to the calibration bit in account. The TCP coordinate frame is orientated with the z axis pointing along the bit shaft.

At Vanderbilt, a customized optical tracking marker was made with a detent at its centre in which the surgical drill tip fits. This tracking marker is then pivoted around the drill tip while collecting optical tracking data for both the tracking marker and the tool frame marker frame. From these two synchronized data sets, ^toolT_tcp is estimated using least squares.

5 ROBOT CONTROL, FILTERING, AND DATA FUSION

Though a serial industrial robot that has not undergone extensive application-specific calibration is highly precise, it has relatively lower absolute accuracy. In order to achieve the overall system accuracies necessary for inner-ear procedures, the present robot controller relies on external data. Feedback is gained by optical tracking data, which are filtered and fused with robot encoder information. The block diagram of this control algorithm is shown in Fig. 6.

Fig 6.

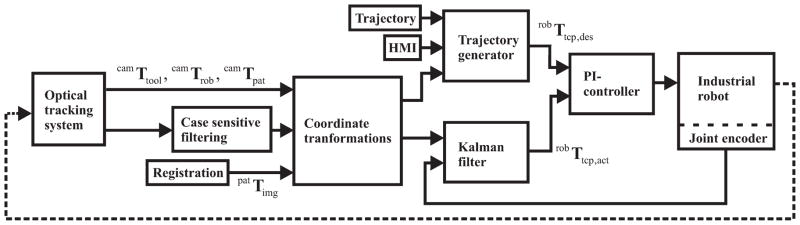
Control circuit block diagram

5.1 Control circuit

The controller implements proportional and integral (PI) control on the position and orientation of the drill tip, which is referred to as the TCP. The actual and desired poses are computed as follows

$${{}^{\text{rob}}\mathbf{T}}_{\text{tcp},\text{act}}={({{}^{\text{cam}}\mathbf{T}}_{\text{rob}})}^{-1}{{}^{\text{cam}}\mathbf{T}}_{\text{tool}}{{}^{\text{tool}}\mathbf{T}}_{\text{tcp}}$$ (5)

and

$${{}^{\text{rob}}\mathbf{T}}_{\text{tcp},\text{des}}={({{}^{\text{cam}}\mathbf{T}}_{\text{rob}})}^{-1}{{}^{\text{cam}}\mathbf{T}}_{\text{pat}}{{}^{\text{pat}}\mathbf{T}}_{\text{img}}{{}^{\text{img}}\mathbf{T}}_{\text{tcp},\text{des}}$$ (6)

respectively.

To remove quantization and sensor noise from optical tracking signals (they are only updated at 25 Hz as described in section 3.2), we also use a Kalman filter to combine velocity information calculated from robot encoder data with the optical robot position estimate, as described in section 5.3 below.

It is noted that control of position and orientation is implemented by separate PI controllers. The error for the position control is simply the difference between desired and actual TCP Cartesian positions, whereas for orientation control the quaternion error is computed using the quaternion product [26] between the desired quaternion and the inverse of the actual quaternion. PI control is then implemented on each quaternion component except the q₀ element. The controller aims for a zero rotation error, which implies an error quaternion of q_err = [1, 0, 0, 0]. Assuming only small rotation errors, q₀ can simply be set to 1 with the controller used to drive the other three elements to zero. Note that a normalization has to be done after calculating the new control value to derive a unit quaternion for further processing as an orientation control variable.

5.2 Filtering of patient motion

An optical tracking marker is attached to the patient. In a clinical system this marker could be attached using bone screws inserted into the skull, or possibly via a bite block fitted to the patient’s teeth. It is useful to filter the patient coordinate frame data provided by the optical tracking system to remove high-frequency noise. Note that patient motion is intermittent and generally contains much lower frequency content than optical tracking noise, so fairly heavy filtering is required most of the time. However, conventional filters can introduce a significant phase lag when heavy filtering is required, in the event of patient motion. Hence, an alternate case was adopted depending on the filter approach, where the filter parameters adapt with respect to the patient motion.

Here, two cases exist: ‘moving body’ and ‘static body’. The system is usually in the static body state with heavy filtering. When the patient moves further than a predefined noise threshold with respect to the last filtered pose value, the filter coefficients switch to the moving body case with lighter filtering. This method allows for the usage of a conventional low-pass filter with the advantages of both heavy and light filtering simultaneously. Note that the computational power required is minimal, making case-dependent filters appealing for real-time applications. The low-pass filter is implemented using the standard digital filter

$${\overline{\mathit{x}}}_k=\mathrm{\alpha }{\overline{\mathit{x}}}_{k-1}+(1-\mathrm{\alpha }){\mathit{x}}_k\text{with}0\le \mathrm{\alpha }\le 1$$ (7)

where x̄_k stands for the actual filtered value, x̄_k−1 for the filtered value of the last cycle, and x_k for the measured value. The experimentally determined values for α were α=0.9 for the static body case and α=0.05 for the moving body case.

Rotational filtering was handled differently, using a method that explicitly accounts for the non-linear structure of rotation representation: the spherical linear interpolation (SLERP) algorithm [35] was applied. Given two orientations q_a and q_b SLERP provides the following equations for interpolation

$$\begin{array}{l}\text{SLERP}({\mathit{q}}_{\mathrm{a}},{\mathit{q}}_{\mathrm{b}},t)=\frac{sin[(1-t)\theta ]}{sin(\theta )}{\mathit{q}}_{\mathrm{a}}+\frac{sin(t\theta )}{sin(\theta )}{\mathit{q}}_{\mathrm{b}}\\ \text{with}cos(\theta )={\mathit{q}}_{\mathrm{a}}·{\mathit{q}}_{\mathrm{b}}\end{array}$$ (8)

as the n-dimensional dot product of the quaternion unit vectors. The interval of t is [0...1].

Interpreting equation (8) as a low-pass filter with q_a=q̄_k−1 representing the filtered orientation of the last cycle, q_b=q_k the measured orientation, and t=α, the following low-pass filter for orientation is obtained

$${\overline{\mathit{q}}}_k=\frac{sin[(1-\mathrm{\alpha })\theta ]}{sin(\theta )}{\overline{\mathit{q}}}_{k-1}+\frac{sin(\mathrm{\alpha }\theta )}{sin(\theta )}{\mathit{q}}_k$$ (9)

A high value for α provides light filtering and a small value for α provides heavy filtering. The empirically determined values were α=0.9 and α=0.05.

5.3 Data fusion

Because the robot moves continuously rather than intermittently like the patient does, a different filtering strategy was implemented for the robot. Due to the low update rate of optical tracking, there is significant quantization. Additionally, sensor noise and lag in optical tracking signals occurs. To smooth the optical tracking information and account for all these issues, a Kalman filter was used (see reference [29]) to fuse velocity information computed from robot encoder readings to the signals. While filtering could be done using simple low-pass filters, it is possible to obtain better results (e.g. reducing phase lag) via this sensor fusion approach.

To accomplish this, we handle translation and orientation separately, each with their own Kalman filters, which differ only in their state vectors and corresponding parameters. For the translational components, the Kalman filter is implemented as follows. The 12×1 state vector is

$${\mathit{x}}_k={[\begin{array}{cccc}{\mathit{p}}_{k-2},& {\mathit{p}}_{k-1},& {\mathit{p}}_k,& {\stackrel{.}{\mathit{p}}}_k\end{array}]}^{\mathrm{T}}$$ (10)

where p_k, p_k−1, and p_k−2 denote the Cartesian positions of the tool at sample time k, k−1, and k−2 respectively and ṗ_k gives the velocity of the TCP at sample time k. Note that these additional sample times account for a latency of two cycles due to the time delay between acquiring data from the robot and optical tracking system (see reference [36] for further information about time delay modelling). The governing equations of the Kalman filter are the general state-space equations of a dynamic system with no inputs or disturbances

$$\stackrel{.}{\mathit{x}}=\mathbf{A}\mathit{x}\text{and}\mathit{y}=\mathbf{C}\mathit{x}$$ (11)

The 12×12 system matrix A and the 6×12 observer matrix C are

$$\mathbf{A}=\left[\begin{array}{cccc}\mathbf{0}& \mathbf{1}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{1}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{1}& \mathbf{T}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{1}\end{array}\right],\mathbf{C}=\left[\begin{array}{cccc}\mathbf{1}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{1}\end{array}\right]$$ (12)

where 0 denotes a 3×3 null matrix, 1 a 3×3 identity matrix, and T a 3×3 diagonal matrix containing the sample time of the Kalman filter (0.02 seconds, in this implementation).

The Kalman filter for orientation works in exactly the same way as the translational filter described above. Rotation is parameterized using quaternions, which are converted to Euler angles before filtering and then converted back to quaternions after filtering. Redefining the state vector to contain these Euler angles, equations (10) to (12) hold for the rotational Kalman filter exactly as written.

The further processing of the data in a prediction and correction step is a standard procedure, as discussed in reference [37]. The optimal Kalman filter gain is a measurement of trust in sensor values versus model prediction, and such trust depends upon the noise present in the system. The gain is adjusted according to the error covariance, consisting of both the process noise covariance and the measurement noise covariance.

The measurement noise covariance is a diagonal matrix computed from noise readings of the optical tracking system. The values of the process noise covariance represent uncertainty in the model. They were empirically chosen, but smaller than the measurement noise covariance; i.e. measured values are trusted somewhat more than model predictions, but a combination of the two is the most effective estimate of the robot position.

In our systems, the Kalman filter implementation performs sensor fusion, combining noisy tool position data from the optical tracking system and smoother velocity data from the robot. By doing so, it was possible to lower the overall noise and to enhance the robustness of the system. Additionally, the system benefits from the lower delay due to earlier arriving signals from the robot compared to the above-mentioned delay of two sample times from the optical tracking system.

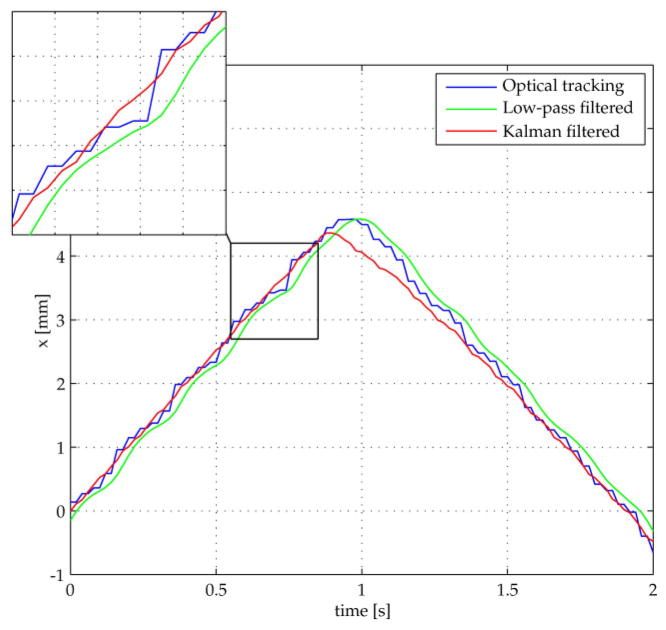
To illustrate the advantages of this Kalman sensor fusion technique in comparison to the standard low-pass filter, the robot performed motions with changes in direction of the movement. Since all degrees of freedom produced similar results, one representative degree of freedom is shown in Fig. 7. It depicts the position in the x direction derived from the unfiltered optical tracking system, the same values low-pass filtered with a corner frequency of 3 Hz, and the Kalman filtered position data.

Fig 7.

Kalman filtered optical tracking data are nearly as smooth as low-pass filtered values with a 3 Hz corner frequency and do not suffer from the low-pass phase shift. Additionally, it reduces the time lag introduced by the optical tracking system

It is easy to see that the Kalman filter performs with higher dynamics than the low-pass filter giving similar smoothed values. Even more, the applied low-pass filter incorporates a significant phase lag. The robot data have a delay of 12 ms whereas the optical tracking system introduces a delay of approximately 40 ms. Therefore, the Kalman filter (taking both signals into account) reacts earlier to changes in the robot motion as the unfiltered optical tracking data. After a short time the Kalman signal converges towards the value of the tracking system, gaining back absolute accuracy.

6 EXPERIMENTS

Two types of phantom experiments were conducted to analyse the performance of the two robot systems described in previous sections of this paper. The first experiment did not involve any imaging and was performed with both the Hannover system and the Vanderbilt system. For this experiment, a phantom was made using a computer numerically controlled (CNC) milling machine such that the outer dimensions are fabricated precisely (± 0.1 mm). The second experiment includes the CT imaging of a different phantom. The markers and the trajectories were determined from the CT scan in a manner envisaged for use in real otologic surgery. This experiment was only performed at Vanderbilt where a portable intraoperative CT machine was available. In order to determine the accuracy of the image guided robots, the deviation of the drilled holes was measured in both experiments, and a statistical analysis was performed.

6.1 Lateral accuracy experiment

An accurately fabricated aluminium block (125× 75×35 mm³) was equipped with 24 drilled holes with a diameter of 10 mm in a grid pattern (see Fig. 8). Each hole was filled with plaster (Hannover) and body filler (Vanderbilt), respectively. Additionally, five threaded holes were added to mount 5 mm titanium spheres for registering the block to physical space. The exact positions of the spheres relative to the block were determined using a calliper (resolution 0.01 mm). Optical tracking markers were fixed to the block using a custom-made base. To register the markers to the block, the point-based registration process was applied (see section 4.2). Subsequently, the milling tool (Lindemann burr NS1808.036, KOMET MEDICAL, Lemgo, Germany) was calibrated as described in section 4.3 using the calibration pins in Hannover and the calibration frame in Vanderbilt.

Fig 8.

The experimental set-up for the lateral accuracy experiment consists of an aluminium block with 24 plaster-filled holes in it, fixed relative to the robot, and optically tracked

For trajectory planning 24 desired trajectories were defined to drill along the centres of the filled bore holes. The centre of the hole on the top side was specified as the entry point _(img)x_e and the centre on the bottom side as the target point _(img)x_t, adding an additional 2 mm to ensure that the drill bit reached the outside of the block. During the experiment, the 24 holes were drilled in a sequence while the optical tracking system and the block remained motionless. The progression of the TCP along the trajectory was commanded manually using the HMI. While the trajectory execution could have been performed completely pre-programmed, it seems to be desirable that a human user (the surgeon in the clinical setting) maintains control of the drill progress. The rotational speed of the drilling tool was adjusted to 10 000 r/min and held constant during both drilling and retraction.

After drilling, the positions of the centres of each hole were determined at the top and at the bottom of the block (the drill bit passed all the way through it), using a coordinate measuring machine (CMM) Zeiss ZMC 530 (Carl Zeiss IMT GmbH, Oberkochen, Germany) with an accuracy of approximately 1 μm. This experiment enables precise assessment of x-and y-direction accuracy of drilling, although drill depth cannot be evaluated by this procedure.

6.2 Lateral accuracy experiment results

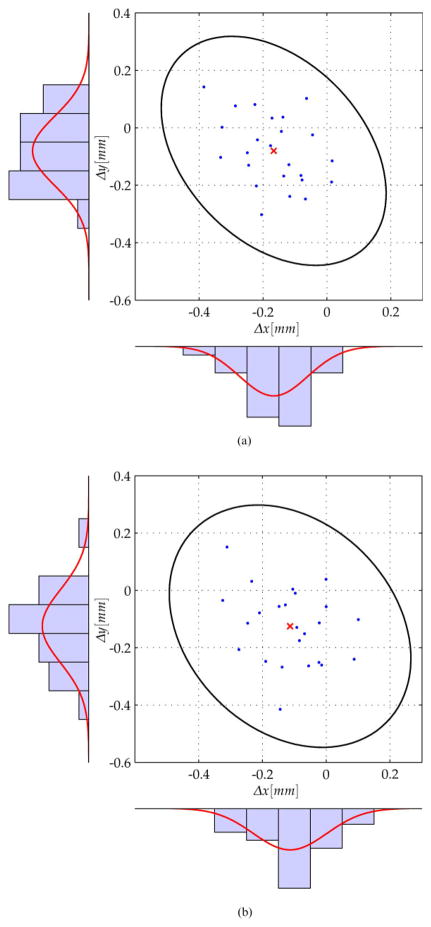
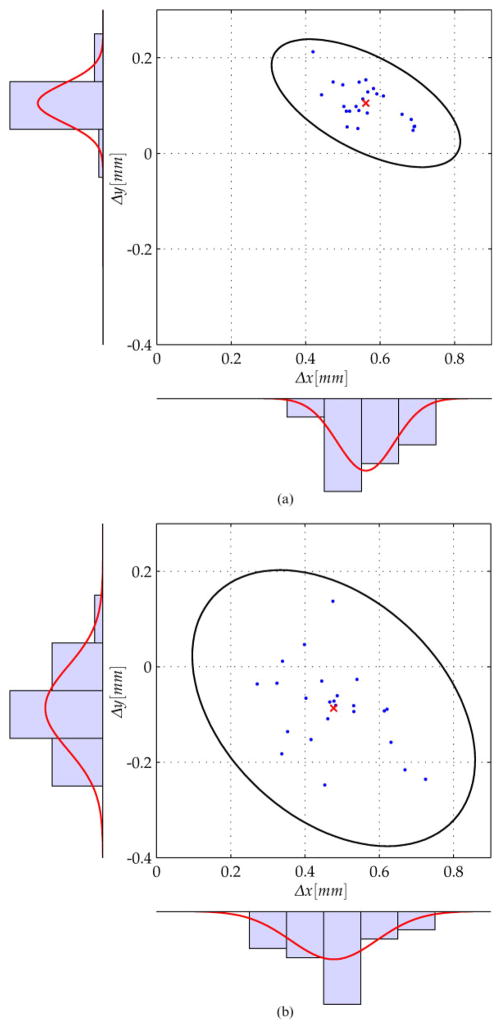
Figures 9 and 10 depict the measured deviations Δx and Δy of the drilled holes within the aluminium block. The mean error is indicated by a red cross and the deviations are marked with a small dot. Furthermore, the plot shows the histograms as well as the corresponding Gaussian distribution in the x and y directions. Assuming a two-dimensional normal distribution, a confidence region for the system accuracy can be calculated using the covariance of the deviation results. Also, 99.9 per cent confidence ellipses are shown on the plots.

Fig 9.

Deviations and 99.9 per cent confidence region for the drilling experiments performed at Hannover using the KUKA KR3 robot and ARTtrack2 optical tracker. (a) top side, (b) bottom side

Fig 10.

Deviations and 99.9 per cent confidence region for the drilling experiments performed at Vanderbilt using the Mitsubishi RV-3S and Polaris Spectra® optical tracker. (a) top side, (b) bottom side

Table 1 summarizes the performed experiments on both systems. Since the standard deviation varies with respect to the direction, its value is given not only in the x and y directions but also in the direction of its principle axes. It can be seen that the Hannover experiments were performed with a lower mean value and the Vanderbilt experiments with a lower standard deviation. See section 7 for a discussion of the significance of these results with respect to otolaryngology surgery.

Table 1.

Mean and standard deviation of the drilling results

Experiment	Mean value (mm)		Standard deviation (mm)				99.9% confidence region (mm), major axis	Mean + confidence region (mm), maximum
	x	y	x axis	y axis	Major axis	Minor axis
Hannover, top side	−0.167	−0.080	0.107	0.121	0.135	0.089	0.444	0.629
Hannover, bottom side	−0.113	−0.125	0.115	0.128	0.138	0.103	0.455	0.624
Vanderbilt, top side	0.562	0.105	0.077	0.041	0.082	0.031	0.268	0.840
Vanderbilt, bottom side	0.477	−0.087	0.116	0.088	0.124	0.076	0.408	0.893

6.3 Absolute accuracy experiment

To assess the absolute accuracy of the system, a phantom made of an acrylic block with three embedded spherical fiducial markers was used (see Fig. 11). The three spheres enable registration between the image and physical space. They were immobilized by embedding them in epoxy. A CT scan of the phantom with the spherical markers was acquired using the xCAT^TM ENT mobile CT scanner (Xoran Technologies, Ann Arbor, MI, USA). The locations of the spheres in the image space were determined by identifying their centres in the CT scan using automatic image processing techniques. Six arbitrary drill trajectories relative to these spheres were then defined in the image space.

Fig 11.

Phantom with three spherical fiducial markers used for the absolute accuracy experiments

An optical tracking marker frame was then attached to the phantom and the locations of the respective spheres in the physical space were acquired using a calibrated probe. A point-based rigid registration was then applied to register image space to physical space, as mentioned in section 4.2. The robot was then programmed to align the drill with the desired trajectory and advance along it under the control of an HMI consisting of a marble mouse (the HMI was included here for the same reason as in the lateral accuracy experiment above). The drill was maintained at 20 000 r/min until the robot reached the target. The drill was then stopped and retracted in the same manner in which it was inserted.

To assess the accuracy of the drilled hole, the phantom was scanned again after drilling using the xCAT^TM ENT CT scanner. To determine accuracy, the pre- and post-drill CT scans were registered to each other using the fiducial sphere locations in both the scans. The desired trajectory from the pre-drill scan was transformed to the post-drill scan and compared to the actual drill path.

6.4 Absolute accuracy experiment results

Figure 12 shows one desired drill trajectory transformed to the post-drill CT scan. It can be seen that the drilled path is along the desired trajectory. The distance between the drilled target and desired target _(img)x_t and between the mid-axis of the drilled trajectory and the mid-axis of the desired trajectory at the target were measured for each trajectory. The mean ± standard deviations of these distances were measured to be 0.62 ± 0.25 mm and 0.56 ± 0.27 mm, respectively.

Fig 12.

A drilled trajectory as seen in the post-drill CT scan. The dotted line indicates the desired drill path and the cross indicates the desired target location

These results demonstrate how an image-guided robot system such as the ones proposed here might be used in a real clinical setting. In summary, it has been shown that submillimetric absolute accuracy can be achieved using established registration procedures and a workflow equivalent to the one that is envisaged for real surgery.

7 DISCUSSION

The results of both experiments described in section 6 demonstrate submillimetric accuracy. The levels of accuracy currently seen in these experimental systems are likely to be sufficient for some applications in inner-ear surgery (e.g. petrous apex access), and may need some enhancement in future work before they are sufficient for other applications (e.g. percutaneous cochlear implantation, where only a 2 mm window is available between the nerves through which the drill must pass). Fortunately, there are several promising areas for possible future work that may enhance the accuracy of our systems even further.

For example, the Hannover system (KR3/ARTtrack2) exhibited a higher standard deviation in the lateral accuracy experiment than the Vanderbilt system (RV-3S/Polaris Spectra®), which is affected by the system noise. This may rely on the use of a camera with a higher noise level. Furthermore, mistuned Kalman filter parameters lead to the same effect. Further experiments have to be performed to figure out the problem. In contrast, the lower mean errors may indicate that the registration procedures were accomplished more accurately, which may be due to the calibration procedures used.

We note furthermore that one potential explanation for the relatively high bias in the x direction in the Vanderbilt experiments is that this corresponds to the direction in which the calibration frame was oriented towards the tool tip during the calibration process, and it is possible that some small inadvertent force was applied during calibration that deflected the drill tip.

The results of the statistical analysis are very important in order to propose safety margins of the drill channel to the critical anatomic structures during the planning process. In this way, maximal safety of these structures can be predicted and no violation of the nerves or blood vessels takes place. For instance, the 99 per cent confidence radius was used for planning the incision on temporal bone specimens in the authors’ recent experiments.

8 CONCLUSION

This paper has reported the authors’ initial work to build robotic systems with sufficient accuracy for percutaneous access to challenging targets in the inner ear, including percutaneous cochlear implantation and petrous apex access. These applications impose challenging accuracy requirements on surgical CAD/CAM robots. In this paper a system architecture designed to meet these challenging requirements has been described. It consists of an external control computer that interfaces with the industrial robot control box and makes use of differential motion commands for Cartesian control based on feedback from optical tracking of the robot and patient. Also described are various filtering strategies designed to deal with sensor latency, slow sensor update rates, and sensor noise, as well as segmentation, planning, and registration strategies.

Two physical mirror systems implementing the proposed architecture and control methods were constructed, one using a KUKA KR3 robot with an ARTtrack2 optical tracker, and the other using a Mitsubishi RV-3S robot with a Polaris Spectra® optical tracker. Using these systems, two feasibility studies for image-guided CAD/CAM robots in inner-ear surgery were performed – both designed to assess system accuracy. The results of these experiments show that CAD/CAM robots are a promising alternative to manual milling in otolaryngology procedures. A robotic approach has the potential to enable percutaneous access to targets in the inner ear, without requiring a mastoidectomy. In these initial feasibility studies, submillimetric overall system accuracy was found. However, from the statistical point of view, the mean values and the confidence regions of the experimental results show that the navigated robots are not able to assure an accuracy of better than 0.5 mm in 99.9 per cent of all cases.

Whether the accuracies achieved in these initial experiments are sufficient for various inner-ear applications is a topic of ongoing study by the authors. In general, they believe that the accuracies they have reached so far are sufficient for some inner-ear applications, and that further research will be needed to enable others. Furthermore, before an industrial robot can be moved from the research lab to an operating room, many layers of redundant sensing and failsafe software must be implemented, which are topics of ongoing work by the authors. They are also continuing to work towards enhancing overall system accuracy and believe that accuracy enhancement will be possible. Strategies for this, which are currently being investigated, include non-contact calibration, data fusion, other sources of information including inertial measurement units, improved optical tracking hardware, and the potential use of redundant optical trackers to reduce the possibility of fiducial occlusion.

In summary, the initial results reported in this paper illustrate the authors’ early efforts towards applying image-guided CAD/CAM robots to inner-ear surgical procedures. This work lays the foundation for bringing the advantages of robots (e.g. precision and ability to accurately apply preoperative image information to guide surgical tools to sub-surface targets in the presence of obstacles) to many new surgical procedures for which robotic assistance has not yet been attempted.