A conservative algorithm for parabolic problems in domains with moving boundaries

Abstract

We describe a novel conservative algorithm for parabolic problems in domains with moving boundaries developed for modeling in cell biology. The spatial discretization is accomplished by applying Voronoi decomposition to a fixed rectangular grid. In the vicinity of the boundary, the procedure generates irregular Voronoi cells that conform to the domain shape and merge seamlessly with regular control volumes in the domain interior. Consequently, our algorithm is free of the CFL stability issue due to moving interfaces and does not involve cell-merging or mass redistribution. Local mass conservation is ensured by finite-volume discretization and natural-neighbor interpolation. Numerical experiments with two-dimensional geometries demonstrate exact mass conservation and indicate an order of convergence in space between one and two. The use of standard meshing techniques makes extension of the method to three dimensions conceptually straightforward.

1. Introduction

In this paper, we describe a fully conservative algorithm for solving parabolic problems in domains with moving boundaries. The work was motivated by the need to develop a capability of modeling cell migration within the Virtual Cell (VCell), a computational framework for simulating cellular phenomena in realistic geometries [1–5].

Mechanisms underlying dynamical changes of cell shape and cell migration have long been of interest to cell biologists and biophysicists [6,7]. Mathematical models of varying degree of complexity have been proposed [8–17], and a recently released computer program called ‘Cytopede’ was specifically designed for modeling mechanical and signaling behaviors of plated cells [18]. Implementation of numerical algorithms, required for the modeling of dynamic cell shape and cell migration, within a general-purpose computational framework will further facilitate research in this area.

Numerical methods for solving systems with time-dependent discontinuities constitute an area of active research in applied mathematics and computational physics. They involve particular techniques for tracking boundaries and are often classified as Lagrangian and Eulerian, depending on whether the spatial grids are moving or stationary [19]. The interface-tracking techniques used in Lagrangian methods treat dynamic discontinuities as explicit sharp interfaces. The moving grids, constructed so that they fit the boundary, are recomputed each time the surface is updated [20]. This type of approach is used in the Cytopede code [18] that simulates shape changes of fibroblasts cultured on flat surfaces. In Eulerian methods, computations are performed on fixed grids, often based on structured meshes. These methods usually employ interface-capturing techniques in which the shape of the surface is defined implicitly. One class of interface-capturing techniques is level-set methods [21], in which the surface is determined by a zero level of an auxiliary volumetric scalar field.

There are also hybrid methods, in which an Eulerian approach to solving a governing equation is combined with a particular method of tracking or capturing the moving interface [22–26]. These methods are attractive as they avoid complexities of maintaining moving grids, which is particularly challenging in three dimensions, and have the advantages of using regular volumetric grids. Combining the Eulerian approach with interface-tracking techniques allows one to define explicit grids on the surface that are beneficial for cell-biological applications which often include membrane-bound molecules. However, exact mass conservation, another extremely valuable feature for applications in cell biology, becomes an issue in the hybrid methods, because the conservative discretization of equations subjected to boundary conditions at interfaces moving with respect to a fixed grid is nontrivial [23].

The conservative formulations of hyperbolic problems in domains with moving boundaries [23, 25] interpret the intersection of the Cartesian cells with the regions on either side of a moving front as a collection of time-dependent control volumes, over which the conservation law is integrated in space-time to derive a finite-volume discretization. The presence of arbitrary small control volumes in this approach leads to a Courant-Friedrich-Lewy (CFL) stability issue, which is resolved differently by different methods.

In an algorithm proposed by Glimm and co-workers [23], the CFL singularities are resolved through merging the small control volumes with adjacent cells [27]. The method works in conjunction with robust front-tracking methods implemented in FronTier [28], a publicly available C++ library for accurate tracking of moving interfaces both in two (2D) and three dimensions (3D). A similar approach was used by Udaykumar and coworkers [29, 30] in applications to solidification and fluid dynamics problems. Cell-merging, however, while well-defined in one and two dimensions, may not be straightforward to apply to 3D problems.

In the embedded boundary methods [24] based on the Volume-of-Fluid front-capturing techniques [31], cell-merging is avoided by performing two updates, a conservative update and a nonconservative, but CFL stable, update. The difference between the two updates is then redistributed to neighboring computational cells to maintain overall stability and local conservation. Recent improvements to the method have been shown to yield second-order accuracy in one dimension [25]. While the redistribution of mass is simpler to apply in multiple dimensions, maintaining the second-order accuracy of the method in 2D and 3D is a challenging problem.

In a recently published hybrid algorithm [26], specifically designed for applications to cell biology, the contour of a moving cell is captured by a level-set technique. Still, the algorithm constructs and maintains the grid on the contour by projecting nearby rectangular grid points onto the interface at each integration time step. The method employs finite-volume discretization with the grid becoming unstructured near the membrane. Because of non-conservative interpolation of displaced grid points, the method does not conserve mass locally, but global mass conservation is enforced on the assumption that the total mass inside the domain is known in advance.

This paper is focused on the description of a fully conservative discretization scheme for parabolic (diffusion-advection-reaction) equations with Rankine-Hugoniot boundary conditions imposed at moving interfaces. For simplicity, we defer the discussion of the front-tracking technique and assume that the position of a moving piecewise-linear interface is known at any time.

In our algorithm, spatial discretization is based on Voronoi decomposition [32] applied to a fixed set of regularly spaced gridpoints. Voronoi meshes were used previously in modeling cell migration by Bottino et al. [33] and in our algorithm for modeling diffusion on a surface coupled to diffusion in embedding volume [3]. Utilizing this meshing technique for purposes of the algorithm described in this article has a number of practical advantages. Voronoi polygons are well suited for conservative finite volume discretization. The procedure automatically generates control volumes of comparable sizes, and the CFL stability issue due to crossings of a moving front with the mesh does not arise. Thus, there is no need in our method to adjust positions of the grid points, nor it requires cell-merging or redistributing mass between control volumes. While the control volumes adjacent to a moving interface conform to the shape of the domain and are therefore irregular, they merge seamlessly with regular Voronoi cells in the interior of the domain. In fact, the procedure of Voronoi decomposition needs to be applied only to the gridpoints in the vicinity of the interface. Finally, the use of the standard meshing technique makes extension of the method to three dimensions conceptually straightforward.

Fully conservative formulation is achieved through finite-volume discretization and natural-neighbor interpolation [34] (interpolation is required to reinitialize unknowns at the nodes crossed by a propagating front and at their neighbors). The formulae of the natural-neighbor interpolation are derived from the requirement that mass be not relocated when boundaries between Voronoi cells are redrawn, thus preserving local mass conservation. Test cases with two-dimensional geometries demonstrate exact mass conservation and indicate an order of convergence of the error between 1 and 2.

2. Mathematical problem

Consider a system defined in a spatial domain Ω(t) ∈Rⁿ (n is the dimensionality of the space) whose boundary ∂Ω(t) changes with time. The system is governed by the continuity (mass conservation) equation,

$$\frac{\partial u}{\partial t}=-\text{div}\mathbf{J}+R,$$ (1)

where u is the concentration of a molecular species, J = −D∇u + vu is the diffusive-advective flux density, and R is the reaction term. Eq (1) is subject to the Rankine-Hugoniot boundary condition at the moving boundary ∂Ω(t), which in the case of the interface representing an impermeable membrane is written as

$$(\mathbf{J}-{\mathbf{v}}_{b}u)\mathbf{n}{|}_{\partial \Omega }=0,$$ (2)

where n is the outward normal and v_b stands for the velocities of the boundary points. For simplicity, the diffusion coefficient, D, and the velocity field in the volume, v, are assumed to be time-independent. We also assume that the membrane velocities, v_b, are given at any time, so that the position of ∂Ω(t) is either known exactly or can be computed with sufficiently high accuracy for any t.

3. Algorithm

Consider a box that would contain Ω(t) for any t ∈ [0, T_max]. The boundary of the domain, ∂Ω(t), is assumed to be piecewise-linear. A cell-centered, uniform orthogonal mesh of size h is applied to the box to generate a regular set of cell centers{r_i}. Our algorithm approximates the solution of Eqs (1),(2) at cell centers inside ∂Ω(t). Because ∂Ω(t) changes with time, these cell centers comprise a time-dependent subset of grid points S(t) = {r_i (t)}. Indeed, the time dependence of this subset is piecewise constant, because only at discrete times t_k (k = 1,2,…) do one or more cell centers abruptly become interior or exterior points as the boundary crosses them, and in between those times, the set S(t) remains unchanged. The set of the interior nodes in the time interval (t_k−1, t_k) will be denoted by S_k.

To ensure mass conservation, we apply the finite volume spatial discretization of Eqs (1), (2) [19]. In this discretization scheme, Ω(t) is decomposed into small control volumes {ω_i(t)}, each including a single computational node r_i. Eq (1) is then integrated over ω_i(t). Taking into account the Rankine-Hugoniot boundary conditions, Eq (2), imposed at the moving boundary, this integration yields

$$\frac{\partial }{\partial t}\underset{{\omega }_i}{\int }udv=\underset{\partial {\omega }_i}{\int }(D\frac{\partial u}{\partial n}-\mathbf{v}\mathbf{n}u)ds+\underset{{\omega }_i}{\int }Rdv,$$ (3)

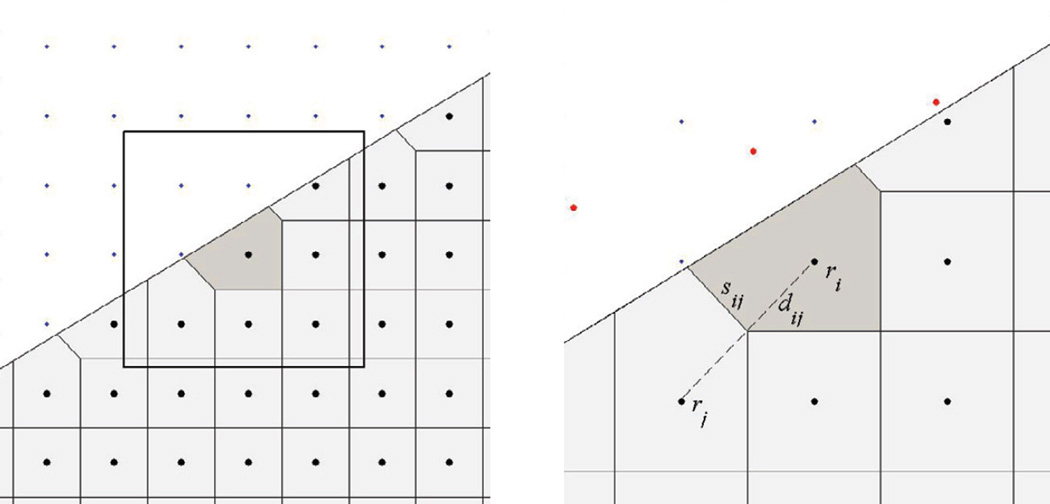
where n is the outer normal to ∂ω_i. In our method, the control volumes {ω_i} are obtained by means of Voronoi decomposition [32], a 2D example of which is shown in Figure 1. Note that at the boundary, the Voronoi decomposition automatically generates a layer of irregular control volumes that conform to the geometry of the front and at the same time mesh seamlessly with neighboring regular cells. Later in this section, we describe two methods of constructing irregular control volumes, with exact and approximate matching of ∂Ω(t).

Figure 1.

Generation of control volumes by Voronoi decomposition. The blow-up of the delineated square at the right includes meshing parameters and illustrates a simple way of constructing a boundary layer of irregular Voronoi cells. The “ghost” points (shown in red), obtained by reflecting the adjacent grid points in the front, are used to “close” a Voronoi cell.

The discretized form of Eq (3) yielded by this meshing scheme is

$$\frac{d(u_i(t)V_i(t))}{dt}\approx \sum _{j\in G(i)}(D\frac{u_j(t)-u_i(t)}{d_{ij}}-{\mathbf{n}}_{ij}\cdot \frac{{\mathbf{v}}_j+{\mathbf{v}}_i}{2}\cdot \frac{u_j+u_i}{2})\cdot s_{ij}(t),i\in S(t),$$ (4)

where u_i and u_j are the concentration values at the corresponding grid points, V_i =| ω_i | is the volume (area in 2D) of the ith Voronoi cell, d_ij is the distance between the ith and jth grid points, s_ij is the area (length) of the shared face (edge) separating the cells i and j, ${\mathbf{n}}_{ij}=\frac{{\mathbf{r}}_j-{\mathbf{r}}_i}{|{\mathbf{r}}_j-{\mathbf{r}}_i|}$ is the outer normal to s_ij, and G(i) is the set of nodes in S(t) that correspond to the Voronoi cells adjacent to the ith cell. The reaction term, whose spatial discretization is trivial, is omitted in Eq (4) for simplicity. While the discretization of the flux terms in the right-hand side of Eq (4) is second-order accurate at the interior grid points representing regular Voronoi cells, the accuracy is lower for irregular control volumes, because the fluxes in this case are approximated by our algorithm at the points that are different from the face centroids. As a result, the overall order of accuracy in space is between 1 and 2 (see the results of convergence studies and the discussion of the accuracy of the method in Section 4).

We now describe two methods of constructing irregular control volumes adjacent to the propagating front. By definition, a Voronoi polygon is a locus of points that are closer to a given node than to any other node. Based on this definition, our method of generating irregular control volumes that exactly conform to the domain shape includes two steps. First, Voronoi polygons are constructed for all grid points in S_k, assuming (theoretically) that the space they are in is infinite. Second, the intersection of the polygons obtained in step 1 and Ω(t) is computed. While theoretically some of the polygons obtained in step 1 will not be closed, in practice they are closed by boundaries of the box containing Ω(t) (see the beginning of this section). This is implemented by adding ‘ghost’ points to S_k, which are created in this method by reflecting in the box boundaries the nodes in S_k close to ∂Ω(t). The intersection of polygons in step 2 is performed using the Vatti clipping algorithm [35].

The second method, illustrated in Figure 1, right, approximates a domain boundary with the Voronoi convex polygons (polyhedrons). It also employs ‘ghost’ points for closing irregular Voronoi polygons, but in this case, the “ghost” points (shown in red) are obtained by reflecting the gridpoints in ∂Ω(t). This method is computationally less expensive but, unlike the first one, introduces additional errors due to local curvature, which are O(h/ρ), where h is the mesh size and ρ is the radius of curvature.

Eqs (4) are integrated over time using first-order fixed time step methods. For regular ω_i, which are not adjacent to ∂Ω(t) and therefore remain regular throughout the time step, V_i and s_ij are independent of time, and standard time discretization schemes [19], explicit or implicit, can be applied to the corresponding grid points. For the Voronoi cells adjacent to ∂Ω(t), the integration within the periods (t_k−1, t_k), for which S(t) ≡ S_k remains unchanged, is not much different: the only distinction is that V_i and s_ij of the irregular Voronoi cells are time-dependent and need to be updated for each integration step Δt. In particular, the time discretization of the left-hand side of Eqs (4) for the corresponding grid points is Δt⁻¹ (u_i (t + Δt)V_i (t + Δt) − u_i (t)V_i (t)).

Our algorithm assumes that the irregular cells do not disappear within one time step due to the repositioning of the front. This imposes a constraint on the integration time step, $\mathrm{\Delta }t<\frac{h}{\underset{\partial \Omega }{2\text{max}}\left|{\mathbf{v}}_b\mathbf{n}\right|}$, mathematically resembling the regular CFL condition. Note that unlike the CFL stability issue that usually arises in hybrid methods, the upper bound for the time step in our method is finite. This is because the sizes of the Voronoi cells centered around uniformly spaced grid points are comparable by construction.

Special care is required for integrating across t = t_k, when the set of unknowns {u_i} changes because of the changing position of ∂Ω(t). At those times, Eqs (4) must be properly re-initialized for the nodes that become interior and the nodes whose natural neighbors change. The structure and parameters of Eqs (4) should be adjusted correspondingly, and the new initial values of the unknowns at the affected nodes must be computed. The reinitialization is an interpolation procedure, in which the values of u(x) at the affected nodes are approximated on the basis of known values of u at surrounding gridpoints. In our algorithm, this is done by means of the natural-neighbor interpolation [34] that ensures local mass conservation. In what follows, we use the superscripts “− ” and “+” to denote the values of variables at t = t_k − 0 and t = t_k + 0, respectively, so that S_k ≡ S⁻, S_k+1 ≡ S⁺, u(r, t_k − 0) ≡u⁻ (r), u(r, t_k + 0)≡ u⁺ (r), etc.

The initial conditions for the new set of variables are derived from the requirement that mass be conserved locally while the borders of the Voronoi cells are redrawn [34]. Thus, the mass within ${\omega }_i^{+}(i\in S^{+}),m^{+}({\omega }_i^{+})=u_i^{+}{V}_i^{+}$, must equal the mass that existed in the same volume before the new borders between the Voronoi cells were drawn. The latter is ${\sum }_{j\in S^{-}}{u}_j^{-}|{\omega }_i^{+}\cap {\omega }_j^{-}|$ because ${\omega }_i^{+}$ is composed of the parts of the control volumes ${\omega }_j^{-}(j\in S^{-})$ which existed before the “redistricting”, i.e. ${\omega }_i^{+}={\cup }_{j\in S^{-}}({\omega }_i^{+}\cap {\omega }_j^{-})$. Therefore,

$$m^{+}({\omega }_i^{+})=\sum _{j\in S^{-}}{u}_j^{-}|{\omega }_i^{+}\cap {\omega }_j^{-}|.$$ (5)

The initial values for the new set of variables, $u_i^{+}=\frac{m^{+}({\omega }_i^{+})}{V_i^{+}}$, then follow from Eqs (5):

$$u_i^{+}=\frac{1}{V_i^{+}}\sum _{j\in S^{-}}{u}_j^{-}|{\omega }_i^{+}\cap {\omega }_j^{-}|.$$ (6)

Because equations (5) and (6) are based on local mass conservation, the total mass in Ω is conserved as well. This can be verified by summing Eqs (5) over all i ∈ S⁺ and taking into account that $V_j^{-}=\sum _{i\in S^{+}}|{\omega }_i^{+}\cap {\omega }_j^{-}|$, which yields $\sum _{i\in S^{+}}{u}_i^{+}{V}_i^{+}=\sum _{j\in S^{-}}{u}_j^{-}{V}_j^{-}$.

Note that the reinitialization of the concentration is not required for the nodes whose natural neighbors remain unchanged during the transition S⁻ → S⁺. Indeed, in this case, $\sum _{j\in S^{-}}{u}_j^{-}|{\omega }_i^{+}\cap {\omega }_j^{-}|=\sum _{j\in S^{+}}{u}_j^{-}\left|{\omega }_i^{+}\right|{\delta }_{ij}=V_i^{+}\sum _{j\in S^{+}}{u}_j^{-}{\delta }_{ij}$ (δ_ij is the Kronecker delta) and from Eqs (6), $u_i^{+}=u_i^{-}$.

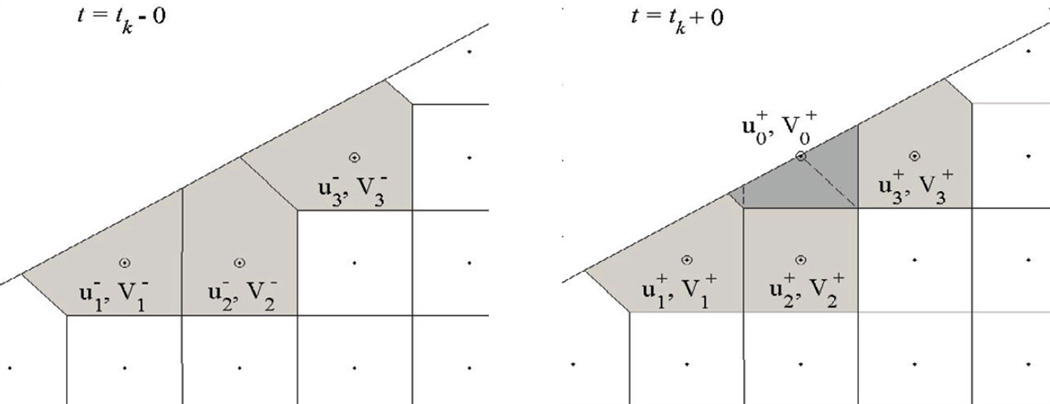
We now use Eqs (6) to derive re-initialization formulae for situations where a node is added to or lost from S⁻ as a result of the transition S⁻ → S⁺. If a new node i is added to S⁻ at t = t_k (Figure 2), then, using Eqs (6), the corresponding concentration $u_i^{+}$ is

$$u_i^{+}=\frac{1}{V_i^{+}}\sum _{j\in G(i)}{u}_j^{-}|{\omega }_i^{+}\cap {\omega }_j^{-}|=\frac{1}{V_i^{+}}\sum _{j\in G(i)}{u}_j^{-}(V_j^{-}-V_j^{+}).$$ (7)

Figure 2.

Creation of an additional Voronoi cell ω₀ around the node r₀ that becomes an interior point of a moving domain. Because the masses previously assigned to cells ω₁, ω₂, and ω₃ are not reallocated, the corresponding unknown u₀ is initialized according to Eq (7), whereas the unknowns, u₁, u₂, u₃ remain unchanged.

Note that $(V_j^{-}-V_j^{+})$ in Eqs (7) are guaranteed to be positive because ${\omega }_j^{+}\subset {\omega }_j^{-}(j\in G(i))$. For the neighboring nodes j ∈ G (i), Eqs (6) yield $u_j^{+}=u_j^{-}$, again due to ${\omega }_j^{+}\subset {\omega }_j^{-}$.

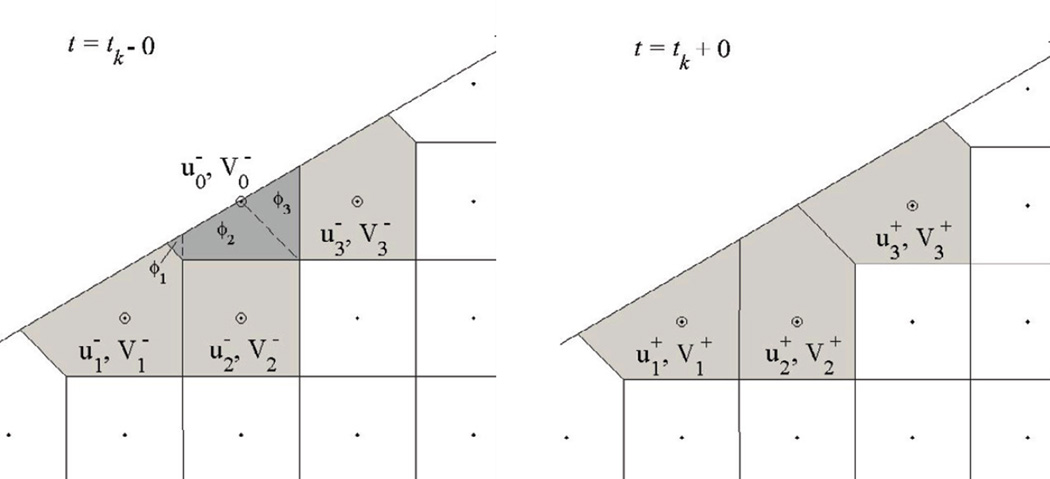
For the situation where a node i is lost from S₋ at t = t_k (Figure 3), Eqs (6) yield the following new initial values $u_j^{+}$ at the neighboring nodes j ∈ G(i) :

$$u_j^{+}=\frac{1}{V_j^{+}}(u_i^{-}|{\omega }_i^{-}\cap {\omega }_j^{+}|+u_j^{-}|{\omega }_j^{-}\cap {\omega }_j^{+}|)=\frac{1}{V_j^{+}}(u_i^{-}{V}_i^{-}{\varphi }_j+u_j^{-}{V}_j^{-}),$$ (8)

where ${\varphi }_j=(V_j^{+}-V_j^{-}){[\sum _{j\in G(i)}(V_j^{+}-V_j^{-})]}^{-1}$ is the volume fraction of the part of ${\omega }_i^{-}$ included into ${\omega }_j^{+}$ (Figure 3, left panel). Note that $\sum _{j\in G(i)}{\varphi }_j=1$ and ϕ_j > 0 for all j because in this case, ${\omega }_j^{+}\supset {\omega }_j^{-}$.

Figure 3.

Voronoi cells ω₁, ω₂, and ω₃ are redrawn when the node r₀ becomes an exterior point, as the cell 0 that has included r₀ is eliminated. The mass, however, is not reallocated, and the unknowns u₁, u₂, u₃ are reinitialized according to Eqs (8).

In Figures 2 and 3, the added (lost) node is located exactly at the interface, consistently with the definition of t_k. It is easy to see, however, that Eqs (7) and (8) and their derivation would not change if the update of the Voronoi decomposition for the nodes adjacent to ∂Ω(t)were done at a slightly different time with the added (lost) node being a little behind (or ahead of) the front. This means that one does not have to look for the exact values of t_k but rather can check for changes in the subset of the adjacent nodes at each time step.

Note that Eqs (7) and (8) were derived for cases where nodes crossed by a moving boundary within one time step are far from each other (or they are crossed one at a time). If the time step is insufficiently small, several nodes that are close to one another might be crossed within the same time step, a situation that is not covered by Eqs (7) and (8). There are various ways to deal with this type of events. In a simple approach employed in our algorithm, all nodes that change their status from interior to exterior or vice versa within a given time step are tagged for reinitialization, and Eq (7) or (8) is applied to them one at a time in the order they were listed in the array {r_i}. Importantly, the set of interior nodes S_k must also be updated consecutively each time Eq (7) or (8) has been used. The method may introduce slight asymmetry due to the ordering of gridpoints. But because the situations in which neighboring nodes change their status simultaneously become rarer as the time step decreases, the possible asymmetry is not a factor for the overall convergence, as demonstrated by the convergence studies described in the next section. An alternative approach would be to apply the natural-neighbor interpolation simultaneously to all gridpoints changing their status [35]. For this, one should compute an intersection of the new decomposition and the old mesh to determine all non-overlapping clips that change their association with the nodes, and Eqs (7) and (8) should be appropriately generalized.

In summary, our algorithm includes the following steps:

• Initializing the problem:

  • (i)
    given ∂Ω(0), identify the set of interior nodes S(0) and the subset of nodes adjacent to ∂Ω (0);
  • (ii)
    perform Voronoi decomposition for the initial subset of nodes adjacent to ∂Ω (0) (for other grid points in S(0), the control volumes are regular orthogonal boxes);
  • (iii)
    compute d_ij (0) (distances between Voronoi neighbors), s_ij (0) (lengths of the edges (areas of the faces) of the irregular Voronoi cells), and V_i (0) (areas (volumes) of the irregular Voronoi cells). Parameters of the regular cells are precomputed, given the mesh size h.
• Advancing the solution in time:

  • (iv)
    find ∂Ω(t + Δt) ;
  • (v)
    update the Voronoi decomposition for the nodes adjacent to ∂Ω(t + Δt) ;
  • (vi)
    compute s_ij (t + Δt) and V_i (t + Δt) for the irregular Voronoi cells (as in step (iii));
  • (vii)
    solve Eqs (4) to find u_i (t + Δt) ; (Note: steps (iv)-(vii) are performed for S(t) ; if S(t + Δt) is different from S(t), the results of step (vii) are used in step (ix).)
  • (viii)
    identify the set of interior nodes S(t + Δt) by updating the subset of the nodes adjacent to ∂Ω(t + Δt) ;
  • (ix)
    if during the time step a computational node changes its status from exterior to interior (from interior to exterior), adjust Eqs (4) and use Eqs (7) (Eqs (8)) to update u_i (t + Δt) for this node and its natural neighbors. This involves computing the corresponding new distances d_ij (t + Δt) and areas (lengths) s_ij (t + Δt). If there are several such nodes in one time step, treat them one by one in an arbitrary order.

4. Convergence studies and tests of mass conservation

Accuracy of the proposed algorithm is affected by several factors. As mentioned in the previous section, the finite volume discretization is second-order accurate only for regular control volumes in the bulk of the domain. For irregular Voronoi cells adjacent to the boundary, approximation of fluxes at the points that are not centroids of the faces lowers the order of convergence in space by approximately ½ (see results below). In addition, the reinitialization of unknowns at grid points in the vicinity of a moving front is a first-order procedure, which in multiple dimensions¹ results in L_∞ -norm error close to O(h). However, the error due to reinitialization occurs only at few nodes at a time and does not affect significantly other nodes. This is because it dissipates quickly to its spatial average, which is zero due to exact local mass conservation built in the algorithm. Indeed, the solution error averaged over the layer of irregular points remains to be O(h^1.4) or higher, whereas convergence in the L₂ -norm is closer to the second order. Overall, the order of convergence of our algorithm in space is between 1 and 2.

The convergence of the algorithm was studied using a number of test problems whose numerical solutions obtained with the algorithm were tested either against exact analytical solutions or precise numerical solutions computed by alternative methods. Total mass inside moving domains has been monitored in all tests and indicates exact mass conservation.

We evaluated several versions of the algorithm that differed by their time discretization scheme (explicit or implicit) and/or by a method of constructing irregular cells near the boundary: the method in which ∂Ω(t) is approximated by irregular Voronoi polygons (illustrated in Figure 1) or the method where irregular control volumes are obtained by exact intersection of Ω(t) and (theoretically) open Voronoi polygons. While various versions of the algorithm have similar orders of convergence, the magnitude of the error was significantly lower for the solutions obtained with irregular control volumes that conform to ∂Ω (t) precisely. The results presented below were obtained using the explicit time discretization and precise construction of irregular control volumes.

4.1. Diffusion inside a moving box: steady-state solutions

A problem of diffusion in a steadily moving box can be solved exactly and therefore provides a convenient test for our algorithm. Consider a gas in an a × a box Ω'(t) = {x'(t), y'(t) : | x'−v_bt |≤a / 2, | y'|≤a / 2} that moves with a constant velocity, v_b = (v_b,0). By changing to a frame of reference moving with the same velocity v_b, the problem reduces to that in a fixed domain,

$${\partial }_{t}u=\text{div}(D\nabla u+{\mathbf{v}}_{b}u),(D\nabla u+{\mathbf{v}}_{b}u)\mathbf{n}{|}_{\partial \Omega }=0,$$ (9)

where u is now defined in Ω ={x, y : | ≤x |≤a / 2, | y|≤a / 2}.

Finding the steady state of the system is particularly straightforward. The problem becomes one-dimensional, with the density u(x) satisfying the following equations: D∂²_xxu + v_b∂_xu = 0, (D∂ _xu + v_bu)|_{x=±a / 2}=0. The exact solution of these equations is u(x) =u₀ exp(−kx), where k = v_b / D and the pre-exponential factor u₀ = u(0) that can be expressed in terms of a given average gas concentration, ū = ∬_Ω udxdy. For ū = 1, u₀ = (ka / 2)(sinh(ka / 2))⁻¹. The corresponding traveling wave solution in the laboratory frame of reference, u(x', t) = u₀ exp(−k(x'−v_bt)), was used for evaluating errors of the numerical solutions obtained with the algorithm.

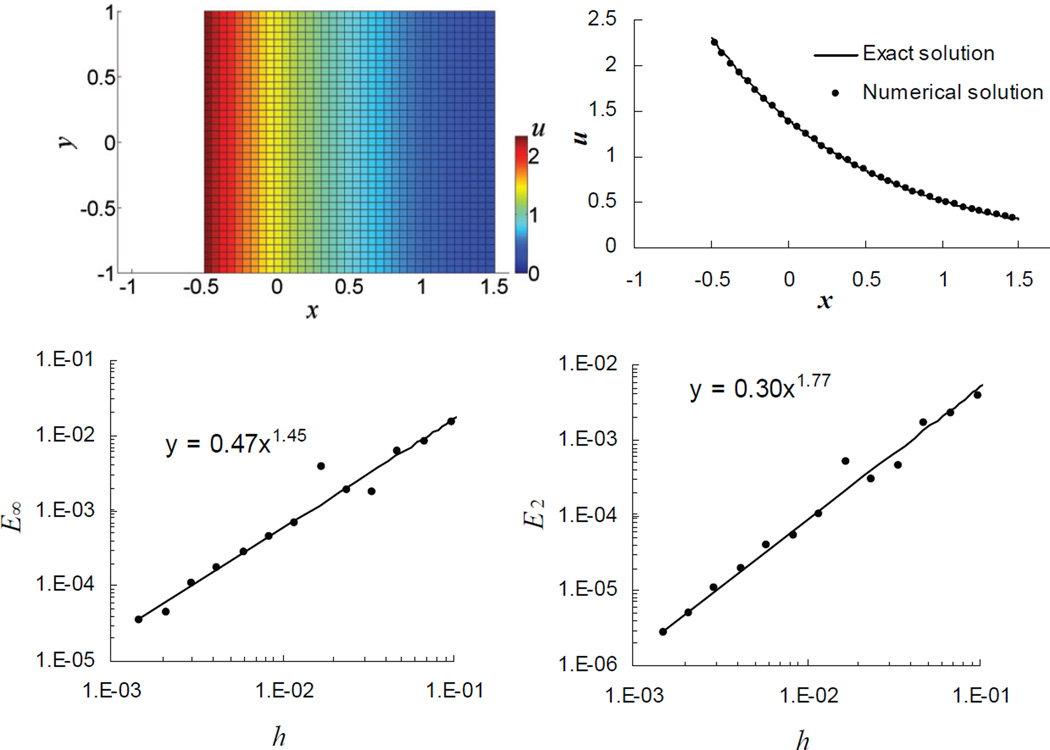
In the test, numerical solutions of Eqs (1), (2) were obtained for D = 1, v = 0, and R = 0 in a square box with a = 2 moving with the speed v_b = 1. Given the initial condition u(x', 0) = u₀ exp(−x'), the solver quickly settles on a numerical steady state. The snapshot in Figure 4 (upper left) illustrates a numerical solution at t = 0.5obtained with h = 0.048 and Δt = 5.76 × 10⁻⁴. The upper right panel of Figure 4 shows a horizontal line scan of the snapshot (dots) superimposed on the corresponding exact solution (solid curve).

Figure 4.

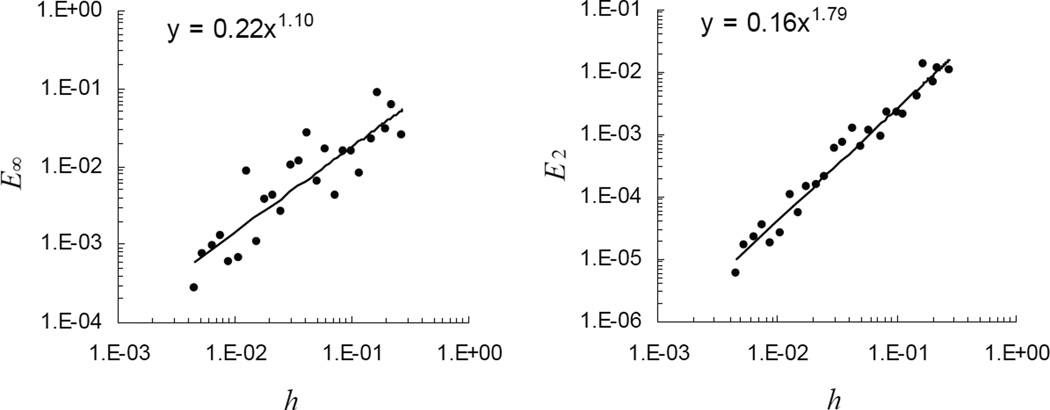
Diffusion in a moving square box. A numerical solution, upper left, obtained for D=1, v_b=1, a=2, is compared with the corresponding exact solution, upper right. In the lower panel, plots of L_∞- (left) and L₂- (right) norms of absolute error as functions of the mesh size h illustrate convergence of the algorithm. All results are based on solutions at t = 0.5.

The lower panel of Figure 4 illustrates orders of convergence of the L_∞ - and L₂ - norms of the solution error, E_∞ and E₂. Because the problem is essentially one-dimensional, the low-order reinitialization procedure is performed rarely and therefore does not affect E_∞ appreciably. Thus, the order of convergence of E_∞ in this test largely reflects the effect of irregularity of the control volumes adjacent to the boundary.

Interestingly, the traveling wave solution, u(x', t) = u₀ exp(−k(x'−v_bt)), holds true regardless of the domain shape, provided the shape remains fixed during the motion and the problem is solved for the zero-flux boundary conditions. We therefore conducted a similar test for a circular domain where the problem is fundamentally two-dimensional. The results indicate that in multiple dimensions, the order of convergence of the L_∞ -norm error, E_∞, is indeed affected by the first-order reinitialization error (Figure 5, left). This error, however, is local in nature and does not affect the accuracy of the solution even within the boundary layer of irregular Voronoi cells. Indeed, when averaged over irregular control volumes, the error exhibits convergence of O(h^1.39), comparable to that of E_∞ in 1D. The convergence of E₂ for the circular domain is similar to that for the square domain (Figure 5, right).

Figure 5.

Diffusion in a moving circular domain: testing against exact steady state. Convergence of L_∞- norm error, E_∞, is affected by reinitialization of unknowns at the boundary, but L₂-norm error, E₂, is O(h^1.79), which is similar to E₂ for diffusion in a moving square. All results are based on solutions at t = 0.2.

4.2. Diffusion inside a moving circle: time-varying solutions

Here we test the accuracy of time-varying solutions to the problem of diffusion in a circular domain moving with velocity v_b = (1, 0), Ω'(t) = {x'(t), y'(t) | (x'−v_bt)² + y'² ≤1}, by comparing them with precise numerical solutions obtained by different methods. To find baseline numerical solutions, the problem is reformulated, similarly to the previous case, as an equivalent diffusion-advection problem in a fixed domain Ω(t) = {x, y | x² + y ² ≤1} (see Eqs (9)). The accurate numerical solutions are then obtained by solving the equivalent problem with high precision using two “conventional” PDE solvers, a VCell diffusion-advection solver [1] and a COMSOL MULTIPHYSICS® PDE solver (http://www.comsol.com/products/multiphysics/).

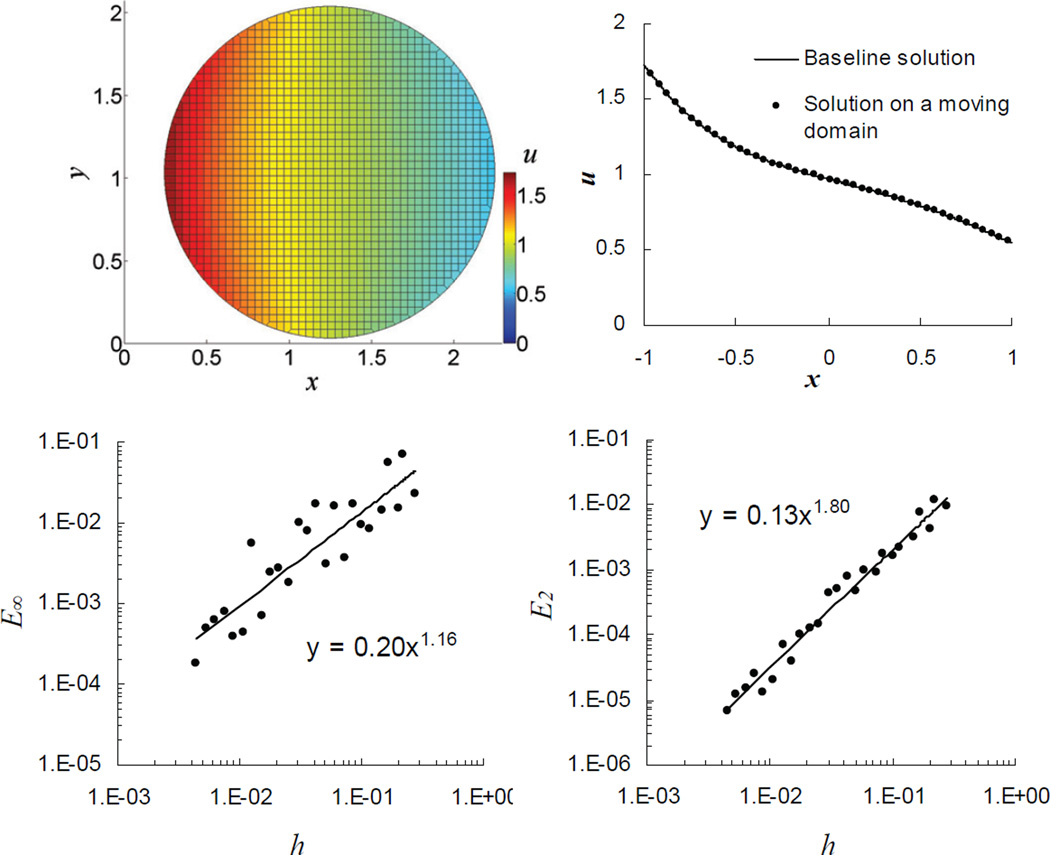
Test results are presented in Figure 6. The snapshot in the upper left pictures a solution of the moving boundary problem at t = 0.2. The solution was obtained with the initial concentrations u(r,0) = 1, using the following discretization parameters: h = 0.044, Δt = 4.84 × 10⁻⁴. In the upper right of Figure 6, the results scanned along the equator of the snapshot (dots) are superimposed on the baseline solution obtained with the VCell diffusion-advection solver (solid curve); the latter was computed with h = 0.0015 and the absolute and relative tolerances set at 10⁻⁹ and 10⁻⁷, respectively, which yielded absolute error ~ 10⁻⁵, estimated by Richardson extrapolation.

Figure 6.

Testing time-varying solutions. Solution at t = 0.2 (upper left) is compared, along the equator, with a precise numerical solution obtained by a regular VCell solver (right). Lower panel: convergence of E_∞ and E₂ ; errors of the solutions at t = 0.2 are computed against a precise numerical solution obtained with COMSOL®.

The solution of the test problem over the entire simulation time was recorded in Supplementary Movie 1, that also provides comparison with the VCell baseline solution over time. In addition, the movie includes a third panel that demonstrates exact mass conservation by displaying the total mass inside the moving domain as a function of time.

The lower panel of Figure 6 illustrates the convergence in space of the L_∞ - and L₂ - norms of the solution error at t = 0.2. The dependencies E_∞ (h) and E₂ (h), obtained in this case against an accurate solution computed with COMSOL MULTIPHYSICS®, are similar to the ones observed in the previous test (Figure 5). The error averaged over irregular control volumes was O(h^1.45), also comparable to the result of the previous test.

In computing the baseline solution with COMSOL MULTIPHYSICS®, the absolute and relative tolerances were set at 10⁻⁹ and 10⁻⁸, respectively, and the mesh was refined to yield at least 7 accurate digits after the decimal point. The error of the baseline solution was estimated by computing system’s steady state, for which the exact solution is available (see section 4.1).

4.3. Diffusion-advection in a moving circle

In living cells, diffusion of macromolecules occurs in cytosol (intracellular fluid), and in a moving cell, the cytosol moves as well. The realistic models of migrating cells will therefore require solving the diffusion-advection equations in moving domains. Here we evaluate the accuracy of the algorithm when it is applied to diffusion-advection systems, using a simple test problem with an analytical solution.

Consider a situation where the fluid is stationary with respect to the domain. Then, in a frame of reference that moves with the domain, the problem reduces to solving a diffusion equation in a fixed domain with zero-flux boundary conditions, a problem that has an analytical solution for simple domain shapes. Specifically, we solve Eq (1) with R = 0, $D=\frac{1}{4}$ and v =(1,0) in a unit circle Ω(t) moving with the velocity v_b = v. For certain initial conditions, the problem has closed-form solutions. In particular, one can verify that u(x, y,t) = exp(−λ² D t)xJ₁ (λ((x − v_bt)² + y²)^1/2) + J₁(λ), where J₁ (z) is the first-order Bessel function of the first kind and λ = 1.841183781340659, is an exact solution of the original problem in Ω(t) ={(x, y) : (x− v_bt)² + y ² ≤ 1}. The corresponding initial condition is u(x, y, 0) = xJ₁ (λ(x² + y²)^1/2) + J₁ (λ), which was used in the numerical test.

The error analysis was performed for solutions at t = 0.2 with varying h. One such solution is shown in Figure 7, along with the plots of E_∞ (h) (circles) and E₂ (h) (triangles). The enhanced convergence of E_∞ and an essentially second order of E₂ are likely because of the smallness of gradients of the solution near the boundary, which is in part, due to the zero-flux boundary condition. In particular, the error due to reinitialization, that would normally dominate E_∞, is significantly reduced in the absence of steep gradients at the boundary.

Figure 7.

A diffusion-advection system in a moving circle. A snapshot of a numerical solution at t = 0.2, left, and plots of E_∞ (h) (circles) and E₂(h) (triangles), right, computed for solutions at t = 0.2.

4.4. Mass conservation in domains with varying shape and velocities

Exact mass conservation was observed in all tests described in the previous sections. In addition, mass conservation was also tested using problems for which we did not have exact solutions, such as diffusion in domains with changing shapes and non-constant translational velocities. The solutions of these problems obtained with our algorithm are demonstrated in Supplementary Movies 2 and 3.

In Movie 2, a circular domain abruptly changes direction of its motion. A color code is used to illustrate changes in the density of a diffusing gas from low (blue) to high (red). A similar color code is used in Movie 3 to demonstrate a solution of a diffusion problem in a cell that changes its shape. The vectors shown in the movie depict velocities of the points of the cell boundary. The solutions demonstrate physically reasonable dynamics and conservation of mass within machine precision.

5. Concluding remarks

In this article, we described and analyzed a conservative algorithm for solving reaction-diffusion-advection systems in domains with moving boundaries. The algorithm was developed for applications in cell biology, where ensuring rigorous conservation of mass is of particular importance.

The proposed algorithm is a hybrid method where dynamic boundaries move relative to a fixed regular grid. The CFL stability issue that arises in hybrid methods due to intersections of a moving front with the underlying mesh is avoided by applying Voronoi decomposition. Control volumes produced by this technique in the vicinity of a front conform to the shape of the domain and merge seamlessly with regular control volumes in the interior of the domain. Local mass conservation is achieved through the built-in finite-volume discretization and by applying the mass-conserving natural-neighbor interpolation to nodes affected by crossings with a propagating front.

The algorithm was tested against exact analytical solutions as well as precise numerical solutions obtained by different algorithms. The results indicate the order of convergence in space between 1 and 2. The exact, within machine precision, conservation of mass was observed in all tests, including those for which we did not have exact solutions. The latter involved domains with changing shapes and domains moving with non-constant velocities.

Certain limitations must be relaxed before the described algorithm can be integrated into a general-purpose computational tool. The method is currently implemented and tested for 2D geometries. Because it employs standard meshing techniques, extension to 3D is conceptually straightforward. Still, for a 3D version of the algorithm to be practical, additional optimization of the method will likely be necessary.

The test problems of the previous section are solved in domains with explicitly defined geometries and given kinematics. In actual applications, the algorithm should be able to handle cases where the positions of moving boundaries are not known a priori, but rather determined based on given or computed velocity fields, and with geometries defined more generally, e.g. by implicit functions. It therefore must work in conjunction with robust front-tracking (capturing) techniques. We evaluated several existing methods, by testing them against “exact” kinematics, and found a recent version of FronTier [28] particularly appealing. It combines advantages of front-tracking and front-capturing techniques and maintains surface grids. The latter is of particular importance, given that applications to cell biology often include variables defined on moving interfaces.

Front-tracking with FronTier is illustrated by Supplementary Movies 4 and 5. The examples used in the movies mimic dynamic changes of cell membranes. In Movie 4, the solid curve represents a dynamic shape of a 2D “cell”, with the “exact” kinematics ∂Ω(t) = {x(t), y(t)} described by x = f (φ, t) cos φ, y = f (φ, t) sin φ, where f (φ, t) = 1+0.1 cos(5φ + 5t) + 0.2 cos(7φ + 3.5t) and φ∈ [0,2π], t ∈ [0,25]. The dots shown in the movie are the boundary points computed by FronTier on the basis of the input velocities x'(t), y'(t).

Similarly, the “exact” kinematics of a 3D “cell”, ∂Ω(t) = {x(t), y(t), z(t)}, described by x(t) = f (φ, θ, t) cos φ cos θ, y(t) = f (φ, θ, t) sin φ cos θ, z(t) = f (φ, θ, t) sin θ, where $f(\phi ,\theta ,t)=1+0.9\text{cos}(10t+4.8)Y_4^2(\phi ,\theta )+0.9\text{cos}(3t+1.44)Y_7^3(\phi ,\theta ),Y_4^2(\phi ,\theta )$ and $Y_7^3(\phi ,\theta )$ are the spherical harmonics, and φ ∈ [0,2π], θ ∈ [0,π], t ∈[0,8] (Movie 5a), were used to compute velocities x'(t), y'(t), z'(t) which were an input for FronTier. Based on this input, FronTier computed the dynamics of boundary points shown in Movie 5b for a cross-section z = 0, along with the cross-section of the exact surface (solid curve).

Upon the implementation of the algorithm in VCell, the users will be able to solve problems where the velocities of the membrane points are either known or can be evaluated as functions of state variables. Because velocities are determined by forces exerted on, and generated by, the cell, the algorithm will ultimately be integrated with cell mechanics. The latter typically includes forces generated by molecular motors and by polymerization of the cytoskeleton, viscoelasticity of the cytoskeleton and its adhesion to extracellular matrix [36].

Supplementary Material

01. Supplementary Movie 1. Diffusion in a moving circle.

A problem of diffusion of gas in a moving circular domain is used to test accuracy of time-varying solutions generated by our algorithm (section 4.2). The solution obtained by our method (left panel) is validated against a precise numerical solution obtained with a different solver for an equivalent diffusion-advection problem in a stationary domain. Detailed comparison of values along the horizontal diameter (middle panel) demonstrates good agreement between the solution obtained with our algorithm (dots) and the baseline solution (solid curve) at all times. The right panel illustrates exact conservation of the mass inside the moving domain.

02. Supplementary Movie 2. Diffusion in a circle moving with varying velocity.

The movie illustrates a test in which a gas diffuses in a circle that abruptly changes direction of its motion. The solution generated by our algorithm is physically correct and characterized by exact mass conservation. A color code is used to illustrate changes in the density of a diffusing gas from low (blue) to high (red).

03. Supplementary Movie 3. Diffusion in a domain with dynamic shape.

Solutions generated by our algorithm for diffusion of gas in a domain with varying shape are physically intuitive and exhibit exact mass conservation. The vectors shown in the movie depict velocities of boundary points. The color illustrates changes in the density of a diffusing gas from low (blue) to high (red).

04. Supplementary Movie 4. Front-tracking with FronTier in 2D.

Prescribed (“exact”) kinematics (see Concluding remarks for details) are used to generate an input to FronTier - an initial shape of a 2D “cell” and time-dependent velocities of the points at the membrane. FronTier, then, recovers the cell kinematics (dots) which are superimposed in the movie on the prescribed kinematics (solid curve).

05. Supplementary Movie 5a. Front-tracking in 3D: prescribed kinematics.

The movie illustrates prescribed (“exact”) kinematics of a 3D “cell” (see Concluding remarks for details), used to generate an input to FronTier - an initial shape of the 'cell' and time-dependent velocities of the points at the membrane.

06. Supplementary Movie 5b. Front-tracking in 3D: results from FronTier vs. exact kinematics.

Given the initial shape and time-dependent velocities at the front as an input, FronTier recovers kinematics of a 3D “cell”. In the movie, the results from FronTier for the horizontal midsection (dots) are superimposed on the exact (prescribed) kinematics in the same cross-section (solid curve).