Abstract
A wide variety of priors have been proposed for nonparametric Bayesian estimation of conditional distributions, and there is a clear need for theorems providing conditions on the prior for large support, as well as posterior consistency. Estimation of an uncountable collection of conditional distributions across different regions of the predictor space is a challenging problem, which differs in some important ways from density and mean regression estimation problems. Defining various topologies on the space of conditional distributions, we provide sufficient conditions for posterior consistency focusing on a broad class of priors formulated as predictor-dependent mixtures of Gaussian kernels. This theory is illustrated by showing that the conditions are satisfied for a class of generalized stick-breaking process mixtures in which the stick-breaking lengths are monotone, differentiable functions of a continuous stochastic process. We also provide a set of sufficient conditions for the case where stick-breaking lengths are predictor independent, such as those arising from a fixed Dirichlet process prior.
Keywords: Asymptotics, Bayesian nonparametrics, Density regression, Dependent Dirichlet process, Large support, Probit stick-breaking process
1. Introduction
One of the most common problems in data analysis is the need to characterize the dependence of a response on predictors in a flexible manner. We want to avoid parametric assumptions on the response density and how features, such as the mean, variance, skewness, shape and even modality, change with predictors. Nonparametric estimates of the conditional distribution [1, 2] are appealing in this context, but in most applications one requires not just a point estimate but also a characterization of uncertainty. For this reason, and because of excellent practical performance in a rich variety of application areas, Bayesian approaches for conditional distribution estimation have become popular in recent years. The most common class of models are infinite mixture models due in part to the rich literature on algorithms for posterior computation using Markov chain Monte Carlo (MCMC) [3–5] and fast approximations [6]. Such MCMC algorithms are straightforward to implement, and the output can be used to estimate exact posterior densities for functionals of interest.
The ever increasing literature on new nonparametric Bayes models and exciting new applications in areas ranging from finance to biostatistics to machine learning has generated considerable enthusiasm. However, there is a clear lack of frequentist asymptotic theory supporting these models. The emphasis of this article is on substantially closing this gap focusing on a new class of generalized stick-breaking process (gSB) priors, which encompasses a number of the most widely applied priors as special cases.
In the absence of predictors, there is a rich theory and methods literature on nonparametric Bayes methods for estimating a density f using mixture models of the form
| (1.1) |
where Π is a mixture prior of the form for suitably chosen kernel k, atoms and weights {(θh, πh), h = 1, …, ∞} with almost surely. The most common choice of Π is the Dirichlet process mixture of normals, first introduced by [7]. Original works on Dirichlet process can be found in [8, 9]. Support of Π in (1.1) and asymptotic properties of the posterior are now well-understood [10–15].
Recent literature has focused on generalizing model (1.1) to the density regression setting in which the entire conditional distribution of y given x changes flexibly with predictors. Bayesian density regression views the entire conditional density f(y | x) as a function valued parameter and allows its center, spread, skewness, modality and other such features to vary with x. For data {(yi, xi), i = 1, …, n} let
| (1.2) |
where
 is the predictor space and
is the predictor space and
 is a prior for the class of conditional densities {fx, x ∈
is a prior for the class of conditional densities {fx, x ∈
 } indexed by the predictors. Refer, for example, to [16–21] and [22] among others.
} indexed by the predictors. Refer, for example, to [16–21] and [22] among others.
The primary focus of this recent development has been infinite mixture models of the form
| (1.3) |
where ϕ is the standard normal density, {πh(x), h = 1, 2, …} are predictor-dependent probability weights that sum to one almost surely for each x ∈
 , and (μh, σh) ~ G0 independently, with G0 a base probability measure on
, and (μh, σh) ~ G0 independently, with G0 a base probability measure on
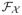 ×ℜ+,
×ℜ+,
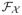 ⊂
⊂
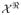 , the space of all
, the space of all
 → ℜ functions. A single finite mixture of Gaussians is inadequate to represent the shape of the density f(y | x) for different levels of the predictor x unless the number of components is huge. By using an infinite mixture we inherently allow for uncertainty in the number of components needed to characterize the data and bypass the difficult issue of selecting the number of components.
→ ℜ functions. A single finite mixture of Gaussians is inadequate to represent the shape of the density f(y | x) for different levels of the predictor x unless the number of components is huge. By using an infinite mixture we inherently allow for uncertainty in the number of components needed to characterize the data and bypass the difficult issue of selecting the number of components.
(1.1) is similar in spirit to kernel mixtures used in non-parametric smoothing approaches. However, a major advantage of using a Bayesian paradigm is that we do not need to deal with optimizing tuning parameters, which becomes difficult in higher dimensions. The new adaptation results [23, 24] reveal that even a single prior specification can adapt to the unknown correct smoothness level of the true density and optimizes estimation in an asymptotic minimax sense. For conditional densities, smoothing needs to be done over the response space as well as the predictor space, making the choice of optimal smoothing even more difficult, especially when the predictors have varying degrees of influence on the response. A Bayesian approach offers an easier practical solution in this case.
To our knowledge, only [25] have considered formalizing the notions of support for dependent stick-breaking processes. We focus on a novel class of gSB processes, which express the probability weights πh(x) in stick-breaking form, with the stick lengths constructed through mapping continuous stochastic processes to the unit interval using a monotone differentiable link function. This class includes dependent Dirichlet processes [26] as a special case.
Only a few papers have considered asymptotic properties of the posterior in conditional density estimation. [22] considers posterior consistency in estimating conditional distributions focusing exclusively on logistic Gaussian process priors [27]. Such priors lack the computational simplicity of the countable mixture priors in (1.3). [28] considers posterior consistency in conditional distribution estimation through a limited information approach by approximating the likelihood by the quantiles of the true distribution. [29, 30] provide sufficient conditions for showing posterior consistency in estimating an autoregressive conditional density and a transition density rather than regression with respect to another covariate.
In this article, focusing on model (1.3), we initially provide sufficient conditions on the prior and true data-generating model under which the prior leads to weak and various types of strong posterior consistency. In this context, we first define notions of weak and L1-integrated neighborhoods. We then show that the sufficient conditions are satisfied for gSB priors. The theory is illustrated through application to a model relying on probit transformations of Gaussian processes, an approach related to the probit stick-breaking process of [21] and [31]. We also considered Gaussian mixtures of fixed-π dependent processes [26, 32].
[33] showed posterior consistency in conditional density estimation using kernel stick breaking process mixtures of Gaussians in a very recent unpublished article. They approximated a conditional density by a smooth mixture of linear regressions as in [34] to demonstrate the KL property. In this paper, we have shown KL support using a more direct approach of approximating the true density by a kernel mixture of a compactly supported conditional measure.
The fundamental contribution of this article is formalizing the notion of support of the gSB process mixture of Gaussians on the space of conditional densities and formulating sufficient conditions to ensure that it leads to a consistent posterior. In doing so, a key technical contribution is the development of a novel method of constructing a sieve for the proposed class of priors. It has been noted by [35] that the usual method of constructing a sieve by controlling prior probabilities is unable to lead to a consistency theorem in the multivariate case. This is because of the explosion of the L1-metric entropy with increasing dimension. They developed a technique specific to the Dirichlet process in the multivariate case for showing weak and strong posterior consistency. The proposed sieve1 avoids the pitfall mentioned by [35] in showing consistency using multivariate mixtures. Our sieve construction has been recently used for studying convergence rates in multivariate density estimation [36, 37].
2. Notations
Throughout the paper, Lebesgue measure on ℜ or ℜp is denoted by λ and the set of natural numbers by ℕ. The supremum and the L1-norms are denoted by ||·||∞ and ||·||1 respectively. The indicator function of a set B is denoted by 1B. Let Lp(ν, M) denote the space of real valued measurable functions defined on M with ν-integrable pth absolute power. For two density functions f, g, the Kullback-Leibler divergence is given by K(f, g) = ∫ log(f/g)fdλ. A ball of radius r with centre x0 relative to the metric d is defined as B(x0, r; d). The diameter of a bounded metric space M relative to a metric d is defined to be sup{d(x, y) : x, y ∈ M}. The ε-covering number N(ε, M, d) of a semi-metric space M relative to the semi-metric d is the minimal number of balls of radius ε needed to cover M. The logarithm of the covering number is referred to as the entropy. “≾” stands for inequality up to a constant multiple or if the constant multiple is irrelevant to the given situation. δ0 stands for a distribution degenerate at 0 and supp(ν) for the support of a measure ν.
3. Conditional density estimation
In this section, we will define the space of conditional densities and construct a prior on this space. It is first necessary to generalize the topologies to allow appropriate neighborhoods to be constructed around an uncountable collection of conditional densities indexed by predictors. With such neighborhoods in place, we then state our main theorems providing sufficient conditions under which various modes of posterior consistency hold for a broad class of predictor-dependent mixtures of Gaussian kernels.
Let
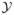 = ℜ be the response space and
= ℜ be the response space and
 be the covariate space which is a compact subset of ℜp. Unless otherwise stated, we will assume
be the covariate space which is a compact subset of ℜp. Unless otherwise stated, we will assume
 = [0, 1]p without loss of generality. Let
= [0, 1]p without loss of generality. Let
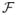 denote the space of densities on
denote the space of densities on
 ×
×
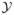 w.r.t. the Lebesgue measure and
w.r.t. the Lebesgue measure and
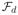 denote a subset of the space of conditional densities satisfying,
denote a subset of the space of conditional densities satisfying,
Suppose yi is observed independently given the covariates xi, i = 1, 2, … which are drawn independently from a probability distribution Q on
 . Assume that Q admits a density q with respect to the Lebesgue measure.
. Assume that Q admits a density q with respect to the Lebesgue measure.
If we define h(x, y) = q(x)f(y | x) and h0(x, y) = q(x)f0(y | x) then h, h0 ∈
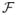 . Throughout the paper, h0 is assumed to be a fixed density in
. Throughout the paper, h0 is assumed to be a fixed density in
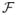 which we alternatively refer to as the true data generating density and {f0(· | x), x ∈
which we alternatively refer to as the true data generating density and {f0(· | x), x ∈
 } is referred to as the true conditional density. The density q(x) will be needed only for theoretical investigation. In practice, we do not need to know it or learn it from the data.
} is referred to as the true conditional density. The density q(x) will be needed only for theoretical investigation. In practice, we do not need to know it or learn it from the data.
We propose to induce a prior
 on the space of conditional densities through a prior
on the space of conditional densities through a prior
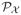 for a collection of mixing measures
for a collection of mixing measures
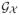 = {Gx, x ∈
= {Gx, x ∈
 } using the following predictor-dependent mixture of kernels
} using the following predictor-dependent mixture of kernels
| (3.1) |
where ψ = (μ, σ), and
| (3.2) |
where πh(x) ≥ 0 are random functions of x such that
a.s. for each fixed x ∈
 .
are i.i.d. realizations of a real valued stochastic process, i.e., G0 is a probability distribution over
.
are i.i.d. realizations of a real valued stochastic process, i.e., G0 is a probability distribution over
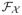 ×ℜ+, where
×ℜ+, where
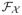 ⊂
⊂
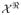 ,
,
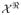 being the space of functions from
being the space of functions from
 to ℜ. Hence for each x ∈
to ℜ. Hence for each x ∈
 , Gx is a random probability measure over the measurable Polish space (ℜ × ℜ+,
, Gx is a random probability measure over the measurable Polish space (ℜ × ℜ+,
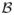 (ℜ × ℜ+)). We are interested the following two important special cases.
(ℜ × ℜ+)). We are interested the following two important special cases.
3.1. Predictor dependent countable mixtures of Gaussian linear regressions
We define the predictor dependent countable mixtures of Gaussian linear regressions (MGLRx) as
and
| (3.3) |
where πh(x) ≥ 0 are random functions of x such that
a.s. for each fixed x ∈
 and G0 = G0,β × G0,σ is a probability distribution on ℜp × ℜ+ where G0,β and G0,σ are probability distributions on ℜp and ℜ+ respectively. For a particular choice of πh(x)’s, we obtain the probit stick-breaking mixtures of Gaussians which have been previously applied to real data applications by [21, 31, 38]. The latter two articles considered probit transformations of Gaussian processes in constructing the stick-breaking weights.
and G0 = G0,β × G0,σ is a probability distribution on ℜp × ℜ+ where G0,β and G0,σ are probability distributions on ℜp and ℜ+ respectively. For a particular choice of πh(x)’s, we obtain the probit stick-breaking mixtures of Gaussians which have been previously applied to real data applications by [21, 31, 38]. The latter two articles considered probit transformations of Gaussian processes in constructing the stick-breaking weights.
3.2. Gaussian mixtures of fixed-π dependent processes
In (3.1), set Gx as in (3.2) with πh(x) ≡ πh for all x ∈
 where πh ≥ 0 are random probability weights
a.s. and
are as in (3.2). Examples include fixed-π dependent Dirichlet process mixtures of Gaussians [26]. Versions of the fixed π-DDP have been applied to ANOVA [32], survival analysis [39, 40], spatial modeling [41], and many more.
where πh ≥ 0 are random probability weights
a.s. and
are as in (3.2). Examples include fixed-π dependent Dirichlet process mixtures of Gaussians [26]. Versions of the fixed π-DDP have been applied to ANOVA [32], survival analysis [39, 40], spatial modeling [41], and many more.
A Gaussian process is a common choice for constructing stochastic processes πh(x)’s and μh(x)’s. Recall that a Gaussian process {α(x) : x ∈
 } is defined as a stochastic process for which any finite dimensional representation {α(x1), …, α(xp)}, p ≥ 1 has a joint Gaussian distribution. We denote by GP(μ, c) a Gaussian process with mean function μ :
} is defined as a stochastic process for which any finite dimensional representation {α(x1), …, α(xp)}, p ≥ 1 has a joint Gaussian distribution. We denote by GP(μ, c) a Gaussian process with mean function μ :
 → ℝ and c :
→ ℝ and c :
 ×
×
 → ℝ.
→ ℝ.
4. Notions of posterior consistency for conditional densities
We recall the definition of posterior consistency through yn = (y1, …, yn) and xn = (x1, …, xn).
Definition 4.1
The posterior
 (· | yn, xn) is consistent at {f0(· | x), x ∈
(· | yn, xn) is consistent at {f0(· | x), x ∈
 } with respect to a given topology if
} with respect to a given topology if
 (Uc | yn, xn) → 0 a.s. for an arbitrary neighborhood U of {f0(· | x), x ∈
(Uc | yn, xn) → 0 a.s. for an arbitrary neighborhood U of {f0(· | x), x ∈
 } in that topology.
} in that topology.
Here a.s. consistency at {f0(· | x), x ∈
 } means that the posterior distribution concentrates around a neighborhood of {f0(· | x), x ∈
} means that the posterior distribution concentrates around a neighborhood of {f0(· | x), x ∈
 } for almost every sequence
generated by i.i.d. sampling from the joint density q(x)f0(y | x).
} for almost every sequence
generated by i.i.d. sampling from the joint density q(x)f0(y | x).
We define the weak and ν-integrated L1 neighborhoods of a collection of conditional densities {f0(· | x), x ∈
 } in the following. A sub-base of a weak neighborhood is defined as
} in the following. A sub-base of a weak neighborhood is defined as
| (4.1) |
for a bounded continuous function g :
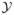 ×
×
 → ℜ. A weak neighborhood base is formed by finite intersections of neighborhoods of the type (4.1). Define a ν-integrated L1 neighborhood
→ ℜ. A weak neighborhood base is formed by finite intersections of neighborhoods of the type (4.1). Define a ν-integrated L1 neighborhood
| (4.2) |
for any measure ν with supp(ν) ⊂
 . Observe that under the topology in (4.2),
. Observe that under the topology in (4.2),
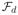 can be identified to a closed subset of L1(λ×ν,
can be identified to a closed subset of L1(λ×ν,
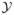 ×supp(ν)) making it a complete separable metric space. Thus measurability issues won’t arise with these topologies.
×supp(ν)) making it a complete separable metric space. Thus measurability issues won’t arise with these topologies.
In the following, we define the Kullback-Leibler (KL) property of
 at a given f0 ∈
at a given f0 ∈
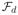 . Note that we define a KL-type neighborhood around the collection of conditional densities f0 through defining a KL neighborhood around the joint density h0, while keeping Q fixed at its true unknown value.
. Note that we define a KL-type neighborhood around the collection of conditional densities f0 through defining a KL neighborhood around the joint density h0, while keeping Q fixed at its true unknown value.
Definition 4.2
For any f0 ∈
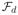 , such that h0(x, y) = q(x)f0(y | x) is the true joint data-generating density, we define an ε-sized KL neighborhood around f0 as
, such that h0(x, y) = q(x)f0(y | x) is the true joint data-generating density, we define an ε-sized KL neighborhood around f0 as
where KL(h0, h) = ∫ h0 log(h0/h). Then,
 is said to have KL property at f0 ∈
is said to have KL property at f0 ∈
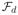 , denoted f0 ∈ KL(
, denoted f0 ∈ KL(
 ), if
), if
 {Kε(f0)} > 0 for any ε > 0.
{Kε(f0)} > 0 for any ε > 0.
Another definition we would require for showing the KL support is the notion of weak neighborhood of a collection of mixing measures
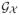 = {Gx, x ∈
= {Gx, x ∈
 } where Gx is a probability measure on S × ℜ+ for each x ∈
} where Gx is a probability measure on S × ℜ+ for each x ∈
 . Here S = ℜp or ℜ depending on the cases considered above. We formulate the notion of a sub-base of the weak neighborhood of
. Here S = ℜp or ℜ depending on the cases considered above. We formulate the notion of a sub-base of the weak neighborhood of
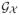 = {Gx, x ∈
= {Gx, x ∈
 } below.
} below.
Definition 4.3
For a bounded continuous function g : S × ℜ+ ×
 → ℜ and ε > 0, a sub-base of the weak neighborhood of a conditional probability measure {Fx, x ∈
→ ℜ and ε > 0, a sub-base of the weak neighborhood of a conditional probability measure {Fx, x ∈
 } is defined as
} is defined as
| (4.3) |
A conditional probability measure {Gx, x ∈
 } lies in the weak support of
} lies in the weak support of
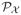 if
if
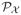 assigns positive probability to every basic neighborhood generated by the sub-base of the type (4.3). In the sequel, we will also consider a neighborhood of the form
assigns positive probability to every basic neighborhood generated by the sub-base of the type (4.3). In the sequel, we will also consider a neighborhood of the form
| (4.4) |
for a bounded continuous function g : S × ℜ+ → ℜ.
5. Posterior consistency in MGLRx mixture of Gaussians
5.1. Kullback-Leibler property
We will work with a specific choice of
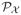 motivated by the probit stick breaking process construction in [21]. Let
motivated by the probit stick breaking process construction in [21]. Let
| (5.1) |
where αh ~ GP(0, ch), for h = 1, 2, …, ∞. Assume the following holds.
-
S1
ch is chosen so that αh ~ GP(0, ch) has continuous path realizations
-
S2for any continuous function under the GP(0, ch) prior for αh g :
 ↦ ℜ,
↦ ℜ,
h = 1, …, ∞ and for any ε > 0.
-
S3
G0 is absolutely continuous with respect to λ(ℜp × ℜ+).
Consider the subset satisfying the following conditions.
-
A1
f is nowhere zero and bounded by M < ∞.
-
A2
|
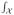
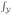 f(y | x) log f(y | x)dyq(x)dx| < ∞.
f(y | x) log f(y | x)dyq(x)dx| < ∞. -
A3
,
where ψx(y) = inft∈[y−1,y+1] f(t | x).
-
A4
∃ η > 0 such that
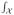
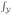 |y|2(1+η)
f(y | x)dyq(x)dx < ∞.
|y|2(1+η)
f(y | x)dyq(x)dx < ∞. -
A5
(x, y) ↦ f(y | x) is jointly continuous.
Remark 5.1
A1 is usually satisfied by common densities arising in practice. A4 imposes a minor tail restriction; e.g., a mean regression model with continuous mean function and a heavy-tailed t residual density with 4 degrees of freedom satisfies A4. Conditions A2 and A3 are more subtle, but are also mild. A flexible class of models which satisfies A1–A5 is as follows. Let yi = μ(xi) + εi, with μ :
 → ℜ continuous and εi ~ fxi, where
for some H ≥ 1,
, πh :
→ ℜ continuous and εi ~ fxi, where
for some H ≥ 1,
, πh :
 → [0, 1] continuous and ψ is Gaussian or t with greater than 2 degrees of freedom.
→ [0, 1] continuous and ψ is Gaussian or t with greater than 2 degrees of freedom.
Remark 5.2
S2 is satisfied if ch(x, x′) = e−Ah||x−x′||2 and the prior for Ah has full support on ℝ+.
The following theorem characterizes the subset of
 for which
for which
 has the KL property. The proof of Theorem 5.3 is provided in Appendix C.
has the KL property. The proof of Theorem 5.3 is provided in Appendix C.
Theorem 5.3
f0 ∈ KL(
 ) for each f0 in
if
) for each f0 in
if
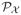 satisfies S1–S3.
satisfies S1–S3.
Remark 5.4
The conditions are satisfied for a class of gSB process mixtures in which the stick-breaking lengths are constructed through mapping continuous stochastic processes to the unit interval using a monotone differentiable link function.
To prove Theorem 5.3, we need several auxiliary results related to the support of the prior
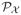 which might be of independent interest. The key idea for showing that the true f0 satisfies
which might be of independent interest. The key idea for showing that the true f0 satisfies
 {Kε(f0)} > 0 for any ε > 0 is to impose certain tail conditions on f0(y | x) and approximate it by
, where {G̃x, x ∈
{Kε(f0)} > 0 for any ε > 0 is to impose certain tail conditions on f0(y | x) and approximate it by
, where {G̃x, x ∈
 } is compactly supported. Observe that,
} is compactly supported. Observe that,
| (5.2) |
We construct such an f̃ in Theorem 5.3 which makes the first term in the right hand side of (5.2) sufficiently small. The following lemma (which is similar to Lemma 3.1 in [12] and Theorem 3 in [11]) guarantees that the second term in the right hand side of (5.2) is also sufficiently small if {Gx, x ∈
 } lies inside a finite intersection of neighborhoods of {G̃x, x ∈
} lies inside a finite intersection of neighborhoods of {G̃x, x ∈
 } of the type (4.4).
} of the type (4.4).
Lemma 5.5
Assume that f0 ∈
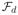 satisfies
satisfies
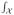
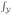 y2f0(y | x)dyq(x)dx < ∞. Suppose
, where ∃a > 0 and 0 < σ < σ̄ such that
y2f0(y | x)dyq(x)dx < ∞. Suppose
, where ∃a > 0 and 0 < σ < σ̄ such that
| (5.3) |
so that G̃x has compact support for each x ∈
 . Then given any ε > 0, ∃ a finite intersection W of neighborhoods of {G̃x, x ∈
. Then given any ε > 0, ∃ a finite intersection W of neighborhoods of {G̃x, x ∈
 } of the type (4.4) such that for any conditional density
, x ∈
} of the type (4.4) such that for any conditional density
, x ∈
 , with {Gx, x ∈
, with {Gx, x ∈
 } ∈ W,
} ∈ W,
| (5.4) |
The proof is similar to Theorem 3 in [11] and is omitted here. In order to ensure that the weak support of
 is sufficiently large to contain all densities f̃ satisfying the assumptions of Lemma 5.5, we define a collection of fixed conditional probability measures on (ℜp × ℜ+,
is sufficiently large to contain all densities f̃ satisfying the assumptions of Lemma 5.5, we define a collection of fixed conditional probability measures on (ℜp × ℜ+,
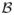 (ℜp × ℜ+)) denoted by
satisfying
(ℜp × ℜ+)) denoted by
satisfying
x ↦ Fx(B) is a continuous function of x ∈
 , ∀ B ∈
, ∀ B ∈
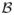 (ℜp × ℜ+).
(ℜp × ℜ+).For any sequence of sets An ⊂ ℜp × ℜ+ ↓ ∅,
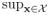 Fx(An) ↓ 0.
Fx(An) ↓ 0.
Next we state the theorem characterizing the weak support of
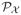 which will be proved in Appendix B.
which will be proved in Appendix B.
Theorem 5.6
If
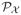 satisfies S1–S3, then any
lies in the weak support of
satisfies S1–S3, then any
lies in the weak support of
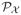 .
.
Corollary 5.7
Assume S1–S3 hold and assume is compactly supported, i.e., there exists a, σ, σ̄ > 0 such that Fx([−a, a]p × [σ, σ̄]) = 1. Then for a bounded uniformly continuous function g : ℜp × ℜ+ → [0, 1] satisfying g(β, σ) → 0 as ||β|| → ∞, σ → ∞,
| (5.5) |
Proof
The proof is similar to Theorem 5.6 with the L1 convergence in (B.1) replaced by convergence uniformly in x. This is because under the assumptions of Corollary 5.7, the uniformly continuous sequence of functions
on
 monotonically decreases to ∫C g(β, σ)dFx(β, σ) as n → ∞ where C is given by [−a, a]p × [σ, σ̄].
monotonically decreases to ∫C g(β, σ)dFx(β, σ) as n → ∞ where C is given by [−a, a]p × [σ, σ̄].
The proof of the following corollary is along the lines of the proof of Theorem 5.6 and is omitted here.
Corollary 5.8
Under the assumptions of Corollary 5.7 for any k0 ≥ 1,
| (5.6) |
where Uj’s are neighborhoods of the type (5.5).
5.2. Strong Consistency with the q-integrated L1 neighborhood
To obtain strong consistency in the q-integrated L1 topology, we need a very straight forward extension of Theorem 2 of [11] below.
Theorem 5.9
Suppose f0 ∈ KL(
 ) and there exist subsets
) and there exist subsets
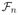 ⊂
⊂
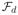 with
with
log N (ε,
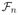 , ||·||1) = o(n),
, ||·||1) = o(n),for some c2, β2 > 0,
then the posterior is strongly consistent with respect to the q-integrated L1 neighborhood.
Before stating the main theorem on strong consistency, we consider a hierarchical extension of MGLRx where the bandwidths are taken to be random. We define a sequence of random inverse-bandwidths Ah of the Gaussian process αh, h ≥ 1 each having ℜ+ as its support. Since the first few atoms suffice to explain most of the dependence of y on x, we expect that the variability due to the covariate in the stochastic process Φ{αh} decreases as h increases. This is achieved through a carefully chosen prior for the covariance kernel ch of the Gaussian process αh.
Let α0 denote the base Gaussian process on [0, 1]p with covariance kernel c0(x, x′) = τ2e−||x−x′||2. Then
for each x∈
 The variability of αh with respect to the covariate is shrunk or stretched to the rectangle
as Ah decreases or increases. Ah’s are constructed to be stochastically decreasing to δ0 in the following manner. We assume that there exist η, η0 > 0 and a sequence δn = O((log n)2/n5/2) such that P (Ah > δn) ≤ exp{−n−η0h(η0+2)/η log h} for each h ≥ 1. Also assume that there exists a sequence rn ↑ ∞ such that
and P (Ah > rn) ≤ e−n. We will discuss how to construct such a sequence of random variables in the Remark 5.12 following Theorem 5.10.
The variability of αh with respect to the covariate is shrunk or stretched to the rectangle
as Ah decreases or increases. Ah’s are constructed to be stochastically decreasing to δ0 in the following manner. We assume that there exist η, η0 > 0 and a sequence δn = O((log n)2/n5/2) such that P (Ah > δn) ≤ exp{−n−η0h(η0+2)/η log h} for each h ≥ 1. Also assume that there exists a sequence rn ↑ ∞ such that
and P (Ah > rn) ≤ e−n. We will discuss how to construct such a sequence of random variables in the Remark 5.12 following Theorem 5.10.
The following theorem provides sufficient conditions for strong posterior consistency in the q-integrated L1 topology. The proof is provided in Appendix D.
Theorem 5.10
Let πh’s satisfy (5.1) with αh ~ GP(0, ch) where ch(x, x′) = τ2e−Ah||x−x′||2, h ≥1, τ2 > 0 fixed.
-
C1
There exist sequences an, hn ↑ ∞, ln ↓ 0 with , and constants d1, d2 > 0 such that G0{B(0; an) × [ln, hn]}c < d1e−d2n for some d1, d2 > 0.
-
C2
Ah’s are constructed as in the second last paragraph before Theorem 5.10.
then f0 ∈ KL(
 ) implies that
) implies that
 achieves strong posterior consistency in q-integrated L1 topology at f0.
achieves strong posterior consistency in q-integrated L1 topology at f0.
Remark 5.11
Verification of condition C1 of Theorem 5.10 is particularly simple. For example, if G0 is a product of multivariate normals on β and an inverse Gamma prior on σ2, the condition C1 is satisfied with
, hn = en,
. It follows from [42] that f0 ∈ KL(
 ) is still satisfied when we have the additional assumptions C1–C2 together with S1–S3 on the prior
) is still satisfied when we have the additional assumptions C1–C2 together with S1–S3 on the prior
 .
.
Remark 5.12
Since we need can be chosen to be O(nη1) for some 0 < η1 < 1. Let d be such that dη1/p ≥ 1 and set η0 = 3d. Let Ah = chBh, where and ch = (h(3d+2)/η log h)−1/d for any 0 < η < 1. Then P (Ah > nη1/p) ≤ P(Bh > nη1/p) ≤ e−ndη1/p ≤ e−n and P(Ah > (log n)2n−5/2) ≤ exp{−n−3dh(3d+2)/η log h}.
Remark 5.13
The theory of strong posterior consistency can be generalized to an arbitrary monotone differentiable link function L : ℜ ↦ [0, 1] which is Lipschitz, i.e., there exists a constant K > 0 such that |L(x) − L(x′)| ≤ K |x − x′| for all x, x′ ∈
 . Also, as long as the πh(x)’s satisfy the hypothesis of Lemma Appendix A.1 and possess the required tail probability in Lemma 5.15, general predictor dependent mixing weights can be used.
. Also, as long as the πh(x)’s satisfy the hypothesis of Lemma Appendix A.1 and possess the required tail probability in Lemma 5.15, general predictor dependent mixing weights can be used.
Below we will develop several auxiliary results required to prove Theorem 5.10. They are stated below as some of them might be of independent interest. Let
for y ∈
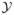 and x ∈
and x ∈
 . From [12], we obtain for
and for each x ∈
. From [12], we obtain for
and for each x ∈
 ,
,
Construct a sieve for (β, σ) as
| (5.7) |
In the following Lemma, we provide an upper bound to N (Θa,h,l, ε, dSS). The proof is omitted as it follows trivially from Lemma 4.1 in [12].
Lemma 5.14
There exist constants d1, d2 > 0 such that .
In the proof of Theorem 5.10, we will verify the sufficient conditions of Theorem 5.9. We calibrate
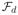 by a carefully chosen sequence of subsets
by a carefully chosen sequence of subsets
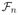 ⊂
⊂
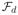 . The fundamental problem with mixture models ∫ N (y; μ, σ2Ip)dP (μ) in estimating a multivariate density lies in attempting to compactify the model space by {∫ N (y, μ, σ2Ip)dP (μ) : P ((−an, an]p) > 1 − δ} for each σ leading to an entropy
growing exponentially with the dimension p. Here we marginalize P in ∫ N(y; μ, σ2Ip)dP (μ) to yield the following construction
, h = 1, …, mn,
leading to an entropy mn log an where mn is related to the tail-decay of
. With this idea in place, we extend the construction of
. The fundamental problem with mixture models ∫ N (y; μ, σ2Ip)dP (μ) in estimating a multivariate density lies in attempting to compactify the model space by {∫ N (y, μ, σ2Ip)dP (μ) : P ((−an, an]p) > 1 − δ} for each σ leading to an entropy
growing exponentially with the dimension p. Here we marginalize P in ∫ N(y; μ, σ2Ip)dP (μ) to yield the following construction
, h = 1, …, mn,
leading to an entropy mn log an where mn is related to the tail-decay of
. With this idea in place, we extend the construction of
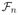 for conditional densities below.
for conditional densities below.
Before constructing a sieve, we briefly review alternative definitions [43] of a Gaussian process as a Banach space valued element below. A Borel measurable random element W with values in a separable Banach space (
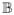 , ||·||) is called Gaussian if the random variable b*W is normally distributed for any element b* ∈
, ||·||) is called Gaussian if the random variable b*W is normally distributed for any element b* ∈
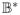 , the dual space of
, the dual space of
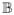 . Recall that in general, the reproducing kernel Hilbert space (RKHS) ℍ attached to a zero-mean Gaussian process W is defined as the collection of all EHW for H ranging over the closed linear span of the variables b*W in L2(ν, M) with inner product
. Recall that in general, the reproducing kernel Hilbert space (RKHS) ℍ attached to a zero-mean Gaussian process W is defined as the collection of all EHW for H ranging over the closed linear span of the variables b*W in L2(ν, M) with inner product
| (5.8) |
The RKHS can be viewed as a subset of
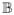 and the RKHS norm ||·||ℍ stronger than the Banach space norm ||·||.
and the RKHS norm ||·||ℍ stronger than the Banach space norm ||·||.
In particular, if W is a Borel measurable zero-mean Gaussian random element in a complete separable subspace of ℓ∞ (T), the Banach space of uniformly bounded functions g : T → ℝ equipped with the uniform norm ||g|| = sup{|g(t)| : t ∈ T }, then the RKHS is actually the completion of the linear space of functions t ↦ EW (t)H relative to the inner product (5.8) where H, H1 and H2 are finite linear combinations of the form Σi aiW (si) with ai ∈ ℝ and si in the index set of W. See Theorem 2.1 of [43] for details.
Next we turn to constructing the sieve. Assume ε > 0 is given. Let
denote a unit ball in the RKHS of the covariance kernel τ2e−a||x−x′||2and
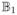 is a unit ball in ℂ [0, 1]p. For numbers M, m, r, δ, construct a sequence of subsets {Bh, h = 1, …, m} of ℂ [0, 1]p as follows.
is a unit ball in ℂ [0, 1]p. For numbers M, m, r, δ, construct a sequence of subsets {Bh, h = 1, …, m} of ℂ [0, 1]p as follows.
The idea is to construct
| (5.9) |
for appropriate sequences am, ln, hn, Mn, mn, rn, δn to be chosen in the proof of Theorem 5.10.
The following lemma is also crucial to the proof of Theorem 5.10 which allows us to calculate the rate of decay of P(
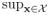 πh(x) > ε) with mn.
πh(x) > ε) with mn.
Lemma 5.15
Let πh’s satisfy (5.1) with αh ~ GP(0, ch) where ch(x, x′) = τ2e−Ah||x−x′||2, h ≥ 1, τ2 > 0 fixed. Then for some constant C7 > 0,
| (5.10) |
Proof
Let where , Zh ~ Ga(1, γ0). We will choose an appropriate value for γ0 in the sequel. Let t0 = −log ε > 0. Observe that
Observe that
where Λh ~ Ga(mn, 1). Then it is easy to show that
 (Λh < t0) ≾ e−mn log mn. However, the calculation gets complicated when αh’s are i.i.d realizations of a zero mean Gaussian process. The proof relies on the fact that the supremum of Gaussian processes has sub-Gaussian tails.
(Λh < t0) ≾ e−mn log mn. However, the calculation gets complicated when αh’s are i.i.d realizations of a zero mean Gaussian process. The proof relies on the fact that the supremum of Gaussian processes has sub-Gaussian tails.
Below we calculate the rate of decay of with mn. We will show that there exists γ0, depending on ε and τ but not depending on n, such that
| (5.11) |
where there exists a constant C5 > 0 such that ξ(x) = C5xp/2 for x > 0. Observe that .
Since for some τ′ < 1, we can re-parameterize t0 as τ′t0/τ and τ as τ′. Hence without loss of generality we assume τ < 1.
Define g : [0, t0] → ℜ, t ↦ −Φ−1(1 − e−t). It holds that g is a continuous function on (0, t0]. Assume α0 ~ GP(0, c0) where c0(x, x′) = τ2e−||x−x′||2. For ,
Below we estimate for large enough λ following Theorem 5.2 of [44]. However extra care is required to identify the role of δn. Since ,
for some constant C2 > 0. Hence
for constants C3, C4 > 0. The last inequality holds for all large λ because τ < 1. Hence there exists t1 ∈ (0, t0) sufficiently small and independent of n such that for all t ∈ (0, t1), . Observe that
for any γ0 > 1. Further choose γ0 large enough such that 2(1 − e−γ0t) > 1 ∀ t ∈ [t1, t0]. Hence P(Wh ≤ t, Ah ≤ δn) ≤ ξ(δn)P(Zh < t) ∀ t ∈ (0, t0] where , with C5 = max{2, C4}. Applying Lemma Appendix E.1, we conclude (5.11) by induction. Lemma Appendix E.1 is proved in Appendix E. As for some constant C6 > 0. Since for some constant C7 > 0, the result follows immediately.
5.3. Prior specification and posterior computation
To illustrate the applicability of the proposed methods, we mention the prior choices and key steps for posterior computation for the MGLRx model. Recall that
| (5.12) |
| (5.13) |
where πh(x) = Φ{αh(x)}Πl<h{1−Φ{αl(x)}. We assume αh ~ GP(0, ch), where , τα ~ Ga(να/2, να/2). See Remark 5.12 for constructing prior for Ah’s. If the yi’s are standardized, we would expect that the total variance should be around 1. Hence choose aσ = 1, bσ = 10 so that the . We can resort to an MCMC algorithm, which is a hybrid of data augmentation, the exact block Gibbs sampler of [45] and Metropolis Hastings sampling to sample from the posterior of (5.12). [45] proposed the exact block Gibbs sampler as an efficient approach to posterior computation in infinite-dimensional Dirichlet process mixture models, modifying the block Gibbs sampler of [46] to avoid truncation approximations. The exact block Gibbs sampler combines characteristics of the retrospective sampler [47] and the slice sampler [4, 48]. Introduce γ1, …, γn such that πh(xi) = P(γi = h), h = 1, 2, …, ∞. Then
where ui ~ U(0, 1).
We continue up to , where is the minimum integer satisfying , i = 1, …, n. The Markov chain adaptively estimates the desired number of components h* at each iteration of the MCMC, thus making it more efficient than a finite mixture model with a pre-specified large number of components. Here we describe the key steps for the posterior computation.
-
Update ui’s and stick breaking random variables: Generatewhere πh(xi) = Φ{αh(xi)}Πl<h[1 − Φ{αl(xi)}]. For i = 1, …, n, introduce latent variables Zh(xi), h = 1, 2, … such that Zh(xi) ~ N(αh(xi), 1). Thus πh(xi) = P(Zh(xi) > 0, Zl(xi) < 0 for l < h). ThenLet Zh = (Zh(x1), …, Zh(xn))′ and αh = (αh(x1), …, αh(xn))′. Letting (Σh)ij = e−Ah||xi−xj||, Zh ~ N(αh, I) and ,Continue up to , where is the minimum integer satisfying , i = 1, …, n. Now
while κα is updated using a Metropolis Hastings step.
- Update allocation to atoms: Update (γ1, …, γn)|– as multinomial random variables with probabilities
-
Update component-specific locations and precisions: Let nh = #{i : γi = h}, l = 1, 2, …, h*. Let Yh = (yi : γi = h) be a nh dimensional vector and Xh is the corresponding nh × p dimensional covariate matrix.
Update Ah’s in a Metropolis Hastings step.
At each iteration of the MCMC, we obtain samples from the full conditional distributions of the parameters, which after discarding a burn-in can be used to get summary statistics of posterior distribution of the parameters or functionals of interest.
6. Posterior consistency in Gaussian mixture of fixed-π dependent processes
6.1. Kullback-Leibler property
The following theorem verifies that
 has KL property at
. The proof of Theorem 6.1 is somewhat similar to that of Theorem 5.3 and can be found in Appendix F.
has KL property at
. The proof of Theorem 6.1 is somewhat similar to that of Theorem 5.3 and can be found in Appendix F.
Theorem 6.1
f0 ∈ KL(
 ) for each f0 in
if
) for each f0 in
if
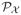 satisfies
satisfies
-
T1
G0 is specified by μh ~ GP(μ, c), σh ~ G0,σ where c is chosen so that GP(0, c) has continuous path realizations and Πσ is absolutely continuous w.r.t. Lebesgue measure on ℜ+.
-
T2
For every k ≥2, (π1, …, πk) is absolutely continuous w.r.t. to the Lebesgue measure on Sk−1.
-
T3For any continuous function g :
 ↦ ℜ,
↦ ℜ,
h = 1, …, ∞ and for any ε > 0.
6.2. Strong consistency with the q-integrated L1 neighborhood
Next we summarize the consistency theorem with respect to the q-integrated L1 topology. The proof of Theorem 6.2 is also similar to that of Theorem 5.10 and is provided in Appendix G.
Theorem 6.2
Let μh(x) = x′βh + ηh(x), βh ~ Gβ and ηh ~ GP(0, c), h = 1, …, ∞ where c(x, x′) = τ2e−A||x−x′||2, Ap(1+η2)/η2 ~ Ga(a, b) for some η2 > 0.
-
F1
There exist sequences an, hn ↑ ∞, ln ↓ 0 with , and constants d1, d2, d3 and d4 > 0 such that Gβ{B(0; an)}c < d1e−d2n and G0,σ{[ln, hn]}c ≤ d3e−d4n.
-
F2
.
then f0 ∈ KL(
 ) implies that
) implies that
 achieves strong posterior consistency at f0 with respect to the q-integrated L1 topology.
achieves strong posterior consistency at f0 with respect to the q-integrated L1 topology.
Remark 6.3
F2 is satisfied if πh’s are made to decay more rapidly than the usual Beta(1, α) stick-breaking random variables, e.g, if πh = νhΠl<h(1−νh) and if νh ~ Beta(1, αh) where αh = h1+η2(log h)p+1α0 for some α0 > 0, then F2 is satisfied. Large value of αh for the higher indexed weights favors smaller number of components.
Remark 6.4
A Gaussian kernel is used here for technical simplification. One can obtain similar results using a variety of kernels e.g. t, Laplace, etc. However, the KL support conditions A1–A5 will be different for different kernels. Refer to [49] for a catalogue of conditions for various kernels in a density estimation framework.
7. Discussion
We have provided sufficient conditions to show posterior consistency in estimating the conditional density via predictor dependent mixtures of Gaussians which include probit stick-breaking mixtures of Gaussians and the fixed-π dependent processes as special cases. The problem is of interest, providing a more flexible and informative alternative to the usual mean regression. For both the models, we need the same set of tail conditions (mentioned in ) on f0 for KL support. Although the first prior is flexible in the weights and the second one in the atoms through their corresponding GP terms, S1, S2, T1 and T3 show that verification of KL property only requires that both the GP terms have continuous path realizations and desired approximation property. Moreover, for the second prior, any set of weights summing to one a.s. T2 suffices for showing KL property. Careful investigations of the prior for the GP kernel for the first model and the probability weights for the second one are required for strong consistency. For the first one we need the covariate dependence of the higher indexed GP terms in the weights to fade off. On the other hand, for the second model, the atoms can be i.i.d. realizations of a GP with Gaussian covariance kernel with inverse- Gamma bandwidth while limiting the model complexity through a sequence of probability weights which are allowed to decay rapidly. This suggests that full flexibility in the weights should be down-weighted by an appropriately chosen prior while full flexibility in the atoms should be accompanied by a restriction imposing fewer number of components. It would be interesting to see how the conditions on the bandwidth can be modified when we actually use a sieve Bayes prior, i.e. a prior with number of components kn diverging to ∞.
Another interesting direction is to consider rates of convergence of the posterior and Bernstein von-Mises (BvM) type results. For infinite dimensional parameters [50], there has been quite a few positive BvM results very recently for linear functionals of a probability density function [51] and for general classes of linear and non-linear functionals in a Gaussian white noise model [52]. We conjecture that such BvM-type results hold for linear functionals of conditional density (e.g. conditional mean, conditional cdf) too under appropriate conditions on the prior and the true data generating conditional density.
Acknowledgments
This work was supported by Award Number R01ES017240 from the National Institute of Environmental Health Sciences. We also thank the Associate Editor and the referees for the comments which significantly improved the exposition of the paper.
Appendix A. A useful lemma
To prove Theorem 5.6, we need an auxiliary lemma which we state below.
Lemma Appendix A.1
If {πh(x), h = 1, …, ∞} constructed as in (5.1) satisfies S1 and S2 then
| (A.1) |
for a measurable partition {Ai, i = 1, …, k} of ℜp × ℜ+, εi > 0 and a conditional cdf {Fx, x ∈
 }.
}.
Proof
Without loss of generality, let 0 < Fx(Ai) < 1, i = 1, …, k ∀ x ∈
 . We want to show that for any εi > 0, i = 1, …, k, (A.1) holds. Construct continuous functions gi :
. We want to show that for any εi > 0, i = 1, …, k, (A.1) holds. Construct continuous functions gi :
 ↦ ℜ, 0 < gi(x) < 1 ∀x ∈
↦ ℜ, 0 < gi(x) < 1 ∀x ∈
 , i = 1, …, k−1 such that
, i = 1, …, k−1 such that
| (A.2) |
As 0 < Fx(Ai) < 1, i = 1, …, k ∀ x ∈
 , it is trivial to find gi, i = 1, …, k satisfying (A.2) since one can solve back for the gi’s from (A.2).
enforces gk ≡1. Since Φ is a continuous function, for any εi > 0, i = 1, …, k − 1,
, it is trivial to find gi, i = 1, …, k satisfying (A.2) since one can solve back for the gi’s from (A.2).
enforces gk ≡1. Since Φ is a continuous function, for any εi > 0, i = 1, …, k − 1,
| (A.3) |
and for i = k,
| (A.4) |
Choose M > Φ−1(1 − εk) + εk. We have 0 < M < 1 and
Hence by assumption,
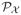 {
{
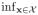 αk(x) > Φ−1(1 − εk)} > 0. Let Sk−1 denote the k-dimensional simplex. For notational simplicity let pi(x) = Φ{αi(x)}, gi(x) = Fx(Ai), i = 1, …, k−1 and gk(x) = 1. Let z = (z1, …, zp)′, fi : Sk−1 → ℜ, z ↦ ziΠl<i(1 − zl), i = 2, …, k and f1(z) = z1. Let p(x) = (p1(x), …, pk(x)) and g(x) = (g1(x), …, gk(x)). Then we need to show that
αk(x) > Φ−1(1 − εk)} > 0. Let Sk−1 denote the k-dimensional simplex. For notational simplicity let pi(x) = Φ{αi(x)}, gi(x) = Fx(Ai), i = 1, …, k−1 and gk(x) = 1. Let z = (z1, …, zp)′, fi : Sk−1 → ℜ, z ↦ ziΠl<i(1 − zl), i = 2, …, k and f1(z) = z1. Let p(x) = (p1(x), …, pk(x)) and g(x) = (g1(x), …, gk(x)). Then we need to show that
Note that for 2 ≤i ≤k,
Thus one can get , i = 1, …, k, such that
But since , the result follows immediately.
Appendix B. Proof of Theorem 5.6
Fix
. Without loss of generality it is enough to show that for a uniformly continuous function g : ℜp×ℜ+×
 → [0, 1] and ε > 0,
→ [0, 1] and ε > 0,
Furthermore, it suffices to assume g(β, σ, x) → 0 uniformly in x ∈
 as ||β|| → ∞, σ → ∞.
as ||β|| → ∞, σ → ∞.
Fix ε > 0, there exist a, σ, σ̄ > 0 not depending on x such that Fx([−a, a]p×[σ, σ̄]) > 1 − ε for all x ∈
 . Let C = [−a, a]p × [σ, σ̄].
. Let C = [−a, a]p × [σ, σ̄].
where πh’s are specified by 5.1 with ch satisfying S1 and S2 and (βh, σh) ~ G0. Now for each x ∈
 , construct a Riemann sum approximation of ∫C g(β, σ, x)dFx(β, σ).
, construct a Riemann sum approximation of ∫C g(β, σ, x)dFx(β, σ).
Let {Ak,n, k = 1, …, n} be a sequence of partitions of C with increasing refinement as n increases. Assume max1≤k≤n diam(Ak,n) → 0 as n ↑ ∞. Fix (β̃k,n, σ̃k,n) ∈ Ak,n, k = 1, …, n. Then by DCT as n → ∞,
| (B.1) |
Hence there exists n1 such that for n ≥ n1
Consider the set
By Lemma Appendix A.1 which is proved in Appendix A,
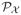 (Ω1) > 0. Since
a.s. there ∃ Ω with
(Ω1) > 0. Since
a.s. there ∃ Ω with
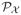 (Ω) = 1, such that for each ω= {πh, h = 1, …, ∞} ∈ Ω,
as n → ∞ for each x in
(Ω) = 1, such that for each ω= {πh, h = 1, …, ∞} ∈ Ω,
as n → ∞ for each x in
 . Note that this convergence is uniform since, gn(·), n ≥ 1 are continuous functions defined on a compact set monotonically increasing to a continuous function identically equal to 1. Hence for each ω = {πh, h = 1, …, ∞} ∈ Ω, gn(x) → 1 uniformly in x. By Egoroff’s theorem, there exists a measurable subset Ω2 of Ω1 with
. Note that this convergence is uniform since, gn(·), n ≥ 1 are continuous functions defined on a compact set monotonically increasing to a continuous function identically equal to 1. Hence for each ω = {πh, h = 1, …, ∞} ∈ Ω, gn(x) → 1 uniformly in x. By Egoroff’s theorem, there exists a measurable subset Ω2 of Ω1 with
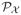 (Ω2) > 0 such that within this subset gn(x) → 1 uniformly in x and uniformly in ω in Ω2. Thus there exists a positive integer nε ≥ n1 not depending on x and ω, such that
on Ω2. Moreover, one can find a K > 0 independent of x such that g(β, σ, x) < ε if ||β|| > K and σ > K. Let A1 = {(β, σ) : ||β|| > K, σ > K}. Let Ω3 = Ω2 ∩ {(βn1+1, σn1+1) ∈ A1, …, (βnε−1, σnε−1) ∈ A1}. For ω ∈ Ω3,
(Ω2) > 0 such that within this subset gn(x) → 1 uniformly in x and uniformly in ω in Ω2. Thus there exists a positive integer nε ≥ n1 not depending on x and ω, such that
on Ω2. Moreover, one can find a K > 0 independent of x such that g(β, σ, x) < ε if ||β|| > K and σ > K. Let A1 = {(β, σ) : ||β|| > K, σ > K}. Let Ω3 = Ω2 ∩ {(βn1+1, σn1+1) ∈ A1, …, (βnε−1, σnε−1) ∈ A1}. For ω ∈ Ω3,
and
There exists sets Bk, k = 1, …, n1 depending on n1 but independent of x such that if (βk, σk) ∈ Bk,|g(βk, σk, x) − g(β̃k,n1, σ̃k,n1, x)|< ε. So for ω ∈ Ω4 = Omega;3 ∩ {(β1, σ1) ∈ B1, …, (βn1, σn1) ∈ Bn1},
Now since
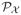 (Ω2) > 0 and the sets {(βn1+1, σn1+1) ∈ A1, …, (βnε−1, σnε−1) ∈ A1} and {(β1, σ1) ∈ B1, …, (βn1, σn1) ∈ Bn1} are independent from Ω2 and have positive probability, it follows that
(Ω2) > 0 and the sets {(βn1+1, σn1+1) ∈ A1, …, (βnε−1, σnε−1) ∈ A1} and {(β1, σ1) ∈ B1, …, (βn1, σn1) ∈ Bn1} are independent from Ω2 and have positive probability, it follows that
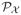 (Ω4) > 0.
(Ω4) > 0.
Appendix C. Proof of Theorem 5.3
Without loss of generality, assume that the covariate space
 is [ζ, 1]p for some 0 < ζ < 1. The proof is essentially along the lines of Theorem 3.2 of [12]. The f̃ in (5.2) will be constructed so as to satisfy the assumptions of Lemma 5.5 and such that
for any ε > 0. Define a sequence of conditional densities
, n ≥ 1 where for σn = n−η,
is [ζ, 1]p for some 0 < ζ < 1. The proof is essentially along the lines of Theorem 3.2 of [12]. The f̃ in (5.2) will be constructed so as to satisfy the assumptions of Lemma 5.5 and such that
for any ε > 0. Define a sequence of conditional densities
, n ≥ 1 where for σn = n−η,
| (C.1) |
Define
| (C.2) |
Proceeding as in Theorem 3.2 of [12], an application of DCT using the conditions A1–A5 yields
Therefore one can simply choose f̃ = fn0 for sufficiently large n0. fn0 satisfies the assumptions of Lemma 5.5 since {Gn0,x, x ∈
 } is compactly supported. Also
as x → Gn0,x(A) is continuous. Hence there exists a finite intersection W of neighborhoods of {Gn0,x, x ∈
} is compactly supported. Also
as x → Gn0,x(A) is continuous. Hence there exists a finite intersection W of neighborhoods of {Gn0,x, x ∈
 } the type (5.5) such that for any {Gx, x ∈
} the type (5.5) such that for any {Gx, x ∈
 } ∈ W, the second term of (5.2) is arbitrarily small. The conclusion of the theorem follows immediately from Corollary 5.8.
} ∈ W, the second term of (5.2) is arbitrarily small. The conclusion of the theorem follows immediately from Corollary 5.8.
Appendix D. Proof of Theorem 5.10
Consider the sequence of sieves defined by (5.9) for given ε > 0 and for sequences an, hn, ln, Mn, mn, rn to be chosen later with
for some constant K1. We will first show that given ξ > 0, there exist c1, c2 > 0 and sequences mn and Mn, such that
and log N (δ,
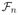 , ||·||) < nξ.
, ||·||) < nξ.
For f1, f2 ∈
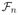 , we have for each x ∈
, we have for each x ∈
 ,
,
Let Θπ,n = {πmn = (π1, π2, …, πmn) : αh ∈ Bh,n, h = 1, …, mn}. Fix . Note that since |Φ(x1) − Φ(x2)| < K2 |x1 − x2| for a global constant K2 > 0, we have
The above fact together with the proof of Lemma Appendix A.1 show that if we can make , h = 1, …, mn, we would have . From the proof of Theorem 3.1 in [42] it follows that for and for sufficiently large Mn, rn,
| (D.1) |
for global constants K3, K4 > 0. For , rn > 1 we have for ,
| (D.2) |
Hence for sufficiently large Mn, we have for ,
| (D.3) |
For ,
where denotes the concentration function of the Gaussian process with covariance kernel c(x, x′) = τ2e−κ||x−x′||2. Now
for some constant K6 > 0. Hence if for some K7 > 0, then it follows from the proof of Theorem 3.1 in [42] that
| (D.4) |
| (D.5) |
We will show that with for some ξ0 assumption C1, we have
| (D.6) |
With mn = O(n/log n), .
With for large enough n and it follows from Lemma 5.15 that
| (D.7) |
Thus with Mn = O(n1/2),
| (D.8) |
(D.6), (D.7) and (D.8) together imply that .
Also for the choice of the sequence rn. With mn = n/(C log n) for some large C > 0, one can make
| (D.9) |
for any ξ > 0. Also from Lemma 5.14,
| (D.10) |
for any ξ > 0. Combining (D.9) and (D.10), log N (
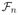 , 4ε, ||·||1) < nξ for any ξ > 0.
, 4ε, ||·||1) < nξ for any ξ > 0.
Appendix E. Another useful lemma
We state without proof the following Lemma needed to prove Theorem 6.1.
Lemma Appendix E.1
For non-negative r.v.s Ai, Bi, if P(Ai ≤ u) ≤ Ci P(Bi ≤ u) for u ∈ (0, t0), t0 > 0, i = 1, 2, P(A1 + A2 ≤ t0) ≤ C1C2P(B1 + B2 ≤ t0).
Appendix F. Proof of Theorem 6.1
Proof
Once again we approximate f0(y|x) by
, so that the first term of 5.2 is arbitrarily small. We construct such an f̃ analogous to that in Theorem 5.3. Lemma Appendix F.1 is a variant of Lemma 5.5 which ensures that the second term in (5.2) is also sufficiently small. Before that we need a different notion of neighborhood of {Fx, x ∈
 } which we formulate below.
} which we formulate below.
| (F.1) |
Lemma Appendix F.1
Assume that f0 ∈
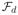 satisfies
satisfies
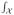
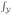 y2f0(y | x)dyq(x)dx < ∞. Suppose
, where ∃ a > 0 and 0 < σ < σ̄ such that
y2f0(y | x)dyq(x)dx < ∞. Suppose
, where ∃ a > 0 and 0 < σ < σ̄ such that
| (F.2) |
so that G̃x has compact support for each x ∈
 . Then given any ε > 0, ∃ a neighborhood W of {G̃x, x ∈
. Then given any ε > 0, ∃ a neighborhood W of {G̃x, x ∈
 } which is a finite intersection of neighborhoods of the type (F.1) such that for any conditional density
, x ∈
} which is a finite intersection of neighborhoods of the type (F.1) such that for any conditional density
, x ∈
 , with {Gx, x ∈
, with {Gx, x ∈
 } ∈ W,
} ∈ W,
| (F.3) |
The proof of Lemma Appendix F.1 is similar to that of Lemma 5.5 and is omitted here. To characterize the support of
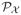 , we define a collection of fixed conditional probability measures {Fx, x ∈
, we define a collection of fixed conditional probability measures {Fx, x ∈
 } on (ℜ × ℜ+,
} on (ℜ × ℜ+,
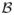 (ℜ × ℜ+)) denoted by
satisfying x ↦ ∫ℜ×ℜ+
g(μ, σ)dFx(μ) is a continuous function of x for all bounded uniformly continuous functions g : ℜ × ℜ+ → [0, 1].
(ℜ × ℜ+)) denoted by
satisfying x ↦ ∫ℜ×ℜ+
g(μ, σ)dFx(μ) is a continuous function of x for all bounded uniformly continuous functions g : ℜ × ℜ+ → [0, 1].
Theorem Appendix F.2
Assume the following holds.
-
T1
G0 is specified by μh ~ GP(μ, c), σh ~ G0,σ where c is chosen so that GP(0, c) has continuous path realizations and Πσ is absolutely continuous w.r.t. Lebesgue measure on ℜ+.
-
T2
For every k ≥ 2, (π1, …, πk) is absolutely continuous w.r.t. to the Lebesgue measure on Sk−1.
-
T3For any continuous function g :
 ↦ ℜ,
↦ ℜ,
h = 1, …, ∞ and for any ε > 0.
Then for a bounded uniformly continuous function g : ℜ × ℜ+ : [0, 1] satisfying g(μ, σ) → 0 as |μ| → ∞, σ → ∞,
| (F.4) |
Proof
It suffices to assume that g is coordinatewise monotonically increasing on ℜ × ℜ+. Let ε > 0 be given and ψ(x) = ∫ℜ×ℜ+
g(μ, σ)dFx(μ, σ). Let nε be such that
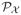 (Ω1) > 0 where
. Then in Ω1,
(Ω1) > 0 where
. Then in Ω1,
Define Ω2 = {
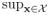 |g(μk(x), σk) − ψ(x)|< ε, k = 1, …, nε}. For a fixed σk, there exists a δ such that
|g(μk(x), σk) − ψ(x)|< ε, k = 1, …, nε}. For a fixed σk, there exists a δ such that
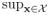 |g(μk(x), σk) − ψ(x)|< ε/2 if
where
denotes the inverse of g(·, σk) for fixed σk. Hence there exists a neighborhood Bk of σk such that for σk ∈ Bk and
, we have
|g(μk(x), σk) − ψ(x)|< ε/2 if
where
denotes the inverse of g(·, σk) for fixed σk. Hence there exists a neighborhood Bk of σk such that for σk ∈ Bk and
, we have
 |g(μk(x), σk) − ψ(x)| < ε. Since for each k = 1, …, nε,
|g(μk(x), σk) − ψ(x)| < ε. Since for each k = 1, …, nε,
 (Ω2) > 0. The conclusion of the theorem follows from the independence of Ω1 and Ω2.
(Ω2) > 0. The conclusion of the theorem follows from the independence of Ω1 and Ω2.
f̃ in (5.2) will be constructed so as to satisfy the assumptions of Lemma Appendix F.1 and such that for any ε > 0. Define a sequence of conditional densities , n ≥ 1 where for σn = n−η,
| (F.5) |
As before define the approximator
| (F.6) |
f̃ will be chosen to be fn0 for some large n0. fn0 satisfies the assumptions of Lemma Appendix F.1 since {Gn0,x, x ∈
 } is compactly supported. Moreover
as x → ∫ℜ×ℜ+
g(μ, σ)dGn0,x(μ, σ) is continuous function of x for all bounded uniformly continuous function g. Hence there exists a finite intersection W of neighborhoods of {Gn0x, x ∈
} is compactly supported. Moreover
as x → ∫ℜ×ℜ+
g(μ, σ)dGn0,x(μ, σ) is continuous function of x for all bounded uniformly continuous function g. Hence there exists a finite intersection W of neighborhoods of {Gn0x, x ∈
 } the type (F.1) such that for any {Gx, x ∈
} the type (F.1) such that for any {Gx, x ∈
 } ∈ W, the second term of (5.2) is arbitrarily small. The conclusion of the theorem follows immediately from a variant of Corollary 5.8 applied to neighborhoods of the type (F.1).
} ∈ W, the second term of (5.2) is arbitrarily small. The conclusion of the theorem follows immediately from a variant of Corollary 5.8 applied to neighborhoods of the type (F.1).
Appendix G. Proof of Theorem 6.2
Proof
As before we establish q-integrated L1 consistency of Gaussian mixtures of fixed-π dependent processes by verifying the conditions of Theorem 5.9. Let
for y ∈
 and x ∈
and x ∈
 . Construct Bn as
. Construct Bn as
with for some constant K1 > 0. Let
| (G.1) |
It is easy to see that
| (G.2) |
Note that and . It follows from the proof of Theorem 3.1 of [42] that
if . Since Ap(1+η2)/η2 ~ Ga(a, b), Lemma 4.9 of [42] indicates that . Hence with Mn = O(n1/2), mn = O{n/(log n)p+1}1/(1+η2) and and
| (G.3) |
Also, the first term in the right hand side of (G.2) can be made smaller than nξ since . Also by F1, the last two terms of the right hand side of (G.2) can be made to grow at o(n).
Footnotes
A similar sieve appears in [33] with a citation to an earlier draft of our paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Fan J, Yao Q, Tong H. Estimation of conditional densities and sensitivity measures in nonlinear dynamical systems. Biometrika. 1996;83:189–206. [Google Scholar]
- 2.Rojas A, Genovese C, Miller C, Nichol R, Wasserman L. Conditional density estimation using finite mixture models with an application to astrophysics. 2005. [Google Scholar]
- 3.Jain S, Neal R. A split-merge markov chain monte carlo procedure for the dirichlet process mixture model. Journal of Computational and Graphical Statistics. 2004;13:158–182. [Google Scholar]
- 4.Walker S. Sampling the Dirichlet mixture model with slices. Communications in Statistics-Simulation and Computation. 2007;36:45–54. [Google Scholar]
- 5.Papaspiliopoulos O, Roberts G. Retrospective Markov chain Monte Carlo methods for Dirichlet process hierarchical models. Biometrika. 2008;95:169. [Google Scholar]
- 6.Minka T. PhD thesis. Massachusetts Institute of Technology; 2001. A family of algorithms for approximate Bayesian inference. [Google Scholar]
- 7.Lo A. On a class of Bayesian nonparametric estimates: I. Density estimates. The Annals of Statistics. 1984;12:351–357. [Google Scholar]
- 8.Ferguson T. A Bayesian analysis of some nonparametric problems. The Annals of Statistics. 1973;1:209–230. [Google Scholar]
- 9.Ferguson T. Prior distributions on spaces of probability measures. The Annals of Statistics. 1974;2:615–629. [Google Scholar]
- 10.Barron A, Schervish M, Wasserman L. The consistency of posterior distributions in nonparametric problems. The Annals of Statistics. 1999;27:536–561. [Google Scholar]
- 11.Ghosal S, Ghosh J, Ramamoorthi R. Posterior consistency of Dirichlet mixtures in density estimation. The Annals of Statistics. 1999;27:143–158. [Google Scholar]
- 12.Tokdar S. Posterior consistency of Dirichlet location-scale mixture of normals in density estimation and regression. Sankhyâ: The Indian Journal of Statistics. 2006;67:90–110. [Google Scholar]
- 13.Ghosal S, van der Vaart A. Entropies and rates of convergence for maximum likelihood and Bayes estimation for mixtures of normal densities. The Annals of Statistics. 2001;29:1233–1263. [Google Scholar]
- 14.Ghosal S, van der Vaart A. Posterior convergence rates of Dirichlet mixtures at smooth densities. The Annals of Statistics. 2007;35:697–723. [Google Scholar]
- 15.Bhattacharya A, Dunson D. Strong consistency of nonparametric bayes density estimation on compact metric spaces with applications to specific manifolds. Annals of the Institute of Statistical Mathematics. 2011:1–28. doi: 10.1007/s10463-011-0341-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Müller P, Erkanli A, West M. Bayesian curve fitting using multivariate normal mixtures. Biometrika. 1996;83:67–79. [Google Scholar]
- 17.Griffin J, Steel M. Order-based dependent Dirichlet processes. Journal of The American Statistical Association. 2006;101:179–194. [Google Scholar]
- 18.Griffin J, Steel M. Bayesian nonparametric modelling with the dirichlet process regression smoother. Statistica Sinica. 2010;20:1507–1527. [Google Scholar]
- 19.Dunson D, Pillai N, Park J. Bayesian density regression. Journal of the Royal Statistical Society, Series B. 2007;69:163–183. [Google Scholar]
- 20.Dunson D, Park J. Kernel stick-breaking processes. Biometrika. 2008;95:307–323. doi: 10.1093/biomet/asn012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chung Y, Dunson D. Nonparametric Bayes conditional distribution modeling with variable selection. Journal of the American Statistical Association. 2009;104:1646–1660. doi: 10.1198/jasa.2009.tm08302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tokdar S, Zhu Y, Ghosh J. Bayesian density regression with logistic Gaussian process and subspace projection. Bayesian Analysis. 2010;5:1–26. [Google Scholar]
- 23.Kruijer W, Rousseau J, Van Der Vaart A. Adaptive bayesian density estimation with location-scale mixtures. Electronic Journal of Statistics. 2010;4:1225–1257. [Google Scholar]
- 24.Scricciolo C. Posterior rates of convergence for dirichlet mixtures of exponential power densities. Electronic Journal of Statistics. 2011;5:270–308. [Google Scholar]
- 25.Barrientos F, Jara A, Quintana F. On the support of MacEachern’s dependent Dirichlet processes. Bayesian Analysis. 2012;7:1–34. [Google Scholar]
- 26.MacEachern S. Dependent nonparametric processes. 1999. pp. 50–55. [Google Scholar]
- 27.Tokdar S, Ghosh J. Posterior consistency of logistic Gaussian process priors in density estimation. Journal of Statistical Planning and Inference. 2007;137:34–42. [Google Scholar]
- 28.Yoon J. Unpublished manuscript. Claremont Mckenna College; 2009. Bayesian analysis of conditional density functions: a limited information approach. [Google Scholar]
- 29.Tang Y, Ghosal S. A consistent nonparametric Bayesian procedure for estimating autoregressive conditional densities. Computational Statistics & Data Analysis. 2007;51:4424–4437. [Google Scholar]
- 30.Tang Y, Ghosal S. Posterior consistency of Dirichlet mixtures for estimating a transition density. Journal of Statistical Planning and Inference. 2007;137:1711–1726. [Google Scholar]
- 31.Rodriguez A, Dunson D. Nonparametric Bayesian models through probit stick-breaking processes. Bayesian Analysis. 2011;6:145–178. doi: 10.1214/11-BA605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.De Iorio M, Mueller P, Rosner G, MacEachern S. An ANOVA model for dependent random measures. Journal of the American Statistical Association. 2004;99:205–215. [Google Scholar]
- 33.Norets A, Pelenis J, editors. Unpublished manuscript. Princeton Univ; 2010. Posterior consistency in conditional density estimation by covariate dependent mixtures. [Google Scholar]
- 34.Norets A. Approximation of conditional densities by smooth mixtures of regressions. The Annals of Statistics. 2010;38:1733–1766. [Google Scholar]
- 35.Wu Y, Ghosal S. The L1-consistency of Dirichlet mixtures in multivariate Bayesian density estimation. Journal of Multivariate Analysis. 2010:2411–2419. [Google Scholar]
- 36.Shen W, Tokdar S, Ghosal S. Adaptive Bayesian multivariate density estimation with Dirichlet mixtures. 2011. Arxiv preprint arXiv:1109.6406. [Google Scholar]
- 37.Tokdar S. Adaptive convergence rates in Dirichlet process mixtures of multivariate normals. 2011. Arxiv preprint arXiv:1111.4148. [Google Scholar]
- 38.Pati D, Dunson D. Unpublished paper. 2009. Bayesian nonparametric regression with varying residual density. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.De Iorio M, Johnson W, Müller P, Rosner G. Bayesian nonparametric nonproportional hazards survival modeling. Biometrics. 2009;65:762–771. doi: 10.1111/j.1541-0420.2008.01166.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Jara A, Lesaffre E, De Iorio M, Quintana F. Bayesian semiparametric inference for multivariate doubly-interval-censored data. The Annals of Applied Statistics. 2010;4:2126–2149. [Google Scholar]
- 41.Gelfand A, Kottas A, MacEachern S. Bayesian nonparametric spatial modeling with Dirichlet process mixing. Journal of the American Statistical Association. 2005;100:1021–1035. [Google Scholar]
- 42.van der Vaart A, van Zanten J. Adaptive Bayesian estimation using a Gaussian random field with inverse Gamma bandwidth. The Annals of Statistics. 2009;37:2655–2675. [Google Scholar]
- 43.van der Vaart A, van Zanten J. Reproducing kernel Hilbert spaces of Gaussian priors. IMS Collections. 2008;3:200–222. [Google Scholar]
- 44.Adler R. An introduction to continuity, extrema, and related topics for general Gaussian processes. Vol. 12. Institute of Mathematical Statistics; 1990. [Google Scholar]
- 45.Papaspiliopoulos O. Technical Report. 2008. A note on posterior sampling from Dirichlet mixture models. [Google Scholar]
- 46.Ishwaran H, James L. Gibbs sampling methods for stick-breaking priors. Journal of the American Statistical Association. 2001;96:161–173. [Google Scholar]
- 47.Papaspiliopoulos O, Roberts G. Retrospective Markov chain Monte Carlo methods for Dirichlet process hierarchical models. Biometrika. 2008;95:169–183. [Google Scholar]
- 48.Kalli M, Griffin J, Walker S. Slice sampling mixture models. Statistics and computing. 2010:1–13. [Google Scholar]
- 49.Wu Y, Ghosal S. Kullback Leibler property of kernel mixture priors in Bayesian density estimation. Electronic Journal of Statistics. 2008;2:298–331. [Google Scholar]
- 50.Freedman D. Wald lecture: On the Bernstein-von Mises theorem with infinite-dimensional parameters. The Annals of Statistics. 1999;27:1119–1141. [Google Scholar]
- 51.Rivoirard V, Rousseau J. Bernstein–von Mises theorem for linear functionals of the density. The Annals of Statistics. 2012;40:1489–1523. [Google Scholar]
- 52.Castillo I, Nickl R. Nonparametric bernstein-von mises theorems. 2012. arXiv preprint arXiv:1208.3862. [Google Scholar]


