MEASURING ECONOMIC GROWTH FROM OUTER SPACE

Abstract

GDP growth is often measured poorly for countries and rarely measured at all for cities or subnational regions. We propose a readily available proxy: satellite data on lights at night. We develop a statistical framework that uses lights growth to augment existing income growth measures, under the assumption that measurement error in using observed light as an indicator of income is uncorrelated with measurement error in national income accounts. For countries with good national income accounts data, information on growth of lights is of marginal value in estimating the true growth rate of income, while for countries with the worst national income accounts, the optimal estimate of true income growth is a composite with roughly equal weights. Among poor-data countries, our new estimate of average annual growth differs by as much as 3 percentage points from official data. Lights data also allow for measurement of income growth in sub- and supranational regions. As an application, we examine growth in Sub Saharan African regions over the last 17 years. We find that real incomes in non-coastal areas have grown faster by 1/3 of an annual percentage point than coastal areas; non-malarial areas have grown faster than malarial ones by 1/3 to 2/3 annual percent points; and primate city regions have grown no faster than hinterland areas. Such applications point toward a research program in which “empirical growth” need no longer be synonymous with “national income accounts.”

Gross Domestic Product (GDP) is the most important variable in analyses of economic growth. The conceptual problems in defining GDP, let alone using it as a measure of welfare, are the stuff of introductory economics courses. Just as serious, however, is the problem that GDP itself is often badly measured, especially in developing countries. Relative to developed countries, in many developing countries a much smaller fraction of economic activity is conducted within the formal sector, the degree of economic integration and price equalization across regions is lower, and, most significantly, the government statistical infrastructure is weaker. These factors make the calculation of nominal GDP (total value added, in domestic prices) difficult.

This paper focuses on measurement of real GDP growth over time within a country, which besides measuring nominal GDP requires the construction of reliable domestic price indices, again a problem for many developing countries. We focus exclusively on real GDP growth within countries. If, in addition, we wanted to compare real GDP levels across countries, that would require purchasing power parity exchange (PPP) rates based on prices for a comparable set of goods across countries.

In the Penn World Tables (PWT), one of the standard compilations of cross-country data on income, countries are given grades corresponding to subjective data quality, with a grade of A indicating a margin of error of 10%, B indicating 20%, C indicating 30%, and D indicating 40%. The grading is based in part on the ability to construct good PPP measures, but also reflects a country’s capacity to produce reliable national income accounts and domestic price indices. Almost all industrialized countries receive a grade of A. By contrast, for the 43 countries of sub-Saharan Africa, 17 get a D and 26 get a C. (Deaton and Heston 2008). In the worst case, some countries simply have no national accounts data available. For example, Iraq, Myanmar, Somalia, and Liberia are among the countries not included in the most recent (6.2) version of PWT.

An illustration of the degree of measurement error in the PWT comes from Johnson et al.’s (2009) study of revisions to the PWT data. Specifically, the authors compared version 6.1 of the PWT, released in 2002, with version 6.2, released in 2006. The standard deviation of the change in countries’ average growth over the period 1970-1999 was 1.1% per year – an enormous change in comparison to the average growth rate over this period of 1.56% per year. To give a striking example, the authors calculated the ten worst growth performers in Africa based on the 6.1 data and similarly based on the 6.2 data. Only five countries were on both lists.¹ As another example of how poorly measured GDP data creates problems for research and policy making, Dawson et al. (2001) claim that the asserted empirical link between output volatility and income growth in the PWT data is purely a product of measurement error in annual income

Besides the PWT, as detailed later the IMF and World Bank both rank sets of countries as to the reliability of their national income accounts. In applications later in the paper we use this ranking rather than the PWT. In the PWT we couldn’t fully disentangle whether poorly rated countries had low quality national accounts data or just poor baseline information for PPP comparisons. The World Bank and IMF ratings concern just the quality of a country’s national accounts data, which is our concern.

In addition to all the problems of measurement error in GDP, a second issue is that in most countries GDP numbers are not available on any consistent basis at the sub-national level. Much of the interesting variation in economic growth takes place within rather than between countries. Similarly, many of the theories about factors that affect growth, for example those that look at the importance of geography, pertain to regions made up of parts of one or more countries. However, for the vast majority of economics research, “empirical analysis of growth” has become synonymous with use of national accounts data. We think the tools are available to set aside this limitation.

In response to the problems of measuring GDP, there is a long tradition in economics of considering various proxies that cover periods or regions for which GDP data are not available at all or not available in a timely fashion. For example, until the year 2005, the Federal Reserve Board based its monthly index of industrial production in part on a survey of utilities that measured electricity delivered to different classes of industrial customers. Similarly, an IMF study examining electricity consumption in Jamaica over the decade of the 1990s concluded that officially measured GDP growth, which averaged 0.3% per year, understated true output growth by 2.7% per year, the gap being explained by growth of the informal sector (IMF, 2006). Young (2009) constructs proxies for the level and growth rate of consumption in 56 developing countries by using microeconomic data in the Demographic and Health Surveys. Economic historians have also employed a variety of proxies for studying economic outcomes in the period before the creation of national income accounts and in order to examine growth in sub-national units. For example, Good (1994) estimates output in 22 sub-regions of the Habsburg Empire in the period 1870-1910 using proxies such as the number of letters mailed per capita. The essays in Steckel and Rose (2002) use skeletal remains to measure both the average standard of living and the degree of inequality in the Americas over the last two millennia.

In this paper we explore the usefulness of a different proxy for economic activity: the amount of light that can be observed from outer space. More particularly, our focus will be on using changes in “night lights” as a measure of economic growth. We will show that lights growth gives a very useful proxy for GDP growth over the long term and also tracks short term fluctuations in growth.

How might we use this new proxy? First we can use the change in night light intensity as an additional measure of income growth at the national level. Even if changes in light observable from space are subject to measurement error, it is well known that several error-prone measures are better than one, especially if there is no reason to think that the measurement errors are correlated. In the paper, we develop a simple framework showing how to combine our lights measure, which is in a different metric than income, with income measures to improve estimates of true economic growth (c.f., Browning and Crosley, 2009 or Krueger and Lindahl, 2001). We illustrate the methodology with an application to a set of countries that are rated by the World Bank as having very low capacity in generating reliable national income accounts and price indices. For these countries we provide new estimates of their economic growth over the period 1992/3 to 2005/6.

Second, we can use night lights data to tell us about economic growth in circumstances where we have no measures of income growth. Most compelling is that night lights data are available at a far greater degree of geographic fineness than is attainable in any standard income and product accounts. As discussed later, we can map data on light observed from space on approximately one-kilometer squares and aggregate them to the city or regional level. This makes the data uniquely suited to spatial analyses of economic activity. Economic analysis of growth and of the impacts of policies and events on cities and regions of many countries is hindered by a complete absence of any regular measure of local economic activity. While population data are sometimes regularly available for cities above a certain size, almost no countries have city level GDP data.² Night lights data give us such a measure. Note also that data from satellites are available at a much higher time frequency than standard output measures. They are also available well in advance of income measures from national accounts and provide an early signal of country growth changes. Further, as will be illustrated below, they allow us to assess the time patterns on regional income growth of events such as discovery of minerals, civil strife, and the like.

This is the first paper we are aware of that uses night lights data to measure real income growth. A number of researchers have shown that night lights reflect human economic activity (e.g., Croft (1978), Elvidge et al. (1997b), Sutton and Costanza (2002), Ebener et al (2005), Doll et al. (2006) and Sutton et al (2007))³, but have not used lights in a statistical framework to measure real economic growth. Satellite data on land cover has been used to examine the spatial expansion of settlements in the USA (e.g., Burchfield et al., 2006). Chen and Nordhaus (2010) adapt the statistical methodology of the first version of our paper and apply lights data to a somewhat different context than the ones here.⁴

Finally we note that lights data has an advantage over other proxies which could serve a similar purpose, such as electricity consumption. Night lights data are available over time and all space. Data on electricity consumption is unavailable for many lower income countries and is generally unavailable for most countries at sub-national levels.

The rest of this paper is organized as follows. Section 1 gives a brief introduction to the night lights data and discusses more obvious examples of how they represent differences in income levels or growth across countries and the effects of political-economic shocks on growth or income levels. In Section 2 we develop the statistical framework to show how information on changes in lights is related to changes in measured income, as well as developing the framework for combining measures of lights growth with existing measures of GDP growth to get improved estimates of true income growth. In Section 3 we estimate the relationship between GDP and lights growth, examining annual and long difference changes, functional specification, use of electricity data and other issues. In Section 4 we turn to the application where we use lights growth measures to improve estimates of true income growth for countries with poor data quality. In Section 5, we present some further applications in which night lights data can be used to assess growth in regions defined by geography, economic, or health metrics, rather than by political borders. Section 6 concludes.

1. Night lights data

Several US Air Force weather satellites circle the earth 14 times per day, recording the intensity of Earth-based lights. Each satellite observes every location on the planet every night at some instant between 8:30 and 10:00 pm local time. Scientists at the National Oceanic and Atmospheric Administration’s (NOAA) National Geophysical Data Center (NGDC) process these raw data and distribute the final data to the public. In processing, they remove observations for places experiencing the bright half of the lunar cycle, the summer months when the sun sets late, auroral activity (the northern and southern lights) and forest fires. These restrictions remove intense sources of natural light, leaving mostly man-made light. Observations where cloud cover obscures the Earth’s surface are also excluded. Finally, data from all orbits of a given satellite in a given year are averaged over all valid nights to produce a satellite-year dataset.⁵ It is these datasets that are distributed to the public.

Each satellite-year dataset is a grid reporting the intensity of lights as a six-bit digital number, for every 30 arc-second output pixel (approximately 0.86 square kilometers at the equator) between 65 degrees south and 75 degrees north latitude.⁶ The exclusion of high latitude zones affects approximately ten thousand people, or 0.0002% of the global total, in four countries or country-equivalents, two of which (Canada and Russia) have GDP data. In our analysis below, we exclude areas north of the Arctic Circle (66 degrees, 32 arc-minutes North), because a disproportionate percentages of pixels there have missing data for entire satellite-years, most likely because of auroral activity. Only 0.036% of global population, in 7 countries, lives there.⁷ Datasets currently exist for 30 satellite-years covering the years 1992 to 2008, for a total of about 22 billion satellite-year-pixels, 6.4 billion of which fall on land. We calculate simple averages across satellites within pixel-years for all analysis below.

The digital number is an integer between 0 (no light) and 63. A small fraction of pixels (less than 0.1%), generally in rich and dense areas, are censored at 63. De facto sensor settings vary over time across satellites and with the age of a satellite, so that comparisons of raw digital numbers over years can be problematic. In statistical work we will control for such issues with year fixed effects. The digital number is not exactly proportional to the physical amount of light received (called true radiance) for several reasons. The first is sensor saturation, which is analogous to top coding. Further, the scaling factor (“gain”) applied to the sensor in converting it into a digital number varies for reasons that are not explained, possibly to allow Air Force analysts to get clearer information on cloud cover. Unfortunately, the level of gain applied to the sensor is not recorded in the data. In an experiment carried out for 18 days during the winters of 1996 and 1997, the settings of one of the satellites were altered so that a true radiance measure could be calculated.⁸ The resulting experimental radiance-calibrated dataset, averaged across all 18 days, is also distributed by NOAA. We find close to unit elasticity in comparing lit pixels from this experiment to lit pixels from the standard data from 1997 (the year of the majority of the 18 days). Details of this exercise and more information about the lights are in the Appendix.

Intensity of night lights reflects outdoor and some indoor use of lights. However, more generally, consumption of nearly all goods in the evening requires lights. As income rises, so does light usage per person, in both consumption activities and many investment activities. Obviously this a complex relationship, and we abstract from such issues as public versus private lighting, relative contributions of consumption versus investment, and the relationship between daytime and nighttime consumption and investment. This paper is concerned with poor or non-existent data on national and local income. For the other aspects of economic activity just listed there are no consistent measures over time and countries, so we can’t directly incorporate these aspects into our analysis, although we will illustrate a variety of considerations in the course of the paper. However, because we will look at growth in lights in the statistical work, cross-country level differences in these other variables will be accounted for in the statistical formulation.

Table 1 gives some sense of the data, describing the distribution of digital numbers across pixels for ten countries covering a broad range of incomes and population densities. For reference, we also include data on GDP per capita at PPP, population density, and the fraction of the population living in urban areas. Our economic and population measures are taken from the World Development Indicators (WDI).

Table 1. Night Lights Data for Selected Countries, 1992-2008 average.

DN	Bangladesh	USA	Canada	Netherlands	Brazil	Costa Rica	Guatemala	Madagascar	Mozambique	Malawi
0	66.72%	69.32%	93.89%	1.00%	94.02%	59.26%	79.23%	99.73%	99.47%	97.67%
1-2	0.637%	0.110%	0.001%	0.000%	0.001%	1.060%	0.244%	0.005%	0.031%	0.000%
3-5	24.48%	10.85%	1.65%	3.45%	2.60%	24.79%	13.84%	0.15%	0.28%	0.93%
6-10	5.27%	9.60%	2.48%	24.04%	1.83%	9.26%	4.17%	0.06%	0.11%	0.85%
11-20	1.69%	4.53%	1.09%	28.83%	0.77%	3.00%	1.46%	0.03%	0.05%	0.27%
21-62	1.13%	5.02%	0.83%	41.10%	0.73%	2.33%	0.95%	0.03%	0.05%	0.27%
63-66	0.06%	0.58%	0.05%	1.58%	0.06%	0.31%	0.10%	0.0001%	0.0003%	0.0012%
% unlit	66.94%	66.20%	92.54%	1.05%	94.31%	60.70%	80.42%	99.74%	99.51%	97.15%
avg. DN	2.0108	4.6648	0.9381	23.5244	0.6342	3.1401	1.4059	0.0233	0.0435	0.3010
gini(DN)	0.7879	0.8471	0.9643	0.3925	0.9689	0.7734	0.8822	0.9985	0.9974	0.9865
pop. density (per sq. km)	1,080	31	3	469	21	76	105	26	23	125
percent urban	24%	79%	79%	76%	81%	59%	45%	27%	30%	15%
GDP per capita, PPP (2005 $)	917	37,953	31,058	32,226	8,046	8,167	3,905	892	546	672
GDP per capita (2000 $)	344	33,582	22,531	23,208	3,760	4,084	1,693	249	252	143
annual %ΔGDP, 1992-2008	5.38%	3.04%	3.18%	2.70%	3.21%	5.02%	3.96%	3.18%	7.52%	3.65%
annual %Δ lights, 1992-2008	0.57%	0.38%	−0.42%	0.36%	2.92%	4.10%	6.35%	2.41%	6.71%	2.06%

Notes:

1) % area unlit accounts for differences in cell area, whereas the percentage of cells having digital number 0, 1-2, etc. does not.

2) Each figure is calculated within satellite-years, averaged across satellites within a year, and then across years.

Table 1 shows the fraction of pixels assigned to different reading intervals on the 0-63 scale for different countries. In many countries a high fraction of pixels are unlit. In the United States and Canada respectively 69.3% and 93.9% of pixels are unlit, while in a high density country like the Netherlands only 1% are unlit. The percentage of unlit pixels falls with income holding density constant; Bangladesh, with higher population density than the Netherlands, has 66.7% of pixels unlit. Among poor, sparsely populated countries like Mozambique and Madagascar, over 99% of pixels are unlit. Note the small difference in fraction of pixels that are unlit (first row of the table) versus the area of a country that is unlit (later row) occurs because of variation in area per pixel within a country as one moves north and south.

Among the countries in Table 1 (and more generally in the sample) there are remarkably few pixels with digital numbers of 1 or 2. Among middle and lower income countries, the most commonly observed range for the digital number is from 3-5; for Canada, it is 6-10; and for the Netherlands, it is 21-62. The minimal fraction of pixels with digital numbers of 1 or 2 reflects, we believe, algorithms used to filter out noise in the raw data. More generally the censoring of data at the low end means some low density-low income pixels do not get counted, so to some extent we will undercount lights nationally. Pixels with a value of 63 are top-coded. The fraction of top coded pixels in low and middle income countries is zero or almost so, while in a densely-populated rich country like the Netherlands 1.58% of pixels are top-coded.

Table 1 also shows the mean digital number and the within-country Gini for the digital number. The mean ranges from 23.5 in the Netherlands to 0.023 in Madagascar. While richer countries tend to have higher average digital numbers, geography and population density also play a strong role, so Bangladesh has a higher average digital number than Canada. For that reason night lights data are best for measuring differences in economic growth across countries because geographic variation across counties is differenced out over time, rather than measuring differences in income levels across countries. Below in the empirical work we will explore whether dispersion measures like the Gini, as well as fraction unlit and fraction top-coded, additionally contribute to our ability to predict income growth.

1.1 Simple examples of what night lights data reflect

A global view

A quick look at the world in Figure 1 suggests that lights do indeed reflect human economic activity, as pointed out as early as Croft (1978). In the figure unlit areas are black, and lights appear with intensity increasing from gray to white. Lights in an area reflect total intensity of income, which is increasing in both income per person and number of people. In the United States, where living standards are fairly uniform nationally, the higher concentration of lights in coastal areas and around the Great Lakes reflects the higher population densities there. The comparison of lights in Western Europe and India reflects huge differences in per capita income, as does the comparison between Brazil and the Democratic Republic of Congo. Again, given cultural differences in use of lights and geographic differences in unlit and top-coded areas, our focus in this paper is on using lights to measure income growth and fluctuations.

Figure 1.

Lights at night, 2008

We now illustrate the relationship between income changes and night lights with several examples that highlight what night lights record and issues in their application.

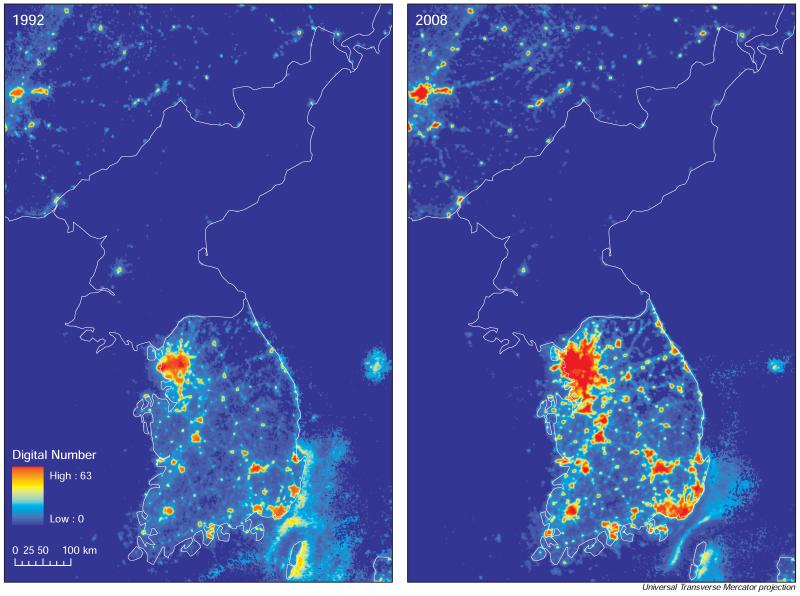
Korean peninsula

Figure 2 shows lights for North and South Korea at two different points in time, 1992 and 2008, indicating scales of luminance. The lights for South Korea illustrate how lights reflect long term growth. In this time period South Korea’s real GDP (in constant local currency units) increased by 119%. This overall growth in GDP for South Korea is matched in the figure by increasing light intensity, with expanding areas of high and medium coding, in red and yellow shades respectively. The average digital number for South Korea increases by 72% in the same time period. Even if the elasticity of lights growth with respect to income growth is close to one, we don’t expect the percentage growth in income and lights to be the same because the lights measures were done by different satellites in 1992 and 2008, the sensor settings of which will not exactly match. Off-shore lights near South Korea in 1992 are from fishing boats shining bright lights to attract photophilic creatures like squid. Figure 2 also shows the dismal comparative situation in North Korea, with little or no growth in the same time period. The average digital number fell by 7.4%.

Figure 2.

Long term growth: Korean peninsula

Indonesia

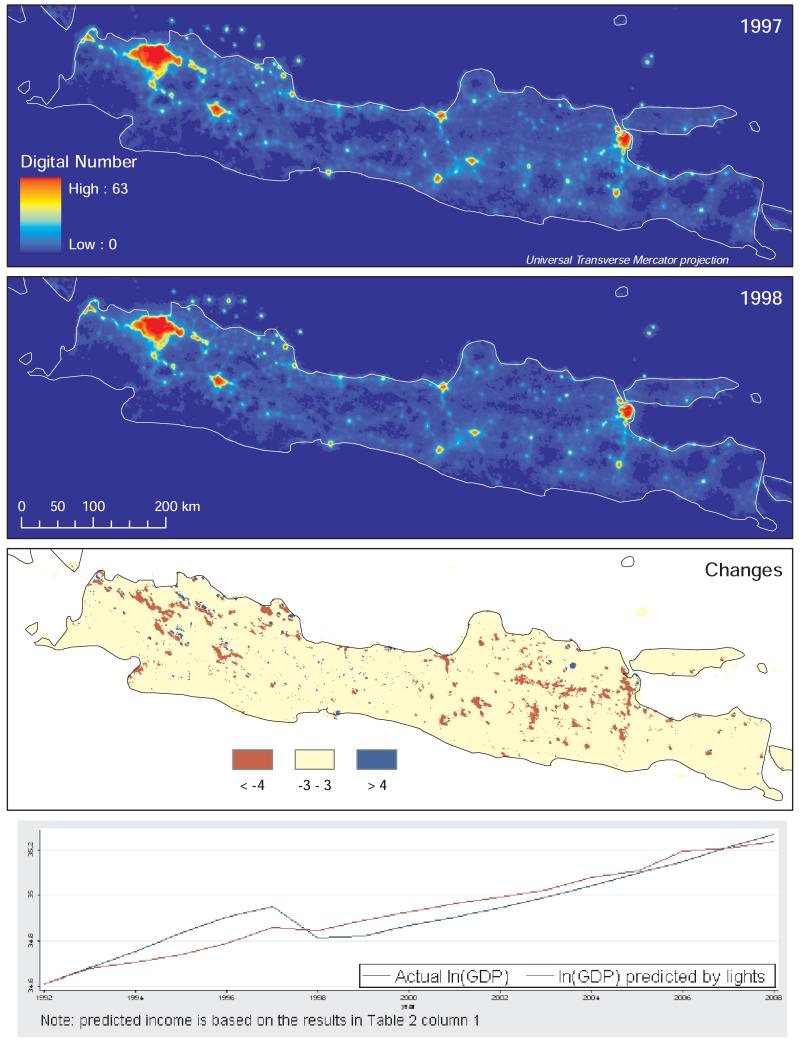
To illustrate the high frequency response of lights to an economic downturn, we use data from Indonesia in 1997, before the Asian fiscal crisis, and in 1998, when Indonesia was at a GDP low. Overall for Indonesia the digital number declined by 6% from 1997 to 1998 and real GDP declined by 13%. To improve visualization we focus just on the main island of Java, pictured in Figure 3. In Figure 3, lights in 1997 are in the top panel; lights in 1998 are in the second; and large positive and negative changes for 1997-1998 are in the third panel. In Figure 3, while one can stare at the first and second panels and see light decreases between 1997 and 1998 especially around the fringe of large urban areas, the third panel shows large light declines in red, where digital numbers change by more than 3. There are large patches of light declines in west Java around Jakarta and its suburban areas and in east Java around the growth pole of Surabaya and its hinterlands, going south-west from Surabaya. In some rural areas there is an increase in lights, depicted in blue. We know that there was some return to rural areas by urban migrants in the crisis and that there is also drilling and refining of petroleum in some of these areas. In the bottom panel, we show the plot of real GDP in local currency units around the time period. In this box we also show predicted incomes from the statistical model presented later in the paper, where lights data are used to predict incomes in a panel framework.

Figure 3.

Asian financial crisis: Java, Indonesia

Rwandan genocide

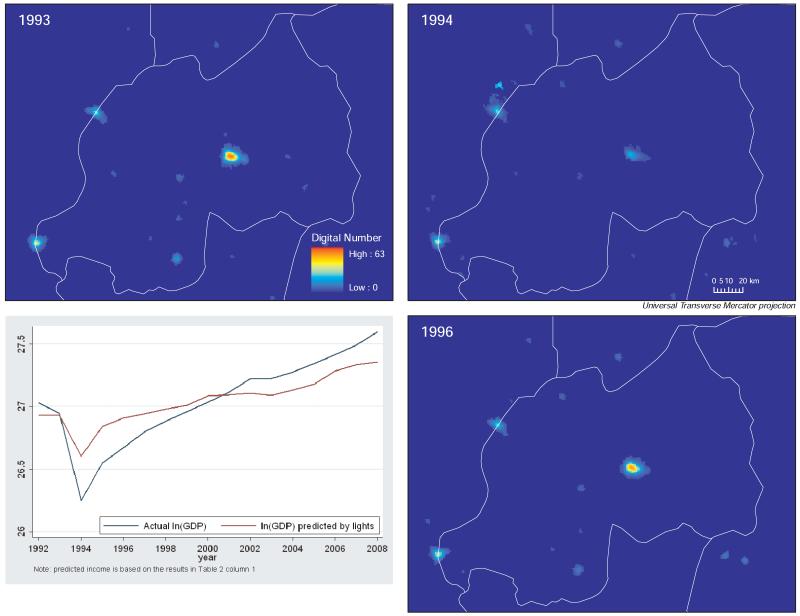
To illustrate how a traumatic crisis event is reflected in lights, the box in Figure 4 shows the huge decline in income during the 1994 genocide in Rwanda, with the partial recovery by 1996, along with income predictions from the panel analysis in Section 3. Here the overall raw lights data clearly mark the sharp temporary economic decline as lights dim from 1993 to 1994 and then mostly relight by 1996. The capital Kigali in particular dims in 1994 and then relights by 1996, as well as more minor urban centers.

Figure 4.

Genocide event: Rwanda

We note that, in Figures 3 and 4 in comparing measured income versus our predictions from lights data, in both cases, lights under-predict the extent of measured income declines. For Indonesia where national income data are relatively good, this could be under-prediction of the true income decline. For Rwanda, national income data are less reliable and economic activity may have been poorly recorded in the period of genocide. Still there is the issue of how well lights predict real income fluctuations, especially the extent to which lights actually dim with economic downturns. Later we look explicitly at a form of generalized ratchet effects and reject them, but still there may be some smoothing in the lights data of short term fluctuations. We believe lights data are best suited to predicting long term growth and that is the focus of applications later in the paper.

Gemstones in Madagascar

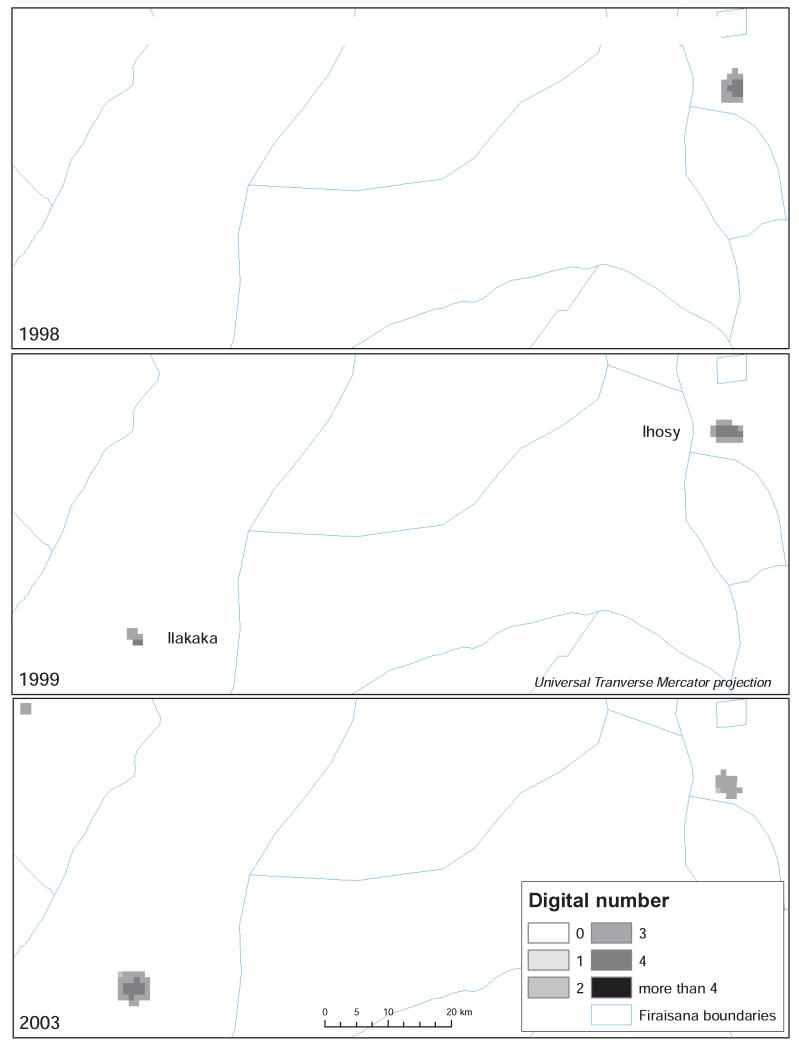
As mentioned above, a major advantage of night light data is that they can be used to examine changes in economic activity at a very local scale. In late 1998, large deposits of rubies and sapphires were accidentally discovered in southern Madagascar, near the town of Ilakaka. The region is now thought to contain the world’s largest sapphire deposit, accounting for around 50% of world supply, and Ilakaka has become a major trading center for sapphires. Previously little more than a truck stop, Ilakaka’s population is now estimated at roughly 20,000.⁹ The story of these developments can clearly be seen in the night lights data in Figure 5. In 1998 (and all of the previous six years for which we have data) there were no lights visible in Ilakaka. Over the next five years there was a sharp growth in the number of pixels for which light is visible at all, and in the intensity of light per pixel. The other town visible in the figure, Ihosy, shows no such growth. If anything, Ihosy’s light gets smaller and weaker, as it suffers in the competition across local towns for population.

Figure 5.

Discovery of sapphire and ruby deposits in Madagascar

2. Lights as a measure of economic activity

In this section we specify the estimating equation to relate lights to GDP growth, specify our assumptions concerning error structure, and develop a statistical framework to show how measures of lights growth can be combined with measures of GDP growth to arrive at an improved estimate of true income growth.

Let y be the growth (or log difference) in true real GDP, z the growth of real GDP as measured in national income accounts, and x the growth of observed light. The variance of true income growth is ${\sigma }_y^2$. For country j (with year subscripts suppressed for now), we assume that there is classical measurement error in GDP growth as recorded in national income accounts:

$$z_j=y_j+{\epsilon }_{z,j},$$ (1)

where the variance of ε_z is denoted ${\sigma }_z^2$. Later we allow for the variance of the measurement error in national income data, ${\sigma }_z^2$, to vary among country groups.

The relationship between growth of lights and growth of true income is given by

$$x_j=\beta y_j+{\epsilon }_{x,j},$$ (2)

where the variance of ε_x is denoted ${\sigma }_x^2$. The assumption underlying this specification is that there is a simple constant elasticity relationship between total observable light in a region (X) and total income (Y): $X_j=Y_j^{\beta }$, where β is the elasticity of lights with respect to income. As reported later we consider different functional forms and controls for changes in light dispersion. Those experiments suggest (2) is appropriate. Since y is the growth rate of total income, we are assuming that observable light is increasing at the same rate in the number of people and per capita income.

The error term in equation (2) we think of as noise in the way measured lights growth reflects GDP growth. This noise includes measurement error in lights, that is, a difference between true light emanating into space and what the satellite records. But the measurement error also includes variation among countries in the relationship between GDP growth and growth of light emanation, due to variation in the mix of products consumed and produced. For example, the increased consumption of automobile services and educational services both represent additions to GDP, but the former results in a larger increase in visible light than the latter. In estimation of the relationship between output and light fluctuations, we will allow for country specific factors in the error specification. Because we don’t think measurement error in GDP is related in any consistent fashion to the error in the equation determining observable light, we assume that Cov(ε_x, ε_z) = 0.

While equation (2) specifies a production relationship between income and lights, in most applications we are concerned with using lights growth to predict income growth. As such, for predictive purposes, we want a regression of growth of income on growth of lights, or

$$z_j=\widehat{\psi }{x}_j+e_j,$$ (3)

We present estimates of this equation in the next section, to look at how well lights reflect fluctuations in income growth and long differences. The OLS parameter $\widehat{\psi }$ is cov(x, z) / var(x). Using the moments in (9b) and (9c) below, the relationship between $\widehat{\psi }$ and the structural parameter β is

$$\mathrm{plim}\left(\widehat{\psi }\right)=\frac{1}{\beta }\left(\frac{{\beta }^2{\sigma }_y^2}{{\beta }^2{\sigma }_y^2+{\sigma }_x^2}\right).$$ (4)

While the parameter $\widehat{\psi }$ is an estimate of the inverse of the elasticity of lights with respect to income, by construction (inversion of the production relationship and measurement error in x), as equation (4) indicates it is a biased estimate. However, equation (3) using $\widehat{\psi }$ is a best fit relationship to be used in producing proxies for income growth. Call these proxies ${\widehat{z}}_j=\widehat{\psi }{x}_j$.

Fitted values of income growth based on lights growth, that is $\widehat{z}$, can be created for sub-national units such as cities as well as for countries in which there are no available income data. Further, however, even where there are available income data, fitted values from lights can be used to improve the precision of estimated income growth. Specifically, $\widehat{z}$ is a separate estimate of income growth which can be combined with a national account measure to arrive at a composite estimate of income growth which will have lower error than either one separately. Specifically, consider a composite estimate of income growth, $\widehat{y}$:

$${\widehat{y}}_j=\lambda z_j+(1-\lambda ){\widehat{z}}_j,$$ (5)

What are the optimal weights on z_j and ${\widehat{z}}_j$ to use in calculating an estimate of true income growth? We specify weights that minimize the variance of measurement error in this estimate relative to the true value of income growth. Based on our assumptions about error structure, the variance of this composite estimate is

$$Var(\widehat{y}-y)=Var\left(\lambda \right(z-y)+(1-\lambda \left)\right(\widehat{z}-y\left)\right)={\lambda }^2{\sigma }_z^2+{(1-\lambda )}^{2}Var(\widehat{z}-y)$$ (6)

The last term in this equation can in turn be expanded as follows:

$$Var(\widehat{z}-y)=Var(\widehat{\psi }x-y)=Var(\widehat{\psi }\beta y+\widehat{\psi }{\epsilon }_x-y)={(\widehat{\psi }\beta -1)}^2{\sigma }_y^2+{\widehat{\psi }}^2{\sigma }_x^2$$

Using the value of $\widehat{\psi }$ from equation (4), this can be rewritten as

$$Var(\widehat{z}-y)=\frac{{\sigma }_y^2{\sigma }_x^2}{{\beta }^2{\sigma }_y^2+{\sigma }_x^2}$$

Substituting this into the equation for variance:

$$Var(\widehat{y}-y)={\lambda }^2{\sigma }_z^2+{(1-\lambda )}^2\frac{{\sigma }_y^2{\sigma }_x^2}{{\beta }^2{\sigma }_y^2+{\sigma }_x^2}.$$ (7)

From (7), we solve for the weight λ which minimizes this variance, where

$${\lambda }^{\ast }=\frac{{\sigma }_x^2{\sigma }_y^2}{{\sigma }_z^2({\beta }^2{\sigma }_y^2+{\sigma }_x^2)+{\sigma }_x^2{\sigma }_y^2}.$$ (8)

λ* is a function of four unknown parameters (${\sigma }_y^2$, ${\sigma }_1^2$, ${\sigma }_2^2$, and β), but the observed data provide only three sample moments:

$$\begin{array}{c}\hfill \mathrm{var}\left(z\right)={\sigma }_y^2+{\sigma }_z^2\left(a\right)\hfill \\ \hfill \mathrm{var}\left(x\right)={\beta }^2{\sigma }_y^2+{\sigma }_x^2\left(b\right)\hfill \\ \hfill \mathrm{cov}(x,z)=\beta {\sigma }_y^2\left(c\right)\hfill \end{array}$$ (9)

. Note for the last moment, cov(y,x) = cov(z,x). To solve the system and to solve for λ*, we need one more equation. Our approach to that equation is as follows.¹⁰

In general one needs to make an assumption about the ratio of signal to total variance in measured GDP growth, z for a set of countries. Define this ratio as

$$\varphi =\frac{{\sigma }_y^2}{{\sigma }_y^2+{\sigma }_z^2}$$ (10)

If we assume a specific value for φ then the optimal λ is given by

$${\lambda }^{\ast }=\frac{\varphi \mathrm{var}\left(z\right)\mathrm{var}\left(x\right)-\mathrm{cov}{(z,x)}^2}{\mathrm{var}\left(z\right)\mathrm{var}\left(x\right)-\mathrm{cov}{(z,x)}^2}=\frac{\varphi -{\rho }^2}{1-{\rho }^2},$$ (11)

where ρ is the correlation between z and x.

We use a variant of this approach which uses information on the relative quality ratings of national income data provided by the IMF and World Bank. Suppose we impose the same lights-economic structure on a set of countries—that is assume the last two moments (and the estimate of ψ) apply to all countries in the set. But then we allow the income noise term, ${\sigma }_z^2$, to vary by country group within the set, using information on the quality of GDP measurement in different countries. Consider a simple case where the set of countries is divided into two groups with different levels of measurement error in GDP. Let g denote countries with good GDP measurement and b denote countries with bad measurement. Now the first moment in (9) becomes two equations:

$$\begin{array}{cc}\hfill \mathrm{var}\left(z_g\right)=& {\sigma }_y^2+{\sigma }_{z,g}^2\left(a\right)\hfill \\ \hfill \mathrm{var}\left(z_b\right)=& {\sigma }_y^2+{\sigma }_{z,b}^2\left(b\right)\hfill \end{array}$$ (12)

Along with the equations for var(x) and cov(z, x), we now have four equations with five unknowns(β, ${\sigma }_y^2$, ${\sigma }_x^2$, ${\sigma }_{z,g}^2$, ${\sigma }_{z,b}^2$). For the fifth, we only need to specify the value of signal to total variance, φ_g for, say, the good data countries which, with (12a), then solves ${\sigma }_y^2$ and ${\sigma }_{z,g}^2$. Those parameters imply φ_b and ${\sigma }_{z,b}^2$ for bad data countries, given (8) and (12b). Given the value of ${\sigma }_y^2$, the equation for cov(z, x) defines β and then the equation for var(x) tells us ${\sigma }_x^2$. With all parameters solved, we can then calculate λ_g and λ_b for good and bad data countries respectively in equation (8).

At an extreme for good data countries, if φ_g=1 and thus ${\sigma }_{z,g}^2=0$ and λ_g = 1, then (12) (where now $\mathrm{var}\left(z_g\right)={\sigma }_y^2$) plus the equations for var(x) and cov(z, x) give the complete solution for parameters. If we have more than two data quality groups, we can proceed in a similar fashion, where the φ for the best data countries implies ${\sigma }_y^2$, and in turn the ${\sigma }_z^2$’s and φ’s for other groups. In Section 4 below we present an application of this process.

2.1 Data quality rankings

The procedure described above requires a measure of data quality or a classification of countries into different data quality groups. The grade rankings in the Penn World Table are an example of such a classification, but as noted earlier much of the concern in the PWT grading is with whether baseline surveys were conducted for PPP comparisons which is not relevant here. Fortunately there are other rating schemes.

The IMF grades countries’ statistical bureaus as high versus lower capability. High capability means countries are subscribers to the IMF’s Special Data Dissemination Standard (SDDS) and meet a set of specifications for data provided to the IMF (with a view to data quality requirements desired in international capital markets). The SDDS grade defines a set of countries with reliable domestic income and price data. Most high income countries meet that standard, but many low and middle income ones do not. Unfortunately the set of non-SDDS countries is large and heterogeneous, and the IMF provides little guidance on varying capabilities within the group. Moreover some countries do not subscribe to the IMF dissemination system and are not graded.

The World Bank (2002) reports an indicator of statistical capacity based on the availability, timeliness, and standard of several kinds of national accounts data for 122 low- and middle-income countries with populations of more than one million.¹¹ The measure runs from 0 to 10. Within the group, ratings are positively correlated with income, although some low income countries such as India get good scores. IMF SDDS countries that appear in the World Bank report all have scores of 5 or above, and most have scores of 7 or more. We will use this World Bank grading scheme to define countries that have better or worse data. In particular we will isolate a group of very low quality data countries which have scores of 3 or less. These include Liberia and the Central African Republic which have essentially no capability to produce reliable data and countries like Burundi, Congo, Iraq, and Angola which have extremely weak capabilities.

3. Predicting GDP with lights

Our data’s capacity to measure true luminance varies across countries by climate and auroral activity. Further, measured luminance for the same GDP may vary with variation in the composition of income between consumption and investment, the division of economic activity between night and day, population density, and land area across counties. Finally, worldwide lighting technology may vary over time, which will affect the relationship between luminance and GDP. To mitigate these problems, we restrict attention to growth formulations and we estimate (3) in several ways. These ways emphasize different cuts on prediction—predicting annual growth and fluctuations, focusing more on predicting annual fluctuations, and predicting long term growth.

First, in a panel context for 1992-2008, we generalize the error structure in (3) to be

$${\tilde{e}}_{jt}=c_j+d_t+e_{jt},$$ (13)

for country j in year t. In (13), year fixed effects (d_t) control for any differences in light sensitivity across satellites, as well as sweeping out effects of changes in worldwide economic conditions, technological advance, and energy costs. Country fixed effects control for cross-country cultural differences in the use of night lights versus day time activities as well as economic factors such as differences in investment and consumption, public versus private lighting, national conditions for generating electricity, and the like. Identification is from within-country relative variation in lights and income over time, relating growth and fluctuations in lights within countries to annual growth and fluctuations in measured income.

If we want to focus more on annual income fluctuations in equation (3) and less on growth, in addition to the error structure in (13), we add a country specific time trend, κ_jt. This formulation asks, for a country on a particular growth path, how well do lights predict fluctuations about that growth path? A country specific time trend also allows for country specific trends in activities generating light and in socio-economic uses of lights. In addition we look at the possibility of “ratchet effects”: whether relative (to the country mean over time) increases and decreases in lights are symmetrically related to increases and decreases in income.

Finally we estimate (3) directly to focus on long run growth, with a long differenced relationship. We examine the period 1992/93 to 2005/06, because 2007 and 2008 are missing data for more countries than any other years in the sample. In our application in section 4 of the statistical model developed in Section 2, we rely on the long differenced model.

3.1 Baseline results

3.1.1 Annual growth and fluctuations

Table 2 presents some basic results for a slightly unbalanced panel of 188 countries over 17 years. Lack of balance arises primarily because some countries lack GDP data in certain years, particularly the most recent. There are also 23 country-years excluded because at least 5% of their land area south of the Arctic Circle is missing data, because of summer lights, auroral activity and/or cloud cover. On average, 177 countries appear in each year. The smallest number in any year is 163 in 2008 (the second smallest is 172). Column 1 shows the fixed effect results, with an estimate of ψ of 0.275. The coefficient is highly significant. Note the R² of 0.77 is a within- R², but accounts for the role of year dummies. Later we report the R²(about 0.21) for data demeaned over countries and years.

Table 2. Baseline results for the world: 1992-2008; growth in real GDP (constant LCU).

	(1) ln(GDP)	(2) ln(GDP)	(3) ln(GDP)	(4) ln(GDP)	(5) ln(GDP)	(6) ln(GDP)	(7) ln(GDP)	(8) ln(GDP)
ln(lights/area)	0.275*** [0.031]	0.260*** [0.034]	0.265*** [0.031]	0.286*** [0.034]	0.282*** [0.046]		0.167*** [0.051]	0.283*** [0.030]
ln(lights/area) sq.		−0.0060 [0.0060]
ln(count top-coded + 1)		0.0116* [0.0059]
ln(unlit)			−0.012 [0.011]
Spatial Gini				0.179 [0.193]
ln(KWH)						0.283*** [0.047]	0.201*** [0.041]
Observations	3014	3014	3014	3014	1853	1853	1853	3014
Countries	188	188	188	188	128	128	128	188
(within) R-sq	0.768	0.769	0.770	0.769	0.757	0.767	0.782	0.769

All specifications include country and year fixed effects

Column (8) excludes regions identified with gas flares.

Robust standard errors in brackets

^***p<0.01

^**p<0.05

^*p<0.1

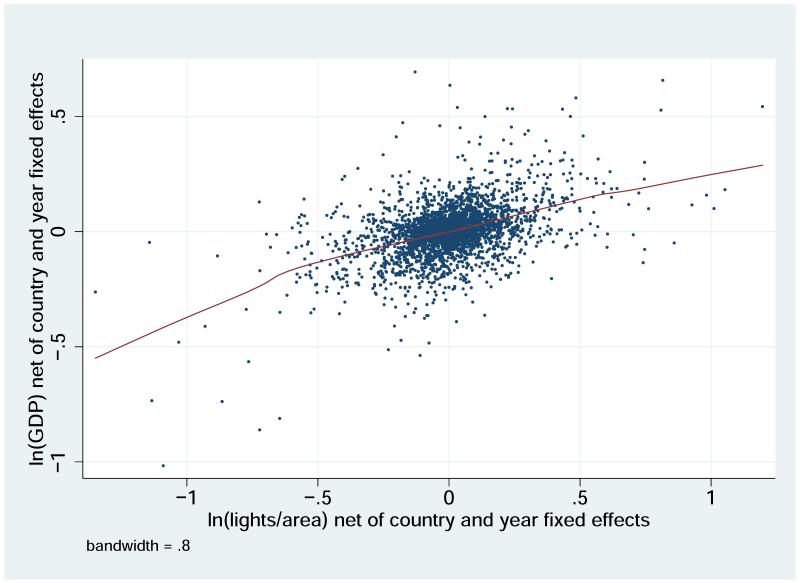
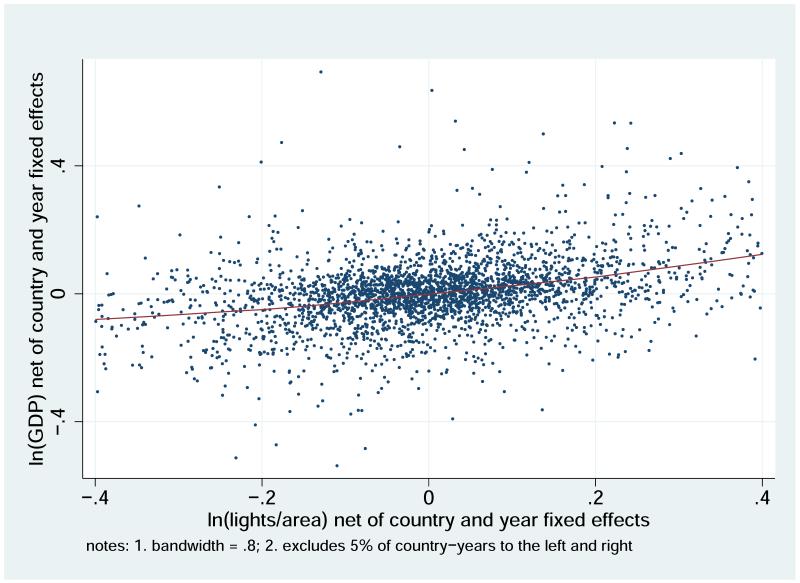
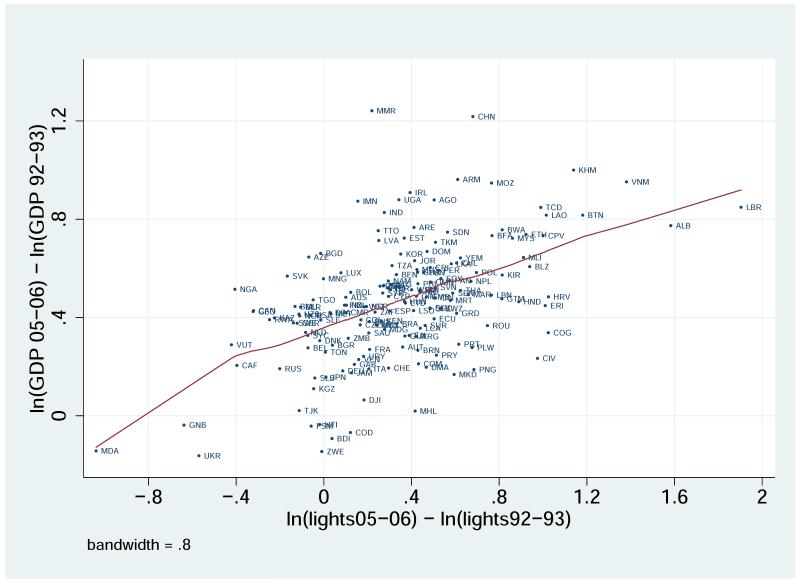
Column 2 of Table 2 suggests a quadratic specification does not fit the data. Figures 6a and 6b show this non-parametrically for the data overall and then over a restricted domain. The figure graphs the z_jt, x_jt relationship net of year and country effects. The pictured relationship indicates a linear specification in the growth rates is appropriate. We also conducted a RESET (Ramsey 1969) test of this specification (net of year and country fixed effects). Linearity for the overall sample is rejected (p-value of 0.008), but there is no compelling higher order specification. In quadratic through a fifth order polynomials expansions, the higher order terms are always insignificant. Below we will show that a long difference specification is distinctly linear, meeting the RESET standard.

Figure 6.

a. GDP versus lights: overall panel

b. GDP versus lights: restricted interval panel

c. GDP versus lights: long differences

Column 3 controls for the number of pixels which are top-coded and the number which are unlit. The former is significant but the estimate of ψ is virtually unchanged as is the R². In column 4, we control for dispersion of lights within a country by using the Gini coefficient for lights among pixels within a country. Given the panel formulation, the coefficient on lights is the same as in column 1 and the Gini has a zero coefficient. These experiments suggest country fixed effects deal with issues of varying light dispersion and unlit areas across countries.¹²

In columns (5) - (7) of Table 2 we explore the relationship between GDP, lights, and electricity consumption. We use electric power consumption in total kilowatt hours (KWH) from the World Development Indicators database. The measure encompasses output from power plants, but excludes small generators unconnected to the power grid. Much light observable from space is from electric illumination. For example if we estimate a panel regression of log lights on the log of KWH, we get a highly significant elasticity of 0.49, and a within R² of 0.54, including the effect of year dummy variables.

Could we substitute electricity consumption for lights data and could we gain by using both, ignoring the issue that electricity consumption data are only available for 60% of our observations? To start, column (5) repeats the specification of column (1) for the sample of country-years for which electricity consumption data are available, showing results are little changed by the reduction in sample. In columns (6) and (7) we look at the predictive power of electricity. Column (6) shows a regression corresponding to columns (1) and (5), except the log of total electricity consumption replaces lights, while column (7) includes both measures. In column (6), electricity consumption has essentially the same predictive power for GDP and the same elasticity as does lights. When the two measures are included together in column (7) both remain significant, indicating they may not capture exactly the same aspects of economic activity, but explanatory power is only modestly improved by inclusion of both. We might also worry that lights are produced on an intensive margin (more usage by those connected to an existing grid) versus an extensive margin (extensions of the grid and more connections to an existing grid). Does knowing about the extensive margin help predictive power? For a very small sample of country-years, the nationally representative Demographic and Health Surveys (DHS)¹³ contains information on the household connections, with which we can try to explore whether adding information on the extensive margin improves our ability to predict measured GDP growth. In the sample, growth in connections yields insignificant effects and no increased explanatory power relative to either just controlling for lights or controlling for both electricity consumption and lights.¹⁴

In sum, while electricity consumption could be used to predict GDP growth, the key issue is that electricity data are available for far fewer countries than are lights. Only 16 of the 30 countries we will later define as bad GDP data countries have electricity data, and many of the countries with no GDP data (such as Afghanistan and Somalia) also do not have electricity data. Second and very critically, electricity usage is generally unavailable for sub-national areas, whereas lights are available for pixels of size less than a square kilometer across the globe.

As discussed above, our data are filtered to remove natural sources of night light, such as auroral activity. Of the remaining man-made light, the majority is artificial light generated so that people can see things at night. The largest exception is light generated by the flaring of natural gas, as a byproduct of oil production. Elvidge et al. (2009) delineate polygons in which observed light in 1992, 2000, or 2007 is primarily from gas flares. 1.0% of the world’s land area, with 0.34% of world population in 2000, fell into these polygons. 3.6% of land-based light emanated from them. In column (8) we report results from a regression corresponding to column (1) in which we exclude all pixels that fell within the gas flare polygons. The results change very little.

3.1.2 Annual fluctuations

Table 3 explores the two other types of income change in which we are interested: annual fluctuations in income and long term growth. Column 1 shows the baseline fixed effects result from Table 2. Column 2 in Table 3 adds country time trends, so lights now just explain deviations of GDP about a country’s growth path. While the value of ψ falls to 0.18 from 0.275, it is still highly significant, suggesting the data do a reasonable job of just predicting annual fluctuations, consistent with the examples we looked at in Section 2. Later when we turn to our sample of low and middle income countries where we apply the lights data, the value of ψ remains around 0.3 with or without country specific time trends.

Table 3. Lights up/down, time trend, long difference.

	(1) Fixed Effects	(2) Country time trend	(3) Demeaned Plus/Minus	(4) Long difference	(5) Long difference
lndn	0.275*** [0.031]	0.180*** [0.035]		0.317*** [0.037]	0.299*** [0.037]
|+Δ ln lights |			0.271*** [0.038]
|− Δln lights |			−0.280*** [0.055]
Ln (top-coded + 1)					0.021 [0.015]
Ln (unlit)					−0.0075 [0.023]
Time effects	Yes	Yes	In demean	No	No
Country effects	Yes	Yes	In demean	No	No
Observations	3014	3014	3014	170	170
Countries	188	188	188	170	170
(within) R-sq	0.768	0.905	0.207	0.273	0.282

Robust standard errors in brackets

^***p<0.01

** p<0.05

* p<0.1

In columns 4 and 5, long differences are formed by averaging the first and last two years of levels data

To explore fluctuations further, in column 3, we examine the ratchet issue: the possibility that because some light growth reflects the installation of new capacity, lights are non-decreasing, so that economic downturns will not be reflected in lights. For column 3, we completely demean the data by regressing GDP and lights on year and country fixed effects and then regressing the GDP residuals on two variables: absolute value positive and negative lights residuals. Positive residuals indicate deviations of lights above average for the time interval for that country and negative residuals are deviations below. They have virtually identical coefficients (of opposite sign given absolute values), consistent with an absence of ratchet effects. Further, the coefficient estimates are almost identical to that in column 1. The R² of 0.21 now reflects the contribution of lights to explaining within-country and within-year variation in income.

3.1.3 Long term growth

The last two columns of Table 3 explore the original equation (3) formulation: how well long term growth in lights predicts long-term measured GDP growth. For this we use long differences between 1992/93 and 2005/06. The long difference estimate of ψ is 0.32, a little higher than the fixed effect value of 0.27, but close and also highly significant. The R² is 0.27. Column (5) adds controls for top-coded and unlit pixels, which have little effect on the ψ and R². Figure 6c shows the plot of the raw long differences in lights versus GDP for each country. As in Figures 6a and 6b, the non-parametric fit of raw numbers appears linear. And in this case, the Ramsey RESET test distinctly cannot reject linearity, with a p-value of 0.73.

3.2 Sample of low and middle income countries

We now turn to a sub-sample of 118 low and middle income countries where we have ratings of their statistical capacity by the World Bank. There are also 27 high income countries not rated by the World Bank which we know from IMF ratings have high quality data. We omit these from the sample we now analyze for several reasons. First has to do with light measurement. These high income countries include a number of northern countries where in some years lights have poor coverage because of aurora activity, lit summer nights, and cloud cover in the winter. Second, we believe the economic structure for these countries as given in the last two moments in (9) may differ from low-middle income countries. For example, in the long difference specification we use in the next section, these countries’ ψ (and also β) seems to differ from our middle-low income countries. While the sample is too small to get strong results, for a pooled sample of these high income countries with our low-middle income ones, the overall coefficient (s.e.) for ψ is 0.322 (0.042), and the differential in coefficient for the high income countries is −0.145 (0.144). This suggestion of a lower ψ for high income countries persists in all formulations.

For the 118 (113 in long differences) low-middle income countries with a World Bank rating, we repeat the estimates of the three cases – fixed effects, fixed effects with a country specific time trend, and long differences. Results are in Table 4. They are similar to what we had before, except that now ψ is about 0.3 in all formulations; in particular it doesn’t drop off once country growth trends are added.

Table 4. Results for rated low-middle income countries; growth in real GDP (local currency units).

	Fixed effects (1)	Country time trend (2)	Long difference (3)
ln(lights/area)	0.308*** [0.037]	0.270*** [0.043]	0.329*** [0.046]
Constant	n/a	n/a	0.365*** [0.028]
Observations	1953	1953	113
Number of isonv10	118	118	113
(Within-country) R-sq	0.780	0.903	0.301
Country fixed effects	Yes	Yes	No
Year fixed effects	Yes	Yes	No
Country time trend	No	Yes	No
Difference in ψ for good data countries (reestimated base ψ not shown)	0.041 [0.063]	-0.013 [0.063]	0.095 [0.092]
Heteroskedasticity:
Breusch-Pagan p-value	<0.00005	<0.00005	0.0396
Regression of squared residuals:
Good data dummy	−0.0055*** [0.0017]	−0.0017* [0.0010]	−0.029 [0.018]

Robust standard errors in brackets

^***p<0.01

** p<0.05

^*p<0.1

In column 3, long differences are formed by averaging the first and last two years of levels data

With this sample, we now explore the idea that countries with different statistical ratings have different variances of measurement error in income (${\sigma }_z^2$), with variances declining as ratings improve. In particular, the regression results can be used to directly calculate the variance of $z-\widehat{\psi }x$. Under our assumptions this variance can be shown to equal $[{\sigma }_y^2-{\beta }^2{\sigma }_y^4∕\mathrm{var}(x\left)\right]+{\sigma }_z^2$. By imposing a common economic-lights structure across all low and middle income countries, we are assuming only ${\sigma }_z^2$ varies across sets of countries, as in equation (12a) versus (12b). In this context, we separate out from our sample of 113 countries, 30 low-middle income countries that have very bad ratings: 0-3 out of 10, to compare with the remaining better data low-middle income countries.

In the bottom part of Table 4, in the first row, we show the results from a regression which allows the slope coefficient on lights to differ from the whole sample for bad data countries. As the row reveals, the differential between good and bad data counties is generally small for the different empirical formulations and in all cases is insignificant. This supports the idea that good rated versus bad rated low and middle countries have similar ψ ’s and economic-lights structure. However in the next line in the bottom part of the table, Bruesch-Pagan tests indicate heteroskedasticity in the residuals between the two groups of countries. Given that, the third line reports results of a simple regression of squared residuals (${(z-\widehat{\psi }x)}^2$) for each column for the model in the top part of the table on a constant term and a dummy variable for good data countries. This asks whether the ${\sigma }_z^2$ in $\mathrm{var}(z-\widehat{\psi }x)=[{\sigma }_y^2-{\beta }^2{\sigma }_y^4∕\mathrm{var}(x\left)\right]+{\sigma }_z^2$ differs for good data countries; that is, whether ${\sigma }_{z,b}^2>{\sigma }_{z,g}^2$. In columns 1 and 2 the differential for good data countries is negative and significant; in the third column the point estimate is also negative but insignificant.

It is also interesting to do a finer cut on good data countries, to look at all the best data low-middle income countries, those with a rating greater than 6 (as opposed to just greater than 3). Following the Table 4 column format, we regress the squared residuals on a constant and 2 dummy variables: 1) if a country has a rating of 4-6 and 2) if it has one 7 or more. The constant term [s.e.] and coefficient [s.e.] on the dummy variable for 7 or more are respectively for the fixed effect, trend and long difference cases: {0.016 (.0014); −0.0101 (0.0021)}; {0.0068 (0.0008); −0.0044 (0.0013)}; and {0.068 (.016); −0.041 (.023)}. ¹⁵ That is, relative to bad data countries (the constant term), the best data countries on average have squared residuals that are less than half those of bad data countries. The data fits the best data countries well, noting however this is all applied to a limited number of countries. In sum, given the evidence, we proceed under the assumption that bad data countries have a higher ${\sigma }_z^2$ in equation (12) and a lower signal to total variance ratio, φ, in equation (10), (i.e. φ_b < φ_g).

4. Improving estimates of true GDP growth

As an application of the model we turn to the issue of how to augment measured GDP growth data with lights data to obtain an improved estimate of true income growth. The sample we use is the 113 low-middle income countries whose statistical capacity is rated by the World Bank and who have GDP data for 1992/93 and 2005/06. We focus on the set of 30 bad data countries whose ratings are between 0 and 3 (out of 10), but also examine the rest of low-middle income countries.

To solve the model, as presented in Section 2, we impose the same economic-lights structure, or use the moments (9b) and (9c) for all 113 countries together. We also solved the model treating bad countries as having a separate economic-lights structure. We comment on these latter results, but they are very similar to what we present for the overall sample. We use (12a) as applied to the 83 good data countries and (12b) as applied to the 30 bad data countries, where ${\sigma }_{z,b}^2>{\sigma }_{z,g}^2$. To close the model we assume a specific φ_g for good data countries in (10) which together with (12a) gives us ${\sigma }_y^2$ and ${\sigma }_{z,g}^2$, which in turn defines ${\sigma }_{z,b}^2$ in (12b) and φ_b in (10). Given ${\sigma }_y^2$, the moments (9a) and (9b) define the rest of the parameters of the model, including β. Given all the parameters, we can then solve for the weights on measured GDP growth and predicted GDP growth from lights for both good and bad data countries to use in getting an improved estimate of true income growth, $\widehat{y}$, in equation (5). In equation (5), for good [bad] data countries λ_g [λ_b] is the weight on measured GDP growth.

Table 5 presents some basic calculations. We do the calculations for different assumed values of signal to total variance ratios for good data countries, φ_g, looking at φ_g = 1, 0.9, 0.8,0.7 and 0.6. For these values of φ_g, the implied weights on measured income for good data countries are respectively 1, 0.85, 0.71, 0.58, and 0.45, indicating that the measured income weight drops off sharply as the signal to total variance ratio declines somewhat modestly. For the same φ_g ’s the implied φ_b ’s are 0.66, 0.59, 0.53, 0.46 and 0.40 and implied λ_b ’s are 0.56, 0.48, 0.41, 0.33, and 0.26 respectively. By construction bad data countries have much lower signal to total variance ratios and weights for measured income. The resulting β ’s vary from 1.03 to 1.72.

Table 5. Solving the statistical model.

30 bad data countries, 83 good data countries

Signal to total variance of measured income		Structural effect of true income growth on lights growth	Weight for measured income growth in calculation of true growth
Good data countries: ψg	Bad data countries: ψb	β	Good data countries: λg	Bad data countries: λb
1	0.660	1.032	1.0	0.563
0.9	0.594	1.147	0.852	0.484
0.8	0.528	1.290	0.710	0.407
0.7	0.462	1.474	0.575	0.333
0.6	0.396	1.720	0.449	0.262

In the next section, we will present our estimates of true income growth for the bad data countries for the case in row 2 of Table 5 where φ_g =0.9 and hence φ_b =0.594. Since we focus on this case, we note the full set of results for it. In particular, Table 5 tells us that for this case β = 1.15; and we note that ${\sigma }_y^2=0.054$, ${\sigma }_{z,g}^2=0.006$, ${\sigma }_{z,b}^2=0.037$, ${\sigma }_x^2=0.127$.

β = 1.15 is the “structural” elasticity of lights growth with respect to income growth, an elasticity that is close to one, so that the long term rate of lights growth approximately equals the long term rate of true income growth. This estimate of β for this case is from a specification where we assume a common economic-lights structure across all low-middle income countries, so that we pool all low-middle income countries in using the moments (9a) and (9b). If we assumed poor data countries have a different economic structure from good ones, solved the model by using (9a)-(9c) applied just to those 31 countries, and specified φ_b=0.594 in (10), we would calculate β = 1.50 and λ_b = 0.48. That β is higher than the estimate in Table 5 but based on a very small sample. When we bootstrap its standard errors, the estimate in Table 5 is well within its confidence interval.

4.1 Estimates of true income growth for bad data low-middle income countries

For our 30 bad data countries, following row 2 of Table 5, we apply the weight 0.48 to the reported GDP growth rates in local currency units and a weight of 0.52 to our fitted values from equation (3), to get an estimate of the average annual growth rate of true income, $\widehat{y}$, for each of the 30 countries. For good data countries, the corresponding weight on measured income is 0.85. Under that measured income weight for good data countries, measured and true income growth estimates are very close, so we don’t report on them.

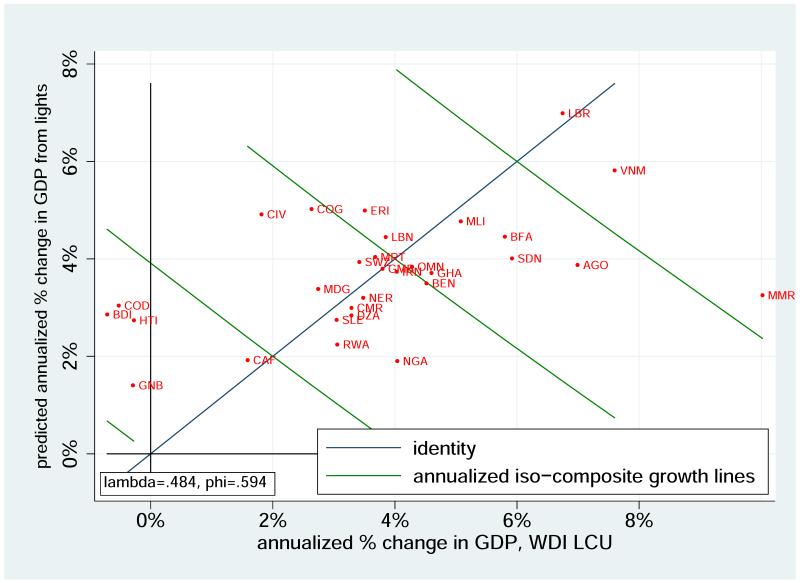
For bad data countries, in Table 6, for comparison, we report measured income growth, predicted income growth from lights and our estimate of true income growth. We also report the difference between our estimate of the true growth rate and the official WDI growth rate. Figure 7 presents a graphical version of the comparison. The horizontal axis records the annualized growth rate of GDP over the decade as measured in the WDI while the vertical axis shows the same thing as measured by the lights data. Points near the 45 degree line in Figure 7 are countries where the two measures give similar results. The further above (below) the 45 degree line is a data point, the higher (lower) is growth in lights data in comparison to growth in the WDI data. The figure also shows a set of iso-composite growth lines, where each iso-composite growth line shows the combinations of lights and WDI based growth rates for which our calculated true growth rate is the same. The slope of these iso-composite growth lines (but not the position of the data points on the graph) will vary with the assumed value of λ_b ; as the weights on lights based growth rates decline, lines become steeper but the points at which they intersect the 45 degree line do not change.

Table 6. Average annual growth rates in true income, for bad data countries (1992/93-2005/06).

Country	ISO code	WDI LCU)	fitted lights	optimal combination of WDI and fitted lights	difference
Myanmar	MMR	10.02%	3.25%	6.47%	−3.22%
Angola	AGO	6.99%	3.88%	5.37%	−1.51%
Nigeria	NGA	4.04%	1.90%	2.93%	−1.07%
Sudan	SDN	5.92%	4.01%	4.93%	−0.94%
Vietnam	VNM	7.60%	5.82%	6.67%	−0.86%
Burkina Faso	BFA	5.80%	4.46%	5.10%	−0.66%
Benin	BEN	4.52%	3.50%	3.99%	−0.50%
Ghana	GHA	4.60%	3.71%	4.14%	−0.44%
Rwanda	RWA	3.06%	2.24%	2.63%	−0.41%
Algeria	DZA	3.29%	2.84%	3.06%	−0.22%
Oman	OMN	4.28%	3.84%	4.05%	−0.22%
Mali	MLI	5.08%	4.77%	4.92%	−0.15%
Sierra Leone	SLE	3.04%	2.75%	2.89%	−0.15%
Cameroon	CMR	3.29%	2.99%	3.14%	−0.15%
Iran, Islamic Rep.	IRN	4.03%	3.74%	3.88%	−0.15%
Niger	NER	3.48%	3.20%	3.34%	−0.14%
Gambia, The	GMB	3.80%	3.80%	3.80%	0.00%
Liberia	LBR	6.75%	6.99%	6.87%	0.12%
Central African
Republic	CAF	1.59%	1.92%	1.76%	0.17%
Mauritania	MRT	3.68%	4.04%	3.86%	0.18%
Swaziland	SWZ	3.42%	3.94%	3.69%	0.26%
Lebanon	LBN	3.85%	4.45%	4.16%	0.30%
Madagascar	MDG	2.74%	3.38%	3.07%	0.32%
Eritrea	ERI	3.51%	4.99%	4.27%	0.74%
Guinea-Bissau	GNB	−0.29%	1.41%	0.58%	0.88%
Congo, Rep.	COG	2.63%	5.02%	3.86%	1.20%
Haiti	HTI	−0.28%	2.74%	1.27%	1.55%
Cote d'lvoire	CIV	1.82%	4.91%	3.40%	1.56%
Congo, Dem. Rep.	COD	−0.52%	3.04%	1.30%	1.83%
Burundi	BDI	−0.71%	2.86%	1.12%	1.84%

Figure 7.

Growth in fitted lights vs. WDI for WBDQ<3.5 countries 1992–2006

The figure and table suggest that, as would be predicted by a standard analysis of measurement error, growth is more likely to be underestimated in the WDI for countries with low measured income growth rates, and overestimated in the WDI for some countries showing very high growth rates. But there is a lot of variation across countries in the adjustment. By reading the true growth rates versus WDI and lights based numbers in Table 6 or by viewing the divergence between the WDI versus lights based numbers in Figure 7, one can see, that after adjustment, countries like the Republic of Congo (COG), Cote d’Ivoire (CIV), and Haiti (HTI) have noticeably higher growth rates, while the number for The Gambia (GMB) is the same. We somewhat downgrade certain higher growth rate countries like Angola (AGO) and Nigeria (NGA) but not Liberia (LBR) or Mali (MLI).

For these bad data countries at the tails of high or low recorded growth such as Myanmar (MMR) and Burundi (BDI), we strongly amend recorded growth rates. For example, in Burundi, the WDI data imply an annual average growth of GDP of −0.71% per year while the satellite data imply growth of 2.86% per year. The optimally weighted average is 1.12%. In Myanmar, the WDI data say that GDP grew at an annual rate of 10.0% while the lights data imply an annual growth rate of 3.2%. In both these cases, there is reason, beyond the night lights data, to suspect that GDP is particularly poorly measured in the WDI. Burundi experienced civil war and reconstruction for much of the period for which we have satellite data, while the economy in Myanmar was largely autarkic and non-market, with a governing regime that would not be averse to exaggerating GDP growth.

4.2 Elasticity of Light with Respect to Income

Our focus in this paper is on producing improved estimates of GDP growth in countries with bad data and on producing estimates of GDP growth for subnational regions. However, a byproduct of this procedure, interesting in its own right, is the estimate of the elasticity of light with respect to income. As discussed above, the parameter $\widehat{\psi }$ is a biased estimate of the inverse of this elasticity. However, using the auxiliary assumptions about measurement error required to form proxies for income growth, we also produce direct estimates of the elasticity, β. For a high signal to total variance ratio which we expect in good data countries, the elasticities in column 3 of Table 5 are close to one. Recall also as reported earlier and in the Appendix, for a limited sample, the estimated elasticity of true radiance with respect to night lights is close to one. This implies that the elasticity of true radiance with respect to GDP is also close to one.

We can think of mechanisms that would tend to push the elasticity both higher and lower than one. There are large fixed costs associated with electricity distribution, which could lead to a convex relationship between income and light output around some income threshold, and thus an elasticity greater than one. On the other hand, there could be diminution in the rate of increase of light as income rises. For example, with more urbanization there is a greater likelihood of people living above one another, so that some light is blocked from reaching space; and there may be economies of scale in the use of lights, such as street lamps. These factors would, a priori, produce an elasticity lower than one. Regardless, for low and middle income countries, it appears that using an elasticity of one between true income and true light growth is reasonable.

5. Additional Applications

As discussed above, one natural application of the night lights data is to improve estimates of GDP growth at the national level. However, night lights data are also well suited to looking at growth in both sub-national regions and in spatial groupings that cross national borders. In these cases typically no reliable real income data are available on a consistent basis. Thus night lights data allow us to broaden the set of questions researchers investigate. The recent rapid development of spatially based analytical tools and datasets points to a number of research directions in which empirical growth analysis need no longer be tied exclusively to availability of national income data.

To illustrate this point, we apply the night lights data to growth issues that require subnational data but go beyond national borders. The application is to sub-Saharan Africa, where alternative sources of data are of lowest quality and where the issues we look at are compelling.¹⁶ The issues concern coastal versus non-coastal growth (Gallup, Sachs, and Mellinger, 1999), primate city versus hinterland growth (Ades and Glaeser, 1995 and Davis and Henderson, 2004), and growth in malarial versus non-malarial areas (Weil, 2010). In addressing these issues, we are not trying to resolve particular debates, since that would require much more detailed analysis. Instead we provide a few facts about where growth is occurring in sub-Saharan Africa overall, from which further analyses could proceed.

For each of our three cases, we start by dividing up the continent into two or more zones (e.g., coastal versus non-coastal) based on a particular criterion. We then sum the digital number for all pixels in each zone and look at the log difference between the average for the first two years in our data (1992 and 1993) and the last two years (2007 and 2008). We then compare this log change across zones. This procedure implicitly allows for both zone and time fixed effects. Note that we are able to include an extra two years of data, in comparison to the analysis in Section 4 of the paper, because we are not constrained to look at years in which GDP data are available.

The issue of light from gas flares, mentioned above in the context of our global regressions, is particularly acute in sub-Saharan Africa. Recall that for the world as a whole, polygons containing gas flares represented 1.0% of land area, 0.34% of population, 3.6% of light emanation. For sub-Saharan Africa as we have defined it, these figures (for the year 2000) are 0.22% of land area, 1.5% of population, and 30.2% of light emanation.¹⁷ For this reason, we conduct our analysis in this section excluding areas with gas flaring.

5.1 Growth on the Coast vs. in the Interior

Mellinger, Sachs, and Gallup (2000) report that the 49.9% of the world’s population that lives within 100 kilometers of the ocean or of an ocean-navigable waterway produces 67.6% of world GDP – twice the level of GDP per capita of people who live away from the sea. Gallup, Sachs, and Mellinger (1999) find that the fraction of a country’s population that lives within 100 km of an ocean or ocean-navigable river has a significantly negative coefficient in a standard growth regression. They follow Adam Smith in arguing that distance from the ocean means that some regions are excluded from the opportunity to reap benefits from trade, and thus impeded in their ability to develop economically. In their work, population data are widely available for sub-national regions that can mapped into the geographic categories that they define. But sub-national income data were available for only 19 of 152 countries in their sample, almost all of them wealthy.

We revisit this issue for Sub-Saharan Africa with its 15 landlocked countries and poor quality road system linking interior areas to the coast (Buys et al., 2010). During the period for which we have lights data, world trade volume increased by a factor of 2.5, making the examination particularly compelling. We are thus interested in the relative performance of regions with and without access to the sea over this period.

To generate the coastal variable, we started with the 100-km buffer of coastlines and navigable rivers from Mellinger, Sachs, and Gallup (2000). Because their coastlines didn’t line up exactly with ours, we added all areas that fell in the ocean in their classification to our coastal zone. Our finding is that, in sub-Saharan Africa, inland lights grew 0.133 log points more than coastal areas over the 15 year period 1992/93 to 2007/08. Using the $\widehat{\psi }$ coefficient of 0.329 from the long difference estimation in column 3 of Table 4, the lights data imply that the increase in total GDP inland was 4.4% greater than on the coast – a difference of 1/3 of a percent per year. While we cannot say anything about the long-run benefits over centuries of being on the coast, during a period of rapidly growing trade, coastal areas in Africa grew more slowly than non-coastal areas. There may be a number of competing explanations for this, including the new economic geography debate about whether increases in external trade benefit coastal versus interior areas (Fujita et al., 1999). The supposedly inherent advantage of coastal location for growth in this period in sub-Saharan Africa does not dominate other forces that may have been at work.

5.2 Primate Cities vs. Hinterland

Increased urbanization is an integral part of economic growth. However, over the past several decades, many observers have argued that in the context of developing world, there has been an unhealthy focus of growth in very large, dominant cities, which are known as “primate cities.” In particular it is noted that in many developing countries, the largest city is disproportionately large in comparison to the rest of the distribution of city sizes. This size discrepancy is believed to result from superior provision of public goods and opportunities for rent seeking (Ades and Glaeser, 1995 and Davis and Henderson, 2004). Henderson (2003) provides empirical evidence that economic growth in developing countries is slowed by over-concentration of cities, although, because of data requirements there are almost no sub-Saharan African cities in his sample. Duranton (2009), summarizing this literature, concludes that “The potentially large misallocation of resources associated with primate cities suggests that policies to reduce urban primacy are needed.”

We ask how the growth of primate cities has compared to growth in other places (either non-primate cities or rural areas) for the period for which we have data. For our analysis, we define primate cities as follows. First, lights are summed across all satellite-years. Contiguously lit polygons are defined based on this set of summed lights. Then we use data from a gazetteer of city populations in which cities are defined as points in longitude-latitude space. We add up the populations of all city points that fall within three kilometers of the polygon border (this buffer allows for measurement error in locations). The polygon with the highest population in each country is designated as the primate city. The remainder of each country is designated as hinterland. ¹⁸ Again we are doing an aggregate comparison across the nations of sub-Saharan Africa to see what the overall differential growth pattern has been in this time period.

The change in log digital number was .029 larger in hinterland areas than primate cities. Again using the $\widehat{\psi }$ coefficient from Table 4, column 3, this differential translates into a tiny (1% over 15 years) difference in GDP growth between the two types of areas. A detailed study would be required to explain the result. It could be that primate cities have reached the point of strong diminishing returns to scale. Perhaps less likely, it might be that sub-Saharan African countries have increased their relative investment in hinterland areas compared to primate cities. Regardless of whether sub-Saharan countries are continuing to favor primate cities in policy making, hinterland areas are growing at least as fast as primate cities. Of course if primate cities have continued to be heavily favored in this time period, this suggests that the money is being wasted—it is not producing higher growth rates.

5.3 The Effect of Malaria on Growth

An extensive literature examines the effect of disease in general, and malaria in particular, on economic growth in sub-Saharan Africa. Although the negative correlation between income levels and malaria prevalence is striking, the existence of a causal link from malaria to underdevelopment is a highly contentious issue (see Weil, 2010, for a discussion of the literature). Because our methodology looks only at recent growth, we cannot address the question of whether malaria has been a source of underdevelopment over the centuries. However, the period for which we have satellite data, especially the second half of it, corresponds to a renewed effort on the part of the international community and affected states to combat the disease. The Roll Back Malaria Partnership, bringing together key international agencies, was launched in 1998. This was followed by a significant increase in resources devoted to the disease. For example, international funding disbursements for malaria increased by a factor of 2.8 from 2004 to 2007 (Roll Back Malaria, 2008). New technologies, such as long-lasting insecticide treated bed nets and artemisinin-based combination therapy were introduced over this period. Thus, one might like to know how growth has differed between regions with high and low malaria prevalence over this time period. If growth were higher in areas with historically high malaria prevalence, that might be taken as evidence that the anti-malaria campaign has borne economic as well as humanitarian fruit.

As our measure of malaria prevalence, we use an index developed by Kiszewski et al (2004). This measure assigns to each grid square (one half degree longitude by one half degree latitude) a value corresponding to the stability of malaria transmission, which in turn is based on data about climactic factors and the dominant vector species. For our analysis, we generated quartiles from the original distribution for the sample region.¹⁹ We then compared growth rates in each other quartile to the first (lowest index) quartile. Our findings are that the second quartile grew 0.146 log points less; the third grew 0.324 points less; and the fourth 0.184 points less than the first quartile. These relative gaps are experienced more in the 2000-2008 time period after the start of the malarial initiatives than before 2000. These gaps translate to annual income growth differences relative to the first quartile of between 1/3 and 2/3 percent per year. However might one think of these gaps, apart from the notion that being non-malarial is still helpful despite anti-malarial campaigns? Malarial quartiles may differ in other ways. For example the lowest prevalence quartile includes many low density arid areas. The application of anti-malaria programs may also have differed across quartiles. Nonetheless these facts are not encouraging.

6. Conclusion

Satellite night-lights data are a useful proxy for economic activity at temporal and geographic scales for which traditional data are of poor quality or are unavailable. In this paper, we develop a statistical model to combine data on changes in night lights with data on measured income growth to improve estimates of true income growth. One assumption of the model is that measurement error in growth as depicted in the national income accounts is uncorrelated with the measurement error that occurs when the change in light is used to measure growth. While there are many potential sources of error in using lights growth to measure income growth, none of them suggest this assumption is inappropriate. But if one wanted to, the framework could be adjusted to allow for such correlation.

Our methodology involves estimating both a coefficient that maps light growth into a proxy for GDP growth and also an optimal weight to be applied in combining this proxy with national accounts data. For countries with high-quality national accounts data, the information contained in lights growth is of little value in improving income growth measures. However, for countries with low-quality national accounts data, the optimal composite estimate puts roughly equal weight on lights growth and national accounts data. We apply the methodology to low and middle income countries with very low quality national accounts data, as rated by the World Bank. For these 30 countries, we get a new set of income growth numbers for the years 1992/3–2005/6. These estimates differ from measured WDI real GDP growth numbers by up to 3.2% per year. We also estimate that among low and middle income countries, the elasticity of growth of light emanating into space with respect to income growth is close to one.

For all countries, lights data can play a key role in analyzing growth at sub- and supranational levels, where income data at a detailed spatial level are unavailable. To illustrate this and build on the theme that research directions in empirical growth need no longer be synonymous with national income accounts data, we examine three issues in growth analysis applied to sub-Saharan Africa. We look at whether over the last 17 years coastal areas have grown faster than non-coastal areas; whether primate cities have grown faster than hinterlands; and whether malarial areas have had a better growth experience compared to non-malarial areas. The answer to all these questions is no, which leaves for future research the question of why.

Appendix: Data

Lights

The Version 4 Defense Meteorological Satellite Program Optical Linescan System (DMSP-OLS) Nighttime Lights Time Series data used in this paper are available from the National Oceanic and Atmospheric Administration’s (NOAA) National Geophysical Data Center (NGDC) .²⁰ Key aspects of the data are discussed in the text. Here we give more details of a few of these aspects. The first has to do with the light that is recorded. As noted in the text, the sensor saturates at a level of light that is common in the cities of rich countries, resulting in top-coded values. At high latitudes no summer data can be used because sunlight is still contaminating images at local pass times of 8:30 to 10 pm. This effect is diminished closer to the equator. The data are subject to overglow or blooming, which means that lights tend to appear larger than they actually are, especially for bright lights and over water. Snow tends to magnify light values. Humidity is known to affect the performance of other sensors but has never been studied in relation to the DMSP-OLS. Many of these problems are not likely to be important in poorer countries, as there are few instances of top-coding, and many are tropical countries with no long summer nights, and virtually no snow in populated areas. In addition to spatial coverage and resolution, sensors also have spectral range and resolution. The DMSP-OLS sensor covers the visual-near infrared portion of the spectrum, from 500 to 900 nanometers. Different lighting technologies have different emissions profiles, but they all have substantial emissions in this range, because the human eye can only see radiation between approximately 380 and 750 nanometers. Further details about the lights data and processing can be found in Elvidge et al. (1997a, 1999, 2003, 2005, 2010), Lieske (1981), and Small et al. (2005).

Across all 30 satellite years, an average of 2.7% of land-based pixels, representing 1.5% of land area, are missing data for entire satellite-years. As noted in the text, they are overwhelmingly at high latitudes, which is why we exclude areas above the Arctic Circle. Below the Arctic Circle, this phenomenon affects pixels representing 0.45% percent of land area. We exclude 23 country-years in which at least one constituent country-satellite year was missing data for at least 5% of its land area.

Because de facto sensor setting may vary across satellites and as a satellite ages, Elvidge et al. (2009) perform an “intercalibration”, relating the different satellite years of data to each other, without tying them directly to physical quantities, based on the identifying assumption that lights in Sicily did not change between 1994 and 2008. Rather than use the formulas in Elvidge et al. (2009) to do that specific intercalibration, in statistical work we control for these problems with year fixed effects, which we find to be more readily interpretable.

As briefly reported in the text, in an experiment carried out for 18 days during the winters of 1996 and 1997, the settings of one of the satellites were altered so that a true radiance measure could be calculated with no top-coding (Elvidge et al. 1999). Settings alternated across these nights between low and high magnification in order to capture both intense and weak lighting. The resulting experimental radiance-calibrated dataset, averaged across all 18 days, is also distributed by NGDC. After a scaling factor is applied, each 30 arc-second pixel reports the radiance in Watts per cm² per steradian.

Since the grid for the radiance calibrated data is in principle the same as that for the annual composites, individual pixels can be compared across datasets. However, the real-world location of each pixel is measured with an error of approximately 2 km (Elvidge et al. 2004), so that the pixels in the two data sets don’t exactly overlap. In Table A1, column 1, we report the results of a regression of the log of digital number from the most comparable of the 30 uncalibrated datasets (F-12, 1997) on the log of radiance, for the 8.6 million cells that are lit in both datasets. The elasticity is 0.587. We expect the elasticity is biased downwards because of measurement error from pixels not exactly overlapping. In the remaining columns, we run the same regressions after aggregating all lit cells into larger square cells, with the linear scale factor noted. So in column 2, 2-by-2 arrays of the original cells are merged to become cells with four times the original cell area, and in column 3, 5-by-5 arrays are formed. By column 3, there are still over six hundred thousand cells, but the elasticity now is close to one. Additional aggregation doesn’t change the elasticity much.

Table A1. Radiance versus digital numbers.

	(1) F-12 DN	(2) F-12 DN	(3) F-12 DN	(4) F-12 DN	(5) F-12 DN	(6) F-12 DN	(7) F-12 DN	(8) F-12 DN
Radiance	0.587*** [0.00020]	0.79876*** [0.00039]	0.94694*** [0.00058]	0.97767*** [0.00072]	0.98090*** [0.00092]	0.97117*** [0.00125]	0.95957*** [0.00174]	0.95548*** [0.00198]
Constant	0.674*** [0.00076]	0.05970*** [0.00187]	0.62278*** [0.00333]	0.78730*** [0.00474]	0.78213*** [0.00679]	0.67790*** [0.01028]	0.55325*** [0.01599]	0.50717*** [0.01888]
Observations	8657670	2590447	606988	229774	93423	38013	14792	10848
R-squared	0.47	0.678	0.862	0.917	0.944	0.958	0.966	0.969
linear scale factor	1	2	5	10	20	40	80	100

Table A2. Summary statistics.

variable	mean	sd	min	Max	count	sample
ln(lights)	−0.0645	2.0364	−5.9498	3.8753	3014	full
ln(GDP, LCU)	25.2829	4.0326	0.3811	35.2722	3014	full
ln(electricity use)	23.5009	1.9024	18.5946	29.0303	1853	full
fraction topcoded	0.0030	0.0126	0.0000	0.2204	3014	full
fraction unlit	0.7123	0.3246	0.0000	0.9998	3014	full
spatial gini	0.8255	0.2020	0.1662	0.9999	3014	full
ln(lights)	−0.6927	1.8768	−5.9498	3.0628	1953	low-middle income
ln(GDP, LCU)	25.9829	4.0438	0.3811	35.2722	1953	low-middle income
ln(lights)	−1.8696	1.9654	−5.4424	3.0628	541	low-middle income, DQ score 0-3
ln(GDP, LCU)	24.8654	5.9608	0.3811	33.8656	541	low-middle income, DQ score 0-3
delta ln(lights)	0.3385	0.4017	−1.0390	1.9036	170	full
delta ln(GDP, LCU)	0.4600	0.2441	−0.1624	1.2415	170	full
delta ln(lights)	0.3823	0.4348	−1.0390	1.9036	113	low-middle income
delta ln(GDP, LCU)	0.4904	0.2605	−0.1624	1.2415	113	low-middle income
delta ln(lights)	0.4106	0.5447	−0.6379	1.9036	30	low-middle income, DQ score 0-3
delta ln(GDP, LCU)	0.4689	0.3021	−0.0928	1.2415	30	low-middle income, DQ score 0-3