Gradient-based high precision alignment of cryo-electron subtomograms

Abstract

Whole cell cryo-electron tomography emerges as an important component for structural system biology approaches. It allows the localization and structural characterization of macromolecular complexes in near living conditions. However, the method is hampered by low resolution, missing data and low signal-to-noise ratio (SNR). To overcome some of these difficulties one can align and average a large set of subtomograms. Existing alignment methods are mostly based on an exhaustive scanning and sampling of all but discrete relative rotations and translations of one subtomogram with respect to the other. In this paper, we propose a gradient-guided alignment method based on two subtomogram similarity measures. We also propose a stochastic parallel optimization that increases significantly the efficiency for the simultaneous refinement of a set of alignment candidates. Results on simulated data of model complexes and experimental structures of protein complexes show that even for highly distorted subtomograms and with only a small number of very sparsely distributed initial alignment seeds, our method can accurately recover true transformations with a significantly higher precision than scanning based alignment methods.

I. Introduction

Whole cell cryo-electron tomography emerges as an important component for structural system biology approaches [1], [2]. Cryo-electron tomograms of whole cells essentially contain information on the systems level about the abundance, spatial distributions and orientations of all large macromolecular complexes at a given time point in a cell [3], [4], [5], [6]. However, detecting these complexes in whole-cell cryo-electron tomograms is a challenging task due to low signal-to-noise ratio (SNR), distortions and low non-isotropic resolution (> 5 nm) of the tomograms [6]. Therefore traditional image registration methods derived for low distortion images usually cannot be applied to alignment of subtomograms. One strategy is to segment the tomogram into a large number of single complex subtomograms, which are then classified into like objects by a pair-wise comparison to each other. After subtomogram classification averaging of the aligned subtomograms in each class reveals the shapes of macromolecular complexes in each class at an increased SNR, which can then be assigned to the corresponding positions in the whole cell tomogram.

Subtomogram alignment methods are key to such processes and have been applied to several complexes, including membrane-bound complexes [7], [8]. However, due to the potentially large number of subtomograms in whole cell tomo-grams alignment protocols must not only be precise but also computationally very efficient. Existing alignment methods are typically based on the exhaustive sampling over discrete sets of rotations and translations of one subtomogram with respect to a second. The optimal alignment is then detected using the cross-correlation similarity measure between both subtomograms [9], [10]. However, due to the heavy computational cost, the exhaustive rotational search can only sample a limited number of angles. Moreover the typically applied Fast Fourier Transform (FFT) based translational alignment can only approximate best translations at the resolution of the unit voxels. To enhance computational efficiency an approximate alignment method has been proposed to generate alignment candidates based on a fast translation-invariant rotational search [11]. Then a local refinement was used starting from the alignment candidates close to the optimal solution. However, the full potential of purely using local refinement on very sparsely distributed starting candidates has not been investigated yet. In this paper, we propose an efficient gradient-guided alignment method based on two subtomogram dissimilarity scores. In addition, we design a stochastic parallel framework that significantly speeds up the simultaneous refinement of multiple alignment candidates.

We demonstrate on realistically simulated data of models and real macromolecular structures that for highly distorted subtomograms, even given a small number of evenly sampled initial angles with a large interval of 60°, our method can accurately recover true transformation with very high precision.

II. Methods

Here we provide a gradient-guided refinement framework for subtomogram alignment that minimizes a dissimilarity score defined by the squared sum of the differences between a parameter fixed function and a function whose parameters are optimized. We consider two types of dissimilarity scores for subtomogram alignment, which both incorporate missing wedge corrections. A real space constrained dissimilarity score (Section II-B) and a Fourier space constrained dissimilarity score (Section II-D). In principle one would like to refine each of the solutions independently, however this is computationally expensive and not feasible for large scale subtomogram classifications necessary in whole cell tomography. We therefore provide also a stochastic parallel refinement framework (Section II-C) to efficiently reduce the total number of refinement steps.

A. Parameter definitions

For simplicity, we denote two subtomograms as two integrable functions $f,g:{\mathbb{R}}^3\to \mathbb{R}$. For $\mathbf{a}\in {\mathbb{R}}^3$, let τ_a be the translation operator (τ_ag)(x) := g(x – a). For a rotation R in the three-dimensional rotational group SO(3), let Λ_R be the rotation operator, such that (Λ_Rg)(x) := g[R⁻¹(x)]. R can be represented as a 3 by 3 rotation matrix R. In this case, (τ_aΛ_Rg)(x) = g(R⁻¹(x – a)).

The collection of linear transformation parameters combining both rotation and translation can be expressed as β = (R, a) = (φ, θ, ψ, a₁, a₂, a₃)^T, where (φ, θ, ψ)^T are Euler angles with the ’ZYZ’ convention [12] to correspond rotation R, and translation parameters a = (a₁, a₂, a₃)^T. In addition, for simplicity, we denote the combined linear transform operator κ_β := τ_aΛ_R.

B. Local optimization of subtomogram alignment based on a real space constrained dissimilarity score (RCS)

We now describe the refinement of the subtomogram alignment, given a coarse solution for R and a. The goal is to identify the exact solution given the current values of R and a as starting parameters. To perform the scoring one must define a dissimilarity measure for the alignment of the two subtomograms. Besides the low resolution and SNR of subtomograms, distortions due to missing data (ie, the missing wedge effect) make subtomogram alignment challenging, and these effects must be explicitly considered in the alignment process.

To address this problem, Förster et al proposed a constrained correlation measure with missing wedge corrections [9]. It is based on a transform that eliminates the coefficients in the missing wedge region. Let $\mathcal{M}:{\mathbb{R}}^3\to \{0,1\}$ be a missing wedge mask function that defines valid and missing Fourier coefficients. Then for a given subtomogram f one can define a modified subtomogram function $f_1≔\Re \left\{{\mathcal{F}}^{-1}\left[\left(\mathcal{F}f\right)\mathcal{M}\left({\Lambda }_R\mathcal{M}\right)\right]\right\}$, where ℜ denotes the real part a complex function, and $\mathcal{F}$ is the Fourier transform operator. Correspondingly, a modified subtomgram function for the second subtomogram g is defined as $g_1:=\Re \left\{{\mathcal{F}}^{-1}\left[\left(\mathcal{F}{\tau }_{\mathbf{a}}{\Lambda }_{R}g\right)\mathcal{M}\left({\Lambda }_R\mathcal{M}\right)\right]\right\}$.

The normalized subtomogram transforms can be defined as $\mathcal{N}f:=\frac{f_1-\mu \left(f_1\right)}{\sqrt{\int {(f_1-\mu \left(f_1\right))}^2}}$ and ${\mathcal{N}}_{{\kappa }_{\beta }}g≔\frac{g_1-\upsilon \left(g_1\right)}{\sqrt{\int {(g_1-\mu \left(g_1\right))}^2}}$ where μ is the mean operator, defined as $\mu f=\frac{\int f\left(\mathbf{x}\right)}{\mathcal{S}f}$, and $\mathcal{S}f$ denotes the size of the subtomogram f. μf is therefore the average intensity value of subtomogram f.

Then the constrained correlation is calculated as

$$c≔\int \mathcal{N}f{\mathcal{N}}_{{\kappa }_{\beta }}g$$ (1)

Because of the subtomogram normalization, this constrained correlation is equivalent to a constrained dissimilarity score:

$$d_{\beta }^{\mathrm{F}}≔\int {\mid \mathcal{N}f-{\mathcal{N}}_{{\kappa }_{\beta }}g\mid }^2=2-2c$$ (2)

For a given initial guess of the rotation R (for instance one of the local minima in a rotational search) one can determine the corresponding best translation τ_a that minimizes the distance criteria d efficiently using Fast Fourier Transform (FFT)). Given any initial Λ_R and τ_a, we seek to obtain an increment Λ_ΔR and corresponding τ_Δa so that

$$d_{({\Lambda }_{\Delta R}{\Lambda }_R,{\tau }_{\Delta \mathbf{a}}{\tau }_{\mathbf{a}})}^{\mathrm{F}}\le d_{({\Lambda }_R,{\tau }_{\mathbf{a}})}^{\mathrm{F}}$$ (3)

Since $\mathcal{N}f$ is fixed with respect to β, we use the Levenberg-Marquardt algorithm [13] to obtain such increments. This algorithm converges very fast.

Let x_j, j = 1 . . . n be the locations of all n voxels in the grid of the subtomogram, then we have a discrete form of the constrained dissimilarity score

$$\widetilde{d_{\beta }^{\mathrm{F}}}≔\sum _j{[\left(\mathcal{N}f\right)\left({\mathbf{x}}_j\right)-\left({\mathcal{N}}_{{\kappa }_{\beta }}g\right)\left({\mathbf{x}}_j\right)]}^2$$ (4)

According to the Levenberg-Marquardt algorithm, Δβ = (ΔR, Δa) can be obtained by computing

$$\Delta \beta ={({\mathbf{J}}^T\mathbf{J}+\lambda \mathrm{diag}{\mathbf{J}}^T\mathbf{J})}^{-1}{\mathbf{J}}^T(\mathbf{f}-{\mathbf{g}}_{\beta })$$ (5)

Here f and g_β are vector representations

$$\mathbf{f}={(\left(\mathcal{N}f\right)\left({\mathbf{x}}_1\right),\dots ,\left(\mathcal{N}f\right)\left({\mathbf{x}}_n\right))}^T$$ (6)

and

$${\mathbf{g}}_{\beta }={(\left({\mathcal{N}}_{{\kappa }_{\beta }}g\right)\left({\mathbf{x}}_1\right),\dots ,\left({\mathcal{N}}_{{\kappa }_{\beta }}g\right)\left({\mathbf{x}}_n\right))}^T$$ (7)

J is the Jacobian matrix whose jth row is $\frac{\partial \left({\mathcal{N}}_{\beta }g\right)\left({\mathbf{x}}_j\right)}{\partial \beta }$, which is approximated by numerical differentiation; λ is a damping factor to control the rate of convergence.

The final result of this section provides the refined alignment parameters R₂ = R₁ + ΔR₁ and a₂ = a₁ + Δa₁ given the initial parameter set R₁ and a₁. To perform a complete refinement this process must be repeated iteratively until convergence is achieved (next section).

C. Stochastic parallel refinement process

To carry out a global optimization it is necessary to perform multiple refinement runs starting each time from a different candidate rotation angle. However, to carry out these individual optimizations independently is time consuming, which would prevent large-scale applications of subtomogram alignments. Therefore, we propose a stochastic parallel refinement framework to prioritize for those candidate transform parameters with smaller dissimilarity scores. The basic idea of this iterative algorithm is to store the scores of all m candidate transformation parameters β₁, . . . , β_m, where each β = (R, a) consists of both rotation and translation parameters. The choice of which β_j to refine next is stochastically decided according to a probability obtained from d_βj.

In other words, at each iteration candidate angles β_j with smaller d_βj compared to other d_βk, k ≠ j, have a higher probability of being selected for refinement using the incremental method described in section II-B.

We define a sampling probability that considers both rank and magnitude of d. Suppose the candidate parameters are ordered such that

$$d_{{\beta }_1}\ge \cdots \ge d_{{\beta }_m}$$ (8)

Then for j = 1 . . . m the sampling probability of β_j is proportional to p_j with

$$p_j=p_{j-1}\max ({10}^{t∕(m-1)},d_{{\beta }_{j-1}}∕d_{{\beta }_j}),\forall j=2\dots m$$ (9)

where p₁ = 1 and t is a scaling threshold such that the distinction between p_j and p_j–1 is at least 10^t/(m–1), and p_m/p₁ ≥ 10^t. The iterative process is terminated when changes in d compared to its initial value are below a given threshold.

To further enhance the computational efficiency, similar candidate transforms β are removed from the list to omit redundant optimization runs. The similarity of two transforms β_j and β_k is defined as the the Frobenius norm ∥D_βjβk∥_F, where

$${\mathbf{D}}_{{\beta }_j{\beta }_k}≔\left[{\mathbf{R}}_j^{-1}(\mathbf{I}-({\mathbf{a}}_j,{\mathbf{a}}_j,{\mathbf{a}}_j))\right]-\left[{\mathbf{R}}_k^{-1}(\mathbf{I}-({\mathbf{a}}_k,{\mathbf{a}}_k,{\mathbf{a}}_k))\right]$$ (10)

$\forall j,k=1,\dots ,m$. If ∥D_βjβk∥_F ≤ γ is lower than a predefined threshold γ, then the transform leading to the larger of the two dissimilarity scores d is removed from the target list.

To terminate the optimization process, at each iteration the ratio between the smallest and the initial minimum score is calculated. The iterative process is terminated when convergence is achieved, which is identified by a linear regression ratio over the minimal scores in last iterations. In case convergence cannot be achieved the optimization is terminated after a large number of iterations n^max_iter.

In this section we have introduced a parallel iterative refinement method that relies on a similarity measure and local optimization process as described in Section II-B. In the following section, we introduce another refinement method based on a different similarity measure between subtomograms.

D. Local optimization of subtomogram alignment based on a Fourier space constrained subtomogram dissimilarity score (FCS)

After having introduced an iterative refinement process, and introduced a dissimilarity measure in Section II-B, we now test the refinement process further with a second dissimilarity score. This new score is based on a constrained dissimilarity score computed directly in Fourier space [11]:

$$d_{\beta }^{\mathrm{B}}≔\frac{\int {\mid \left(\mathcal{F}f\right)-\left(\mathcal{F}{\tau }_{\mathbf{a}}{\Lambda }_{R}g\right)\mid }^2\mathcal{M}\left({\Lambda }_R\mathcal{M}\right)}{\int \mathcal{M}\left({\Lambda }_R\mathcal{M}\right)}$$ (11)

By properties of the Fourier transform

$$\left(\mathcal{F}{\tau }_{\mathbf{a}}{\Lambda }_{R}g\right)\left(\xi \right)=e^{-2\pi {\mathbf{a}}^{\mathsf{T}}\xi }\left({\Lambda }_R\mathcal{F}g\right)\left(\xi \right)$$ (12)

, given a fixed initial R, the initial a can be efficiently calculated using FFT. Because $d_{\beta }^{\mathrm{B}}$ is not expressed as the summed square of differences, here the Levenberg-Marquardt algorithm cannot be directly applied. However, because $\int \mathcal{M}\left({\Lambda }_R\mathcal{M}\right)$ has a regular structure containing only binary 0 and 1 values, one can approximate $d_{\beta }^{\mathrm{B}}$ as

$$d_{\beta }^{\mathrm{B}}\approx c\int {\mid \left(\mathcal{F}f\right)-\left(\mathcal{F}{\tau }_{\mathbf{a}}{\Lambda }_{R}g\right)\mid }^2\mathcal{M}\left({\Lambda }_R\mathcal{M}\right)$$ (13)

where $c≔\frac{1}{\int \mathcal{M}\left({\Lambda }_R\mathcal{M}\right)}$ is treated as a constant in the whole refinement step.

Let ξ_j, j = 1 ... n be the locations of all n voxels in the grid of the Fourier transform of the tomogram such that $\mathcal{M}\left({\Lambda }_R\mathcal{M}\right)\left({\xi }_j\right)=1$. Then a discrete form of the dissimilarity score can be formulated

$$\widetilde{d_{\beta }^{\mathrm{B}}}≔c\sum _j{\mid \left(\mathcal{F}f\right)\left({\xi }_j\right)-\left(\mathcal{F}{\kappa }_{\beta }g\right)\left({\xi }_j\right)\mid }^2$$ (14)

Because the above score is based on a complex function, the Levenberg-Marquardt algorithm cannot be directly applied. Therefore in the following section we derive a new version of the Levenberg-Marquardt algorithm for complex functions. In this version, Δβ can be obtained by computing

$$\Delta \beta ={\mathbf{A}}^{-1}\mathbf{b}$$ (15)

where

$$\mathbf{A}=[\Re {\left(\mathbf{J}\right)}^T\Re \left(\mathbf{J}\right)+\Im {\left(\mathbf{J}\right)}^T\Im \left(\mathbf{J}\right)]+\lambda \mathrm{diag}[\Re {\left(\mathbf{J}\right)}^T\Re \left(\mathbf{J}\right)+\Im {\left(\mathbf{J}\right)}^T\Im \left(\mathbf{J}\right)]$$ (16)

and where ℜ and ℑ denote real and imaginary parts and

$$\mathbf{b}=\Re {\left(\mathbf{J}\right)}^T[\Re \left(\mathbf{f}\right)-\Re \left({\mathbf{g}}_{\beta }\right)]+\Im {\left(\mathbf{J}\right)}^T[\Im \left(\mathbf{f}\right)-\Im \left({\mathbf{g}}_{\beta }\right)]$$ (17)

Here f and g_β are vector representations of Fourier transform of the two subtomograms

$$\mathbf{f}={(\left(\mathcal{F}f\right)\left({\xi }_1\right),\dots ,\left(\mathcal{F}f\right)\left({\xi }_n\right))}^T$$ (18)

and

$${\mathbf{g}}_{\beta }={(\left(\mathcal{F}{\kappa }_{\beta }g\right)\left({\xi }_1\right),\dots ,\left(\mathcal{F}{\kappa }_{\beta }g\right)\left({\xi }_n\right))}^T$$ (19)

J is the Jacobian matrix whose jth row is $\frac{\partial \left(\mathcal{F}{\kappa }_{\beta }g\right)\left({\xi }_j\right)}{\partial \beta }$, where the derivative with respect to the translational parameters can be determined analytically (according to Equation (12)) and the derivative with respect to the rotational parameters is approximated by numerical differentiation. λ is a damping factor to control convergence speed.

E. Generating simulated cryo-electron tomograms

For a reliable assessment of the method tomograms must be simulated as realistic as possible. We follow a previously applied methodology for realistically simulating the tomographic image formation [4], [6], [9], [14]. Initial density maps at 4 nm resolution are generated and used as samples for simulating electron micrograph images at different tilt angles. The tilt angles are set within a certain maximal range with steps of 1°. As a result our data contains a wedge-shaped region in Fourier space for which no data has been measured (missing wedge effects), similar to experimental measurements. The missing wedge effect leads to distortions of the density maps in real space along the tilt-axis. To generate realistic micrographs, noise is added to the images and the resulting image map is convoluted with a Contrast Transfer Function (CTF), which describes the imaging in the transmission electron microscope in a linear approximation. Any negative contrast values beyond the first zero of the CTF are eliminated. We also consider the modulation Transfer Function (MTF) of a typical detector used in whole cell tomography, and convolute the density map with the corresponding MTF. The CTF and MTF describe distortions from interactions between electrons and the specimen and distortions due to the image detector [15], [14]. Typical acquisition parameters used during actual experimental measurements of whole cell tomograms [4] were used: voxel grid length = 1 nm, the spherical aberration = 2 × 10^–3m, the defocus value = –4 × 10^–6m, the voltage = 200kV, the MTF corresponded to a realistic electron detector [16], defined as sinc(πω/2) where ω is the fraction of the Nyquist frequency.

Finally, we use a backprojection algorithm to generate a tomogram from the individual 2D micrographs that were generated at the various tilt angles [4]. To test the influence of increasing noise, we add different amount of noise to the images, so that the SNRs range between ∞ and 0.1, respectively. Figure 1(b) shows the reconstructed subtomograms of a phantom model at different noise levels and different tilt angle ranges.

Fig. 1.

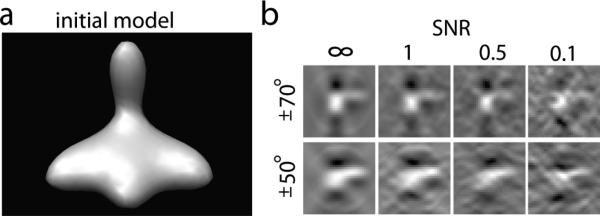
(a) Density map of an unsymmetric phantom model consisting of four different 3D Gaussian functions. This density map is used to simulate subtomograms of 32³ voxels. (b) A slice of the reconstructed tomograms at different levels of noise (∞, 1, 0.5, 0.1), and different tilt angle ranges leading to different levels of missing wedge distortions. The Isodensity contour plot are generated using the Chimera software package [17]. The slices are plotted using MATLAB.

All our methods are implemented in MATLAB.

III. Results

We test our method on phantom models and actual structures of protein complexes.

To assess the general performance, 100 pairs of subtomograms with randomly placed phantom models were generated for different SNR levels and tilt angle ranges (Figure 1(b)). Our stochastic parallel refinement method is tested using both the RCS and FCS distance scores¹.

We test our approach with respect to two factors. First, the maximal alignment error obtained from the refinement and second, the number of iterative steps that are needed to determine the optimal solution.

We show that even at a low SNR level of 0.5 and a typical range of tilt angles between −70° and +70° our method can still achieve a very low alignment error (Table I). For example even when the rotational sampling is performed at only 60° intervals the stochastic iterative refinement process together with the RCS scoring produces on average errors of 3.1° , while the FCS scoring achieves 2.9° error (Table I). This angle error is significantly lower than would be expected from exhaustive scanning where sampling of rotational angles is usually performed at 10° or 5° sampling intervals without additional refinement. At 5° intervals a total of 168,634 candidate orientations must be processed while at 60° rotational intervals only 108 candidate orientations are processed. Also our method can in general achieve a small error for the translation of subtomograms that cannot be reached by an FFT based exhaustive sampling, which on average cannot be less than 0.5 (Table II).

TABLE I.

Subtomgram alignment error in terms of the difference in the determined and true rotational angle of the subtomograms. Shown are the medians and median absolute deviations of all 100 subtomogram alignments.

RCS
SNR	∞	1	0.5	0.1
Tilt
±90°	0.71 ± 0.49	3.3 ± 2.8	2.6 ± 1.4	14 ± 9.3
±80°	0.85 ± 0.54	2.5 ± 1.8	3.5 ± 2.4	21 ± 14
±70°	1.2 ± 0.53	1.9 ± 1.3	3.1 ± 1.7	19 ± 12
±60°	0.97 ± 0.49	2 ± 0.97	3.7 ± 2.4	49 ± 45
±50°	1.8 ± 0.9	2.9 ± 1.6	7 ± 5.2	87 ± 63
±40°	1.6 ± 1	9 ± 8.3	55 ± 53	123 ± 31
FCS
	∞	1	0.5	0.1
±90°	0.89 ± 0.54	2.6 ± 2.1	2.4 ± 1.1	8.5 ± 4.5
±80°	1.1 ± 0.61	2.2 ± 1.6	3.2 ± 2.2	12 ± 7.7
±70°	2 ± 0.86	2.1 ± 1	2.9 ± 1.3	16 ± 11
±60°	1.5 ± 0.82	2.4 ± 1.2	3.8 ± 2.1	34 ± 30
±50°	2.6 ± 1.1	3.4 ± 1.8	6.3 ± 4.2	43 ± 37
±40°	15 ± 14	92 ± 40	106 ± 37	113 ± 26

TABLE II.

Subtomogram alignment error in terms of the difference in the Euclidean distance between determined and true subtomogram translations. Shown are the medians and median absolute deviations of all 100 subtomogram alignments.

RCS
SNR	∞	1	0.5	0.1
Tilt
±90°	0.035 ± 0.023	0.16 ± 0.12	0.19 ± 0.12	0.96 ± 0.66
±80°	0.045 ± 0.029	0.24 ± 0.2	0.21 ± 0.15	1.3 ± 0.89
±70°	0.078 ± 0.037	0.25 ± 0.17	0.3 ± 0.18	1.3 ± 0.74
±60°	0.068 ± 0.036	0.19 ± 0.12	0.43 ± 0.3	2.2 ± 1.3
±50°	0.14 ± 0.078	0.26 ± 0.17	0.65 ± 0.51	2.3 ± 1.3
±40°	0.15 ± 0.092	0.74 ± 0.64	1.7 ± 1.3	3.2 ± 1.6
FCS
	∞	1	0.5	0.1
±90°	0.047 ± 0.023	0.12 ± 0.081	0.11 ± 0.053	0.49 ± 0.31
±80°	0.053 ± 0.03	0.15 ± 0.1	0.18 ± 0.1	0.85 ± 0.66
±70°	0.11 ± 0.057	0.13 ± 0.074	0.21 ± 0.1	0.95 ± 0.58
±60°	0.11 ± 0.061	0.2 ± 0.094	0.3 ± 0.15	1.6 ± 1.2
±50°	0.19 ± 0.1	0.28 ± 0.16	0.44 ± 0.26	1.8 ± 1.2
±40°	0.61 ± 0.54	3.3 ± 2.7	4.3 ± 2.6	6.2 ± 3

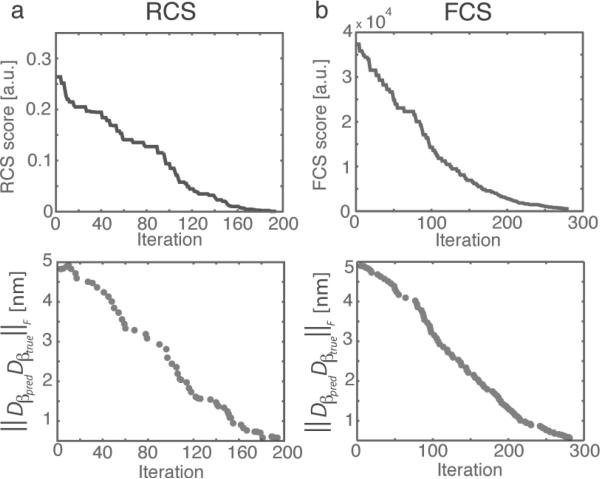
The parallel stochastic refinement process reduces considerably the number of refinement iterations that are needed to reach the global solution. At a rotational sampling of 60° , there are 108 candidate orientations that can potentially serve as starting points for a refinement process. Without the parallel stochastic optimization method, a refinement of a candidate orientation takes on average about 60 iterations per run, totaling about 6480 iterative refinement steps to find the global optimum among all candidate orientations if all candidate orientations are refined independently. However, our parallel stochastic refinement process reaches convergence already within 200-300 iterative refinement steps (Figure 2). We estimate that the parallel stochastic refinement is on average about 20 to 40 fold faster in comparison to the independent refinement of all candidate orientations (Table III).

Fig. 2.

Top panels: The minimum dissimilarity scores obtained at different iterations subtracted from the true distance. Bottom panels: The difference ∥D_βpredβtrue∥_F between predicted and true transforms at those iterations where minimum dissimilarity scores are obtained. Top, (a) Subtomogram alignments based on the real space constrained dissimilarity score (RCS), and (b) based on the Fourier space constrained dissimilarity score (FCS). Shown is the performance for subtomograms with SNR 0.5, missing wedge angle 30°. The method was tested with rotational angles sampled at angle interval 60°

TABLE III.

Fold change for the decrease in the iteration number needed by stochastic parallel optimization compared to exhaustive independent refinement. Shown are the medians and median absolute deviations of all 100 subtomogram alignments.

RCS
SNR	∞	1	0.5	0.1
Tilt
±90°	28 ± 5.4	23 ± 3.4	21 ± 1.8	21 ± 2.3
±80°	28 ± 4.6	23 ± 2.7	21 ± 2.2	21 ± 2.8
±70°	27 ± 4.2	21 ± 2.4	22 ± 2.7	20 ± 2.4
±60°	28 ± 4.1	21 ± 2.5	21 ± 1.8	21 ± 3
±50°	23 ± 3.1	22 ± 2.4	20 ± 2.4	21 ± 2.9
±40°	23 ± 3.2	20 ± 2.5	20 ± 2.3	20 ± 2.2
fcs
	∞	1	0.5	0.1
±90°	40 ± 12	28 ± 6.3	26 ± 4.2	21 ± 2
±80°	37 ± 11	26 ± 4.7	24 ± 3.3	21 ± 1.8
±70°	36 ± 5.3	26 ± 4.6	24 ± 3.6	20 ± 2.1
±60°	36 ± 8.4	26 ± 4.6	24 ± 3.2	21 ± 1.8
±50°	29 ± 6.4	24 ± 3.9	23 ± 2.8	21 ± 2.1
±40°	24 ± 4.6	22 ± 3.2	20 ± 2.5	20 ± 3.3

Next, we further test our alignment methods for refining density maps of complexes by averaging all aligned subtomograms. We generated 1000 subtomograms (at SNR 0.5, tilt angle range ±60°) containing randomly oriented models. We then aligned the tomograms against the initial template using our methods and rotational sampling with 60° angle intervals. From the resulting averaged density maps it can be seen that our methods can successfully recover the initial model structure (Figure 3).

Fig. 3.

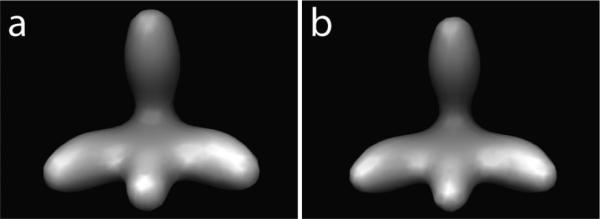
Averaged subtomograms. Left, aligned using RCS. Right, aligned using FCS.

A. Pairwise alignment of subtomograms from real macromolecular complexes

A whole cell cryo-electron tomogram consists of instances of macromolecular complexes of different types. These instances are segmented into subtomograms and can be classified after pairwise alignment, which is fundamental for successful structural systems biology analysis of these instances. In this section, we test our methods on subtomograms of four macromolecular complexes obtained from the Protein Data Bank (PDB id 1KP8, 2GHO, 1W6T, 1YG6). The density map of each complex is calculated from its atomic structure by applying a low pass filter at 4 nm resolution using the PDB2VOL program of the Situs 2.0 package [18] and voxel spacing of 1 nm. The resulting density maps are used to simulate 20 subtomograms for each randomly placed macromolecular complex, at SNR 0.5 and tilt angle range ±60° (Section II-E).

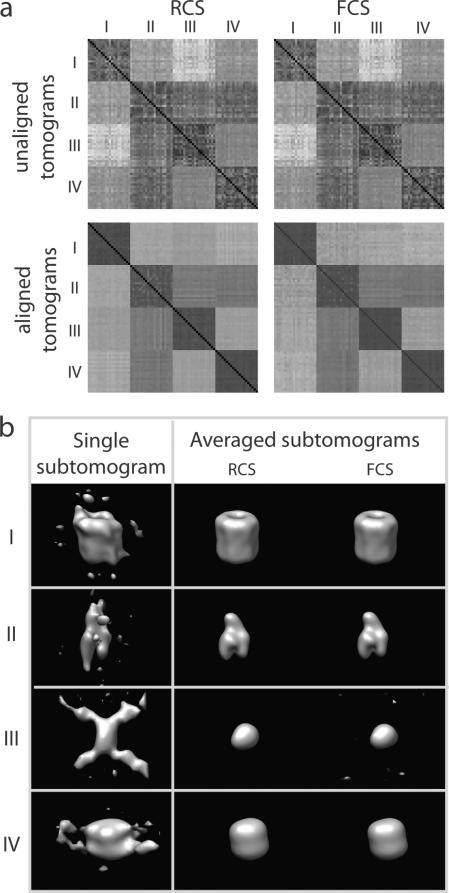
We perform all pairwise alignments between all 80 subtomograms with sampling of 60° rotational angle intervals. After alignment the resulting dissimilarity score matrix for subtomogram classification is significantly improved in comparison to the dissimilarity score matrix generated from the initial starting structures (Figure 4 (a)).

Fig. 4.

(a) Dissimilarity score matrices for subtomogram classification. The matrix elements representing the same complexes are in consecutive order. (Top row) Dissimilarity score matrix based on the initial subtomogram orientations before alignment for (left column) RCS score and (right column) FCS score. (Bottom row) RCS and FCS score matrices after subtomogram alignments. The alignment is performed at a sampling with 60° rotation angle intervals. (b) Density maps of complexes generated after averaging of the aligned subtomograms in the same class. (Left column) Isodensity contour plot of the density distribution in single subtomogram for each complex. (Middle and right columns) Isodensity contour plot of the resulting density maps generated by averaging the 20 subtomograms aligned with the RCS and FCS scores, respectively.

After classification and alignment, the resulting averaged tomograms are very similar to the original density maps. The distortions evident in the individual subtomograms are greatly reduced after averaging (Figure 4 (b)).

IV. Conclusion

In this paper, we have proposed a new gradient based method for high precision subtomogram alignments. Combined with the RCS and FCS scores, this method can achieve significantly lower alignment error in comparison to an exhaustive sampling method. We show that this accuracy can already be reached with only a relatively small number of sampled candidate orientations, for example at rotational intervals of 60°. Moreover, we have proposed a very efficient stochastic parallel refinement method, which is able to find the global optimum with only a small fraction of iterations in comparison to the independent sampling and refinement with the same sampling angle intervals. Together, these improvements increase significantly the efficiency and accuracy for subtomogram alignments, which is a key factor for the systematic classification of macromolecular complexes in cryo-electron tomograms of whole cells.