Abstract
Greater skill in solving single-digit multiplication problems requires a progressive shift from a reliance on numerical to verbal mechanisms over development. Children with math learning disability (MD), however, are thought to suffer from a specific impairment in numerical mechanisms. Here we tested the hypothesis that this impairment might prevent MD children from transitioning towards verbal mechanisms when solving single-digit multiplication problems. Brain activations during multiplication problems were compared in MD and typically developing (TD) children (3rd to 7th graders) in numerical and verbal regions which were individuated by independent localizer tasks. We used small (e.g. 2 × 3) and large (e.g. 7 × 9) problems as these problems likely differ in their reliance on verbal versus numerical mechanisms. Results indicate that MD children have reduced activations in both the verbal (i.e. left inferior frontal gyrus and left middle temporal to superior temporal gyri) and the numerical (i.e. right superior parietal lobule including intra-parietal sulcus) regions suggesting that both mechanisms are impaired. Moreover, the only reliable activation observed for MD children was in the numerical region when solving small problems. This suggests that MD children could effectively engage numerical mechanisms only for the easier problems. Conversely, TD children showed a modulation of activation with problem size in the verbal regions. This suggests that TD children were effectively engaging verbal mechanisms for the easier problems. Moreover, TD children with better language skills were more effective at engaging verbal mechanisms. In conclusion, results suggest that the numerical and language related processes involved in solving multiplication problems are impaired in MD children.
Keywords: arithmetic, multiplication, fMRI, dyscalculia, learning disability
1. Introduction
Several alternative accounts advance that mathematical learning disability (MD or dyscalculia) stems from a specific impairment in basic numerical processing. The “Core Deficit Theory” (Wilson and Dehaene, 2007) argues that MD is a deficit in the approximate number sense, whereas the “Numerosity Coding” theory suggests that the deficit lies in the ability to represent numerosities in a discrete and precise way (Butterworth, 2010). In support of a primary impairment in numerical processing, MD children show poor number acuity (i.e. the ability to compare collections of items based on their numerical quantity) compared to same age peers (Mazzocco, et al., 2011; Moeller, et al., 2009; Piazza et al., 2010). Evidence from structural and functional neuroimaging studies also supports a core deficit in numerical processing. First, MD children have reduced grey matter in the right intraparietal sulcus (IPS) (Rotzer et al., 2008), an area thought to be involved in the processing of both symbolic and non-symbolic numerical information (Ansari, 2008; Nieder and Dehaene, 2009; Piazza, et al., 2004; Pinel, et al., 2001). Second, the majority of functional neuroimaging studies using non-symbolic tasks show abnormalities in IPS in MD children (Kaufmann et al., 2009; Price, et al., 2007). Neurofunctional differences in MD children have also been observed in symbolic tasks. For example, in a single-digit comparison task, MD children exhibited weak involvement of bilateral IPS, with no modulation of activations due to the distance between the two digits (Mussolin et al., 2010). Such a modulation is typically present in adults and children without specific math impairments (Mussolin et al., 2010; Pinel et al., 2001). All together, these studies indicate that the quality of numerical representations supported by the IPS are crucial for math skill and may be central to math disability.
A small number of imaging studies comparing typically developing (TD) to MD children have further suggested that altered IPS processing might also underpin impaired performance in arithmetic tasks. A study examining addition showed that MD children had weaker activations in the bilateral IPS and middle and inferior frontal gyri for an approximate condition, whereas no group differences were observed for an exact condition (Kucian et al., 2006). The authors argued that the impairment in MD children may lie in the evaluation of numerical distance, but not in counting or fact retrieval mechanisms. In contrast to the wide age range studied in Kucian et al. (2006), Davis et al. (2009) tested exact and approximate addition problems within third graders. Stronger activations for MD children were observed in the right insula and precentral gyrus, suggesting the possible use of immature finger counting strategies to solve the task (Jordan and Montani, 1997). Davis et al. (2009) also showed greater activation for the MD children during approximate calculation in the right inferior parietal lobe; an area associated with processing spatial information (Pinel et al., 2001). In summary, studies on arithmetic are broadly consistent with the results on numerical processing, suggesting alterations in the parietal cortex in MD children.
As suggested by De Smedt et al. (2011), such an impaired system of numerical representations in the IPS could prevent MD children from moving towards more efficient retrieval strategies for solving arithmetic problems over the course of development. In TD children, operations such as single-digit addition and multiplication are thought to become familiar with schooling so that by adulthood these do not require computation but are retrieved from long term verbal memory (Ashcraft, 1992; Groen and Parkman, 1972; Parkman and Groen, 1971). MD children, however, are less accurate and slower when retrieving the solutions to single-digit arithmetic problems (Geary and Hoard, 2001; Geary, 1993; Shalev and Gross-Tsur, 2001) probably because they use less efficient and immature calculation strategies (Jordan and Montani, 1997). This is consistent with the results of two recent neuroimaging studies. First, De Smedt et al. (2011) found that, in TD children, the IPS was more activated during larger addition problems (thought to mostly depend upon calculation mechanisms) than during smaller addition problems (thought to mostly depend upon retrieval). Conversely, the authors showed that MD children failed to modulate brain responses in the right IPS based on problem size, suggesting that they rely on numerical mechanisms even for small problems (and thus may fail to use retrieval mechanisms). Second, Ashkenazi et al. (Ashkenazi, et al., 2012) also manipulated arithmetic complexity to study the neural bases of single-digit addition in MD and TD children. The authors confirmed that MD children had reduced sensitivity to complexity in bilateral IPS and superior parietal lobules, suggesting that all problem types engage calculation mechanisms. However, this paper also reported a weaker response to complexity for MD children in the left middle temporal gyrus (MTG). Because the left MTG could play an important role in retrieving verbally stored arithmetical facts (Prado et al., 2011; Prado, et al., under review), these findings suggest that MD children might not be able to store arithmetic facts in memory as effectively as TD children. Indeed, a number of behavioral studies have highlighted the role of verbal competences, such as phonological awareness, as unique predictor of later mathematical performance, in particular for multiplication problems (De Smedt et al., 2010; Hecht et al., 2001). Because the problem and the correct answer need to be present simultaneously in short-term memory to be stored as long-term verbal representations (Geary, 1993), children struggling with the manipulation of numerical quantities would not be able to create such associations. It follows that the IPS impairments observed in MD might be associated with impaired representation of math facts in verbal regions of the MTG.
The aim of this study was to investigate whether MD children differ from typical children in their reliance on both numerical and verbal mechanisms when retrieving arithmetic facts. Although the neural bases of single-digit subtraction and addition have been compared between MD and TD children (De Smedt et al., 2011; Ashkenazi, et al., 2012), we chose to examine single-digit multiplication because these problems are thought to be retrieved from verbal memory whereas subtraction and addition might rely more on calculation procedures (Fayol and Thevenot, 2012). We also manipulated problem size because small problems are more likely to engage verbal mechanisms, whereas large problems should engage numerical mechanisms to a greater degree (Siegler, 1988). Although MD children have been shown to have behavioral deficits in multiplication, ours is the first study to examine the neural basis of group differences in multiplication. To identify the underlying mechanisms, we used localizer tasks that have successfully identified verbal and numerical regions in previous studies (Prado et al., 2011, Prado et al., in press). Because MD children show poor number acuity (Piazza et al., 2010) and abnormal activation of right IPS in non-symbolic tasks (Price et al., 2007), our numerical localizer aimed at identifying the region involved in the manipulation of numerical quantities. We compared MD children to age matched TD children (8 to 14-years of age) in their reliance on these mechanisms. Overall, we expected MD children to show weaker modulation of neural responses as a function of problem size and weaker involvement of both the left MTG and right IPS. This would be consistent with the hypothesis that both impaired numerical and verbal mechanisms underlie MD deficits when solving multiplication problems.
2. Materials and Method
2.1. Participants
Third to 7th grade children (N=40) were recruited to participate in the study by advertising in the Chicago public transportation system and in local school districts (see Table 1). Participants were included in the study if they were native English speakers, were free of past and present neurological or psychiatric disorders and had a full scale IQ equal or above 80 (as measured by the Wechsler Abbreviated Scale of Intelligence, WASI; Wechsler, 1999) thus excluding participants with intellectual deficits. Twenty children were classified as having math learning disability (MD) based on performances to both the Basic Composite Score of Comprehensive Mathematical Abilities Test (CMAT; Hresko et al., 2003) and the Math Fluency subtest from the Woodcock-Johnson III Test of Achievement (WJ-III; Woodcock, McGrew and Mather, 2001). The former test is composed of 4 untimed subtests, each evaluating one of the four basic mathematical operations. The latter subtest requires solving basic addition, subtraction and multiplication problems in a 3-minute time limit. MD children are particularly challenged in chronometric tasks where time consuming back up strategies may not be used. However, to ensure that low performance was not due to stress or fatigue, we also added the non-timed task. To be included in the MD group, a child had to score below 95 on both tests and equal to or below 85 on at least one of the two tests. For the 20 typically developing (TD) peers, both scores had to be 95 or above. All participants succeeding in just one of the two tasks were eliminated from the study. These criteria guarantee no overlap between the two groups. The two groups were also matched on age and gender distribution. Response bias to the tasks performed in the scanner was also evaluated for each child combining a False Alarm (FA) index with a FA/Misses ratio. Children included in the study had less than 50% of FA and a FA/Misses ratio smaller than 2. Therefore, for two comparable performances, a child with a similar number of accepted false trials and rejections of true trials was included in the study whereas a child with a disproportionate number of accepted false trials with no rejections was discarded.
Table 1.
Scores on standardized tests for children in the TD and MD groups
| TD (N=20) |
MD (N=20) |
Sig |
|
|---|---|---|---|
| Mean (SD) [min-max] | Mean (SD) [min-max] | ||
| Male/Female | 9/11 | 7/13 | n.s. |
| Age (years:months) | 11:6 (1:7) [8:6–13:10] | 11:5(1:6) [9:2-13:10] | n.s. |
| WASIa | |||
|
| |||
| Verbal | 114.3 (13.7) [90–141] | 101.5 (13.7) [81–139] | <.005 |
| Performance | 110.6 (15.4) [84–138] | 92.6 (9.6) [77–109] | <.001 |
| Full | 114 (15.4) [86–144] | 96.4 (9.2) [82–116] | <.001 |
| CMATa | |||
|
| |||
| Basic Composite Score | 113 (9.5) [95–159] | 79 (6.0) [62–93] | <.001 |
| Woodcock-Johnson IIIa | |||
|
| |||
| Math Fluency | 108.1 (12.7) [95–143] | 80 (5.2) [71–94] | <.001 |
| Spatial Relations | 106.5 (13.6) [75–130] | 94.3 (17.3) [32–115] | <.05 |
| CTOPPb | |||
|
| |||
| Blending words | 11.4 (2.7) [6–15] | 9.7(3.1) [5–15] | n.s. |
Note. SD, Standard Deviation; WASI, Wechsler Abbreviated Scale of Intelligence; CMAT, Comprehensive Mathematical Abilities Test; CTOPP, Comprehensive Test of Phonological Processing;
Standard Scores (M = 100 and SD = 15);
Scaled Scores (M =10, SD = 3).
Spatial processing was tested with the Spatial Relation subtest of the WJ-III. This subtest requires participants to individuate, among a selection of smaller geometrical shapes, the pieces that constitute a larger shape. Phonological abilities were assessed with the Blending Word subtest from the Comprehensive Test of Phonological Processing (CTOPP; Wagner, et al., 1999). This test evaluates the ability to synthetize sounds to form words. Mean scores, standard deviations and t-test significance for all standardized measures are presented separately for each group in Table 1.
Written consent was obtained from children and their parents or guardians. All experimental procedures were approved by the Institutional Review Board at Northwestern University.
2.2. Multiplication task
Participants were presented with single-digit multiplication problems (see Figure 1B). Trials were subdivided into small and large problems depending on the size of the operands (i.e., problem size). Twelve small problems had the two operands equal or smaller than 5 (e.g., 2 × 4) and 12 large problems had both operands larger than 5 (e.g., 6 × 9). Each problem was repeated twice with a true answer and once with a false answer. This yielded 72 trials total for each problem type (36 smaller and 36 larger). Due to experimental time-limit constraints, false answers were only within-operation results from the preceding or following fact based on the first operand (e.g., 20 or 28 as the false answer to 6 × 4). Presenting cross-operation results may have involuntarily induced addition procedures introducing undesired variability in brain activations (LeFevre, Bisanz, and Mrkonjic, 1988). Problems involving 0 (e.g., 3 × 0 or 0 × 3) or 1 as operand (e.g., 3 × 1) and ties (e.g., 3 × 3) were excluded in the main experiment but used as practice items. Twenty-four null trials were included to control for motor responses. In these trials a blue square appeared for the same duration as the experimental condition and participants had to press a button when it turned red. The practice session was composed of 48 problems, half of which with a correct answer and half with a false answer (see Prado et al., 2011).
Figure 1.
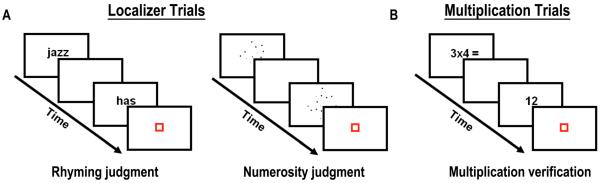
Localizer and multiplication tasks. (A) In the Rhyming localizer (left), participants decided whether two visually presented English words rhymed or not. In the Numerosity localizer (right), participants decided which of two dot arrays had the largest number of dots. (B) In the Multiplication Task, participants were asked to evaluate whether the given answer was the correct solution to the previously seen arithmetical fact.
2.3. Localizer tasks
Each subject also performed two functional localizer scans containing verbal and numerical trials (see Prado et al., 2011). In the Rhyming Task (see Figure 1A, left), participants were sequentially presented with two monosyllabic English words and were required to decide whether they rhymed or not. Orthography and phonology were manipulated independently to ensure that judgments were not based solely on orthographic similarities between words. The two dimensions were orthogonally crossed yielding 4 conditions of 12 trials each: both orthography and phonology are similar (e.g., dime – lime), orthography is similar but phonology is dissimilar (e.g., pint – mint), orthography is dissimilar but phonology is similar (i.e., jazz – has) and finally both orthography and phonology are discordant (e.g., press – list). Twelve null trials were included. Twelve different pairs of words per condition were used as practice trials during the familiarization sessions.
In the Numerosity Task (see Figure 1A, right), participants were sequentially presented with two arrays of dots. Participants had to decide which array contained the larger number of dots. In half of the trials the larger set was presented first. The ratio between the two sets was manipulated and varied across trials. The three ratios used were: 0.33 (i.e., 12 vs. 36 dots), 0.5 (i.e., 18 vs. 36 dots) and 0.66 (i.e., 24 vs. 36 dots) making three conditions from hardest to easiest, respectively. Six different dot sizes were used to make the sets, and stimuli were controlled for differences in cumulative surface area and distribution of dot sizes. Each condition was composed of 24 pairs making a total of 72 trials to which 24 null trials were added. Twelve different pairs per condition were used as practice trials during the familiarization sessions.
2.4. Experimental protocol
Participants were familiarized with tasks and the fMRI environment during a practice session after giving informed consent and having completed standardized testing. During this session, they learned to minimize head movement in a mock fMRI scanner by means of an infrared-tracking feedback device and practiced all tasks. This session was completed within a week prior to actual fMRI data acquisition. In the fMRI scanner, the Multiplication Task and the Numerosity Task were split into two 4-minutes runs. Only the Rhyming Task was acquired in a single 7-minute run. The order of the tasks was fully counterbalanced across participants and the timing and order of trials within each run were optimized for estimation efficiency using optseq2 (http://surfer.nmr.mgh.harvard.edu/optseq/). Behavioral responses were recorded using an MR-compatible keypad placed in the right hand. Stimuli were generated using E-prime software (Psychology Software Tools, Pittsburgh, PA) and projected onto a translucent screen that was viewed through a mirror attached to the head-coil.
2.5. Stimulus timing
Stimulus timing was identical for all tasks. A trial started with the presentation of a first stimulus (a multiplication, a set of dots or a single word) for 800 msec followed by a blank screen for 200 msec. A second stimulus (the multiplication answer, the second set of dots or the second word) was presented for 800 msec and then followed by a red fixation square for 200 msec. The red square indicated the need to give a response during an interval ranging from 2800 msec to 3600 msec. Moreover, null trials were composed of a blue square that lasted for the same duration as the experimental conditions and participants had to press a button when it turned red.
2.6. fMRI data acquisition
fMRI data were collected at the Northwestern University's Center for Translational Imaging (CTI), using a Siemens 3T TIM Trio MRI scanner (Siemens Healthcare, Erlangen, Germany). The fMRI blood oxygenation level dependent (BOLD) signal was measured with a susceptibility weighted single-shot echo planar imaging (EPI) sequence. The following parameters used were: TE = 20 ms, flip angle = 80°, matrix size = 128 × 120, field of view = 220 × 206.25 mm, slice thickness = 3 mm (.48 mm gap), number of slices = 32, TR = 2000 ms. Before functional image acquisition, a high resolution T1 weighted 3D structural image was acquired for each subject (TR = 1570 ms, TE = 3.36 ms, matrix size = 256 × 256, field of view = 240 mm, slice thickness = 1 mm, number of slices = 160).
2.7. fMRI preprocessing
Data analysis was performed using SPM8 (www.filion.ucl.ac.uk/spm). After discarding the first six images of each run, functional images were corrected for slice acquisition delays, realigned to the first image of the first run and spatially smoothed with a Gaussian filter equal to twice the voxel size (4 × 4 × 8 mm3 full width and half maximum). Prior to normalizing images with SPM8, we used ArtRepair (Mazaika, et al., 2009; http://cibsr.standford.edu/tools/ArtRepair/ArtRepair.htm) to suppress residual fluctuations due to large head motion and to identify volumes with significant artifact and outliers relative to the global mean signal (i.e., 4% from the global mean). Volumes showing rapid scan-to-scan movements of greater than 1.5 mm were excluded via interpolation of the 2 nearest non-repaired volumes. Interpolated volumes were then partially deweighted when first-level models were calculated on the repaired images (Mazaika, et al., 2007). Finally, functional volumes were co-registered with the segmented anatomical image and normalized to the standard T1 Montreal Neurological Institute (MNI) template volume (normalized voxel size, 2 × 2 × 4 mm3). All participants included in the analysis had less than 6% of the total number of volumes replaced and these did not differ between groups for any task (all ps > 0.1).
2.8. fMRI processing
Event-related statistical analysis was performed according to the general linear model. Activation was modeled as epochs with onsets time-locked to the presentation of the first stimulus in each trial and with a duration of 2 seconds (i.e., the trial duration). For the multiplication task, trials were classified for problem type (true, false) and for problem size (small, large). However, only true trials were considered of interest in behavioral and fMRI analyses. Indeed, true trials are a cleaner measure of participants' performance because it is impossible to establish whether false trials were discarded by reaching the correct solution. For localizers scans, trials were sorted by trial type (language, numerical). Null trials were further modeled in a separate regressor for each localizer scan and the multiplication task. All epochs were convolved with a canonical hemodynamic response function. The time series data were high-pass filtered (1/128 Hz) and serial correlations were corrected using an autoregressive AR (1) model.
2.9. ROI analyses
Verbal and numerical processing ROIs were defined using the localizer tasks. First, for each subject, a first level contrast of rhyming versus null trials greater than numerosity versus null trials generated the rhyming localizer contrast. The numerosity localizer contrast was the converse (i.e., numerosity versus null greater than rhyming versus null). A second-level random effects analysis across all participants (i.e., both TD and MD) was used to generate ROI masks. Because of specific a priori hypothesis on brain areas involved in language-related and spatial-numerical processing, we constrained the second-level statistical analysis with atlas based anatomical masks (defined using the aal template). The inferior frontal gyrus, superior temporal gyrus and middle temporal gyrus for the left hemisphere were used as anatomical masks on the rhyming localizer (Booth, 2010) and the superior and inferior parietal lobules for the right hemisphere were used as anatomical masks for the numerosity localizer (Prado et al., 2011; see Figure 2). Within these masks, we submitted individual contrasts to a one-sample t-test across all participants. The resulting statistical maps were thresholded using a voxelwise threshold of p < .005 (uncorrected) and a cluster extent threshold of 30 contiguous voxels. Voxels reaching this threshold in the second-level analysis for the rhyming and numerosity localizer contrasts were taken as language-related and numerical processing ROIs, respectively.
Figure 2.
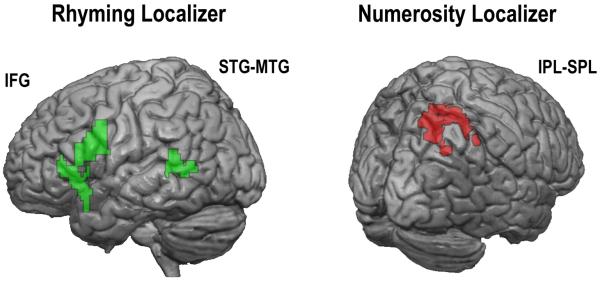
Brain regions activated in the localizer tasks. (A) The language-related network involves the left IFG and left MTG-STG. (B) The numerical processing network is situated in the right SPL.
Significance thresholds for the multiplication task within the ROIs were determined using 3dClustSim, which calculates cluster size threshold (k) for false positive (noise-only) clusters at specified uncorrected alpha level (available as part of the AFNI fMRI analysis package, available at http://afni.nimh.nih.gov/afni/download). Briefly, 3dClustSim carries out a user-specified number of Monte Carlo simulations of random noise activations at a particular voxel-wise alpha level within a masked brain volume. Ten thousand such simulations were performed for the Rhyming and Numerosity ROIs. The number of simulations in which clusters of various sizes appear within each volumetric mask is tallied among these simulations. These data are then used to calculate size thresholds across a range of probability values for that region. In particular, in a specified volume using a voxel-wise alpha of 0.05, if clusters of size 39 mm3 or greater appear in 50 of 10,000 iterations by chance, this corresponds to a p < 0.05 cluster level significance threshold. In other words, within the specified volume using a voxel-wise alpha of 0.05, clusters exceeding 39 mm3 are unlikely to occur by chance. Clusters exceeding these size thresholds were deemed significant.
3. Results
3.1. Behavioral results
For true trials, mean accuracies were transformed with the 2*arcsin√(proportion) formula and RTs were transformed using the √(RT) formula (Kirk, 2013). An ANOVA was run on accuracy and reaction times (RTs) for the Multiplication Task with group (MD vs. TD) as between-subject factor and problem size (small vs. large) as within-subject factor. Mean accuracies and RTs are reported in Table 2 for the two groups. For accuracies, both main effects were significant (F(1,38)=34, p<.001 for group and F(1,38)=39, p<.001 for problem size) but the interaction between problem size and group was not significant (p>.5). Problem size and the interaction between problem size and group were significant for RTs (F(1,38)=17, p<.001 and F(1,38)=8, p<.01, respectively). Simple effects revealed that the manipulation was significant only within the TD group (F(1,19)=42, p<.001) and that RTs for the two problem sizes did not significantly differ between groups. These results show that the TD children were more accurate than MD children and that the problem size manipulation was effective specifically for TD children, as larger problems were associated with lower accuracy and longer RTs. The absence of size manipulation for MD children could be explained by the presentation rate pressuring children in responding faster for larger problems. However, it is also possible that children were overwhelmed by larger problems and gave up earlier compared to peers. Separate ANOVAs were also run on the localizer tasks with group as a between subjects factor. In both tasks, only accuracy differed significantly between groups (F(1,38)=15, p<.001 for rhyming and F(1,38)=8, p<.01 for numerosity), with TD children showing higher accuracy in both tasks (see Table 2).
Table 2.
Mean accuracy and response times for children in the TD and MD groups for all tasks.
| TD |
MD |
||||
|---|---|---|---|---|---|
| Task | Condition | % Accuracy | RT in msec | % Accuracy | RT in msec |
| Rhyming Task | |||||
|
| |||||
| Rhyming trials | 86.4 (9.9) | 1201 (237) | 71.9 (14.8) | 1203 (328) | |
| Numerosity Task | |||||
|
| |||||
| Numerosity trials | 92.1(8.9) | 1010 (304) | 86.3 (7.9) | 962 (301) | |
| Multiplication Task | |||||
|
| |||||
| Small problems | 98.1 (2.9) | 862 (285) | 78.1 (21.2) | 1131 (483) | |
| Large problems | 84.9 (14.6) | 1167 (298) | 56.1 (21.2) | 1181 (424) | |
Note. Values in parenthesis denote standard deviations.
3.2. ROI definition
For each subject, verbal and numerical ROIs were identified by contrasting rhyming minus null with numerosity minus null trials and vice-versa (see Figure 2, left panel, and Table 3). For rhyming trials, the cluster in the inferior frontal gyrus (IFG) included parts of the pars opercularis, triangularis and orbitalis. The cluster in the temporal cortex spanned the middle and superior temporal gyri. The peak coordinates of the left IFG and left MTG clusters were close (an Euclidean distance of 21 mm for the IFG and 13 mm for the MTG) to those defined using an identical rhyming task in a previous study with children (Prado et al., under review). For numerical trials, the cluster in the right parietal cortex covered the rostral parts of the inferior and superior parietal lobules including the IPS (see Figure 2, right panel, and Table 3). The peak coordinates were very close (an Euclidean distance of 7 mm) to the coordinates reported in a study investigating the role of this region in multiplication and subtraction processing in adults (Andres, et al., 2012) and near the peak reported by Piazza and colleagues (an Euclidean distance of 14 mm) to respond selectively to the numerical but not the physical properties of sets of dots (Piazza, et al., 2004). All further contrasts were run within these ROIs (see point 2.9. for further details)
Table 3.
Brain regions activated for all tasks
| MNI coordinates | |||||||
|---|---|---|---|---|---|---|---|
| Anatomical location | ~BA | X | Y | Z | k | z-value | Sig* |
| Localizer Tasks | |||||||
|
| |||||||
| Rhyming Task [Rhyming > Numerosity] | |||||||
| L. Inferior Frontal Gyrus | 47, 45, 44 | − 46 | 20 | − 10 | 374 | 4.59 | 0.0001 |
| L. Middle/Superior Temporal Gyrus | 21, 22 | − 48 | − 32 | − 6 | 154 | 3.63 | 0.01 |
| Numerosity Task [Numerosity > Rhyming] | |||||||
| R. Superior/Inferior Parietal Lobule | 7,39 | 26 | − 68 | 46 | 312 | 4.33 | 0.0002 |
| Multiplication Task | |||||||
|
| |||||||
| Rhyming Localizer | |||||||
| TD [Small - Large] > MD [Small - Large] | |||||||
| L. Inferior Frontal Gyrus | 47, 45 | − 42 | 18 | − 22 | 86 | 3.01 | 0.006 |
| L. Middle/Superior Temporal Gyrus | 21, 22 | − 56 | − 50 | 6 | 128 | 3.47 | 0.0006 |
| TD [Small - Large] | |||||||
| L. Inferior Frontal Gyrus | 47, 45 | − 48 | 32 | 2 | 81 | 4.35 | 0.007 |
| L. Middle/Superior Temporal Gyrus | 21,22 | − 56 | − 50 | 6 | 146 | 4.64 | 0.0001 |
|
| |||||||
| Numerosity Localizer | |||||||
| MD [Small - Large] > TD [Small - Large] | |||||||
| R. Superior Parietal Lobule | 7 | 28 | − 64 | 50 | 32 | 2.15 | 0.09 |
| MD [Small - Large] | |||||||
| R. Superior Parietal Lobule | 7 | 16 | − 70 | 54 | 69 | 2.81 | 0.009 |
Notes. L, left; R, right; ~BA, approximate Brodmann Area; MNI, Montreal Neurological Institute; Sig, significance determined by Monte Carlo simulation with 10000 iterations.
3.3. Activations within the numerical ROI
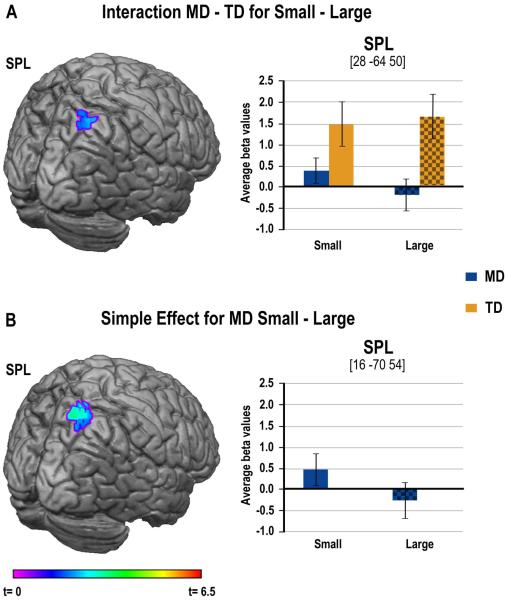
We expected TD children to show greater activation of numerical regions for large compared to small problems, and that this problem size effect should be more robust for TD compared to MD children. In contrast to our expectations, we found a trend (32 voxels while the threshold for a p=0.05 significance was of 39 voxels) for an interaction between group and problem size in the contrast of small versus large problems in a right SPL cluster extending into the IPS. Examination of the means shows that activations were higher for TD children than MD children for both problem sizes, but that MD children appeared to show greater activation for small compared to large problems (Figure 3A and Table 3). This was confirmed by a simple effect analysis showing that MD children showed greater involvement of the right SPL cluster for small compared to large problems, whereas the TD group failed to show modulation with problems size (see Figure 3B and Table 3). There was neither a significant interaction nor simple effects within groups for the contrast of large minus small problems. Although the greater engagement of numerical regions for the TD children was consistent with our predictions, we did not expect that MD children would show greater modulation of activation based on problem size, an issue that we will come back to in the discussion.
Figure 3.
Group differences in activation for multiplication in numerical ROIs. (A) On the left-hand side, image of the cluster in SPL showing greater activation for Small compared to Large problems for the MD children compared to the TD children. On the right-hand side, bar charts represent average activations for each group and for each problem size. (B) On the left-hand side, image of the cluster showing greater activation for Small compared to Large problems only in the MD children. On the right-hand side, bar charts represent average activations for each problem size.
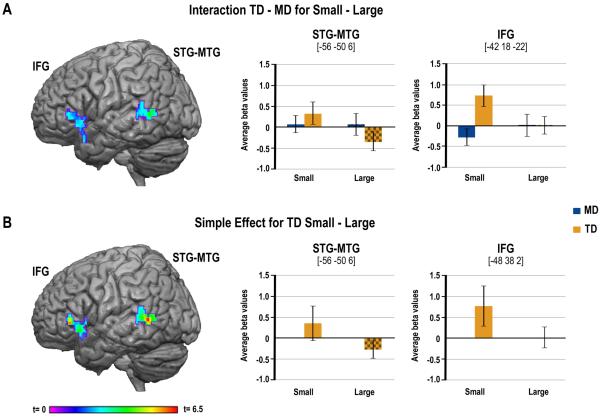
3.4. Activations within the verbal ROIs
We hypothesized that processing impairments in the IPS might lead to deficits in verbal retrieval in MD. Consistent with this expectation, clusters in both the MTG/STG and IFG were significantly more activated in the TD group compared to the MD group for the small minus large problem contrast (see Figure 4A, and Table 3). Examination of this interaction effect suggests that it was driven by greater activation for the small compared to large problems in the TD group. This was confirmed by simple effect analysis within groups showing that the TD exhibited greater activation for the small compared to large problems in both clusters (see Figure 4B, and Table 3), but that there was no reliable modulation of activation for this contrast in the MD group. There was neither a significant interaction nor simple effects within groups for the contrast of large minus small problems.
Figure 4.
Group differences in activation for multiplication in verbal ROIs. (A) On the left-hand side, images of the clusters in the STG-MTG and IFG showing greater activation for Small compared to Large problems for the TD children compared to the MD children. On the right-hand side, bar charts represent average activations from the two clusters for each group and for each problem size. (B) On the left-hand side, images of the clusters showing greater activation for Small compared to Large problems only in the TD children. On the right-hand side, bar charts represent average activations from the two clusters for each problem size.
3.4. Control analyses
Because our groups differed in IQ, with MD children being significantly lower than TD, we ran control analyses on a smaller sample of participants that were equated for IQ. After eliminating the TD children with the highest IQ scores and the MD children with the lowest IQ scores, 14 participants were retained in each group (MD: mean= 100.6, SD= 7.5 and for TD: mean= 105.9, SD= 9.6). Behavioral analyses yielded the same results as the larger groups.
The Numerosity and Rhyming localizers were defined using the same procedures and thresholds as for the entire group and yielded clusters of similar extent in the same areas. Within the numerical ROI, the same clusters were found for the interaction small versus large between groups and for the simple effect for MD children (<10 mm Euclidean distance between peaks) at a more lenient threshold due to the smaller sample. Importantly, at this lenient threshold, no relevant cluster was found in any other contrast. Within the rhyming ROIs, the same patterns of activations were found for the interaction small versus large between groups and for the simple effect for TD children. Despite the smaller sample, the STG/MTG cluster remained significant (<13 mm distance between peaks) at the same threshold as the main analysis. The IFG cluster was also found but failed to reach significance (<19 mm distance between peaks).
3.5. Brain-behavior correlations
To characterize the relations of skill with activations observed in verbal and numerical ROIs, average activations from the interaction clusters were correlated to standardized scores. Our standardized measures consisted of a phonological awareness and spatial relations test (see Table 1). We were interested in whether the phonological awareness measure was correlated with activation in the verbal ROIs, and whether the spatial relations measure was correlated with activation in the numerical ROIs. These correlations were done separately for each group. Values outside 2.5 standard deviations were excluded from analyses. Bonferroni's correction for multiple tests was calculated and the p-value threshold was adjusted to 0.008 to assess the significance of each correlation. Fisher transformation was then used to assess significant differences between the two correlation coefficients.
Phonological awareness was differentially correlated in the two groups in the verbal ROIs (see Figure 5). For the TD group, higher phonological awareness was associated with greater activation in the STG/MTG for small problems (r(20)=.70, p<.001), whereas this correlation was not significant for MD children (r(20)=−.18, n.s.). The two correlations were significantly different (Z=−3.08, p<.005). Moreover, MD children with lower phonological awareness showed greater activation in IFG for small problems (r(19)=−.54, p<.05). Although this correlation did not survive after correcting for multiple comparisons, the difference with TD children was significant (TD: r(19)=.21, n.s.; Z=−2.32, p<.05).
Figure 5.
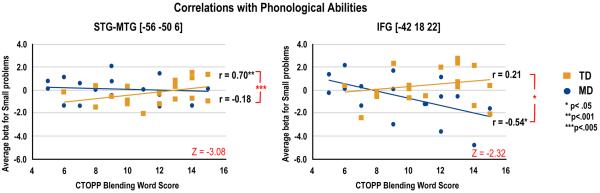
Correlations of activation during multiplication with standardized measures. (A) Correlations of phonological awareness (Blending Words) with activation in the STG-MTG for small problems showing a stronger positive relationship for the TD children. (B) Correlations of phonological awareness (Blending Words) with activation in the IFG for small problems showing a stronger negative relationship for the MD children.
All other correlations involving large problems and the spatial relations test were not significant after correcting for multiple comparisons or did not show a significant difference between groups.
4. Discussion
It has been proposed that an impaired system of numerical representations in the IPS could prevent MD children from moving towards verbal retrieval mechanisms over the course of development (De Smedt et al., 2011). Therefore, MD children should differ from typical children in their reliance on both numerical and verbal mechanisms when solving problems that normally rely on retrieval. Our study tested this hypothesis by comparing MD and TD children in their use of numerical and verbal regions while solving single-digit multiplication problems. To identify the regions involved in verbal and numerical processing we used independent localizers to improve specificity and selectivity of our analyses. Because small multiplication problems are more likely to be verbally retrieved compared to large multiplication problems (Siegler, 1988), problem size was manipulated to observe differences in modulation of neural responses in the two mechanisms.
Alterations in numerical mechanisms when solving multiplication problems
In the numerical ROI, which included both the right SPL and IPS, we expected to observe differences in activations between groups because MD is thought to stem from an impaired numerical system (Price et al., 2007; De Smedt et al., 2011). Although the interaction of group by problem size fell short of significance at the cluster level, the average beta weights in Figure 3 reveal that TD children show greater activation in the IPS as compared to MD children. This is in line with the general finding that the IPS is less activated in MD children when comparing quantities (Mussolin et al., 2010; Kucian et al., 2006) and when solving arithmetical facts (Ashkenazi et al., 2012). Our findings provide additional support for the hypothesis of a core deficit in the numerical system in MD.
We expected differences in the modulation of the IPS with problem size for the two groups. Previous studies have reported modulation of activation for TD children with task difficulty or complexity (Ashkenazi et al., 2012; Price et al., 2007; De Smedt et al., 2011) with greater activation for harder problems. However, activations in our numerical ROI did not show modulation with size for the TD group: both problem sizes elicited comparable activations. This could be explained by the relatively young age range tested here. Indeed, when the learning process is still ongoing, children are inconsistent in using the retrieval strategy (Cooney, et al., 1988) and eventually they might double check their answer through calculation procedures (Siegler, 1988). Moreover, children of different ages might use different strategies such that the youngest children in our group could be using more calculation strategies, whereas older children could rely more frequently on retrieval (Imbo and Vandierendonck, 2007; Steel and Funnell, 2001). The absence of modulation by problem size for our TD group is in contrast with that observed in the IPS by De Smedt et al. (2011). In this study, however, the authors did not use multiplication but rather addition problems. Critically, addition problems are learned earlier and tend to be easier than multiplication problems (Parkman and Groen, 1971; Groen and Parkman, 1972; Zbrodoff, 1995). Therefore, participants in De Smedt et al. (2011) might have more strongly engaged verbal representations, as compared to our participants, and might have almost exclusively relied on verbal retrieval for small problems.
In contrast to typically developing children, MD children showed a modulation of the neural response in the numerical ROI with greater activation for small compared to large problems. This result suggests that MD children were relying on calculation-based procedures to a greater extent in small compared to large problems. This result seems to be contradictory with the study from De Smedt et al. (2011) where the MD group relied on numerical calculations for small and large addition problems and did not show any modulation of the neural response with problem size in the right IPS. The authors argue that MD children were still relying on numerical calculations for both large and small problems. The difference in activation patterns in the IPS between our study and De Smedt et al. (2011) study is probably due to the difference in operation. Because addition problems are learned earlier and are easier compared to multiplication problems (Groen and Parkman, 1972; Zbrodoff, 1995), MD children in the De Smedt et al. (2011) study may have been able to engage their numerical representations for all problem sizes. Our study suggests that, although MD children might engage some numerical representations for solving smaller multiplication problems, they might fail to engage such representations for larger multiplication problems.
Alterations in verbal mechanisms when solving multiplication problems
The verbal ROI included the left STG/MTG as well as the left IFG. We found that this ROI was more activated for small problems compared to large problems for the TD group. This suggests that, in TD children, small problems were retrieved from verbal memory to a greater extent than larger problems. Because smaller problems are more frequent when starting to learn multiplication problems and are mastered earlier (Ashcraft, 1992; Siegler, 1988), the creation of long-term verbal representations might be facilitated. This result is consistent with previous findings showing an increase of involvement of the temporal cortex for multiplication problems with age (Prado et al., under review). Moreover, both training by repetition (Ischebeck, et al., 2007) and practice aiming at rote verbal memorization (Prado et al., 2013) have resulted in greater activations in the MTG. Therefore, the STG/MTG identified through our verbal localizer task may be associated with retrieval of stored verbal representations of problems and their solution. The modulation in IFG with greater activation for small problems might instead be related to the effortful control in individuating the correct answer from plausible competitors. In our paradigm, false trials presented answers that were strong competitors in the network (i.e. the solution to the adjacent problem). This might have increased the effort required to identify the correct answer. Our findings are consistent with the left IFG being more activated in adult participants with greater expertise and a larger number of stored arithmetical facts (Zamarian, et al., 2009), as well as being selectively activated in adults for large, thus harder, multiplication problems suggesting that weaker representations in MTG required greater cognitive control (Prado, et al. 2011).
The positive correlation between phonological awareness and activations elicited during small multiplication problems in the STG/MTG suggests that TD children with better language skills appear to rely more on verbal representations. We argue that better phonological skills may facilitate the consolidation of robust verbal representations of multiplication facts. Indeed, arithmetical facts, in particular those problems that are verbally retrieved, are assumed to be stored as phonological codes in a long-term verbal representation (Simmons and Singleton, 2008). Behavioral studies have highlighted a relation between phonological awareness and arithmetical fact performance (De Smedt, et al., 2010; Hecht, et al., 2001; Simmons and Singleton, 2008). Indeed, phonological awareness uniquely predicts improvement in general mathematical skills (Hecht et al., 2001) and more specifically, it is related to multiplication problems (De Smedt et al., 2010). Our study is the first neuroimaging evidence of a relation between phonological abilities and activations elicited during arithmetical fact retrieval. Because performance on phonological awareness is an index of the quality of children's long-term phonological representations (Fowler, 1991), this correlation more generally supports the conclusion that STG/MTG is responsible for the quality of the verbal representation of multiplication facts.
MD children did not show reliable activations of verbal regions, nor did they show modulations by problem size, suggesting that they do not consistently retrieve solutions verbally even for smaller problems. This result is in agreement with the finding from Ashkenazi et al. (2012) who observed weaker MTG activations in MD children compared to TD children when retrieving addition problems. Together with the weaker involvement of the numerical ROI in MD, the weaker involvement of the verbal ROI suggests that the impaired numerical system of MD children might prevent them from moving towards a verbally-based retrieval strategy. Being able to efficiently solve arithmetical facts requires the ability to verbally store and retrieve the solution from long-term memory (Ashcraft, 1992). A recent study has demonstrated that the brain areas involved when solving arithmetical facts are dependent on both the operation to be solved and the learning stage: with schooling there is a decreasing reliance on numerical processing areas with a consequent increasing use of verbal areas for multiplications, indicating a shift towards retrieval of verbal representations with arithmetical proficiency (Prado et al. under review). However, for an association to be stored in long-term memory, it has been argued that both the problem and the answer have to be present simultaneously in short-term memory (Baddeley, 1992; Geary, 1993). Because MD children take longer and have lower accuracies when learning multiplication problems (Geary, 2004), these associations may fail to develop or require a greater number of exposures of the same problem. Interference theories of arithmetical fact retrieval assume that a problem is associated with more answers than only the correct solution and the weaker the association with the correct answer, the greater the interference (Campbell, 1995). This interference argument is supported by the brain-behavior correlation where MD children with lower phonological awareness showed greater activation in IFG when processing small problems. Because MD children appear to have weak verbal representations of multiplication facts, any attempts to retrieve these representations by frontal regions are exacerbated by low phonological skills. Indeed, as lower phonological awareness has been associated with lower quality verbal representations (Elbro and Pallesen, 2002), it is possible that the task was more demanding on control processes in MD children.
Alternative explanations for the findings need to be reviewed. First, the groups differed in IQ, with MD children being significantly lower than TD. Although arguments have been raised against the necessity and adequacy in considering IQ in studies on learning disabilities (see Dennis, Francis, Cirino, Schachar, Barnes, and Fletcher, 2009), we ran the same analyses on a subset of participants that resulted in no statistical differences in IQ. Similar clusters and peaks, as well as same pattern of results were found. The results found in the equated groups mitigate concerns about an influence of IQ on the findings. Second, a possible contributing factor for the reduced brain activity for the MD group could be ascribed to a difference in brain integrity. Indeed, a study has found that MD children have lower gray matter density in the right IPS and in the left IFG compared to TD children (Rotzer et al., 2008). This structural difference could therefore contribute to the group differences but should not account for the within group modulation observed for the numerical processing. Finally, because MD children are more prone in giving up when challenged, we were concerned whether the modulation observed in the numerical ROI was due to lower percentage of no responses (i.e. not pressing the button for that trial) for larger problems, however, for both groups the difference in no responses for large and small problems was non-significant (p=.12 and p=.08 for MD and TD, respectively).
In conclusion, our results suggest that the creation of long-term verbal representations of the association between problems and answers are crucial for effectively solving multiplication problems. Typically developing children with higher phonological awareness are better able to form high quality verbal representations of the association between the problem and answer. The ability to rely on these representations for solving multiplication problems is a gradual process that might be compromised in children with math disability. It is possible that impaired numerical representations in children with math disability may hinder the creation of stable verbal representations for these arithmetic facts. To answer this question, it is crucial to perform longitudinal studies determining whether early neural processing of numerical information in the intra-parietal sulcus is predictive of later engagement of the verbal system in the middle temporal gyrus.
Acknowledgments
This project has been funded by the National Institute of Child Health and Human Development (grant number HD059177) awarded to J.R.B.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ansari D. Effects of development and enculturation on number representation in the brain. Nature reviews. Neuroscience. 2008;9(4):278–291. doi: 10.1038/nrn2334. [DOI] [PubMed] [Google Scholar]
- Andres M, Michaux N, Pesenti M. Common substrate for mental arithmetic and finger representation in the parietal cortex. NeuroImage. 2012;62(3):1520–1528. doi: 10.1016/j.neuroimage.2012.05.047. [DOI] [PubMed] [Google Scholar]
- Ashcraft MH. Cognitive arithmetic: A review of data and theory. Cognition. 1992;44:75–106. doi: 10.1016/0010-0277(92)90051-i. [DOI] [PubMed] [Google Scholar]
- Ashkenazi S, Rosenberg-Lee M, Tenison C, Menon V. Weak task-related modulation and stimulus representations during arithmetic problem solving in children with developmental dyscalculia. Developmental Cognitive Neuroscience. 2012;2(Suppl 1):S152–166. doi: 10.1016/j.dcn.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley A. Working Memory. Science. 1992;255(5044):556–559. doi: 10.1126/science.1736359. [DOI] [PubMed] [Google Scholar]
- Booth JR. Development and language. In: Koob G, Le Moal M, Thompson RF, editors. Encyclopaedia of Behavioral Neuroscience. Volume 1. Academic Press; Oxford: 2010. pp. 287–295. [Google Scholar]
- Butterworth B. Foundational numerical capacities and the origins of dyscalculia. Trends in Cognitive Sciences. 2010;14(12):534–541. doi: 10.1016/j.tics.2010.09.007. [DOI] [PubMed] [Google Scholar]
- Campbell JID. Handbook of mathematical cognition. Psychology Press; New York: 1995. [Google Scholar]
- Cooney JB, Swansons HL, Ladd SF. Acquisition of mental multiplication skill: Evidence from the transition between counting and retrieval strategies. Cognition and Instruction. 1988;5(4):323–345. [Google Scholar]
- Davis N, Cannistraci CJ, Rogers BP, Gatenby JC, Fuchs LS, Anderson AW, Gore JC. Aberrant functional activation in school age children at-risk for mathematical disability: a functional imaging study of simple arithmetic skill. Neuropsychologia. 2009;47(12):2470–2479. doi: 10.1016/j.neuropsychologia.2009.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennis M, Francis DJ, Cirino PT, Schachar R, Barnes MA, Fletcher JM. Why IQ is not a covariate in cognitive studies of neurodevelopmental disorders. Journal of the International Neuropsychological Society. 2009;15(3):331–343. doi: 10.1017/S1355617709090481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Smedt B, Holloway ID, Ansari D. Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency. NeuroImage. 2011;57(3):771–781. doi: 10.1016/j.neuroimage.2010.12.037. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Taylor J, Archibald L, Ansari D. How is phonological processing related to individual differences in children's arithmetic skills? Developmental Science. 2010;13(3):508–520. doi: 10.1111/j.1467-7687.2009.00897.x. [DOI] [PubMed] [Google Scholar]
- Elbro C, Pallesen BR. The quality of phonological reprsentations and phonological awareness: A causal link? In: Verhoeven L, Elbro C, Reitsma P, editors. Precursors of functional literacy. John Benjamins; Amsterdam and Philadelphia: 2002. pp. 17–32. [Google Scholar]
- Fayol M, Thevenot C. The use of procedural knowledge in simple addition and subtraction problems. Cognition. 2012;123(3):392–403. doi: 10.1016/j.cognition.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Fowler AE. How early phonological development might set the stage for phoneme awareness. In: Brady SA, Shankweiler D, editors. Phonological processes in literacy: A tribute to Isabelle Y. Liberman. Erlbaum; Hillsdale, NJ: 1991. pp. 97–117. [Google Scholar]
- Geary DC. Mathematical disabilities: Cognitive, neuropsychological and genetic components. Psychological Bulletin. 1993;114(2):345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematics and Learning Disabilities. Journal of Learning Disabilities. 2004;37(1):4–15. doi: 10.1177/00222194040370010201. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK. Numerical and arithmetical deficits in learning-disabled children: Relation to dyscalculia and dyslexia. Aphasiology. 2001;15(7):635–647. [Google Scholar]
- Groen GJ, Parkman JM. A chronometric analysis of simple addition. Psychological Review. 1972;79(4):329–343. [Google Scholar]
- Hecht SA, Torgesen JK, Wagner RK, Rashotte CA. The relations between phonological processing abilities and emerging individual differences in mathematical computation skills: a longitudinal study from second to fifth grades. Journal of Experimental Child Psychology. 2001;79(2):192–227. doi: 10.1006/jecp.2000.2586. [DOI] [PubMed] [Google Scholar]
- Hresko W, Schlieve P, Herron S, Swain C, Sherbenou R. Comprehensive Mathematical Abilities Test: Esaminer's manual. PRO-ED; Austin, TX: 2003. [Google Scholar]
- Imbo I, Vandierendonck A. The development of strategy use in elementary school children: working memory and individual differences. Journal of Experimental Child Psychology. 2007;96(4):284–309. doi: 10.1016/j.jecp.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Ischebeck A, Zamarian L, Egger K, Schocke M, Delazer M. Imaging early practice effects in arithmetic. NeuroImage. 2007;36(3):993–1003. doi: 10.1016/j.neuroimage.2007.03.051. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Montani TO. Cognitive arithmetic and problem solving: a comparison of children with specific and general mathematics difficutlies. Journal of Learning Disabilities. 1997;30(6):624–634. doi: 10.1177/002221949703000606. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Vogel SE, Starke M, Kremser C, Schocke M, Wood G. Developmental dyscalculia: compensatory mechanisms in left intraparietal regions in response to nonsymbolic magnitudes. Behavioral and Brain Functions. 2009;5:35. doi: 10.1186/1744-9081-5-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirk RE. Experimental design: Procedures for the behavioral sciences. 4th Ed. Sage; Thousand Oaks, CA: 2013. [Google Scholar]
- Kucian K, Loenneker T, Dietrich T, Dosch M, Martin E, Von Aster M. Impaired neural networks for approximate calculation in dyscalculic children: a functional MRI study. Behavioral and Brain Functions. 2006;2:31. doi: 10.1186/1744-9081-2-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazaika PK, Whitfield-Gabrieli S, Reiss AL. Artifact repair for fMRI data from high motion clinical subjects. Presentation at The Organization of Human Brain Mapping, 13th Annual Meeting.2007. [Google Scholar]
- Mazaika PK, Hoeft F, Glover G, Reiss A. Methods and software for fMRI analysis for clinical subjects. Paper presented at The Organization of Human Brain Mapping, 15th Annual Meeting.Jun 18–23, 2009. [Google Scholar]
- Mazzocco MMM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability (dyscalculia) Child Development. 2011;82(4):1224–1237. doi: 10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller K, Neuburger S, Kaufmann L, Landerl K, Nuerk H-C. Basic number processing deficits in developmental dyscalculia: Evidence from eye tracking. Cognitive Development. 2009;24(4):371–386. [Google Scholar]
- Mussolin C, De Volder A, Grandin C, Schlögel X, Nassogne M-C, Noël M-P. Neural correlates of symbolic number comparison in developmental dyscalculia. Journal of Cognitive Neuroscience. 2010;22(5):860–874. doi: 10.1162/jocn.2009.21237. [DOI] [PubMed] [Google Scholar]
- Nieder A, Dehaene S. Representation of number in the brain. Annual Review of Neuroscience. 2009;32:185–208. doi: 10.1146/annurev.neuro.051508.135550. [DOI] [PubMed] [Google Scholar]
- Parkman JM, Groen GJ. Temporal aspects of simple addition and comparison. Journal of Experimental Psychology. 1971;89:335–342. [Google Scholar]
- Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D, Dehaene S, Zorzi M. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010;116(1):33–41. doi: 10.1016/j.cognition.2010.03.012. [DOI] [PubMed] [Google Scholar]
- Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron. 2004;44(3):547–555. doi: 10.1016/j.neuron.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Pinel P, Dehaene S, Rivière D, LeBihan D. Modulation of parietal activation by semantic distance in a number comparison task. NeuroImage. 2001;14(5):1013–1026. doi: 10.1006/nimg.2001.0913. [DOI] [PubMed] [Google Scholar]
- Prado J, Lu J, Liu L, Dong Q, Zhou X, Booth JR. The neural bases of the multiplication problem-size effect across countries. Frontiers in Human Neuroscience. 2013;7 doi: 10.3389/fnhum.2013.00189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado J, Mutreja R, Booth JR. Developmental Science. Developmental dissociation in the neural responses to simple multiplication and subtraction problems. under review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado J, Mutreja R, Zhang H, Mehta R, Desroches AS, Minas JE, Booth JR. Distinct representations of subtraction and multiplication in the nueral system for numerosity and language. Human Brain Mapping. 2011;32(11):1932–1947. doi: 10.1002/hbm.21159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GR, Holloway I, Räsänen P, Vesterinen M, Ansari D. Impaired parietal magnitude processing in developmental dyscalculia. Current Biology. 2007;17(24):R1042–1043. doi: 10.1016/j.cub.2007.10.013. [DOI] [PubMed] [Google Scholar]
- Rotzer S, Kucian K, Martin E, Von Aster M, Klaver P, Loenneker T. Optimized voxel-based morphometry in children with developmental dyscalculia. NeuroImage. 2008;39(1):417–422. doi: 10.1016/j.neuroimage.2007.08.045. [DOI] [PubMed] [Google Scholar]
- Shalev RS, Gross-Tsur V. Developmental dyscalculia. Pediatric Neurology. 2001;24(5):337–342. doi: 10.1016/s0887-8994(00)00258-7. [DOI] [PubMed] [Google Scholar]
- Schneider W, Eschman A, Zuccolotto A. E-Prime User's Guide. Psychology Software Tools Inc; Pittsburgh: 2002b. [Google Scholar]
- Siegler RS. Strategy choice procedures and the development of multiplication skill. Journal of Experimental Psychology: General. 1988;117(3):258–275. doi: 10.1037//0096-3445.117.3.258. [DOI] [PubMed] [Google Scholar]
- Simmons FR, Singleton C. Do weak phonological Representations Impact on Arithmetic Development? Review of Research into Arithmetic and Dyslexia. Dyslexia. 2008;94:77–94. doi: 10.1002/dys.341. [DOI] [PubMed] [Google Scholar]
- Steel S, Funnell E. Learning multiplication facts: a study of children taught by discovery methods in England. Journal of Experimental Child Psychology. 2001;79(1):37–55. doi: 10.1006/jecp.2000.2579. [DOI] [PubMed] [Google Scholar]
- Wagner RK, Torgesen JK, Rashotte CA. The Comprehensive Test of Phonological Processing. PRO-ED; Austin, TX: 1999. [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. The Psychological Corporation; San Antonio, TX: 1999. [Google Scholar]
- Wilson AJ, Dehaene S. Number sense and developmental dyscalculia. In: Coch D, Dawson G, K Fischer, editors. Human behavior, learning, and the developing brain: atypical development. Guildford Press; New York: 2007. pp. 212–238. [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson III Tests of Achievement. The Riverside Publishing Company; Itasca, IL: 2001. [Google Scholar]
- Zamarian L, Ischebeck A, Delazer M. Neuroscience of learning arithmetic - Evidence from brain imaging studies. Neuroscience and Biobehavioral Reviews. 2009;33(6):909–925. doi: 10.1016/j.neubiorev.2009.03.005. [DOI] [PubMed] [Google Scholar]
- Zbrodoff NJ. Why is 9+7 harder than 2+3? Strength and interference as explanations of the problem-size effect. Memory & cognition. 1995;23(6):689–700. doi: 10.3758/bf03200922. [DOI] [PubMed] [Google Scholar]