Detection of large ions in time-of-flight mass spectrometry: effects of ion mass and acceleration voltage on microchannel plate detector response

Abstract

In time-of-flight mass spectrometry (TOF-MS), ion detection is typically accomplished by the generation and amplification of secondary electrons produced by ions colliding with a microchannel plate (MCP) detector. Here, the response of an MCP detector as a function of ion mass and acceleration voltage is characterized, for peptide/protein ions ranging from 1 kDa to 290 kDa in mass, and for acceleration voltages from 5 kV to 25 kV. A non-destructive inductive charge detector (ICD) employed in parallel with MCP detection provides a reliable reference signal to allow accurate calibration of the MCP response. MCP detection efficiencies were very close to unity for smaller ions at high acceleration voltages (e.g. angiotensin, 1,046.5 Da, at 25 kV acceleration voltage), but decreased to ~11% for the largest ions examined (Immunoglobulin G (IgG) dimer, 290 kDa) even at the highest acceleration voltage employed (25 kV). The secondary electron yield γ (average number of electrons produced per ion collision) is found to be proportional to mv^3.1 (m: ion mass, v: ion velocity) over the entire mass range examined, and inversely proportional to the square root of m in TOF-MS analysis. The results indicate that although MCP detectors indeed offer superlative performance in the detection of smaller peptide/protein species, their performance does fall off substantially for larger proteins, particularly under conditions of low acceleration voltage.

INTRODUCTION

The critical protein actors in biological systems are the intact proteoforms, namely the different forms of proteins, produced from the genome in a variety of splice forms, and adorned with a myriad of post-translational modifications that modulate their function [1]. However, today’s dominant “bottom-up” proteomic strategies, which identify and quantify peptides derived from proteins, rather than the proteins themselves, do not deliver this crucial protein-level information to biologists. A challenging problem in biological mass spectrometry is thus the development of new approaches to the analysis of complex proteoform mixtures, revealing the identities and abundances of all detectable proteoforms present [2, 3].

Protein ions are generally produced for mass spectrometry (MS) analysis in either of two forms: as the distribution of highly charged ions produced by electrospray ionization (ESI)[4]; or as singly charged ions produced either by matrix-assisted laser desorption/ionization (MALDI)[5, 6], or by charge reduction of ESI-generated ions [7–9]. In the latter case, which has the advantage of greatly decreased spectral complexity and correspondingly increased ion intensity, the ions must be analyzed by time-of-flight mass spectrometry (TOF-MS), as this is the only mass analyzer able to accommodate the high m/z range of such singly charged proteins. Although this is an attractive approach to the analysis of proteoform mixtures, in fact relatively little work has been reported of this type, largely due to limitations of existing MS instrumentation [10, 11]. One of the significant instrumentation challenges to consider is the efficiency of detection of the large, slow-moving protein ions produced in TOF-MS.

There are three primary mechanisms for the detection of ions in mass spectrometry; these are direct charge detection (as in the Faraday cup detector), image charge detection (as in the inductive detector), and secondary electron generation (as in electron multiplier (EM) and microchannel plate (MCP) detectors)[12]. Direct charge detection is important historically, but finds use almost solely in magnetic sector instruments because of its relatively low sensitivity compared to other detector types. Inductive detectors, although even less sensitive than direct charge detectors, are the only non-destructive detection modality, and hence are critical to Fourier transform instruments such as the Fourier transform ion cyclotron resonance (FTICR) and Orbitrap mass analyzers, where signal averaging of circulating ion packets is fundamental to the instruments operation. TOF ion detectors need to have large areas, rapid response times to provide good timing resolution and correspondingly accurate m/z determinations, and high sensitivity. These criteria are best met by the EM and MCP detectors, based upon their generation of secondary electrons [10, 13–18]. Our focus in the present work is upon the performance of MCP detectors, as these are far more widely employed than EM detectors.

In TOF mass analyzers, all ions generated in the source are subjected to the same acceleration voltage U, and thus, to first order, all singly charged ions acquire the same kinetic energy, qU = 1/2mv², where q is the ion charge, m is the ion mass, and v is the ion velocity [19]. Singly charged ions of greater mass therefore necessarily move more slowly than smaller ions, and thus impinge upon the detector with lower velocity. Previous work has characterized MCP response as a function of ion mass and velocity, and shown a strong dependence of the efficiency of secondary electron generation upon both, with detector response increasing proportionally to ion mass, but decreasing with a roughly fourth-order dependence on ion velocity [17]. However, this work only examined a mass range up to 66 kDa, and accordingly left unaddressed the question of how MCPs respond to protein ions outside that range. In the human proteome, for example, more than a third of proteins have masses over 50 kDa [3], and thus the issue of ion detection sensitivity for these large macromolecular species is critical. It is important to characterize the performance of these existing detectors in order to be able to evaluate their merits relative to potential alternative detection modalities [20–22].

We present here a detailed characterization of MCP response as a function of ion mass and acceleration voltage. We analyzed a set of 10 peptide/protein ions ranging in mass from 1 to 294 kDa, a four-fold greater mass range than previous studies, and subjected them to acceleration voltages from 5 to 25 kilovolts (kV). Ions were generated by MALDI, and detected in parallel by both an in-line non-destructive inductive charge detector (ICD) mounted in the flight tube, and an MCP detector positioned at the end of the flight tube. The ICD provides an absolute measure of the number of ions present in the ion packet, allowing an accurate calibration of the MCP response. The values of the secondary electron yield γ (average number of electrons produced per ion collision), and the detection efficiency ε (probability of generation of one or more secondary electrons) were determined for each peptide/protein and acceleration voltage.

EXPERIMENTAL

Reagents and Materials

All peptides, proteins, matrices and solvents were obtained from Sigma-Aldrich (St. Louis, MO). The peptide/protein standards are listed in Table 1. Angiotensin II, adrenocorticotropic hormone (ACTH) fragment 18–39, insulin, cytochrome c, apomyoglobin, aldolase, and albumin were purchased as ProteoMass^™ MALDI-MS standards and dissolved in 0.1% trifluoroacetic acid (TFA) to 100 μM, except for insulin in 1% TFA. Phosphorylase b (rabbit muscle) and IgG (rabbit serum) were dissolved in 50% acetonitrile/50% (0.05% TFA) to 100 μM. α-Cyano-4-hydroxycinnamic acid (CHCA) and sinapinic acid were prepared as nearly saturated solutions at 10 mg/mL in 50% acetonitrile/50% (0.05% TFA). CHCA was used as matrix for angiotensin II, ACTH fragment, insulin and cytochrome c, while sinapinic acid was employed for the other proteins. MALDI samples were prepared by combining 0.7 μL of matrix solution with 0.7 μL of sample solution directly on the stainless steel MALDI sample plate, followed by solvent evaporation at atmospheric pressure and room temperature.

Table 1.

Peptide/protein standards

peptides/proteins	molecular weight (Da)
angiotensin II	1045.5
ACTH fragment	2464.2
insulin	5729.6
cytochrome c	12361
apomyoglobin	16951
aldolase	39211
albumin	66429
phosphorylase b	97,200
IgG	145,000

Instrumentation

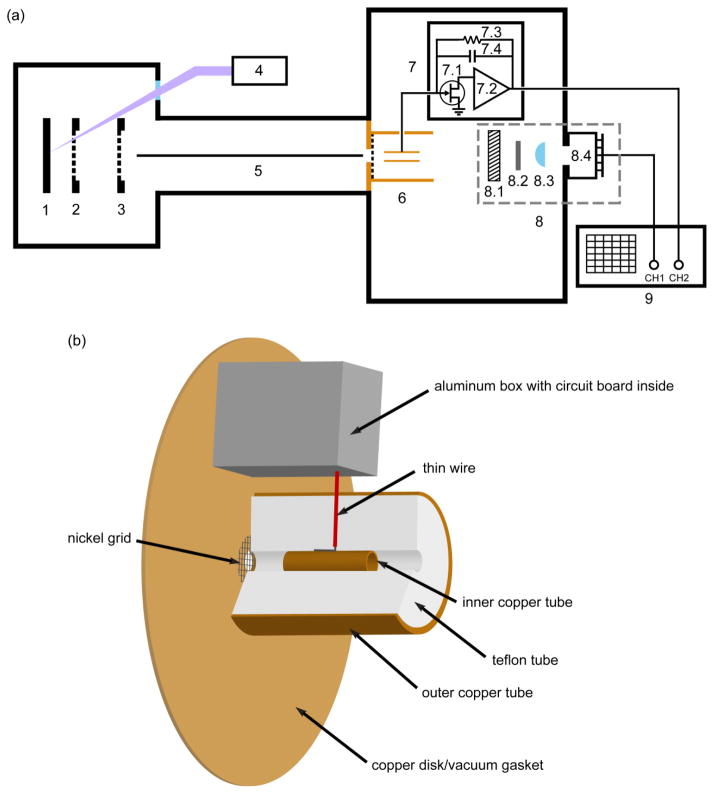
Experiments were performed on a modified linear Voyager-DE STR mass spectrometer (Perseptive Biosystems Inc, Framingham, MA) diagrammed in Figure 1(a). The ions were detected at the end of the flight tube with the manufacturer-supplied High Current Detector (HCD). This detector consists of a nichrome-coated MCP followed by a scintillator that converts electrons to photons, which are then detected with a photosensor module (Type No. H5773, Hamamatsu Photonics, Bridgewater, NJ). This single MCP detector is less susceptible to saturation than the dual chevron MCP employed in a previous study [10]. The MCP has the following properties; 40 mm quality diameter, 32 μm channel center-to-center spacing, 25 μm channel diameter, 8° bias angle, 40:1 aspect ratio, 30–125 μA bias current, and was obtained from JBI Scientific (Huntsville, TX) to replace the original MCP. The MCP was operated at a potential of 960 V for all experiments reported here. The photosensor module is controlled by an attached circuit board that also provides a suitable output voltage (referred to below as the “MCP voltage”), which was monitored in the present work with a Tektronix DPO 2024B oscilloscope (Tektronix Inc., Beaverton, OR).

Figure 1.

(a) Instrument schematic diagram showing the MALDI mass spectrometer with two detectors. 1: sample plate. 2: variable-voltage grid. 3: ground grid. 4: nitrogen laser. 5: guide wire. 6: inductive charge detector (ICD). 7: ICD circuit board. 7.1: 2SK152 FET. 7.2: A250 charge-sensitive preamplifier. 7.3: 1 GΩ feedback resistor. 7.4: parasitic capacitance shown as a symbolic feedback capacitor. 8: high current detector (HCD). 8.1: MCP. 8.2: scintillator. 8.3: focusing lens. 8.4: photosensor module with attached circuit board. 9: oscilloscope. (b) Expanded view of the ICD assembly, components 6 and 7.

An inductive charge detector (ICD) was placed in the ion path in front of the MCP detector to provide an absolute reference signal for the number of ions present in each ion packet. The ICD (illustrated in Figure 1(b)) was constructed based on the design of Fuerstenau and Benner [23]. As shown in the diagram, it consists of three concentric tubes: The innermost tube is copper, 1.18″ in length, with a 0.25″ outer diameter and 0.20″ inner diameter, and serves as the image charge sensing element. It is positioned in contact with a piece of 22 gauge stranded silver coated copper wire in the center of the second tube, which is made of Teflon, 2.00″ in length, with a 1.51″ outer diameter and 0.25″ inner diameter, and serves as an insulating spacer. The third outer tube is copper, also 2.00″ in length, with a 1.62″ outer diameter and 1.51″ inner diameter, and serves as a radiofrequency (RF) shield for the image charge pickup tube. The front end of the Teflon tube is mounted on a home-made 4.74″ diameter copper disk with a center hole of 0.25″ diameter, which also served as the vacuum flange gasket used to join two segments of the flight tube. An 88% transmission electroformed nickel grid (Industrial Netting, Minneapolis, MN) was inserted between the flange and the Teflon tube to provide an RF shield (keeping electric fields due to approaching ions from inducing charge on the detector). This design positions the ICD coaxial with the flight tube while providing important RF shielding protecting the image charge sensor from external fields. The distance between the exit of the ICD and the MCP front surface is 5.0″. With this short distance and the large quality diameter of the MCP, all ions passing through the ICD strike the MCP.

Ions passing through the inner tube induce image charges on the tube surface. The tube is connected by the 22-gauge wire to a 2SK152 field-effect transistor (FET) coupled to an A250 charge-sensitive preamplifier (Amptek Inc. Bedford, MA) for signal processing (see Figure 1(a)). The electronic components are installed on an in-house fabricated circuit board, which is enclosed in an aluminum box placed inside of the flight tube to minimize RF pickup. The feedback loop of the preamplifier contains a 1 GΩ resistor and a parasitic capacitance C_f estimated to be about 0.13 picofarad (pF). This estimate is obtained by using the circuit to measure a known quantity of charge placed on a 2.2 pF test capacitor (C_test) with an 80 mV input voltage (V_in). The output voltage peak value is given by V_out = V_in × C_test/C_f. This equation also shows that maximum gain is obtained when the feedback capacitance is minimized. A similar measurement applying V_in to the outer copper tube instead of a test capacitor yields a capacitance between the two copper tubes of 3.4 pF. The large feedback resistor is required to keep the RC time constant (in this case, 130 μs) much longer than the time required for the slowest ion packet to pass entirely through the ICD. This prevents the output signal from starting to decrease before it reaches the peak value. The output of the preamplifier is connected to the oscilloscope with the input impedance set to 1 MΩ.

MALDI-TOF analysis

Mass spectra were acquired in positive ion mode at five acceleration voltages (5kV, 10kV, 15kV, 20kV, 25 kV), with acquisition parameters (grid voltage, delayed extraction time and guide wire voltage) optimized for each analyte. At least 3 spectra were taken at six to eight different laser intensities in order to vary the ion yield. Each spectrum was an average of signals from 50 laser shots. Spectra obtained from the ICD and MCP were acquired simultaneously on different channels of an oscilloscope, and were thereby automatically synchronized in data acquisition, for both channels were triggered by the same signal provided by the laser upon firing.

MCP detector efficiency measurements

Overview

The ICD is employed here to provide an absolute measure of the number of ions present in each ion packet, allowing an accurate calibration of the MCP response. The manner in which this is accomplished is described below.

ICD signal

When an ion packet with N_i ions carrying a charge Q is present in the ICD, an opposite charge less than or equal to Q is induced on the ICD and converted to a voltage by the charge-sensitive preamplifier. The intensity of the ICD signal I_ICD is a voltage proportional to the amount of charge

$${\mathrm{I}}_{\text{ICD}}={\mathrm{V}}_{\text{ICD}}=\mathrm{Q}/{\mathrm{C}}_{\mathrm{f}}={\mathrm{N}}_{\mathrm{i}}\text{ze}/{\mathrm{C}}_{\mathrm{f}}$$ (1)

where C_f is the feedback capacitance of the preamplifier, z is the number of charges on each ion and e is the charge of an electron [24]. (For clarity, the induced charge is approximated here as equal to Q.).

MCP signal

In contrast to the ICD, which responds to the charges within it collectively, MCP detectors respond to the ions individually. Each ion entering one of the microchannels may eject zero to n secondary electrons from the channel wall, and these electrons then generate more electrons when they are accelerated into the channel wall by the voltage applied to the MCP. If no secondary electron is emitted initially, the ion is not detected. It has been shown previously that the secondary electron multiplicity is described by a Poisson distribution

$${\mathrm{P}}_{\mathrm{n}}={\mathrm{\gamma }}^{\mathrm{n}}{\mathrm{e}}^{-\mathrm{\gamma }}/(\mathrm{n}!)$$ (2)

where P_n is the probability of emitting n secondary electrons per ion impact, and γ is the average number of secondary electrons emitted per ion impact, known as the secondary electron yield [25].

Calibrating the MCP response with the ICD

To use the ICD signal as a calibration for the MCP response, it is necessary to account for several important differences between the signals at the two detectors. First, the MCP is located further down the flight tube than the ICD, and thus the signals are offset in time. Second, the ion packets expand as they travel down the flight tube, and thus have different lengths at the two detectors. Third, the ion packets are substantially longer in space (typically 10–20 cm) than the length of the ICD (3 cm). It is thus essential to compare only the same part of the ion packets for both detectors, namely the center region yielding the maximum signal intensity. Finally, whereas the ICD signal corresponds to the voltage produced by the ions inside the image charge sensor, the MCP detector produces voltage independently from each microchannel that is activated by an ion collision, and thus the MCP signal for an ion packet corresponds to a sum of the voltages produced from each time point taken across the peak. The following procedure was employed to process the detector signals to yield a correct calibration, based upon these considerations.

1. Obtain peak time and magnitude of the ion packet from the ICD spectrum.

2. Obtain peak time of the ion packet from the corresponding MCP spectrum.

3. Calculate the velocity of the center ions from the MCP peak time and the distance between the MCP and the sample plate.

4. Calculate the time when the center ions are at the middle of the inner copper tube of the ICD based on their velocity (from 3) and the distance between the ICD and the sample plate.

5. Calculate the velocities of the ions at the inlet and outlet of the inner copper tube separately based on the result of 4) and the inner copper tube length.

6. Calculate the difference in time (Δt) for the inlet and outlet ions (from 5) to arrive at the MCP based on the result of 5) and the distance between the MCP and sample plate.

7. Integrate the MCP voltage across the peak over the time range Δt. Move the integral across the MCP peak and find the maximum (the portion of the peak containing the maximum area).

8. A correction is also needed to compensate for the fact that the time interval between data points was longer for spectra acquired on larger, slower-moving ions. Intervals between data points were 32 nsec (angiotensin II, ACTH fragment (15 to 25 kV)), 64 nsec (ACTH fragment (5 kV and 10 kV), insulin), 128 nsec (cytochrome c, apomyoglobin, aldolase (10 to 25 kV)), or 320 nsec (aldolase (5 kV), albumin, phosphorylase b, IgG). The correction factor f_c is calculated as the time interval employed for the sample, divided by 32 nsec, which was the time interval employed for the shortest mass spectra acquired. The correction factors employed thus have values of 1, 2, 4, or 10.

The intensity of the MCP signal for each spectrum is then given by

$${\mathrm{I}}_{\text{MCP}}=\mathrm{\sum }{\mathrm{V}}_{\text{MCP}}\times {\mathrm{f}}_{\mathrm{c}}$$ (3)

and may also be expressed as

$${\mathrm{I}}_{\text{MCP}}={\mathrm{N}}_{\mathrm{e}}\mathrm{G}$$ (4)

where N_e is the number of total secondary electrons generated by the ion packet on the MCP channel wall, and G is the voltage resulting from one secondary electron. N_e is given by

$${\mathrm{N}}_{\mathrm{e}}={\mathrm{N}}_{\mathrm{i}}\mathrm{f}\mathrm{\gamma }$$ (5)

where f is the open area ratio of the MCP (the ratio of the active MCP area to the entire MCP area). Combining equations (1), (4), and (5) yields the following expression for γ, the secondary electron emission yield:

$$\mathrm{\gamma }={\mathrm{N}}_{\mathrm{e}}/({\mathrm{N}}_{\mathrm{i}}\mathrm{f})=({\mathrm{I}}_{\text{MCP}}/{\mathrm{I}}_{\text{ICD}})\mathrm{z}(\mathrm{e}/{\mathrm{C}}_{\mathrm{f}}\text{fG})$$ (6)

The constant e/C_ffG has a value of 0.50 based upon the results reported by Geno et al [13]. They determined this value for the bradykinin [M+H]⁺ ion (1060 Da) at 3.0×10⁴ m/s, which is very close to that for the angiotensin II [M+H]⁺ ion (1046.5 Da) at 3.0×10⁴ m/s in the present work due to the similarity in their masses and velocities. Thus, all of the factors in equation (6) are either known, or measured, permitting the calculation of γ for each mass spectrum obtained.

The Poisson distribution shown in equation (2) above permits calculation of the probability that an ion collision with the MCP is detected, by producing one or more secondary electrons. Thus

$$\mathrm{\epsilon }=1-{\mathrm{P}}_0=1-{\mathrm{e}}^{-\mathrm{\gamma }}$$ (7)

where ε is the MCP detection efficiency [13].

MCP detector saturation

The MCP detector is normally operated at high gain (~1000 V) for TOF analysis, in order to provide maximum detection sensitivity [26]. In this mode, substantial numbers of electrons are depleted from the channel wall as the secondary electrons produced in the initial ion collision are amplified exponentially along the channel. Due to the low recharge current, which is limited by the high resistance of the MCP material, the charges depleted from the channel wall require time to be fully replenished. If ions strike the MCP before sufficient recharge time has passed, the gain of the channel is lower and the MCP appears “saturated”. This period of time, called “dead time”, is on the order of milliseconds. This millisecond period is longer than the flight time of the slowest ions in this study (0.6 ms) but shorter than the intervals between two laser shots (333 ms).

MCP saturation requires special attention when ion quantification involves signals from the MCP detector. Three situations where the MCP signals are at risk of being reduced by saturation are as follows.

1. Peaks following large matrix ion peaks.

2. Peaks following large analyte peaks within the same spectrum; for example, a singly charged dimer ([2M+H]⁺) signal may be reduced by a previous large monomer peak ([M+H]⁺).

3. When the ion density in an ion packet is high, two ions have a higher chance of entering the same channel.

Spectra in which saturation effects were present were identified and eliminated during data processing as described in the following section.

Data processing

The acquired spectra were smoothed by locally weighted scatterplot smoothing (LOESS) to improve signal-to-noise [27]. LOESS employs a smoothing parameter α, which is a measure of the number of data points included in the local averaging process. Larger values of α thus correspond to more smoothing, and lower values of α to less smoothing. As the velocity of the ion increases, the ion packet expands less in its flight direction (due to the shorter flight time) and its peaks on both detectors are narrower. It is thus necessary to reduce α in order to maintain optimum smoothing while retaining peak shape. We found empirically that using the relations α_MCP = 13 (km/sec)/velocity (km/sec) for MCP spectra and α_ICD = 4α_MCP = 52 (km/sec)/velocity (km/sec) for ICD spectra yielded good results. The smoothing parameter employed for the ICD spectra was 4 times greater than that employed for the MCP spectra due to the innate differences in time response of the two detectors. MATLAB was used to perform LOESS for each spectrum and to then calculate I_ICD and I_MCP.

It was also necessary to estimate baselines in order to calculate peak heights in I_ICD and I_MCP calculations. In the case of the ICD, the estimated peak start point and end point were connected to form a local baseline. I_ICD was then calculated by subtracting the value of the baseline at the time of the peak maximum from the peak value. For the MCP spectra, the last 60 data points of the spectrum were taken as the baseline, and I_MCP was calculated by subtracting the average value of the baseline from each data point. The (I_ICD, I_MCP) data set was eliminated if I_ICD was below 0.2 mV, as these ICD peaks were too weak to be quantified accurately.

The data sets impacted adversely by MCP saturation were identified by comparing the I_ICD/I_MCP ratios obtained for a given analyte at the same acceleration voltage. Saturation is more of a problem when higher laser pulse intensities are employed, as this produces higher levels of both matrix and analyte ions. We purposely used a range of laser intensities from near threshold to substantially higher levels, in order to be able to observe the onset of saturation effects. When the MCP exhibits saturation, the I_ICD/I_MCP ratio rises due to the lower I_MCP value. The five (I_ICD, I_MCP) data sets corresponding to the lowest I_ICD values, but still above the 0.2 mV I_ICD threshold, were used to calculate the average I_ICD/I_MCP ratio and its standard deviation. Data sets lying 2 or more standard deviations away from the average ratio were discarded. This allowed elimination of all spectra in which saturation was occurring.

RESULTS AND DISCUSSION

The major results of this study consist of the experimentally determined values for the MCP secondary electron yield γ and detection efficiency ε for the set of 10 peptide/protein ions ranging in mass from 1 to 290 kDa, and subjected to acceleration voltages from 5 to 25 kV. These results are presented in Table 2; representative spectra are shown in Figure 2; and selected plots illustrating the important trends are shown in Figures 3–5.

Table 2.

Data summary showing the measured velocity (v), secondary electron yield (γ) and detection efficiency (ε) for the 10 peptide/protein ions at various acceleration voltages.

peptide/protein (ion mass)	acceleration voltage (kV)	v (km/s)	γ	γ/m	ε
angiotensin II (1046.5 Da)	25	68	1.6	1.5E-03	0.79
	20	61	1.4	1.3E-03	0.74
	15	53	1.5	1.5E-03	0.78
	10	43	1.2	1.1E-03	0.69
	5	30	0.49	4.7E-04	0.39
ACTH fragment (2465.2 Da)	25	44	2.0	7.9E-04	0.86
	20	39	0.83	3.4E-04	0.56
	15	34	1.1	4.6E-04	0.68
	10	28	0.40	1.6E-04	0.33
	5	20	0.11	4.5E-05	0.10
insulin (5730.6 Da)	25	29	1.4	2.4E-04	0.74
	20	26	1.1	1.9E-04	0.66
	15	22	0.54	9.5E-05	0.42
	10	18	0.22	3.9E-05	0.20
	5	13	0.051	8.9E-06	0.050
cytochrome c (12362 Da)	25	19	0.69	5.6E-05	0.50
	20	17	0.48	3.9E-05	0.38
	15	15	0.32	2.6E-05	0.28
	10	12	0.16	1.3E-05	0.15
	5	8.6	0.086	6.9E-06	0.082
apomyoglobin (16952 Da)	25	17	0.44	2.6E-05	0.36
	20	15	0.32	1.9E-05	0.27
	15	13	0.29	1.7E-05	0.25
	10	10	0.15	8.7E-06	0.14
	5	7.4	0.070	4.1E-06	0.068
aldolase (39212 Da)	25	11	0.31	7.9E-06	0.27
	20	9.7	0.27	6.9E-06	0.24
	15	8.4	0.26	6.7E-06	0.23
	10	6.8	0.14	3.6E-06	0.13
	5	4.8	0.023	5.9E-07	0.023
albumin (66430 Da)	25	8.3	0.30	4.5E-06	0.26
	20	7.5	0.30	4.5E-06	0.26
	15	6.4	0.21	3.2E-06	0.19
	10	5.2	0.079	1.2E-06	0.076
	5	3.6	0.0088	1.3E-07	0.0087
phosphorylase b (97.2 kDa)	25	6.9	0.29	2.9E-06	0.25
	20	6.2	0.26	2.7E-06	0.23
	15	5.3	0.16	1.7E-06	0.15
	10	4.3	0.037	3.8E-07	0.036
	5	-	-	-	-
IgG (145 kDa)	25	5.6	0.28	1.9E-06	0.24
	20	5.0	0.17	1.2E-06	0.16
	15	4.3	0.077	5.3E-07	0.074
	10	3.5	0.013	9.3E-08	0.013
	5	-	-	-	-
IgG [2M+H] (290 kDa)	25	4.0	0.12	4.1E-07	0.11
	20	3.5	0.052	1.8E-07	0.052
	15	-	-	-	-
	10	-	-	-	-
	5	-	-	-	-

- indicates signal on one or both detectors is below limit of detection.

Figure 2.

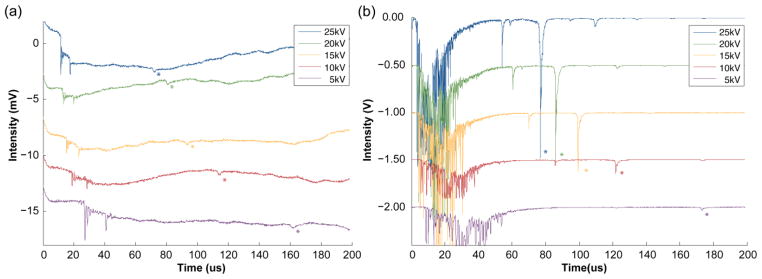
Comparison of insulin MALDI spectra acquired with the (a) ICD and (b) MCP detector at different acceleration voltages. [M+H]⁺ peaks are denoted with an asterisk. Peak heights in the ICD spectra are all of comparable magnitudes, while peak heights in the MCP spectra vary by ~50 fold. The mass spectra corresponding to acceleration voltages of 20 to 5 kV are offset vertically from the 25 kV spectrum by −5 mV increments in (a) and −0.5 V increments in (b) to create a stacking view. (Matrix peaks (those peaks occurring before ~50 μsec) in the 10kV and 5kV spectra in (b) were truncated during data acquisition due to the oscilloscope setting employed to expand the low intensity analyte peaks.)

Figure 3.

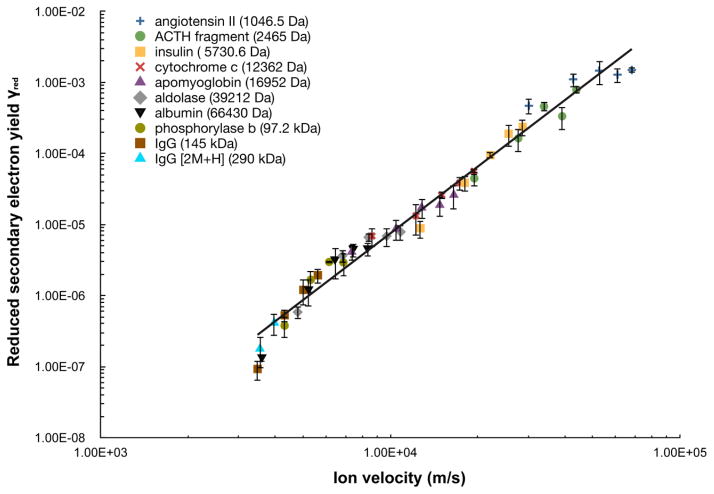
Reduced secondary electron yield γ_red of the MCP detector for 10 peptide/protein ions plotted as a function of ion velocity. Note that multiple ion velocity data points are present for each peptide/protein due to the various acceleration voltages employed. All ions are [M+H]⁺ ion except for the singly charged dimer of IgG. The solid line is a power law fit to the data with the function γ_red = γ/m = 2.6×10⁻¹⁸ v^3.1 (R² = 0.978). Error bars correspond to ± one standard deviation.

Figure 5.

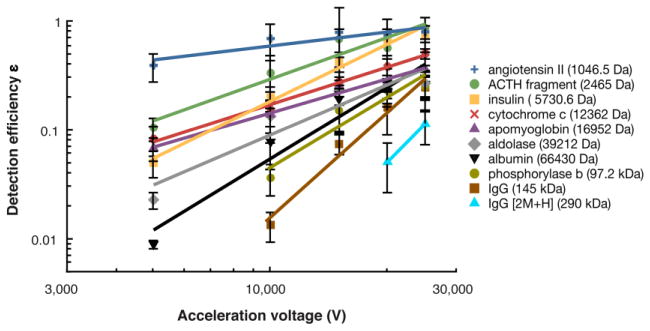
MCP secondary electron yield ε plotted as a function of acceleration voltage. For each peptide/protein ion, the data is fit to a power law function as indicated by the solid lines. Error bars correspond to ± one standard deviation.

ICD and MCP mass spectra

Figure 2 shows examples of typical MALDI-TOF mass spectra obtained for insulin (5729.6 Da) simultaneously from the ICD and MCP detectors at acceleration voltages from 5 to 25 kV. Important aspects of the detector responses are evident in these spectra. First, the insulin peaks (indicated by the asterisks) observed in the ICD spectra (panel a) are all similar in magnitude across the full range of acceleration voltages. This contrasts markedly with the peaks obtained from the MCP detector (panel b), which show dramatically decreased intensities at the lower acceleration voltages (compare 25kV and 5 kV in panel b). At a 5kV acceleration voltage, the two detectors have comparable sensitivity, but at higher acceleration voltages the MCP shows much better sensitivity than the ICD. In both cases the ion flight times increase at lower acceleration voltages as expected for a TOF measurement. The ICD signal also permits the number of ions that give rise to the analyte peaks in the mass spectra to be estimated: in the spectra shown in Figure 2, the insulin peaks correspond to approximately 400 – 450 ions; the ion packets corresponding to the data in Table 2 contain 200 – 3000 ions.

MCP secondary electron yield and detection efficiency

Two detector parameters are of particular utility for evaluating MCP detector response: the secondary electron yield γ (average number of electrons produced per ion collision), and the detection efficiency ε (probability of generation of one or more secondary electrons).

MCP secondary electron yield

Table 2 shows the values obtained for the secondary electron yield γ for all peptides/proteins and acceleration voltages examined. The values range from somewhat greater than unity for the two peptides (1.6 and 2.0 respectively for the 1 kDa angiotensin ion and the 2.5 kDa ACTH fragment ion at 25 kV acceleration voltage) to as low as 0.013 for the 145 kDa IgG ion at 10 kV acceleration voltage. In accord with previous studies [13, 17], the results show a linear dependence of γ on ion mass, and a power law dependence on ion velocity. Figure 3 shows a log-log plot of the “reduced” secondary electron yield γ_red = γ/m as a function of velocity, which fits well (R² = 0.978) to the power law function

$${\mathrm{\gamma }}_{\text{red}}=\mathrm{\gamma }/\mathrm{m}=2.6\times {10}^{-18}{\mathrm{v}}^{3.1}$$ (8)

Interestingly, the value of the velocity exponent, 3.1, differs from values of 4.3 previously reported by Westmacott et al [17] and of 4.4 by our group [10], but is similar to the value of 3.2 reported by Qiao et al [28] and the value of 3.3 reported for a CsI surface by Westmacott et al [16] in an earlier study. These differences are likely due at least in part to the different properties of the detector surface materials, which affect both the work function and the secondary electron yield. In addition, in our previous work we employed the result of Gajewski [29], indicating that the charge induced on a conducting ring is proportional to ion velocity; we have since determined that this relationship is not appropriate for this application, and developed the alternative analysis described in the experimental section above to obtain the velocity dependence shown. A striking feature of the plot shown in Figure 3 is the excellent fit obtained to this single function over four orders of magnitude in γ_red.

Approximating the value of the velocity exponent in equation (8) as 3.0, and combining that equation with the basic equation of TOF-MS

$$\mathrm{v}={(2\text{Uze}/\mathrm{m})}^{1/2}$$ (9)

where U is the acceleration voltage, yields the relation

$$\mathrm{\gamma }=7.4\times {10}^{-18}{(\text{Uez})}^{3/2}{\mathrm{m}}^{-1/2}$$ (10)

This shows that for a given acceleration voltage, the MCP secondary electron yield of the ions varies inversely with the square root of ion mass. Figure 4(a) shows log-log plots (γ vs mass) of equation (10) for each of the five acceleration voltages. The slopes range from −0.48 (25kV) to −0.78 (5 kV), in reasonable agreement with the value of −0.5 expected from equation (10).

Figure 4.

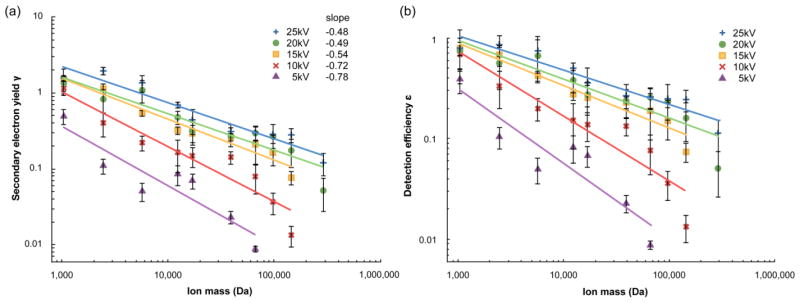
MCP secondary electron yield γ (a) and detection efficiency ε (b) plotted as a function of ion mass. At each acceleration voltage, the data is fit to a power law function as indicated by the solid lines. Error bars correspond to ± one standard deviation.

MCP detection efficiency

Table 2 shows the values obtained for the MCP detection efficiency ε for all peptides/proteins and acceleration voltages examined, and plots are shown in Figure 4(b). This parameter is very useful as it directly reports the probability that an ion will be detected, since firing even a single MCP channel is generally sufficient for detection, in either analog or ion counting modes [30]. The values range from a high of 0.86 (2.5 kDa ACTH fragment ion at 25 kV acceleration voltage) to as low as 0.013 (the 145 kDa IgG ion at 10kV acceleration voltage). At a 25 kV acceleration voltage, the largest protein examined, the IgG dimer at 290 kDa, is detected with 11% efficiency, corresponding to ~1 in 9 ions. It may be noted that since e^−γ ≈ 1- γ for small γ, then from equation (7), ε also approaches γ when γ is small. The two values are almost identical for γ below 0.1. This similarity in the behavior of γ and ε is responsible for their similar behavior in the plots of Figures 4(a) and 4(b).

Effect of acceleration voltage on MCP detection

Figure 5 shows a plot of detection efficiency ε as a function of acceleration voltage for the set of peptides/proteins. It is notable that whereas the ion detection efficiencies vary widely at low acceleration voltage, they become much more similar at the higher acceleration voltages. This behavior reflects the fact that while low mass ions are detected with high efficiency even at low acceleration voltage, high mass ions require high acceleration voltage for efficient MCP detection. This fact has practical consequence, as it shows that high acceleration voltages are needed to efficiently detect large singly charged ions in TOF-MS, such as those generated by charge reduction of ESI-generated protein ions [7].

CONCLUSION

This study comprises the most comprehensive analysis to date of MCP response to singly charged peptide/protein ions as a function of ion mass and acceleration voltage. A mass range of 1 kDa to 290 kDa was examined, 4-fold greater than previous studies, and acceleration voltages from 5 kV to 25 kV. The use of a non-destructive inductive charge detector in parallel with MCP detection provided a reliable reference signal to allow accurate calibration of the MCP response. In accord with previous studies, the generation of secondary electrons by ion collisions is shown to vary linearly with ion mass, and as a power function with ion velocity. It is shown that for singly charged ions the secondary electron yield in a TOF experiment varies inversely with the square root of ion mass. At 25 kV acceleration voltage, all proteins are detectable, with efficiencies of ~80% for 1–2 kDa peptides, dropping to ~10% for the largest protein ion examined (IgG dimer, 290 kDa). At lower acceleration voltages, detection efficiency is significantly reduced in all cases, and the larger proteins become undetectable.