Communication: Comment on the effective temporal and spectral resolution of impulsive stimulated Raman signals

Abstract

A compact correlation-function expression for time-resolved stimulated Raman signals, generated by combining a spectrally narrow (picosecond) with a broad (femtosecond) pulse, is derived using a closed time path loop diagrammatic technique that represents forward and backward time evolution of the vibrational wave function. We show that even though the external spectral and temporal parameters of the pulses may be independently controlled, the effective temporal and spectral resolution of the experiment may not exceed the fundamental bandwidth limitation.

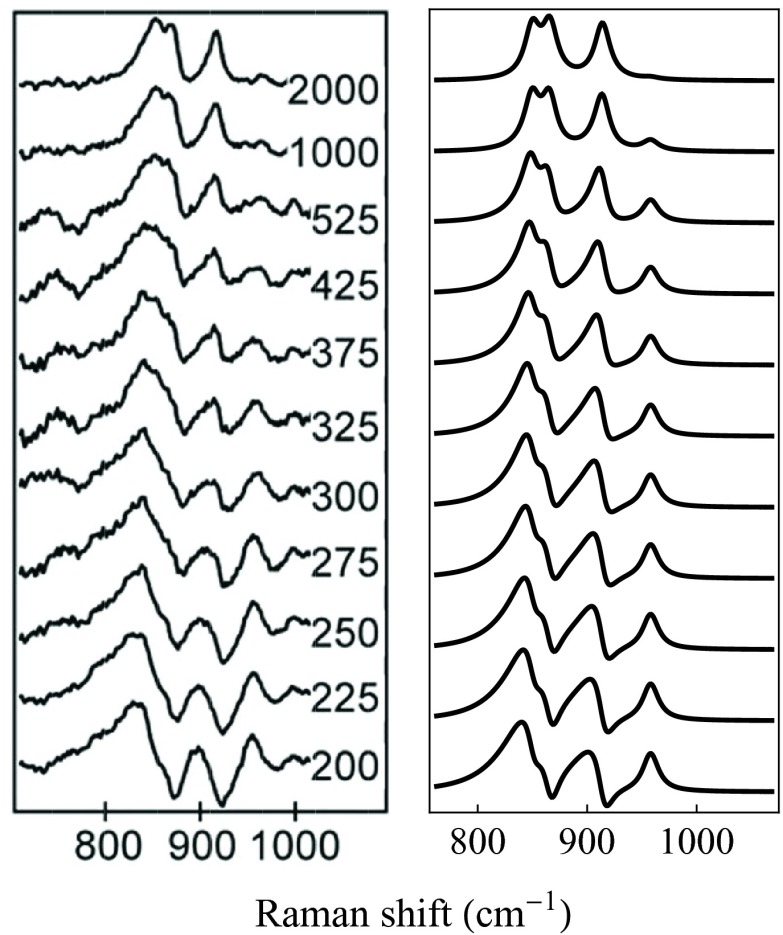
Stimulated Raman spectroscopy (SRS) has found powerful applications in biomedical imaging.^1,2 Closely related coherent Raman spectroscopy (coherent anti-Stokes Raman spectroscopy) has been proposed for remote sensing.^3,4 Pulse shaping techniques have been used for manipulating these signals.^5–7 Impulsive stimulated Raman scattering uses femtosecond pulses to measure simultaneously molecular vibrations over a broad bandwidth.^8–10 It has been argued that by using a combination of a femtosecond and a picosecond pulse it is possible to achieve both high spectral and temporal resolution that exceed the fundamental transform limit. This was denoted “circumventing Heisenberg.”^11,12 Experiments on deuterated chloroform¹³ and other systems¹¹ show how the phase of the Raman-like features changes with a time resolution $(<50\mathrm{fs})$ while the spectral resolution is less than $30{\mathrm{cm}}^{-1}$. Typical experimental data on rhodopsin¹⁶ are shown in Fig. 1 (left panel).

FIG. 1.

Stimulated Raman signals from rhodopsin for different values of the delay time T (in femtoseconds). Left panel: Experimental data adopted from Ref. 16. Right panel: Fit to the data obtained using Eq. (4) and the same four vibrational mode model used in Ref. 16 but with different parameters (From Science 310, 1006 (2005). Reprinted with permission from AAAS).

Here we present a microscopic calculation and intuitive analysis of these signals by using a compact loop diagram representation. We show that when the temporal and the spectral resolution are properly defined, their product may not violate the transform limit. Only higher-order measurements with more pulses can have non-conjugate time and frequency axes that are not subject to the transform limit.

We focus on the experimental pulse configuration shown in Figs. 2 and 3(a). A femtosecond pulse (${\mathit{k}}_1$) brings the molecule to an electronically excited state where isomerization is launched. A long picosecond pulse (${\mathit{k}}_2$) then excites the system while a third short pulse (${\mathit{k}}_3$) centered at τ = T stimulates the Raman signal which is dispersed in a spectrometer and recorded versus frequency. The apparent time-resolution Δt is controlled by the delay T between the two femtosecond pulses, and the spectral resolution Δω is determined by the spectrometer. Since these are independent devices, there is no lower limit on the ΔωΔt product. It is tempting to think that since the Raman signal is stimulated by the second short pulse, its time is well defined and the dispersed Raman signal (left panel of Fig. 1) thus gives high resolution snapshots of the vibrational frequencies at that time. As we show below, this interpretation is false.

FIG. 2.

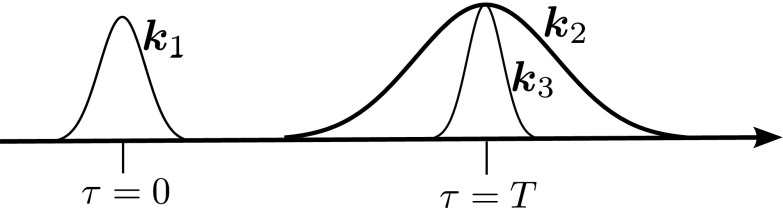
Pulse sequence for the stimulated Raman experiment considered here. The arrival time of the electronically resonant pulse ${\mathit{k}}_1$ defines the time origin (τ = 0) and launches the vibrational dynamics. The electronically off-resonant pulse pair, ${\mathit{k}}_2$ and ${\mathit{k}}_3$, arrive at the sample at τ = T.

FIG. 3.

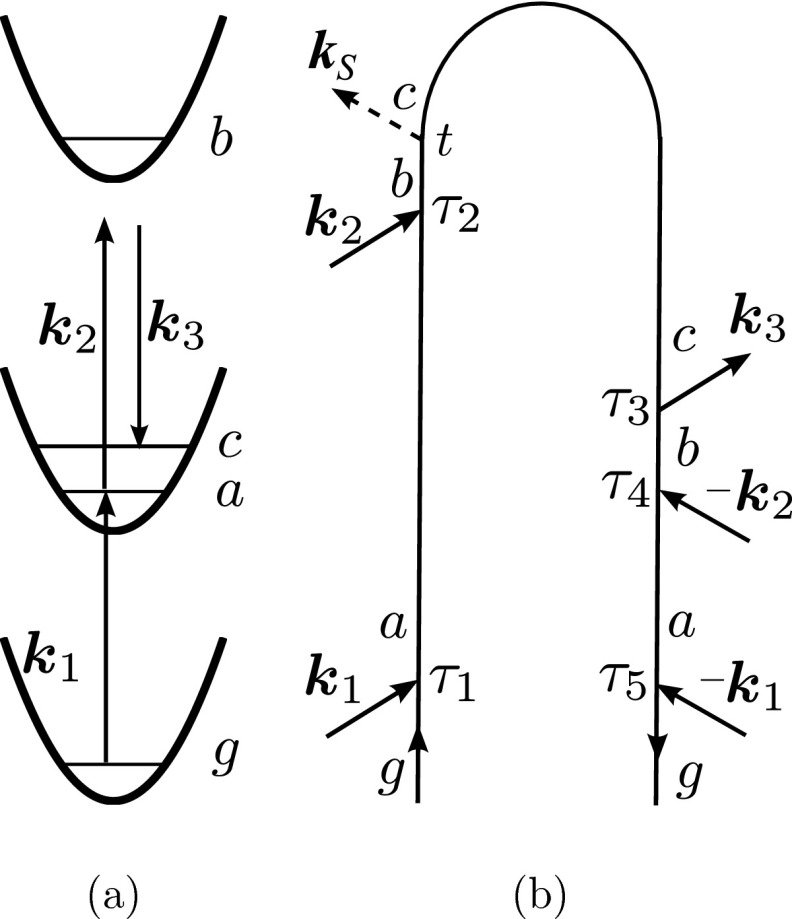
(a) Level scheme for the time-resolved Raman process. g is the system ground state, a and c are vibrational states belonging to the excited electronic state accessed by the first pulse, whereas b is a higher-lying excited state accessed transiently in the Raman process. (b) Closed-time path-loop diagram for the polarization P⁽⁵⁾(t) [Eq. (1)] responsible for the stimulated Raman signal. The loop describes the propagation of the wave function by moving clockwise (forward (backward) in the left (right) branch). The interaction times are denoted τ_i. t is chronologically the last time. Time variables are ordered within each branch but not between branches. The density matrix formulation, in contrast, maintains complete time ordering and separates the diagram into several Feynman diagrams. Due to the short duration of the electronically resonant pulse, ${\mathit{k}}_1$, the interaction times τ₁ and τ₅ are localized near τ = 0. Pulse ${\mathit{k}}_3$ is also impulsive, and τ₃ is confined to the vicinity of τ = T. τ₂ and τ₄ are loosely controlled by the envelope of the picosecond ${\mathit{k}}_2$ pulse whereas the observation time t is not controlled by the pulses. The t − τ₃ interval is limited by the vibrational dephasing timescale ${\gamma }_{ca}^{-1}$.

Nonlinear optical signals are most commonly described using double sided Feynman diagrams that represent the evolution of the density matrix in Liouville space.¹⁷ That approach keeps track of the forward evolution in real time and is particularly appealing for time domain (impulsive) techniques. It was extensively used by Lee et al. to calculate the Raman signals.¹⁸

We shall adopt a different, loop diagram, representation¹⁹ as shown in Fig. 3(b). We shall explain its advantages for this application after presenting the result. The left branch of the loop represents forward propagation of the wave function, and the right branch corresponds to backward propagation as we move clockwise (for rules see Ref. 19). The loop gives the time-dependent polarization (or scattered field) at time t, P(t). Pulse ${\mathit{k}}_1$ will not be treated explicitly. Instead we assume that this pulse is impulsive and initiates a reaction, making the Hamiltonian time dependent through its variation with a classical reaction coordinate.²⁰ The polarization induced by the five interactions can be directly read from Fig. 3(b) and is given by

$$\begin{array}{ccc}\hfill P^{\left(5\right)}\left(t\right)& =& {\int }_{-\infty }^{t}d{\tau }_2{\int }_{-\infty }^{t}d{\tau }_3{\int }_{-\infty }^{{\tau }_3}d{\tau }_4{\mathit{}\mathcal{E}}_2^{*}\left({\tau }_4\right){\mathit{}\mathcal{E}}_3\left({\tau }_3\right){\mathit{}\mathcal{E}}_2\left({\tau }_2\right)\hfill \\ & & \times 〈V{G}^{†}\left({\tau }_3,{\tau }_4\right){\text{VG}}^{†}\left(t,{\tau }_3\right)VG\left(t,{\tau }_2\right)V〉.\hfill \end{array}$$ (1)

The electric fields are decomposed into the positive frequency $\left(\mathit{}\mathcal{E}\right)$ and negative frequency $\left({\mathit{}\mathcal{E}}^{*}\right)$ components as $E_i\left(t\right)={\mathit{}\mathcal{E}}_i{e}^{-i{\omega }_{i}t}+{\mathit{}\mathcal{E}}_i^{*}{e}^{i{\omega }_{i}t}$. V is the dipole operator, and the two-time Green's function G(t₂, t₁)G†(t₂, t₁) represents forward (backward) propagation from t₁ to t₂ under the time-dependent Hamiltonian. The frequency-dispersed signal is given by¹⁷

$$S_{\mathrm{SRS}}\left(\omega \right)=\Im P^{\left(5\right)}\left(\omega \right){\mathit{}\mathcal{E}}_3^{*}\left(\omega \right),$$ (2)

where

$$P^{\left(5\right)}\left(\omega \right)={\int }_{-\infty }^{\infty }dt{P}^{\left(5\right)}\left(t\right)e^{i\omega t}.$$ (3)

Note that P⁽⁵⁾(t) is the positive frequency part of the polarization so that S(ω) = 0 for ω < 0.

For clarity we further assume that pulse ${\mathit{k}}_2$ is monochromatic $({\mathit{}\mathcal{E}}_2\left(\tau \right)\approx {\mathit{}\mathcal{E}}_2\exp (-i{\omega }_2\tau ))$, and ${\mathit{k}}_3$ as impulsive $({\mathit{}\mathcal{E}}_3\left(\tau \right)\approx {\mathit{}\mathcal{E}}_3\delta (\tau -T))$. Our conclusions are more general and hold for other pulse shapes. Equation (1) then results in

$$\begin{array}{cc}& P^{\left(5\right)}\left(t\right)=i{\left|{\mathit{}\mathcal{E}}_2\right|}^2{\mathit{}\mathcal{E}}_3\frac{{\left|V_{ab}\right|}^2{\left|V_{cb}\right|}^2}{{\left({\omega }_2-{\omega }_{\mathit{\text{ab}}}\right)}^2}\hfill \\ & \times \exp \left(-i{\omega }_2(t-T)+i{\int }_T^t{\omega }_{ca}\left(\tau \right)d\tau -{\gamma }_{ca}|t-T|\right),\hfill \end{array}$$ (4)

where V_ij, ω_ij(τ), and γ_ij, are the dipole matrix element, time-dependent frequency, and dephasing rate for the i ← j transition, respectively. The dephasing rate is due to finite lifetime as well as pure dephasing.

As we can see, the signal depends on the entire trajectory of the frequency ω_ca(τ) between the stimulation time T and the detection time t. It may not be simply related to a single snapshot of ω_ca(T). In a frequency-dispersed measurement [Eqs. (2) and (3)] t varies between −∞ and ∞, thus the control parameter T does not represent the actual time of measurement. Equation (4) for the time-dependent polarization is to be contrasted with the phenomenological expression used in the simulations of Ref. 16, where ω_ca(t)(t − T) replaces the integral over the changing vibrational frequency.

Some insight into the effective time resolution of these measurements can be obtained by considering a model system of a single vibrational mode whose frequency changes according to

$${\omega }_{ca}\left(t\right)=\left\{\begin{array}{cc}\hfill {\omega }_{ca}^{\mathrm{final}}+e^{-t/t^{\prime }}\left({\omega }_{ca}^{\mathrm{initial}}-{\omega }_{ca}^{\mathrm{final}}\right)& \hfill :t\ge 0\\ \hfill {\omega }_{ca}^{\mathrm{initial}}& \hfill :t<0\end{array}\right..$$ (5)

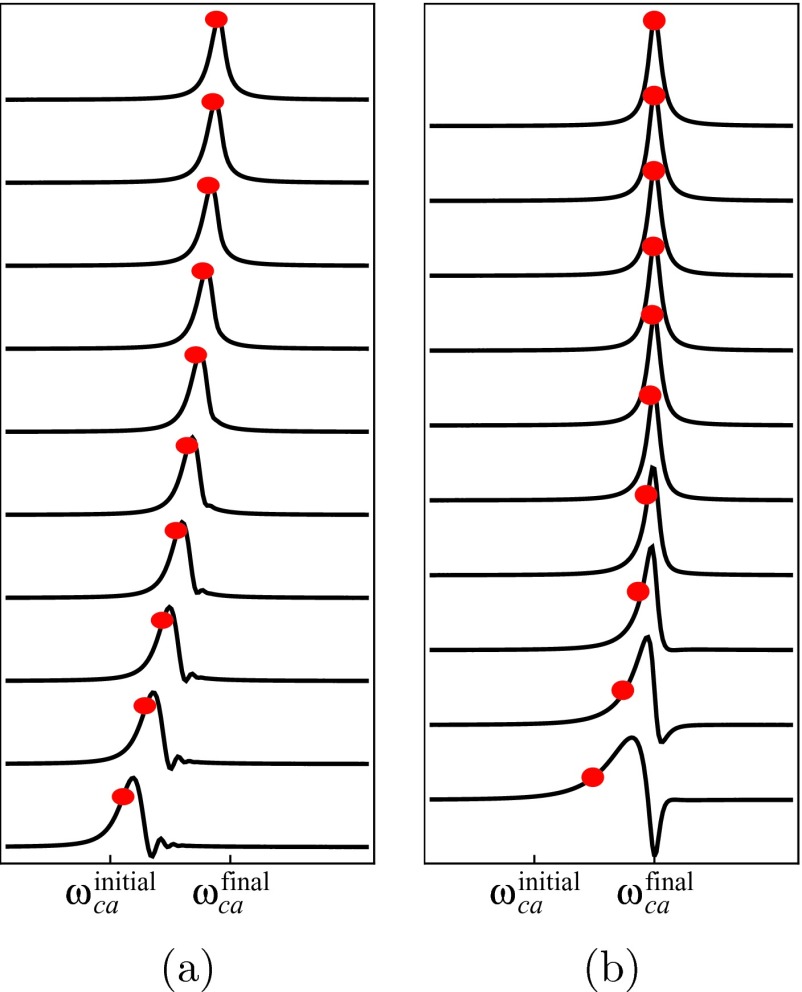
In Fig. 4, we use Eq. (4) to model the signal for this model with the dephasing time set to ${\gamma }_{ca}^{-1}=620\mathrm{fs}$. The vibrational frequency at the arrival time of pulse ${\mathit{k}}_3$ is shown by a red circle in each case. In Fig. 4(a) t′ = 5 ps and spectra are shown for values of T in increments of 500 fs. Here the timescale t′ over which the vibrational frequency changes is much shorter than the dephasing time ${\gamma }_{ca}^{-1}$, and the peak position in the detected polarization is in quite good agreement with the nominal vibrational frequency ω_ca(T). Figure 4(b) has t′ = 300 fs and 200 fs increments between measurements. Only for the very slow reaction is the vibrational frequency well resolved.

FIG. 4.

Stimulated Raman signals calculated for a model system consisting of a single vibrational mode whose frequency varies according to Eq. (5) for successive values of the interpulse delay T, starting with T = 200 fs, with fixed increments from bottom to top. The vibrational frequency ω_ca(T) is indicated as a red circle, and the dephasing time is ${\gamma }_{ca}^{-1}=620\mathrm{fs}$. (a) The frequency changes very slowly ($t^{\prime }=5\mathrm{ps}$) compared with ${\gamma }_{ca}^{-1}$. The increment is ΔT = 1.2 ps. (b) The frequency changes rapidly (t′ = 300 fs) compared with ${\gamma }_{ca}^{-1}$, and the increment is ΔT = 200 fs.

We had further applied the theory to simulate the signals of Ref. 16 from rhodopsin. The simulation shown in Fig. 1 includes four vibrational modes, one of which has a constant frequency of 959 cm⁻¹ and three of which vary according to Eq. (5). The polarization is modeled according to Eq. (4), with ${\gamma }_{ca}^{-1}=620\mathrm{fs}$. This fit is of similar quality of that of Ref. 16 but the fitting parameters are different. The results from a crude fit give $t^{\prime }=300\mathrm{fs},$ initial frequencies ${\omega }_{ca}^{\mathrm{initial}}$ of 750, 770, and 820 cm⁻¹, and final frequencies ${\omega }_{ca}^{\mathrm{final}}$ 867, 851, and 915 cm⁻¹. Including finite-duration pulses did not significantly affect these results.

Observing the oscillation period from a Raman mode is not the same as having that time-frequency resolution. For example, when one obtains an interferometric autocorrelation, one is able to observe oscillations with the period of the optical carrier frequency. For 800 nm one would observe oscillations that are 2.7 fs in period regardless of the pulse duration. The data used in Ref. 16 to support the violation of the time-bandwidth product only detected the phase of the Raman oscillations and does not prove superior time resolution.

The closed-time path loop follows the wave function in Hilbert space and requires both forward and backward time evolutions.¹⁹ It is more compact since it only maintains partial time ordering of interactions (on the forward and on the backward branches, but not between branches). When describing experiments with temporally overlapping pulses the loop representation contains fewer terms since there is no need to maintain complete time ordering. This is particularly helpful in the present application where we need only one diagram [plus its complex conjugate, this is why we have imaginary part in Eq. (2)].

The stimulated Raman signal obtained by employing a broad and a narrow pulse offers a high spectral resolution of vibrational lines and some useful but limited (integrated) information on the time dependent vibrational frequencies. The loop diagram provides a convenient tool for computing and interpreting these signals. It clearly reveals the origin of the Raman resonances: They are generated during a single time interval in this diagram where the system's wave function propagates backward from the observation time t to τ₃ which is close to the delay time T. Note that t − T is a time interval between two successive interactions along the loop but not in real time. The natural time variables in the double sided approach are the intervals between successive interactions in real time. This is why the loop representation is so natural for the description of this signal. The alternative description of these resonances in terms of the density matrix is fully time ordered and involves only forward propagation.¹⁷ However, it will be much less intuitive since the loop diagram is then split into several double-sided diagrams and there is no single interval responsible for the resonances.

Figure 3(b) shows that the temporal and spectral resolutions are conjugates: both are determined by a single time interval t − τ₃. The observed narrow vibrational lines indicate that t is long and hence the temporal resolution must be low. In fact, the signal from the isomerization product ${\omega }_{ca}^{\mathrm{final}}$ appears even at T = 0. This does not imply a fast reaction, but rather reflects the low temporal resolution of the measurement. It is true that the control parameters satisfy ΔωΔt < 1, but these do not reflect the intrinsic resolution of the measurement.

By comparing Eqs. (1) and (2), we see that the femtosecond pulse envelope ${\mathit{}\mathcal{E}}_3$ appears twice in the signal: as ${\mathit{}\mathcal{E}}_3\left({\tau }_3\right)$ and ${\mathit{}\mathcal{E}}_3^{*}\left(\omega \right)$. ${\mathit{}\mathcal{E}}_3\left({\tau }_3\right)$ in the right branch is impulsive and ensures that the interaction time τ₃ is centered at τ₃ = T within the pulse envelope. For the detection (top interaction in the left branch), Eq. (2) selects a single Fourier component, ${\mathit{k}}_3$ then provides the broad bandwidth for its detection via Eq. (2). The time t is not restricted by the duration of pulse 3. The long t − T interval is the reason for the low temporal resolution and the high spectral resolution (narrow Raman lines). The dispersed signal for the delay time T depends on the entire time evolution between T and ∞. The signal does depend parametrically on T since only the dynamics between T and ∞ is monitored. This dependence contains useful information, but technically there is no temporal resolution for the subsequent vibrational dynamics. The ΔωΔt > 1 inequality for the effective resolution is maintained.

Different detection modes have different degrees of control over t, which determine the effective spectral and temporal resolution of the signal. The temporal resolution of the frequency dispersed signal considered here, $\Im P^{\left(5\right)}\left(\omega \right){\mathit{}\mathcal{E}}_3^{*}\left(\omega \right)$, is determined by ${\gamma }_{ca}^{-1}$ which limits the range of t values that contribute to the integral in Eq. (3). Time-resolved detection, $\Im P^{\left(5\right)}\left(t\right){\mathit{}\mathcal{E}}_3^{*}\left(t\right)$, will sharply restrict the t − T interval since ${\mathit{}\mathcal{E}}_3^{*}\left(\omega \right)$ is replaced by ${\mathit{}\mathcal{E}}_3^{*}\left(t\right),$ but the spectral resolution will be poor. Intermediate resolutions can be achieved by a proper gating.²¹ It should be possible to control the temporal and spectral resolution of the signal by using three pulses and looking at the homodyne four-wave mixing signal generated spontaneously in the direction ${\mathit{k}}_2-{\mathit{k}}_{2^{\prime }}+{\mathit{k}}_3.$ The signal can then be gated²¹ and the gating spectrogram may be varied to adjust the resolution. The two extreme limits for the gated spontaneous signal will be |P(ω)|² [ideal spectral resolution, resembling Eq. (2)] and |P(t)|² (ideal temporal resolution).

The present diagram may be extended to include more elaborate pulse sequences²² as well as pulse shaping effects.²³ We have shown that electronically off resonant stimulated Raman measurements cannot possess both high temporal and spectral resolution, beyond the transform limit. The signal is determined by the evolution during a single time interval, representing backward propagation from t to T.²⁴ Since T is sharply defined by the delay of the two short pulses (${\mathit{k}}_1$ and ${\mathit{k}}_3$), the effective temporal and spectral resolutions are determined by the degree of control of the detection time t. Strict control will result in a time resolved measurement with no spectral resolution. As this control is relaxed, spectral resolution emerges at the expense of the temporal one, since the two resolutions are Fourier conjugates and are bounded by the transform limit. Multidimensional techniques involving additional pulses can acquire both high temporal and spectral resolutions, by controlling different time intervals.¹⁷ Another interesting extension will be to replace the electronic excitation by ${\mathit{k}}_1$ considered here by a broadband Raman initiation.^8,9 This will create a wave packet of low frequency vibrational modes. The initiation process must then be treated quantum mechanically²⁰ rather than in terms of a classical coordinate.