Abstract
This paper examines the interplay of the effect of cross immunity and antibody-dependent enhancement (ADE) in multistrain diseases. Motivated by dengue fever, we study a model for the spreading of epidemics in a population with multistrain interactions mediated by both partial temporary cross immunity and ADE. Although ADE models have previously been observed to cause chaotic outbreaks, we show analytically that weak cross immunity has a stabilizing effect on the system. That is, the onset of disease fluctuations requires a larger value of ADE with small cross immunity than without. However, strong cross immunity is shown numerically to cause oscillations and chaotic outbreaks even for low values of ADE.
The spreading of infectious diseases having multiple strains in a population can exhibit very complex dynamics, ranging from periodic and quasiperiodic outbreaks to high-dimensional chaotic behavior. Several sociological and epidemiological factors characterize the disease spread at different levels, such as interactions among the disease strains, social contacts, and human immune responses. In this work we focus on dengue fever, a vector borne disease which has exhibited as many as four different strains, and is endemic in large areas of Southeast Asia, Africa, and the Americas. A notable feature of dengue is its interaction with the human immune system. When an individual is infected with dengue, the immune system triggers an antibody response which will temporarily protect against secondary infections. However, when the level of protection decreases, secondary infections may be possible and the presence of low level antibodies triggers an increase in the infectiousness of the individual. This effect is called antibody-dependent enhancement (ADE). In this paper we study a mathematical model for the spreading of dengue fever. While ADE alone is proved to trigger large amplitude chaotic oscillations, we show that including weak temporary cross immunity stabilizes the system. In contrast, we also show that strong cross immunity destabilizes the dynamics. These results will help understand the implementation of proper control strategies when using future vaccines.
I. INTRODUCTION
Understanding the dynamics of multistrain diseases is a key topic in population biology. A suitable model class for such diseases, which include influenza, malaria, and dengue,19 must take into account the possibility of interactions among the serotypes or strains. The nature of multistrain interactions strongly affects the impact of the disease on the population as well as the mechanisms for its control.
One prominent example of an endemic multistrain disease is that of dengue and dengue hemorrhagic fever. Located in Africa, the Americas, and Southeast Asia, dengue is one of several emerging tropical diseases.15 There is no vaccine, although clinical trials are underway in order to generate an immune response across all strains.18 Approximately people are at risk for contracting dengue,32,33 and between and cases are reported each year.15 The dominant four dengue viruses have progressively spread geographically to virtually all tropical countries to create a global pandemic resulting in several hundred thousand hospitalizations every year.20 Since dengue is so far reaching and endemic, it is important to understand how it fluctuates in time, so that when proper vaccines are developed, implementation may be guided by a more thorough understanding of the disease.
Dengue is known to exhibit as many as four coexisting serotypes (strains) in a region such as Thailand. The dynamics of dengue spread is believed to be governed by two types of interactions between serotypes, ADE and temporary cross immunity. Once a person is infected and recovers from one serotype, lifelong immunity to that serotype is conferred. Antibodies are developed specifically for the first challenging serotype. In the presence of a new secondary infection, low level antibodies developed from the first infection form complexes with the second challenging serotype so that the virus can enter more cells, increasing viral production.8 Viral loads are associated with transmissibility, and it is hypothesized that individuals with secondary infection are more infectious than during their first infection. This increased transmission rate in subsequent infections is known as ADE. In vitro studies of dengue fever suggest that the ADE phenomenon may be due to the increasing of the infection of cells bearing the IgG receptor (G-immunoglobulin).21
The impact of ADE on the modeling of multistrain diseases such as dengue is quite profound.12 In general, the first models were of susceptible-infected-recovered (SIR) type, with ADE included, and they showed that for sufficiently high ADE, oscillations were possible. In contrast, single strain SIR models only have isolated equilibria and cannot show fluctuations without external seasonal drives or noise. Recent work has begun to analyze in detail the effect of ADE quantitatively on the dynamics,29,30 as well as the competition between serotypes.9 It is also still unclear if ADE increases transmission of the disease or increases mortality, shortening the effective infectious period. Theoretical studies suggest that the former case allows for coexistence of strains with periodic and chaotic disease outbreaks,9 while in the latter the phenomenon may decrease persistence.24 Throughout this work we shall assume the first case to hold.
In addition to ADE, another type of interaction between the strains occurs. Recently, cross protection, or cross immunity between serotypes, has been conjectured to play a role in the dynamics of dengue.3,25 While a primary dengue infection with a particular serotype may confer lifelong immunity to that strain,22,28 it may also confer temporary cross immunity to the other serotypes. Cross immunity may act like a prophylactic to different strains and may also possess different efficacies. That is, cross immunity may be complete (i.e., individuals cannot contract a secondary infection during the cross immune period) or partial (i.e., cross immune individuals have a reduced but nonzero probability to contract the disease). In general, the length of the cross immunity period may vary depending on the disease. Cross immunity may result from an immunological response to the disease. It acts to reduce the susceptibility to a secondary infection, lowering the effective probability for reinfection to happen.2 In the case of dengue fever, cross immunity may last from 2 to 9 months,31 after which the antibodies have dropped to sufficiently low levels that allow infection with other strains and subsequent ADE. Cross immunity plays a crucial role in the cocirculation of strains4,27 and the pathogen diversity.1,17
Several studies involving separately cross immunity1,6,11,17 and ADE7,9,12,29 have been published in the past. The presence of both ADE and cross immunity in such models has not been extensively studied, although some recent models have begun to address this interaction. As an example of such a model, Ref. 5 studied the impact of ADE on the dynamics of a multistrain disease with temporary cross immunity, giving particular importance to the “inverse ADE” hypothesis (i.e., reduced infectivity of secondary infections). Reference 2 considered different types of ADE while allowing for lifelong partial cross immunity. Reference 31 showed that including both ADE and temporary cross immunity is necessary to produce periodicities consistent with epidemiological data. Finally, Ref. 25 included different mechanisms of cross immunity in a model with ADE in order to test the impact of a period of cross protection on the incidence of secondary dengue cases. They found that including clinical cross immunity, in which immunity to a second serotype can be generated by exposure during the cross immunity period but without a detectable infection of the second serotype, gives incidence patterns of secondary dengue infections that are compatible with collected data.
The aim of our work is to study in detail the impact of both ADE and temporary, partial cross immunity on the dynamics of the multistrain diseases. The outline of the paper is as follows. In Sec. II we introduce the model, in Sec. III we analyze the effect of weak cross immunity on the system, in Sec. IV we restrict ourselves to the case of no ADE to investigate the impact of strong cross immunity on the dynamics, and in Sec. V we include also ADE and study the interplay between cross immunity and ADE. Section VI concludes with a summary and discussion.
II. DESCRIPTION OF THE MODEL
The dynamical system considered in this paper is based on the SIR model and is a generalization of a multistrain model with ADE studied previously.7,29 We write the model for an arbitrary number of serotypes, and we include both ADE and cross immunity in the dynamics. A set of ordinary differential equations describes the rate of change in the population in each of the classes. We assume the population size to be normalized to unity, so each state represents a fraction of the total population. The quantities that enter the equations are the fraction of susceptibles to all serotypes, denoted by ; the primary infectives with strain , ; the cross immunes that are recovered from strain and have temporary cross immunity to all strains, ; those recovered from strain that are immune to strain only, ; and the secondary infectives with strain previously infected with strain , . The flow of an individual through the population in the two strain case is shown in Fig. 1. Tertiary infections are not included,26 so all individuals enter the completely immune class after recovery from a secondary infection. The dynamical system is as follows:
| (1) |
where the parameters are the number of strains , the contact rate , the recovery rate , the ADE factor , the strength of cross immunity , the rate for cross immunity to wear off , the birth rate , and the mortality rate . The model of Eq. (1) allows for one reinfection. The parameter determines how susceptible the cross immune compartments are to a secondary infection, where means no cross immunity effect (the compartments are infected as easily as the recovered compartments ) and confers complete cross immunity ( are not susceptible to a secondary infection).
FIG. 1.
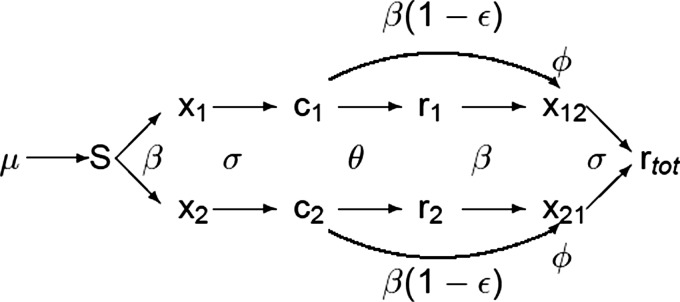
Flow diagram of how an individual would proceed through the model in the case of two serotypes. Note the reduction of susceptibility to a secondary infection through the cross immunity factor and the enhancement of secondary infectiousness due to the ADE factor . Death terms for each compartment are not included in the graph for ease of reading.
Throughout this paper, we use serotypes, , , , and in all numerical simulations.29 The choice of and corresponds to a basic reproductive number of .7 The parameter is the average time span of cross immunity, which typically ranges from 2 to 9 months.31 We choose , corresponding to six months of cross immunity, but we have used , equivalent to three months of cross immunity, with no significant difference in the results. For convenience, we choose the mortality rate to be either to maintain a constant population or in our analytical approximation for ease of analysis. Parameter values are summarized in Table I. We vary the ADE and cross immunity strength as bifurcation parameters.
Table I.
Parameters used in the model.
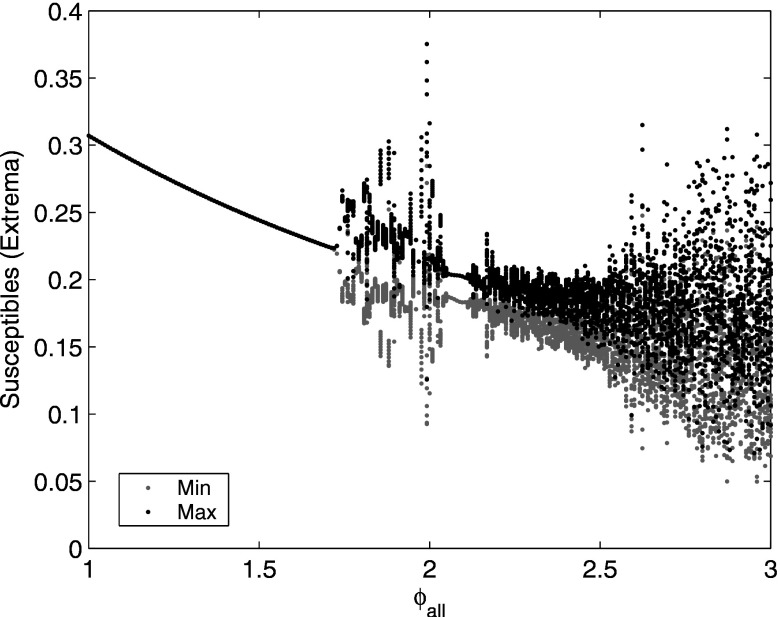
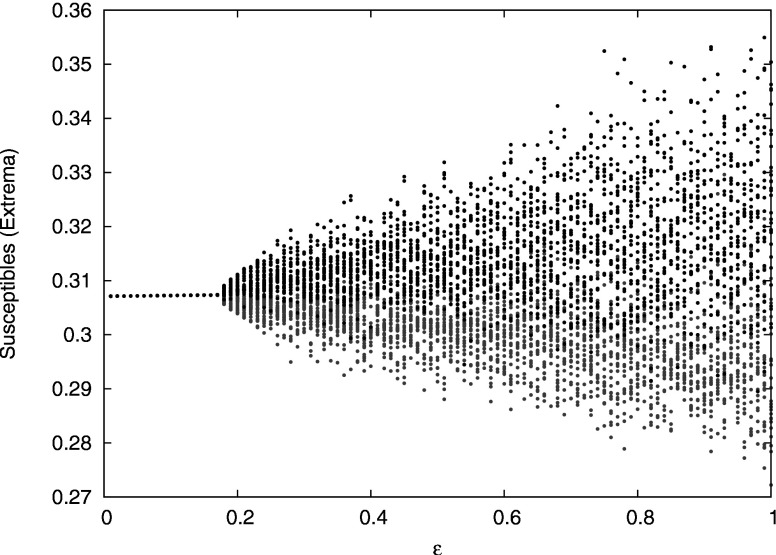
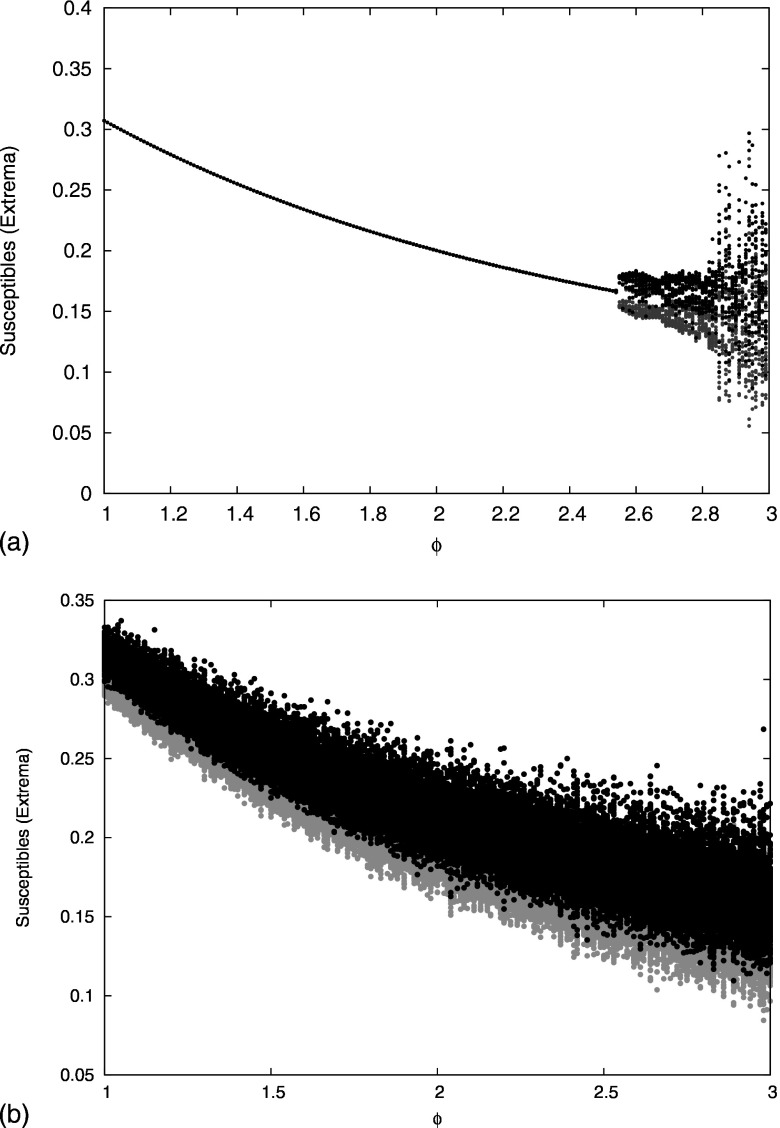
The case without cross immunity, , reduces to a previously studied model with only ADE7,29 because the cross immune and recovered compartments have the same infection rate and are treated identically. It has been shown7,29 that as ADE is increased, the system undergoes a Hopf bifurcation to stable periodic oscillations and then to chaos (Fig. 2). Desynchronization between strains occurs in the regions of chaotic outbreaks, but all strains are synchronized near the Hopf bifurcation when the outbreaks are periodic. The system has been analyzed in the neighborhood of the Hopf bifurcation using a reduced model that assumes a lower-dimensional, synchronized system. In Sec. III, we extend this analysis to the case of weak cross immunity.
FIG. 2.
Bifurcation diagram in ADE for the multistrain system with no cross immunity. For each ADE value, we show the local maxima (black) and local minima (gray) of the susceptibles during a 100 year time series after removal of transients. [Reprinted with permission from Schwartz et al., Phys. Rev. E 72, 066201 (2005). Copyright © 2005, American Physical Society.]
III. STABILIZING EFFECT OF WEAK CROSS IMMUNITY
We consider first the effect of weak cross immunity, , and show that it helps stabilize the steady state. Numerical simulations indicate that when is small, the system undergoes a Hopf bifurcation as ADE is increased, as it does for the system without cross immunity, and the compartments are identical across all strains near the Hopf bifurcation. Thus the system’s dimensionality reduces. Assuming symmetry between strains, we rewrite Eq. (1) as follows:
| (2) |
where represents the fraction of the population that is susceptible to the disease, the primary infectives, the cross immunes, the recovered, and the secondary infectives. Since is a small parameter, for ease of analysis we set the mortality rate . This approximation is equivalent to assuming that all mortality occurs in the class, those who have recovered from infections with two serotypes. In a region where dengue is very common and dengue infections occur early compared with the human life expectancy, it may be an accurate assumption. The endemic steady state for Eq. (2) is
| (3) |
Evaluating the eigenvalues of the Jacobian of Eq. (2) at the endemic steady state allows us to study its stability as a function of . Since both and are small parameters, we expand the root of the characteristic polynomial of the Jacobian matrix as follows:
| (4) |
Let us also use the following transformation for the characteristic polynomial ,
| (5) |
Substituting Eq. (4) into the characteristic polynomial and using Eq. (5), four of the five eigenvalues can be obtained,
| (6) |
| (7) |
| (8) |
The last eigenvalue can be obtained by performing the following substitution in the characteristic polynomial:
| (9) |
The fifth eigenvalue is then found to be
| (10) |
The real part of the pair of complex eigenvalues determines the stability of the system, since the other eigenvalues are clearly negative. Notice that the parameter occurs in both the real and imaginary parts of the eigenvalues. Therefore, we expect that will modify not only the stability of the endemic state but also the ensuing frequency of oscillations. To first order, the real part of is
| (11) |
Notice that the onset of a Hopf bifurcation is clearly a function of , , and . By visual inspection of Eq. (11), we see that when is increased from 0, the eigenvalue becomes more negative, so cross immunity is stabilizing in the limit of small and .
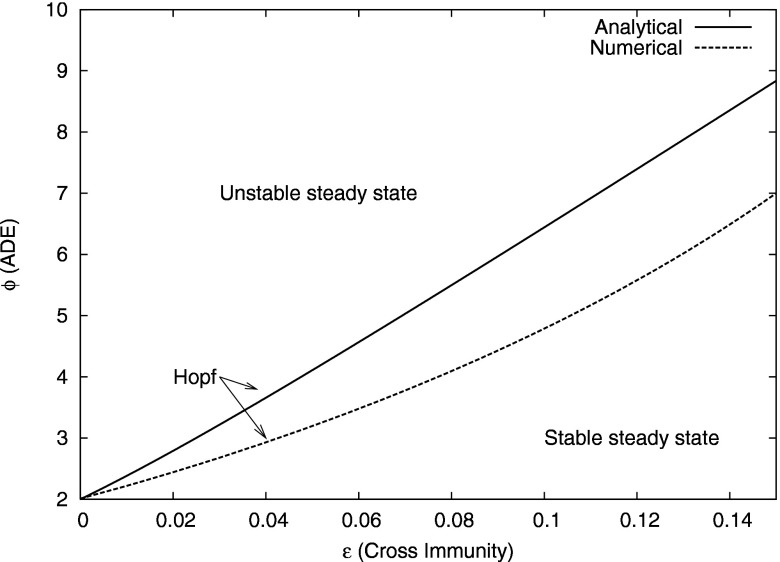
In Fig. 3, we plot the zeros of Eq. (11) in space, showing the predicted location of the Hopf bifurcation in the presence of ADE and weak cross immunity. Below the curve, the steady state is stable. As the cross immunity is increased, a larger ADE value is needed to destabilize the steady state. Thus weak cross immunity is stabilizing. Figure 3 also shows the actual location of the Hopf bifurcation for Eq. (1). These were computed using a continuation routine.10 Note that the Hopf bifurcation in Fig. 3, where both the numerical and the analytical curves were obtained in the case of no mortality, occurs at a larger value of ADE than in the system with mortality. However, the predicted trend of stabilization due to weak cross immunity is observed in either case (cf. Figs. 9 and 10).
FIG. 3.
Predicted and actual location for Hopf bifurcation as a function of and for weak cross immunity in the case of no mortality . The full curve is the analytic approximation [zeros of Eq. (11)], while the dashed curve is the actual location of the Hopf bifurcation obtained numerically for the full system in the case of no mortality. The number of strains is , and other parameters are as listed in the text.
FIG. 9.
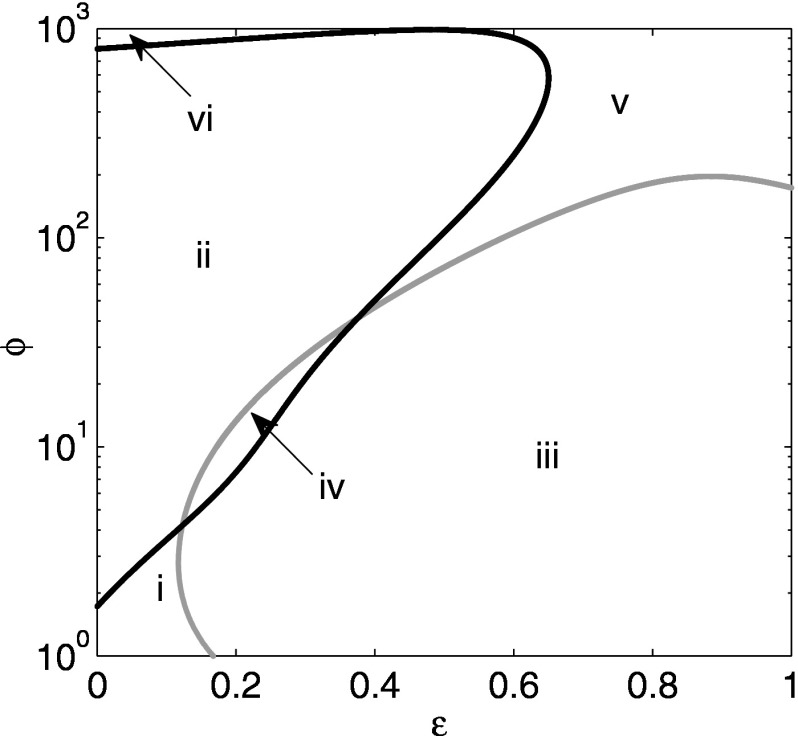
Full bifurcation diagram in cross immunity and ADE . Curves indicate location of Hopf bifurcations. See text for details.
FIG. 10.
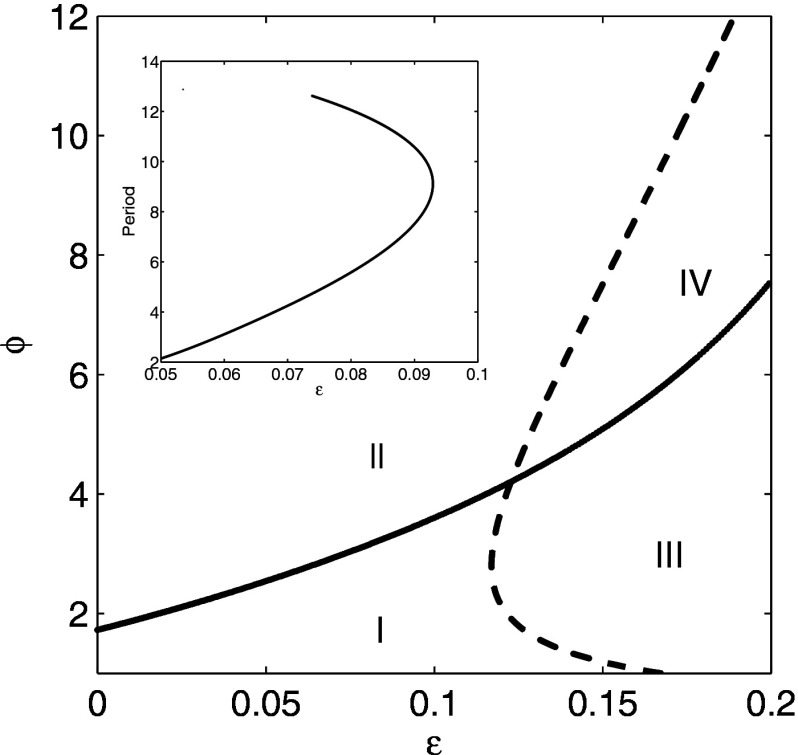
Blowup of bifurcation diagram in Fig. 9 for small cross immunity and ADE . Curves indicate location of Hopf bifurcations. Only region I has stable steady states. The inset shows the period of a branch of unstable orbits as a function of for in region II. See text for details.
IV. CROSS IMMUNITY AS CRITICAL PARAMETER
We next study numerically the effect of stronger cross immunity. We first consider the case of no ADE and fix the number of strains to as for dengue. We introduce partial cross immunity by increasing the value of continuously from (no cross immunity) to (complete cross immunity). The attracting bifurcation structure is depicted in Fig. 4.
FIG. 4.
Bifurcation diagram for the system of ordinary differential equations [Eq. (1)] in the absence of ADE . The cross immunity parameter is varied from 0 to 1. For each cross immunity value we plot the maxima (black) and the minima (gray) of the susceptibles during a 100 year time series after removal of a transient. A transition to chaos occurs at .
For weak cross immunity, the endemic steady state is stable. A loss of stability occurs at . Numerical analysis of the eigenvalues of the Jacobian of Eq. (1) at the steady state shows that a supercritical Hopf bifurcation occurs, and simulations show that the periodic orbit that appears just past the Hopf point is stable over a very small range of . The strains are desynchronized on the periodic branch, so it is not possible to analyze this bifurcation using a reduced model as in Sec. III. Also in contrast to the Hopf bifurcation for weak cross immunity studied in Sec. III, for which one complex pair of eigenvalues loses stability, at the Hopf bifurcation three identical complex pairs of eigenvalues become unstable simultaneously.14
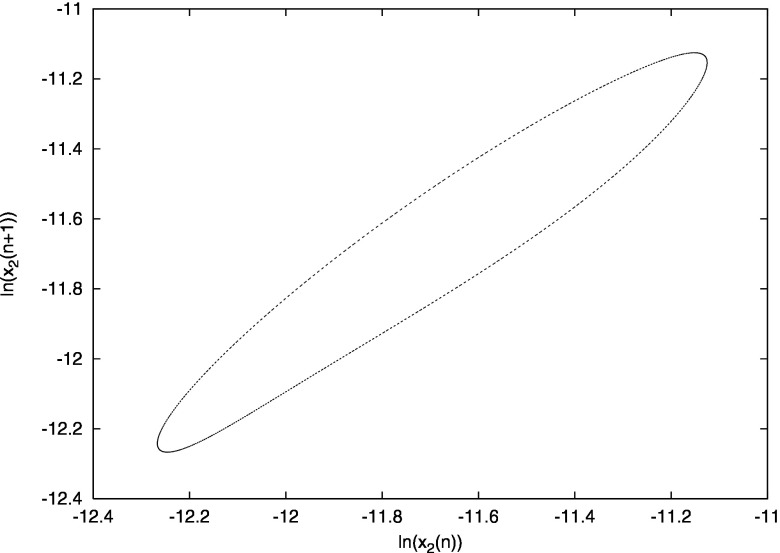
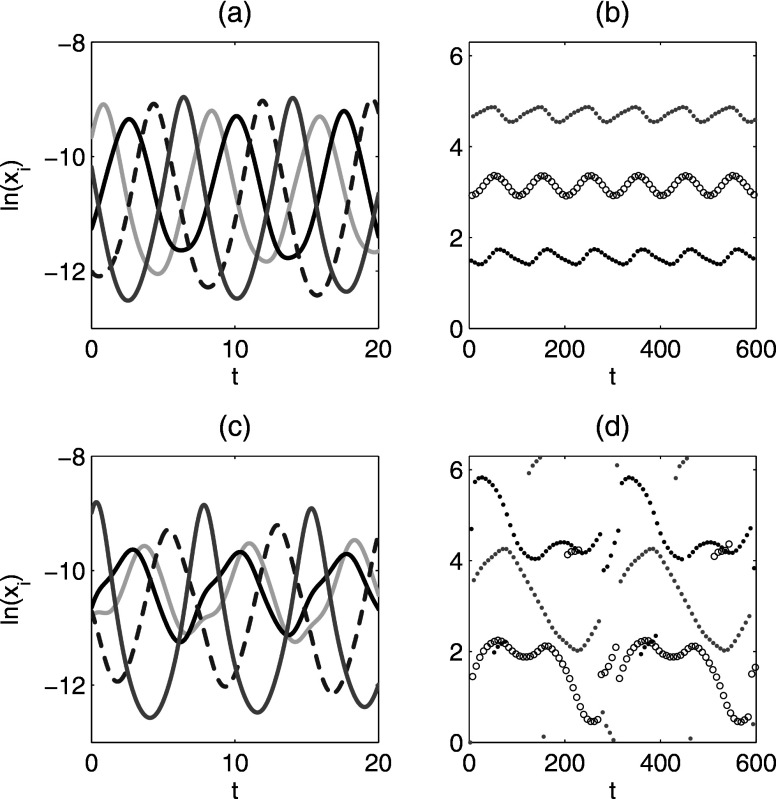
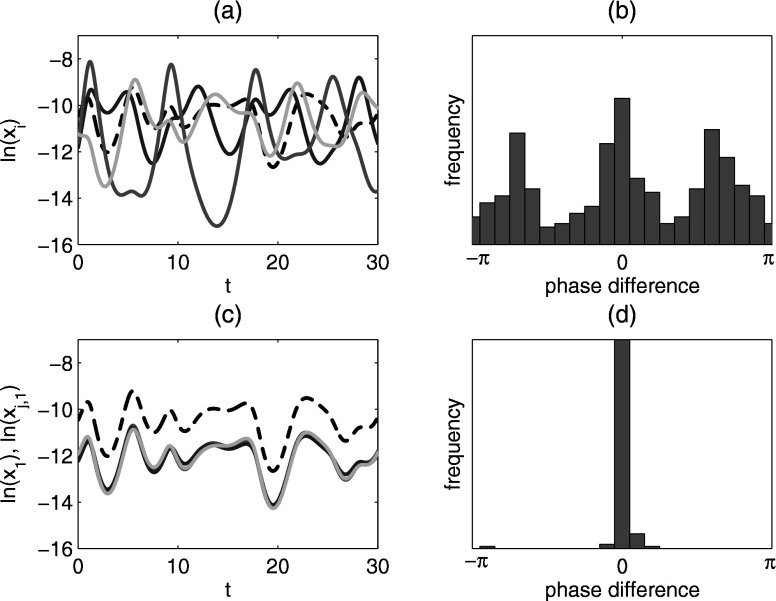
For , where , the system displays quasiperiodicity. Figure 5 shows a Poincaré map for , where the system is quasiperiodic. The map is obtained as follows: in the -dimensional phase space an -dimensional surface is introduced by fixing the value of one of the variables, in this case the number of primary infectives currently infected with strain 1, . We then sample the other variables every time their path crosses the hyperplane, that is, every time is identical to a fixed value [namely, ]. If the system is periodic, then the Poincaré map would result in a point, whereas if the system is quasiperiodic we obtain a closed curve, which is indeed what happens for the times series of Fig. 5. We have observed two attracting quasiperiodic attractors with overlapping regions of stability. Sample time series for the quasiperiodic attractors are shown in Figs. 6(a) and 6(c). The four strains are desynchronized on the quasiperiodic attractors, but with different phase dynamics.
FIG. 5.
Poincaré section showing vs . , . See text for details.
FIG. 6.
Quasiperiodic attractors for [panels (a) and (b)] and [panels (c) and (d)]. Time series of primary infectives (log variables) are shown in (a) and (c). Phase differences of primary infectives relative to primary infective are shown in (b) and (d). The time series in (a) and (c) are the beginning of those used to generate (b) and (d). The reference strain is the lightest gray curve in (a) and (c). Other parameters: .
To study the strain desynchronization in more detail, we define a phase difference between compartments, as in Ref. 29. Let be the reference compartment and another compartment. Let denote the sequence of times for local maxima of and the sequence of times for local maxima of . For , define the phase of relative to as . The phases of the other primary infective compartments relative to for the quasiperiodic attractors are shown in Figs. 6(b) and 6(d). For the attractor at weaker cross immunity, the phases of the strains relative to each other are approximately constant. This is sometimes called a splay phase state in the coupled oscillator literature. In contrast, the behavior at stronger cross immunity is more complex and qualitatively different, with the order of the strain outbreaks changing over time. Finally, since all the strains have identical parameters, we note that any permutation of strain labels gives another similar quasiperiodic state.
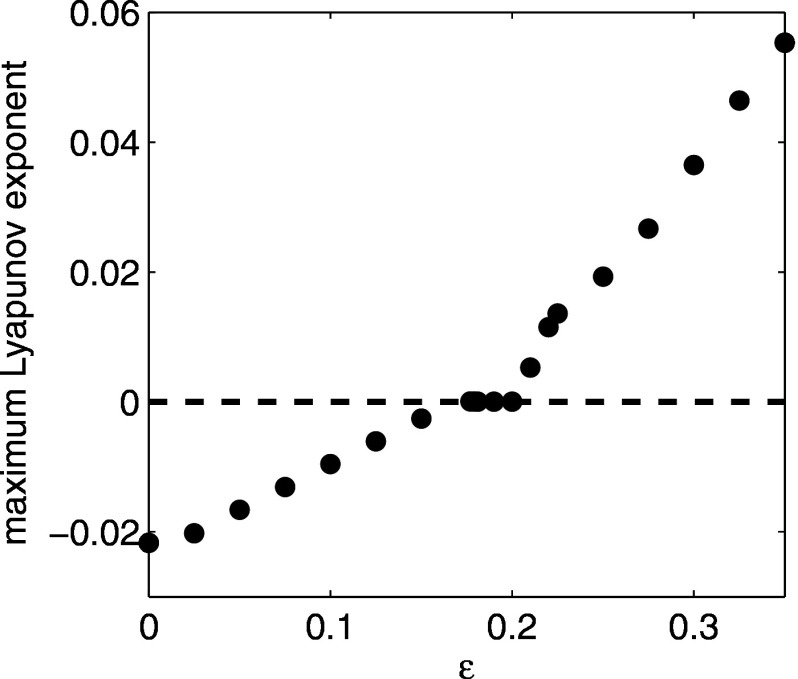
When the cross immunity is increased above , the system bifurcates to chaos. The presence of chaos in SIR multistrain models with cross immunity has been already revealed by several studies in the past.6,11,17,23 We have confirmed the chaotic behavior by computing the maximum Lyapunov exponent for Eq. (1). The maximum Lyapunov exponent was obtained by integrating the linear variational equations along solutions to Eq. (1) for after removal of transients. Results are shown in Fig. 7. For , the endemic steady state is stable and the maximum Lyapunov exponent is negative. For , the system exhibits quasiperiodic solutions and the maximum Lyapunov exponent is zero. For , the system is chaotic and positive Lyapunov exponents are observed.
FIG. 7.
Maximum Lyapunov exponent of Eq. (1) for as a function of cross immunity strength . Equations were integrated for after removal of transients.
Sample time series for chaotic solutions are shown in Figs. 8(a) and 8(c). Panel (a) shows the four primary infective compartments, which are desynchronized. We measured the phase differences of the other primary infectives relative to primary infective , and they are frequently nonzero, although there appears to be some structure with certain phase differences more probable than others, as shown in Fig. 8(b). Figure 8(c) shows times series of all primary and secondary infective compartments that are currently infected with strain 1. We observe that primary and secondary infective compartments infected with the same strain (i.e., and the three compartments, where ) are usually synchronized. Figure 8(d), a histogram of phase differences of the relative to , shows the synchronization more clearly. This effect has been observed previously for the model with ADE only29 and has been explained by a collapse of the dynamics onto a lower-dimensional center manifold.30 The same reduction in dimension is observed in the system with cross immunity (Fig. 8) as well as in the system with both ADE and cross immunity (data not shown).
FIG. 8.
Chaotic attractor for . (a) Time series of all four primary infectives (log variables). Black dashed curve: ; darkest gray curve: . (b) Histogram of phase differences of primary infective relative to primary infective . (c) Time series of the first primary infective and the secondary infectives currently infected with strain 1 (log variables). Black dashed curve: . (d) Histogram of phase differences of secondary infective relative to primary infective . Phase difference histograms are collected for 2000 yr time series.
V. INTERACTION OF STRONG CROSS IMMUNITY AND ADE
We now turn to the interaction of both ADE and cross immunity, computing bifurcation diagrams using a continuation routine.10 Figure 9 shows the full bifurcation diagram in space. Here, the cross immunity ranges from 0 to 1. The vertical axis is a logarithmic scale for . The curves show the parameters of at which a Hopf bifurcation occurs. However, the curves denote different types of stability exchange. When crossing the black curve, only one pair of eigenvalues crosses the imaginary axis, indicating a simple bifurcation to or from periodic orbits. In contrast, when crossing the gray curve, the situation is degenerate in that three identical pairs of eigenvalues cross the imaginary axis. In this case, it is expected that complicated dynamics such as torus bifurcations may come into existence. For example, when traversing regions i, ii, and vi by increasing , we go from steady state through a periodic orbit and possibly aperiodic behavior, and then through another Hopf bifurcation to return to a steady state. On the other hand, if we go from region iii to v by increasing , we go from periodic or aperiodic behavior through a reverse degenerate Hopf bifurcation to steady state.
Notice that there are two relatively large regions of stable steady behavior: one for small and small in region i, and one for large and large in region v. (Note that the latter region of stable endemic states extends to small and large , labeled region vi in the figure.) For large cross immunity where is between 0.65 and 1, a sufficiently large value of will stabilize the steady state again. However, the value of is so large (the Hopf bifurcation has values of on the order of 100) that it is unrealistic. Therefore, to explore in more detail the bifurcations occurring at reasonable values of , we examine the case where is small, which is shown in Fig. 10.
In Fig. 10, there are four distinct regions describing the stability of the steady state behavior. In region I, the endemic steady state is stable. The solid curve is a line of Hopf bifurcations where one complex pair of eigenvalues becomes unstable. The dashed curve is a line of Hopf bifurcations where three identical complex pairs of eigenvalues become unstable. Therefore, the system has zero unstable eigenvalues in region I, one unstable pair in region II, three unstable pairs in region III, and four unstable pairs in region IV. At the Hopf bifurcation between regions I and II, a stable periodic orbit emerges for which all four strains are synchronized and identical. This bifurcation was studied in Sec. III using a reduced model that assumed symmetry between the strains. This periodic orbit has a narrow region of stability, and then it quickly bifurcates to chaos, so the majority of region II displays chaotic dynamics. At the Hopf bifurcation between regions I and III, the region of stable periodic orbits is even smaller, and then the system goes to a quasiperiodic attractor. When becomes sufficiently large, the system bifurcates to chaos. Although quasiperiodic orbits are observed for portions of region III shown in Fig. 10, the majority of region III for displays chaotic dynamics. Chaotic dynamics is also observed in most of region IV. Figure 10 (inset) also partially explores the sensitivity of the average oscillation period in region II with respect to . Here , and we vary to compute a branch of periodic orbits. Plotted is the period of the branch of periodic orbits (unstable). Notice that in the linear range near the bifurcation point where , the slope is on the order of 100, showing a clear sensitive dependence of the oscillation period on the cross immune response. For larger values of , the period exhibits a nonlinear response at the turning point, resulting in a biunstable branch of periodic orbits.
Finally, we show the interplay between ADE and cross immunity by comparing the bifurcation diagram of Fig. 2, which was obtained with a model equivalent to the model of Eq. (1) with no cross immunity, with the case of weak and strong cross immunity. In other words, we fixed the value of and built the bifurcation diagram using as critical parameter. Figure 11(a) shows the effect of the inclusion of weak cross immunity . By visual comparison with Fig. 2, it is clear that the region of stability is increased: a value of is needed to destabilize the system in comparison to needed in the case of no cross immunity. Figure 11(b) shows the effect of strong cross immunity on the bifurcation structure . The system is observed to be chaotic for all the considered values of ADE.
FIG. 11.
Bifurcation diagrams in ADE for cases with nonzero cross immunity. For each ADE value, we show maxima (black) and minima (gray). (a) Weak cross immunity, . (b) Strong cross immunity, . (For comparison, Fig. 2 shows the case of no cross immunity.)
VI. CONCLUSIONS AND DISCUSSION
In this work we analyzed the impact of two types of strain interactions in a multistrain model for epidemics, cross immunity and ADE. The ADE parameter measured an increase in infectiousness of secondary infectives, and the cross immunity strength determined the reduction in susceptibility to other strains during a temporary period after recovering from primary infection with one strain.
The nature of the observed dynamics depended on the strength of the cross immunity. Weak cross immunity was found to stabilize the endemic steady state. This effect was motivated analytically by studying a reduced model for weak cross immunity with symmetry between strains. Although the analysis was performed for a perturbed system without mortality, both the analytical treatment and numerical simulations of the full system were in good qualitative agreement. Since the onset of fluctuations is determined by Hopf bifurcations in models for dengue, the stabilizing effect of cross immunity shows that it is an important parameter to include when modeling disease fluctuations about equilibria. In addition, since cross immunity has a strong effect on the period of oscillation, it will play a role in determining the timing of efficient disease control strategies.
When considering strong cross immunity, most of the parameter regions predict unstable steady state behavior, as shown in Fig. 9. In fact, when the cross immunity parameter is greater than 0.65, stable endemic behavior was achieved only for unrealistically large values of ADE. As a result, strong cross immunity destabilized the system, and we observed complicated aperiodic fluctuations, such as quasiperiodic behavior and chaotic outbreaks. In contrast to the synchronized periodic behavior seen for weak cross immunity, we observed that both quasiperiodic and chaotic attractors exhibited strains that were unsynchronized. Asynchrony in chaotic outbreaks has also been observed in multistrain models with ADE and no cross immunity.29
Because time series data for dengue fever show asynchronous outbreaks for the different strains and nonperiodic behavior,26 our work suggests possible refined parameter ranges for dengue in terms of ADE and cross immunity. Specifically, either the ADE or the temporary cross immunity must be strong enough to put the system in the chaotic, desynchronized region, where certain types of unstable steady states were observed. There is now a need to quantify multistrain models against existing data sets (such as Ref. 26) and further refine parameter estimates. It should be noted that the model presented here does not include seasonality. Because dengue is carried by mosquitoes and displays outbreaks with a seasonal component, including annual variations in the contact rate will likely be necessary for good quantitative agreement between models and data. However, other longer period components exist in the data, and are probably due to the interaction between the seasonal contact rate fluctuations and the instabilities induced by the ADE and cross immunity parameters. From the ADE model analyzed in Refs. 7 and 29, it was observed that the mean period of oscillations was very sensitive with respect to the ADE parameter. In the current work, we have also done a preliminary sensitivity analysis of the mean oscillation period on the cross immune response parameter. Here we found that small changes in may yield very large changes in the oscillation period. Therefore, in order to connect the model with measured mean periods from the data, both ADE and cross immunity will play an important role in model prediction and control. In closing, there are many other modeling variations that we have omitted but which will refine model fidelity in future work. These include inhomogeneity in contact rate due to spatial density variation in the mosquito populations and fluctuations in the sociological parameters such as contact, birth and death rates, as well as general stochastic fluctuations in the population itself. Such stochastic effects in finite populations, which can lead to fade-out of the disease, may also impact future disease controls.
ACKNOWLEDGMENTS
L.B.S. and S.B. were partially supported by the Jeffress Memorial Trust. I.B.S. was supported by the Office of Naval Research and the Armed Forces Medical Intelligence Center. The authors acknowledge helpful discussions with Derek Cummings.
REFERENCES
- 1.Abu-Raddad, L. J. and Ferguson, N. M. , “The impact of cross-immunity, mutation and stochastic extinction on pathogen diversity,” Proc. R. Soc. London, Ser. B 271, 2431–2438 (2004). 10.1098/rspb.2004.2877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Adams, B. and Boots, M., “Modelling the relationship between antibody-dependent enhancement and immunological distance with application to dengue,” J. Theor. Biol. 242, 337–346 (2006). 10.1016/j.jtbi.2006.03.002 [DOI] [PubMed] [Google Scholar]
- 3.Adams, B., Holmes, E. C. , Zhang, C., Mammen, M. P. , Nimmannitya, S., Kalayanarooj, S., and Boots, M., “Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok,” Proc. Natl. Acad. Sci. U.S.A. 103, 14234–14239 (2006). 10.1073/pnas.0602768103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Adams, B. and Sasaki, A., “Cross-immunity, invasion and coexistence of pathogen strains in epidemiological models with one-dimensional antigenic space,” Math. Biosci. 210, 680–699 (2007). 10.1016/j.mbs.2007.08.001 [DOI] [PubMed] [Google Scholar]
- 5.Aguiar. M. and Stollenwerk, N., “A new chaotic attractor in a basic multi-strain epidemiological model with temporary cross-immunity,” e-print arXiv:cond-mat/0704.3174
- 6.Andreasen, V., Lin, J., and Levin, S. A. , “The dynamics of cocirculating influenza strains conferring partial cross-immunity,” J. Math. Biol. 35, 825–842 (1997). 10.1007/s002850050079 [DOI] [PubMed] [Google Scholar]
- 7.Billings, L., Schwartz, I. B. , Shaw, L. B. , McCrary, M., Burke, D. S. , and Cummings, D. A. T. , “Instabilities in multiserotype disease models with antibody-dependent enhancement,” J. Theor. Biol. 246, 18–27 (2007). 10.1016/j.jtbi.2006.12.023 [DOI] [PubMed] [Google Scholar]
- 8.Center For Disease Control Website, http://www.cdc.gov/ncidod/dvbid/dengue/slideset/index.htm, 2006
- 9.Cummings, D. A. T. , Schwartz, I. B. , Billing, L., Shaw, L. B. , and Burke, D. S. , “Dynamic effect of antibody-dependent enhancement on the fitness of viruses,” Proc. Natl. Acad. Sci. U.S.A. 102, 15259–15264 (2005). 10.1073/pnas.0507320102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Doedel, E., Oldeman, B., Champneys, A., Dercole, F., Fairgrieve, T., Kuznetsov, Y., Paffenroth, R., Sandstede, B., Wang, X., and Zhang, C., “Auto97: Continuation and bifurcation software for ordinary differential equations,” 1997. Available from ftp://ftp.cs.concordia.ca/pub/doedel/auto/auto.ps.gz
- 11.Esteva, L. and Vargas, C., “Coexistence of different serotypes of dengue virus,” J. Math. Biol. 46, 31–47 (2003). 10.1007/s00285-002-0168-4 [DOI] [PubMed] [Google Scholar]
- 12.Ferguson, N., Anderson, R., and Gupta, S., “The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens,” Proc. Natl. Acad. Sci. U.S.A. 96, 790–794 (1999). 10.1073/pnas.96.2.790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ferguson, N. M. , Donnelly, C. A. , and Anderson, R. M. , “Transmission dynamics and epidemiology of dengue: Insights from age-stratified sero-prevalence surveys,” Philos. Trans. R. Soc. London, Ser. B 354, 757–768 (1999). 10.1098/rstb.1999.0428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Golubitsky, M. and Stewart, I., “Hopf bifurcation in the presence of symmetry,” Arch. Ration. Mech. Anal. 87, 107–165 (1985). 10.1007/BF00280698 [DOI] [Google Scholar]
- 15.Gubler, D. J. , “Epidemic dengue/dengue hemorrhagic fever as a public health, social and economic problem in the 21st century,” Trends Microbiol. 10, 100–103 (2002). 10.1016/S0966-842X(01)02288-0 [DOI] [PubMed] [Google Scholar]
- 16.Gubler, D. J. , Suharyono, W., Tan, R., Abidin, M., and Sie, A., “Viremia in patients with naturally acquired dengue infection,” Bull. World Health Organ 59, 623–630 (1981). [PMC free article] [PubMed] [Google Scholar]
- 17.Gupta, S., Ferguson, N., and Anderson, R., “Chaos, persistence, and evolution of strain structure in antigenically diverse infectious agents,” Science 280, 912–915 (1998). 10.1126/science.280.5365.912 [DOI] [PubMed] [Google Scholar]
- 18.Guy, B. and Almond, J. W. , “Towards a dengue vaccine: Progress to date and remaining challenges,” Comp. Immunol. Microbiol. Infect. Dis. 31, 239–252 (2008). 10.1016/j.cimid.2007.07.011 [DOI] [PubMed] [Google Scholar]
- 19.Halstead, S. B. , “Dengue,” Lancet 370, 1644–1652 (2007). 10.1016/S0140-6736(07)61687-0 [DOI] [PubMed] [Google Scholar]
- 20.Halstead, S. B. and Deen, J., “The future of dengue vaccines,” Lancet 360, 1243–1245 (2002). 10.1016/S0140-6736(02)11276-1 [DOI] [PubMed] [Google Scholar]
- 21.Halstead, S. B. and O’Rourke, E. J. , “Antibody-enhanced dengue virus infection in primate leukocytes,” Nature (London) 265, 739–741 (1977). 10.1038/265739a0 [DOI] [PubMed] [Google Scholar]
- 22.Innis, B. L. , Dengue and Dengue Hemorrhagic Fever (CABI, Wallingford, UK, 1997). [Google Scholar]
- 23.Kamo, M. and Sasaki, A., “The effect of cross-immunity and seasonal forcing in a multi-strain epidemic model,” Physica D 165, 228–241 (2002). 10.1016/S0167-2789(02)00389-5 [DOI] [Google Scholar]
- 24.Kawaguchi, I., Sasaki, A., and Boots, M., “Why are dengue virus serotypes so distantly related? Enhancement and limiting serotype similarity between dengue virus strains,” Proc. R. Soc. London, Ser. B 270, 2241–2247 (2003). 10.1098/rspb.2003.2440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nagao, Y. and Koelle, K., “Decreases in dengue transmission may act to increase the incidence of dengue hemorrhagic fever,” Proc. Natl. Acad. Sci. U.S.A. 105, 2238–2243 (2008). 10.1073/pnas.0709029105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nisalak, A., Endy, T. P. , Nimmannitya, S., Kalayanarooj, S., Thisayakorn, U., Scott, R. M. , Burke, D. S. , Hoke, C. H. , Innis, B. L. , and Vaughn, D. W. , “Serotype specific virus circulation and dengue disease in Bangkok, Thailand from 1973 to 1999,” Am. J. Trop. Med. Hyg. 68, 191–202 (2003). [PubMed] [Google Scholar]
- 27.Nuño, M., Feng, Z., Martcheva, M., and Castillo-Chavez, C., “Dynamics of two-strain influenza with isolation and partial cross-immunity,” SIAM J. Appl. Math. 65, 964–982 (2005). 10.1137/S003613990343882X [DOI] [Google Scholar]
- 28.Sabin, S. B. , “Research on dengue during World War II,” Am. J. Trop. Med. Hyg. 1, 30–50 (1952). [DOI] [PubMed] [Google Scholar]
- 29.Schwartz, I. B. , Shaw, L. B. , Cummings, D. A. T. , Billings, L., McCrary, M., and Burke, D. S. , “Chaotic desynchronization of multistrain diseases,” Phys. Rev. E 72, 066201 (2005). 10.1103/PhysRevE.72.066201 [DOI] [PubMed] [Google Scholar]
- 30.Shaw, L. B. , Billings, L., and Schwartz, I. B. , “Using dimension reduction to improve outbreak predictability of multistrain diseases,” J. Math. Biol. 55, 1–19 (2007). 10.1007/s00285-007-0074-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wearing, H. J. and Rohani, P., “Ecological and immunological determinants of dengue epidemics,” Proc. Natl. Acad. Sci. U.S.A. 103, 11802–11807 (2006). 10.1073/pnas.0602960103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.WHO website, http://www.who.int/mediacentre/factsheets/fs117/en/, 2006
- 33.WHO website, http://w3.whosea.org/en/section10/section332/section520_2417.htm, 2006