Abstract
In radiation therapy applications, deformable image registrations (DIRs) are often carried out between two images that only partially match. Image mismatching could present as superior-inferior coverage differences, field-of-view (FOV) cutoffs, or motion crossing the image boundaries. In this study, the authors propose a method to improve the existing DIR algorithms so that DIR can be carried out in such situations. The basic idea is to extend the image volumes and define the extension voxels (outside the FOV or outside the original image volume) as NaN (not-a-number) values that are transparent to all floating-point computations in the DIR algorithms. Registrations are then carried out with one additional rule that NaN voxels can match any voxels. In this way, the matched sections of the images are registered properly, and the mismatched sections of the images are registered to NaN voxels. This method makes it possible to perform DIR on partially matched images that otherwise are difficult to register. It may also improve DIR accuracy, especially near or in the mismatched image regions.
Keywords: deformable image registration, adaptive radiotherapy, motion estimation
I. INTRODUCTION
Image registration is a procedure for transforming different image datasets into a common coordinate system so that the corresponding points in the images are matched and allow complementary information from the different image datasets to be used for various diagnostic and therapeutic purposes.1 Image registration plays increasingly important roles in radiation therapy applications since more and more anatomical images (kVCT, daily megavoltage-CT or cone-beam-CT, MRI, etc.) and functional images (PET, SPECT, fMRI, etc.) are adopted into patient radiation treatment management. Image registration algorithms can be generally grouped into rigid and deformable (nonrigid) registrations.2 While rigid registration applies only affine transformations with a limited number of free parameters (up to 12), deformable image registration (DIR) uses a much larger number of parameters to describe tissue deformation.
DIR3 can be computed based on features extracted from the images (e.g., points,4 lines,5 and surfaces6) or based on similarity metrics directly derived from image intensity values [e.g., sum of squared differences (SSD),7 mutual information (MI),8 cross correlation,9 and correlation ratio10]. There are also different categories of algorithms based on the transformation models and the optimization schemes, for example, the thin-plate spline algorithm,11 B-spline algorithm,12,13 optical flow algorithms,7,14,15 diffeomorphic algorithms,16,17 block matching algorithms,18 finite element model (FEM) based algorithms,19,20 etc. Single modality CT-to-CT DIR is especially important for radiation therapy applications such as patient response monitoring, treatment adaptation, dose tracking, and patient motion modeling.15,21,22
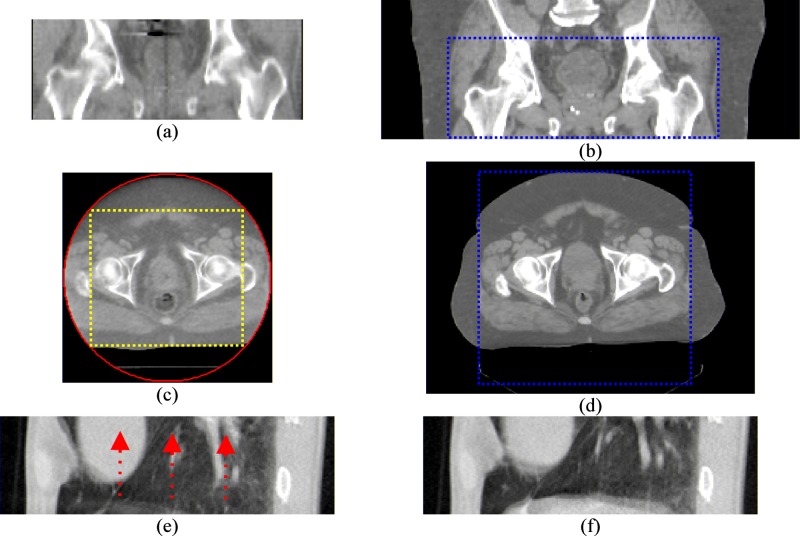
There are many situations that DIR needs to be carried out between two image datasets that only partially match. For example, (1) the daily CT images (kV-CBCT, MV-CBCT, or tomotherapy MVCT) have smaller field of views (FOVs) and superior-inferior coverage than the corresponding treatment planning CT images, as shown in Figs. 1(a)–1(d), (2) two multiple-slice free-breathing ciné mode lung CT scans at the same couch table position but different breathing phases may have different image contents due to breathing motion, as shown in Figs. 1(e) and 1(f). DIR algorithms usually assume that the two images to be registered have matching contents in the whole image domain. If the two images are only partially matched, there will be registration problems associated with the mismatched image contents, as shown in Fig. 2. Currently, a general solution is to crop the images so that the moving image can cover the fixed image entirely in both volume and image content. The disadvantages are (1) registration results will be only defined on the smaller cropped image volumes and (2) useful image information is lost because of cropping.
FIG. 1.
Examples of images partially matching situations. (a)–(d) are the scans of a prostate cancer patient. (a) and (c) are tomotherapy MVCT scans. (b) and (d) are the corresponding conventional kVCT scans. (a) and (b) demonstrate the different superior-inferior coverage between the MVCT and kVCT. The dashed lines in (b) and (d) mark the boundaries of the corresponding MVCT volume. (c) and (d) demonstrate the differences in FOV. The circle in (c) is the tomotherapy MVCT FOV circle. The rectangle marks the maximal cropped region if the MVCT image is cropped to be completely within the FOV. (e) and (f) are two 64-slice axial CT lung scans at the same couch position but at different phases of the breathing cycle. The arrows in (e) demonstrate the directions of tissue motion to match the scan in (f).
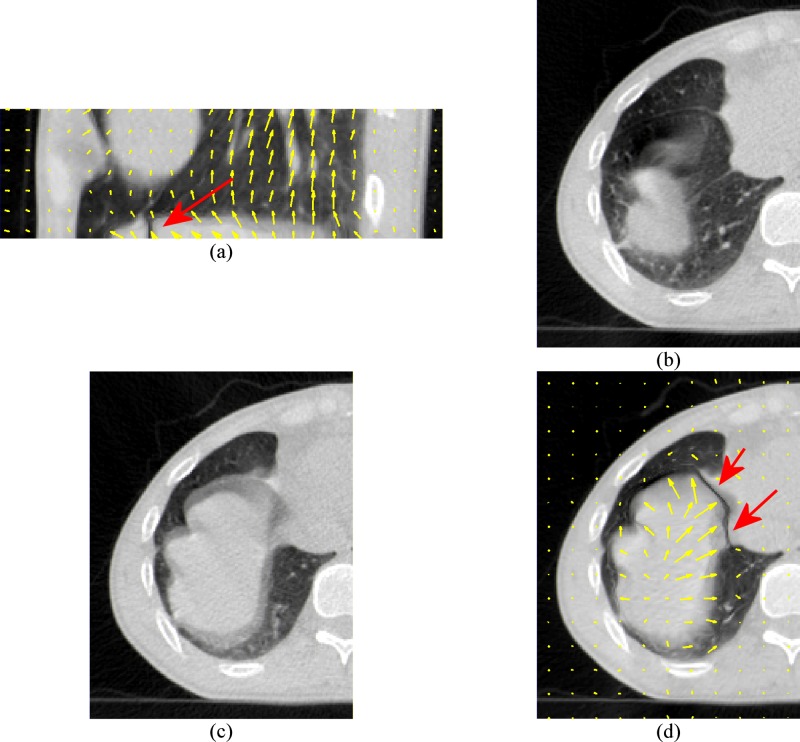
FIG. 2.
Demonstration of registration problems on the 64-slice lung CT scans. The CT scan in Fig. 1(e) is used as the moving image and the CT scan in Fig. 1(f) is used as the fixed image. (a) and (d) are the deformed moving image. (b) is the moving image in transverse view. (c) is the fixed image in transverse view. The arrows indicate the most significant registration errors. The motion vectors in (a) and (d) also show the incorrect transverse motions as the diaphragm should move mainly in the superior-inferior direction instead of in the transverse direction.
II. METHOD
In this article, we propose a method to improve the existing DIR algorithms so that DIR can be carried out in such image mismatching situations. The basic idea is to use NaN values to extend the image volumes instead of cropping them and to allow NaN voxels to match to any voxels in the registration computation. As the results, the matched sections between the images are registered and the mismatched sections of the images will be mapped to NaN voxels.
For two images ( and ) to be registered, let be the moving image and be the fixed image, a deformation vector field (DVF) registers to when the general system energy equation is optimized,
| (1) |
where is the deformed moving image , is the similarity function, is the smoothness constraint function, is the image domain, and is a configurable constant. To allow mismatched images, we slightly modify the system energy equation to
| (2) |
where and are the images with their volumes extended with NaN values, is the extended image domain, the similarity measurement function is slightly modified to take only valid (non-NaN) voxels. For example, if SSD is used as the similarity metric, the similarity term can be written as
| (3) |
where the NaN value checking function is defined as
| (4) |
However, adding the function into the system energy equation (2) makes Eq. (2) not differentiable because is not differentiable and there is no simple way to write it in a differentiable formulation. One approximation is to defer the NaN checking from the system energy equation to iterative solutions by which the system equation is solved. To demonstrate such an approximation, we use the Horn–Schunck14 (HS) optical flow algorithm which computes using the following iterative equation:
| (5) |
where is the at iteration and is averaged in the neighborhood of every voxel. is initialized to all 0 for . To check the NaN values in the iteration, this equation is modified to
| (6) |
Even though there are only slight modifications in the system energy equation and the iterative solution, there are several aspects that require further explanation. First, the reason to use NaN instead of other floating values for undefined voxels is that NaN is transparent to all arithmetic operations that DIR computations are based on. The results of arithmetic operations, such as addition, multiplication, etc., will be NaN if any operand of an arithmetic operation is a NaN. The undefined voxels need to be tracked through out the DIR iterative computations. NaN values are appropriate as the indicators for these voxels while other floating-point values, such as 0 or negative values, could not straightforwardly serve the same purpose because they could not maintain their values throughout arithmetic operations as NaN values do.
The second issue is whether allowing NaN voxels to be registered to any voxels (whether or not they are NaN voxels) would cause inaccurate registrations. Image intensity information is not available for undefined voxels; so there is no way to determine the image motion for these voxels. Assigning NaN values to these voxels and allowing them to match to any voxels is equivalent to not computing image motion on these undefined voxels. Global smoothing mechanisms of the DIR algorithms help to propagate motion from the valid image regions to the NaN region. Therefore, image motions on the undefined voxels are estimated using image motion information from the neighboring voxels containing valid intensity values.
For the modified HS algorithm, the function checks the adjustment [the operand of function in Eq. (6)], denoted as , at every iteration. will be NaN for the undefined voxels as well as neighboring voxels because of image gradient and deformation computations that use neighboring voxel intensities. How a NaN voxel affects in its neighborhood depends on the actual implementation of image gradient computation and image deformation. In our implementation, the image gradient is computed in a way similar to and trilinear interpolation is used for image deformation. A NaN voxel will affect in the neighboring voxels but not further. One should note that the in Eq. (6) will not have NaN values after the function is used. This ensures that global smoothness mechanisms applied during the iterations will continue to work and will diffuse the DVF into the undefined image regions.
Finally, an image boundary should be extended far enough to cover the maximal image displacement at the boundary. Smoothing operations, such as Gaussian low-pass filtering, will propagate NaN values into the neighboring voxels. Necessary image smoothing should be carried out before the image volumes are expanded with NaN voxels.
III. RESULTS AND VALIDATION
Figure 3 shows the results of registration between two 64-slice axial CT scans with mismatched image contents. Both CT images were with voxel size of . They were acquired at the same couch table position but different breathing tidal volumes. This 4DCT registration situation has been an interested problem for respiratory motion studies23,24 but has never been successfully solved previously. The proposed method in this paper makes a better solution for this problem. As shown in Fig. 3, we can directly register these two 4DCT scans by extending them in the superior and inferior directions by eight slices with NaN voxels before registration. Compared to the results in Fig. 2, the results in Fig. 3 are visually better.
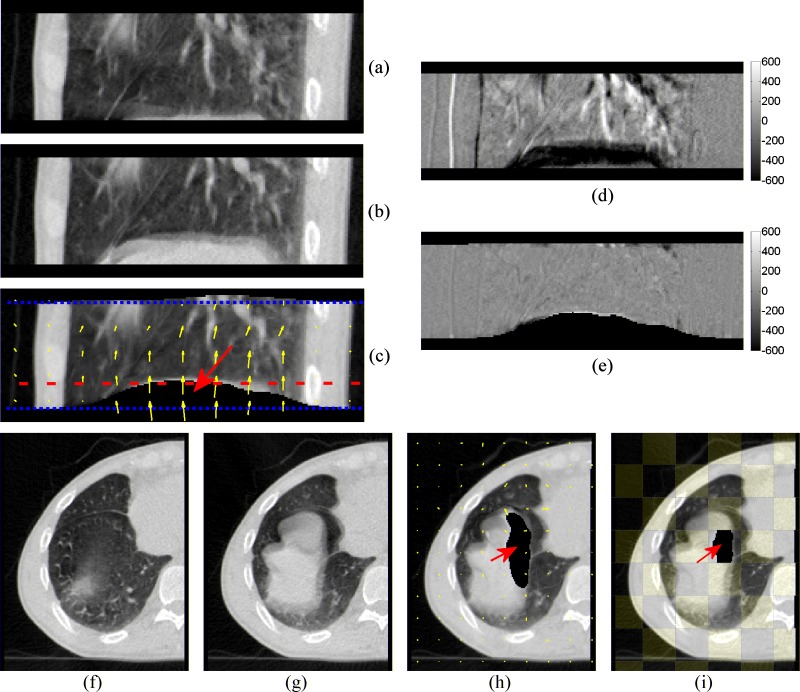
FIG. 3.
New registration results using the NaN voxel extension. Both CT scans are extended in the superior-inferior and lateral directions with NaN voxels. (a) and (f) are the moving image. (b) and (g) are the fixed image. (c) and (h) are the deformed moving image. The dotted lines in (c) mark the original CT scan boundary before NaN voxel extension. (d) is the different image before registration. (e) is the different images after registration. (i) is the checkerboard image after registration. The arrows in (c), (h), and (i) indicate the deformed NaN voxels. The transverse slice shown in (f) to (i) is marked by the dashed line in (c).
We have performed landmark-based validation for this 4DCT example. For 20 manually selected corresponding landmarks (lung-bronchi bifurcation points) in both CT scans, the average distance between the corresponding landmark pairs was before registration. The registration errors, which are defined as the absolute distances from the registered landmark points in the deformed moving image to the target landmark points in the fixed image, were .
We have also performed quantitative validation for the MVCT and kVCT volume and FOV mismatching situations shown in Fig. 1. We used a digital phantom (a kVCT image defined by a known ) with an artificial FOV cutoff. We carried DIR using the original kVCT as the moving image and the digital phantom as the fixed image. We quantitatively compared the registration errors against those from a regular DIR without using NaN extension. The results listed in Table I suggest that the proposed method could reduce registration errors, comparing to regular DIR results for the FOV mismatching situations.
TABLE I.
Registration results comparison for the MVCT FOV truncation situations.
| Image region | Ground truth imagedisplacement(mm) | Registration errors (mm)after setting voxelsoutside FOV to NaN | Registration errors(mm) after settingvoxels outside FOV to 0 |
|---|---|---|---|
| Entire image | |||
| Inside FOV | |||
| Outside FOV | |||
| Within insideFOV | |||
| Within outsideFOV |
IV. DISCUSSION AND CONCLUSION
The proposed method is able to estimate the DVF in the image mismatching image regions. Therefore, it has the advantage to allow DIR computation in larger image volumes comparing to the regular approach which crops the image volumes before DIR computation. Allowing the NaN voxels to match to any other voxels is also the primary limitation of the proposed method. The DVFs computed on the undefined voxels are not obtained by image intensity matching, but by propagating the DVF from the neighborhood valid voxels. While DVF propagating is a reasonable method for estimating DVF on the undefined voxels where image information is not available, the accuracy cannot be guaranteed.
In conclusion, we have proposed a method to improve the existing DIR algorithms to handle partially matched images. The core concept is to extend the image volumes with NaN voxels and to allow such NaN voxels to match to any voxels in the other image. The proposed method could be applied to many radiotherapy applications similar to the examples used in this paper. It is also possible to apply this method in similar ways to other algorithms that are based on different similarity metrics, including mutual information and cross correlation, even though we have to leave out such discussions from this short paper.
ACKNOWLEDGMENT
This work supported in part by a grant from Tomotherapy, Inc.
REFERENCES
- 1.Kessler M. L., “Image registration and data fusion in radiation therapy,” Br. J. Radiol. 79, S99–108 (2006). 10.1259/bjr/70617164 [DOI] [PubMed] [Google Scholar]
- 2.Maintz J. B. and Viergever M. A., “A survey of medical image registration,” Med. Image Anal. 2, 1–36 (1998). 10.1016/S1361-8415(01)80026-8 [DOI] [PubMed] [Google Scholar]
- 3.Crum W. R., Hartkens T., and Hill D. L. G., “Non-rigid image registration: theory and practice,” Med. Image Anal. 77, S140–153 (2004). [DOI] [PubMed] [Google Scholar]
- 4.Kessler M. L., Pitluck S., Petti P., and Castro J. R., “Integration of multimodality imaging data for radiotherapy treatment planning,” Int. J. Radiat. Oncol., Biol., Phys. 21, 1653–1667 (1991). [DOI] [PubMed] [Google Scholar]
- 5.Balter J. M., Pelizzari C. A., and Chen G. T., “Correlation of projection radiographs in radiation therapy using open curve segments and points,” Med. Phys. 19, 329–334 (1992). 10.1118/1.596863 [DOI] [PubMed] [Google Scholar]
- 6.van Herk M. and Kooy H. M., “Automatic three-dimensional correlation of CT-CT, CT-MRI, and CT-SPECT using chamfer matching,” Med. Phys. 21, 1163–1178 (1994). 10.1118/1.597344 [DOI] [PubMed] [Google Scholar]
- 7.Thirion J. P., “Image matching as a diffusion process: An analogy with Maxwell’s demons,” Med. Image Anal. 2, 243–260 (1998). 10.1016/S1361-8415(98)80022-4 [DOI] [PubMed] [Google Scholar]
- 8.Viola P. and Wells W. M. III, “Alignment by maximization of mutual information,” presented at the IEEE Proceedings of Fifth International Conference on Computer Vision, 1995 [Google Scholar]
- 9.Kim J. and Fessler J. A., “Intensity-based image registration using robust correlation coefficients,” IEEE Trans. Med. Imaging 23, 1430–1444 (2004). 10.1109/TMI.2004.835313 [DOI] [PubMed] [Google Scholar]
- 10.Roche A., Malandain G., Pennec X., and Ayache N., “The correlation ratio as a new similarity measure for multimodal image registration,” in Proceedings of the First International Conference on Medical Image Computing and Computer-Assisted Intervention (Springer-Verlag, New York, 1998). [Google Scholar]
- 11.Fred L. B., “Thin-plate splines and the Atlas problem for biomedical images,” in Proceedings of the 12th International Conference on Information Processing in Medical Imaging (Springer-Verlag, New York, 1991). [Google Scholar]
- 12.Xie Z. and Farin G. E., “Image registration using hierarchical B-splines,” IEEE Trans. Vis. Comput. Graph. 10, 85–94 (2004). 10.1109/TVCG.2004.1260760 [DOI] [PubMed] [Google Scholar]
- 13.Rueckert D., Sonoda L. I., Hayes C., Hill D. L., Leach M. O., and Hawkes D. J., “Nonrigid registration using free-form deformations: application to breast MR images,” IEEE Trans. Med. Imaging 18, 712–721 (1999). 10.1109/42.796284 [DOI] [PubMed] [Google Scholar]
- 14.Horn B. K. P. and Schunck B. G., “Determining optical flow,” Artif. Intell. 17, 185–203 (1981). 10.1016/0004-3702(81)90024-2 [DOI] [Google Scholar]
- 15.Wang H., Dong L., O’Daniel J., Mohan R., Garden A. S., Ang K. K., Kuban D. A., Bonnen M., Chang J. Y., and Cheung R., “Validation of an accelerated ‘demons’ algorithm for deformable image registration in radiation therapy,” Phys. Med. Biol. 50, 2887–2905 (2005). 10.1088/0031-9155/50/12/011 [DOI] [PubMed] [Google Scholar]
- 16.Dupuis P., Grenander U., and Miller M. I., “Variational problems on flows of diffeomorphisms for image matching,” Q. Appl. Math. LVI, 587–600 (1998). [Google Scholar]
- 17.Ashburner J., “A fast diffeomorphic image registration algorithm,” Neuroimage 38, 95–113 (2007). 10.1016/j.neuroimage.2007.07.007 [DOI] [PubMed] [Google Scholar]
- 18.Malsch U., Thieke C., Huber P. E., and Bendl R., “An enhanced block matching algorithm for fast elastic registration in adaptive radiotherapy,” Phys. Med. Biol. 51, 4789 (2006). 10.1088/0031-9155/51/19/005 [DOI] [PubMed] [Google Scholar]
- 19.Crouch J. R., Pizer S. M., Chaney E. L., Hu Y.-C., Mageras G. S., and Zaider M., “Automated finite-element analysis for deformable registration of prostate images,” IEEE Trans. Med. Imaging 26, 1379–1390 (2007). 10.1109/TMI.2007.898810 [DOI] [PubMed] [Google Scholar]
- 20.Brock K. K., Sharpe M. B., Dawson L. A., Kim S. M., and Jaffray D. A., “Accuracy of finite element model-based multi-organ deformable image registration,” Med. Phys. 32, 1647–1659 (2005). 10.1118/1.1915012 [DOI] [PubMed] [Google Scholar]
- 21.Lu W., Chen M. L., Olivera G. H., Ruchala K. J., and Mackie T. R., “Fast free-form deformable registration via calculus of variations,” Phys. Med. Biol. 49, 3067–3087 (2004). 10.1088/0031-9155/49/14/003 [DOI] [PubMed] [Google Scholar]
- 22.Sarrut D., Sarrut D., Delhay S., Villard P. F., Boldea V. A. B. V., Beuve M. A. B. M., and Clarysse P. A. C. P., “A comparison framework for breathing motion estimation methods from 4-D imaging,” IEEE Trans. Med. Imaging 26, 1636–1648 (2007). 10.1109/TMI.2007.901006 [DOI] [PubMed] [Google Scholar]
- 23.Ehrhardt J., Werner R., Saring D., Frenzel T., Lu W., Low D., and Handels H., “An optical flow based method for improved reconstruction of 4D CT data sets acquired during free breathing,” Med. Phys. 34, 711–721 (2007). 10.1118/1.2431245 [DOI] [PubMed] [Google Scholar]
- 24.Yang D., Lu W., Low D. A., Deasy J. O., Hope A. J., and El Naqa I., “4D-CT motion estimation using deformable image registration and 5D respiratory motion modeling,” Med. Phys. 35, 4577–4590 (2008). 10.1118/1.2977828 [DOI] [PMC free article] [PubMed] [Google Scholar]