The role of nonlinearity in computing graph-theoretical properties of resting-state functional magnetic resonance imaging brain networks

Abstract

In recent years, there has been an increasing interest in the study of large-scale brain activity interaction structure from the perspective of complex networks, based on functional magnetic resonance imaging (fMRI) measurements. To assess the strength of interaction (functional connectivity, FC) between two brain regions, the linear (Pearson) correlation coefficient of the respective time series is most commonly used. Since a potential use of nonlinear FC measures has recently been discussed in this and other fields, the question arises whether particular nonlinear FC measures would be more informative for the graph analysis than linear ones. We present a comparison of network analysis results obtained from the brain connectivity graphs capturing either full (both linear and nonlinear) or only linear connectivity using 24 sessions of human resting-state fMRI. For each session, a matrix of full connectivity between 90 anatomical parcel time series is computed using mutual information. For comparison, connectivity matrices obtained for multivariate linear Gaussian surrogate data that preserve the correlations, but remove any nonlinearity are generated. Binarizing these matrices using multiple thresholds, we generate graphs corresponding to linear and full nonlinear interaction structures. The effect of neglecting nonlinearity is then assessed by comparing the values of a range of graph-theoretical measures evaluated for both types of graphs. Statistical comparisons suggest a potential effect of nonlinearity on the local measures—clustering coefficient and betweenness centrality. Nevertheless, subsequent quantitative comparison shows that the nonlinearity effect is practically negligible when compared to the intersubject variability of the graph measures. Further, on the group-average graph level, the nonlinearity effect is unnoticeable.

Nowadays many real-world systems are often understood as networks of mutually dependent subsystems. The connectivity between subsystems is evaluated by various statistical measures of dependence. For a given system the mutual dependencies between the corresponding subsystems can be represented as a discrete structure called a weighted graph, where each subsystem is represented by a single vertex and each dependence by a connection (an edge) between two such vertices. Each edge can be labeled with a number called a weight. A weighted graph can be imagined as a set of points in a space connected by lines with different widths according to the weights. The graph representation of a system can be used to study the system’s underlying properties with the help of graph theory. Commonly a set of graph-theoretical measures is computed that characterize properties of the underlying graph and consequently of the whole system. A potentially critical part of the whole process is the choice of the statistical dependence measure used for derivation of the weights during the graph construction. For this purpose, the simple linear (Pearson) correlation coefficient of observations from any given two vertices is most commonly used. Such a choice may have the disadvantage that linear correlation does not take into account the nonlinear dependences possibly occurring in data. However there are measures that capture nonlinearities, e.g., mutual information. The main task of this paper is to study the relevance of nonlinear measures for graph-theoretical analysis of large-scale brain networks. We do so by assessing the influence of canceling the data nonlinearities, through the use of linearized surrogate data, on various graph-theoretical measures when a general nonlinear dependence measure, namely mutual information, is used as a measure of connectivity. Apart from its direct relevance for the analysis of resting-state fMRI brain networks, this study presents an approach and a general framework for assessing the relevance of nonlinear measures for graph-theoretical analysis in other fields.

I. INTRODUCTION

Graph-theoretical measures are becoming popular for characterization of complex networks,¹ such as those describing the interactions or interdependence structure of large-scale, real-world, potentially highly nonlinear dynamical systems. The examples of such systems range from climatic networks² to large-scale neural systems.³

The individual interactions between nodes of a given network can be measured by a variety of methods. While linear measures such as the Pearson correlation coefficient (referred to as linear correlation throughout this paper to stress the distinction from nonlinear correlation coefficient indices) or coherence are commonly applied, potential advantages of nonlinear measures are receiving increased attention.^2,4

Nonlinear measures potentially offer higher sensitivity due to generality of the dependence structures they are able to capture. On the other hand, linear measures have the advantage of typically easier implementation and robustness, as well as straightforward interpretation and accessibility to a wider community of researchers outside the field of nonlinear dynamics.

However, the question of which interdependence or connectivity measures should be used cannot be answered in general. The trade-off between the crucial factors is likely to depend on a particular dataset and scientific problem considered. For instance, the use of mutual information, a very general nonlinear dependence measure, has been recently proposed as advantageous for the analysis of climatic networks.²

While the linear dependence measures (correlation, partial correlation, coherence, partial coherence, partial directed coherence) constitute a relatively narrow family corresponding to “singular” simplifying linear models of the system, there is a virtually boundless number of nonlinear dependence measures stemming from various perspectives taken by the analysts. We refer the reader to a selection of reviews of some of the nonlinear dependence measures proposed so far with some emphasize on methods applied in neuroscience.^4–6 Importantly among the nonlinear measures, some stand out due to the generality of the concepts they build upon. For a system with two variables, a classical example is that of mutual information, which is a general measure of dependence between two variables in the context of information theory, corresponding to the amount of common information contained in two variables. Mutual information is also deeply rooted to the probability theory, as it can be conveniently viewed as the Kullback–Leibler divergence of the bivariate distribution from a hypothetical bivariate distribution of two independent variables with the same marginal distributions as the original ones. Thus, instead of having to test a virtually infinite number of possible nonlinear dependence measures, we use mutual information as an unbiased information-theoretically rooted measure of departure from statistical independence.

Various approaches have been developed for estimating of information-theoretical functionals.⁷ A relatively simple estimator based on marginal equiquantization⁸ has been proposed for detecting nonlinearity^9–11 in combination with the technique of surrogate data.¹² Although other estimators may have better performance considering estimator bias, in statistical tests the correct value of mutual information is less important than the distinction of the data value from a range related to a null hypothesis, realized using surrogate data. Considering that the surrogate data reliably reflect sources of estimator bias, estimator variance is more important that the estimator bias. In such a situation, the simple equiquantal box-counting algorithm is not outperformed by more complex and computationally more intensive estimators with lower bias.¹³ The equiquantal mutual information estimator has been successfully used in detection and quantification of nonlinearity in the dynamics of various complex systems, ranging from the Earth’s atmosphere¹⁴ to the human heart¹⁵ and brain.^16–19

In neuroscience, functional magnetic resonance imaging (fMRI) is one of the prominent methods for the study of large-scale brain dynamics. Following the increase of interest in the study of complex network properties, a wealth of graph-theoretical studies utilizing resting-state fMRI data has been published in the last 5 yr.²⁰ Importantly, linear connectivity measures such as Pearson or partial linear correlation of the local activity time series are used to derive the connectivity matrix that is then transformed to the network representation.

Notably, the suitability of the use of linear correlation as a dependence measure depends on the Gaussianity of the joint bivariate distribution. Recent work has shown that while there is a statistically detectable non-Gaussianity in the resting brain state fMRI data,²¹ the approximation of mutual information by linear correlation is relatively close.

In the analysis of complex systems, the question of linearity is often discussed. Although not always fully specified, linearity is often understood in terms of existence of an underlying linear Gaussian stationary stochastic process generating the observed data—the question whether the observed data could be generated by such a process is often posed and statistically tested.¹² Wherever we refer to “linearity assumptions,” these assumptions are considered. Nonlinearity then refers to deviation from this data property.

As mentioned above, rather than on testing the linearity assumptions, this paper focuses on a different though related question whether linear correlation is a sufficient measure of bivariate dependences for the purposes of characterization of the system by graph-theoretical properties of the corresponding connectivity graph. Clearly, if the bivariate distributions p(X_i, X_j) for each two variables X_i, X_j are Gaussian (which is trivially valid under the relatively strong linearity assumptions), then linear correlation fully captures the full bivariate dependencies. When we speak about data Gaussianity, we refer to this Gaussianity of the bivariate distributions of the marginally normalized data (or surrogates) and non-Gaussianity refers to deviation from this property. Note that deviation from this bivariate data Gaussianity might, but not necessarily, lead to substantial differences in the graph-theoretical properties between graphs constructed using linear or nonlinear dependence measures.

A question arises, whether the observed deviation of the fMRI time series from the linear Gaussian properties is relevant for the graph-theoretical properties of the brain interaction network. In other words, does the non-Gaussianity present in the dependence structure of large-scale brain activity data sufficiently motivate and justify potential use of nonlinear measures of connectivity in graph-theoretical studies of resting-state fMRI data?

In this report, we contribute to the discussion of this question by comparing the graph-theoretical properties obtained when using mutual information as a dependence measure of original and linearized (surrogate) fMRI data. Using this approach, we circumvent the issues associated with different numerical properties of mutual information and linear correlation.

The paper is organized as follows: First, a description of the acquisition and preprocessing of the data is given in Sec. II. The section is divided into a description of the data in Sec. II A, the generation of linear surrogate datasets in Sec. II B, and the nonlinear connectivity measure we applied in Sec. II C. Section III provides a brief overview of graph-theoretical notions in Sec. III A and describes the applied graph-theoretical measures in Sec. II B. Further in Sec. IV we outline the process of analysis. After a general account of the procedure in Sec. IV A, we continue with descriptions of particular concepts used in the analysis itself: dominances are introduced in Sec. IV B, shadow datasets in Sec. IV C, and additional statistics in Sec. IV D. The results and conclusions are provided in Secs. V and VI.

II. DATA AND PREPROCESSING

A. Data

Resting-state fMRI data from 12 healthy volunteers (5 males and 7 females, age range 20–31 yr) were obtained using a 3T Philips Achieva MRI scanner, operating at ITAB (Chieti, Italy). Functional images were obtained using T2-weighted echo-planar imaging (EPI) with blood oxygenation level-dependent²² (BOLD) contrast using sensitivity encoding (SENSE) imaging. EPIs [time to repetition (TR)/time to echo (TE) = 2000/35 ms] comprised 32 axial slices acquired continuously in ascending order covering the entire cerebrum (voxel size = 3 × 3 × 3.5 mm³).

Each subject underwent two scanning runs. In each scanning run the initial five dummy volumes allowing the MRI signal to reach steady state were discarded. The subsequent 300 functional volumes forming a 10-min data session were then used for the analysis. Therefore the data available for analysis consist of 24 sessions, each containing activity time series with 300 timepoints for each brain voxel.

A three-dimensional high-resolution T1-weighted image (TR/TE=9.6/4.6 ms, voxel size = 0.98 × 0.98 × 1.2 mm³) covering the entire brain was also acquired for each subject and used for anatomical reference.

Standard data preprocessing was performed using the spm5 software package (Wellcome Department of Cognitive Neurology, London, UK) running under matlab (The Mathworks). The preprocessing steps involved the following: (1) correction for slice-timing differences, (2) correction of head-motion across functional images, (3) coregistration of the anatomical image and the mean functional image, and (4) spatial normalization of all images to a standard stereotaxic space (Montreal Neurological Institute, MNI) with a voxel size of 3 × 3 × 3 mm³. For details of the preprocessing methods we refer the reader to the comprehensive book by Friston et al.²³

Ninety parcels from the automated anatomical labeling (AAL) atlas were used to extract mean BOLD time series after masking out nongray matter voxels. The anatomical positions of the parcels are described in the literature.²⁴ Every parcel time series was orthogonalized with respect to the motion parameters and global mean signal and high-pass filtered at 1/120 Hz.

Before any calculations with resulting time series a specific “normalization step” was performed. This “normalization” step consists in assigning the appropriate percentile to each value of a given variable, and then replacing the original values of the variable by the values corresponding to these percentiles in the standard normal distribution. Note that this normalization step does not affect mutual information between the time series if the mutual information is estimated using equiprobable binning, as described below. Reasons for inclusion of this step are described in Sec. II B.

After all preprocessing step calculations, the data consist of 24 sessions, each one consisting of 90 time series with 300 data points each.

B. Generation of linear surrogate data

To assess the effect of nonlinearity on the graph-theoretical properties of the resting-state fMRI brain networks, we compare the network representations of the data with those of their linear counterparts.

The linear counterpart of a single session dataset is considered as a realization of a linear Gaussian process with the same “linear properties” as the original data. Such realizations, called surrogate datasets, are created using the method of multivariate Fourier transform (FT) surrogates^25,26—realizations of multivariate linear Gaussian stochastic process which mimics individual spectra of the original time series as well as their cross-spectrum. The multivariate FT surrogates are obtained by computing the Fourier transform (FT) of the series, keeping unchanged the magnitudes of the Fourier coefficients (the spectrum), but adding the same random number to the phases of coefficients of the same frequency bin; the inverse FT into the time domain is then performed. The multivariate FT surrogates preserve (the part of) synchronization, if present in the original data, which can be explained by a multivariate linear Gaussian stochastic process.

For each session, 99 such multivariate surrogates are generated to build a solid statistical ensemble to compare the original data. While the fMRI data marginals typically do not deviate strongly from Gaussianity, to correct for potential differences due to univariate non-Gaussianity of the original data (that would not appear in the linear surrogates), an initial normalization step described in Sec. II A is performed.

Note that the applied rescaling effectively corresponds to the initial step of the amplitude adjusted Fourier transform (AAFT) surrogate generation method^12,27—i.e., the normalization of the univariate distributions. As in the AAFT, this is followed by the Fourier transform and phase randomization. The final readjustment of the marginals present in the AAFT method is not carried out in our analysis. There are two main reasons for this. First, such a rescaling does not change the bivariate mutual information and, therefore, does not affect our results. Secondly, we choose to follow the same framework as used in the earlier paper,²¹ where the assumption of Gaussianity of the marginals gives us a convenient bound on the mutual information $I_{X,Y}\ge I_{\mathrm{Gauss}}(r_{X,Y})=-\frac{1}{2}\text{log}(1-r_{X,Y}^2)$, where r_X,Y is the linear correlation of X and Y, I_X,Y is mutual information between X and Y and I_Gauss(r) is mutual information between two variables with a bivariate Gaussian joint distribution with correlation coefficient r. This bound on mutual information is in general not valid when the marginals are not kept Gaussian.

C. Computing functional connectivity by mutual information

For each session, the network is represented by a functional connectivity matrix. To be sensitive both to linear and nonlinear connectivity contributions, we use a general dependence measure—mutual information.

For two discrete random variables X₁, X₂ with sets of values Ξ₁ and Ξ₂, mutual information is defined as

$$I(X_1,X_2)=\sum _{x_1\in {\Xi }_1}\sum _{x_2\in {\Xi }_2}p(x_1,x_2)\text{log}\frac{p(x_1,x_2)}{p(x_1)p(x_2)},$$

where the probability distribution function is defined by p(x_i) = Pr{X_i = x_i}, x_i ∈ Ξ_i and the joint probability distribution function p(x₁, x₂) is defined analogously. When the discrete variables X₁, X₂ are obtained from continuous variables in a continuous probability space, then the mutual information depends on a partition chosen to discretize the space. Here a simple box-counting algorithm based on the marginal equiquantization method^8,9 was used, i.e., a partition was generated adaptively in one dimension (for each variable) so that the marginal bins become equiprobable. This means that there is approximately the same number of data points in each marginal bin. The number Q of marginal bins is limited by the amount of available data.²⁸ Several empirical criteria have been proposed, e.g., Paluš^8,9,28 recommends that N ≥ Q^n + 1 when computing mutual information of n variables using time series consisting of N samples. Severity of the “overquantization” bias depends on the properties of the analyzed data.²⁸ On the other hand, too coarse quantization (e.g., Q = 4) can neglect some subtle nonlinear effects. Therefore we used a pragmatic choice of Q = 8 bins which has been found to be sensitive to nonlinear dependence and even to nonlinear causal effects in a large number of studied model and real systems.^28,29

For each session, we computed the MI for each pair of parcels, yielding a symmetric 90 × 90 matrix of MI values.

III. COMPLEX NETWORKS

Graph theory is a well established field of mathematical science^30–32 with many applications in various natural and social sciences.^33–35 For analysis of neurological data its most important subfield is probably the theory of complex networks.^1,3 This theory deals with various types of graphs representing complex behavior of the underlying systems that these graphs represent. Such analysis usually focuses on several key graph-theoretical measures. In the following text, we give a brief overview of the definitions of the concepts from graph theory that we use, in order to provide a clear context for the introduction of specific graph-theoretical measures typically used in complex network analysis.

A. Terms and notations from graph theory

A graph G is a pair, G = (V, E), where V stands for a set of nodes (or vertices) and E is a set of edges where each edge represents a connection between two nodes. All graphs considered in this work are undirected.³¹ For complex network analysis a simple generalization of graph called weighted graph is used.³⁰ In weight graphs a weight w is introduced for each edge by the so-called weight function $W:E\to \mathbb{R}$. Graphs without weights can be called unweighted if there is a need to distinguish them from the weighted ones.

Nodes are usually denoted as v_i or only by their index i when there is an enumeration of nodes or simply by v if indices are not important. A similar situation is in the case of edges for which notations e_i,j or {i,j} are used. The number of vertices is denoted by n = |V| and the number of edges by m = |E|. From an algebraic point of view the most important notion for us is the adjacency matrix.³² An adjacency matrix A is a matrix $A={(a_{i,j})}_{i,j=1}^n$ whose elements are a_i,j = 1 if e_i,j ∈ E and 0 otherwise. It is useful to conceptualize the set of vertices that are connected with a given vertex v by edges—this set is denoted as Γ(v). A density, defined as ρ = 2m/(n(n − 1)), represents the relative number of edges present in the graph with respect to the total number of edges possible. For a set T ⊂ V of vertices E(T) ⊂ E denotes a subset of edges of the original graph that connects only vertices from set T. Another algebraic structure used here is the distance matrix³² D, defined as $D={(d_{ij})}_{i,j=1}^n$, where d_i, j is a distance between vertices i and j that means a shortest path connecting corresponding vertices where a path is informally a sequence of vertices that are consecutively connected by the edges, number of which defines the length of the path.³⁰ If there is no path connecting two vertices then we set d_i, j = ∞, while the diagonal entries of the distance matrix are naturally set to d_i, i = 0.

B. Network characteristics

In this paper, the graph-theoretical properties of undirected unweighted graphs are analyzed, following the most common analysis approach applied in complex network analysis.¹ The undirected unweighted graphs are obtained by binarization of the symmetric connectivity matrix using some thresholds. The main objective of this work is to study the influence of nonlinearities on various graph characteristics that are also called graph measures. The number of potentially useful characteristics used is very high and still rising.¹ Therefore testing all possible measures is impractical. For this reason a subset of measures covering several general classes of complex network characteristics is chosen. The considered classes differ in their locality and in the amount of used information. The following text describes the nature and calculation of all the measures we used.

The first class involves the local characteristics. Measures in this class are defined for each node v ∈ V(G) and they do not depend on the aspects of the structure of G that are located far from the studied vertex v. A classical representative of this class is the degree of vertex v defined as³⁶

$$k_i=\sum _{j\in V}{a}_{i,j}.$$ (1)

Another widely used local characteristic is the local clustering coefficient which determines whether vertices that are linked to a particular vertex v_i are likely to be linked to each other.³⁷ It can be also considered as a measure of how far a subgraph on a set Γ(i) is from a complete graph (a graph with all possible edges present). The local clustering coefficient is defined as

$$c_i=\frac{2|E(\mathbf{\Gamma }(i))|}{k_i(k_i-1)}=\frac{{\sum }_{j,\ell }{a}_{i,j}{a}_{j,\ell }{a}_{\ell ,i}}{k_i(k_i-1)}.$$ (2)

We will refer to the second class of measures as mesoscopic characteristics. These are still calculated for particular vertices, but a distant structure of G also becomes more important. A key mesoscopic measure is betweenness centrality (also called the shortest path betweenness centrality) defined as³⁸

$$C_b(i)=\sum _{j,k\in V,j\ne i\ne k}\frac{{\sigma }_{j,k}(i)}{{\sigma }_{j,k}},$$ (3)

where σ_j,k denotes the number of all the shortest paths between vertices j and k and σ_j,k (i) denotes the number of the shortest paths between the same vertices that go through the vertex i (note that particularly in unweighted graphs, it is common for several or many different shortest paths between two vertices to exist). This measure expresses how important the particular vertex is from a perspective of “information flow” from one vertex to any other vertex. In other words, how important this vertex is as a mediator between any pair of vertices. In this paper, the computation was performed using the algorithm of Brandes.³⁹ This measure is one from a large family of graph centralities, where the shortest path betweenness is probably the most used.⁴⁰ In the following text, local and mesoscopic measures are often abbreviated together as local measures and where distinction is needed a term strictly local is used.

The last class of measures to be considered in this paper is the class of global characteristics. These measures are not evaluated for specific vertices, but express the properties of the whole network. Some of the local or mesoscopic graph characteristics have their counterparts in this class. An example of this case is the global clustering coefficient or simply a clustering coefficient calculated as the average of the values of the local clustering coefficient over all vertices

$$C=\frac{1}{n}\sum _{i\in V}{c}_i.$$ (4)

In the same way as the global clustering coefficient, global betweenness centrality or betweenness centrality is defined as

$$C_b=\frac{1}{n}\sum _{i\in V}{c}_b(i).$$ (5)

Another important global measure is characteristic path length, defined as³⁷

$$L=\frac{1}{n(n-1)}\sum _{i,j\in V,i\ne j}{d}_{i,j},$$ (6)

where d_i,j ∈ D are elements of the distance matrix. For disconnected graphs characteristic path length defined according to Eq. ((6)) is not finite and therefore if often not very convenient. Since this characteristic was shown to correspond to global betweenness centrality⁴¹ for connected graphs and since global betweenness centrality has no computational problems with infinite values, only global betweenness centrality, and not characteristic path length, is used in further computations.

Another characteristic called efficiency is commonly used at the place of the characteristic path length for both theoretical and computational reasons.^42,43 However as efficiency and characteristic path length are not fully equivalent,^42,43 we also include an analysis of efficiency, defined as

$$E=\frac{1}{n(n-1)}\sum _{i,j\in V,i\ne j}\frac{1}{d_{i,j}}.$$ (7)

The last global characteristic to be considered in this paper deals with the general tendency in connectivity as a function of the vertex degree.⁴⁴ One type of such a general tendency is whether high-degree nodes are likely to connect with other high-degree nodes, or to low-degree ones. This property is called assortativity, or disassortativity, respectively.^44–46 Detection of such a behavior is usually a nontrivial task, often replaced by a simple coefficient called the assortative coefficient, defined as^44,46

$$r=\frac{{\displaystyle \sum _{(i,j)\in E}}{k}_i{k}_j-\frac{1}{m}{\left[{\displaystyle \sum _{(i,j)\in E}}\frac{1}{2}(k_i+k_j)\right]}^2}{{\displaystyle \sum _{(i,j)\in E}}\frac{1}{2}(k_i^2+k_j^2)-\frac{1}{m}{\left[{\displaystyle \sum _{(i,j)\in E}}\frac{1}{2}(k_i+k_j)\right]}^2}.$$ (8)

This coefficient can be used to approximately describe the behavior of the underlying network from the perspective of assortativity. Deeper discussion of this topic can be found in the corresponding literature.^47,44

A very important property of the resulting network is the number of components where a component is the maximal subset of vertices which is connected, i.e., any vertex from this set can be reached by a path from any other. While network characteristics are typically well defined even for graphs that are not connected, i.e., have several components, the comparison of some measures, especially mesoscopic and global, can be very sensitive to the resulting component structure. For these reasons we restrict some parts of our analysis to the results obtained for such values of the binarization threshold for which all compared graphs are connected.

IV. NETWORK ANALYSIS METHOD

The main task of this paper is to detect the potential influence of nonlinearities possibly present in real fMRI brain activity data on commonly used graph characteristics. For this purpose 24 data sessions were preprocessed and analyzed by the methods described in Sec. II A, giving N_sess = 24 basic datasets, each containing the original time series together with N_surr = 99 multivariate surrogate time series generated from the original data by the method outlined in Sec II B. This section describes how the connectivity matrices corresponding to the multivariate time series are transformed to graphs and further analyzed.

A. Network analysis process overview

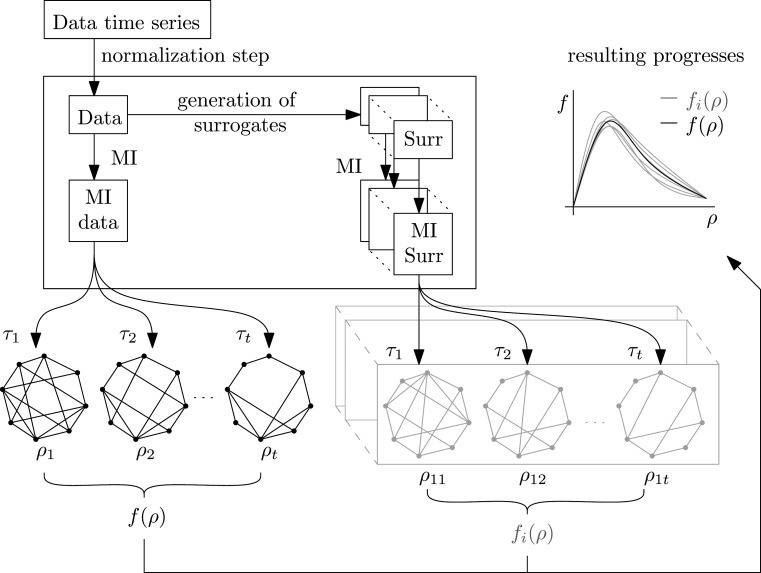
For each connectivity matrix from any dataset various thresholds can be used to construct unweighted graphs for which a general graph-theoretical characteristic f can be determined. The whole process containing the steps described in Sec. II is shown in Fig. 1.

FIG. 1.

Data analysis pipeline: An initial normalization step described in Sec. II A is performed using the data time series. For resulting data, MI is computed for all pairs, see Sec. II C. In parallel, linear surrogate data are generated, see Sec. II B, from the same data and for each surrogate its MI matrix is computed in the similar way. Each matrix (corresponding to data or surrogate) was then threshold at multiple thresholds providing a collection of graphs. For each such graph a chosen characteristic f is computed and analyzed (e.g., plotted as a function of density).

For binarization of the connectivity matrices into unweighted graphs, thresholds from 0.0 to 1.0 with a step 0.001 were used in general. Mutual information can have values above 1. Nevertheless results show that these values are very sparse for our analysis process and therefore we chose an upper bound of 1. We are interested in the network structure rather than in the connectivity strength. For comparing graph-theoretical properties of different connectivity matrices, it is more suitable to match the graph density rather than the thresholds.² Therefore, for each matrix we evaluate each characteristic f as a function of density: f = f (ρ).

While for n = 90 vertices the maximum Ω = 4005 possible density values can be obtained by thresholding, in practice only a subset of densities is attained with adaptive thresholding of the connectivity matrix. To achieve comparable results across the matrices, the function f = f(ρ) is interpolated in Voronoi manner⁴⁸—to each value of ρ the value f (ρ_neigh) is assigned, corresponding to the closest density ρ_neigh attained by thresholding. In further description, a data value of the global characteristic for a specific session s and density ρ is denoted as f^D (s, ρ). We drop some of the indices to simplify notation where confusion is unlikely. We further write f_j(s, ρ) for the values obtained for surrogates, where j = 1, 2, … , N_surr are the indices of the surrogates. When local versions of characteristics are used, a parameter i for vertices has to be also used as in f^D(s, ρ, i) and f_j(s, ρ, i).

For each session, global characteristics are simply computed as functions of density for data and corresponding N_surr surrogates. Then functions representing surrogates and data can be compared using the process depicted in Fig. 1. The results for surrogates are usually plotted by two gray lines—minimal and maximal, forming a “belt” of values typical under linearity. When the black data line falls into this belt, it suggests that the data nonlinearity does not have a substantial effect on the particular graph measure—the deviation from linear process is within the natural variation due to numerical estimation of the connectivity measure from a finite-size sample. This process is repeated for each session and the goal is to check whether data functions evade significantly from the “belt” representing the linear surrogate values.

B. Dominances

While the visual inspection of the belt plot provides an intuitive grasp of the strength of any nonlinearity effect on the studied graph-theoretical measures, a more formal quantitative analysis is beneficial, particularly in the case of mesoscopic and local characteristics. An intuitive formalization of the concept of data “leaving the belt” of surrogates by the concept of dominance is provided below.

Let s and ρ be fixed. For mesoscopic or local graph characteristic, let us call a vertex i a maximal dominant vertex when it holds that max_j{f_j(i)} < f^D(i) and similarly minimal dominant vertex if min_j{f_j(i)} > f^D(i). We further define the maximal dominance indicator function as

$$f_M^{\mathrm{dom}}(s,\rho ,i)=\{\begin{array}{cc}\multicolumn{1}{c}{1,}& \hfill i\mathrm{is}\mathrm{maximal}\mathrm{dominant}\hfill \\ \multicolumn{1}{c}{0,}& \hfill \mathrm{otherwise}.\hfill \end{array}$$ (9)

Similarly, the minimal dominance indicator function $f_m^{\mathrm{dom}}(s,\rho ,i)$ is defined. Finally, the dominance function is defined as $f^{\mathrm{dom}}(s,\rho ,i)=f_m^{\mathrm{dom}}(s,\rho ,i)+f_M^{\mathrm{dom}}(s,\rho ,i)$. The following steps can be performed for any of these functions but we concentrate on the dominance function only. Using simple summation the graph dominance function can be defined as

$$f^{G,\mathrm{dom}}(s,\rho )=\sum _{i=1}^n{f}^{\mathrm{dom}}(s,\rho ,i),$$ (10)

and finally the overall dominance function is computed as

$$f^{T,\mathrm{dom}}(\rho )=\frac{1}{N_{\mathrm{sess}}}\sum _{s=1}^{N_{\mathrm{sess}}}{f}^{G,\mathrm{dom}}(s,\rho ).$$ (11)

This function is then further analyzed. The same approach is used for the global characteristic, with the exception that dominance indicators are not functions of vertices and the summation step (10) is therefore omitted. Note that the expected values of the dominances under strict linearity are about 2%, corresponding to the probability of a single value out of a set of 100 values (1 data value and 99 surrogate values) being the highest or the lowest under the simplifying assumption of existence of a single maximum (or single minimum) value.

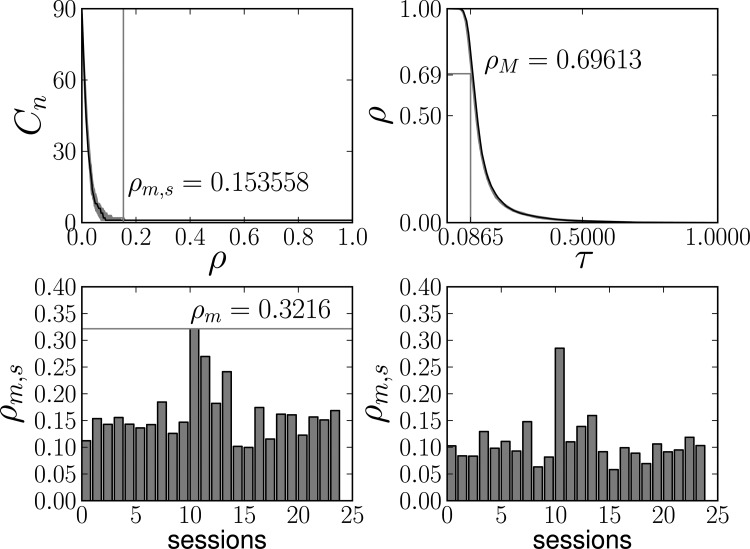
To achieve robustness in the statistical comparison of the dominances, these were further averaged across a range of relevant densities. The resulting upper and lower density bounds are presented in Fig. 2. The lower bound is determined so that for all sessions, all the resulting graphs are connected, i.e., consist of a single component to guarantee good comparability across graphs. For each session s a minimal density ρ_m,s is determined, assuring that the data graph and all graphs of surrogates are connected. We use ρ_m = max_s ρ_m,s = 0.3216 as the lower bound of the interval of interest. The upper bound is equal to ρ_M = 0.69613, above which the resulting graphs are likely to be extremely influenced by noise. This density corresponds to threshold τ_M = 0.0865 for the mutual information. This is the estimated expected mutual information for the equiquantization method and sample size (see Sec. II C) under the condition of total independence of the two variables. The value was estimated as the mean of mutual information values generated for 50 000 bivariate samples from a bivariate distribution with zero correlation, each with N = 300 observations.

FIG. 2.

Generation of the relevant density interval for dominance averaging. Top left: number of components C_n in a chosen session and it surrogates with lower bound for single-component graphs ρ_m,s. Top right: dependence between density and threshold with indicated upper bound ρ_M. Bottom left: values of ρ_m,s for various sessions (showing also the across-subject maximum ρ_m). Bottom right: the same as bottom left but using only data; without maximization across all surrogates.

C. Control for numerical bias using shadow datasets

To explicitly control for any potential bias in the numerical generation of the surrogate distributions, we repeat for each session the whole procedure for N_shadow = 39 linear, “shadow” datasets. For each session, 39 shadow datasets were created as a multivariate FT surrogate of the marginally normalized original dataset. Thus the shadow dataset preserved only the linear (correlation) structure of the original dataset of the respective session. Subsequently, each shadow dataset has undergone the same procedure as original data, including the initial normalization, generation of multivariate surrogates, computation of MI, and generation of binary graphs using the appropriate thresholds. In this way, we mimic the full procedure of processing the original data while using linear shadow datasets, accounting for any potential slight bias introduced by numerical properties of the algorithm. Then, the dominances for relevant graph measures computed from the data are compared with the distribution obtained from the linear, shadow datasets. In particular, if the data dominance value is higher than at least 38 out of the 39 dominance values obtained from the shadow datasets, this would correspond to the significance level p < 2/40 = 0.05 (no correction for multiple comparisons applied).

D. Additional statistics

To support the results obtained from the dominance quantification we carry out one more statistically potentially stronger and quantitatively more informative analysis step. The key idea is to compare the bias and extra variability contained in the nonlinear results with the random intersurrogate variance observed in the linear results and further with the intersession variability capturing the differences within and between subjects. In other words, we want to quantify the nonlinear effects and compare them to random error and a realistic true effect, to see if the potential nonlinear effects would be relevant in practice.

To derive these comparisons, we first consider a general global characteristic f. For a given session s an average value of the general characteristic f for surrogates can be determined as

$${\stackrel{\wedge }{f}}^S(s,\rho )=\frac{{\sum }_{j=2}^{N_{\mathrm{surr}}}{f}_j(s,\rho )}{N_{\mathrm{surr}}-1}.$$ (12)

We have omitted the first surrogate as it is going to serve as a reference element for all comparisons with the data values. As the order of surrogates bears no relevant information, the first one can be technically considered to be chosen at random.

We estimate the average difference of (nonlinear) data with respect to (linearized) surrogates by

$${\stackrel{\wedge }{f}}^D(\rho )=\frac{{\sum }_{s=1}^{N_{\mathrm{sess}}}(f^D(s,\rho )-{\stackrel{\wedge }{f}}^S(s,\rho ))}{N_{\mathrm{sess}}},$$ (13)

and also estimate the standard deviation of such differences as

$${\stackrel{\wedge }{\sigma }}^D(\rho )=\sqrt{\frac{{\sum }_{s=1}^{N_{\mathrm{sess}}}(f^D(s,\rho )-{\stackrel{\wedge }{f}}^S(s,\rho )-{\stackrel{\wedge }{f}}^D(\rho )){}^2}{N_{\mathrm{sess}}-1}}.$$ (14)

These values are compared to similar quantities computed using the “reference” linear surrogate (that was previously excluded from the average surrogate value comparison to achieve independence of the estimates)

$$\stackrel{\wedge }{\delta }(\rho )=\frac{{\sum }_{s=1}^{N_{\mathrm{sess}}}(f_1(s,\rho )-{\stackrel{\wedge }{f}}^S(s,\rho ))}{N_{\mathrm{sess}}}$$ (15)

and

$$\stackrel{\wedge }{\sigma }(\rho )=\sqrt{\frac{{\sum }_{s=1}^{N_{\mathrm{sess}}}(f_1(s,\rho )-{\stackrel{\wedge }{f}}^S(s,\rho )-\stackrel{\wedge }{\delta }(\rho )){}^2}{N_{\mathrm{sess}}-1}}.$$ (16)

For local characteristics just one extra step is included in that all the described statistics are at first determined for each vertex and subsequently the graph values are computed by averaging over vertices.

V. RESULTS

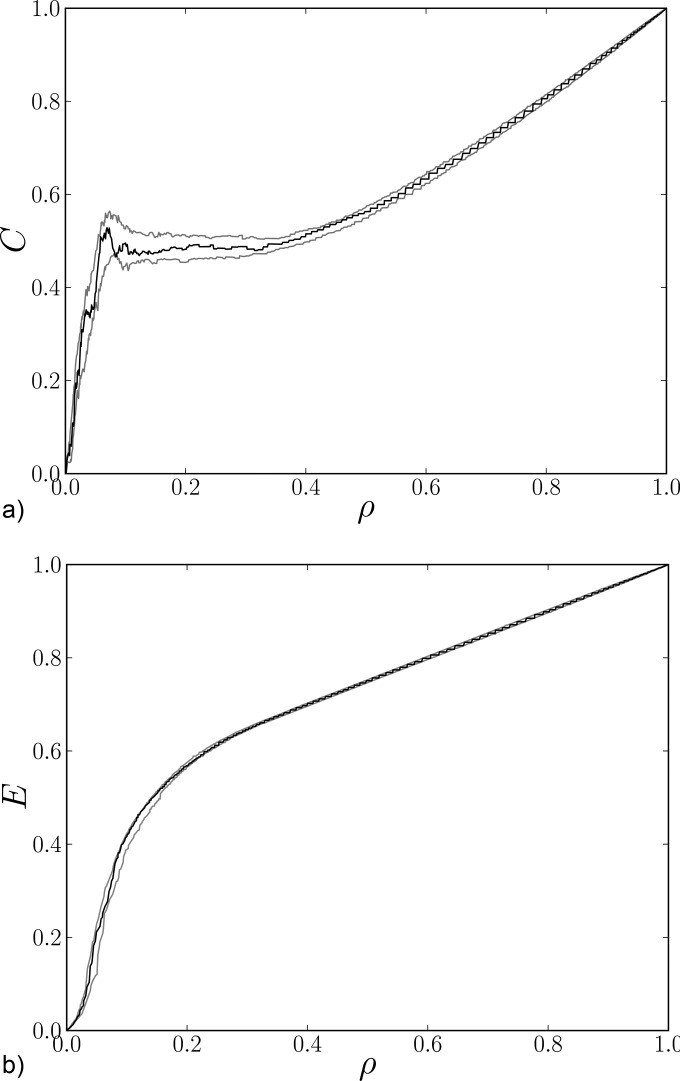
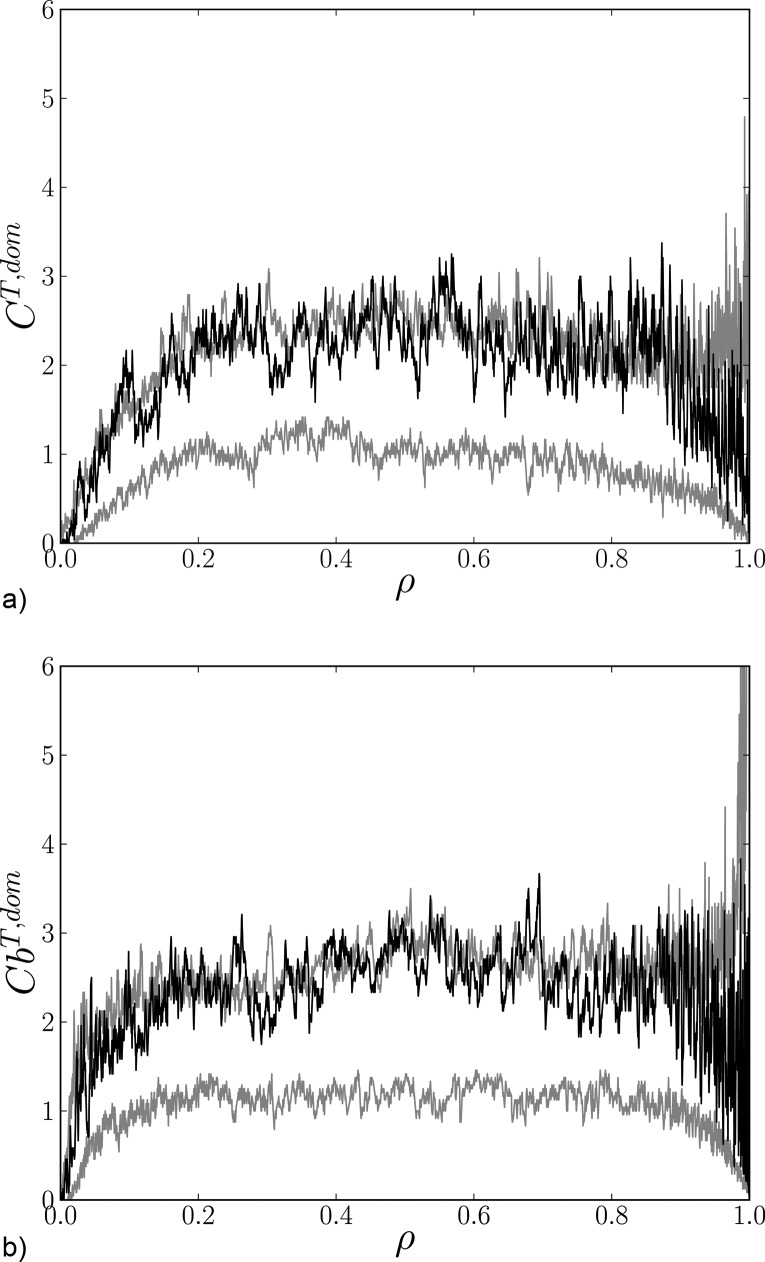
We first present a graphical comparison of the graph-theoretical measures evaluated for data and linear surrogate graphs. The results for the global clustering coefficient calculated using Eq. ((4)) from a representative session are shown in Fig. 3(a). Similar results can be found for other sessions. The figure shows that the original data line is not leaving the “belt” defined by the minimal and maximal values of the linear surrogates, suggesting that the nonlinear effect is negligible with respect to the error variance due to mutual information estimation.

FIG. 3.

Two graph characteristics as functions of density ρ for a graph representing original data (black line) and minimal and maximal surrogate lines (gray lines) for a representative session.

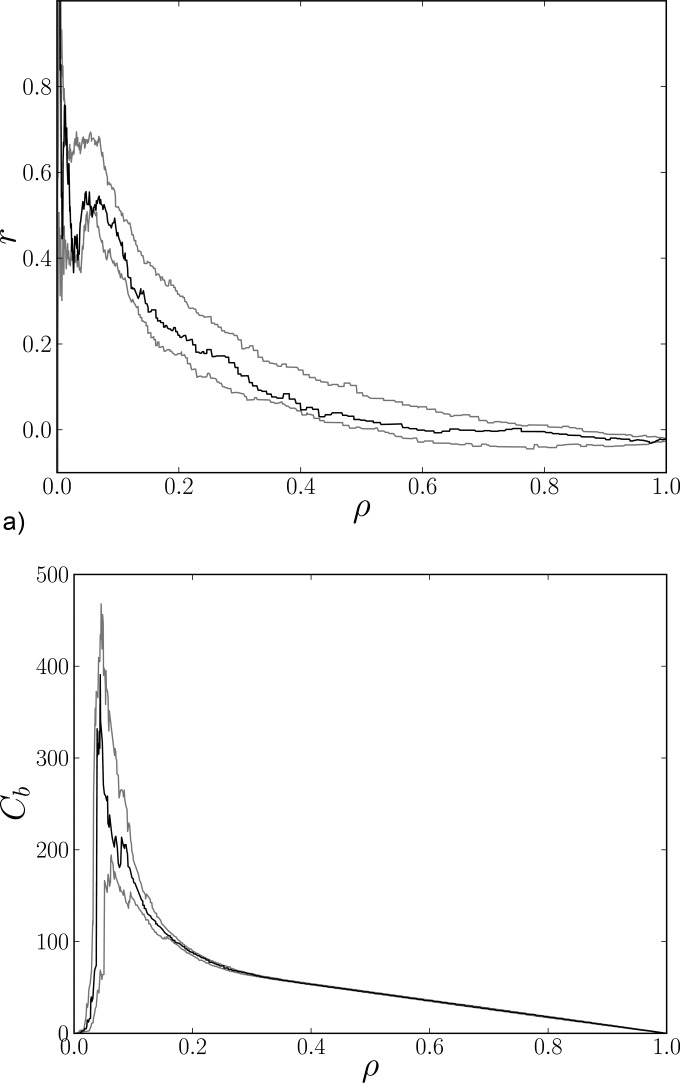
A similar picture can be observed in Fig. 3(b), where the global values of efficiency given in Eq. ((7)) are depicted. Similarly to the previous case, the data line is located well within the belt created from corresponding surrogates. The same behavior can be observed in the case of the assortative coefficient and global betweenness centrality (Fig. 4).

FIG. 4.

Two graph characteristics as functions of density ρ for a graph representing original data (black line) and minimal and maximal surrogate lines (gray lines) for a representative session.

In general, the global network characteristics we considered do not seem to be substantially influenced by possible fMRI data nonlinearities, since similar graphs were obtained for the other sessions, too. To analyze this behavior in a more formal way the dominances described in Sec. IV A were calculated for the data and the generated shadows datasets as described in Sec. IV C.

For each global characteristic, the dominances form a set of 40 functions of density that express the single dominance function for the original dataset and 39 dominances for the shadow datasets. As the global characteristic dominances do not include the extra step of averaging over vertices, extra robustness and easier interpretation is attained by averaging the values across a range of densities (see Sec. IV B).

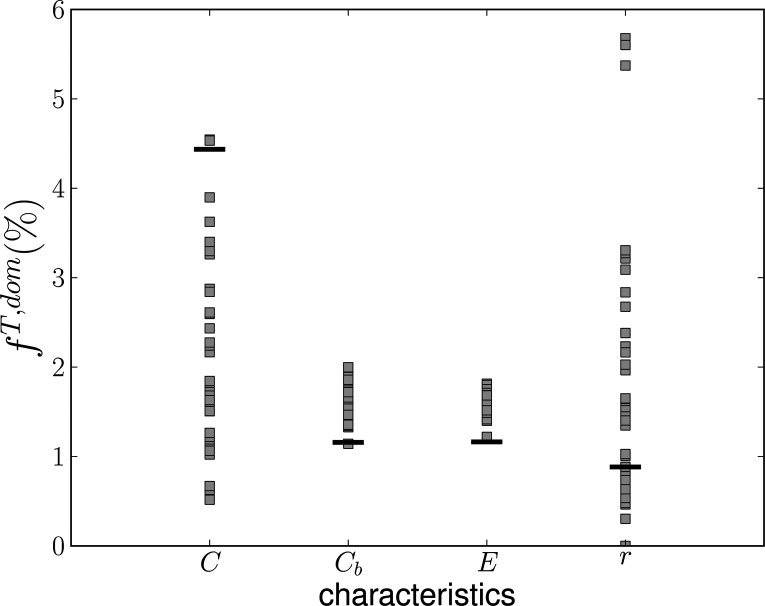
The resulting comparisons of the observed data value and the 39 shadow data values for all characteristics are shown in Fig. 5. For all characteristics except efficiency the dominances observed for the original dataset stay within the range of dominances observed for shadow datasets. Dominance of the original dataset for efficiency is out of this interval. However it is a minimum of this set placed not far from the set itself. Such placement would suggest that the dominance effects in shadows were stronger than in the original data which therefore cannot be caused by nonlinearities (original data more similar to linear surrogates than observed for typical shadow dataset). This more detailed analysis confirmed that nonlinearity does not have a substantial effect on the graph-theoretical properties of the resulting graph, with the data giving similar results as completely linearized shadow datasets.

FIG. 5.

Values of global dominances averaged over an interval of interest for shadow datasets (gray squares) and original dataset (black lines) for global clustering coefficient (C), global betweenness centrality (C_b), efficiency (E), and assortative coefficient (r). Values on y axis are dominances in percent.

In the following we present results obtained for the local graph-theoretical characteristics that might potentially be more sensitive to some localized nonlinearity. Due to the extra dependence on choice of vertex, the resulting diagrams such as those in Figs. 3 and 4 are not easily readable and therefore only the resulting dominances are shown. On the other hand, due to averaging over vertices the dominance functions are robust and smooth enough to be visually interpretable. Such a graph for the local clustering coefficient is shown in Fig. 6(a).

FIG. 6.

Values of two local dominances f^T,dom as a function of density for shadow datasets presented by minimal and maximal curves (gray color) and original dataset (black color). Values on y axis are dominances in percent.

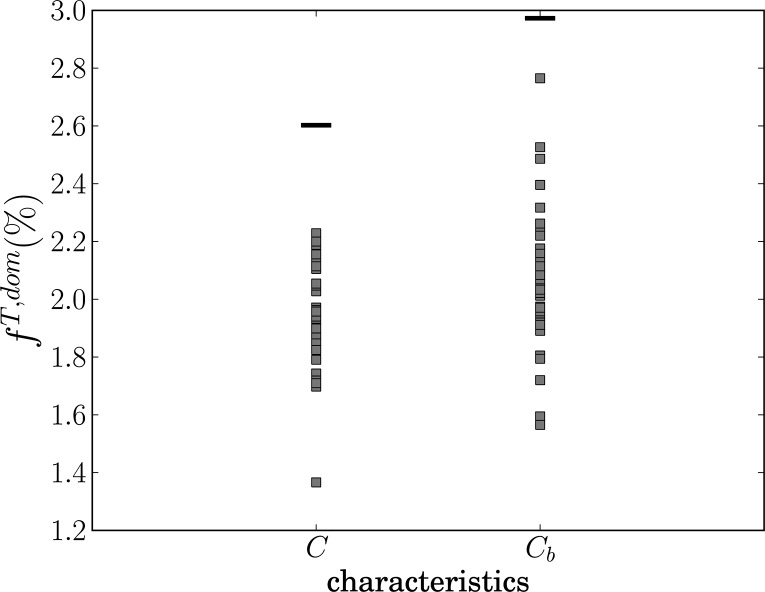
Similar results were obtained for dominances computed for betweenness centrality, see Fig. 6(b). This time, one may suspect some nonlinear effects from visual inspection of the diagram—while the data line is not consistently outside the gray belt, it follows its top boundary across a wide range of densities. The diagram comparing the data and shadow data dominance is shown in Fig. 7. Here we see that the data dominances are significantly higher than dominances for the shadow datasets, which stay close to the expected value of 2%. This again suggests some influence of nonlinearities.

FIG. 7.

Values of local dominances averaged over the interval of interest for shadow datasets (gray squares) and original dataset (black lines) for clustering coefficient and betweenness centrality. Values on y axis are dominances in percent.

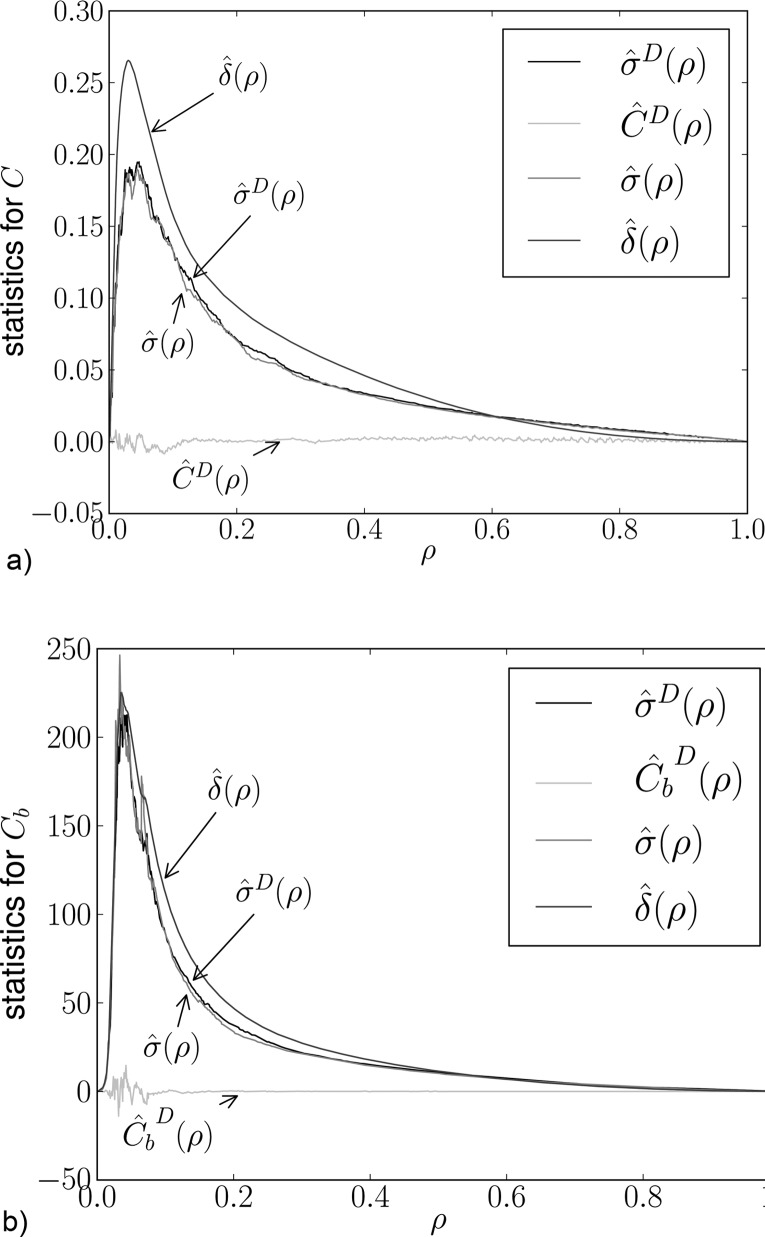
To assess this influence and its practical relevance quantitatively, the statistics described in Sec. IV D were calculated. The results for the clustering coefficient are presented in Fig. 8(a). Here it is possible to see that the difference between ${\stackrel{\wedge }{\sigma }}^D(\rho )$ and $\stackrel{\wedge }{\sigma }(\rho )$, which represents the extra variability due to nonlinearity (on top of random estimation error), is almost negligible. Moreover, the intersession variability represented by $\stackrel{\wedge }{\delta }(\rho )$ is at least an order of magnitude higher than the nonlinearity effect ${\stackrel{\wedge }{C}}^D(\rho )$ (which is practically zero) as well as the difference ${\stackrel{\wedge }{\sigma }}^D(\rho )-\stackrel{\wedge }{\sigma }(\rho )$. In other words, while potentially detectable by a sensitive statistical approach on the group level, the nonlinearity effect even on these local graph-theoretical characteristics is negligible when compared to the intersession and intersubject variabilities. A similar diagram obtained for betweenness centrality is shown in Fig. 8(b).

FIG. 8.

Statistics described in Sec. IV D for local version of two characteristics.

VI. DISCUSSION AND CONCLUSIONS

We have assessed the effect of accounting for nonlinear dependences on the results of graph-theoretical analysis of large-scale brain networks. In particular, we used resting-state fMRI, a type of data recently receiving increased attention.

For the global graph-theoretical measures, we have shown that the results obtained from data are well in the range of the results obtained for linear multivariate surrogates (in which nonlinearities are removed by construction). This indicates that potential nonlinearity in the studied fMRI resting state data does not significantly affect the calculation of the global graph-theoretical measures. This observation has been shown to be valid for a wide range of global graph-theoretical measures differing in the complexity of graph properties utilized in their computations. For instance, assortative coefficient uses only the degree values, while efficiency already uses some basic structural information represented by shortest paths. On the other side, clustering coefficient takes into account the neighboring structures of each vertex. Finally, global betweenness centrality is an average of local betweenness centralities that each reflects the full graph structure.

For the clustering coefficient and betweenness centrality a more detailed local analysis was performed. Here, we have observed a statistically significant deviation of results from those obtained from control linearized shadow datasets. Nevertheless, a quantitative comparison showed that the nonlinearity effect is practically negligible when compared to the intersession variability.

It is worth mentioning that the slight differences observed might be due not only to nonlinearity, but also due to nonstationarity of the time series. Therefore the observed miniscule deviation from linearity might actually already be inflated over the true value by potential nonstationarity contributions. While this offers an alternative explanation to the slight deviations observed, it does not alter the conclusion regarding the unimportance of non-Gaussian contributions to graph-theoretical measures in networks constructed from fMRI resting-state time series. However, the problem of conflation of nonlinearity and nonstationarity is worth mentioning, in general, in this context as it might become crucial if the conclusion were to be that a substantial deviation is observed from the linear Gaussian stationary stochastic process—in this case, false positives due to nonstationarity should be considered. For a discussion of such scenarios and proposed nonstationarity tests we refer the reader to the relevant literature.^49–52

To assess the general (potentially nonlinear) dependence between the network nodes, we used mutual information—a fully general, information-theoretical rooted bivariate dependence measure. This represents a natural nonlinear counterpart to the use of linear correlation—in fact, mutual information can be considered as a generalization of linear correlation in the specific sense that for bivariate Gaussian distribution the two are linked by a functional relation $I(X,Y)=I_{\mathrm{Gauss}}(r_{X,Y})=-\frac{1}{2}\text{log}(1-r^2)$.

A potential limitation of the current study is that, at least in theory, “exotic” processes may exist, for which the departure from Gaussian dependence would not show in bivariate dependencies but only if multivariate dependencies including temporal embeddings were taken into account. Thus, only measures that incorporate these multivariate patterns such as mutual information between the symbolic sequences of ordinal patterns (proposed originally in the context of complexity estimation⁵³), would theoretically be sensitive in these cases to properties of the signals that the corresponding linear model would not detect.

Note that in the framework of the multivariate information functionals such as ordinal patterns mutual information, the comparison with simple linear correlation would be biased against the linear correlation, as this measure utilizes only information in the equal-time bivariate distribution. Therefore a comparison with a suitable candidate linear dependence measure derived from a linear model of corresponding order would be necessary. On the one hand, we believe that such a generalization of our procedure is of real theoretical interest, and potentially may be also valuable for some specific applications. On the other hand, an unbiased testing using information-theoretical functionals of the various multivariate dependence scenarios is limited. This limitation lies in the computational expense and the demand for long observation time series due to the curse of dimensionality and in the problems with the estimation of appropriate model order. Importantly, the detection of an effect of non-Gaussianity in equal-time bivariate dependencies on graph-theoretical properties of complex networks, as presented in the current paper, is reasonably tractable and already provides important insights valuable for the many practical applications where equal-time dependencies are generally considered informative.

Regarding the methodology of the statistical testing, a careful reader might notice the potential degree of freedom in the choice of the dominance indicator functions in Sec. IV B—instead of the maximum and minimum, a suitably chosen couple of “extreme” percentiles (e.g., 95th and 5th) could have been used in the definition of dominant vertices. The corresponding redefined dominance function would then have a different expected value (e.g., 10% with the above choice), but may potentially represent a more robust dominance estimate yielding higher sensitivity of the subsequent statistical comparisons. Nevertheless, a control analysis with dominance definition based on the (convenient but still rather arbitrary) 95th and 5th percentiles did not substantially alter the results. Thus we have chosen to keep in this report the definition with maximum and minimum—mainly for simplicity and consistence of the presented methods. Moreover, as the statistical tests did reveal some significant differences and are moreover complemented by the quantitative analysis for the two most “suspicious” graph measures, we find the general issue of potentially suboptimal sensitivity of particular statistical tests used not crucial for the results presented.

In general, it remains an open question to what extent our results regarding observable dependence nonlinearities generalize to the connectivity during psychological task rather than resting-state conditions, or to data acquired in patient cohorts. We believe it is not unreasonable to conjecture that the general nature of the activity process in terms of the degree of (non)linearity is going to be preserved. While the ultimate answer would require extensive testing in various settings and task or disease conditions, in the following paragraphs we review some of the relevant evidence.

On the one hand, the overall pattern of spontaneous brain activity represented by the correlated low-frequency fluctuations of the so-called resting-state networks is generally ongoing, although altered, even under task conditions—for a review of the interactions between intrinsic and stimulus driven activity we refer the reader to a recent publication by Northoff et al.⁵⁴ Moreover, the resting-state networks have been shown to correspond to the major functional networks as discovered in task studies.⁵⁵ Similar arguments apply to generalization of our findings to fMRI data acquired in patients—while specific differences in the spatiotemporal patterns of intrinsic brain activity have been observed in various patient groups, the overall spontaneous activity pattern is generally conserved. For detailed review of current knowledge of alterations of spontaneous brain activity in disease we refer the reader to two recent overview papers.^56,57

On the other hand, it is indeed possible that specific task conditions might lead to spatiotemporal activity dynamics that would manifest itself in activity interdependencies with relatively higher degrees of nonlinearity than observed in typical resting-state conditions. While extensive evidence regarding this is still lacking, we refer the reader at least to a brief review of some relevant research that is included in a recent modeling study.⁵⁸ Of potential interest, the main message of the cited paper lies in proposing an ambitious nonlinear multivariate interaction model for task-condition activations. Unfortunately, the specificity of the model introduced therein and of its analysis precludes direct quantitative comparison to the analysis of the resting-state activity dependence structure presented in Ref. 21 and in the current paper.

In summary, we have provided quantitative evidence suggesting that linear correlation is a satisfactory connectivity measure for graph-theoretical analysis of resting-state fMRI brain networks and application of nonlinear dependence measures is not likely to bring substantial new information. While we have focused on the particular application to fMRI studies of intrinsic brain activity, we suggest that the approach used in this paper may be applied to data describing other complex networks of interest not limited to neuroscience—this could be of special interest for fields such as meteorology or geophysics. In general, this would facilitate informed decisions regarding the application of nonlinear dependence measures for graph-theoretical study of real-world complex networks.