Validating plastic scintillation detectors for photon dosimetry in the radiologic energy range

Abstract

Purpose:

Photon dosimetry in the kilovolt (kV) energy range represents a major challenge for diagnostic and interventional radiology and superficial therapy. Plastic scintillation detectors (PSDs) are potentially good candidates for this task. This study proposes a simple way to obtain accurate correction factors to compensate for the response of PSDs to photon energies between 80 and 150 kVp. The performance of PSDs is also investigated to determine their potential usefulness in the diagnostic energy range.

Methods:

A 1-mm-diameter, 10-mm-long PSD was irradiated by a Therapax SXT 150 unit using five different beam qualities made of tube potentials ranging from 80 to 150 kVp and filtration thickness ranging from 0.8 to 0.2 mmAl + 1.0 mmCu. The light emitted by the detector was collected using an 8-m-long optical fiber and a polychromatic photodiode, which converted the scintillation photons to an electrical current. The PSD response was compared with the reference free air dose rate measured with a calibrated Farmer NE2571 ionization chamber. PSD measurements were corrected using spectra-weighted corrections, accounting for mass energy-absorption coefficient differences between the sensitive volumes of the ionization chamber and the PSD, as suggested by large cavity theory (LCT). Beam spectra were obtained from x-ray simulation software and validated experimentally using a CdTe spectrometer. Correction factors were also obtained using Monte Carlo (MC) simulations. Percent depth dose (PDD) measurements were compensated for beam hardening using the LCT correction method. These PDD measurements were compared with uncorrected PSD data, PDD measurements obtained using Gafchromic films, Monte Carlo simulations, and previous data.

Results:

For each beam quality used, the authors observed an increase of the energy response with effective energy when no correction was applied to the PSD response. Using the LCT correction, the PSD response was almost energy independent, with a residual 2.1% coefficient of variation (COV) over the 80–150-kVp energy range. Monte Carlo corrections reduced the COV to 1.4% over this energy range. All PDD measurements were in good agreement with one another except for the uncorrected PSD data, in which an over-response was observed with depth (13% at 10 cm with a 100 kVp beam), showing that beam hardening had a non-negligible effect on the PSD response. A correction based on LCT compensated very well for this effect, reducing the over-response to 3%.

Conclusion:

In the diagnostic energy range, PSDs show high-energy dependence, which can be corrected using spectra-weighted mass energy-absorption coefficients, showing no considerable sign of quenching between these energies. Correction factors obtained by Monte Carlo simulations confirm that the approximations made by LCT corrections are valid. Thus, PSDs could be useful for real-time dosimetry in radiology applications.

I. INTRODUCTION

Plastic scintillation detectors (PSDs) are promising dosimeters owing to their multiple advantages over other detector types. Beddar et al.¹ demonstrated that, in the entire radiotherapy energy range, PSDs are water-equivalent, have excellent reproducibility and stability, are dose-rate independent, and have a high spatial resolution because of their small size. These detectors have been studied extensively with high-energy photon and electron beams.^1–8 For high-energy photon beams, in which Compton interactions are dominant, the main advantage of PSDs is their near water-equivalence;¹ this feature is due to the low effective atomic number (Z_eff) of the polystyrene sensitive volume which is 5.74 according to the calculation method proposed by Attix.⁹ This is much lower than that of other detectors, such as thermoluminescent dosimeters, optically stimulated luminescent dosimeters, or metal-oxide field-effect transistors.

The water-equivalence of PSDs requires investigation at radiologic photon energies because the photoelectric cross section may be affected by small Z_eff differences. Some studies^10–12 have shown that the dose linearity, reproducibility, and angle independence of PSD are maintained in the diagnostic energy range, but these studies also found a positive variation in the energy response over the energy range of interest. Hyer et al.¹⁰ reported an increase of 10% in the PSD response at 15-cm depth owing to beam hardening and scattered radiation with a 120-kVp beam.

To our knowledge, no systematic approach has been developed to obtain PSD correction factors that can be adapted to a wide range of x-ray systems with specific tube potential and added filtrations. With low-energy photons, for which secondary particles range is negligible, it is reasonable to assume local energy deposition occurring where the photons interact. In that case, the cross section ratio between two media is equivalent to their mass energy absorption coefficient (μ_en/ρ) ratio.⁹ In this work, this approximation is referred as the large cavity theory (LCT). Polystyrene, which is the main material found in some PSD sensitive volume, presents a significant variation in the μ_en/ρ ratio between water and air below 100 keV.¹³ In this study, we used a method based on LCT to compensate for the PSD energy response and validated it using Monte Carlo (MC) simulations. The dose to soft tissue, bone, or any other media can be extracted from a PSD measurement.

II. MATERIALS AND METHODS

II.A. Photon beam source

A Therapax SXT 150 (Pantak Inc., Branford, CT) was used to deliver the radiation. Only five of the eight commissioned beam qualities (Effective energies from 26 to 86 keV) were used because the reference ion chamber was not calibrated for the lower beam qualities. The beam ranged from 80 kVp (1.26 mmAl first half-value layer [HVL]) to 150 kVp (12.87 mmAl or 1.17 mmCu first HVL), with filtration thicknesses varying from 0.8 to 0.2 mmAl + 1.0 mmCu (see Table I). The tube anode was made of tungsten, had a 40° angle, and had an inherent filtration of 2 mm of beryllium. Measurements were performed in a 3-cm-diameter field at a source-to-surface distance (SSD) of 15 cm.

TABLE I.

Available beam qualities specifications from the Therapax SXT 150 used in this work. The effective energy is used to specify the beam quality.

Peak	Anode			Effective
energy	current		HVL	energy
(keV)	(mA)	Filtration	(mmAl)	(keV)
80	4.0	0.8 mmAl	1.26	26
80	8.0	2.0 mmAl	2.33	30
100	10.5	1.8 mmAl + 0.1 mmCu	5.20	44
120	11.2	1.1 mmAl + 0.3 mmCu	8.84	59
150	13.2	0.2 mmAl + 1.0 mmCu	12.87	86

II.B. PSD

The PSD used was made of a BCF-60 green scintillating fiber (diameter, 1 mm; length, 10 mm; Saint-Gobain Crystal, Paris, France), which had been polished using polishing films with decreasing grain sizes (5 μm, 3 μm, 1 μm, and 0.3 μm). The PSD was coupled to an 8-m-long, polished, clear optical fiber (Eska GH-4001; Mitsubishi International Corporation, New York, NY) following the method described by Ayotte et al.¹⁴ The optical fiber was aligned to the photodetection surface using an SMA connector. Light was collected by a polychromatic photodiode (Sensor-ICs True Color Sensor; MAZeT GmbH, Jena, Germany). This photodetector converts light to an electrical current in three optical channels (red, blue, and green) without applied bias. Because of the absence of Cerenkov radiation production in the investigated energy range (<150 keV), no spectral correction¹⁵ was applied to the readings. Only the photodiode's green output was used because it filtered the fluorescence noise signal, which is distributed around the blue part of the spectrum (460 nm).¹⁶

II.C. Primary incident spectra

II.C.1. Computed spectra

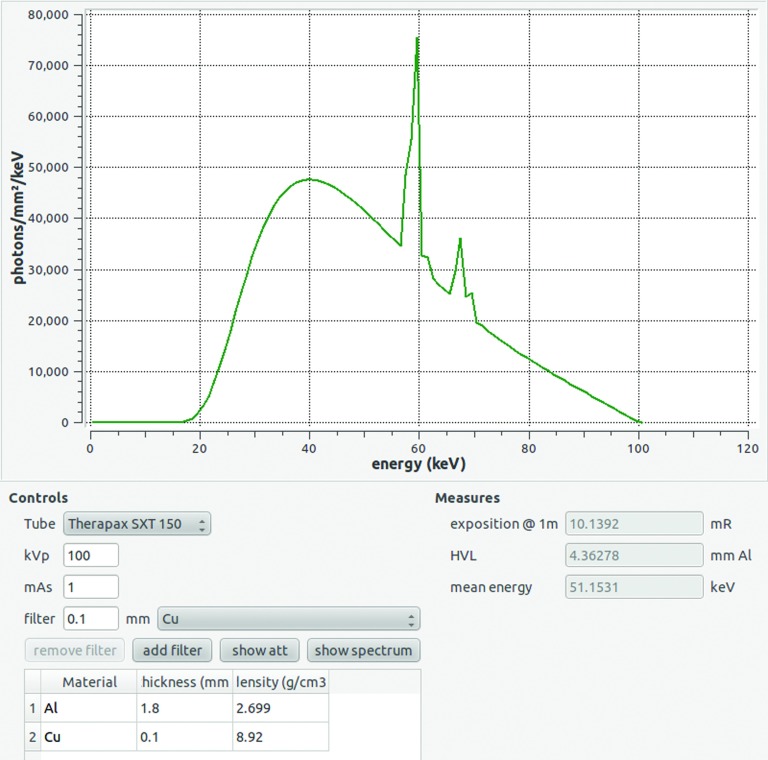
Primary incident spectra were determined with the open source software SpectrumGUI (Ref. 17) (see Fig. 1). This software is based on the work of Tucker and Barnes,^18,19 and the inherent filtration, anode angle, and composition values were adapted for the x-ray tube used. Tube potential and filtration were set for each beam qualities to obtain the associated fluence spectra.

FIG. 1.

Main window of SpectrumGUI (Ref. 17) used to determine primary incident spectra. The user can choose the x-ray tube type and then define the peak kilovoltage, current, and filtration. The corresponding fluence spectrum, exposition at 1 m, HVL, and effective energy are then displayed in less than a second.

II.C.2. Measured spectra

To confirm the validity of the computed spectra, we made direct measurements with a commercial CdTe spectrometer detector (XR-100-CdTe triple stack; Amptek Inc., Bedford, MA). The thickness of the sensitive volume was 2.25 mm, which provided detection efficiency of about 50% for 150-keV photons. The stripping method developed by Di Castro et al.²⁰ and adapted by Maeda et al.²¹ and Bazalova et al.²² was applied to the detector raw response. This Monte Carlo-based correction procedure was applied to correct the detector response for spurious effects such as photoelectric detection efficiency, cadmium and tellurium K-escape, and partial energy deposition. It is important to note that for the current analysis, no Compton scatterer was used and primary photons were measured directly.

II.D. Correction for medium difference

According to the American Association of Physicists in Medicine Task Group 61 (TG-61),²³ reference dosimetry should be based on in-air kerma measurements for the low-energy range. Dose is assumed to be equal to the kerma because the radiative losses by secondary charged particles are less than 0.1% for photons below 300 keV.²³ For the sizes that we considered in this application, LCT was applicable for this energy range because of the short electron range.

At diagnostic x-ray energies, the deposited dose is highly dependent upon the medium. Because in our study the PSD sensitive volume was made of polystyrene and the reference dose rates were measured in free air, the dose in the medium, D_med, can be expressed as

$$D_{\mathrm{med}}\cong K_{\mathrm{med}}=K_{\mathrm{air}}·{\left[\overline{\frac{{\mu }_{\mathrm{en}}}{\rho }}\right]}_{\mathrm{air}}^{\mathrm{med}},$$

where K_med is the kerma in the medium of interest and K_air is reference air kerma. Therefore, to relate a measurement made with a PSD, M_PSD, to a dose in air, one should apply:

$$D_{\mathrm{air}}=M_{\mathrm{PSD}}{\left[\overline{\frac{{\mu }_{\mathrm{en}}}{\rho }}\right]}_{\mathrm{polystyrene}}^{\mathrm{air}}.$$

Because the radiation used was not monoenergetic, exact correction factors were not straightforward to obtain, prompting us to test various methods.

II.D.1. Effective energy correction factor

Every spectrum can be approximated to a monoenergetic beam corresponding to its effective energy. The simplest method to obtain this value experimentally is to measure the beam HVL and obtain its effective energy from published data.²⁴ The correction factor $C_{\mathrm{LCT}{E}_{\mathrm{eff}}}$ becomes the μ_en/ρ ratio taken at the effective energy

$$C_{\mathrm{LCT}{E}_{\mathrm{eff}}}={\left[\overline{\frac{{\mu }_{\mathrm{en}}}{\rho }}\right]}_{\mathrm{air}}^{\mathrm{med}}=\frac{{\left[\frac{{\mu }_{\mathrm{en}}}{\rho }\left(E_{\mathrm{eff}}\right)\right]}_{\mathrm{med}}}{{\left[\frac{{\mu }_{\mathrm{en}}}{\rho }\left(E_{\mathrm{eff}}\right)\right]}_{\mathrm{air}}},$$ (1)

where (μ_en/ρ)(E_eff) is the mass energy-absorption coefficient taken for the corresponding effective energy.

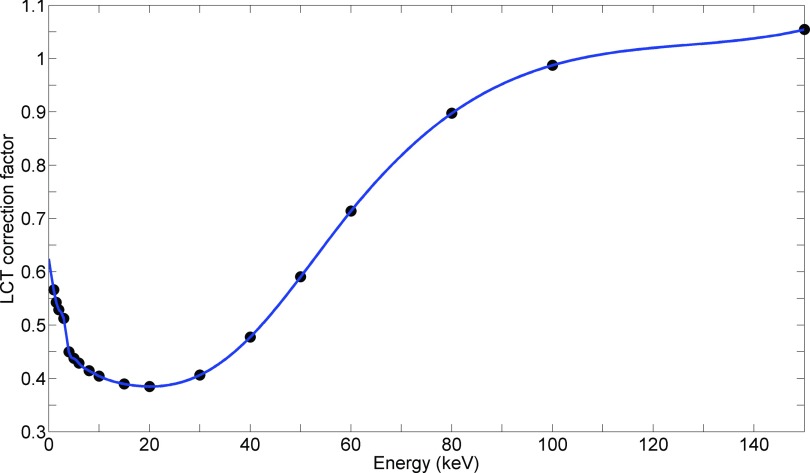
This method is correct only if ${\left[{\mu }_{\mathrm{en}}/\rho \right]}_{\mathrm{air}}^{\mathrm{med}}$ is linear within the energy range. With polystyrene as the medium, this assumption was partially false, as shown in Fig. 2, where the data from National Institute of Standards and Technology tables are presented.²⁵

FIG. 2.

μ_en/ρ ratio between polystyrene and air in the low-energy range, taken from the National Institute of Standards and Technology (Ref. 25). According to LCT, this ratio is the correction factor to obtain deposited dose in polystyrene from a measurement in air.

II.D.2. Correction weighted on spectra

Another method we used was to average ${\left[{\mu }_{\mathrm{en}}/\rho \right]}_{\mathrm{air}}^{\mathrm{med}}$over the complete fluence spectra:

$$\begin{array}{ccc}\hfill C_{\mathrm{LCT}\mathrm{spectra}}& =& {\left[\overline{\frac{{\mu }_{\mathrm{en}}}{\rho }}\right]}_{\mathrm{air}}^{\mathrm{polystyrene}}\hfill \\ & =& \frac{{\int }_0^{E_{\max }}{\left(\frac{{\mu }_{\mathrm{en}}}{\rho }\left(E\right)\right)}_{\mathrm{polystyrene}}·E·\Phi \left(\mathrm{E}\right)·\mathrm{dE}}{{\int }_0^{E_{\max }}{\left(\frac{{\mu }_{\mathrm{en}}}{\rho }\left(E\right)\right)}_{\mathrm{air}}·E·\Phi \left(\mathrm{E}\right)·\mathrm{dE}},\hfill \end{array}$$ (2)

where E_max is the maximum incident photon energy and Φ(E) is the fluence spectrum.

Equation (2) was used to obtain correction factors for the computed and measured spectra as described in Sec. II C. Note that the uncertainty on this parameter is a function of parameters such as spectrum uncertainty, the precision of the value of μ_en/ρ and interpolation method that are difficult to quantify. According to TG-61 (Ref. 23) an uncertainty value of ±1.5% should be assumed for C_{LCT spectra}. Because ${\left[\overline{{\mu }_{\mathrm{en}}/\rho }\right]}_{\mathrm{air}}^{\mathrm{polystyrene}}$varies slowly with energy (Fig. 2), some discrepancy between computed and measured spectra may not affect the correction factor substantially.

II.D.3. Correction based on Monte Carlo simulation

Monte Carlo simulations were performed to confirm the LCT method. In Geant4,^26,27 a phase space made of an isotropic point source collimated to a 3-cm-diameter beam at an SSD of 15 cm was modeled. Both simulated and measured spectra were used. For each beam qualities and spectrum, a simulation of 4 × 10⁸ photons impinging on a fully modeled PSD in air was run. The geometry consisted of a 10-mm-long scintillating fiber made of a 0.97-mm-diameter polystyrene core and surrounded by a 0.015-mm-thick poly(methyl methacrylate) (PMMA) cladding coupled to a long PMMA clear fiber with a 0.99-mm diameter. The entire assembly was surrounded by a 0.6-mm-thick polyethylene jacket. Dose was scored in the PSD's polystyrene core as well as in an equivalent volume made of air, in the absence of the PSD. The Monte Carlo correction factor, C_MC, was defined as

$$C_{\mathrm{MC}}=\frac{D_{\mathrm{polystyrene}}}{D_{\mathrm{air}}}.$$ (3)

The standard deviation of the simulation is estimated with the batch method from ten independent simulations. The error values presented in Table II correspond to 1 standard deviation. With these simulations, it is possible to consider the effect of some parameters that are neglected in LCT, such as beam divergence and its finite diameter, the presence of a PSD jacket, scattered radiation, beam attenuation through the detector, and electron range.

TABLE II.

Correction factors (C) for plastic scintillation detector, obtained using LCT and MC. The LCT factor errors correspond to the ±1.5% error range estimated by the American Association of Physicists in Medicine Task Group 61 (Ref. 23). Monte Carlo errors correspond to ±1 standard deviation of the simulation estimated with the batch method. Correction factors have no unit.

		CLCT spectra		CMC
Effective energy (keV)	CLCT Eeffa	Weighted on theoretical spectrum	Weighted on experimental spectrum	Using theoretical spectrum	Using experimental spectrum
26	0.390 ± 0.006	0.420 ± 0.006	0.423 ± 0.006	0.411 ± 0.004	0.432 ± 0.002
30	0.410 ± 0.006	0.448 ± 0.007	0.458 ± 0.007	0.440 ± 0.003	0.465 ± 0.004
44	0.501 ± 0.008	0.556 ± 0.008	0.571 ± 0.009	0.549 ± 0.005	0.578 ± 0.006
59	0.700 ± 0.010	0.690 ± 0.010	0.700 ± 0.010	0.691 ± 0.009	0.710 ± 0.009
86	0.920 ± 0.010	0.870 ± 0.010	0.870 ± 0.010	0.883 ± 0.006	0.890 ± 0.009

^aUsing the spectrum effective energy.

II.E. PSD measurements

II.E.1. Absolute dose rate determination

For the reference dose rate, measurement was made with a calibrated Farmer NE2571 ionization chamber (NE Technology Limited, Berkshire, England). The chamber was calibrated for various HVL beam qualities, and the calibration factors were interpolated for our measured HVLs. Measurements were taken in a 3-cm-diameter beam at an SSD of 15 cm. Reference air dose rates were obtained following the TG-61 protocol for low-energy x-rays.²³

Under the same conditions, the ionization chamber was replaced with the PSD. Given the dose rate in terms of air kerma, the PSD response A (in pC/Gy) was calculated for all beam qualities as

$$A=\frac{Q}{D_{\mathrm{polystyrene}}}=\frac{Q}{K_{\mathrm{air}}·C},$$ (4)

where Q is the charge (in pC) measured by the photodiode green channel and C is the applied correction factor (either from Eq. (1) and (2), or (3)). The energy dependence of A was characterized according to each correction factor obtained in Sec. II D.

II.E.2. Percent depth dose (PDD) measurements

PDD was measured with a 3-cm-diameter beam at an SSD of 15 cm in an MT150M water phantom (Civco, Kalona, IA). A constant irradiation time of 1 min was chosen for all depths. Data were taken for effective energy beams of 26, 44, and 86 keV. The PSD was positioned perpendicularly to the x-ray tube axis to minimize the heel effect. Because these measurements were relative to the surface dose, we knew the energy dependence would be caused by beam hardening and scattered radiation variation with depth. To obtain the primary and secondary photon fluence spectra as a function of depth, we conducted Monte Carlo simulations using the EGSnrc/FLURZnrc code.²⁸ The same beam parameters as in Sec. II D 3 was used. With the calculated spectra as a function of depth, the PSD response was converted to dose-to-water for each depth,

$${\mathrm{PSD}}_{\mathrm{corrected}}\left(z\right)={\mathrm{PSD}}_{\mathrm{raw}}\left(z\right).{\left[\overline{\frac{{\mu }_{\mathrm{en}}}{\rho }}\right]}_{\mathrm{polystyrene}}^{\mathrm{water}}\left(z\right).$$ (5)

PDD was also measured using Gafchromic EBT2 film (International Specialty Products (ISP), Wayne, NJ), which was calibrated at 44 keV effective energy using the method recommended by Delage.²⁹ The same calibration curve was used for other beam qualities. The film was placed vertically in a water phantom to measure the dose at any depth along the beam central axis. PDD measurements were further compared with the data from Jurado et al.³⁰ who used a PTW chamber. Monte Carlo simulations performed using the EGSnrc/DOSRZnrc code²⁸ were considered as the reference data for comparison purposes. The statistical uncertainties on these simulations were evaluated with a history by history method.²⁸

III. RESULTS

III.A. Primary incident spectra

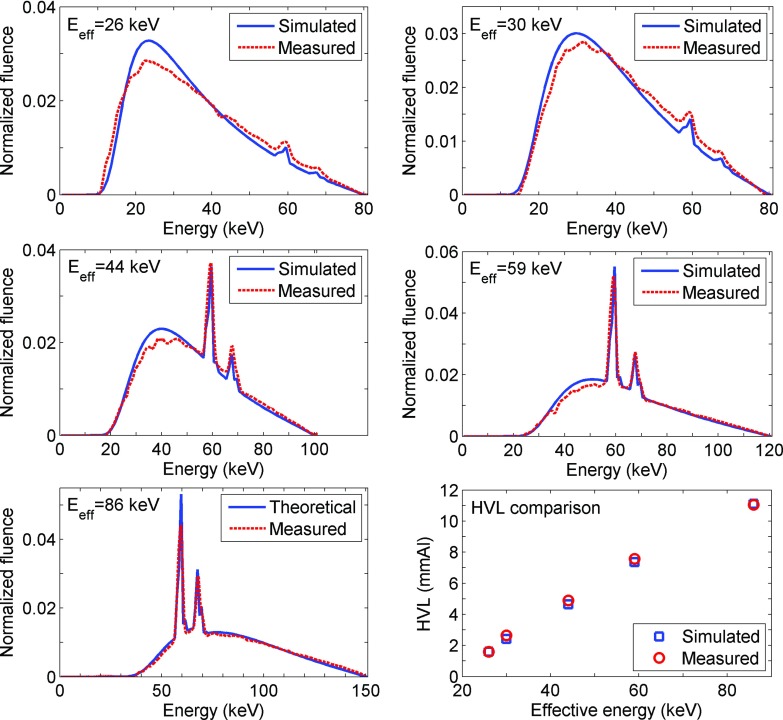
Spectra predicted with SpectrumGUI were consistent with measured spectra for every beam qualities, as shown in Fig. 3. The HVLs obtained from these spectra were also in good agreement with one another (Fig. 3, bottom right panel).

FIG. 3.

Simulated (computed with SpectrumGUI) and measured (with CdTe detector) spectra for beam effective energies of 26, 30, 44, 59, and 86 keV. Each area under the curve is normalized to 1. Bottom right: Computed HVL comparison for each beam qualities.

III.B. Correction for medium difference

The correction factors as defined in Sec. II D are presented in Table II. These factors differed considerably between beam qualities: correction factors varied by a factor of 2 between 26 and 86 keV effective energy. The LCT correction factors based on the effective energy most differed from those obtained with other methods. The C_{LCT spectra} factors obtained using theoretical spectra were consistent with those obtained using experimental spectra within the ±1.5% error range suggested by the TG-61 document.²³ Monte Carlo correction factors were also consistent with LCT correction factors. These results suggest that LCT was a reasonable approximation and that the primary cause of error among the correction factors was the method used to evaluate the spectra.

III.C. Absolute dose rate measurements

Table III shows the PSD calibration factors (in pC/Gy) for each beam qualities. The differences between them were caused by the energy response of the scintillator. Without any correction, the PSD response varied by more than a factor of 2 over the analyzed energy range, demonstrating that the polystyrene PSD core was not equivalent to air. Even the simplest corrected energy response (effective energy) was much more stable between 80 and 150 kVp with a coefficient of variation (COV) of 4.5% about its mean value. The corrected energy responses weighted on the theoretical and experimental spectra were almost energy independent, with COV values of 2.1% and 2.9%, respectively. For the Monte Carlo correction factor, the COVs decreased to 1.4% with theoretical incident spectra and 2.7% with experimental spectra. The uncertainties presented are a combination of the correction factor uncertainty and 1 standard deviation obtained on five consecutive PSD measurements.

TABLE III.

Plastic scintillation detector absolute energy responses [Eq. (4)] according to each correction factor described in the paper. The no correction column corresponds to the uncorrected PSD response to dose in air. The COV for the parameter is presented for each method.

	Energy response (pC/Gy)
Effective energy (keV)	No correction	LCT effective energy correction	LCT theoretical spectra correction	LCT experimental spectra correction	Monte Carlo theoretical spectra correction	Monte Carlo experimental spectra correction
26	16.1 ± 0.2	41.0 ± 1.0	38.3 ± 0.9	38.1 ± 1.0	39.2 ± 0.8	37.3 ± 0.7
30	17.1 ± 0.2	42.0 ± 1.0	38.3 ± 0.9	37.4 ± 1.0	38.9 ± 0.6	36.9 ± 0.8
44	20.9 ± 0.2	41.0 ± 0.9	37.6 ± 0.9	36.6 ± 0.9	38.1 ± 0.7	36.2 ± 0.8
59	26.6 ± 0.3	38.0 ± 0.9	38.4 ± 1.0	37.7 ± 1.0	38.4 ± 0.9	37.4 ± 0.9
86	34.9 ± 0.3	37.8 ± 0.9	40.1 ± 0.9	39.9 ± 0.9	39.5 ± 0.8	39.2 ± 0.9
Mean	23.1	40.0	38.6	37.9	38.8	37.4
COV	30.0%	4.5%	2.1%	2.9%	1.4%	2.7%

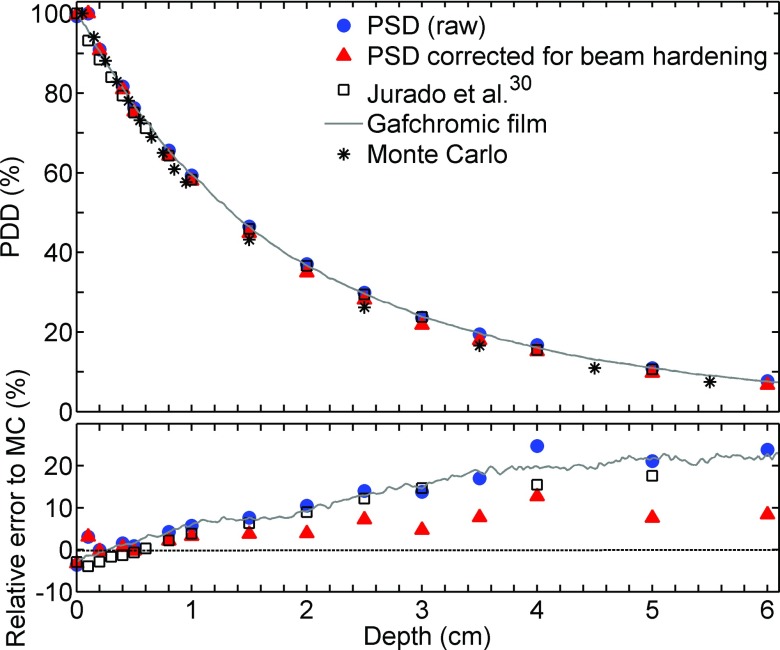
III.D. PDD measurements

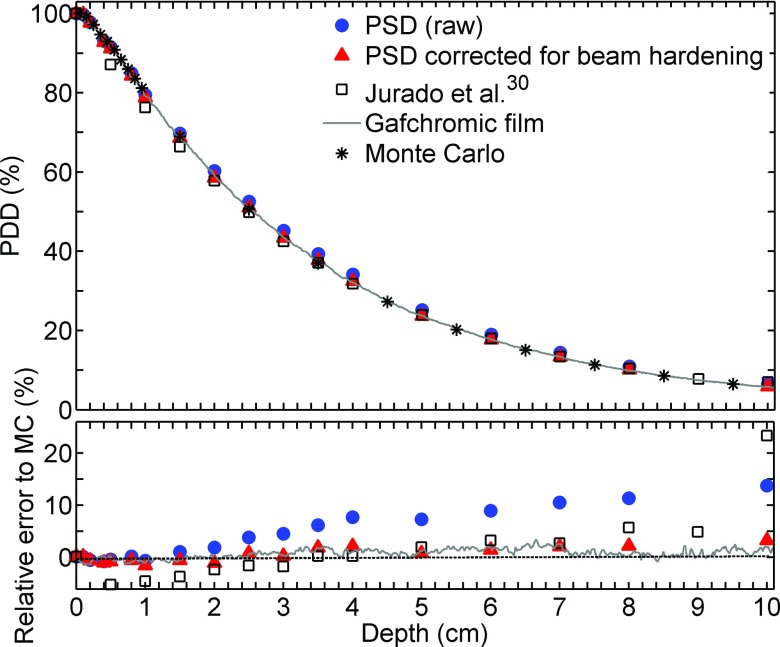
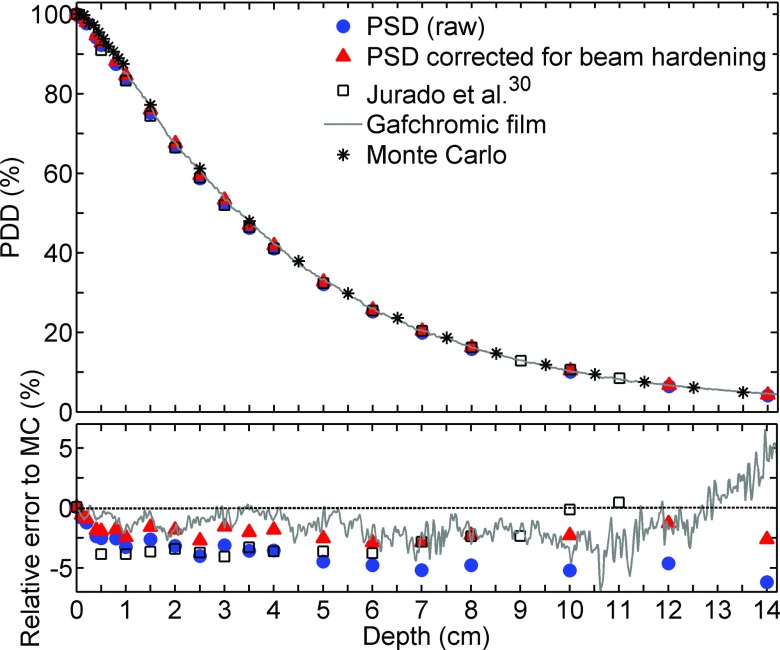
PDD measurements obtained using the various methods are plotted in Figs. 4–6 for effective energies spectra of 26, 44, and 86 keV, respectively. The statistical error on the Monte Carlo simulations used as the reference is less than 0.5%. When the PSD raw data were compared with Monte Carlo simulations, the differences increased with depth, up to 13% at 10 cm with 44 keV effective energy. The LCT correction method for beam hardening partially compensated for this effect, reducing the difference to 3%. The data from Jurado et al.³⁰ lie between the PSD raw data and the PSD corrected data. It is important to specify that PDD from Jurado et al. that are illustrated in Fig. 4 were measured in PMMA instead of water. According to Hill et al.,³¹ this may result in an over response of 7% compared to PDD in water.

FIG. 4.

(Top) 26 keV effective energy beam relative PDD obtained using various detectors. (Bottom) Relative error to MC simulation.

FIG. 5.

(Top) 44 keV effective energy beam relative PDD obtained using various detectors. (Bottom) Relative error to MC simulation.

FIG. 6.

(Top): 86 keV effective energy beam relative PDD obtained using various detectors. (Bottom) Relative error to MC simulation.

IV. DISCUSSION

In this investigation of the performance of a PSD over five beam qualities ranging from 80 to 150 kVp, we found that a simple spectrum-weighted correction based on LCT that accounts for medium composition differences could be applied to compensate for the energy dependence. In our studies, the spectrum was easily obtained with x-ray spectrum simulation software, and the results were in good agreement with the Monte Carlo simulations. However, for PDD measurements, it was important to consider beam hardening in the analysis.

The results from our measured spectra were quite similar to those of the spectra predicted by SpectrumGUI, and the correction factors extracted from the theoretical and experimental spectra are in agreement within ±1.5%. SpectrumGUI has proven to be easily adaptable open-source software, providing reliable spectra for the diagnostic energy range. Considering the complexity of measuring spectra, we suggest using computed spectra for further application in the field of radiology. It could be interesting to obtain every spectrum with complete Monte Carlo simulation to rigorously benchmark the results, but the gain in precision would be eclipsed by the uncertainty of interpolated μ_en/ρ values using a cubic spline between 10 and 150 keV in the National Institute of Standards and Technology tables.²⁵

The correction factors obtained using effective energy ($C_{\mathrm{LCT}{E}_{\mathrm{eff}}}$) were the simplest to obtain, but this method seems to be inaccurate because the values were quite different from those obtained with the Monte Carlo simulation. Calculating C_{LCT spectra} instead of $C_{\mathrm{LCT}{E}_{\mathrm{eff}}}$ is slightly more complex, but the complexity is justified by the gain in accuracy. C_{LCT spectra} values were consistent with those obtained in the Monte Carlo simulations, showing that the presence of the PSD jacket had negligible effects and that LCT was applicable. Keeping a clinically applicable approach in mind, the best compromise between complexity and accuracy is therefore to use LCT factors weighted on spectra obtained from a tool such as SpectrumGUI.

A single energy response factor A (=39 ± 1 pC/Gy) may be applicable to our detector for the energy range most widely used in radiology and superficial x-ray therapy. The main source of uncertainty comes from the measurement of air kerma with the ionization chamber. TG-61 (Ref. 23) states that this error is composed of the calibration factor from standard laboratory (0.7%), the effect of the beam quality difference between calibration and measurement (2.0%), stem effect (1.0%) and measurement error (1.5%). All these random errors sum to a RMS value of approximately 3%, which is similar to the energy response COV that we obtained. When corrected for medium differences with LCT, the PSD clearly did not present any energy dependence or quenching effects in the analyzed energy range. Williamson et al.,³² in a similar study, measured a decrease in the PSD energy response below 133 keV compared to iridium-192 (408 keV). The composition difference between PSD and reference medium alone could not explain this effect. In our study, the narrow window of diagnostic energies allowed us to assume that the quenching effect was constant or within the uncertainties and thus did not affect the measurements. Thus, it should be kept in mind that the PSD must be calibrated in the middle of the radiologic energy range (around 100 kVp) rather than at higher reference energies like iridium-192, cesium-137, or cobalt-60. Some authors^16,33 have also measured the fluorescence contamination signal from the clear collecting plastic fibers. The stability of our corrected data indicates that fluorescence production, if present in the green channel, was constant over the energy range studied.

For surface measurements, the backscatter factor may be measured with PSDs, but because the scattered radiation energy spectrum differs from the spectrum of primary photons, Monte Carlo simulation should be used to obtain the scattered radiation energy spectrum.

Beam hardening showed a non-negligible effect on the PSD response. The good match obtained between Monte Carlo simulation and PSD corrected data shows that the correction method applied was valid. PSD response data were also consistent with data from Jurado et al.,³⁰ who performed measurements using another Therapax SXT 150 unit. Gafchromic films might have the potential to serve as good reference detectors as long as a calibration curve can be obtained for each film batch. For 26 keV beam, the substantial over-response of each detector compared with Monte Carlo in our experiments suggests that the simulation used a spectrum slightly softer than the real spectrum. Increasing the spectrum effective energy by 1 keV provided simulated PDD much more in agreement with the detectors. This may suggest that PDD measurements/simulations are good methods to benchmark the spectrum validity.

V. CONCLUSIONS

Using the LCT-based correction method presented in this research, PSDs clearly have the potential to be used for real-time in vivo measurements in the diagnostic radiology and superficial therapy energy range. If no correction is applied to compensate the medium difference, an under-response of 50% may be observed between hard and soft beams. This gap was reduced to 5% with the proposed correction method. Since the medium composition effect on deposited dose was proven to be non-negligible, the proposed method may be used to convert measured dose to any medium of interest such as skin, soft tissues, bone, or muscle.