Dose optimization with first-order total-variation minimization for dense angularly sampled and sparse intensity modulated radiation therapy (DASSIM-RT)

Abstract

Purpose:

A new treatment scheme coined as dense angularly sampled and sparse intensity modulated radiation therapy (DASSIM-RT) has recently been proposed to bridge the gap between IMRT and VMAT. By increasing the angular sampling of radiation beams while eliminating dispensable segments of the incident fields, DASSIM-RT is capable of providing improved conformity in dose distributions while maintaining high delivery efficiency. The fact that DASSIM-RT utilizes a large number of incident beams represents a major computational challenge for the clinical applications of this powerful treatment scheme. The purpose of this work is to provide a practical solution to the DASSIM-RT inverse planning problem.

Methods:

The inverse planning problem is formulated as a fluence-map optimization problem with total-variation (TV) minimization. A newly released L1-solver, template for first-order conic solver (TFOCS), was adopted in this work. TFOCS achieves faster convergence with less memory usage as compared with conventional quadratic programming (QP) for the TV form through the effective use of conic forms, dual-variable updates, and optimal first-order approaches. As such, it is tailored to specifically address the computational challenges of large-scale optimization in DASSIM-RT inverse planning. Two clinical cases (a prostate and a head and neck case) are used to evaluate the effectiveness and efficiency of the proposed planning technique. DASSIM-RT plans with 15 and 30 beams are compared with conventional IMRT plans with 7 beams in terms of plan quality and delivery efficiency, which are quantified by conformation number (CN), the total number of segments and modulation index, respectively. For optimization efficiency, the QP-based approach was compared with the proposed algorithm for the DASSIM-RT plans with 15 beams for both cases.

Results:

Plan quality improves with an increasing number of incident beams, while the total number of segments is maintained to be about the same in both cases. For the prostate patient, the conformation number to the target was 0.7509, 0.7565, and 0.7611 with 80 segments for IMRT with 7 beams, and DASSIM-RT with 15 and 30 beams, respectively. For the head and neck (HN) patient with a complicated target shape, conformation numbers of the three treatment plans were 0.7554, 0.7758, and 0.7819 with 75 segments for all beam configurations. With respect to the dose sparing to the critical structures, the organs such as the femoral heads in the prostate case and the brainstem and spinal cord in the HN case were better protected with DASSIM-RT. For both cases, the delivery efficiency has been greatly improved as the beam angular sampling increases with the similar or better conformal dose distribution. Compared with conventional quadratic programming approaches, first-order TFOCS-based optimization achieves far faster convergence and smaller memory requirements in DASSIM-RT.

Conclusions:

The new optimization algorithm TFOCS provides a practical and timely solution to the DASSIM-RT or other inverse planning problem requiring large memory space. The new treatment scheme is shown to outperform conventional IMRT in terms of dose conformity to both the targetand the critical structures, while maintaining high delivery efficiency.

I. INTRODUCTION

IMRT (Refs. 1–4) and VMAT (Refs. 5–7) are currently widely used for RT of various cancers. Each technique captures certain desirable features of RT, but compromises in other aspects. IMRT achieves a reasonable dose distribution by intensity modulation with limited angular beam sampling (typically 5–10 fixed gantry beams). IMRT inverse planning can be broadly divided into two types of optimization algorithms: direct aperture optimization (DAO) (Refs. 8–12) and beamlet based optimization (BBO).^13–18 Although DAO takes the physical constraints of the delivery system into consideration, it suffers from the problem of multiple local minima due to the nonconvex cost function. In BBO, on the other hand, the level of intensity modulation is generally unconstrained and the resultant number of segments is usually large in order to generate a reasonable dose distribution. In terms of the planning quality in IMRT, due to the sparse angular sampling, the conformity and maneuverability of the resultant dose distribution are often limited.¹⁹ On the other hand, VMAT produces conformal dose distributions by continuously rotating the gantry while modulating the aperture shape and dose rate. Because each beam is limited to a single aperture in an arc-based delivery, it does not provide the desired beam intensity modulation in some or all directions. In many clinical cases, single-arc VMAT may unduly compromise the quality of the dose distribution.^20,21 The use of multiple arcs could be a possible solution to the problem, but it fails to address the need for intensity modulation of each individual beam and may defeat the purpose of fast delivery. VMAT involves gantry rotation during dose delivery and thus requires additional attention in QA. Inability to change beam energy during rotational arc therapy also presents potential pitfalls in practice.

Recently, an alternative treatment scheme, termed dense angularly sampled and sparse intensity modulated RT (DASSIM-RT), has been proposed.²⁰ It is achieved by increasing the angular sampling of radiation beams while eliminating dispensable segments of the incident fields. DASSIM-RT combines the desirable features of both VMAT (by increasing the angular sampling) and conventional IMRT (by allowing multiple field specific segments). It explores a large area of uncharted territory in terms of the number of beams and level of intensity modulation and bridges the gap between conventional IMRT and VMAT. Two recent advancements in RT support the applications of DASSIM-RT in clinical practice. On the planning side, IMRT inverse planning with total-variation (TV) regularization^22–24 has been proposed, which is capable of dispensing unnecessary segments in intensity modulated beams to produce easily deliverable piecewise constant fluence maps. On the delivery side, DASSIM-RT is made efficient by the high dose-rate beams and by autofield sequencing available on TrueBeam^TM, which eliminates the unnecessary operator control of gantry rotation during dose delivery.²⁰ DASSIM-RT improves conformity in dose distributions while maintaining high delivery efficiency. Hybrids of rotational arc and fixed-gantry dose deliveries and/or treatment with mixed beam energies for different directions are readily achievable with DASSIM-RT.

Although the proof of concept for DASSIM-RT has been successfully demonstrated, there remains a major challenge in practice, and if not resolved, it could hinder the clinical applications of this powerful treatment scheme. Such a challenge arises from the fact that DASSIM-RT utilizes a large number of incident beams and thus involves many more variables to be optimized. This leads to a several-fold expansion of the search space and entails a much larger memory in the optimization process. Although the total-variation regularization with quadratic programming (QP) (Ref. 25) was successfully applied to optimize the fluence map in conventional IMRT,^22–24 direct application of the method to deal with the DASSIM-RT inverse planning is rather challenging because of the dramatically increased scale of problem. The use of a second-order Newton step in QP for large matrix sizes may significantly lower the convergence speed and, more computationally problematic, requires prohibitively large memory space for the optimization. Therefore, there is an unmet practical need to develop optimization algorithms that are tailored to the special challenges arising from the inverse planning for DASSIM-RT or alike.

In this paper, we utilize a novel optimization framework, called template for first-order conic solvers (TFOCS),²⁶ to address the above challenges in DASSIM-RT planning. Specifically, TFOCS tackles the computation by using first-order methods and dual variable updates, which allows for substantially reduced memory usage and assures faster convergence rates during the fluence-map optimization process. Furthermore, TFOCS provides effective solutions for the problem of ill-conditioned dose matrices, which has been one of the major difficulties in total-variation minimization. The approach thereby ensures more stable and consistent results. This work demonstrates that the promise of DASSIM-RT can indeed be realized with the TFOCS-based optimization algorithm.

II. METHODS AND MATERIALS

II.A. Conventional total-variation minimization techniques for RT planning and their pitfalls

The idea of total-variation regularization has been successfully applied to generate piecewise constant fluence maps. In the original work, the optimization problem in Eq. (1)

$$\mathrm{Minimize}{‖Ax-d‖}_2^2+\beta {‖Wx‖}_1$$ (1)

was solved using QP,^22–25 where A is the dose matrix, d is the prescribed dose, $x\in {\mathbb{R}}^n$ is the beamlet-intensity map to be optimized, $W\in {\mathbb{R}}^{2n\times n}$ is the difference matrix for total-variation in 2D-sense, and β is the regularization parameter to be determined. QP-based total-variation regularization uses a second-order Newton update, represented by Hessian, whose matrix size is n × n, where n is the number of beamlets multiplied by the number of beams. As the number of beams increases, the size of Hessian becomes much larger, thereby requiring a huge amount of memory and reducing the convergence speed of optimization. Additionally, to reformulate L1-norm based total-variation regularization in Eq. (1) as a QP problem, the resultant Hessian matrix is increased to a size of 3n × 3n. This leads to an additional increase in the requirement for memory space, on top of the original large Hessian matrix. The DASSIM-RT fluence-map optimization using QP is not practical due to the large number of beams involved in the problem.

The increased demand for memory is a well recognized problem in dealing with problems involving L1-norm regularization.^27–30 With widespread interest in compressed sensing,^31–33 several first-order based L1-solvers^34–38 have been developed, which normally refer to the model shown below

$$\begin{array}{c}\mathrm{Minimize}{‖Wx‖}_1\hfill \\ \mathrm{subject}\mathrm{to}{‖Ax-d‖}_2\le \varepsilon ,x\succ 0.\hfill \end{array}$$ (2)

The main advantage of the first-order methods lies in their faster convergence and minimal usage of memory. However, the application of L1-solvers with the first-order methods in RT planning is still quite limited for several reasons. First, as the difference matrix W for the total-variation is neither square nor a projection matrix, the inverse operation is not available, making it computationally intractable. Second, the dose matrix A has such a large condition number, called ill-conditioned, that a necessary inverse operation such as inverse of A^TA is entirely unreliable. Third, adding a constraint such as x ⩾ 0 can disrupt the process of acquiring the solution in some cases. Those three factors coupled with the memory issue prevent these techniques from being practical solutions to the fluence-map optimization problem in DASSIM-RT.

II.B. TFOCS as an effective and practical solution for DASSIM-RT planning

A newly released L1-solver, called TFOCS,²⁶ can effectively tackle the DASSIM-RT plan optimization problem with the conic forms, the dual-variable updates and the optimal first-order approaches, while assuring flexibility and efficiency. Especially, dual-variable updates can not only accelerate the speed of convergence, but can also overcome the problems caused by ill-conditioned dose matrices. The greatest benefit of TFOCS for DASSIM-RT planning with a large number of beams is that, as TFOCS is based upon the first-order method without acquisitions of the enlarged second-order Newton step, it helps save memory space and achieves faster convergence to the optimal solution than QP-based techniques. For these reasons, as the number of radiation beams increases in DASSIM-RT, both the computational time and memory requirement for TFOCS-based optimization is expected to grow linearly, rather than exponentially. The basic model for the optimization of DASSIM-RT used in this study is expressed in the following way:

$$\begin{array}{c}\mathrm{Minimize}{‖Wx‖}_1+\mu {‖x-x_0‖}_2^2\hfill \\ \mathrm{subject}\mathrm{to}{‖\sqrt{{\lambda }_i}(A_{i}x-d_i)‖}_2\le {\varepsilon }_i=k_i·m_i\hfill \\ x\succ 0\hfill \end{array},$$ (3)

where $x_0\in {\mathbb{R}}^n$ is the initial guess for iterations, μ is a sufficiently small positive constant. The primary goal of the second term in the cost function is to ensure the numerical stability by composing a strongly convex primal objective and make the dual function differentiable so that the dual objective can be optimized by means of efficient first-order methods. $A_i\in {\mathbb{R}}^{m_i\times n}$ is the dose matrix, and d_i is the dose distribution, m_i represents the number of voxels, λ_i is the importance factor of structure i, and n is the entire number of beamlet elements (size of beamlet multiplied by the number of beams). The residue imposed on PTV and each structure i is denoted by ɛ_i, which is defined as the product of positive constant k_i and the number of voxels of each structure m_i, i.e., ɛ_i = k_i·m_i. The details of the mathematical techniques used in TFOCS such as conic forms, dual updates, and first-order methods can be found in Boyd and Bandenberghe²⁵ and Becker et al.²⁶

II.C. Design considerations and algorithm implementation

Dose matrices which describe the relationship between the dose distributions and the beamlet-intensity map are calculated using voxel-based Monte Calro simulations.^39,40 Each field is comprised of 16 × 20 beamlets, with the beamlet size of 5 mm × 5 mm.

For a fair comparison between DASSIM-RT and conventional IMRT, both the prescribed residues and the importance factors of the critical structures are maintained to be the same for all plans in this work. The respective prescribed residues assigned to PTV and OARs are ɛ_PTV = 0.03·m_PTV, ɛ_i = 0.02·m_i for a prostate study and ɛ_i = 0.015·m_i for a head-neck study. The importance factors of the critical structures represented by λ_i are heuristically determined considering the residues imposed on the structures for the different number of incident beams.

The optimization algorithm was based on the TFOCS software package (http://tfocs.stanford.edu) and was modified to fit the specific needs of RT inverse planning. The initial guess was defined to be zeros, namely, x₀ = 0, and the difference matrices were designed to give the beamlet intensity differences between neighboring pixels for total-variation operation. The algorithm stops when the difference in L2-norm between two consecutive iterations is less than 10⁻⁴, namely, ‖x_k+1 − x_k‖₂ ⩽ 10⁻⁴. After fluence-map optimization, the resultant beamlet intensity map is converted into deliverable MLC segments using the method described by Zhu et al.²² For the comparison to TFOCS for toal-variation in algorithmic performance at the same condition, QP-based approach was performed by MOSEK software package (http://www.mosek.com) with appropriate modifications in parameter setting. The algorithms were implemented with MATLAB R 2008a on a PC with 4 GB memory and Intel Core i5 CPU, 2.67 GHz.

II.D. Evaluation

Two previously treated cases, a prostate case and a head and neck (HN) case, were selected to evaluate the performance of the TFOCS algorithm for DASSIM-RT planning. For both cases, the number of incident beams is assigned to 15 and 30 beams for DASSIM-RT, with the gantry angles uniformly distributed with a spacing of 24° and 12°, respectively. For comparison, we also applied the TFOCS algorithm for conventional IMRT planning with 7 fixed-gantry beams. The gantry angles are set up to be 20°, 70°, 120°, 170°, 220°, 270°, 320° for the HN case and 30°, 80°, 130°, 180°, 230°, 280°, 330° for the prostate patient.

For the prostate patient, the target shape is relatively regular. The critical structures involved were bladder, rectum, seminal vesicle, and femoral heads. A total dose of 78 Gy was prescribed to the PTV. For the HN case, the target shape is quite complicated, as shown in Fig. 1. The critical structures involved in optimization were spinal cord, brainstem, mandible, and oral cavity. For this case, a total dose of 60 Gy was prescribed to the PTV. In this work, all plans were designed such that 95% of the PTV receives the prescribe dose about at 75–80 entire beam segments.

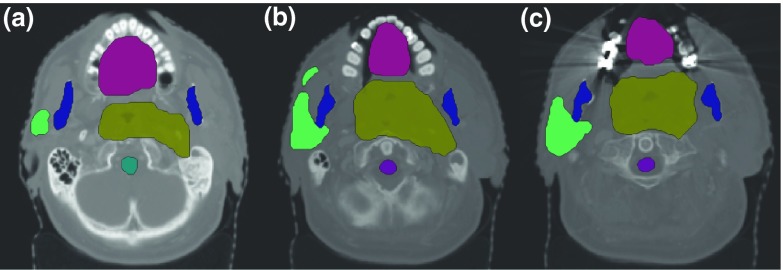
FIG. 1.

(a)–(c) Three axial slices showing all structures on CT images in the HN case. Target volumes, which are quite complex in shape, are surrounded by critical structures such as brainstem, cord, mandible, and oral cavity.

The criteria for dosimetric assessment of the planning results are dose volume histogram (DVH) and iso-dose distributions. Of diverse techniques proposed to quantitatively evaluate the dose conformity to the target in the name of conformality index,^41–45 this study adopts the notion of conformation number (CN), which consist of two different terms multiplied as shown in Eq. (4), suggested by Van't Riet et al.⁴¹ and Oozeer et al.,⁴²

$$\mathrm{Conformation}\mathrm{Number}\left(\mathrm{CN}\right)=\frac{V_{\tau ,\mathrm{ref}}}{V_{\tau }}·\frac{V_{\tau ,\mathrm{ref}}}{V_{\mathrm{ref}}}$$ (4)

where V_τ is the volume of PTV, V_{τ, ref} represents the target volume receiving the dose greater than or equal to the reference dose, and V_ref is the total volume receiving the dose greater than or equal to the reference dose. The first term of CN, denoted by CN1 for convenience, describes the coverage of target volume, which is normally required to be greater than or equal to 95%. The second term, CN2, also called the spill factor, summarizes the fractional volume of healthy tissue irradiated by a dose greater than or equal to the reference dose. Increasing the number of incident beams in DASSIM-RT compared with IMRT can improve the second term of conformation number, and thus the overall dose conformality.

In addition to the dose conformity, another important practical aspect in inverse planning is the delivery efficiency of the resultant treatment plans. For step-and-shoot techniques, the delivery efficiency is closely related to the total number of segments and the modulation index (MI).^24,46 In this work, we will evaluate the change of conformality index with respect to these two factors for each plan. The MI is defined as

$$\begin{array}{c}\hfill \begin{array}{c}{\Delta }_u=\Vert x_{u,v,f}-x_{u-1,v,f}\Vert ,{\Delta }_v=\Vert x_{u,v,f}-x_{u,v-1,f}\Vert \hfill \\ N\left(f\right)=(\mathrm{Number}\mathrm{of}\mathrm{beamlets}\mathrm{such}\mathrm{that}{\Delta }_u,{\Delta }_v>f·\sigma )\hfill \\ (f=0.01,0.02,...,2)\hfill \\ {\displaystyle z\left(f\right)=\frac{N\left(f\right)}{(N_u-1)N_v+N_u(N_v-1)}}\hfill \\ {\displaystyle \mathrm{MI}={\int }_0^{0.5\sigma }z\left(f\right)df}\hfill \end{array}\end{array}$$ (5)

where x is the resultant fluence map, N_u and N_v are the size of beamlet, Δ_u and Δ_v are the intensity change between adjacent beamlets in perpendicular and horizontal directions, σ is the standard deviation of the beamlet intensities, and N(f) is the number of beamlets satisfying the condition above.

The proposed first-order approach is compared with second-order QP-based approaches for DASSIM-RT planning. The QP equivalent model with the total-variation minimization is optimized for the prostate and HN cases with 15 and 30 beams. The comparison is made in terms of algorithmic performance such as the convergence speed and required memory usage.

III. RESULTS

III.A. Plan quality

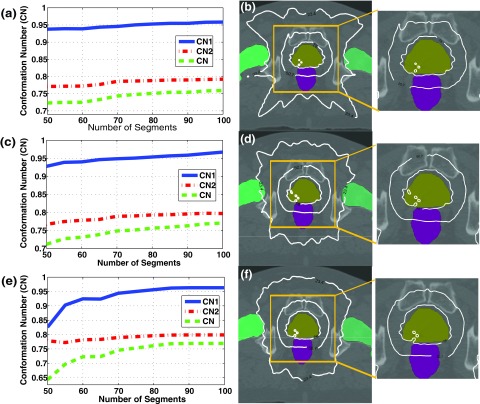
The dose conformity to the PTV for both cases is demonstrated in Figs. 2 and 3, which show the CN and iso-dose distributions for plans with 7, 15, and 30 beams. From Figs. 2, 3(a), 3(c), and 3(e), it can be seen that CN increases as the number of beams rises. The improvement in the dose conformity to the PTV is clearly shown in iso-dose distributions in Figs. 2, 3(b), 3(d), and 3(f), where the dose distribution is more conformal to the target at the same beam segments as the number of beam increases. The extent of the improvement in target dose conformity appears to be more remarkable in the HN case, where the shape of the PTV is bigger and more complicated than that in the prostate case. This indicates that DASSIM-RT with an increased beam angular frequency may be more effective in complicated cases. Table I lists the numerical results of CNs and its two components for the three different plans for the three different plans in the prostate and HN cases with 80 beam segments. With CN1 greater than or equal to 0.95, both CN and CN2 are improved as the number of beams is increased. A similar, yet more noticeable, trend is observed in Table II for the HN case with 75 beam segments. These results demonstrate the dosimetric advantages of DASSIM-RT over IMRT, by increasing the beam angular sampling.

FIG. 2.

Planning results in the prostate case. (a), (c), (e) The variations of CN, CN1; and CN2, (b), (d), (f) iso-dose distributions with 80 segments for 7, 15, and 30 beams. CN and visualized dose conformity to the PTV tend to increase as the number of beams increases. Also, the dose distribution with 30 beams is better nearby the femoral heads and normal tissues than that with 7 beams.

FIG. 3.

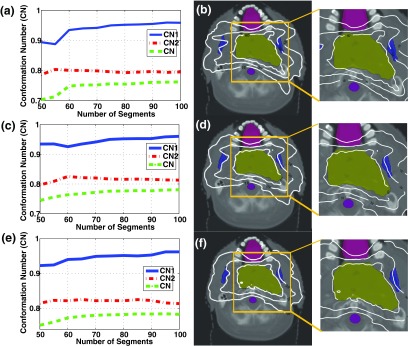
Planning results in the HN case. (a), (c), (e) The variations of CN, CN1, and CN2, (b), (d), (f) iso-dose distributions with 75 segments for 7, 15, and 30 beams. Improvement in dose conformity to the PTV becomes more remarkable than the prostate case.

TABLE I.

Conformation number, optimization time, modulation index, maximum and mean beam intensity for the prostate treatment plans with 7, 15, and 30 beams at 80 beam segment using the proposed methods.

	Conformality index					Beam intensity
	CN	CN1	CN2	Time for fluence-map optimization (s)	MI	Maximum intensity	Mean of intensity
7 beams	0.7509	0.9527	0.7882	120	4.33	742	297
15 beams	0.7565	0.9535	0.7934	255	3.61	425	139
30 beams	0.7611	0.9545	0.7974	524	2.51	242	68

TABLE II.

Conformation number, optimization time, modulation index, maximum and mean beam intensity for HN treatment plans with 7, 15, and 30 beams at 75 beam segments using the proposed methods.

	Conformality index					Beam intensity
	CN	CN1	CN2	Time for fluence-map optimization (s)	MI	Maximum intensity	Mean of intensity
7 beams	0.7554	0.9501	0.7951	97	4.40	1304	96
15 beams	0.7758	0.9501	0.8165	168	3.12	695	45
30 beams	0.7819	0.9504	0.8224	352	1.73	394	23

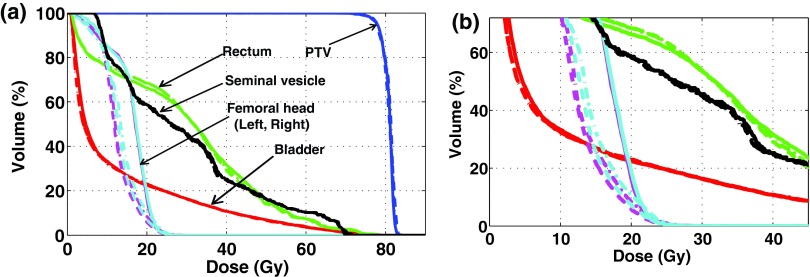
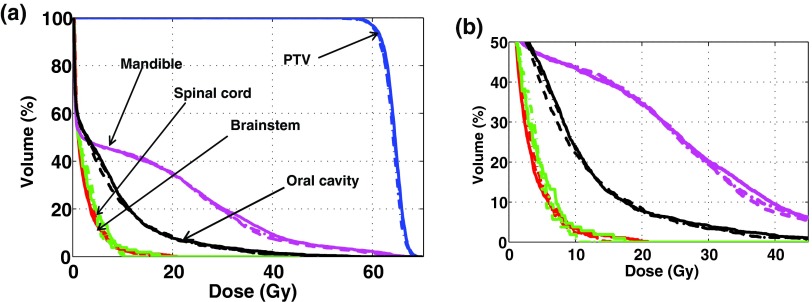
Figures 4 and 5 show the DVHs of all structures involved in the fluence-map optimizations with 7, 15, and 30 beams for the prostate and HN cases. The planning results were obtained with 80 and 75 beam segments for the two cases, respectively. They show that normal tissues can be better spared with higher beam angular frequencies in DASSIM-RT. The advantage of using more beams in protecting normal tissues is also evident from Tables III and IV. For instance, in the prostate case, the mean dose to femoral heads is decreased from 16 Gy to ∼13 Gy when the number of beams is increased from 7 to 15 and 30. In the HN case, the maximum dose to the brainstem and spinal cord is reduced by ∼25% and ∼43% with 15 beams and the dose reduction is even more with 30 beams. Doses to other organs are also reduced with DASSIM-RT, although by a smaller amount.

FIG. 4.

(a) DVHs of the resultant plans with 7, 15, and 30 beams in the prostate case and (b) the magnified views, where the solid(-), the dashed-dotted(-•), and the dashed lines(–) correspond to 7, 15, and 30 beams, respectively. The DVHs were acquired with 80 segments for all plans. The dose conformity to the critical structures, especially left/right femoral heads, is noticeably enhanced with DASSIM-RT (15 and 30 beams) over IMRT (7 beams).

FIG. 5.

(a) DVHs of the resultant plans with 7, 15, and 30 beams in the HN case, and (b) the magnified views, where the solid(-), the dashed-dotted(-•), and the dashed lines(–) correspond to 7, 15, and 30 beams, respectively. The DVHs were acquired with 75 segments for all plans. The dose conformity to the critical structures, such as brainstem and spinal cord, is improved with the greater number of beams.

TABLE III.

Planning results compared with the clinical acceptance criteria in the prostate case.

		Results
	Acceptance criteria	7 beams	15 beams	30 beams
PTV	% vol ⩾ 78Gy > 95	95	95	95
Rectum	% vol ⩾ 40Gy ⩽ 35	31.68	30.03	29.08
	% vol ⩾ 65Gy ⩽ 17	3.84	3.92	3.86
	vol > 79.6Gy ⩽ 1cc	0 cc	0 cc	0 cc
Bladder	% vol ⩾ 40Gy ⩽ 50	10.81	10.71	10.67
	% vol ⩾ 65Gy ⩽ 25	2.59	2.34	2.41
Femoral heads	% vol ⩾ 45Gy ⩽ 1	0 (mean: 16.06 Gy)	0 (mean: 13.03 Gy)	0 (mean: 12.56 Gy)
Seminal vesicle	–	Mean: 30.45 Gy	Mean: 30.26 Gy	Mean: 30.23 Gy

Note: As seminal vesicle has no specific criteria, its mean dose is shown here.

TABLE IV.

Planning results compared with the clinical acceptance in the HN case.

		Results
	Acceptance criteria	7 beams	15 beams	30 beams
PTV	% vol ⩾ 60Gy > 95	95	95	95
Brainstem	Maximum <54 Gy	Max.: 20.90 Gy (Mean: 2.52 Gy)	Max.: 15.75 Gy (Mean: 2.42 Gy)	Max.: 14.25 Gy (Mean: 2.39 Gy)
Spinal cord	Maximum <45 Gy	Max.: 17.41 Gy (Mean: 2.62 Gy)	Max.: 9.97 Gy (Mean: 2.34 Gy)	Max.: 10.03 Gy (Mean: 2.36 Gy)
Mandible	–	Mean: 14.10 Gy	Mean: 13.82 Gy	Mean: 13.84 Gy
Oral cavity	–	Mean: 6.64 Gy	Mean: 6.61 Gy	Mean: 6.46 Gy

Note: Since mandible and oral cavity have no specific criterions, the mean dose of the structures was provided.

Figures 6 and 7 show the dose conformity to the target (or CN) as a function of the total number of segments and MI. It can be seen that in both cases, DASSIM-RT (15 and 30 beams) is able to achieve a higher CN than IMRT (7 beams) with a similar number of beam segments, and with a significantly reduced MI. For instance, as shown in Table I for the prostate case, the MI is reduced by 40% with the 30-beam DASSIM-RT plan compared to the 7-beam IMRT plan. The reduction in MI is even more dramatic in the HN case, by as much as 60%, as shown in Table I. The reduction in MI is a manifestation of the simplicity of the resultant fluence maps, which are illustrated in Figs. 8 and 9, for the prostate case and HN case. This demonstrates that as the number of beams increases in DASSIM-RT, the fluence maps become more piecewise constant and thus are more efficient to deliver.

FIG. 6.

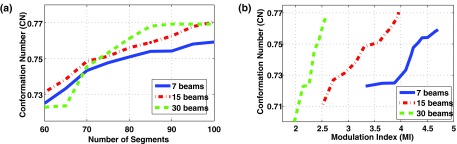
Conformation number as a function of (a) the number of beam segments and (b) the modulation index for the IMRT plan (7 beams) and the DASSIM-RT plans (15 and 30 beams) in the HN case. DASSIM-RT is able to achieve higher dose conformity with less intensity modulation and similar or even less number of segments.

FIG. 7.

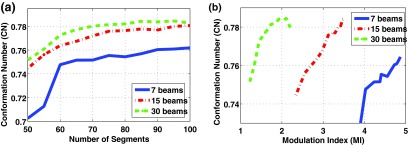
Conformation number as a function of (a) the number of beam segments and (b) the modulation index for the IMRT plan (7 beams) and the DASSIM-RT plans (15 and 30 beams) in the HN case. The improvement in the PTV dose conformity is more noticeable in the HN case than the prostate case mainly due to more complicated PTV structure.

FIG. 8.

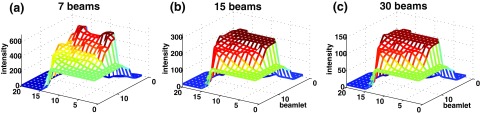
Optimized fluence maps for the three prostate plans (gantry angle 280° for 7 beam, and gantry angle 288° for 15 and 30 beams) before passing through the leaf-sequencing algorithm. As the beam angular sampling increases, the resultant fluence maps become simple and tend to be piecewise constant.

FIG. 9.

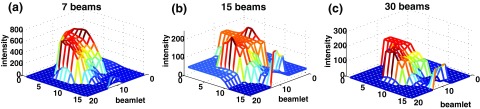
Optimized fluence maps acquired by the three HN plans (gantry angle 120°) before passing through the leaf-sequencing algorithm.

Regarding the plan quality comparison between TFOCS and QP-based methods, the DVHs and iso-dose distributions are very similar with the same beam configuration for the prostate and HN cases as shown in Fig. 10 although minor differences are present. With respect to the dose conformity to the target, TFOCS yields greater CN than QP-based methods for both cases as presented in Table V.

FIG. 10.

Comparisons of the plans from the proposed methods (solid lines) and the QP-based approaches with TV form (dotted lines) in (a), (c) DVHs, and (b), (d) iso-dose distribution for the prostate and HN cases.

TABLE V.

Comparisons in algorithmic performance between TFOCS and QP-based approaches for HN case with 15 beams DASSIM-RT with respect to (1) the computational time and (2) the actual memory space required for the fluence-map optimization and (3) conformality index by CN.

	Prostate			HN
	Time for fluence-map	Actual memory		Time for fluence-map	Actual memory
	optimization (s)	usage (GB)	CN	optimization (s)	usage (GB)	CN
TFOCS	255	0.92	0.7565	168	0.56	0.7758
QP	3911	2.54	0.7014	3597	2.41	0.7665

III.B. Optimization efficiency

Tables I and II list the time elapsed for fluence-map optimization at 7, 15, and 30 beams, for the prostate and HN cases, respectively. For most of the plans, the results were achieved within 2000 iterations using TFOCS algorithm with the stopping criterion given, ‖x_k+1 − x_k‖₂ ⩽ 10⁻⁴, except for the HN case with 7 beams, where the complexity of the fluence map becomes high. In such a case, the stopping criterion was strengthened by lowering the difference in L2-norm between two consecutive iterations to less than 10⁻⁵. The optimization time required for a 30-beam DASSIM-RT plan is <9 min and ∼6 min for the prostate and HN cases, respectively. It is worth noticing that in both cases, the computational time for fluence-map optimization increases only linearly with respect to the number of beams instead of exponentially as the number of variables to be updated at every iteration linearly increases in the TFOCS based approach. This is a main practical benefit of the proposed algorithm for the DASSIM-RT.

Table V lists the time elapsed for fluence-map optimization with the proposed method and QP-based approach for DASSIM-RT plans with 15 beams. The QP-based approaches converge to the solution ∼15–20 times slower than the TFOCS based algorithm in both cases. Even worse, the QP-based approaches cannot even process the DASSIM-RT plans with 30 beams because its memory requirement exceeds what our current computing platform can offer (4 GB memory), which can demonstrate the superiority of the proposed algorithm for DASSIM-RT plans in memory efficiency. Table V also shows the actual memory usage spent in each algorithm in the unit of gigabyte (GB), which is ∼2.5–4 times greater in QP-based method than that in the first-order method, TFOCS.

IV. DISCUSSION

DASSIM-RT has recently been proposed to fully utilize the degrees of freedom of angular and intensity modulation in unison. A major obstacle in the practical implementation of DASSIM-RT is how to find the solution that best balances the intrabeam modulation and angular sampling. The complication here arises from the fact that a large number of incident beams are involved, which necessitates a much larger memory in the optimization process. Conventional total-variation regularization techniques based upon the QP do not handle these large-scale problems properly due to the computational time and memory expenses.

In this work, we tackle the issue of computational efficiency by adopting a novel L1-solver called TFOCS. It utilizes first-order methods and assures faster convergence time to the solutions than conventional second-order methods such as QP. In addition, because it does not involve the enlarged Hessian matrix for the second-order Newton step, TFOCS requires much less usage of memory than the QP-based methods. These desirable features are ideally suited for DASSIM-RT where the size of dose matrix becomes much larger than in conventional IMRT. Indeed, as the results showed in both cases, the computational time for fluence-map optimization increases almost linearly (instead of exponentially) with respect to the number of beams. Significantly, the fact that QP-based approaches cannot process the DASSIM-RT plans with 30 beams, while the first-order TFOCS method can perform with our computing platform, demonstrates the superiority of the proposed method in memory efficiency. Specifically, in the TFOCS-based approach, the memory charge is mostly determined by the total number of voxels of entire structures multiplied by the entire beamlet elements ($({\sum }_{i=1}^{N+1}{m}_i)\times n$), where the N+1 is the total number of organs. Contrarily, the QP-based approach for TV form requires a much bigger matrix for composing additional matrix element (3n × 3n). At each iteration, the first-order method only updates multiple times of n elements for primal and dual variables, whereas QP based second-order approach updates 3n × 3n variables. These make an enormous difference between the two methods in terms of memory usage and convergence time. It clearly shows the practical applicability of the TFOCS algorithm for large-scale optimization problems such as the DASSIM-RT inverse planning.

The results from two patient studies demonstrate that, by increasing the angular beam sampling and effectively eliminating the dispensable segments using TFOCS based total-variation minimization, DASSIM-RT provides better dose conformity to both the critical structures and the target than conventional IMRT. The improvement of dose conformity was demonstrated in various aspects such as DVHs, iso-dose distribution, and conformality index.

Although the organ doses are all within the planning limits in both cases, it can be argued that in radiation therapy, fewer doses to normal tissues are always better with the same PTV coverage. Further, the dosimetric advantages of DASSIM-RT can prove important for more complex cases or for patients who have received RT before or are receiving hypofractionated RT.

In addition to a highly conformal dose distribution, it is also important to maintain the delivery efficiency. DASSIM-RT achieves this goal by greatly reducing the complexity of intensity modulation, measured by MI and the number of beam segments. As the number of beams increases in DASSIM-RT, the complexity of intensity modulation measured by MI significantly decreases and the resultant fluence maps become nearly piecewise constant, which should translate into efficiency in the dose delivery process. In our original paper,²⁰ we have compared the estimated delivery time of DASSIM-RT, IMRT, and VMAT. We found that for three clinical cases, the estimated dose delivery time for a DASSIM-RT plan with 15 beams and 5 intensity levels is around 4.5 min, which is similar to the delivery time of step-and-shoot IMRT plans with 7 beams and 10 intensity levels. VMAT plans take less time to deliver (1.5 and 2.5 min for a 1-arc and 2-arc plan, respectively).

The actual need of the number of beams is case-dependent. Our results suggest that the effect of increasing the angular sampling frequency would be more dramatic when (1) the shape of the target is more complicated as in the head-neck patient data used in this study, or/and (2) the critical structures are located quite close to the target, thereby requiring high dose sparing to the critical structures. In one of those two cases, just as confirmed in the results of the HN patient study, dose conformity to the PTV is noticeably better with the same or fewer beam segments and with much less fluence-map complexity.

Future work of DASSIM-RT planning includes a more comprehensive evaluation on more clinical cases in more anatomic sites. The optimal number of beams and the exact beam orientation will also be investigated in a general framework for DASSIM-RT planning. The proposed first-order based L1-solver can be used in other medical applications which require large-scale optimization, such as CS-based iterative cone-beam CT reconstruction.²⁸

V. CONCLUSIONS

Angular beam sampling and intrabeam intensity modulation represent two important aspects in conformal radiation therapy. DASSIM-RT combines the desirable features of both VMAT and conventional IMRT, by increasing the angular sampling of radiation beams while eliminating dispensable segments of the incident fields. Computationally, the use of a large number of beams may be problematic for conventional second-order optimization methods, leading to a slow convergence and large memory expense. We have applied a newly available first-order based L1-solver to address the computational challenges of large-scale optimization in DASSIM-RT inverse planning. For DASSIM-RT planning with 15 beams, the algorithm converges in ∼5 and 3 min in the prostate and HN case. Compared with conventional QP-based approaches, the proposed algorithm achieves faster convergence by a factor of ∼15–20 and smaller memory requirements. This work provides a practical and timely solution to the DASSIM-RT inverse planning problem and could lead to new treatments that provide quality dose distributions in clinical practice. The proposed first-order based L1-solver can also be applied in other medical applications, which require large-scale optimization, such as CS-based iterative cone-beam CT reconstruction.