Bidirectional local distance measure for comparing segmentations

Abstract

Purpose:

To accurately quantify the local difference between two contour surfaces in two- or three-dimensional space, a new, robust point-to-surface distance measure is developed.

Methods:

To evaluate and visualize the local surface differences, point-to-surface distance measures have been utilized. However, previously well-known point-to-surface distance measures have critical shortfalls. Previous distance measures termed “normal distance (ND),” “radial distance,” or “minimum distance (MD)” can report erroneous results at certain points where the surfaces under comparison meet certain conditions. These skewed results are due to the monodirectional characteristics of these methods. ComGrad distance was also proposed to overcome asymmetric characteristics of previous point-to-surface distance measures, but their critical incapability of dealing with a fold or concave contours. In this regard, a new distance measure termed the bidirectional local distance (BLD) is proposed which minimizes errors of the previous methods by taking into account the bidirectional characteristics with the forward and backward directions. BLD measure works through three steps which calculate the maximum value between the forward minimum distance (FMinD) and the backward maximum distance (BMaxD) at each point. The first step calculates the FMinD as the minimum distance to the test surface from a point,p_ref on the reference surface. The second step involves calculating the minimum distances at every point on the test surface to the reference surface. During the last step, the BMaxD is calculated as the maximum distance among the minimum distances found at p_ref on the reference surface. Tests are performed on two- and three-dimensional artificial contour sets in comparison to MD and ND measure techniques. Three-dimensional tests performed on actual liver and head-and-neck cancer patients.

Results:

The proposed BLD measure provides local distances between segmentations, even in situations where ND, MD, or ComGrad measures fail. In particular, the standard deviation measure is not distorted at certain geometries where ND, MD, and ComGrad measures report skewed results.

Conclusions:

The proposed measure provides more reliable statistics on contour comparisons. From the statistics, specific local and global distances can be extracted. Bidirectional local distance is a reliable distance measure in comparing two- or three-dimensional organ segmentations.

I. INTRODUCTION

In the last decade, many researchers have actively studied similarity evaluations between reference segmentation and a test segmentation. Many atlas-based segmentation tools in medicine have been introduced with evaluations based on comparing experts’ manual segmentations vs the algorithm's segmentation.^1–3 In the scientific arena, quantitative and objective measures of similarity for contours (or in topological terms: “surfaces”) are essential to verify the accuracy and precision of a segmentation. The most widely used similarity measures are the Dice⁴ and Jaccard⁵ similarity indices that are calculated on the combined volumes enclosed by two surfaces. Even though the Dice and Jaccard indices are good metrics, it has a critical shortcoming where severe local discrepancies between surfaces are masked since total volume differences are addressed. Moreover, visualization of discrepancies between surfaces is not possible with these kinds of global volumetric similarity indices.

For radiation treatment planning applications, it is desirable to know quantified errors in geometric displacement to ensure target coverage, normal tissue avoidance, and similar analyses. Therefore, some researchers have utilized distance measures to quantify the similarity/discrepancy between two different segmentations.^6–8 For computer graphics, it is very important to visualize the regional discrepancy between two surface meshes.^9–11 Similarity may be indexed using the geometric displacement which is calculated by measuring distances between points on two surfaces. Since this approach takes into account distance differences, the ambiguity of volume-based similarity indices, such as Dice and Jaccard is eliminated.

The Hausdorff distance is a well-known distance measure between two data sets.¹² In a Hausdorff calculation, the minimum distance is measured twice. First, the distances from the reference surface to the test surface are measured, and then the distances from the test surface to the reference surface are measured. There are many modified Hausdorff measures using this information.^13–15 The main differences among these modified measures depend on how they select a final Hausdorff distance from the minimum distances. However, all of these original and modified Hausdorff distances are global distance measures. A single representative distance value is calculated for two surfaces or data sets. With only the single value, the discrepancy of any particular part of a surface or data set cannot be quantified or analyzed. These distance measures cannot be utilized for distributed statistical analyses of distance measures between the organ surfaces or visualization of discrepancies.

A local distance measure, a point-to-surface distance, is needed for the quantified visualization or statistical analysis of similarity/discrepancy between two different surfaces/segmentations. The distances should be mapped at each point on the reference surface and the distance should represent the distance to the test surface. Typical methods used in measuring the local distance differences from all points on a reference surface to a test surface are: the radial distance (RD) measure,^16–18 the normal (perpendicular) distance (ND) measure,^6,19 the minimum distance (MD) measure,^20,21 and the ComGrad measure.²²

The radial distance is defined as the distance from the center of mass point (or line) of a segmentation to its surface per each radial direction. The RD as a similarity index calculates differences between the radial distances of the reference and test surfaces in the same radial direction from the center of mass point of the reference surface. However, the RD measure is limited to radial and cylindrical shapes²³ and is thus dropped from further considerations for comparison.

I.A. Normal distance measure

The normal distance is defined as the Euclidean magnitude of the normal vector which starts from a point on the reference surface and ends at the test surface. Let R be a reference surface, and T a test surface. The ND at a point p_ref on R is defined as $d(p_{\mathrm{ref}},T)=\left|\vec{N}\right|$, where N is R's normal vector starting at the point p_ref, and ending where N is intersecting with the surface T. d(p_ref,T) is the magnitude of the vector N. Deurloo et al.⁶ utilized the ND measure to analyze the shape variation of seminal vesicles for prostate cancer patients. Wu et al.⁸ also utilized this measure to quantify the segmentation uncertainty. They utilized the ND to measure the distances from the average segmentation to the individual segmentations. Wu et al. generated a standard deviation surface map (SDSM) using the measured distances. This kind of statistical analysis is only possible with local (point-to-surface) distance measures.

However, the ND technique may result in erroneously long distances when the reference surfaces are not a smooth spherical surface. Wu et al. also utilized a smoothed surface since the normal distance was not reasonable when the average segmentation is not smooth enough.⁸

Consider a reference surface R (solid line) with severe curves and a test surface T (dotted line) with simple curves as shown in Fig. 1(a). The ND approach has two problems. First, distances cannot be calculated when the normal vector of the point p₁ on surface R cannot find an intersecting point on the surface T as illustrated in Fig. 1(a). Second, distances can be miscalculated if the two surfaces are anything but parallel as shown at the point p₂ in the same figure.

FIG. 1.

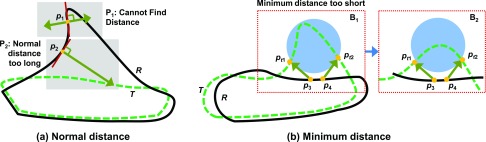
Shortfalls of normal and minimum distance measures: (a) ND cannot be found at the point p₁ since the normal vector on the reference surface does not intersect with the test surface. The ND measure may report longer distances when two surfaces are not parallel such as at the point p₂. (b) The MD measure may report shorter distances when the test surface is winding and the reference surface is flat as highlighted circle. Although the local discrepancy between the surfaces in the circle area is larger at B₁ than B₂, the MD at the points, p₃ and p₄ will be reported as the same as at points p_t1 and p_t2, respectively. The reference surface R is drawn as a solid line and the test surface T is drawn as dotted line.

I.B. Minimum distance measure

The minimum distance measure is defined as

$$d(p_{\mathrm{ref}},T)=d_{\min }(p_{\mathrm{ref}},T)=\underset{p_t\in T}{min}{‖p_{\mathrm{ref}}-p_t‖}_2,$$ (1)

where d_min(p_ref,T) is the minimum distance from a point p_ref on a reference surface R to all points p_t on a test surface T, and ‖·‖₂ is the Euclidean norm. Some researchers referred this MD measure as a Hausdorff distance since a Hausdorff distance utilizes the minimum distance measure in its initial calculations.^20,24,25 Rizzo et al. utilized the minimum distance measure to calculate the average symmetric distance, which is one type of Hausdorff distance.²⁶ However, the Hausdorff distance is a global distance measure as mentioned above. It is not able to locate the regional discrepancy. Therefore, they are the minimum distance measure although they called it (one-side or one-directional) Hausdorff distance.^20,25 To avoid confusion, the term Hausdorff distance will not be used since it was originally proposed to be a single valued global distance measure.¹²

MD measures can miscalculate distances at the points on the reference surfaces which are geometrically adjacent to the strongly winding curves of a test surface. For example, consider the two contours in Fig. 1(b). The goal is to calculate the distance from a point belonging to the reference surface R to the test surface T as shown in Fig. 1(b). Let the points, p₃ and p₄ on the surface R be neighboring points. The MD at the points, p₃ and p₄ to the surface T are found at the points, p_t1 and p_t2, respectively, as shown in Fig. 1(b). In this example, the MD measure ignores the points in the circle area between points, p_t1 and p_t2 on the surface T. Although B₁ has larger local discrepancy between the surfaces, R and T in the circle area compared to B₂, the MD at the points, p₃ and p₄ in B₂ are found at the same points, p_t1 and p_t2, as same as in B₁. The MD measure calculates the same minimum distances in the example of Fig. 1(b) despite obvious differences between the two test surfaces. The MD measure tends to report smaller distances than the actual local discrepancy.

I.C. ComGrad measure

The distance measures described above are all asymmetric because the resultant distances are different when the reference and test surfaces are switched. van der Put et al. proposed a symmetric method.²² They named it the ComGrad, which calculates the combined gradient of the signed distance transforms²⁷ produced from the reference and the test contours. The ComGrad uses the unit vectors along the gradient direction to identify corresponding points between the reference and the test contours.²² The final distances are calculated by adding the scalars of the unit vectors along each gradient direction. It is a reliable distance measure in case spatial information needs to be preserved. However, as authors mentioned in their discussion, the ComGrad cannot find proper corresponding points when either of the contours has a concave region or a folding region like the shortfall of ND.

I.D. Bidirectional local distance (BLD), a new measure to compare segmentations

Previous distance measures work well for prostate cases since the contours are round and relatively smooth. However, they fail to quantify local contour variations for head-and-neck tumors or lung tumors, which include complicated concave, folding, or horse shoe regions.

Bidirectional local distance, a more reliable bidirectional distance measure is presented, overcomes these shortfalls.

II. MATERIALS AND METHODS

II.A. Theory of bidirectional local distance measure

The concept of the minimum distance technique is utilized in the new BLD measure. As shown in Fig. 2, the first step calculates the forward minimum distance (FMinD) that is defined as the minimum of distances from a point on a reference surface R to all points on a test surface T:

$$\mathrm{FMinD}(p_{\mathrm{ref}},T)=d_{\min }(p_{\mathrm{ref}},T)=\underset{p_t\in T}{min}{‖p_{\mathrm{ref}}-p_t‖}_2,$$ (2)

where p_ref ∈ R.

FIG. 2.

An example illustrates the BLD measure scheme; FMinD at the point p_ref is marked as ①. During the BMaxD calculation ② and ③ are the candidates. Since BMaxD selects the maximum distance among the candidates, ② is chosen as BMaxD. The final BLD(p_ref, T) is the maximum between FMinD and BMaxD. Therefore, BMaxD, ② is chosen as the final BLD(p_ref, T) in this example.

This step is the same as the MD measure, the initial calculation of the Hausdorff distance measure. An additional step is devised to resolve the problem of monodirectional distances as described in the Introduction. The second step calculates the backward maximum distance (BMaxD) at p_ref on the reference surface R. Actual calculations of BMaxD(T,p_ref) are composed of three stages. The first calculation is to determine the backward minimum distance, d_min(p_t,R) at every point p_t on the test surface T. Then points are selected whose d_min(p_t,R) is found at the point p_ref on the reference surface R and designate these as p_t. Finally, BMaxD(T,p_ref) is the maximum value from the set {d_min(p_t,R)}. These calculations are presented in one equation:

$$\begin{array}{c}\hfill \mathrm{BMaxD}(T,p_{\mathrm{ref}})=\underset{p_t\in T}{max}\left\{d\right|d=d_{\min }(p_t,R),d=\Vert p_t-p_{\mathrm{ref}}{\Vert }_2\}.\end{array}$$ (3)

The final measured distance BLD(p_ref,T) is decided by finding the maximum distance between FMinD(p_ref,T) and BMaxD(T,p_ref):

$$\mathrm{BLD}(p_{\mathrm{ref}},T)=\max (\mathrm{FMinD}(p_{\mathrm{ref}},T),\mathrm{BMaxD}(T,p_{\mathrm{ref}})).$$ (4)

Utilizing a minimum distance measure in both directions can resolve the shortfall of the ND technique shown in Fig. 1(a). Determining the final distance using the maximum between FMinD and BMaxD gives us a meaningful distance between two surfaces at the point p_ref on the reference surface R. Therefore, the shortfalls of the MD measure shown in Fig. 1(b) can be avoided.

II.B. Benchmarking bidirectional local distance measure

Three methods are implemented to benchmark our new measure.

II.B.1. Measuring rigid-shifted contours

First, a distance map measured from one case of 20 mm laterally shifted contours is compared. The tested contour is a two-dimensional (2D) contour with sharp and smooth edged curves as shown in Fig. 3. The solid black lines show the reference contours. The dotted lines show the test contours which are 20 mm shifted from the reference contours. Our BLD method is compared to the ND, MD, and ComGrad measures. The simplicity of this test allows us to characterize and compare the three distance measures in verifiable way, while confirming the calculation accuracy.

FIG. 3.

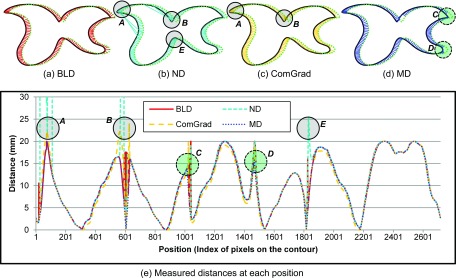
Analyses of measured distances between shifted contours along the contour perimeter position. (a)–(d) Distances measured for BLD, ND, ComGrad, and MD. (c) Distances profile at each pixel on the reference contour. Solid lines represent the BLD measure, and the dotted lines represent the MD measure at every point on the reference contour. The dashed lines show the ND measure. The long dashed orange lines show the ComGrad measure. The ND erroneously measures longer than 20 mm shifts at several points (shown in three regions as marked with A, B, E). MD erroneously measures shorter than 20 mm at two regions as marked with C and D. The ComGrad measures longer than 20 mm shifts at the region as marked with E.

II.B.2. Measuring deformed 2D contours

Second, distance maps for 2D contours sharing characteristics of various shapes of tumors are compared. Four typical cases are shown. Those four example cases are created to represent the possible variations between the reference and test contours as found in clinical practice which includes shifting and deformation. Especially, the forth case includes folded and concave curves. The BLD measure is compared to the ND, MD, and ComGrad measures. Due to the importance of this test, software is developed that implements and analyzes all four techniques. The software allows a user to create a reference contour and a test contour in two-dimensional space.

II.B.3. Application to three-dimensional structures

Third, distance measurement is compared between pairs of three-dimensional (3D) contours for two patients. For the 3D comparison, a software tool is developed implementing BLD, ND, and MD measures using the Visualization Toolkit (VTK).²⁸ Two actual patient cases, a liver case and a head-and-neck, case are tested. Differences are measured between two liver contours from treatment plans generated a year apart from a returning patient. Two plans are registered using automatic and manual rigid-body registration methods. Two contour sets are manually delineated by expert physicians using the Pinnacle3 radiation treatment planning system (version 8.0, Philips Healthcare, Madison, WI). The head-and-neck patient went through offline adaptive radiation treatment planning procedure due to the significant tumor shrinkage in the middle of treatment course. The two plans are registered using automatic rigid-body registration.²⁹ Distances between the original primary CTV contour and the new shrunken primary CTV contour are measured.

Three-dimensional organ volumes are generated from the 2D DICOM-RT contours by designating 1 for the voxels inside the contour, 0.5 for the voxels on the contour, and 0 for the voxels outside the contour. Next, a marching cube algorithm is used to generate a surface mesh from the organ volume with 0.5 threshold value.^30–32 Since the CT image set is captured in 3 mm slice thickness, the physician segmented contours had 3 mm intervals in superior–inferior axis. Voxel sizes of 2 × 2 × 3 mm³ voxel are used to achieve a smooth mesh surface.³³ Mesh surface smoothing is also applied to reduce sharp edges in the surface meshes.³⁴

II.C. Effect of smoothing volumes

The effect of volume smoothing is investigated using the liver patient data set. For this comparison, recursive Gaussian smoothing algorithm is utilized before applying the marching cube algorithm.^35,36 Various standard deviation values for smoothing are tested. Gaussian smoothing is applied before creating the organ mesh. A higher standard deviation yields a smoother mesh but the detailed organ contour will be diminished. BLD measure is compared to MD and ND. ND is known to be affected by smoothing.

II.D. Calculating the standard deviation surface map

Wu et al.⁸ introduced the concept of a SDSM to present uncertainty in contouring organ models of prostate cancer patients. SDSM can enhance the accuracy of deformable model based automatic segmentation by providing the localized range of uncertainty associated with an organ template. Wu et al. constructed an average contour derived from multiple experts’ segmentations, and then measured the ND from the averaged contour to each individual expert's contour. The standard deviation of the ND at each point of the averaged contour is mapped. Since they utilized ND measure, they had to smooth the averaged contour. ND measure is unable to measure correct distances on surfaces with high degree of curvature (see Fig. 4) and rapidly undulating surfaces. By smoothing the contour, the original shape may be lost along with the accuracy of the analysis.

FIG. 4.

Comparison of ND, MD, ComGrad, and BLD measures: Case 1—high similarity and weakly winding contours; Case 2—low similarity and weakly winding contours; Case 3—medium similarity and strongly winding contours; Case 4—winding contours with concave and folded curves. The solid lines are reference contours and the dashed lines are test contours. For easy illustration, the linked lines between contours indicate measured distances.

The BLD measure is used to build a SDSM from nine prostate segmentations. The SDSM is calculated using our BLD measure to first generate the distance difference maps between the individual contours and the averaged contour. From this information, standard deviations are generated and used to create the SDSM while minimizing the influence of the curvature of the segmentations.

III. RESULTS

III.A. Measuring shifted contours

Figures 3(a)–3(d) graphically illustrate the distances measured from the contour example which have the complicated curves such as concave and fold. Each subfigure represents BLD, ND, ComGrad, and MD measures. A solid circle (label A, B, and E) indicates the problematic region resulting in distances overestimated and a dashed circle (label C and D) is the problematic region measuring distances underestimated. Distance profiles are created from the measured distances as shown in Fig. 3(e). Our BLD measurement is shown as a solid line and the MD, ND, and ComGrad distances are shown as a dashed short line, a dashed long line, and a dotted line, respectively, in the measured distance graphs. The maximum distance should be equal to or less than 20 mm. The BLD and MD measures do not report any shifts larger than 20 mm (the maximum actual shifted distance). However, the ND measure estimates actual go to infinity at several sharp corner areas A and B, which forces the smoothing approximation in an attempt to compensate. Even in the smoothed corner, the ND measure reports 25 mm which is more than 20 mm of shift as shown in the area E in Fig. 3(e). The ComGrad and ND measures have similar problems. ComGrad reports 22 and 24 mm, respectively, as shown in the areas A and B in Fig. 3(e). The cause of the overestimated distances is because the distance line calculated along with vector field flow is curved. The areas C and D in Fig. 3(b) indicate that MD measure reports smaller than 20 mm at the outer tips of the curve.

III.B. Distance measure comparisons for various 2D shapes

Figure 4 graphically illustrates the distances measured between a reference contour and a test contour for the four cases characterized. The solid lines are reference contours and the dashed lines are test contours. The matching points for measuring distances between two contours are shown as linked lines for visualizing the measured distances, and the lengths of these lines are the distances measured.

For Case 1, the reference contour and the test contour have high similarity while the curves are weakly winding. All measures calculate correct distances between the contours for this case. However, the second case shows that the MD measure falls short where the curvature has a high degree of winding and low similarity. BLD and the ND measures can report more accurate shift distances compared to the MD measure. Finally, Case 3 shows that the ND measure reports erroneous distances. Normal vectors at the points where the reference contour is strongly winding do not find any intersecting points on the test contour, or find geometrically unrelated far-off points on the test contour. Finally, Case 4 with folded and concave curves shows that the proposed BLD outperforms the others. In case of the concave-like curve, the ND measure reports erroneous distances, and the ComGrad measure overestimates distances because it calculates distances along with vector field flow estimated after applying the distance transform and the Gaussian derivative filter. For the fold-like curve, the ND and ComGrad measures fall short. These experimental results show that BLD is the best for measuring differences between contours, succeeding in cases where other measures fail.

III.C. Application to three-dimensional structures

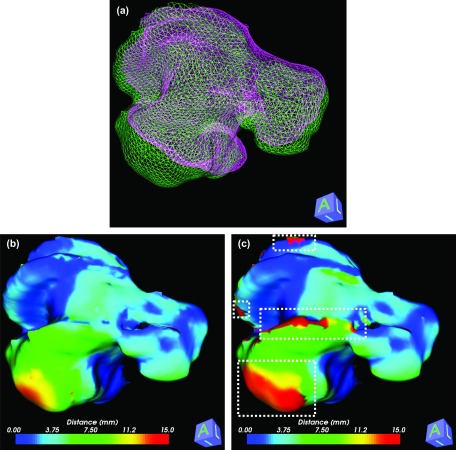
BLD measure is used to quantify organ deformation after rigid-body image registrations. Two clinical cases are used for this test: a liver case shown in Fig. 5 and a head-and-neck case shown in Fig. 6. Figure 5(a) shows 3D mesh models that are generated from the contours. Two 3D livers are reconstructed from the first and second plans. The first plan is set as a reference for both cases. Therefore, the measured distances are mapped on the mesh surface from the first plan. Distances are measured using our proposed BLD measure and the ND measure as shown in Figs. 5(b) and 5(c), respectively. Although a mesh smoothing scheme is utilized to get a better result for the ND measure, the ND measure does not calculate reasonable distances in areas of sharp edged corners and strongly winding curves. Problematic regions for the ND measure are marked as white-dashed boxes in Fig. 5(c). The Hausdorff distance between two surfaces is 29 mm, which means the global maximum discrepancy between two surfaces is 29 mm. Therefore, it is unreasonable a distance measure reports a local distance greater than 29 mm. BLD measured in these areas are 29 mm or less. ND measure reported the distance in these areas up to 117 mm.

FIG. 5.

Two liver contours from two treatment plans are constructed as mesh structures. After rigid-body image registration and smoothing are performed, BLD and ND distances are displayed in a color map. (a) Two 3D livers are reconstructed from the first and second plans. (b) BLD measure and (c) ND measure. BLD measure reports distances in these areas up to 29 mm. However, ND measure calculates the distances in these areas up to 117 mm. [URL: http://dx.doi.org/10.1118/1.4754802.1]Download video file ^{(12.6MB, avi)} DOI: 10.1118/1.4754802.1

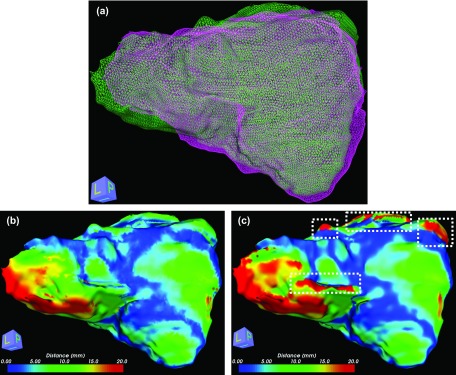
FIG. 6.

Distances between two clinical target volumes from two head-and-neck treatment plans are measured. Distances between contours are displayed in a color map after rigid-body image registration and smoothing. (a) 3D CTV structures from the head-and-neck case. Two 3D head-and-neck cases are reconstructed from the first and second plans. (b) BLD measure and (c) ND measure. The maximum distance measured by BLD measure is 17 mm, but ND measure reported the maximum distance of 32 mm.

For the head-and-neck case, our proposed BLD measure outperforms ND measure. Problematic regions for ND measure are shown in white-dashed box in Fig. 6(c). The problematic regions observed are similar to the 2D case (Case 3) in Fig. 4 at the outer tip of the horse shoe shape. The Hausdorff distance for the head-and-neck case is 17 mm. The maximum distance measured by BLD measure is 17 mm, but ND measure reported the maximum distance is 32 mm.

Distance histograms from three distance measures are compared as shown in Fig. 8(a). The MD measure shows higher frequency in short distances because it searches the closest points. On the contrary, the ND measure reports erroneous distances beyond 30 mm (compressed on the graph at the distance 30 mm for readability) at the locations of severe curvature. The BLD measure does not show abnormal frequency at any distances.

FIG. 8.

Distances between two contours displayed as histograms. Three different distance measures are applied to the same contours. (a) Distance histogram comparison without smoothing—the MD measure showed high frequency at short distances and the ND measure shows erroneous measurements beyond 30 mm (compressed at 30 mm for readability) not observed in other histograms calculated using other measures. (b)–(d) Analyses are performed following three different levels of volume surface smoothing.

III.D. Effect of smoothing organ volumes on distance measurements

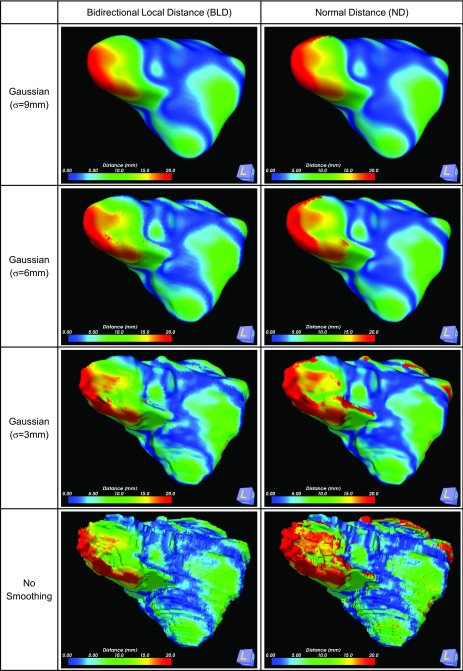
Recursive Gaussian smoothing is applied to the liver volume using three different sigma values (3, 6, and 9 mm). Measured distances between contours using two distance measure techniques are displayed in a color map as shown in Fig. 7, and plotted as histograms in Figs. 8(b)–8(d). The distribution of distances between three different levels of smoothing changed insignificantly when our proposed BLD measure is used. However, ND measure showed recognizable changes in the distribution of distances. In Fig. 7 the distance map between BLD and ND measures are shown for three different levels of Gaussian smoothing. Changes in calculating the larger displacement distances (red colored area) are less obvious when our proposed measure is used compared to ND measure. Even when a severe smoothing (σ = 9 mm) is applied, 1.1% (295 points among 25 854 points) of the surface points could not find the corresponding surface point when using ND measure. Without smoothing, 4.2% (1759 points among 41 745 points) of the total surface points could not find the normal distance. This does not happen when using the MD technique or the BLD technique.

FIG. 7.

The effect of Gaussian smoothing is compared between our proposed BLD measure and the ND measure.

Distance histograms are compared between three distance measures after three different smoothings are performed as shown in Fig. 8. Changes in distance distributions are investigated. MD measure shows the more variations in short distance distributions. ND measure shows more variations among larger distance distribution. Our proposed BLD measure shows the least changes in both short and long distance distributions.

III.E. A standard deviation surface map generated using the BLD measure

Standard deviation maps as a probability distribution has been proposed to measure the variability or dispersion of multiple contours.⁸ For example, the portion of a prostate contour with a low standard deviation means that the multiple contours tend to be very close to the mean, whereas a high standard deviation indicates that contours are spread out or disagree with each other in that region. Figure 9(a) shows multiple manually delineated contours and Fig. 9(b) indicates the standard deviation map at each circumferential point along the average contour. The contour in Fig. 9(b) is the average contour calculated from the multiple contours, and the color map represents the standard deviation. Red color representing a high standard deviation means the contours are spread out.

FIG. 9.

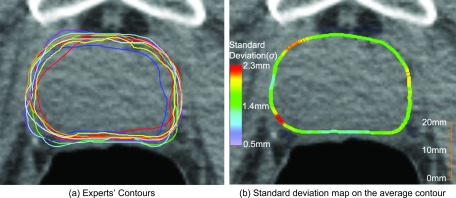
A standard deviation map built from nine expert's contours for a prostate. (a) Nine expert's contours. (b) Standard deviation map.

IV. DISCUSSIONS AND CONCLUSION

To accurately quantify the local difference between two contour surfaces in two- or three-dimensional space, one must use a measure that is both accurate and robust. Minimum distance measure and normal distance measure report erroneous results in high degrees of curvature, and ComGrad measure cannot estimate correct distances in concave and folded curves. Smoothing surfaces improves the ND measure performance but changes the surface shape of the contour.

Our bidirectional local distance measure can measure the distance between contours for many complicated organ shapes, which is not possible with the ND measure. As shown in Figs. 3 and 4, ND measure can overestimate distances between contours. Although the BLD is asymmetric, it can find the most realistic and reasonable distance for complicated contours compared to existing methods. Furthermore, smoothing is not required for BLD analysis.

Applications of the BLD measure include accuracy analysis of atlas-based automatic segmentations, and organ deformation measurements in radiation therapy. During image guided radiation therapy, target(s) can be tracked, and their position and shape variation can be analyzed using BLD analysis. Planning target volumes can thus be examined to determine adequate coverage. Metastudy analysis of large databases of contours can be mined for future medical studies with a high degree of confidence. Applications using BLD measure can be expanded to 3D model analysis, computer graphics, and pattern recognition in engineering.