Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2014 Jul 17;5:4402. doi: 10.1038/ncomms5402

Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum

Lihua Wang 1,6, Jiao Teng 2,6, Pan Liu 3,6, Akihiko Hirata 3, En Ma 4,a, Ze Zhang 1,5,b, Mingwei Chen 3, Xiaodong Han 1,c
PMCID: PMC4109021  PMID: 25030380

Abstract

Grain rotation is a well-known phenomenon during high (homologous) temperature deformation and recrystallization of polycrystalline materials. In recent years, grain rotation has also been proposed as a plasticity mechanism at low temperatures (for example, room temperature for metals), especially for nanocrystalline grains with diameter d less than ~15 nm. Here, in tensile-loaded Pt thin films under a high-resolution transmission electron microscope, we show that the plasticity mechanism transitions from cross-grain dislocation glide in larger grains (d>6 nm) to a mode of coordinated rotation of multiple grains for grains with d<6 nm. The mechanism underlying the grain rotation is dislocation climb at the grain boundary, rather than grain boundary sliding or diffusional creep. Our atomic-scale images demonstrate directly that the evolution of the misorientation angle between neighbouring grains can be quantitatively accounted for by the change of the Frank–Bilby dislocation content in the grain boundary.

Inline graphicGrain rotation is proposed as an active deformation mechanism in nanocrystalline metals at room temperature. Here, during in-situ atomic scale experimentation, the authors observe that grains with a size <6 nm deform by coordinated rotation of multiple grains, associated with dislocation climb at grain boundaries.

Grain rotation is a well-known phenomenon for polycrystalline materials during deformation at high (homologous) temperatures1,2,3,4,5,6,7,8. It is also common during annealing and recrystallization in polycrystalline materials9,10,11. The proposed mechanisms mediating grain rotation include intra-grain dislocation processes (that is, the cross-grain glide of a large number of dislocations that re-orient the grains with respect to surrounding grains2), diffusive mechanisms3,4 as well as sliding5,6,7,8 at the grain boundaries (GBs). In recent years, grain rotation has also been proposed as a plasticity phenomenon at low temperatures (for example, room temperature for metals), especially for nanocrystalline (NC) grains with a very small diameter (d)12,13,14,15,16,17,18,19,20,21. In the latter case, however, the underlying mechanism remains unclear: the glide of cross-grain dislocations is expected to subside in such tiny grains12,13,14,15,22,23,24,25,26,27,28,29,30,31,32,33, and diffusional processes may also be insufficient to mediate fast GB sliding at room temperature. Then how can grain rotation be realized to carry plasticity in such an NC system?

The classical theories developed in the 1950’s and later9,34,35,36,37 stipulate that such low-temperature grain rotation (that is, change of the misorientation angle between grains but not the apparent grain size) can be accomplished primarily by GB dislocations. However, so far there has been no direct and quantitative experimental evidence to verify that this is indeed the case.

Here, by using a newly developed deformation device in a high-resolution transmission electron microscope (HRTEM), the atomic-scale and dynamic deformation process of NC Pt has been recorded in situ. We show direct and quantitative evidence that when the grain size is below ~6 nm, the plastic deformation mode becomes grain rotation, involving multiple grains in a collective manner. This particular process is mediated by the climb of GB dislocations, rather than cross-grain dislocation slip or GB sliding.

Results

In situ deformation of Pt NC thin film

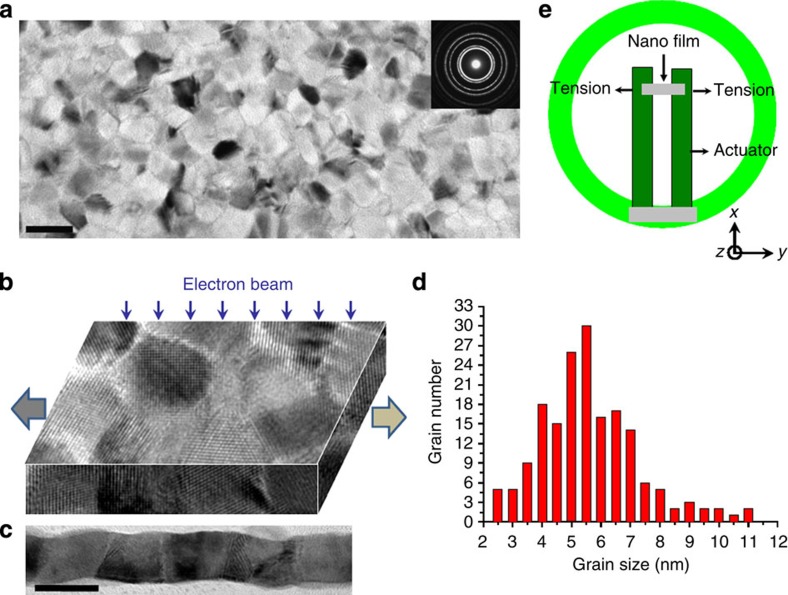
As shown in the bright-field TEM image of Fig. 1a, the Pt film has nanometre-sized and equi-axed grains, with no obvious texture (see the selected area diffraction patterns in the inset and Supplementary Fig. 1). The HRTEM image in Fig. 1b shows that most grains are separated by high-angle GBs, without visible porosity or micro-cracks. The cross-sectional TEM images indicate that the thin film is ~10 nm in thickness, and consists of one or two grains in the thickness direction (Fig. 1c). The distribution of grain sizes, as measured for ~180 grains, is shown in Fig. 1d. The grain diameters range from 2 to 12 nm and most of the grains have a diameter below 10 nm, with an average d of ~6 nm. Tensile experiments were carried out using our TEM tensile stage as shown in the schematic in Fig. 1e. This special stage allows slow and gentle deformation of the electron-transparent film, and at the same time retains the double-tilt capability such that the grains can be oriented appropriately to a low-index crystallographic zone orientation for high-resolution imaging (see refs 28, 29 for details). The tensile pulling was realized by heating the sample holder to ~80 °C, causing bending of the bimetallic strips due to thermal expansion. The real-time evolution of the film was captured in situ along with deformation, in a JEOL-2010 field-emission TEM operating at 200 kV.

Figure 1. TEM observations of the Pt nanocrystalline thin film.

Figure 1

Open in a new tab

(a) Bright-field transmission electron microscope (TEM) image of the Pt film, with a selected area diffraction pattern in the inset. (b) High-resolution TEM (HRTEM) image showing grains separated by high-angle grain boundaries (GBs). (c) Cross-sectional TEM image of the thin film. (d) Statistical distribution of the grain size. (e) Home-made testing device used for in situ tensile pulling of the Pt thin film in a TEM. Scale bars, 10 nm.

Atomic-scale in situ observation of grain rotation in small grains

Figure 2 is a series of HRTEM images, showing the GB dislocation-mediated grain rotation process observed at the atomic scale. For convenience, we define the in-plane motion about the axis parallel to the electron beam as ‘rotation’ and the out-of-plane rotation around an axis in the film plane as ‘tilt’. We define Gi–j as the GB between grains Gi and Gj. As shown in Fig. 2a, both G1 and G2 exhibit a clear [110] (axis) lattice and the GB angles are 8.3° and 6.4° for G1–2 and G1–3, respectively. In the figure, the double-ended arrow indicates the loading axis, relative to the grains G1, G2 and G3. As revealed in Fig. 2b–d, during the straining, the number of the dislocations at G1–2 increases and the average spacing of the GB dislocations decreases from 3.1 to 1.2 nm. This increased number of GB dislocations leads to the increased misorientation angle of G1–2, from 8.3° to 13.5°, as well as that of G1–3, from 6.4° to 10.6°. No dislocations were observed inside the small grains throughout the deformation process. During the straining, G1 and G2 exhibit no obvious lattice fringe change, indicating that the grain rotation is not caused by a global tilt of specimen during deformation.

Figure 2. HRTEM images taken at different points of time showing the GB dislocation-mediated grain rotation.

Figure 2

Open in a new tab

(a) Two GB dislocations (as marked with ‘T’) at GB1–3. (b–d) During straining, the number of the dislocations increased, leading to the GB angle at G1–2 increasing from 8.3° to 13.5°. Scale bars, 2 nm.

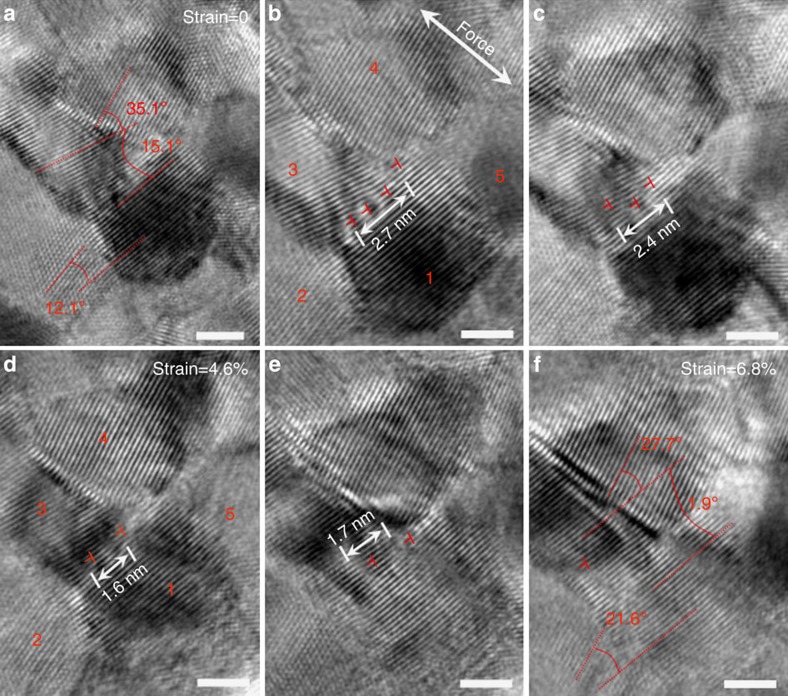
As the grain size decreases, the grain rotation is more obvious. Figure 3 is a series of HRTEM images, showing the GB dislocation-mediated grain rotation process at the atomic scale. Figure 3a highlights five grains (d~5 nm, marked as ‘1’ to ‘5’), separated by high-angle GBs. During the straining, G3 and G4 exhibit no obvious fringe change, indicating that there is no global tilt and shift of the specimen during deformation. The double-ended arrow in Fig. 3b indicates the loading axis. The GB angles are 12.1°, 15.1° and 35.1° for G1–2, G1–3 and G3–4, respectively. As noted with ‘T’ in Fig. 3a, an array of GB dislocations can be seen at G1–3. As shown in Fig. 3b–f, during the in situ straining, the number of the dislocations at G1–3 decreases and the average spacing of the GB dislocations increases from 0.9 to 1.7 nm. This corresponds to a reduced misorientation angle at G1–3, decreasing from 15.1° to 1.9°. Figre. 3e,h show that the GB dislocations have climbed towards the triple junction (TJ) points, and the dislocation annihilation/absorption in the TJ (or other GBs) is the reason of the decrease in the number of GB dislocations. For G1–3, the GB angle increased from 12.1° to 21.6°, while that for the G3–4 decreased from 35.1° to 27.7°. Here again, no intra-grain dislocations were observed inside these tiny grains throughout the deformation process. It is noted that G1 rotates about 9.5° with respect to G2 but 13.2° with respect to G3. If only G1 underwent the rotation process, the rotation angle of G1 with respect to others would be the same. We also measured the rotation angles of G1–4, G2–4 and G2–3. The rotation angles all exhibited different values. This indicates that these grains underwent a simultaneous rotation process, that is, they all participated in rotations relative to one another in a coordinated manner during straining. A number of in situ observations consistently show that for those grains surrounded by small grains, they underwent collective rotation together (Supplementary Tables 1 and 2, and Supplementary Fig. 2). For the grains surrounded by large grains, only the smaller grains underwent rotation (see next paragraph, Supplementary Table 3 and Supplementary Figs 3 and 4).

Figure 3. Atomic-scale in situ observation of grain rotation in smaller grains.

Figure 3

Open in a new tab

(a) An array of dislocations (as marked with ‘T’) forms a wedge-shaped disclination at the GB. (b–e) During straining, the number of the dislocations decreases, leading to decreasing GB angle G1–3. (e,f) The dislocation number decreases, caused by the GB dislocations climbing into the TJs or other GBs. Meanwhile, the GB angle at G1–2 increased from 12.1° to 21.6°. Scale bars, 2 nm.

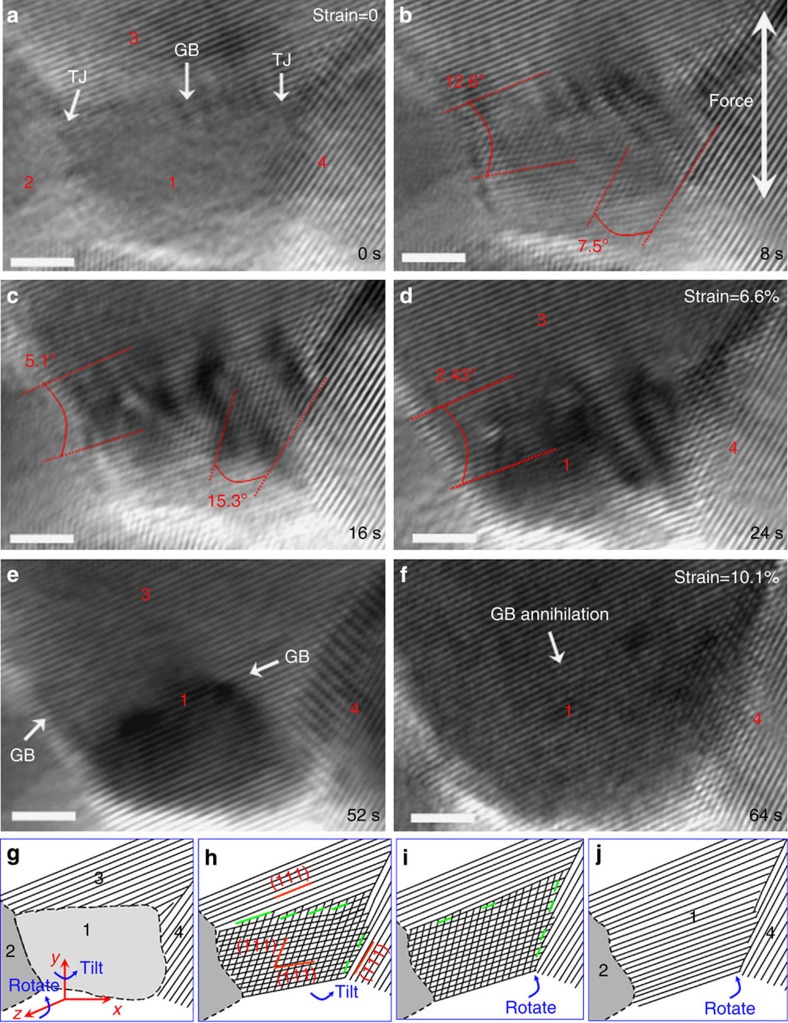
Figure 4 presents a series of HRTEM images, showing another scenario for the rotation of a small grain, which underwent not only rotation but also tilt. As described above, the small grain G1 (d=4.8 nm) clearly exhibits GB dislocation-mediated grain rotation. In a larger grain, G4 (d>10 nm), full dislocations were frequently observed28,29, in lieu of grain rotation. During straining, no change was observed for the lattice/fringe in grains G3 and G4 (Supplementary Figs 3 and 4), indicating that there was no rotation/tilt between G3 and G4. In comparison, the contrast of the G1 grain, and the GB structure of G1–3 and G1–4, changed quickly. From Fig. 4a, G1 is surrounded by high-angle GBs: no fringes were observed in G1, while G3 and G4 exhibit obvious fringes. The TJs are indicated by arrows. With increasing straining, we observed a clear [110] (axis) lattice (Fig. 4b) in G1, and the GB angles are 12.6° and 7.5° for G1–3 and G1–4 (they changed into small-angle GBs), respectively. This is obviously caused by the tilting of G1, together with GB structural changes. On further loading, the lattice in G1 changed into fringes and then became the same as the grain G3 (Fig. 4c–f), involving both in-plane and out-of-plane grain re-orientation. The G1–3 changed from a high-angle GB to a small-angle GB and then disappeared, and the TJ changed into a GB. For G1–4, it changed from a small-angle GB (7.5° in Fig. 4b) to a high-angle GB (15.3° in Fig. 4c). Although the angle of G1–3 cannot be measured after Fig. 4c, it continued to increase because of the rotation and tilt of the grain G1. In Fig. 4d,e, G1–4 shows the features of a typical high-angle GB. Figure 4g–j presents the schematic view corresponding to Fig. 4a–f, for illustrating the rotation process of G1. As illustrated in Fig. 4g,h, the rotation and tilting of G1 led to the appearance of lattice fringe in the image. The G1–3 and G1–4 consist of arrays of GB dislocations (as marked in green lines). With extensive deformation, G1 rotated via GB dislocation motion and annihilation. The GB angles decreased (or increased) as the dislocation number changed, as shown in Fig. 4h,i. The continued rotation and tilting of G1 eventually led to the merge of the grain as the GB in between and the TJ disappear (Fig. 4j). Here, G1 was surrounded by relatively large grains (such as G2, G3 and G4). We can see that the rotation angle of G1 with respect to G3 and G4 is the same, while the rotation angle of G3 with respect to G4 is nearly zero. Thus, only G1 underwent the rotation process during deformation (Supplementary Table 3).

Figure 4. In situ observation of the grain rotation for a 4.8 nm × 6.8 nm sized grain.

Figure 4

Open in a new tab

The white arrow in b indicates the loading axis. In a, G1 is surrounded by high-angle GBs. (b,c) With straining, G1 exhibits the [110] lattice, and the GB G1–3 and G1–4 have changed into small-angle GBs. (d,e) With further straining, the [110] axial-lattice in G1 changed into fringes. (f) The GB G1–2 disappeared and G1–4 extended to become a long GB. (g–j) Schematics corresponding to a–f to illustrate the rotation process of G1 under tensile stress. Scale bars, 2 nm.

We also used black lines drawn on the {111} planes in grains G1, G3 and G4 to reveal the details of the GB dislocation-mediated grain rotation. These dark lines were derived from the actual atomic positions visible in HRTEM images to indicate an array of dislocations at G1–3. During straining, the number of dislocations at G1–3 decreased along with the increased average spacing of the GB dislocations. This gradually decreased the GB angle of G1–3 until its final annihilation (Supplementary Fig. 5a–c,f–h). For G1–4, the number of dislocations in the GB increased, leading to an increasing GB angle (Supplementary Fig. 5d,e,i,j). During the rotation process, the GB dislocations adjusted their spacing by climbing along the GBs concurrently, with increasing/decreasing number of GB dislocations. Meanwhile, the GB angle continuously changed. The dislocations climbed short distances to GB TJs and free surfaces, with no obvious cross-grain dislocation glide.

Grain rotation and Frank–Bilby equation

Clearly, the low-temperature grain rotation is not mediated by cross-grain glide of a large number of dislocations that re-orient the grain with respect to the surrounding grains35,38,39, nor diffusional creep processes12,13,14,15,17 and GB sliding17,18. Instead, the grain rotation is found to be accomplished primarily by the change in the content of GB dislocations34,35,36,37. Such an evolution of GB dislocations is expected to cause a change in the GB angle between neighbouring grains, as indicated by the well-known Frank–Bilby equation36,37:

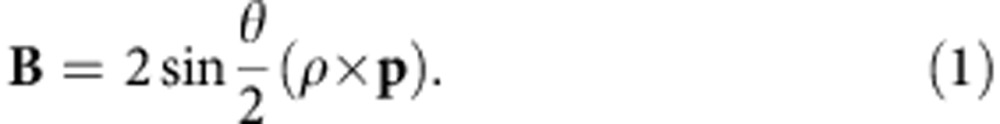graphic file with name ncomms5402-m1.jpg

Here we choose a proper vector p (lying in the GB) such that the Burgers circuit encloses all the GB dislocations. B is the sum of the Burgers vectors of the GB dislocations, θ is the GB angle and ρ is the rotation axis (|ρ|). According to equation (1), an increase in the number of GB dislocations would lead to increased B, and consequently increased GB angle θ. Conversely, decreasing the number of GB dislocations would reduce B and hence θ. This picture is exactly what we observe under the Cs-corrected HRTEM (see figures and discussions above).

Let us now consider the GB dislocations visualized in our HRTEM images, which are responsible for the in-plane rotation. Then, p is perpendicular to ρ. The Frank–Bilby equation can be written as:

graphic file with name ncomms5402-m2.jpg

Here, b is the edge component of the Burgers vectors, ~0.243 nm, and h is the average dislocation spacing. We can then compare the prediction by equation (2) with our experimental observation. From Fig. 3b–e, the measured average dislocation spacing is 0.9, 1.2, 1.6 and 2.0 nm, respectively. The calculated GB angle is correspondingly 15.5°, 11.6°, 8.7° and 7.0°, respectively, which is very consistent with the measured GB angles (15.1°, 11.2°, 8.5° and 7.2°, respectively). From Fig. 4b,c, the measured average dislocation spacing for GB1–3 is 1.06 and 2.25 nm. The calculated GB angle is then 13.2° and 6.2° for GB1–3, also close to the HRTEM measurements of 12.6° and 5.1°. For GB1–4, the measured average dislocation spacing is 1.95 and 1.10 nm. The calculated GB angle is 7.1° and 12.7° for GB1–4, consistent with the measured GB angle of 7.5° and 15.3° (see summary in Supplementary Table 4). It should be noted that for the above application of the Frank–Bilby equation, we only examine the dislocation Burgers vector perpendicular to the tilt GB plane, that is, the edge component of the Burgers vectors, because the screw component of the Burgers vectors cannot be detected and quantified in the HRTEM images. The edge component leads to the rotation, while the screw component (parallel to the GB plane) leads to tilt.

In the current study, the mis-orientation angle between grains was defined as the angle between the corresponding lattices of two nearest neighbouring grains observed in the HRTEM imaging. The statistics of the mis-orientation angle distribution of the observed nearest neighbouring grains (that is, 215 nearest neighbouring grain pairs) shows that the GB with mis-orientation angles ranging from 8° to 35° are the high-frequency ones (Supplementary Fig. 6). For high-angle GBs (larger than 15°, per Brandon’s criterion), we also observed collective grain rotation without obvious GB sliding and migration (Fig. 3). This suggests that high-angle GB can also undergo rotation; the mechanism may be similar to that of low-angle GBs, but could also be assisted by possible GB atomic diffusion and shuffling.

Cross-grain dislocation-mediated plasticity in larger grains

For larger grains, on loading we frequently observed movements and interactions of cross-grain dislocations. Figure 5a provides a typical HRTEM observation of full dislocation (marked with ‘T’) in a ~11-nm-sized grain, with a Burgers vector of a/2[011]. For d between 6 and 10 nm, full dislocations become much less, and stacking faults resulting from the passage of partial dislocations (as noted by the arrows in Fig. 5b) become more frequent. In fact, >100 grains (with d from 3 to ~25 nm) were monitored during and at the end of the pulling. These include 48 in situ examples, and the others are ex-situ ones (see the many examples in Supplementary Figs 2–11). There is a clear trend with decreasing d: the dislocations in action transition from full to partial inside the grains, and eventually to those in the GB to mediate grain rotation. The mechanisms are depicted schematically in Supplementary Fig. 12. The former (cross-grain dislocation) mechanism has been treated in many previous studies, so our data in that regard are only displayed in Supplementary Materials for interested readers.

Figure 5. HRTEM images show the intra-grain dislocations in larger grains.

Figure 5

Open in a new tab

(a) Full dislocation (marked with ‘T’) in a ~11-nm-sized grain. (b) Partial dislocations resulting in stacking faults (as noted by the arrows) in an ~7-nm-sized grain. Scale bars, 2 nm.

Discussion

The GB dislocation-mediated grain rotation described here is different from that reported in several earlier experiments on NC metals. In Au with d~20 nm (ref. 38), the grains are sufficiently large that the cross-grain dislocation activities were active and led to the formation of disclinations that move to the GBs. Murayama et al.39 observed disclination dipoles in bcc Fe and suggested that they may facilitate the re-orientation of grains. Such disclination processes and crystal lattice rotation in the grains are more closely related to grain fragmentation processes38,39. The grain rotations in these cases are the consequence of cross-grain dislocations40,41. In recent MD simulations, GB sliding was found to be the controlling mechanism during compressive deformation of Pt42. A difference between reference42 and our observation is that the GBs in their pillar were relaxed within MD timescale only and the specimens were deformed at high strain rates.

We now discuss why GB dislocation-mediated grain rotation was observed here, in lieu of GB sliding and diffusional creep. Our experiments were carried out at ~353 K (far below the melting point of Pt, Tm=2045 K). At such low temperatures, the GB sliding and diffusional creep only contributed a strain rate well below our experimental strain rate of ~10−3 s−1. This is different from the cases of Cu and Au, which have much lower melting temperatures, and the GB sliding and diffusional creep contributions could account for most of the strain rate imposed in experiments. See estimates made in Supplementary Discussion. In comparison, the grain rotation mediated by GB dislocation in Pt can result in a much higher strain rate (of the order of ~3 × 10−4 s−1, see Supplementary Discussion). At d<6 nm, the GB dislocations only need short-distance climb to reach nearby TJs along the GB and climb to free surfaces in the thin film specimens. This explains why GB dislocation-mediated grain rotation becomes favourable when the grain size becomes very small.

Our experimental observation of the GB dislocation-controlled grain rotation process involves multiple grains, resembling a grain-switching process in which the coordinates of each individual grain change, as shown in Supplementary Fig. 13. This is reminiscent of the Ashby–Verrall (A–V) grain-switching model43,44,45. However, in the A–V model, the switching process is through translational movement of an assembly of grains via GB diffusion, rather than rotation via inter-grain dislocation activities only. In the A–V model, the dislocation density along GB does not change dramatically, due to additional help from diffusion and the translational character of the sliding. Our grain rotation is largely of geometry-necessary character with the change in GB dislocation density as the main mechanism, which may be assisted by GB atomic diffusion and shuffling. Although various GB deformation mechanisms have been explored by many groups both experimentally and computationally11,17,18,21,22,23,24,25,26,46,47,48, our results provide for the first time a direct, atomic-scale and quantitative experimental proof that GB dislocation-mediated grain rotation can be active in NC metals near room temperature.

Our thin film samples have bottom and top free surfaces and are only a couple of grains thick. A conceivable role of the free surfaces is to enhance atomic diffusion, and dislocation nucleation and climb49,50,51. The very thin films with large free surface areas may have facilitated grain rotation in the current study. For thick samples, grain rotation may still occur via GB dislocations, but may require more accommodation from GB atomic diffusion and shuffling. Recently, the A–V deformation mode was also suggested by MD simulation in both thin films and three-dimensional NC samples44,45: even when the samples have more than five grains in the thickness direction, grain rotation can still occur via GB dislocations assisted by GB atomic diffusion and shuffling.

In conclusion, using in situ atomic scale straining inside TEM, we have captured atomic-scale images of the dynamic processes of grain rotation in Pt nanograins. Our work focuses on a grain size regime (d<~6 nm) hitherto rarely explored in experiments. In this regime, cross-grain dislocations subside while grain rotation becomes the most prevalent mode. This is a new room-temperature plasticity process in NC metals with extremely small grains, as the grain rotation in this case is found to be mediated by the climb and absorption/generation of Frank–Bilby dislocations in the GB, distinct from the previously proposed mechanism of GB sliding or diffusional creep (e.g., Coble creep). Moreover, our observation has general significance in physical metallurgy, as it directly illustrates for the first time the grain rotation via GB dislocations in a quantitative way consistent with the Frank–Bilby equation. Specifically, the difference in grain orientation (increase or decrease of GB misorientation angle) is entirely accounted for by a change in the density of GB dislocations.

Methods

In situ TEM tensile device

The TEM extensor is made of two thermally actuated bimetallic strips. They were fixed, in opposing positions, on a TEM Cu-ring grid, using superglue or epoxy resin. Each bimetallic strip is made of two layers of different materials (Mn72Ni10Cu18 and Fe-Ni36 alloys) that have a large mismatch in thermal expansion coefficient (26 × 10−6 and 2.9 × 10−6 K−1, respectively), to achieve a significant deflection at relatively low operation temperatures. A significant deflection was clearly visible under gentle heating conditions. The conventional TEM specimen holder (hot stage), now with the bimetallic strips, can therefore act as a double tilt, displacement controlled, deformation stage. The tensile straining of the Pt film was carried out at an estimated strain rate of 10−3~10−4. The two bimetallic strips, heated to <80 °C (read from the controller of the sample holder), bent in opposite directions to provide the tensile pulling force.

Transferring thin film to the tensile devices

A Pt thin film ~10 nm in thickness was deposited on a (001)-oriented NaCl single crystal substrate (3 × 3 cm2) at 300 °C by magnetron sputtering. Operated under optical microscope, the bimetallic extensors (two metallic bars) can be well aligned to be vertical to the thin film samples. Using epoxy resin on the surfaces of the bimetallic extension actuator, the thin films can be attached on the surface of the extensor in almost ideal geometrical configuration. Thus, the uni-axiality of the deformation can be ensured during loading process. Dissolving away the NaCl substrate, free-standing bimetallic strips together with thin film tensile samples are released for loading onto the TEM-tensile stage. During TEM observation, the temperature controller can accurately increase the temperature of the TEM-tensile stage for the bimetallic actuator to exert uniaxial tensile force on the thin films.

GB angle measurement method

With our double-tilt in situ tensile testing device for TEM, lattice fringe images are easily observed for properly oriented grains. Because of the small scattering angle for electron diffraction, fringe images can be observed for those crystal planes with normal perpendicular to the incident beam direction. The grain rotation (angles) were tracked by grain lattice (fringes) rotation, revealed in HRTEM images. No intra-grain dislocations were revealed in this grain lattice rotation process, and perfect linearity of the grain lattices/fringes were preserved through the grain rotation. It is therefore believed that the rotation is a whole grain rotation. This technique works very well, as long as the axis of rotation is nearly parallel to the electron beam and film normal; otherwise, the lattice fringes will go out of contrast as the diffracting planes are rotated away from the beam.

Author contributions

L.H.W., J.T. and P.L. contributed equally to this work. X.D.H., Z.Z. and E.M. designed the project and guided the research. L.H.W., P.L. and A.H. conducted the in situ TEM experiments under the guidance of X.D.H. and M.W.C. J.T synthesized the thin films. X.D.H. and E.M. wrote the manuscript. All authors contributed to the extensive discussions of the results.

Additional information

How to cite this article: Wang, L. et al. Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum. Nat. Commun. 5:4402 doi: 10.1038/ncomms5402 (2014).

Supplementary Material

Supplementary Information

Supplementary Figures 1-13, Supplementary Tables 1-5, Supplementary Discussion and Supplementary References

ncomms5402-s1.pdf (1.5MB, pdf)

Acknowledgments

This work was supported by the National Natural Science Foundation (11234011, 11127404 and 10102001201304), the Beijing PXM201101420409000053 and Beijing 211 Project, and Specialized Research Fund for the Doctoral Program of Higher Education of China (3C102001201301). E.M. was supported at JHU by Materials Sciences and Engineering Division, Office of Basic Energy Sciences (BES), US Department of Energy (DOE, DE-FG02-09ER46056). M.W.C. was sponsored by ‘World Premier International (WPI) Research Center Initiative for Atoms, Molecules and Materials’, MEXT, Japan.

References

  1. Nieh T. G., Wadsworth J. & Sherby O. D. Superplasticity in Metals and Ceramics Cambridge University Press (1997). [Google Scholar]
  2. Gifkins R. C. Grain-boundary sliding and its accommodation during creep and superplasticity. Metall. Trans. A 7, 1225–1232 (1976). [Google Scholar]
  3. Nabarro F. R. N. Steady state diffusional creep. Phil. Mag. A. 16, 231–237 (1967). [Google Scholar]
  4. Herring C. Diffusional viscosity of a polycrystalline solid. J. Appl. Phys. 21, 437–445 (1951). [Google Scholar]
  5. Lee D. The strain rate dependent plastic flow behavior of zirconium and its alloys. Metall. Trans. 1, 1607–1617 (1970). [Google Scholar]
  6. Ashby M. F., Edward G. H., Davenport J. & Verrall R. A. Application of bound theorems for creeping solids and their application to large strain diffusional flow. Acta Metall. 26, 1379–1388 (1978). [Google Scholar]
  7. Zelin M. G. & Mukherjee A. K. Geometrical aspects of superplastic flow. Mater. Sci. Eng. A 208, 210–225 (1996). [Google Scholar]
  8. Matsuki K., Morita H., Yamada M. & Murakami Y. Relative motion of grains during superplastic flow in an Al-9Zn-l wt.%Mg alloy. Met. Sci. 11, 156–163 (1977). [Google Scholar]
  9. Li James C. M. Possibility of subgrain rotation during recrystallization. J. Appl. Phys. 33, 2958–2965 (1962). [Google Scholar]
  10. Humphreys F. J. & Hatherly M. Recrystallization and Related Annealing Phenomena Elsevier Science (1995). [Google Scholar]
  11. Farkas D., Mohanty S. & Monk J. Linear grain growth kinetics and rotation in nanocrystalline Ni. Phys. Rev. Lett. 98, 165502 (2008). [DOI] [PubMed] [Google Scholar]
  12. Yip S. The strongest size. Nature 391, 532 (1998). [Google Scholar]
  13. Yamakov V., Wolf D., Phillpot S. R., Mukherjee A. K. & Gleiter H. Deformation-mechanism map for nanocrystalline metals by molecular dynamics simulation. Nat. Mater. 3, 43–47 (2004). [DOI] [PubMed] [Google Scholar]
  14. Greer J. R. & De Hosson J. T. M. Plasticity in small-sized metallic systems: intrinsic versus extrinsic size effect. Prog. Mater. Sci. 56, 654–724 (2011). [Google Scholar]
  15. Schiotz J., Di Tolla F. D. & Jacobsen K. W. Softening of nanocrystalline metals at very small grain sizes. Nature 391, 561–563 (1998). [Google Scholar]
  16. Schiotz J. & Jacobson K. W. A maximum in the strength of nanocrystalline copper. Science 301, 1357–1359 (2003). [DOI] [PubMed] [Google Scholar]
  17. Cahn J. W. & Taylor J. E. A unified approach to motion of grain boundaries, relative tangential translation along grain boundaries, and grain rotation. Acta Mater. 52, 4887–4898 (2004). [Google Scholar]
  18. Swygenhoven H. V. & Derlet P. M. Grain-boundary sliding in nanocrystalline fcc metals. Phys. Rev. B 64, 224105 (2001). [Google Scholar]
  19. Wolf D., Yamakov V., Phillpot S. R., Mukherjee A. & Gleiter H. Deformation of nanocrystalline materials by molecular-dynamics simulation: relationship to experiments? Acta Mater. 53, 1–40 (2005). [Google Scholar]
  20. Chokshi A. H., Rosen A., Karch J. & Gleiter H. On the validity of the hall-petch relationship in nanocrystalline materials. Scripta Metall. 23, 1679–1683 (1989). [Google Scholar]
  21. Farkas D., Mohanty S. & Monk J. Strain-driven grain boundary motion in nanocrystalline materials. Mater. Sci. Eng. A 493, 33–40 (2008). [Google Scholar]
  22. Shan Z. W. et al. Grain boundary–mediated plasticity in nanocrystalline nickel. Science 305, 654–657 (2004). [DOI] [PubMed] [Google Scholar]
  23. Chen M. W. & Yan X. Q. Comment on ‘‘Grain boundary–mediated plasticity in nanocrystalline nickel’’. Science 308, 356C (2005). [DOI] [PubMed] [Google Scholar]
  24. Rupert T. J., Gianola D. S., Gan Y. & Hemker K. J. Experimental observations of stress-driven grain boundary migration. Science 326, 1686–1689 (2009). [DOI] [PubMed] [Google Scholar]
  25. Jin M., Minor A. M., Stach E. A. & Morris J. W. In situ TEM observations of fast grain-boundary motion in stressed nanocrystalline aluminum films. Acta Mater. 52, 5381–5387 (2004). [Google Scholar]
  26. Legros M., Gianola D. S. & Hemker K. J. In situ TEM observations of fast grain-boundary motion in stressed nanocrystalline aluminum films. Acta Mater. 56, 3380–3393 (2008). [Google Scholar]
  27. Chen M. W. et al. Deformation twinning in nanocrystalline aluminum. Science 300, 1275–1277 (2003). [DOI] [PubMed] [Google Scholar]
  28. Wang L. H., Zhang Z. & Han X. D. In situ experimental mechanics of nanomaterials at the atomic scale. NPG Asia Mater. 5, e40 (2012). [Google Scholar]
  29. Wang L. H. et al. In situ observation of dislocation behavior in nanometer grains. Phys. Rev. Lett. 105, 135501 (2010). [DOI] [PubMed] [Google Scholar]
  30. Wang L. H., Zhang Z., Ma E. & Han X. D. Transmission electron microscopy observations of dislocation annihilation and storage in nanograins. Appl. Phys. Lett. 98, 051905 (2011). [Google Scholar]
  31. Milligan W. W., Hackney S. A., Ke M. & Aifantis E. C. In situ studies of deformation and fracture in nanophase materials. Nanostruct. Mater. 2, 267–276 (1993). [Google Scholar]
  32. Hugo R. C., Kung H. J. R., Weertman R. M., Knapp J. A. & Follstaedt D. M. In-situ TEM tensile testing of DC magnetron sputtered and pulsed laser deposited Ni thin films. Acta Mater. 51, 1937–1943 (2003). [Google Scholar]
  33. Youssef K. M., Scattergood R. O., Murty K. L., Horton J. A. & Koch C. C. Ultrahigh strength and high ductility of bulk nanocrystalline copper. Appl. Phys. Lett. 87, 091904 (2005). [Google Scholar]
  34. James C. M. L. Mechanical grain growth in nanocrystalline copper. Phys. Rev. Lett. 96, 215506 (2006). [DOI] [PubMed] [Google Scholar]
  35. Ovid’ko I. A. & Sheinerman A. G. Special rotational deformation in nanocrystalline metals and ceramics. Scripta Mater. 59, 119–122 (2008). [Google Scholar]
  36. Frank F. C. A Symposium on the Plastic Deformation of Crystalline Solids Office of Naval Research: Pittsburgh, 150 (1950). [Google Scholar]
  37. Bilby B. A., Bullough R. & Smith E. Continuous distributions of dislocations: a new application of the methods of non-riemannian geometry. Proc. R. Soc. Lond. A 231, 263–273 (1955). [Google Scholar]
  38. Liu P., Mao S. C., Wang L. H., Han X. D. & Zhang Z. Direct dynamic atomic mechanisms of strain-induced grain rotation in nanocrystalline, textured, columnar-structured thin gold films. Scripta Mater. 64, 343–346 (2011). [Google Scholar]
  39. Murayama M., Howe J. M., Hidaka H. & Takaki S. Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe. Science 295, 2433–2435 (2002). [DOI] [PubMed] [Google Scholar]
  40. Gutkin M. Y., Ovid’ko I. A. & Skiba N. V. Crossover from grain boundary sliding to rotational deformation in nanocrystalline materials. Acta Mater. 51, 4059–4071 (2003). [Google Scholar]
  41. Ovid’ko I. A. Super plasticity and ductility of superstrong nanomaterials. Rev. Adv. Mater. Sci. 10, 89–104 (2005). [Google Scholar]
  42. Gu X. W. et al. Size-dependent deformation of nanocrystalline Pt nanopillars. Nano Lett. 12, 6385–6392 (2012). [DOI] [PubMed] [Google Scholar]
  43. Ashby M. F. & Verrall R. A. Diffusion-accommodated flow and surperplasticity. Acta Metall. 21, 149–163 (1973). [Google Scholar]
  44. Kumar S., Li X. Y., Haque A. & Gao H. J. Is stress concentration relevant for nanocrystalline metals? Nano Lett. 11, 2510–2516 (2011). [DOI] [PubMed] [Google Scholar]
  45. Shimokawa T., Nakatani A. & Kitagawa H. Mechanical properties depending on grain size of face-centered-cubic nanocrystalline metals using molecular dynamic simulation. JSME Int. J. Ser. A 47, 83–91 (2004). [Google Scholar]
  46. Trautt Z. T. & Mishin Y. Grain boundary migration and grain rotation studied by molecular dynamics. Acta Mater. 60, 2407–2424 (2012). [Google Scholar]
  47. Hasnaoui A., Swygenhoven H. V. & Derlet P. M. Cooperative processes during plastic deformation in nanocrystalline fcc metals: A molecular dynamics simulation. Phys. Rev. B 66, 184112 (2002). [Google Scholar]
  48. Haslam A. J. et al. Stress-enhanced grain growth in a nanocrystalline material by molecular-dynamics simulation. Acta Mater. 51, 2097–2112 (2003). [Google Scholar]
  49. Gianola D. S., Farkas D., Gamarra M. & He M. R. The role of confinement on stress-driven grain boundary motion in nanocrystalline aluminum thin films. J. Appl. Phys. 112, 124313 (2012). [Google Scholar]
  50. Derlet P. M. & Swygenhoven H. V. The role played by two parallel free surfaces in the deformation mechanism of nanocrystalline metals: a molecular dynamics simulation. Philos. Mag. A 82, 1 (2002). [Google Scholar]
  51. Mompiou F. et al. Inter- and intragranular plasticity mechanisms in ultrafine-grained Al thin films: an in situ TEM study. Acta Mater. 61, 205–216 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-13, Supplementary Tables 1-5, Supplementary Discussion and Supplementary References

ncomms5402-s1.pdf (1.5MB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES