Abstract
Tumors generate physical forces during growth and progression. These physical forces are able to compress blood and lymphatic vessels, reducing perfusion rates and creating hypoxia. When exerted directly on cancer cells, they can increase their invasive and metastatic potential. Tumor vessels - while nourishing the tumor - are usually leaky and tortuous, which further decreases perfusion. Hypo-perfusion and hypoxia contribute to immune-evasion, promote malignant progression and metastasis, and reduce the efficacy of a number of therapies, including radiation. In parallel, vessel leakiness together with vessel compression cause a uniformly elevated interstitial fluid pressure that hinders delivery of blood-borne therapeutic agents, lowering the efficacy of chemo- and nano-therapies. In addition, shear stresses exerted by flowing blood and interstitial fluid modulate the behavior of cancer and a variety of host cells. Taming these physical forces can improve therapeutic outcomes in many cancers.
Keywords: tumor microenvironment, vessel compression, tumor perfusion, vascular hyper-permeability, vascular normalization, residual stress, stress alleviation
Introduction
A solid tumor is an aberrant tissue made of cancer cells and a variety of host cells – all embedded in an extracellular matrix – nourished by blood vessels and drained by lymphatic vessels (1). Solid tumors stiffen as they grow in a host normal tissue. Stiffening, which is perhaps the only mechanical aspect of a tumor that clinicians and patients can feel/sense, is caused by an increase in the amount of the structural components of the tumor, particularly the cancer cells, stromal cells and the extracellular matrix constituents. As tumor tissue becomes stiffer than the surrounding tissue, the continued generation of forces by the tumor constituents displaces the surrounding normal tissue and allows the tumor to invade and grow in size. Thus tumor growth involves the generation of mechanical forces within the tumor, and between the tumor and the host tissue. These mechanical forces, coupled with aberrant tumor vessels, induce abnormal solid and fluid stresses (i.e., force per unit area) that facilitate tumor progression and hinder response to various treatments.
Solid stress - the mechanical forces exerted by non-fluid components of the tumor - is accumulated within tumors as the rapid proliferation of cancer cells strains the tumor microenvironment, which itself pushes against and deforms the surrounding normal tissue (Fig. 1). The solid stress held solely within a tumor - that remains in the tissue after it is excised and external loads are removed - is referred to as growth-induced or residual stress. An additional, externally applied stress is generated as the growing tumor deforms the normal tissue, which in turn, resists tumor expansion (2, 3). Solid stresses affect tumor pathophysiology in at least two ways: directly by compressing cancer and stromal cells and indirectly by deforming blood and lymphatic vessels. Cell compression alters gene expression, cancer cell proliferation, apoptosis and invasiveness, stromal cell function, and extracellular matrix synthesis and organization (4-10). Blood and lymphatic vessel compression reduces the delivery of oxygen, nutrients and drugs, creating a hypoxic and acidic microenvironment and compromising therapeutic outcomes (1, 2, 11-15).
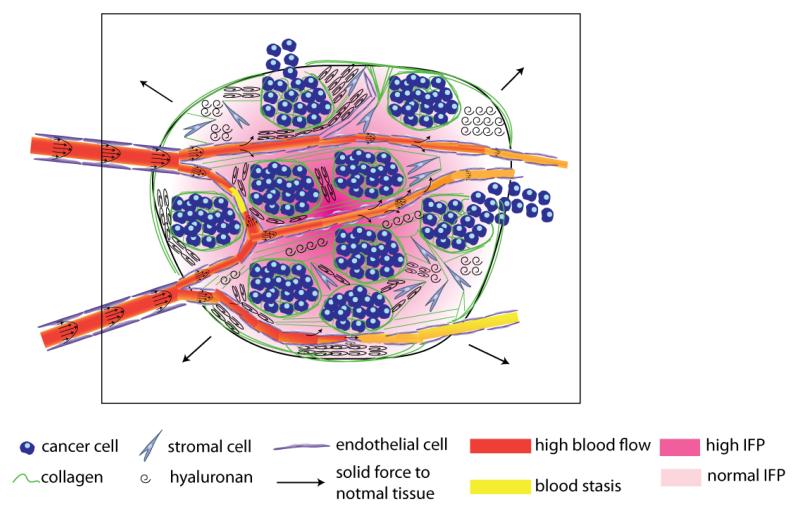
Figure 1.
Schematic of the tumor mechanical microenvironment. Cancer cells along with myfibroblasts (stromal cells) stretch collagen fibers and compress hyaluronan storing growth-induced solid stress. This stress can compress or even collapse intratumoral vessels reducing blood flow. The remaining uncompressed vessels are often leaky resulting in excessive fluid crossing the vessel wall and contributing to elevated interstitial fluid pressure. Vessel leakiness further reduces perfusion and along with vessel compression can cause blood stasis. At the macroscopic scale the tumor pushes against the surrounding normal tissue, which in turn restricts tumor expansion.
Fluid stress - the forces exerted by the fluid components of the tumor - includes the microvascular and interstitial fluid pressures (MVP and IFP, respectively), as well as the shear stress exerted by blood and lymphatic flow on the vessel wall and by interstitial flow on cancer and stromal cells as well as extracellular matrix (16). Fluid stresses are determined in large part by the combined effect of the structure of tumor vessels, and the compression of blood and lymphatic vessels. Blood vessel compression reduces the effective “flow” cross-section of the vessel and thus, increases the resistance to blood flow, which can affect MVP, shear stress and perfusion (17) (Fig. 1). In addition, compression of lymphatic vessels hinders the drainage of excessive interstitial fluid (18, 19). This in turn results in accumulation of fluid in the interstitial space and formation of edema, which is often seen in patients. Furthermore, the hyper-permeability of the tumor vessels, formed during the process of angiogenesis, usually lead to increased fluid flux from the vascular to the interstitial space. This fluid leakage reduces tumor perfusion and, along with the loss of functional lymphatics through physical compression, elevates IFP (18). This is a vicious cycle, as elevated IFP also reduces perfusion, because the upstream microvascular pressure is communicated to the extravascular space and then to downstream vessels, minimizing the pressure drop between upstream and downstream segments of vessels leading to reduced flow. Taken together, the effects of elevated IFP make it a major barrier to drug delivery (19-23).
Here, we review the existing knowledge on solid and fluid mechanics of tumors and describe the mechanisms with which tumor mechanics affect cancer cell growth and metastasis and inhibit the delivery of drugs. We also propose therapeutic strategies that can alter the tumor mechanical microenvironment and improve the delivery of therapeutic agents and thus, the efficacy of cancer treatment.
Solid Mechanics of Tumors
Externally applied and growth-induced stresses are additive and affect tumor progression and treatment either directly by being exerted on cancer and stromal cells and extracellular matrix constituents or indirectly by deforming blood and lymphatic vessels. The sum of the two is the total solid stress, which begins to evolve from the early stages of carcinogenesis (24). Contrary to fluid pressure, solid stress can be direction dependent. Thus, total solid stress is compressive in the interior of the tumor in all directions, while at the interface with the normal tissue, it is compressive in the radial and tensile in the circumferential directions as shown in Fig. 2 (2, 3). We review separately the external and growth-induced solid stress.
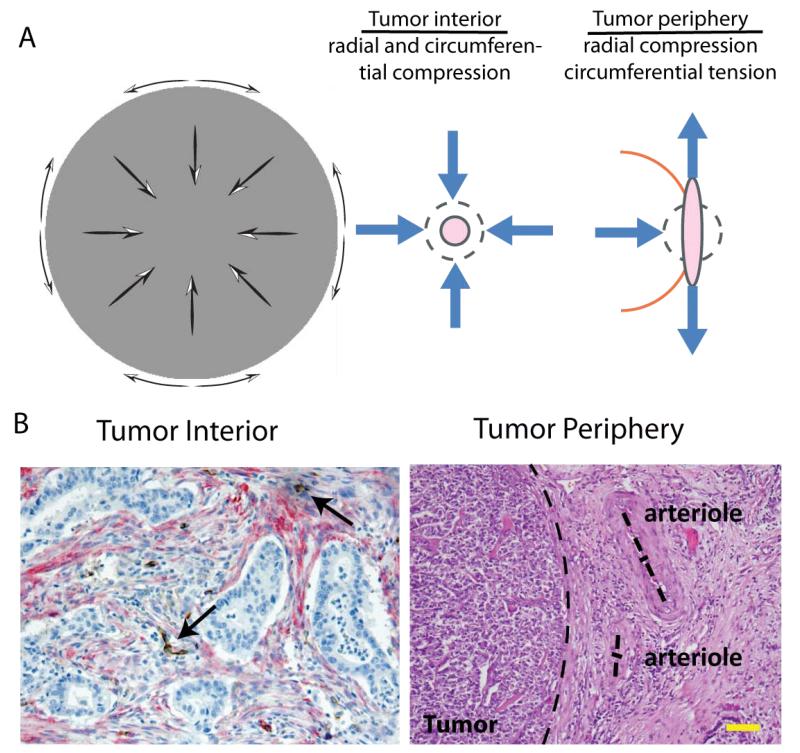
Figure 2.
Solid stress profile in tumors and evidence of vessel compression. A | Solid stresses are compressive in the interior of the tumor in both radial and circumferential direction, while at the periphery radial stresses are compressive and circumferential stresses are tensile. [Reproduced from Reference (3)]. B | This stress profile can collapse intratumor vessels (histologic section of human pancreatic tumor [Reproduced from Reference (135)], arrows show position of collapsed vessels), while peripheral vessels obtain elliptical shapes (histologic section of human pancreatic neuroendocrine tumor [Reproduced from Reference (3)], dash lines show tumor margin and the two main axes of the arterioles). Scale bar 100 μm.
Externally applied solid stress
The effect of solid stress exerted externally by the surrounding tissue on solid tumors has been studied in vitro, by growing avascular tumor spheroids within a polymer matrix (4, 8, 9, 25). We first grew cancer cells within an agarose gel of varying concentration to increase the compressive stress exerted on the cells, and found that increasing compressive stress inhibits spheroid growth (4). The inhibitory effect of stress on growth is, however, reversible and growth-inhibited spheroids resume normal growth once the stress is removed. Later, we repeated the experiment to investigate the underlying mechanisms (8) and found that compressive stresses suppress cancer cell proliferation and induce apoptotic cell death via the mitochondrial pathway. More specifically, anisotropic (i.e., non-uniform) mechanical loads can induce apoptosis in regions of high compressive stress, and allow proliferation in low-stress regions of the tumor spheroid (8) (Fig. 3A). As a result, external forces can define tumor morphology, isotropic (i.e., uniform) loads lead to the growth of spherical cancer cell aggregates, while anisotropic loads force cancer cells to grow preferentially in the direction of least stress. Tumor spheroid growth patterns are again reversible and the aggregates can be remodeled by altering the stress field. Moreover, compressive stress can enhance the invasive phenotype of cancer cells (10) (Fig. 3B) and increase the expression of genes that remodel the extracellular matrix and tumor vessels (9, 26, 27). Estimates of the external stress levels in the spheroids are in the range of 28-120 mmHg (3.7 - 16.0 kPa) depending on the concentration of the matrix (4, 8). Recently, with the use of mathematical modeling we found that the externally applied stress at the tumor interior can exceed 150 mmHg (20 kPa) based on experimental data for murine tumors (3). These stresses are sufficient to compress fragile intratumoral blood and lymphatic vessels, while the tensile circumferential stress at the interface of the tumor with the normal tissue can deform peritumoral vessels to elliptical shapes (Fig. 2B).
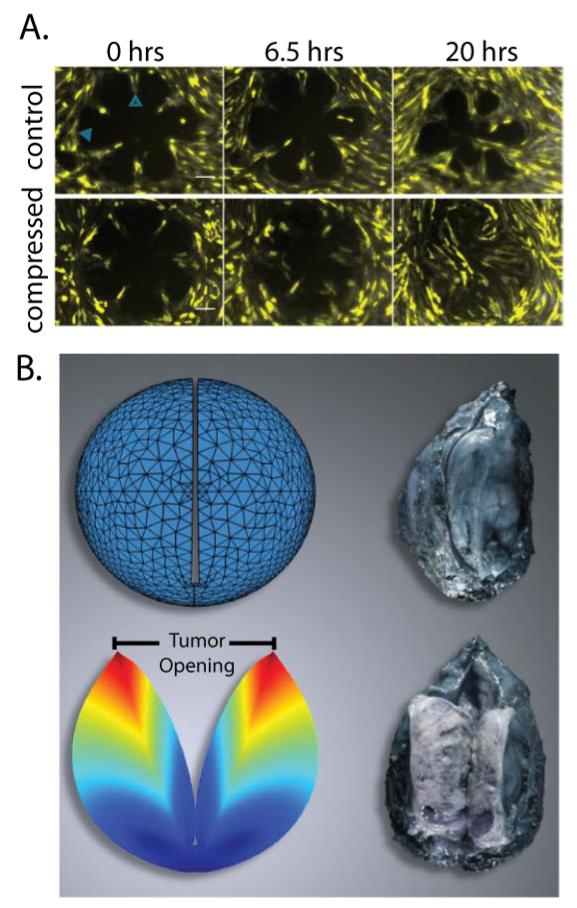
Figure 3.
External and growth induced stress. A | Direct cancer cell compression enhances the invasive phenotype of 67NR cells. 67NR monolayers form a rosette shape, the control group is stress-free, while the compressed group is subject to 773 Pa compressive stress. Under compressive stress the 67NR cells move faster towards the center of the rosette, which suggests increased motility and invasiveness. Scale bar 100 μm [Reproduced from Reference (10)]. B | Evidence of growth-induced stress. Cutting of an excised tumor along its longest axis (80% of its thickness) causes retraction of the surface and swelling of the interior of the tumor. These deformation modes are caused by relaxation of the growth-induced stress and result in a measurable tumor opening. Thus, even though no external loads are exerted on the excised tumor, the tumor still holds growth-induced, residual stress. Growth-induced stress is estimated with the use of mathematical modeling by simulating the cutting experiment [Reproduced from Reference (2)]. The tumor in the figure is a soft tissue sarcoma.
Growth-induced solid stress
Growth-induced or residual solid stress is accumulated within tumors during progression as the growth of proliferating cancer cells strains the tumor microenvironment and stores strain energy (Fig. 1)(2). This stress is evident when one excises a tumor, so that no external loads are applied, and makes a cut along its longest axis. The cut releases the stress and allows the tissue to relax, resulting in simultaneous swelling at the center and retraction at the boundary of the tumor. These relaxations lead to a significant “opening” at the location of the cut (Fig. 3B). The retraction of the tissue is indicative of tension at the tumor periphery. The swelling at the center indicates that the intratumoral region is in compression, which presumably balances the tension at the periphery. The tensile growth-induced stress at the periphery causes a smooth transition of the circumferential stress from compressive inside the tumor to tensile at the interface with the normal tissue (3).
Based on experimental data and with the use of mathematical models, the levels of compressive growth-induced stress at the intratumoral region were estimated to be in the range of 35-142 mmHg (4.7 - 18.9 kPa) for human tumors, 2-60 mmHg (0.3 - 8.0 kPa) for murine tumors and 0-10 mmHg (0 - 1.3 kPa) for avascular tumor spheroids (2, 28, 29). Interestingly, tumors with higher growth-induced stress levels exhibited lower growth rates, presumably due to reduced cancer cell proliferation and increased apoptosis (2, 8). Finally, according to our calculations, growth-induced stress contributes less than 30% to the total solid stress of a tumor, suggesting that the contribution of the external stress from the host tissue is more significant (3).
Cancer cells, stromal cells, and the extracellular matrix participate in the accumulation of growth-induced stress (2). Cancer and stromal cells contribute to growth-induced stress by generating forces during proliferation and contraction. They both also contribute to the remodeling of matrix components. The extracellular matrix constituents, such as collagen and hyaluronic acid, store and transmit stress in a manner dependent on their mechanical properties. Collagen fibers, which are remarkably stiff in tension and provide tensile strength to tissues, can contribute to growth-induced stress by virtue of the ability of the collagen fibers to resist stretching when connected cells are forced apart. Collagen fibers are also remodeled and pulled by fibroblasts. On the other hand, hyaluronic acid provides compressive resistance because of its capacity to trap water molecules. Water is incompressible and because water molecules cannot escape from the tumor, they resist the compressive stress developed in the tumor interior (Fig. 1).
Desmoplasia and solid stress accumulation
It is notable that during tumor progression, extensive extracellular matrix synthesis and remodeling takes place. One pathway through which this occurs is the activation or over-expression of transforming growth factor-β (TGF-β). TGF-β can regulate the production of matrix-modifying enzymes (e.g., metalloproteinases (MMPs) and lysil oxidase (LOX)) in order to increase matrix protein synthesis and crosslinking and decrease matrix proteinase activity (30-32), thereby increasing matrix stiffness (30). Stiffening of the matrix and the resulting increase of the stress levels can in turn induce production of fibronectin, enhance focal adhesions, and increase cytoskeletal tension by Rho/Rock signaling activation (33, 34). Matrix stiffening can also promote integrin clustering and enhance PI3 kinase activity that regulates tumor invasion (35, 36).
In addition, mechanical stress and TGF-β activation can convert fibroblasts or other quiescent precursor cells into contractile myo-fibroblasts, also known as cancer associated fibroblasts, that produce extracellular molecules (collagen-I, fibronectin, glycosaminoglycans) and remodel the extracellular matrix (5, 37, 38). Production of new extracellular matrix again increases tissue stiffness and solid stress, while myo-fibroblast contraction further activates latent TGF-β from the extracellular matrix (7, 37), creating a positive feedback loop. TGF-β may also play a role in both endothelial-to-mesenchymal transition (EndMT) and epithelial-to-mesenchymal transition (EMT), which are associated with loss of intercellular adhesion and acquisition of a motile phenotype that promotes cancer cell invasion and metastasis (39, 40).
Consequences of vessel compression to cancer progression and treatment
Blood vessel compression reduces tumor perfusion and thus, the supply of oxygen and nutrients (11). Limited oxygen and nutrient supply results in the formation of necrotic tissue at the tumor interior. But since oxygen and nutrients are essential for tumor progression, this paradox raises questions about the role of vessel compression and solid stress in cancer progression. Our hypothesis is that vessel compression and solid stress protect cancer cells from the immune system of the host (1, 41). The cells of the immune system continuously patrol the human body through the circulation. Therefore, lack of functional intratumoral vessels would inhibit immune cells from reaching the tumor. But even if these cells arrive in the tumor tissue, hypoxia compromises their killing potential (42). Hypoxia also produces growth factors (e.g. VEGF, TGF-β) that suppress the activity of macrophages and have the potential to convert macrophages to protumorigenic (tumor-friendly) cells (43). Furthermore, a hypoxic microenvironment can select for cells that can survive in a harsh microenvironment, which enhances the invasive and metastatic potential of cancer cells and lowers the efficacy of radiation and immunotherapy (1, 43-45).
Vessel compression can also exclude large tumor regions from the systemic administration of therapeutic agents by reducing blood flow and creating vascular shunts (i.e., short, high flow vascular pathways that bypass long downstream pathways) (46-48). Therefore, drugs might not be able to reach certain regions of tumors in sufficient amounts. Furthermore, the collapse of intratumoral lymphatic vessels contributes to the uniform elevation of IFP, which can be equal to or locally exceed MVP transiently (18, 19, 21, 49, 50). As we will discuss in detail later, IFP elevation eliminates pressure gradients across the tumor vasculature and in the interstitial space of tumors, and thus inhibits convective transport of drugs.
Mathematical modeling of solid mechanics of tumors
Several mathematical models have been developed to study the biomechanical response of solid tumors. Most of them make use of the multiplicative decomposition of the deformation gradient tensor to account for tumor growth, evolution of growth-induced stress and/or the mechanical interactions with the surrounding normal tissue (2, 3, 51-54). Methodologies also exist that involve the incorporation of a growth strain factor to direct tumor expansion (28, 29). While the mathematical framework for tumor growth is well defined, little work has been done to-date regarding constitutive modeling of solid tumors, at least compared to other biological tissues, such as arteries, heart valve leaflets and articular cartilage. Tumors are usually modeled as isotropic, hyper-elastic materials (e.g. Neo-Hookean or Blatz-Ko) (2, 51, 53, 54), isotropic poroelastic materials composed of a solid and a fluid phase (3, 55) or a mixture of more than two components (52). These models, however, are limited in that tumors are not isotropic and their structure is too complex to be described by continuum-level constitutive equations. A main reason for the uncertainty of the mechanical behavior of tumors is the lack of experimental studies as most of the models developed to date lack experimental validation. Spatial and temporal heterogeneities in the structure of a tumor, differences between the primary tumor and its metastases, as well as among tumors of the same type or tumors of different types render the derivation of a global constitutive equation a challenging task. To deal with the structural heterogeneity of tumors, structure-based models that incorporate directly tumors’ heterogeneity by utilizing multi-scale methodologies similar to these developed for other soft tissues is a promising approach (56, 57).
Fluid mechanics of tumors
Fluid mechanics of tumors involve flow along the tumor vasculature, through the tumor interstitial space and drainage of excessive fluid by the lymphatic network. Abnormalities in the tumor microenvironment due to the formation of hyper-permeable tumor blood vessels and the accumulation of solid stress affect blood flow, MVP, IFP and fluid shear stresses (16, 58). As a result, tumors are often hypo-perfused, MVP drops while IFP increases uniformly throughout the tumor interior, fluid shear stresses cause remodeling of the vascular network and lymphatic flow is limited only to the tumor periphery. Here, we review separately vascular, interstitial and lymphatic flow and their effects on tumor progression and treatment.
Vascular Fluid Mechanics
Blood flow rate, Q, in the vasculature of normal and tumor tissues is given by the microvascular pressure drop, ΔMVP, divided by the flow resistance, FR, . The resistance to fluid flow can be either due to vascular network geometry (e.g. vessel morphology, tortuosity) or due to changes in blood viscosity. In solid tumors both geometric and viscous resistances are elevated (17, 59, 60).
Rapid tumor growth requires a sufficient vascular network to feed cancer cells with nutrients and oxygen. For that reason pro-angiogenic factors (e.g VEGF, PDGF), which induce angiogenesis, are over-expressed in order to recruit endothelial cells to form new vessels (61, 62). Tumor vessels are usually immature and have an abnormal structure and function (1, 48, 63, 64). The endothelial lining that forms the vascular network can have wide junctions, large numbers of fenestrae and transendothelial channels, and be accompanied by a discontinuous or absent basement membrane and poor pericyte coverage. As a result, the openings in the tumor vessel wall can be as large as a few micrometers in size, much larger than the pores of normal vessels, which are less than 10nm (65-67). The large pores of tumor vessels enhance leakage of blood plasma to the interstitial space, which in turn increases red blood cell concentration (hemoconcentration) and blood viscosity (60, 68, 69). In addition, tumor vessels can be dilated and tortuous (64), and create vascular shunts (46). Finally, as mentioned previously, blood and lymphatic vessels can be compressed due to solid stresses, which further increases geometric resistance to blood flow. As a result of all these abnormalities, blood velocity in tumors is highly heterogeneous and is not correlated with vessel diameter. It can also be an order of magnitude lower than the velocity in normal vessels, ranging from 0.001 to 10 mm/s (47, 70) (Fig. 4A). In normal vessels with higher velocities, shear stress contributes to the regulation of an important step in metastasis. Shear stress controls whether circulating tumor cells (CTCs) adhere to normal blood vessel walls in distant organs. Increasing shear increases the amount of collisions of CTCs with vessel walls, but it reduces their residence time of adhesion, which could impair extravasation (71).
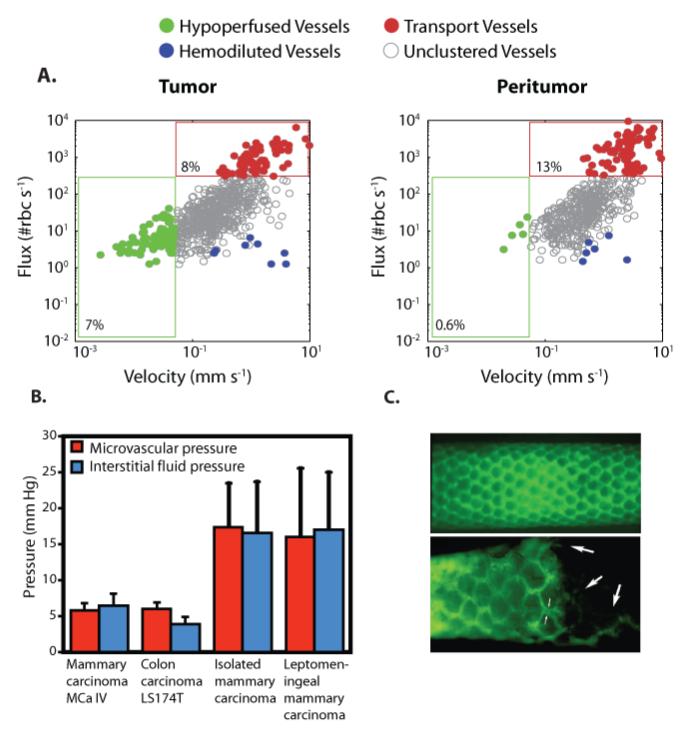
Figure 4.
Abnormal fluid flow in tumors. A | Red blood cell (RBC) flux and blood velocity in interior and peripheral vessels of a glioma growing in a mouse brain. A significantly larger proportion of interior vessels are hypo-perfused with velocities less than 0.1 mm/s compared to peripheral vessels [Reproduced from Reference (47)]. B | Interstitial fluid pressure in tumors is elevated and comparable to microvascular pressure [Reproduced from Reference (108)]. C | Lymphatics are absent from the tumor interior and hyperplastic at the periphery. Fluorescence lymphangiography images of a normal (top) and a sarcoma-bearing (bottom) mouse tail. At the normal tissue, lymphatics form a functional network (green). At the tumor interior (right side of bottom panel) lymphatics are absent, but have a larger diameter at the margin. Large arrows indicate attenuated vessels inside the tumor. Small arrows indicate the increased diameter of the lymphatic capillary at the margin [Reproduced from Reference (91)]).
Within intratumoral vessels, the lower shear stress applied to endothelial cells contributes to the regulation of angiogenesis and tumor vascular network abnormalities. Shear stress from blood flow on the endothelial lining is transmitted by the glycocalyx layer. This layer is a negatively-charged fibrous structure of proteins and macromolecules and is connected to the cytoskeleton of endothelial cells (72). This connection allows the layer to mediate the transduction of fluid shear stress to the endothelial cell lining. Through this mechanism, high and low shear stress regulate different steps of angiogenesis. A lack of shear stress, indicative of a poorly-perfused vessel, induces endothelial cells to sprout to seek new sources of blood flow. Nitric oxide production, however, with moderate levels of shear stress results in the attenuation of sprouting (73). While low shear stress encourages endothelial cells to seek alternate sources of nutrients, higher shear stress induce vessel branching, termed intussusceptive angiogenesis (74). This process occurs as endothelial cells, protruding into the vessel lumen, connect to form a pillar within the vessel. The pillar’s location is governed by shear stress, because it forms where there was high velocity and thus low shear in the original vessel. As a result of the branching, there is a stress reduction in the individual endothelial cells but the flow rate within the original, single vessel is maintained by the combination of the two vessels. Therefore, high and low shear stress affect angiogenesis in single vessels in different ways.
The effect of shear stress on a single vessel can have a substantial impact on the blood flow through nearby regions of the vascular network. Functional shunts are an interesting example of this relationship. They occur in situations where there is a short arterio-venous connection through which blood flow can bypass the downstream vascular network. The shear stress is often high in the short vessel serving as the functional shunt, which causes the shunt to dilate, allowing more blood to flow through the shunt (75). The feeding arteriole downstream of the shunt senses less flow and shear stress. As a consequence, it reduces in diameter, further discouraging flow throughout the vascular network downstream of the branch point to the shunt (46). Abnormal shear stress in a single vessel can impair blood flow to downstream regions of tumors, contributing to the low perfusion found in multiple, large volumes within most solid tumors.
Interstitial fluid mechanics
The driving forces for interstitial flow are hydrostatic and osmotic pressure gradients between the vascular and interstitial space. The interstitial space of solid tumors is composed of a network of collagen fibers, along with other fibrillar and space-filling proteins and molecules, such as proteoglycans and glycosaminoglycans (e.g., hyaluronic acid) (76, 77). The compressive stress throughout a tumor compresses the matrix into a dense and tortuous network that hinders transport of fluid. We provided the first measurements of the interstitial fluid velocity and found on the order of 0.2-0.8 μm/s (78), resulting in very low Reynolds number (i.e., Stokes flow). Even with low flow velocity, shear stress can be high when there are small pores. Nonetheless, in tumors the shear stress remains low because the matrix shields the cells from stress and local gradients in hydraulic conductivity divert flow from cells (79).
Despite the low velocity of the interstitial fluid, studies have shown that fluid shear stress - similar to solid stress - can upregulate TGF-β, causing myo-fibroblasts differentiation and contraction and extracellular matrix reorganization and stiffening (80, 81). Therefore, the role of fluid and solid stresses on TGF-β dependent pathways appear to be synergetic. Furthermore, despite the fact that the interstitial shear stresses are up to two orders of magnitude lower than the intravascular shear stresses, when applied to cancer cells they can stimulate oncogenic signaling pathways (82). Stromal cells present in large numbers in many tumors may increase their motility in response to interstitial flow as a result of a small shear gradient across the cell (83). Thus, interstitial shear stress influences cancer cell and stromal cell behavior. Shear stress generated by interstitial flow also affects angiogenesis. Interstitial flow increases the rate of the vessel morphogenesis, which is the rearrangement of the vessel wall microanatomy preceding sprouting. After sprouting, invading endothelial cells preferentially protrude against the direction of interstitial flow (73). In this way, a vessel, which began sprouting because of low intravascular shear stress, sprouts in the direction of another leaky vessel, or in other words, towards a higher pressure region.
Interstitial fluid flow is governed in large part by the hydraulic conductivity of the interstitial space, a measure of the resistance to fluid flow in porous and fibrous media. The higher the conductivity, the more easily fluid will percolate through the extravascular space of the tissue. Importantly, hydraulic conductivity - along with vessel leakiness and lymphatic dysfunction - is a regulator of IFP and the low conductivity values often found in tumors contribute to the elevation of IFP to values comparable to MVP (Fig. 4B). For fibrous media, which is the case of our interest, hydraulic conductivity depends on the volume fraction, surface charge and organization of the fibers (84, 85). Therefore, tumors rich in collagen might exhibit an order of magnitude lower hydraulic conductivity than those of low collagen content tumors (86). As has been already mentioned, in many tumors an accumulation of fibrillar collagen types I and III occurs presumably due to increased activity of tumorigenic factors, such as TGF-β, that might stiffen the extracellular matrix and induce fibrosis (32, 87). Therefore, this desmoplastic response of tumors would further decrease hydraulic conductivity. The hydraulic conductivity of the interstitium is also influenced by the negatively-charged proteoglycans and glycosaminoglycans. Increasing the glycosaminoglycan concentration leads to increased flow resistance due to their capacity to trap water (84). Accordingly, depletion of glycosaminoglycans with matrix metalloproteinases-1 and -8 increases the hydraulic conductivity and thus, the interstitial fluid velocity (88). Cancer and stromal cells form another barrier to interstitial fluid flow. The high cellular density, which is common in many cancers, reduces the space available for flow, and thus increases fluid resistance. Also plasma proteins, soluble collagen, and the thin and elongated glycosaminoglycan chains that are contained in the interstitial fluid might increase significantly the viscosity of the interstitial space (89, 90).
Lymphatic fluid mechanics
The lymphatic network drains excessive fluid from the interstitial space and returns it back to the blood circulation. By doing so, it regulates the fluid balance in tissues and prevents formation of edema. Tumor lymphatics have two characteristics, common in many cancers. They are not functional in the intratumoral region (91, 92), and they are hyperplastic and exhibit increased flow at the periphery (93, 94). The loss of functionality is attributed to compressive solid stress that is developed in tumors. This stress has been shown to collapse intratumoral lymphatic vessels, and thus eliminates lymph flow. Lymphagiogenesis in the tumor periphery is regulated by the expression of the vascular endothelial growth factors C and D (VEGF-C and VEGF-D). Overexpression of these growth factors in tumors might result in hyperplasia of the vessels, dilation of their lumen, and increased volumetric flow rate (Fig. 4C) (94-96). The lymph fluid velocity in tumors has been measured to be on the order of μm/s, about an order of magnitude higher than the interstitial fluid velocity (97-100). The increase in lymph flow rate of the peritumor lymphatic vessels might lead to a 200-fold increase in the accumulation of cancer cells in lymph nodes and a 4-fold increase in metastasis, despite the absence of intratumoral lymphatics (92, 94). Therefore lymph flow plays a crucial role to cancer dissemination.
Another regulator of lymphatic function is nitric oxide (NO) (1, 101, 102). Nitric oxide is synthesized by NO synthase (NOS) and can be neuronal (nNOS), endothelial (eNOS) or inducible (iNOS). nNOS and eNOS are constitutively expressed by neuronal and endothelial cells, while iNOS is induced by inflammatory cytokines, endotoxin, hypoxia, and oxidative stress. We have shown that eNOS maintains strong lymphatic contractions and its inhibition decreases lymphatic fluid velocity (100). We attributed this effect to the regulation of the deeper collecting lymphatics of eNOS, as the velocity of the superficial lymphatics did not change with eNOS inhibition. iNOS levels can maintain lymphatic pumping during inflammation and infection (103, 104). Lymphatic flow is also susceptible to changes in the interstitial flow. An increase in interstitial flow can stimulate lymphatic endothelial cell morphogenesis and increase lymphatic permeability (105, 106). Therefore, the composition of the interstitial space and particularly the hydraulic conductivity can regulate not only interstitial but also lymphatic flow (81).
Consequences of fluid stresses to cancer progression and treatment
Heterogeneous and compromised vascular flow results in heterogeneous distribution of therapeutic agents in the tumor, and thus it can reduce the efficacy of the treatment. In addition, because not all tumor vessels are leaky, the delivery of large therapeutic agents (e.g. nanotherapeutics), through the enhanced permeability and retention (EPR) effect, is not uniform (107). Furthermore, the excessive leakage of blood plasma from the abnormal vascular network in conjunction with the lack of functional lymphatic vessels to maintain fluid balance as well as the increased resistance to interstitial fluid flow due to low hydraulic conductivity result in interstitial hypertension (19, 21, 50, 108-111). Young and co-workers reported the first measurements of elevated IFP in tumors growing in rabbits in 1950 (112), but the implications of this interstitial hypertension for tumor progression and treatment were not fully revealed for nearly four decades. In 1988, we showed mathematically and confirmed later with experimental measurements that IFP is uniformly elevated throughout the bulk of a tumor (Fig. 4B) with a precipitous drop to normal values in the tumor margin creating a steep pressure gradient (18) (Fig. 1). Elevated IFP can compromise the efficacy of therapeutics and facilitate metastasis in multiple ways. First, the uniform elevation of IFP can reach and locally exceed MVP transiently, which as we already discussed eliminates transvascular and interstitial pressure gradients, and thus the convective transport of drugs across the vessel wall and in the interior of the tumor (21, 23, 49, 50, 113). Second, the steep pressure gradients in the periphery would cause fluid leaking from the blood vessels located in the tumor margin – but not from the vessels in the tumor interior – to “ooze” into the surrounding normal tissue (1, 22). This oozing fluid would facilitate transport of growth factors and cancer cells into the surrounding tissue – fueling tumor growth, progression and lymphatic metastasis. It also reduces the retention time of small drugs (less than 10nm in diameter), and thus inhibits their homogeneous distribution inside the tumor.
Mathematical modeling of fluid mechanics of tumors
Modeling blood flow in the highly irregular structure of the tumor vasculature is a challenging task. Direct solution of the equations of flow in a three-dimensional vascular network is computationally intensive. For that reason, most studies assume an idealized, one-dimensional blood flow (i.e., axial flow), which follows Poiseuille’s equation (23, 114, 115),
| (1) |
where R is the vessel radius, ΔP the pressure difference along a vessel of length L, and μapp an apparent viscosity that describes the rheological properties of both blood plasma and cells. Empirical equations have been derived that correlate μapp with the hematocrit (red blood cell concentration) and vessel diameter (Fahraeus-Lindqvist effect) (116). Based on this approach several methodologies have been developed to model tumor progression taking into account the concentration of oxygen and nutrients, shear forces, cell proliferation and apoptosis, the evolution and remodeling of the tumor vascular network and other biochemical processes (117-119).
Coupled to Eq. 1 is the equation that describes the fluid exchange rate, Qtrans , between the vascular and interstitial space. This equation is given by Starling’s approximation as (19)
| (2) |
where Lp is the hydraulic conductivity of the vessel wall, S the surface area of the vessel, Pv and Pi the vascular and interstitial fluid pressure, πv and πi the osmotic pressure in the vascular and interstitial space and σ the osmotic reflection coefficient for plasma proteins.
In addition, mathematical models have been developed to study blood rheology taking into account red blood cells, white blood cells, as well as their interactions (120-124). These models provide predictions not only for the fluid flow, but also for the viscosity of the blood, and for the deformation and distribution of the cells in the vessel. In other models, remodeling of the vascular network is considered as a function of the shear stress exerted on the endothelial lining of the vessel wall, the vascular pressure, and the metabolic stimuli (e.g. partial oxygen pressure) (125). Vascular remodeling usually involves changes in the structure, diameter and wall thickness of the vessel, while for low vascular pressures it might also include vessel collapse.
As in every fibrous medium subject to low Reynolds number flow, the interstitial fluid velocity, v, can be described by the well known Darcy’s equation as
| (3) |
or the Brinkman’s equation
| (4) |
where K is the hydraulic conductivity of the interstitial space, Pi the IFP and μ the viscosity. Brinkman’s equation can be seen as Darcy’s equation with an additional term for viscous stresses in the fluid phase. Both hydraulic conductivity and IFP can severely affect fluid flow in the tumor interstitium.
Several mathematical expressions have been derived to predict the hydraulic conductivity of a fibrous medium. Many of them refer to two-dimensional solutions of low Reynolds number flows parallel and transverse to spatially periodic arrays of fibers (126). These expressions relate the hydraulic permeability (i.e., the hydraulic conductivity multiplied by the viscosity) to the fiber volume fraction and might include more than one family of fibers (127). More recently, mathematical approaches to calculate hydraulic conductivity in three-dimensional fiber structures have been developed. These approaches apart from the fiber volume fraction might also account for fiber organization and/or surface charge (85, 128). Caution has to be taken, however, when such methods are to be used to calculate the hydraulic conductivity of tumors. The complex structure of the tumor interstitial space involves heterogeneously distributed fibers with multiple orientations, sizes and surface charges that cannot be represented directly by the idealized structures of these models. Alternatively, empirical equations that are based on experimental studies exist and provide the hydraulic conductivity of tumors as a function of collagen, proteoglycan and glycosaminoglycan content (84, 129).
Finally, the flow rate entering the lymphatic circulation from the interstitial space, Ql is given by Starling’s approximation as (20)
| (5) |
where Lpl is the hydraulic conductivity of the lymphatic wall, Sl the surface area of the lymphatic vessel, Pi the IFP, and Pl the pressure of the lymphatic vessel. As we have mentioned earlier, intratumoral lymphatics are dysfunctional and thus, it is common to consider lymphatic flow to be negligible. More detailed approaches for modeling lymphatic drainage and pumping utilizing homogenization or Lattice Boltzmann methods exist (130, 131). Particularly in (131) increases in shear stress were modeled to trigger NO emission by the endothelium, which in turn causes dilation of the vessel and increased lymph flow, suggesting a direct mechanism of fluid stress control of lymph flow.
Therapeutic Strategies
Given the fact that solid and fluid mechanics in tumors are mainly determined by the accumulation of solid stress and the formation of abnormal vessels, we proposed two therapeutic strategies to improve drug delivery and efficacy (1). On one hand, stress-alleviation treatments have the ability to re-open compressed blood vessels and thus, improve perfusion and drug delivery in hypo-perfused tumors (2, 15). On the other hand, vascular normalization strategies aim to decrease the leakiness in hyper-permeable tumors, which is a different mechanism to improve perfusion and delivery of therapeutic agents (2, 15) (Fig. 5). Which of the two strategies is more beneficial depends on the microenvironment of the tumor and particularly on whether tumor vessels are hyper-permeable, compressed, both or neither. Use of these two strategies alone or in combination could improve therapeutic outcomes.
Figure 5.
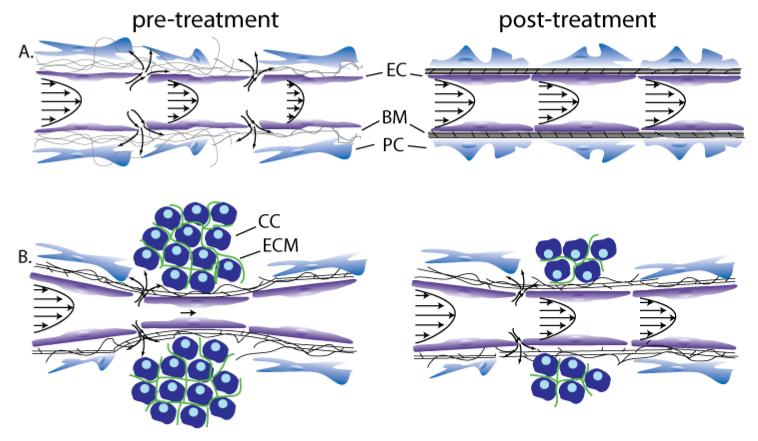
Strategies to improve perfusion and drug delivery in solid tumors. (A) Vascular normalization increases pericyte coverage, which decreases vessel permeability and improves perfusion, (B) Stress-alleviation treatment depletes structural components of the tumor microenvironment, which decompresses tumor vessels and improves perfusion [Reproduced from Reference (15)]. Improved perfusion rates will increase the delivery of drugs. These strategies can be used either alone or in combination based on whether tumor vessels are leaky, compressed, both or none. Abbreviations EC: endothelial cell, BM: basement membrane, PC: pericyte, CC: cancer cell, ECM: extracellular matrix.
Stress alleviation treatment to decompress vessels
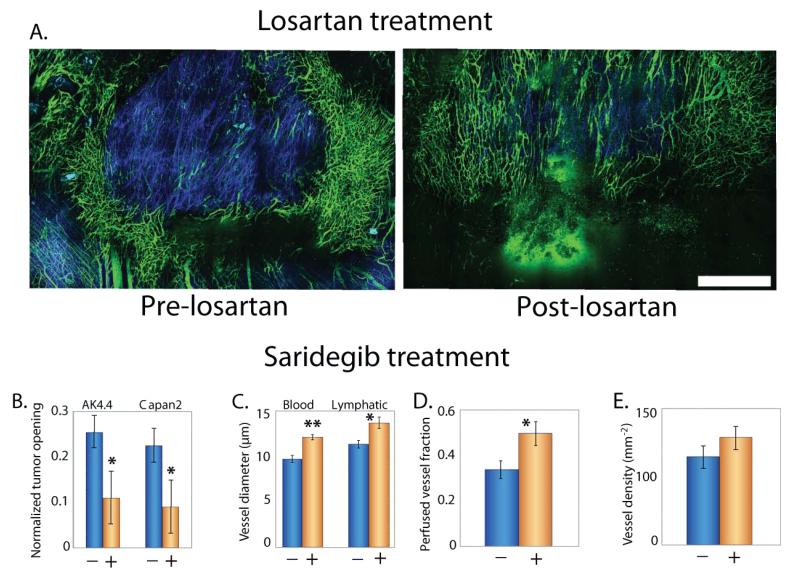
A stress alleviation strategy is based on the following sequence of events: alleviate stress levels, re-open compressed tumor blood vessels, improve perfusion, enhance drug delivery, and efficacy resulting in improved overall survival. Stress reduction also increases the diameter of intratumor lymphatic vessels, but their function is not restored – presumably due to impaired lymphatic valves in the draining lymphatics (1, 13). Constituents of the tumor microenvironment – other than cancer cells – that contribute to the generation of solid stress include stromal cells and extracellular matrix components (2). Indeed, we have shown that pharmacological depletion of tumor stroma with Saridegib, an inhibitor of the Hedghog pathway, alleviates stress levels and increases blood vessel diameter and tumor perfusion (Fig. 6) (2), while in another study use of Saridegib improved chemotherapy in murine pancreatic cancers and the overall survival of the mice (132). In addition, enzymatic degradation of hyaluronan when combined with cytotoxics has been shown to decompress blood vessels, improve tumor perfusion, drug delivery and the overall survival of mice bearing pancreatic tumors (14, 133). Modification of the extracellular matrix can be also achieved by inactivation of cancer-associated fibroblasts by inhibiting signaling pathways that drive their activation (134). We have been able to achieve this by inhibiting either the activity of Angiotensin II with angiotensin-converting enzyme inhibitors or the signaling of Angiotensin II with angiotensin receptor blockers (135). Many of these drugs are widely prescribed as anti-hypertensive therapies. Specifically, the clinically approved anti-hypertensive drug losartan, an angiotensin receptor blocker reduces collagen and hyaluronan levels in murine tumors by decreasing stromal expression of TGF-β as well as other fibrosis signaling molecules (135). This in turn, alleviates solid stress levels and improves tumor perfusion as well as the delivery of both chemotherapeutic agents and nanomedicines, and thereby increasing the overall survival of mice bearing tumors (135, 136). These findings have led to a clinical trial at Massachusetts General Hospital in patients with advanced pancreatic ductal adenocarcinoma – a uniformly fatal disease with very poor prognosis (see ClinicalTrials.GOV – trial identifier number NCT01821729). Retrospective clinical studies have also shown that treatment with angiotensin receptor blockers and angiotensin-converting enzyme inhibitors may contribute to prolonged survival in patients with pancreatic, lung and renal cancers (137-139).
Figure 6.
Stress alleviation treatment. A | Intravital multiphoton microscopy images show treatment with the angiotensin receptor blocker, losartan lowers collagen levels (blue) and increases the density of perfused vessels (green) in an orthotopic mammary adenocarcinoma (EO771) [Reproduced from Reference (135)]. Treatment with the sonic hedgehog inhibitor Saridegib, B | reduces solid stress levels, measured as a function of tumor opening (Fig. 3), in two pancreatic ductal adenocarcinomas (AK4.4 and Capan2), C | increases blood and lymphatic vessel diameter and D | the fraction of perfused vessels, E | without affecting vascular density [Panels B-E reproduced from Reference (135)] (2). Scale bar 1 mm. Asterisks represent a statistically significant deference (P < 0.05).
Normalization of tumor vasculature
Compromised blood flow rates in tumors are also due to the formation of leaky and tortuous vessels. Therefore, the goal of a therapeutic strategy should be to change the phenotype of the abnormal tumor vasculature to a more functional phenotype that resembles the structure of normal vessels. We coined this strategy as vascular normalization and suggested to use judicious doses of anti-angiogenic therapy to realize this goal (1, 43, 62, 140).
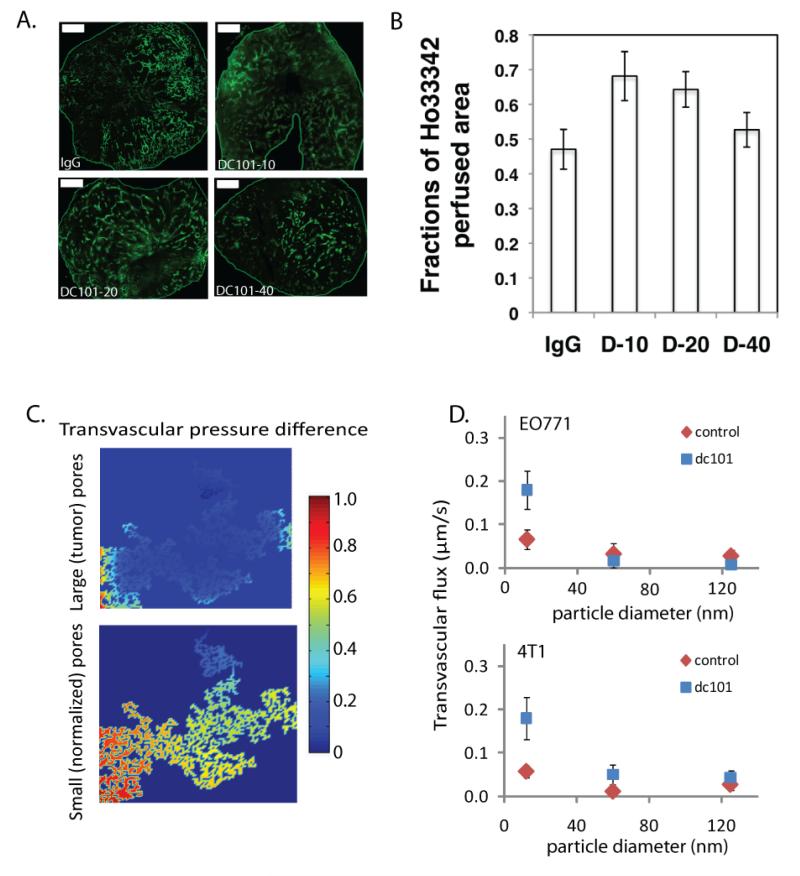
Indeed, vascular normalization remodels the tumor vasculature by increasing pericyte coverage of blood vessels and thus decreasing vessel leakiness. As a result, tumor perfusion is increased and interstitial fluid pressure is decreased to more normal levels (Fig. 7 A & B). Therefore, the pressure difference across the vessel wall is restored, which in turn enhances the extravasation of therapeutic agents and oxygen transport (Fig. 7C) (23, 141-147). A decrease in vessel wall openings, however, will decrease the maximum size of particles that can pass through the vessel wall, and thus vascular normalization adversely affects the delivery of nanoparticles larger than 20 nm in diameter (23) (Fig. 7D). Furthermore, normalization is dose-dependent and high doses will prune the vessels and reduce perfusion and drug delivery (1, 145). Also, vascular normalization has a transient effect, resulting in a time window within which drug delivery is improved, but when anti-VEGF treatment is continued the tumors may shrink or the cancer cells may employ other angiogenic signaling pathways (1, 43, 62, 148). Clinical studies have verified in humans that anti-angiogenic agents can normalize tumor vasculature. Agents that have been used include a monoclonal antibody (bevacizumab) to block VEGF-A in patients with rectal cancer, and an inhibitor of all three vascular endothelial growth factor receptor (VEGF-1,-2,-3) tyrosine kinases (cediranib) in patients with recurrent or newly diagnosed glioblastoma (110, 111, 146-150).
Figure 7.
Vascular normalization treatment with the monoclonal antibody DC101. Normalization of tumor vessels improve tumor perfusion in a dose-dependent manner. A | Perfusion images of whole tumor tissue taken by multispectral confocal microscopy. Animals treated with IgG (control) and 10, 20, or 40 mg/kg bw DC101. Green, Sytox staining. (Scale bars, 1,000 μm.). B | Quantification of fractions of Hoechst 33342-positive area in whole tumor area show perfused regions in the tumors for the three DC101 doses (*P < 0.05) [Panels A adapted from and panel B reproduced from Reference (145)]. C | Model predictions for the effect of vessel wall pore size on the pressure difference across the tumor vessel wall. Decrease in vessel wall pore size with vascular normalization restores a transvascular pressure difference [Reproduced from Reference (23)]. D | Normalization of tumor vasculature and the resulting increase in transvascular pressure difference, improves flux of nanoparticles across the tumor vessel wall in a size-dependent manner in orthotopic mammary adenocarcinomas (EO771 and 4T1) [Reproduced from Reference (23)].
Guidelines for the optimal use of stress-based therapeutic strategies
With the use of mathematical modeling, we recently showed that stress-alleviation treatments to decompress vessels and improve perfusion could be effective in poorly or moderately permeable tumors, such as pancreatic and colon cancers, and various sarcomas (15). On the other hand, vascular normalization treatment will be more effective in hyper-permeable tumors with open vessels, such as a subset of glioblastomas, melanomas, and ovarian carcinomas. These tumors are expected to have low solid stress levels, with perfusion mainly determined by the permeability of the tumor vasculature. In this case, normalization treatment will decrease permeability and improve perfusion and drug delivery. Finally, if a tumor is hyper-permeable with abundant compressed vessels, such as a subset of mammary carcinomas, the two treatments have to be combined so that stress alleviation will open-up the vessels and vascular normalization will make them less permeable. Identification of which tumors have vasculatures that are leaky, compressed, or both is a challenging task. We can make some general statements, such as pancreatic cancers have compressed vessels, but there are many tumors such as breast cancers, where the levels of solid stress and the permeability are highly variable from one tumor to the next and potentially from the primary site to the metastatic site, and thus it could be hard to choose an appropriate strategy until the state of that individual tumor is known. Existing and/or emerging imaging modalities may be able to help in this selection (146, 147).
Conclusions
Our hypothesis is that the abnormal mechanical microenvironment of tumors enables them to be protected from the immune system of the host body, resist anti-cancer therapies, and coordinate their progression. The tumor mechanical microenvironment is quite different from that of normal tissues, characterized by accumulation of solid stress, low perfusion rates and elevation of IFP. To improve treatment, we need to revert tumors from their abnormal path back towards a normal state. This can be achieved with the modification of the tumor microenvironment and modulation of mechanical stresses. We propose two complementary therapeutic strategies: the normalization of the tumor vasculature with judicious doses of anti-VEGF therapy and the normalization of the tumor interstitial space with stress-alleviation therapy. The fact that certain drugs that normalize the tumor microenvironment are already clinically approved and/or are being used in the clinical practice for other diseases is encouraging. The scope of the scientific effort should now be to indentify new, safe and well-tolerated drugs that normalize tumor microenvironment and can be used in a combinatorial treatment with chemo-, immune- or radiation therapy (1). Specific guidelines for the optimal use of these therapeutic strategies is essential given the dynamic and highly heterogeneous nature of tumors and the differences between primary tumors and metastases. Importantly, these strategies have to be tailored to individual patients, and techniques, such as imaging methods, must be developed to enable this personalization.
Acknowledgments
We thank Drs. James Baish, Vikash Chauhan, Lance Munn and Mei Ng for useful comments on the manuscript. RKJ would like to thank the National Cancer Institute for continuously supporting his research on the role of physical forces in tumor growth and treatment since 1980, and would like to acknowledge his current support from the National Cancer Institute (P01-CA080124, R01-CA126642, R01-CA115767, R01-CA096915, R01-CA085140, R01-CA098706, T32-CA073479), a DoD Breast Cancer Research Innovator award (W81XWH-10-1-0016), and a grant from the Lustgarten Foundation via the Bridge Program. TS is supported by the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement no 336839-ReEngineeringCancer.
Footnotes
Conflict of Interests: R.K.J. received research grants from Dyax, MedImmune and Roche; consultant fees from Enlight, Noxxon, SynDevRx and Zyngenia; owns equity in Enlight, SynDevRx and XTuit, serves on the Board of Directors of XTuit and Board of Trustees of H&Q Healthcare Investors and H&Q Life Sciences Investors. No reagents or funding from these companies was used in these studies. Therefore, there is no significant financial or other competing interest in the work.
Cited Literature
- 1.Jain RK. Normalizing tumor microenvironment to treat cancer: Bench to bedside to biomarkers. J Clin Oncol. 2013;31:2205–18. doi: 10.1200/JCO.2012.46.3653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stylianopoulos T, Martin JD, Chauhan VP, Jain SR, Diop-Frimpong B, et al. Causes, consequences, and remedies for growth-induced solid stress in murine and human tumors. Proc. Natl. Acad. Sci. U. S. A. 2012;109:15101–8. doi: 10.1073/pnas.1213353109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Stylianopoulos T, Martin JD, Snuderl M, Mpekris F, Jain SR, Jain RK. Coevolution of solid stress and interstitial fluid pressure in tumors during progression: Implications for vascular collapse. Cancer Res. 2013;73:3833–41. doi: 10.1158/0008-5472.CAN-12-4521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Helmlinger G, Netti PA, Lichtenbeld HC, Melder RJ, Jain RK. Solid stress inhibits the growth of multicellular tumor spheroids. Nat Biotechnol. 1997;15:778–83. doi: 10.1038/nbt0897-778. [DOI] [PubMed] [Google Scholar]
- 5.Tomasek JJ, Gabbiani G, Hinz B, Chaponnier C, Brown RA. Myofibroblasts and mechano-regulation of connective tissue remodelling. Nat Rev Mol Cell Biol. 2002;3:349–63. doi: 10.1038/nrm809. [DOI] [PubMed] [Google Scholar]
- 6.Paszek MJ, Weaver VM. The tension mounts: Mechanics meets morphogenesis and malignancy. J Mammary Gland Biol Neoplasia. 2004;9:325–42. doi: 10.1007/s10911-004-1404-x. [DOI] [PubMed] [Google Scholar]
- 7.Wipff PJ, Hinz B. Myofibroblasts work best under stress. J Bodyw Mov Ther. 2009;13:121–7. doi: 10.1016/j.jbmt.2008.04.031. [DOI] [PubMed] [Google Scholar]
- 8.Cheng G, Tse J, Jain RK, Munn LL. Micro-environmental mechanical stress controls tumor spheroid size and morphology by suppressing proliferation and inducing apoptosis in cancer cells. PLoS One. 2009;4:e4632. doi: 10.1371/journal.pone.0004632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Demou ZN. Gene expression profiles in 3D tumor analogs indicate compressive strain differentially enhances metastatic potential. Ann Biomed Eng. 2010;38:3509–20. doi: 10.1007/s10439-010-0097-0. [DOI] [PubMed] [Google Scholar]
- 10.Tse JM, Cheng G, Tyrrell JA, Wilcox-Adelman SA, Boucher Y, et al. Mechanical compression drives cancer cells toward invasive phenotype. PNAS. 2012;109:911–916. doi: 10.1073/pnas.1118910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Helmlinger G, Yuan F, Dellian M, Jain RK. Interstitial pH and pO2 gradients in solid tumors in vivo: High-resolution measurements reveal a lack of correlation. Nat Med. 1997;3:177–82. doi: 10.1038/nm0297-177. [DOI] [PubMed] [Google Scholar]
- 12.Griffon-Etienne G, Boucher Y, Brekken C, Suit HD, Jain RK. Taxane-induced apoptosis decompresses blood vessels and lowers interstitial fluid pressure in solid tumors: Clinical implications. Cancer Res. 1999;59:3776–82. [PubMed] [Google Scholar]
- 13.Padera TP, Stoll BR, Tooredman JB, Capen D, di Tomaso E, Jain RK. Pathology: Cancer cells compress intratumour vessels. Nature. 2004;427:695. doi: 10.1038/427695a. [DOI] [PubMed] [Google Scholar]
- 14.Provenzano PP, Cuevas C, Chang AE, Goel VK, Von Hoff DD, Hingorani SR. Enzymatic targeting of the stroma ablates physical barriers to treatment of pancreatic ductal adenocarcinoma. Cancer Cell. 2012;21:418–29. doi: 10.1016/j.ccr.2012.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stylianopoulos T, Jain RK. Therapeutic strategies to improve perfusion and drug delivery in solid tumors. Proc Natl Acad Sci U S A. 2013;110:18632–18637. doi: 10.1073/pnas.1318415110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Koumoutsakos P, Pivkin I, Milde F. The fluid mechanics of cancer and its therapy. Annual Review of Fluid Mechanics. 2013;45:325–55. [Google Scholar]
- 17.Jain RK. Determinants of tumor blood flow: A review. Cancer Res. 1988;48:2641–58. [PubMed] [Google Scholar]
- 18.Jain RK, Baxter LT. Mechanisms of heterogeneous distribution of monoclonal antibodies and other macromolecules in tumors: Significance of elevated interstitial pressure. Cancer Res. 1988;48:7022–32. [PubMed] [Google Scholar]
- 19.Baxter LT, Jain RK. Transport of fluid and macromolecules in tumors. I. role of interstitial pressure and convection. Microvasc Res. 1989;37:77–104. doi: 10.1016/0026-2862(89)90074-5. [DOI] [PubMed] [Google Scholar]
- 20.Baxter LT, Jain RK. Transport of fluid and macromolecules in tumors. II. role of heterogeneous perfusion and lymphatics. Microvasc Res. 1990;40:246–63. doi: 10.1016/0026-2862(90)90023-k. [DOI] [PubMed] [Google Scholar]
- 21.Boucher Y, Baxter LT, Jain RK. Interstitial pressure gradients in tissue-isolated and subcutaneous tumors: Implications for therapy. Cancer Res. 1990;50:4478–84. [PubMed] [Google Scholar]
- 22.Jain RK, Tong RT, Munn LL. Effect of vascular normalization by antiangiogenic therapy on interstitial hypertension, peritumor edema, and lymphatic metastasis: Insights from a mathematical model. Cancer Res. 2007;67:2729–35. doi: 10.1158/0008-5472.CAN-06-4102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chauhan VP, Stylianopoulos T, Martin JD, Popovic Z, Chen O, et al. Normalization of tumour blood vessels improves the delivery of nanomedicines in a size-dependent manner. Nat Nanotechnol. 2012;7:383–388. doi: 10.1038/nnano.2012.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hagendoorn J, Tong R, Fukumura D, Lin Q, Lobo J, et al. Onset of abnormal blood and lymphatic vessel function and interstitial hypertension in early stages of carcinogenesis. Cancer Res. 2006;66:3360–4. doi: 10.1158/0008-5472.CAN-05-2655. [DOI] [PubMed] [Google Scholar]
- 25.Kaufman LJ, Brangwynne CP, Kasza KE, Filippidi E, Gordon VD, et al. Glioma expansion in collagen I matrices: Analyzing collagen concentration-dependent growth and motility patterns. Biophys J. 2005;89:635–50. doi: 10.1529/biophysj.105.061994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Koike C, McKee TD, Pluen A, Ramanujan S, Burton K, et al. Solid stress facilitates spheroid formation: Potential involvement of hyaluronan. Br J Cancer. 2002;86:947–53. doi: 10.1038/sj.bjc.6600158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rivron NC, Vrij EJ, Rouwkema J, Le Gac S, van den Berg A, et al. Tissue deformation spatially modulates VEGF signaling and angiogenesis. Proc. Natl. Acad. Sci. U. S. A. 2012;109:6886–91. doi: 10.1073/pnas.1201626109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Roose T, Netti PA, Munn LL, Boucher Y, Jain RK. Solid stress generated by spheroid growth estimated using a linear poroelasticity model. Microvasc Res. 2003;66:204–12. doi: 10.1016/s0026-2862(03)00057-8. [DOI] [PubMed] [Google Scholar]
- 29.Sarntinoranont M, Rooney F, Ferrari M. Interstitial stress and fluid pressure within a growing tumor. Ann Biomed Eng. 2003;31:327–35. doi: 10.1114/1.1554923. [DOI] [PubMed] [Google Scholar]
- 30.Branton MH, Kopp JB. TGF-beta and fibrosis. Microbes Infect. 1999;1:1349–65. doi: 10.1016/s1286-4579(99)00250-6. [DOI] [PubMed] [Google Scholar]
- 31.Butcher DT, Alliston T, Weaver VM. A tense situation: Forcing tumour progression. Nat Rev Cancer. 2009;9:108–22. doi: 10.1038/nrc2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Egeblad M, Rasch MG, Weaver VM. Dynamic interplay between the collagen scaffold and tumor evolution. Curr Opin Cell Biol. 2010;22:697–706. doi: 10.1016/j.ceb.2010.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Paszek MJ, Zahir N, Johnson KR, Lakins JN, Rozenberg GI, et al. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–54. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 34.Samuel MS, Lopez JI, McGhee EJ, Croft DR, Strachan D, et al. Actomyosin-mediated cellular tension drives increased tissue stiffness and beta-catenin activation to induce epidermal hyperplasia and tumor growth. Cancer Cell. 2011;19:776–91. doi: 10.1016/j.ccr.2011.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Friedland JC, Lee MH, Boettiger D. Mechanically activated integrin switch controls alpha5beta1 function. Science. 2009;323:642–4. doi: 10.1126/science.1168441. [DOI] [PubMed] [Google Scholar]
- 36.Levental KR, Yu H, Kass L, Lakins JN, Egeblad M, et al. Matrix crosslinking forces tumor progression by enhancing integrin signaling. Cell. 2009;139:891–906. doi: 10.1016/j.cell.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wipff PJ, Rifkin DB, Meister JJ, Hinz B. Myofibroblast contraction activates latent TGF-beta1 from the extracellular matrix. J Cell Biol. 2007;179:1311–23. doi: 10.1083/jcb.200704042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Karagiannis GS, Poutahidis T, Erdman SE, Kirsch R, Riddell RH, Diamandis EP. Cancer-associated fibroblasts drive the progression of metastasis through both paracrine and mechanical pressure on cancer tissue. Mol. Cancer. Res. 2012;10:1403–18. doi: 10.1158/1541-7786.MCR-12-0307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Potenta S, Zeisberg E, Kalluri R. The role of endothelial-to-mesenchymal transition in cancer progression. Br J Cancer. 2008;99:1375–9. doi: 10.1038/sj.bjc.6604662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kalluri R, Weinberg RA. The basics of epithelial-mesenchymal transition. J Clin Invest. 2009;119:1420–8. doi: 10.1172/JCI39104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Huang Y, Goel S, Duda DG, Fukumura D, Jain RK. Vascular normalization as an emerging strategy to enhance cancer immunotherapy. Cancer Res. 2013;73:2943–8. doi: 10.1158/0008-5472.CAN-12-4354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Facciabene A, Peng X, Hagemann IS, Balint K, Barchetti A, et al. Tumour hypoxia promotes tolerance and angiogenesis via CCL28 and T(reg) cells. Nature. 2011;475:226–30. doi: 10.1038/nature10169. [DOI] [PubMed] [Google Scholar]
- 43.Goel S, Duda DG, Xu L, Munn LL, Boucher Y, et al. Normalization of the vasculature for treatment of cancer and other diseases. Physiol Rev. 2011;91:1071–121. doi: 10.1152/physrev.00038.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wilson WR, Hay MP. Targeting hypoxia in cancer therapy. Nat. Rev. Cancer. 2011;11:393–410. doi: 10.1038/nrc3064. [DOI] [PubMed] [Google Scholar]
- 45.Carmeliet P, Jain RK. Molecular mechanisms and clinical applications of angiogenesis. Nature. 2011;473:298–307. doi: 10.1038/nature10144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pries AR, Hopfner M, le Noble F, Dewhirst MW, Secomb TW. The shunt problem: Control of functional shunting in normal and tumour vasculature. Nat Rev Cancer. 2010;10:587–93. doi: 10.1038/nrc2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kamoun WS, Chae SS, Lacorre DA, Tyrrell JA, Mitre M, et al. Simultaneous measurement of RBC velocity, flux, hematocrit and shear rate in vascular networks. Nat Methods. 2010;7:655–60. doi: 10.1038/nmeth.1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Baish JW, Stylianopoulos T, Lanning RM, Kamoun WS, Fukumura D, et al. Scaling rules for diffusive drug delivery in tumor and normal tissues. Proc Natl Acad Sci U S A. 2011;108:1799–803. doi: 10.1073/pnas.1018154108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Boucher Y, Kirkwood JM, Opacic D, Desantis M, Jain RK. Interstitial hypertension in superficial metastatic melanomas in humans. Cancer Res. 1991;51:6691–4. [PubMed] [Google Scholar]
- 50.Less JR, Posner MC, Boucher Y, Borochovitz D, Wolmark N, Jain RK. Interstitial hypertension in human breast and colorectal tumors. Cancer Res. 1992;52:6371–4. [PubMed] [Google Scholar]
- 51.Ambrosi D, Mollica F. On the mechanics of a growing tumor. International journal of engineering science. 2002;40:1297–316. [Google Scholar]
- 52.Ambrosi D, Preziosi L. Cell adhesion mechanisms and stress relaxation in the mechanics of tumours. Biomech. Model. Mechanobiol. 2009;8:397–413. doi: 10.1007/s10237-008-0145-y. [DOI] [PubMed] [Google Scholar]
- 53.MacLaurin J, Chapman J, Jones GW, Roose T. The buckling of capillaries in solid tumours. Proc. R. Soc. A. 2012;468:4123–45. [Google Scholar]
- 54.Ciarletta P. Buckling instability in growing tumor spheroids. Phys Rev Lett. 2013;110:158102. doi: 10.1103/PhysRevLett.110.158102. [DOI] [PubMed] [Google Scholar]
- 55.Byrne H, Preziosi L. Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. 2003;20:341–66. doi: 10.1093/imammb/20.4.341. [DOI] [PubMed] [Google Scholar]
- 56.Stylianopoulos T, Barocas VH. Multiscale, structure-based modeling for the elastic mechanical behavior of arterial walls. J Biomech Eng. 2007;129:611–8. doi: 10.1115/1.2746387. [DOI] [PubMed] [Google Scholar]
- 57.Sander E, Stylianopoulos T, Tranquillo R, Barocas V. Image-based biomechanics of collagen-based tissue equivalents. IEEE Eng Med Biol Mag. 2009;28:10–8. doi: 10.1109/MEMB.2009.932486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chauhan VP, Stylianopoulos T, Boucher Y, Jain RK. Delivery of molecular and nanomedicine to tumors: Transport barriers and strategies. Annual Reviews Chemical and Biomolecular Engineering. 2011;2:281–98. doi: 10.1146/annurev-chembioeng-061010-114300. [DOI] [PubMed] [Google Scholar]
- 59.Sevick EM, Jain RK. Geometric resistance to blood flow in solid tumors perfused ex vivo: Effects of tumor size and perfusion pressure. Cancer Res. 1989;49:3506–12. [PubMed] [Google Scholar]
- 60.Sevick EM, Jain RK. Viscous resistance to blood flow in solid tumors: Effect of hematocrit on intratumor blood viscosity. Cancer Res. 1989;49:3513–9. [PubMed] [Google Scholar]
- 61.Carmeliet P, Jain RK. Angiogenesis in cancer and other diseases. Nature. 2000;407:249–57. doi: 10.1038/35025220. [DOI] [PubMed] [Google Scholar]
- 62.Jain RK. Normalization of tumor vasculature: An emerging concept in antiangiogenic therapy. Science. 2005;307:58–62. doi: 10.1126/science.1104819. [DOI] [PubMed] [Google Scholar]
- 63.Leunig M, Yuan F, Menger MD, Boucher Y, Goetz AE, et al. Angiogenesis, microvascular architecture, microhemodynamics, and interstitial fluid pressure during early growth of human adenocarcinoma LS174T in SCID mice. Cancer Res. 1992;52:6553–60. [PubMed] [Google Scholar]
- 64.Vakoc BJ, Lanning RM, Tyrrell JA, Padera TP, Bartlett LA, et al. Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging. Nat Med. 2009;15:1219–23. doi: 10.1038/nm.1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Jain RK. Transport of molecules across tumor vasculature. Cancer Metastasis Rev. 1987;6:559–93. doi: 10.1007/BF00047468. [DOI] [PubMed] [Google Scholar]
- 66.Hobbs SK, Monsky WL, Yuan F, Roberts WG, Griffith L, et al. Regulation of transport pathways in tumor vessels: Role of tumor type and microenvironment. Proc Natl Acad Sci U S A. 1998;95:4607–12. doi: 10.1073/pnas.95.8.4607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Hashizume H, Baluk P, Morikawa S, McLean JW, Thurston G, et al. Openings between defective endothelial cells explain tumor vessel leakiness. Am J Pathol. 2000;156:1363–80. doi: 10.1016/S0002-9440(10)65006-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Less JR, Posner MC, Skalak TC, Wolmark N, Jain RK. Geometric resistance and microvascular network architecture of human colorectal carcinoma. Microcirculation. 1997;4:25–33. doi: 10.3109/10739689709148315. [DOI] [PubMed] [Google Scholar]
- 69.Sun C, Jain RK, Munn LL. Non-uniform plasma leakage affects local hematocrit and blood flow: Implications for inflammation and tumor perfusion. Ann Biomed Eng. 2007;35:2121–9. doi: 10.1007/s10439-007-9377-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Yuan F, Salehi HA, Boucher Y, Vasthare US, Tuma RF, Jain RK. Vascular permeability and microcirculation of gliomas and mammary carcinomas transplanted in rat and mouse cranial windows. Cancer Res. 1994;54:4564–8. [PubMed] [Google Scholar]
- 71.Wirtz D, Konstantopoulos K, Searson PC. The physics of cancer: The role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer. 2011;11:512–22. doi: 10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Tarbell JM, Weinbaum S, Kamm RD. Cellular fluid mechanics and mechanotransduction. Ann. Biomed. Eng. 2005;33:1719–23. doi: 10.1007/s10439-005-8775-z. [DOI] [PubMed] [Google Scholar]
- 73.Song JW, Munn LL. Fluid forces control endothelial sprouting. Proc. Natl. Acad. Sci. U. S. A. 2011;108:15342–7. doi: 10.1073/pnas.1105316108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Djonov VG, Kurz H, Burri PH. Optimality in the developing vascular system: Branching remodeling by means of intussusception as an efficient adaptation mechanism. Dev. Dyn. 2002;224:391–402. doi: 10.1002/dvdy.10119. [DOI] [PubMed] [Google Scholar]
- 75.Kamiya A, Ando J, Shibata M, Masuda H. Roles of fluid shear stress in physiological regulation of vascular structure and function. Biorheology. 1988;25:271–8. doi: 10.3233/bir-1988-251-236. [DOI] [PubMed] [Google Scholar]
- 76.Nagy JA, Dvorak AM, Dvorak HF. Vascular hyperpermeability, angiogenesis, and stroma generation. Cold Spring Harb Perspect. Med. 2012;2:a006544. doi: 10.1101/cshperspect.a006544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Kalluri R, Zeisberg M. Fibroblasts in cancer. Nat. Rev. Cancer. 2006;6:392–401. doi: 10.1038/nrc1877. [DOI] [PubMed] [Google Scholar]
- 78.Chary SR, Jain RK. Direct measurement of interstitial convection and diffusion of albumin in normal and neoplastic tissues by fluorescence photobleaching. Proceedings of the National Academy of Sciences of the United States of America. 1989;86:5385–9. doi: 10.1073/pnas.86.14.5385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Pedersen JA, Lichter S, Swartz MA. Cells in 3D matrices under interstitial flow: Effects of extracellular matrix alignment on cell shear stress and drag forces. J. Biomech. 2010;43:900–5. doi: 10.1016/j.jbiomech.2009.11.007. [DOI] [PubMed] [Google Scholar]
- 80.Ng CP, Hinz B, Swartz MA. Interstitial fluid flow induces myofibroblast differentiation and collagen alignment in vitro. J. Cell. Sci. 2005;118:4731–9. doi: 10.1242/jcs.02605. [DOI] [PubMed] [Google Scholar]
- 81.Swartz MA, Lund AW. Lymphatic and interstitial flow in the tumour microenvironment: Linking mechanobiology with immunity. Nat. Rev. Cancer. 2012;12:210–9. doi: 10.1038/nrc3186. [DOI] [PubMed] [Google Scholar]
- 82.Avvisato CL, Yang X, Shah S, Hoxter B, Li W, et al. Mechanical force modulates global gene expression and beta-catenin signaling in colon cancer cells. J. Cell. Sci. 2007;120:2672–82. doi: 10.1242/jcs.03476. [DOI] [PubMed] [Google Scholar]
- 83.Shieh AC. Biomechanical forces shape the tumor microenvironment. Ann. Biomed. Eng. 2011;39:1379–89. doi: 10.1007/s10439-011-0252-2. [DOI] [PubMed] [Google Scholar]
- 84.Levick JR. Flow through interstitium and other fibrous matrices. Q J Exp Physiol. 1987;72:409–37. doi: 10.1113/expphysiol.1987.sp003085. [DOI] [PubMed] [Google Scholar]
- 85.Stylianopoulos T, Yeckel A, Derby JJ, Luo XJ, Shephard MS, et al. Permeability calculations in three-dimensional isotropic and oriented fiber networks. Phys Fluids. 2008;20:123601. doi: 10.1063/1.3021477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Netti PA, Berk DA, Swartz MA, Grodzinsky AJ, Jain RK. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer Res. 2000;60:2497–503. [PubMed] [Google Scholar]
- 87.Huijbers IJ, Iravani M, Popov S, Robertson D, Al-Sarraj S, et al. A role for fibrillar collagen deposition and the collagen internalization receptor endo180 in glioma invasion. PLoS One. 2010;5:e9808. doi: 10.1371/journal.pone.0009808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Mok W, Boucher Y, Jain RK. Matrix metalloproteinases-1 and -8 improve the distribution and efficacy of an oncolytic virus. Cancer Res. 2007;67:10664–8. doi: 10.1158/0008-5472.CAN-07-3107. [DOI] [PubMed] [Google Scholar]
- 89.Clayes IL, Brady JF. Suspensions of prolate spheroids in stokes flow. part 2. statistically homogeneous dispersions. Journal of Fluid Mechanics. 1993;251:443–77. [Google Scholar]
- 90.Stylianopoulos T, Diop-Frimpong B, Munn LL, Jain RK. Diffusion anisotorpy in collagen gels and tumors: The effect of fiber network orientation. Biophys J. 2010;99:3119–28. doi: 10.1016/j.bpj.2010.08.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Leu AJ, Berk DA, Lymboussaki A, Alitalo K, Jain RK. Absence of functional lymphatics within a murine sarcoma: A molecular and functional evaluation. Cancer Res. 2000;60:4324–7. [PubMed] [Google Scholar]
- 92.Padera TP, Kadambi A, di Tomaso E, Carreira CM, Brown EB, et al. Lymphatic metastasis in the absence of functional intratumor lymphatics. Science. 2002;296:1883–6. doi: 10.1126/science.1071420. [DOI] [PubMed] [Google Scholar]
- 93.Isaka N, Padera TP, Hagendoorn J, Fukumura D, Jain RK. Peritumor lymphatics induced by vascular endothelial growth factor-C exhibit abnormal function. Cancer Res. 2004;64:4400–4. doi: 10.1158/0008-5472.CAN-04-0752. [DOI] [PubMed] [Google Scholar]
- 94.Hoshida T, Isaka N, Hagendoorn J, di Tomaso E, Chen YL, et al. Imaging steps of lymphatic metastasis reveals that vascular endothelial growth factor-C increases metastasis by increasing delivery of cancer cells to lymph nodes: Therapeutic implications. Cancer Res. 2006;66:8065–75. doi: 10.1158/0008-5472.CAN-06-1392. [DOI] [PubMed] [Google Scholar]
- 95.Jeltsch M, Kaipainen A, Joukov V, Meng X, Lakso M, et al. Hyperplasia of lymphatic vessels in VEGF-C transgenic mice. Science. 1997;276:1423–5. doi: 10.1126/science.276.5317.1423. [DOI] [PubMed] [Google Scholar]
- 96.Alitalo K, Tammela T, Petrova TV. Lymphangiogenesis in development and human disease. Nature. 2005;438:946–53. doi: 10.1038/nature04480. [DOI] [PubMed] [Google Scholar]
- 97.Berk DA, Swartz MA, Leu AJ, Jain RK. Transport in lymphatic capillaries. II. microscopic velocity measurement with fluorescence photobleaching. Am J Physiol. 1996;270:H330–7. doi: 10.1152/ajpheart.1996.270.1.H330. [DOI] [PubMed] [Google Scholar]
- 98.Fischer M, Franzeck UK, Herrig I, Costanzo U, Wen S, et al. Flow velocity of single lymphatic capillaries in human skin. Am J Physiol. 1996;270:H358–63. doi: 10.1152/ajpheart.1996.270.1.H358. [DOI] [PubMed] [Google Scholar]
- 99.Swartz MA, Berk DA, Jain RK. Transport in lymphatic capillaries. I. macroscopic measurements using residence time distribution theory. Am J Physiol. 1996;270:H324–9. doi: 10.1152/ajpheart.1996.270.1.H324. [DOI] [PubMed] [Google Scholar]
- 100.Hagendoorn J, Padera TP, Kashiwagi S, Isaka N, Noda F, et al. Endothelial nitric oxide synthase regulates microlymphatic flow via collecting lymphatics. Circ Res. 2004;95:204–9. doi: 10.1161/01.RES.0000135549.72828.24. [DOI] [PubMed] [Google Scholar]
- 101.Gasheva OY, Zawieja DC, Gashev AA. Contraction-initiated NO-dependent lymphatic relaxation: A self-regulatory mechanism in rat thoracic duct. J Physiol. 2006;575:821–32. doi: 10.1113/jphysiol.2006.115212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Kajiya K, Huggenberger R, Drinnenberg I, Ma B, Detmar M. Nitric oxide mediates lymphatic vessel activation via soluble guanylate cyclase alpha1beta1-impact on inflammation. FASEB J. 2008;22:530–7. doi: 10.1096/fj.07-8873com. [DOI] [PubMed] [Google Scholar]
- 103.Liao S, Cheng G, Conner DA, Huang Y, Kucherlapati RS, et al. Impaired lymphatic contraction associated with immunosuppression. Proc. Natl. Acad. Sci. U. S. A. 2011;108:18784–9. doi: 10.1073/pnas.1116152108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Kesler CT, Liao S, Munn LL, Padera TP. Lymphatic vessels in health and disease. Wiley Interdiscip. Rev. Syst. Biol. Med. 2013;5:111–24. doi: 10.1002/wsbm.1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Ng CP, Helm CL, Swartz MA. Interstitial flow differentially stimulates blood and lymphatic endothelial cell morphogenesis in vitro. Microvasc Res. 2004;68:258–64. doi: 10.1016/j.mvr.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 106.Miteva DO, Rutkowski JM, Dixon JB, Kilarski W, Shields JD, Swartz MA. Transmural flow modulates cell and fluid transport functions of lymphatic endothelium. Circ Res. 2010;106:920–31. doi: 10.1161/CIRCRESAHA.109.207274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Yuan F, Leunig M, Huang SK, Berk DA, Papahadjopoulos D, Jain RK. Microvascular permeability and interstitial penetration of sterically stabilized (stealth) liposomes in a human tumor xenograft. Cancer Res. 1994;54:3352–6. [PubMed] [Google Scholar]
- 108.Boucher Y, Jain RK. Microvascular pressure is the principal driving force for interstitial hypertension in solid tumors: Implications for vascular collapse. Cancer Res. 1992;52:5110–4. [PubMed] [Google Scholar]
- 109.Nathanson SD, Nelson L. Interstitial fluid pressure in breast cancer, benign breast conditions, and breast parenchyma. Ann Surg Oncol. 1994;1:333–8. doi: 10.1007/BF03187139. [DOI] [PubMed] [Google Scholar]
- 110.Willett CG, Boucher Y, di Tomaso E, Duda DG, Munn LL, et al. Direct evidence that the VEGF-specific antibody bevacizumab has antivascular effects in human rectal cancer. Nat Med. 2004;10:145–7. doi: 10.1038/nm988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Willett CG, Duda DG, di Tomaso E, Boucher Y, Ancukiewicz M, et al. Efficacy, safety, and biomarkers of neoadjuvant bevacizumab, radiation therapy, and fluorouracil in rectal cancer: A multidisciplinary phase II study. J Clin Oncol. 2009;27:3020–6. doi: 10.1200/JCO.2008.21.1771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Young JS, Lumsden CE, Stalker AL. The significance of the ‘tissue pressure’ of normal testicular and of neoplastic (brown-pearce carcinoma) tissue in the rabbit. J Path Bact. 1950;62:313–33. doi: 10.1002/path.1700620303. [DOI] [PubMed] [Google Scholar]
- 113.Stylianopoulos T, Soteriou K, Fukumura D, Jain RK. Cationic nanoparticles have superior transvascular flux into solid tumors: Insights from a mathematical model. Ann Biomed Eng. 2013;41(1):68–77. doi: 10.1007/s10439-012-0630-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Baish JW, Netti PA, Jain RK. Transmural coupling of fluid flow in microcirculatory network and interstitium in tumors. Microvasc Res. 1997;53:128–41. doi: 10.1006/mvre.1996.2005. [DOI] [PubMed] [Google Scholar]
- 115.Pozrikidis C, Farrow DA. A model of fluid flow in solid tumors. Ann Biomed Eng. 2003;31:181–94. doi: 10.1114/1.1540103. [DOI] [PubMed] [Google Scholar]
- 116.Pries AR, Secomb TW, Gaehtgens P, Gross JF. Blood flow in microvascular networks. experiments and simulation. Circ Res. 1990;67:826–34. doi: 10.1161/01.res.67.4.826. [DOI] [PubMed] [Google Scholar]
- 117.Welter M, Bartha K, Rieger H. Emergent vascular network inhomogeneities and resulting blood flow patterns in a growing tumor. J Theor Biol. 2008;250:257–80. doi: 10.1016/j.jtbi.2007.09.031. [DOI] [PubMed] [Google Scholar]
- 118.Cai Y, Xu S, Wu J, Long Q. Coupled modelling of tumour angiogenesis, tumour growth and blood perfusion. J. Theor. Biol. 2011;279:90–101. doi: 10.1016/j.jtbi.2011.02.017. [DOI] [PubMed] [Google Scholar]
- 119.Wu M, Frieboes HB, McDougall SR, Chaplain MA, Cristini V, Lowengrub J. The effect of interstitial pressure on tumor growth: Coupling with blood and lymphatic vascular systems. J Theor Biol. 2012;320:131–51. doi: 10.1016/j.jtbi.2012.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Pozrikidis C. Axisymmetric motion of a file of red blood cells through capillaries. Phys Fluids. 2005;17:1–14. [Google Scholar]
- 121.Sun C, Munn LL. Particulate nature of blood determines macroscopic rheology: A 2-D lattice boltzmann analysis. Biophys J. 2005;88:1635–45. doi: 10.1529/biophysj.104.051151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Dupin MM, Halliday I, Care CM, Alboul L, Munn LL. Modeling the flow of dense suspensions of deformable particles in three dimensions. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;75:066707. doi: 10.1103/PhysRevE.75.066707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Pivkin IV, Karniadakis GE. Accurate coarse-grained modeling of red blood cells. Phys. Rev. Lett. 2008;101:118105. doi: 10.1103/PhysRevLett.101.118105. [DOI] [PubMed] [Google Scholar]
- 124.Li X, Vlahovska PM, Karniadakis GE. Continuum- and particle-based modeling of shapes and dynamics of red blood cells in health and disease. Soft Matter. 2013;9:28–37. doi: 10.1039/C2SM26891D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Pries AR, Cornelissen AJ, Sloot AA, Hinkeldey M, Dreher MR, et al. Structural adaptation and heterogeneity of normal and tumor microvascular networks. PLoS Comput Biol. 2009;5:e1000394. doi: 10.1371/journal.pcbi.1000394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Jackson GW, James DF. The permeability of fibrous porous-media. Canadian Journal of Chemical Engineering. 1986;64:364–74. [Google Scholar]
- 127.Ethier R. Flow through mixed fibrous porous materials. AIChE J. 1994;37:1227–36. [Google Scholar]
- 128.Mattern KJ, Nakornchai C, Deen WM. Darcy permeability of agarose-glycosaminoglycan gels analyzed using fiber-mixture and donnan models. Biophys J. 2008;95:648–56. doi: 10.1529/biophysj.107.127316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Jain RK. Transport of molecules in the tumor interstitium: A review. Cancer Research. 1987;47:3039–51. [PubMed] [Google Scholar]
- 130.Roose T, Swartz MA. Multiscale modeling of lymphatic drainage from tissues using homogenization theory. J. Biomech. 2012;45:107–15. doi: 10.1016/j.jbiomech.2011.09.015. [DOI] [PubMed] [Google Scholar]
- 131.Kunert C, Padera TP, Munn LL. Nitric oxide kinetics drive lymphatic pumping. 2013. Under review.
- 132.Olive KP, Jacobetz MA, Davidson CJ, Gopinathan A, McIntyre D, et al. Inhibition of hedgehog signaling enhances delivery of chemotherapy in a mouse model of pancreatic cancer. Science. 2009;324:1457–61. doi: 10.1126/science.1171362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Jacobetz MA, Chan DS, Neesse A, Bapiro TE, Cook N, et al. Hyaluronan impairs vascular function and drug delivery in a mouse model of pancreatic cancer. Gut. 2012;62:112–20. doi: 10.1136/gutjnl-2012-302529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Liu J, Liao S, Diop-Frimpong B, Chen W, Goel S, et al. TGF-beta blockade improves the distribution and efficacy of therapeutics in breast carcinoma by normalizing the tumor stroma. Proc Natl Acad Sci U S A. 2012;109:16618–23. doi: 10.1073/pnas.1117610109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Chauhan VP, Martin JD, Liu H, Lacorre DA, Jain SR, et al. Angiotensin inhibition enhances drug delivery and potentiates chemotherapy by decompressing tumor blood vessels. Nature Communications. 2013;4:2516. doi: 10.1038/ncomms3516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Diop-Frimpong B, Chauhan VP, Krane S, Boucher Y, Jain RK. Losartan inhibits collagen I synthesis and improves the distribution and efficacy of nanotherapeutics in tumors. Proc Natl Acad Sci U S A. 2011;108:2909–14. doi: 10.1073/pnas.1018892108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Nakai Y, Isayama H, Ijichi H, Sasaki T, Sasahira N, et al. Inhibition of renin-angiotensin system affects prognosis of advanced pancreatic cancer receiving gemcitabine. Br. J. Cancer. 2010;103:1644–8. doi: 10.1038/sj.bjc.6605955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Wilop S, von Hobe S, Crysandt M, Esser A, Osieka R, Jost E. Impact of angiotensin I converting enzyme inhibitors and angiotensin II type 1 receptor blockers on survival in patients with advanced non-small-cell lung cancer undergoing first-line platinum-based chemotherapy. J Cancer Res Clin Oncol. 2009;135:1429–35. doi: 10.1007/s00432-009-0587-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Keizman D, Huang P, Eisenberger MA, Pili R, Kim JJ, et al. Angiotensin system inhibitors and outcome of sunitinib treatment in patients with metastatic renal cell carcinoma: A retrospective examination. Eur. J. Cancer. 2011;47:1955–61. doi: 10.1016/j.ejca.2011.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Jain RK. Normalizing tumor vasculature with anti-angiogenic therapy: A new paradigm for combination therapy. Nat Med. 2001;7:987–9. doi: 10.1038/nm0901-987. [DOI] [PubMed] [Google Scholar]
- 141.Lee CG, Heijn M, di Tomaso E, Griffon-Etienne G, Ancukiewicz M, et al. Anti-vascular endothelial growth factor treatment augments tumor radiation response under normoxic or hypoxic conditions. Cancer Res. 2000;60:5565–70. [PubMed] [Google Scholar]
- 142.Izumi Y, Xu L, di Tomaso E, Fukumura D, Jain RK. Tumour biology: Herceptin acts as an anti-angiogenic cocktail. Nature. 2002;416:279–80. doi: 10.1038/416279b. [DOI] [PubMed] [Google Scholar]
- 143.Wildiers H, Guetens G, De Boeck G, Verbeken E, Landuyt B, et al. Effect of antivascular endothelial growth factor treatment on the intratumoral uptake of CPT-11. Br J Cancer. 2003;88:1979–86. doi: 10.1038/sj.bjc.6601005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Tong RT, Boucher Y, Kozin SV, Winkler F, Hicklin DJ, Jain RK. Vascular normalization by vascular endothelial growth factor receptor 2 blockade induces a pressure gradient across the vasculature and improves drug penetration in tumors. Cancer Res. 2004;64:3731–6. doi: 10.1158/0008-5472.CAN-04-0074. [DOI] [PubMed] [Google Scholar]
- 145.Huang Y, Yuan J, Righi E, Kamoun WS, Ancukiewicz M, et al. Vascular normalizing doses of antiangiogenic treatment reprogram the immunosuppressive tumor microenvironment and enhance immunotherapy. Proc. Natl. Acad. Sci. U. S. A. 2012;109:17561–6. doi: 10.1073/pnas.1215397109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Emblem KE, Mouridsen K, Bjornerud A, Farrar C, Jennings D, et al. Vascular architecture imaging identifies patient responders to anti-angiogenic therapy. Nat Med. 2013;19:1178–1183. doi: 10.1038/nm.3289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Batchelor TT, Gerstner ER, Emblem KE, Duda DG, Kalpathy-Cramer J, et al. Increased perfusion due to vascular normalization improves oxygenation and survival in glioblastoma patients treated with cediranib and chemoradiation. Proc Natl Acad Sci U S A. 2013;110:19059–19064. doi: 10.1073/pnas.1318022110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Batchelor TT, Sorensen AG, di Tomaso E, Zhang WT, Duda DG, et al. AZD2171, a pan-VEGF receptor tyrosine kinase inhibitor, normalizes tumor vasculature and alleviates edema in glioblastoma patients. Cancer Cell. 2007;11:83–95. doi: 10.1016/j.ccr.2006.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Sorensen AG, Batchelor TT, Zhang WT, Chen PJ, Yeo P, et al. A “vascular normalization index” as potential mechanistic biomarker to predict survival after a single dose of cediranib in recurrent glioblastoma patients. Cancer Res. 2009;69:5296–300. doi: 10.1158/0008-5472.CAN-09-0814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Sorensen AG, Emblem KE, Polaskova P, Jennings D, Kim H, et al. Increased survival of glioblastoma patients who respond to anti-angiogenic therapy with elevated blood perfusion. Cancer Res. 2012;72:402–407. doi: 10.1158/0008-5472.CAN-11-2464. [DOI] [PMC free article] [PubMed] [Google Scholar]