Inter-modality Relationship Constrained Multi-Task Feature Selection for AD/MCI Classification

Abstract

In conventional multi-modality based classification framework, feature selection is typically performed separately for each individual modality, ignoring potential strong inter-modality relationship of the same subject. To extract this inter-modality relationship, L_2,1 norm-based multi-task learning approach can be used to jointly select common features from different modalities. Unfortunately, this approach overlooks different yet complementary information conveyed by different modalities. To address this issue, we propose a novel multi-task feature selection method to effectively preserve the complementary information between different modalities, improving brain disease classification accuracy. Specifically, a new constraint is introduced to preserve the inter-modality relationship by treating the feature selection procedure of each modality as a task. This constraint preserves distance between feature vectors from different modalities after projection to low dimensional feature space. We evaluated our method on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset and obtained significant improvement on Alzheimer’s Disease (AD) and Mild Cognitive Impairment (MCI) classification compared to state-of-the-art methods.

1 Introduction

Alzheimer’s Disease (AD) that is highly related to the central nervous system is a genetically complex and irreversible neurodegenerative disorder. AD is the most common form of dementia diagnosed in people over 65 years of age, and is characterized by a decline in cognitive and memory functions [1]. Efforts have been made for the past few decades to understand the pathophysiological underpinnings of AD and its intermediate stage, i.e., Mild Cognitive Impairment (MCI) [2]. Previous study suggest that individuals with MCI tend to progress to AD at a rate of approximately 10% to 15% per year, compared to Normal Controls (NC) who tend to develop dementia at a rate of 1% to 2% per year [3]. Due to high progression rate, it is crucial to accurately identify AD in its early stage for possible treatment and intervention.

There is ample evidence showing individuals with AD are significantly affected in their brain functions and structures. For example, Greicius et al. found that disrupted connectivity between posterior cingulate and hippocampus accounted for the posterior cingulate hypometabolism [4]. In addition, Guo et al. reported that patients with AD exhibited significant decrease of gray matter volume in the hippocampus, parahippocampal gyrus, insula and superior temporal gyrus, suggesting the potential of using these regions as an imaging marker for AD [5]. However, these findings are solely based on univariate or group-level statistical methods, and thus are of limited utility for individual-level disease diagnosis. In fact, disease diagnosis at individual level is important for clinical usage that can be accomplished through pattern classification technique. This technique is sensitive to the fine-grained spatial discriminative patterns and is effective in providing predictive value to diseases. To date, pattern classification method has been widely used on neuroimaging data to identify AD and MCI from NC [6, 7].

Recent studies demonstrate that complementary information from different neuroimaging modalities can be used jointly to improve AD/MCI diagnosis [8, 9]. However, feature selection procedure in these studies is typically performed separately for each individual modality, ignoring strong within-subject inter-modality relationship. Recently, L_2,1 norm-based multi-task learning has been proposed to simultaneously select features from different tasks based on intrinsic relationship between different tasks [10]. Learning multiple related tasks simultaneously has shown to often perform better than learning each task separately [11]. This learning approach, although enables the joint selection of common features from different modalities, unfortunately may overlook different yet complementary information conveyed by different modalities.

To address this issue, a novel multi-task learning based feature selection method is proposed to better preserve the complementary information conveyed by different modalities. In the proposed feature selection method, a new constraint is imposed to preserve the inter-modality relationship after feature projection while enforcing the sparseness of the selected features. A multi-kernel Support Vector Machine (SVM) is then adopted to combine these selected features. The proposed method has been evaluated on ADNI dataset and obtained promising results.

2 Materials and Methods

2.1 Data Acquisition and Preprocessing

Data used in this study are obtained from the ADNI dataset (http://www.loni.ucla.edu/ADNI). In total, we use 202 subjects from ADNI dataset: 51 patients with AD, 99 patients with MCI, and 52 NC. Image preprocessing is carried out separately for magnetic resonance imaging (MRI) and Fluorodeoxyglucose (FDG) Positron-Emission Tomography (PET) data. The preprocessing steps of MRI data include skull-stripping [12], dura removal, intensity inhomogeneity correction, cerebellum removal, spatial segmentation and registration. We then parcellate the preprocessed images into 93 regions according to the template in [13]. Only gray matter volume of these 93 regions-of-interest is used in the study. For the preprocessing of PET images, we align the PET image of each subject to its corresponding MRI image using a rigid transformation and the average intensity of each regions-of-interest is calculated as a feature. Therefore, we have two 93-dimensional feature vectors for each subject.

2.2 Multi-Task Feature Selection

Feature selection is treated as a multi-task regression problem that incorporates the relationship between different modalities. Let ${\mathit{X}}^j={\left[{\mathit{x}}_1^j,\dots ,{\mathit{x}}_i^j,\dots ,{\mathit{x}}_n^j\right]}^T$ be a n × d matrix that represents d features of n training samples for modality j, j = 1, …, m, where m is the total number of modalities. Let ${\mathit{y}}^j={[y_1^j,\dots ,y_i^j,\dots ,y_n^j]}^T$ be a n dimensional corresponding target vector (with classification labels as values of +1 or −1 in this study) for modality j. In our application, we have two modalities (MRI and PET) and the same target vectors, i.e., m = 2 and y¹ = y². According to [14], the linear model used for prediction is defined as follows:

$${\widehat{\mathit{y}}}^j={\mathit{X}}^j{\mathit{w}}^j$$ (1)

where w^j ∈ R^d×1 and ŷ^j are the regression coefficient vector and the predicted label vector of the j-th modality, respectively. One of the popular approaches to estimate W = [w¹, …, w^j, … , w^m] is by minimizing the following objective function:

$$\underset{\mathit{w}}{min}\sum _{j=1}^m{\Vert {\mathit{X}}^j{\mathit{w}}^j-{\mathit{y}}^j\Vert }_F^2+{\lambda }_1{\Vert \mathit{W}\Vert }_1$$ (2)

where λ₁ > 0 is a regularization parameter, and ||W||₁ is the L₁ norm of W defined as ${\sum }_{i=1}^d{\sum }_{j=1}^m\left|w_{i,j}\right|$. The first term of Eq. (2) measures the empirical error on the training data while the second term controls the sparseness. This regression model is known as Least Absolute Shrinkage and Selection Operator (LASSO) [15].

The limitation of this regression model is that all tasks are assumed to be independent. Although we can use group sparsity (i.e., L_2,1 norm) to guide the selection of features for same regions from different modalities, the complementary information conveyed by different modalities might be eliminated after this group constraint. To address this problem, one effective way is to preserve the relative distance between feature vectors of different modalities of the same subject (also called as inter-modality relationship) after feature projection via the following constraint:

$$D=\sum _{i=1}^n\sum _{j=1}^m\sum _{k=1,k\ne j}^m\frac{{\Vert {\mathit{x}}_i^j{\mathit{w}}^j-{\mathit{x}}_i^k{\mathit{w}}^k\Vert }_F^2}{{\Vert {\mathit{x}}_i^j-{\mathit{x}}_i^k\Vert }_F^2}$$ (3)

where ${\mathit{x}}_i^j$ and ${\mathit{x}}_i^k$ denote the feature vectors of the j-th and k-th modalities in the i-th subject, respectively. ${\Vert {\mathit{x}}_i^j-{\mathit{x}}_i^k\Vert }_F^2$ measures the relative distance between the feature vectors ${\mathit{x}}_i^j$ and ${\mathit{x}}_i^k$ before feature projection, and ${\Vert {\mathit{x}}_i^j{\mathit{w}}^j-{\mathit{x}}_i^k{\mathit{w}}^k\Vert }_F^2$ measures the respective distance after feature projection (or the distance between the corresponding predictions). Basically, for two initial vectors with small distance, they are constrained to have small distance after projection. While for the two initial vectors with very large distance, we will put less constraint on their mapping since the inverse of their initial distance is almost zero. This constraint preserves the inter-modality relationship after projection of feature vectors from different modalities onto the low-dimensional feature space.

By incorporating this constraint into Eq. (2), we can obtain a new objective function:

$$\underset{w}{min}\sum _{j=1}^m{\Vert {\mathit{X}}^j{\mathit{w}}^j-{\mathit{y}}^j\Vert }_F^2+{\lambda }_1{\Vert \mathit{W}\Vert }_1+{\lambda }_{2}D$$ (4)

where λ₂ > 0 is the regularization parameter that controls the degree of preserving the inter-modality relationship. Of note, features from different modalities are normalized to have zero mean and unit standard deviation to enable direct combination of different types of features. In this study, we use Accelerated Proximal Gradient method [16] to optimize the objective function in Eq. (4). After feature selection, only those features with non-zero regression coefficients are used for final classification.

2.3 Multi-kernel SVM Classification

A multi-kernel SVM method is applied to integrate features from different modalities (i.e., PET and MRI) for classification via a weighted linear combination [8]. In brief, for each modality, we calculate the corresponding kernel on the basis of the features selected by the aforementioned feature selection method. Subsequently, multi-kernel SVM is used to construct a mixed kernel matrix by linearly combining kernels from different modalities. It is worth noting that the optimal parameters used for combining different kernels are determined by using grid search approach. SVM classifier with linear kernel is implemented via the LIBSVM toolbox [17].

A nested ten-fold cross-validation strategy is used to evaluate classification performance. Specifically, the inner cross-validation loop is used to determine the parameters, i.e., the regularization parameters λ₁, λ₂ and the above-mentioned kernel combination parameter from training set. The outer loop is then used to evaluate the generalizability of the SVM model by using an independent testing set. SVM model that perform the best during the inner cross-validation stage is considered as the optimal model and is used to classify unseen test samples. This process is repeated 10 times to avoid the bias introduced by randomly partitioning dataset in the cross-validation. Accuracy, sensitivity, and specificity are calculated to quantify the performance of all compared methods.

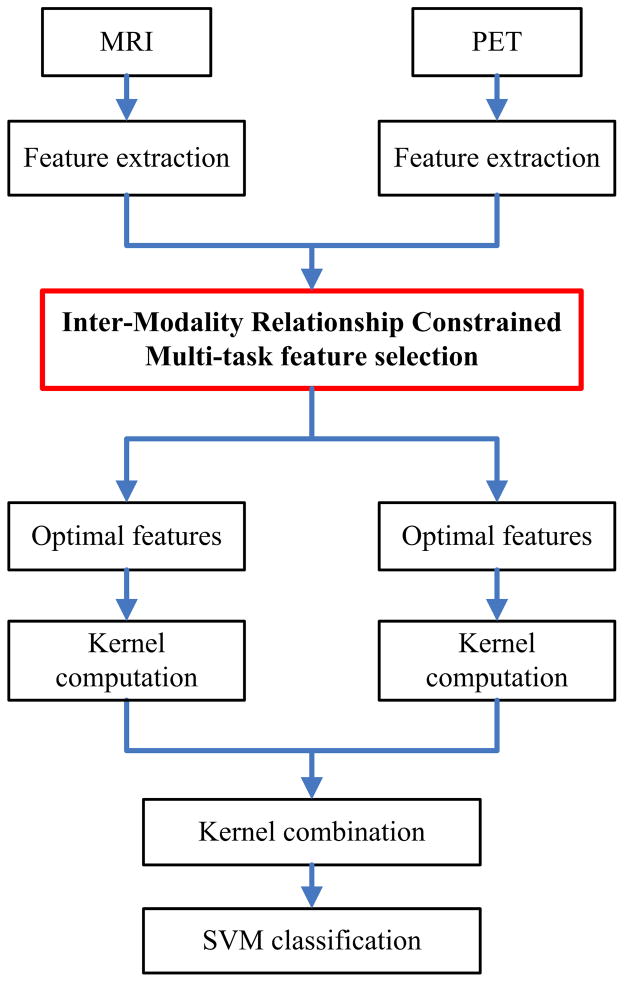
An overview of the proposed AD/MCI classification pipeline is illustrated in Fig. 1.

Fig. 1.

Schematic diagram illustrating the proposed AD/MCI classification framework

3 Experimental Results

The performance of our method is compared with the 1) Single-Task feature selection (i.e., LASSO) integrated with the Multi-modality Multi-kernel (STMM) SVM, 2) Single-Task feature selection integrated with the Single-modality Single-kernel (STSS) SVM, and 3) Joint feature Selection (i.e., L_2,1 norm) integrated with Multimodality Multi-kernel (JSMM) SVM. It is worth noting that we use the same training and testing data across the experiments for all the methods for fair comparison. For each comparison, the performance of each comparison method is evaluated through the classification of AD vs. NC and MCI vs. NC, respectively.

As shown in Table 1 and Fig. 2, the proposed method outperforms all comparison methods in AD/MCI classification. Specifically, for distinguishing AD from NC, our method achieves accuracy of 94.37%, with a sensitivity of 94.71%, a specificity of 94.04%, and the Area Under the receiver operating characteristic Curve (AUC) of 0.9724. On the other hand, for distinguishing MCI from NC, our method achieves a classification accuracy of 78.8%, with a sensitivity of 84.85%, a specificity of 67.06%, and the AUC of 0.8284. We also perform paired t-tests on the accuracies of all comparison methods with our method and obtain p values smaller than 0.05 for all comparisons, indicating significant improvement by our method on AD/MCI classification. These results demonstrate that preserving inter-modality relationship improves the classification performance. The numbers of support vectors used in our method are 29~40 and 57~69 for AD and MCI classifications, respectively. The numbers of selected features used for final classification are 8~14 and 41~64 for AD and MCI classifications, respectively. The whole classification pipeline requires 10 and 30 minutes for AD and MCI classifications, respectively.

Table 1.

Classification performance of all comparison methods. ACC, SEN, SPE stand for the accuracy, sensitivity, and specificity, respectively.

Method	AD vs. NC				MCI vs. NC
	ACC (%)	SEN (%)	SPE (%)	AUC	ACC (%)	SEN (%)	SPE (%)	AUC
STMM	91.02	89.02	92.88	0.9655	72.08	75.56	65.38	0.7826
STSS	88.25	84.91	91.54	0.9004	71.41	77.78	59.23	0.7575
JSMM	91.10	91.57	90.58	0.9584	73.54	81.01	59.23	0.7706
Proposed	94.37	94.71	94.04	0.9724	78.80	84.85	67.06	0.8284

Fig. 2.

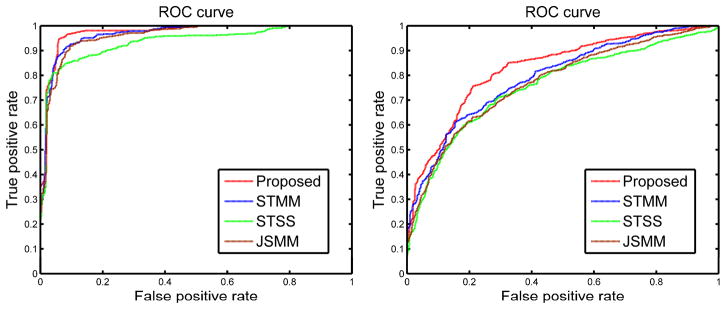
Receiver Operating Characteristic (ROC) curves of different methods (with feature selection) for AD (left) and MCI (right) classifications

In order to validate the effectiveness of the proposed feature selection method, we compare the AD/MCI classification performance with and without the proposed feature selection step. The same multi-kernel SVM framework is applied for both the comparison methods. As seen in Table 2, the proposed feature selection method outperforms the approach without feature selection. For further comparison, we summarize the results of recent multi-modal classification studies. Hinrichs et al. used 48 AD patients and 66 NC for classification, and obtained an accuracy of 87.6% by using two modalities (PET + MRI), and an accuracy of 92.4% by using five types of features (MRI + PET + cerebrospinal fluid (CSF) + Apolipoprotein E (APOE) + cognitive scores) [8]. Gray et al. used 37 AD patients, 75 MCI patients and 35 NC, reporting an accuracy of 89% for AD classification and an accuracy of 74.6% for MCI classification by using four types of features (CSF + MRI + PET + Genetic features) [9]. As seen in Table 3, our method performs better than the two aforementioned studies, even though they used more modalities. Although direct comparison with these studies is not appropriate due to possible use of different subjects (although from the same ADNI dataset), the obtained results validate the promising performance of our method for AD classification to some extent.

Table 2.

Classification performance with and without feature selection step

Method	Subjects	Modalities	AD vs. NC (%)	MCI vs. NC (%)
Without	51AD+99MCI+52NC	PET+MRI	89.90	70.89
With	51AD+99MCI+52NC	PET+MRI	94.37	78.80

Table 3.

Comparison of classification accuracies reported in the literature

Method	Subjects	Modalities	AD vs. NC (%)	MCI vs. NC (%)
Hinrichs et al. [8]	48AD+66NC	PET+MRI	87.60	-
Hinrichs et al. [8]	48AD+66NC	MRI+PET+CSF+APOE+cognitive scores	92.40	-
Gray et al. [9]	37AD+75MCI+35NC	PET+MRI+CSF+Genetic	89.00	74.60
Proposed	51AD+99MCI+52NC	PET+MRI	94.37	78.80

4 Conclusion

We propose a novel multi-task learning based feature selection method to effectively integrate the complementary information from multiple modalities neuroimaging data to improve AD/MCI identification. Specifically, we treat the selection of features from each modality as a task and preserve the inter-modality relationship after projection of feature vectors from different modalities onto the low-dimensional feature space. Experimental results on ADNI dataset demonstrate that our proposed multitask feature selection technique, integrated with the multi-kernel SVM, outperforms all comparison methods. In the future, we will extend our work to include more modalities (such as CSF or genetic features) to improve AD/MCI classification performance.