Abstract
Chikungunya and dengue are re-emerging mosquito-borne infectious diseases that are of increasing concern as human travel and expanding mosquito ranges increase the risk of spread. We seek to understand the differences in transient and endemic behavior of chikungunya and dengue; risk of emergence for different virus-vector assemblages; and the role that virus evolution plays in disease dynamics and risk. To address these questions, we adapt a mathematical mosquito-borne disease model to chikungunya and dengue in Aedes aegypti and Aedes albopictus mosquitoes. We derive analytical threshold conditions and important dimensionless parameters for virus transmission; perform sensitivity analysis on quantities of interest such as the basic reproduction number, endemic equilibrium, and first epidemic peak; and compute distributions for the quantities of interest across parameter ranges. We found that chikungunya and dengue exhibit different transient dynamics and long-term endemic levels. While the order of most sensitive parameters is preserved across vector-virus combinations, the magnitude of sensitivity is different across scenarios, indicating that risk of invasion or an outbreak can change with vector-virus assemblages. We found that the dengue-A. aegypti and new Rèunion strain of chikungunya-A. albopictus systems represent the highest risk across the range of parameters considered. These results inform future experimental and field research efforts and point toward effective mitigation strategies adapted to each disease.
Keywords: chikungunya, dengue, Aedes albopictus, Aedes aegypti, mathematical model
1. Introduction
Mosquito-borne pathogens pose a significant threat to human health around the world. Dengue has caused increasing concern in tropical and subtropical regions and is emerging in areas where it has been absent for years, infecting millions every year [1] and potentially increasing with climate change [2]. Recently, chikungunya virus re-emerged in Asia and caused outbreaks in Italy and several Indian Ocean islands [3, 4]. Dengue modeling and control efforts are extensive although there is much still to do [5]. Chikungunya is just starting to receive attention after several recent outbreaks. Although chikungunya and dengue have many similarities, how they interact with different mosquito species and the human host can vary considerably. The primary vectors for both chikungunya and dengue are Aedes aegypti and Aedes albopictus and both viruses generate acute immunizing infections in humans. However, the vector extrinsic incubation period is shorter for a new 2005 Rèunion strain of chikungunya (CHIK-R) than it is for dengue [6, 7, 8]. There is also evidence that A. albopictus is a more competent vector for CHIK-R than it is for dengue (DENV) and the older Asian genotype of chikungunya (CHIK-A). In this paper, we adapt models for malaria and Rift Valley fever [9, 10] to both dengue and chikungunya. We compute the basic reproduction number and endemic equilibrium as well as simulate transient dynamics. Using different baseline parameter sets for each pathogen and mosquito species, sensitivity analysis highlights differences and similarities between these important mosquito-borne pathogens. We find that different virus-vector combinations can behave differently from one another in invasion capability (initial transmission), transient dynamics, and long-term endemic states.
Dengue is a virus that persists primarily in an urban transmission cycle between mosquitoes and humans, common in Asia and Central and South America. Dengue was almost extinct in South America after a large campaign to eradicate A. aegypti mosquitoes from human populations. However, as A. aegypti have been re-introduced into urban environments across most of South and Central America, dengue incidence has risen dramatically there [11, 12]. Cases of dengue have been confirmed in southern Texas and southern Florida, increasing concern about continued emergence in the United States. There are four major serotypes of dengue and infection with one does not necessarily confer immunity to another.
Dengue is primarily transmitted by A. aegypti, but A. albopictus can be an important secondary vector. Both mosquito species are diurnal, biting mostly in the morning and evening rather than at night. In general, the dengue virus takes between 8 and 12 days to disseminate in mosquitoes before it can be transmitted. Humans have a latent period of around 5 days and are infectious for approximately a week. It is common for people infected with dengue to exhibit relatively mild to severe flu-like symptoms, although in rare cases hemorrhagic fever can result. Mitigation strategies for dengue include reduction of the mosquito population via indoor spraying (adulticides), larvicides, lethal ovitraps [13], removing man-made oviposition sites and reduction of human exposure to mosquito bites via the use of screens, mosquito repellent, etc. Vaccines are also in development and currently in clinical trials [14].
Chikungunya is an arbovirus first identified in 1953 [15] and is also transmitted primarily by A. albopictus and A. aegypti. As with dengue, chikungunya has a low death rate, but often causes disease with symptoms similar to dengue fever accented by severe arthritis-type pain [15]. The sudden outbreak of the disease in Rèunion in 2005 and India in 2006, more than 40 years after the last known outbreak in India, has prompted ongoing modeling and biological studies [16], although chikungunya remains relatively uncommon and poorly documented [16]. The primary chikungunya vector has traditionally been A. aegypti. Reports from sequencing chikungunya virus isolated from patients in Rèunion and Seychelles described a mutation which was previously absent [17]. The effects of this mutation documented by [6, 7] showed that the new strain caused faster dissemination rates in mosquitoes than the original counterpart, and that the mutated virus was more effectively transmitted by A. albopictus. Traditionally, A. albopictus has been considered to be a less competent vector for chikungunya, but A. albopictus is starting to play a more prominent role [18] in part due to the virus mutation. Once infected, immunity is thought to last for life and there is thought to be cross-immunity between strains. For the older Asian strain (associated with a different genotype than CHIK-R), the extrinsic incubation period in mosquitoes is about 7–15 days, similar to dengue. However, CHIK-R needs only 2–6 days to incubate in mosquitoes. In addition to re-emerging in India, Asia and islands such as Rèunion, a recent outbreak in Italy has caused concern that chikungunya will be successfully introduced to Europe and the Americas while becoming more of a problem in areas where it is endemic. Mitigation strategies for chikungunya are similar to those used for dengue.
There is a growing need to understand the critical parameters in the transmission and persistence of these diseases and to develop effective strategies for prevention and control. There are many models for dengue in the literature investigating different aspects of its spread and behavior [19, 20, 21] from standard mosquito-borne disease models [22] to models incorporating space [12], seasonality and temperature dependence [23, 24], cross-immunity with multiple strains [25, 26, 27], and effectiveness of control measures [28]. For the purposes of this study, we will restrict our model to one representative dengue serotype and to models without explicit seasonality.
There have been several efforts to model chikungunya since the recent outbreaks (e.g. [29, 30]). Dumont et al. 2008 and 2010 [31, 32] modeled chikungunya spread for the recent Rèunion Island strain, including control measures and a faster incubation period in A. albopictus. Moulay et al. 2011 and 2012 [33, 34] analyzed a similar model with a focus on mosquito population dynamics to explore optimal control strategies for chikungunya outbreaks. Recently, Yakob & Clements [35] modeled the first outbreak of chikungunya on Rèunion Island, focusing on asymptomatic versus symptomatic human cases in order to better fit reported data. These modeling efforts provided important analysis and parameter estimates for chikungunya, which had previously received little attention from the modeling community.
Mathematical modeling can play a unique role in comparing the effects of control strategies and understanding how virus evolution could impact transmission. We begin such a comparison by determining the relative importance of model parameters in chikungunya transmission and prevalence levels to those of dengue. We adapt the Chitnis et al. [9] and [10] models for malaria and Rift Valley fever to chikungunya and dengue while keeping the original structure of the model intact for comparison purposes. We first describe the mathematical models for dengue and chikungunya, including the definition of a domain where the models are mathematically and epidemiologically well-posed. This model is different from most other chikungunya and dengue models in that rather than lumping ‘transmission rate’ into one parameter, it differentiates between the components of successful transmission, including mosquito biting rates, densities of both hosts and vectors, and host availability that can be modified by mitigation strategies (exceptions include [36, 37]). Both host and vector population dynamics are also included. We use baseline parameter sets for dengue (DENV), an Asian strain of chikungunya (CHIK-A) and the newer Rèunion (CHIK-R) strain from the current literature. Additionally, for chikungunya and dengue, we compile differential parameter sets for both A. aegypti and A. albopictus mosquitoes.
We found that chikungunya and dengue exhibit different transient dynamics and long-term endemic levels. While the order of most sensitive parameters is preserved across vector-virus combinations, the magnitude of sensitivity is different for various scenarios and quantities of interest. CHIK-R has a higher basic reproduction number, faster initial transmission, and higher potential endemic levels than CHIK-A. We also find that CHIK-R is less sensitive to small changes in mosquito-related parameters than CHIK-A and is comparable to dengue transmission in A. aegypti, DENV(A. aegypti). In our model, the DENV(A. aegypti) and CHIK-R(A. albopictus) systems represent the highest risk for invasion and persistence across the range of parameters considered. We posit that invasion of chikungunya in areas where it is previously unknown, and difficulty of control if an outbreak were to occur could be more likely than for dengue, particularly in areas with mixed A. albopictus/A. aegypti or primarily A. albopictus mosquito populations. These varying dynamics indicate that the risk of invasion or an outbreak can change with different vector-virus combinations. Finally, the model shows that virus evolution, as recently observed in chikungunya, can increase risk of emergence and that sensitivity analysis may elucidate likely future directions of virus evolution.
2. Description of Model Framework
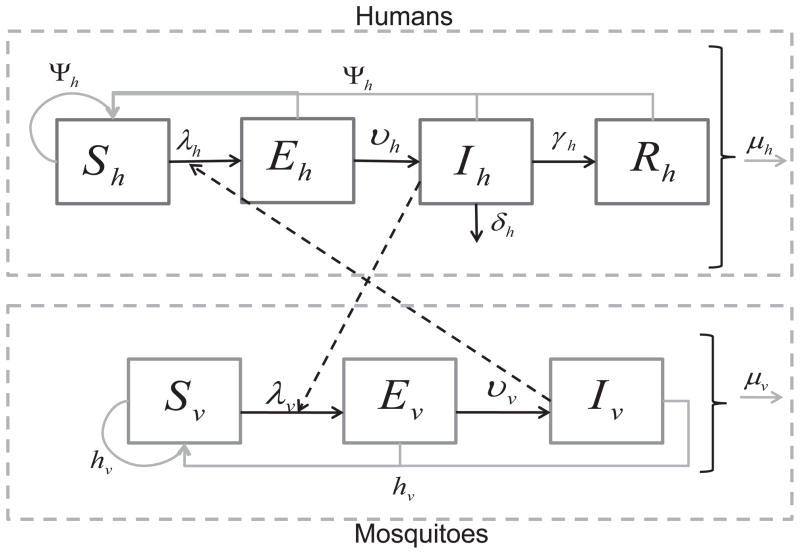
The model (Figure 1) divides the human population into 4 classes: susceptible, Sh, exposed (infected but not infectious), Eh, infectious, Ih, and recovered (immune), Rh. Humans enter the susceptible class, Sh through a per-capita birth rate Ψh. When an infectious mosquito bites a susceptible human, there is a finite probability that the human becomes infected. After being successfully infected by an infectious mosquito, humans move from the susceptible class Sh to the exposed class, Eh. After an intrinsic incubation period, they move to the infectious class, Ih, in which humans can infect mosquitoes if bitten. Unlike malaria, chikungunya and dengue do not have long periods of time over which asymptomatic hosts can transmit. After some time, infectious humans recover and move to the recovered class, Rh. We assume recovered humans have immunity to the pathogen for life. In the case of dengue, recovered individuals are thought to be immune to the particular serotype they contracted but may be susceptible to one of the other three serotypes of dengue after a period of 4–6 months. Humans leave the population through a per capita natural death rate, μh. We assume that death due to disease, δh, is negligible, so will be left out of subsequent equations. We will assume that the human population size is stable and relatively constant, hence that Ψh = μh.
Figure 1.
Disease transition arrows are in black, contacts between humans and mosquitoes are represented by the dashed arrows, and population dynamics are in grey. Susceptible humans hosts, Sh, can be infected when they are bitten by infectious mosquitoes. Infected humans become exposed (infected but not infectious), Eh, then infectious, Ih. Infectious humans recover with a constant per capita recovery rate to enter the recovered, Rh, class. Susceptible mosquito vectors, Sv, can become infected when they bite infectious humans. The infected mosquitoes then move through the exposed, Ev, and infectious, Iv, classes. Births and deaths of the population are shown as well.
We assume migration of mosquitoes and humans is negligible for the scales considered and questions being asked here. If we assume that all humans migrating into the simulation region are susceptible, then our assumption that human migration is negligible can be relaxed by expanding the definition of the birth and death terms in the model to include migration. We do not consider the case of chikungunya and dengue co-circulation, concentrating instead on comparing the dynamics of each virus alone.
We divide the adult female mosquito population into 3 classes: susceptible, Sv, exposed, Ev, and infectious, Iv. Mosquitoes enter the susceptible class through recruitment from the pupal stage. The recruitment term for mosquitoes accounts for and is proportional to the egg-laying rate of adult female mosquitoes; survival and hatching rate of eggs; and survival of larvae and pupae. If any of these are increased or decreased, the recruitment rate is affected accordingly. Since most density-dependent survival of mosquitoes occurs in the larval stage, we assume a density-dependent recruitment rate.
When a susceptible mosquito bites an infectious human and the virus infects the mosquito, the mosquito moves to the exposed class, Ev. The exposed class models the delay before infected mosquitoes become infectious, or the extrinsic incubation period. In mosquitoes, this delay is important because it is on the same order as their expected life span. Thus, many infected mosquitoes die before they become infectious. After the extrinsic incubation period, which can depend on the ambient temperature and humidity, the mosquito moves from the exposed class to the infectious class, Iv. The mosquito remains infectious for life. Adult female mosquitoes leave the population through a per capita natural death rate, μv. We assume here that dengue or chikungunya infection does not affect the lifespan of a mosquito.
We analyze the relative importance of the parameters for three model outputs:
The initial rate of disease spread and its invasion potential
The transient disease dynamics
The endemic persistence of disease
using three quantities of interest (QOI), namely the basic reproduction number, the timing and magnitude of the first epidemic peak, and the endemic equilibrium. A knowledge of the relative importance of parameters can help guide the development of efficient intervention strategies in chikungunya and dengue endemic or epidemic areas where resources are scarce, as well as quantify the risk of pathogen invasion and the key processes most susceptible to virus evolution.
2.1. Model Equations
The state variables (Table 1) and parameters (Table 2) for the chikungunya and dengue model (Figure 1) satisfy the equations
Table 1.
State variables for the model (2.1).
| Sh: | Number of susceptible humans |
| Eh: | Number of exposed humans |
| Ih: | Number of infectious humans |
| Rh: | Number of recovered humans |
| Sv: | Number of susceptible mosquitoes |
| Ev: | Number of exposed mosquitoes |
| Iv: | Number of infectious mosquitoes |
| Nh: | Total human population size |
| Nv: | Total mosquito population size |
Table 2.
Parameters for the model (2.1) and their dimensions.
| H0: | Stable population size of humans. Humans. |
| Ψh: | Per capita birth rate of humans. We assume that Ψh = μh and the human population is at equilibrium. Time−1. |
| Ψv: | Per capita recruitment rate of mosquitoes. Time−1. |
| σv: | Number of times one mosquito would bite a human per unit time, if humans were freely available. This is a function of the mosquito’s gonotrophic cycle (the amount of time a mosquito requires to produce eggs) and its preference for human blood. Time−1. |
| σh: | The maximum number of mosquito bites a human can sustain per unit time. This is a function of the human’s exposed surface area and any vector control interventions in place to reduce exposure to mosquitoes. Time−1. |
| βhv: | Probability of pathogen transmission from an infectious mosquito to a susceptible human given that a contact between the two occurs. Dimensionless. |
| βvh: | Probability of pathogen transmission from an infectious human to a susceptible mosquito given that a contact between the two occurs. Dimensionless. |
| νh: | Per capita rate of progression of humans from the exposed state to the infectious state. 1/νh is the average duration of the latent period. Time−1. |
| νv: | Per capita rate of progression of mosquitoes from the exposed state to the infectious state. 1/νv is the average duration of the extrinsic incubation period. Time−1. |
| gamma;h: | Per capita recovery rate for humans from the infectious state to the recovered state. 1/gamma;h is the average duration of the infectious period. Time−1. |
| μh: | Per capita death (and emigration) rate for humans. Time−1. |
| μv: | Density-independent death rate for mosquitoes. Time−1. |
| Kv: | Carrying capacity of mosquitoes. Mosquitoes. |
| rv: | Natural growth rate of mosquitoes with no density dependence. Time−1. |
| (2.1a) |
| (2.1b) |
| (2.1c) |
| (2.1d) |
| (2.1e) |
| (2.1f) |
| (2.1g) |
The total population sizes are Nh = Sh + Eh + Ih + Rh and Nv = Sv + Ev + Iv with the mosquito birth rate
| (2.2) |
where Ψv is the natural birth rate in the absence of density dependence, rv = Ψv − μv is the intrinsic growth rate of mosquitoes in the absence of density dependence, and Kv is the carrying capacity of the mosquitoes in the region considered. We include density dependence in the birth term because evidence suggests that mosquito populations are controlled by availability of egg-laying sites and competition between larvae [38], both of which are factored into the recruitment rate of adult female mosquitoes. Then,
and the positive mosquito population equilibrium point is M0 = Kv. We assume that the forces of infection are
and that all parameters are strictly positive.
In this model, following [9], σv is the maximum rate at which a mosquito would bite a human (related to the gonotrophic cycle length), and σh is the maximum number of bites that a human can support per unit time. Then, σvNv is the optimal number of bites a mosquito seeks per unit time and σhNh is the maximum available number of human bites per unit time. The total number of mosquito-human contacts is then
| (2.3) |
which depends on the population densities of humans and mosquitoes. We define bh = bh(Nh, Nv) = b(Nh, Nv)/Nh as the number of bites per human per unit time, and bv = bv(Nh, Nv) = b(Nh, Nv)/Nv as the number of bites per mosquito per unit time. The advantage of using this biting rate, as opposed to the more standard frequency-dependent contact rates, is that it can handle the whole range of possible vector-to-host ratios, whereas frequency or density-dependent contact rates have limited ranges of vector-to-host ratios across which they are applicable (see, e.g. [64]).
The force of infection from mosquitoes to humans, λh(t), is the product of the number of times one human is bitten by mosquitoes per unit time, bh, the probability that the mosquito is infectious, Iv/Nv, and the probability of pathogen transmission from the mosquito to the human, βhv. The force of infection from humans to mosquitoes, λv(t), is defined as the number of times one mosquito bites a human per unit time, bv, the probability that the human is infectious, Ih/Nh, and the probability of pathogen transmission from an infected human to the mosquito, βvh.
The model (2.1) is epidemiologically and mathematically well-posed in the domain,
| (2.4) |
This domain,
 , is valid epidemiologically as the populations, Eh, Ih, Rh, Ev, and Iv are all nonnegative and have sums over their species type that are less than or equal to the total population. The human population, Nh, is positive and bounded by its stable disease-free value, H0, while the mosquito population, Nv is bounded by its stable disease-free value, M0 = Kv. We use the notation f′ to denote df/dt. We denote points in
, is valid epidemiologically as the populations, Eh, Ih, Rh, Ev, and Iv are all nonnegative and have sums over their species type that are less than or equal to the total population. The human population, Nh, is positive and bounded by its stable disease-free value, H0, while the mosquito population, Nv is bounded by its stable disease-free value, M0 = Kv. We use the notation f′ to denote df/dt. We denote points in
 by x = (Nh, Eh, Ih, Rh, Nv, Ev, Iv).
by x = (Nh, Eh, Ih, Rh, Nv, Ev, Iv).
Theorem 2.1
Assuming that the initial conditions lie in
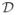 , the system of equations for the chikungunya/dengue model (2.1) has a unique solution that exists and remains in
, the system of equations for the chikungunya/dengue model (2.1) has a unique solution that exists and remains in
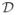 for all time t ≥ 0.
for all time t ≥ 0.
Proof
The right hand side of (2.1) is continuous with continuous partial derivatives in
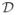 , so (2.1) has a unique solution. Next, we show that
, so (2.1) has a unique solution. Next, we show that
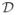 is forward-invariant. We can see from (2.1) that if Eh = 0, then
; if Ih = 0, then
; if Rh = 0, then
; if Ev = 0, then
; and if Iv = 0, then
. It is also true that if Sh + Eh + Ih + Rh ≥ H0 then
; and if Sv + Ev + Iv ≥ M0 then
. Finally, we note that if Nh = 0, then
; if Nh > 0 at time t = 0, then Nh > 0 for all t > 0; and if Nh = H0, then
. Similarly, if Nv = 0, then
; if Nv > 0 at time t = 0, then Nv > 0 for all t > 0; and if Nv = M0, then
. Therefore, none of the orbits leave
is forward-invariant. We can see from (2.1) that if Eh = 0, then
; if Ih = 0, then
; if Rh = 0, then
; if Ev = 0, then
; and if Iv = 0, then
. It is also true that if Sh + Eh + Ih + Rh ≥ H0 then
; and if Sv + Ev + Iv ≥ M0 then
. Finally, we note that if Nh = 0, then
; if Nh > 0 at time t = 0, then Nh > 0 for all t > 0; and if Nh = H0, then
. Similarly, if Nv = 0, then
; if Nv > 0 at time t = 0, then Nv > 0 for all t > 0; and if Nv = M0, then
. Therefore, none of the orbits leave
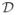 and a unique solution exists for all time.
and a unique solution exists for all time.
3. Quantities of Interest
3.1. Disease-Free Equilibrium and Basic Reproduction Number
Disease-free equilibrium points are steady-state solutions where there is no disease. We define the “diseased” classes as humans or mosquitoes that are either exposed or infectious; that is, Eh, Ih, Ev, and Iv for model (2.1). We denote the positive orthant in ℝn by and the boundary of by .
Theorem 3.1
The model for chikungunya/dengue model(2.1) has exactly one equilibrium point,
| (3.1) |
with no disease in the population (on ).
Proof
By inserting xdfe in (2.1), we see that all derivatives are equal to zero so xdfe is an equilibrium point of (2.1). By setting any of Eh, Ih, Rh, Ev, or Iv equal to zero, we also see that the other four diseased variables have to be zero while Nv = M0 = Kv and Nh = H0 for the system to be at equilibrium.
In a model assuming a homogeneously mixed population, the basic reproductive number,
 , is defined as the expected number of secondary infections that one infectious individual would cause over the duration of the infectious period in a fully susceptible population. For this model, we use the next generation operator approach, as described by van den Driessche and Watmough [65], to derive the basic reproductive number,
, is defined as the expected number of secondary infections that one infectious individual would cause over the duration of the infectious period in a fully susceptible population. For this model, we use the next generation operator approach, as described by van den Driessche and Watmough [65], to derive the basic reproductive number,
 , which defines a threshold condition for when the disease-free equilibrium loses stability (see Appendix A for details). Let
, which defines a threshold condition for when the disease-free equilibrium loses stability (see Appendix A for details). Let
| (3.2) |
be the number of secondary infections created in humans by one newly introduced infected mosquito and let
| (3.3) |
be the number of secondary infections created in mosquitoes by one newly infected introduced human, both in fully susceptible populations. Then, the basic reproductive number is the spectral radius of the next generation matrix, , and the geometric mean of Rvh and Rhv,
| (3.4) |
where s(A) denotes the absolute value of the largest eigenvalue of A. We define the basic reproduction number here as the expected number of human to mosquito or mosquito to human secondary cases. The type reproduction number, or expected number of secondary human cases resulting from one infected human, is . For this model the human-to-human type reproduction number is equivalent to the mosquito-to-mosquito type reproduction number.
Theorem 3.2
The disease-free equilibrium point, xdfe of the model for chikungunya/dengue (2.1), is locally asymptotically stable when
 < 1 and unstable when
< 1 and unstable when
 > 1.
> 1.
Proof
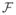 (x),
(x),
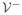 (x), and
(x), and
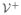 (x) satisfy assumptions (A1)–(A5) in [65] so this theorem is a straightforward application of Theorem 2 in [65].
(x) satisfy assumptions (A1)–(A5) in [65] so this theorem is a straightforward application of Theorem 2 in [65].
3.1.1. Important Dimensionless Numbers
The components of Rhv and Rvh can be described as the product of dimensionless numbers that provide intuition about the basic reproduction number and how it will vary as parameters change. The expected number of secondary infections in fully susceptible humans resulting from one newly introduced infected mosquito, Rhv, can be written as the product of four dimensionless numbers:
| (3.5) |
The first term, , is the probability that an exposed mosquito will survive the extrinsic incubation period. When μv and νv are of similar value, we expect more sensitivity to both μv and νv, while for the case where νv > μv (i.e. the extrinsic incubation period is much less than the average lifespan), then sensitivity to νv will be reduced since will be close to 1.
Some models for mosquito-borne disease assume a constant (rather than exponentially distributed) extrinsic incubation period. Under that assumption, the term would be replaced by e−μv/νv. With a constant incubation period, sensitivity to μv and νv is qualitatively similar to sensitivity under our model assumptions (i.e. if νv > μv then Rhv is less sensitive to νv while if νv ≈ μv then sensitivity to νv is higher).
The product of the second and third terms is the expected number of times an infectious mosquito will bite humans while infectious. The term is the number of human bites an infectious mosquito would make if humans were freely available. The term is a measure of the actual availability of humans, or the proportion of desired human bites that will occur. We chose a vector-to-host ratio of 2:1 for our simulations, so the total number of bites per day depends primarily on mosquito density. In this situation, human availability is close to 1 and we expect Rhv not to vary significantly with local changes in σh. Sensitivity to σh will increase as the vector-to-host ratio becomes large, as the biting rate increases significantly, or as the maximum number of bites sustained by an average human decreases.
The last term, βhv, is the probability of transmission from mosquito to human given that the human is bitten by an infectious mosquito. This is a measure of host susceptibility and infectiousness of the mosquito. Rhv is directly proportional to βhv, so
 will be sensitive to and vary directly with βhv. Unfortunately, βhv is a difficult parameter to measure directly.
will be sensitive to and vary directly with βhv. Unfortunately, βhv is a difficult parameter to measure directly.
The number of secondary infections in fully susceptible mosquitoes resulting from one newly introduced infected human, Rvh, can be written as the product of four dimensionless numbers:
| (3.6) |
The first term is the probability that an exposed human will survive the incubation period. since the probability of a human dying of natural causes while in the intrinsic incubation period is small.
The product of the second and third terms of Rvh are the expected number of mosquito bites an infectious human will get while infected. The term
is the maximum number of bites an infectious human will get before recovery with unlimited availability of mosquitoes. Notice that
since μh (the natural death rate of humans) is comparatively small. We expect
 to vary directly with σh but, for our chosen parameters, to not be especially dependent on σh. As the vector to host ratio increases, dependence on σh will increase as well. The term
is a measure of the actual availability of mosquitoes, or the proportion of potential bites on a human that will actually occur. This term will be small for the vector-to-host ratio at baseline parameters. The availability terms in Rvh and Rhv highlight dependence on Kv/H0.
to vary directly with σh but, for our chosen parameters, to not be especially dependent on σh. As the vector to host ratio increases, dependence on σh will increase as well. The term
is a measure of the actual availability of mosquitoes, or the proportion of potential bites on a human that will actually occur. This term will be small for the vector-to-host ratio at baseline parameters. The availability terms in Rvh and Rhv highlight dependence on Kv/H0.
The last term, βvh, is the probability of transmission from human to mosquito given that a susceptible mosquito bites an infectious human. This is a measure of mosquito susceptibility and infectiousness of the human host. As before, we expect
 to be sensitive to and vary directly with the value of βvh.
to be sensitive to and vary directly with the value of βvh.
3.2. First Epidemic Peak and Endemic Equilibrium
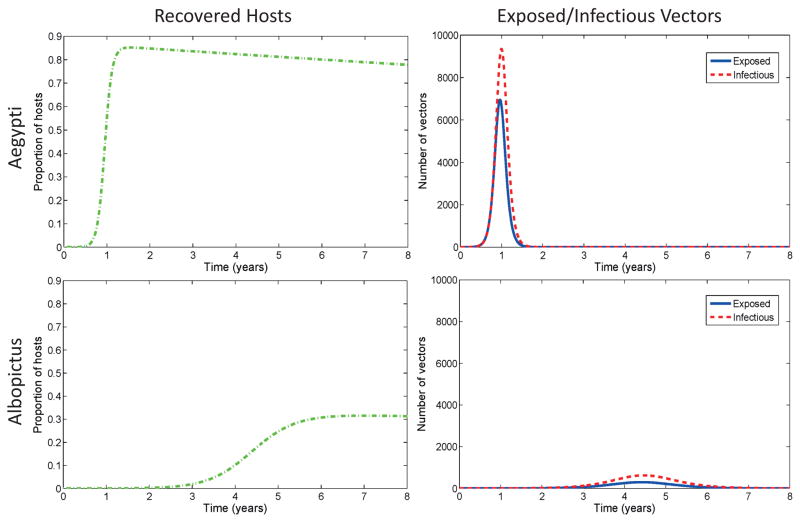
First we consider the timing and magnitude of the first peak of infection after initial introduction of the disease by one infectious human into a fully susceptible population. The magnitude of the first peak is related to the basic reproduction number as well as initial conditions, but we have no analytical representation of the peak, so we use numerical simulations to analyze the first peak of infection. A simulation with dengue baseline parameters in Table 3 is shown in Figure 2. A dengue epidemic in a naive population with A. aegypti mosquitoes will result in higher prevalence than a similar epidemic with A. albopictus as the primary vector. The time to first epidemic peak in A. aegypti is a little over a quarter of the time to first epidemic peak in A. albopictus alone for dengue.
Table 3.
The parameters for dengue (left) for (2.1) with baseline values, range, and references. Time is in days, unless otherwise specified. The parameters for chikungunya (right) for (2.1) with values, range, and references and for old (Asian) and new (Rèunion) strains. The baseline vector-to-host ratio is 2:1, but is varied between 1:1 and 10:1 for both dengue and chikungunya.
| Par | Baseline | Range | Reference | Par | Baseline | Range | Reference |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Dengue | Chikungunya | ||||||
| Human | Human | ||||||
|
| |||||||
| σh | 19 | 0.1 – 50 | [39] | σh | 19 | 0.1 – 50 | [39] |
| 1/νh | 5 | 4 – 7 | [40, 41] | 1/νh | 3 | 2 – 4 | [32, 42, 43, 16] |
| 1/gamma;h | 6 | 4 – 12 | [44, 45] | 1/gamma;h | 6 | 3 – 7 | [33, 43] |
| 1/μh | 70 yrs | 68 – 76 | [39] | 1/μh | 70 yrs | 68 – 76 | [39] |
|
| |||||||
| DENV(Aedes aegypti) | CHIK-A(Aedes aegypti) | ||||||
|
| |||||||
| βhv | 0.33 | 0.10 – 0.75 | [46, 47] | βhv | 0.24 | 0.001 – 0.35 | [16, 48, 49] |
| βvh | 0.33 | 0.10 – 0.75 | [46, 47] | βvh | 0.24 | 0.005 – 0.35 | [16, 48, 49] |
| Ψv | 0.30 | 0.28 – 0.32 | [50, 39, 51] | Ψv | 0.30 | 0.28 – 0.32 | [50, 39, 51] |
| σv | 0.5 | 0.33 – 1 | [52, 53] | σv | 0.5 | 0.33 – 1 | [52, 53] |
| 1/νv | 10 | 7 – 14 | [40, 54] | 1/νv | 11 | 7 – 15 | [48] |
| 1/μv | 14 | 8 – 42 | [55, 52, 56] | 1/μv | 14 | 8 – 42 | [55, 52, 56] |
|
| |||||||
| DENV(Aedes albopictus) | CHIK-R(Aedes albopictus) | ||||||
|
| |||||||
| βhv | 0.31 | 0.1 – 0.5 | [47, 57] | βhv | 0.33 | 0.001 – 0.54 | [31, 32, 49] |
| βvh | 0.31 | 0.1 – 0.5 | [47, 57] | βvh | 0.33 | 0.3 – 0.9 | [31, 48, 58, 49] |
| Ψv | 0.24 | 0.22 – 0.26 | [50, 39, 59] | Ψv | 0.24 | 0.22 – 0.26 | [50, 39, 59] |
| σv | 0.26 | 0.19 – 0.39 | [60, 61] | σv | 0.26 | 0.19 – 0.39 | [60, 61] |
| 1/νv | 10 | 7 – 14 | [50] | 1/νv | 3.5 | 2 – 6 | [62, 6, 63, 32, 33] |
| 1/μv | 21 | 14 – 42 | [32, 42, 50] | 1/μv | 21 | 14 – 42 | [32, 42, 33, 43] |
Figure 2.
Disease progression of dengue with A. albopictus and A. aegypti. The y-axis for the hosts is proportion of hosts (rather than number) and the x-axis is time in years. Columns are plotted on same scale. The timing and magnitude of the first epidemic differs between mosquito species. Notice that the model output for chikungunya (Figure 3) are quite different than the dengue plots, indicating different dynamics and relative risk for the two pathogens. The size and timing of the epidemic peak is driven by differences and tradeoffs between vector biting rates, the extrinsic incubation period, transmission probabilities (vector/host competence), and the infectious time for humans. Baseline parameters from Table 3 are used with initial conditions (Sh, Eh, Ih, Rh, Sv, Ev, Iv) = (H0 − 1, 0, 1, 0, Kv, 0, 0) where H0 = 100, 000 and Kv = 2H0.
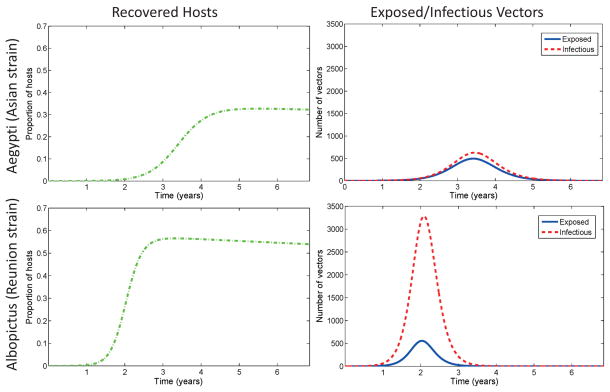
Transient dynamics vary with different mosquito-virus combinations. In Figure 3, we show the results of simulations when chikungunya is introduced into a completely naive population via one infected human with baseline parameters as in Table 3. CHIK-A in its primary A. aegypti vector results in lower prevalence after the first peak than CHIK-R strain in A. albopictus. The time to first epidemic peak for the CHIK-R is a little more than half the time to peak for CHIK-A. Thus, as has been observed, the CHIK-R results in higher prevalence and faster-moving epidemics. All four scenarios exhibit damped oscillations for decades before reaching a stable endemic equilibrium (not shown).
Figure 3.
Disease progression of Rèunion strain chikungunya with A. albopictus and Asian strain of chikungunya with A. aegypti. The y-axis for the hosts is proportion of hosts (rather than number) and the x-axis is time in years. Columns are plotted on same scale. Both timing and magnitude of the first epidemic peak is different for the different strains of chikungunya and different mosquito species. Initial conditions are the same as in Figure 2 with baseline parameters from Table 3.
These also highlight the importance of susceptible host availability. Without mitigation or outside forcing such as seasonality, a DENV(A. aegypti) outbreak in a naive host population can infect up to 80% of the population, resulting in low availability of susceptible hosts for future outbreaks. In that scenario, changes in transmission rates or the extrinsic incubation period could result in extinction of the virus (without reintroduction) via loss of available hosts. However, virus evolution resulting in strains for which previous exposure to another strain does not confer full immunity against the new strain would increase virus fitness from the perspective of long term virus persistence, without affecting the basic reproductive number (
 ).
).
Endemic equilibrium points are steady-state solutions where disease persists in the population. If either dengue or chikungunya is introduced into a fully susceptible population, it takes decades to reach the endemic equilibrium. This is because there is a large initial outbreak, then very little transmission until the number of susceptible hosts is replenished, then another outbreak will occur, and so on, until the oscillations damp to the steady endemic state. While we do not prove stability of the endemic equilibrium point for the model, we conjecture that it is locally asymptotically stable when
 > 1.
> 1.
The endemic equilibrium for human hosts is
| (3.7) |
| (3.8) |
| (3.9) |
| (3.10) |
and for mosquito vectors is
| (3.11) |
| (3.12) |
| (3.13) |
where is the type reproduction number, Mh = A/(1 + A) with , and where Mv = B/(1 + B) with . As expected, the endemic equilibrium values are proportional to and to non-dimensional terms similar to those in section 3.1.1. The total number of humans in a disease stage at the endemic equilibrium is . Mh and the total number of mosquitoes in an infection stage at the endemic equilibrium is .
The proportions assigned to each one of the infection stages depends upon the probability of surviving the previous infection stage. The probability of a mosquito surviving the extrinsic incubation period is , so the number of infectious mosquitoes, , depends on this term. Then, the number of mosquitoes in the exposed class, is proportional to which is equal to . Similar reasoning can be used to understand how humans are distributed among , and . The endemic equilibrium states are also dependent on the relative contributions of the vectors and the hosts to new cases (Rhv and Rvh) as well as the relative ‘herd turnover’ rates of mosquitoes (μvKv) and humans (μhH0) as seen in the terms Mv and Mh.
Table 5 gives the endemic equilibrium values, the magnitude of the first epidemic peak in a naive population, and the time to first epidemic peak for the various virus-vector combinations. Both DENV(A. aegypti) and the CHIK-R(A. albopictus) have higher endemic equilibrium values, higher first epidemic peak values, and move faster through a naive population. DENV(A. albopictus) and CHIK-A(A. aegypti) have low endemic equilibrium values indicating that the magnitude (rather than just the ratio) of human and mosquito populations and environmental stochasticity will play a large role in the persistence of the viruses in these scenarios. As expected, the magnitude of the first epidemic peak is lower and the time to the first peak is longer for these scenarios as well. Thus, both invasion potential and persistence probability are higher for DENV(A. aegypti) and CHIK-R(A. albopictus).
Table 5.
Endemic equilibrium (eh, ih, rh, ev, iv) and properties of the first peak: maximum proportion humans infected (ih,P), time to ih,P (Tih,P), maximum proportion of mosquitoes infected (iv,P), time to iv,P (Tiv,P), maximum proportion of immune humans (rh,P), and time to rh,P (Trh,P) for dengue and chikungunya. The proportions written as percent of the total populations and the time is in years. DENV(A. aegypti) and CHIK-R(A. albopictus) reach the epidemic peak faster (Tih,P) and result in more total infections (rh,P) by the end of an outbreak. They also result in a greater percent of immune hosts at the endemic state (rh).
| Virus | eh | ih | rh | ev | iv | ih,P | Tih,P | iv,P | Tiv,P | rh,P | Trh,P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||
|
Aedes aegypti
| ||||||||||||
| 1. | DENV | 0.011 | 0.014 | 58.41 | 0.012 | 0.017 | 4.15 | 0.95 | 4.67 | 1.0 | 85.22 | 1.6 |
| 2. | CHIK-A | 0.0021 | 0.0043 | 18.17 | 0.0030 | 0.0038 | 0.35 | 3.4 | 0.31 | 3.45 | 32.69 | 5.5 |
|
| ||||||||||||
|
Aedes albopictus
| ||||||||||||
| 1. | DENV | 0.0020 | 0.0041 | 17.56 | 0.0023 | 0.0049 | 0.26 | 4.4 | 0.31 | 4.5 | 31.5 | 7.0 |
| 2. | CHIK-R | 0.0039 | 0.0079 | 33.58 | 0.0020 | 0.012 | 1.13 | 2.0 | 1.64 | 2.1 | 56.56 | 3.3 |
4. Model Analysis and Uncertainty Quantification
Climate, vector biology, human susceptibility, control methods, and transmission rates can vary for both dengue and chikungunya. In order to understand how this variation could affect our results, we quantify the impact of changes in parameters on the relevant outputs of the model. We identify three types parameters of interest (POI) in a model. They are the parameters we can control, the ones we only know approximately, and the parameters that cannot be defined to be a specific value because of random stochastic effects. Uncertainties in the POI can affect the solution at every stage of computation; they may cause our quantities of interest to grow or shrink as the solution evolves. The usefulness of the model depends on understanding how the uncertainties in our parameters affect predictions of quantities of interest (QOI). Often it is the response of the QOI to these POI that provide the most useful information into understanding the underlying complex transmission dynamics.
We recognize that mathematical equations are a simplistic model of the real world. Fortunately, often the relative ranking of the response of the QOI to the POI is a more robust measurement, even though the exact model predictions can be in error. In this paper we consider all the variables listed in Table 3 as POI and use local sensitivity analysis to focus on a reduced set of POI. Other choices include combinations of these parameters, such as the dimensionless numbers listed in Table 4. In determining how best to reduce human mortality and morbidity due to chikungunya and dengue and to predict risk of invasion into new areas, it is necessary to know the relative importance of the different factors (POI) responsible for transmission and prevalence (QOI).
Table 4.
Important dimensionless parameters for the chikungunya and dengue models based on dimensional analysis of the basic reproduction number,
 , in section 3.1.1. The first 5 dimensionless numbers can be affected by virus evolution, whereas the last three are largely governed by vector and host population dynamics.
, in section 3.1.1. The first 5 dimensionless numbers can be affected by virus evolution, whereas the last three are largely governed by vector and host population dynamics.
| Number | Description | |
|---|---|---|
| βhv | Probability of transmission from an infectious mosquito to a susceptible human given that a contact between the two occurs; measure of human susceptibility and mosquito infectiousness | |
|
|
Probability that an exposed mosquito will survive the extrinsic incubation period | |
| βvh | Probability of transmission from an infectious human to a susceptible mosquito given that a contact between the two occurs; measure of mosquito susceptibility and human infectiousness | |
|
|
Expected number of times that an infectious human will be bitten by mosquitoes if mosquitoes are freely available | |
|
|
Probability that an exposed human will survive the intrinsic incubation period (i.e. not die of natural death) | |
|
|
Expected number of human bites an infectious mosquito will have with humans freely available | |
|
|
Measure of actual availability of humans for mosquitoes to bite (proportion of desired mosquito bites that occur) | |
|
|
Measure of actual availability of mosquitoes to bite humans (proportion of potential bites on humans that actually occur) |
The solution of the mathematical models for the baseline parameters, shown in Figures 2–3, and the related QOI are functions of the parameters of interest. Because POI are only known approximately, it can be difficult to quantify the full range of possible model predictions. We will use three approaches to quantify the change and uncertainty in these QOI:
Local Sensitivity Analysis: In its simplest form, local sensitivity analysis defines the derivative of the model quantities of interest as a function of the model parameters for a particular reference (baseline) solution. The sensitivity indices (derivatives) can quantify how small changes in the input POI cause variability in the output QOI and determine the relative importance of the model parameters on the model predictions [66].
Extended Sensitivity Analysis: Extended sensitivity analysis calculates the response of the model to variations in each parameter of interest over its range of possible values, while fixing all of the other parameters at their baseline values.
Global Uncertainty Quantification: The QOI are investigated over the full range of possible parameter values. Each parameter is treated as a random variable and each QOI has a distribution dependent on the POI distributions.
4.1. Description of Local Sensitivity Analysis
In local sensitivity analysis, we perturb a reference (baseline) solution to quantify how the QOI change in response to small changes in the parameters of interest (POI). For example, it can be used to understand how the basic reproductive number or the endemic equilibrium states will change in response to small perturbations in the model parameters. The sign of the index indicates the direction of the response, and its magnitude tells us the relative importance of each parameter in our model predictions. Because the analysis is based on a linearization of the solution with the baseline parameters, the sensitivity indices are only valid for POIs very close to these baseline values. There is a detailed example of evaluating these sensitivity indices for mosquito-borne disease transmission models in [39].
We calculate the normalized sensitivity indices for
 , the magnitude of the first peak, the time to first peak, and the endemic equilibrium to the POIs at the baseline values (Table 3). The indices tell us the relative importance of each parameter to the QOIs for dengue and chikungunya and how sensitive a virus-mosquito system is to changes in parameters due to mitigation strategies, behavior change, or virus mutation. We use this sensitivity analysis to inform intervention strategies by determining which parameters have the largest impact on transmission and prevalence. The local sensitivity analysis indices are only valid in a small neighborhood of the baseline reference solution.
, the magnitude of the first peak, the time to first peak, and the endemic equilibrium to the POIs at the baseline values (Table 3). The indices tell us the relative importance of each parameter to the QOIs for dengue and chikungunya and how sensitive a virus-mosquito system is to changes in parameters due to mitigation strategies, behavior change, or virus mutation. We use this sensitivity analysis to inform intervention strategies by determining which parameters have the largest impact on transmission and prevalence. The local sensitivity analysis indices are only valid in a small neighborhood of the baseline reference solution.
The local normalized relative sensitivity index, , is the percent change in the output given the percent change in an input parameter. That is, if the parameter, p, changes by x%, then the quantity of interest, q, will change by . Note that the sign of the sensitivity index indicates whether the QOI increases (> 0) or decreases (< 0) with the POI. We describe this analysis in more detail in Appendix A.
4.2. Local Sensitivity Indices of

The growth of the early epidemic is partly characterized by
 and the sensitivity indices quantify how small changes in each of the POI affects
and the sensitivity indices quantify how small changes in each of the POI affects
 . We analytically computed the sensitivity indices
for
. We analytically computed the sensitivity indices
for
 (Table 6) by evaluating partial derivatives of Eq. 3.4 at the baseline parameter values (Table 3). The indices
, or the local sensitivity of
(Table 6) by evaluating partial derivatives of Eq. 3.4 at the baseline parameter values (Table 3). The indices
, or the local sensitivity of
 to a parameter p, are recorded in Table 6 for dengue and for chikungunya.
to a parameter p, are recorded in Table 6 for dengue and for chikungunya.
Table 6.
Sensitivity indices of
 (3.4) with respect to the POI for the dengue and chikungunya models at the baseline parameter values in Table 3. The most sensitive parameter is the mosquito biting rate, σv, and the least sensitive parameter is the human death rate, μh. A negative sensitivity index indicates if the parameter increases,
(3.4) with respect to the POI for the dengue and chikungunya models at the baseline parameter values in Table 3. The most sensitive parameter is the mosquito biting rate, σv, and the least sensitive parameter is the human death rate, μh. A negative sensitivity index indicates if the parameter increases,
 decreases, while a positive sensitivity index means that
decreases, while a positive sensitivity index means that
 increases as the parameter increases. Notice that the relative ranking of the order of importance of the parameters is the same for all four virus-vector combinations.
increases as the parameter increases. Notice that the relative ranking of the order of importance of the parameters is the same for all four virus-vector combinations.
| Parameter | DENV | DENV | CHIK-A | CHIK-R |
|---|---|---|---|---|
| A. aegypti | A. albopictus | A. aegypti | A. albopictus | |
| mathcalR0 = 1.55 | mathcalR0 = 1.07 | mathcalR0 = 1.10 | mathcalR0 = 1.27 | |
|
| ||||
| σv | +0.95 | +0.97 | +0.95 | +0.97 |
| μv | −0.71 | −0.66 | −0.72 | −0.57 |
| βvh | +0.50 | +0.50 | +0.50 | +0.50 |
| βhv | +0.50 | +0.50 | +0.50 | +0.50 |
| γh | −0.50 | −0.50 | −0.50 | −0.50 |
| H0 | −0.45 | −0.47 | −0.45 | −0.47 |
| Kv | +0.45 | +0.47 | +0.45 | +0.47 |
| νv | +0.21 | +0.16 | +0.22 | +0.07 |
| σh | +0.05 | +0.03 | +0.05 | +0.03 |
| μh | −0.0002 | −0.0002 | −0.0002 | −0.0002 |
| νh | +0.0001 | +0.0001 | +0.0001 | +0.0001 |
We see that, as expected, the basic reproduction number near the baseline parameter values is most sensitive to the mosquito biting rate, σv, and the mosquito death rate (inverse of the average mosquito lifespan), μv, for all scenarios. The basic reproduction number is also sensitive to transmission probabilities given a contact, βvh and βhv, and to γh, the rate at which a human recovers from infection. The basic reproduction number for all strains considered is also sensitive to Kv/H0, or the vector-to-host ratio.
The basic reproduction number near the baseline parameter values is most sensitive to, and increases with, the mosquito biting rate, σv. The second largest (in magnitude) sensitivity index for
 , μv, is negative. Therefore, as the death rate increases,
, μv, is negative. Therefore, as the death rate increases,
 will decrease. After identifying that σv and μv are the largest sensitivity indices for
will decrease. After identifying that σv and μv are the largest sensitivity indices for
 , the next step is to determine why these variables are so important. In equation 3.5 for
, the next step is to determine why these variables are so important. In equation 3.5 for
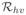 , both of these variables contribute to the expected maximum number of bites that an infected mosquito will make, σv/μv. That is, these two POIs both contribute to this underlying driving factor for the epidemic.
, both of these variables contribute to the expected maximum number of bites that an infected mosquito will make, σv/μv. That is, these two POIs both contribute to this underlying driving factor for the epidemic.
A noticeable difference among the sensitivities for the virus-vector combinations is that for CHIK-R(A. albopictus),
 is less sensitive to the extrinsic incubation period (EIP), 1/νv than the other combinations. The average time that an infected mosquito is infectious is a function of the difference between the average lifetime of the mosquito and the EIP (and the average age that a mosquito becomes infected). If the EIP is significantly shorter than any of the other virus-vector combinations (as it is for CHIK-R (A. albopictus)), then the average time an infected mosquito is infected is longer, making
is less sensitive to the extrinsic incubation period (EIP), 1/νv than the other combinations. The average time that an infected mosquito is infectious is a function of the difference between the average lifetime of the mosquito and the EIP (and the average age that a mosquito becomes infected). If the EIP is significantly shorter than any of the other virus-vector combinations (as it is for CHIK-R (A. albopictus)), then the average time an infected mosquito is infected is longer, making
 less sensitive to relative changes in the EIP. Therefore, decreasing the EIP for DENV and CHIK-A by a small amount will have a greater impact on initial transmission than will decreasing the EIP for CHIK-R by a small amount. We can also see that for chikungunya,
less sensitive to relative changes in the EIP. Therefore, decreasing the EIP for DENV and CHIK-A by a small amount will have a greater impact on initial transmission than will decreasing the EIP for CHIK-R by a small amount. We can also see that for chikungunya,
 is more sensitive to the human infectious period (1/γh) than is dengue.
is more sensitive to the human infectious period (1/γh) than is dengue.
4.3. Sensitivity indices for endemic equilibrium and epidemic peak
In addition to the basic reproduction number, we compute sensitivity of the timing and magnitude of the first epidemic peak and of the endemic equilibrium to the baseline parameter values. In order to compute sensitivity of the timing and magnitude of the first epidemic peak, we set initial conditions to be the same for all scenarios, namely one infectious human is introduced into fully susceptible human and mosquito populations that are at carrying capacity. Table 7 records local normalized sensitivity indices of the endemic equilibrium and first epidemic peak for dengue and for chikungunya. We only record values for the first eight most sensitive parameters.
Table 7.
Dengue and chikungunya model local normalized sensitivity indices of the endemic equilibrium and the magnitude and timing of the first epidemic peak. The endemic equilibrium is denoted by (eh, ih, rh, ev, iv) and properties of the first peak are maximum proportion humans infected (ih,P), time to ih,P (Tih,P), maximum proportion of mosquitoes infected (iv,P), time to iv,P (Tiv,P), maximum proportion of immune humans (rh,P), and time to rh,P (Trh,P). DENV(A. albopictus) and CHIK-A(A. aegypti) are more sensitive to changes in the parameters. Generally, the characteristics of the epidemic peak are more sensitive to parameter changes than the endemic equilibrium or mathcalR0 are.
| Parameter | eh | ih | rh | ev | iv | ih,P | Tih,P | iv,P | Tiv,P | rh,P | Trh,P |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| DENV(A. aegypti)
| |||||||||||
| σv | 1.35 | 1.35 | 1.35 | 2.30 | 2.30 | 3.31 | −2.42 | 3.74 | −1.40 | 0.82 | −1.94 |
| μv | −1.01 | −1.01 | −1.01 | −1.42 | −2.42 | −2.00 | 1.69 | −3.01 | 0.73 | −0.61 | 0.34 |
| γh | −0.71 | −1.71 | −0.71 | −1.71 | −1.71 | −2.51 | 1.40 | −2.23 | 0.42 | −0.42 | 1.23 |
| βhv | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 1.79 | −1.70 | 1.54 | −0.74 | 0.44 | −0.26 |
| βvh | 0.71 | 0.71 | 0.71 | 1.71 | 1.71 | 1.71 | −1.70 | 2.40 | −0.74 | 0.42 | −0.25 |
| Kv | 0.64 | 0.64 | 0.64 | 0.59 | 0.59 | 1.61 | −1.59 | 1.34 | −0.64 | 0.40 | −0.22 |
| H0 | −0.64 | −0.64 | −0.64 | −0.59 | −0.59 | −0.02 | 0.00 | −0.02 | 0.00 | −0.01 | 0.02 |
| νv | 0.30 | 0.30 | 0.30 | −0.29 | 0.71 | 0.85 | −0.45 | 1.16 | −0.42 | 0.18 | −0.16 |
|
| |||||||||||
| DENV(A. albopictus)
| |||||||||||
| σv | 9.11 | 9.11 | 9.11 | 10.09 | 10.09 | 18.56 | −8.35 | 19.37 | −8.30 | 8.60 | −8.23 |
| μv | −6.20 | −6.20 | −6.20 | −6.53 | −7.53 | −12.02 | 5.08 | −13.24 | 5.09 | −5.84 | 4.97 |
| γh | −4.69 | −5.69 | −4.69 | −5.69 | −5.69 | −10.38 | 4.13 | −10.30 | 4.12 | −4.42 | 4.30 |
| βhv | 4.69 | 4.69 | 4.69 | 4.69 | 4.69 | 9.57 | −4.23 | 9.49 | −4.21 | 4.43 | −4.42 |
| βvh | 4.69 | 4.69 | 4.69 | 5.69 | 5.69 | 9.54 | −4.23 | 10.46 | −4.21 | 4.42 | −4.42 |
| Kv | 4.42 | 4.42 | 4.42 | 4.39 | 4.39 | 9.02 | −4.11 | 8.92 | −4.11 | 4.18 | −4.20 |
| H0 | −4.42 | −4.42 | −4.42 | −4.39 | −4.39 | −0.47 | 0.04 | −0.46 | 0.03 | −0.28 | −0.04 |
| νv | 1.51 | 1.51 | 1.51 | 0.84 | 1.84 | 3.21 | −1.61 | 3.50 | −1.60 | 1.43 | −1.47 |
|
| |||||||||||
| CHIK-A(A. aegypti)
| |||||||||||
| σv | 8.55 | 8.55 | 8.55 | 9.50 | 9.50 | 17.41 | −8.01 | 18.20 | −8.02 | 7.99 | −8.15 |
| μv | −6.48 | −6.48 | −6.48 | −6.92 | −7.92 | −12.63 | 5.25 | −13.96 | 5.24 | −6.05 | 5.65 |
| γh | −4.50 | −5.50 | −4.50 | −5.50 | −5.50 | −9.94 | 3.98 | −9.86 | 3.98 | −4.19 | 4.06 |
| βhv | 4.50 | 4.50 | 4.50 | 4.50 | 4.50 | 9.18 | −4.10 | 9.10 | −4.09 | 4.21 | −4.09 |
| βvh | 4.50 | 4.50 | 4.50 | 5.50 | 5.50 | 9.15 | −4.10 | 10.06 | −4.09 | 4.20 | −4.09 |
| Kv | 4.05 | 4.05 | 4.05 | 4.00 | 4.00 | 8.26 | −3.89 | 8.14 | −3.92 | 3.79 | −3.97 |
| H0 | −4.05 | −4.05 | −4.05 | −4.00 | −4.00 | −0.33 | 0.01 | −0.33 | 0.01 | −0.20 | 0.02 |
| νv | 1.98 | 1.98 | 1.98 | 1.42 | 2.42 | 4.15 | −2.01 | 4.56 | −1.98 | 1.85 | −1.72 |
|
| |||||||||||
| CHIK-R(A. albopictus)
| |||||||||||
| σv | 3.84 | 3.84 | 3.85 | 4.82 | 4.81 | 8.26 | −4.21 | 8.90 | −4.16 | 3.22 | −4.43 |
| μv | −2.26 | −2.26 | −2.26 | −2.40 | −3.40 | −4.23 | 1.70 | −5.16 | 2.35 | −1.89 | 1.88 |
| γh | −1.97 | −2.97 | −1.98 | −2.97 | −2.97 | −5.04 | 2.22 | −4.87 | 2.24 | −1.65 | 1.67 |
| βhv | 1.97 | 1.97 | 1.98 | 1.97 | 1.97 | 4.27 | −2.43 | 4.10 | −2.45 | 1.67 | −1.8 |
| βvh | 1.97 | 1.97 | 1.98 | 2.97 | 2.97 | 4.22 | −2.43 | 5.04 | −2.45 | 1.64 | −1.81 |
| Kv | 1.87 | 1.87 | 1.87 | 1.84 | 1.84 | 4.04 | −2.33 | 3.86 | −2.37 | 1.58 | −1.78 |
| H0 | −1.87 | −1.87 | −1.87 | −1.84 | −1.84 | −0.10 | −0.08 | −0.09 | −0.09 | −0.06 | −0.13 |
| νv | 0.28 | 0.28 | 0.28 | −0.58 | 0.42 | 0.68 | −0.36 | 0.80 | −0.35 | 0.24 | −1.03 |
Sensitivity of the endemic equilibrium for all scenarios retains the same general order of parameter importance as for the basic reproduction number. However, the magnitude of the sensitivity is different. The endemic equilibrium is more sensitive to all of the parameters, so small changes in parameter values will result in a larger change in the endemic equilibrium than in the basic reproduction number. We notice here a significant difference between mosquito species for dengue. For the endemic equilibrium, DENV(A. albopictus) is much more sensitive to the POI than DENV(A. aegypti).
The timing and magnitude of the first epidemic peak is about twice as sensitive to the parameters as the endemic equilibrium is. So, small changes in parameter values will have the most effect on the timing and magnitude of the first epidemic peak when introduced into a naive population. The one exception to this is that the first peak is much less sensitive than
 is to the number of hosts (humans) in the system. As in the endemic case, the first peak for DENV(A. albopictus) is much more sensitive to local changes in parameter values than is the first peak for DENV(A. aegypti).
is to the number of hosts (humans) in the system. As in the endemic case, the first peak for DENV(A. albopictus) is much more sensitive to local changes in parameter values than is the first peak for DENV(A. aegypti).
The ranking of sensitivity indices for chikungunya and dengue are similar. The sensitivity indices are generally largest for the timing and magnitude of the first peak, then for the endemic equilibrium, and finally for the basic reproduction number. As with dengue, we see a significant difference in magnitude of sensitivity between mosquito species. The endemic equilibrium for CHIK-R(A. albopictus) is about half as sensitive to the top parameters as DENV(A. albopictus). Furthermore, the endemic equilibrium for CHIK-A(A. aegypti) is nearly three times as sensitive as CHIK-R(A. albopictus). Similarly, sensitivity of the timing and magnitude of the first epidemic peak for the CHIK-R(A. albopictus) is less than half that for CHIK-A(A. aegypti). As with dengue, the peak is not sensitive to the number of humans, meaning there are sufficient hosts available for the first epidemic. If the number of humans were significantly reduced, this could change. It would be interesting to explore this further for different vector-to-host ratios and initial conditions.
For both dengue and chikungunya any change in the important parameters will have the most effect on the magnitude and timing of the first epidemic peak. The endemic equilibrium values are less sensitive, while the basic reproduction number is the least sensitive to parameter changes. This result highlights the fact that reducing the size of a new epidemic or driving a disease to very low levels in the endemic stage is easier than reducing
 below one, or eradicating the disease permanently without possibility of an outbreak if re-introduced. From a management and mitigation perspective, the size and timing of an outbreak can be greatly reduced by changes in the sensitive parameters (POI).
below one, or eradicating the disease permanently without possibility of an outbreak if re-introduced. From a management and mitigation perspective, the size and timing of an outbreak can be greatly reduced by changes in the sensitive parameters (POI).
4.4. Extended Sensitivity Analysis
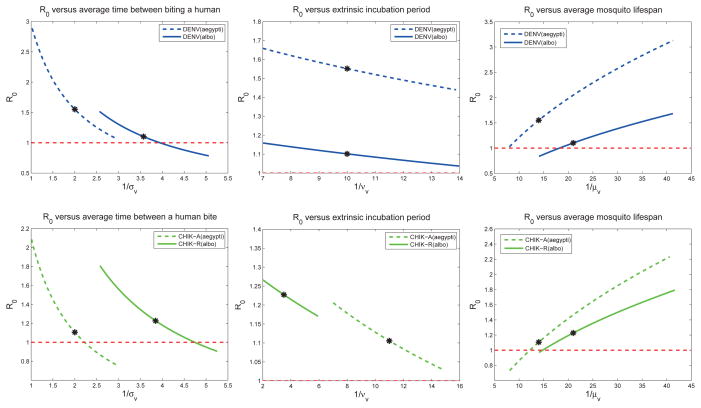
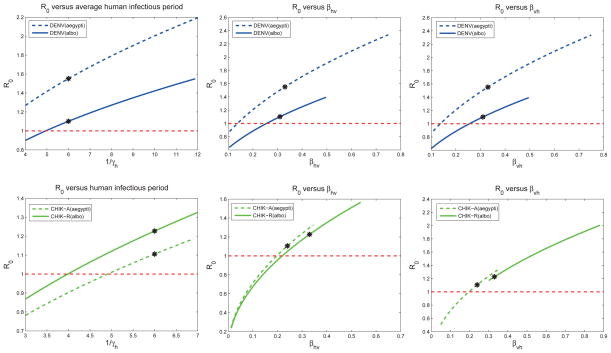
Local sensitivity analysis is a useful tool, but is valid for only small changes in any of the baseline POI. Extended sensitivity analysis expands the range of the analysis along the axis of each POI. It quantifies the univariate model response for each of the POI over the parameter’s entire range of values (holding the other POI fixed at the baseline values).
If the response curves in Figure 4 were straight lines, then the local sensitivity analysis would be exact over the entire range of the POI. Because most of the response curves are close to a straight line, the local sensitivity indices (Table 7) are good approximations over the entire range of feasible parameters given in Table 2. One exception to the linear behavior are the plots of
 versus the average time between mosquito bites, 1/σv. The magnitude of sensitivity for
versus the average time between mosquito bites, 1/σv. The magnitude of sensitivity for
 is higher at higher biting rates (or fewer number of days between human bites).
is higher at higher biting rates (or fewer number of days between human bites).
Figure 4.
These plots show how the
 for dengue (top 3 plots) and chikungunya (bottom 3 plots) change as the parameters vary (one at a time) within the ranges given in Table 2, while all other parameters are set at baseline values. Baseline values for the models (indicated by a *) correspond to Table 6. The local sensitivity indices in Table 6 are the scaled slope at the baseline values. For sensitivity curves close to a straight line (e.g. for νv), the local sensitivity index is relatively accurate across the parameter range. However, if the sensitivity curve is more nonlinear (e.g. for σv), the local sensitivity index is indeed only accurate locally. Effective early mitigation strategies target the control POI that reduce
for dengue (top 3 plots) and chikungunya (bottom 3 plots) change as the parameters vary (one at a time) within the ranges given in Table 2, while all other parameters are set at baseline values. Baseline values for the models (indicated by a *) correspond to Table 6. The local sensitivity indices in Table 6 are the scaled slope at the baseline values. For sensitivity curves close to a straight line (e.g. for νv), the local sensitivity index is relatively accurate across the parameter range. However, if the sensitivity curve is more nonlinear (e.g. for σv), the local sensitivity index is indeed only accurate locally. Effective early mitigation strategies target the control POI that reduce
 the most.
the most.
The extended sensitivity analysis plots provide visual comparison between the scenarios. For example, reducing the time that an infectious human is exposed to mosquito bites can have a significant impact on chikungunya transmission, but would be less effective for dengue when implemented alone. Reducing susceptibility of humans (βhv) for chikungunya via vaccines, for example, could significantly reduce
 for chikungunya even with relatively low efficacy. For dengue, however, significant reduction in vector-to-host transmission would be needed to significantly reduce
for chikungunya even with relatively low efficacy. For dengue, however, significant reduction in vector-to-host transmission would be needed to significantly reduce
 . For the virus-vector scenarios, and in particular for DENV(A. aegypti) and CHIK-R(A. albopictus),
. For the virus-vector scenarios, and in particular for DENV(A. aegypti) and CHIK-R(A. albopictus),
 > 1 across most of each parameter’s range. Thus, the model predicts that the most effective mitigation strategies to mitigate chikungunya or dengue would be an integrated strategy that changed multiple parameters simultaneously.
> 1 across most of each parameter’s range. Thus, the model predicts that the most effective mitigation strategies to mitigate chikungunya or dengue would be an integrated strategy that changed multiple parameters simultaneously.
4.5. Global Uncertainty Quantification
Local sensitivity analysis is valid at particular parameter values assuming that all other parameters are fixed. The extended sensitivity analysis varies one parameter at a time, but still only samples a very small region in the space of possible parameter values. There is uncertainty in parameter values and combinations of parameter values depending on location, climate, individual behavior, and intrinsic stochasticity, so we computed distributions for each of the QOI while varying all parameters across their ranges simultaneously. The goal of global uncertainty quantification is to characterize the response of the model over the entire feasibility space. In particular, it can be used to identify regions of the feasible POIs that create outliers (extreme events) in the QOI and to quantify the distributions of, and correlations between, the QOI.
We begin by solving for the QOI as the POI are sampled throughout their range (Table 3). In our global uncertainty analysis, we have assumed that each of the POIs are varying independently of each other. If the POIs are correlated, then this must be taken into account in the sampling algorithm. We assumed uniform distributions for the parameter ranges. If more information is known about these distributions, then the sampling can reflect the known distribution. By tabulating all of the sample responses for a single QOI q, we can create the one-dimensional distribution for the QOI. This simple approach provides a quick analysis of the possible range of QOI within the parameter ranges and indicates the frequency with which QOI values will occur.
The ordering of the sensitivity of the QOIs with respect to the POIs is robust over the full range of parameter values. That is, the relative importance of the model parameters is insensitive their specific values. The
 distribution for the CHIK-A(A. aegypti) is relatively narrow with the peak just below one (see Figure 5(a)). The
distribution for the CHIK-A(A. aegypti) is relatively narrow with the peak just below one (see Figure 5(a)). The
 distribution for DENV(A. albopictus) peaks just above one but is still lower than the CHIK-R and DENV(A. aegypti). The
distribution for DENV(A. albopictus) peaks just above one but is still lower than the CHIK-R and DENV(A. aegypti). The
 distribution for both CHIK-R(A. albopictus) and DENV(A. aegypti) have longer tailed distributions, thus more variation in outcome.
distribution for both CHIK-R(A. albopictus) and DENV(A. aegypti) have longer tailed distributions, thus more variation in outcome.
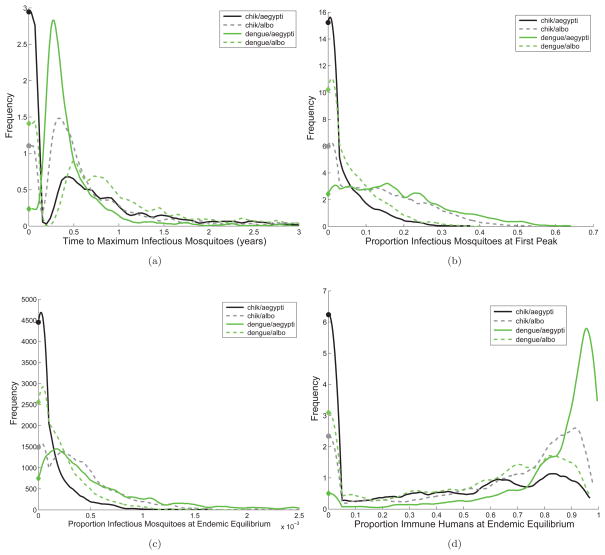
Figure 5.
Distributions for
 , first epidemic peak, and the endemic equilibrium, sampling uniformly from the ranges of the 8 most sensitive parameters (POIs). The x-axis is the value of the output variable being considered and the y-axis is the value of the associated probability distribution function (pdf). The vertical dashed red line at
, first epidemic peak, and the endemic equilibrium, sampling uniformly from the ranges of the 8 most sensitive parameters (POIs). The x-axis is the value of the output variable being considered and the y-axis is the value of the associated probability distribution function (pdf). The vertical dashed red line at
 = 1 in subfigure (a) indicates the threshold value for an epidemic. For CHIK-A(A. aegypti) 64.5% of parameter combinations result in an outbreak with mathcal R0 > 1, while for CHIK-R(A. albopictus) 85.4%, for DENV(A. aegypti) 96.3%, and for DENV(A. albopictus) 79.8% do. Subfigures (b)–(d) show distributions for the magnitude of the first epidemic peak in humans, time to the first epidemic peak after introduction, and proportion of humans infectious at the endemic equilibrium. The far left side of the plots (b)– (d) (filled circles) are cases for which there is no epidemic (i.e.
= 1 in subfigure (a) indicates the threshold value for an epidemic. For CHIK-A(A. aegypti) 64.5% of parameter combinations result in an outbreak with mathcal R0 > 1, while for CHIK-R(A. albopictus) 85.4%, for DENV(A. aegypti) 96.3%, and for DENV(A. albopictus) 79.8% do. Subfigures (b)–(d) show distributions for the magnitude of the first epidemic peak in humans, time to the first epidemic peak after introduction, and proportion of humans infectious at the endemic equilibrium. The far left side of the plots (b)– (d) (filled circles) are cases for which there is no epidemic (i.e.
 < 1). For subfigure (d), the x-axis units are in 10−4 and for (c) the x-axis units are in years. Notice that DENV(A. aegypti) and CHIK-R(A. albopictus) consistently have higher values for
< 1). For subfigure (d), the x-axis units are in 10−4 and for (c) the x-axis units are in years. Notice that DENV(A. aegypti) and CHIK-R(A. albopictus) consistently have higher values for
 , a larger first epidemic peak, and move faster when first introduced. At the endemic equilibrium, however, the proportion of humans infectious at any given time is higher in general for systems with A. aegypti, even while accounting for virus strain. This indicates that the first epidemic depends strongly on the virus-vector-host interactions, but once endemic, vector characteristics are more important.
, a larger first epidemic peak, and move faster when first introduced. At the endemic equilibrium, however, the proportion of humans infectious at any given time is higher in general for systems with A. aegypti, even while accounting for virus strain. This indicates that the first epidemic depends strongly on the virus-vector-host interactions, but once endemic, vector characteristics are more important.
The fraction of cases, F, for which the basic reproduction number exceeds the threshold value,
 > 1, over the full range of possible parameter values indicates the fraction of parameter values that can sustain an epidemic. These fractions vary widely over different virus-vector combinations:
> 1, over the full range of possible parameter values indicates the fraction of parameter values that can sustain an epidemic. These fractions vary widely over different virus-vector combinations:
| CHIK-A(A. aegypti) |
F(
 > 1) = 0.65 > 1) = 0.65 |
| CHIK-R(A. albopictus) |
F(
 > 1) = 0.85 > 1) = 0.85 |
| DENV(A. aegypti) |
F(
 > 1) = 0.96 > 1) = 0.96 |
| DENV(A. albopictus) |
F(
 > 1) = 0.80 > 1) = 0.80 |
Overall, DENV(A. aegypti) is most likely to spread, followed by CHIK-R(A. albopictus), both of which result in general in the fastest and largest outbreaks and highest endemic seroprevalence levels. This observation is consistent with the rapid spread of dengue across South America with the reintroduction of A. aegypti.
Figure 5(b) shows the distribution of the proportion of humans immune to the virus at first epidemic peak. The size of the first outbreak is zero for the parameter values where
 < 1. For parameters where
< 1. For parameters where
 > 1, at the epidemic peak, a larger fraction of people are infected with CHIK-R(A. albopictus) than they are to CHIK-A(A. aegypti). Similarly, at the epidemic peak, there are many more people immune to dengue in an A. aegypti epidemic than when A. albopictus is the primary vector. We see similar rankings of virus-vector combinations for Figures 5(c) and 5(d). The position of the peaks of the distributions for proportion of infectious humans at endemic equilibrium align for each virus regardless of the vector, presumably because of differences in the human infectious periods. Distributions for other POI can be found in Figure B.6.
> 1, at the epidemic peak, a larger fraction of people are infected with CHIK-R(A. albopictus) than they are to CHIK-A(A. aegypti). Similarly, at the epidemic peak, there are many more people immune to dengue in an A. aegypti epidemic than when A. albopictus is the primary vector. We see similar rankings of virus-vector combinations for Figures 5(c) and 5(d). The position of the peaks of the distributions for proportion of infectious humans at endemic equilibrium align for each virus regardless of the vector, presumably because of differences in the human infectious periods. Distributions for other POI can be found in Figure B.6.
The distribution of values for
 for dengue are similar to previous estimates, e.g. see [35] and references therein, and the wide range of possible values for
for dengue are similar to previous estimates, e.g. see [35] and references therein, and the wide range of possible values for
 for DENV(A. aegypti) is consistent with variation in the basic reproduction number seen from year to year and between locations for dengue. Seroprevalence after the first epidemic peak is within observed ranges for both CHIK-A and CHIK-R. For the CHIK-R(A. albopictus) outbreak on Réunion island, seroprevalence was estimated between 35–41% [67]; for CHIK-R(A. albopictus) in Mayotte seroprevalence was estimated at 32.7% [68]. Both Réunion and Mayotte implemented wide-spread mitigation strategies, thus presumably reducing the size of the first peak. In Lamu Island, Kenya the CHIK-R(A. aegypti) combination resulted in an outbreak with up to 75% seroprevalence [69]; and CHIK-R(A. aegypti) on Comore island resulted in 62% seroprevalence [70], both with minimal to no mitigation implemented. Distributions computed for the endemic equilibrium for CHIK-A also match well with existing data. An outbreak of CHIK-A(A. aegypti) in Senegal in 1996–1997 resulted in 35% seroprevalence and endemic prevalence of the CHIK-A in Southeast Asia with primarily A. aegypti was estimated to be 1–42% with mean 18% [71, 72].
for DENV(A. aegypti) is consistent with variation in the basic reproduction number seen from year to year and between locations for dengue. Seroprevalence after the first epidemic peak is within observed ranges for both CHIK-A and CHIK-R. For the CHIK-R(A. albopictus) outbreak on Réunion island, seroprevalence was estimated between 35–41% [67]; for CHIK-R(A. albopictus) in Mayotte seroprevalence was estimated at 32.7% [68]. Both Réunion and Mayotte implemented wide-spread mitigation strategies, thus presumably reducing the size of the first peak. In Lamu Island, Kenya the CHIK-R(A. aegypti) combination resulted in an outbreak with up to 75% seroprevalence [69]; and CHIK-R(A. aegypti) on Comore island resulted in 62% seroprevalence [70], both with minimal to no mitigation implemented. Distributions computed for the endemic equilibrium for CHIK-A also match well with existing data. An outbreak of CHIK-A(A. aegypti) in Senegal in 1996–1997 resulted in 35% seroprevalence and endemic prevalence of the CHIK-A in Southeast Asia with primarily A. aegypti was estimated to be 1–42% with mean 18% [71, 72].
Distributions for the magnitude and timing of the first peak also maintain the general rankings of the virus-vector combinations as seen in Figures 5(c) and B.6(a). The timing of the first peak highlights differences among the initial growth rates of the different virus-vector combinations. Global uncertainty quantification via distributions of the QOI across the full range of POI confirms that the pathogen-vector systems resulting in the highest risk across the QOI is DENV(A. aegypti) and the new strain of CHIK-R(A. albopictus), as was seen in local sensitivity analysis.
Figure B.6.
Subfigures (a) – (b) are distributions for the time to the first epidemic peak and the magnitude of the first peak in mosquitoes. Subfigures (b) – (c) are the proportion of infectious mosquitoes at the endemic equilibrium and proportion of recovered and immune humans at the endemic equilibrium. The x-axis is the value of the variable being considered and the y-axis is the value of the associated probability distribution function. The far left of each plot represents scenarios for which the disease does not take off.
5. Discussion and Conclusion
We extended the Chitnis et al. [9, 10] models to chikungunya and dengue for both A. aegypti and A. albopictus mosquito vectors. We derived an explicit formula for the basic reproduction number and endemic equilibrium, and compiled two baseline parameter ranges: one for dengue and one for chikungunya, each with A. aegypti and A. albopictus. Our analysis focused on three quantities of interest:
 , the endemic equilibrium, and the timing and magnitude of the first epidemic peak. We then used local sensitivity analysis to determine which parameters are most important to disease persistence and transmission. Local sensitivity differences between the scenarios were more pronounced for the endemic equilibrium and most pronounced for the timing and magnitude of the first peak. We also sampled from parameter ranges to find distributions for the quantities of interest.
, the endemic equilibrium, and the timing and magnitude of the first epidemic peak. We then used local sensitivity analysis to determine which parameters are most important to disease persistence and transmission. Local sensitivity differences between the scenarios were more pronounced for the endemic equilibrium and most pronounced for the timing and magnitude of the first peak. We also sampled from parameter ranges to find distributions for the quantities of interest.
Insights into mitigation strategies and the effects of virus evolution were gained by dimensional analysis of the basic reproduction number. From a mitigation perspective, the basic reproduction number is one indicator for risk of outbreaks. From a virus evolution perspective, the basic reproduction number is one measure of virus fitness [73]. From both a mitigation and virus evolution perspective, close inspection of the dimensionless parameters under the parameter ranges for chikungunya and dengue indicates that the largest effect is attained by small changes in the mosquito portion of the transmission cycle, with the notable exception of the amount of time a human host spends infectious and host susceptibility to infection (e.g., prior immunity). The less robust viruses, as measured by our quantities of interest, would benefit more from small changes in parameter values as opposed to the more efficient virus-vector combinations which get relatively little benefit from the same relative magnitude change in parameters.
We found that mitigation strategies affecting the most sensitive parameters can have a large impact on the magnitude and timing of the first epidemic peak if the viruses are introduced into a fully susceptible population. This is particularly true for DENV(A. albopictus) and CHIK-A(A. aegypti), indicating that given a fast response, outbreaks should be relatively easy to control. For the new strain CHIK-R(A. albopictus) and DENV(A. aegypti), mitigation strategies affecting the most sensitive parameters will be effective but will need to be implemented on a larger scale and in concert to result in the same reduction in epidemic peak size. Therefore, the new strain of chikungunya poses a higher risk for places with high densities of A. albopictus and can potentially spread quickly in such scenarios when invading a naive area, as does dengue in a naive area with high densities of A. aegypti.
Reducing the mosquito biting rate and vector-to-host ratio via repellents, adulticides, larvicides, or other methods will be effective for all vector-virus scenarios. Reducing the mosquito lifespan (e.g., use of lethal ovitraps) will work well for dengue and the old strain of chikungunya, but not as well for the new strain of chikungunya, since the extrinsic incubation period is shorter and thus sensitivity to mosquito lifespan is reduced. Reducing the amount of time a human spends infectious (or an infectious human’s availability to mosquitoes), and thus the expected number of mosquito bites an infectious person gets, will also serve to reduce initial transmission. Thus, quarantine of infectious humans from mosquito exposure could be an effective measure.
From the perspective of virus fitness, decreasing the extrinsic incubation period will increase the basic reproduction number and the probability of infected mosquitoes surviving the EIP to become infectious and transmit to humans. The virus can also gain increased fitness indirectly from changes in mosquito population dynamics such as higher human biting rates, shorter gonotrophic cycles, and longer lifespans, due to mosquito evolution, climate change, urbanization, and other natural or anthropogenic changes in the environment. These results highlight that even small changes in mosquito population dynamics, mosquito species distribution, and/or virus-mosquito interactions can have a significant effect on the basic reproduction number.
Based on our analysis, the Asian strain of chikungunya would have room for improvement when balancing initial transmission, transient epidemic dynamics, and endemic state, since it is more sensitive to small parameter changes. This helps explain why the new Rèunion strain is so successfully invading, since fitness would be significantly increased by small parameter changes resulting from virus mutation, such as the observed reduction in the extrinsic incubation period. Because overall immunity to chikungunya in humans is low, invasion of a new strain is not hampered by low host availability as in the dengue case. It remains to be seen if the new strain of chikungunya will successfully invade dengue-endemic urban areas. Reduced sensitivity of the new strain of chikungunya to small parameter changes suggests the new strain is moving toward a peak in fitness.
Since dengue in A. aegypti is close to maximal in terms of invasion (i.e. in the first peak more than 80% of the population become immune in most scenarios and remain immune for life) and persistence, and since small changes in the parameters have relatively little effect, it seems it would be difficult for a new strain of dengue to invade the endemic system. Evolution of the virus would give relatively little fitness advantage unless it could significantly change some aspect of the dynamics, such as host immunity. Dengue virus is comprised of four serotypes for which exposure to a previous serotype does not confer full immunity. This type of strain evolution in the presence of immune pressure (i.e., availability of susceptible hosts) makes sense in the context of our sensitivity analysis and distributions of the quantities of interest.
For dengue in A. albopictus, small changes in the virus or mosquito apart from host immunity could potentially result in large changes in virus fitness as measured by successful invasion potential and long-term persistence. This will only be the case if available humans in A. albopictus dominated areas are not already immune, as could occur in temperate regions such as Europe [74] or the United States. With high human mobility, previous exposure in areas dominated by A. aegypti may minimize potential significant advantages for adaptation in regions where dengue is already present. However, in places where A. albopictus is dominate and dengue is not currently circulating, a mutation in dengue similar to the one we saw in chikungunya could pose an increased risk. So for some scenarios, a change in parameters via virus mutation, climate change, or change in mosquito distributions can significantly affect risk for disease invasion, particularly as regards the timing and size of the first epidemic peak.
The model analyzed in this paper does not address the scenario in which multiple serotypes of dengue are circulating and thus prior exposure can lead to immune interactions, such as temporary cross-immunity and the increased risk of severe disease. As far as is currently known, this is only an issue for dengue (with four distinct serotypes) and not chikungunya (all strains belong to a single serotype and are assumed to confer complete cross-immunity). The work presented here is relevant for the introduction of dengue and chikungunya strains into novel areas, which is timely in the light of recent events including spread of chikungunya to the Caribbean [8] and evidence of autochthonous dengue cases in Houston [75].
 and the timing and magnitude of the first epidemic peak are naturally defined within the context of an introduction into a fully susceptible population. The proportion infected with dengue at endemic equilibrium could be impacted by the presence of multiple serotypes. In endemic regions where the availability of susceptible human hosts is modulated by immunity, we expect that the relative sensitivity of the non-immune-related parameters will be similar to what we found here. We focused on the consequences of viral variation in traits such as the extrinsic incubation period. However, immune pressure could overwhelm small changes in viral or mosquito traits that are not related to immunity. More work will be needed to understand the relative importance of strain variability within the context of hyperendemicity, where multiple serotypes circulate and immunity plays a key role in dengue dynamics.
and the timing and magnitude of the first epidemic peak are naturally defined within the context of an introduction into a fully susceptible population. The proportion infected with dengue at endemic equilibrium could be impacted by the presence of multiple serotypes. In endemic regions where the availability of susceptible human hosts is modulated by immunity, we expect that the relative sensitivity of the non-immune-related parameters will be similar to what we found here. We focused on the consequences of viral variation in traits such as the extrinsic incubation period. However, immune pressure could overwhelm small changes in viral or mosquito traits that are not related to immunity. More work will be needed to understand the relative importance of strain variability within the context of hyperendemicity, where multiple serotypes circulate and immunity plays a key role in dengue dynamics.
Although this model gives important insight when comparing chikungunya and dengue, we make several assumptions that are not realistic for all geographic regions or virus-vector-host scenarios. We did not consider the Rèunion strain of chikungunya in A. aegypti, but evidence suggests that CHIK-R has a shorter incubation period in A. aegypti as well. Our baseline vector-to-host ratio of 2:1 with a range of 1:1–10:1 may be high or low for some regions while the baseline maximum bites a human sustains may also be high or low depending on the region. We ignore seasonality, but it could play an important role in the long-term persistence of the virus and in the size of an initial outbreak by limiting mosquito density as seasons change. We also did not consider chikungunya and dengue co-circulating in a population, although this is certainly a possibility. Future work incorporating seasonality and stochasticity will be important. We also assume closed human and mosquito populations, but human movement could play an important role in patterns of infection within a region and in long-term persistence via re-introduction of the virus from movement of infectious humans or mosquitoes. Finally, we did not consider sylvatic cycling, which may play a role in persistence. Choice of which of these added complexities to include will depend on the characteristics of specific regions or systems we wish to understand.
We summarize the key public health related findings from the model analysis here:
For both dengue and chikungunya any change in the most sensitive parameters will have the most effect on the magnitude and timing of the first epidemic peak upon introduction
The most effective mitigation for chikungunya or dengue would be an integrated strategy that changed multiple parameters simultaneously
For CHIK-R(A. albopictus) and DENV(A. aegypti), mitigation strategies will need to be implemented on a larger scale and in concert to result in the same reduction in epidemic peak size
Reducing the mosquito biting rate and vector-to-host ratio will be effective for all vector-virus scenarios
Reducing the mosquito lifespan could work well for DENV, but not as well for CHIK
Reducing the amount of time a human spends infectious (or an infectious human’s availability to mosquitoes) will also serve to reduce initial transmission
A change in parameters via virus mutation, climate change, or change in mosquito distributions can affect risk for disease invasion, particularly as regards the timing and size of the first epidemic peak
Acknowledgments
CAM, HJW and JMH are partially supported through grants from the NIH/NIGMS grant in the Models of Infectious Disease Agent Study (MIDAS) program, U01-GM097661-01 and CAM is partially supported by the NSF MPS Division of Mathematical Sciences grant DMS-1122666 and NSF SEES Science, Engineering and Education for Sustainability Fellow grant CHE-1314029. KSH is partially supported by NIH/NIGMS MIDAS grant U01-GM097658. SX was supported by the Center for Computational Science at Tulane University. We thank Christopher Mores, Dawn Wesson, and Rebecca Christofferson for helpful conversations and comments. Thank you to two anonymous reviewers for helpful comments.
Appendix A. Computing

For the model (2.1), we let x = (Eh, Ih, Ev, Iv, Rh, Nh, Nv) and dx/dt =
 (x) −
(x) −
 (x), where
(x), where
 (x) represents the rate of new infections entering the population, and
(x) represents the rate of new infections entering the population, and
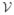 (x) =
(x) =
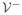 (x) −
(x) −
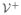 (x) represents the rate of movement (by other means) out of, and into, each compartment, respectively. We let F0 and V0 be the Jacobian matrices of the first four elements of
(x) represents the rate of movement (by other means) out of, and into, each compartment, respectively. We let F0 and V0 be the Jacobian matrices of the first four elements of
 and
and
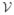 , respectively, evaluated at the disease-free equilibrium, xdfe. Then,
, respectively, evaluated at the disease-free equilibrium, xdfe. Then,
| (A.1) |
and,
| (A.2) |
where,
| (A.3) |
The next generation matrix is
| (A.4) |
where the kij entry of R is the average number of cases in class i resulting from an infectious individual in class j.
Appendix B. Local and Global Sensitivity Analysis
We start by describing local sensitivity analysis for the simple situation where a single QOI, q, is a differentiable function of a POI, p. Suppose we have solved our model for the baseline POI p̂ and know the baseline QOI, q̂ = q(p̂). (We use the notation .^ to indicate that a variable is evaluated at the model baseline values.) Perturbing the POI by a small relative fractional amount θp, p = p̂(1 + θp), will create a relative change θq in the QOI, q = q(p̂ + θpp̂). Using Taylor series,
| (B.1) |
Where is the fractional change in q̂, given a fractional change in p̂ of θp. This motivates us to define the dimensionless relative sensitivity index as
| (B.2) |
In addition to highlighting the relative importance of parameters to output, the forward normalized sensitivity index can be used to approximate output quantities of interest locally given a percent change in an input parameter using equation B.2. For example, for DENV(A. aegypti),
indicating that a θσv= 10% increase in the mosquito desired biting rate (σv) will result in a
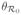 = 9.5% relative increase in the basic reproduction number (Table 6) and will result in a 13.5% relative increase in prevalence at endemic equilibrium (
, Table 7). For DENV(A. aegypti) at the baseline,
= 9.5% relative increase in the basic reproduction number (Table 6) and will result in a 13.5% relative increase in prevalence at endemic equilibrium (
, Table 7). For DENV(A. aegypti) at the baseline,
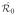 = 1.55. Therefore, if σv increases by 10%, then θσv = 0.1 and
= 1.55. Therefore, if σv increases by 10%, then θσv = 0.1 and
 will increase by a factor of
. Hence, the new reproductive number will be
will increase by a factor of
. Hence, the new reproductive number will be
 = (1 + 0.095)
= (1 + 0.095)
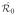 = 1.70. As another example, if the A. aegypti mosquito lived for one less day, then let θμv= (1/10 – 1/11)10 = 0.091, and the new
for dengue.
= 1.70. As another example, if the A. aegypti mosquito lived for one less day, then let θμv= (1/10 – 1/11)10 = 0.091, and the new
for dengue.
For the global sensitivity analysis, each input POI p = (p1, p2,…, pn) ∈ ℝn satisfies, for i = 1, 2, … n. We sample in this feasibility space N times using Sobol sampling [76, 77], yielding , j = 1, N. We solve the model for each pj to generate the corresponding QOI, qj. To form a distribution of the QOI from these samples we use a kernel density estimate (KDE) [78] where the estimate of the probability density function for qi is given by
| (B.3) |
Here K(u) is a compactly supported function on ℝ and h > 0 is the bandwidth of the KDE. For this paper we take K(u) to be the Epanechnikov kernel
which has been shown to have a good combination of smoothing and cutoff properties [78]. The bandwidth h > 0 is chosen so that f̂h(q) is sufficiently regularized to show the shape of the distribution. Distributions and sensitivity for remaining quantities of interest are shown in Figures B.6–B.7.
Figure B.7.
These plots show how the
 for dengue (top 3 plots) and chikungunya (bottom 3 plots) change as the parameters vary (one at a time) within the ranges given in Table 2, while all other parameters are set at baseline values. Baseline values for the models (indicated by a *) correspond to Table 6.
for dengue (top 3 plots) and chikungunya (bottom 3 plots) change as the parameters vary (one at a time) within the ranges given in Table 2, while all other parameters are set at baseline values. Baseline values for the models (indicated by a *) correspond to Table 6.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Guzman A, Istúriz RE. Update on the global spread of dengue. International Journal of Antimicrobial Agents. 2010;36:S40–S42. doi: 10.1016/j.ijantimicag.2010.06.018. [DOI] [PubMed] [Google Scholar]
- 2.Åström C, Rocklöv J, Hales S, Béguin A, Louis V, Sauerborn R. Potential distribution of dengue fever under scenarios of climate change and economic development. EcoHealth. 2013:1–7. doi: 10.1007/s10393-012-0808-0. [DOI] [PubMed] [Google Scholar]
- 3.Thiboutot MM, Kannan S, Kawalekar OU, Shedlock DJ, Khan AS, Sarangan G, Srikanth P, Weiner DB, Muthumani K. Chikungunya: A potentially emerging epidemic? PLoS Neglected Tropical Diseases. 4(4) doi: 10.1371/journal.pntd.0000623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Anyamba A, Linthicum KJ, Small JL, Collins KM, Tucker CJ, Pak EW, Britch SC, Eastman JR, Pinzon JE, Russell KL. Climate teleconnections and recent patterns of human and animal disease outbreaks. PLoS Neglected Tropical Diseases. 2012;6(1):e1465. doi: 10.1371/journal.pntd.0001465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Reiner RC, Perkins TA, Barker CM, Niu T, Chaves LF, Ellis AM, George DB, Le Menach A, Pulliam JR, Bisanzio D, et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. Journal of The Royal Society Interface. 10(81) doi: 10.1098/rsif.2012.0921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dubrulle M, Mousson L, Moutailler S, Vazeille M, Failloux A. Chikungunya virus and Aedes mosquitoes: saliva is infectious as soon as two days after oral infection. PLoS One. 2009;4 (6):e5895. doi: 10.1371/journal.pone.0005895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tsetsarkin KA, Vanlandingham DL, McGee CE, Higgs S. A single mutation in chikungunya virus affects vector specificity and epidemic potential. PLoS pathogens. 2007;3 (12):e201. doi: 10.1371/journal.ppat.0030201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vega-Rúa A, Zouache K, Girod R, Failloux A-B, Lourenço-de Oliveira R. High vector competence of aedes aegypti and aedes albopictus from ten american countries as a crucial factor of the spread of chikungunya. Journal of virology. 2014:JVI–00370. doi: 10.1128/JVI.00370-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chitnis N, Cushing J, Hyman J. Bifurcation analysis of a mathematical model for malaria transmission. SIAM Journal on Applied Mathematics. 2006;67 (1):24–45. [Google Scholar]
- 10.Chitnis N, Hyman JM, Manore CA. Modelling vertical transmission in vector-borne diseases with applications to Rift Valley fever. Journal of Biological Dynamics. 2013;7:11–40. doi: 10.1080/17513758.2012.733427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pinheiro FP, Corber SJ, et al. Global situation of dengue and dengue haemorrhagic fever, and its emergence in the Americas. World Health Statistics Quarterly. 1997;50:161–169. [PubMed] [Google Scholar]
- 12.Chowell G, Diaz-Dueñas P, Miller JC, Alcazar-Velazco A, Hyman JM, Fenimore PW, Castillo-Chavez C. Estimation of the reproduction number of dengue fever from spatial epidemic data. Mathematical Biosciences. 2007;208 (2):571–589. doi: 10.1016/j.mbs.2006.11.011. [DOI] [PubMed] [Google Scholar]
- 13.Wesson D, Morrison A, Paz Soldan V, Moudy R, Long K, Ponnusamy L, Mohler J, Astete H, Ayyash L, Halsey E, et al. Lethal ovitraps and dengue prevention: report from Iquitos, Peru. International Journal of Infectious Diseases. 2012;16:e473. [Google Scholar]
- 14.Sabchareon A, Wallace D, Sirivichayakul C, Limkittikul K, Chanthavanich P, Suvannadabba S, Jiwariyavej V, Dulyachai W, Pengsaa K, Wartel TA, Moureau A, Saville M, Bouckenooghe A, Viviani S, Tornieporth NG, Lang J. Protective efficacy of the recombinant, live-attenuated, CYD tetravalent dengue vaccine in thai schoolchildren: a randomised, controlled phase 2b trial. The Lancet. 2012;380 (9853):1559–1567. doi: 10.1016/S0140-6736(12)61428-7. [DOI] [PubMed] [Google Scholar]
- 15.Robinson MC. An epidemic of virus disease in Southern Province, Tanganyika Territory, in 1952–53. Transactions of the Royal Society of Tropical Medicine and Hygiene. 1955;49 (1):28–32. doi: 10.1016/0035-9203(55)90080-8. [DOI] [PubMed] [Google Scholar]
- 16.Pialoux G, Gaüzère B, Jauréguiberry S, Strobel M. Chikungunya, an epidemic arbovirosis. The Lancet Infectious Diseases. 2007;7 (5):319–327. doi: 10.1016/S1473-3099(07)70107-X. [DOI] [PubMed] [Google Scholar]
- 17.Bonn D. How did chikungunya reach the Indian Ocean? The Lancet Infectious Diseases. 2006;6 (9):543. doi: 10.1016/s1473-3099(06)70559-x. [DOI] [PubMed] [Google Scholar]
- 18.Paupy C, Kassa Kassa F, Caron M, Nkoghé D, Leroy EM. A chikungunya outbreak associated with the vector Aedes albopictus in remote villages of Gabon. Vector-Borne and Zoonotic Diseases. 2012;12 (2):167–169. doi: 10.1089/vbz.2011.0736. [DOI] [PubMed] [Google Scholar]
- 19.Focks DA, Daniels E, Haile DG, Keesling JE. A simulation model of the epidemiology of urban dengue fever: literature analysis, model development, preliminary validation, and samples of simulation results. American Journal of Tropical Medicine and Hygiene. 1995;53 (5):489–506. doi: 10.4269/ajtmh.1995.53.489. [DOI] [PubMed] [Google Scholar]
- 20.Ferguson NM, Donnelly CA, Anderson RM. Transmission dynamics and epidemiology of dengue: insights from age–stratified sero–prevalence surveys. Philosophical Transactions of the Royal Society of London Series B: Biological Sciences. 1999;354 (1384):757–768. doi: 10.1098/rstb.1999.0428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Favier C, Dégallier N, Rosa-Freitas M, Boulanger JP, Costa Lima JR, Luitgards-Moura JF, Menkès C, Mondet B, Oliveira C, Weimann E, Tsouris P. Early determination of the reproductive number for vector-borne diseases: the case of dengue in Brazil. Tropical Medicine & International Health. 2006;11 (3):332–340. doi: 10.1111/j.1365-3156.2006.01560.x. [DOI] [PubMed] [Google Scholar]
- 22.Esteva L, Vargas C. Analysis of a dengue disease transmission model. Mathematical Biosciences. 1998;150 (2):131–151. doi: 10.1016/s0025-5564(98)10003-2. [DOI] [PubMed] [Google Scholar]
- 23.Hartley LM, Donnelly CA, Garnett GP. The seasonal pattern of dengue in endemic areas: mathematical models of mechanisms. Transactions of the Royal Society of Tropical Medicine and Hygiene. 2002;96 (4):387–397. doi: 10.1016/s0035-9203(02)90371-8. [DOI] [PubMed] [Google Scholar]
- 24.Massad E, Coutinho FAB, Lopez LF, da Silva DR. Modeling the impact of global warming on vector-borne infections. Physics of Life Reviews. 2011;8(2):169–199. doi: 10.1016/j.plrev.2011.01.001. doi: http://dx.doi.org/10.1016/j.plrev.2011.01.001. URL http://www.sciencedirect.com/science/article/pii/S1571064511000029. [DOI] [PubMed] [Google Scholar]
- 25.Wearing HJ, Rohani P. Ecological and immunological determinants of dengue epidemics. Proceedings of the National Academy of Sciences. 2006;103 (31):11802–11807. doi: 10.1073/pnas.0602960103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Feng Z, Velasco-Hernandez JX. Competitive exclusion in a vector-host model for the dengue fever. Journal of Mathematical Biology. 1997;35 (5):523–544. doi: 10.1007/s002850050064. [DOI] [PubMed] [Google Scholar]
- 27.Adams B, Holmes E, Zhang C, Mammen M, Jr, Nimmannitya S, Kalayanarooj S, Boots M. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. Proceedings of the National Academy of Sciences. 2006;103 (38):14234–14239. doi: 10.1073/pnas.0602768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chao DL, Halstead SB, Halloran ME, Longini IM. Controlling dengue with vaccines in Thailand. PLoS Neglected Tropical Diseases. 2012;6 (10):e1876. doi: 10.1371/journal.pntd.0001876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bacaër N. Approximation of the basic reproduction number R0 for vector-borne diseases with a periodic vector population. Bulletin of Mathematical Biology. 2007;69 (3):1067–1091. doi: 10.1007/s11538-006-9166-9. [DOI] [PubMed] [Google Scholar]
- 30.Poletti P, Messeri G, Ajelli M, Vallorani R, Rizzo C, Merler S. Transmission potential of chikungunya virus and control measures: the case of Italy. PLoS One. 2011;6 (5):e18860. doi: 10.1371/journal.pone.0018860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dumont Y, Chiroleu F, Domerg C. On a temporal model for the Chikungunya disease: Modeling, theory and numerics. Mathematical Biosciences. 2008;213 (1):80–91. doi: 10.1016/j.mbs.2008.02.008. [DOI] [PubMed] [Google Scholar]
- 32.Dumont Y, Chiroleu F. Vector control for the Chikungunya disease. Mathematical Biosciences and Engineering. 2010;7 (2):315–348. doi: 10.3934/mbe.2010.7.313. [DOI] [PubMed] [Google Scholar]
- 33.Moulay D, Aziz-Alaoui M, Cadivel M. The chikungunya disease: modeling, vector and transmission global dynamics. Mathematical Biosciences. 2011;229 (1):50–63. doi: 10.1016/j.mbs.2010.10.008. [DOI] [PubMed] [Google Scholar]
- 34.Moulay D, Aziz-Alaoui M, Kwon HD. Optimal control of chikungunya disease: larvae reduction, treatment and prevention. Mathematical Biosciences and Engineering. 2012;9 (2):369–392. doi: 10.3934/mbe.2012.9.369. [DOI] [PubMed] [Google Scholar]
- 35.Yakob L, Clements AC. A mathematical model of chikungunya dynamics and control: The major epidemic on Réunion Island. PLoS One. 2013;8 (3):e57448. doi: 10.1371/journal.pone.0057448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Smith DL, Dushoff J, McKenzie FE. The risk of a mosquito-borne infectionin a heterogeneous environment. PLoS Biology. 2004;2 (11):e368. doi: 10.1371/journal.pbio.0020368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Smith DL, McKenzie FE, Snow RW, Hay SI. Revisiting the basic reproductive number for malaria and its implications for malaria control. PLoS Biology. 2007;5 (3):e42. doi: 10.1371/journal.pbio.0050042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lord C. Density dependence in larval Aedes albopictus (Diptera: Culicidae) Journal of Medical Entomology. 1998;35 (5):825–829. doi: 10.1093/jmedent/35.5.825. [DOI] [PubMed] [Google Scholar]
- 39.Chitnis N, Hyman J, Cushing J. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bulletin of Mathematical Biology. 2008;70 (5):1272–1296. doi: 10.1007/s11538-008-9299-0. [DOI] [PubMed] [Google Scholar]
- 40.Siler JF, Hall MW, Hitchens AP. Dengue: the history, epidemiology, mechanism of transmission etiology, clinical manifestations, immunity, and prevention. Philippine Journal of Science. 1926;29:1–304. [Google Scholar]
- 41.Sabin SB. Research on dengue during World War II. American Journal of Tropical Medicine and Hygiene. 1952;1:30–50. doi: 10.4269/ajtmh.1952.1.30. [DOI] [PubMed] [Google Scholar]
- 42.Lahariya C, Pradhan SK. Emergence of chikungunya virus in Indian subcontinent after 32 years: a review. Journal of Vector Borne Diseases. 2006;43 (4):151. [PubMed] [Google Scholar]
- 43.Schwartz O, Albert M. Biology and pathogenesis of chikungunya virus. Nature Reviews Microbiology. 2010;8 (7):491–500. doi: 10.1038/nrmicro2368. [DOI] [PubMed] [Google Scholar]
- 44.Gubler DJ, Suharyono W, Tan R, Abidin M, Sie A. Viraemia in patients with naturally acquired dengue infection. Bulletin of the World Health Organization. 1981;59:623–630. [PMC free article] [PubMed] [Google Scholar]
- 45.Vaughn DW, Green S, Kalayanarooj S, Innis BL, Nimmannitya S, Suntayakorn S, Endy TP, Raengsakulrach B, Rothman AL, Ennis FA, Nisalak A. Dengue viremia titer, antibody response pattern, and virus serotype correlate with disease severity. Journal of Infectious Diseases. 2000;181:2–9. doi: 10.1086/315215. [DOI] [PubMed] [Google Scholar]
- 46.Newton EAC, Reiter P. A model of the transmission of dengue fever with an evaluation of the impact of ultra-low volume (ULV) insecticide applications on dengue epidemics. American Journal of Tropical Medicine and Hygiene. 1992;47:709–720. doi: 10.4269/ajtmh.1992.47.709. [DOI] [PubMed] [Google Scholar]
- 47.Paupy C, Ollomo B, Kamgang B, Moutailler S, Rousset D, Demanou M, Hervé J, Leroy E, Simard F. Comparative role of Aedes albopictus and Aedes aegypti in the emergence of dengue and chikungunya in Central Africa. Vector-Borne and Zoonotic Diseases. 2010;10 (3):259–266. doi: 10.1089/vbz.2009.0005. [DOI] [PubMed] [Google Scholar]
- 48.Massad E, Ma S, Burattini M, Tun Y, Coutinho F, Ang L. The risk of chikungunya fever in a dengue-endemic area. Journal of Travel Medicine. 2008;15 (3):147–155. doi: 10.1111/j.1708-8305.2008.00186.x. [DOI] [PubMed] [Google Scholar]
- 49.Turell M, Beaman J, Tammariello R. Susceptibility of selected strains of Aedes aegypti and Aedes albopictus (Diptera: Culicidae) to chikungunya virus. Journal of Medical Entomology. 1992;29 (1):49–53. doi: 10.1093/jmedent/29.1.49. [DOI] [PubMed] [Google Scholar]
- 50.Nur Aida H, Abu Hassan A, Nurita A, Che Salmah M, Norasmah B. Population analysis of Aedes albopictus (Skuse)(Diptera: Culicidae) under uncontrolled laboratory conditions. Tropical Biomedicine. 2008;25:117–125. [PubMed] [Google Scholar]
- 51.Costero A, Edman J, Clark G, Scott T. Life table study of Aedes aegypti (Diptera: Culicidae) in Puerto Rico fed only human blood versus blood plus sugar. Journal of Medical Entomology. 1998;35 (5):809–813. doi: 10.1093/jmedent/35.5.809. [DOI] [PubMed] [Google Scholar]
- 52.Trpis M, Haussermann W. Dispersal and other population parameters of Aedes aegypti in an African village and their possible significance in epidemiology of vector-borne diseases. American Journal of Tropical Medicine and Hygiene. 1986;35:1263–1279. doi: 10.4269/ajtmh.1986.35.1263. [DOI] [PubMed] [Google Scholar]
- 53.Putnam JL, Scott TW. Blood feeding behavior of dengue-2 virus-infected Aedes aegypti. American Journal of Tropical Medicine and Hygiene. 1995;55:225–227. doi: 10.4269/ajtmh.1995.52.225. [DOI] [PubMed] [Google Scholar]
- 54.Watts DM, Burke DS, Harrison BA, Whitmore RE, Nisalak A. Effect of temperature on the vector efficiency of Aedes aegypti for dengue 2 virus. American Journal of Tropical Medicine and Hygiene. 1987;36:143–152. doi: 10.4269/ajtmh.1987.36.143. [DOI] [PubMed] [Google Scholar]
- 55.Sheppard PM, Macdonald WM, Tonn RJ, Grabs B. The dynamics of an adult population of Aedes aegypti in relation to dengue haemorrhagic fever in Bangkok. Journal of Animal Ecology. 1969;38:661–701. [Google Scholar]
- 56.Trpis M, Haussermann W, Craig GB. Estimates of population size, dispersal, and longevity of domestic Aedes aegypti by mark-release-recapture in the village of Shauri Moyo in eastern Kenya. Journal of Medical Entomology. 1995;32:27–33. doi: 10.1093/jmedent/32.1.27. [DOI] [PubMed] [Google Scholar]
- 57.Lambrechts L, Scott T, Gubler D. Consequences of the expanding global distribution of Aedes albopictus for dengue virus transmission. PLoS Neglected Tropical Diseases. 2010;4 (5):e646. doi: 10.1371/journal.pntd.0000646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Pesko K, Westbrook C, Mores C, Lounibos L, Reiskind M. Effects of infectious virus dose and bloodmeal delivery method on susceptibility of Aedes aegypti and Aedes albopictus to chikungunya virus. Journal of Medical Entomology. 2009;46 (2):395. doi: 10.1603/033.046.0228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Costanzo K, Mormann K, Juliano S. Asymmetrical competition and patterns of abundance of Aedes albopictus and Culex pipiens (Diptera: Culicidae) Journal of Medical Entomology. 2005;42 (4):559. doi: 10.1093/jmedent/42.4.559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sivanathan M. PhD thesis. Universiti Sains Malaysia; 2006. The ecology and biology of Aedes aegypti (l.) and aedes albopictus (skuse)(diptera: Culicidae) and the resistance status of aedes albopictus (field strain) against organophosphates in penang, malaysia [ql536. m266 2006 f rb] [Google Scholar]
- 61.Delatte H, Gimonneau G, Triboire A, Fontenille D. Influence of temperature on immature development, survival, longevity, fecundity, and gonotrophic cycles of Aedes albopictus, vector of chikungunya and dengue in the Indian Ocean. Journal of Medical Entomology. 2009;46 (1):33–41. doi: 10.1603/033.046.0105. [DOI] [PubMed] [Google Scholar]
- 62.Vazeille M, Moutailler S, Coudrier D, Rousseaux C, Khun H, Huerre M, Thiria J, Dehecq J-S, Fontenille D, Schuffenecker I, et al. Two chikungunya isolates from the outbreak of La Reunion (Indian Ocean) exhibit different patterns of infection in the mosquito. Aedes albopictus, PLoS One. 2(11) doi: 10.1371/journal.pone.0001168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sebastian M, Lodha R, Kabra S. Chikungunya infection in children. Indian Journal of Pediatrics. 2009;76 (2):185–189. doi: 10.1007/s12098-009-0049-6. [DOI] [PubMed] [Google Scholar]
- 64.Wonham MJ, Lewis MA, Rencławowicz J, Van den Driessche P. Transmission assumptions generate conflicting predictions in host–vector disease models: a case study in West Nile virus. Ecology Letters. 2006;9 (6):706–725. doi: 10.1111/j.1461-0248.2006.00912.x. [DOI] [PubMed] [Google Scholar]
- 65.Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences. 2002;180 (1):29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 66.Arriola L, Hyman J. [Google Scholar]
- 67.Gérardin P, Guernier V, Perrau J, Fianu A, Le Roux K, Grivard P, Michault A, De Lamballerie X, Flahault A, Favier F. Estimating chikungunya prevalence in La Réunion Island outbreak by serosurveys: two methods for two critical times of the epidemic. BMC Infectious Diseases. 2008;8 (1):99. doi: 10.1186/1471-2334-8-99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sissoko D, Moendandze A, Malvy D, Giry C, Ezzedine K, Solet JL, Pierre V. Seroprevalence and risk factors of chikungunya virus infection in Mayotte, Indian Ocean, 2005–2006: a population-based survey. PLoS One. 2008;3 (8):e3066. doi: 10.1371/journal.pone.0003066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sergon K, Njuguna C, Kalani R, Ofula V, Onyango C, Konongoi LS, Bedno S, Burke H, Dumilla AM, Konde J, Njenga MK, Sang R, Breiman RF. Seroprevalence of chikungunya virus (CHIKV) infection on Lamu Island, Kenya, October 2004. The American Journal of Tropical Medicine and Hygiene. 2008;78 (2):333–337. [PubMed] [Google Scholar]
- 70.Sergon K, Yahaya AA, Brown J, Bedja SA, Mlindasse M, Agata N, Allaranger Y, Ball MD, Powers AM, Ofula V, Onyango C, Konongoi LS, Sang R, Njenga MK, Breiman RF. Seroprevalence of chikungunya virus infection on Grande Comore Island, Union of the Comoros, 2005. The American Journal of Tropical Medicine and Hygiene. 2007;76 (6):1189–1193. [PubMed] [Google Scholar]
- 71.Kanamitsu M, Taniguchi K, Urasawa S, Ogata T, Wada Y, Wada Y, Saroso JS. Geographic distribution of arbovirus antibodies in indigenous human populations in the Indo-Australian archipelago. American Journal of Tropical Medicine and Hygiene. 1979;28 (2):351–363. doi: 10.4269/ajtmh.1979.28.351. [DOI] [PubMed] [Google Scholar]
- 72.Rao TR. Immunological surveys of arbovirus infections in South-East Asia, with special reference to dengue, chikungunya, and Kyasanur Forest disease. Bulletin of the World Health Organization. 1971;44 (5):585. [PMC free article] [PubMed] [Google Scholar]
- 73.Gandon S. Evolution of multihost parasites. Evolution. 2004;58 (3):455–469. [PubMed] [Google Scholar]
- 74.Vega-Rua A, Zouache K, Caro V, Diancourt L, Delaunay P, Grandadam M, Failloux AB. High effciency of temperate Aedes albopictus to transmit chikungunya and dengue viruses in the southeast of France. PloS one. 2013;8 (3):e59716. doi: 10.1371/journal.pone.0059716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Murray KO, Rodriguez LF, Herrington E, Kharat V, Vasilakis N, Walker C, Turner C, Khuwaja S, Arafat R, Weaver SC, et al. Identification of dengue fever cases in houston, texas, with evidence of autochthonous transmission between 2003 and 2005. Vector-Borne and Zoonotic Diseases. 2013;13 (12):835–845. doi: 10.1089/vbz.2013.1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Sobol’ IM. On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki. 1967;7 (4):784–802. [Google Scholar]
- 77.Caflisch RE. Monte carlo and quasimonte carlo methods. Acta Numerica. 1998;1998:1–49. [Google Scholar]
- 78.Izenman AJ. Review papers: Recent developments in nonparametric density estimation. Journal of the American Statistical Association. 1991;86 (413):205–224. [Google Scholar]