Experimental validation of the TOPAS Monte Carlo system for passive scattering proton therapy

Abstract

Purpose:

TOPAS (TOol for PArticle Simulation) is a particle simulation code recently developed with the specific aim of making Monte Carlo simulations user-friendly for research and clinical physicists in the particle therapy community. The authors present a thorough and extensive experimental validation of Monte Carlo simulations performed with TOPAS in a variety of setups relevant for proton therapy applications. The set of validation measurements performed in this work represents an overall end-to-end testing strategy recommended for all clinical centers planning to rely on TOPAS for quality assurance or patient dose calculation and, more generally, for all the institutions using passive-scattering proton therapy systems.

Methods:

The authors systematically compared TOPAS simulations with measurements that are performed routinely within the quality assurance (QA) program in our institution as well as experiments specifically designed for this validation study. First, the authors compared TOPAS simulations with measurements of depth-dose curves for spread-out Bragg peak (SOBP) fields. Second, absolute dosimetry simulations were benchmarked against measured machine output factors (OFs). Third, the authors simulated and measured 2D dose profiles and analyzed the differences in terms of field flatness and symmetry and usable field size. Fourth, the authors designed a simple experiment using a half-beam shifter to assess the effects of multiple Coulomb scattering, beam divergence, and inverse square attenuation on lateral and longitudinal dose profiles measured and simulated in a water phantom. Fifth, TOPAS’ capabilities to simulate time dependent beam delivery was benchmarked against dose rate functions (i.e., dose per unit time vs time) measured at different depths inside an SOBP field. Sixth, simulations of the charge deposited by protons fully stopping in two different types of multilayer Faraday cups (MLFCs) were compared with measurements to benchmark the nuclear interaction models used in the simulations.

Results:

SOBPs’ range and modulation width were reproduced, on average, with an accuracy of +1, −2 and ±3 mm, respectively. OF simulations reproduced measured data within ±3%. Simulated 2D dose-profiles show field flatness and average field radius within ±3% of measured profiles. The field symmetry resulted, on average in ±3% agreement with commissioned profiles. TOPAS accuracy in reproducing measured dose profiles downstream the half beam shifter is better than 2%. Dose rate function simulation reproduced the measurements within ∼2% showing that the four-dimensional modeling of the passively modulation system was implement correctly and millimeter accuracy can be achieved in reproducing measured data. For MLFCs simulations, 2% agreement was found between TOPAS and both sets of experimental measurements. The overall results show that TOPAS simulations are within the clinical accepted tolerances for all QA measurements performed at our institution.

Conclusions:

Our Monte Carlo simulations reproduced accurately the experimental data acquired through all the measurements performed in this study. Thus, TOPAS can reliably be applied to quality assurance for proton therapy and also as an input for commissioning of commercial treatment planning systems. This work also provides the basis for routine clinical dose calculations in patients for all passive scattering proton therapy centers using TOPAS.

I. INTRODUCTION

Monte Carlo simulations are widely used in radiation therapy and are considered the most accurate methods for dose calculation in proton therapy. Routine use of Monte Carlo for clinical dose calculation could potentially allow a reduction of uncertainty margins in treatment planning, which in turn might significantly reduce side effects.¹ Several general-purpose Monte Carlo codes are currently used in particle radiation therapy: Geant4,^2,3 MCNPX,⁴ FLUKA,⁵ and Shield-Hit.⁶ Other codes are more specifically focused on medical applications. Codes to simulate proton therapy include VMCPro,⁷ GATE,⁸ and PTSIM.⁹ In spite of their value, Monte Carlo codes are currently underutilized mainly because of their complexity.

TOPAS (TOol for PArticle Simulation) (Ref. 10) is a Monte Carlo platform layered on top of Geant4 recently developed with the specific aim of making Monte Carlo simulations user-friendly for research and clinical physicists in the proton therapy community. All simulations are performed with the same exact compiled code, built and tested by the TOPAS collaboration. Therefore the user can, for example, produce complex simulations of sophisticated treatment head nozzles, import a patient CT data set, and control particle sources, physics settings, scoring, and graphical output, all without the need of a detailed understanding of the underlying “native Geant4” and with no need of writing any Geant4 user-code. Indeed, each specific user-simulation is fully defined through simple text files.

In this work, we present a thorough experimental validation of TOPAS in a variety of setups relevant to proton therapy applications. This paper focuses on beams delivered with the passive scattering system. A similar validation for pencil beam systems will be the object of a forthcoming publication.

This study had two aims. The first aim was to validate the accuracy of TOPAS for clinical dose calculations. TOPAS will soon be used at Massachusetts General Hospital (MGH) as a routine clinical Monte Carlo dose calculation tool for treatment planning support. Therefore it was mandatory to perform a thorough experimental validation of the system. Though Geant4 has already a long history in proton therapy, e.g.,^11,12 and it has been validated for clinical and Quality Assurance (QA) proton therapy applications, e.g.,^13,14 users concerned with validation must differentiate between the Geant4 toolkit as a whole and any specific user application built from Geant4. Individual parts of the Geant4 toolkit, such as its physics models, have already been “unit tested” in the above references. But the second and equally important aspect of validation, “end-to-end testing,” must be performed separately each time a user assembles some set of Geant4 toolkit parts into a specific user code. As a particularly complex and flexible user code, TOPAS must itself be validated. Moreover, the presence of 4D behaviors in the TOPAS simulation framework makes end-to-end testing all the more critical.

The second aim of our study was to suggest a comprehensive set of validation measurements as a comprehensive testing strategy recommended for all clinical centers planning to rely on TOPAS or any other Monte Carlo code for quality assurance or patient dose calculations.

We systematically compared TOPAS simulations with measurements routinely performed within the QA-program of our institution as well as experiments specifically designed for this validation study. More specifically:

• •The range and modulation width of depth-dose curves of spread-out Bragg peak (SOBP) fields were compared.
• •Absolute dose simulations were benchmarked against measured machine output factors.
• •Field flatness, symmetry, and usable field size were compared.
• •Lateral and longitudinal dose profiles in a water phantom placed downstream of a half-beam block consisting of two sections of different Lucite thickness were compared to assess the effects of multiple Coulomb scattering, beam divergence and inverse square attenuation.
• •Time-dependent simulations were benchmarked against measurements of dose rate functions (i.e., dose per unit time vs time) at different depths along an SOBP field.¹⁵
• •Simulations of the charge deposited by protons fully stopping in two different types of multilayer Faraday cups (MLFCs) were compared with measurements previously published by our group to benchmark the nuclear interaction models underlying the simulations^11,16

II. METHODS

II.A. Description of the Gantry nozzles in double scattering mode and general TOPAS simulation settings

The simulations and measurements presented in this work are based on the two gantry rooms of the Francis H. Burr Proton Therapy Center (FHBPTC) at MGH. A detailed description of the beam delivery system can be found in Paganetti et al.¹³ A figure showing one of the gantry nozzles, as modeled in TOPAS in double scattering mode, can be found in Perl et al.¹⁰ The beam passes through a vacuum window, ion chamber, first scatterer, gantry-specific range modulator wheel (RMW), second scatterers, scanning magnets, movable x-y collimators (jaws), a second ion chamber (IC2), and an interchangeable snout selected according to required field dimensions.

In this study we focus on beams delivered with the passive scattering system where SOBP fields are produced using an assortment of RMWs for different treatment depths covering the range from 4.6 to 29 cm.

TOPAS “time features” allow the RMW to rotate during the simulation and the beam current to vary to reproduce the time dependent behavior of the system.¹⁷ The synchronization of the RMW with beam current modulation achieves the desired SOBP distribution.¹⁸

No variance reduction (VR) techniques have been used in this work. VR techniques supported by TOPAS (Russian roulette and geometrical splitting) have been benchmarked in a separate study¹⁹ and they will be included in a future release of the code.

All the simulations presented in this work were based on Geant4 version 9.6 and a physics list containing the Geant4 modules: g4em-standard_opt3, g4h-phy_QGSP_BIC_HP, g4decay, g4ion-binarycascade, g4h-elastic_HP, and g4q-stopping. This physics list follows the one suggested by Zacharatou et al.,² with some module name changes to keep up with name changes in the underlying Geant4 code. The default step size for particle transport, i.e., the maximum length before Geant4 forces a particle to perform a calculation step, was set to 1 m, a very large number so that, in effect, no artificial step limitation is being applied. For all simulations except the MLFC simulations, secondary particles were produced and transported only when their estimated range was longer than 0.05 mm. Otherwise their energy was deposited locally. For MLFC simulations, the production range cutoff was set to 0.001 mm for photons, electrons and positrons and to 0.0001 mm protons, alphas, deuterons, and tritons. Because of the higher density of the MLFC detectors, a smaller scoring grid and a dedicated method for charge scoring was implemented as described in Sec. II D.

II.B. Comparison between TOPAS simulations and quality assurance measurements

II.B.1. Depth-dose curves measurements and simulations of pristine peaks and SOBP fields

Depth-dose measurements are routinely performed within the QA program to verify the consistency of measured ranges and modulation widths with the corresponding nominal values requested by the user through the treatment control system. For each SOBP, the specific combination of range and modulation width determines which particular track (so-called “option”) of the RMW will be used. Table I shows the combinations used for each option analyzed during QA. The measurements are for 6 cm radius circular fields produced using a 12 cm diameter brass aperture.

TABLE I.

Nominal range and modulation width (Mod) for the options used during QA to measure depth-dose curves and 2D field flatness profiles. Options A correspond to gantry room 1 and option B to gantry room 2. Output factors are measured for the same options as the SOBP depth-dose curves.

	Nominal settings for		Nominal settings for
	measurements of		measurements of 2D field
	depth-dose curves		flatness profiles
Option	Range (cm)	Mod (cm)	Range (cm)	Mod (cm)
A1	5.1	2.7	5.2	4.0
A2	6.5	4.2	6.6	4.0
A3	8.1	4.4	8.5	6.0
A4	10.2	7.2	10.6	6.0
A5	12.7	7.0	13.5	10.0
A6	19.2	11.8	17.6	10.0
A7	23.5	4.2	22.3	10.0
A8	26.0	8.5	25.7	10.0
B3	8.7	3.2	8.5	6.0
B4	10.3	4.2	10.6	6.0
B5	12.8	3.4	13.5	10.0
B6	16.7	6.3	17.6	10.0
B7	22.5	6.0	22.3	10.0
B8	25.5	9	24.8	10.0

Depth-dose measurements are acquired in a water tank using a horizontal one-dimensional scanner with a point spacing of 0.25 mm (Computerized Radiation Scanners, Inc. Vero Beach, FL). In-house software is used to control the scanner and analyze the depth-dose curves to obtain range and modulation width.²⁰ A parallel-plate ion chamber (Markus chamber, PTW Freiburg, Germany) is used to measure the dose in water while a thimble ion chamber (Extradin A1 chamber, Standard Imaging Inc.) is placed in air, at the edge of field, in front of the water tank, to account for fluence fluctuations. The water phantom was precisely modeled in TOPAS. It consists of a Lexan water tank (40 × 20 × 20 cm³; wall thickness 5.5 mm; ρ = 1.15 g/cm³) filled with water (mean ionization potential I = 75 eV). The Markus ion chamber was not simulated. Instead we scored the energy deposited in a cylindrical scoring volume (radius 3 cm) placed in water with depth bin thickness of 0.5 mm. The diameter of the scoring volume was chosen to achieve a good trade-off between detection statistics and simulation speed.

For each option from Table I, we also measured and simulated the depth-dose curves for the deepest pristine peak constituting the SOBP. These Bragg-peaks are of particular interest since they have the highest weight among all constituent Bragg-peaks and have the most affect on the range of the SOBP. Pristine peaks are produced by modulating the beam current so that the beam only passes through the thinnest layer of a particular RMW. TOPAS simulations are performed for a single position of the RMW corresponding to the first rotation step of the wheel.

II.B.2. Output factors measurements and simulations for absolute dosimetry

The output factor (OF) of a particular field is the ratio of the dose at a specified point in that field to the number of monitor units (MU) delivered. A detailed description of absolute dosimetry Monte Carlo simulations to determine the OFs has been described in Ref. 21. Here we will briefly review the main aspects relevant to this study.

Monitor units are facility dependent. At the FHBPTC a MU corresponds to a charge of 3 nC collected in a segmented transmission ion chamber named IC2 placed in the nozzle close to the snout. At our institution, a theoretical model, based on the observation that the OF is the ratio of the SOBP plateau dose to the dose measured in the reference chamber IC2, is clinically used to predict the OF and for their constancy verification for any specific SOBP.²² Output factors are measured routinely within the QA program for each option reported in Table I.

We reproduced in TOPAS the experimental setup used for OF measurements. Such a setup utilizes the same water tank described for depth-dose curves measurements with a Markus ion chamber placed along the beam axis in the middle of the SOBP. The collecting volume of the IC2 monitor chamber is a cylinder whose axis is aligned parallel to the beam axis. The IC2 was precisely reproduced in TOPAS according to the manufacturer specifications. The radius of the active area is 0.95 cm and the distance between the parallel plates is 1 cm. In the Monte Carlo simulations we scored the dose D_IC2 delivered in the IC2 air volume. Assuming that the charge collection has 100% efficiency, the charge q_IC2 collected in the ion chamber was calculated as

$$\frac{q_{\mathrm{IC}2}{\rho }_{\mathrm{air}}·{\mathrm{Vol}}_{\mathrm{IC}2}}{W_{\mathrm{air}}}·D_{\mathrm{IC}2},$$

where the air density ρ_air is 1.196 × 10⁻³ g cm⁻³ (the value at 22 °C and 1013 hPa), Vol_IC2 is the air volume of IC2 at this temperature and pressure (2.83 cm³) and W_air is the mean energy to produce an ion pair that we assumed equal to 33.97 J/C for electrons and photons and to 34.2 J/C for all other particles heavier than electrons.²¹

The output factor ψ is defined as

$$\Psi =\frac{D_{\mathrm{Water}}}{q_{\mathrm{IC}2}}\left[\frac{\mathrm{cGy}}{\mathrm{MU}}\right],$$

where q_IC2 is expressed in MU through the conversion 1 MU = 3 nC and D_Water is the dose in water measured by the Markus ion chamber placed at the isocenter in the middle of the SOBP that was modeled in TOPAS as a cylindrical scoring volume (diameter 6 cm, thickness 1 mm) in water. We systematically performed TOPAS simulations for all options analyzed during QA.

II.B.3. Two-dimensional dose profile measurements and simulations

The QA program also prescribes the analysis of field flatness and symmetry and usable field size for all options reported in Table I. Measurements are performed with a commercial 2D detector (MatriXX IBA, Belgium) and the largest available snout (diameter 25 cm). The MatriXX consists of an array of 1020 cylindrical ion chambers (diameter 4.5 mm, length 5 mm) arranged in a square grid with 7.62 mm spacing to cover an area of 24.4 × 24.4 cm². It provides an accuracy in dose measurements of ∼1% (Ref. 23) and a spatial resolution of ∼1 mm when bilinear interpolation of raw data is performed. All the irradiations were performed with the nozzle in vertical position (gantry at 0°). The MatriXX is positioned on the treatment couch. For each option, water equivalent plastic plates (Solid Water) are placed on top of the MatriXX to place the array of ion chambers of the detector at the center of the SOBP, corresponding to the isocenter. The air gap between the snout and the Solid Water plates is set, for all options, at 80 ± 1 mm.

In TOPAS, a cubic water phantom (30 × 30 × 40 cm³) was placed at the exit of the treatment head, maintaining the same air gap as in the measurements. The energy deposited by protons was scored in a planar 1 mm thick slab (voxel size 1 × 1 × 1 mm³) positioned 3 mm downstream from the center of the SOBP to take into account the intrinsic detector build-up thickness (3.3 mm water equivalent, manufacturer specification).

II.C. Comparison between TOPAS simulations and dedicated experimental validation measurements

II.C.1. Effects of the half beam shifter on lateral and longitudinal dose profiles

We designed a simple experiment using a half-beam shifter to compare the effects of multiple Coulomb scattering, beam divergence, and inverse square attenuation on measured and simulated dose profiles. A schematic view of the experimental setup is reported in Fig. 13 of Perl et al.¹⁰ A half-beam shifter consisting of a uniform block of Lucite, covering half of the proton field is placed in the beam path upstream to the water phantom. Lateral and longitudinal dose profiles were acquired using the water tank and ion chambers used to measure depth-dose curves. Measurements were performed for two different thicknesses of the Lucite shifter (2 and 4 cm) and for two SOBP fields (range: 20 cm, modulation width: 20 cm and range: 16 cm, modulation width: 10 cm).

The TOPAS simulation included the square brass aperture (8 cm width) used to shape the beam and the experimental air gap (120 ± 1 mm) between the snout and the water tank. The energy deposited by protons in the water-phantom was scored on a three-dimensional grid (voxel size 2 × 2 × 2 mm³).

II.C.2. Measurements and simulations of dose rate functions

At FHBPTC the RMW spins at a constant speed of 600 rpm. The beam passes through different thicknesses of the wheel as it spins, delivering a series of Bragg peaks spread out in depth. The dose deposited in a medium thus varies in a periodic manner with time, with a period of 100 ms. The temporal dependence of these dose rate functions (DRFs) has been measured in a water tank by sampling, in time, the signal generated by a Markus ion chamber.¹⁵ DRFs were acquired at different depths along a SOBP (range: 16 cm and modulation width: 10 cm) using the system described for depth-dose scan measurements. Measured DRFs were compared with TOPAS simulations to perform a specific benchmark of the TOPAS time features.¹⁷ TOPAS allows time-dependent scoring of any scored quantity. We emulated the time sampling of the charge recorded by the ion chamber by scoring the energy deposited in the water tank after each rotation step of the RMW corresponding to a time step of ∼0.2 ms. The Markus ion chamber was modeled in TOPAS as a cylindrical water scoring volume as described for the OF simulations.

II.D. Comparison between TOPAS simulations and multilayer Faraday cup (MLFC) measurements

The measurement of the charge distribution produced by protons fully stopping in a MLFC provides a rather simple benchmark for the accuracy of nuclear interactions models used in Monte Carlo simulations. MLFC simulations are described in detail in Refs. 11 and 16. Here we briefly review the basic features relevant to this study. MLFC measurements allow the separation of the nuclear and electromagnetic (EM) interaction processes that are responsible for secondary particle emission and finite proton range, respectively. The longitudinal charge distribution inside the MLFC consists of two regions, a build-up region attributable entirely to nuclear interactions and a sharp peak attributable entirely to protons stopping by EM interactions.

In this paper we used the experimental results of two MLFC measurements described in two previous works from our group^11,16 to validate the nuclear models used in the simulations. We used a proton point source 1.5 m upstream (in air) of the MLFC (proton energy = 158 MeV for the Copper-Kapton MLFC and 160 MeV for the Polyethylene MLFC; energy-spread σ = 0.5 MeV) impinging on the center of the MLFC. The experiments were performed with two different MLFCs that have been carefully modeled in TOPAS. One MLFC is a stack of 66 copper (Cu) plates (7.6 × 7.6 × 0.0529 cm) separated by Kapton insulating plates (7.6 × 7.6 × 0.00255 cm), while the second one is a stack of 66 brass collector plates (15 × 15 × 0.00254 cm) separated by polyethylene (CH₂) plates (15 × 15 × 0.317 cm). In both cases, 64 collecting channels were connected to individual current integrators.

Any MLFC, whether made mainly with conducting or insulating materials, detects only the charge from the proton beam. The efficiency is assumed to be 100%. If a proton happens to stop in a conductor plate, its contribution to the integrated current is detected directly. On the other hand, if a proton stops in an insulator, it attracts electrons to the neighboring conducting plates, which, again, flow through their integrators.

In TOPAS the charge is scored as the net charge of all particles that reach kinetic energy of zero in the scoring volume minus the charge of any particles that are produced in the scoring volume if they leave the scoring volume. As in any Monte Carlo simulation involving thin plates or small cavities, extra care must be taken so that the secondary particle production cuts required to keep computation time reasonable do not unduly affect the result. In Geant4, production cuts are applied as “range cuts.” Before a secondary is produced, Geant4 checks whether this secondary would have sufficient energy to travel the given range (distance) in the current medium. If the energy is below this cut, the secondary is not produced, and instead the energy that would have been transferred to the secondary is lost by the primary in a continuous energy loss process over the primary's next step. This process in itself would not affect what particles exit one plate to travel to another (potentially carrying charge with them), since Geant4 does not invoke range cuts for secondaries that leave the current volume. But these secondaries may have descendants which exit the current volume, so cutting production of these secondaries can affect whether their descendants carry charge out of the current volume. Following the standard procedure for tuning range cuts, we selected a range cut for which lower values of the range cut have no significant effect on the result. Reducing the range cut further drives up computation time with no significant change to the result. Specifically, we reduced the range cut value from the TOPAS default of 0.05 to 0.0001 mm for heavy particles and 0.001 mm for electrons, positrons and photons. As in our previous work^11,16 asymmetric charge sharing in the dielectric layers has not been taken into account. The impact of this approximation is small and relevant only in the proximity of the Bragg peak.²⁴

III. RESULTS AND DISCUSSION

III.A. Comparison between TOPAS simulations and quality assurance measurements

III.A.1. Depth-dose curves measurements and simulations of pristine peaks and SOBP fields

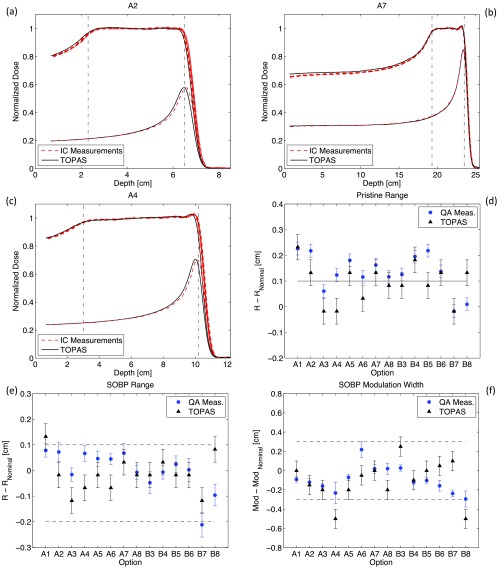
Figure 1 shows the analysis of measured and simulated pristine peaks and SOBP fields for each option (see Table I). SOBPs simulated with TOPAS are compared to six series of QA measurements performed over a period of four months. For the benchmarking of pristine peaks a single series of measurement has been carried out. Three examples of depth-dose curves are reported in Figs. 1(a)–1(c) showing a representative set of QA measurements. The variation in the measurements was small and graphically, the depth-dose curves of the six QA measurements are hardly distinguishable. Nevertheless their difference is shown by the error bars of the mean values of range and modulation width in Figs. 1(e) and 1(f). Here, for all options, the variation from the nominal values of range and modulation width (listed in Table I) is plotted for measured and simulated SOBP, respectively. Results from QA measurements differ slightly from day to day due to not perfect reproducibility of beam delivery and experimental setup. The error bars of measured data represent the standard deviation between the six series of measurements while the error bars for TOPAS simulations is set to the bin dimension (0.5 mm) of the depth-scoring volume. The range is defined as the point of the depth-dose curve at the distal 90% of the maximum dose value while the modulation width is defined by the distance between the points at the proximal 98% and distal 90% dose values. Measured and simulated profiles have been normalized to their mean dose level along a 2 cm region in the center of the SOBP.

FIG. 1.

(a)–(c) Depth-dose scan measurements and simulations of SOBPs and most distal pristine peaks. Data are presented for a selection from all options that are routinely analyzed during QA. Vertical dashed lines represent the nominal position of points at 98% and 90% dose levels as reported in Table I. (d) Comparison between measured and simulated range of the deepest pristine peak constituting the SOBP for all options (e) and (f) Comparison between measured and simulated SOBP range and modulation width for all options. Horizontal dashed lines represent the acceptable clinical tolerances for QA measurements. Nominal range and modulation width values are presented in Table I. Note that the simulations are based on treatment head blueprints provided by the manufacturer.

The simulations of SOBPs represent first a validation of the source and geometry details used in the Monte Carlo along with the physics models handling the interactions of protons and secondary particles with the traversed materials. Second, they represent a consistency test of TOPAS time features since the modulation width is caused by the rotation of the RMW. Moreover, to achieve a flat dose distribution a precise synchronization is required between the RMW rotation and the beam current modulation. Such a requirement is realized in TOPAS by simulating a different number of particles for each individual position of the RMW. The comparison between the flatness of measured and simulated SOBP is better than 1%. Even more interesting is the way TOPAS closely reproduces the measured oscillations along the plateau region of the SOBP for option B6 [see Fig. 1(c)] and the distal dose rise for option A7 [see Fig. 1(b)]. Such dose rise is an intended effect designed to better fit the requested and delivered range especially for options with deep range where the effects of energy and angular scattering of protons are more significant.

Figures 1(a)–1(c) also show the deepest pristine peaks composing the SOBPs. The pristine peaks are normalized to their relative dose-weight and are designed to have a range ∼1 mm longer than the range of the SOBPs. This is done in order to increase the steepness of the dose fall-off of the SOBPs. Figure 1(d) shows, for all options, the difference from the pristine range and the nominal SOBP range. Note that the nominal range for a SOBP in our planning system is given by the range of its deepest pristine peak. Therefore, SOBP ranges presented in Fig. 1(e) are expected to systematically be 1 mm shallower than nominal range for both TOPAS simulations and QA measurements.

TOPAS simulations reproduce measured SOBP and pristine peak ranges more closely for B options (using gantry room 2) than for A options (using gantry room 1). This behavior can be seen in Figs. 1(d) and 1(e). More precisely, a rather systematic shift with respect to measured data of about −1 mm is visible for all SOBPs and pristine peaks from options A. This suggests a systematic error in the source or geometry, in particular, the water equivalent thickness of a treatment head component for gantry room 1 may deviate slightly from design parameters. Indeed, discrepancies between range but also modulation width or SOBP flatness, between measured data and Monte Carlo simulations can be caused by inaccurate knowledge of the actual materials used in the delivery system, which sometimes vary from the blueprints. Note that the simulations presented in Fig. 1 are based on original drawings or technical reports and specifications from the manufacturer of the facility.¹³ Nevertheless, the water equivalent thickness of the treatment head is prone to some uncertainties and therefore adjustments of the proton energy source at nozzle entrance can be applied for “fine tuning”.

The result of such “tuning” is presented in Fig. 2 where, analogously to Fig. 1, we show the analysis of measured and simulated pristine peaks and SOBP fields. Only for simulations of options A (using gantry 1), the energy of the proton source has been increased by a quantity corresponding to a rise in range of +1 mm water equivalent.

FIG. 2.

(a)–(f) Comparison of measurement and simulation as for Fig. 3. Simulations for options A (corresponding to gantry room 1) are obtained by increasing the energy of the proton source by a quantity corresponding to an increase in range of +1 mm water equivalent. This adjustment has been performed in order to take into account a systematic range shift.

The improved agreement between simulations and measurements is graphically visible, for example, on the depth-dose curves for option A2 [see Figs. 1(a) and 2(a)]. From the systematic analysis of SOBP fields presented in Figs. 2(e) and 2(f) we see that for the majority of options, simulated range and modulation width are within the clinical tolerance accepted for QA measurements that are represented by the horizontal dashed lines. Such tolerances, defined internally at MGH, are +1/−2 mm for range and ±3 mm for modulation width, respectively. An option-dependent extra fine-tuning of the WET of the nozzle could still potentially improve the agreement between measurements and simulations. Nevertheless we aim at using TOPAS as a robust and reliable clinical verification tool and therefore we wanted to keep all the “tuning” adjustments as simple as possible.

There are a few options where TOPAS simulations are slightly out of clinical tolerances. The range of option A1 went out of tolerances in Fig. 2(e) because of the range tuning. It was within tolerances for the unmodified SOBPs shown in Fig. 1(e). However, measured and simulated ranges are in good agreement and the tuning was to be applied to all A options to be consistent. The modulation widths of options A4 and B8 are also slightly out of tolerances. Nevertheless, for both options, the agreement between TOPAS and measured data is within 2 mm. Moreover, for option A4 [see Fig. 2(c)], the very smooth shoulder at the proximal beginning of the plateau of the SOBP, combined with a slight tilt of the dose-plateau region, leads to increased statistical uncertainty in determining the location of the longitudinal point at 98% dose level of the simulated depth-dose curve used to calculate the modulation width. Option B8 utilizes a special carbon track of the RMW for which we can expect increased uncertainty due to insufficient knowledge of the material density.

The agreement of range and modulation width between TOPAS simulations and QA measurements is within clinical tolerances for the large majority of options. Each simulation has been run for 5 × 10⁷ original proton histories. Minor statistical fluctuations can be seen from the range and modulation width analysis for B options, comparing Figs. 1(d)–1(f) and 2(d)–2(f). In general, TOPAS simulations overestimate the dose by ∼1%–2% in the entrance region of the SOBP compared to measurement. This is likely due to a slight deviation of the time-dependent angular step position of the RMW from design parameter. In any case, the overestimation of dose is not clinically significant.

III.A.2. Output factor measurements and simulations for absolute dosimetry

Figure 3(a) shows the absolute output factors, expressed in cGy/MU, for the options used during routine QA listed in Table I. Figure 3(b) shows the relative variation from the predictive theoretical model of output factors simulated with TOPAS and measured during QA. For each option, simulated output factors are compared to six series of QA measurements performed over a period of four months. The error bars of measured data represent the standard deviation between the six series of measurements. For Monte Carlo simulations, the rigorous systematic evaluation of statistical fluctuations is cumbersome because of the long computational time required to accumulate high enough statistics. This is due to the low density of the air contained in the IC2 chamber and to its relative small scoring volume. From separate verifications on a restricted number of options we can assume that, for the actual number of original proton histories (5 × 10⁸), the statistical fluctuations of TOPAS simulations affect the relative output factors by less than 1.5%.

FIG. 3.

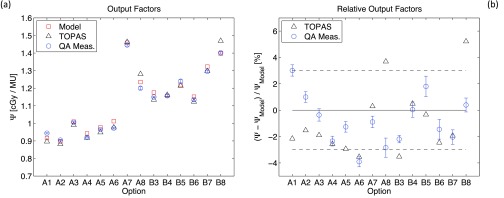
(a) Absolute output factors expressed in cGy/MU for all the options analyzed during QA and listed in Table I. Data are reported for theoretical model calculations, TOPAS simulations and QA measurements. (b) Relative variation from the predictive theoretical model of output factors simulated with TOPAS and measured during QA. The horizontal dashed lines represent the acceptable clinical tolerances for QA measurements.

For the majority of options, simulated output factor is within the clinical accepted tolerance for QA measurements (±3%) that are represented by the horizontal dashed lines. Few options are slightly out of tolerances (A8, B3, B8) while some other options present a relatively large deviation from measured values (A1, A8, B8). These deviations are not systematic and their reason is unclear but a possible explanation could be the approximation in charge scoring in the ion chamber by the Monte Carlo (see above). To determine the charge collected by IC2 we assume the mean energy value required to create an ion pair for all massive particles to be equal to the one of electrons. Moreover, the already mentioned systematic overestimation, compared to measurements, of TOPAS dose for shallow regions of SOBP depth-dose curves, could be the reason of the underestimate of TOPAS output factors for some options. Indeed, the output factor is the ratio of the SOBP plateau dose to the dose measured in the reference chamber IC2 that is correlated to the entrance dose of depth-dose curves.

III.A.3. Two-dimensional dose profile measurements and simulations

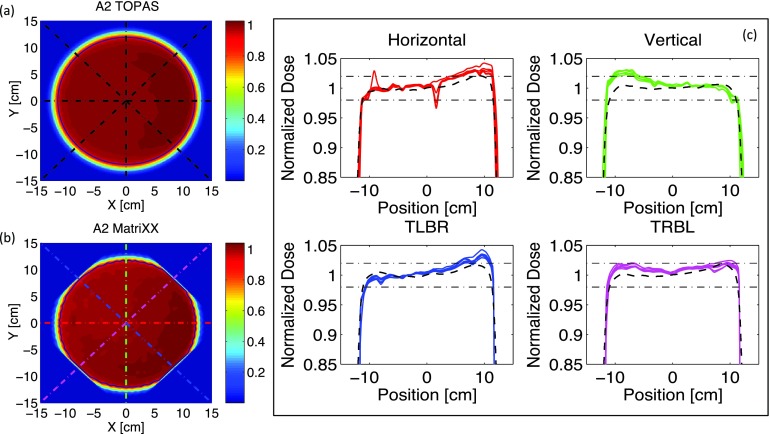
Figures 4(a) and 4(b) show an example of simulated and measured 2D dose profiles of the SOBP used for option A2. Profiles are measured and simulated at the isocenter and normalized to their mean central dose, calculated over a square area of 4 cm². Measurements and simulations have been performed systematically for all the options listed in Table I. Note that the field of view (FOV) of the MatriXX used for the measurements (24.4 × 24.4 cm²) is slightly smaller than the field size used during QA (diameter 25 cm). For this reason, the measurements are performed with the MatriXX placed at 45° with respect to the couch transverse axis. During the data analysis a prebuilt Matlab (MathWorks Inc.) rotation-interpolation function is applied to expand the FOV while rotating the 2D dose distribution back 45°. Nevertheless, such FOV-expansion does still not fully encompass the round field used for the measurements and residual effects of the limited FOV are shown by the slightly chopped edges of the 2D profile presented in Fig. 4(b).

FIG. 4.

(a) and (b) Simulated and measured 2D dose distributions of the SOBP used for option A2 (see Table I). Profiles are measured and simulated at the isocenter and normalized to their mean central dose. The round contours denote the 90% isodose lines. (c) Dose profiles along the dashed lines shown in Figs. 4(a) and 4(b). Full lines refer to five series of measured data. Dashed lines are TOPAS simulations. Horizontal dashed-dotted lines represents the acceptable clinical tolerances for field flatness. In the plot titles, TLBR stands for top-left-bottom-right and TRBL for top-right-bottom-left. The dip at ~1 cm in the measured horizontal profiles is due to few damaged ion chambers in the MatriXX detector.

Dose profiles are extracted along the horizontal, vertical, and diagonal cuts represented by the dashed lines of Figs. 4(a) and 4(b). The results are plotted in Fig. 4(c). TOPAS simulations are compared to five series of QA measurements acquired over a period of six months. Such profiles are used to assess the field symmetry and the field flatness of each option. The horizontal dashed lines shown in Fig. 4(c) represent the acceptable clinical tolerances (±2%) for field flatness.

From the systematic analysis of the profiles, we observed that, for all options, TOPAS simulations are always within the clinical tolerances for field flatness. Moreover, the qualitative assessment of the field symmetry of all the profiles shows that Monte Carlo simulations are systematically in good agreement with commissioned profiles. This is not always the case for QA measurements. Indeed both field flatness and field symmetry depend on the fine-tuning of several beam optics settings that are affected by unavoidable beam fluctuations. One purpose of QA measurements is detecting when the database of beam optics parameters has to be retuned because the measured profiles went out of tolerance. Such tuning is performed by adjusting the skewness of the pencil beam at nozzle entrance and its radial position in front of the first scatterer. Figure 5(b) shows the qualitative effect of the radial position of the beam in front of the first scatterer on TOPAS simulations. By applying a radial shift of 2 mm (gray line) on the position of the proton pencil beam at nozzle entrance, we could partially reproduce the asymmetry in the profile measured at the isocenter. As already mentioned, in reality, also the beam skewness is tuned in order to get the flattest possible dose-profiles. Our TOPAS simulations, on the other hand, are performed with symmetric pencil beams with a radial Gaussian distribution and fixed spot size of 6.5 mm. We did not investigate the influence of skewed beams since this would go beyond the scope of this validation paper.

FIG. 5.

(a) Relative difference between measured and simulated mean field radius for all options listed in Table I. (b) Effect of the radial position of the proton pencil beam position at nozzle entrance on the lateral dose profiles measured and simulated at the isocenter. (c) Effect of the angular beam spread of the proton pencil beam at nozzle entrance on the lateral dose profiles measured and simulated at the isocenter.

Another parameter routinely analyzed during QA is the usable field size, which is defined as the mean radius of the 90% isodose line of the same 2D dose distribution measured for field flatness. An example of such isodose lines calculated with a prebuilt Matlab contour algorithm is displayed in Figs. 4(a) and 4(b) for Monte Carlo simulations and QA measurements, respectively. Once again, the analysis of the mean usable field radius has been performed systematically for all the options analyzed during QA.

Figure 5(a) shows the relative difference, for all the options listed in Table I, between measurements and TOPAS simulations for the mean usable field radius. Simulations have been run for 5 × 10⁸ protons. Error bars are relative to the field radius and they account for the standard deviation between all the points on the isodose contour and the pixel size of the 2D dose distribution (1 × 1 mm² for interpolated MatriXX measurement and 2 × 2 mm² for TOPAS simulations). Note that the larger error bars for options A8 and B8 are due to the smaller field size achievable for these long-range options as shown in Fig. 5(c). The mean difference between simulated and measured field radii is within ±2% for all options.

As already discussed in Sec. II A, the size of the beam spot and the beam angular spread at nozzle entrance are two input parameters of the Monte Carlo simulations that affect the size of the delivered field. The angular beam spread was estimated by the manufacturer of the facility to be 3.2 mm-mrad from beam-optics calculations. Nevertheless, as pointed out in the following, this value represents only a rough estimate since it does not take into account its dependence on the beam-energy. Moreover, the measurements of the beam spot size performed with the segmented ion chamber at nozzle entrance are affected by inevitable variability due to specific adjustments of the magnet-parameters used for beam-tuning that have to take into account unavoidable beam fluctuations. In Fig. 5(c) we investigated the influence of the beam angular spread on the mean field radius. For long-range options we found that the original angular spread of 3.2 mm-mrad underestimated the measured field radii by ∼10% while this same angular spread led to good agreement with measurements for short-range options. This suggested the need for an energy-dependent parameterization of the angular spread. A quadratic parameterization has then been applied to all TOPAS simulations and the value of the angular spread necessary to fit measured radii for the longest available range has been empirically found to be 9 mm-mrad. Note that with such angular spread, the profiles presented in Fig. 5(c) are not only in good agreement for field radius but also for their general shape, suggesting that the beam has then a realistic size before interacting with the second scatterer.

The above shows that some simulation parameters are largely unknown in clinical delivery systems and need to be adjusted. The adjustments presented in this work are small variations of input parameters that are not explicitly known and therefore do not reflect on the validation of our Monte Carlo system.

III.B. Comparison between TOPAS simulations and dedicated benchmarking measurements

III.B.1. Effects of a half beam shifter on lateral and longitudinal dose profiles

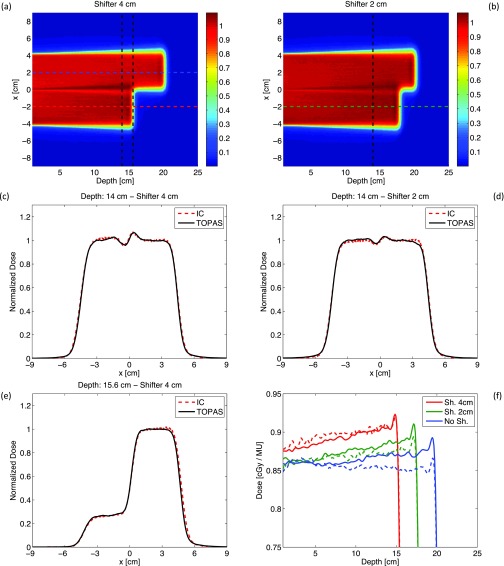
Figures 6(a) and 6(b) show 2D profiles of dose deposited in the water phantom for TOPAS simulations with two different thicknesses (4 and 2 cm) of half-beam shifters. Both profiles are normalized to the dose scored at the point located at 8 cm depth and x = 2 cm. Simulations have been run for 1 × 10⁸ protons and the 2D profiles are obtained projecting the scored dose over the latitude direction.

FIG. 6.

(a) and (b) TOPAS simulations of 2D dose profiles in the water phantom placed downstream the half-beam shifter of thickness 4 and 2 cm. (c)–(f) Lateral and longitudinal dose profiles obtained along the dashed lines shown in Figs. 6(a) and 6(b). Full lines are TOPAS simulations; dashed lines refer to ion chamber (IC) measurements. The SOBP used for measurements and simulations has range: 20 cm and modulation width: 20 cm.

Figures 6(c) and 6(d) show the lateral profiles measured and simulated at depth = 14 cm for a shifter thickness of 4 and 2 cm, respectively. The oscillations on the dose profiles around x = 0 cm are caused by proton multiple Coulomb scattering at the shifter interface. Scattering is higher for lower energy protons, i.e., a drift in the dose is produced from the shifted part of the beam towards the unshifted section. Note that, as expected, the amplitude of these oscillations depends on the shifter thickness. TOPAS simulations reproduce ion chamber measurements within ∼1% for all the points in the high dose region of the curves. Moreover the lateral field size, that is determined first by the dimension of the square brass aperture (side 8 cm) and secondly by the distance from the point of measure and the snout, is also reproduced. This implies that the lateral beam divergence of the beam is implemented correctly in our simulations.

Figure 6(e) shows the lateral profiles measured and simulated at depth = 15.6 cm for shifter thickness of 4 cm. Point-by-point differences between TOPAS simulations and IC measurements are less than 1% for 98% of bins in the high dose region. Note the almost perfect matching between simulations and measurements for −6 cm ≤ x ≤ 0 cm, corresponding to the penumbra region of the longitudinal dose fall-off for the shifted part of the beam. In this region the dose gradient is very steep (∼−65%/mm) and the accuracy in the longitudinal position of the ion chamber used to perform the lateral scan was only ∼0.3 mm.²⁵

Figure 6(f) shows the longitudinal depth-dose curves obtained along the shifted and unshifted part of the beam for the two thicknesses of the Lucite shifter. The depth-dose curves measured with the ion chamber are normalized to the output factors measured independently for each curve at the point at 8 cm depth along the scan direction. TOPAS simulations are normalized to the dose scored on the 2D dose profiles at the point located at 8 cm depth and x = 2 cm. To allow an easier comparison between measurements and simulations, all the simulated depth-dose curves of Fig. 6(f) have been multiplied by the output factor measured for the unshifted part of the beam (0.86 cGy/MU). This allows a direct comparison of the relative increase in the plateau dose between measurements and simulations. The plateau dose of shifted depth-dose curves increases because of the inverse square attenuation effect of the beam. Additionally, the Lucite shifter affects the slope of shifted profiles. This is not surprising since the beam current modulation is optimized, taking into account also the inverse square attenuation effect, in order to deliver flat depth-dose curves for open fields (this effect is corrected for in clinical beam delivery where compensator are used). Point-by-point differences between TOPAS simulations and measurements are less than 2% for ∼90% of bins in the plateau dose region and the longitudinal dose fall-off is reproduced correctly. Note that it would not have been practical to normalize the simulated profiles to output factors that are also obtained by Monte Carlo simulations. The average variation between simulated and measured output factors is of the same order [∼2%–3%, see Fig. 3(b)] of the relative increase in the plateau dose, which is the endpoint that we wanted to benchmark with this simulation. Measured profiles are affected by the uncertainties on the output factor measurements [∼1%, see error bars of Fig. 3(b)] and by some beam fluctuations that led, for example, to acquire not regularly flat depth-dose curves along the unshifted part of the beam [see dashed blue curve of Fig. 6(f)].

Figure 7(b) shows the comparison between measured and simulated longitudinal depth-dose curves obtained along the dashed lines shown in Fig. 7(a). Full lines refer to ion chamber measurements and dashed lines to TOPAS simulations. All the longitudinal profiles are normalized to the point at 8 cm depth and are obtained for a SOBP with range 16 cm and modulation width of 10 cm. They show the transition from the shifted to the unshifted part of the beam. Such transition is dominated by the penumbra of the lateral dose fall-off of the unshifted part of the field that extends for ∼1.5 cm.

FIG. 7.

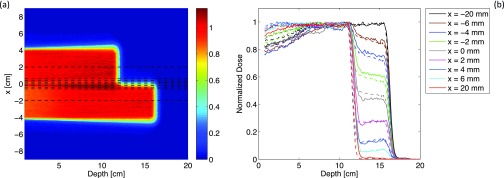
(a) TOPAS simulations of 2D dose profile scored in a water phantom placed downstream the Lucite half-beam shifter (thickness: 4 cm) for a SOBP with range: 16 cm and modulation width: 10 cm. (b) Depth-dose curves obtained along the dashed lines shown in Fig. 7(a). Dashed lines are TOPAS simulations; full lines refer to ion chamber measurements.

Point-by-point differences between TOPAS simulations and IC measurements are less than 2% for 90% of bins in the plateau dose region. Two main factors affect the accuracy of measured and simulated curves. The measurements at different x locations [see Fig. 7(a)] were performed by moving the patient couch on which the water tank was seated along the lateral direction. The accuracy of such lateral positioning is about 1 mm. The dimension of the surface of the Markus ion chamber (radius 3 mm) used for the measurements does not perfectly match the dimension of the squared scoring grid used in the simulation (2 × 2 mm). Moreover, the uncertainties on the lateral position of the table are sufficient to explain the differences between measurements and simulations.

III.B.2. Measurements and simulations of dose rate functions (DRFs)

Figure 8 shows the comparison between measured and simulated DRFs at different depths inside the plateau region of a SOBP (range 16 cm; modulation width 10 cm). The pattern of each DRF depends uniquely on its depth inside the SOBP and, by definition, the integral over each curve determines the plateau dose of the SOPB.^15,26 Such a dose has then been used to normalize all the DRFs.

FIG. 8.

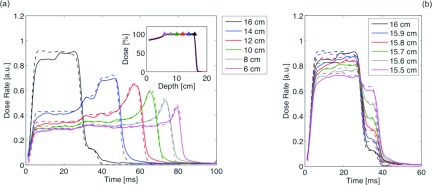
(a) and (b) DRFs at different locations inside the SOBP (range: 16 cm, modulation width: 10 cm). Full lines refer to ion chamber measurements; dashed lines are TOPAS simulations. Inset of Fig. 8(a): measured and simulated SOBP; triangles indicate the positions where DRFs were measured and simulated.

Point-by-point differences between measurements and simulations are less than 2% for 95% of bins with dose rates higher than 20% of the maximum dose rate values. However, for example, the DRF at 16 cm depth shows a 10% deviation between simulations and measurements. This can be due, first, to a slight shift in TOPAS of the time-dependent angular step position of the RMW from the design parameter and, second, to a potential mismatch between the longitudinal location of measured and simulated profiles. Indeed, as can be seen in Fig. 8(b), even a sub-millimeter difference in the depth location can be reflected, especially towards the end of range, in a different pattern of the DRFs. At depths deeper than 12 cm DRFs show traces of stepwise structures. In fact, the time structure of DRFs should consist of a succession of steps, each corresponding to a separate segment of the RMW track. The feature is more obvious at earlier times (<50 ms) corresponding to the first few segments of the RMW track that have substantially wider angles than the others. It becomes unrecognizable at later times for the smaller segments of the RMW track. This is consistent with the manner of beam delivery in the range modulation system described in Sec. II C 2. Indeed, as the RMW spins, the beam spot travels along the circular modulator track whose individual steps get smaller and smaller. Therefore, because of its finite size, the beam spot potentially overlaps adjacent steps leading to range mixing that produces less sharp DRFs.²⁶ The results presented in Fig. 8(b) show that the four-dimensional modeling of the rotating RMW, including the beam current modulation, was implemented correctly and millimeter accuracy can be achieved in reproducing measured data.

The shape of the raw measured data must be deconvolved in time to be compared with TOPAS simulations because the measuring circuit of the ion chamber has a finite resistor-capacitor (RC) time constant. Such deconvolution is quite straightforward, nevertheless it is still affected by the accuracy in the determination of the RC time constant of the measuring circuit.¹⁵ As an example, note that for the DRF at 6 cm depth (the shallowest depth measured) the beam current switches off at ∼82 ms. The simulated DRF is then interrupted abruptly while the measured DRF falls to the background value in ∼3 ms although the beam current cut-off is almost instantaneous.

III.C. Comparison between TOPAS simulations and multilayer Faraday cup measurements

Figure 9 displays the results from TOPAS simulations and measurements at the Harvard Cyclotron of two types of MLFCs, one Copper/Kapton and one Polyethylene/Brass MLFC. Details of the MLFCs and the experimental setup can be found in Refs. 11 and 16. Protons (10⁷) were simulated for each MLFC. The total charge scored in the MLFCs was reproduced with an accuracy of 0.05%. The shape of the measured data was reproduced within statistical fluctuations of the measurements (point-by-point differences were around 10% in low statistics bins (<30) and <2% above bin 30 up to the Bragg peak). The shapes of the simulated data show the same behavior as in previous publications¹¹ and follow the shapes of the measurements.

FIG. 9.

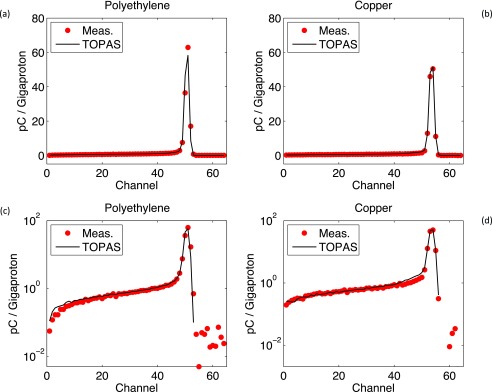
Charge deposited in polyethylene (a) and (c) and copper (b) and (d) MLFC. Data from Figs. 9(a) and 9(b) are replotted in logarithmic scale in Figs. 9(c) and 9(d).

IV. SUMMARY AND CONCLUSIONS

We performed a comprehensive validation of the TOPAS Monte Carlo simulations used at MGH in a variety of phantom setups relevant for proton therapy applications. Through the comparison between measurements and simulations presented in this work, we demonstrated the accuracy of all physics settings and physics models we used in TOPAS as well as the accuracy of the geometrical modeling of the treatment heads at the Francis H. Burr Proton Therapy Center, including time-dependent behaviors. In addition, beam parameters to characterize the beam at treatment head entrance were assessed. More specifically, through the systematic comparison of all types of beam irradiation measurements performed in the QA program of our institution, we could verify that our TOPAS simulations are within the clinical accepted tolerances for the majority of the investigated cases. The few exceptions are attributed mainly to inaccurate knowledge of the actual material or geometry used for some of the treatment head components, which sometimes vary from the information provided by the manufacturer. As demonstrated, “ad hoc” adjustments for such cases could be done. Thus, this shows the intrinsic limitation of Monte Carlo simulations based only on manufacturer's drawings without any adjusted parameters.

The simulations presented in this paper are purely based on original drawings and technical specifications from the manufacturer of the treatment head nozzles installed in the two gantry rooms of our facility. All treatment head devices, amounting to more than one thousand components, have been modeled with submillimeter accuracy. Only the angular spread to be applied in the pencil beam proton source at nozzle entrance had to be slightly adjusted since the manufacturer of the facility only provided approximations. This was done based on the full set of field size measurements performed during QA. Moreover, from a first series of TOPAS simulations of depth-dose curve for SOBPs and pristine peaks produced with treatment head nozzle of gantry room 1 we observed a systematic shift of about −1 mm with respect to QA measurements. This suggested that the water equivalent thickness of a treatment head component deviated slightly from the original design parameter provided by the manufacturer of the facility. Therefore, the energy of the proton source was increased by a quantity corresponding to a rise in range of +1 mm water equivalent for all our following simulations using gantry room 1.

In conclusion, TOPAS can reliably be applied to quality assurance for proton therapy and also as an input for commissioning of commercial treatment planning. TOPAS will soon be used at the Francis H Burr Proton Therapy Center, Massachusetts General Hospital as a routine clinical Monte Carlo dose calculation system for treatment planning support in proton therapy.