SUMMARY
Previous work has hinted that prospective and retrospective coding modes exist in hippocampus. Prospective coding is believed to reflect memory retrieval processes, whereas retrospective coding is thought to be important for memory encoding. Here, we show in rats that separate prospective and retrospective modes exist in hippocampal subfield CA1 and that slow and fast gamma rhythms differentially coordinate place cells during the two modes. Slow gamma power and phase-locking of spikes increased during prospective coding; fast gamma power and phase-locking increased during retrospective coding. Additionally, slow gamma spikes occurred earlier in place fields than fast gamma spikes, and cell ensembles retrieved upcoming positions during slow gamma and encoded past positions during fast gamma. These results imply that alternating slow and fast gamma states allow the hippocampus to switch between prospective and retrospective modes, possibly to prevent interference between memory retrieval and encoding.
INTRODUCTION
Place cells are neurons in the hippocampus that fire selectively in specific locations in space that are called ‘place fields’ (O’Keefe and Dostrovsky, 1971; O’Keefe, 1976). Place cells do not code spatial location uniformly on all traversals through their place fields. Spikes from individual place cells are often ‘misaligned’ with respect to their average place field (Muller and Kubie, 1989; Battaglia et al., 2004). Place field shifts in the direction opposite to the animal’s direction of motion have been termed ‘prospective’ firing events, and forward shifts in the same direction as the rat’s motion have been termed ‘retrospective’ firing events (Battaglia et al., 2004). Analogous prospective and retrospective firing properties have been observed in grid cells in the medial entorhinal cortex (MEC) (De Almeida et al., 2012). In grid cells, prospective and retrospective coding events have been shown to be coordinated across simultaneously active cells, suggesting that these events reflect different information processing modes in the entorhinal network. The prospective mode may reflect retrieval of stored information, whereas the retrospective mode may serve as a short-term memory buffer that facilitates memory encoding (De Almeida et al., 2012). Considering that prospective and retrospective firing occurs in individual place cells (Muller and Kubie, 1989; Battaglia et al., 2004), it is possible that prospective and retrospective network modes also exist in the hippocampus. In support of this idea, ensembles of place cells represent upcoming positions at some times (Gupta et al., 2012) and represent recent positions at other times (Barbieri et al., 2005; Gupta et al., 2012). If such modes exist in the hippocampal network, a mechanism must exist to ensure that simultaneously active cells carry out the same type of coding at the same time.
One possibility is that gamma rhythms provide a mechanism for coordinating simultaneously active cells during prospective and retrospective coding. Gamma rhythms are thought to coordinate neuronal ensembles by synchronizing the activity of cells that code related information (Bragin et al., 1995; Harris et al., 2003; Fries, 2009; Colgin and Moser, 2010). Additionally, gamma rhythms split into distinct fast and slow subtypes that differentially route separate streams of information (Colgin et al., 2009). Fast gamma couples the hippocampus with inputs from medial entorhinal cortex (MEC), which convey information about current spatial location (Brun et al., 2002; Fyhn et al., 2004; Hafting et al., 2005) that is necessary for new memory encoding (Brun et al., 2008). Slow gamma rhythms link hippocampal subfield CA1 to inputs from CA3 that appear to play a role in memory retrieval (Brun et al., 2002; Sutherland et al., 1983; Steffenach et al., 2002). Additionally, slow and fast gamma emerge on different phases of the theta rhythms with which they co-occur (Colgin et al., 2009), and encoding and retrieval processes operate most effectively when separated on different phases of theta (Hasselmo et al., 2002).
If fast gamma rhythms regulate the hippocampal network during spatial memory encoding, then fast gamma would be expected to coordinate cell ensembles during retrospective coding. If slow gamma rhythms reflect a memory retrieval mode, then slow gamma would be expected to coordinate cell ensembles during prospective coding. We tested these hypotheses by recording the activity of ensembles of place cells in the hippocampus of rats running on a linear track. We found that CA1 place cells preferentially represent recent locations during fast gamma rhythms and upcoming locations during slow gamma rhythms. These findings provide the first evidence that fast and slow gamma rhythms reflect different spatial memory processing modes in the hippocampal network.
RESULTS
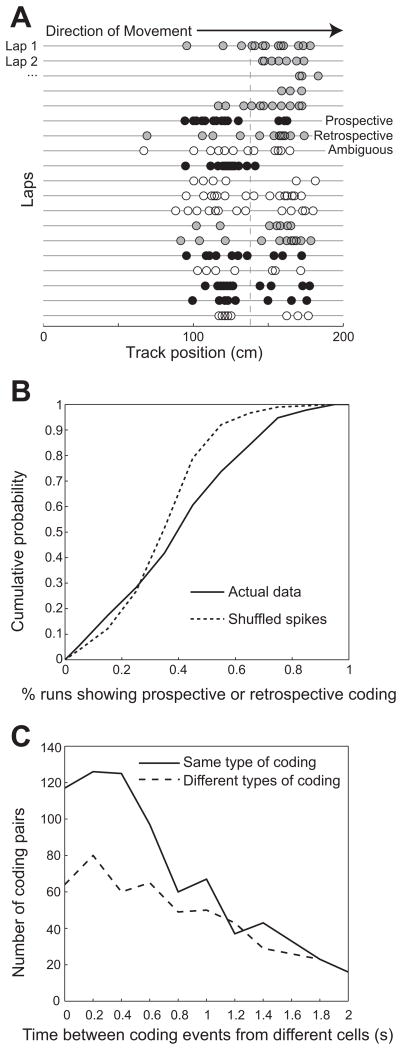
To investigate whether spatial coding differs during slow and fast gamma rhythms, we recorded neuronal ensembles from the dorsal hippocampus in a group of 5 rats that ran stereotyped paths on a linear track. We first characterized spatial coding in 692 CA1 place cells. We followed a theoretical framework that has been proposed previously (Battaglia et al., 2004; De Almeida et al., 2012). In this framework, prospective coding is defined to occur when a place cell’s firing peak is in the first half of the place field, and retrospective coding is defined to occur when the cell mainly fires in the second half of the field (Figure 1A). We observed prospective and retrospective coding modes significantly more often in the experimental data than in surrogate data in which spikes were randomly shuffled across runs (χ2(1) = 56.826, p < 0.0001; Figure 1B), indicating that coding modes were not merely a random process. Classification of prospective and retrospective coding modes was not affected by inhomogeneous spatial sampling across place fields that overlap with the ends of the track because such fields were excluded from analyses (see Experimental Procedures). Retrospective and prospective coding events did not reflect position tracking errors because no differences in tracked areas from raw video recordings were observed between prospective, retrospective, and ambiguous events (Figure S1A). Previous findings have shown that place cells code locations ahead of an animal’s actual location when the animal is leaving a reward site and represent locations behind the actual location when the animal is approaching a reward site (Gupta et al., 2012). Consistent with these previous results, we found that prospective coding events tended to occur when rats were leaving a reward location (i.e., the ends of the track), whereas retrospective coding events tended to occur as rats approached a reward location (Figure S1B).
Figure 1. Prospective and retrospective coding modes in CA1 place cells.
(A) Individual spike positions for an example CA1 place cell recorded in a rat running on a linear track. Successive laps in the rightward direction are shown for an ~10 minute session. The mean field position across all laps is indicated with a vertical dashed line. Passes through a place field were classified as ‘prospective’ (black circles) if ≥2/3 of spikes were in the 1st half of the field and ‘retrospective’ (gray circles) if ≥2/3 of spikes were in the 2nd half of the field. Passes that did not fall under either of these definitions were classified as ambiguous (white circles). See also Figure S1. (B) Prospective and retrospective coding occur more often than expected by chance. The percentage of runs showing some type of coding (i.e., either prospective or retrospective, not ambiguous) is shown. A greater proportion of runs exhibit some type of coding mode, either prospective or retrospective, in the actual data compared to shuffled data, in which a larger number of ambiguous runs occur. (C) Prospective and retrospective coding events were detected for all recorded CA1 place cells. Successive coding events from place cell pairs were likely to be of the same type if they occurred closely in time (i.e., < 0.8 s).
We next investigated whether the occurrence of prospective and retrospective coding modes was correlated across different cells, as has been shown for grid cells in MEC (De Almeida et al., 2012). We found that pairs of cells were likely to exhibit the same type of coding when the time interval between traversals through the cells’ place field centers was relatively short. When two cells fired within time windows less than 800 ms, cell pairs exhibited the same type of coding significantly more often than they exhibited different types of coding (Figure 1C; χ2(1)= 15.5, p = 0.0001 for t = 0–200 ms; χ2(1) = 10.3, p = 0.001 for t = 200–400 ms; χ2(1) = 22.8, p = 0.0001 for t = 400–600 ms; χ2(1) = 6.3, p = 0.01 for t = 600–800 ms). This indicates that the majority of cells that are active at the same time engage in the same type of coding, either prospective or retrospective, and that prospective and retrospective coding modes are coordinated across the CA1 network. The time scale of this coordination is similar to the time scale of switching between slow and fast gamma states in the hippocampus (Colgin et al., 2009). Moreover, local field potentials (LFPs) should reflect activity in the majority of neurons that show coordinated coding more than activity in the minority of neurons that do not show coordinated coding. Therefore, we set out to examine the hypothesis that slow and fast gamma rhythms coordinate place cells during prospective and retrospective coding at the level of single units and cell ensembles.
Prospective and retrospective coding in single units during slow and fast gamma
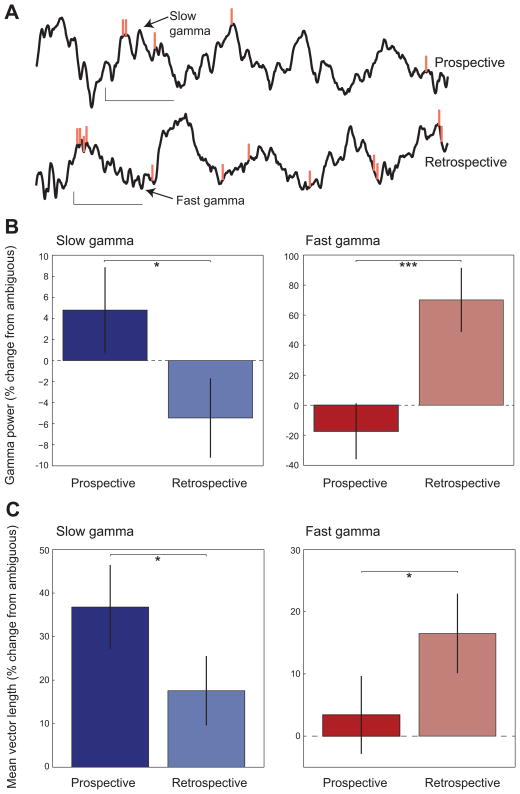
To investigate whether slow and fast gamma rhythms coordinate single unit firing during prospective and retrospective coding, we first quantified the power of slow and fast gamma rhythms in CA1 stratum pyramidale during prospective and retrospective events in individual cells (Figures 2A and 2B). We found that slow and fast gamma power were differentially enhanced depending on the type of coding that was occurring (interaction between gamma type and coding type: two-way repeated measures ANOVA, F(1, 3642) = 20.0, P = 0.0001). Slow gamma power was significantly higher during prospective coding modes than retrospective coding modes (t(3642) = 2.1, p = 0.04). In contrast, fast gamma power was significantly higher during retrospective coding events (prospective vs retrospective: t(3642) = 3.5, p = 0.0004). These differential effects of prospective and retrospective coding on slow and fast gamma power are consistent with the hypothesis that slow and fast gamma coordinate cells during prospective and retrospective coding, respectively. Interestingly, a significant main effect of gamma type was also found (F(1,3642) = 1477.1, p = 0.0001), indicating that fast gamma power increases during retrospective coding were significantly greater than slow gamma power increases during prospective coding. This may suggest that many place cells become synchronized by fast gamma during retrospective coding, while perhaps a more limited number of place cells get recruited by slow gamma during prospective coding.
Figure 2. Slow and fast gamma during prospective and retrospective coding in CA1.
(A) Example LFP recordings from CA1 s. pyramidale are shown with corresponding spikes from an example place cell (orange vertical lines, same place cell as shown in Figure 1A). Slow gamma during a prospective coding event is shown above, and fast gamma during a retrospective coding event is shown below (calibration: 100 ms, 0.2 mV). The top recording corresponds to one of the prospective coding events shown in Figure 1A (5th row from the bottom), and the bottom recording corresponds to a retrospective coding event in Figure 1A (5th row from the top). (B) Slow (blue) and fast (red) gamma power in CA1 during prospective and retrospective coding events. Power is plotted as the percent change (mean ± SEM) relative to power during ambiguous runs (see Figure S2A). Slow gamma power was higher during prospective coding than during retrospective coding. Fast gamma power was greater for retrospective coding compared to prospective coding. (C) Phase-locking of interneuron spike times (mean ± SEM) to slow and fast gamma during prospective and retrospective coding events. Slow gamma phase-locking was greater during prospective coding than during retrospective coding. Fast gamma phase-locking was greater during retrospective coding than during prospective coding. See also Figure S2B.
‘Ambiguous’ runs are runs in which approximately equal numbers of spikes occurred in the first and second halves of the place field. Such runs could reflect a switch from prospective to retrospective coding as the rat passed through the field. We thus analyzed whether slow and fast gamma power changed between the first and second halves of place fields during ambiguous runs. We found that slow gamma power was significantly greater in the first half of place fields than in the second half (2-tailed paired t-test: t(4417) = 2.65, p = 0.01; Figure S2A). However, no difference in fast gamma power was observed between the first and second halves of place fields (t(4417) = −0.34, p = 0.7). These findings imply that slow gamma in ambiguous runs may be slightly stronger during the early component of a cell’s place field compared to the later component. However, fast gamma occurs evenly in both the initial and late parts of a place field when spikes occur across the entire field.
CA1 gamma rhythms reflect rhythmic inhibitory potentials in pyramidal neurons produced by rhythmic firing of GABA-ergic interneurons (Soltesz and Deschenes, 1993; Penttonen et al., 1998). We investigated whether putative interneurons exhibited slow gamma rhythmic firing during prospective coding and fast gamma rhythmic firing during retrospective coding. We analyzed slow and fast gamma phase-locking in 201 putative interneurons in CA1 that were recorded simultaneously with CA1 place cells. We found that the degree of gamma phase-locking seen in interneurons during prospective and retrospective coding events was different for slow and fast gamma rhythms (Figure 2C; interaction between gamma type and coding type: two-way repeated measures ANOVA, F(1, 502) = 12.2, P = 0.001). Interneurons were significantly more phase-locked to slow gamma rhythms during prospective coding (prospective vs retrospective: t(502) = 2.0, p = 0.05) and fast gamma rhythms during retrospective coding (prospective vs retrospective: t(502) = 1.9, p = 0.05; Figure S2B). Analogous results were not obtained for individual place cells. Because of the low firing rate of place cells compared to interneurons, the low number of spikes remaining after selection of spikes during periods of prospective or retrospective coding likely prevented effective detection of phase-locking. Moreover, previous work indicated that spikes occurring during slow and fast gamma periods must first be selected in order to reliably detect slow and fast gamma phase-locking in place cells (Colgin et al., 2009). This is because slow and fast gamma rhythms are not stationary across time (i.e., not continuously present), and thus many phase estimates are meaningless if slow and fast gamma are not pre-selected (Colgin et al., 2009). Pre-selection of slow and fast gamma spikes was not possible in this analysis because spikes were selected for each place field traversal (i.e., for prospective and retrospective coding events), not according to the presence of slow or fast gamma.
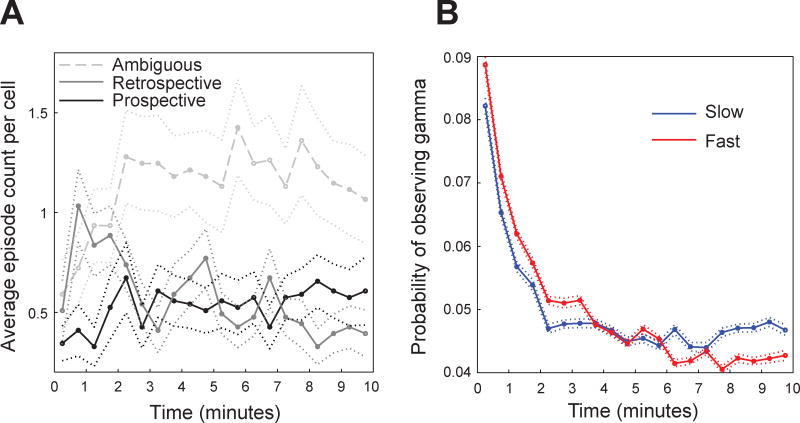
The above results raise the possibility that spatial representations in place cells differ during slow and fast gamma states. We investigated this possibility by comparing place fields during slow and fast gamma. We found that the center of mass for place fields during slow gamma was shifted 1.2 ± 9.4 cm before the overall place field center (i.e., the center of mass of the place field constructed from all spikes). The center of mass for fast gamma-associated place fields was shifted 0.3 ± 5.5 cm after the overall place field center (fast gamma center of mass after slow gamma center of mass: t(368) = 1.9, p = 0.05; Figures 3 and S3). The backward shift observed during slow gamma is reminiscent of the backward shift that CA1 place fields develop within the first few track laps each day (Mehta et al., 1997; Mehta et al., 2000; Lee et al., 2004). Consistent with this earlier research, few prospective coding events were observed during the first minute on the track each day (Figure 4A). However, the probability of observing slow gamma was high during this same time period (Figure 4B), which was surprising considering that increases in slow gamma power were associated with prospective coding when all laps across all recording sessions were analyzed (Figure 2B; see Discussion).
Figure 3. Place fields constructed from spikes emitted during slow and fast gamma periods in CA1.
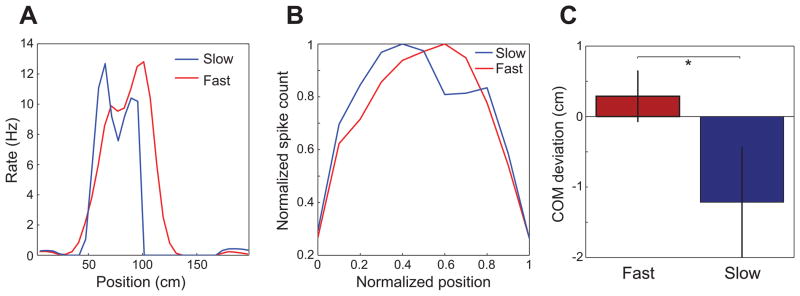
(A) Rate maps constructed for spikes occurring during slow and fast gamma for an example CA1 place cell from a rat running in the rightward direction (B) Spike counts across position combined for all spikes from all cells, subsampled for non-overlapping slow and fast gamma periods. Spike counts were normalized according to each cell’s maximum, and the x-axis shows normalized position within each cell’s place field (ranging from 0 to 1). Leftward runs were reversed so that place fields from runs in both directions could be combined, such that animals were running from position = 0 to position = 1 in all cases. See also Figure S3. (C) Center of mass (COM) deviations (mean ± SEM) for place fields subsampled for non-overlapping slow and fast gamma periods. Zero represents the place field COM for all spikes. Place field COMs were shifted significantly forward during fast gamma compared to place field COMs during slow gamma.
Figure 4. Time course of slow and fast gamma episodes and prospective and retrospective coding events in CA1.
(A) The mean (± SEM) distribution of ambiguous, retrospective, and prospective coding events during the first 10-minute session of each day is shown. (B) The mean (± SEM) probability of detecting slow and fast gamma episodes across the first 10-minute recording session for each day is shown.
Theta phase precession during periods of slow and fast gamma
The above results indicate that place cells tend to code upcoming places during slow gamma and recent places during fast gamma. Place cell spikes occur on earlier and earlier phases of theta as a rat progresses through a cell’s place field in a phenomenon termed ‘theta phase precession’ (O’Keefe and Recce, 1993; Skaggs et al., 1996). Theta phase precession has been proposed to represent a prospective network mode involving the cued retrieval of upcoming places (Tsodyks et al., 1996; Jensen and Lisman, 1996; Jensen and Lisman, 2005; Lisman and Redish, 2009), as well as a mechanism for compressing spatial sequences into a temporal structure that is ideal for memory encoding (Skaggs et al., 1996). We examined the relationship between theta phase and position for spikes emitted during periods of slow and fast gamma and combined the data across all place cells and all animals (Figure 5). As expected, normal theta phase precession was observed when all spikes were included (Figure 5A). Remarkably, we found that slow gamma spikes did not tend to occur across the full range of theta phases and positions within the place field but instead tended to be restricted to late theta phases and early portions of the place field (Figure 5B). On the other hand, spikes emitted during fast gamma periods occurred across all positions and displayed theta phase precession (Figure 5C). Theta phase distributions during slow gamma periods and fast gamma periods were significantly different when all phases were considered (Watson-Williams test, F(1,80725) = 123.7, p = 0.0001) and when data were randomly downsampled such that each cell had an equal number of phase estimates during slow and fast gamma periods (Watson-Williams test, F(1,35563) = 59.9, p = 0.0001). Moreover, the correlation between phase and position differed depending on whether slow or fast gamma was present (F(2,2004) = 15.6, p = 0.0001) and was significantly higher for periods of fast gamma compared to periods of slow gamma (t(1192) = 3.2, p = 0.002). These differences again remained significant when data were randomly downsampled such that each cell had an equal number of theta phase estimates for slow and fast gamma (F(2,948) = 13.0, p = 0.0001; correlation between phase and position greater for fast gamma compared to slow gamma: t(474) = 3.4, p = 0.001). These effects did not appear to be due to discrepancies in theta phase estimation resulting from theta power and frequency differences between track positions associated with slow and fast gamma (Figure S4).
Figure 5. Theta phase precession during slow and fast gamma periods in CA1.
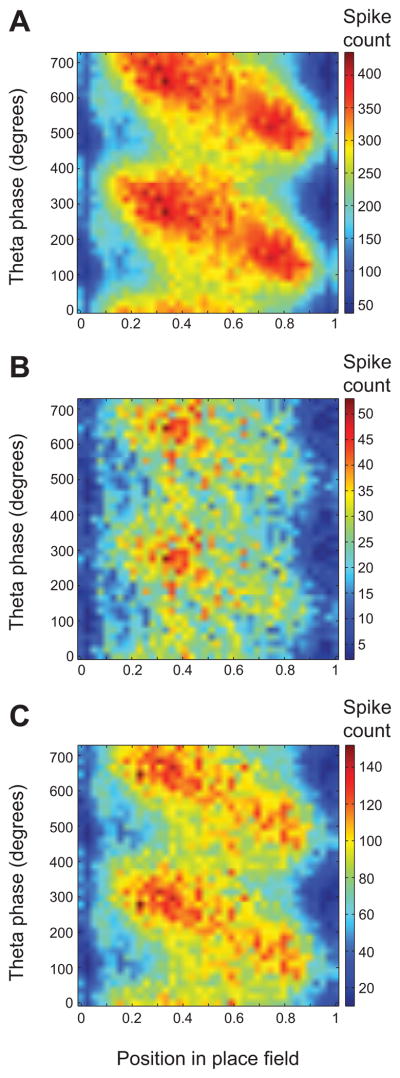
For each panel, normalized position within the place field is plotted on the x-axis, and the theta phase at which each spike occurred is plotted on the y-axis. (A) Theta phase precession is depicted for all spikes. (B) The relationship between theta phase and position is shown during periods of slow gamma. Note how spikes primarily occur in the first half of the place field. (C) The relationship between theta phase and position is shown during periods of fast gamma. Spikes occur across the full range of positions and theta phases. Note that spike counts in (B) and (C) do not sum to spike counts in (A) because (A) also includes periods when neither fast nor slow gamma were detected. See also Figure S4.
Controlling for other factors, such as running speed
Were differences in spatial coding during slow and fast gamma simply a side effect of the relationship between running speed and gamma frequency (Ahmed and Mehta, 2012)? This is unlikely for several reasons. Running speeds on the linear track follow a stereotypical pattern in well-trained rats: rats begin each lap slowly, reach maximal speed in the middle of the track, and then slow down again before reaching the other end (Figure S4B). If slow and fast gamma effects merely reflected changes in running speed, we would expect to observe slow gamma at the ends of the track and fast gamma in the center of the track. In contrast, we found that both slow and fast gamma tended to occur near the ends and in the middle of the track (Figure S4B). Additionally, we accounted for running speed using a general linear model with gamma power as a repeated factor and running speed as a covariate. Accounting for the interaction between gamma type and running speed, and accounting for running speed, we found that the interaction between gamma type and coding type remained significant (F(1,3641) = 24.891, p < 0.0001). Lastly, we matched prospective and retrospective coding events according to running speed and found that the slow and fast gamma effects persisted. Specifically, a significant interaction between coding type and gamma type was again observed (F(1, 3446) = 25.508, P < 0.0001). Post-hoc testing showed that slow gamma during prospective coding exhibited greater power than during retrospective coding (t(1723) = −2.00, p = .05), and fast gamma exhibited higher power for retrospective coding compared to prospective coding (t(1723) = 4.34, p < 0.0001). Our results were also not explained by differences due to track location because effects remained significant when the location of each coding event was included as a covariate (gamma type by coding type interaction: F(1,3641) = 22.88, P < .0001) and when data were randomly downsampled such that each location exhibited equivalent amounts of each coding type (F(1,2536) = 11.88, P < .001).
Spatial coding at the ensemble level during slow and fast gamma
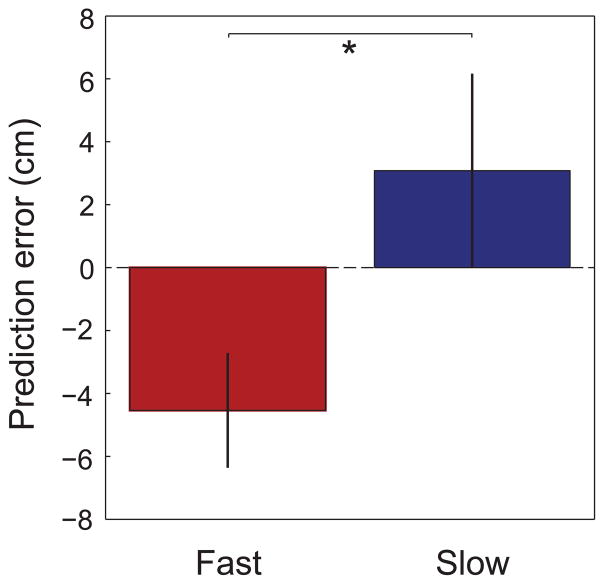
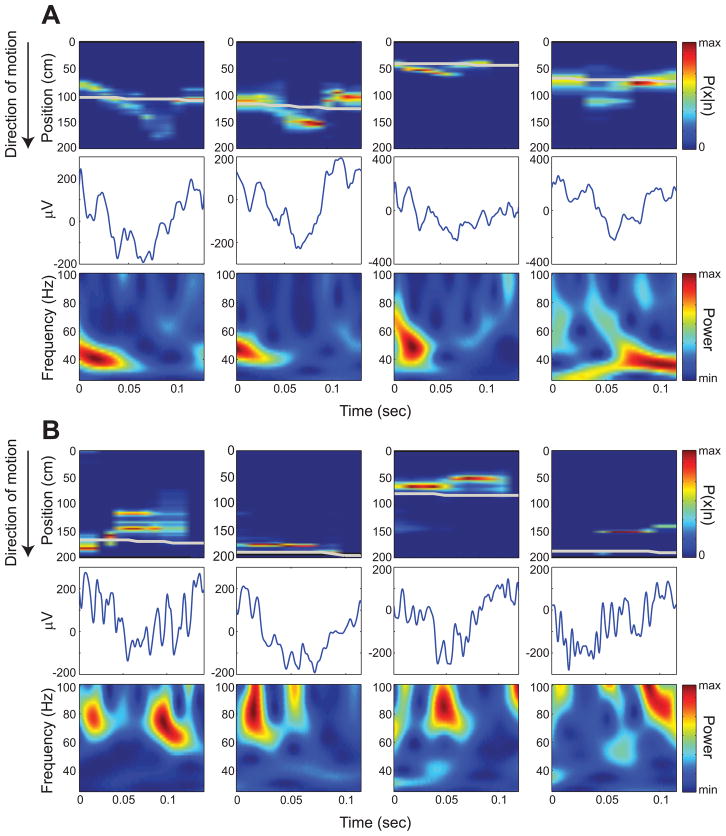
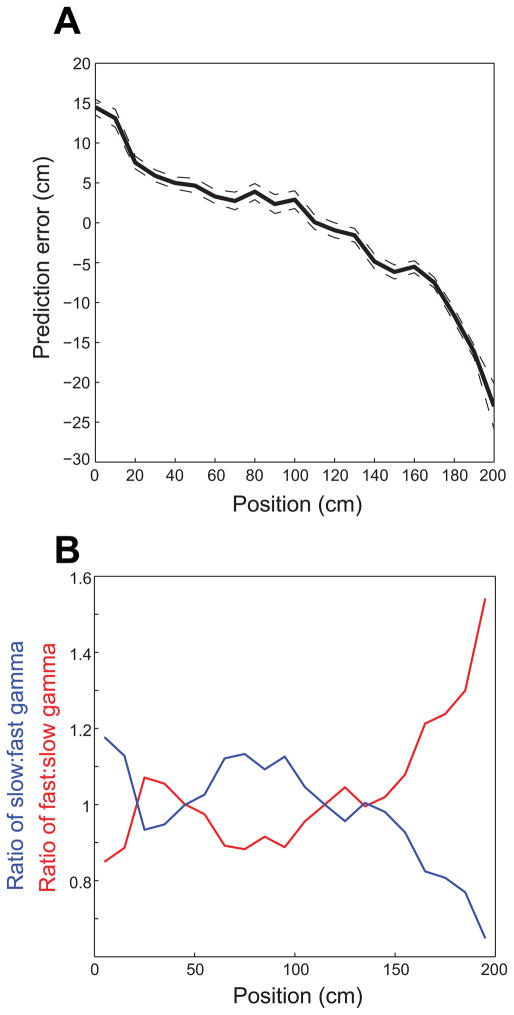
The above results imply that slow and fast gamma rhythms coordinate prospective and retrospective coding, respectively, in place cells. Yet, the above results were obtained from isolated single units and did not directly address the question of whether slow and fast gamma rhythms coordinate spatial coding at the network level. To address this question, we detected theta cycles containing sequences of active place cells (‘theta sequences’) and employed Bayesian decoding (Brown et al., 1998; Zhang et al., 1998; Jensen and Lisman, 2000) to estimate the spatial trajectory represented by the spikes in each theta sequence (as in Gupta et al., 2012). We then measured the prediction error (i.e., predicted position – actual position) for theta sequences associated with slow and fast gamma. We found that prediction errors during slow and fast gamma were significantly different (t(511) = 2.1, p = 0.04; Figure 6), with slow gamma associated with positive prediction errors (3.1 ± 50.2 cm) and fast gamma associated with negative prediction errors (−4.5 ± 28.8 cm). We then compared slow and fast gamma during theta sequences having cumulative prediction errors less than or greater than zero and found significantly greater fast gamma power for negative prediction errors (t(51648) = −10.6, p < 0.0001). We found a trend toward higher slow gamma power for positive prediction errors compared to negative prediction errors (t(51648) = 1.7, p = 0.09). However, when we omitted theta cycles with prediction errors close to 0 cm and examined those theta cycles with prediction errors greater than 1 cm or less than 1 cm, slow gamma power was significantly higher for positive errors compared to negative errors (t(49216) = 2.1, p = 0.04) and, again, fast gamma power was significantly greater for negative errors than for positive errors (t(49216) = −10.5, p < 0.0001). The slow gamma effect became more pronounced when only those theta cycles with prediction errors greater than or less than 2 cm were considered (slow gamma power significantly higher for positive errors than negative errors: t(46127) = 2.5, p = 0.01; fast gamma power significantly higher for negative errors than positive errors: t(46127) = −10.1, p < 0.0001). Examples of theta sequences showing positive and negative prediction errors associated with slow and fast gamma, respectively, are shown in Figure 7. Note how theta sequences associated with positive prediction errors (i.e., predicted position ahead of the actual position, Figure 7A) resemble ‘ahead sequences’ that have been reported previously by Gupta and colleagues (2012) to occur predominantly as animals leave reward sites. Such sequences may be related to sequences that reactivate during sharp waves (Figure S5). On the other hand, theta sequences that are associated with negative prediction errors (i.e., predicted position behind the actual position, Figure 7B) match ‘behind sequences’, which have been reported to occur as animals approach reward sites (Gupta et al., 2012). In the current study, reward sites were located at the ends of the track. The present data are consistent with the findings of Gupta and colleagues because positive prediction errors tended to occur (Figure 8A), and slow gamma occurred more often than fast gamma (Figure 8B), as rats left the end of the track. On the other hand, as rats approached the end of the track, negative prediction errors were more prevalent, and fast gamma occurred more often than slow gamma.
Figure 6. Reconstruction errors (difference between the position estimated by Bayesian decoding and the animal’s actual position) during periods of slow and fast gamma in CA1.
Prediction errors (mean ± SEM) were negative on average during fast gamma and positive on average during slow gamma. Negative prediction errors indicate that the decoded position is behind the actual position, whereas positive prediction errors indicate that the decoded position is ahead of the actual position. See Figure S7 for example place cell recording sites used in Bayesian decoding analyses.
Figure 7. Examples of reconstructed positions from theta cycles showing slow or fast gamma.
Top panels show Bayesian decoded spatial probability distributions for example theta cycles (raw traces shown in middle panels); the gray line indicates the rat’s actual position. Rats were running from 0 to 200 cm. The bottom panels depict color-coded power across time (x-axis) for the range of gamma frequencies (y-axis). (A) Examples showing positive prediction errors associated with slow gamma. (B) Examples showing negative prediction errors associated with fast gamma. See also Figure S5.
Figure 8. Negative and positive prediction errors from Bayesian decoding are associated with particular locations, and slow and fast gamma predominate at different locations, on the linear track.
Leftward runs were reversed (as described in Figure 3). (A) Mean prediction errors ± 95% confidence intervals are plotted against position on the track. Note that positive prediction errors were associated with positions where rats were leaving the end of the track, and negative prediction errors were associated with positions where rats were approaching the end of the track. (B) The ratio of the probability of slow gamma occurrence to the probability of fast gamma occurrence (blue) and the ratio of the probability of fast gamma occurrence to the probability of slow gamma occurrence (red) are plotted against position on the track. Note that these results are a transformed version of what is shown in the left panel of Figure S4B. See also Figure S6.
Theta modulation of slow and fast gamma
Earlier findings indicated that both slow and fast gamma are modulated by theta phase but tend to occur on different theta phases and cycles (Colgin et al., 2009). Consistent with these earlier findings, plotting gamma power within individual theta cycles revealed theta phase-locked slow gamma as rats began a track run and theta phase-locked fast gamma as rats ended a track run (Figure S6). Moreover, slow gamma was most strongly phase-locked to theta during prospective coding events (mean vector length (MVL) = 0.035) compared to retrospective coding events (MVL = 0.002) and ambiguous events (MVL = 0.022). On the other hand, fast gamma exhibited strongest phase-locking to theta during retrospective events (MVL = 0.025) compared to prospective (MVL = 0.011) and ambiguous events (MVL = 0.012). These results suggest that the phenomena reported above involve theta-modulated slow and fast gamma rather than slow and fast gamma in isolation.
DISCUSSION
The present results suggest that distributed place cells participate in distinct network processing modes that alternate according to whether slow and fast gamma rhythms are present. The results indicate that the slow and fast gamma modes coordinate place cell assemblies during prediction of upcoming locations and encoding of recent locations, respectively. Similarly alternating prospective and retrospective modes have been reported in entorhinal cortex grid cells (De Almeida et al., 2012), but they were not linked to any type of oscillation. These prospective and retrospective coding modes are believed to reflect distinct memory processing states in the entorhinal-hippocampal network. Prospective coding is reminiscent of the backward expansion of CA1 place fields that develops with experience (Mehta et al., 1997; Mehta et al., 2000; Lee et al., 2004). Development of such expansion is blocked by NMDA receptor antagonists (Ekstrom et al., 2001), which also block spatial learning (Morris et al., 1986). For these reasons, this expansion is believed to reflect the retrieval of spatial representations that formed during earlier experiences. Retrospective coding may be driven by persistent firing in entorhinal cortex neurons (Klink and Alonso et al., 1997; Yoshida et al., 2008), which may be involved in short-term memory encoding (Suzuki et al., 1997).
It should be noted that the present work uses the terms ‘prospective coding’ and ‘retrospective coding’ to describe representations of locations at the spatial scale of individual place fields, following the terminology used in earlier studies of similar phenomena (Muller and Kubie, 1989; Battaglia et al., 2004; De Almeida et al., 2012). However, the same ‘prospective’ and ‘retrospective’ terminology has been used to refer to place cell coding at a larger spatial scale (Ferbinteanu and Shapiro, 2003). The Ferbinteanu and Shapiro study defined prospective coding as place cell firing rate changes that signal which way a rat is headed and retrospective coding as firing rate changes that indicate from which direction the rat has come. The present findings do not address the question of whether gamma rhythms are involved in these phenomena.
In the present study, prospective and retrospective coding events tended to occur at the beginning and end, respectively, of the linear track, consistent with findings reported by Gupta and colleagues (2012). However, the present findings additionally show that prospective and retrospective coding events were associated with the occurrence of slow and fast gamma, respectively. Prospective firing is thought to occur as a result of current place input triggering retrieval of upcoming spatial sequences that were previously associated with a given location (Hasselmo and Eichenbaum, 2005). Prospective ‘sweep ahead’ events have also been observed in CA3 place cells at choice points on a T-maze, locations where ~40 Hz gamma (i.e., slow gamma) also prominently occurred (Johnson and Redish, 2007). Together, these findings suggest that slow gamma coordination of place cells during prospective coding facilitates retrieval of representations of future locations in the hippocampal network. A previous study linked gamma coherence between CA3 and CA1 to memory retrieval but did not discriminate between slow and fast variants of gamma (Montgomery and Buzsaki, 2007). The CA3-CA1 coupling they observed, however, most likely involved slow gamma considering that CA3-CA1 coherence has been reported to be maximal in the slow gamma range (Colgin et al., 2009). Moreover, slow gamma has been proposed to mediate memory retrieval during sharp wave-associated replay in quiescent behavioral states (Carr et al., 2012; Figure S5).
If slow gamma-mediated prospective coding is related to retrieval of learned locations, as we propose, then it should be related to the backward shifts of place fields that develop with experience (Mehta et al., 1997; Mehta et al., 2000; Lee et al., 2004). Consistent with this, we observed few prospective events in CA1 during the first 30 seconds on the linear track each day (Figure 4A). However, we also observed that the probability of slow gamma occurrence was high during this time (Figure 4B), which seems to contradict our results linking slow gamma with prospective coding. Differences between CA3 and CA1 may provide a possible explanation for this paradox. In a well-learned environment, CA1 place fields shift backward over the course of the first few laps of each day, but stable spatial representations emerge immediately in CA3 (Lee et al., 2004; Roth et al., 2012). This suggests that CA3 maintains long-term memories of spatial locations and that these memories are transmitted to CA1 during the first few laps of each day. Slow gamma may occur during the first few laps of each day as stored spatial memories are reactivated in CA3, but emergence of these memories in CA1 may follow a slower time course. CA1 cells may not respond to slow gamma-mediated inputs from CA3 until after CA3-CA1 synapses have undergone NMDA receptor-dependent synaptic strengthening that occurs during this time (Ekstrom et al., 2001). This could explain why few prospective coding events were seen in CA1 during the first few laps of each day.
Here, we posit that prospective coding relies on slow gamma coupling of CA1 and CA3 during retrieval of stored memory representations. Yet, this does not explain prospective coding in grid cells (De Almeida et al., 2012). It is possible that grid cell representations of upcoming locations are inherited from CA1, considering that CA1 projects to MEC layer V (Swanson and Cowan, 1977), which projects to layers II and III (van Haeften et al., 2003). However, this remains an interesting question for later study.
Our findings also provide novel insights regarding the functional significance of theta phase precession (O’Keefe and Recce, 1993; Skaggs et al., 1996). It is unlikely that theta phase precession simply reflects retrieval of upcoming locations because prospective coding was associated with slow gamma, and phase precession was less pronounced during periods of slow gamma. Specifically, spikes were largely restricted to the late theta phase component of theta phase precession. In other words, upcoming locations were preferentially represented and spiking was suppressed at early theta phases when slow gamma rhythms were present (Figure 5B). Theta phase precession did occur, however, during fast gamma periods (Figure 5C) when cells preferentially represented locations in the recent past. These findings support the interpretation that spikes occurring on early theta phases code recently visited locations (Dragoi and Buzsaki, 2006), not current location as otherwise suggested (Lisman and Redish, 2009). Recent events are thought to be maintained in short-term memory by persistent firing in entorhinal cortex (Jensen and Lisman, 2005; Suzuki et al., 1997; Hasselmo and Stern, 2006), and fast gamma promotes inputs from entorhinal cortex (Colgin et al., 2009). Fast gamma inputs from MEC may also activate representations of current location slightly later in the theta cycle. Representations of upcoming locations could then be triggered as a result of associations that were formed across sequentially activated place cells during prior learning. We predict that cells coding current location would not trigger firing of cells coding upcoming locations in a novel environment, and thus spikes on late theta phases would be absent during fast gamma in a novel environment. However, the theta phases at which spikes occurred were only weakly correlated with position during the first lap on a linear track on a given day (Mehta et al., 2002). Thus, it is possible that the relationship between theta phase and position would be greatly diminished during periods of fast gamma in a novel environment. In any case, this remains an interesting question for later study.
Another interesting question is how slow and fast gamma modes relate to different classes of gamma-modulated cells in CA1 reported by Senior and colleagues (Senior et al., 2008). In that study, ‘TroPyr’ cells fired at the trough of gamma and fired across the full range of theta phases during theta phase precession, whereas ‘RisPyr’ cells fired at the rising phase of gamma as the animal was leaving a cell’s place field. The study did not differentiate between different frequencies of gamma. However, TroPyr cells may correspond to fast gamma-modulated cells. Place cells fired across the full range of theta phase precession during fast gamma in the present study (Figure 5C), and earlier work showed that cells that were significantly phase-locked to fast gamma tended to fire on the fast gamma trough (Colgin et al., 2009). The relationship between RisPyr cells and slow and fast gamma remains unclear, however. Place cells that were significantly phase-locked to slow gamma did tend to fire on the rising phase of slow gamma (Colgin et al., 2009). However, place cells fired in the initial part of their place fields during periods of slow gamma (Figure 5B), whereas RisPyr cells tended to fire in the later portions of their place fields (Senior et al., 2008).
Although it is possible that our results were influenced by factors unrelated to memory (e.g., consumption of reward), the relationship of slow and fast gamma rhythms to prospective and retrospective coding modes suggests that different frequencies of gamma coordinate different types of spatial memory processing. Fast gamma may correspond to an encoding mode, similar to that proposed previously for theta-modulated gamma during learning (Jensen and Lisman, 1996; Lisman and Otmakhova, 2001). In this mode, representations for recently visited locations may be held in a short-term memory buffer that provides the repetitive firing necessary to encode new memories. On the other hand, slow gamma may correspond to a retrieval mode, in which firing is facilitated before the center of the place field and suppressed in the later part of the place field. This may prevent ongoing encoding from interfering with retrieval of previously stored spatial memories, as can occur if these processes are engaged at the same time (Hasselmo et al., 2002). Considering that slow and fast gamma rhythms occur in other brain regions (Kay, 2003; van der Meer and Redish, 2009; Igarashi et al., 2013; Manabe and Mori, 2013), separate slow and fast gamma modes may mediate different types of information processing throughout the brain.
EXPERIMENTAL PROCEDURES
Subjects
Five male Long Evans rats weighing approximately 350–500 grams were used in the study. Animals were housed on a reverse light dark cycle (lights off from 8 a.m.–8 p.m.) and tested during the dark phase. After surgery, animals were housed individually in cages (~40 cm × 40 cm × 40 cm) built from clear acrylic and containing enrichment materials (e.g., plastic balls, cardboard tubes, wooden blocks). Rats were allowed to recover from surgery for at least one week prior to the start of training. During the data collection period, rats were placed on a food deprivation regimen that maintained them at ~90% of their free-feeding body weight. All experiments were conducted according to the guidelines of the United States National Institutes of Health Guide for the Care and Use of Laboratory Animals under a protocol approved by the University of Texas at Austin Institutional Animal Care and Use Committee.
Tetrode placement
Over the course of a few weeks after drive implantation, tetrodes were slowly lowered toward their target locations. 11–12 of the tetrodes (11 in one rat, 12 in the other four rats) were targeted toward CA3 and CA1 cell body layers. Another tetrode was targeted toward the apical dendritic layers of CA1 and was used for hippocampal depth estimation as the rest of the tetrodes were turned down. Another tetrode was used as a reference for differential recording. This reference tetrode was placed at the level of the corpus callosum or higher and was recorded against ground to make sure that it was placed in a quiet location. All recording locations were verified histologically after experiments were finished. Representative examples of final recording locations are shown in Figure S7. Final hippocampal recording sites used in the study were located in or near CA1 and CA3 strata pyramidale. In one rat, two tetrodes targeted toward CA1 appeared in histological sections to be on the border of CA2-CA1. However, place cells and LFPs recorded from these tetrodes were indistinguishable from other CA1 recordings collected simultaneously. Therefore, place cells, interneurons, and LFPs from these tetrodes were included in this study. The majority of CA3 tetrodes were located in CA3c (i.e., in the hilus, see Figure S7 for an example). Because gamma oscillations exhibit large amplitudes in the hilus (Buzsaki et al., 1983; Bragin et al., 1995), volume-conducted gamma oscillations from the hilus contaminated LFP recordings from these tetrodes. Thus, we did not include recordings from CA3 tetrodes in our main analyses involving LFPs. Single unit recordings from CA3 tetrodes were, however, included in Bayesian decoding analyses of activity during periods of slow and fast gamma in CA1. In 2 rats, some of the tetrodes targeted toward CA3 ended up in the dentate gyrus (1 tetrode in 1 of the rats and 2 tetrodes in the other). Recordings from dentate gyrus tetrodes were not used in this study.
Classification of individual place cell coding modes (Figures 1, 2, and 4; Figures S1 and S2)
692 CA1 cells from 5 rats were used for classification of coding modes. If multiple days of the same cell were recorded, only data from the first acceptable day was used for that cell. Animals’ movements along the linear track were collapsed into one dimension for ease of analysis. Place field passes in which the animal’s running speed dropped below 5 cm/s were discarded. The average place field center was then defined as the center of mass of the positions of the remaining spikes. Prospective passes were defined as those in which >= 2/3 of spikes occurred before the place field center. Retrospective passes were defined as those in which >= 2/3 of spikes occurred after the place field center. All remaining passes through the place field were categorized as ambiguous. To determine the time difference between cell pairs exhibiting the same or different type of coding (Figure 1C), ambiguous passes were excluded. The time point for each coding event was defined as the time when the rat passed through the center of the spiking activity for that particular traversal through the field. To determine whether the place cell population exhibited coding modes more often than expected by chance, we determined the proportion of passes through the place field that would randomly exhibit coding modes for each cell (Figure 1B). To do this, we preserved the number of spikes for each place cell, and preserved the number of spikes that occurred on each pass through a place field, but randomly shuffled the spikes’ assignments to particular passes.
Gamma power during prospective and retrospective coding (Figure 2B)
Prospective, retrospective, and ambiguous passes through a place field were defined as described above for the population of CA1 cells. For each categorized place field traversal, the period of time during which the place cell emitted spikes in the field defined the time windows that were used to estimate slow and fast gamma power. Time-varying slow and fast gamma power estimates were obtained for these time windows as described below.
Estimating slow and fast gamma power
For fast and slow gamma estimates (see Supplemental Experimental Procedures), time-varying power was computed across the 60–100 Hz and 25–55 Hz frequency bands, respectively. Although fast gamma has previously been defined as extending up to 140 Hz (Colgin et al., 2009), we chose to cut it off at 100 Hz to avoid overlap with the recently defined epsilon band (90–150 Hz; Belluscio et al., 2012) and to avoid contamination by spike waveforms, which can generate power across a broad range of high frequencies, sometimes extending down to ~150 Hz (Colgin et al., 2009). A single estimate of slow gamma power and a single estimate of fast gamma power were then obtained for each categorized place field traversal by averaging power for each gamma type across the time window and across the frequency band of interest (i.e., 60–100 Hz for fast gamma and 25–55 Hz for slow gamma).
Matching prospective and retrospective coding events according to running speed
Counts of retrospective and prospective events were binned by average running speed using intervals of 5 cm/s. The number of events was randomly downsampled so that the numbers of retrospective and prospective events within each speed bin were equal. Measurements of slow and fast gamma were then obtained for the remaining events, as described above.
Detection of gamma episodes (Figures 3, 4B, 5B, 5C, 8B, S3, and S4B)
To extract periods of slow and fast gamma activity in the LFP recordings, time-varying slow and fast gamma power were calculated, using the method described above. Power at each time point was averaged across the slow and fast gamma frequency ranges to obtain an estimate of slow and fast gamma power for each time point. Time points were collected during which slow and fast gamma power exceeded 2 SD above the mean power of slow and fast gamma, respectively, across all time points. This method of slow and fast gamma detection has been used previously (Colgin et al., 2009). Time windows, 125 ms in length, were cut around the selected time points. In each 125 ms segment, the slow and fast gamma amplitude maxima were determined from the slow and fast gamma bandpass filtered versions of the recordings. Duplicated gamma windows, a consequence of detecting overlapping time windows, were avoided by discarding identical maxima values within a given gamma subtype and further requiring that maxima of a given gamma subtype be separated by at least 100 ms. The maxima were then used to define the centers of slow and fast gamma episodes. Slow and fast gamma episodes/periods were defined as 125 ms-long windows centered around the slow and fast gamma maxima.
Theta phase precession (Figure 5)
Theta phase was determined by band-pass filtering the LFP signal in the theta range (6–10Hz) and performing a Hilbert transform. Each spike was assigned a theta phase using the signal from the tetrode from which it was recorded. Spike locations were normalized using the boundaries of the place field (ranging from 0 to 1). Leftward runs were reversed such that movement always occurred from 0 to 1. Gamma episodes were detected as described above, and spikes occurring within slow and fast gamma episodes were used to construct the position-phase plots shown in Figures 5B and 5C.
Detecting individual theta cycles for Bayesian decoding (Figures 6, 7, and 8A)
The LFP signal was chosen from the tetrode with the most recorded CA1 cells for that particular recording. The signal was separately band-pass filtered for theta (6–12 Hz) and delta (2–4 Hz), and the power for each was determined using a convolving Morlet wavelet (as described in Supplemental Experimental Procedures). The presence of theta activity was defined when theta power was greater than delta by 3 times or more. The maxima of the bandpass filtered signal were then identified as theta peaks for each recording. Individual theta cycles were cut from peak to peak, as in Gupta et al. (2012), and spikes occurring within those theta cycles were used to reconstruct position estimates for each theta cycle using a Bayesian decoding approach, described below.
Bayesian decoding analyses (Figures 6, 7, and 8A)
The most likely position represented by spiking activity from a population of 456 CA1 cells and 87 CA3 cells was estimated using a Bayesian decoding approach (Zhang et al., 1998; Brown et al., 1998; Jensen and Lisman, 2000). Recording sessions with fewer than 20 cells were not used, and cells were not excluded from Bayesian analyses on the basis of the place field acceptance criteria (see Supplemental Experimental Procedures). These factors explain why the number of CA1 cells listed here differs from the number used for the single unit analyses. Only theta cycles containing at least 2 active place cells were included in the analysis. Additionally, theta epochs were selected using the same theta/delta threshold method described above; spikes that occurred during non-theta epochs were not included. Place fields for each of the cells were constructed from each recording session on the linear track, as described in the “Place fields” section in Supplemental Experimental Procedures. Decoding was performed for each theta cycle using a 40-ms sliding time window shifted by 10 ms at each step, as in Gupta et al. (2012). The probability of the animal to be at position x, given the number of spikes n from each cell collected in the time window t was estimated using Bayes rule:
P(x) was calculated from the experimental tracking data. P(n|x) was estimated using the firing rates from the experimentally obtained place fields in the same 10-minute linear track session, assuming that the firing rates of different place cells are statistically independent and that the number of spikes from each cell has a Poisson distribution (Zhang et al., 1998; Jensen and Lisman, 2000). P(n), the normalizing constant, was set so that P(x|n) summed to 1. Reconstructed positions were identified for each time bin as the center of mass of the probability distribution, P(x|n).
The reconstructed location at each time bin was then compared with the actual location identified from position tracking data. A prediction error was calculated for each time bin by subtracting the actual position from the reconstructed position. Errors were then averaged across all time bins within a theta cycle to obtain a single prediction error estimate for each theta cycle.
Slow and fast gamma power estimates were calculated for each theta cycle in the following manner. For every tetrode with cells that were used for Bayesian decoding, slow and fast gamma power were estimated within the theta cycle using the method described above. Slow and fast gamma power estimates were then averaged across tetrodes, and averaged across time within the theta cycle, to obtain a single slow gamma power estimate and a single fast gamma power estimate for each theta cycle. Theta cycles associated with slow or fast gamma (Figure 6) were then detected by identifying theta cycles with slow and fast gamma power estimates that were 2 SD greater than the mean slow and fast gamma power, respectively, across all theta cycles.
Supplementary Material
Highlights.
Place cells code current location during fast gamma
Place cells predict upcoming locations during slow gamma
Spikes precess across the full range of theta phases during fast gamma
Place cells mainly spike in the first half of their fields during slow gamma
Acknowledgments
We thank S. Amen from the Division of Statistics and Scientific Computation at UT Austin for advice regarding statistical analyses used to control for running speed. We thank A. Enenmoh for help with cell sorting analyses, S.G. Trettel for valuable contributions to video analyses, and C.T. Tulisiak for assistance with data collection. We also thank O. Jensen and J.W. Pillow for helpful comments. This work was supported by the Esther A. and Joseph Klingenstein Fund, the Alfred P. Sloan Foundation, grant P30 MH089900 from NIMH, and 1F30MH100818-01A1 from NIMH (to K.W.B.).
Footnotes
Supplemental Information includes seven figures and Supplemental Experimental Procedures, and can be found with this article online.
AUTHOR CONTRIBUTIONS
K.W.B. and L.L.C. designed experiments and analyses; K.W.B. performed the majority of the experiments, with input from L.L.C.; K.W.B. performed the majority of the analyses, with input from L.L.C.; K.N.B. performed some of the cell sorting analyses and identification of putative interneurons, with input from K.W.B. and L.L.C. K.W.B. and L.L.C. wrote the paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahmed OJ, Mehta MR. Running speed alters the frequency of hippocampal gamma oscillations. J Neurosci. 2012;32:7373–7383. doi: 10.1523/JNEUROSCI.5110-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri R, Wilson MA, Frank LM, Brown EN. An analysis of hippocampal spatio-temporal representations using a Bayesian Algorithm for Neural Spike Train Decoding. IEEE Trans Neural Syst Rehabil Eng. 2005;13:131–136. doi: 10.1109/TNSRE.2005.847368. [DOI] [PubMed] [Google Scholar]
- Battaglia FP, Sutherland GR, McNaughton BL. Local sensory cues and place cell directionality: additional evidence of prospective coding in the hippocampus. J Neurosci. 2004;24:4541–4550. doi: 10.1523/JNEUROSCI.4896-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belluscio MA, Mizuseki K, Schmidt R, Kempter R, Buzsaki G. Cross-frequency phase-phase coupling between theta and gamma oscillations in the hippocampus. J Neurosci. 2012;32:423–435. doi: 10.1523/JNEUROSCI.4122-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bragin A, Jando G, Nadasdy Z, Hetke J, Wise K, Buzsaki G. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown EN, Frank LM, Tang D, Quirk MC, Wilson MA. A statistical paradigm for neural spike train decoding applied to position prediction from ensemble firing patterns of rat hippocampal place cells. J Neurosci. 1998;18:7411–7425. doi: 10.1523/JNEUROSCI.18-18-07411.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brun VH, Leutgeb S, Wu HQ, Schwarcz R, Witter MP, Moser EI, Moser MB. Impaired spatial representation in CA1 after lesion of direct input from entorhinal cortex. Neuron. 2008;57:290–302. doi: 10.1016/j.neuron.2007.11.034. [DOI] [PubMed] [Google Scholar]
- Brun VH, Otnass MK, Molden S, Steffenach HA, Witter MP, Moser MB, Moser EI. Place cells and place recognition maintained by direct entorhinal-hippocampal circuitry. Science. 2002;296:2243–2246. doi: 10.1126/science.1071089. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Leung LW, Vanderwolf CH. Cellular bases of hippocampal EEG in the behaving rat. Brain Res. 1983;287:139–171. doi: 10.1016/0165-0173(83)90037-1. [DOI] [PubMed] [Google Scholar]
- Carr MF, Karlsson MP, Frank LM. Transient slow gamma synchrony underlies hippocampal memory replay. Neuron. 2012;75:700–713. doi: 10.1016/j.neuron.2012.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser MB, Moser EI. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Colgin LL, Moser EI. Gamma oscillations in the hippocampus. Physiology (Bethesda) 2010;25:319–329. doi: 10.1152/physiol.00021.2010. [DOI] [PubMed] [Google Scholar]
- De Almeida L, Idiart M, Villavicencio A, Lisman J. Alternating predictive and short-term memory modes of entorhinal grid cells. Hippocampus. 2012;22:1647–1651. doi: 10.1002/hipo.22030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragoi G, Buzsaki G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron. 2006;50:145–157. doi: 10.1016/j.neuron.2006.02.023. [DOI] [PubMed] [Google Scholar]
- Ekstrom AD, Meltzer J, McNaughton BL, Barnes CA. NMDA receptor antagonism blocks experience-dependent expansion of hippocampal “place fields”. Neuron. 2001;31:631–638. doi: 10.1016/s0896-6273(01)00401-9. [DOI] [PubMed] [Google Scholar]
- Ferbinteanu J, Shapiro ML. Prospective and retrospective memory coding in the hippocampus. Neuron. 2003;40:1227–1239. doi: 10.1016/s0896-6273(03)00752-9. [DOI] [PubMed] [Google Scholar]
- Fries P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu Rev Neurosci. 2009;32:209–224. doi: 10.1146/annurev.neuro.051508.135603. [DOI] [PubMed] [Google Scholar]
- Fyhn M, Molden S, Witter MP, Moser EI, Moser MB. Spatial representation in the entorhinal cortex. Science. 2004;305:1258–1264. doi: 10.1126/science.1099901. [DOI] [PubMed] [Google Scholar]
- Gupta AS, van der Meer MA, Touretzky DS, Redish AD. Segmentation of spatial experience by hippocampal theta sequences. Nat Neurosci. 2012;15:1032–1039. doi: 10.1038/nn.3138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME, Bodelon C, Wyble BP. A proposed function for hippocampal theta rhythm: separate phases of encoding and retrieval enhance reversal of prior learning. Neural Comput. 2002;14:793–817. doi: 10.1162/089976602317318965. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME, Eichenbaum H. Hippocampal mechanisms for the context-dependent retrieval of episodes. Neural Networks. 2005;18:1172–1190. doi: 10.1016/j.neunet.2005.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, Stern CE. Mechanisms underlying working memory for novel information. Trends Cogn Sci. 2006;10:487–493. doi: 10.1016/j.tics.2006.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Igarashi J, Isomura Y, Arai K, Harukuni R, Fukai T. A θ-γ oscillation code for neuronal coordination during motor behavior. J Neurosci. 2013;33:18515–18530. doi: 10.1523/JNEUROSCI.2126-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen O, Lisman JE. Hippocampal CA3 region predicts memory sequences: accounting for the phase precession of place cells. Learn Mem. 1996;3:279–287. doi: 10.1101/lm.3.2-3.279. [DOI] [PubMed] [Google Scholar]
- Jensen O, Lisman JE. Position reconstruction from an ensemble of hippocampal place cells: contribution of theta phase coding. J Neurophysiol. 2000;83:2602–2609. doi: 10.1152/jn.2000.83.5.2602. [DOI] [PubMed] [Google Scholar]
- Jensen O, Lisman JE. Hippocampal sequence-encoding driven by a cortical multi-item working memory buffer. Trends Neurosci. 2005;28:67–72. doi: 10.1016/j.tins.2004.12.001. [DOI] [PubMed] [Google Scholar]
- Johnson A, Redish AD. Neural ensembles in CA3 transiently encode paths forward of the animal at a decision point. J Neurosci. 2007;27:12176–12189. doi: 10.1523/JNEUROSCI.3761-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay LM. Two species of gamma oscillations in the olfactory bulb: dependence on behavioral state and synaptic interactions. J Integr Neurosci. 2003;2:31–44. doi: 10.1142/s0219635203000196. [DOI] [PubMed] [Google Scholar]
- Klink R, Alonso A. Muscarinic modulation of the oscillatory and repetitive firing properties of entorhinal cortex layer II neurons. J Neurophysiol. 77:1813–1828. doi: 10.1152/jn.1997.77.4.1813. [DOI] [PubMed] [Google Scholar]
- Lee I, Rao G, Knierim JJ. A double dissociation between hippocampal subfields: differential time course of CA3 and CA1 place cells for processing changed environments. Neuron. 2004;42:803–815. doi: 10.1016/j.neuron.2004.05.010. [DOI] [PubMed] [Google Scholar]
- Lisman J, Redish AD. Prediction, sequences and the hippocampus. Philos Trans R Soc Lond B Biol Sci. 2009;364:1193–1201. doi: 10.1098/rstb.2008.0316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman JE, Otmakhova NA. Storage, recall, and novelty detection of sequences by the hippocampus: elaborating on the SOCRATIC model to account for normal and aberrant effects of dopamine. Hippocampus. 2001;11:551–568. doi: 10.1002/hipo.1071. [DOI] [PubMed] [Google Scholar]
- Manabe H, Mori K. Sniff rhythm-paced fast and slow gamma-oscillations in the olfactory bulb: relation to tufted and mitral cells and behavioral states. J Neurophysiol. 2013;110:1593–1599. doi: 10.1152/jn.00379.2013. [DOI] [PubMed] [Google Scholar]
- Mehta MR, Barnes CA, McNaughton BL. Experience-dependent, asymmetric expansion of hippocampal place fields. Proc Natl Acad Sci U S A. 1997;94:8918–8921. doi: 10.1073/pnas.94.16.8918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta MR, Quirk MC, Wilson MA. Experience-dependent asymmetric shape of hippocampal receptive fields. Neuron. 2000;25:707–715. doi: 10.1016/s0896-6273(00)81072-7. [DOI] [PubMed] [Google Scholar]
- Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature. 2002;417:741–746. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
- Montgomery SM, Buzsaki G. Gamma oscillations dynamically couple hippocampal CA3 and CA1 regions during memory task performance. Proc Natl Acad Sci U S A. 2007;104:14495–14500. doi: 10.1073/pnas.0701826104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris RGM, Anderson E, Lynch GS, Baudry M. Selective impairment of learning and blockade of long-term potentiation by an N-methyl-D-aspartate receptor antagonist, AP5. Nature. 1986;319:774–776. doi: 10.1038/319774a0. [DOI] [PubMed] [Google Scholar]
- Muller RU, Kubie JL. The firing of hippocampal place cells predicts the future position of freely moving rats. J Neurosci. 1989;9:4101–4110. doi: 10.1523/JNEUROSCI.09-12-04101.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J. Place units in the hippocampus of the freely moving rat. Exp Neurol. 1976;51:78–109. doi: 10.1016/0014-4886(76)90055-8. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
- Penttonen M, Kamondi A, Acsady L, Buzsaki G. Gamma frequency oscillation in the hippocampus of the rat: intracellular analysis in vivo. Eur J Neurosci. 1998;10:718–728. doi: 10.1046/j.1460-9568.1998.00096.x. [DOI] [PubMed] [Google Scholar]
- Roth ED, Yu X, Rao G, Knierim JJ. Functional differences in the backward shifts of CA1 and CA3 place fields in novel and familiar environments. PLoS One. 2012;7:e36035. doi: 10.1371/journal.pone.0036035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senior TJ, Huxter JR, Allen K, O’Neill J, Csicsvari J. Gamma oscillatory firing reveals distinct populations of pyramidal cells in the CA1 region of the hippocampus. J Neurosci. 2008;28:2274–2286. doi: 10.1523/JNEUROSCI.4669-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL, Wilson MA, Barnes CA. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus. 1996;6:149–172. doi: 10.1002/(SICI)1098-1063(1996)6:2<149::AID-HIPO6>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- Soltesz I, Deschenes M. Low- and high-frequency membrane potential oscillations during theta activity in CA1 and CA3 pyramidal neurons of the rat hippocampus under ketamine-xylazine anesthesia. J Neurophysiol. 1993;70:97–116. doi: 10.1152/jn.1993.70.1.97. [DOI] [PubMed] [Google Scholar]
- Steffenach HA, Sloviter RS, Moser EI, Moser MB. Impaired retention of spatial memory after transection of longitudinally oriented axons of hippocampal CA3 pyramidal cells. Proc Natl Acad Sci U S A. 2002;99:3194–3198. doi: 10.1073/pnas.042700999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutherland RJ, Whishaw IQ, Kolb B. A behavioural analysis of spatial localization following electrolytic, kainate- or colchicine-induced damage to the hippocampal formation in the rat. Behav Brain Res. 1983;7:133–153. doi: 10.1016/0166-4328(83)90188-2. [DOI] [PubMed] [Google Scholar]
- Suzuki WA, Miller EK, Desimone R. Object and place memory in the macaque entorhinal cortex. J Neurophysiol. 1997;78:1062–1081. doi: 10.1152/jn.1997.78.2.1062. [DOI] [PubMed] [Google Scholar]
- Swanson LW, Cowan WM. An autoradiographic study of the organization of the efferent connections of the hippocampal formation in the rat. J Comp Neurol. 1977;172:49–84. doi: 10.1002/cne.901720104. [DOI] [PubMed] [Google Scholar]
- Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL. Population dynamics and theta rhythm phase precession of hippocampal place cell firing: a spiking neuron model. Hippocampus. 1996;6:271–280. doi: 10.1002/(SICI)1098-1063(1996)6:3<271::AID-HIPO5>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- van der Meer MA, Redish AD. Low and High Gamma Oscillations in Rat Ventral Striatum have Distinct Relationships to Behavior, Reward, and Spiking Activity on a Learned Spatial Decision Task. Front Integr Neurosci. 2009;3:9. doi: 10.3389/neuro.07.009.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Haeften T, Baks-te-Bulte L, Goede PH, Wouterlood FG, Witter MP. Morphological and numerical analysis of synaptic interactions between neurons in deep and superficial layers of the entorhinal cortex of the rat. Hippocampus. 2003;13:943–952. doi: 10.1002/hipo.10144. [DOI] [PubMed] [Google Scholar]
- Yoshida M, Fransen E, Hasselmo ME. mGluR-dependent persistent firing in entorhinal cortex layer III neurons. Eur J Neurosci. 2008;28:1116–1126. doi: 10.1111/j.1460-9568.2008.06409.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K, Ginzburg I, McNaughton BL, Sejnowski TJ. Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. J Neurophysiol. 1998;79:1017–1044. doi: 10.1152/jn.1998.79.2.1017. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.