Automated refinement and inference of analytical models for metabolic networks

Abstract

The reverse engineering of metabolic networks from experimental data is traditionally a labor-intensive task requiring a priori systems knowledge. Using a proven model as a test system, we demonstrate an automated method to simplify this process by modifying an existing or related model – suggesting nonlinear terms and structural modifications – or even constructing a new model that agrees with the system’s time-series observations. In certain cases, this method can identify the full dynamical model from scratch without prior knowledge or structural assumptions. The algorithm selects between multiple candidate models by designing experiments to make their predictions disagree. We performed computational experiments to analyze a nonlinear seven-dimensional model of yeast glycolytic oscillations. This approach corrected mistakes reliably in both approximated and overspecified models. The method performed well to high levels of noise for most states, could identify the correct model de novo, and make better predictions than ordinary parametric regression and neural network models. We identified an invariant quantity in the model, which accurately derived kinetics and the numerical sensitivity coefficients of the system. Finally, we compared the system to dynamic flux estimation and discussed the scaling and application of this methodology to automated experiment design and control in biological systems in real-time.

Introduction

Many remarkable behaviors in nature arise from complex signaling or metabolic networks. A mathematical description is one way to represent the dynamics of a network that is amenable to human interpretation. Mathematical models also often permit the prediction of new or rare behavior. A predictive network model is essential for external control of complex cellular behaviors. However, manually finding a full analytical expression can be an arduous task – particularly in multidimensional biological systems with nonlinear reactions, feedback, and oscillations. Models can either be reductionist with the utmost possible detail [1-3], or effective or surrogate models that capture specific dynamics, often using simplified mathematical representations [4-10]. In both cases, the identification of metabolic and signaling network models and their parameters is of pressing practical interest [11, 12].

Active-learning methods applied to the metabolic inverse problem [13] offer the possibility of using a computational system not only to test hypotheses but to generate new ones. The “robot scientist” project [14-17] is developing systems that can 1) assemble the background knowledge into a model in the form of a logical graph, 2) use that knowledge to design the best experiment to identify the location of a genetic perturbation on that graph, 3) perform and analyze microbial experiments, and 4) use the results to design the next experiment or genetic modification, and it provides significant savings in cost and time over human or random selection of experiments.

Here we propose a new method that could accelerate the task of model inference by automatically correcting hypothesized models – simplifying terms or proposing new nonlinear structures – to improve the agreement between model and experimental observations. The proposed approach does not require the assumption that the variables being modeled obey power-law or piecewise power-law representations. We also test the ability to model de novo, without prior knowledge of the structure of the metabolic system under study. This approach can be applied either to existing time-series data, in silico simulations of experiments, or wet-lab experiments suggested (or controlled) by the algorithm. Finally, we adapt the process to identify an invariant quantity in the system that plays a key role in predicting the system dynamics.

We performed computational experiments to analyze a seven-dimensional nonlinear model of glycolytic oscillation in yeast by perturbing and collecting noisy observations based on a well-characterized target model that could serve as a benchmark for validation of our methodology. Past research [18-20] has demonstrated the construction of a model of a biological system using automated experimental design. Here, we provide new advances into automated modeling: the ability to utilize exceedingly large data sets efficiently with fitness prediction, improved representations of mathematical models in the computational search, and integration of these approaches with automated experiment design. The advances presented here enable the first automated dynamical modeling of a realistic and biologically interesting system, where the system is an order of magnitude more complex and nonlinear, and in the presence of an order of magnitude higher measurement noise than we have previously shown.

A variety of methods has been used to infer gene regulatory networks (GRN) [21, 22], including genetics, biochemistry, molecular biology, and medicine [23]. Most often, preexisting models are used to provide a functional form, and then an optimization technique is used to fit the model parameters. Because of the breadth of data available, much of signaling network inference is based upon high-throughput mRNA microarray data for gene arrays, while metabolic network analysis considers both gene expression and high-throughput mass spectrometry of metabolites [24]. There are various challenges specific to the inference of metabolic networks from such data [25], since metabolism includes not only transcriptional regulation of enzymes, but also the conversion of substrate species with stoichiometric constraints. The computational challenge is exacerbated by the range of metabolic time constants and concentrations, each of which can easily span many orders of magnitude.

While there remain many unsolved problems in the inference of GRN models, metabolic networks surpass many other biological networks in terms of their breadth, detail, quantitative nature, and experimental validation. Currently, it is possible to obtain quantitative, dynamic measurements of metabolic concentrations, metabolite fluxes, and genetic modification simultaneously, providing an important connection between the transcriptome/proteome and cellular phenotype [26, 27]. The speed and efficiency with which these data can be acquired suggest that metabolic networks are well suited for automated inference using computer-designed and - controlled wet-lab experiments.

The most common mathematical form used to represent a metabolic network is a set of ordinary differential equations (ODEs) that describe the time derivatives of chemical concentrations [28] in the system as a function of its current state. ODEs are amenable to human interpretation because they are deterministic models and explicitly encode causal relationships [29], including feedback loops that are difficult to model using other methods. Terms in the differential equations correspond to reactions occurring in the system based on their connectivity, such as first- and second-order rate laws, power laws, and Michaelis-Menten kinetics [30].

Methods such as symbolic regression [31-34] are capable of identifying and adapting differential equations automatically from experimental data [18, 35, 36]; however, substantial challenges remain to scale this approach to the dimensionality and functional complexity necessary for biological applications. We describe how an integrated framework of equations, graph-based symbolic encoding [36], fitness prediction [35, 37], and estimation-exploration [18-20] can for the first time provide the degree of symbolic regression required for biological applications. In addition, this symbolic regression approach also allows the extraction of an algebraic expression that remains essentially invariant under all dynamic conditions of the model, shown by means of an example involving the yeast glycolytic oscillatory model. This result has key implications for enabling wet-lab automation via computation of kinetics and the related sensitivity coefficients for the observed variable in the model, constructed via symbolic regression with data from biological experiments.

Background

Metabolic modeling

While our approach is generally applicable to a variety of biological networks, we restrict the present analysis to metabolism. Given the breadth of metabolic networks, we find it useful to organize metabolic models into three categories: comprehensive versus localized, static versus dynamic, and linear versus nonlinear. All metabolic modeling approaches share these three categories, as shown in Table 1. Among these approaches, Metabolic Control Analysis (MCA) examines sensitivity of steady-state metabolic fluxes and concentrations to small perturbations of control variables. This provides some insights into the metabolic inverse problem [38], which involves determining the nature of the equation network that underlies observed behavior using techniques such as reverse engineering or systems identification. MCA analysis further suggests that the metabolome may provide more information about cellular phenotype than the transcriptome, as changes in individual enzymes have little effect on metabolite fluxes but major effects on metabolite concentrations [39]. The propagation of impulse perturbations in such chemical concentrations can also be used to infer kinetic network topology [40, 41]. Genetic programming techniques, previously demonstrated for the reverse engineering of chemical reaction networks from observed time-series data, can be used to infer both the topology and numerical parameters of metabolic networks [30, 41]. For example, evolutionary programming produced the best solution for a three-enzyme problem despite its large computation time [42], while gradient methods performed the worst.

Table 1.

Properties of various modeling approaches used to study metabolic systems

Name of Modeling Approach	Linear or Nonlinear	Static or Dynamic	Localized or Comprehensive
Genome-scale modeling using generalized mass action kinetics [38]	Linear	Dynamic	Comprehensive
Flux Balance Analysis (FBA)	Linear	Static
Metabolic Control Analysis (MCA)	Linear	Static
Dynamic Flux Balance Analysis (dFBA) [40,41]	Linear	Static	Between Localized and Comprehensive
Dynamic Metabolic Control Analysis (dMCA) [42-44]	Linear	Static
Cybernetic Modeling [47]	Nonlinear	Dynamic
Biochemical Systems Theory (S-Systems Approach) [45,46]	Nonlinear	Dynamic	Localized

Reverse engineering a deterministic model of a metabolic network consists of determining both the correct functional form of a set of ODEs to describe the system and the proper set of model parameters to fit experimentally collected data to within a given tolerance. The inverse metabolic problem is universally recognized as very hard [14, 39] and is most likely NP complete [21, 43]. A number of approaches, including global nonlinear optimization approaches [44-47], have been developed to solve this problem. Similarly, neural networks have also been used to address the metabolic inverse problem, where the measurable variables are the inputs and the unknown parameters are the outputs. The method is predicated on knowledge of the pathway structure and requires multiple hidden layers in the case of nonlinear kinetics (such as Michaelis-Menten) [43]. Alternatively, a neural network can be used to map the relationships between concentration gradients directly from data. In both cases, the resulting network is used to primarily predict performance, rather than to gain insight into the structure of the underlying system.

Within the past decade, a variety of techniques have been introduced to accelerate the estimation of model parameters [48]. A more daunting challenge is to determine the mathematical representation of the model’s system dynamics. This requires incorporation of steady-state solutions and constraints that ensure stoichiometric consistency. A difficulty with the application of such a priori constraints is the possibility that the system will deviate significantly from the assumed optimal condition under transient abnormal conditions, such as myocardial ischemia. While this can be overcome with dynamic flux balance analysis (dFBA) [49], the researcher must still choose an appropriate set of constraints to describe the transient behavior of the system, which can be challenging.

In the larger context, it is recognized that traditional metabolic flux analysis must be extended to include functional genomic information [24, 50], particularly since the regulation of metabolic behavior is shared by both metabolic constraints and transcriptional regulation [51]. Further, metabolic modeling and detailed comprehensive models of biological networks increasingly suffer from the identifiability problem [52], where there is an inability to distinguish experimentally between parameter combinations that produce identical measurements. Consequently, additional methods are needed to reduce model complexity of large biochemical systems [28]. We address this need by presenting an approach that can identify local or effective models for nonlinear and dynamic subsets of larger systems. This will aid in exploring the underlying physiology and enable accurate external control of the system [53] and the optimized design of wet-lab experiments to address these challenges.

Dynamics of biological systems and their invariants

In recent years, the application of concepts from dynamical systems theory to biological systems has led to the development of Systems Biology [54]. This has enabled the study of complex biochemical systems with nonlinear enzyme kinetics and regulatory feedback loops. Models of such systems can aid in recreating phenomena such as glycolytic oscillations [55] with the help of tools that are also used in many other disciplines [56] to study behaviors such as bifurcations and limit cycles. Often, these are identified using a system linearized about its steady state [57] and can lead to the discovery of structures in phase space called attractors [58]. These include stable, unstable, and center manifolds, collectively known as invariant manifolds [56]. Similar studies have also been attempted using alternative approaches, such as Fourier transforms, to identify control mechanisms for autonomous oscillations [59]. For example, variations in gene expressions in multistable systems are reduced over the course of time in a process known as canalization, which has recently been investigated by means of invariant manifolds [60]. This is computationally expensive, however, and has therefore led to alternate approximation methods [61, 62] that can improve the performance of many model reduction algorithms [63, 64] and the partitioning of the system into slow and fast components [65]. Identification of these invariant manifolds is therefore of interest to fields such as chemical kinetics [66], as it enables the reduction of a complex model with many variables to one containing only a few. Such advances show the applicability of methods from dynamical systems theory to understanding problems of interest in metabolic networks.

Classical mechanical systems such as the double pendulum can be described in terms of Hamiltonians, Lagrangians, and equations of motion which are derived from the physical principles that govern their dynamics. In contrast, biochemical systems were not expected to be governed by similar laws. However, symbolic regression applied to an oscillatory physical system has uncovered such invariant expressions using only observable data [67]. Herein we apply this approach to the model of yeast glycolysis. While the relationship between the derived invariants and the model dynamics is yet to be fully understood, the invariant form yields the equations for the observed variables, which are selected from species amenable to measurement, and their numerical sensitivities.

Methods

Overview of the approach

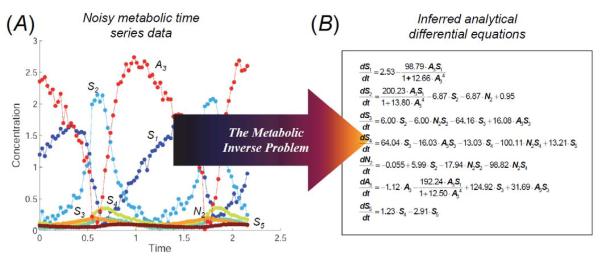
We first provide a brief overview of the proposed approach for adapting and modeling dynamical models before describing the methods in more detail. The purpose of our approach, illustrated in Figure 1, is to identify the differential equations that describe the reactions taking place in the metabolic network by designing numerical experiments and searching for dynamical equations automatically. Initially, we have no data, and the first experiments could either be to observe the system performance for a randomly selected set of initial conditions within the normal bounds of the system, or to make simple observations of nominal stable behavior, such as stable nodes and limit cycles. Later, these experiments are chosen optimally to discriminate among the candidate models in the equation search. We perform experiments in a virtual wet-lab, where a glycolysis system is simulated by a black box that outputs noisy time-series data (also see Methods in the Supporting Information).

Figure 1. Concept and flow chart for automated model inference.

A: Noisy time-series data reflecting anaerobic metabolism concentrations over time (presented with a higher-than-required sampling rate). B: The noisy time-series data are automatically translated into a set of coupled analytical differential equations without prior knowledge of the system structure.

Once we have initial time-course data from the system, we then begin searching for each differential equation of the system using symbolic regression [31-34] and fitness prediction [35, 37] (also see Methods in the Supporting Information). Symbolic regression searches both the structure, i.e., analytical form, and the parameters of an equation to fit and explain the data in the most parsimonious way. The second component in our method, fitness prediction, simplifies large data sets to accelerate the equation search while maintaining accurate ranking among all candidate differentials in the search. Our representation of a differential equation in the search is an acyclic graph [36]. This encoding also accelerates the equation search while producing more parsimonious expressions on average in comparison to traditional encodings. We have made software implementing these techniques available online for download at [68].

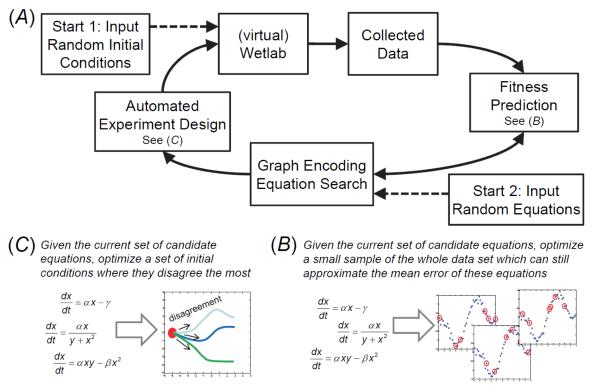
As many differential equations compete to fit the training data, it is likely that multiple equations are able to explain the behavior in different ways. Given these multiple explanations, we use an estimation-exploration algorithm (EEA) to search in parallel for experiments that will maximize disagreement in the predictions of the evolving set of models [18-20]. For a dynamical system such as glycolysis, we represent an experiment as a set of initial conditions that we apply in silico to the black-box system so we can observe its transient trajectory and behavior. We dictate the most informative experiment to be the set of initial conditions in which the current population of equations has the highest statistical variance in its predicted dynamics. Periodically, we perform the best experiment on the black-box system, collect new data, and once again evolve equations to explain them. We repeat this process until a dominant model emerges. Figure 2 outlines the overall approach, whose steps we now describe in detail.

Figure 2. Workflow detailing the steps involved in our approach.

A: The method starts with a set of randomly chosen experimental data. Next, fitness predictors are optimized to approximate the complete data set (B). The graph encoding is initiated with random equations, and candidate models are then coevolved to optimize to the fitness predictors. The new candidate models are then used to design new experiments (C) which maximize disagreement among model predictions to refine their structure, and the cycle is repeated.

Symbolic regression and fitness prediction

Genetic programming is a widely studied class of evolutionary algorithms inspired by biological evolution [34] that can be used to search for mathematical models. In a traditional genetic program, an initially random population of individuals evolves iteratively in computer memory to maximize some objective – for example, equations to model experimental data with the lowest squared error. Equations with the highest fitness, i.e., the lowest error, persist in the population to recombine (genetic crossover) and mutate to replace less-fit individuals.

Symbolic regression uses genetic programming to evolve (compete) algebraic expressions to explain experimental data [34]. Unlike polynomial (parametric) regression or neural networks which also fit data, symbolic regression searches a space of analytical equations to explain available experimental observations. Symbolic regression composes equations using basic algebraic building blocks with the aim to formulate simpler (e.g., fewer parameters) or more natural expressions (robust to perturbations) that are most likely to correspond to the underlying intrinsic mechanisms of the system.

Symbolic regression compares candidate equations by calculating their residual errors on the experimental data – also known as the equation’s fitness metric – for example, using square-error or correlation. The scaling of symbolic regression is dominated by the size of the equations that need to be evaluated, which can be exponential in the worst case, rather than the dimensionality of the system [36].

This paper emphasizes that this approach can be made tractable for appreciable systems. In past research, algorithms have used all available data at once to evaluate the fit. However, this metric can be overly stringent and inhibit equations from building intermediate expressions needed for the final model.

Instead, we have developed a method called fitness prediction to reduce overall computational cost and to approximate the local search gradient [35, 37]. A fitness predictor is a small subset of all collected data samples that approximates the entire data set. For example, if a data set contains 1000 data points, a fitness predictor could be a list of 10 points from the full data set. If the samples in the predictor are chosen well, measuring fitness on the smaller sample is sufficient to rank and discriminate the candidate equations in the population of equations.

The data subset is adapted within a separate population of fitness predictors (data subsets) that evolves in parallel with the symbolic regression of differential equations. The fitness of a fitness predictor is its ability to approximate error on the full data set for the current population of equations.

The differential equation and the fitness predictor populations coevolve together throughout the equation search. In the symbolic regression population, the fitness of each equation is calculated using the data samples in the top-ranked predictor at all times. In contrast to standard symbolic regression alone, equations still compete to fit the experimental data, but are free to drift in more trajectories; the predictors adapt with the goal of defeating poor deviations.

Fitness prediction allows a genetic algorithm to search a wider range of equations by adapting the fitness heuristic and reducing its computational cost. An interesting result [37] shows that symbolic regression is more successful when equations are pressured to explain only key features of the systems at any given time rather than the entire data set at once. The effect of overfitting is actually reduced when using fitness prediction as the predictors adapt (coevolve) to defeat overfitting to the subset [37], and consequently further overfitting. This allows equations to drift from the objective gradient, but the focus adapts with the population to prevent excessive divergence from the intended gradient.

Here, we have introduced the key concepts of symbolic regression and fitness prediction. Additional details and implementation information are available in [37] and the Supporting Information, where we provide the algorithm settings. We have developed our own software to perform all computational searches described in this paper, available at [68], but the procedure could be implemented in many ways on different software platforms.

Acyclic graph encoding of the model

The ability to identify an accurate and parsimonious differential equation model using symbolic regression can rely strongly on the genetic encoding (e.g., the genotype organization of a symbolic expression within the algorithm) used in the equation search. In particular, the encoding needs to be amenable to crossover and mutation operations of the evolutionary algorithm.

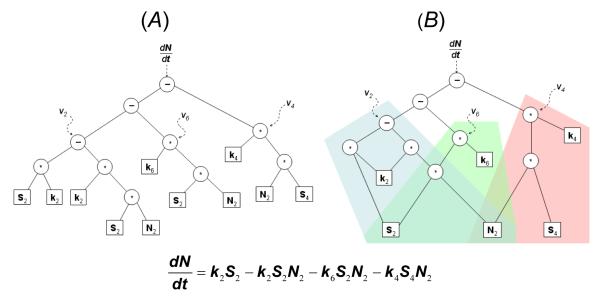
Traditionally, symbolic expressions have been represented as binary-trees, where parent nodes represent algebraic operations such as addition or multiplication, and leaf nodes represent symbolic variables and parameter constants (Figure 3A). While tree encodings are simple and easy to manipulate in an evolutionary search, they are susceptible to producing complex and bloated equations, often resulting in unsuitable models for understanding the underlying system.

Figure 3. Two analytical model representations for NADH in the cell glycolysis model.

A: Tree encoding, and B: graph encoding of the same equation (below). While the tree encoding is simpler to manipulate algorithmically (e.g., alter subexpressions), it requires redundant subtrees and is prone to produce large equations that may not accurately represent the biological system. The graph encoding couples subtrees, thereby biasing equations to preserve simpler shared expressions.

Instead of a tree, we use an acyclic graph encoding for symbolic regression that scales well computationally and exploits the shared structures found in differential equations [36]. The acyclic graph encoding represents a symbolic expression similarly to a tree encoding – interpreting parent nodes as mathematical operations such as addition and multiplication and leaf nodes as state-variables or parameter constants – however, subexpressions can be reused (Figure 3B). In our implementation, the encoding for the graph is an ordered list of operations much like assembly code: each operation builds up successive subexpressions in the final expression, using any preceding operations and symbolic variables.

The graph encoding takes advantage of redundant subexpressions, such as coupled reactions in metabolic networks. Effectively, a reused subexpression constrains the genotype of the equation, making these subexpressions more stable and less likely to drift to more bloated equivalents and thereby biasing the search against bloated equations and overfitting [36]. In the end, the graph-encoded equations are simpler and faster to evaluate on average, allowing us to scale the modeling procedure to more complex systems. Additional details are provided in [36] and the Supporting Information.

Automated experimental design

Once the symbolic regression step has evolved a population of candidate equations to fit the current set of training data, there may be several coherent equations that model the data in different ways – particularly in high-dimensional domains with sparse data where many equivalent explanations exist for the simplest behavior. But which of these several mathematical explanations of the system is correct?

The estimation-exploration algorithm (EEA) is a method to automatically design a new experiment that can help differentiate the current model candidates and refine their structure [18-20, 69]. The purpose of the EEA is to decipher which model is likely to be correct by searching for experiment settings, initial conditions, perturbations, or procedures that cause current models to disagree most in their predictions.

The EEA designs and conducts the experiments in parallel with the equation search. Different experiments compete in a population to maximize the variance they produce in the current differential equations. Periodically, every 50,000 iterations (or roughly every 10 minutes), we take the best experiment and perform it on the black-box system to collect new data to test predictions made by the current population of differential equations.

Generating data

For our experiments in this paper, we collect data in a virtual wet-lab by numerically integrating the glycolysis model from an initial state and recording the state-variables over the transient trajectory. The initial state is either randomly chosen (for collecting initial data before modeling) or chosen by the algorithm. For a given initial state, we record the system’s state-variables every 0.1 minutes until we have acquired 100 samples.

In our results, we report performance on two data sets: a training data set and a test data set. Only the training data set is used to evolve and select the differential equation models, while the larger test data set is used to help analyze and compare the different modeling methods considered in our results.

We confined all initial states to realistic environments indicated in Table 2 for the training data. These constraints are the ranges each metabolite experiences when the system is left alone to oscillate naturally on its stable limit cycle. Therefore, each initial condition is a combination of typical individual metabolite levels found in the metabolic network’s natural oscillations. In the case of the test data set, however, the upper-bound constraints were doubled to expand the phase space by a factor of 2⁷. The looser constraints used for the test data set measure how well models extrapolate and predict new behavior in locations in phase space distant from those used in the inference of the model.

Table 2.

Model variables, the allowed range of initial states for the training data set, and the standard deviation of the limit cycle used to compute the amount of added noise.

Variable	Name	Range	Standard deviation
S1	Glucose	[0.15, 1.60]	0.4872
S2	Glyceraldehydes-3-phosphate and dihydroxyacetone phosphate pool	[0.19, 2.16]	0.6263
S3	1,3-bisphosphoglycerate	[0.04, 0.20]	0.0503
S4	Cytosolic pyruvate and acetaldehyde pool	[0.10, 0.35]	0.0814
N2	NADH	[0.08, 0.30]	0.0379
A3	ATP	[0.14, 2.67]	0.7478
S5	Extracellular pyruvate and acetaldehyde pool	[0.05, 0.10]	0.0159

As part of the black-box glycolysis model, we simulate taking physical measurements on a real system by adding normally distributed random noise to each state-variable in each time-sample. The standard deviation of the random noise added to each state is relative to the standard deviation of the state-variable in the system’s stable limit cycle. This gives variables with large magnitude oscillations higher noise than variables with smaller magnitudes and makes the noise impact independent of measurement units. We used 10% noise in most experiments, i.e., the ratio between the noise standard deviation and the metabolite standard deviation is 0.1. This is consistent with reports of ~10% average standard errors of the measured metabolic oscillation amplitudes (with the percentage errors smaller on large-amplitude variables) [70] and added noise amplitudes of 10% used in other metabolic system estimates [48]. We estimated the numerical derivative of the data using Loess locally weighted polynomial fitting [71] with window size of 50 (also see Methods and Figure S3 in Supporting Information).

In later experiments, we sweep the amount of noise from zero to 50% noise. The 10% noise is the first level where identifying the exact system structure becomes nontrivial. After this point, five of the seven states can be modeled exactly up to 30% noise, and four of the seven at 50% noise. It is worth noting that many real biological systems may also contain different types of noise, such as asymmetrical noise, and a modified equation search method could be used in these cases, such as explicitly including symbolic noise sources in the ODE model [72].

The glycolytic oscillation models

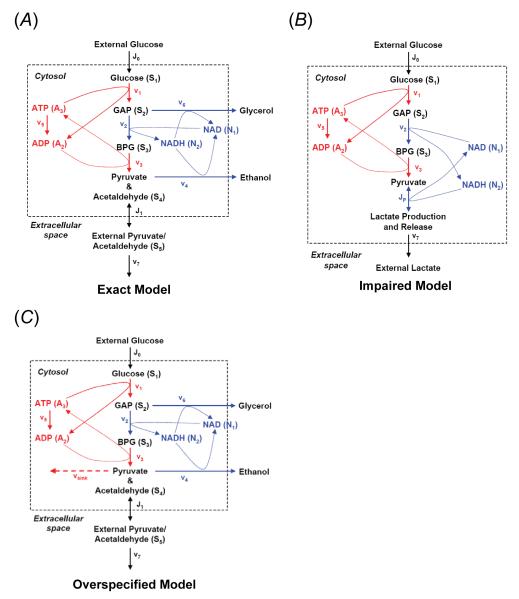
For our in silico demonstration of this process, we begin with a published numerical model [73, 74] of glycolytic oscillation in yeast for the system upon which our algorithm experiments. Tables 2 and 3 and other tables in the Supporting Information provide details of the models shown in Figure 4. In this seven-variable model, the respiratory chain (mitochondrial oxidative phosphorylation) is completely inhibited. The reaction network for this system, shown in Figure 4A, contains the main reactions of glycolysis and adjacent reactions producing ethanol and glycerol. We provide additional model details in the Supporting Information. During the original model development, the complexity of the model was reduced by omitting many of the glycolytic reactions, and by lumping together other reactions, so that several of the model variables denote concentrations of pools of intermediates rather than concentrations of the individual compounds, e.g., the pools of triose phosphates (glyceraldehydes-3-phosphate, dihydroxyacetone phosphate) and pyruvate and acetaldehyde. This simplification has been rigorously justified using a judiciously applied quasi-steady-state approximation [75]. This particular model is capable of reproducing glycolytic oscillations with a period in the range of 0.10 to 12 minutes and has been used to study the temperature dependence and temperature compensation of yeast glycolytic oscillations [74].

Table 3.

The differential equations describing glycolytic oscillation of the generating model (left pane) and the inferred model from the training data, which had 10% noise (right pane).

Original system	Automatically inferred system
$\frac{{\mathit{dS}}_1}{\mathit{dt}}=2.5-\frac{{100}^{\ast }{\mathit{A}}_3{\mathit{S}}_1}{1+{13.68}^{\ast }{{\mathit{A}}_3}^4}$	$\frac{{\mathit{dS}}_1}{\mathit{dt}}=2.53-\frac{98.79\cdot {\mathit{A}}_3{\mathit{S}}_1}{1+12.66\cdot {{\mathit{A}}_3}^4}$
$\frac{{\mathit{dS}}_2}{\mathit{dt}}=\frac{{200}^{\ast }{\mathit{A}}_3{\mathit{S}}_1}{1+{13.68}^{\ast }{{\mathit{A}}_3}^4}-6^{\ast }{\mathit{S}}_2-6^{\ast }{\mathit{S}}_2{\mathit{N}}_2$	$\frac{{\mathit{dS}}_2}{\mathit{dt}}=\frac{200.23\cdot {\mathit{A}}_3{\mathit{S}}_1}{1+13.80\cdot {{\mathit{A}}_3}^4}-6.87\cdot {\mathit{S}}_2-6.87\cdot {\mathit{N}}_2+0.95$
$\frac{{\mathit{dS}}_3}{\mathit{dt}}=6^{\ast }{\mathit{S}}_2-6^{\ast }{\mathit{N}}_2{\mathit{S}}_2-{64}^{\ast }{\mathit{S}}_3+{16}^{\ast }{\mathit{A}}_3{\mathit{S}}_3$	$\frac{{\mathit{dS}}_3}{\mathit{dt}}=6.00\cdot {\mathit{S}}_2-6.00\cdot {\mathit{N}}_2{\mathit{S}}_2-64.16\cdot {\mathit{S}}_3+16.08\cdot {\mathit{A}}_3{\mathit{S}}_3$
$\frac{{\mathit{dS}}_4}{\mathit{dt}}={64}^{\ast }{\mathit{S}}_3-{16}^{\ast }{\mathit{A}}_3{\mathit{S}}_3-{13}^{\ast }{\mathit{S}}_4-{100}^{\ast }{\mathit{N}}_2{\mathit{S}}_4+{13}^{\ast }{\mathit{S}}_5$	$\frac{{\mathit{dS}}_4}{\mathit{dt}}=64.04\cdot {\mathit{S}}_3-16.03\cdot {\mathit{A}}_3{\mathit{S}}_3-13.03\cdot {\mathit{S}}_4-100.11\cdot {\mathit{N}}_2{\mathit{S}}_4+13.21\cdot {\mathit{S}}_5$
$\frac{{\mathit{dN}}_2}{\mathit{dt}}=6^{\ast }{\mathit{S}}_2-{18}^{\ast }{\mathit{N}}_2{\mathit{S}}_2-{100}^{\ast }{\mathit{N}}_2{\mathit{S}}_4$	$\frac{{\mathit{dN}}_2}{\mathit{dt}}=-0.055+5.99\cdot {\mathit{S}}_2-17.94\cdot {\mathit{N}}_2{\mathit{S}}_2-98.82\cdot {\mathit{N}}_2{\mathit{S}}_4$
$\frac{{\mathit{dA}}_3}{\mathit{dt}}=-{1.28}^{\ast }{\mathit{A}}_3-\frac{{200}^{\ast }{\mathit{A}}_3{\mathit{S}}_1}{1+{13.68}^{\ast }{{\mathit{A}}_3}^4}+{128}^{\ast }{\mathit{S}}_3+{32}^{\ast }{\mathit{A}}_3{\mathit{S}}_3$	$\frac{{\mathit{dA}}_3}{\mathit{dt}}=-1.12\cdot {\mathit{A}}_3-\frac{192.24\cdot {\mathit{A}}_3{\mathit{S}}_1}{1+12.50\cdot {{\mathit{A}}_3}^4}+124.92\cdot {\mathit{S}}_3+31.69\cdot {\mathit{A}}_3{\mathit{S}}_3$
$\frac{{\mathit{dS}}_5}{\mathit{dt}}={1.3}^{\ast }{\mathit{S}}_4-{3.1}^{\ast }{\mathit{S}}_5$	$\frac{{\mathit{dS}}_5}{\mathit{dt}}=1.23\cdot {\mathit{S}}_4-2.91\cdot {\mathit{S}}_5$

Figure 4. Reaction networks for anaerobic metabolism in a yeast cell.

A: The exact model includes membrane transport of glucose and pyruvate/acetaldehyde. Reactions in red involve ATP production/usage, and reactions in blue involve redox species production/usage. B: The impaired model does not produce either glycerol or ethanol. C: The overspecified model has an additional sink for pyruvate/acetaldehyde (S₄).

Reverse engineering glycolytic oscillation in yeast

We used the model of glycolytic oscillations in yeast shown in Figure 4A to simulate experimenting on a wet system. Glycolytic oscillation is one of the most common examples of oscillatory behavior at the cellular level and enables a broader understanding of the underlying dynamic processes that lead to rhythmic behavior. Of such systems, anaerobic glucose metabolism in yeast is one of the most commonly studied. In a particular region of parameter space, all of the glycolytic intermediates show an oscillatory behavior with a variation in the frequency of oscillation observed across species. In the vicinity of the attractor that is responsible for these oscillations, the system never reaches steady state and hence this behavior cannot be readily analyzed by equilibrium or stoichiometric approaches such as metabolic flux balance analysis [76]. We use this oscillatory system to demonstrate the capability of our approach to infer the equations governing a nonlinear dynamical metabolic system.

Our experiments placed the yeast glucose model (Figure 4A and Figure S1) in a numerical black box and then allowed our algorithm to conduct in silico experiments on this black box. For our studies, we collect data by numerically integrating the differential equations in the black-box glycolysis model and adding noise. Initial states, i.e., the initial conditions, are constrained to a specified range, and the initial states for the test data are sampled over a larger volume in state-variable space to determine how well models can extrapolate and predict new behavior.

Our goal is to find the exact differential equations of the unknown system algorithmically. More specifically, we are interested in modeling metabolic networks as a dynamical system – a set of ODEs. In a system of N state-variables that we observe experimentally (e.g., extracellular concentrations of glucose (S₁) or NADH (N₂) over time), we must identify N (possibly nonlinear) differential equations. Synthesizing these mathematical models of a dynamical system is the most computationally intensive task in our procedure. We first smooth and then differentiate the observed time-series data to produce its derivatives. We then search for the differential equations that reproduce each numerically estimated derivative.

We calculate the numerical time derivative of each variable at each data point in order to compare it with the value of the candidate differential equation explicitly. Accumulating errors of the derivative values avoids the need to integrate each differential equation, which can be computationally expensive [18].

Regression procedure for all methods

During regression for each compared algorithm – symbolic regression, nonlinear regression, and neural network regression – we track accuracy on both the training and test data sets over time. Only the training data set is used to update the models. By recording the accuracy of the model of the test data set over time, we can analyze later how well the regression procedure identifies models that generalize and extrapolate to data not in the training set (e.g., Figure 6 below).

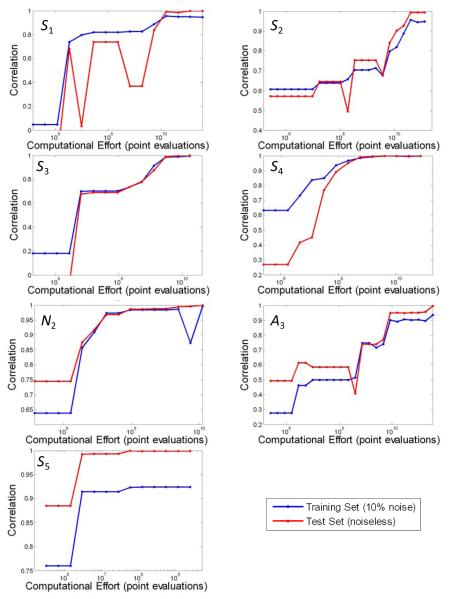
Figure 6. The fit to the data of the highest ranked equation during regression for each glycolysis variable.

The blue series show the correlation coefficient to the training data, and the red to the test data. The training data contain 10% noise while the test data have none. The test data contain a larger range of allowed state-variables (i.e., sampled with weaker constraints to explore a variable phase space that is 2⁷ times larger than for the training set) to determine whether the model identified from the training data can extrapolate and predict new behavior. The variables are identified in Figure 4 and Table 2.

In nonlinear regression and neural network regression, the training set was constant, with 200 trajectories (random experiments on the black box). In contrast, the symbolic regression algorithm’s training set begins with10 trajectories that were produced following 10 different, random initial conditions, but subsequently adds new black-box trajectories from initial conditions chosen by the algorithm throughout regression for a maximum of 200 total experiments, with 100 measurements per experiment. Hence such a single black-box experiment provides 100 measurements of each variable over the duration of each experiment. As we discussed above, each black-box experiment is followed by approximately 50,000 EEA iterations conducted during 10 minutes of real time, an interval that would be consistent with an automated wet-lab experiment [53]. For all algorithms, the test data set was held constant. The test data set contained 100 random trajectories. We do not perform early stopping on any of the methods; however, performance trends such as overfitting can be gleaned from the fitness of the test data set using values from the training data set (also see Methods and Figure S7 in Supporting Information).

Construction of an invariant expression

The search for a conserved quantity used a similar symbolic regression search as that which produced the dynamical model, but instead of modeling a specific signal, such as a numerical derivative, the search looked for an invariant expression.

Searching for invariant equations, however, is particularly challenging because an error metric is difficult to define [77]. For example, in any data set there are infinitely many trivial equations that satisfy a conserved quantity, such as x-x, or other more complicated identities that simplify to, or nearly simplify to, a constant. Instead, the invariant search looked for equations that accurately predict implicit derivatives estimated from the data [67, 77]. This requirement identifies invariant expressions that can also derive nontrivial dynamical relations in the data.

We searched for an invariant in the glycolysis system that used the variables S₁, N₂, A₂, and v₁, i.e., glucose, NADH, ADP, and the rate of the S₁ reaction (glucose to GAP), respectively, as shown in Figure 4A. Invariant equations were rewarded for predicting the implicit derivatives between each pair (such as dS₁/dN₂, dS₁/dA₃, etc.) and for using all four in the expression (a requirement for our post-analysis). If an expression used less than four of these variables it was removed from the search population. We selected the most parsimonious invariant equation on the resulting search Pareto frontier (see for example, Figure S2 in the Supporting Information).

Finally, we used nonlinear regression on the resulting invariant form to fine-tune the parameter coefficients because the invariants have some freedom in their exact coefficient values. In this step, we solve the invariant equation (e.g., f(S₁,N₂,A₃,v₁) = 0) for S₁. We then used Mathematica to tune parameters to predict the S₁ signal. The resulting model is predictive of both the implicit derivatives of the data set and the explicit S₁ signal while still remaining invariant.

Results

We used the proposed automated modeling procedure to analyze the seven-dimensional model of glycolytic oscillations in yeast. We tested the ability of the algorithm to adapt and correct a partially correct hypothesized model chosen by the experimenter to fit the exact system, i.e., to augment expert modeling. We tested the regression of the entire system de novo (without prior knowledge of the system structure) and compared predicted results with those obtained from nonlinear parametric regression and fitting to neural networks. Finally, we modified the procedure to identify an invariant quantity of the biochemical system that is distinct from any conserved moieties that may exist in the model. The invariant also predicts kinetics of an observed variable of the system (in our case v₁) which in turn allows for computation of the numerical sensitivities to a high degree of accuracy.

Correcting hypothesized models

The first experiment is to adapt or improve upon an existing hypothesized model, given a hypothesized differential equation. For example, the algorithm can modify a partially correct model by altering its existing structure and terms, pruning unnecessary terms, or synthesizing new terms to identify the exact intrinsic model. While methods for simplifying models already exist [52], these techniques do not compose new terms in a model or correct erroneous terms. Using automated data acquisition, the algorithm can also design experiments to differentiate multiple hypothesized models and test their correctness where they disagree most.

In order to use the algorithm to refine a given model, we first initialize its search population by seeding the initial population with the chosen models. Effectively, this biases the algorithm to reuse the structure of the given model, but does not restrict the algorithm from making large alterations. We first test the impact of this seeding procedure to correctly model the glycolysis S₄ differential equation using the impaired and overspecified models. (The hypothesized differential equations for S₄ in this experiment are given in Table S5.)

There are two possible impacts that seeding a hypothesized model can have on symbolic regression. In the best case, the seeded model may be very close and the algorithm only needs to make minor adjustments to converge to the intrinsic model. Alternatively, the seeded model may be absurd, in which case there is no benefit and the algorithm evolves de novo. Figure 5B and D exemplifies these two symbolic regression behaviors for the S₄ differential equation.

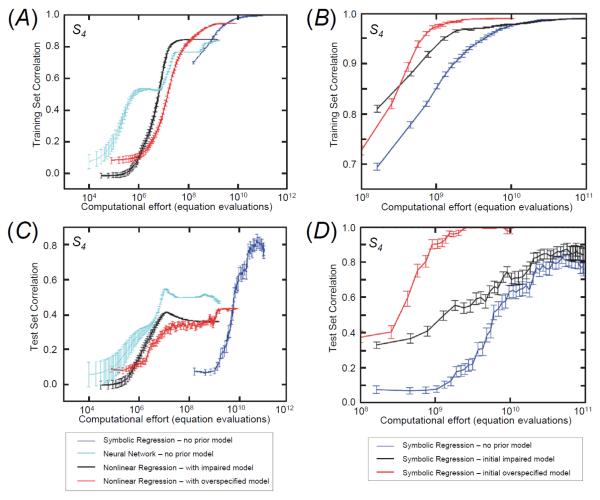
Figure 5. Performance comparison between symbolic, nonlinear, and neural network regression.

Left: Nonlinear parametric regression to the impaired and overspecified models, and neural network regression, as compared to symbolic regression without a prior model. Training data performance (A) shows that all algorithms accurately explain the training data. The test data performance (C) of the same equations plotted for the training data shows that not all methods extrapolate well to the larger test set. Note that symbolic regression uses more point evaluations in the same amount of running time because it is a parallel search, whereas nonlinear regression and neural network back-propagation use serial updates. Right: Performance comparison of symbolic regression when correcting a hypothesized model. B: The blue curves represent the performance of the algorithm to the S₄ equation without any prior model. For the other two pairs of curves, the symbolic regression algorithm was seeded with an incorrect hypothesized model (black = impaired, red = overspecified) and the algorithm had to modify the seeded model to fit the original training data, i.e., to return to the model that was inferred during the progress of the blue curve. The figure shows the performance for the training data (B) and the test data (D) on the same equations. For both A) and B) results are averaged over 100 trials – error bars represent the standard error.

As shown in Figure 5B and D, in the overspecified case, the seeding has improved by a factor of ten both the speed to regress and the reliability of the results in comparison to regression without a prior model (shown below). In effect, the algorithm has corrected the model by removing the sink term and fixing the differences in parameters. In the impaired model case, the effect is much less dramatic. The algorithm must construct the two missing terms. However, the seeding improves the reliability of convergence on average. There is also the possibility that the initial seeding might trap the algorithm in a local error minimum from which the present algorithm cannot escape. Similar problems have been encountered and addressed in conventional nonlinear regression schemes by, for example, choosing random data points at some distance from the regressed data to ensure that the solution is in fact a global rather than local minimum. Similar approaches could be taken with our method, although it is unclear whether this would provide any advantage to ab initio regression.

Modeling without a prior model

When modeling without a prior model, we do not assume an initial hypothesis model. The initial equations in the search are randomly initialized; therefore, the algorithm’s search for each ODE equation starts at a random point. Table S4 provides an example of how the equation for S₂ evolves during regression. We conducted ten independent trials to collect data and model each equation (Table 3) corresponding to Figure 4A. We show in Figure 6 the runs that reached the highest performance on the training data (blue). Additionally, at each level of computation we measured performance of the same equations on the test data (shown in red). Variables S₃ (1,3-bisphosphoglycerate), S₄ (cytosolic pyruvate and acetaldehyde pool), N₂, and S₅ were the fastest equations to infer, and their performance curves gradually converge monotonically during regression. Equations for S₁, S₂ (glyceraldehydes-3-phosphate and dihydroxyacetone phosphate pool) and A₃, which have the most nonlinear structure, show performance that is more rugged. Dips in the training data performance indicate that data from a new black-box experiment revealed dynamics that were not in the current data set (or perhaps underemphasized). Such dips tend to precede large improvements in performance.

The equations with the best fits to the training data obtained from the model in Figure 4A for the ten trials are shown in Table 3. The automatically inferred equations are nearly identical to the black-box generating numerical model. Some slight differences remain: most notably, the parameters are inexact, which results in a slight mass imbalance, and one nonlinear term is approximated by a linear term in the S₂ equation. Specifically in our ab initio model inference, the S₂ equation approximates the N₂*S₂ term and adds a constant term (0.9467) to the ODE in Table 3. The N₂*S₂ term comes from the balance of v₂ and v₆, where v₂ is the conversion of S₂ to S₃, and v₆ is the loss of S₂ to glycerol production. Both the v₆ and v₂ fluxes are NAD dependent, which gives rise to the N₂*S₂ term through a simple application of mass action kinetics. The decoupled N₂*S₂ dependence is now represented as a linear combination of (N₂ + S₂). For the N₂ equation, the combined action of v₂ and v₆ is properly inferred. However, there is (once again) a small constant term (−0.0549) in the N₂ ODE that compensates for the fact that the NAD pool is not being strictly conserved.

Figure 7 shows integration of the inferred model compared to the exact model (Figure 4A), with the differences in frequency being the results of the small mass imbalances that are compensated for with the additional terms. Despite these small differences, Figure 7 shows the same behavior as the original system. Since symbolic regression does not have any inbuilt “chemical logic,” it is unable to recognize and constrain reaction rate expressions that appear in multiple ODEs. The ramifications of this are twofold: first, the inferred model incurs small mass imbalances within the system that manifest themselves as a carbon loss or a source term in the energetic pools (ATP and NADH); second, the inferred model compensates for the imbalances by adding compensatory terms.

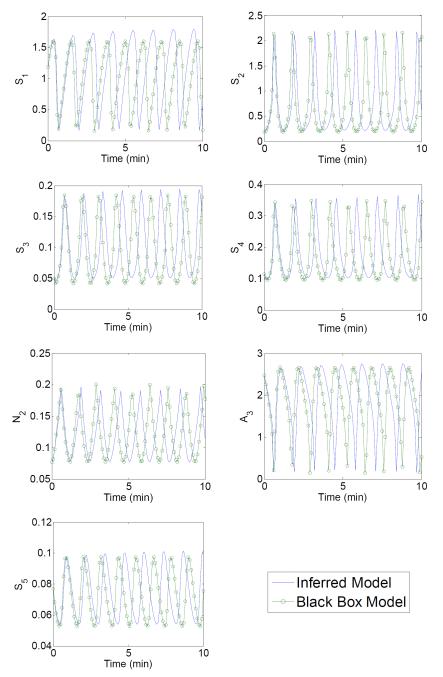
Figure 7. Integration over time of the exact black-box and inferred models.

The inferred model shown in Table 3 differs from the exact model by a slight mass imbalance. Integrated over 10 minutes, the inferred model captures the same behavior. While small differences in derivative values tend to accumulate during integration, the inferred model captures the integrated behavior remarkably well. The inferred model predicts early behavior accurately and exhibits the same qualitative dynamics later in time, differing only slightly in the phase.

Identification of the simplest equation, S₅ (external pyruvate/acetaldehyde), without a priori information required approximately one minute for ~3 × 10⁶ evaluations for ab initio modeling, and ~1 model/experiment/evolution cycle. In contrast, the time to regress the most complex differential equations in the glycolysis model, A₃ (ATP), was approximately 1-2 hours, and involved ~4 × 10¹¹ point evaluations on four workstations (eight 2.4 GHz cores), representing ~200 model/experiment evolution cycles and ~2 × 10⁹ point evaluations/cycle.

Comparison to established methods

Searching the space of symbolic differential equations is unique in that it does not require prior information about the system or a prior model. Hence it is difficult to compare this model inference process with the process of historical development of an existing metabolic model. To demonstrate the capabilities of this approach to specify a compact representation of a model, as might be needed for prediction and control of metabolism in a bioreactor[53], we have compared our approach with two relevant methods: nonlinear regression and neural network regression.

Neural networks are recognized as being useful for predicting a time series when the underlying mechanism is unknown or is too complex to be easily represented, or noisy data limit the analysis [44]. Such numerical models are less amenable to human interpretation, but can model and predict data similar to that used for training. In the neural network regression, we use a 1024-neuron hidden layer network mapping the seven state-variables to their seven respective time derivatives. The output layer consists of linear perceptrons. We use standard back-propagation to train the network and bias-node weights.

In nonlinear regression, a preexisting mathematical model is chosen to be fitted to the data. The selected preexisting model is assumed to closely relate to the actual, underlying model of the system but may have a slightly different structure – it may be missing key terms, or have unnecessary terms, or incorrect terms. Regressing data to the wrong model may provide a low-error fit, but with parameter values that are in fact quite different from the actual ones because of the adjustments required to fit the wrong model to the data. We fit the nonlinear regression models via gradient-descent, with initial parameters given by their theoretical values (see Table S3 of the Supporting Information).

For the nonlinear parametric regression comparison, we chose two slightly different preexisting glycolysis models, also shown in Figure 4B and C – one that is a simplification of the exact model (the “impaired” model) and one that is more complex in that it replaces some dynamics with an additional sink term (the “overspecified” model). The impaired model is produced by eliminating the glycerol (v₆) and ethanol (v₄) production and having the NADH→NAD recycle occur with the production of lactate from pyruvate. This essentially converts the yeast model into that of a mammalian cell. The overspecified model is produced by relaxing the assumption of no carbon loss to other cellular synthetic processes in the yeast model (fatty acid biosynthesis, amino acid production, etc.). This is accomplished by adding a carbon sink term (v_sink) to the pyruvate pool, whose rate is primarily controlled by the presence of ATP.

On average, all three algorithms model the training data equally well, but some do not generalize well when the regression results are applied to the broader test data set that was not used for training (Figure 5C). It is clear that nonlinear regression of both related models can explain a substantial amount of the S₄ dynamics, particularly within the training data. However, extrapolation to the wider domain of the test data only reaches correlation of approximately one half. Similarly, the neural network accurately models the training data, but as shown by the early dip in correlation, it significantly overfits before converging, possibly due to the added noise. Additional details are provided in the Supporting Information.

Invariant-derived model results

Finally, we tested the ability to find an invariant quantity directly from the data. We modified our procedure by changing the fitness metric from the error in predicting the rate of change of each variable to the error in estimating implicit derivatives between pairs of variables in the system [67]. We chose the equation with the lowest magnitude (most invariant) in the resulting models as closest to a true invariant of the system.

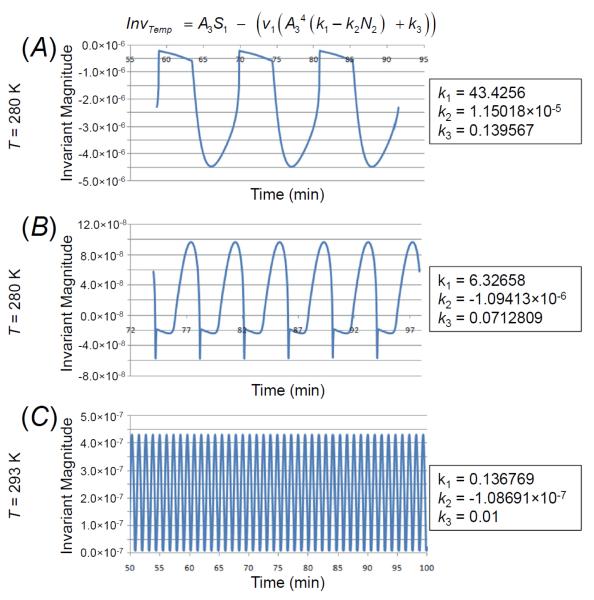
This analysis was carried out for three different temperatures of 280 K, 284 K, and 293 K, as is it known that the period of yeast glycolytic oscillations increases with temperature. An invariant with the same form was extracted for all three temperatures, and contained three coefficients. This invariant had the form I_Temp = A₃S₁ − (v₁ (A₃⁴ (k₁ – k₂N₂) + k₃)) where k₁, k₂, and k₃ are coefficients of the terms in the invariant that vary with temperature. These coefficients are listed to the right of each panel in Figure 8 for all three temperatures, and the time-courses of the corresponding invariants are shown in Figure 8A, Figure 8B, and Figure 8C, respectively. It can be seen that the invariants, computed by solving the equation f(S₁,N₂,A₃,v₁) = 0 for S₁, have small magnitudes relative to the oscillations of the variables themselves in Figure 7.

Figure 8. Description of the invariant expression obtained by means of symbolic regression at three temperatures.

All invariants are equations of the form at the top of the figure. To the right are shown the coefficients of the invariant that was constructed for each temperature using data from the published model. The graphs show the invariant plotted as a function of time for the three temperatures. Note that the invariant oscillates with a period whose length equals that of the model, and has very small magnitude (10⁻⁶ to 10⁻⁸ as shown on the left-side scale) relative to the scale of the oscillations of the system variables (Fig. 7). Numerical experiments have shown that the invariant is sensitive to the number of significant digits included, implying that accuracy can be improved by allowing the symbolic regression algorithm to run for a longer time, leading to an invariant with smaller magnitudes that are even closer to zero.

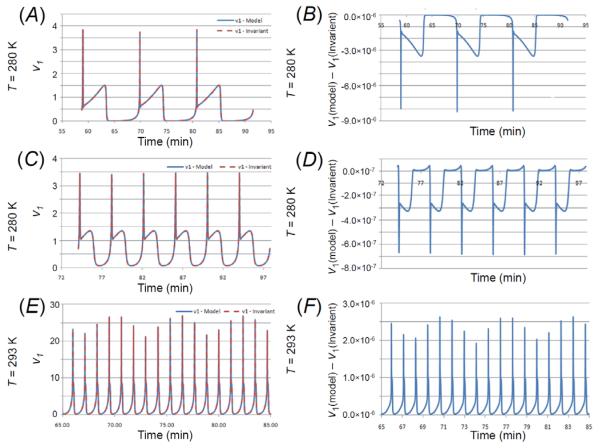
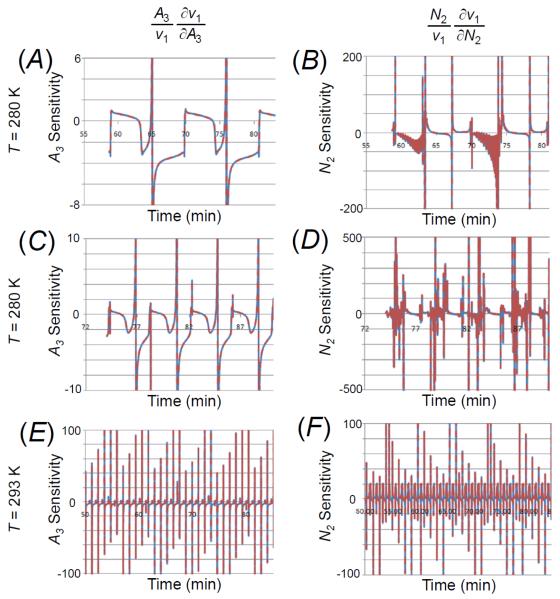
As a demonstration of the utility of the invariant, the variable v₁ can be obtained by solving the invariant expression for v₁, which has been plotted versus time in Figure 9a, 9c, and 9e, respectively, along with the corresponding v₁ from the analytical model. The error between the invariant-derived and analytical model v₁ is shown in Figure 9b, 9d, and 9f, respectively (see also Figure S8 in the Supporting Information). Numerical sensitivities can be obtained from the invariant expression by differentiating with respect to the species of interest. We computed sensitivities of v₁ with respect to A₃ and N₂ using the invariants for the three temperatures, which have been plotted in Figure 10 along with the corresponding difference with respect to the actual model-derived sensitivities (see also Figure S9 and Figure S10 in the Supporting Information).

Figure 9. A comparison of the glucose reaction rate obtained from the invariant and the analytical model.

v₁ is plotted versus time and compared with the v₁ obtained from the analytical model for each of the temperatures considered (panels A, C, and E). Panels B, D, and F show the difference between v₁ derived from the invariant and the v derived from the model. Note that the amplitude of the difference is 10⁻⁵ 1 to 10⁻⁶ smaller than that of either v₁.

Figure 10. The invariant-determined sensitivity of v₁ with respect to A₃ and N₂.

The invariant was used to compute the sensitivity of v₁ with respect to A₃ (equation at the top of the left column) and N₂ (equation at the top of right column) for 280 K (panels A and B); for 284 K (C and D); and for 293 K (E and F).

This result shows that searching for invariants directly can closely model the kinetics of the observed variable and its associated numerical sensitivities without access to any additional internal model structure. It could also be useful to use an existing dynamical system from which to then identify an invariant expression to derive the kinetics and sensitivities, yielding a compact representation of the model’s dynamics.

Modeling limitations

Modeling any dynamical system requires some baseline assumptions, such as the set of state variables with which to model the system [78]. This is a form of implicit prior knowledge, whereas we ordinarily refer to prior knowledge as higher level assumptions, such as known model relationships or structures. We therefore implicitly assume that the system’s key dynamics can be accurately derived and represented by the choice of variables.

While our present implementation does not require chemical mass balance other than what is provided by the ODEs, mass-balance logic could be built into future implementations, albeit with some performance costs. For example, one could assume the current best model and use it to test for constraint violations. Models and experiments could then be penalized or rejected accordingly, focusing the search on the valid equations as shown in [48]. Alternatively, it may be possible to enforce chemical logic [79, 80] by providing the SRA algorithm with an appropriate chemical operator set rather than just the four algebraic operations we allowed.

A potential difficulty when modeling the dynamics of biological systems arises when only a few relevant states in the system can be observed directly. In such cases, these variables must be estimated or inferred in parallel. For example, missing state-variables could be represented by one or more parameters that vary with time (e.g., a Taylor series). Missing states can also be estimated, or sometimes exactly derived, by the available observables – as is done in inferential sensing [81]. Finally, missing states could be encoded directly into the model as latent variables. In this case, an initial condition and a corresponding equation could be included for each latent variable in the model search, and this variable would then be simulated using the observable data to produce the missing time series. If the missing states are ignored completely, the inferred dynamical models will necessarily be higher-level approximations of the system’s dynamics. These are important areas of future research; in this paper, however, we focus on the case where we can observe, or have already accurately estimated, the relevant states.

Finally, searching for a dynamical model from scratch can be computationally intensive. A previous study [36] showed that the performance is dominated by the size of the target expression rather than the dimensionality of the problem. Therefore, systems with an increasing number of state-variables take linearly more computation effort (an additional search for each additional state-variable). However, modeling systems with extremely dense and complex equations (e.g., equations that are difficult to write or even read manually) could require substantially more computational effort with the depth of the expression. Finally, in cases where the algorithm could not deduce exact equations in detail, it can still provide an approximate high-level model of the major dynamics., i.e., an effective or surrogate model that could be used for controlling the system [53].

Discussion

Our experiments tested the proposed method to modify a related or hypothesized mathematical model – suggesting nonlinear terms or modifications – to make it agree with data, or to propose complete dynamical models without a prior model. The modeling process searches the space of symbolic differential equations using symbolic regression and fitness prediction for building mathematical equations and an estimation-exploration algorithm for designing new in silico or even wet-lab experiments to test and refine candidate models. While this method is general enough to be applied to many types of modeling problems, we focus on metabolic networks because they are known to be difficult to model with conventional methods due to their dimensionality, feedback loops, and rich dynamics, yet should be well suited for automated wet-lab experimentation.

Our in silico experiments showed that seeding symbolic regression with a hypothesized model or closely related model can significantly improve the ability and speed to find the exact model for the unknown metabolic network. In contrast to other techniques for model reduction, this approach can also expand a nonlinear model to include features not present in the hypothesized or baseline model. Similarly, the approach can be used to identify a set of initial conditions that could be used to discriminate between two models, i.e., design experiments that can test hypotheses and correct subtle differences using experimental data to identify how a particular metabolic system differs from one described by an established model.

We also demonstrated that our approach could identify the complete set of differential equations without a prior model. All equations were identified reliably with up to 10% observation noise, and five of the seven were identified reliably with up to 50% noise. It is worth noting that this system also represents one of the largest and most realistic experiments where the set of ODEs was identified automatically from data. While the understanding of nonlinear interactions of glycolytic oscillations in yeast has required several years of analysis [73, 74], our results indicate that the proposed method could help accelerate this task.

We also compared the ability of our symbolic regression based-approach to predict future trajectories of the system with the nonlinear regression of two approximate glycolysis models, neural network regression, and the proposed method. While each algorithm modeled the training data well, the proposed method found models that extrapolated accurately to the test data set better than the ordinary regression and neural network methods. This suggests that the method could also be beneficial for numerical simulations in addition to analytical analysis.

Finally, we showed that the symbolic regression approach can be applied to find an invariant expression for the metabolic network. The invariant of the biochemical network identified by the algorithm can be considered to be a closed object embedded in the multidimensional phase space of the model variables. The projection of this surface onto the subspace of the observed variables accurately derived its kinetics and respective sensitivity coefficients. We have yet to identify formally the relationship between the invariants that we derive and invariant manifolds [56, 59-66]. Similarly, we have not yet determined whether the modeling process for the entire system could be accelerated by first searching for a single invariant equation.

We are currently developing the substantial experimental hardware and algorithms required to allow the EEA to conduct wet-lab experiments on yeast and other biochemical systems [53, 82]. A fascinating possibility would be to add near-real-time measurements of the transcriptome into robot metabolic scientists by measuring the expression of selected genes through optical detection of green fluorescent protein (GFP) markers. This would be particularly important when studying systems that demonstrate rapid coupling between metabolic dynamics and gene expression [83, 84]. Expansion of the robot scientists’ techniques to large numbers of genes would require, for example, chemostats capable of providing a steady supply of cells for mRNA analysis, and an mRNA identification technique that was both rapid and required only small numbers of cells. A major challenge will be to infer long-term metabolic network dynamics, where metabolic changes are driven by complex gene regulatory networks and the transcriptional factors that they control, some of which are themselves metabolites, and neither the active network topology nor the network parameters are fixed [85]. At issue would be whether in a wet-lab environment the algorithm can infer a model faster than the system itself evolves, i.e., whether the biological system can be treated as quasistatic during model inference.