Efficient network meta-analysis: a confidence distribution approach

Summary

Network meta-analysis synthesizes several studies of multiple treatment comparisons to simultaneously provide inference for all treatments in the network. It can often strengthen inference on pairwise comparisons by borrowing evidence from other comparisons in the network. Current network meta-analysis approaches are derived from either conventional pairwise meta-analysis or hierarchical Bayesian methods. This paper introduces a new approach for network meta-analysis by combining confidence distributions (CDs). Instead of combining point estimators from individual studies in the conventional approach, the new approach combines CDs which contain richer information than point estimators and thus achieves greater efficiency in its inference. The proposed CD approach can e ciently integrate all studies in the network and provide inference for all treatments even when individual studies contain only comparisons of subsets of the treatments. Through numerical studies with real and simulated data sets, the proposed approach is shown to outperform or at least equal the traditional pairwise meta-analysis and a commonly used Bayesian hierarchical model. Although the Bayesian approach may yield comparable results with a suitably chosen prior, it is highly sensitive to the choice of priors (especially the prior of the between-trial covariance structure), which is often subjective. The CD approach is a general frequentist approach and is prior-free. Moreover, it can always provide a proper inference for all the treatment effects regardless of the between-trial covariance structure.

Introduction

Recent advances in computing and data storage technology have greatly facilitated data gathering from many disparate sources. The demand for efficient methodologies for combining information from independent studies or disparate sources has never been greater. So far, meta-analysis is one of the most, if not the most, commonly used approaches for synthesizing findings from different sources for pairwise comparisons. For example, it is used in medical research for summarizing estimates from a set of randomized controlled trials (RCTs) of the relative efficacy of two treatments (cf. Normand, 1999; Sutton and Higgins, 2008). For more complicated comparative effectiveness research, where the comparisons involve a network of more than two treatments, several generalizations have been developed for combining information from various sources. A useful survey can be found in the report of the ISPOR Task Force on Indirect Treatment Comparisons Good Research Practices (Jansen et al., 2011; Hoaglin et al., 2011) and the references therein. A key advantage of network meta-analysis is that it can perform indirect comparisons among multiple treatments.

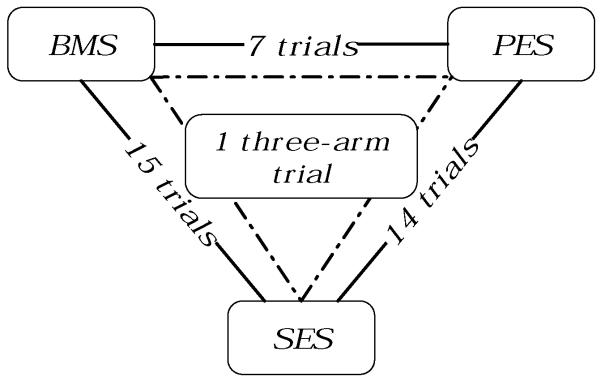
We describe network meta-analysis in a general setting with a working example. In the general setting, the process begins with a systematic research for RCTs that compare treatments for a particular condition. The trials that satisfy a set of eligibility criteria yield a network of evidence, in which each node represents a treatment and each edge represents a direct comparison in one or more trials. We assume that the network is connected, and denote the total number of treatments by p and the number of treatments in trial i by p_i (2 ≤ p_i ≤ p). For example, Stettler et al. (2007) assembled data from 37 trials for comparing the performance of three types of stents, namely EMS, PES and SES, used in patients with coronary artery disease. Figure 1 illustrates the network of comparisons among the three stents. Each stent is connected to the other two through a number of direct comparisons, and these three stents form a network. The primary objective is to assess the effectiveness of these three stents (more broadly all treatments in the network). The network meta-analysis yields estimates of all pairwise comparisons.

Figure 1.

Network of comparisons for bare-metal stents (BMS), paclitaxel-eluting stents (PES), and sirolimus-eluting stents (SES) in 37 trials (Stettler et al., 2007)

There exist several network meta-analysis approaches in the literature. Lumley (2002) introduced a model for combining evidence from trials with pairwise comparisons between treatments. Although this method allows borrowing evidence from indirect comparisons to strengthen the results of direct comparisons, it can be restrictive in practice because it requires that each individual trial be a two-arm trial (i.e., comparing exactly two treatments). Thus, this method cannot deal with multi-arm trials as in the example of Figure 1. Generalizing the method in Smith et al. (1995), Lu and Ades (2004) introduced a network meta-analysis approach using a Bayesian hierarchical model. Although this approach can include multi-arm trials, its inference is quite sensitive to the choice of priors, as seen in the simulation studies in Section 4. More specifically, if the assumption of the prior distribution does not meet the underlying true model (the unknown between-trial covariance structure), the resulting credible interval may fail to achieve the nominal coverage probability, falling far below the nominal level in some cases.

This paper aims to introduce a new network meta-analysis approach that: i) can e ciently synthesize evidence from a number of independent trials on multiple treatments; ii) can include trials with multiple arms; and iii) does not need to specify priors for parameters of interest or other parameters. The proposed new approach is derived from combining multivariate confidence distributions.

To some extent, our proposed CD approach extends of the method developed in Lumley (2002) to include multi-arm trials. Compared with the Bayesian method in Lu and Ades (2004), the proposed CD approach is a pure frequentist approach and it does not require specification of priors. In fact, the proposed CD approach can be viewed as a frequentist counterpart of the Bayesian method of Lu and Ades (2004).

The general idea of combining CDs has been developed in Singh et al. (2005) and Xie et al. (2011). The concept of CD and its utility in statistical inference have been researched intensely; see, e.g., Schweder and Hjort (2002) and Singh et al. (2005, 2007). A detailed survey of the recent developments on CD can be found in Xie and Singh (2013). Roughly speaking, a CD bases inference on a sample-dependent distribution function, rather than a point or an interval, on the parameter space. A CD can be viewed as a frequentist “distribution estimator” of an unknown parameter, as described in Xie and Singh (2013) and Cox (2013). As a distribution function, a CD naturally contains more information than a point or interval estimator, and is thus a more versatile tool for inference. For example, point or interval approaches may fail to provide inference for an odds ratio when the 2x2 table observes zero events, but the CD approach remains valid, as shown in Liu et al. (2012). CDs have been demonstrated in Singh et al. (2005) and Xie et al. (2011) to be especially useful for combining information on a single parameter. In particular, Xie et al. (2011) has shown not only that the CD combining approach can provide a unifying framework for almost all univariate meta-analysis applications, but it can also provide new estimates that achieve desirable properties such as high efficiency and robustness.

Network meta-analysis generally involves multiple parameters, and the information on each parameter may have non-negligible impact on the inferences for other parameters. To fully utilize the joint information on multiple parameters, we construct multivariate joint CD functions for the entire set of parameters from each study. The combination of these joint CD functions leads to a novel frequentist approach to network meta-analysis.

Our numerical studies show that the proposed CD approach compares favorably with, and is often superior to, traditional meta-analysis and the hierarchical Bayesian network meta-analysis method proposed in Lu and Ades (2004). Specifically, in comparison with the traditional method, the CD method is more efficient because it also uses indirect evidence. In comparison with the Bayesian method, the CD approach is prior-free and can always provide a proper inference (i.e., confidence intervals with correct coverage rates) for treatment effects, regardless of the between-trial covariance structure. Moreover, our simulation studies show that the performance of the Bayesian approach is sensitive to the choice of prior distributions, which should be chosen to reflect the underlying between-trial covariance structure.

The paper is organized as follows. Section 2 reviews the concept of CD and develops a general method for combining multivariate normal CDs to facilitate network meta-analysis. Section 3 uses two real data examples to illustrate the proposed CD approach in the analysis of a three-treatment network, and to compare it with the traditional meta-analysis and Bayesian network meta-analysis. In Section 4, several simulation studies are presented to show that the proposed CD approach can always provide proper inferences for all treatments in the network. These inference results are also compared with those from the traditional and Bayesian network meta-analysis approaches. Moreover, we devise a simple adaptive CD approach to address possible inconsistent (or contradictory) evidence from indirect and direct comparisons. This adaptive approach can alleviate undue influence from indirect comparisons whose evidence contradicts the direct comparisons. Section 5 provides a summary and further remarks.

2 A CD approach for network meta-analysis

Assume that the network comprises k independent studies (or clinical trials) and involves the effects of p treatments, denoted by the vector θ ≡ (θ₁, … , θ_p)^T. The individual studies may have involved only a subset of the p treatments. More specifically, the i-th study involves p_i (p_i ≤ p) treatments. If p_i < p, the i-th study provides only partial information about θ, in the sense that only the p_i-dimensional parameter θ_i ≡ A_iθ is identifiable. Here A_i is the p_i × p selection matrix associated with the i-th study and is obtained by removing from the p × p identity matrix (or, more generally, any p × p orthogonal matrix A) the rows corresponding to the parameters which are missing in the i-th study. In this paper, we propose the following multivariate random-effects model for network meta-analysis, which can be viewed as a multivariate extension of the univariate hierarchical random-effects model reviewed in Normand (1999):

$$y_i\mid {\theta }_i{\Sigma }_i\stackrel{\mathrm{ind}}{\sim }N({\theta }_i,{\Sigma }_i),{\theta }_i\mid \theta ,\mathrm{S}\stackrel{\mathrm{ind}}{\sim }N({\mathrm{A}}_i\theta ,{\mathrm{A}}_i{\mathrm{SA}}_i^{\mathrm{T}}),i=1,2,\dots ,k,$$ (1)

where y_i is a summary statistic from the i-th study, Σ_i is the covariance matrix of y_i, and S is the covariance matrix of random-effects distribution. In practice, it has been assumed in conventional meta-analysis (see, for example, Normand (1999)) that samples from individual studies may not be available, but their summary statistics y_i’s (often sufficient statistics of θ_i’s) are. The same assumption is also made in the hierarchical random-effects model (1). Note that, if model (1) holds only asymptotically when the sample size of each individual study n_i → 1, the results provided in this paper also hold only asymptotically. In any event, model (1) covers a broad range of settings, including many non-normal ones. A case in point is the multinomial real data example in Section 3.

In this paper, the number of treatments of interest p is assumed to be finite, while the number of studies k is allowed to be either finite or infinite.

Different from the usual meta-analysis applications, a key question in network meta-analysis is how the information on θ_i (which may provide only partial information on θ) can be integrated to make efficient inference about the entire θ. Our proposed approach of combining multivariate normal CDs for θ_i’s can provide a solution.

Before presenting our CD approach for network meta-analysis, we review the procedure for combining CDs in the univariate case in Section 2.1 and then extend it to the multivariate case in Section 2.2.

2.1 CD approach for univariate meta-analysis

When the parameter of interest is univariate, model (1) simplifies to model (2)-(3) in Normand (1999), namely,

$$y_i\mid {\theta }_i{\sigma }_i^2\stackrel{\mathrm{ind}}{\sim }N({\theta }_i,{\sigma }_i^2),{\theta }_i\mid \theta ,{\tau }^2\stackrel{\mathrm{ind}}{\sim }N(\theta ,{\tau }^2),i=1,2,\dots ,k,$$ (2)

where θ_i is the study-specific mean (random-effect) and θ and τ² are hyper-parameters for θ_i. Again, y_i is only a summary statistic of which the individual sample may not be necessarily available. In addition, model (2) may hold only asymptotically.

For the univariate case, all current meta-analysis estimators used in practice (c.f., Table IV of Normand, 1999) are nothing but various versions of weighted average of the summary statistics y_i’s. Following the CD concept, those estimators can all be obtained through the unifying framework developed in Xie et al. (2011). Xie et al. (2011) further showed that the CD approach is far more flexible and can reach beyond the conventional methods of weighted averages, including for example the development of robust and non-linear combining approaches.

In contract with the usual point or interval estimator, a CD can be viewed as a frequentist “distribution estimator” of a given parameter of interest. It has been loosely referred to as a distribution function on the parameter space that can represent confidence intervals of all levels for a given parameter of interest. More specifically, the following formal definition of CD is proposed in Schweder and Hjort (2002) and Singh et al. (2005):

Definition 1Suppose Θ is the parameter space of the unknown parameter of interest θ, and χ is the sample space corresponding to data X = {x₁, …, x_n}. Then a function H(·) = H(X,·) on χ × Θ → [0, 1] is a confidence distribution (CD) if:

1. For each given X ∈ χ, H(·) is a continuous cumulative distribution function on Θ; and

2. At the true parameter value θ= θ₀, H(θ₀) = H(X, θ₀), as a function of the sample X, follows the uniform distribution U [0, 1].

The function H(·) is an asymptotic CD (aCD) if the U[0, 1] requirement holds only asymptotically and the continuity requirement on H(·) is dropped.

In other words, a confidence distribution is a function defined on both the parameter space and the sample space, satisfying requirements (i) and (ii). Requirement (i) simply says that a CD should be a distribution on the parameter space. Requirement (ii) imposes some restrictions to facilitate desirable frequentist properties such as unbiasedness, consistency and/or efficiency. The CD concept is broad, covering examples from regular parametric (fiducial distribution) to bootstrap distributions, significance functions (also called p-value functions), normalized likelihood functions, and, in some cases, Bayesian priors and posteriors; see, e.g., Singh et al. (2007) and Xie and Singh (2013). A CD can be used to draw various inferences for the unknown parameter. For example, the median/mean of the distribution function H(·) can be used as a point estimator of θ, and the interval (−∞, H⁻¹(1 − ∞))forms a level (1 − α) confidence interval, an immediate consequence Requirement (ii).

Example 1 (CDs for univariate normal mean) Let {y_i, i = 1, …, n} be an iid sample from N(θ, σ²) with mean ȳ. Suppose that the parameter θ is of primary interest. If σ² is known, then $H_{\Phi }\left(\theta \right)=\Phi \left(\sqrt{n}\right(\theta -\stackrel{‒}{y})∕\sigma )$ satisfies the two requirements in Definition 1, and it is a CD for θ. If σ² is unknown, one can show that $H_t\left(\theta \right)=F_{t_{n-1}}\left(\sqrt{n}\right(\theta -\stackrel{‒}{y})∕s)$ is a CD for θ. Here σ² is the sample variance, and F_tn−1 is the cumulative distribution function of the student-t distribution with (n − 1) degrees of freedom. However, $H_A\left(\theta \right)=\Phi \left(\sqrt{n}\right(\theta -\stackrel{‒}{y})∕s)$ is only an asymptotic CD for θ.

To combine individual CDs, say, H_i(θ) for i = 1, …, k, Singh et al. (2005) proposed a general recipe that uses a coordinate-wise monotonic function that maps the k-dimensional cube [0, 1]^k to the real line. Specifically, a combined CD can be constructed following

$$H^{\left(c\right)}\left(\theta \right)=G^{\left(c\right)}\left\{g^{\left(c\right)}\right(H_1\left(\theta \right),\dots ,H_k\left(\theta \right)\left)\right\},$$ (3)

where the function G^(c) is defined as G^(c)(t) = Pr{g^(c)(U₁, …, U_k) ≤ t} in which U₁, …, U_k are independent U[0, 1] random variables. Xie et al. (2011) applied this general recipe to meta-analysis, with a special choice of g^(c):

$$g^{\left(c\right)}(u_1,\dots ,u_k)={\tilde{w}}_1{a}_0\left(u_1\right)+\dots +{\tilde{w}}_k{a}_0\left(u_k\right),$$ (4)

where a₀(·) is a given monotonic function and ${\tilde{w}}_i\ge 0$, with at least one ${\tilde{w}}_i\ne 0$, are generic weights for the combination. Xie et al. (2011) and subsequent research showed that, with suitable choices of g^(c), almost all combining methods currently used in meta-analysis can be unified under the framework of Equation (3), including p-value combination methods, model-based meta-analysis (fixed-effect and random-effects models), the Mantel-Haenszel method, Peto’s method, and also the method in Tian et al. (2009) by combining confidence intervals.

For the special model in (2), one can construct $H_i\left(\theta \right)=\Phi \left(\right(\theta -y_i)∕{({\sigma }_i^2+{\tau }^2)}^{1∕2})$ based on the ith study and take a₀(·) = Φ⁻¹(·) and ${\tilde{w}}_i=1∕{({\sigma }_i^2+{\tau }^2)}^{1∕2}$ in (4). Here τ² is assumed known. If τ² is unknown, one can replace it with the DerSimonian and Laird estimator ${\widehat{\tau }}_{\mathrm{DL}}^2$ (DerSimonian and Laird, 1986) or preferably the restricted-maximum-likelihood estimator ${\widehat{\tau }}_{\mathrm{REML}}^2$. Then the combined CD function for θ is

$$H^{\left(c\right)}\left(\theta \right)=\Phi \left({\left(\sum _{i=1}^k\frac{1}{{\sigma }_i^2+{\tau }^2}\right)}^{1∕2}(\theta -{\widehat{\theta }}^{\left(c\right)})\right),$$ (5)

where ${\widehat{\theta }}^{\left(c\right)}=\left\{{\Sigma }_{i=1}^k\frac{y_i}{{\sigma }_i^2+{\tau }^2}\right\}∕\left\{{\Sigma }_{i=1}^k\frac{1}{{\sigma }_i^2+{\tau }^2}\right\}$. The combined CD function is normal with mean ${\widehat{\theta }}^{\left(c\right)}$ and variance $s_c^2={\left\{{\Sigma }_{i=1}^k\frac{1}{{\sigma }_i^2+{\tau }^2}\right\}}^{-1}$, which is ready for making point estimates and constructing confidence intervals for the parameter θ.

From Definition 1, a CD function H(·) is a cumulative distribution function on the parameter space for each given sample X_n. Thus, we can construct a random variable ξ defined on χ × Θ such that, conditional on the sample, ξ has the distribution H(·). We call this random variable ξ a CD random variable (see, e.g., Singh et al., 2007; Xie and Singh, 2013). Conversely, suppose we have a CD random variable ξ ∈ χ × Θ whose conditional distribution, conditional on the sample, has a cumulative distribution function H(·). Then H(·) is a CD for the parameter of interest θ. In special cases when τ² is replaced by ${\widehat{\tau }}_{\mathrm{DL}}^2$ or ${\widehat{\tau }}_{\mathrm{REML}}^2$, the inference by (5) is, respectively, the same as the conventional method of moments or the REML approach that are listed in Table IV of Normand (1999).

We can express the normal CD combination (5) as a combination of CD random variables. Specifically, for a CD-random variable ${\xi }_i\mid y_i\sim H_i\left(\theta \right)=\Phi \left(\right(\theta -y_i)∕{({\sigma }_i^2+{\tau }^2)}^{1∕2})$ derived from the i-th study, we can define ${\xi }^{\left(c\right)}={\Sigma }_{i=1}^k{w}_i{\xi }_i$, where $w_i=1∕({\sigma }_i^2+{\tau }^2)$, and its corresponding combined CD is

$$H^{\left(c\right)}\left(\theta \right)=\mathrm{Pr}({\xi }^{\left(c\right)}\le \theta \mid data),\text{for any}\theta \in ϴ.$$ (6)

It is straightforward to show that the H^(c)(·) defined in (6) is the same as the one defined in (5).

The concept of CD random variable has been investigated in several recent publications. For example, Xie and Singh (2013) explored the connection of CD random variables with boot-strap estimators when the bootstrap approach applies. Hannig and Xie (2012) discussed the association of a CD random variable with the so-called belief random set, a fundamental concept in the Dempster-Shafer theory of belief functions (cf. Dempster, 2008; Martin and Liu, 2013).

2.2 A general procedure to combine multivariate normal CDs

Constructing and combining CDs for multi-dimensional parameters is not a straightforward extension of the univariate case. One difficulty is that the cumulative distribution function is not a useful notion in the multivariate case, because (a) the region F(x) ≤ α is not of main interest and (b) the property $F\left(\mathrm{X}\right)\stackrel{L}{=}U[0,1]$ when $\mathrm{X}\stackrel{L}{=}F$ does not hold in ${\mathfrak{R}}^p$ (Singh et al., 2007). Research thus far suggests that we either limit our interest to center-outward confidence regions (instead of all Borel sets) in the p × 1 parameter space or use asymptotic normality; see Xie and Singh (2013) and also De Blasi and Schweder (2012). In the present context, it suffices to consider only the multivariate normal CDs because individual CDs are based on asymptotic normality. We use a multivariate normal CD definition proposed in Singh et al. (2007). Intuitively, a distribution function H(·) is a multivariate normal CD for a p × 1 vector θ if and only if the projected distribution of H(·) on any direction $\lambda \in {\mathfrak{R}}^p$, ||λ||₂ = 1, is a univariate normal CD for λ^Tθ. Here is a formal definition of a multivariate normal CD:

Definition 2 Let ξ be a random vector on ${\mathfrak{R}}^p$. For any given p × 1 vector λ, ||λ||² = 1, we denote by H_λ(·) the conditional distribution of λ^Tξ given X. We also denote by H(·) the conditional distribution of ξ given X. Then we call H(·) the multivariate normal CD (or, asymptotic multivariate normal CD) for a p × 1 parameter vector θ if and only if, for any given λ, H_λ(·) is a univariate normal CD (or asymptotic CD) function for λ^Tθ. Also, the random vector ξ is called a CD random vector for θ.

Example 2 (CDs for multivariate normal mean) Suppose x_i, i = 1, …, n are identically and independently distributed observations from a multivariate normal distribution with mean θ and covariance matrix Σ. If Σ is known, then the sample-dependent distribution N(y, Σ) is a multivariate normal CD function for θ, where y = x̄ is the sample mean. If Σ is unknown but can be estimated consistently, say by $\widehat{\Sigma }$, then the sample-dependent distribution $N(y,\widehat{\Sigma })$ is an asymptotic multivariate normal CD function for θ.

The CD combination method for the multivariate case cannot be easily specified by following (3) and (4), especially under the setting of (1), where p_i may differ. Instead, we utilize the concept of CD random vector and an extension of (6) to propose the following scheme for combining multivariate normal CDs.

Theorem 1 Let H_i(_i) H_i(X_i, θ_i), i = 1 …, k are multivariate normal CD functions for the multivariate parameters θ_i from k independent samples X_i, where θ_i = A_iθ for the same p-dimensional target parameter vector θ. Additionally, let ξ_i be the CD random vector for θ_i. For any $\mathrm{t}\in {\mathfrak{R}}^p$, we define

$$H^{\left(c\right)}\left(\mathrm{t}\right)=\mathrm{Pr}\left\{{\left(\sum _{i=1}^k{W}_i\right)}^{-1}\sum _{i=1}^k{W}_i{\mathrm{A}}_i^{+}{\xi }_i\le \mathrm{t}\mid {\mathrm{X}}_1,\dots ,{\mathrm{X}}_k\right\},$$ (7)

where ${\mathrm{A}}_i^{+}$ is the Moore–Penrose pseudo-inverse of A_i. Then H^(c)(·) = H(X₁, … ,X_k; ·) is a multivariate normal CD for θ provided the following conditions hold:

1. Each p × p matrix W_i is positive semi-definite.

2. e(W_i) = V_i, where e(W_i) is the column space of W_i and V_i is the row space of A_i.

3. $V_1+V_2+\dots ,+V_k={\mathfrak{R}}^p$, where $V_1+V_2+\dots ,+V_k\triangleq \{{\Sigma }_{i=1}^k{v}_i\mid v_i\in V_i,i=1,\dots ,k\}$.

In Theorem 1, conditions (2) and (3) state that, even if rank(A_i) < p for all i, so that θ is not identifiable in any individual study, we can still derive a multivariate normal CD for θ as long as the treatments are connected in a network.

Recall the multivariate model introduced in (1). We first consider the case in which Σ_i and S are known. From Example 2, we know that $N(y_i,{\Sigma }_i+{\mathrm{A}}_i{\mathrm{SA}}_i^{\mathrm{T}})$ is a multivariate normal CD function for θ_i based on the i-th study. Let ξ_i be the corresponding CD random vector for inference on θ_i and $W_i={\mathrm{A}}_i^{+}{({\Sigma }_i+{\mathrm{A}}_i{\mathrm{SA}}_i^{\mathrm{T}})}^{-1}{\mathrm{A}}_i$. It follows that ${\left({\Sigma }_{i=1}^k{E}_i\right)}^{-1}{\Sigma }_{i=1}^k{W}_i{\mathrm{A}}_i^{+}{\xi }_i$ is normally distributed with mean vector ${\widehat{\theta }}^{\left(c\right)}={\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}\left({\Sigma }_{i=1}^k{W}_i{\mathrm{A}}_i^{+}{y}_i\right)$ and variance ${\mathrm{S}}_c={\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}$, given the sample. Thus, following the recipe in Equation (7), the combined CD for θ is

$$H^{\left(c\right)}\left(\theta \right)=\Psi \left({\mathrm{S}}_c^{-1∕2}\right(\theta -{\widehat{\theta }}^{\left(c\right)}\left)\right)$$ (8)

where Ψ(·) is the cdf of the standard p×1 multivariate normal distribution function. Conditions (1) and (2) of Theorem 1 are satisfied by the specification of W_i, and condition (3) is satisfied as long as the comparisons involved in the studies form a connected network. Based on the combined multivariate CD function in (8), we can use ${\widehat{\theta }}^{\left(c\right)}$ as a point estimator for θ with variance S_c. Furthermore, inferences on any linear contrasts λ^Tθ of θ can be obtained from λ^Tξ^(c), where ξ^(c) follows the distribution specified in Equation (8).

If Σ_i and S are unknown, we can replace them with the sample estimators ${\widehat{\Sigma }}_i$ and S_REML. Then, as long as these estimators are consistent, the distribution $N(y_i,{\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{REML}{\mathrm{A}}_i^{\mathrm{T}})$ is asymptotically a multivariate normal CD for θ_i. Here ${\widehat{\Sigma }}_i$ is the sample covariance matrix, and S_REML is the restricted-maximum-likelihood estimator of the heterogeneity between studies. As a result, the combined CD function (8) is an asymptotic multivariate normal CD for θ with Σ_i and S replaced by ${\widehat{\Sigma }}_i$ and S_REML, respectively. For the estimation of S, Jackson et al. (2010) developed a direct extension of the DerSimonian and Laird estimator of heterogeneity to multivariate case. Hereafter, we denote by S_DL and S_REML respectively the estimator derived from Jackson et al. (2010) and the restricted-maximum-likelihood estimator. We apply and examine both estimators in our numerical study of real examples and simulations in Sections 3 and 4. Further discussions on the performance of the DL and REML estimators for the heterogeneity in univariate random-effects models can be found in Sidik and Jonkman (2007) and Thorlund et al. (2011).

As shown in Liu (2012) and Yang (2013), if individual samples in all studies are given, our approach in (8) yields exactly the same or asymptotically equivalent results (depending on whether (1) holds exactly or approximately) as the likelihood approach, and thus the two approaches have the same statistical accuracy. We stress that our approach uses only summary statistics and does not need individual observations, which generally is the setting in conventional meta-analysis. One can also use an approximate likelihood approach by treating y_i’s as if they are “individual” observations. This in fact yields the same results as our CD approach.

One advantage of our CD approach is its flexibility, in that, for example, one can easily adapt the approach to address possible inconsistent (or contradictory) evidence from indirect and direct comparisons, as illustrated in Section 4. Another advantage of our approach is that it uses explicit expressions, so its computational cost is minimal. The discussion and comparison with likelihood-based approaches are similar to those provided in Xie et al. (2011) for univariate meta-analysis problems.

Note that our model and approach cover many non-normal cases so long as the summary statistic y_i’s are normal or asymptotically normally distributed, such is the case with the real data example in Section 3 below.

3 Real data examples

In this section, we illustrate the proposed CD approach for network meta-analysis using two real data examples, one on coronary artery disease and the other on cirrhosis. For comparison, we also include the traditional pairwise meta-analysis and the Bayesian hierarchical model.

3.1 An example on coronary artery disease (CAD)

Stettler et al. (2007) used data from a network of 37 trials to compare the performance of three types of stent: bare metal stent (BMS), sirolimus-eluting stent (SES), and paclitaxel-eluting stent (PES), in patients with coronary artery disease. Each trial involved at least two of the three treatments; we analyze the data on a negative outcome, whether patients required target lesion revascularisation (TLR) within one year (cf. Figure 1). One trial, TAXUS I, had zero events and is thus excluded from the analysis. Of the remaining 36 trials, listed in Table 1, 15 trials compared BMS with SES, 6 trials compared BMS with PES, 14 trials compared SES with PES, and 1 trial compared all three treatments. The network is connected, so simultaneous inference on the treatment effects is possible.

Table 1.

CAD Trial Data, Target Lesion Revascularisation at 1 year

Study	BMS (A)		SES (B)		PES (C)
	rij	nij	rij	nij	rij	nij
BASKET	35	281	25	264	25	281
C-SIRIUS	11	50	2	50	—	—
DECODE	8	29	5	54	—	—
DIABETES	27	80	6	80	—	—
E-SIRIUS	44	177	8	175	—	—
Ortolani 2007	11	52	6	52	—	—
Pache 2005	51	250	25	250	—	—
PRISON II	20	100	4	100	—	—
RAVEL	16	118	1	120	—	—
RRISC	10	37	6	38	—	—
SCANDSTENT	47	159	4	163	—	—
SCORPIUS	20	95	5	95	—	—
SESAMI	19	160	7	160	—	—
SES-SMART	27	128	9	129	—	—
SIRIUS	106	525	26	533	—	—
TYPHOON	45	357	13	355	—	—
HAAMUS-TENT	9	82	—	—	3	82
PASSION	23	309	—	—	16	310
TAXUS II	39	269	—	—	13	260
TAXUS IV	96	652	—	—	28	662
TAXUS V	107	579	—	—	62	577
TAXUS VI	46	227	—	—	19	219
Cervinka 2006	—	—	1	37	2	33
CORPAL	—	—	22	331	25	321
Han 2006	—	—	9	202	11	196
ISAR-DESIRE	—	—	14	100	22	100
ISAR-DIABETES	—	—	9	125	15	125
ISAR-SMART3	—	—	16	180	29	180
LONG DES II	—	—	6	250	18	250
Petronio 2007	—	—	1	42	1	43
PROSIT	—	—	3	116	9	115
REALITY	—	—	44	684	43	669
SIRTAX	—	—	30	503	54	509
SORT OUT II	—	—	40	1065	46	1033
TAXi	—	—	4	102	2	100
Zhang 2006	—	—	14	225	16	187

3.1.1 A multivariate random-effects model

We use treatments A, B, and C to denote the three types of stents BMS, SES and PES, respectively. We use T_i to denote the set of treatments compared in the i-th trial; for example, T_i = {A, C} for TAXUS IV. Further, let n_ij and r_ij be the number of total patients and number of patients who experienced a TLR in the i-th study with treatment j. Then with a binary individual responses we would assume

$$r_{ij}\mid p_{ij}\sim \text{Binomial}(n_{ij},p_{ij}),i=1,2,\dots ,36,j\in T_i$$ (9)

where p_ij denotes the probability that a patient on treatment j experiences an event in the i-th trial.

The target parameter is p = (p_A, p_B, p_C)^T, the overall probability of an event for BMS, SES, and PES, respectively. In practice, one often applies a log transformation to the observed odds of an event. Owing to the rapid convergence to a normal distribution on the log-odds scale, it is customary to consider a general random-effects model for θ_i = (logit(p_ij))^T, ∀_j ∈ T_i with parameter θ = (logit(p_A), logit(p_B), logit(p_C))^T; cf. DerSimonian and Laird (1986); Normand (1999). Here, logit(p) = log(p/(1 − p)). Specifically, we have

$$\begin{array}{cc}\hfill \text{level 1}:& r_{ij}\mid p_{ij}\sim \text{Binomial}(n_{ij},p_{ij}),i=1,2,\cdots ,36,j\in T_i\hfill \\ \hfill \text{level 2}:& {\theta }_i\sim N({\mathrm{A}}_i\theta ,{\mathrm{A}}_i{\mathrm{SA}}_i^T)\hfill \end{array}$$ (10)

where A_i is the selection matrix associated with T_i; for example, ${\mathrm{A}}_i=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right]$ if T_i = {A, B}, ${\mathrm{A}}_i=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$ if T_i = {A, C}, ${\mathrm{A}}_i=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$ if T_i = {B,C}, and A_i = I₃ if T_i = {A,B,C}.

Further, let $y_{ij}=\log \left(\frac{r_{ij}}{n_{ij}-r_{ij}}\right)$, ${\widehat{\sigma }}_{ij}^2=\frac{1}{r_{ij}}+\frac{1}{n_{ij}-r_{ij}}$ and y_i = [y_ij, j ∈ T_i]^T ${\widehat{\Sigma }}_i=\mathrm{diag}({\widehat{\sigma }}_{ij}^2,j\in T_i)$. Then an asymptotically equivalent model is

$$\begin{array}{cc}\hfill \text{level 1}:& y_i\mid {\theta }_i\sim N({\theta }_i,{\widehat{\Sigma }}_i),i=1,2,\dots ,36\hfill \\ \hfill \text{level 2}:& {\theta }_i\sim N({\mathrm{A}}_i\theta ,{\mathrm{A}}_i{\mathrm{SA}}_i^{\mathrm{T}}).\hfill \end{array}$$ (11)

Finally, if that our primary concern is the efficacy of SES vs BMS, the parameter of interest is the log-odds ratio reflecting the relative efficacy of treatment B vs A, that is δ_AB ≡ θ_B − θ_A. We proceed to compare the results obtained from the proposed CD procedure with those-from the traditional pairwise meta-analysis and the Bayesian network meta-analysis.

3.1.2 The CD approach

Consider the random-effects model in (11). We estimate the covariance matrix S by the restricted-maximum-likelihood estimator S_REML. We can construct a multivariate normal aCD function for θ_i based on the i-th individual study, namely $N(y_i,{\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{\mathrm{REML}}{\mathrm{A}}_i^{\mathrm{T}})$. We use ${\xi }_i\mid y_i\sim N(y_i,{\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{\mathrm{REML}}{\mathrm{A}}_i^{\mathrm{T}})$ to denote the associated CD random variable and take $W_i={\mathrm{A}}_i^{+}{({\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{\mathrm{REML}}{\mathrm{A}}_i^{\mathrm{T}})}^{-1}{\mathrm{A}}_i$. Then, by (8), $H^{\left(c\right)}\left(\theta \right)=\Psi \left({\mathrm{S}}_c^{-1∕2}\right(\theta -{\widehat{\theta }}^{\left(c\right)}\left)\right)$ is the combined CD for θ, where ${\widehat{\theta }}^{\left(c\right)}={\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}\left({\Sigma }_{i=1}^k{W}_i{\mathrm{A}}_i^{+}{y}_i\right)$ and ${\mathrm{S}}_c={\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}$. Since we have ${\mathrm{A}}_i^{+}={\mathrm{A}}_i^{\mathrm{T}}$ in the current case, we can replace ${\mathrm{A}}_i^{+}$ with ${\mathrm{A}}_i^{\mathrm{T}}$ in the above formulas.

To make inferences for δ_AB ≡ θ_B − θ_A, we can use the marginal distribution of ${\lambda }_{AB}^{\mathrm{T}}{\xi }^{\left(c\right)}$ where λ_AB = (−1, 1, 0)^T and ${\xi }^{\left(c\right)}\mid data\sim N({\widehat{\theta }}^{\left(c\right)},{\mathrm{S}}_c)$. Therefore, the point estimator ${\widehat{\delta }}_{AB}$ and its variance based on the CD procedure are

$$\begin{array}{cc}\hfill {\widehat{\delta }}_{AB}=& {\lambda }_{AB}^{\mathrm{T}}{\left\{\sum _{i=1}^k{\mathrm{A}}_i^{+}{({\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{\mathrm{REML}}{\mathrm{A}}_i^{\mathrm{T}})}^{-1}{\mathrm{A}}_i\right\}}^{-1}\sum _{i=1}^k{\mathrm{A}}_i^{+}{({\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{\mathrm{REML}}{\mathrm{A}}_i^{\mathrm{T}})}^{-1}{\mathrm{A}}_i{\mathrm{A}}_i^{\mathrm{T}}{y}_i\hfill \\ \hfill & \mathrm{var}\left({\widehat{\delta }}_{AB}\right)={\lambda }_{AB}^{\mathrm{T}}{\left\{\sum _{i=1}^k{\mathrm{A}}_i^{+}{({\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{\mathrm{REML}}{\mathrm{A}}_i^{\mathrm{T}})}^{-1}{\mathrm{A}}_i\right\}}^{-1}{\lambda }_{AB}.\hfill \end{array}$$

In practice, we might also be interested in simultaneous inferences on, say, q linear combinations of θ, e.g., Qθ where $\mathrm{Q}\in {\mathfrak{R}}^{q\times p}$. The Bayesian approach often uses the marginal posterior distribution of Qθ as the basis for statistical inference. Similarly, to draw inferences for θ, the proposed CD network meta-analysis approach can use the marginal distribution of Qξ^(c) given the data. Here ξ^(c) is the CD random vector associated with the combined CD function H^(c)(·) for θ.

3.1.3 Traditional pairwise meta-analysis

A traditional meta-analysis for such a problem uses only the direct evidence, e.g., clinical trials that explicitly compared BMS vs SES; see, e.g., Simmonds and Higgins (2007) and Hoaglin et al. (2011). Let ${\widehat{\delta }}_{AB,i}=\log \left(\frac{r_{iB}(n_{iA}-r_{iA})}{r_{iA}(n_{iB}-r_{iB})}\right)$ for A,B ∈ T_i. A random-effects model (Der-Simonian and Laird, 1986) is considered:

$$\begin{array}{cc}\hfill \text{level 1}:& {\widehat{\delta }}_{AB,i}\sim N({\delta }_{AB,i},{\sigma }_{AB,i}^2),is.t.A,B\in T_i\hfill \\ \hfill \text{level 2}:& {\delta }_{AB,i}\sim N({\delta }_{AB},{\tau }_{AB}^2).\hfill \end{array}$$ (12)

An overall estimate of the common log-odds ratio δ_AB, based on the direct evidence, is often a weighted average of the estimates ${\widehat{\delta }}_{AB,i}$ from individual studies (Hardy and Thompson, 1996):

$${\widehat{\delta }}_{AB,direct}=\frac{{\Sigma }_i{w}_i{\widehat{\delta }}_{AB,i}}{{\Sigma }_i{w}_i}\text{with}\mathrm{var}\left({\widehat{\delta }}_{AB}\right)=\frac{1}{{\Sigma }_i{w}_i},$$ (13)

where the weight w_i is often taken as the empirical weight determined by the reciprocal of the variance ${\sigma }_{AB,i}^2$ adjusted to incorporate the heterogeneity ${\tau }_{AB}^2$, for example $w_i=1∕({\sigma }_{AB,i}^2+{\tau }_{AB}^2)$, as suggested in DerSimonian and Laird (1986).

In practice, when the variance ${\sigma }_{AB,i}^2$ and the heterogeneity ${\tau }_{AB}^2$ are unknown, they are often replaced by their corresponding estimates ${\widehat{\sigma }}_{AB,i}^2$ and ${\widehat{\tau }}_{AB}^2$, where ${\widehat{\sigma }}_{AB,i}^2=\frac{1}{r_{iA}}+\frac{1}{n_{iA}-r_{iA}}+\frac{1}{r_{i}B}+\frac{1}{n_{iB}-r_{iB}}$, provided that r_ij ≠ 0 and r_ij ≠ r_ij, and ${\widehat{\tau }}_{AB}^2$ is the REML estimate.

Similarly, we can obtain estimates ${\widehat{\delta }}_{AC}$ and ${\widehat{\delta }}_{BC}$ for the pairwise comparisons of BMS vs PES and SES vs PES, respectively, based on the 7 and 15 trials that compared them directly. Then an indirect comparison of BMS vs SES can be obtained by taking

$${\widehat{\delta }}_{AB,direct}={\widehat{\delta }}_{AC}-{\widehat{\delta }}_{BC}\text{and}\mathrm{var}\left({\widehat{\delta }}_{AB}\right)=\mathrm{var}\left({\widehat{\delta }}_{AC}\right)+\mathrm{var}\left({\widehat{\delta }}_{BC}\right).$$ (14)

We can then combine the ${\widehat{\delta }}_{AB,direct}$,direct and ${\widehat{\delta }}_{AB,indirect}$,indirect to obtain an estimator that integrates the two sources of information, provided that the direct and indirect comparisons are consistent with each other or at least not contradictory. Here is a simple illustration of inconsistent/contradictory evidence: the direct comparison concludes that the effect of treatment X is larger than that of treatment Y, but the indirect comparison concludes the opposite. Some discussion on issues of inconsistent evidence in network meta-analysis can be found in Lumley (2002), Lu and Ades (2006), and Dias et al. (2010).

Although one can always apply the procedure above to combine the direct and indirect estimates, this procedure splits the three-arm trial into three two-arm trials and uses them for three difference estimates. This is a drawback for traditional pairwise meta-analysis — Trials with more than two arms cannot be fully incorporated in the meta-analysis unless they are split into multiple two-arm trials. Those two-arm trials are treated as if they were independent; whereas they came from the same trial. Consequently, such a network meta-analysis often incurs bias and loss of efficiency, as observed in Jansen et al. (2011) and Hoaglin et al. (2011). Taking into account this drawback, we consider ${\widehat{\delta }}_{AB,direct}$ and ${\widehat{\delta }}_{AB,indirect}$ as two separate estimators of δ_AB in the analysis in later sections.

We show later that the CD approach can combine the direct and indirect evidence for δ_AB efficiently, provided that the observed evidences from the direct and indirect comparisons are consistent with each other or at least not contradictory.

3.1.4 Bayesian hierarchical model

Similar to the CD approach, a Bayesian approach can also incorporate all trials. However, the Bayesian approach has to rely on prior distributions, which then impose additional assumptions.

To carry out network meta-analysis on clinical trials with direct and indirect treatment comparisons, Lu and Ades (2004, 2006) proposed the following hierarchical Bayesian model:

$$\begin{array}{cc}\hfill \text{level 1}:& r_{ij}\mid p_{ij}\sim \text{Binomial}(n_{ij},p_{ij}),i=1,2,\dots ,36,j=A,B,C\hfill \\ \hfill \text{level 2}:& {({\delta }_{AB,i},{\delta }_{AC,i})}^{\mathrm{T}}\mid \delta ,\mathrm{C}\sim N(\delta ,\mathrm{C})\perp {\mu }_i\mid \mu ,{\sigma }_{\mu }^2\sim N(\mu ,{\sigma }_{\mu }^2)\hfill \\ \hfill \text{level 3}:& \text{hyper prior distributions for}\delta ,\mathrm{C}\hfill \\ \hfill & \text{and parameters in the distribution of}\mu ,{\sigma }_{\mu }^2\text{if necessary}\hfill \end{array}$$ (15)

where

$$\left[\begin{array}{c}\hfill {\delta }_{AB,i}\hfill \\ \hfill {\delta }_{AC,i}\hfill \\ \hfill {\mu }_i\hfill \end{array}\right]={\mathrm{T}}_{\mathrm{BS}}\left[\begin{array}{c}\hfill \mathrm{logit}\left(p_{iA}\right)\hfill \\ \hfill \mathrm{logit}\left(p_{iB}\right)\hfill \\ \hfill \mathrm{logit}\left(p_{iC}\right)\hfill \end{array}\right]\text{and}{\mathrm{T}}_{\mathrm{BS}}\triangleq \left[\begin{array}{ccc}\hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1∕3\hfill & \hfill 1∕3\hfill & \hfill 1∕3\hfill \end{array}\right].$$

As stated in Lu and Ades (2004), this model extends the one proposed by Smith et al. (1995) to address the issues of incorporating indirect comparisons and to fully incorporate trials with more than two arms.

Specifically, Lu and Ades (2004) considered two sets of prior distributions, Bayesian-HOM prior and Bayesian-HET prior. The first set of prior distributions (“Bayesian-HOM”) assumes a homogenous variance for δ_AB,i and δ_AC,i:

$$\begin{array}{c}\hfill \delta \sim N(0,{10}^3{\mathrm{I}}_2)\hfill \\ \hfill \mathrm{C}={\sigma }^2\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1∕2\hfill \\ \hfill 1∕2\hfill & \hfill 1\hfill \end{array}\right],{\sigma }^{-2}\sim \text{Gamma}({10}^{-3},{10}^{-3})\hfill \\ \hfill \mu \sim N(0,{10}^3),{\sigma }_{\mu }^{-2}\sim \text{Gamma}({10}^{-3},{10}^{-3})\hfill \end{array}$$ (16)

The second set of prior distributions (“Bayesian-HET”) allows heterogenous variances for δ_AB,i and δ_AC,i:

$$\begin{array}{c}\hfill \delta \sim N(0,{10}^3{\mathrm{I}}_2)\hfill \\ \hfill \mathrm{C}=\left[\begin{array}{cc}\hfill {\sigma }_1^2\hfill & \hfill \rho {\sigma }_1{\sigma }_2\hfill \\ \hfill \rho {\sigma }_1{\sigma }_2\hfill & \hfill {\sigma }_2^2\hfill \end{array}\right],\text{where}\rho =0.5\hfill \\ \hfill {\sigma }_j^2\sim \text{Gamma}(a,b),a\sim \mathrm{Exp}\left(0.01\right),b\sim \text{Gamma}({10}^{-3},{10}^{-3}),j=1,2\hfill \\ \hfill \mu \sim N(0,{10}^3),{\sigma }_{\mu }^{-2}\sim \text{Gamma}({10}^{-3},{10}^{-3})\hfill \end{array}$$ (17)

Except for the different assumptions on the structure of covariance matrix C, both Bayesian-HOM and Bayesian-HET impose the same noninformative priors on δ, μ, and ${\sigma }_{\mu }^2$. The assumptions of priors are subjective and often difficult to verify. Our numerical studies in Section 4 suggest that the Bayesian approach is sensitive to the choice of priors.

3.1.5 Results

We consider the following six methods and compare their inferences on δ_AB:

• Traditional-Direct: Traditional frequentist meta-analysis on direct pairwise comparisons.

• Traditional-Indirect: Traditional frequentist meta-analysis on indirect pairwise comparisons.

• Bayesian-HOM: Bayesian network meta-analysis with homogeneous variance structure on δ.

• Bayesian-HET: Bayesian network meta-analysis with heterogeneous variance structure on δ.

• CD[S_DL]: The proposed CD procedure with S estimated by an extension of the DerSimonian and Laird method to the multivariate case (Jackson et al. (2010)).

• CD[S_REML]: The proposed CD procedure with S estimated by maximizing restricted likelihood.

The values of ${\widehat{\delta }}_{AB}$ and its corresponding 95% confidence interval (CI) or 95% credible interval (CrI) from all six methods are summarized in Table 2.

Table 2.

Results of meta-analyses on CAD data

Method	${\widehat{\delta }}_{AB}$	s.d.(${\widehat{\delta }}_{AB}$)	95% CI	Length of 95% CI
Traditional-Direct	−1.3757	0.1672	(−1.7035, −1.0479)	0.6556
Traditional-Indirect	−1.2874	0.5129	(−2.2926, −0.2822)	2.0104
Bayesian-HOM	−1.3681	0.1084	(−1.5900, −1.1650)	0.4250
Bayesian-HET	−1.3770	0.1312	(−1.6170, −1.1028)	0.5142
CD[SDL]	−1.2984	0.1174	(−1.5285, −1.0683)	0.4602
CD[SREML]	−1.2957	0.1096	(−1.5104, −1.0809)	0.4295

Table 2 shows that all six methods yield similar point estimates of δ_AB. However, because they use both direct and indirect evidence, the Bayesian methods and the CD methods yield smaller variance estimates and tighter confidence interval, in comparison with traditional pairwise meta-analysis. Also, the results from indirect comparisons are in line with those obtained from direct comparisons, although less e cient. It seems appropriate to combine the trials with direct and indirect evidence.

3.2 An example on cirrhosis

As another example, we consider the data presented in Pagliaro et al. (1992) and used in Lu and Ades (2004). The authors analyzed 26 trials of non-surgical treatments intended to prevent first bleeding in patients with cirrhosis and esophageal varices who had never bled, in order to assess the effectiveness of three types of treatments: beta-blockers, endoscopic sclerotherapy and non-active treatment (control), denoted by A, B, and C, respectively. Of the 26 trials, 2 trials compared all three treatments, 7 trials compared beta-blockers vs control, and 17 trials compared sclerotherapy vs control. In Table 3, for trial i and treatment j, r_ij is the number of patients who had a first bleeding event and n_ij is the total number of patients. Our concern is with the relative performance of the active treatments: beta-blockers vs sclerotherapy. However, the only trials that compared them directly were the two three-arm trials, which were not sufficiently large. In this situation direct evidence is not strong enough, and incorporating indirect evidence is particularly important for making inferences.

Table 3.

Cirrhosis data: number of patients who had a first bleeding event.

Study	Beta-blockers (A)		Sclerotherapy (B)		Control (C)
	rij	nij	rij	nij	rij	nij
1	2	43	9	42	13	41
2	12	68	13	73	13	72
3	4	20	—	—	4	16
4	20	116	—	—	30	111
5	1	30	—	—	11	49
6	7	53	—	—	10	53
7	18	85	—	—	31	89
8	2	51	—	—	11	51
9	8	23	—	—	2	25
10	—	—	4	18	0	19
11	—	—	3	35	22	36
12	—	—	5	56	30	53
13	—	—	5	16	6	18
14	—	—	3	23	9	22
15	—	—	11	49	31	46
16	—	—	19	53	9	60
17	—	—	17	53	26	60
18	—	—	10	71	29	69
19	—	—	12	41	14	41
20	—	—	0	21	3	20
21	—	—	13	33	14	35
22	—	—	31	143	23	138
23	—	—	20	55	19	51
24	—	—	3	13	12	16
25	—	—	3	21	5	28
26	—	—	6	22	2	24

We apply the same six methods as in the CAD data set. The parameter of interest is δ_AB, the log-odds ratio of first bleeding for beta-blockers vs sclerotherapy. The results are presented in Table 4.

Table 4.

Results of meta-analysis on cirrhosis data

Method	${\widehat{\delta }}_{AB}$	s.d.(${\widehat{\delta }}_{AB}$)	95% CI	Length of 95% CI
Traditional-Direct	0.7284	0.8439	(−0.9256,2.3824)	3.3080
Traditional-Indirect	−0.0927	0.8069	(−1.6738,1.4884)	3.1622
Bayesian-HOM	0.5228	0.3171	(−0.0969,1.1461)	1.2430
Bayesian-HET	0.6466	0.3250	( 0.0410, 1.3151)	1.2741
CD[SDL]	0.5688	0.2588	( 0.0617, 1.0761)	1.0144
CD[SREML]	0.6381	0.2445	( 0.1589, 1.1174)	0.9585

In Table 4, we again observe that the Bayesian methods and the CD procedures have substantially lower variance as a result of integrating all treatment comparisons. Therefore, the network-meta-analysis approaches have effectively strengthened the results obtained from direct comparisons by borrowing information from indirect comparisons. Unlike the results in the CAD example, pairwise meta-analysis using only direct comparisons does not achieve significant results, whereas the Bayesian and CD approaches yield significant or almost significant results. However, the validity of combining direct and indirect treatment comparisons should be carefully investigated, the difference between ${\widehat{\delta }}_{AB,indirect}$ and ${\widehat{\delta }}_{AB,direct}$ raises concerns about consistency between direct and indirect evidence. The topic of inconsistent evidence is discussed in Higgins et al. (2002, 2003). We also discuss this topic further in Section 4.3 and Section 5.

In these two examples, the CD and Bayesian approaches yield similar results. The confidence intervals derived from the CD approach are only slightly tighter than those derived from the Bayesian approach. However, our simulation studies in the next section show that the Bayesian credible intervals may not achieve the nominal coverage probability, and their empirical coverage probabilities may be far below the nominal level when the assumed prior on the between-trial covariance structure does not agree with the underlying true model. This latter condition is almost impossible to verify in practice. In contrast, the proposed CD combining approach does not require any prior, and the derived confidence intervals can maintain adequate coverage probability regardless of the between-trial covariance structure.

4 Simulation studies

We conducted simulation studies to compare the performance of the proposed CD combining approach with traditional pairwise meta-analysis and the Bayesian method.

4.1 Simulation settings

We based our simulation on the structure of the cirrhosis data. Specifically, the evidence network involves three treatments (A, B, and C). The problem of interest is to infer the relative effectiveness of A vs B.

Consider two scenarios, one with 24 trials and the other with 96 trials. In the first scenario, the 24 clinical trials, comprise 1 trial comparing all three treatments, 3 trials comparing A and B, 10 trials comparing treatments A and C, and 10 trials comparing B and C. The number of patients in each arm of each trial is 100, i.e., n_ij = 100, ∀i and j ∈ T_i. In the second scenario the number of trials of each type is four times that in the first scenario. The simulation is designed to show the benefit of borrowing strength from indirect evidence when direct evidence (trials directly comparing treatments A and B) is somewhat limited.

We generate the simulated data from the model:

$$\begin{array}{c}\hfill r_{ij}\mid p_{ij}\sim \text{Binomial}(n_{ij},p_{ij}),p_{ij}=\frac{\exp \left({\theta }_{ij}\right)}{1+\exp \left({\theta }_{ij}\right)},i=1,2,\dots ,24\text{or}96,j\in T_i\hfill \\ \hfill {\theta }_i\sim N({\mathrm{A}}_i\theta ,{\mathrm{A}}_i{\mathrm{SA}}_i^{\mathrm{T}})\hfill \end{array}$$ (18)

where A_i consists of the rows of the identity matrix corresponding to the treatments in T_i.

We specify the true value of θ = (−1.82, −1.21, 0.80)^T as the values are close to those estimated from the cirrhosis data. It follows that the probabilities of observing an event in treatment A, B, and C are p = (0.14, 0.23, 0.31)^T. For the covariance matrix S, we consider three cases:

Case 1:

$$\mathrm{S}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\iff B=\left[\begin{array}{ccc}\hfill 2\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1∕3\hfill \end{array}\right];$$

Case 2:

$$\mathrm{S}=\left[\begin{array}{ccc}\hfill 2.5736\hfill & \hfill -1.2868\hfill & \hfill 1,7132\hfill \\ \hfill -1.2868\hfill & \hfill 4.8528\hfill & \hfill -0.5660\hfill \\ \hfill 1.7132\hfill & \hfill -0.5660\hfill & \hfill 1.8528\hfill \end{array}\right]\iff \mathrm{B}=\left[\begin{array}{ccc}\hfill 10\hfill & \hfill 1.5811\hfill & \hfill 0\hfill \\ \hfill 1.5811\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right];$$

Case 3:

$$\mathrm{S}=\left[\begin{array}{ccc}\hfill 3.1070\hfill & \hfill 0.4314\hfill & \hfill 1.2358\hfill \\ \hfill 0.4314\hfill & \hfill 0.7557\hfill & \hfill 0.4693\hfill \\ \hfill 1.2358\hfill & \hfill 0.4693\hfill & \hfill 0.8645\hfill \end{array}\right]\iff \mathrm{B}=\left[\begin{array}{ccc}\hfill 3.0000\hfill & \hfill 1.9092\hfill & \hfill -1.0392\hfill \\ \hfill 1.9092\hfill & \hfill 1.5000\hfill & \hfill -0.7348\hfill \\ \hfill -1.0392\hfill & \hfill -0.7348\hfill & \hfill 1.0000\hfill \end{array}\right],$$

where $\mathrm{B}=\mathrm{cov}({\delta }_{AB,i},{\delta }_{AC,i},{\mu }_i)={\mathrm{T}}_{\mathrm{BS}}{\mathrm{ST}}_{\mathrm{BS}}^{\mathrm{T}}$, and δ_AB,i, δ_AC,i, μ_i and T_BS are defined as in model (15). Here “ ⇔ ” indicates the one-to-one correspondence between the covariance matrix S in model (18) and the covariance matrix B in the Bayesian models.

In Case 1, S is set to an identity matrix to ensure that the true model (18) meets the assumptions of Bayesian-HOM in Section 3.1.4, and is thus equivalent to the case of (16) with σ² = 2. Similarly, the covariance matrix S in Case 2 allows the true model (18) to meet the assumptions of Bayesian-HET, and is thus equivalent to the case of ${\sigma }_1^2=10$, ${\sigma }_2^2=1$ and ρ = 0.5 in (17). As suggested in Joseph et al. (1997), we further extend the model to incorporate correlations between δ_AB,i, δ_AC,i and μ_i, instead of assuming independence. Therefore, in Case 3, the covariance matrix S is specified to give an arbitrary covariance structure such that B fails to meet the assumptions of either Bayesian-HOM or Bayesian-HET. In summary, we consider a total of six (= 2 × 3) settings in our simulation study: 24 and 96 trials each with three specifications of the covariance matrix S.

4.2 Results

We consider and compare the performance of a total of nine approaches. They include the six methods listed in Section 3.1.5: Traditional-Direct and Traditional-Indirect, Bayesian-HOM and Bayesian-HET, and CD[S_DL] and CD[S_REML]. Additionally, we include three other CD approaches: two semi-Bayesian approaches, CD[S_BHOM] and CD[S_BHET], in which the covariance matrix S is estimated by the Bayesian method with prior in (16) and (17), respectively, and CD[S_TRUE], which uses the true covariance matrix S. The CD[S_TRUE] method allows us to separate the effect of estimating the mean alone and study the potential impacts on estimation of the mean when different approaches are used to estimate S. Thus, the nine methods are:

• Traditional frequentist methods:

  • -
    Traditional-Direct: Traditional frequentist meta-analysis of direct pairwise comparisons.
  • -
    Traditional-Indirect: Traditional frequentist meta-analysis via indirect pairwise comparisons.
• Bayesian methods:

  • -
    Bayesian-HOM: Bayesian network meta-analysis with homogenous variance structure on δ.
  • -
    Bayesian-HET: Bayesian network meta-analysis with heterogenous variance structure on δ.
• CD methods:

  • -
    CD[S_DL]: S estimated by S_DL.
  • -
    CD[S_REML]: S estimated by S_REML.
  • -
    CD[S_BHOM]: S estimated by S_BHOM.
  • -
    CD[S_BHET]: S estimated by S_BHET.
  • -
    CD[S_TRUE]: using the known true S.

In simulation Scenario 1 Case 1, for example, we generate data according to the model specified in (18), and then apply each method to estimate δ_AB and calculate the corresponding 95% confidence (credible) interval. We repeat this process 1000 times. For each method, we report the mean and standard deviation of the 1000 ${\widehat{\delta }}_{AB}$ and the percentage of times (coverage) that the 1000 95% CIs cover the true δ_AB = 0.6070 and the average interval length. The results for Scenarios 1 and 2 with Case 1 (S = I_{3 × 3}) are presented in Table 6. Similarly, the results for Case 2 and Case 3 are presented in Tables 7 and 8. It is straightforward to verify that the chance that no trial has zero events in the entire 1000 replications is at least 99.97%. Thus the zero events issue is not considered in the simulation study.

Table 6.

Summary of results of simulation studies - Case 1

Method	${\widehat{\delta }}_{AB}$	s.d.(${\widehat{\delta }}_{AB}$)	95% CI coverage	Average Length of 95% CI
Scenario 1 - Small Number of Trials k = 24
Traditional-Direct	0.5952	0.7167	0.867	2.7041
Traditional-Indirect	0.5913	0.6312	0.941	2.5225
Bayesian-HOM	0.5796	0.4097	0.937	1.5704
Bayesian-HET	0.5736	0.4104	0.938	1.5712
CD[SREML]	0.5677	0.4057	0.897	1.3766
CD[STRUE]	0.5732	0.3850	0.955	1.5554
CD[SDL]	0.5718	0.4195	0.862	1.2550
CD[SBHOM]	0.5719	0.3925	0.940	1.5337
CD[SBHET]	0.5714	0.3927	0.943	1.5225
Scenario 2 - Large Number of Trials k = 96
Traditional-Direct	0.5843	0.3658	0.927	1.3950
Traditional-Indirect	0.6104	0.3118	0.962	1.2681
Bayesian-HOM	0.6126	0.2016	0.948	0.7663
Bayesian-HET	0.6126	0.2016	0.943	0.7701
CD[SREML]	0.5780	0.1915	0.936	0.7242
CD[STRUE]	0.5856	0.1900	0.966	0.7777
CD[SDL]	0.5762	0.1932	0.904	0.6536
CD[SBHOM]	0.5852	0.1920	0.959	0.7716
CD[SBHET]	0.5852	0.1918	0.954	0.7680

Table 7.

Summary of results of simulation studies - Case 2

Method	${\widehat{\delta }}_{AB}$	s.d.(${\widehat{\delta }}_{AB}$)	95% CI coverage	Average Length of 95% CI
Scenario 1 - Small Number of Trials k = 24
Traditional-Direct	0.6176	1.4759	0.849	5.4220
Traditional-Indirect	0.5905	0.8818	0.937	3.4753
Bayesian-HOM	0.6095	0.7450	0.887	2.4177
Bayesian-HET	0.5706	0.7360	0.913	2.6355
CD[SREML]	0.5793	0.6922	0.916	2.5426
CD[STRUE]	0.5820	0.6865	0.973	2.9649
CD[SDL]	0.6165	0.7289	0.811	2.0011
CD[SBHOM]	0.6323	0.7030	0.901	2.3815
CD[SBHET]	0.6044	0.6930	0.906	2.4856
Scenario 2 - Large Number of Trials k = 96
Traditional-Direct	0.6433	0.7431	0.924	2.8474
Traditional-Indirect	0.6287	0.4279	0.951	1.7643
Bayesian-HOM	0.6852	0.3540	0.899	1.1858
Bayesian-HET	0.6454	0.3436	0.960	1.3952
CD[SREML]	0.6200	0.3226	0.959	1.3164
CD[STRUE]	0.6261	0.3254	0.980	1.4823
CD[SDL]	0.6455	0.3227	0.864	0.9721
CD[SBHOM]	0.6636	0.3324	0.933	1.2085
CD[SBHET]	0.6279	0.3256	0.968	1.3876

Table 8.

Summary of results of simulation studies - Case 3

Method	${\widehat{\delta }}_{AB}$	s.d.(${\widehat{\delta }}_{AB}$)	95% CI coverage	Average Length of 95% CI
Scenario 1 - Small Number of Trials k = 24
Traditional-Direct	0.4706	0.8260	0.868	3.0721
Traditional-Indirect	0.4250	0.4582	0.915	1.8193
Bayesian-HOM	0.4135	0.4400	0.855	1.4116
Bayesian-HET	0.4065	0.4388	0.853	1.4186
CD[SREML]	0.4834	0.4201	0.892	1.4924
CD[STRUE]	0.5010	0.4058	0.953	1.7241
CD[SDL]	0.3957	0.4510	0.787	1.2756
CD[SBHOM]	0.3750	0.4169	0.855	1.3811
CD[SBHET]	0.3753	0.4141	0.852	1.3824
Scenario 2 - Large Number of Trials k = 96
Traditional-Direct	0.4823	0.4132	0.912	1.5936
Traditional-Indirect	0.4472	0.2250	0.896	0.9051
Bayesian-HOM	0.4603	0.2131	0.807	0.6828
Bayesian-HET	0.4589	0.2097	0.822	0.6996
CD[SREML]	0.5057	0.1943	0.919	0.7724
CD[STRUE]	0.5261	0.1978	0.949	0.8620
CD[SDL]	0.4435	0.2029	0.749	0.6242
CD[SBHOM]	0.3959	0.2027	0.754	0.6954
CD[SBHET]	0.3950	0.2002	0.759	0.7042

From the results in Tables 6, 7 and 8, it is evident that the traditional pairwise meta-analysis is much less e cient than the CD network meta-analysis approaches. Specifically, compared with the results from the CD[S_REML] method, the lengths of 95% CIs obtained from traditional meta-analysis methods are much greater, even though the probabilities of covering the true value are comparable. This suggests that, when the parameter of interest is a vector, information on one parameter may be potentially useful for inferences on other parameters. Thus, mixed treatment comparisons should be considered in our settings.

Consider the probability that the nominal 95% CI covers the true δ_AB as one criterion for assessing the performance of each meta-analysis method. It is evident from the simulation study that the results of the Bayesian methods are sensitive to the specifications of their prior distributions. Specifically, Bayesian-HOM fails to achieve appropriate coverage in Cases 2 and 3 (e.g., 89% and 90% in Table 7 and 86% and 81% in Table 8), regardless whether the number of studies is small or large. Similarly, Bayesian-HET fails to provide satisfactory coverage in the Case 3 (85% and 82% in Table 8) when its assumption on prior cannot cover the true model. In summary, both Bayesian methods are able to estimate δ_AB properly only if their prior assumptions cover the underlying true covariance model, and they fail to do so when their prior assumptions are not compatible with the underlying true covariance model. So the Bayesian procedures are vulnerable to their assumptions on priors, and we should make as few assumptions as possible when specifying priors.

In examining the results of the CD procedures, we first observe that CD[S_TRUE] achieves desirable coverage rates in all cases (95%–98% in Tables 6, 7, and 8). Therefore, the performance of the CD procedure is satisfactory for combining information on θ. However, the performance of the CD procedure is strongly affected by the quality of estimating the covariance matrix S. To help establish a practical guideline, we compare the quality of estimates based on the extended DL method S_DL and the REML method S_REML. Specifically, we plug in the corresponding estimates in the process of constructing and combining individual CDs, and again we study the performance of estimates ${\widehat{\delta }}_{AB}$ and the corresponding 95% CIs. The performance of CD[S_REML] is reasonable in all settings, i.e., close to the nominal 95% coverage (see, e.g., 92%–96% in Tables 6, 7, and 8) as long as the number of studies is sufficiently large. Further, the coverage rate of CD[S_REML] improves from 89%–92% to 92%–96% as the number of studies increases from 24 to 96. On the other hand, the coverage rate of CD[S_DL] is relatively low, around 79%–86%, when the sample size is small. Moreover, the performance of CD[S_DL] does not always improve as the number of studies increases. For example, the coverage rate of CD[S_DL] drops from 78.7% to 74.9% in Table 8. Thus, the REML method is preferable to the extended DL method for estimating the covariance matrix S. This observation is consistent with the shortcomings of the DL method reported in univariate random-effects models by Emerson et al. (1993). Between the REML and DL methods, we recommend the CD procedure with S_REML for network meta-analysis when S is unknown.

Finally, the results for the semi-Bayesian CD procedures appear to be similar to the results for the corresponding Bayesian procedures. Specifically, the performance of CD[S_BHOM] is in line with Bayesian-HOM. It achieves appropriate coverage in Case 1 (94% and 96% in Table 6), but fails in Cases 2 and 3 (90% and 93% in Table 7 and 86% and 75% in Table 8), regardless of the number of studies k = 24 or 96. Similarly, the results for CD[S_BHET] are in line with Bayesian-HET. It provides satisfactory coverage in Cases 1 and 2 (94% and 95% in Table 6 and 91% and 97% in Table 7), but fails Case 3 (85% and 76% in Table 8). Once again, the CD procedure is sensitive to the quality of estimation of S. Also, the confidence distribution H^(c)(·) in (8) is an asymptotic CD that is more suitable for making inferences on θ when k → ∞, under which both the mean vector θ and the between-trials covariance matrix S can be estimated consistently.

4.3 A CD approach with adaptive weights

As we observed from in Section 4.2, the overall findings for a network can be quite unreliable when indirect evidence and direct evidence inconsistent. In this section, an adaptive weighting system improves resistance to the impact of inconsistent indirect comparisons by down-weighting the trials that contribute to the inconsistent evidence. Here, the degree of inconsistency from an indirect comparison is measured by how the trials in the indirect comparison deviate from the overall outcome for the direct comparison. The precise formulation of this measure, which we loosely call “distance,” is given after Model (19). Taking into account this distance, the CD combining process can still use indirect comparisons that provide outcomes consistent with those from the direct comparisons, but it can also reduce the impact of inconsistent indirect comparisons. We demonstrate this property through the following simulation studies.

We consider the model (18) used in Scenario 1 in Section 4.1, with two modifications. First, we increase the total number of trials from 24 to 33 so that three trials, instead of one trial, compare treatments A, B, and C, and ten trials, instead of three trials, directly compare treatments A and B. We still have ten trials comparing treatments A and C and ten trials comparing treatments B and C. Thus, for inferences on δ_AB, we have 13 direct comparisons and 20 trials with information on the indirect comparison. Second, the trials containing information on the direct comparison are consistent, but some of the remaining 20 trials containing information on the indirect comparison may be biased. Specifically, we consider the following model to generate the simulation data:

$$\begin{array}{c}\hfill r_{ij}\mid p_{ij}\sim \text{Binomial}(n_{ij},p_{ij}),p_{ij}=\frac{\exp \left({\theta }_{ij}\right)}{1+\exp \left({\theta }_{ij}\right)},i=1,2,\dots ,33,j\in T_i\hfill \\ \hfill {\theta }_i\sim (1-∊)N({\mathrm{A}}_i\theta ,{\mathrm{A}}_i{\mathrm{SA}}_i^{\mathrm{T}})+∊N\left({\mathrm{A}}_i\right(\theta -{\eta }_i),{\mathrm{A}}_i{\mathrm{SA}}_i^{\mathrm{T}})\hfill \end{array}$$ (19)

where

$$\begin{array}{c}\hfill ∊=0\text{and}{\eta }_i=0\text{for}is.t.T_i=\{A,B,C\}\text{or}{T}_i=\{A,B\}\hfill \\ \hfill ∊=0.4\text{and}{\eta }_i=\{\begin{array}{cc}{({\eta }_{A,i},0,0)}^{\mathrm{T}}\hfill & \text{for}is.t.T_i=\{A,C\}\hfill \\ {(0,{\eta }_{B,i},0)}^{\mathrm{T}}\hfill & \text{for}is.t.T_i=\{B,C\}\hfill \end{array}\phantom{\}}\hfill \end{array}$$

Here, the values of η_A,i and η_B,i are fixed numbers simulated from N(2, 4).

Model (19) indicates that all trials that compare both treatments A and B directly have the same underlying true parameter θ, whereas some trials involving A only or B only may have different underlying true parameters. If we are to include the trials that provide the indirect comparison in our analysis, it would be desirable to exclude or down-weight those trials. In this case, we devise the following notion of distance d_i,

$$d_i=\{\begin{array}{cc}\frac{({\widehat{\delta }}_{AC,i}-{\text{median}}_{ls.t.}{T}_l=\{B,C\left\}{\widehat{\delta }}_{BC,l}\right)-{\widehat{\delta }}_{AB,\text{direct}}}{\sqrt{\mathrm{var}\left({\widehat{\delta }}_{AB,direct}\right)}}\hfill & \text{for}is.t.T_i=\{A,C\}\hfill \\ \frac{({\text{median}}_{ls.t.}{T}_l=\{A,C\}{\widehat{\delta }}_{AC,l}-{\widehat{\delta }}_{BC,i})-{\widehat{\delta }}_{AB,direct}}{\sqrt{\mathrm{var}\left({\widehat{\delta }}_{AB,direct}\right)}}\hfill & \text{for}is.t.T_i=\{B,C\},\hfill \end{array}\phantom{\}}$$

where ${\widehat{\delta }}_{AB,direct}$ and $\left({\widehat{\delta }}_{AB,direct}\right)$ are obtained from Equation (13). Heuristically, d_i for each indirect comparison trial measures its deviation from the overall outcome given by all direct comparison trials. For example, we could consider including only the studies with distance |d_i| ≤ 1 in the meta-analysis. In other words, we would define $w_i^{\ast }$ as

$$w_i^{\ast }=\{\begin{array}{cc}1\hfill & \text{if}\mid d_i\mid \le 1\hfill \\ 0\hfill & \text{if}\mid d_i\mid >1,\hfill \end{array}\phantom{\}}$$

and use $w_i^{\ast }$ in the method CD[S_REML]-adjusted. Specifically, we set $W_i=w_i^{\ast }\times {\mathrm{A}}_i^{+}{({\widehat{\Sigma }}_i+{\mathrm{A}}_i{\mathrm{S}}_{\mathrm{REML}}{\mathrm{A}}_i^{\mathrm{T}})}^{-1}{\mathrm{A}}_i$, and take the cdf of the random vector in (7) as the combined multivariate normal CD. We show that in this way the combined CD is able to exclude those inconsistent indirect trials – trials with large d_i. There are many other choices of adaptive weights. For convenience, we use here the simple, though somewhat restrictive, |d_i| ≤ 1 to remove inconsistent studies from combination. A detailed discussion of choices of adaptive weights and their applications to combining CDs can be found in Xie et al. (2011).

In a further simulation study (Case 4), we consider two settings. In Setting 1, we generate the simulated data using model (18), in which all studies have the same underlying true parameter value, but modify it to have 33 trials with the same composition of trials as model (19). In Setting 2, the simulated data are generated from model (19). In this case, some trials used in the indirect comparison have a different underlying true parameter value. In both settings, three trials compare all three treatments, ten trials compare treatments A and B, ten trials A and C, and ten trials B and C. The number of patients involved in each arm of each study is 100. We apply CD[S_REML], CD[S_REML]-adjusted, and CD[S_TRUE] to the simulated data sets. We repeat the entire process 1000 times and report the results in Table 9.

Table 9.

Summary of results of simulation studies - Case 4

Method	${\widehat{\delta }}_{AB}$	s.d.(${\widehat{\delta }}_{AB}$)	95% CI coverage	Average Length of 95% CI
Setting 1-33 Trials without Inconsistent Indirect Trials
CD[SREML]	0.5733	0.2984	0.9200	1.1122
CD[SREML]-adjusted	0.5780	0.3705	0.9230	1.4078
CD[STRUE]	0.5818	0.2955	0.9520	1.2139
Setting 2 - 33Trials with Inconsistent Indirect Trials
CD[SREML]	1.1425	0.3932	0.7190	1.4808
CD[SREML]-adjusted	0.6479	0.3934	0.9770	1.9963
CD[STRUE]	1.1001	0.3367	0.6260	1.2250

All three methods are able to achieve appropriate coverage rate (92% – 95% in Setting 1) if all trial outcomes are consistent with one another. However, in Setting 2, with inconsistent indirect trials, only CD[S_REML]-adjusted provides appropriate inference on δ_AB. In particular, the estimate ${\widehat{\delta }}_{AB}=0.6479$ by CD[S_REML]-adjusted is not far from the true δ_AB = 0.6070, and its 95% CI has a coverage rate of 97.7%. Therefore, with carefully designed study-specific weights, the CD procedure is able to provide some resistance to the impact of inconsistent indirect trials mistakenly included in the meta-analysis.

5 Concluding remarks

In this paper, we have proposed a frequentist method for network meta-analysis by combining multivariate normal confidence distributions (CDs) associated with individual studies. This proposed CD approach can perform indirect comparisons in a network of mixed treatment comparisons, and it can use the findings from indirect comparisons e ciently to enhance the overall inference of the entire network. The CD approach can also be modified by using an adaptive weighting scheme to reduce the effect of indirect comparisons whose findings contradict those from the direct comparisons. Overall, the proposed CD approach can effectively and e ciently integrate direct and indirect information from disparate sources. In fact, the CD approach can estimate consistently and e ciently the parameters of interest as well as the between-trials covariance matrix when the number of studies goes to infinity. Through simulation studies, we have also demonstrated that the CD approach generally outperforms traditional pairwise meta-analysis and the Bayesian hierarchical model. In conclusion, the CD approach is highly competitive for network meta-analysis.

Even though model (1) and our network meta-analysis in this paper are formulated under the normality assumption, this assumption can be easily relaxed to accommodate non-normal cases, such as any location-scale distribution families (including the t-model, etc.). Moreover, we stress that the normality in model (1) is assumed only for the summary statistics, but not for the model that underlies the individual observations. If the sample sizes of individual studies are sufficiently large, model (1) holds for many non-normal settings, following the central limit theorem. In any case, the normal model (1) is not as restrictive as it appears, and it in fact covers many non-normal cases.

In comparing the approaches on the CAD data in Section 3.1, we excluded the TAXUS I trial to avoid addressing the issue of zero events there. In traditional pairwise meta-analysis, one customarily adds 0.5 to zero events. This correction is arbitrary and introduces bias in the inferences. By removing zero-event trials from the analysis, one would lose the information they contain. For example, for TAXUS I, zero event is a favorable outcome for both BMS and PES. This loss can cause concerns as well, especially if the zero-event trials constitute a sizable portion of the data. For an exact inference method involving zero events, the approach of combining significance functions proposed in Liu et al. (2012) can avoid the shortcomings of the earlier approaches.

In network meta-analysis, it is important to assess the consistency of the evidence from all trials in the network. However, such assessment is often difficult. One reason is that designs often differ between the trials yielding direct comparisons and the trials leading to indirect comparisons. Furthermore, it is practically impossible to distinguish between inconsistency and heterogeneity of random effects. See Higgins et al. (2002, 2003) for further discussion of this topic.

Although our examples involve clinical trials in medical studies, we emphasize that the proposed CD approach can be applied broadly for any multiple comparison studies in many other domains. For example, to establish ratings for a list of restaurants based on a survey of customer ratings, customers would be able to provide data only on the restaurants that they have patronized. The CD approach could be applied by constructing and combining CDs based on the ratings given to those restaurants by a group of customers.

Table 5.

Simulation Settings - Number of Trials k and Patients Involved in Each Group n_ij

Total Number of Trials k[CKR]Type of Trial		ABC	AB	AC	BC	nij
Simulation Scenario 1	k=24	1	3	10	10	100
Simulation Scenario 2	k=96	4	12	40	40	100

Appendix

Lemma 1Suppose W_i, i = 1, …, k are p × p positive semi-definite symmetric matrices and V_i is the column space of W_i. Let $V=V_1+V_2+\dots +V_k\triangleq \{{\Sigma }_{i=1}^k{v}_i\mid v_i\in V_i,i=1,\dots ,k\}$. Then ${\Sigma }_{i=1}^k{W}_i$ is positive definite provided that $V={\mathfrak{R}}^p$.

Proof of Lemma 1:

It is a direct result that ${\Sigma }_{i=1}^k{W}_i$ is positive semi-definite. Suppose there exists a p × 1 vector v ≠ 0 such that ${\mathrm{v}}^{\mathrm{T}}\left({\Sigma }_{i=1}^k{W}_i\right)\mathrm{v}=0$. Then, for any fixed i, we have v^TW_iv = 0, which implies that $W_i^{1∕2}\mathrm{v}=0$. It follows that $\mathrm{v}\in \text{kernel}\left(W_i^{1∕2}\right)$, and immediately v ∈ kernel(W_i) since W_i is symmetric. Thus v ⊥ V_i. Since i is arbitrary, we conclude that $\mathrm{v}\perp V={\mathfrak{R}}^p$ and v has to be 0, which contradicts the assumption that v ≠ 0.

Proof of Theorem 1:

Let ${\xi }^{\left(c\right)}={\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}{\Sigma }_{i=1}^k{W}_i{\mathrm{A}}_i^{+}{\xi }_i$ and H^(c)(t) = Pr{ξ^(c) ≤ t|Y₁, … ,Y_k}. We need to show that H^(c)(·) = H(Y₁, … ,Y_k; ·) is a multivariate normal CD for θ. Define H_λ(t) = Pr{λ^Tξ^(c) ≤ t|Y₁, … ,Y_k} for any given vector λ satisfying ||λ||₂ = 1. By Definition 2, it suffices to show that H_λ(t) is a univariate normal CD function for λ^Tθ.

To do so, we first note that H_λ(t) goes from 0 to 1 monotonically as t goes from −∞ to ∞. Thus, H_λ(t) is a cdf. Second, we note that ξ_i, defined by ξ_i|Y_i = y_i ~ N(y_i, var(Y_i)), is a CD random vector for θ_i, and furthermore, ${\mathrm{A}}_i^{+}{\xi }_i$ is a CD random vector for θ in the sense that the distribution function of ${\eta }^{\mathrm{T}}{\mathrm{A}}_i^{+}{\xi }_i$ is a CD for η^Tθ for any η ∈ V_i. Since ${\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}$ exists by Lemma 1, we consider the conditional distribution of ${\left(W_i{\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}\lambda \right)}^{\mathrm{T}}{\mathrm{A}}_i^{+}{\xi }_i$ given Y_i.

Clearly, it is a univariate normal CD for ${\left(W_i{\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}\lambda \right)}^{\mathrm{T}}\theta$, because $W_i{\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}\lambda \in V_i$. Therefore, it is straightforward to show that, at the true parameter value θ = θ₀,

$$\mathrm{Pr}\left\{H_{\lambda }\right({\mathrm{Y}}_1,\dots ,{\mathrm{Y}}_k)\le s\}=\mathrm{Pr}\left\{\Phi \left(\frac{{\Sigma }_{i=1}^k{\left(W_i{\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}\lambda \right)}^{\mathrm{T}}{\mathrm{A}}_i^{+}{\mathrm{Y}}_i-{\lambda }^{\mathrm{T}}{\theta }_0}{\sqrt{{\Sigma }_{i=1}^k{\sigma }_i^2}}\right)\le s\right\}=s$$

where ${\sigma }_i^2=\mathrm{var}\left({\left(W_i{\left({\Sigma }_{i=1}^k{W}_i\right)}^{-1}\lambda \right)}^{\mathrm{T}}{\mathrm{A}}_i^{+}{\xi }_i\right)$. Thus, we have established that, at the true θ = θ₀ and as a function of the sample Y₁, … ,Y_k, H_λ(Y₁, … ,Y_k) follows the uniform distribution U[0, 1]. This completes the proof.