Conducting Simulation Studies in the R Programming Environment

Abstract

Simulation studies allow researchers to answer specific questions about data analysis, statistical power, and best-practices for obtaining accurate results in empirical research. Despite the benefits that simulation research can provide, many researchers are unfamiliar with available tools for conducting their own simulation studies. The use of simulation studies need not be restricted to researchers with advanced skills in statistics and computer programming, and such methods can be implemented by researchers with a variety of abilities and interests. The present paper provides an introduction to methods used for running simulation studies using the R statistical programming environment and is written for individuals with minimal experience running simulation studies or using R. The paper describes the rationale and benefits of using simulations and introduces R functions relevant for many simulation studies. Three examples illustrate different applications for simulation studies, including (a) the use of simulations to answer a novel question about statistical analysis, (b) the use of simulations to estimate statistical power, and (c) the use of simulations to obtain confidence intervals of parameter estimates through bootstrapping. Results and fully annotated syntax from these examples are provided.

Introduction

Simulations provide a powerful technique for answering a broad set of methodological and theoretical questions and provide a flexible framework to answer specific questions relevant to one’s own research. For example, simulations can evaluate the robustness of a statistical procedure under ideal and non-ideal conditions, and can identify strengths (e.g., accuracy of parameter estimates) and weaknesses (e.g., type-I and type-II error rates) of competing approaches for hypothesis testing. Simulations can be used to estimate the statistical power of many models that cannot be estimated directly through power tables and other classical methods (e.g., mediation analyses, hierarchical linear models, structural equation models, etc.). The procedures used for simulation studies are also at the heart of bootstrapping methods, which use resampling procedures to obtain empirical estimates of sampling distributions, confidence intervals, and p-values when a parameter sampling distribution is non-normal or unknown.

The current paper will provide an overview of the procedures involved in designing and implementing basic simulation studies in the R statistical programming environment (R Development Core Team, 2011). The paper will first outline the logic and steps that are included in simulation studies. Then, it will briefly introduce R syntax that helps facilitate the use of simulations. Three examples will be introduced to show the logic and procedures involved in implementing simulation studies, with fully annotated R syntax and brief discussions of the results provided. The examples will target three different uses of simulation studies, including

1. Using simulations to answer a novel statistical question

2. Using simulations to estimate the statistical power of a model

3. Using bootstrapping to obtain a 95% confidence interval of a model parameter estimate

For demonstrative purposes, these examples will achieve their respective goals within the context of mediation models. Specifically, Example 1 will answer a novel statistical question about mediation model specification, Example 2 will estimate the statistical power of a mediation model, and Example 3 will bootstrap confidence intervals for testing the significance of an indirect effect in a mediation model. Despite the specificity of these example applications, the goal of the present paper is to provide the reader with an entry-level understanding of methods for conducting simulation studies in R that can be applied to a variety of statistical models unrelated to mediation analysis.

Rationale for Simulation Studies

Although many statistical questions can be answered directly through mathematical analysis rather than simulations, the complexity of some statistical questions makes them more easily answered through simulation methods. In these cases, simulations may be used to generate datasets that conform to a set of known properties (e.g., mean, standard deviation, degree of zero-inflation, ceiling effects, etc. are specified by the researcher) and the accuracy of the model-computed parameter estimates may be compared to their specified values to determine how adequately the model performs under the specified conditions. Because several methods may be available for analyzing datasets with these characteristics, the suitability of these different methods could also be tested using simulations to determine if some methods offer greater accuracy than others (e.g., Estabrook, Grimm, & Bowles, 2012; Luh & Guo, 1999).

Simulation studies typically are designed according to the following steps to ensure that the simulation study can be informative to the researcher’s question:

1. A set of assumptions about the nature and parameters of a dataset are specified.

2. A dataset is generated according to these assumptions.

3. Statistical analyses of interest are performed on this dataset, and the parameter estimates of interest from these analyses (e.g., model coefficient estimates, fit indices, p-values, etc.) are retained.

4. Steps 2 and 3 are repeated many times with many newly generated datasets (e.g., 1000 datatsets) in order to obtain an empirical distribution of parameter estimates.

5. Often, the assumptions specified in step 1 are modified and steps 2–4 are repeated for datasets generated according to new parameters or assumptions.

6. The obtained distributions of parameter estimates from these simulated datasets are analyzed to evaluate the question of interest.

The R Statistical Programming Environment

The R statistical programming environment (R Development Core Team, 2011) provides an ideal platform to conduct simulation studies. R includes the ability to fit a variety of statistical models natively, includes sophisticated procedures for data plotting, and has over 3000 add-on packages that allow for additional modeling and plotting techniques. R also allows researchers to incorporate features common in most programming languages such as loops, random number generators, conditional (if-then) logic, branching, and reading and writing of data, all of which facilitate the generation and analysis of data over many repetitions that is required for many simulation studies. R also is free, open source, and may be run across a variety of operating systems.

Several existing add-on packages already allow R users to conduct simulation studies, but typically these are designed for running simulations for a specific type of model or application. For example, the simsem package provides functions for simulating structural equation models (Pornprasertmanit, Miller, & Schoemann, 2012), ergm includes functions for simulating social network exponential random graphs (Handcock et al., 2012), mirt allows users to simulate multivariate-normal data for item response theory (Chalmers, 2012), and the simulate function in the native stats package allows users to simulate fitted general linear models and generalized linear models. It should be noted that many simulation studies can be conducted efficiently using these pre-existing functions, and that using the alternative, more general method for running simulation studies described here may not always be necessary. However, the current paper will describe a set of general methods and functions that can be used in a variety of simulation studies, rather than describing the methods for simulating specific types of models already developed in other packages.

R Syntax

R is syntax-driven, which can create an initial hurdle that prevents many researchers from using it. While the learning curve for syntax-driven statistical languages may be steep initially, many people with little or no prior programming experience have become comfortable using R. Also, such a syntax-driven platform allows for much of the program’s flexibility described above.

The simulations used in the following tutorials utilize several basic R functions, with a rationale for their use provided below and a brief description with examples given in Table 1. A full tutorial on these basic functions and on using R in general is not given here; instead, the reader is referred to several open-source tutorials introducing R (Kabacoff, 2012; Owen, 2010; Spector, 2004; Venables, Smith, & R Development Core Team, 2012). Some commands that serve a secondary function that are not directly related to generating or analyzing simulation data (e.g., the write.table command for saving a dataset) are not discussed here but descriptions of such functions are included in the annotated syntax examples in the appendices. More information about each of the functions used in this tutorial can be obtained from the help files included in R or by entering ?<command> in the R command line (e.g., enter ?c to get more information about the c command).

Table 1.

Common R commands for simulation studies.

Commands for working with vectors
Command	Description	Examples
c	Combines arguments to make vectors	#create vector called a which contains the values 3, 5, 4
		a = c(3,5,4)
		#identical to above, uses <- instead of =
		a <- c(3,4,5)
		#return the second element in vector a, which is 5
		a[2]
		#remove the contents previously stored in vector a
		a = NULL
length	Returns the length of a vector	#return length of vector a, which is 3
		a = c(3,5,4)
		length(a)
rbind and cbind	Combine arguments by rows or columns	#create matrix d that has vector a as row 1 and vector b as row 2.
		a = c(3,5,4)
		b = c(9,8,7)
		d = rbind(a,b)
		#create matrix e that has two copies of matrix d joined by column
		e = cbind(d,d)

Commands for generating random values
Command	Description	Examples
rnorm	Randomly samples values from normal distribution with a given population M and SD	#randomly sample 100 values from a normal distribution with a population M = 50 and SD = 10
		x = rnorm(100, 50, 10)
sample	Randomly sample values from another vector	#randomly sample 8 values from vector a, with replacement
		a = c(1,2,3,4,5,6,7,8)
		sample(a, size=8, replace=TRUE)
		#e.g., returns 3 1 3 6 5 4 2 2
set.seed	Allows exact replication of randomly-generated numbers between simulations	#The same 5 random numbers returned each time the following lines are run
		set.seed(12345)
		rnorm(5, 50, 10)

Command for statistical modeling
Command	Description	Examples
lm	fits linear ordinary least squares models	#Regress y onto x1 and x2
		y = c(2,2,5,4,3,6,4,6,5,7)
		x1 = c(1,2,3,1,1,2,3,1,2,2)
		x2 = c(0,0,0,0,0,1,1,1,1,1)
		mymodel = lm(y ~ x1 + x2)
		summary(mymodel)
		#retrieve fixed effect coefficients from a lm object
		mymodel$coefficients

Commands for programming
Command	Description	Examples
function	generate customized function	# function that returns the sum of x1 and x2
		myfunction = function(x1, x2){
		mysum = x1 + x2
		return(mysum)
		}
for	create a loop, allowing sequences of commands to be executed a specified number of times	#Create vector of empirical sample means (stored as mean_vector) from 100 random samples of size N = 20, sampled from a population M = 50 and SD = 10.
		mean_vector = NULL
		for (i in 1:100){
		x = rnorm(20, 50, 10)
		m = mean(x)
		mean_vector = c(mean_vector, m)
		}

Note: Text appearing after the # symbol is not processed by R and is typically reserved for comments and annotation. List of commands is not exhaustive.

R is an object-oriented program that works with data structures such as vectors and data frames. Vectors are one of the simplest data structures and contain an ordered list of values. Vectors will be used throughout the examples described in this tutorial to store values for variables in simulated datasets and to store parameter estimates that are retained from statistical analyses (e.g., p-values, parameter point estimates, etc.). The examples here will make extensive use of commands for generating, indexing, and combining vectors, including the c command for generating and combining vectors, the length command for obtaining the number of items in a vector, and the rbind and cbind commands for combining vectors by row or column, respectively.

Two functions for creating random numbers, rnorm and sample, will be used in the simulation examples in this paper in order to generate values for random variables or to sample subsets of observations from an existing dataset, respectively. An additional function for setting the randomization seed, set.seed, is useful for generating the same sets of random numbers each time a simulation study is run, allowing exact replications of results.

Statistical models in these tutorials will be fit using the lm command, which models linear regression, analysis of variance, and analysis of covariance (however, note that there are many additional native and add-on R packages that can fit a variety of models outside of the general linear model framework). The lm command returns an object with information about the fitted linear model, which may be accessed through additional commands. For example, fixed effect coefficients for the lm object called mymodel shown in Table 1 (under the lm command) can be extracted by calling for the coefficients values of mymodel, such that the syntax

     > f = mymodel$coefficients

returns the regression coefficients for the intercept and effects of x1 and x2 in predicting y from the data in Table 1 and saves it to vector f, which has the following values:

     (Intercept)          x1        x2
      3.07692308 0.07692308 2.36923077

Specific fixed effects could be further extracted by indexing values from vector f; for example, the command f[2] would extract the second value in vector f, which is the fixed effect coefficient for x1.

The function command allows users to generate their own customized functions, which provides a useful way of reducing syntax when a procedure is repeated many times. For example, the first tutorial below computes several Sobel statistics each time a dataset is generated, and declaring a function that computes the Sobel statistic allows the program to call on one function each time the statistic must be computed, rather than repeating several lines of the same syntax within the simulation. The for command is used to create loops, which allow sequences of commands that are specified once to be executed several times. This is useful in simulation studies because datasets often must be generated and analyzed hundreds or thousands of times.

Tutorials

This section will outline examples of questions that may be answered using simulation studies and describes the methods used to answer those questions. In each example, the underlying assumptions and procedures for generating and analyzing data will be discussed, and fully annotated syntax for the simulations will be provided as appendices.

Example 1: Answering a Novel Question about Mediation Analysis

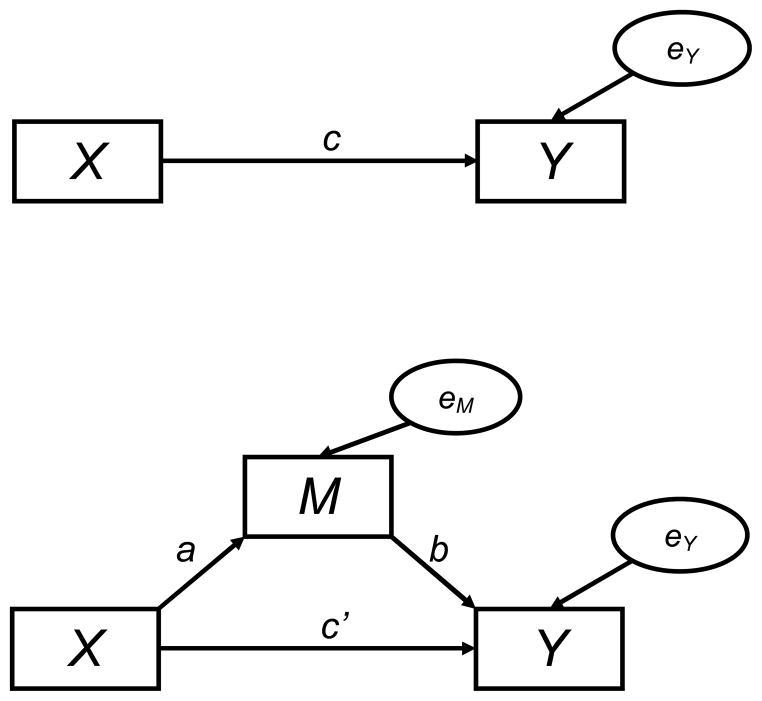
Mediation analysis is a statistical technique for analyzing whether the effect of an independent variable (X) on an outcome variable (Y) can be accounted for by an intermediate variable (M; see Figure 1 for graphical depiction; see Hayes 2009 for pedagogical review). When mediation is present, the degree to which X predicts Y is changed when M is added to the model in the manner shown in Figure 1 (i.e., c – c′ ≠ 0 in Figure 1). The degree to which the relationship between X and Y changes (c – c′) is called the indirect effect, which is mathematically equivalent to the product of the path coefficients ab shown in Figure 1. The product of path coefficients ab (or equivalently, c – c′) represents the amount of change in outcome variable Y that can be attributed to being caused by changes in the independent variable X operating through the mediating variable M. In situations where a mediator variable cannot be directly manipulated through experimentation, mediation analysis has often been championed as a method of choice for identifying variables that may cause an observed outcome (Y) as part of a causal sequence where X affects M, and M in turn affects Y.

Figure 1.

Direct effect model (top) and mediation model (bottom).

For example, in psychotherapy research, the number of times participants receive drink-refusal training (X) may impact their self-efficacy to refuse drinks (M), and enhanced self-efficacy may in turn cause improved abstinence from alcohol (Y; e.g., Witkiewitz, Donovan, & Hartzler, 2012). Self-efficacy cannot be directly manipulated by experiment, so researchers may use mediation analysis to test whether a particular psychotherapy increases self-efficacy, and whether this in turn increases abstinence outcomes. However, little research has identified the consequences of wrongly specifying which variables are mediator variables (M) versus outcome variables (Y). For example, it could also be possible that drink-refusal training (X) enhances abstinence from alcohol (Y), which in turn enhances self-efficacy (M; e.g., X causes Y, Y causes M). Support for this alternative model would guide treatment providers and subsequent research efforts toward different goals than the original model, and therefore it is important to know whether mediation models are likely to produce significant results even when the true causal order of effects is incorrectly specified by investigators.

The present example uses simulations to test whether mediation models produce significant results when the implied causal ordering of effects is switched within the tested model. Data is generated for three variables, X, M, and Y, such that M mediates the relationship between X and Y (“X-M-Y” model) using ordinary least-squares (OLS) regression. Path coefficients for a (X predicting M; see Figure 1) and b (M predicting Y, controlling for X) will each be manipulated at three levels (−0.3, 0.0, 0.3), c′ (X predicting Y, controlling for M) will be manipulated at three levels (−0.2, 0.0, 0.2), and sample size (N) will be manipulated at two levels (100, 300). This results in a 3 (X) × 3 (M) × 3 (Y) × 2 (N) design. One thousand simulated datasets will be generated in each condition. Data will be generated for an X-M-Y model, and mediation tests will be conducted on the original X-M-Y models and with models that switch the order of M and Y variables (i.e., X-Y-M models). The Sobel test (MacKinnon, Warsi, & Dwyer, 1995; Sobel, 1982) will be computed and retained for each type of mediation model, with p < 0.05 indicating significant mediation for that particular model.

Assumptions about the nature and properties of a dataset

Data in this example are generated in accordance with OLS regression assumptions, including the assumptions that random variables are sampled from populations with normal distributions, that residual errors are normally distributed with a mean of zero, and that residual errors are homoscedastic and serially uncorrelated. Assumptions about the relationships among X, M, and Y variables from Figure 1 are guided by the equations provided by Jo (2008),

$$M_i={\alpha }_m+\alpha X_i+{\epsilon }_{mi}$$ (1)

and

$$Y_i={\alpha }_y+{bM}_i+c^{\prime }{X}_i+{\epsilon }_{yi},$$ (2)

where X_i, M_i, and Y_i represent values for the independent variable, mediator, and outcome for individual i, respectively; α_m and α_y represent the intercepts for M and Y after the other effects are accounted for, and a, b, and c′ correspond with the mediation regression paths shown in Figure 1.

Generating data

Data for X, M, and Y with sample size N can be generated using the rnorm command. If N, a, b, and c′ (c′ is named cp in the syntax below) are each specified as single numeric values, then the following syntax will generate data for the X, M, and Y variables.

     > X = rnorm(N, 0, 1)
     > M = a*X + rnorm(N, 0, 1)
     > Y = cp*X + b*M + rnorm(N, 0, 1)

The first line of the syntax above creates a random variable X with a mean of zero and a standard deviation of one for N observations. The second line creates a random variable M that regresses onto X with regression coefficient a and a random error with a mean of zero and standard deviation of one (error variances need not be fixed with a mean of zero and standard deviation of one, and can be specified at any value based on previous research or theoretically-expected values). The third line of syntax creates a random variable Y that regresses onto X and M with regression coefficients cp and b, respectively, with a random error that has a mean of zero and standard deviation of one. It will be shown below that the intercept parameters do not affect the significance of a mediation test, and thus the intercepts were left at zero in the three lines of code above; however, the intercept parameter could be manipulated in a similar manner to a, b, and c′ if desired.

Statistical analyses are performed and parameters are retained

Once the random variables X, M, and Y have been generated, the next step is to perform a statistical analysis on the simulated data. In mediation analysis, the Sobel test (MacKinnon et al., 1995; Sobel, 1982) is commonly employed (although, see section below on bootstrapping), which tests the significance of a mediation effect by computing the magnitude of the indirect effect as the product of coefficients a and b (ab) and compares this value to the standard error of ab to obtain a z-like test statistic. Specifically, the Sobel test uses the formula

$$\mathit{Sobel}z=\frac{ab}{\sqrt{b^2{s_a}^2+a^2{s_b}^2}}$$ (3)

where s_a and s_b are the standard errors of the estimates for regression coefficients a and b, respectively. The product of coefficients ab reflects the degree to which the effect of X on Y is mediated through variable M, and is contained in the numerator of Equation 3. The standard error of the distribution of ab is in the denominator of Equation 3, and the Sobel statistic obtained in the full equation provides a z-like statistic that tests whether the ab effect is significantly different from zero. Because the Sobel test will be computed many times, making a function to compute the Sobel test provides an efficient way to compute the test repeatedly. Such a function is defined below and called sobel_test. The function takes three arguments, vectors X, M, and Y as the first, second, and third arguments, respectively, and computes regression models for M regressed onto X and Y regressed onto X and M. The coefficients representing a, b, s_a, and s_b in Equation 3 are extracted by calling coefficients, then a Sobel test is computed and returned.

     > sobel_test <- function (X, M, Y){
     >   M_X = lm (M ~ X)
     >   Y_XM = lm (Y ~ X + M)
     >   a = coefficients (M_X) [2]
     >   b = coefficients (Y_XM) [3]
     >   stdera = summary (M_X) $coefficients [2,2]
     >   stderb = summary (Y_XM) $coefficients [3,2]
     >   sobelz = a*b / sqrt(b^2*stdera^2 + a^2*stderb^2)
     >    return(sobelz)
     > }

Data are generated and analyzed many times under the same conditions

So far syntax has been provided to generate one set of X, M, and Y variables and to compute a Sobel z-statistic from these variables. These procedures can now be repeated several hundred or thousand times to observe how this model behaves across many samples, which may be accomplished with for loops, as shown below. In the syntax below, the procedure for generating data and computing a Sobel test is repeated reps number of times, where reps is a single integer value. For each iteration of the for loop, data are saved to a matrix called d to retain information about the iteration number (i), a, b, and c′ parameters (a, b, and cp), the sample size (N), an indexing variable that tells whether the test statistic corresponds with an X-M-Y or X-Y-M mediation model (1 vs. 2), and the computed Sobel test statistic which calls on the sobel_test function above.

       > for (i in 1:reps){
          >  X = rnorm (N, 0, 1)
          >  M = a*X + rnorm (N, 0, 1)
          >  Y = cp*X + b*M + rnorm (N, 0, 1)
          >  d = rbind (d, c(i, a, b, cp, N, 1,
              sobel_test(X, M, Y
)))
          >  d = rbind(d, c(i, a, b, cp, N, 2,
              sobel_test(X, Y, M
)))
       > }

The above steps can then be repeated for datasets generated according to different parameters. In the present example, we wish to test three different values of a, b, c′, and N. Syntax for manipulating these parameters is included below. The values selected for a, b, c′, and N are specified as vectors called a_list, b_list, cp_list, and N_list, respectively. Four nested for loops index through each of the values in a_list, b_list, cp_list, and N_list and extract single values for these parameters that are used for data generation. For each combination of a, b, c′, and N, reps number of datasets are generated and subjected to the Sobel test using the same syntax presented above (some syntax is omitted below for brevity, and full syntax with more detailed annotation for this example is provided in Appendix A), and the data are then saved to a matrix called d:

          > N_list = c(100, 300)
          > a_list = c(-.3, 0, .3)
          > b_list = c(-.3, 0, .3)
          > cp_list = c(-.2, 0, .2)
          > reps = 1000
          > for (N in N_list){
          >    for (a in a_list){
          >       for (b in b_list){
          >           for (cp in cp_list){
          >              for (i in 1:reps){
          >                  X = rnorm(N, 0, 1)
          >                  M = a*X + rnorm(N, 0, 1)
                             #... syntax omitted
           >                 d = rbind(d, c(i, a, b, cp,
                                 N, 2, sobel_test(X, Y,
                                 M
)))
          >              }
          >           }
          >       }
          >    }
          > }

Retained parameter estimates are analyzed to evaluate the question of interest

Executing the syntax above generates a matrix d that contains Sobel test statistics for X-M-Y (omitted for brevity) and X-Y-M mediation models (shown above) generated from a variety of a, b, c′, and N parameters. The next step is to evaluate the results of these models. Before this is done, it will be helpful to add labels to the variables in matrix d to allow for easy extraction of subsets of the results and to facilitate their interpretation:

          > colnames(d) = c(“iteration”, “a”, “b”, “cp”, “N”,
               “model”, “Sobel_z”
)

It is also desirable to save a backup copy of the results using the command

          > write.table(d,”C:\\...\\mediation_output.csv”,
               sep=“,”, row.names=FALSE
)

In the syntax above, “...” must be replaced with the directory where results should be saved, and each folder must be separated by double backslashes (“\\”) if the R program is running on a Windows computer (on Macintosh, a colon “:” should be used, and in Linux/Unix, a single forward slash “/” should be used).

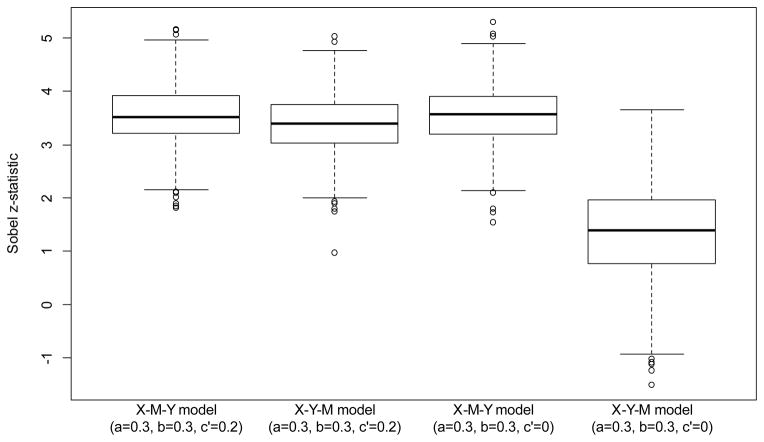
Researchers can choose any number of ways to analyze the results of simulation studies, and the method chosen should be based on the nature of the question under examination. One way to compare the distributions of Sobel z-statistics obtained for the X-M-Y and X-Y-M mediation models in the current example is to use boxplots, which can be created in R (see ?boxplot for details) or other statistical software by importing the mediation_output.csv file into other data analytic software. As seen in Figure 2, in the first two conditions where the population parameters a = 0.3, b = 0.3, and c′ = 0.2, Sobel tests for X-M-Y and X-Y-M mediation models produce test statistics with nearly identical distributions and Sobel test-values are almost always significant (|z| > 1.96, which corresponds with p < .05, two-tailed) when N = 300 and other assumptions described above are held. In the latter two conditions where the population parameters a = 0.3, b = 0.3, and c′ = 0, Sobel tests for X-M-Y models remain high, while test statistics for X-Y-M models are lower even though approximately 25% of these models still had Sobel z-test statistics with magnitudes greater than 1.96 (and thus, p-values less than 0.05).

Figure 2.

Boxplot of partial results from Example 1 with N = 300.

The similarity of results between X-M-Y and X-Y-M models suggests limitations of using mediation analysis to identify causal relationships. Specifically, the same datasets may produce significant results under a variety of models that support different theories of the causal ordering of relations. For example, a variable that is truly a mediator may instead be specified as an outcome and still produce “significant” results in a mediation analysis. This could imply misleading support for a causal chain due to the way researchers specify the ordering of variables in the analysis. This finding suggests that mediation analysis may produce misleading results in some situations, particularly when data are cross-sectional because of the lack of temporal-ordering for observations of X, M, and Y that could provide stronger testing of a proposed causal sequence (Maxwell & Cole, 2007; Maxwell, Cole, & Mitchell, 2011). One implication of these findings is that researchers who perform mediation analysis should test alternative models. For example, researchers could test alternative models with assumed mediators modeled as outcomes and assumed outcomes modeled as mediators to test whether other plausible models are also “significant” (e.g., Witkiewitz et al., 2012).

Example 2: Estimating the Statistical Power of a Model

Simulations can be used to estimate the statistical power of a model -- i.e., the likelihood of rejecting the null hypothesis for a particular effect under a given set of conditions. Although statistical power can be estimated directly for many analyses with power tables (e.g., Maxwell & Delaney, 2004) and free software such as G*Power (Erdfelder, Faul, & Buchner, 2006; see Mayr, Erdfelder, Buchner, & Faul, 2007 for a tutorial on using G*Power), many types of analyses currently have no well-established method to directly estimate statistical power, as is the case with mediation analysis.

The steps in Example 1 provide the necessary data to estimate the power of a mediation analysis if the assumptions and parameters specified in Example 1 remain the same. Thus, using the simulation results saved in dataset d generated in Example 1, the power of a mediation model under a given set of conditions can be estimated by identifying the relative frequency in which a mediation test was significant.

For example, the syntax below extracts the Sobel test statistic from dataset d under the condition where a = 0.3, b = 0.3, c′ = 0.2, N = 300, and “model” = 1 (i.e., an X-M-Y mediation model is tested). The vector of Sobel test statistics across 1000 repetitions is saved in a variable called z_dist. The absolute value each of the numbers in z_dist is compared against 1.96 (i.e., the z-value that corresponds with p < 0.05, two-tailed), creating a vector of values that are either TRUE (if the absolute value is greater than 1.96) or FALSE (if the absolute value is less than or equal to 1.96). The number of TRUE and FALSE values can be summarized using the table command (see ?table for details), which if divided by the length of the number of values in the vector will provide the proportion of Sobel tests with absolute value greater than 1.96:

          > z_dist = d$Sobel_z[d$a==0.3 & d$b==0.3 & d$cp==0.2 & d$N==300 &
              d$model==1]
          > significant = abs(z_dist) > 1.96
          > table(significant)/length(significant)

When the above syntax is run, the following result is printed

          significant
          FALSE TRUE
          0.003   0.997

which indicates that 99.7% of the datasets randomly sampled under the conditions specified above produced significant Sobel tests, and that the analysis has an estimated power of 0.997.

One could also test the power of mediation models with different parameters specified. For example, the power of a model with all the same parameters as above except with a smaller sample size of N = 100 could be examined using the syntax

          > z_dist = d$Sobel_z[d$a==0.3 & d$b==0.3 & d$cp==0.2 &
               d$N==100 & d$model==1]
          > significant = abs(z_dist) > 1.96
          > table(significant)/length(significant)

which produces the following output

          significant
          FALSE TRUE
          0.485   0.515

The output above indicates that only 51.5% of the mediation models in this example were significant, which reflects the reduced power rate due to the smaller sample size. Full syntax for this example is provided in Appendix B.

Example 3: Bootstrapping to Obtain Confidence Intervals

In the above examples, the Sobel test was used to determine whether a mediation effect was significant. Although the Sobel test is more robust than other methods such as Baron and Kenny’s (1984) causal steps approach (Hayes, 2009; McKinnon et al., 1995), a limitation of the Sobel test is that it assumes that the sampling distribution of indirect effects (ab) is normally distributed in order for the p-value obtained from the z-like statistic to be valid. This assumption typically is not met because the sampling distributions for a and b are each independently normal, and multiplying a and b introduces skew into the sampling distribution of ab. Bootstrapping can be used as an alternative to the Sobel test to obtain an empirically derived sampling distribution with confidence intervals that are more accurate than the Sobel test.

To obtain an empirical sampling distribution of indirect effects ab, N randomly selected participants from an observed dataset are sampled with replacement, where N is equal to the original sample size. A dataset containing the observed X, M, and Y values for these randomly resampled participants is created and subject to a mediation analysis using Equations 1 and 2. The a and b coefficients are obtained from these regression models, and the product of these coefficients, ab, is computed and retained. This procedure is repeated many times, perhaps 1000 or 10,000 times, with a new set of subjects from the original sample randomly selected with replacement each time (Hélie, 2006). This provides an empirical sampling distribution of the product of coefficients ab that no longer requires the standard error of the estimate for ab to be computed.

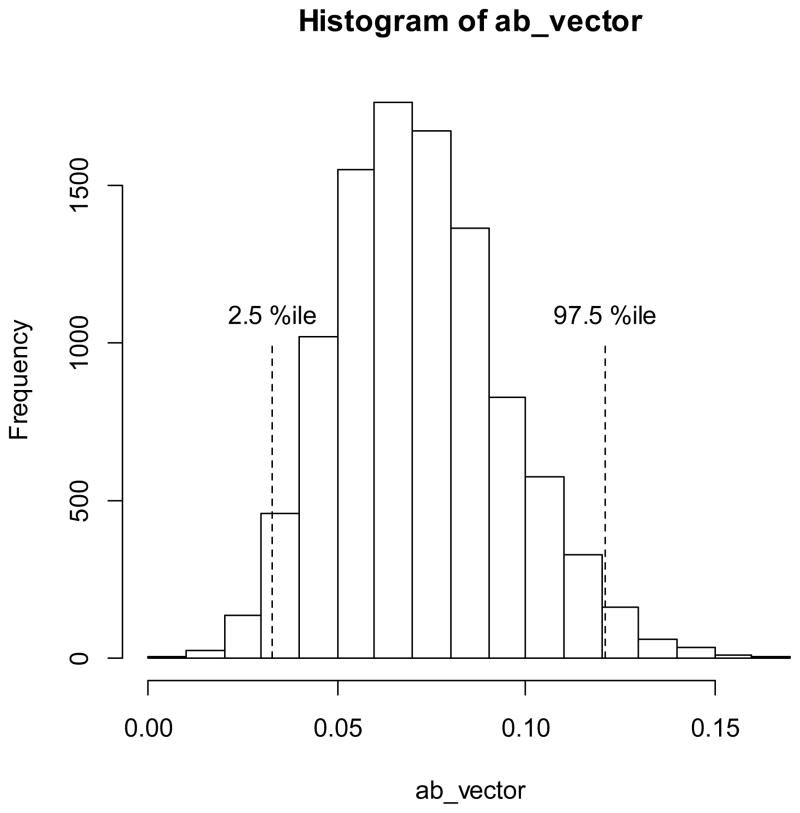
The syntax below provides the steps for bootstrapping a 95% confidence interval of an indirect effect for variables X, M, and Y. A variable called ab_vector holds the bootstrapped distribution of ab values, and is initialized using the NULL argument to remove any data previously stored in this variable. A for loop is specified to repeat reps number of times, where reps is a single integer representing the number of repetitions that should be used for bootstrapping. Variable s is a vector containing row numbers of participants that are randomly sampled with replacement from the original observed sample (raw data for X, M, and Y in this example is provided in the supplemental file mediation_raw_data.csv; see Appendix C for syntax to import this dataset into R). The vectors Xs, Ys, and Ms store the values for X, Y, and M, respectively, that correspond with the subjects resampled based on the vector s. Finally, M_Xs and Y_XMs are lm objects containing linear regression models for Ms regressed onto Xs and for Ys regressed onto Xs and Ms, respectively, and the a and b coefficients in these two models are extracted. The product of coefficients ab is computed and saved to ab_vector, then the resampling process and computation of the ab effect are repeated. Once the repetitions are completed, 95% confidence interval limits are obtained using the quantile command to identify the values in ab_vector at the 2.5th and 97.5 percentiles (these values could be adjusted to obtain different confidence intervals; enter ?quantile in the R console for more details), and the result is saved in a vector called bootlim. Finally, a histogram of the ab effects in ab_vector is printed and displayed in Figure 3.

Figure 3.

Empirical distribution of indirect effects (ab) used for bootstrapping a confidence interval.

          > ab_vector = NULL
          > for (i in 1:reps){
          >   s = sample(1:length(X), replace=TRUE)
          >   Xs = X[s]
          >   Ys = Y[s]
          >   Ms = M[s]
          >   M_Xs = lm(Ms ~ Xs)
          >   Y_XMs = lm(Ys ~ Xs + Ms)
          >    a = M_Xs$coefficients[2]
           >   b = Y_XMs$coefficients[3]
          >    ab = a*b
          >    ab_vector = c(ab_vector, ab)
          > }
          > bootlim = c(quantile(ab_vector, 0.025),
              quantile(ab_vector, 0.975))
          > hist(ab_vector)

Full syntax with annotation for the bootstrapping procedure above is provided in Appendix C. Calling the bootlim vector returns the indirect effects that correspond with the 2.5th and 97.5th percentile of the empirical sampling distribution of ab, giving the following output:

               2.5%      97.5%
          0.06635642    0.17234665

Because the 95% confidence interval does not contain zero, the results indicate that the product of coefficients ab is significantly different than zero at p < 0.05.

Discussion

The preceding sections provided demonstrations of methods to implement simulation studies for different purposes, including answering novel questions related to statistical modeling, estimating power, and bootstrapping confidence intervals. The demonstrations presented here used mediation analysis as the content area to demonstrate the underlying processes used in simulation studies, but simulation studies are not limited only to questions related to mediation. Virtually any type of analysis or model could be explored using simulation studies. While the way that researchers construct simulations depends largely on the research question of interest, the basic procedures outlined here can be applied to a large array of simulation studies.

While it is possible to run simulation studies in other programming environments (e.g., the latent variable modeling software MPlus, see Muthén & Muthén, 2002), R may provide unique advantages to other programs when running simulation studies because it is free, open source, and cross-platform. R also allows researchers to generate and manipulate their data with much more flexibility than many other programs, and contains packages to run a multitude of statistical analyses of interest to social science researchers in a variety of domains.

There are several limitations of simulation studies that should be noted. First, real-world data often do not adhere to the assumptions and parameters by which data are generated in simulation studies. For example, unlike the linear regression models for the examples above, it is often the case in real world studies that residual errors are not homoscedastic and serially uncorrelated. That is, real-world datasets are likely to be more “dirty” than the “clean” datasets that are generated in simulation studies, which are often generated under idealistic conditions. While these “dirty” aspects of data can be incorporated into simulation studies, the degree to which these aspects should be modeled into the data may be unknown and thus at times difficult to incorporate in a realistic manner.

Second, it is practically impossible to know the values of true population parameters that are incorporated into simulation studies. For example, in the mediation examples above, the regression coefficients a, b, and c’ often may be unknown for a question of interest. Even if previous research provides empirically-estimated parameter estimates, the exact value for these population parameters is still unknown due to sampling error. To deal with this, researchers can run simulations across a variety of parameter values, as was done in Examples 1 and 2, to understand how their models may perform under different conditions, but pinpointing the exact parameter values that apply to their question of interest is unrealistic and typically impossible.

Third, simulation studies often require considerable computation time because hundreds or thousands of datasets often must be generated and analyzed. Simulations that are large or use iterative estimation routines (e.g., maximum likelihood) may take hours, days, or even weeks to run, depending on the size of the study.

Fourth, not all statistical questions require simulations to obtain meaningful answers. Many statistical questions can be answered through mathematical derivations, and in these cases simulation studies can demonstrate only what was shown already to be true through mathematical proofs (Maxwell & Cole, 1995). Thus, simulation studies are utilized best when they derive answers to problems that do not contain simple mathematical solutions.

Simulation methods are relatively straightforward once the assumptions of a model and the parameters to be used for data generation are specified. Researchers who use simulation methods can have tight experimental control over these assumptions and their data, and can test how a model performs under a known set of parameters (whereas with real-world data, the parameters are unknown). Simulation methods are flexible and can be applied to a number of problems to obtain quantitative answers to questions that may not be possible to derive through other approaches. Results from simulation studies can be used to test obtained results with their theoretically-expected values to compare competing approaches for handling data, and the flexibility of simulation studies allows them to be used for a variety of purposes.

Appendix A. Syntax for Example 1

#Answering a novel question about mediation analysis
#This simulation will generate mediational datasets with three variables,
#X, M, and Y, and will calculate Sobel z-tests for two competing mediation
#models in each dataset: the first mediation model proposing that M mediates
#the relationship between X and Y (X-M-Y mediation model), the second
#mediation model poposes that Y mediates the relationship between X and M
#(X-Y-M mediation model).
#Note this simulation may take 10-45 minutes to complete, depending on
#computer speed
#Data characteristics specified by researcher -- edit these as needed
N_list = c(100, 300)   #Values for N (number of participants in sample)
a_list = c(-.3, 0, .3)    #values for the “a” effect (regression coefficient
                   #for X->M path)
b_list = c(-.3, 0, .3)    #values for the “b” effect (regression coefficient
                   #for M->Y path after X is controlled)
cp_list = c(-.2, 0, .2)   #values for the “c-prime” effect (regression
                    #coefficient for X->Y after M is controlled)
reps = 1000          #number of datasets to be generated in each condition
#Set starting seed for random number generator, this is not necessary but
#allows results to be replicated exactly each time the simulation is run.
set.seed(192)
#Create a function for estimating Sobel z-test of mediation effects
sobel_test <- function(X, M, Y){
     M_X = lm(M ~ X)
     #regression model for M predicted by X
     Y_XM = lm(Y ~ X + M)
     #regression model for Y predicted by X and M
     a = coefficients(M_X)[2]
     #extracts the estimated “a” effect
     b = coefficients(Y_XM)[3]
     #extracts the estimated “b” effect
     stdera = summary(M_X)$coefficients[2,2]  #extracts the standard error
                                         #of the “a” effect
     stderb = summary(Y_XM)$coefficients[3,2] #extracts the standard error
                                         #of the “b” effect
     sobelz = a*b / sqrt(b^2 * stdera^2 + a^2 * stderb^2)   #computes the
                                  #Sobel z-test statistic
     return(sobelz)
     #return the Sobel z-test statistic when this function is called
}
#run simulation
d = NULL #start with an empty dataset
#loop through all of the “N” sizes specified above
for (N in N_list){
     #loop through all of the “a” effects specified above
     for (a in 1:a_list){
          #pick one “a” effect with which data will be simulated. This
          #will start with #the value a = -0.3.
          #loop through all of the “b” effects specified above
          #pick one “b” effect with which data will be simulated
          for (b in b_list){
               #loop through all of the “c-prime” effects specified above
               for (cp in cp_list){
                    #loop to replicate simulated datasets within each
                    #condition
                    for (i in 1:reps){
                         #Generate mediation based on MacKinnon,
                         #Fairchild, & Fritz (2007) equations for
                         #mediation. This data is set-up so that X, M,
                         #and Y are conformed to be the idealized
                         #mediators
                         #generate random variable X that has N
                         #observations, mean = 0, sd = 1
                         X = rnorm(N, 0, 1)
                         #generate random varible M that inclues the “a”
                         #effect due to X and random error with mean =
                         #0, sd = 1
                         M = a*X + rnorm(N, 0, 1)
                         #generate random variable Y that includes “b”
                         #and “c-prime” effects and random error with
                         #mean = 0, sd = 1
                         Y = cp*X + b*M + rnorm(N, 0, 1)
                         #Compute Sobel z-test statistic for X-M-Y
                         #mediation and save parameter information to
                         #dtemp
                         d = rbind(d, c(i, a, b, cp, N, 1,
                              sobel_test(X, M, Y)))
                         #Compute Sobel z-test statistic for M-Y-X
                         #mediation and save parameter information to
                         #dtemp
                         d = rbind(d, c(i, a, b, cp, N, 2,
                              sobel_test(X, Y, M)))
                    }
               }
          }
     }
}
#add column names to matrix “d” and convert to data.frame
colnames(d) = c(“iteration”, “a”, “b”, “cp”, “N”, “model”, “Sobel_z”)
d = data.frame(d)
#save data frame “d” as a CSV file (need to change save path as needed)
write.table(d, “C:\\Users\\...\\novel_question_output.csv”, sep=“,”,
row.names=FALSE)
#save raw data from last iteration to data.set to illustrate bootstrapping
#example (change file path as needed)
d_raw = cbind(X, M, Y)
write.table(d_raw, “C:\\Users\\...\\mediation_raw_data.csv”, sep=“,”,
row.names=FALSE)
#Make a boxplot of X-M-Y and X-Y-M models when a=0.3, b=0.3, c’ = 0.2, N =
#300, and when a=0.3, b=0.3, c’=0, N = 300.
boxplot(d$Sobel_z[d$a == 0.3 & d$b == 0.3 & d$cp == 0.2 & d$model == 1 & d$N
== 300],
        d$Sobel_z[d$a == 0.3 & d$b == 0.3 & d$cp == 0.2 & d$model == 2 & d$N ==
300],
        d$Sobel_z[d$a == 0.3 & d$b == 0.3 & d$cp == 0 & d$model == 1 & d$N ==
300],
        d$Sobel_z[d$a == 0.3 & d$b == 0.3 & d$cp == 0 & d$model == 2 & d$N ==
300],
        ylab=“Sobel z-statistic”,
        xaxt = ‘n’,
        tick=FALSE) #suppress x-axis labels to remove tick marks
#Add labels to x-axis manually
axis(1,at=c(1:4),labels=c(“X-M-Y model\n(a=0.3, b=0.3, c’=0.2)”, “X-Y-M
model\n(a=0.3, b=0.3, c’=0.2)”, “X-M-Y model\n(a=0.3, b=0.3, c’=0)”, “X-Y-M
model\n(a=0.3, b=0.3, c’=0)”),tick=FALSE)

Appendix B. Syntax for Example 2

#Estimating power of a mediation test
#read simulated dataset (change file path as needed)
d = read.csv(“C:\\Users\\...\\novel_question_output.csv”, header=TRUE,
sep=“,”)
#Example where a = 0.3, b=0.3, c’=0.2, N = 300
#extract Sobel z-statistic from the condition of interest
z_dist = d$Sobel_z[d$a==0.3 & d$b==0.3 & d$cp==0.2 & d$N==300 & d$model==1]
#identify which z-values are large enough to give p-value < 0.05
significant = abs(z_dist) > 1.96
#identify the proportion of z-values with p-value < 0.05. The proportion of
#values that are TRUE is equal to the proportion of times the null hypothesis
#of no indirect effect is rejected and is equivalent to power.
table(significant)/length(significant)
#Example where a = 0.3, b=0.3, c’=0.2, N = 100
#extract Sobel z-statistic from the condition of interest
z_dist = d$Sobel_z[d$a==0.3 & d$b==0.3 & d$cp==0.2 & d$N==100 & d$model==1]
#identify which z-values are large enough to give p-value < 0.05
significant = abs(z_dist) > 1.96
#identify the proportion of z-values with p-value < 0.05. The proportion of
#values that are TRUE is equal to the proportion of times the null hypothesis
#of no indirect effect is rejected and is equivalent to power.
table(significant)/length(significant)
#Other example where a = 0.3, b=0, c’=0.2, N = 300
#extract Sobel z-statistic from the condition of interest
z_dist = d$Sobel_z[d$a==0.3 & d$b==0 & d$cp==0.2 & d$N==300 & d$model==1]
#identify which z-values are large enough to give p-value < 0.05
significant = abs(z_dist) > 1.96
#identify the proportion of z-values with p-value < 0.05. The proportion of
#values that are TRUE is equal to the proportion of times the null hypothesis
#of no indirect effect is rejected and is equivalent to power.
table(significant)/length(significant)

Appendix C. Syntax for Example 3

#Bootstrapping a 95% CI for mediation test
#Create a function for bootstrapping
mediation_bootstrap <- function(X, M, Y, reps){
      ab_vector = NULL #remove any data that is stored under the variable
                      #ab_vector
      for (i in 1:reps){ #loop the number of times specified by the reps
                      #parameter
          s = sample(1:length(X), replace=TRUE)  #sample cases N cases
                                             #WITH replacement
          Xs = X[s] #extract X variable for the sampled cases indexed by s
          Ys = Y[s] #extract Y variable for the sampled cases indexed by s
          Ms = M[s] #extract M variable for the sampled cases indexed by s
          M_Xs = lm(Ms ~ Xs)      #perform a regression model of M
                                  #predicted by X
          Y_XMs = lm(Ys ~ Xs + Ms) #perform a regression model of Y
                                  #predicted by X and M
          a = M_Xs$coefficients[2]   #extract beta coefficient for magnitude
                                  #of X->M relationship
          b = Y_XMs$coefficients[3]       #extract beta coefficient for
                                       #magnitude of M->Y relationship
                                       #(with X covaried)
          ab = a*b     #compute product of coefficients
          ab_vector = c(ab_vector, ab)      #save each computed product of
                                       #coefficients to vector called
                                       #ab_vector
      }
     bootlim = c(quantile(ab_vector, 0.025), quantile(ab_vector, 0.975))
          #identify ab values at 2.5 and 97.5 percentile, representing 95%
          #CI
     hist(ab_vector)
     segments(bootlim, y0=0, y1=1000, lty=2)
     text(bootlim, y=1100, labels=c(“2.5 %ile”, “97.5 %ile”))
     return(bootlim) #return the 95% CI
}
#Set starting seed for random number generator, this is not necessary but
#allows results to be replicated exactly each time the simulation is run.
set.seed(192)
#import raw data for bootstrapping (change file path as needed)
d_raw = read.csv(“C:\\Users\\...\\mediation_raw_data.csv”, header=TRUE,
sep=“,”)
#identify 95% confidence interval for indirect effect in X-M-Y mediation
#model
mediation_bootstrap(d_raw$X, d_raw$M, d_raw$Y, 1000)