Patterns of Cognitive Strengths and Weaknesses: Identification Rates, Agreement, and Validity for Learning Disabilities Identification

Abstract

Purpose

Few empirical investigations have evaluated LD identification methods based on a pattern of cognitive strengths and weaknesses (PSW). This study investigated the reliability and validity of two proposed PSW methods: the concordance/discordance method (C/DM) and cross battery assessment (XBA) method.

Methods

Cognitive assessment data for 139 adolescents demonstrating inadequate response to intervention was utilized to empirically classify participants as meeting or not meeting PSW LD identification criteria using the two approaches, permitting an analysis of: (1) LD identification rates; (2) agreement between methods; and (3) external validity.

Results

LD identification rates varied between the two methods depending upon the cut point for low achievement, with low agreement for LD identification decisions. Comparisons of groups that met and did not meet LD identification criteria on external academic variables were largely null, raising questions of external validity.

Conclusions

This study found low agreement and little evidence of validity for LD identification decisions based on PSW methods. An alternative may be to use multiple measures of academic achievement to guide intervention.

In recent years, advocates of cognitive discrepancy frameworks have proposed that children with LD be identified according to patterns of cognitive processing strengths and weaknesses (PSW; Hale et al., 2010). Three methods have been proposed to operationalize this approach: (a) the concordance/discordance method (C/DM; Hale &Fiorello, 2004), (b) the cross battery assessment method (XBA; Flanagan, et al., 2007), and (c) the Discrepancy/Consistency Method (D/CM; Naglieri, 1999). Although often treated as interchangeable, these methods differ in important ways, including: (a) how achievement deficits and cognitive weaknesses are theoretically linked; (b) the role of exclusionary factors that may preclude LD identification (e.g., emotional, economic factors); (c) specified thresholds for achievement deficits; and (d) methods for establishing a cognitive discrepancy.

Proponents contend that PSW methods are important because cognitive assessment can be used to plan treatment and to differentiate students with “specific” learning disabilities from “slow learners” with more global deficits. Despite the strong claims by PSW advocates, empirical studies demonstrating the reliability and validity of PSW methods have been slow to emerge. No published empirical study has investigated the reliability and validity of LD identification decisions resulting from PSW methods. Further, no study has investigated the implementation of these LD identification methods following a determination of inadequate response to intervention, a “hybrid” model that provides early intervention through RTI service delivery models, followed by comprehensive assessment for LD identification for students who demonstrate inadequate response to Tier 2 intervention (Fiorello, Hale, & Snyder, 2010; Hale et al., 2010). In the present study, we utilized a sample of inadequate responders to Tier 2 intervention to investigate: (a) LD identification rates; (b) extent of agreement; and (c) academic attributes of groups resulting from two proposed PSW methods for LD identification: the C/DM and XBA methods. A third proposed PSW method, the D/CM, requires a specific assessment battery (Cognitive Assessment System, Naglieri & Das, 1997) and is therefore not included in the present study.

The Concordance/Discordance Method (C/DM)

The C/DM specifies that LD is marked by an intraindividual pattern of concordance and discordance that includes: (a) a concordance between a theoretically related academic achievement weakness and a cognitive processing weakness; (b) a discordance between the academic achievement weakness and a cognitive processing strength; and (c) a discordance between the cognitive processing weakness and a cognitive processing strength (Hale & Fiorello, 2004). Determinations of concordance and discordance between academic and cognitive processing deficits and strengths are based on thresholds for significant differences. These thresholds are based on calculations employing one of two estimates of the distribution of differences: (a) the standard error of the difference or (b) the standard error of the residual. Observed score differences are then compared to determine if the differences are: (a) concordant (i.e. the observed difference does not exceed the significant difference threshold); or (b) discordant (i.e. the observed difference exceeds the significant difference threshold). LD identification is based on: (a) identification of the C/DM pattern; (b) consideration of exclusionary clauses; and (c) professional judgment.

The Cross Battery Assessment

The XBA method specifies four necessary conditions to establish a PSW: (a) a normative deficit in academic achievement; (b) a normative deficit in a cognitive processing skill; (c) a theoretical relation between deficits in achievement and cognitive processing; and (d) an otherwise “normal” cognitive profile (Flanagan et al., 2007). An academic achievement or cognitive processing deficit is defined as a score more than one standard deviation below the population mean on a standardized assessment (standard score < 85).

Flanagan et al. (2007) specified procedures to determine whether the student demonstrated “normal” cognitive abilities based on the Cattell-Horn-Carroll (CHC) theory. Performance within seven CHC broad clusters is dichotomized as either deficient or normal. The dichotomous (0/1) variable in each CHC broad cluster is multiplied by a g loading specified in the SLD scoring assistant (Flanagan et al, 2007). The products are summed across the clusters and if the sum is greater than one, the student demonstrates normal cognitive abilities. LD identification is based on the necessary XBA PSW pattern and a consideration of exclusionary clauses.

Cognitive Assessment and Cattell-Horn-Carroll Theory

The two PSW methods emphasize flexibility in the selection of measures constituting a comprehensive psychoeducational assessment battery. The C/DM method is compatible with both CHC and Lurian approaches to designing and interpreting cognitive assessments, while the XBA method implements tests based on the CHC theory of cognitive abilities. In the present study, we utilized an assessment battery consistent with CHC theory to evaluate and empirically classify inadequate responders as meeting or not meeting LD criteria according to PSW methods.

Modern CHC theory is based on the three stratum theory of cognitive ability (Carroll 1993) and extended G_f-G_c theory (Horn & Noll, 1997). It synthesizes these theories into a single, hierarchical taxonomy of cognitive functioning (McGrew, 2009). Within CHC Theory, cognitive ability is divided into three strata. Stratum III represents overall cognitive ability or general intelligence (g). Stratum II consists of identified broad ability domains or clusters. Most theorists identify nine broad abilities (G_f, G_c, G_v, G_a, G_sm, G_lr, G_s, G_q, G_rw). Stratum I consists of over 80 identified narrow abilities, which are subsumed under the 9 identified broad abilities. CHC theory has been regarded as a significant advance in the assessment of cognitive processing and has been proposed as the foundation of a common nomenclature for describing research and testing theory (McGrew, 2009).

Research on PSW Methods

Much of the research cited by PSW proponents is correlational, investigating relations between specific cognitive processes and reading achievement (Hale, Fiorello, Kavanagh, Hoeppner, & Gaither, 2001) or whether specific cognitive profiles can be identified (Fiorello et al., 2010). However, the reliability, validity, and utility of profile analyses of psychometric tests have been questioned (Watkins, 2000). Further, evidence for the existence of distinct disability subtypes is not ipso facto evidence for the reliability, validity, or utility of PSW methods for LD identification.

If PSW methods are to be validated, direct investigations of the reliability and validity of classification decisions will be necessary. Stuebing et al. (2012) used simulated data to investigate the technical adequacy of three proposed PSW methods: C/DM. XBA, and D/CM. Results indicated that all three methods demonstrated good specificity but poor sensitivity, suggesting that a large number of students who did not respond adequately to Tier 2 intervention would not be identified as LD and that if identified, many would be false positives. Further, all three methods identified a small percentage of the population (1-2%), raising important questions about the efficiency of the methods. To date no empirical investigation has evaluated PSW methods for LD identification, although other studies (Fletcher et al., 2011; Vellutino, Scanlon, Small, & Fanuele, 2006) have not been able to demonstrate evidence of specific cognitive profiles associated with inadequate response to intervention.

Rationale for the Present Study

The present study addressed this gap in research with a sample of adolescent inadequate responders to Tier 2 intervention for two proposed PSW methods for LD identification: the C/DM and XBA methods. We utilized the dichotomous determinations to answer three research questions:

1. What are the rates of LD identification for the two PSW methods?

2. To what extent do the two PSW methods agree in LD identification decisions?

3. What are the academic profiles of inadequate responders that meet PSW LD criteria, and how do they compare to inadequate responders that do not meet proposed PSW LD criteria?

Methods

Participants

This study was conducted with the approval of the Institutional Review Boards of the respective universities and school districts. Participants were drawn from a larger study investigating the effects of a response to intervention framework in middle school (see Vaughn, Cirino et al., 2010; Vaughn, Wanzek et al., 2010; Vaughn, et al., 2011; and Vaughn et al. 2012 for full reports on participant flow, methods, and intervention effectiveness across all three years of the study). Participants attended seven middle schools in two large urban cities in the southwestern United States.

All participants received a full year of Tier 2 intervention in year 1 of the larger study (2006-2007). A total of 326 6th and 7th graders began the Tier 2 intervention. Sixteen students did not complete the intervention and were unavailable for academic assessment in spring of year 1 (remaining n = 310). An additional 70 students did not return to any of the participating schools and did not matriculate in the school system in the summer between year 1 and year 2, before the proposed battery of cognitive and academic measures was administered (remaining n =240).

Students who did not return (n = 70) were compared with students who returned (n = 240) on three standardized measures of reading performance administered in the previous spring: (a) Woodcock Johnson III: Basic Reading (WJ-III; Woodcock, McGrew, & Mather, 2001), (b) Test of Word Reading Efficiency (TOWRE; Torgesen, Wagner, & Rashotte, 1999), and (c) WJ-III Passage Comprehension (Woodcock et al., 2001). A multivariate analysis of variance (MANOVA) revealed no significant between group differences on the set of outcomes, F(3, 306) < 1. Of the 240 students that returned in year 2, 12 students did not complete the full assessment battery and could not be empirically classified by PSW methods, leaving 228 sixth and seventh graders who completed both the Tier 2 intervention and the comprehensive assessment battery in year 2. Eighty-nine students scored above the adequate response cut point on all three tests and were excluded from further analysis. The final sample of 139 students included all students that scored below the adequate response cut point on at least one criterion measure.

Demographic information for all participants is presented in Table 1. The sample reflects what will emerge in many schools that complete mass screening of all secondary students to identify struggling readers. It includes a large number of economically disadvantaged students and students from linguistically and culturally diverse backgrounds. The sample of inadequate responders includes a higher percentage of students receiving free and reduced lunch and a larger percentage of students with a history of ESL (all students received English-only core instruction and completed the Tier 2 intervention in English).

Table 1. Demographic statistics for both adequate and inadequate responders.

Variable	Inadequate Responders	Adequate Responders
	N = 139	N = 89
Age
M	11.92	11.44
SD	0.75	0.51
% Male	51.8	47.19
% F/R Lunch	83.46	75.32
% ESL	13.53	4.49
Race/Ethnicity
% Black	43.88	46.07
% White	5.04	17.98
% Hispanic	48.92	34.83
% Other	2.16	1.12

Measuring Adequate Response to Instruction

Adequate response to intervention was defined as a standard score of 90 or above on three standardized assessments of reading: (a) WJ-III Basic Reading, (b) TOWRE, and (c) WJ-III Passage Comprehension. This cut point on nationally normed assessments aligns with previous studies investigating response to intervention and is frequently used in studies of LD as a cut point for participant inclusion (Fletcher et al., 2011; Vellutino et al., 2006). The use of multiple indicators results in greater sensitivity and minimizes false negatives. This is important because: (a) single indicators of adequate response demonstrate poor to moderate agreement in classification decisions (Barth et al., 2008; Brown-Waesche, Schatschneieder, Maner, Ahmed, & Wagner, 2011) and (b) false negatives are comparatively deleterious because students who may need intervention will not be identified. The utilization of multiple final status indicators directly addresses the fundamental question of whether a student requires additional intervention and is sensitive to students that demonstrate specific reading deficits because multiple reading skills are assessed.

Although many RTI models rely on growth or dual discrepancy criteria for a determination of inadequate response (Fuchs & Deshler, 2007), recent investigations have not found that slope explains unique variance beyond final status for the purpose of identifying inadequate responders (Schatschneider, Wagner, & Crawford, 2008), including in this sample (Tolar Barth, Fletcher, Francis, &Vaughn, under review). This is especially true in middle school, because growth rates are much lower than in early elementary grades (Tolar et al., 2012). While an evaluation of growth is essential to instructional planning, there is not compelling evidence that the calculation of slope contributes meaningful information to a determination of inadequate response that is not contained in the final status assessment. To evaluate whether the adequate response criteria applied in the present study influenced results, all analyses were also conducted with a subset sample that met final status criteria and demonstrated discrepant, low growth (i.e. dual discrepancy criteria; n = 25). All results were consistent with those documented for the larger sample, providing evidence that the results of the present study are not due to the adequate response criteria applied for sample identification.

Procedures

Tier 2 intervention

Students assigned to the Tier 2 intervention attended a supplementary reading intervention in groups of 10-15 for one period (45-50 min.) each day as part of their regular schedule for the entire school year. The multi-component intervention addressed: (a) word study, (b) reading fluency, (c) vocabulary, and (d) comprehension. Early lessons focused on word study and reading fluency activities, such as structured partner reading. In subsequent lessons, the emphasis shifted to vocabulary learning routines and comprehension activities around expository texts and novels.

Intervention teachers participated in approximately 60 hours of intervention training plus ongoing coaching. A trained member of the research team collected information on the fidelity of implementation for each intervention teacher across the year. Fidelity data was collected up to five times, with a median of four observations per teacher. Intervention teachers were evaluated for program adherence and quality of instruction on Likert-type scales ranging from 1 (low) to 3 (high). In sixth grade, the mean teacher score for fidelity of implementation was 2.53 (SD = .30) and for quality of implementation was 2.60 (SD = .27). In seventh grade, average fidelity of implementation scores ranged from 2.22-3.00 and average quality of instruction scores ranged from 2.00-3.00.

Intervention effectiveness

Intervention students in sixth grade performed significantly better on measures of decoding, fluency, and comprehension in comparison to the control group (median d = +.16). In contrast, intervention students in seventh and eighth grades demonstrated few statistically significant differences in comparison to the control condition. It is not surprising that aggregate treatment effects were smaller than those found in similarly designed studies in early elementary. Annual achievement gains on standardized measures drop precipitously from early elementary to middle school (Lipsey et al., 2012). Effect sizes on standardized measures for one year of intervention in early elementary and middle school are therefore not comparable. Further, the year 1 effects for sixth graders compare favorably with other large scale reading interventions in middle school (Scammacca, Roberts, Vaughn, & Stuebing, in press). Finally, despite strict criteria for inadequate response, a large number of students met adequate response criteria and a large group did not. This winnowing of easy to remediate students is precisely the reason PSW proponents advocate a hybrid RTI-PSW approach for LD identification.

Measures

Assessment procedures

Assessment data were collected at two time points: (a) spring of year 1 to determine adequate response (WJ-III Basic Reading and Passage Comprehension, TOWRE, and KBIT-2: Matrices only) and (b) fall of year 2 (2007-2008; all other measures). All measures with discrepant testing dates are age-adjusted. It was necessary to administer the KBIT-2 in year 1 of the study to identify students with potential intellectual deficits who would not meet inclusion criteria to continue the study. The administration of the full cognitive battery was not logistically feasible in year 1 because of the large number of participants across multiple grades. In year 2, a comprehensive battery assessing a full range of reading and cognitive skills was possible because of the smaller participant sample. The comprehensive battery in fall of year 2 allowed for classification according to PSW methods after a determination of inadequate response to Tier 2 intervention but prior to Tier 3 intervention, providing an empirical test of the hybrid RTI/PSW assessment model.

The assessment battery was selected to assess a broad range of reading, cognitive, and language skills within the time constraints imposed by participating schools. We identified cognitive and language measures that: (a) have been implicated as predictors of intervention response; and (b) align with theoretical models of cognitive processing commonly used as the basis for assessing intraindividual patterns of PSW, such as CHC theory (Carroll, 1993).

Measures to determine response to intervention

Norm-referenced assessments of the three major domains of reading were used to evaluate outcomes in word recognition, fluency, and comprehension.

Woodcock Johnson III Tests of Achievement (WJ-III)

The WJ-III (Woodock, et al., 2001) is a nationally normed assessment of academic achievement. Four subtests were administered: Letter-Word Identification, Word Attack, Passage Comprehension, and Spelling. Test-retest reliability coefficients for students aged 10-13 range from .91- .94 for the Basic Reading composite, .80- .86 for the Passage Comprehension subtest, and .87- .92 for the Spelling subtest.

Test of Word Reading Efficiency (TOWRE)

The TOWRE (Torgesen et al., 1999) is a nationally normed, individually administered test of reading fluency. Two subtests were administered: Sight Word Efficiency (SWE) and Phonemic Decoding Efficiency (PDE). Confirmatory factor analysis indicates a high correlation (.98) of the latent structure of word reading fluency (as in TOWRE) and text reading fluency (Barth, Catts, & Anthony, 2009). The median test-retest reliability for the TOWRE Composite score for students aged 10-18 is .94 (range = .83- .92).

Measures to identify a profile of strengths and weaknesses

We measured phonological awareness, rapid naming, nonverbal reasoning, listening comprehension, spatial working memory, and processing speed. In addition to the established empirical relations with reading achievement and potential representation of strengths in reading LD, the alignment of specific measures with CHC broad clusters is presented in Table 2 and described below. The visual processing cluster was not assessed because it is not strongly related to LD in reading and because we had a measure of nonverbal reasoning that should be a strength in many with reading LD. For the present study, visual processing skill was assumed to be normal in the calculation of profile normality. Age-based standard scores were available for most measures; for the Underlining Test and Test of Spatial Working Memory, the measures were normed within the sample. Note that the standardization sample does not affect the C/DM method because neither measure is used for empirical classification. Within the XBA method, the two measures are utilized only for the purpose of establishing a normal cognitive profile.

Table 2. Cattell-Horn-Carroll clusters and proposed measures.

CHC Cluster	Definition	Measure
Crystallized Intelligence (Gc)	Breadth and depth of acquired knowledge	GRADE: Listening Comprehension
Fluid Intelligence (Gf)	Ability to reason, form concepts, and solve problems	KBIT-2 Matrix Reasoning
Short term Memory (Gsm)	Ability to hold information in immediate awareness and use it again in a few seconds	Test of Spatial Working Memory
Long term storage and retrieval (Glr)	Ability to store information and retrieve it fluently	CTOPP Rapid Automatized Naming (Letters)
Visual Processing (Gv)	Ability to think with visual patterns	Not measured
Auditory Processing (Ga)	Ability to analyze and synthesize auditory stimuli	CTOPP Phonological Awareness Composite
Processing Speed (Gs)	Ability to perform automatic cognitive tasks	Underlining Test

GRADE = Group Reading Assessment and Diagnostic Evaluator; KBIT-2 = Kaufman Brief Intelligence Test- Second Edition; CTOPP = Comprehensive Test of Phonological Processing.

Comprehensive Test of Phonological Awareness (CTOPP)

The CTOPP (Wagner, Torgesen, & Rashotte, 1999) is a nationally normed, individually administered test of phonological processing which is strongly associated with learning to read and inadequate response to reading intervention (Fletcher et al., 2011; Vellutino et al., 2006). We administered the three CTOPP subtests most commonly implicated in studies of reading LD: Blending Words, Elision, and Rapid Automatized Naming- Letters (RAN-L). The CTOPP phonological awareness composite was selected to assess phonological awareness, which is an indicator of auditory processing (G_a; Flanagan et al., 2007, p. 61). Rapid naming was selected to serve as an indicator of long-term retrieval (G_lr; Flanagan et al., p. 61). For students aged 8-17, the test-retest reliability coefficient is .84 for the Phonological Awareness composite, and .72 for RAN-L.

Kaufman Brief Intelligence Test- Second Edition (KBIT-2)

The KBIT-2 (Kaufman & Kaufman, 2004) is a nationally normed, individually administered measure of verbal and nonverbal intelligence. We administered the Matrix Reasoning subtest. In addition to screening for intellectual deficits, nonverbal reasoning (matrices) is an indicator of fluid reasoning (G_f; Flanagan et al., 2007, p. 60). It is often a strength in students with LD in reading. The median test-retest reliability coefficient for students aged 10-13 is .78 (range = .76 - .80) for Matrix Reasoning.

Group Reading Assessment and Diagnostic Evaluation: Listening Comprehension

The GRADE (Williams, 2001) is a nationally normed, group-administered test of listening comprehension. It was selected as an indicator of crystallized abilities (G_c; Flanagan et al., 2007, p. 60). Crystallized abilities, as indicated by verbal knowledge and listening comprehension, are associated with reading comprehension (Evans et al., 2001; Catts et al., 2006) and often seen as a strength in children with word reading and fluency LD. The median test-retest reliability coefficient for grades 6-8 is .90 (range = .88-.94).

Underlining Test

The Underlining Test (Doehring, 1968) is an individually-administered measure of processing speed. It was selected as an indicator of processing speed (G_s; Flanagan et al., 2007, p. 59). The Underlining Test utilizes similar task requirements to the WJ-III Visual Matching subtest, a commonly utilized measure of processing speed. A target stimulus is presented at the top of a page with the target stimulus and distracters below in lines. The student must underline only the target stimulus as quickly and accurately as possible for 30 or 60 seconds. The raw score for the three subtests is the total number of correct stimuli underlined, minus the number of errors. Raw scores on each subtest were converted to z-scores and the mean z-score was utilized for all analyses.

Test of Spatial Working Memory

The Test of Spatial Working Memory (Cirino, 2011) is an assessment of visuospatial working memory. It was selected as an indicator of working memory (G_sm; Flanagan et al., 2007, p. 58). The student is presented with a series of non-namable shapes or a star one at a time in one of four quadrants of a page. The student must indicate if the stimulus was a star following each presentation. After a series of shapes are presented, the student must recall the position of all the shapes in sequential order. The number of stimuli presented within a block increases as the administration progresses. Reliability estimates range from .73 to .84 among kindergarten and college students, respectively (Cirino, 2011). The score was a total raw score, where a point was awarded for each correct sequence recalled. The raw score was converted to a z-score (M = 0, SD = 1), which was used for all analyses.

Other academic measures

Group Reading Assessment and Diagnostic Evaluation: Reading Comprehension (GRADE)

The GRADE (Williams, 2001) Reading Comprehension subtest is a nationally normed, group-administered test of reading comprehension. The test-retest reliability coefficient for 7th grade is .94, and the alternate form reliability coefficient is .88. The GRADE produces a stanine score for the Passage Comprehension subtest.

Test of Silent Reading Efficiency and Comprehension (TOSREC)

The TOSREC (Wagner, Torgesen, Rashotte, & Pearson, 1999) is a nationally normed, group-administered test of reading fluency and comprehension. Within the larger study sample, the mean intercorrelation across the five time points in grade 6-8 ranged from .79 - .86 (Vaughn, Wanzek, et al., 2010).

Woodcock Johnson- Third Edition Spelling (WJ-III)

The Spelling subtest of the WJ-III is a dictated spelling test (Woodcock et al., 2001). Reliability coefficients for students aged 11-14 range from 0.87-0.92.

Applying PSW Methods for LD Identification

C/DM

Hale and Fiorello (2004) proposed utilizing one of two estimates of the distribution of differences between two measures to calculate a significant difference: (a) the standard error of the difference (SED) or (b) the standard error of the residual (SER). In the present study, we utilized the SED to calculate significant differences between measures at p < .05 following specified procedures (Hale & Fiorello, p. 102). Hale and Fiorello recommend utilizing SED first, as it is the more conservative option. Observed scores on all measures were compared and students were classified as meeting or not meeting C/DM criteria based on: (a) the pattern of concordance and discordance (b) observed achievement deficits, and (c) a theoretical link between achievement deficits and a concordant cognitive processing weakness.

XBA

Flanagan et al. (2007) specified that a classification of LD requires: (a) an achievement deficit, (b) a theoretically linked cognitive deficit, and (c) a normal cognitive profile. Deficit scores are defined as a score more than one SD below the population mean score. To create equivalent metrics, all academic and cognitive variables utilized in group formation were scaled to standard score values, with M = 100, SD = 15. We then created a series of dichotomous variables for each academic and cognitive processing measure indicating a normal or deficit score.

To determine whether the student had a normal cognitive profile, we assigned a 0 (below deficit cut point) or 1 (at or above cut point) in each of the seven CHC broad clusters. A list of the measures utilized as indicators of each CHC cluster is presented in Table 2. The dichotomous variable was then multiplied by a g loading derived from the SLD Assistant version 1.0 (Flanagan et al., 2007) and summed across clusters. If the sum is ≥ 1, the student's cognitive profile is considered normal.

Theoretical specification of the PSW methods

The two PSW methods specified that academic and cognitive deficits should be theoretically related, providing a hypothesis for the academic deficit (Flanagan et al., 2007; Hale &Fiorello, 2004). However, neither method specified which academic and cognitive skills are sufficiently linked by theory. Therefore, we established a priori links between cognitive processing skills and the three domains of reading assessed: (a) basic decoding, (b) reading fluency, and (c) reading comprehension.

Considerable empirical evidence supports a strong relationship between basic decoding skills and phonological awareness, which falls within the auditory processing cluster (Catts, Adlof, & Weismar, 2006; Torgesen, Wagner, Rashotte, Burgess, & Hecht, 1997). Thus, students with deficits in basic decoding had to demonstrate a theoretically linked deficit in phonological awareness/auditory processing.

There is a strong association between performance measures of reading fluency and rapid naming tasks, which fall within the long term retrieval cluster (Torgesen, Wagner, Rashotte, Burgess, & Hecht, 1997). Thus, students with deficits in reading fluency had to demonstrate a theoretically linked deficit in rapid naming/long term retrieval.

Reading comprehension deficits are strongly related to vocabulary and listening comprehension, within the crystallized intelligence cluster (Catts et al, 2006). Thus, students with deficits in reading comprehension had to demonstrate a theoretically linked deficit in listening comprehension/crystallized intelligence.

Establishing deficit cut points

The C/DM method is often implemented with a cut point for low achievement of a standard score less than 90 on standardized achievement measures (J. B. Hale, personal communication, April 19, 2013). In contrast, Flanagan et al. (2007) specified a threshold of > 1 SD (SS < 85) below the population mean. In the present study, we classified participants using standard scores less than 85 and, less than 90. This permitted investigation of the implications of different cut points for iterations of the same methods and across methods at equivalent cut points.

Results

Table 3 presents means and standard deviations for all academic and cognitive processing measures for the entire sample. Across reading measures, participants performed in the low average to below average range, which is expected because each participant fell below at least one of three adequate response criteria. Participants scored similarly low on all cognitive processing measures, except the Test of Spatial Working Memory and the Underlining Test, which were normed on the sample of participants, rather than a population sample.

Table 3. Means and standard deviations of full sample of inadequate responders.

Variable	M	SD
Criterion Reading Measures
WJ-III Basic Reading	91.26	9.96
TOWRE	90.58	14.14
WJ-III Passage Comprehension	84.12	9.30
Other Academic Measures
GRADE Reading Comprehension	83.55	9.16
TOSREC	76.45	12.01
WJ-III Spelling	88.86	12.30
Cognitive Processsing Measures
CTOPP Phonological Awareness	89.05	11.60
CTOPP Rapid Letter Naming	87.55	16.02
GRADE Listening Comprehension	87.83	6.46
KBIT-2 Matrix Reasoning	93.40	13.39
Test of Spatial Working Memorya	100.76	13.60
Underlining Testa	99.85	9.79

N = 139;

^aReported score is a converted standard score of (M=100; SD= 15). Norming sample is drawn from larger study and includes both adequate and inadequate responders. WJ-III = Woodcock Johnson- Third Edition; TOWRE = Test of Word Reading Efficiency; GRADE = Group Reading Assessment and Diagnostic Evaluation; TOSREC = Test of Silent Reading Efficiency and Comprehension; CTOPP = Comprehensive Test of Phonological Processing; KBIT-2 = Kaufman Brief Intelligence Test- Second Edition.

Identification Rates

C/DM

Table 4 summarizes the distribution of participants that met C/DM criteria at each cut point in each of the three reading areas and students that met criteria in multiple reading areas. The number of participants that met C/DM LD criteria varied depending upon which cut point for achievement deficits was applied. With a cut point for low achievement less than a standard score of 85 (C/DM < 85), 41 participants were classified as LD (29.4%). As would be expected, a larger number of participants (66; 47.5%) met C/DM criteria when the cut point for achievement deficits was a standard score of 90 (C/DM < 90). At both achievement deficit cut points, participants were most likely to qualify as LD with deficits in reading comprehension or reading fluency. Fewer participants met criteria in multiple areas.

Table 4. Academic deficit area(s) of students meeting and not meeting LD criteria according to PSW methods.

Area of Deficit			C/DM < 85 N (%)	C/DM < 90 N (%)	XBA < 85 N (%)	XBA < 90 N (%)
Basic reading	Reading fluency	Reading comprehension
yes	yes	yes	1 (0.7)	3 (2.1)	0	0
yes	yes	no	4 (2.8)	4 (2.8)	1 (0.7)	2 (1.4)
yes	no	yes	1 (0.7)	3 (2.1)	2 (1.4)	2 (1.4)
yes	no	no	5 (3.6)	7 (5)	6 (4.3)	8 (5.8)
no	yes	yes	0	3 (2.1)	0	0
no	no	yes	19 (13.7)	32 (23)	5 (3.6)	12 (8.6)
no	yes	no	11 (7.9)	14 (10.1)	10 (7.1)	10 (7.1)
no	no	no	98 (70.5)	73 (52.5)	115 (82.7)	105 (75.5)
Total meeting criteria:			41 (29.5)	66 (47.5)	24 (17.3)	34 (24.5)

Note: Basic reading based on performance on Woodcock Johnson-Third Edition Basic Reading Composite; reading fluency based on performance on Test of Word Reading Efficiency; reading comprehension based on Woodcock Johnson- Third Edition Passage Comprehension subtest.

XBA

With a cut point set at a standard score less than 85 (XBA < 85), 24 (17.3%) participants met LD criteria for the XBA method (Table 4). When the cut point was raised to a standard score below 90, the number of participants that met XBA LD criteria increased to 34 (24.5%). Across deficit cut points, the distribution of students qualifying in each reading area was relatively even. Few students met XBA LD criteria in multiple reading areas. In comparison to the C/DM, the XBA method classified fewer students with LD at both cut points.

Agreement between C/DM and XBA Methods

Agreement statistics on the identification decisions of the two PSW methods at different cut points for low achievement are reported in Table 5.

Table 5. Agreement on LD identification between the C/DM and XBA methods at different low achievement cut points.

Approach:	Approach
	C/DM < 85	C/DM < 90	XBA < 85	XBA < 90
C/DM < 85	-	62.1	30.0	13.6
C/DM < 90	-	-	20.0	20.5
XBA < 85	0.31	0.11	-	23.4
XBA < 90	-0.04	0.03	-	-

Below diagonal = kappa; above diagonal = percentage overlap (total identified by both approaches/total identified).

To evaluate agreement in classification decisions, we first calculated percentage overlap. Percentage overlap represents the number of students identified by both approaches divided by the total number of students identified by the two approaches separately. It is an index of agreement among the pool of students that would potentially qualify as LD through different iterations of the two approaches. The percentage overlap varied considerably, ranging from 13.6% - 62.1%. The percentage overlap was highest when comparing the two cut points for the C/DM approach (62.1%). The comparison of the two cut points for the XBA approach was lower (23.4%), as were comparisons between iterations of the two approaches (range 13.6% - 30%). As would be expected, comparisons between approaches demonstrated better agreement when deficit cut points were the same.

Cohen's kappa is an index of agreement for categorical data. It represents the improvement over chance achieved by independent raters or decision rules. It represents agreement for both positive and negative classification decisions. We therefore do not report kappa statistics for the same PSW method at different cut points. This is because each positive classification decision at the highest cut point would also be positive at lower cut points, making kappa an inappropriate index. Kappa achieved between iterations of the two different PSW methods is reported below the diagonal in Table 5. Kappa statistics ranged from -.04 - .31, indicating poor agreement (Cichetti & Sparrow, 1981). Kappa was highest when comparing the two iterations at the lower academic cut point, when fewer students meet LD criteria.

Academic Performance of PSW Groups

We conducted four MANOVAs comparing the academic performance of students that met and did not meet LD criteria at different deficit cut points according the two PSW methods. Each of the four MANOVAs compared the academic performance of the group that met LD criteria with the group that did not meet LD criteria for the four methods and cut point combinations. Dependent variables were three external academic variables: (a) GRADE Reading Comprehension, (b) TOSREC, and (c) WJ-III Spelling.

Figure 1 graphically displays the achievement patterns for LD and not-LD groups across the three academic measures not used to form the groups. All scores are reported in standard score values. Each graph compares the achievement patterns of students that met and did not meet LD criteria according to a specific PSW method at the specified threshold for low achievement (e.g. C/DM < 90). Notably, the patterns of academic achievement are largely parallel with larger differences indicating lower performance by the LD group when the cut point is lower.

Figure 1. Performance on external reading variables of groups that met and did not meet PSW LD identification criteria.

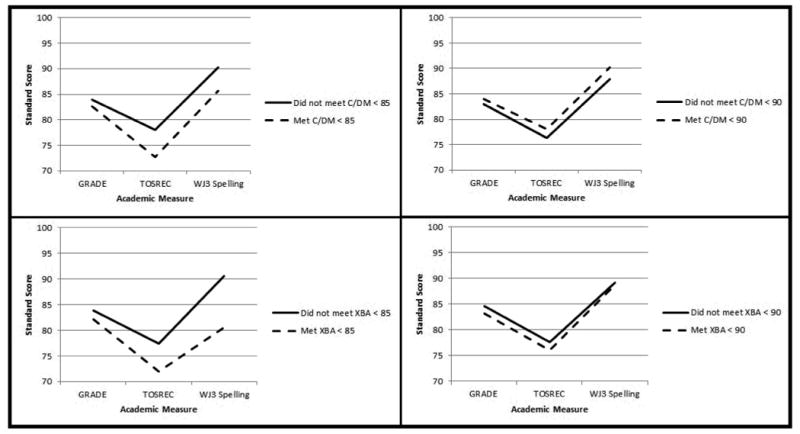
C/DM

For the comparison of LD and not-LD groups resulting from the C/DM < 85 iteration, there was no significant main effect for group status, F(3, 135) = 2.36, p > .05, η² = .05. There was also no significant effect for group status for the C/DM < 90 iteration F(3, 135) = 0.47, p > .05, η² = .01. Effect sizes were negligible.

XBA

For the comparison of LD and not-LD groups resulting from the XBA < 85 iteration, there was a significant main effect for XBA LD group status, F(3, 135) = 4.94, p < .05, η² = .10, with a medium effect size. The comparison of groups resulting from the XBA < 90 did not yield a significant main effect for group, F(3, 135) = 0.25, p > .05, η² = .01.

Discussion

Identification Rates

The identification rates of the two PSW methods at different cut points varied widely. The percentage of participants that met LD identification criteria ranged from 17.3% (XBA < 85) to 47.5% (C/DM < 90). For both methods, the percentage of participants who met LD criteria varied systematically, with each increase in the cut point for low achievement resulting in a greater number of participants who met criteria. Across PSW methods, the C/DM approach identified a much larger percentage of participants than the XBA approach at equivalent deficit cut points (17.3% vs. 29.4% and 24.5% vs. 47.5%).

The most inclusive C/DM iteration (C/DM < 90) identified close to 2.5 times as many participants as the most restrictive XBA iteration (XBA < 85). Even within a single PSW method, the rate of identification was considerably higher when a cut point of 90 rather than 85 was used. Such dramatic shifts highlight the fundamental role that cut points play in determining the rate of identification. The two proposed PSW approaches also differed dramatically in the percentage of participants meeting criteria. At every cut point, the XBA identified a much lower percentage of participants. This disparity could result in large differences in LD identification rates across different schools and districts if the different PSW methods and cut points were used interchangeably.

Altogether, these methods identified at most less than half of the inadequate responders as LD. Considering the sample is limited to students with persistent, intractable reading difficulties it may be expected that the majority would be eligible for referral for comprehensive evaluation for special education. However, it is difficult to determine what the appropriate identification rate would be given that there is no “gold standard” for LD status. Estimates of the prevalence of the disorder vary widely and generally depend on the cut points used to indicate a deficiency in different attributes of LD. To interpret the number of students identified in the present study, it is important to note the large number of middle school students screened (> 5,000) in the larger study. Although the larger study included a 2:1 randomization to the tiered treatment framework and suffered from considerable random attrition, it is remarkable how few students: (a) completed Tier 2 intervention, (b) demonstrated inadequate response, and (c) met PSW criteria (all criteria that would be necessary within recommended PSW methods). The low identification rates from this extant sample are consistent with the simulations of Stuebing et al. (2012), who reported low rates of identification for all three PSW methods across multiple cut points. In that study, only 1%-2% of the population met PSW criteria for LD based strictly on simulated psychometric data. Student mobility and attendance, as well as inconsistent delivery of intervention would further depress the number of students identified as LD in widespread implementation.

Agreement between PSW Methods

PSW methods are often presented interchangeably, as if the same students would be identified by both methods (Hale et al., 2010; Hanson et al., 2008). However, even the classification decisions of the same method at different cut points ranges widely. For the C/DM method at two cut points, the percentage overlap is 62.1%. For the XBA approach, the percentage overlap is lower (23.4%).

This low overlap in identification decisions even within the same method highlights the psychometric difficulty of applying fixed cut points to continuous data. Any comparison of classification decisions based on applying cut points to continuous data is subject to classification variability (Barth et al., 2008). This is an inherent result of imperfect, correlated tests that measure unobservable constructs. Even if an assessment perfectly measured the construct of interest (perfect validity), group membership would fluctuate and agreement would suffer because of imperfect test reliability.

Agreement between the classification decisions of the two distinct PSW methods is poor (kappa range = -.04-.31). This low level of agreement between approaches is not surprising because the two approaches implement the PSW model differently. The C/DM is primarily an ipsative, or within-person approach (Hale &Fiorello, 2004). The pattern of strengths and weaknesses is based on a within-person comparison of scores across a comprehensive assessment battery. In contrast, the XBA method is primarily a normative approach (Flanagan et al., 2007). The pattern of strengths and weaknesses is based on a series of dichotomous contrasts with “normal” expectations. The results of this study raise significant questions about the acceptability of the two approaches as equivalent alternatives of the PSW model.

The results of the present study may understate variability in the dichotomous classifications of the two approaches if widely implemented. The present study utilized the same measures to make all classification decisions. However, it is likely that different schools and districts would utilize different tests to implement PSW methods. This variability would introduce greater variability into the LD identification process. For example, MacMann et al. (1989) evaluated different formulae for identifying an IQ-achievement discrepancy using the same and different measures. While the study found variability as a result of different formulae, “the degree of variation attributed to the different methods of discrepancy score calculation was trivial in comparison to the extreme levels of classification inconsistency introduced by test selection” (emphasis in original; MacMann et al., p. 139). Further, the present study did not utilize the expertise of a multi-disciplinary team or include the application of exclusionary clauses in LD identification, which would be the next step in implementation of a PSW method. The addition of these processes would add another layer of complexity to the LD identification process. The sample in the present study, which includes a large number of economically disadvantaged students and students with a history of ESL instruction (not uncommon demographics in large, urban districts), hints at the challenge created by the interpretation of exclusionary clauses. Such difficulties highlight a fundamental tension of identification processes focused on identifying the right kind of students, rather than students that need additional academic instruction.

Academic Profiles

The third research question investigated differences in the academic performance of participants that met or did not meet LD criteria according to the two PSW methods. The failure to find more robust differences between groups that met and did not meet criteria according to the two approaches raises questions about the external validity of the PSW model. Absent an agreed upon diagnostic standard, resultant groups must be compared on external variables—that is variables not utilized for group formation. If the groups differ on external variables in some practically significant way, the classification system would accrue validity (Morris & Fletcher, 1998).

The failure to find large differences between identified groups for either method also casts doubt on whether the classification decisions reflect qualitative group differences, which is an implicit hypothesis of PSW approaches. Recent studies have found strong linear relations between the cognitive skills underlying reading and reading achievement, with a stepwise progression among groups reflecting the severity of reading impairment (Fletcher et al., 2011; Vellutino et al., 2006). The achievement graphs appear to support this assertion because groups are separated by level, but do not differ in the pattern of their achievement.

Implications for PSW Methods

Conceptual cohesiveness

The C/DM and XBA methods are often presented as equivalent alternatives of the same conceptual model LD identification (see for example Hale et al., 2010; Hanson et al., 2008). However, the results of the present study raise questions about the interchangeability of the two methods. First, the two methods demonstrated poor agreement on classification decisions regardless of the cut point applied. Agreement between classification decisions based on psychometric data inherently suffers as a result of: (a) less than perfect test reliability, (b) imperfect measurement of the latent construct, and (c) variability introduced by different measures. Agreement between the C/DM and XBA approach is impacted further because of the different manner in which the two methods identify a pattern of cognitive processing strengths and weaknesses. At best, the approaches agreed on only 30% of the students potentially classified as LD, a troublingly low level of agreement. In light of this low agreement between approaches on classification decisions, the results of the present study suggest that the process of empirically validating either approach must be undertaken independently, as the two approaches may not be interchangeable.

The necessity of aptitude by treatment interactions

Advocates of a PSW model argue that a comprehensive assessment can help inform subsequent intervention and improve treatment response (Hale et al., 2010; Hanson et al., 2008). However, despite years of research, group by treatment interactions remain largely speculative and unproven (Kearns & Fuchs, 2013; Pashler, McDaniel, Rohrer, & Bjork, 2009). Pashler et al. concluded that the evidence for such interactions is at best fragmentary and often contradicted. Kearns and Fuchs (2013) conducted a separate review of literature investigating group by treatment interactions based on interventions focused on cognitive deficits. The review found no evidence for a group by treatment interaction such that cognitively focused interventions aimed at students with specific cognitive deficits produce better effects (Kearns & Fuchs, 2013).

Questions about efficiency

PSW methods require allocation of considerable resources to complete the assessments. For example, the resources expended to identify a student as LD according to the C/DM < 90 method, the most inclusive iteration in the present study. Following Tier 2 intervention, the student would be referred for a comprehensive evaluation, similar to what was administered in the present study. Given a 50% LD identification rate, it would require individually assessing two students to identify one student as LD. For the XBA < 90 method, which has a lower identification rate of roughly 1 in 4 students, the process to identify one student with LD would require that four students be individually assessed. As cut points are lowered, the number of students who must be assessed to identify a single student spikes, peaking at approximately six students assessed to identify one student as LD through XBA < 85.

Implications for Practice

The results of this study raise questions about the reliability, validity, and efficiency of PSW methods for the identification of LD. Although advocates of PSW methods make strong evidentiary claims (Hale et al., 2010, Hanson et al., 2008), empirical research validating these methods remains limited. Until such evidence exists, the widespread adoption of PSW methods for LD identification would be premature.

A better allocation of resources may focus on directly assessing the academic skills of interest and providing instruction in that area. All classification systems based on psychometric data present methodological difficulties and variability in classification decisions (Barth et al., 2008; MacMann et al., 1989), yet classification decisions will continue to be necessary as long as subsets of students demonstrate increased academic need in a system of finite resources. MacMann et al. (1989) called for an assessment system based on “a coherent psychology of helping” (p. 145). Rather than focus on issues of etiology and classification, assessment could be understood as a means to design and evaluate academic intervention. Through this lens, the question is subtly shifted from which students qualify for help, to which students need help.

Limitations

The results of the present study are specific to the sample and measures described. Several limitations must be acknowledged. First, the present study implemented two PSW methods on a large scale, in order to answer questions that can only be investigated with a large participant sample. However, it should be acknowledged that neither PSW method is designed to be implemented in this way. Although both approaches provide specific formula for identifying a pattern of cognitive processing strengths and weaknesses, the creators of both methods caution against a strict actuarial implementation of the model (Flanagan et al., 2007; Hale & Fiorello, 2004). Both methods advocate that the results of assessment should be supplemented with the expertise of a multi-disciplinary team. Indeed, assessment results should be interpreted by the multi-disciplinary team as hypotheses to explain academic difficulties. It may be that the classification decisions of such a team would differ from the findings of the present study.

Additionally, various limitations arise from the design of the larger study. For example, the KBIT-2 Matrix Reasoning was administered at a different time than other cognitive measures, which was reasonable because standard scores were used and these tests are stable over a school year. This reflected the constraints of a large-scale intervention study and the need to limit the amount of assessment at any one time. An ideal study would have administered the entire assessment battery at one time point. However, the PSW model is premised on a belief that cognitive processing is less malleable than academic achievement and thus less susceptible to intervention than academic achievement.

Because of limited testing time, we were also unable to administer multiple subtests for each CHC broad ability, as recommended by Flanagan et al. (2007). This is a limitation of the present study. An additional measure may have increased the reliability with which each CHC process was assessed. However, tests were carefully selected to assess each CHC process, which are indicated by multiple tests in latent variable studies (McGrew, 2009). Within a latent variable framework, a single indicator accounts for the variability in relating to other correlated measures, for example other CHC broad abilities. Thus, the addition of extra indicators for each CHC factor would be unlikely to affect the results of the present study, which largely reflect the fundamental importance of cut scores on classification decisions and the procedural differences of the C/DM and XBA methods.

Two of the measures utilized as part of the XBA identification process (Underlining Test, Test of Spatial Working Memory) were normed on the sample of struggling readers from the larger intervention study because national norms were unavailable. However, the effect of this limitation is unlikely to change the conclusions of the study. First, the two measures were utilized only for the purpose of establishing a “normal” cognitive profile within the XBA method. The effect of a restricted norming sample would likely result in inflated scores and thus a higher frequency of normal profiles. Utilizing population norms may have decreased the number of normal cognitive profiles and decreased the number of students identified as LD. Second, weak correlations between the two measures and all reading measures suggest that the restriction of range displayed by the reading-impaired sample may have been minimal.

Finally, a sample of inadequate responders in middle school may not represent the population most commonly referred for an assessment of LD. Future studies should investigate the feasibility of a PSW model in elementary school. With a different sample, the results may have been different. Further, while most students are identified with LD with achievement deficits in reading, the results of this study should not be generalized to the identification of LD with achievement deficits in math or other academic areas not assessed in the present study.

Conclusions

The results of this study highlight several potential challenges to the widespread implementation of PSW methods. Both approaches identified a low percentage of students, raising questions about the efficiency of the model. The poor agreement between the models is an inevitable result of measurement error and the different manner in which the approaches implement the PSW model. Such variability in identification decisions suggests that the models may not be interchangeable and should be independently validated. Further, the failure to find large qualitative differences in academic performance between groups that met and did not meet criteria for either approach raises questions about the utility of the identification model. Until empirical research provides more evidence for the validity, reliability, and utility of PSW methods, resources may be better allocated towards directly assessing important academic skills and addressing deficits through intervention.