Time-Frequency Masking for Speech Separation and Its Potential for Hearing Aid Design

Abstract

A new approach to the separation of speech from speech-in-noise mixtures is the use of time-frequency (T-F) masking. Originated in the field of computational auditory scene analysis, T-F masking performs separation in the time-frequency domain. This article introduces the T-F masking concept and reviews T-F masking algorithms that separate target speech from either monaural or binaural mixtures, as well as microphone-array recordings. The review emphasizes techniques that are promising for hearing aid design. This article also surveys recent studies that evaluate the perceptual effects of T-F masking techniques, particularly their effectiveness in improving human speech recognition in noise. An assessment is made of the potential benefits of T-F masking methods for the hearing impaired in light of the processing constraints of hearing aids. Finally, several issues pertinent to T-F masking are discussed.

It is well documented that listeners with hearing loss have greater difficulty in understanding speech with background noise. Modern hearing aids improve the audibility of a speech signal and the comfort of noisy speech. However, the ability of hearing aids to improve the intelligibility of noisy speech is rather limited (Dillon, 2001; Moore, 2007). Because of the ever-present nature of background noise, it is very important for hearing aid research to develop speech separation methods that have the potential to enhance speech intelligibility in noise.

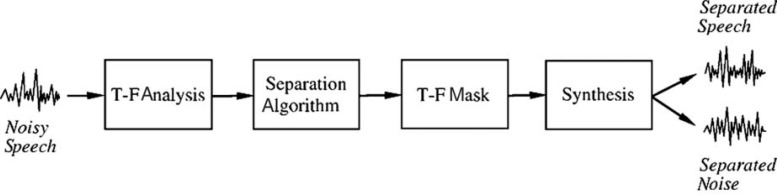
This article intends to review speech separation research under the heading of time-frequency (T-F) masking and appraise the potential of this recent development for hearing aid design. A T-F mask is based on a T-F representation of the signal. Such a representation can be obtained either by a short-time Fourier transform (STFT) or a windowed auditory filterbank in the form of a cochleagram (Wang & Brown, 2006). It should be noted that the term “masking” here means weighting (filtering) the mixture, which is different from the same term used in psychoacoustics where it means blocking the target sound by using acoustic interference. Figure 1 illustrates a typical T-F masking system for speech separation. A noisy speech signal first undergoes T-F analysis, resulting in a T-F representation. A separation algorithm then operates on the representation, and the outcome of the separation is a T-F mask, which can be used in a synthesis step to convert separated speech and background noise from the T-F representation back to the waveform representation.

Figure 1.

Block diagram of a typical time-frequency (T-F) masking system for speech separation.

This article is not intended to be a general topic survey as typically found in the literature. Rather it is written with focus on those studies that have at least some promise for benefiting listeners with hearing loss. As a result, more space is devoted to speech separation algorithms that use two or more microphones (monaural separation is discussed relatively briefly) and studies with human listeners.

The basic idea behind using T-F masking as a technique for sound separation is not new and has been explored for decades. For example, in the field of speech enhancement (Loizou, 2007), the classical Wiener filter can be viewed as a T-F mask where each T-F unit (element) of the mask represents the ratio of target energy to mixture energy within the unit, and so can the commonly used spectral subtraction technique. In addition, time-frequency gain control in hearing aid processing (Dillon, 2001) and binaural systems that perform multiband spatial separation (Bodden, 1993; Kollmeier, Peissig, & Hohmann, 1993) may be treated as cases of T-F masking. The recent development of T-F masking differs, however, in two main aspects. First, T-F masks often take the values of 0 and 1, resulting in binary T-F masking for separation. Second, algorithms for computing T-F masks are typically of the kinds of computational auditory scene analysis (CASA) or independent component analysis (ICA). This review focuses on this recent development. Broadly speaking, CASA aims at segregating sound sources on the basis of perceptual principles of auditory scene analysis (Bregman, 1990). ICA, on the other hand, assumes that source signals are statistically independent, and formulates the separation problem as that of estimating a demixing matrix through machine learning techniques (Hyvärinen, Karhunen, & Oja, 2001).

This article is organized as follows. The next section introduces the concept of binary T-F masking for separation and traces its origins. The subsequent section gives a short description on monaural separation systems. This is followed by reviews of the T-F masking algorithms using two or more microphones and a section that considers perceptual studies that test intelligibility or quality of separated speech produced by T-F masks. In the penultimate section, we assess the potential of the reviewed studies for hearing aid application that places limits on the processing complexity and especially the processing delay. The final section discusses several issues and concludes the article.

Time-Frequency Masking Concept and Its Origins

Although time-varying filters have long been used in signal processing, current interest in T-F masking originates from different considerations. A main motivation behind the current interest is sound separation through binary masking in the T-F domain.

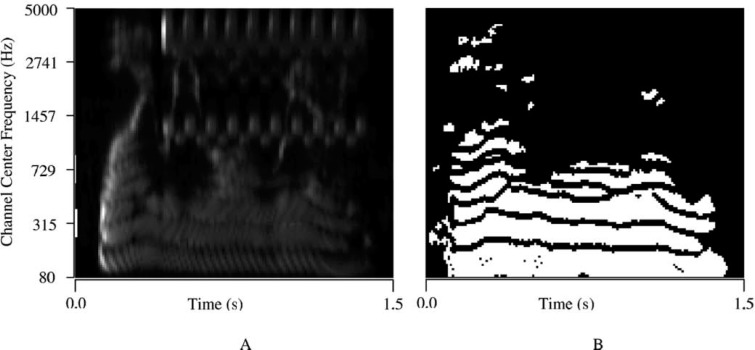
The use of a binary T-F mask for sound separation can be traced back to a 1983 article by Lyon and a 1985 dissertation by Weintraub, which started the field of computational auditory scene analysis or CASA. From the outset, CASA adopts the cochleagram representation, which is created by time windowing responses from a filterbank representing the frequency analysis of the cochlea, hence having the two dimensions of frequency and time (Wang & Brown, 2006). CASA then attempts to segment the cochleagram of a mixture into contiguous T-F regions, or segments, on the cochleagram and then groups segments into streams corresponding to different sound sources. In this framework, the result of the grouping is naturally a binary T-F mask indicating which parts of the input scene belong to the segregated target. The clearest examples of using binary masks include Brown and Cooke (1994) and Wang and Brown (1999). Figure 2 illustrates a binary mask output from the Wang and Brown model in response to a mixture of speech and trill telephone. Figure 2A shows the cochleagram of the mixture and Figure 2B the binary mask as the output of segregation, where a mask value of 1 indicates that the segregation system considers that the acoustic energy in the corresponding T-F unit contains mostly the target signal and hence should be retained and the mask value of 0 indicates that the energy in the corresponding unit should be removed. With this output mask, the segregated speech waveform can be easily constructed in a synthesis step (see Figure 1) by applying the mask as a binary weight matrix to the mixture in the T-F domain (Weintraub, 1985; see also Wang & Brown, 2006).

Figure 2.

Binary time-frequency mask. (A) Cochleagram of a mixture of speech and trill telephone. (B) Target binary mask as segregation output, where white pixels denote 1 and black pixels denote 0.

Source: Reprinted from Wang and Brown (1999), with permission from IEEE Transactions on Neural Networks.

Several interesting developments have been made on binary T-F masks in the last several years. First, Cooke, Green, Josifovsski, and Vizinho (2001) proposed the missing data approach to robust automatic speech recognition (ASR), where a binary T-F mask plays a key role in informing the recognizer which T-F units provide reliable data for target speech recognition. To evaluate their approach, they introduced the so-called a priori mask as one that is supposed to provide a ceiling mask for recognition. The a priori mask is 1 for a T-F unit if the mixture energy is within 3 dB of the premixed target speech energy, and it is 0 otherwise.

Second, Jourjine, Rickard, and Yilmaz (2000) and Roweis (2001) observed that the energy of a speech signal has a sparse distribution in time and frequency (see also Nadas, Nahamoo, & Picheny, 1989), that is, significant energy occurs only in small, isolated regions of a T-F representation. In voiced speech, for example, speech energy is concentrated at frequencies that are multiples of the fundamental frequency F₀. As a result of sparsity, the overlap between different speech signals is small with a high-resolution T-F representation and can be quantitatively measured (Yilmaz & Rickard, 2004). In the extreme case of sparsity where different sources are orthogonal, a binary mask is sufficient to fully extract a single source from the mixture. In practice, high-quality separation can be obtained as long as orthogonality holds approximately.

Third, Wang and colleagues suggested the notion of an ideal binary mask (IBM) as a major computational goal of CASA (Hu & Wang, 2001; Roman, Wang, & Brown, 2003; Wang, 2005), which can then be used as an explicit criterion for evaluating a CASA system. Specifically, within T-F unit u(t, f), let s(t, f) denote the target energy and n(t, f) denote interference energy, both in dB. The ideal binary mask is defined as

$$IBM\left(t,f\right)=\{\begin{array}{ll}1\hfill & if\hspace{0.17em}s\left(t,f\right)-n\left(t,f\right)>LC\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (1)

The threshold LC (standing for local signal-to-noise ratio [SNR] criterion) in dB is typically chosen to be 0, giving a 0-dB SNR criterion, although other SNR criteria can also be chosen. One thing special about the 0-dB criterion is that, under certain conditions, the IBM thus constructed gives the highest SNR gain of all the binary masks treating clean target as the signal (Ellis, 2006; Hu & Wang, 2004; Li & Wang, in press). Figure 3 shows the IBM for a mixture of two speech utterances, whose cochleagrams are shown in the top two panels. The middle left panel shows the cochleagram of the mixture with 0-dB SNR. The IBM is given in the middle right panel. The lower panel of the figure illustrates the masked or IBM-segregated mixture.

Figure 3.

Ideal binary mask. Top left: Cochleagram of a target utterance (“Primitive tribes have an upbeat attitude”). Top right: Cochleagram of an interfering utterance (“Only the best players enjoy popularity”). Middle left: Cochleagram of the mixture. Middle right: Ideal binary mask. Bottom left: Masked mixture using the ideal binary mask.

The notion of the IBM as a CASA objective is directly motivated by the auditory masking phenomenon, which is a fundamental characteristic of auditory perception. Auditory masking refers to the perceptual effect that, roughly speaking, a louder sound renders a weaker sound inaudible within a critical band (Moore, 2003). This justification based on auditory masking should be contrasted with that based on signal sparsity.

In addition to SNR gain, the IBM has proven to be highly effective for robust ASR (Cooke et al., 2001; Roman et al., 2003) and human speech intelligibility in noise (see section titled “Perceptual Studies”). The term has since been used in the community (see, e.g., Li, Guan, Xu, & Liu, 2006; Yilmaz & Rickard, 2004), although it does not always mean the same thing (see “Perceptual Studies” section for a different definition).

Monaural Time-Frequency Masking Algorithms

Much of the work in CASA, where the binary T-F masking concept is originated, is about monaural (single-microphone) processing (see Wang & Brown, 2006, for a comprehensive review). Monaural algorithms typically make use of intrinsic sound properties to perform separation, or auditory scene analysis. For speech separation, commonly used properties include harmonicity, onset and offset, amplitude and frequency modulations, temporal continuity, and trained speech models. As will be discussed in the section titled “Assessment from the Hearing Aid Perspective”, although promising, monaural T-F masking algorithms for speech separation are either too complex or performance is too limited, to be directly applicable to practical hearing prosthesis. As a result, I will describe just a few representative systems to illustrate how T-F masking is done with monaural mixtures and briefly mention other systems.

One of the early CASA models for voiced speech separation was proposed by Brown and Cooke (1994). Their model starts with peripheral processing using a gammatone filterbank (a gammatone filter has an impulse response that is the product of a gamma function and a tone) and a model for hair cell to auditory nerve transduction, leading to a two-dimensional (2-D) cochleagram. The model then computes a number of auditory maps corresponding to frequency modulation (FM), pitch, and onset/offset. The FM map and the correlation of the correlogram (autocorrelation) responses between neighboring filters are then used to segment the cochleagram into a collection of segments. Grouping is based on pitch contour similarity as well as common onset and offset. More specifically, they compute a pitch contour for each segment and then measure similarity between the pitch contours of two segments that overlap in time. In addition, similarity between two segments is increased if they start or end at approximately the same time. With the similarity measures for pitch contours and common onsets and offsets between pairs of segments, the Brown and Cooke system performs scene analysis using an iterative procedure as follows. The system starts a new stream by selecting the longest ungrouped segment, and then evaluates each segment not yet in any stream for potential grouping. An ungrouped segment joins the current stream only when it is similar enough to every segment in the stream. The grouping process repeats until no segment is ungrouped in the auditory scene. Note that each stream thus separated is a binary T-F mask, which is then used to mask the original mixture to produce a separated signal in waveform (see previous section).

Partly motivated by the evidence that the auditory system appears to use different mechanisms to analyze resolved and unresolved harmonics, Hu and Wang (2004, 2006) proposed a CASA model for voiced speech separation that groups resolved and unresolved harmonics in different ways. This model employs the cochleagram representation, and performs auditory segmentation on the basis of cross-channel correlation and temporal continuity. To estimate a pitch track corresponding to the target speech, initial grouping is conducted using the dominant pitch in each time frame. Given the target pitch track, the system labels T-F units as to whether they belong to the target speech using a periodicity criterion in the low-frequency range and an amplitude modulation (AM) criterion in the high-frequency range. The AM criterion is used because channels at high frequencies respond to multiple harmonics (hence unresolved harmonics), resulting in amplitude-modulated responses fluctuating at the F₀ rate of the speech source (Helmholtz, 1863). With all T-F units labeled, a segment is grouped to the target stream if the acoustic energy corresponding to its T-F units labeled as the target exceeds half of the total energy of the segment. Finally, each target segment expands by iteratively grouping its neighboring T-F units with the target label that do not belong to any segment. The resulting target stream is a binary mask. Hu and Wang explicitly estimate the IBM with LC = 0 dB, and evaluate their system performance according to an SNR metric that measures the difference between a computed binary mask and the IBM.

The grouping in the above two studies is based on periodicity, and hence is applicable only to voiced speech. Recently, Hu and Wang (2008) made the first systematic effort to segregate unvoiced speech. Their CASA system has two stages. In the segmentation stage, the input mixture is segmented into T-F regions based on a multiscale analysis of onsets and offsets. In the grouping stage, segments are grouped into the target speech or the background using Bayesian classification of acoustic-phonetic features. This system and their earlier system on voiced speech segregation (Hu & Wang, 2004, 2006) together produce a binary mask for both voiced speech and unvoiced speech that are separated from background interference.

Generally speaking, monaural T-F masking sytems for speech separation can be divided into feature-based and model-based (Wang & Brown, 2006). The aforementioned systems belong to the feature-based category. Other feature-based systems include those by Li et al. (2006), Deshmukh, Espy-Wilson, and Carney (2007), and Pichevar and Rouat (2007). Model-based systems use trained speech and noise models to separate noisy speech (Ellis, 2006), and include those by Roweis (2001), Radfar, Dansereau, and Sayadiyan (2007), and Reddy and Raj (2007). In Roweis's system, for instance, each of the speech sources in a mixture is modeled using a hidden Markov model (HMM). During the separation process, the mixture is decomposed into the underlying HMMs for individual sources using a factorization technique, corresponding to binary T-F masking. The feature- and model-based systems produce either binary or ratio (soft) masks, and the IBM is often used as a measure of ceiling performance.

Binaural and Array-Based Time-Frequency Masking Algorithms

Whereas most of the monaural separation algorithms are developed in the field of CASA, T-F masking techniques using two or more microphones have been developed in both CASA and ICA communities. As noted in the section “Time-Frequency Masking Concept and Its Origins”, T-F masking is based on two different principles: the principle of auditory masking and the principle of signal sparsity. Studies on two-microphone source separation are usually based on one, but not both, of the two principles, depending on which community the studies fall into (CASA or ICA). It is worth pointing out that, although the sparsity principle applies to a range of important signals, including speech and music, the auditory masking principle is more general; for speech separation, it applies whether or not the background is diffusely (e.g., speech babble) or sparsely distributed (e.g., another speech utterance).

Basic Approach

The main approach for two-microphone (or binaural) speech separation is established in two studies by Roman et al. (2003) and Yilmaz and Rickard (2004). Although the backgrounds of these two studies are different, the proposed approaches have similar features: they both employ characteristic clustering in feature space to perform separation and use the IBM as ground truth for performance evaluation. Each is described below.

The segregation system of Roman et al. (2003) is motivated by binaural processing of the human auditory system. Their model starts with the binaural input of a KEMAR dummy head that realistically simulates the filtering process of the head, torso, and external ear (Burkhard & Sachs, 1975). Then binaural cues of interaural time difference (ITD) and interaural intensity difference (IID) are extracted within each corresponding pair of T-F units in the left ear and right ear KEMAR responses. They find that, within a narrow frequency band, modifications to the relative energy of the target source with respect to the interfering energy trigger systematic changes of the binaural cues. This results in characteristic clustering in the joint ITD-IID feature space for a given spatial configuration. The objective of their system is to estimate the IBM at a given ear, which amounts to binary classification in the feature space. The classification is based on a maximum a posteriori (MAP) decision rule, where the likelihood is given by a nonparametric density estimation method. To obtain best results, the training is performed for each frequency channel and each spatial configuration, although training signals need not be similar to test signals.

Roman et al. (2003) evaluated the performance of their model for two- and three-source configurations in anechoic conditions. Estimated binary masks match the IBM very well. They also tested their system using ASR and human speech intelligibility, and reported large improvements (particularly in low SNR conditions).

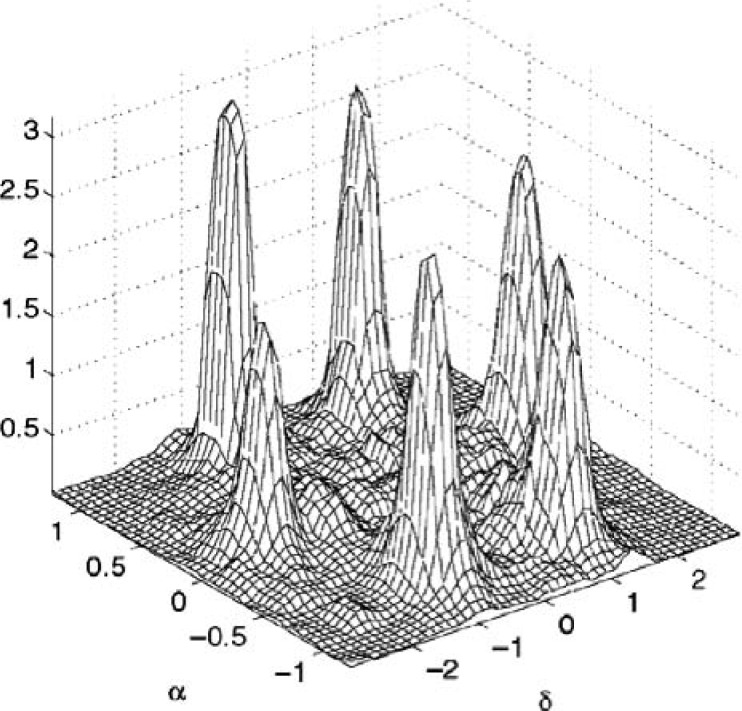
Unlike Roman et al. (2003) who used the binaural input, Yilmaz and Rickard (2004) used the two-microphone input that was obtained from two omnidirectional microphones placed 1.75 cm apart. Their system is based on the sparsity (orthogonality) principle, and they suggested a measure of approximate orthogonality. As expected, sparsity decreases as the number of speech signals comprising a mixture increases or as the amount of reverberation increases. For source separation, Yilmaz and Rickard proposed an algorithm called DUET (degenerate unmixing estimation technique) for underdetermined mixing conditions where the number of microphones is smaller than the number of sources. Similar to Roman et al., the key observation behind the DUET algorithm is the characteristic clustering of pairs of phase and amplitude differences between the corresponding T-F units of the two microphone recordings. This is illustrated in Figure 4, which plots a 2-D histogram along the phase difference and amplitude difference dimensions. Their objective is to separate all the sound sources from the two mixtures. As a result, they use an unsupervised clustering algorithm to extract individual sources. Specifically, the training process amounts to the generation of a 2-D histogram as shown in Figure 4. The histogram is then smoothed, and peaks are located that correspond to distinct sources. Each peak is used to construct a binary T-F mask. The binary mask can then be used to recover an individual sound source from the mixture.

Figure 4.

Two-dimensional smoothed histogram. The histogram is generated from two 6-source mixtures, where α indicates amplitude difference and δ indicates time difference.

Source: Reprinted from Yilmaz and Rickard (2004), with permission from IEEE Transactions on Signal Processing.

Yilmaz and Rickard (2004) tested their system for separating synthetic mixtures of 6 and 10 speech sources. In both cases, they reported large SNR gains although in the latter situation separated sources become highly corrupted and barely intelligible. For tests with actual recordings from two microphones, separation performance is very good in anechoic conditions, but drops significantly in reverberant conditions even with three sources placed at very different arrival angles.

In addition to the differences in motivation and input format, there are several other distinctions between the above two studies. The most important one is the objective: Roman et al. (2003) aim to separate a target signal from the mixture whereas Yilmaz and Rickard (2004) strive to separate all the signals. The different objectives lead to diverging separation algorithms: Roman et al. use a binary classification algorithm whereas Yilmaz and Rickard use a multicluster clustering algorithm. Another difference is that Roman et al. perform classification within individual frequency bands and Yilmaz and Rickard carry out clustering in all frequencies. Roman et al. report that pooling all frequency bands for classification gives worse performance, presumably because their use of the head-related transfer function (HRTF) which yields large interaural intensity differences in the high-frequency range; such differences are absent in the two-microphone setup of Yilmaz and Rickard.

Variations

Aarabi and Shi (2004) presented a related T-F masking approach for speech enhancement. Different from the two studies discussed above, the Aarabi and Shi system uses only intermicrophone differences of arrival time, or phase differences. Similar to Roman et al. (2003), they study the relationship between SNR within each T-F unit and deviations from the phase difference of the given target direction. Given the observed monotonic relationship, the SNR can then be derived from the computed phase deviations. Note that they do not address the issue of sound localization; instead sound directions are provided to their algorithm. This system does not use a binary mask, but a ratio (or soft) mask—a Wiener filter—that optimizes the output SNR. They call it phase-error filter. They evaluate their system on a digit recognition task, and report substantial improvements over standard beamformers in both anechoic and reverberant conditions. In addition, they compare performing T-F masking on each microphone separately and on both microphones followed by a combination. Interestingly, the combined processing does not give better results, even performing a little worse than those at the better-performing microphone.

Linh-Trung, Belouchrani, Abed-Meraim, and Boashush (2005) studied spatial T-F distributions and derived a clustering algorithm to separate sound sources of different spatial origins. They analyze the different properties of same-source cross-correlations (between microphones) versus different-source cross-correlations. These properties are then used in their clustering algorithm which uses the matrix analysis of different T-F distributions, and the clustering amounts to binary T-F masking as done in Yilmaz and Rickard (2004). However, their evaluations are limited to synthetic frequency-modulated tones.

Recognizing the importance of sparseness for the success of T-F masking, Molla, Hirose, and Minematsu (2006) proposed a signal decomposition technique that leads to higher T-F resolutions than STFT and cochleagram. Specifically, they suggested the use of the so-called Hilbert spectrum, which can be derived from empirical mode decomposition and Hilbert transform. The derived Hilbert spectrum has the property that its time resolution is the same as that of signal sampling and the frequency resolution is limited only by the Nyquist frequency (hence the same as the Fourier spectrum). Using this representation, source separation becomes identifying peaks in the 2-D histogram of time and intensity differences. They compared their Hilbert spectrum representation with STFT and found performance improvements. They also report that a mixing model based on HRTF gives better separation results than the two-microphone model. However, their ad hoc evaluation criterion makes it hard to decipher the meaning of the reported performance.

Further Developments

The basic T-F masking approach described earlier has been further developed in many subsequent studies. The later studies are motivated by two primary concerns: (a) the existence of signal distortion referred to as musical noise resulting from a binary mask and (b) the handling of room reverberation. The musical noise is the residual noise after processing that exhibits strong fluctuations in the time-frequency domain (Cappe, 1994). It is called “musical noise” because isolated noise energies resemble and sound like narrowband tones. Although the musical noise problem occurs and has been well studied in speech enhancement algorithms, such as spectral subtraction, the use of binary gains in binary T-F masking algorithms exacerbates the problem.

The following survey is organized depending on whether T-F masking is derived along with ICA or beamforming.

ICA and T-F masking. A main appeal of the T-F masking concept is its ability to deal with underdetermined blind source separation, which poses a major difficulty for ICA. The standard formulation of ICA requires that the number of microphones be no smaller than the number of sources, an often impractical constraint. On the other hand, impressive separation can be obtained when ICA assumptions are met.

The idea of combining the ICA approach and T-F masking was probably first published by Araki, Makino, Blin, Mukai, and Sawada (2004) and Kolossa and Orglmeister (2004). Araki et al. proposed to first extract one source from a mixture by using binary T-F masking and then separate the remaining mixture by using frequency domain ICA. Their system is designed to deal with the situation with two microphones and three sources, an underdetermined situation. One can imagine that this method should be able to extend to extract the first N-M sources using T-F masking and the remaining M sources using ICA, where N refers to the number of sources and M the number of microphones. Their evaluation shows that signal distortion is reduced, but at the expense of reduced output SNR, compared to the binary masking approach without ICA. Kolossa and Orglmeister (2004) proposed a different approach for combining T-F masking and ICA in the determined case, but with reverberation. Their method first applies ICA and then a binary T-F mask to further suppress interference, which is called nonlinear postprocessing. The binary mask is given by comparing the two separated signals from ICA. They observed an average SNR gain of more than 3 dB due to the postprocessing.

A note of caution on the evaluation measure is in order. Studies using binary masks often measure their output SNR on the basis of only active T-F units (those with the value of 1), where the amount of target energy passed through by the same units is considered as the signal and the amount of interference passed through by such units is considered as the noise (see, e.g., Kolossa & Orglmeister, 2004; Wang & Brown, 1999; Yilmaz & Rickard, 2004). Such a measure does not penalize the loss of target energy. For example, one can produce a very conservative mask (i.e., with few active units) and get a very high SNR—indeed infinite SNR results if processing results in a single active unit that contains no intrusion. Such a measure often inflates the output SNR (Hu & Wang, 2004), and hence reported SNR gains should be viewed in this light.

In a later study, Araki, Makino, Sawada, and Mukai (2004) abandoned the use of a binary mask for extracting the first N-M sources in favor of a continuous T-F mask derived from a directivity pattern. The overall processing follows the same two stages as in Araki, Makino, Blin, et al. (2004). In T-F masking, the soft mask is estimated using the directivity pattern of a null beamformer, with a given source direction. Such a beamformer is known to produce little signal distortion. They find that a modified directivity pattern with constant gains in certain regions of the directivity pattern performs better. Again, reduced signal distortion is accompanied by reduced SNR gain.

Saruwatari et al. (2005) investigated two different ways of combining binary masking and ICA. A simple way is to generate a binary mask by comparing ICA-separated sources directly. A more sophisticated way, the one proposed by the authors, is to perform the so-called single-input multiple-output ICA, where multiple outputs are generated at each microphone. They then calculate a separate T-F mask at each microphone to further remove interference. Their comparison using recorded mixtures from a head and torso manikin shows that their proposed combination outperforms the simple method of integration, which in turn is better than using ICA alone. Similar conclusions are drawn from a later evaluation using two directional microphones (Mori et al., 2006).

Sawada, Araki, Mukai, and Makino (2005, 2006) used T-F masking and ICA together for a somewhat different task: extraction of dominant sources—those close to sensors—rather than all sources. Different from their previous work, they first apply ICA to extract M independent components, M being the number of microphones. From the estimated mixing matrix, they obtain a set of basis vectors. T-F masking is then used to attenuate the residual noise from extracted components which, in the underdetermined case, do not necessarily correspond to individual sources. They adopt a sigmoidal mask rather than a binary one, and each mask value is determined by the angle between the basis vector for each extracted component and a T-F sample vector. They experimented with a number of choices for the two parameters of the sigmoid. Their evaluation results demonstrate significant SNR improvements with little more distortions in comparison with just ICA.

A recent study by Araki, Sawada, Mukai, and Makino (2007) addresses the underdetermined separation problem by using normalized amplitude and phase differences between multiple sensor inputs in the k-means clustering method, which is the most commonly used clustering algorithm (Duda, Hart, & Stork, 2001). The normalized features do not require sensor position information, and as a result their separation algorithm can be applied to situations where multiple sensors are arbitrarily arranged. Unlike Araki, Makino, Sawada, et al. (2004), this study uses binary masks, probably necessitated by the use of k-means clustering. As pointed out by the authors, typical musical noise exists in their separation results due to binary masking. On the other hand, they obtain good SNR results. Their algorithm has been evaluated in a number of configurations involving two or more microphones and modest amounts of room reverberation.

Based on a geometrical interpretation of instantaneous ICA, Pedersen, Wang, Larsen, and Kjems (2005, 2008) devised an algorithm for separating many speech sources on the basis of two closely spaced microphones. The key idea of this algorithm is to apply ICA and binary T-F masking iteratively to separate underdetermined mixtures until each separated signal is deemed to contain a single speech utterance. An ICA operation in the underdetermined situation gives two outputs, each of which is generally another linear mixture of the sources. From the two outputs, they compute two binary masks, treating each output as the target. The two binary masks are then applied to the two original mixtures, producing two pairs of separated signals. A stopping criterion is introduced to decide whether a pair of separated signals contains a single source from the one spatial direction or more than one source. In the former case, no further processing is necessary; in the latter case, the separation process continues where the two signals are fed to the same ICA and binary masking operations. The application of the same binary mask to the two mixtures is justified by the use of the closely spaced microphones. They have shown that this iterative algorithm can successfully separate mixtures of up to seven speech signals and also achieve significant SNR gains for recordings in a reverberant room.

Beamforming and T-F masking. Beamforming, or spatial filtering, is a standard signal processing technique that enhances the signal arriving from a specific direction through the use of an array of two or more microphones (van Veen & Buckley, 1988). Beamformers are divided into fixed beamformers and adaptive beamformers. A fixed beamformer, such as a delay-and-sum beamformer, boosts the sound energy from the target direction by arranging the microphones to form a spatial beam. An adaptive beamformer, on the other hand, aims to cancel or attenuate interfering sources through weight adaptation. Beamforming methods have been implemented in hearing aids (Dillon, 2001; Greenberg & Zurek, 2001).

To deal with the difficulty posed by room reverberation, Roman and Wang (2004) and Roman, Srinivasan, and Wang (2006) proposed using adaptive beamforming to provide the basis for binary T-F masking in order to segregate a target source from a reverberant mixture. This use of beamforming to generate a binary mask should be contrasted with the use of a beamformer to produce a soft mask in conjunction with ICA (see Araki, Makino, Sawada, et al., 2004). The basic idea of the Roman et al. system is to first cancel the target source from a known direction using adaptive beamforming. Then an estimate of the IBM is made by comparing the mixture signal and the output from the beamformer within each T-F unit. This algorithm is described in more detail in the section “Assessment From the Hearing Aid Perspective.”

In an attempt to directly calculate the IBM for a mixture input, Boldt, Kjems, Pedersen, Lunner, and Wang (2008) made use of a first-order differential beamformer to produce limacon patterns of directivity (Thompson, 2000). With known directions of a target signal and an interfering signal, the basis of IBM calculation is a comparison between a front cardioid and a back cardioid. More specifically, they derive a theoretical relation between the ratio of the front and back cardioid responses and the LC parameter in the IBM definition of Equation (1). The relation is given in terms of the directional gains of the two cardioids, and thus enables highly accurate estimation of the IBM for the case of two sources with no reverberation. In addition, they show that reasonable IBM estimation can be obtained by simply deciding whether the front cardioid gives a stronger response than the back cardioid. This algorithm is also described in the Section “Assessment From the Hearing Aid Perspective.”

Related Studies

Dubnov, Tabrikian, and Arnon-Targan (2004, 2006) proposed a two-microphone method to separate spatially disjoint sources in two stages. In the first stage, T-F units responding to a single source are extracted. This is done by analyzing the cross-correlation matrix of the two mixture signals at every frequency. Note that a single source with uncorrelated white noise gives the largest eigenvalue of the cross-correlation matrix that is greater than the remaining eigenvalues, which are all equal. The single-source T-F units are clustered for direction estimation. In the second stage, a Gaussian mixture model is used to describe multiple clusters at each frequency, and a Kalman filter is used to track the cluster means across frequencies for an individual source; the Kalman filter is a classical method in control theory for estimating the state of a dynamical system from noisy measurements. The second stage gives a solution to the permutation problem in the frequency domain, which is the problem of grouping the separated subband signals of the same source across frequency. This method is proposed for the convolutive case with a relatively small amount of reverberation. Although it does not employ T-F masking explicitly, the underlying approach bears resemblance to the basic approach described in an earlier section.

Blin, Araki, and Makino (2005) described an algorithm for separating convolutive and underdetermined mixtures. The system is tailored for two microphones and three sources. This is a three-step algorithm. In the first step, for each frequency, the algorithm detects the time frames where only a single source is active. This is done through a geometrical analysis of scatter plots of measured amplitude pairs. In such a plot, points are scattered around three straight lines corresponding to vectors of the mixing matrix. With this geometrical analysis, binary T-F masks are designed to extract single source T-F units. On the basis of these extracted units, the second step estimates the mixing matrix. In addition, the first step also identifies the T-F units where two sources are simultaneously active (their empirical analysis shows very few units containing significant energy from all three sources hence this scenario can be ignored.) This information is necessary for the third step where the mixing matrix becomes determined and can be inverted. Like the related study by Araki, Makino, Sawada, et al. (2004), this work mainly targets the signal distortion problem. Unfortunately, no comparison with their other methods is mentioned.

Not all the work in T-F masking aims at the source separation problem. Several studies have explored binary T-F masks for robust ASR. In the previous subsection, I have discussed a separation technique by Kolossa and Orglmeister (2004) that performs ICA first and then binary T-F masking where the mask is constructed from the ICA outputs. Subsequently, Kolossa, Klimas, and Orglmeister (2005) applied their technique to ASR for noisy and convolutive speech mixtures. The binary mask provides reliable features in the T-F domain. However, high-performance ASR typically uses mel-frequency cepstral coefficients (MFCC) derived in the cepstral domain rather than in the spectral domain. Kolossa et al. suggested techniques that transform spectral features to MFCC for use in ASR. Without feature transformation, SNR gains obtained by T-F masking do not translate to recognition gains. With feature transformation, they report substantial ASR improvements from ICA and T-F masking. In another study, Harding, Barker, and Brown (2006) extended the Roman et al. (2003) approach to estimate a soft T-F mask which is then applied to missing data ASR. In a supervised training process, they obtain within each frequency channel histograms in the ITD-IID space for mixtures as well as for targets presented alone. These two histograms are then used to make a Bayesian decision for estimating the posterior probability of the target occurring in a particular T-F unit given the observed ITD and IID values. A T-F mask thus obtained is a soft mask, which can be used directly in a missing data approach for robust ASR. The difference from the Roman et al. system lies in the use of the histogram data to derive a probability mask. The main purpose of the Harding et al. study is for ASR in reverberant environments, and their evaluations demonstrate good recognition performance using estimated soft masks.

Summary

Table 1 gives an at-a-glance summary of the studies discussed in this section, along five columns: the method used for mask generation, whether a binary or soft mask is computed, whether reverberation is addressed, the mixture type (determined or underdetermined), and the evaluation metrics employed. In addition to SNR and ASR, the following abbreviations are used:

Table 1.

Summary of Time-Frequency Masking Algorithms for Speech Separation

Author(s) (Year)	Method	Mask Type	Reverberation	Mixture Type	Evaluation
Roman et al. (2003	Classification	Binary	No	Underdetermined	SNR, ASR, HSI
Yilmaz and Rickard (2004)	Clustering	Binary	Yes	Underdetermined	SNR, RSR
Aarabi and Shi (2004)	Phase analysis	Soft	Yes	Determined	ASR
Araki, Makino, Blin, et al. (2004)	DOA	Binary	Yes	Underdetermined	SNR, SDR
Araki, Makino, Sawada, et al. (2004)	Beamforming	Soft	Yes	Underdetermined	SNR, SDR
Kolossa and Orglmeister (2004)	ICA	Binary	Yes	Determined	SNR
Blin et al. (2005)	DOA	Binary	Yes	Underdetermined	SNR, SDR
Linh-Trung et al. (2005)	Clustering	Binary	No	Underdetermined	NRR
Saruwatari et al. (2005)	ICA	Binary	Yes	Determined	SNR
Kolossa et al. (2005)	ICA	Binary	Yes	Determined	SNR, ASR
Dubnov et al. (2006)	Classification	Soft	Yes	Determined	SNR
Roman et al. (2006)	Beamforming	Binary	Yes	Underdetermined	SNR, RSR, ASR
Sawada et al. (2006)	ICA	Soft	Yes	Underdetermined	SNR, SDR
Harding et al. (2006)	Classification	Soft	Yes	Underdetermined	ASR
Molla et al. (2006)	Clustering	Binary	No	Underdetermined	NRR
Mori et al. (2006)	ICA	Binary	Yes	Determined	SNR
Araki et al. (2007)	Clustering	Binary	Yes	Undetermined	SNR, SDR
Pedersen et al. (2008)	ICA	Binary	Yes	Underdetermined	SNR, RSR, NRR
Boldt et al. (2008)	Beamforming	Binary	No	Determined	HSI

NOTES: ASR = automatic speech recognition; DOA = direction of arrival; HSI = human speech intelligibility; HSQ = human speech quality; ICA = independent component analysis; NRR = noise-residual ratio; RSR = retained-speech ratio; SDR = speech-to-interference ratio; SNR = signal-to-noise ratio.

• DOA: direction of arrival

• HSI: human speech intelligibility

• HSQ: human speech quality

• NRR: noise-residual ratio

• RSR: retained-speech ratio

• SDR: speech-to-interference ratio

Although none of these studies are formulated for real-time implementation, some algorithms are more suitable for real-time operations than others. Of these, the following algorithms that use beamforming to produce T-F masks are most promising: Aarabi and Shi (2004), Roman et al. (2006), and Boldt et al. (2008). The Aarabi and Shi algorithm based on phase analysis can be viewed as a form of fixed beamforming with given directions of arrival. The Roman et al. algorithm uses adaptive beamforming which is somewhat more complex to implement than fixed beamforming.

In reviewing studies in this section, I focus on binaural or two-microphone mixtures. There are also studies that employ more than two microphones. Examples include Takenouchi and Hamada (2005), Cermak, Araki, Sawada, and Makino (2006), Togami, Sumiyoshi, and Amano (2006), and Araki et al. (2007). Generally speaking, systems with more than 2 microphones employ the same principles as those with two microphones. Actually, many of the two-microphone algorithms are originally formulated for an arbitrary number (greater than 1) of microphones and then tested in two-microphone settings.

Perceptual Studies

Speech Quality

A number of the systems described in the section “Binaural and Array-Based Time-Frequency Masking Algorithms” have been evaluated with listening tests. Except for Roman et al. (2003), these tests are all conducted on some form of speech quality, not speech intelligibility. For example, Araki, Makino, Sawada, and Mukai (2005) evaluated the amount of the perceived musical noise in their subject tests. We should note that speech quality tests are subjective in nature, influenced strongly by the kind of questions posed to the listener. Hence comparisons across different studies are difficult to draw.

Li et al. (2006) conducted a study on monaural speech separation with the aim of improving speech quality. Their separation method is intended to optimize an objective measure of speech quality. They also performed a perceived speech quality test in the form of a mean opinion score (MOS) in the range of 1 to 5 (5 is the best). Their results with 10 listeners show that the IBM yields an MOS of 3.18 whereas original mixtures give 1.33. Their evaluation also shows a substantial MOS improvement for their pitch-based separation algorithm as well as that of Hu and Wang (2004), both of which produce binary masks as output.

Speech Intelligibility

Several studies have directly tested speech intelligibility of binary T-F masking algorithms. The first such test is done by Roman et al. (2003) whose binaural algorithm was described in an earlier section. They tested the speech intelligibility of normal-hearing (NH) listeners using a Bamford-Kowal-Bench corpus of short English sentences (Bench & Bamford, 1979). The segregation result from their system in the form of a binary mask is used to synthesize a sentence presented at a target location diotically. They ran a two-source condition and a three-source condition. In the two-source condition, the interference is presented 5° apart from the target direction. In low SNR conditions, they find large intelligibility gains due to segregation: more than 20 and 60 percentage points for the input SNRs of −5 dB and −10 dB, respectively. In the three-source condition, the two interfering sources—both are speech utterances—are placed on the two sides of the target. In this condition, the intelligibility is increased by about 45 percentage points. Because their estimated masks are very similar to the ideal masks, this performance is indicative of that of the IBM.

Brungart, Chang, Simpson, and Wang (2006; see also Chang, 2004) conducted an intelligibility test on the IBM defined in Equation (1). They systematically vary LC in Equation (1), or the local SNR threshold in the IBM definition, leading to different ideal masks. They use the coordinate response measure English corpus (Bolia, Nelson, Ericson, & Simpson, 2000) to produce mixtures of one target talker and one to three competing talkers, where all talkers are normalized to be equally loud. Their results show that, within the local SNR range from −12 dB to 0 dB, ideal masking produces nearly perfect intelligibility scores, much higher than with no masking. Intelligibility monotonically decreases when LC increases in the positive range, due to the removal of increasingly more target energy, or when LC decreases in the negative range, saturating to the level with no masking, due to increasing interference.

In addition, they found that the intelligibility gain is significantly reduced when interference is speech-shaped noise (SSN) or modulated SSN. For SSN the benefit of ideal masking amounts to a reduction (improvement) of 5 dB in speech reception threshold (SRT) as opposed to an SRT reduction in the range of 22 to 25 dB for same-talker maskers—SRT refers to the input SNR level required to achieve the 50% intelligibility score. Their main explanation for the improved intelligibility is that IBM segregation strongly attenuates or eliminates informational masking, which refers to the nonenergetic form of masking caused by the inability to segregate target speech from similarsounding interfering signals.

Anzalone, Calandruccio, Doherty, and Carney (2006) tested a different version of the ideal binary mask, which is defined not in terms of the local SNR within each T-F unit, but the energy distribution of the target speech alone. The IBM is generated by comparing energy values of individual T-F units against a fixed threshold, which is adjusted in order to retain a certain percentage (e.g., 90%) of the total target energy. The ideal mask generated this way is then used to synthesize from a cochleagram a separated target from the mixture of speech and SSN. The test corpus is the commonly used HINT (hearing-in-noise test) (Nilsson, Soli, & Sullivan, 1994). The tests were conducted on 6 NH and 14 hearing-impaired (HI) listeners. They found that ideal masking leads to substantial SRT reductions: more than 7-dB reduction for NH listeners, and more than 9-dB improvement for HI listeners. In addition, for HI listeners, ideal masking in the low-frequency range (up to 1.5 kHz) contributes much more to reduced SRT than in the high-frequency range; for the NH listeners, on the other hand, ideal masking in the high-frequency range also contributes significantly. To obtain the benefit of ideal masking, the energy threshold for mask generation needs to be at least 90%. Also the benefit occurs with a relatively low frequency resolution but needs a relatively high temporal resolution.

In addition to improving SNR, IBM processing should decrease the spread of masking by interference. Listeners with hearing loss are known to be particularly susceptible to the upward spread of masking (Gagne, 1988). This explanation is consistent with their result that HI listeners show little improvement if binary masking is applied to only high-frequency bands, unlike NH listeners. Another interesting observation from Anzalone et al. (2006) is that HI listeners are less sensitive to binary masking artifacts than NH listeners.

A recent study by Li and Loizou (2008b) on NH listeners extends the findings of Brungart et al. (2006) to different types of speech and interference. Specifically, the speech material in their study consists of sentences from the IEEE database (IEEE, 1969) and the types of interference include speech babble and two-talker utterances in addition to SSN and modulated SSN. Their findings are consistent with those of Brungart et al. In particular, for input SNR levels of −5 and −10 dB, they find broad performance plateaus (near 100% intelligibility) with respect to LC values. For example, a plateau ranges from LC = −20 dB to 5 dB for speech and babble noise mixed at the SNR of −5 dB. In addition, this study has assessed the impact of deviations from the IBM on speech intelligibility. By systematically and randomly flipping binary labels of the IBM, they observed that the intelligibility score drops gradually as the percentage of wrongly labeled T-F units increases. Compared with unprocessed mixtures, there is still performance improvement when the mask error is 40% for babble noise and 20% for SSN and two-talker speech masker. An important finding in their error analysis is that miss errors (1 flipped to 0) and false-alarm errors (0 flipped to 1) have different effects on intelligibility, and false-alarm errors are substantially more harmful to intelligibility.

A subsequent study by Li and Loizou (2008a) examines the effects of spectral resolution and band-limited processing on IBM segregation. The stimuli are processed using a sinewave-excited vocoder with the number of frequency channels systematically varied. Their results on NH listeners show significant intelligibility improvements with as few as 12 channels for IBM-processed stimuli. The improvement is particularly large (by 60 percentage points) with 24 and 36 channels, although the resulting intelligibility is not as high as that reached with 128 channels used in Brungart et al. (2006). Besides the differences in the number of frequency channels, the use of vocoded stimuli in Li and Loizou (2008a) could also contribute to less-than-perfect intelligibility. In addition, Li and Loizou evaluated the intelligibility of IBM processed stimuli in the low-frequency range only (i.e., no ideal masking in the high-frequency range). They observe a monotonic increase of intelligibility as the range of ideal masking extends to higher cutoff frequencies, until performance asymptotes with cutoff frequencies of 1.5 to 2.5 kHz depending on input SNR. This observation suggests that IBM processing in the first and second formant regions is sufficient for intelligibility. These results indicate the potential of T-F masking for cochlear implants.

Wang, Kjems, Pedersen, Boldt, and Lunner (2008) also evaluated the speech intelligibility improvements of IBM processing for both NH and HI listeners. Their study uses the IBM definition in Equation (1) by fixing LC to −6 dB and measures the SRT effects of ideal masking using both SSN and a cafeteria noise. The speech material comprises Danish sentences from the Dantale II corpus (Wagener, Josvassen, & Ardenkjær, 2003). With the SSN background, they found a 7.4-dB SRT reduction for NH listeners and a 9.2-dB SRT reduction for HI listeners. These levels of SRT improvements are compatible with those reported by Anzalone et al. (2006) despite different IBM definitions. For the cafeteria background, Wang et al. (2008) observed a 10.5-dB SRT reduction for NH listeners and a 15.6-dB SRT reduction for HI listeners. The observed SRT improvements for the cafeteria noise are significantly larger than for SSN, suggesting that ideal masking is more effective for modulated noise than for stationary noise (see also Brungart et al., 2006). A striking conclusion from Wang et al.'s study is that IBM processing makes the intelligibility performances for HI listeners and NH listeners comparable. This study also shows that IBM segregation in lower frequency (up to 1.35 kHz) brings more benefit than IBM processing in higher frequency (>1.35 kHz), particularly for HI listeners, confirming a similar finding by Anzalone et al. (2006). Wang et al. point out that one reason is that IBM segregation in low frequency removes more background noise than IBM segregation in high frequency because the distribution of noise energy is heavily tilted towards low frequency.

In the above studies, either input SNR or LC is fixed. What happens if input SNR and LC are co-varied? Exploiting the fact that changing input SNR and LC by the same amount does not alter the IBM, Wang, Kjems, Pedersen, Boldt, and Lunner (in press) tested an extreme version of IBM where both input SNR and LC are set to −∞ dB. In this case, the stimulus contains only noise with no speech at all. More specifically, IBM plays the role of specifying when to turn on or off the filtered noise. With SSN, they observed that listeners can achieve nearly perfect speech recognition from noise gated by the IBM. Only 16 frequency channels and binary gains varying at the rate of 100 Hz are apparently sufficient for high intelligibility scores. This finding is surprising as the information encoded in binary gains is greatly reduced compared with that contained in original speech—both spectral and temporal aspects of the speech signal are severely degraded. It should be noted that, within a frequency channel, vocoded noise in the well-known study of Shannon, Zeng, Kamath, Wygonski, and Ekelid (1995) uses the full speech envelope whereas a binary envelope is used in ideally masked noise (Wang et al., in press).

A few conclusions can be drawn from the above studies. First, IBM processing provides large intelligibility gains. Second, the intelligibility benefit is even larger for HI listeners than for NH subjects, and for modulated noise than for steady noise. Third, binary masking in limited frequency regions (particularly in the low-frequency range) or a small number of frequency channels can still provide substantial intelligibility improvements.

Assessment from the Hearing Aid Perspective

None of the studies on T-F masking have so far targeted the hearing aid application directly. The core of T-F masking is to apply different gains to different T-F units, depending on estimation of local SNRs within these units. So T-F masking is a form of T-F gain control in the range between 0 and 1 (Anzalone et al., 2006). Once T-F gains are computed, a T-F masking strategy can be viewed as a multichannel (multiband) dynamic compression scheme in a hearing aid (Dillon, 2001). In practice, T-F masking would need to be implemented in addition to dynamic compression whose main purpose is to decrease input sound levels to match the dynamic range of HI listeners.

The consideration of hearing aid implementation, however, places a number of constraints on the complexity of an algorithm, including

• The requirement of real-time processing: This constraint limits the processing delay to just a few milliseconds (see, e.g., Kates & Arehart, 2005), which in turns limits the algorithmic complexity and the availability of the data at a particular time.

• Amount of required training: Machine learning has been increasingly applied to speech separation. The amount of training is typically not a concern for algorithmic development, but it is for the hearing aid application. In particular, the amount of training needed during operation, if any, must be small.

• The number of frequency bands in a multichannel hearing aid is relatively small.

With the above constraints in mind, I assess monaural T-F masking algorithms in the next subsection and binaural algorithms in the subsequent subsection. The subsection titled “Musical Noise” discusses how to attenuate the musical noise caused by T-F masking.

Monaural Algorithms

Current monaural separation systems give little consideration to real-time implementation, and algorithms generally involve complex operations for feature extraction, segmentation, grouping, or significant amounts of training. Even without the constraint of operating in real time, the performance of such systems is still not stable or consistent enough for implementation in a hearing aid. Although aspects of this research could be exploited for the hearing aid application in the short term, for example, classification of acoustic environments for hearing aid use (Buchler, Allegro, Launer, & Dillier, 2005), long-term research is required before monaural T-F masking algorithms can be used for noise reduction in hearing aids. Future effort is especially needed in real-time processing, sequential organization (grouping of the same source across time), and robustness to room reverberation.

On the other hand, research on monaural separation techniques holds a great deal of potential for the hearing aid application, as it is based on principles of auditory perception and not subject to fundamental limitations of spatial filtering such as configuration dependency (see next subsection) and the inability of suppressing interfering sounds arriving from directions that are the same as or close to the target direction. In addition, monaural segregation is based on intrinsic sound properties such as periodicity, and it is thus expected to be more robust to room reverberation than spatial filtering provided by beamforming, which is fundamentally susceptible to echoes coming from various directions. Also, incorporating aspects of monaural separation, such as segmentation, likely enhances the noise reduction performance of directional systems.

Binaural and Array-Based Algorithms

Algorithms based on classification or clustering. As explained in the section “Binaural and Array-Based Time-Frequency Masking Algorithms” the basic T-F masking approach builds on the observation that a data histogram of time and amplitude differences from individual T-F units forms characteristic clustering. From these data distributions, unsupervised clustering or supervised classification algorithms are then used to estimate the IBM. These algorithms are simple to apply and their underlying principles are well understood.

The cluster structure is, however, configuration dependent. That is, when sound sources change their locations, a different cluster structure is formed. To perform effective T-F separation retraining is required in order to model the new cluster structure. In other words, effective T-F separation is configuration specific. This is a major drawback of such algorithms from the standpoint of real-time processing. Although techniques can be introduced to relax this limitation, such as the use of approximate but fast update (Rickard, Balan, & Rosca, 2001) or pretraining of configurations to form some lookup table plus interpolation, resulting algorithms become more complex and the performance degrades.

Another limitation of classification/clustering arises when room reverberation is considered. The difficulty posed by reverberation (or convolutive mixtures) is twofold. First, the cluster structure becomes much shallower and noisier with many spurious peaks. Second, extracted time and amplitude differences are less reliable. As a result, separation performance drops significantly (Brown & Palomäki, 2006).

The limitations of configuration specificity and room reverberation make it difficult to apply the algorithms based on clustering or classification to hearing aid design.

Algorithms Based on ICA. Many of the recent T-F algorithms couple the use of ICA and T-F masking. As already mentioned, ICA is based on the assumption that source signals are statistically independent and performs blind source separation by computing a demixing matrix through statistical machine learning. To make ICA applicable requires a number of assumptions, including that the mixing is determined (i.e., the number of microphones is no less than the number of sources) and that the mixing matrix is constant for a period of time to estimate the demixing matrix. The latter assumption is essentially the same as that of configuration specificity. Indeed the limitation of a determined mixture is a major reason for exploring T-F masking. Even for determined mixtures, room reverberation complicates the problem considerably. All of these factors have diminished the early enthusiasm of ICA as an audio separation approach (Hyvärinen et al., 2001). The prospect of ICA-based masking algorithms for the hearing aid application is similarly limited.

Algorithms based on beamforming. Considering the limitations of configuration specificity and ICA, T-F masking algorithms based on beamforming hold promise for the hearing aid application. Both fixed and adaptive beamforming techniques are effective for improving speech intelligibility, and have been implemented in modern hearing aids. Two-microphone beamforming either enhances the signal from a target direction (forming a lobe) or suppresses the noise from a specific direction (forming a null). Recent hearing aids make use of first-order differential microphones with the target sound assumed to occur in the front (look) direction. In addition, subband adaptive beamformers have been built into hearing aids for the purpose of attenuating strong interfering sources originating from the back (e.g. Oticon Syncro).

Two such approaches are of potential interest for hearing aid implementation. The first approach was proposed by Roman et al. (2006). This approach derives a binary mask on the basis of adaptive beamforming, which can be viewed as comparing an adaptively formed beampattern and an omnidirectional pattern, and has been tested in reverberant situations. The second approach is described by Boldt et al. (2008). As mentioned in the section “Binaural and Array-Based Time-Frequency Masking Algorithms” this approach derives T-F masks by comparing the responses from the front cardioid and the back cardioid. The binary masking algorithm is particularly simple, making it feasible for implementation. Each of the two approaches is described in more detail below.

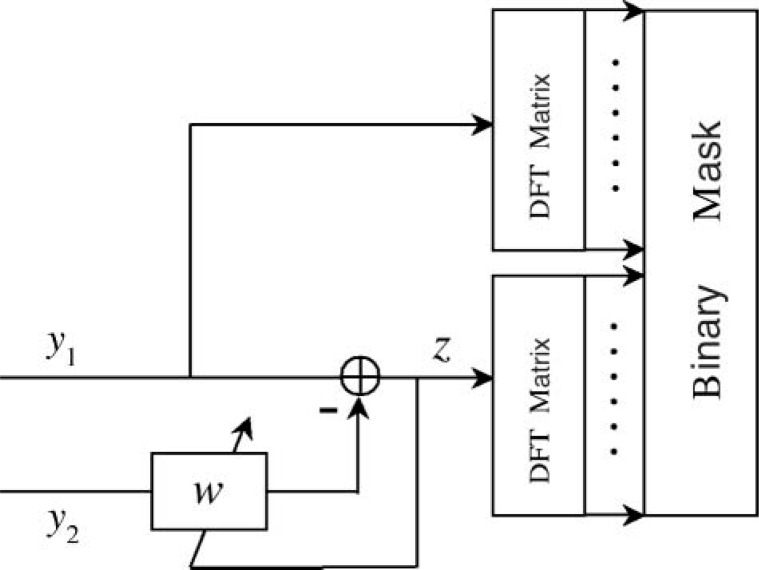
The approach by Roman et al. (2006) was designed to deal with room reverberation. As mentioned earlier, the system has two stages as shown in Figure 5, where y₁ and y₂ denote two microphone signals. In the first stage, an adaptive beamformer is trained to form a null in the front direction. The output of the beamformer is denoted as z. At one of the two microphones (the so-called “better ear”), say microphone 1, STFT transforms the microphone signal and the beamformer output into a T-F representation. The second stage computes the energy ratio of the corresponding T-F unit pairs of the two T-F representations, called output-to-input energy ratio (OIR),

Figure 5.

Diagram of the Roman et al. (2006) system. An adaptive filter is applied for target cancellation in the first stage. The second stage computes a binary time-frequency mask by comparing the mixture signal and the adaptive filter output (DFT = discrete Fourier transform).

Source: Reprinted from Roman et al. (2006), with permission from Journal of the Acoustical Society of America, American Institute of Physics.

$$OIR\left(t,f\right)=\frac{{\left|Z\left(t,f\right)\right|}^2}{{\left|Y_1\left(t,f\right)\right|}^2}$$ (2)

where Z and Y₁ are the Fourier transforms of z andy₁, respectively.

After an analysis of the correlation between OIR and the relative strength of target energy with respect to mixture energy, Roman et al. (2006) set the decision threshold for binary mask generation to −6 dB; that is, u(t, f) = 1 if OIR(t, f) < −6 dB and 0 otherwise. The binary mask is then used to reconstruct the separation result at the better ear (microphone 1). Roman et al. evaluated their system on reverberant mixtures using both SNR and ASR measures, which are found to give similar performance profiles. Their system produces substantial improvements compared to no processing. With the exception of two-source configurations, where an adaptive beamformer designed for reverberant environments gives a better output, the algorithm outperforms the adaptive beamformer, which in turn gives better results than a delay-and-sum beamformer.

It is worth noting that in the Roman et al. (2006) system mixture signals are obtained from the KEMAR, with microphones spaced according to the layout of the human head. If their algorithm is to be implemented on two closely spaced microphones, some adapting work is needed although directional microphones can be turned into an adaptive beamformer. Also, the training for adaptive beamforming is specific to a particular room configuration, and it remains to be investigated to what extent the segregation performance degrades with changing room configurations and whether a simpler adaptive beamformer that is less restrictive in terms of training can still outperform a fixed null beamformer. Currently, a single mask is computed for the better ear, and it would be interesting to see whether improvements can be made by computing two masks for the two microphones and reconstructing a spatial pattern as output.

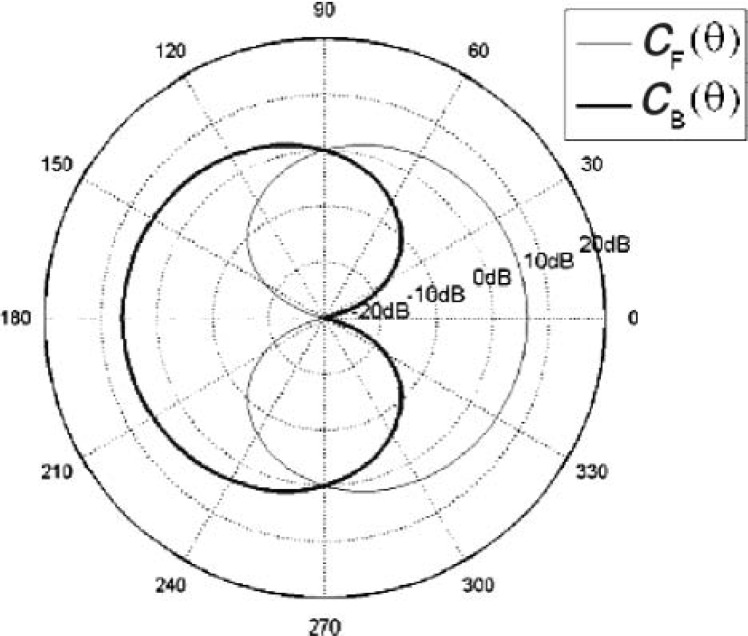
With two closely spaced microphones, two cardioid directivity patterns can be formed. Figure 6 illustrates the two cardioids, where the front cardioid response is denoted by C_F and the back by C_B. Boldt et al. (2008) converted each cardioid response into the T-F domain using a filterbank and then estimated the IBM as follows:

Figure 6.

Two back-to-back cardioid responses. The front direction corresponds to θ = 0°.

$$\stackrel{\circ }{IBM}\left(t,f\right)=\{\begin{array}{ll}1\hfill & \text{if}\hspace{0.17em}{C}_{\text{F}}\left(t,f\right)-C_{\text{B}}n\left(t,f\right)>L{C}^{\prime }\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (3)

where IBM denotes the estimated IBM, and C_F(t, f) and C_B(t, f) denote the energy (in dB) of the front cardioid within u(t, f) and that of the back cardioid, respectively The parameter LC' is a threshold (also in dB).

For two sources in anechoic conditions, Boldt et al. (2008) found that, for a given LC' in Equation (1), LC'in Equation (3) can be chosen accordingly,

$$L{C}^{\prime }=\frac{a_0^{2}LC+a_1^2}{b_0^{2}LC+b_1^2}$$ (4)

where a₀ and a₁ are the directional gains of the front cardioid to the target and the interference, respectively, and b₀ and b₁ are the directional gains of the back cardioid to the two sources.

The evaluation of the system by Boldt et al. (2008) shows that IBM and IBM are nearly identical, indicating that the estimated IBM should perform nearly as well as the IBM in terms of speech intelligibility for two sources in anechoic conditions (see Li & Loizou, 2008b). Even without knowing the directional gains, they suggest that a particularly simple choice of LC' = 0 dB is still expected to produce high levels of speech intelligibility as long as the target signal is located in the front and the interfering signal in the back.

The fixed choice of LC' = 0 dB for generating a binary mask in a directional system corresponds to checking whether C_F(t, f) > C_B(t, f), which is simple to implement. On the other hand, the effectiveness of the method with respect to standard beamforming remains to be evaluated in reverberant or diffuse-noise conditions.

Musical Noise

Many recent T-F masking algorithms have been designed with the musical noise problem in mind. In addition, studies have been conducted to specifically deal with the problem. A few conclusions may be made:

• Temporal smoothing by using relatively smaller frame shifts (Araki et al., 2005) or in selected frequency regions in the cepstral domain (Madhu, Breithaupt, & Martin, 2008) has been shown to be effective in attenuating the musical noise.

• A sigmoidal mask with constant cutoffs at both low and high ends helps to soften the output sound (Araki, Sawada, Mukai, & Makino, 2006; Li, McAllister, Black, & Perez, 2001).

• The output with attenuated musical noise tends to accompanied by lower SNR gains. In other words, there may be an SNR cost associated with improved quality.

Algorithms that attempt to reduce musical noise are typically tested on some quality measure or a speech quality test with listeners, and the effect on speech intelligibility is not known. One should keep in mind that HI listeners might be less sensitive to or bothered by binary-masking distortions than NH listeners (Anzalone et al., 2006). This could result from reduced spectral and temporal resolutions of HI subjects. Hence, effects on HI listeners may not be inferred from tests with NH listeners.

Given the current understanding on the musical noise associated with T-F masking, some combination of smoothing and sigmoidal masking with constant cutoffs guided by auditory masking data, will likely lead to an acceptable level of speech quality for HI listeners. A critical question is whether a smoother sounding output will diminish the potential intelligibility benefit brought about by T-F masking.

Discussion

What Is the target?

In the presence of multiple sound sources, which source should be treated as the target at a particular time? This important question is closely related to the complex issue of auditory attention: That is, what controls the shift of attention from one moment to the next? Current directional hearing aids get around this issue by assuming that the target is in the look direction, which is a practical solution in many listening situations, although there are certainly situations where such an assumption is incorrect. Assuming that sound sources can be separated, a reasonable alternative would be to treat the loudest source (e.g., loudest talker) as the target in light of the Lombard reflex that speakers unconsciously raise their voice level with increasing background noise. This alternative is also unreasonable in certain environments. Perhaps a combination of the two would give a better solution than either one. To apply such a combination would of course require the use of algorithms that achieve reliable separation.

Binary Versus Soft Masks

Should a T-F mask as the output of a separation system be binary or soft? Although it is binary T-F masks that depart from more traditional ratio masks (e.g., a Wiener filter) and trigger much research in the T-F masking paradigm, recent studies have also advocated the use of soft masks, not only for speech separation (Reddy & Raj, 2007; Sawada et al., 2006) but also for ASR (Barker, Josifovski, Cooke, & Green, 2000; Harding et al., 2006; Srinivasan, Roman, & Wang, 2006). As discussed in the section “Binaural and Array-Based Time-Frequency Masking Algorithms,” a main consideration behind the interest in using soft masks is the attenuation of the musical noise although improved quality is often accompanied by reduced SNR gain.

Because a binary mask can be treated as a special case of a soft mask, it should not come as a surprise that soft masks can outperform binary masks. Barker et al. (2000) showed performance benefits in ASR by replacing binary masks with soft masks. Palomäki, Brown, and Barker (2004), however, found no performance gain for reverberant speech recognition. Srinivasan et al. (2006) reported that in a small-vocabulary task, binary masks perform better than ratio masks, whereas the reverse is true for a large-vocabulary task. A subsequent study by Srinivasan and Wang (2007) proposes a new approach to ASR in conjunction of binary masks and shows good performance in a large-vocabulary task. In a direct comparison between the IBM and an ideal ratio mask using both speech and music mixtures, Li and Wang (in press) found, surprisingly, that the SNR gain from the ideal ratio mask is only slightly higher than the IBM. It is therefore likely that no clear-cut conclusion can be drawn concerning whether soft masks are better than binary masks. Which is better probably depends on the task involved and the algorithm used for mask generation.

One should be careful not to generalize SNR or ASR results to speech intelligibility. As discussed in the section “Perceptual Studies,” there is conclusive evidence showing that IBM segregation clearly improves human speech recognition in noise. Binary T-F masking algorithms in some limited cases have also been shown to improve speech intelligibility. Whether soft masking can also improve speech intelligibility remains to be seen, and the history in speech enhancement proves the elusive nature of improving speech intelligibility (Loizou, 2007).

Lastly, I want to remark that, unless soft masking is expected to have significant performance gains, the use of binary masking should be preferred. The reason lies in estimation. Binary masking entails binary decision making, and methods abound in pattern classification and clustering (Duda et al., 2001) that can be employed to make binary decisions. On the other hand, soft decision making often requires approximating an underlying function that tends to be more complex. In other words, computing a binary mask may be considerably simpler than computing a soft mask.

Quality Versus Intelligibility

As discussed in the sections “Binaural and Array-Based Time-Frequency Masking Algorithms” and “Assessment from the Hearing Aid Perspective,” progress has been made in addressing the issue of speech distortion or the musical noise accompanying T-F masking. Techniques introduced to improve speech quality typically “soften” basic operations in T-F masking and come at the expense of reduced SNR gain. It is possible that processing that enhances speech quality ends up hurting speech intelligibility. A core appeal of T-F masking for speech separation is its promise for improving speech intelligibility. Hence, methods for attenuating the musical noise should be evaluated not only on their effects on speech quality but also their impact on speech intelligibility.

To conclude, a substantial amount of research has been recently conducted on T-F masking for speech separation. An appraisal from the hearing aid perspective suggests that, although a majority of the proposed techniques are unlikely useful for hearing prosthesis immediately, T-F masking algorithms based on beamforming may be valuable for noise reduction in hearing aids in the near term.