Abstract
Spatial statistics has seen rapid application in many fields, especially epidemiology and public health. Many studies, nonetheless, make limited use of the geographical location information and also usually assume that the covariates, which are related to the response variable, have linear effects. We develop a Bayesian semi-parametric regression model for HIV prevalence data. Model estimation and inference is based on fully Bayesian approach via Markov Chain Monte Carlo (McMC). The model is applied to HIV prevalence data among men in Kenya, derived from the Kenya AIDS indicator survey, with n = 3,662. Past studies have concluded that HIV infection has a nonlinear association with age. In this study a smooth function based on penalized regression splines is used to estimate this nonlinear effect. Other covariates were assumed to have a linear effect. Spatial references to the counties were modeled as both structured and unstructured spatial effects. We observe that circumcision reduces the risk of HIV infection. The results also indicate that men in the urban areas were more likely to be infected by HIV as compared to their rural counterpart. Men with higher education had the lowest risk of HIV infection. A nonlinear relationship between HIV infection and age was established. Risk of HIV infection increases with age up to the age of 40 then declines with increase in age. Men who had STI in the last 12 months were more likely to be infected with HIV. Also men who had ever used a condom were found to have higher likelihood to be infected by HIV. A significant spatial variation of HIV infection in Kenya was also established. The study shows the practicality and flexibility of Bayesian semi-parametric regression model in analyzing epidemiological data.
Introduction
Globally, people living with HIV were estimated to be 35.3 million in 2012 with 2.2 million new infections. It is estimated that over two thirds of all persons living with HIV are in sub-Saharan Africa [1]. Furthermore, this region also has the highest prevalence and HIV infection incidence in the entire world [1].
Many prevention strategies are being employed to minimize new infections and to improve the living standards of HIV-infected persons. Notably, male circumcision campaigns [2]–[4], introduction of tropical microbicides [5]–[6], vaccine initiatives [7]–[9] and the roll out of antiretroviral therapy [10].
Monitoring the prevalence of HIV in a country using national averages is important, especially for assessing the HIV trend at national level over time and for comparison purposes between countries. However, the approaches can facade HIV prevalence variability among administration units in the country [11]. Subsequently, policies and interventions developed from these approaches might have no effect at the grassroots level.
In Kenya, HIV prevalence in 2007 was estimated to be approximately at 7.1% among adults aged 15–64 years [13]. HIV prevalence varies considerably between sub-regions in the country. Counties like Bungoma, Embu, Isiolo, Kajiado, Machakos, Meru, Wajir and West Pokot having a prevalence of less than 3% while counties close to the Lake Victoria region, in the West having prevalence ranging between 13% and 25% [13]. The dissimilarities in these regions may be explained by cultural factors, demographic factors and socioeconomic factors [14]–[15].
A proper understanding of the spatial component of HIV among the administrative units in a country is key to structuring, developing and implementing apposite strategies that will have an effect on people at the local administrative units [16].
HIV prevalence in Kenya also varies significantly by sex and age. HIV prevalence among women in Kenya is 6.9% and 4.4% among men [12]. HIV prevalence by age has a nonlinear relationship, assuming an inverted U-shape [14], [17]. In particular, HIV prevalence is low among people below the age of 18, the prevalence increases up to the age of 35–40 then starts declining with increase in age.
Several studies on spatial analysis of HIV prevalence at lower administration units in Kenya have been based on proportions [17], [18]. This prevalence estimates and corresponding maps are prone to instability, hence unreliable due to small sample sizes from these administrative units. Some studies have applied spatial smoothing techniques to circumnavigate this sparse data problem [19]. However, these studies have inherently assumed that all covariates in the study have a linear relationship with the response variable. This linear relationship might not be valid for some variables. As noted earlier, HIV prevalence has a nonlinear relationship with age of an individual.
A primary objective of this study is to develop and apply flexible models to capture this nonlinear nature of some covariates while still accounting for the spatial heterogeneity. The study proposes a spatial semi-parametric model based on penalized regression spline to model HIV prevalence data among men, extracted from the Kenya AIDS Indicator Survey (2007).
Methods
Data
The Kenya AIDS Indicator Survey (KAIS) was carried out by the Government of Kenya with financial support from United States President's Emergency Plan for AIDS Relief (PEPFAR) and United Nations (UN). The key objective of survey was to collect high quality data on the prevalence of HIV and Sexually Transmitted Infections (STI) among adults, and to assess knowledge of HIV and STI in the populations.
The survey collected a representative sample of households selected from the eight provinces in the country. It involved men and women in the age of 15–64 years. Two questionnaires were used in the survey. A household questionnaire which was used to collected information about the household head and the characteristics of the dwelling place. The second one, the individual questionnaire collected information from men and women aged 15–64 years, about their demographic characteristics, and their knowledge on HIV and STI. Each individual was then asked for consent to provide a venous blood sample for HIV and HSV-2 testing. Readers are referred to the final survey report regarding survey methodologies used in collecting the data [13]. Even though a new round of KAIS, 2012 [12] has been done, this study uses the 2007 data since the final release of this new study has not been made hence the data was not availlable for use. In this study we use the men's data from this survey. In total, 3,662 men who provided venous blood for testing and also had full covariate information were used in the analysis. In the data, age was captured as both categorical and continous while all the other covariates were continuous. Table 1 gives an initial exploratory analysis used to identify variables that are significantly associated with HIV infection. The variables were categorised in to four groups, namely, demographic, social, biological and behavioural.
Table 1. Exploratory data analysis.
| Variable | p-value | Unadjusted OR | 95% CI for OR |
| Demographic characteristics | |||
| Age(ref 15–19) | 0.000 | 1 | |
| 20–24 | 0.009 | 0.337 | (0.149,0.759) |
| 25–29 | 0.363 | 0.714 | (0.346,1.474) |
| 30–34 | 0.017 | 2.217 | (1.151,4.269) |
| 35–39 | 0.004 | 2.62 | (1.362,5.04) |
| 40–44 | 0.001 | 3.024 | (1.571,5.823) |
| 45–49 | 0.001 | 3.231 | (1.668,6.257) |
| 50–54 | 0.013 | 2.362 | (1.195,4.67) |
| 55–59 | 0.022 | 2.284 | (1.127,4.628) |
| 60–64 | 0.796 | 0.894 | (0.383,2.09) |
| Place of residence (Ref Rural) | 1 | ||
| Urban | 0.016 | 1.326 | (1.055,1.668) |
| Social characteristics | |||
| Number of children dead (ref Never given birth) | 0.658 | 1 | |
| no child died | 0.999 | 0.491 | (0.310,0.803) |
| one child died | 0.802 | 0.763 | (0.093,6.294) |
| more than one child died | 0.970 | 0.960 | (0.116,7.928) |
| Education level (ref None) | 0.047 | 1 | |
| Primary | 0.177 | 1.183 | (0.927,1.511) |
| Secondary | 0.050 | 1.108 | (0.047,0.079) |
| Higher | 0.047 | 0.721 | (0.476,0.991) |
| Wealth quantile (ref Poorest) | 0.889 | 1 | |
| Second | 0.750 | 1.060 | (0.741,1.517) |
| Middle | 0.938 | 1.014 | (0.710,1.449) |
| Fourth | 0.954 | 0.990 | (0.693,1.414) |
| Richest | 0.430 | 1.141 | (0.822,1.584) |
| Marital status (ref Married,1partner) | 0.000 | 1 | |
| Married, +2partner | 0.002 | 1.762 | (1.232,2.520) |
| Divorced/Separated | 0.831 | 1.053 | (0.656,1.689) |
| Widowed | 0.000 | 3.318 | (1.925,5.720) |
| Never Married | 0.000 | 0.310 | (0.230,0.420) |
| Age at first sex (ref Never had sex) | 0.000 | 1 | |
| under 11 | 0.302 | 1.768 | (0.599,5.22) |
| between 12–14 | 0.000 | 6.678 | (3.393,13.144) |
| between 15–17 | 0.000 | 6.264 | (3.282,11.953) |
| over 18 | 0.000 | 5.400 | (2.836,10.284) |
| Perceived risk of HIV (ref No risk) | 0.010 | 1 | |
| Small Risk | 0.001 | 0.424 | (0.253,0.711) |
| Moderate Risk | 0.005 | 0.501 | (0.308,0.813) |
| Great Risk | 0.891 | 1.038 | (0.612,1.759) |
| Biological characteristics | |||
| Circumcision status (ref circumcised) | 1 | ||
| Not circumcised | 0.000 | 4.344 | (3.479,5.423) |
| Had STI in the last 12 months (ref Yes) | 1 | ||
| No | 0.003 | 0.464 | (0.28,0.769) |
| Behavioural characteristics | |||
| Ever used Condom (ref Yes) | 1 | ||
| No | 0.000 | 0.641 | (0.505,0.814) |
| Paid for sex (ref Yes) | 1 | ||
| No | 0.430 | 0.712 | (0.306,1.657) |
| Freq of travel away (ref Did not stay away) | 0.089 | 1 | |
| stayed away 1–2 times | 0.127 | 1.233 | (0.942,1.613) |
| stayed away 3–5 times | 0.024 | 1.415 | (1.047,1.914) |
| stayed away 6–10 times | 0.255 | 1.290 | (0.832,1.999) |
| stayed away >11 times | 0.408 | 0.797 | (0.466,1.363) |
From this initial analysis, the following variables were found to be associated with HIV infection and were included in subsequent analyses: place of residence, age, education level, marital status, age at first sex, perceived risk of HIV, circumcision status, if had STI in the last 12 months and if ever used a condom. Further from this initial analysis, it was evident that age had a nonlinear effect on HIV infection, hence its continous form (mean = 33.70, SD = 13. 45) was used in the subsequent analyses.
Ethics Statement
Ethical clearance was granted by the institutional review board of the Kenya Medical Research Institute (KEMRI) and the US Centers for Disease Control and Prevention. The consent procedure, highlighted below, was approved by these two bodies.
Participants provided separate informed oral consent for interviews, blood draws and blood storage and, the interviewer signed the consent form to indicate whether or not consent was given for each part. An oral informed consent was given for participants in the age of 18–64 while for minors, in the age group 15–17, oral informed consent was obtained from a parent/guardian or other adult responsible for the youth's health and welfare before the youth was asked for his/her consent. Only after the parent or guardian had agreed, was when the consent was asked of the adolescent.
Investigators in the study got a waiver of documentation of informed consent for all participants due to the fact that the research presented very minimal risk of harm to the individuals. The waiver did not adversely affect the rights and welfare of the participants, and the survey involved no procedures for which written consent is normally required outside the research context in Kenya.
Statistical model
Let 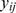 be the HIV status of individual
be the HIV status of individual  in county
in county 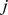 .
. 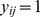 if individual
if individual  in county
in county 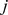 is HIV positive and zero otherwise.
is HIV positive and zero otherwise.
The vector 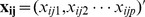 contains
contains 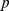 continuous independent random variables and
continuous independent random variables and 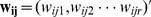 contains
contains  categorical independent random variables with first component accounting for the intercept. In this study,
categorical independent random variables with first component accounting for the intercept. In this study, 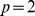 and
and 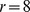 .
.
This study assumes that the dependent variable 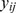 is Bernoulli distributed, i.e
is Bernoulli distributed, i.e 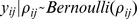 with an unknown
with an unknown 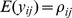 , being related to the independent variables as follows:
, being related to the independent variables as follows:
In this equation, 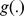 is a logit link function,
is a logit link function, 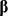 is a
is a 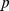 dimensional vector of regression coefficients for the continuous independent variables, and
dimensional vector of regression coefficients for the continuous independent variables, and 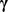 is a
is a  dimensional vector of regression coefficients for the categorical independent variables.
dimensional vector of regression coefficients for the categorical independent variables.
In order to cater for both the nonlinear effects of the continuous covariates and the spatial autocorrelation in the data, a semi-parametric model utilizing the penalized regression spline approach and convolution model was employed.
The penalized regression spline approach relaxed the highly restrictive linear predictor by a more flexible semi-parametric predictor, defined as:
Here, 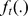 is a nonlinear twice differentiable smooth function for the continuous covariates and
is a nonlinear twice differentiable smooth function for the continuous covariates and 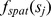 is a factor that caters for the spatial effects of each county. This study considers a convolution approach to these spatial effects, which assumes that the spatial effect can be decomposed in to two pure components, spatially structured and spatially unstructured, i.e
is a factor that caters for the spatial effects of each county. This study considers a convolution approach to these spatial effects, which assumes that the spatial effect can be decomposed in to two pure components, spatially structured and spatially unstructured, i.e 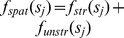 .
.
The final model can be expressed as:
Estimation of parameters
A full Bayesian approach in estimation was used in this study. Prior distributions were assigned to all the parameters as discussed in the following subsections.
Smooth function
There exists a myriad of methods for estimating the smooth functions . Several authors have given a thorough review of these methods [20]–[21]. Of particular importance to this current study is the use of penalized regression splines, which was proposed by Eilers and Marx [22]. In this method, the assumption is that the effect of the continuous covariates can be approximated by a polynomial spline. In particular, they assume that the smooth function
. Several authors have given a thorough review of these methods [20]–[21]. Of particular importance to this current study is the use of penalized regression splines, which was proposed by Eilers and Marx [22]. In this method, the assumption is that the effect of the continuous covariates can be approximated by a polynomial spline. In particular, they assume that the smooth function  can be approximated by a spline of degree
can be approximated by a spline of degree 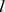 with
with 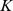 equally spaced knots,
equally spaced knots, 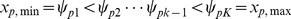 , yielding,
, yielding,
where, 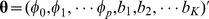 and
and 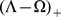 is equal to
is equal to  if
if  is positive and zero otherwise.
is positive and zero otherwise.
Following Caroll and Rupert [23], this study considers 20 knots to ensure enough flexibility and takes the 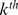 knot to be defined as the sample quantile of the continuous independent variable obtained with a probability equal to
knot to be defined as the sample quantile of the continuous independent variable obtained with a probability equal to 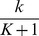 . Furthermore, this study utilizes a quadratic spline, hence degree
. Furthermore, this study utilizes a quadratic spline, hence degree 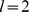 .
.
To avoid getting a smooth function which “wiggles” too much, a roughness penalty, suggested by Green and Silverman [24], given by
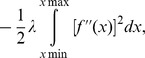 |
is imposed in the log- likelihood yielding the penalized log-likelihood function given by
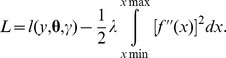 |
The balance between flexibility and smoothness is dictated by the positive parameter 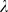 .
.
Spatial components priors
For the prior distribution of the spatially structured effects, this study uses the nearest neighbour Gaussian Markov random field which is specified as follows:
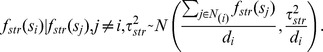 |
Here, 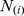 and
and 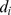 are, respectively, the set and number of neighbours of region
are, respectively, the set and number of neighbours of region  . The neighbourhood can be defined in terms of whether two regions share a border or not. If the two regions share a border then they are neighbours, otherwise they are not. This leads to the intrinsic conditional autoregressive (ICAR) prior distribution [25], [26].
. The neighbourhood can be defined in terms of whether two regions share a border or not. If the two regions share a border then they are neighbours, otherwise they are not. This leads to the intrinsic conditional autoregressive (ICAR) prior distribution [25], [26].
The unstructured spatial effect were assumed to have a Gaussian prior distribution, that is 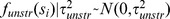 .
.
In addition, the variance hyperparameters, 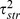 and
and 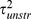 were assigned inverse gamma prior distributions as follows:
were assigned inverse gamma prior distributions as follows:
Other prior distributions
For the fixed effects coefficients, the following prior distributions were assumed:
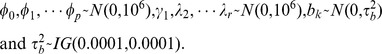 |
Posterior distribution
Posterior distribution refers to the distribution of the parameters after observing the data. It is obtained by updating the prior distribution with observed data. A full Bayesian inference gets its estimates by sampling from this posterior distribution. In reality, the posterior distribution is usually of high dimension and analytically intractable. This is aggravated by the heavy integration required when performing analytical methods. Markov chain Monte Carlo (McMC) methods is a class of techniques used to overcome this problem. It allows for direct sampling from this posterior distribution repeatedly and estimates are calculated from these samples using simple data summaries such as mean and median.
Assuming conditional independence, the posterior distribution of the parameters for the Bernoulli model is given by
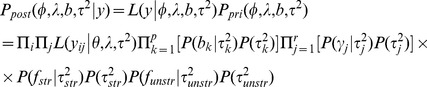 |
All the analyses in this study were carried out using WinBUGS 14 [27]. For each model, 40,000 Markov chain Monte Carlo (McMC) iterations were ran, with the initial 10,000 discarded to cater for the burn-in period and thereafter keeping every tenth sample value. The 3,000 iterations left were used for assessing convergence of the McMC and parameter estimation. We assessed McMC convergence of all models parameters by checking trace plots and autocorrelation plots of the McMC output [28]. Text S1 presents the WinBUGS code used during the analysis.
Model diagnostics
The models were compared using the Deviance Information Criterion (DIC) as suggested by Spiegelhalter et al. [29]. The best fitting model is one with the smallest DIC. DIC value is given by 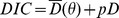 , in which
, in which 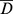 is the posterior mean of the deviance that measures the goodness of fit, and
is the posterior mean of the deviance that measures the goodness of fit, and 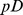 gives the effective number of parameters in the model which penalizes for complexity of the model. In this criterion, low vales of
gives the effective number of parameters in the model which penalizes for complexity of the model. In this criterion, low vales of 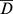 indicate a better fit while small values of
indicate a better fit while small values of 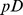 indicate a parsimonious model.
indicate a parsimonious model.
When comparing two models, how big the difference between the DIC values of the two models need to be so as to declare that one model is better than the other is not clear cut. However, several authors have stated that a difference in DIC of 3 between two models cannot be distinguished while a difference between 3 and 7 can be weakly differentiated [26], [29].
Application/Data Analysis
The following set of models were investigated in order to understand the effect of the observed covariates and unobserved effects on the distribution of HIV in Kenya based on the male data:
Model 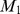 is a model of fixed categorical covariate and one continuous covariate, age, modelled with a non-linear smooth function and linear effects of the categorical covariates, place of residence, education level, marital status, age at first sex, perceived risk of HIV, circumcision status, if had STI in the last 12 months and if ever used a condom. The choice of modelling age with non-linear smoothing prior is supported by results from [14], [17]. This model does not take into account the spatially structured and spatially unstructured random effects.
is a model of fixed categorical covariate and one continuous covariate, age, modelled with a non-linear smooth function and linear effects of the categorical covariates, place of residence, education level, marital status, age at first sex, perceived risk of HIV, circumcision status, if had STI in the last 12 months and if ever used a condom. The choice of modelling age with non-linear smoothing prior is supported by results from [14], [17]. This model does not take into account the spatially structured and spatially unstructured random effects.
Model 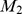 is an additive model that assumes a nonlinear function of the covariate age, linear effects of categorical covariates (listed in model 1 above) and spatially unstructured random effects which cover the unobserved covariates that are inherent within the counties.
is an additive model that assumes a nonlinear function of the covariate age, linear effects of categorical covariates (listed in model 1 above) and spatially unstructured random effects which cover the unobserved covariates that are inherent within the counties.
The third model, 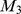 , examines the effect of nonlinear covariate age, linear effects of categorical covariates and spatially structured random effect which accounts for any unobserved covariates that vary spatially among the counties.
, examines the effect of nonlinear covariate age, linear effects of categorical covariates and spatially structured random effect which accounts for any unobserved covariates that vary spatially among the counties.
The final model 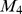 examines the effects of nonlinear effects of age, linear effects of categorical covariates and a convolution of spatially structured and spatially unstructured random effects. Table 2 summarizes the structure of nesting for the four models, under study, in order of complexity. The adjusted odds ratios, were reported, for these multivariate models. The adjustment is to cater for confounding between the variables.
examines the effects of nonlinear effects of age, linear effects of categorical covariates and a convolution of spatially structured and spatially unstructured random effects. Table 2 summarizes the structure of nesting for the four models, under study, in order of complexity. The adjusted odds ratios, were reported, for these multivariate models. The adjustment is to cater for confounding between the variables.
Table 2. Nesting nature of the models under study.
| Model | Nonlinear effect of age | Linear effects of categorical covariates | Spatially unstructured random effects | Spatially structured random effects |
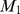
|
√ | √ | - | - |
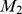
|
√ | √ | √ | - |
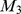
|
√ | √ | - | √ |
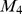
|
√ | √ | √ | √ |
Results
Model assessment and comparison
Table 3 presents model diagnostics for all the fitted models. Model with a small DIC value provides a better fit. Comparing the goodness of fit and complexity of the models, model 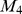 is the preferred model. In what follows, we only present the results based on this best fitting model (
is the preferred model. In what follows, we only present the results based on this best fitting model (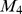 ).
).
Table 3. Models comparison.
| MODELS | ||||
| fit |
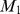
|
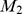
|
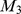
|
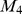
|
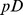
|
22.20 | 29.56 | 33.01 | 36.303 |
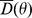
|
1393.89 | 1382.38 | 1377.86 | 1364.02 |
| DIC | 1416.09 | 1411.94 | 1410.87 | 1400.32 |
Fixed effects
Table 4 gives the posterior estimates of the Odds ratios (OR) and their corresponding 95% credible intervals (CI) for the categorical covariates that were assumed to have a linear effect of HIV, based on the best fitting model 4. The following covariates were found to be significantly associated with HIV infection in this model: place of residence, education level, circumcision status, if the individual had an STI in the last 12 months and if the man has ever used a condom.
Table 4. Parameter estimates based on the best fitting model 4.
| Fixed effects | Adjusted OR | 95% CI for OR |
| Demographic characteristics | ||
| Place of residence (ref Rural) | 1 | |
| Urban | 1.88 | (1.196,2.831) |
| Social characteristics | ||
| Education level (ref None) | 1 | |
| Primary | 1.248 | (0.829,1.791) |
| Secondary | 0.726 | (0.449,1.096) |
| Higher | 0.463 | (0.232,0.815) |
| Marital status (ref Married, 1partner) | 1 | |
| Married, +2partner | 1.125 | (0.633,1.818) |
| Divorced/Separated | 1.224 | (0.461,2.459) |
| Widowed | 4.548 | (0.946,12.25) |
| Never Married | 2.209 | (1.062,3.952) |
| Age at first sex (ref Never had sex) | 1 | |
| under 11 | 2.690 | (0.000,21.630) |
| between 12–14 | 5.525 | (0.001,40.850) |
| between 15–17 | 4.383 | (0.001,31.380) |
| over 18 | 3.404 | (0.001,24.650) |
| Perceived risk of HIV (ref No risk) | 1 | |
| Small Risk | 0.632 | (0.282,1.202) |
| Moderate Risk | 0.629 | (0.308,1.172) |
| Great Risk | 0.996 | (0.456,1.937) |
| Biological characteristics | ||
| Circumcision status (ref Circumcised) | 1 | |
| Not circumcised | 4.422 | (2.794,6.537) |
| Had STI in the last 12 months (ref No) | 1 | |
| Yes | 2.946 | (1.428,5.449) |
| Behaviorial characteristics | ||
| Ever used Condom (ref No) | 1 | |
| Yes | 1.506 | (1.071,2.09) |
| Random effects | Estimate | 95% CI |
Spatially unstructured (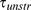 ) ) |
0.100 | (0.000,0.435) |
Spatially structured (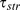 ) ) |
0.169 | (0.001,0.895) |
Spline coefficients (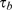 ) ) |
2947 | (950.6,6789) |
HIV infection is negatively related to education. The likelihood of HIV infection was higher for those men with primary education as compared to those with no education, albeit, this was not significant as indicated by the odds ratio and its corresponding credible interval (OR: 1.25, 95% CI: 0.83 to 1.79). The chance of HIV infection was lower for men with secondary education compared to those with no education, although this difference was not significant (OR: 0.73, 95% CI: 0.45 to 1.10). The likelihood of HIV infection was lowest in men with higher education (OR: 0.46, 95% CI: 0.23 to 0.82). Circumcision was found to be significantly associated with HIV infection. The odds of an uncircumcised man to be infected with HIV were 4.42 times the odds of a circumcised man (OR: 4.42, 95% CI: 2.79 to 6.54). Place of residence (Urban/Rural) was also found to be associated with HIV infection among men. The odds of HIV infection among men staying in urban areas was 1.88 times higher than that of men living in the rural areas (OR: 1.88, 95% CI: 1.20 to 2.83). Individuals who had an STI in the last 12 months were found to be 2.95 times more likely to be HIV positive (OR: 2.95, 95% CI: 1.43 to 5.45). Men who have ever used condoms were found to have an elevated likelihood of being infected by HIV (OR: 1.51, 95% CI: 1.07 to 2.09).
Nonlinear effects of age
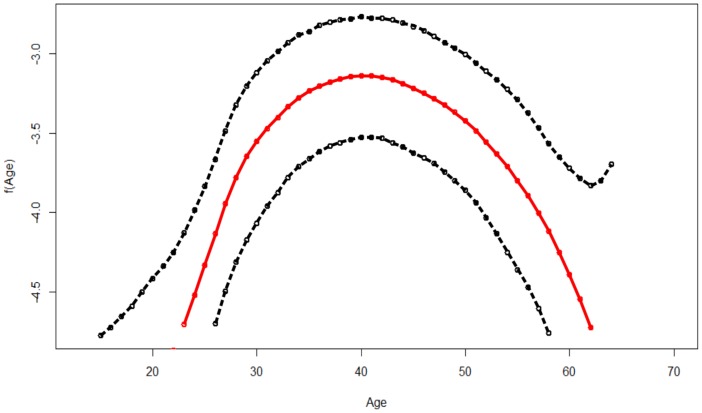
Figure 1 shows the nonlinear association between of age of an individual and the HIV infection. The figure gives the posterior mean of the smooth function and its corresponding 95% CI. It is evident from the figure that the effect of age on HIV infection is nonlinear, and an assumption of a linear effect would have led to specious results and subsequently wrong interpretations. The likelihood of HIV infection is seen to increase with age up to an optimum age of approximately 40 years then starts declining with increase with age.
Figure 1. Estimated mean of the Nonlinear effect of age (in red) and the corresponding 95% credible interval (dotted black lines).
Spatial effects
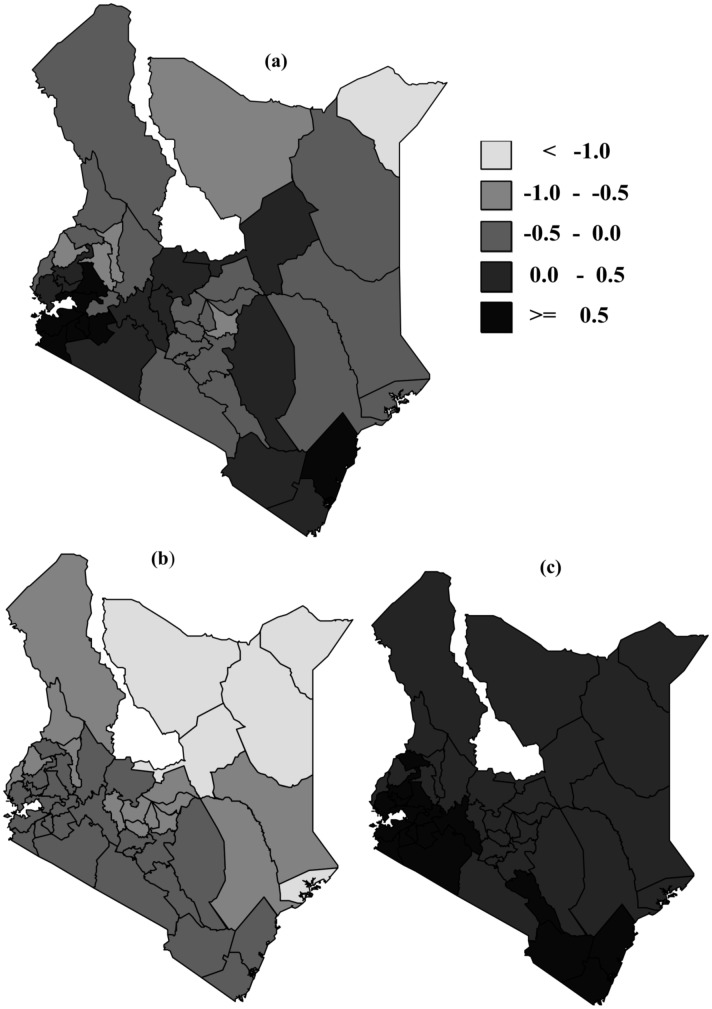
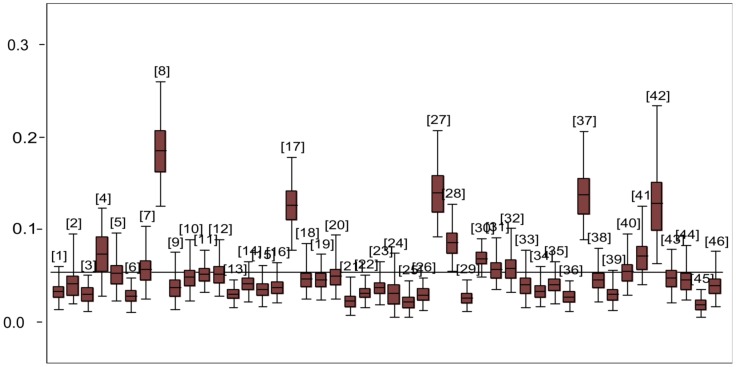
We examined the spatial effects based on the best fitting model 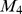 . The spatial effect with the corresponding 95% CI is given in Figure 2. From the figure, counties with light grey colour show low association with HIV infection while black shaded counties have high association with HIV infection prevalence. There is clear evidence of spatial variation of HIV prevalence. From the maps, counties in the Western part, around Lake Victoria region, show high spatial variation. Very high HIV prevalence (>10%) was recorded in the following counties: Homabay, Migori, Siaya, Turkana, and Kisumu. Figure 3 gives a box-plot of HIV prevalence by counties (the counties are numbered from 1 to 46, see Table 5 for corresponding county names) while Table 5 gives the exact estimates.
. The spatial effect with the corresponding 95% CI is given in Figure 2. From the figure, counties with light grey colour show low association with HIV infection while black shaded counties have high association with HIV infection prevalence. There is clear evidence of spatial variation of HIV prevalence. From the maps, counties in the Western part, around Lake Victoria region, show high spatial variation. Very high HIV prevalence (>10%) was recorded in the following counties: Homabay, Migori, Siaya, Turkana, and Kisumu. Figure 3 gives a box-plot of HIV prevalence by counties (the counties are numbered from 1 to 46, see Table 5 for corresponding county names) while Table 5 gives the exact estimates.
Figure 2. Residual spatial effect of county. Shown are the posterior means (a) and the corresponding lower (b) and upper (c) 95% credible limits.
Figure 3. Box plot of HIV prevalence estimates by county. The numbers represent counties (See table 5 for the county numbering codes).
Table 5. Estimated HIV prevalence by county and corresponding 95% Credible interval.
| Code | County | Prevalence (95% CI) |
| 1 | Baringo | 0.033(0.014,0.061) |
| 2 | Bomet | 0.042(0.02,0.096) |
| 3 | Bungoma | 0.03(0.012,0.051) |
| 4 | Busia | 0.074(0.029,0.123) |
| 5 | Elgeyo Marakwet | 0.052(0.023,0.095) |
| 6 | Embu | 0.028(0.011,0.048) |
| 7 | Garissa | 0.058(0.026,0.105) |
| 8 | Homa Bay | 0.186(0.127,0.261) |
| 9 | Isiolo | 0.038(0.014,0.074) |
| 10 | Kajiado | 0.049(0.023,0.091) |
| 11 | Kakamega | 0.052(0.033,0.078) |
| 12 | Kericho | 0.052(0.028,0.09) |
| 13 | Kiambu | 0.03(0.016,0.046) |
| 14 | Kilifi | 0.041(0.022,0.066) |
| 15 | Kirinyaga | 0.036(0.017,0.061) |
| 16 | Kisii | 0.038(0.021,0.064) |
| 17 | Kisumu | 0.126(0.076,0.177) |
| 18 | Kitui | 0.046(0.025,0.083) |
| 19 | Kwale | 0.046(0.024,0.074) |
| 20 | Laikipia | 0.05(0.024,0.097) |
| 21 | Lamu | 0.023(0.007,0.049) |
| 22 | Machakos | 0.031(0.016,0.051) |
| 23 | Makueni | 0.038(0.019,0.067) |
| 24 | Mandera | 0.032(0.005,0.073) |
| 25 | Marsabit | 0.021(0.005,0.043) |
| 26 | Meru | 0.029(0.013,0.048) |
| 27 | Migori | 0.14(0.093,0.204) |
| 28 | Mombasa | 0.086(0.054,0.125) |
| 29 | Muranga | 0.027(0.011,0.046) |
| 30 | Nairobi | 0.069(0.05,0.09) |
| 31 | Nakuru | 0.057(0.037,0.092) |
| 32 | Nandi | 0.059(0.033,0.101) |
| 33 | Narok | 0.04(0.016,0.08) |
| 34 | Nyamira | 0.033(0.016,0.06) |
| 35 | Nyandarua | 0.04(0.02,0.065) |
| 36 | Nyeri | 0.027(0.011,0.044) |
| 37 | Siaya | 0.137(0.089,0.204) |
| 38 | Taita Taveta | 0.046(0.022,0.079) |
| 39 | Tana River | 0.03(0.012,0.057) |
| 40 | Tharaka-Nithi | 0.054(0.028,0.097) |
| 41 | Trans Nzoia | 0.071(0.04,0.127) |
| 42 | Turkana | 0.129(0.064,0.238) |
| 43 | Uasin Gishu | 0.048(0.02,0.078) |
| 44 | Vihiga | 0.045(0.024,0.081) |
| 45 | Wajir | 0.019(0.005,0.036) |
| 46 | West Pokot | 0.039(0.017,0.076) |
The structured spatial effects are dominant over the spatially unstructured random effects as shown by the ratio of variance components, calculated by 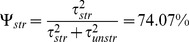 (Table 4).
(Table 4).
Discussion
This study utilizes Bayesian techniques to analyze regional variation and risk factors of HIV infection. The study develops and uses Bayesian semi-parametric regression models to help assess factors associated with HIV infection. We build on existing contributions by Eilers and Marx [22] and Caroll and Rupert [23]. The models used in this study are based on the penalized regression splines, in a semi-parametric modeling paradigm, with allowance for spatial variation in the response variable. Many situations arise where the relationship between the function of the response variable and covariates is not pigeonholed linearly [21]. Semi-parametric models are a class of models which borrows strength from both parametric and non-parametric models. Subsequently, it can be viewed as enriching standard parametric models by exploring the non-parametric domain while still keeping intact the linear structure [30]. Furthermore, the regularly encountered assumption of fully parametric linear predictor for evaluating the effect of covariates on the dependent variable is usually restrictive, unrealistic and can lead to specious conclusions. The spatially structured effects in the model are modeled using a Gaussian Markov Random Field (GMRF) while the spatially unstructured random effects are modeled using a zero mean Gaussian process [25], [26]. Due to the high complexity and intractability owing to this intricacy, the maximum likelihood approaches are not viable in the estimation of these models. Consequently, the Bayesian inference, utilizing McMC techniques is highly favoured.
In this study, we found that the male circumcision reduces the risk of HIV infection, precisely, uncircumcised men were more likely to be HIV positive than circumcised men. This finding is supported by previous studies and therefore adds to the large body of research indicating that circumcision lowers the risk of HIV infection [4]–[6]. The Ministry of Health in Kenya currently runs an aggressive Voluntary Medical Male Circumcision (VMMC) in the country [31]–[32]. With respect to this finding, there will be hope for decline in HIV prevalence due to this campaign.
Place of residence proved to have a significant relationship to HIV infection among men when controlled for other covariates. Men in urban areas were more likely to be HIV positive as compared to men in the rural areas. The effect of place of residence on HIV infection has been reported in many studies but with mixed conclusions [14], [33]. This finding could be used to inform tailormade HIV campaign strategies depending on place of residence.
Another finding from this study is that the likelihood of HIV infection was lowest among men with higher education. Other studies have also shown similar result [14]. The government's introduction of free primary education and subsidized secondary education is hoped to increase the number of young people attaining higher level of education [34]. This is envisaged to increase awareness of this pandemic and further reduce its spread.
It was also found in this study that men who had an STI in the last 12 months were more likely to be HIV positive. In terms of condom usage, men who have ever used a condom were more likely to be infected by HIV. This is an unexpected finding. This finding may be attributed to two possible reasons. Firstly, some men who use condom, with their spouses, will later on end up stopping to use a condom by assuming that they “know” one another properly and trust each other. Subsequently having unprotected sex. Secondly, the way this question was captured in the study, wasn't useful. A better way was to capture consistent use of condom. If this could have been captured then, maybe, opposite and expected results could have been realized.
The nonlinear effect of age on HIV infection was evident from the analysis. The relationship between HIV infection and age has an inverted “U” shape. The likelihood of HIV infection increase with age and reaches a maximum at the age of around 40, then takes a nosedive. This result is in tandem with other bodies of research [14], [17].
Spatial effects in the model acts as surrogate of the unobserved variables. Identification of high prevalence areas can provide insights for designing intervention and campaign programmes that are tailor-made to those regions, hence increasing the impact of the initiative. There was evidence of spatial variation of HIV infection among the counties, with highest prevalence rates being reported on the Western part of the country, around Lake Victoria region.
Vis-a-vis classical regression modeling frameworks, this study uses an approach that allows for flexible and realistic models to be implemented, thereby making it possible to establish and test epidemiological hypotheses. Availability of freely available software like R and WinBUGS makes implementation of these complex models easier and accessible to practitioners in medical, environmental and any other relevant field.
A major limitation of our analysis is that the data used for county estimation was collected when the country was still based on the old administrative units (provinces), the data was not powered to carry out estimation at these new administrative units. The study rides on the advantage that these new administrative units called counties were formed by combining several districts together. This made it easy for the county where an individual belongs to be allocated easily since each district belongs to only one county. Also, in the data, the way some variables were captured was not usefull; ever using a condom should be replaced with consistent use of condom. In terms of methodology, the knots used in the penalized spline regression were assumed to be fixed and were calculated as quantiles from the continuous variable age. A more flexible analysis can allow the knots to be data driven [35].
Despite the limitations highlighted above, the models introduced in this study can be replicated in other countries with similar data.
Supporting Information
WinBUGS code used in the analysis.
(DOCX)
Acknowledgments
We thank, with profound appreciation, The Kenya National Bureau of Statistics (KNBS) for providing the data used in this study.
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. The data is held by the Kenya National Bureau of Statistics and freely available to the public but a request has to be sent to the Kenya National Bureau of Statistics. The link to access it is http://statistics.knbs.or.ke/nada/index.php/catalog/25.
Funding Statement
The authors have no support or funding to report.
References
- 1.UNAIDS (2013) Report on the global AIDS epidemic. Geneva, Switzerland: UNAIDS/WHO.
- 2. Auvert B, Taljaard D, Lagarde E, Sobngwi-Tambekou J, Sitta R, et al. (2005) Randomized, controlled intervention trial of male circumcision for reduction of HIV infection risk: the ANRS 1265 Trial. PLoS medicine 2(11): e298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Bailey RC, Moses S, Parker CB, Agot K, Maclean I, et al. (2007) Male circumcision for HIV prevention in young men in Kisumu, Kenya: a randomised controlled trial. The Lancet 369(9562): 643–656. [DOI] [PubMed] [Google Scholar]
- 4. Gray RH, Kigozi G, Serwadda D, Makumbi F, Watya S, et al. (2007) Male circumcision for HIV prevention in men in Rakai, Uganda: a randomised trial. The Lancet 369(9562): 657–666. [DOI] [PubMed] [Google Scholar]
- 5. Ramjee G, Kapiga S, Weiss S, Peterson L, Leburg C, et al. (2008) The value of site preparedness studies for future implementation of phase 2/IIb/III HIV prevention trials: experience from the HPTN 055 study. Journal of Acquired Immune Deficiency Syndromes 47(1): 93–100. [DOI] [PubMed] [Google Scholar]
- 6. Karim QA, Karim SA, Frohlich JA, Grobler AC, Baxter C, et al. (2010) Effectiveness and safety of tenofovir gel, an antiretroviral microbicide, for the prevention of HIV infection in women. Science 329(5996): 1168–1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Fast PE, Kaleebu P (2010) HIV vaccines: Current status worldwide and in Africa. AIDS 24 (suppl 4)S50–S60. [DOI] [PubMed] [Google Scholar]
- 8. Jaoko W, Nakwagala FN, Anzala O, Manyonyi GO, Birungi J, et al. (2008) Safety and immunogenicity of recombinant low-dosage HIV-1 A vaccine candidates vectored by plasmid pTHr DNA or modified vaccinia virus Ankara (MVA) in humans in East Africa. Vaccine 26(22): 2788–2795. [DOI] [PubMed] [Google Scholar]
- 9. Mugyenyi PN (2002) HIV vaccines: The Uganda experience. Vaccine 20: 1905–1908. [DOI] [PubMed] [Google Scholar]
- 10. Cohen MS, Chen YQ, McCauley M, Gamble T, Hosseinipour MC, et al. (2011) Prevention of HIV-1 infection with early antiretroviral therapy. New England journal of medicine 365(6): 493–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Sandøy IF, Kvåle G, Michelo C, Fylkesnes K (2006) Antenatal clinic-based HIV prevalence in Zambia: Declining trends but sharp local contrasts in young women. Tropical Medicine & International Health 11(6): 917–928. [DOI] [PubMed] [Google Scholar]
- 12.NASCOP (2012) Ministry of Health, Kenya: Kenya AIDS Indicator Survey preliminary report.
- 13.NASCOP (2007) Ministry of Health, Kenya: Kenya AIDS Indicator Survey report.
- 14. Johnson K, Way A (2006) Risk factors for HIV infection in a national adult population: evidence from the 2003 Kenya Demographic and Health Survey. Journal of Acquired Immune Deficiency Syndromes 42(5): 627–636. [DOI] [PubMed] [Google Scholar]
- 15. Madise NJ, Ziraba AK, Inungu J, Khamadi SA, Ezeh A, et al. (2012) Are slum dwellers at heightened risk of HIV infection than other urban residents? Evidence from population-based HIV prevalence surveys in Kenya. Health & Place 18(5): 1144–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Manda SO, Lombard CJ, Mosala T (2012) Divergent spatial patterns in the prevalence of the human immunodeficiency virus (HIV) and syphilis in South African pregnant women. Geospatial health 6(2): 221–231. [DOI] [PubMed] [Google Scholar]
- 17.Mishra V, Montana L, Neuman M (2007) Spatial modeling of HIV prevalence in kenya. In Demographic and Health Research.
- 18.Ngigi MM (2007) A Geographical study on the HIV/AIDS pandemic in Kenya. PhD thesis: University of Tsukuba.
- 19. Ngesa O, Achia T, Mwambi H (2013) Spatial joint disease modeling and mapping with application to HIV and HSV-2. In South African Statistical Journal Proceedings: Proceedings of the 55th Annual Conference of the South African Statistical Association for 2013: 61–68. [Google Scholar]
- 20.Fahrmeir L, Tutz G (2001) Multivariate Statistical Modelling based on Generalized Linear Models. 2nd Edition, New York: Springer.
- 21.Hastie T, Tibshirani R, Friedman J (2001) The Elements of Statistical Learning. New York: Springer-Verlag.
- 22. Eilers PH, Marx BD (1996) Flexible smoothing with B-splines and penalties. Statistical science 11(2): 89–102. [Google Scholar]
- 23.Carroll MR, Ruppert DW (2003) Semi-parametric Regression. Cambridge: Cambridge university Press.
- 24.Green PJ, Silverman BW (1993) Nonparametric regression and generalized linear models.:A roughness penalty approach. CRC Press.
- 25. Besag J, York J, Mollié A (1991) Bayesian image restoration, with two applications in spatial statistics. Annals of the Institute of Statistical Mathematics 43(1): 1–20. [Google Scholar]
- 26. Kazembe LN, Chirwa TF, Simbeye JS, Namangale JJ (2008) Applications of Bayesian approach in modelling risk of malaria-related hospital mortality. BMC medical research methodology 8(1): 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Spiegelhalter TD, Best N, Lunn D (2007) WinBUGS User Manual Version 1.4.3. [Online] Available: http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/contents.shtml. Accessed 2013 July 10.
- 28.Carlin JB, Gelman A, Rubin DB, Stern HS (2003) Bayesian data analysis: Chapman & Hall/CRC.
- 29. Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A (2002) Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society Series B (Statistical Methodology) 64: 583–639. [Google Scholar]
- 30. Fahrmeir L, Kneib T, Lang S (2004) Penalized structured additive regression for space-time data: a Bayesian perspective. Statistica Sinica 14(3): 731–762. [Google Scholar]
- 31. Mwandi Z, Murphy A, Reed J, Chesang K, Njeuhmeli E, et al. (2011) Voluntary medical male circumcision: translating research into the rapid expansion of services in Kenya, 2008–2011. PLoS medicine 8(11): e1001130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Herman-Roloff A, Llewellyn E, Obiero W, Agot K, Ndinya-Achola J, et al. (2011) Implementing voluntary medical male circumcision for HIV prevention in Nyanza Province, Kenya: lessons learned during the first year. PloS one 6(4): e18299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Kleinschmidt I, MacPhail C, Natashia M, Pettifor A, Rees H (2007) Geographic distribution of human immunodeficiency virus in South Africa. The American journal of tropical medicine and hygiene 77(6): 1163–1169. [PMC free article] [PubMed] [Google Scholar]
- 34. Adrienne LM, Mbiti IM (2012) Access, sorting, and achievement: the short-run effects of free primary education in Kenya. American Economic Journal: Applied Economics 4(4): 226–253. [Google Scholar]
- 35. DiMatteo I, Genovese CR, Kass RE (2001) Bayesian curve-fitting with free-knot splines. Biometrika 88(4): 1055–1071. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
WinBUGS code used in the analysis.
(DOCX)
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. The data is held by the Kenya National Bureau of Statistics and freely available to the public but a request has to be sent to the Kenya National Bureau of Statistics. The link to access it is http://statistics.knbs.or.ke/nada/index.php/catalog/25.