Model-based CT performance assessment and optimization for iodinated and noniodinated imaging tasks as a function of kVp and body size

Abstract

Purpose:

The goal of this study was to assess the comparative performance of iterative reconstruction in space (IRIS) and filtered back projection (FBP) reconstruction algorithms in terms of image quality and dose across kVps and phantom sizes.

Methods:

The ACR CT phantom (model 464) was supplemented with the addition of an iodinated spherical capsule (1.5 mm diameter, 3.4 mg iodine per ml) to simulate the contrast filled structures and with an additional circular attachment consisting of an array of 500 um brass beads for spatial resolution measurements. A larger sized phantom was also created by wrapping the original phantom with additional tissue equivalent material of 4 cm thickness. The phantoms were imaged on a 64 detector array multidetector computed tomography scanner (Somatom Definition, Siemens, Germany) using clinically applicable protocols (0.5 s rotation time; 80, 100, 120, and 140 kVp; 64 to 640 mA; 220 to 250 mm field of view). Images were reconstructed using the FBP and the IRIS algorithms. Combining measurements of image noise and spatial resolution with a task function, a figure of merit (FOM) for image quality was generated taking into account the type of visualization required from the image for the detection of either large or small image features with and without iodine content. The FOM was further reported in terms of area under the receiver operating characteristic (ROC) curve (A_Z) to predict the comparative diagnostic performance of the two algorithms at different dose levels.

Results:

For a given dose level, the predicted A_Z for IRIS consistently outperformed that of FBP. At comparative A_Z, depending on protocol and task, the dose requirement for the optimal technique (optimized kVp with IRIS) was 2-3 times lower than that for standard technique (120 kVp with FBP). The potential for dose reduction was found to be higher when performing small feature detection tasks in comparison to larger feature detection tasks. The optimal kVp was from 80 to 100 kVp for the small phantom, 100 to 120 kVp for the larger phantom.

Conclusions:

Overall, greater dose reduction may be achieved with IRIS compared to FBP, with enhanced advantage at thinner slice reconstructions. The results highlight how IRIS may offer a superior balance between image quality and dose across a range of imaging tasks, thus enabling dose reduction at constant quality or image quality improvement at constant dose. The prediction of the investigation can be used toward effective design of subsequent clinical studies.

I. INTRODUCTION

Reconstruction fidelity for filtered back projection (FBP) is limited by noise at low radiation dose settings. This limitation can be minimized by the use of iterative reconstruction (IR). Incorporating the characteristics of the imaging system into the image reconstruction, IR can reduce noise at equivalent or improved spatial resolution, providing for improved image quality for the same radiation dose exposure or a lower dose at comparable image quality. The amount of dose reduction achievable with IR, however, depends on the performance of the specific IR algorithm, CT imaging parameters, and phantom specific characteristics.^1–4 Thus, it is most relevant for the dose reduction potential of IR be evaluated for specific tasks, applicable technical parameters (e.g., kV), and patient size.⁵ Furthermore, given the large number of imaging parameters that can influence image quality, it is imperative that the evaluation to be initially done with a phantom so that any follow-up clinical studies can be planned in the most judicious and targeted fashion.

The purpose of this study was to assess the comparative performance of IR and FBP in terms of expected image quality and dose across kV values with the use of a phantom. The study focused on a specific type of IR, commercially known as Iterative Reconstruction in Space (IRIS) (“Space” referring to the image space). In IRIS, the required IR regularization step is performed on the image data without calculating the forward and back-projection steps, which has certain computational advantages. Image quality was assessed using a task-based metric of diagnostic performance, taking into account the imaging task at hand, while incorporating a description of spatial resolution and noise texture. The results were used to predict the optimum kVp for different detection tasks and patient sizes, and to ascertain the potential dose reduction achievable by IR under an optimized kV condition.

II. METHODS AND MATERIAL

II.A. Theory: Model-based estimation of imaging performance

The complexity of medical imaging systems is constantly increasing, requiring more comprehensive methods of performance assessment. One approach is to perform human observer studies; however, they are costly and time consuming. Alternatively, there are mathematical observers, which attempt to emulate human observer performance and can provide a useful surrogate for imaging performance. This is in comparison to system performance metrics, which simply characterize system performance rather than human performance. ICRU 54 summarizes the development of a task-based methodology for assessing medical images in terms of how well they can perform a given imaging task.⁶ This enables the assessment of system performance in terms of how well an observer is expected to perform a given task given a certain image. Examples of various tasks include the detection of a small or large lesion, the discrimination between two shapes, or the estimation of some quantity in the image (i.e., size and density). This methodology combines conventional system performance metrics (i.e., MTF and NPS) with a description of the imaging task. In its simplest form, this is given as the detectability index (d^′) for the Fisher-Hotelling observer⁷

$$d^{\prime 2}=\int \frac{{\mathrm{MTF}}^2\left(\mathit{f}\right)}{\mathrm{NPS}\left(\mathit{f}\right)}{W}_{\mathrm{Task}}^2\left(\mathit{f}\right)d\mathit{f},$$ (1)

where f denotes the spatial-frequency. The detectability index provides a figure of merit that incorporates system performance and imaging task, and offers an objective function for protocol optimization and design. For a classification task (such as detection), the task function, W_task, is given by the Fourier transform of the difference between two hypothesis functions (e.g., lesion present and lesion absent) as

$$W_{\mathrm{Task}}\left(\mathit{f}\right)=\left|F\{{\mathit{h}}_1\left(\mathbf{x}\right)-{\mathit{h}}_2\left(\mathbf{x}\right)\}\right|,$$ (2)

where ${\mathit{h}}_1\left(\mathbf{x}\right)$ and ${\mathit{h}}_2\left(\mathbf{x}\right)$ denote the hypothesis functions, which describe the signal in the spatial domain for the two hypotheses. In this form, the detectability index can also be understood as a weighted sum of the task function with the MTF and NPS, such that the task function weighs spatial-frequencies of importance associated with the task at hand.

In turn, the detectability index can be mathematically related to the area under the receiver operating characteristic curve (A_Z). Assuming that the internal decision variable employed in assessing the ROC curve is normally distributed for both hypotheses and has equal variance, the detectability index can be related to A_Z as⁸

$$A_Z=\frac{1}{2}\left(1+\frac{2}{\sqrt{\pi }}{\int }_0^{\frac{d^{\prime }}{2}}\exp (-x^2)dx\right),$$ (3)

where the integral is the well known error function.⁸ The derivation of A_z from d^′ assumes normal distribution for the underlying statistical distribution functions, a common assumption in perception metrology. While not fully validated for all interpretive processes, this assumption has proven valid for a wide range of statistical decisions.^9,10

The above strategy provides a mathematical tool for converting system performance metrics to human performance metrics via phantom-based measurements. The approach is theoretically only applicable to imaging systems that are linear and stationary in nature. However, most imaging systems violate these requirements in one way or another. But provided that a system is tested under limited experimental conditions, where reasonable stationary and linearity are maintained (i.e., a quasilinearity state), the methodology can be applicable.¹¹ In this study, we applied the above methodology to assess the performance of a clinical CT system. The measurements of the MTF and the NPS were made using specific sized phantoms. Within the specific conditions of the experimental acquisition (for IRIS and FBP), the MTF was found not to depend on the object contrast (within −1000 to 910 HU), confirmed by a separate investigation.¹² The NPS was similarly found to be constant across the ROIs within the phantom image used for the measurements. Thus a quasilinear system evaluation was found applicable to be of predictive value and relevance.

II.B. Image acquisition

The ACR (model 464) phantom with a cylindrical size of 20 cm in diameter and 16 cm in length was supplemented with an additional attachment, the bead phantom [Fig. 1(a)]. The bead phantom consisted of five brass beads placed into a customized Poly (methyl methacrylate) (PMMA) 10 cm diameter container which was filled with bee's wax (HU = −78 at 120 kVp). Iodinated inserts (in the form of 1.5 mm diameter tubes filled with 3.4 mg iodine per ml) were placed in the phantom's air calibration chamber. The ACR phantom was further supplemented in size by wrapping it with 4 cm thick layer of simulated fat (HU = −2 at 120 kVp) to create an additional 28-cm-diameter phantom.

FIG. 1.

(a) ACR phantom (*) with supplemented bead phantom for resolution measurement. (b) ACR phantom with additional material circumferentially placed. (c) Cross sectional view of the (a) bead phantom and (b) ACR phantom.

Image acquisitions were performed on a dual-source 64 MDCT scanner (Definition, Siemens Health System, Forcheinm, Gemrany) that consists of 32-detector array for each x-ray tube utilizing a 1.2 mm focal spot. All scanning was performed utilizing a single tube mode. The following CT parameters were kept constant for all datasets: scan collimation of 40 mm, rotation time of 0.5 s, and pitch of 0.8. The kVp varied from 80 to 140. The mAs was kept constant during each acquisition by utilizing a constant rotation time of 0.5 s and a fixed mA (range of 64 to 640). Images were reconstructed with the FBP algorithm (B31f kernel) and with the IRIS algorithm (I31f kernel) at 5 mm and 0.625 mm slice thicknesses. These kernels were chosen based on direct input from the manufacturer as the kernels that provide the closest match in spatial detail between the two reconstructions. The mAs values for the larger phantom size were adjusted upward to maintain the same range of noise levels measured in the phantom without the added fat layer.

A list of protocols used for the two phantom sizes is summarized in Table I. The phantom was scanned twice for each protocol. To provide a comparison of technique between protocols, the CT dose index (CTDI_vol) was recorded for each protocol. It should be noted that the protocols used in the study were limited and not meant to offer an optimized condition for each algorithm; they were rather chosen to represent the current, clinically applicable common and reasonably comparable imaging conditions between the two algorithms. As such, the results should be interpreted not as intrinsic reflections of the algorithms, rather as their performance for a set of benchmarked clinical protocols.

TABLE I.

List of image parameters (protocols) used for data acquisition acquired on the Siemens Definition.

kVp	Phantom size	Fov (mm)	Tube current (mA)	Rot. time (s)	Pitch (mm)	CTDI/mA	Recon	Slice thickness (mm)
80	Small	220	496, 356, 302, 192	0.5	0.8	0.0118	FBP/IRIS	0.6, 5.0
100	Small	220	496, 356, 258, 141	0.5	0.8	0.0264	FBP/IRIS	0.6, 5.0
120	Small	220	213, 147, 107, 64	0.5	0.8	0.0451	FBP/IRIS	0.6, 5.0
140	Small	220	213, 147, 107, 64	0.5	0.8	0.0678	FBP/IRIS	0.6, 5.0
80	Large	250	400, 288, 200, 96	0.5	0.8	0.0118	FBP/IRIS	5.0
100	Large	250	480, 360, 240, 120	0.5	0.8	0.0264	FBP/IRIS	5.0
120	Large	250	640, 460, 320, 240	0.5	0.8	0.0451	FBP/IRIS	5.0
140	Large	250	560, 432, 280, 144	0.5	0.8	0.0678	FBP/IRIS	5.0

II.C. Evaluation of imaging performance

System performance was assessed for each protocol in terms of a mathematical estimate of A_Z (the area under the receiver operative characteristic curve). The assessment methodology took into consideration attributes of noise and spatial resolution in the images as well as imaging features of size and contrast of targeted abnormalities defined in terms of task specific functions.

The noise power spectrum (NPS) and pixel standard deviation measurements were made across all the protocols listed in Table I. The NPS was utilized as the measure of pixel noise as it allows for the assessment of both magnitude and texture of the noise. Measurements of noise were obtained by placing 100, 3 × 3 cm² ROI within the uniformity area of the ACR phantom and measuring the normalized amplitude of the Fourier transform of the data using an established methodology.¹³ A custom software using MATLAB (MathWorks, Natick, MA) was used to detrend the two-dimensional sample and average the data across the ROIs. The pixel standard deviation was also measured in the same region of uniformity. The NPS and noise magnitude measurements were repeated as a function of radial distance from the center of rotation, which indicated small location dependencies (no change in the shape of the NPS and up to 6% change in the noise magnitude).

The modulation transfer function (MTF) was used to characterize image resolution. The MTF was evaluated from the reconstructed images of the beads using

$$\mathrm{MTF}(f_x,f_y)=\left|\frac{F\left\{\mathrm{image}\right(x,y\left)\right\}}{F\left\{\mathrm{object}\right(x,y\left)\right\}}\right|,$$ (4)

where “image” denotes the reconstructed bead, modeled as a 500 um disc in two-dimensional, and “object” denotes the “ideal image” of the bead. With the phantom scanned twice, ten MTF realizations for each technique were averaged to yield the ensemble two-dimensional MTF.

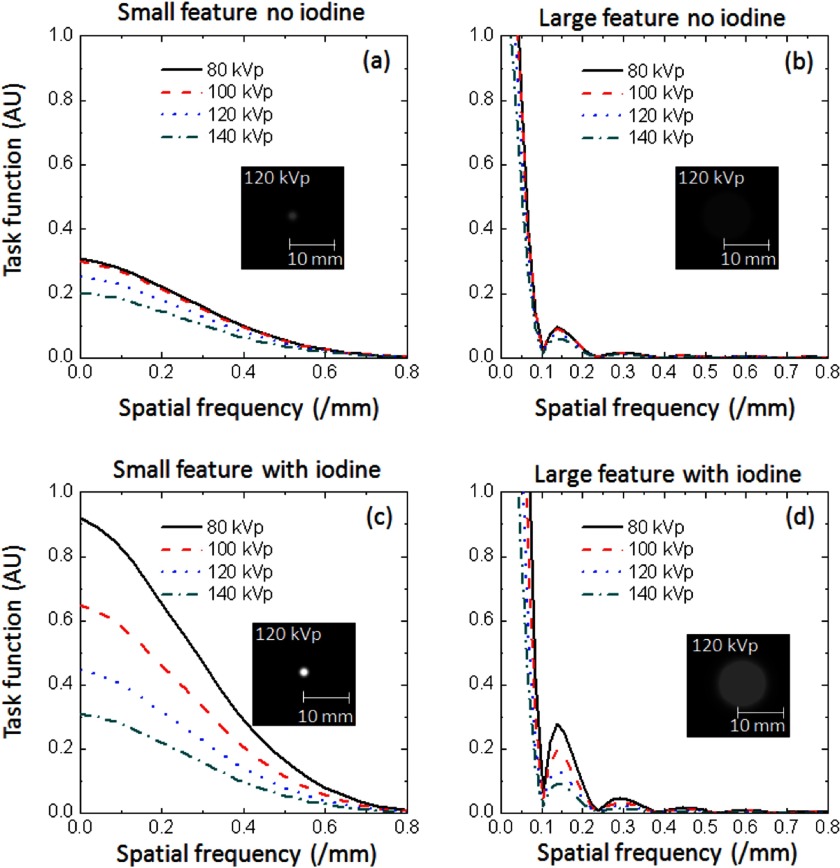
The two-dimensional MTF and NPS measurements were combined to yield a task-based figure of merit for each protocol, the detectability index or d^′, from which to predict the area under the ROC curve (A_Z) as a function of dose and kVp. The model computations were performed as detailed in Sec. II A above. Four classes of imaging tasks were considered in this study (Fig. 2, Table II). The small feature detection task considered hypotheses of a uniform background and a small feature, corresponding to the two-dimensional profile of a 1.2 mm diameter object. The large feature detection task considered hypotheses of a uniform background and a circular lesion, corresponding to the two-dimensional profile of a 10 mm diameter object. These task functions were meant to represent detection of iso-dense features (either individual lesions of lesion details) within a solid organ. The contrast levels for either object was based on Hounsfield unit values of the ACR phantom objects measured using an image analysis tool (ImageJ, NIH, Bethesda, MD). Contrast to noise ratios (CNRs) were also computed for each of these objects.

FIG. 2.

Task function for (a) small and (b) large with no iodine enhancement and (c) small and (d) large feature with iodine enhancement as a function of kVp. The inset images show the idealized feature at 120 kVp depicting the various size and contrast for the different tasks.

TABLE II.

The contrast levels of the lesions used to maintain equal signal power.

	80 KVp	100 kVp	120 kVp	140 kVp
Small with iodine	87	67	46	32
Large with iodine	17.4	13.4	9.2	6.4
Small without iodine	32	31	26	21
Large without iodine	6.4	6.2	5.2	4.2

The performance was evaluated for a combination of four tasks: large and small feature with or without iodine enhancement. The discrete data point relating imaging performance (d^′, A_Z, or CNR) to dose at discrete dose levels were fit by linear regression into continues functions. A standard technique was defined as 120 kVp, 100 mA, 5 mm slice thickness reconstruction with FBP. The dose reduction potential for a given task or patient size was assessed by comparing the performance of the standard technique to that of an alternative technique (with IRIS reconstruction and/or different kVp) that would offer a higher performance. The percentage dose reduction was evaluated by identifying dose differences corresponding to identical performance levels for the two techniques.

III. RESULTS

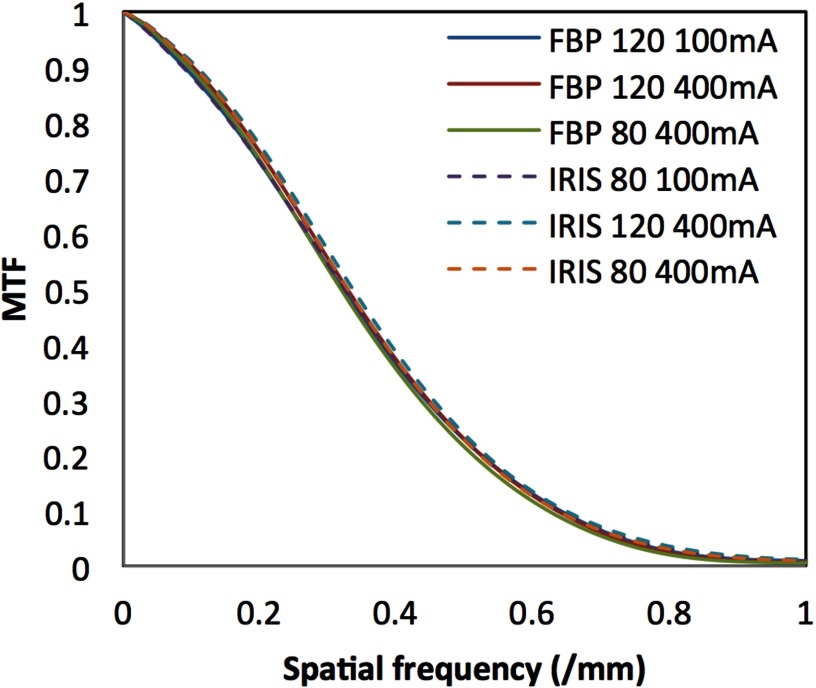
The measured NPS is shown in Figs. 3(a) and 3(b) as a function of mA for FBP and IRIS. The plotted curves represent radially averaged NPS of the two-dimensional NPS to better illustrate the overall trends. The results, shown for the 120 kVp measurements only for the sake of succinctness, showed similar trends at other kVps. The magnitude of the NPS was proportional to the standard deviation of noise, Fig. 3(c). The NPS also provided a comparison of the noise texture between FBP and IRIS images, highlighting slight differences in noise texture appearance. The peaks of the NPS at 0.2 mm⁻¹ for FBP and at 0.18 mm⁻¹ for IRIS demonstrates that, for the same pixel standard deviation, the IRIS images had slightly more correlated noise at low spatial frequencies than FBP. The spatial resolution of this iterative reconstruction was similar to that of FBP and did not vary as a function of dose or kVp as illustrated in the representative MTF data shown in Fig. 4.

FIG. 3.

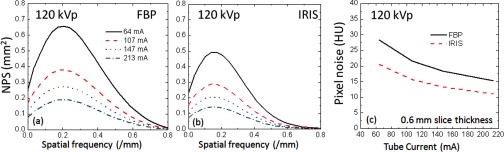
Noise-power spectra as a function of mA for FBP (a) and IRIS (b) reconstructions and the overall pixel noise as a function of mA (c).

FIG. 4.

Modulation transfer function measurements across a representative range of kVp and mA.

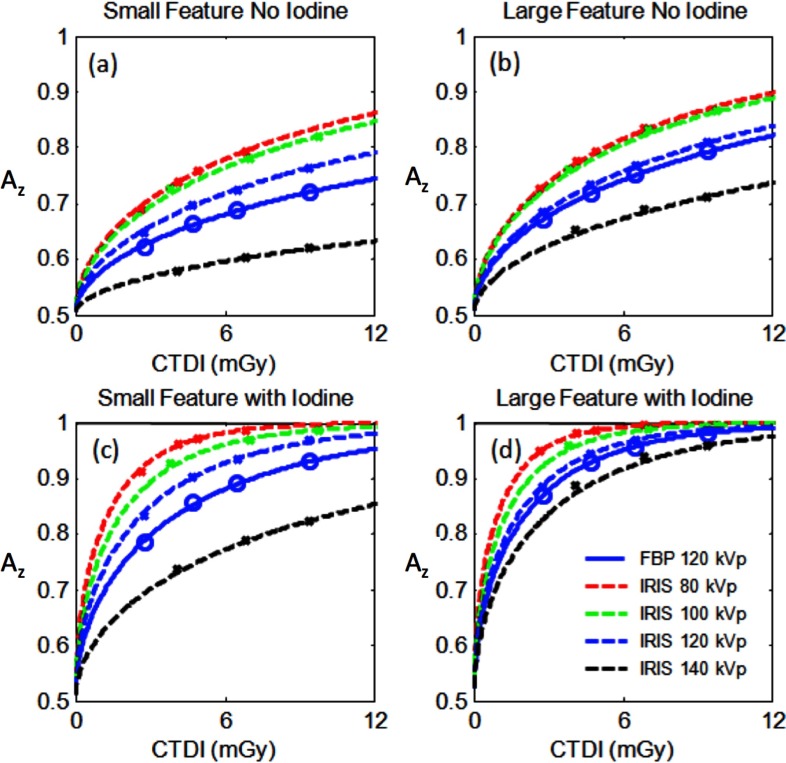
Comparative A_Z performance across protocols are illustrated in Fig. 5. Based on the benchmarked protocols employed, the results show that for the small feature with no contrast, employing the 120 kVp with FBP as a reference, lowering the kVp to 80 or 100 kVp accompanied with the use of IRIS could provide comparable image quality at 52% less dose. For the large feature with no contrast, going from 120 kVp FBP to 80 or 100 kVp IRIS resulted in a potential dose reduction of 36%. For the feature detection with iodine enhancement, the optimal kVp was found to be 80 kVp for both small and large features types. The results indicated that dose reduction of 57% and 40% for the small and large feature detection tasks, respectively, when using 80 kVp/IRIS compared to 120 kVp/FBP. These results indicate that IRIS offers a higher dose advantage for imaging smaller features. These trends are consistent with the dependency of task functions on kV shown earlier (Fig. 2, Table II).

FIG. 5.

Area under the ROC curve (A_Z) as a function of dose for various kVp and reconstruction algorithms for the small phantom and 5 mm slices. Here and throughout the rest of the figures, data points reflect the discrete dose levels at which the performance was measured, while the line reflect fits to that data.

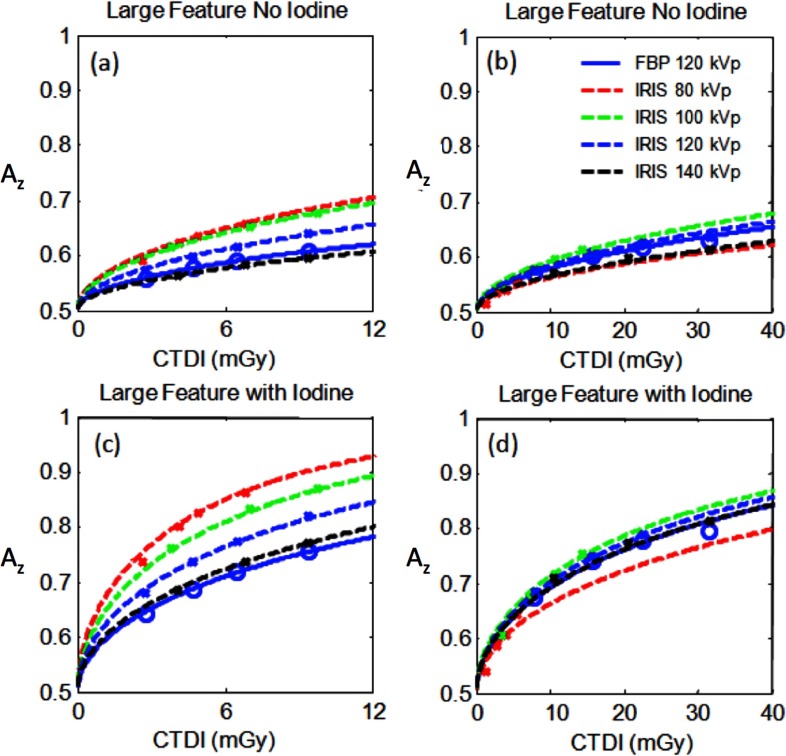
In comparison to the nominal data shown in Fig. 5 (i.e., small phantom and 5 mm reconstruction), Fig. 6 shows the results for thinner slice reconstructions [Figs. 6(a) and 6(c)] and large phantom size [Figs. 6(b) and 6(d)] for the large feature detection task. Assessing the variation based on reconstructed slice thickness for the small phantom, IRIS enabled a 60% dose reduction. Focusing on phantom size, the potential for dose reduction with IRIS compared to FBP was significantly reduced for the larger phantom compared to the small phantom by 10% and 44% for the same task without and with iodine, respectively. As stated earlier, these results are limited to the protocols used in the study.

FIG. 6.

Area under the ROC curve (A_Z) as a function of dose for various kVp and reconstruction algorithms. (a) and (c) reflect small phantom data with 0.6 mm slice thickness and (b) and (d) reflect large phantom data with 5 mm slices.

In terms of performance as a function of noise (as opposed to CTDI noted above), Fig. 7 plots the computed area under the ROC curve as a function of the measured noise in the image. Noise, measured across both the 5 mm and 0.6 mm reconstructions, was plotted for the different kVps across the four tasks. For clarity, a line was fitted across the different dataset. Results show how performance drops with increased noise and across different slice thicknesses. Note that the 120 kVp/FBP and 120 kVp/IRIS curves did not overlap noting that at comparable noise (not dose), FBP outperforms IRIS. This is a reflection of the differing noise texture of the two reconstructions. In another word, at the same dose, IRIS outperforms FBP. But, if dose is adjusted such that the noise magnitude is kept constant for the two, FBP has a more favorable noise texture and thus provides a more favorable background for lesion detection.

FIG. 7.

Area under the ROC curve (A_Z) as a function of pixel noise for various kVp and reconstruction algorithms. The plots contain data from the 5 and 0.6 mm slices. (a) and (c) reflect small phantom data with 0.6 mm slice thickness and (b) and (d) reflect large phantom data with 5 mm slices.

The overall results for all tasks, different phantom size, and function are summarized in Table III. Within the constraint of the exact protocol parameters investigated in the study, the data present the optimum technique to achieve the highest performance for a given task and patient size, and the expected dose saving if the optimum technique (as opposed to the reference technique) is used.

TABLE III.

Summary of optimal technique and possible dose reduction across the various task, phantom sizes, and reconstruction slice thicknesses.

Small patient (5 mm slice)
Task	Optimal technique	% dose reduction (with respect to 120 kVp FBP)
Small/no contrast	80 or 100 kVp with IRIS	52%
Large/no contrast	100 kVp with IRIS	36%
Small/with contrast	80 kVp with IRIS	57%
Large/with contrast	80 kVp with IRIS	40%
Large patient (5 mm slice)
Task	Optimal technique	% dose reduction (with respect to 120 kVp FBP)
Small/no contrast	100 or 120 kVp with IRIS	40%
Large/no contrast	100 or 120 kVp with IRIS	17%
Small/with contrast	100 or 120 kVp with IRIS	34%
Large/with contrast	100 or 120 kVp with IRIS	9%
Small patient (0.625 mm slice)
Task	Optimal technique	% dose reduction (with respect to 120 kVp FBP)
Small/no contrast	80 or 100 kVp with IRIS	69%
Large/no contrast	100 kVp with IRIS	58%
Small/with contrast	80 kVp with IRIS	73%
Large/with contrast	80 kVp with IRIS	62%

IV. DISCUSSION

Iterative reconstruction algorithms are currently being installed on clinical CT systems; however, there is currently no consensus on how to properly and accurately assess the image quality of CT images reconstructed with iterative algorithms. One of the mains challenges posed by these reconstructions is their nonlinearity, the spatial resolution and noise can depend on the dose or contrast of the object. As a result, standard contrast, noise, and contrast to noise ratio (CNR) metric are often too limited to properly assess image quality. Furthermore, iterative reconstruction algorithms are found to alter image texture, which these conventional metrics do not capture. There is a growing consensus in the imaging community that new metrology is needed to properly ascertain the performance of such CT systems.

This work provides a methodology to predict task-dependent performance of a CT system. The methodology can be readily applied to different reconstruction algorithms other than IRIS. The only exception would be for iterative reconstructions that exhibit contrast-dependent MTF, not applicable to IRIS.¹² For those algorithms, the MTF would need to be measured as a function of the contrast level, and be applied to tasks that reflect corresponding contrast levels.¹¹ The findings of our study indicate that noise magnitude cannot be a sole predictor of image quality across reconstruction algorithms; as shown in Fig. 7, the performance for FBP and IRIS do not overlap even though the spatial resolution, pixel noise, kVp, and object contrast are exactly the same in both sets of images.

The method employed in this study was task-specific in the sense that the generated metrics of quality, d^′ and A_z, reflect the characteristics of the task of interest. The d^′ metric that we used is an ideal observer which does not take the visual response of the human eye into consideration. Other d^′ formulations can be used toward that goal.⁶ The findings show a strong task dependency. The difference between the two tasks is a result of different textures between IRIS and FBP as quantified by the NPS shown in Fig. 3. The noise (i.e., NPS) is greater at lower spatial frequencies for IRIS than FBP; therefore, IRIS performance is more heavily penalized than FBP even if the total noise and resolution of the images are the same. However, IRIS offers distinct advantages for smaller features. With the MTF being constant, because the NPS for IRIS has more power than FBP at lower spatial frequencies, a smaller lesion with higher power at higher special frequencies can be more advantageously perceived in a lower frequency background.

Overall, measurements of pixel noise in IRIS overestimates imaging performance compared to FBP by 2%–8% depending on the task and noise level. As an example, at a pixel noise of 5 HU, this overestimation is 2.5% for a small feature and 6.8% for a large feature without iodine and 2.7% for a small feature and 5.5% for a large feature with iodine. These and above observations highlight how pixel noise has to be carefully interpreted when employed as a predictor of performance even if the resolution of the system remains unchanged. This is a somewhat surprising result since the NPS was different between FBP and IRIS and for traditional CT systems using FBP, the change of the reconstruction filter typically alters both the NPS and MTF leading to a conventional trade-off between spatial resolution and pixel noise. These results point to a different paradigm that needs to be assessed and accounted for in protocol optimization when evaluating iterative reconstructions.

This work provides a strategy for identifying the kVp and the mA or dose reduction for various types of imaging tasks. Across all tasks tested, results indicate that a lower kVp (80 or 100) should be employed for smaller patients. Results further indicate that greater dose reduction can be achieved for a small feature in comparison to a large feature. This may seem counterintuitive but can be explained by the fact that a small feature is more noise and spatial resolution sensitive than a large feature task and because IRIS improves the noise properties without affecting the resolution, therefore the relative benefit is larger for a small feature than it is for a large feature detection task.

The detectability index was found to potentially provide a more useful metric than noise or CNR to account for the complex imaging characteristics of CT images when iterative reconstruction algorithms are employed. Overall, this work provides a guideline for the application of IRIS on clinical scanners via an objective assessment of image quality. The application of lower kVp was found to improve image quality especially for smaller sized patients. The added benefit of iterative reconstruction can potentially extend the improved contrast advantage offered with low-kVp imaging to larger patients due to lower noise. Dose reduction was shown to be achievable in all cases, with varying reduction ranging from 9% to 73% depending on phantom size, imaging task, and reconstruction slice thickness. This represents a wide range of dose reduction and therefore careful implementation of the factors need to be considered.

There are several limitations to our work. The proposed methodology, while considered an improvement over CNR-based metrologies, provides only a prediction of clinical performance. The methodology is envisioned not as a replacement of observer studies, but as a precursor, which can make those studies better targeted and more efficient in confirming the clinical utility of iterative reconstructions. Second, our study only used two reasonably matched kernels; we did not fully characterize the performance of the reconstruction across the entire range of possible kernels, as investigated by an earlier study.¹⁴ As such, any claim of optimality is based on the kernels used, and care should be exercised in making a generic claim of one algorithm being better than another. Each algorithm (FBP or IRIS) needs to be optimized across its entire parameter space before a generic conclusion can be reached. The FBP acquisition could by itself be optimized by a targeted selection of acquisition parameters. Nonetheless, the FBP protocol that was used in the study was the state of practice at our institution and many others. As such, the comparison, while not as complete, is relevant.

Third, our methodology did not explicitly characterize possible higher order dependencies of the MTF and the NPS. Higher degrees of stratification had to be avoided for the sake of a higher level of experimental certainty. Quantitative characterizations of directional, locational, and signal dependencies of the MTF and the NPS remain topics of worthy follow up investigations. Those include possible anisotropy, shift-variance, edge-preservation, contrast dependency, and noise dependency of the MTF and the NPS. Of particular challenge is the assessment of the MTF at the exact noise and contrast levels corresponding to a targeted task. Finally, while the current study is meaningful in highlighting the importance of patient size as a factor in system evaluation and optimization, it used only two phantom-patient sizes. The “large patient size” in the study was only 28 cm in diameter, which is still small by current population statistics. Future work should include performance evaluation across a wider range of patient sizes.

V. CONCLUSIONS

Our results highlight the dependence of CT optimal technique on imaging task and provides initial implementation of an experimentally measured figure of merit for CT performance assessment and optimization. The application of metrics which enable spatial resolution and noise texture assessment combined with a description of imaging task provides an objective comparison of imaging performance between protocols and reconstruction algorithms. The application of lower kVp in conjunction with iterative reconstruction was shown to potentially reduce patient dose while maintaining or improving diagnostic image quality.