Predictive equations for the estimation of body size in seals and sea lions (Carnivora: Pinnipedia)

Abstract

Body size plays an important role in pinniped ecology and life history. However, body size data is often absent for historical, archaeological, and fossil specimens. To estimate the body size of pinnipeds (seals, sea lions, and walruses) for today and the past, we used 14 commonly preserved cranial measurements to develop sets of single variable and multivariate predictive equations for pinniped body mass and total length. Principal components analysis (PCA) was used to test whether separate family specific regressions were more appropriate than single predictive equations for Pinnipedia. The influence of phylogeny was tested with phylogenetic independent contrasts (PIC). The accuracy of these regressions was then assessed using a combination of coefficient of determination, percent prediction error, and standard error of estimation. Three different methods of multivariate analysis were examined: bidirectional stepwise model selection using Akaike information criteria; all-subsets model selection using Bayesian information criteria (BIC); and partial least squares regression. The PCA showed clear discrimination between Otariidae (fur seals and sea lions) and Phocidae (earless seals) for the 14 measurements, indicating the need for family-specific regression equations. The PIC analysis found that phylogeny had a minor influence on relationship between morphological variables and body size. The regressions for total length were more accurate than those for body mass, and equations specific to Otariidae were more accurate than those for Phocidae. Of the three multivariate methods, the all-subsets approach required the fewest number of variables to estimate body size accurately. We then used the single variable predictive equations and the all-subsets approach to estimate the body size of two recently extinct pinniped taxa, the Caribbean monk seal (Monachus tropicalis) and the Japanese sea lion (Zalophus japonicus). Body size estimates using single variable regressions generally under or over-estimated body size; however, the all-subset regression produced body size estimates that were close to historically recorded body length for these two species. This indicates that the all-subset regression equations developed in this study can estimate body size accurately.

Introduction

Body size is strongly correlated with numerous aspects of mammalian life history, including range size (Gittleman, 1985), reproduction (Tuomi, 1980), community structure (Van Valkenburgh, 1990), and extinction risk (Cardillo et al. 2005). Among marine mammals, pinnipeds (seals, sea lions, and walruses) show a large range of body sizes, from the 80–90-kg Baikal seal (Pusa sibirica) to the 3600-kg male southern elephant seal (Mirounga leonina; King, 1983). Pinnipeds show an extensive degree of sexual dimorphism within taxa as well, with male southern elephant seals being seven times the size of an adult female of the same species (Lindenfors et al. 2002). Pinniped body size can also affect other aspects of their life history such as reproductive isolation (Miller et al. 1996; Berta & Churchill, 2012), mating strategy (Weckerly, 1998; Lindenfors et al. 2002), and diving ability (Schreer et al. 2001). Changes in pinniped body size through time can reveal important information about the environment, including changes in productivity. For instance, changes in body mass in female Steller's sea lion (Eumetopias jubatus) during their recent population decline in Alaska have been used as evidence of nutritional stress in the population, which was induced by recent changes in abundance of different prey taxa (Calkins et al. 1998). Changes in body size over deep time may also provide important information on the roles that productivity and climate change play in pinniped evolution.

Museums are excellent repositories for information on body size through time, with large collections of historical, archaeological, and fossil material available to researchers. However, much of this material may be fragmentary or lack information on total length or body mass (Pyenson et al. 2013). To make use of this material, methods need to be developed that allow the estimation of body size based on fragmentary material.

Accurate estimates of body size can be produced using allometric relationships between morphological features of the skull and body size (Damuth & MacFadden, 1990). This method has been used successfully to provide estimates of body size in other fossil marine mammals, including sea cows (Sarko et al. 2010) and whales (Pyenson & Sponberg, 2011). However, comprehensive predictive equations for pinniped body size based on cranial measurements are largely absent, and those that have been published have been limited to a single species or a few measurements of size. Itoo & Inoué (1993) provided estimates of body size of the extinct Japanese sea lion (Zalophus japonicus) by comparing features of the skull with the closely related California sea lion (Zalophus californianus). Debey & Pyenson (2013), in their study of orbit size in pinnipeds, found a strong relationship between occipital condyle breadth and body mass. However, they only validated this relationship for two other variables (condylobasal length and orbit length), and only looked at body mass, not total length.

In this study we established predictive equations for pinniped body size using single variable and multivariate techniques for 14 commonly preserved morphological features of the pinniped cranium, and evaluated the accuracy of these equations by comparing the body size estimates with a subset of individuals of known body size. We then applied the best predictive equations to estimate the body size of two historically extinct species of pinniped, the Caribbean monk seal (Monachus tropicalis) and the Japanese sea lion (Z. japonicus).

Materials and methods

Sampling

To maximize the phylogenetic and morphological diversity within our sample, we gathered measurement data from 34 extant species and morphologically distinct subspecies of phocid and otariid seal. Taxonomy largely follows that of Berta & Churchill (2012), although we continue to recognize only one genus of southern fur seal (Arctocephalus), and do not recognize Arctophoca, due to the unsettled state of fur seal taxonomy. We included two subspecies of harbor seal (Atlantic, Phoca vitulina vitulina and Pacific, P. vitulina richardii), three subspecies of southern fur seal (South American Arctocephalus australis australis, Peruvian A. australis ssp. nov., and New Zealand A. australis forsteri), and two subspecies of Cape fur seal (South African Arctocephalus pusillus pusillus and Australian A. pusillus doriferus). Both sexes were sampled and sampling was limited to complete skulls whenever possible. Only mature individuals were sampled, with maturity assessed using a combination of suture indices (Doutt, 1942; Sivertsen, 1954) and cranium length. Because of the limited availability of material, we were unable to sample the following species and sexes: Hawaiian monk seal (Monachus schauinslandi), Juan Fernández fur seal (Arctocephalus philippii philippii), female Australian Sea Lion (Neophoca cinerea) and female Townsend's fur seal (A. philippii townsendi).

Sampling was limited solely to Phocidae and Otariidae, and we did not include odobenids (walruses). Although formerly more diverse (Deméré et al. 2003), Odobenidae is today represented by only one species. The limited range of body size and taxonomic diversity within extant Odobenidae make the development of family-specific predictive body size regression equations difficult. Even with consideration of the different subspecies and sex, a maximum of only four data points is possible using average measurement values, preventing the creation of robust regression equations. Walruses also possess an extensively modified cranium, due to the development of enormous tusks and specialization for benthic suction feeding (Adam & Berta, 2002). This unusual cranial morphology makes comparability of standard cranial measurements difficult between extant odobenids and other pinniped clades. Furthermore, few of the adult Odobenus specimens examined by the authors had associated body size data, preventing the calculation of support values such as percent prediction error.

To reconstruct the body size of historically extinct pinnipeds, we examined complete and fragmentary material from M. tropicalis and Z. japonicus. For M. tropicalis, known total length data are so far limited to one male individual with a total length of 226 cm, and four pregnant females, with total lengths of 199, 214, 216, and 224 cm (Allen, 1887; Ward, 1887; Adam, 2004). The weight of only one of these pregnant females is known (163 kg; Adam, 2004; Anonymous, 1903), and no weight data are available for any males. Material for M. tropicalis included eight crania from four males and four females. These specimens were collected in 1900 from the Triangle Islands of Mexico. No body size data are available for Z. japonicus, although estimates of total length based on archaeological material suggest a total length of 287.9 cm for one individual and a body mass between 437.7–513.7 kg, based on two individuals and comparison with cranial material from extant Z. californianus (Itoo & Inoué, 1993; Ohdachi et al. 2009). The Z. japonicus surveyed in this study were represented by cranial material of 17 male individuals from three different sites on Hokkaido, Japan, of different age (supporting Information Appendix S1): The Funadomari Shell Mound sites (2.6–3.8 ka) on Rebun Island, Hamanaka-2 on Rebun Island (3.2–2.6 ka), and the Aonae site, Okushiri Island (0.8–0.5 ka). We assessed differences in Z. japonicus body size between sites and ages using non-parametric t-tests. Overall, we were able to examine cranial material from ∼600 specimens, including extant and historically extinct taxa (Supporting Information Appendix S2). All institutional abbreviations are listed in Appendix S2.

Fourteen measurements were collected from each specimen (Fig. 1), with the acronyms and definitions of measurements listed in Table 1. All measurements were made with digital calipers to the nearest 0.1 mm. For exceptionally large taxa [e.g. Steller's sea lion (Eumetopias jubatus), South American sea lion (Otaria byronia), and elephant seals (Mirounga spp.)], basal length (BL) was measured using a cloth measuring tape, to the nearest 1 mm. The 14 measurements used in this analysis were chosen based on multiple criteria, including comparability across taxa, ease of measurement, and frequency of preservation within fossil and archaeological material. Measurements were limited solely to the cranial region, due to extensive modification of the postcrania for aquatic locomotion, and their reduced function as weight-supporting structures (Bebej, 2009; Pierce et al. 2011).

Figure 1.

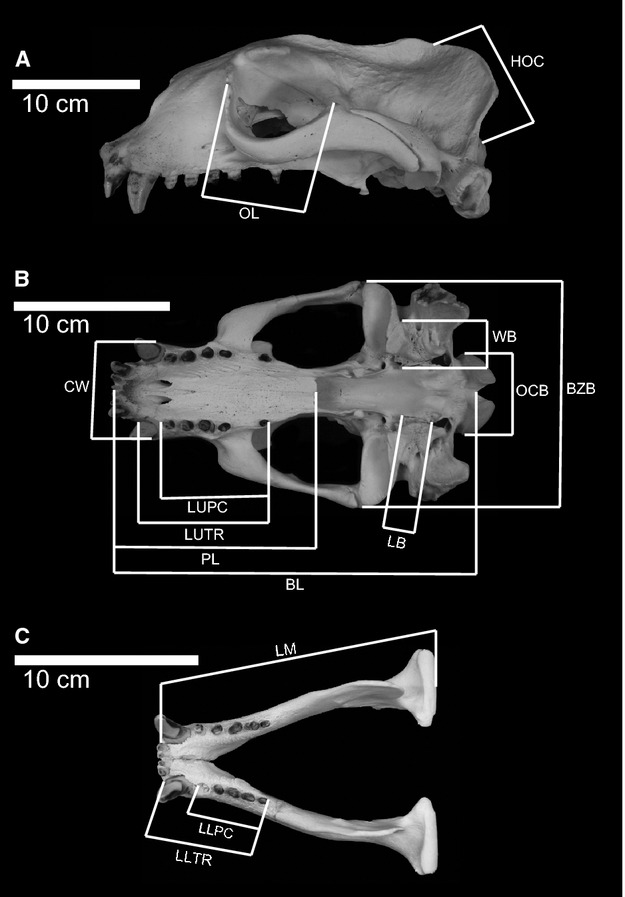
Lateral (A) and dorsal (B) of the cranium and dorsal view (C) of the mandible of Eumetopias jubatus (California Academy of Science (CAS) 23735), illustrating cranial measurements used in this study. Measurements include: BL (basal length); PL (palate length); LUTR (length of upper tooth row); LUPC (length of upper postcanine tooth row); CW (width of rostrum across the canines); BZB (bizygomatic width); LB (length of bullae along the medial border); WB (width across the bullae); OCB (width across the occipital condyles); HOC (height of the occipital); OL (length of orbit); LM (length of mandible); LLTR (length of lower tooth row); LLPC (length of postcanine tooth row).

Table 1.

Measurements used in this study

Acronym	Definition
BM	Body mass
TL	Total length, from tip of snout to tip of tail, measured in supine position
BL	Basal length
PL	Palate length, measured along the ∼ midline of the skull from the anterior to the alveoli for the first incisors to the posterior border of the palate
LUTR	Length of the upper tooth row, from the anterior margin of the C1 alveolus to the posterior margin of the last postcanine alveolus (M1 and M2), as a straight line distance
LUPC	Length of the upper postcanine tooth row, as measured from the anterior margin of the P1 alveolus to the posterior margin of the last postcanine alveolus (either M1 or M2)
CW	Width of the rostrum across the canines
BZB	Bizygomatic width of cranium
LB	Length of the auditory bulla along the medial margin from anterior opening of the auditory tube to the posterior lacerate foramen
WB	Width of the auditory bulla from the lateralmost margin of the eustachian tube to the medial margin of the bulla at the approximate midpoint of its length
OCB	Width across the occipital condyles
HOC	Height of the occipital shield along the midline, from the intercondylar notch to the junction of the sagittal and lambdoidal crests
OL	Length of orbit, the straightline distance between the antorbital process of the maxilla/frontal, to the postorbital process of the jugal
LM	Length of mandible from the anterior terminus to the approximate center of the posterior surface of the mandibular condyle
LLTR	Length of the lower tooth row, from the anterior margin of the C1 alveolus to the posterior margin of the M1
LLPC	Length of the lower postcanine tooth row, as measured from the anterior margin of the P1 alveolus to the posterior margin of the M1

Pinnipeds show some of the highest levels of sexual dimorphism of any mammalian taxa (Lindenfors et al. 2002). For taxa with high sexual dimorphism, we averaged male and female cranial measurements separately. Taxa were considered to show a large degree of sexual dimorphism if the body weight difference of one sex was greater than or equal to 11% of the body mass and 10% of the total length of the larger sex. We treated males and females separately for the following taxa: Otariidae, elephant seals (Mirounga), leopard seal (Hydrurga leptonyx), hooded seal (Cystophora cristata), and gray seal (Halichoerus grypus). A large degree of sexual dimorphism was also present within Mediterranean monk seal (Monachus monachus); however, few specimens available for study had an assigned sex. Because of this, we treated male, female, and individuals of unknown sex as one unit for analysis for M. monachus.

For this study, we examined two metrics of body size. Body mass (BM) is frequently used as a measure of body size within terrestrial mammals (Damuth & MacFadden, 1990). However, body mass can be difficult to measure for marine mammals because they are often very large (Pyenson & Sponberg, 2011). Because of the lack of body weight data for many specimens, we also used total length [TL = standard length (Committee on Marine Mammals, 1967)] as a body size proxy, which is defined as the distance between the tip of the snout and tip of the tail measured while the animal is in a supine position. When available, body mass and total length data were collected for each specimen examined. However, many specimens within museum collections lack associated body size data, particularly for larger and older specimens, limiting known body size data to a small subset of taxa. To increase the taxonomic sampling of our data, we compiled average body mass and average total length data for each sex of each species and distinctive subspecies of interest, from the compilations of King (1983), Bininda-Emonds & Gittleman (2000), and Lindenfors et al. (2002). These average body size values were then compared with the average value of each cranial measurement for each taxon to produce our predictive equations for body size. Measurement data, mean measurement values, and mean BM and TL are presented for each species in Supporting Information Appendix S3.

Principal components analysis

Large differences in morphology (Jones & Goswami, 2010; Debey & Pyenson, 2013; Jones et al. 2013) and long separate evolutionary histories (Higdon et al. 2007) call into question the usefulness of creating single predictive equations for body mass and total length for Pinnipedia. To determine whether family-specific equations would be more appropriate, we performed PCA on the 14 log₁₀-transformed average measurements for each taxon. If Phocidae and Otariidae are clearly separated from one another on the PCA, then family-level predictive equations are more appropriate. If both families are mixed together with little discrimination, predictive equations at the level of Pinnipedia are more appropriate. The PCA also provided a good test of whether our measurements were strongly related to differences in size, or related to other sources of morphological variation. PCA was performed using the factominer package (Lê et al. 2008) in r 2.12.1 (R Development Core Team, 2010).

Phylogenetic independent contrasts

Since different pinniped species share common ancestry, they do not represent statistically independent units, and any analysis of scaling relationships may be influenced by phylogeny (Felsenstein, 1985). To determine the impact of phylogeny on the allometric relationships between different cranial measurements and body size, we performed phylogenetic independent contrasts (PIC; Felsenstein, 1985) to determine whether strong allometric relationships existed between different cranial measurements and body size without the influence of phylogeny.

Separate analyses were performed for each body size proxy and family, resulting in four separate sets of PIC analyses for each measurement variable. Sexes of sexually dimorphic taxa could not be analyzed separately, and male and female body mass, total length, and measurement values were averaged together for PIC. This resulted in differences between datasets used for PIC and calculating the regression equations, with the PIC datasets having a smaller range of body size as well as fewer data points. To accommodate these differences, adjusted R² values were computed for linear regression on the sex-averaged datasets, for comparison with R² produced from the PIC analysis. Non-parametric t-tests were used to assess differences in R² between PIC and non-PIC analyses. For otariid analyses, the combined evidence tree of Churchill et al. (in press ) was used. For phocid analyses, the topology of Fulton & Strobeck (2010) was used. These studies represent the most recent comprehensive phylogenetic analyses available for these clades, and provided tree topologies with no polytomies (Fig. 2). All analyses were performed in r, using the packages APE (Paradis et al. 2004) and GEIGER (Harmon et al. 2008). Because branch lengths were not available for all phylogenies, we randomly generated branch lengths 10 000 times, resulting in 560 000 PIC analyses. This removed the influence of varying branch lengths on PIC.

Figure 2.

Phylogeny used in PIC analyses. The topology for Otariidae is from Churchill et al. (in press ), while the topology for Phocidae is from Fulton & Strobeck (2010). Placement of families within the phylogeny follows Higdon et al. (2007).

Development of predictive equations

To estimate the body size of extinct taxa, we produced predictive equations based on four different approaches: (i) single variable regressions; (ii) multivariate regression using stepwise model selection; (iii) multivariate regression using an all-subsets approach; and (iv) partial least squares regression. Regression equations were created for both average body mass and average total length. Supporting Information Appendix S4 includes the R code used to generate all multivariate regressions.

All data were log₁₀-transformed to simplify the method of analysis and allow more accurate fitting of linear models (Smith, 1993). Since the purpose of these equations was to predict body size based on a given measurement variable, the least squares method of linear regression was used (Gingerich & Smith, 1984; LaBarbera, 1989). To produce the single variable predictive equations, the log₁₀-transformed average BM and TL were regressed onto the log₁₀-transformed average measurement variable for each species and sexually dimorphic taxon.

While single variable predictive equations are frequently used for body size estimation, multivariate approaches can significantly improve estimates by incorporating the size-related variation of multiple measurements (Mendoza et al. 2006). However, not all variables may be equally useful predictors of body size. To find the optimal set of variables which best predicted the body size of extinct taxa, we used two different methods of model selection.

The first method, bidirectional stepwise model selection, was implemented in r using the MASS package (Venables & Ripley, 2002) and the Akaike information criteria (AIC). This method performs an iterative test and determines at each step what variable should be included or excluded, arriving at the single best combination of variables for prediction of body size, as determined by the set of variables with the smallest AIC score.

We also performed an all-subsets method of model selection, as implemented using the leaps (Lumley & Miller, 2009) and cars packages (Fox & Weisberg, 2011) in r. This method selects the single best combination of variables for each subset of variables (e.g. 2 variables, 3 variables...13 variables), using a branch and bound search algorithm. The best variable combination for each subset was then compared using the BIC as implemented in the stats4 package (R Development Core Team, 2010), with the combination with the lowest BIC score selected.

Although adding additional variables can improve the accuracy of predictive equations, many of the morphological variables may not be fully independent from one another and may show strong correlation, reducing further improvement of the model (Pyenson & Sponberg, 2011). One approach to avoid this problem is to isolate the portion of each measurement directly related to body size. This can be done by converting the dataset into canonical components like those produced by PCA, and only using those canonical components that best explain change in size. This multivariate method is referred to as partial least squares (PLS) regression. To produce estimates of body size using a PLS approach, we extracted the canonical variates from the 14 log₁₀-transformed average measurements for each taxon and sexually dimorphic gender, using the package PLS (Mevik & Wehrens, 2007) in r. Root mean squared error of prediction (RMSEP) validation plots were used to assess the individual components, with the number of components which led to the greatest decrease in RMSEP used to predict body size.

To assess the fit of each predictive equation, we determined the adjusted coefficient of determination (R²) and P-value of each regression. Since R² values are often a poor indicator of the robustness of a predictive equation, we also calculated the standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) (Smith, 1981, 1984; Van Valkenburgh, 1990). The PPE represents the offset between the known and estimated body size value, and is calculated using the following equation (Eqn 1):

(1)

The SEE represents the ability of an independent variable or set of variables to predict the dependent variable. Roughly 68% of the actual data should fall within one SEE of the predicted data. It is calculated using the following equation (Eqn 2):

(2)

The SE, PPE, and SEE were calculated from regressions derived from the average body mass and total length of 34 species to calculate the body size of a subset of specimens with known body mass and total length, and comparing the known versus estimated body sizes. All SE, PPE, and SEE values are reported relative to the log₁₀ estimate. Detransforming the estimated body size derived from the regression equations can introduce error, reducing the accuracy of SE, PPE, and SEE. All reported values for SE, PPE, and SEE were the average value for a given variable or for a specific multivariate regression. We also tested for significant differences in the R², PPE, and SEE of different sets of single variable predictive equations, using non-parametric Kruskal–Wallis tests (P > 0.05).

For Otariidae, the data subset of taxa with known total length and/or body mass was composed of three taxa: northern fur seal (Callorhinus ursinus; 19 individuals with known body size), Steller's sea lion (E. jubatus; two individuals with known body mass, 13 with known total length), and California sea lion (Z. californianus; 11 individuals with known body mass, and 31 with known total length). For Phocidae, this dataset was composed of male and female southern elephant seal (M. leonina; four individuals with known total length), Weddell's seal (Leptonychotes weddellii; one individual with known total length), bearded seal (Erignathus barbatus; three individuals with known body size), spotted seal (P. largha; one individual with known body mass, nine with known total length), Pacific harbor seal (P. vitulina richardii; two individuals with known body mass, three with known total length), Caspian seal (P. caspica; 22 individuals with known body size), ringed seal (P. hispida; five individuals with known body mass, eight with known total length), and Baikal seal (P. sibirica; 21 individuals with known body mass, 18 with known total length).

Results

Principal components analysis

Approximately 93% of variation in skull shape was explained by the first two components (Fig. 3). Principal component one explained 82.59% of the variation and reflected differences in body size. Principal component two explained 10.29% of the variation and reflected differences in shape of the bulla and orbit. Principal component two segregated otariids and phocids. Otariidae mostly differed in size, and showed little variation in principal component two. Phocidae showed approximately twice the amount of variation in principal component two, indicating a large degree of morphological diversity within the shape of the bullae and the orbit for this family.

Figure 3.

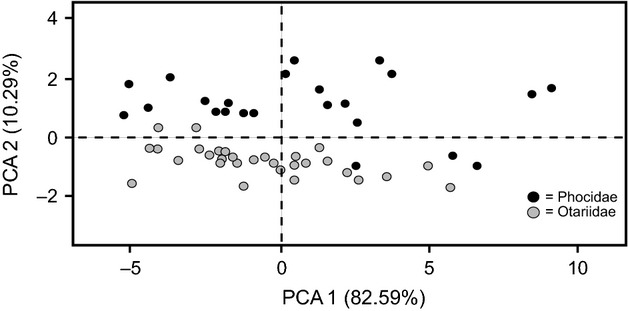
Bivariate plot of principal component one versus principal component two, based on the average 14 Log₁₀ transformed cranial measurements for 34 distinctive species and subspecies of otariid and phocid seal. Male and female otariids, Mirounga, Hydrurga, Cystophora, and Halichoerus are treated as separate data points.

The PCA indicated that the two families can be clearly distinguished using the measurements employed in this study, and that separate regression equations are warranted for the purpose of predicting body size. For the remainder of this paper, measurements of Otariidae and Phocidae will be analyzed separately to produce family-specific predictive equations.

Phylogenetic independent contrasts

Differences in R² between non-PIC and PIC single variable regression analyses are shown in Fig. 4. Significant differences in R² were found for regressions for body mass for Phocidae (t = 3.44, df = 22, P = 0.002) and total length for Otariidae (t = 2.39, df = 26, P = 0.024) and Phocidae (t = 4.71, df = 19, P < 0.001) when phylogeny was controlled. Even with phylogeny taken in account, non-zero slopes were still significant (P < 0.001) for all regressions. Differences in R² values between PIC and non-PIC analyses for Otariidae were usually less than 0.1, while differences between PIC and non-PIC analyses for Phocidae were greater than those of Otariidae, as high as ∼0.45 (Fig. 5). PIC analyses showed that phylogeny influenced the strength of the relationship between the measurement variables and body size. However, the degree of influence appears to vary between Otariidae and Phocidae, with Otariidae showing only minor phylogenetic influence and Phocidae showing greater influence. When phylogeny is taken into account, robust relationships still existed between the measurement variables and body size.

Figure 4.

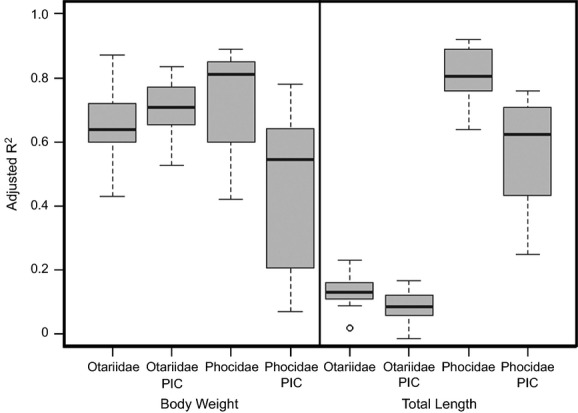
Boxplots comparing R² values for linear regressions with those produced from PIC.

Figure 5.

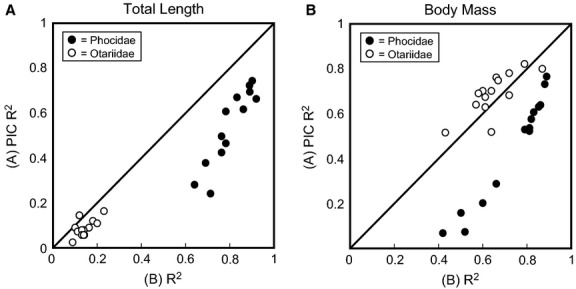
Bivariate plots of R² values from PIC (A) and non-PIC (B) single variable linear regressions. Diagonal line represents a 1 : 1 line: points above the line represent regressions with R² values improved by PIC, and points below the line represent regressions where R² values decreased with PIC.

Single variable regressions

Fifty-six single variable predictive equations are presented for Otariidae and Phocidae in Tables 2–5. Support values were used to assess the accuracy of variables; however, specific support values (R², PPE, SEE) often supported different variables as being the most accurate. Overall, single variables with a low PPE also had a low SEE, although there were exceptions (e.g. the predictive equation for phocid body mass using zygomatic width produced a low PPE but a high SEE value). However, R² was not well correlated with either PPE or SEE values, and many regressions with high R² often had poor PPE and SEE scores, and vice versa. Poor correlations between R² and PPE and SEE can exist when interspecific data are used to produce allometric equations (Smith, 1981). For this reason, we used PPE and SEE to determine the best variables for body size estimation, with the overall best performing equations highlighted in bold in Tables 2–5.

Table 2.

Single variable linear regressions for estimation of body mass for Otariidae, with the adjusted coefficient of determination (R²), standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) reported for each regression. Best predictors for body size estimation (as determined by combination of PPE and SEE) indicated in bold

Equation		ad. R2	SE	PPE (%)	SEE (%)
BL	2.98 × Log(BL) − 2.17	0.75	0.22	13.74	65.24
PL	2.17 × Log(PL) − 0.34	0.77	0.19	11.03	53.57
LUTR	2.52 × Log(LUTR) − 0.30	0.70	0.19	10.78	54.19
LUPC	2.57 × Log(LUPC) − 0.089	0.67	0.19	11.41	56.02
CW	1.64 × Log(CW) + 0.74	0.54	0.21	12.18	63.67
BZB	3.57 × Log(BZB) − 2.14	0.78	0.19	12.05	55.17
LB	2.00 × Log(LB) + 0.89	0.31	0.42	27.52	165.83
WB	2.92 × Log(WB) + 0.42	0.56	0.33	21.55	114.41
OCB	3.05 × Log(OCB) − 0.54	0.60	0.41	26.10	155.49
HOC	3.04 × Log(HOC) − 0.43	0.41	0.20	12.07	42.24
OL	4.53 × Log(OL) − 1.62	0.38	0.31	17.22	102.08
LM	3.05 × Log(LM) − 1.79	0.84	0.20	12.72	59.07
LLTR	2.52 × Log(LLTR) − 0.14	0.73	0.19	10.41	56.24
LLPC	2.86 × Log(LLPC) − 0.07	0.74	0.24	14.04	72.45

Table 5.

Single variable linear regressions for estimation of total length for Phocidae, with the adjusted coefficient of determination (R²), standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) reported for each regression. Best predictors for body size estimation (as determined by combination of PPE and SEE) indicated in bold

Equation		ad. R2	SE	PPE (%)	SEE (%)
BL	1.13 × Log(BL) + 0.77	0.89	0.06	3.63	15.39
PL	0.96 × Log(PL) + 1.32	0.83	0.08	4.47	19.52
LUTR	1.00 × Log(LUTR) + 1.50	0.78	0.08	4.97	21.62
LUPC	0.96 × Log(LUPC) + 1.64	0.65	0.09	5.80	25.59
CW	0.72 × Log(CW) + 1.83	0.91	0.06	2.98	13.71
BZB	1.03 × Log(BZB) + 1.10	0.89	0.11	3.90	28.22
LB	0.75 × Log(LB) + 1.91	0.72	0.08	3.43	19.43
WB	1.08 × Log(WB) + 1.58	0.86	0.06	3.17	15.87
OCB	1.54 × Log(OCB) + 1.02	0.91	0.07	3.60	17.09
HOC	1.30 × Log(HOC) + 1.28	0.91	0.06	3.24	15.70
OL	1.20 × Log(OL) + 1.35	0.81	0.09	5.19	23.73
LM	1.01 × Log(LM) + 1.09	0.90	0.07	4.02	17.29
LLTR	0.97 × Log(LLTR) + 1.54	0.74	0.10	5.60	24.64
LLPC	0.94 × Log(LLPC) + 1.67	0.59	0.11	6.56	29.08

Table 3.

Single variable linear regressions for estimation of body mass for Phocidae, with the adjusted coefficient of determination (R²), standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) reported for each regression. Best predictors for body size estimation (as determined by combination of PPE and SEE) indicated in bold

Equation		ad. R2	SE	PPE (%)	SEE (%)
BL	2.98 × Log(BL) − 1.74	0.80	0.19	13.64	53.60
PL	2.63 × Log(PL) − 0.40	0.81	0.24	18.20	59.92
LUTR	2.52 × Log(LUTR) + 0.25	0.65	0.29	19.64	73.01
LUPC	2.27 × Log(LUPC) + 0.71	0.47	0.29	23.24	97.15
CW	1.95 × Log(CW) + 1.00	0.87	0.17	11.38	47.00
BZB	2.79 × Log(BZB) − 0.98	0.86	0.33	14.49	114.78
LB	1.83 × Log(LB) + 1.34	0.55	0.25	16.24	78.22
WB	3.01 × Log(WB) + 0.26	0.89	0.17	11.76	48.99
OCB	4.09 × Log(OCB) − 1.12	0.85	0.19	13.31	54.91
HOC	3.54 × Log(HOC) − 0.46	0.89	0.21	15.14	61.29
OL	3.39 × Log(OL) − 0.40	0.84	0.24	18.15	72.53
LM	2.65 × Log(LM) − 0.89	0.80	0.20	14.61	57.62
LLTR	2.28 × Log(LLTR) + 0.40	0.58	0.27	21.00	87.03
LLPC	2.13 × Log(LLPC) + 0.86	0.39	0.34	26.93	118.25

Table 4.

Single variable linear regressions for estimation of total length for Otariidae, with the adjusted coefficient of determination (R²), standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) reported for each regression. Best predictors for body size estimation (as determined by combination of PPE and SEE) indicated in bold

Equation		ad. R2	SE	PPE (%)	SEE (%)
BL	1.01 × Log(BL) + 0.91	0.75	0.03	1.97	7.82
PL	0.61 × Log(PL) + 1.63	0.54	0.04	2.26	8.67
LUTR	0.85 × Log(LUTR) + 1.52	0.65	0.05	3.26	13.00
LUPC	0.82 × Log(LUPC) + 1.63	0.56	0.07	3.46	16.68
CW	0.55 × Log(CW) + 1.89	0.63	0.03	1.98	7.43
BZB	0.98 × Log(BZB) + 1.15	0.69	0.02	1.42	5.72
LB	0.70 × Log(LB) + 1.99	0.44	0.05	3.38	12.88
WB	0.67 × Log(WB) + 1.96	0.58	0.04	2.32	9.26
OCB	1.10 × Log(OCB) + 1.47	0.72	0.06	3.17	13.58
HOC	0.85 × Log(HOC) + 1.62	0.51	0.03	2.08	6.30
OL	1.62 × Log(OL) + 1.05	0.61	0.03	2.18	8.13
LM	0.79 × Log(LM) + 1.31	0.71	0.03	1.94	7.44
LLTR	0.77 × Log(LLTR) + 1.64	0.70	0.03	2.23	8.35
LLPC	0.85 × Log(LLPC) + 1.69	0.64	0.04	2.66	9.87

Each predictive equation fits the data with high significance (P < 0.001). The average R², PPE, and SEE for each set of variables are compared in Fig. 6. Adjusted R² values varied from 0.31 to 0.89. A Kruskal–Wallis test revealed no significant difference (K = 4.38, df = 3, P = 0.22) in the R²-values of the four sets of equations.

Figure 6.

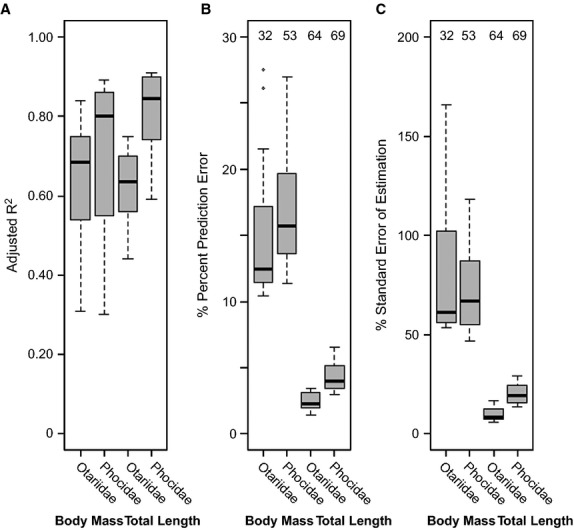
Box plots of adjusted R² (A), percent prediction error (B), and standard error of estimation (C) for estimates of body mass and total length based on 14 cranial measurements. Otariid and phocid body size regressions treated separately. Numbers above the box plots represent the sample size of the subset of individuals with known body mass and total length used to calculate percent prediction error and standard error of estimation. Black line through box represents the median, and the upper and lower limits of the boxes represent the upper and lower quartiles, respectively.

Kruskal–Wallis tests revealed significant differences in the PPE (K = 45.49, df = 3, P < 0.001) and SEE (K = 44.15, df = 3, P < 0.001) values for the four sets of equations. The predictive equations for otariid total length had the lowest PPE (mean = 2.45%, range = 1–3%) and SEE (mean = 9.65%, range = 6–17%). The predictive equations for phocid total length had the second smallest PPE (mean = 4.33%, range = 4–7%) and SEE (mean = 20.49%, range = 14–29%). The regressions for phocid body mass had the third smallest PPE (mean = 16.98%, range = 11–27%) and SEE (mean = 73.16%, range = 47–118%). Regressions for otariid body mass had the largest PPE (mean = 15.20%, range = 10–28%) and SEE (mean = 79.69%, range = 42–166%) values.

Multivariate regressions

The multivariate body size predictive equations generated using stepwise and all-subsets model methods are presented in Table 6, with support values presented in Tables 7 and 8. Few differences were found in R², PPE or SEE for the two multivariate approaches. The largest difference between the two approaches was in the number of variables selected for the predictive equations.

Table 6.

Multivariate regressions for estimation of body size in Otariidae and Phocidae

Method and body size proxy	Equation
Body mass
Otariidae (Stepwise)	10.11 × Log(BL) − 1.35 × Log(PL) − 3.23 × Log(LUTR) − 1.06 × Log(WB) + 3.49 × Log(OL) − 3.60 × Log(LM) + 3.98 × Log(LLTR) − 1.90 × Log(LLPC) − 6.94
Otariidae (All Subsets)	6.82 × Log(BL) − (2.11 × PL) − 4.86
Phocidae (Stepwise)	1.35 × Log(PL) − 3.44 × Log(LUTR) − 0.64 × Log(LB) + 4.26 × Log(OCB) − 1.67 × Log(OL) + 2.03 × Log(LM) + 5.15 × Log(LLTR) − 3.78 × Log(LLPC) − 2.16
Phocidae (All Subsets)	1.12 × Log(PL) + 2.48 × Log(OCB) + 2.34 × Log(LLTR) − 2.70 × Log(LLPC) − 0.94
Total length
Otariidae (Stepwise)	2.89 × Log(BL) − 0.74 × Log(PL) − 0.25 × Log(LB) − 0.55 × Log(LB) − 0.09
Otariidae (All Subsets)	1.9 × Log(BL) − 0.66 × Log(PL) + 0.4
Phocidae (Stepwise)	0.15 × Log(BL) + 0.29 × Log(CW) − 0.08 × Log(LB) + 0.88 × Log(OCB) − 0.17 × Log(OL) + 0.22 × Log(LM) − 0.06 × Log(LLTR) + 1.15
Phocidae (All Subsets)	0.37 × Log(CW) + 0.80 × Log(OCB) + 1.39

Table 7.

Support values for multivariate regressions produced using the stepwise method, with the AIC, adjusted coefficient of determination (R²), standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) reported for each regression

	AIC	ad. R2	SE	PPE (%)	SEE (%)
Body mass
Otariidae	−116.5	0.88	0.52	21.72	118.74
Phocidae	−98.03	0.95	0.30	14.30	99.92
Total length
Otariidae	−176.19	0.84	0.04	2.66	10.73
Phocidae	−142.45	0.93	0.06	3.63	16.22

Table 8.

Support values for multivariate regressions produced using the all subsets method, with the BIC, adjusted coefficient of determination (R²), standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) reported for each regression

	BIC	ad. R2	SE	PPE (%)	SEE (%)
Body mass
Otariidae	−24.88	0.87	0.29	18.97	94.48
Phocidae	−98.03	0.92	0.18	13.00	51.62
Total length
Otariidae	−89.02	0.83	0.04	2.66	10.62
Phocidae	−74.03	0.94	0.05	2.83	13.34

For PLS regression, validation plots (Supporting Information Appendix S5) showed that the first component explained the largest decrease in RMSEP. Therefore, for all regressions only the first component was used. The first component explained 78.92–93.81% of the variation within the 14 log₁₀-transformed measurements, and was related to body size. The variance, R², SE, PPE, and SEE for each PLS regressions are presented in Table 9.

Table 9.

The percent variance, adjusted coefficient of determination (R²), standard error (SE), percent prediction error (PPE), and standard error of estimation (SEE) of body mass and total length for Otariidae and Phocidae using partial least squares regression. Estimation of body size occurred within The r package PLS and equations are not included

	Variance explained (%)	adj. R2	SE	PPE (%)	SSE (%)
Body mass – Otariidae	78.92	0.75	0.11	6.00	27.58
Body mass – Phocidae	84.50	0.79	0.16	11.48	50.97
Total length – Otariidae	72.26	0.75	0.03	2.00	7.61
Total length – Phocidae	93.81	0.92	0.05	2.85	13.07

Body size estimates of historically extinct pinnipeds

Estimates of body size for male and female M. tropicalis and male Z. japonicus were calculated using single variable, all-subsets multivariate, and PLS regressions. Because of the high PPE and SEE support values, only total length was calculated for each individual, not body mass. Body size estimates are presented in Supporting Information Appendix S6.

The average total length for males and female M. tropicalis generated by each predictive equation are plotted on Fig. 7A, and compared with a sample of known mean total length (n = 5, 215.8 cm; Allen, 1887; Ward, 1887). Using single variable regressions, estimates of total length varied from 163 to 283 cm. The single best predictor for total length (CW, width across the upper canines) calculated an average total length of 251 cm (range = 237–259 cm) for males and an average length of 202 cm (range = 138–259 cm) for females. Using the single best multivariate regression equation for body size [all-subsets, palate length (PL) and height of the occipital (HOC)], we calculated an average total length of 209 cm (range = 189–229 cm) for males and an average total length of 203 cm (range = 194–207 cm) for females. PLS regression was only performed on a single female Monachus [National Museum of Natural History (USNM) 100371], due to missing measurement data for the length of orbit. A length of ∼233 cm was estimated for this individual.

Figure 7.

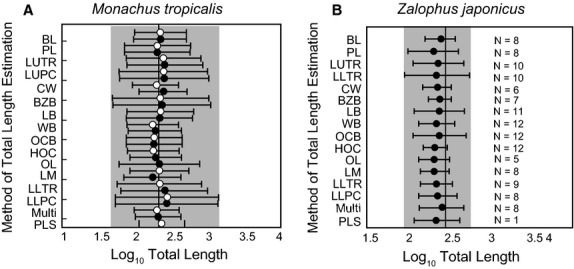
Comparisons of the average estimates of log total length for Monachus tropicalis (left) and Zalophus japonicus (right) for each regression equation, with the known total length of an individual from the literature (vertical line) (Ward, 1887; Itoo & Inoué, 1993). White circles are estimates of average female total length (n = 4) and black circles are estimates of average male total length (n = 4). Sample size for M. tropicalis is four for each sex. Sample sizes for Z. japonicus are listed besides each regression. Estimates are represented by circles, with brackets representing standard error of the estimate calculated for each equation. Estimates using the multivariate regression were calculated using the all subsets equation.

The average total lengths for male Z. japonicus are also listed in Fig. 7B. For single variable regressions, average total length varied from 138 to 248 cm. When we used the single best predictor for total length (LM, length of mandible), we calculated an average total length of ∼212 cm (range = 110–247 cm). Only eight individuals were complete enough to use the all-subsets total length regression equation. If we use the best multivariate predictor [all-subsets, basal length (BL) and palate length (PL)], we calculate an average total length of ∼264 cm (range = 251–277 cm). PLS analysis could only be performed on one specimen [National Museum of Japanese History (HM) 2-97R 60000], and a total length of ∼240 cm was produced. No significant differences in total length of individuals were found between southern and northwestern Hokkaido. Similarly, we observe no significant differences between the 500–800-year-old Aonae site and the 2600–3800-year-old Rebun Island and Funadomari Shell Mound sites.

Discussion

Total length versus body weight

In this study, we assessed whether predictive equations for total length perform better than those produced for body mass, in creating accurate estimates of body size. Total length in general is less prone to seasonal fluctuation, whereas body mass in mammals may fluctuate greatly over the course of a year due to seasonal changes in diet, breeding condition, and ontogeny (Van Valkenburgh, 1990; Pyenson & Sponberg, 2011). These changes in body mass may be even more exaggerated in pinnipeds because many species undergo periods of seasonal fasting related to breeding and molting, and show drastic weight loss on a seasonal basis (Riedman, 1990).

Body mass can also be hard to measure for marine mammals, due to their large body size and the effects of decomposition and sickness on the weight of a stranded animal. Examination of museum material as part of this study has confirmed that body mass data are much less frequently recorded than total length, although often both measures are missing for older specimens. For many of the reasons listed above, Pyenson & Sponberg (2011) only used total length for their predictive equations for estimating body size of fossil whales. Our study supported the conclusions of Pyenson & Sponberg (2011), and found that total length were significantly better than body mass at producing accurate predictions of body size, with total length having smaller PPE and SEE support values. No major differences were found in R² values for either body size proxy.

Although the equations for the estimation of total length produced in this study perform better than those used to estimate body mass, body mass has been the traditional proxy used for body size in evolutionary and ecological studies (Gittleman, 1985; Lindstedt et al. 1986; Damuth & MacFadden, 1990; Johnson, 2002; Rodriguez et al. 2008; Smith et al. 2010; Fitzpatrick et al. 2012). While total length of an organism will be correlated with body mass, the correlation of total length with ecological variables may be less strong. If body mass information is absolutely necessary for a specimen and only an estimate of total length is available, there are ways of converting total length data to body mass data. Trites & Pauly (1998), for instance, using generalized survival models and growth curve data, were able to show a strong linear relationship between total length and body mass, and were able to use this relationship to calculate the mean body mass of 106 extant marine mammals. Using methods similar to these, it should be possible to estimate body mass from total length data.

Single variable predictive equations

When comparing the PPE and SEE values for different variables, predictive equations for otariids performed better than those for phocids. This probably was a result of multiple factors, including sample size (better range of body size present within the dataset of known otariid total length and body mass) and morphological diversity. Otariid cranial shape and morphology are more conservative than those of phocids (Jones & Goswami, 2010), allowing predictive equations to be applied accurately to a range of taxa.

Width across the occipital condyles (OCB) was found to be a poor predictor for body size, with the exception of phocid body mass. However, this measurement has been used as a predictor of body size in whales (Uhen, 2004; Pyenson & Sponberg, 2011) and sea cows (Clementz et al. 2009; Sarko et al. 2010). It has also been suggested to be a good predictor of body size in pinnipeds (Debey & Pyenson, 2013). However, Debey & Pyenson (2013) only examined two other measurements, basal length and length of orbit, and only examined body mass, not total length. Only for phocid body mass is OCB considered within the top four best predictors of body size. The explanation for why OCB is an important predictor of body size in Phocidae but not in Otariidae may be due to differences in sampling and analysis between our study and Debey & Pyenson's. Debey & Pyenson (2013) included walruses within their sample size, a clade excluded from our study, and this may have influenced their results. Furthermore, they also did not account for sexual dimorphism. Doing so increased the number of samples used to generate our regressions. Large differences in R² values were apparent when measurements were averaged across sex (to compare results to the PIC analyses) when compared with analyses that did not average across sex. The influence of sexual dimorphism on the datasets would have a much greater effect on otariids than phocids, and would bias the development or testing of regression equations.

Comparison of multivariate methods

We found little difference in R² values between the stepwise and all-subsets approaches. Both have R² values higher than those recovered for single variable predictive equations. The all-subsets and stepwise approaches also had a R² improved over that reported for PLS, with only slight improvements of R² for PLS over single variable predictive equations. For PPE and SEE, only minor differences were apparent between the three multivariate methods. The only exception was the regression equation for otariid body mass, which showed significant improvement in PPE and SEE for PLS over the other multivariate methods.

The largest difference between the three methods was in the number of variables selected, with the all-subsets approach being the most parsimonious. The difference in number of variables selected between the stepwise and all-subsets approach reflected the difference in variable selection criteria. AIC uses a less harsh penalty than BIC for adding additional variables, which may result in overparameterization of the dataset. The harsher penalty of BIC on the other hand may cause this approach to underestimate the number of variables needed (Burnham & Anderson, 2002). In all cases, the variables selected for the all-subsets were the same as those selected for the stepwise, with the stepwise method selecting additional measurement variables. The R², PPE, and SEE produced using the all-subsets approach were comparable to that of predictive equations employing additional variables produced using the stepwise method. This would suggest that for ease of use and accuracy, the all-subsets approach might be the best method to use for estimating pinniped body size.

Pinniped morphological diversity

Although not a goal of this research, our study found morphometric differences between Otariidae and Phocidae. Our results are congruent with the morphometric landmark analysis of Jones & Goswami (2010) and Jones et al. (2013), which showed that strong differences in cranial shape were related to differences between families. This is confirmed in our study, as both Phocidae and Otariidae clustered separately from one another.

Within families there appears to be little phylogenetic separation. Most otariids showed relatively little variation along the second principal component and cluster tightly. The lack of shape diversity may be related to the geologically young age of the otariid radiation, with most extant taxa only diversifying within the last 5 million years (Yonezawa et al. 2009) and the absence of ecological specialization within the group.

Our study identified greater morphological diversity within Phocidae than Otariidae, consistent with Jones & Goswami (2010). We also found that variation in orbit length varied primarily along the second principal component, as did Jones & Goswami (2010). Debey & Pyenson (2013) also found a much greater degree of variation in proportional orbit length for Phocidae when compared to Otariidae. Unlike the previous studies, our study also found that bullar shape and size contributed significantly to principal component two. The bullae of phocids are more inflated and variable in morphology than the bullae of otariids (Wyss, 1987; Bininda-Emonds & Russell, 1996).

Body size of historically extinct species

Different predictive regression equations for total length yielded different estimates of body size for the extinct taxa examined within this study. The estimated total lengths of M. tropicalis based on width across the canines (CW), the best predictor, were generally far larger than those of historically measured individuals. In contrast, comparing the estimated total length for the multivariate equations with historical values provided a much closer match. Estimates of total length for males (189–229 cm) bracket a historical measurement of 226 cm for this species (Allen, 1887; Ward, 1887). Based on M. tropicalis, the total length estimates produced by the multivariate regression seem to provide the most realistic estimates of body size.

One particular problem that may negatively affect the accuracy of predictive equations for M. tropicalis is the poor representation of Monachus within the dataset, due to the general rarity of monk seals within collections. In addition, our known body mass and total length dataset was biased towards phocine seals, due to the rarity of many taxa within collections (Monachus, Lobodontini). Furthermore, many monachine taxa (e.g. Mirounga) are large in size, making it difficult to collect body mass data for these taxa in the field. This may influence the PPE and SEE, as the PPE and SEE values could reflect the best predictors of body size for phocines, not monachines. Techniques that employ multiple variables may decrease this uncertainty by employing a range of characters with varying degrees of phylogenetic influence. This may explain the better performance of multivariate body size regression in producing reasonable body size estimates for M. tropicalis.

There appears to be no significant sexual dimorphism in estimated body sizes of M. tropicalis. Both extant species of Monachus, M. monachus and M. schauinslandi, show female-biased sexual dimorphism, with females larger than males. This trend is absent both in historical records (Allen, 1887; Ward, 1887; Adam, 2004) as well as the estimates produced here for M. tropicalis. Although all three species of Monachus shared similarities in morphology and ecology, the lack of sexual dimorphism in M. tropicalis suggests that major differences in life history from other Monachus could have existed for this taxon.

Estimation of body size for Z. japonicus indicated total lengths smaller than those of a prior estimate (Itoo & Inoué, 1993). Itoo & Inoué (1993) estimated the total length of a single individual; our analysis suggests that this individual may have been near the upper end of the Z. japonicus size range. While our analysis incorporated more individuals than prior studies that estimated Z. japonicus body size, many of these specimens were difficult to age due to the fragmentary nature of the material preserved. This may have resulted in the inclusion of both adult and immature individuals. This may have biased our body size estimates by incorporating individuals who had yet to achieve maximum adult body size. Similarly, the difference in body size estimates for the best single variable and multivariate equations probably represented differing sample pools, as many of the skulls used for the multivariate estimation lacked mandibles, and some of the mandibles represented isolated, unassociated bones. Finally, Itoo & Inoué (1993) estimated body size by comparing Z. japonicus with Z. californianus. In contrast, our regressions incorporate data from a much wider selection of otariids, and may have less accuracy than regressions or estimates solely based on Zalophus when determining the body size of Z. japonicus.

The material examined for Z. japonicus represented two separate geographic locations on Hokkaido and spanned almost 4000 years, allowing us to examine whether differences in local productivity or food sources may have resulted in differences in Z. japonicus body size. We found no significant differences in total length between different regions and time periods. This suggests that either there were no significant changes in productivity in the region over time or space, or that the changes that did occur did not influence Z. japonicus body size. Alternatively, changes in productivity or food source may have induced minor changes in body size, but our sampling was too coarse or limited to identify any body size trends.

Conclusions

A principal components analysis on the 14 cranial measurements found that otariids and phocids were separated from one another with little overlap, indicating the need for separate sets of body size equations for otariids and phocids. Phylogenetic independent contrasts analyses indicated that phylogeny had a minor influence on the robustness of the allometric equations. Separate sets of equations were produced using multivariate and single variable approaches. Estimates of total length were more accurate than those for body mass, and estimates of otariid body size were more accurate than those for phocids. Comparison of different multivariate techniques revealed the all-subsets method performed the best at predicting body size with the fewest number of variables needed. We used single variable, all-subsets method multivariate, and PLS methods to produce estimates of body size for eight M. tropicalis and 17 Z. japonicus. All-subsets multivariate analysis provided the most accurate estimates of body size for M. tropicalis when compared with historic data. Body size estimates for Z. japonicus are smaller than a prior estimate of Z. japonicus body size, although this may be a result of differences in sampling. This suggests that the estimates of total length provided by the all-subsets regression equations are highly accurate and can provide important information on body size for historical and fossil pinniped material.

Author contributions

M.C.: designed the study and carried out all analyses. M.C. and M.T.C.: wrote the paper. M.C.: and N.K.: collected the measurement data.

Supporting Information

Additional Supporting Information may be found in the online version of this article:

Appendix S3. Cranial measurement data for otariid and phocid taxa.

Appendix S4. R code for multivariate models.

Appendix S6. Body size estimates for Monachus tropicalis and Zalophus japonicus.