Morphometric analysis of variation in the ribs with age and sex

Abstract

Rib cage morphology changes with age and sex are expected to affect thoracic injury mechanisms and tolerance, particularly for vulnerable populations such as pediatrics and the elderly. The size and shape variation of the external geometry of the ribs was characterized for males and females aged 0–100 years. Computed tomography (CT) scans from 339 subjects were analyzed to collect between 2700 and 10 400 homologous landmarks from each rib. Rib landmarks were analyzed using the geometric morphometric technique known as Procrustes superimposition. Age- and sex-specific functions of 3D rib morphology were produced representing the combined size and shape variation and the isolated shape variation. Statistically significant changes in the size and shape variation (P < 0.0001) and shape variation (P < 0.0053) of all 24 ribs were found to occur with age in males and females. Rib geometry, location, and orientation varied according to the rib level. From birth through adolescence, the rib cage experienced an increase in size, a decrease in thoracic kyphosis, and inferior rotation of the ribs relative to the spine within the sagittal plane. From young adulthood into elderly age, the rib cage experienced increased thoracic kyphosis and superior rotation of the ribs relative to the spine within the sagittal plane. The increased roundedness of the rib cage and horizontal angling of the ribs relative to the spine with age influences the biomechanical response of the thorax. With the plane of the rib oriented more horizontally, loading applied in the anterior-posterior direction will result in increased deformation within the plane of the rib and an increased risk for rib fractures. Thus, morphological changes may be a contributing factor to the increased incidence of rib fractures in the elderly. The morphological functions derived in this study capture substantially more information on thoracic skeleton morphology variation with age and sex than is currently available in the literature. The developed models of rib cage anatomy can be used to study age and sex variations in thoracic injury patterns due to motor vehicle crashes or falls, and clinically relevant changes due to chronic obstructive pulmonary disease or other diseases evidenced by structural and anatomic changes to the chest.

Introduction

Thoracic injuries sustained in motor vehicle crashes (MVCs) are a leading cause of mortality, morbidity, and economic cost (Galan et al. 1992; Allen & Coates, 1996; Cavanaugh, 2002; Ruan et al. 2003; Hanna & Hershman, 2009). Injuries to the thorax account for 13% of all minor to moderate injuries, 29% of all serious to fatal injuries, and up to 25% of traumatic deaths (Dougall et al. 1977; Galan et al. 1992; Allen & Coates, 1996; Ruan et al. 2003). MVCs are the leading source of blunt chest trauma (70%), followed by falls (20%), which are more frequent and more harmful in the elderly population (Galan et al. 1992; Adams et al. 2010).

The aging population is a growing concern as the increased fragility and frailty of the elderly results in an elevated incidence of thoracic injuries as well as an increased risk of mortality and morbidity (Burstein et al. 1976; Finelli et al. 1989; Shorr et al. 1989; Zhou et al. 1996; Perdue et al. 1998; Zioupos & Currey, 1998; Bulger et al. 2000; Bergeron et al. 2003; Holcomb et al. 2003; Stawicki et al. 2004; Hanna & Hershman, 2009; Stitzel et al. 2010; Kahane, 2013). In the next 40 years, the USA is projected to experience a rapid growth in its elderly population, with the proportion of adults aged 65+ years in the population increasing from 13% in 2010 to 20% by 2040 (Vincent & Velkoff, 2010). By 2050, the population of persons aged 65+ years is projected to reach 16% globally and 26% in more developed countries (Haub, 2011; U.S. Census Bureau, 2013). The projected increase in the elderly population creates a critical need for further research into the biomechanics of the human thorax with age. Advancements in restraint systems (i.e. airbags, seatbelts, load limiters) have improved vehicle safety; however, the incidence of thoracic injury has been shown in recent studies to increase with age for both belted and unbelted occupants (Hanna & Hershman, 2009). Thoracic injuries are still prevalent in MVCs, especially for particular age groups. Restraint systems that are tailored to account for the biological variation that occurs with age could reduce injuries in vulnerable populations such as pediatrics and the elderly.

Normal pediatric rib cage anatomy has been previously characterized in several studies using select X-ray and computed tomography (CT) measurements (Haller et al. 1987; Derveaux et al. 1989; Daunt et al. 2004; Comeau, 2010; Sandoz et al. 2013). Kent et al. (2005) found a significant age effect on rib angles measured in the sagittal plane from 161 males of ages 18–89 years (Kent et al. 2005). The ribs were found to become more perpendicular to the spine as age increased, with the rib angle of the ninth rib increasing from 50° in an 18-year-old to 57° in an 89-year-old. Gayzik et al. (2008) quantified age-related shape changes in the rib cage using a geometric morphometric technique known as Procrustes superimposition to analyze 106 rib cage landmarks from 63 normal adult males (Slice, 2005; Gayzik et al. 2008). That study found a significant quadratic relationship between the landmark locations and age that resulted in shape changes such as increased kyphosis and rounding of the rib cage with aging. Increased kyphosis of the thoracic spine with age has been well established in other studies (Milne & Williamson, 1983; Puche et al. 1995; Korovessis et al. 1998; Goh et al. 2000; Hammerberg & Wood, 2003; Vafa, 2012). Respiratory system changes with age result in increased chest wall stiffening, declining vital lung capacity, and decreased respiratory muscle strength that likely have an effect on the thoracic skeleton geometry (Campbell & Lefrak, 1978).

Rib cage geometry and material property data have been used to create thoracic finite element (FE) models representative of specific ages for measuring the thoracic response to impact (Kent et al. 2005; Ito et al. 2009; El-Jawahri et al. 2010). Kent et al. (2005) altered rib angles, cortical bone thickness, and bone material properties to create FE models representative of a ‘young’ versus ‘old’ thorax. In FE simulations, the structural versus material property changes had approximately equivalent effects on the force-deflection response of the thorax. Ito et al. (2009) and El-Jawahri et al. (2010) used geometrical measurements from Kent et al. (2005) and Gayzik et al. (2008), as well as material property data from the literature to create thoracic FE models representing a 35-year-old male and a 75-year-old male. Age- and sex-specific models of normal rib cage anatomy can be used to better understand the mechanisms of thoracic injury and how factors such as age and sex affect injury incidence and outcome.

Previous studies that have characterized or modeled pediatric and adult rib cage anatomy are limited in that geometrical changes were quantified using select landmarks or measurements that were often manually collected. The three-dimensional (3D) changes in the rib cage have not been fully characterized and are important for creating models of normal rib cage anatomy. Furthermore, the full spectrum of ages was not investigated in any previous study and females in particular are under-represented. Merging and comparing data from independent studies of pediatric versus adult rib cage geometry is difficult as the measurements and landmarks collected vary between studies. Thus, there is a need for high resolution data that accurately describe the 3D rib cage geometry for males and females across the entire age spectrum (age 0–100 years). These morphometric data could be used to create thoracic FE models representative of particular ages and sexes to study the effects of age and sex on thoracic injury risk. These data could also be used in statistical models, as the inclusion of morphometric variables in addition to vehicle and demographic variables has been shown to improve the predictive power of thoracic injury risk models (Zhang et al. 2013).

The objective of the current study was to quantify size and shape variation in the ribs for males and females aged 0–100 years. This goal was accomplished through the following specific methods:

1. Collection of high resolution homologous landmark data from the ribs of 339 subjects.

2. Geometric morphometrics analysis of rib landmarks using Procrustes superimposition (Slice, 2005).

3. Regression and statistical analysis of landmark data to produce functions of individual rib morphology variation with age and sex.

4. Location and orientation of the individual rib results within the full rib cage to produce age- and sex-specific models of rib cage morphology.

One hypothesis of the study is that the ribs undergo size and shape changes, as well as isolated shape changes, with age and that these changes are statistically significant. Rib geometry, location, and orientation are expected to vary according to age, sex, and rib level. The size of the rib cage is expected to increase during pediatric development. Thoracic kyphosis is expected to increase from young adulthood to elderly age. From young adulthood into elderly age, the ribs are expected to become angled more perpendicular to the spine in the sagittal plane, resulting in increased roundness of the rib cage in the elderly. Both sexes are expected to experience these age-related trends in rib cage morphology, but the rib cage size and shape are also expected to vary between the sexes. A major outcome of this study will be development of functions that describe age- and sex-specific rib cage morphology to a high degree of detail based on 3D rib landmark locations.

Methods

Homologous landmark collection

Homologous rib landmarks that were in comparable locations on each subject were collected by applying a semi-automated image segmentation and registration algorithm to analyze 339 normal chest CT scans of males and females aged 0–100 years. The analyzed scans were de-identified to protect patient confidentiality and Institutional Review Board (IRB) approval was obtained for the study. The homologous landmark collection technique included image segmentation, atlas development, and image registration. The 24 ribs were segmented from the CT scans of each subject using automated bone threshold and region growing operations in conjunction with manual editing to define the external geometry of each rib. Only fully ossified bone in the ribs was included in the segmentation and cartilaginous structures including calcified cartilage were excluded. A rib cage atlas containing the 24 ribs was developed from existing computer-aided design (CAD) geometry of a 50th percentile male thorax (Gayzik et al. 2011). Although the average percentile of the males and females in the study population may not reflect a 50th percentile male size, the atlas was selected because it was an existing, smoothed geometry that could be used for the analysis of every subject, allowing for age- and sex-based comparisons to be made. The rib cage atlas consisted of a stereolithography (STL) model and Neuroimaging Informatics Technology Initiative (NIfTI) binary images created from the existing CAD geometry. Grids of homologous landmarks were placed on each atlas rib at an even spacing of 1.7 mm. Depending on the surface area of the rib, between 2769 (12th rib) to 10 351 (sixth rib) landmarks were placed per rib. The rib cage atlas geometry and landmarks were symmetric about the median plane. An image registration algorithm that applied rigid, affine, and symmetric diffeomorphic transformations was used to register the NIfTI images of the respective rib atlas to binary NIfTI images of each subject's segmented rib. A symmetric image normalization transformation model (SyN) paired with a cross-correlation similarity measure was used in the symmetric diffeomorphic registration, which has been shown to provide consistent, robust, and accurate results for different subjects and anatomical structures (Avants et al. 2008; Klein et al. 2009). Following image registration, custom matlab code (The Math Works, Natick, MA, USA) was used to apply the registration transformations to morph the point cloud of rib atlas landmarks to each subject rib. This effectively transformed the landmarks on each rib atlas to homologous locations on each subject rib. The segmentation and registration algorithm resulted in successful collection of homologous landmarks from 92% of the available subject ribs and the remaining 8% of the subject ribs were excluded due to lower registration quality. Thus, homologous landmarks were not collected from all 24 ribs in some subjects. Homologous landmarks were collected from a total of 7077 ribs with 2769–10 351 homologous landmarks collected per rib. Over 53 million landmarks representing the external rib geometry were collected across all subjects to be utilized in geometric morphometric analysis.

Generalized Procrustes analysis

Rib morphology was quantified from the homologous landmark data using a geometric morphometrics technique known as Procrustes superimposition (Slice, 2005). Procrustes superimposition is a least-squares method to estimate location and orientation parameters that minimizes the sum of the squared distances between homologous landmarks in two or more different configurations. The comparison of more than two structures with a mean configuration is known as the generalized Procrustes analysis (GPA) and is used widely in geometric morphometric studies of anthropology and anatomy (Bookstein et al. 1999; Weber et al. 2001; Slice & Stitzel, 2004; Slice, 2005; Danelson et al. 2008; Gayzik et al. 2008; Neubauer et al. 2009).

Subject ribs of a given level and laterality were grouped into sex-specific samples. The GPA was used to fit the configurations of all ribs in a given sample to a mean configuration to minimize the sum of the squared deviations of the sample configurations around the mean configuration (Gayzik et al. 2011). The respective rib atlas was initially input as the reference mean configuration and the sample configurations were fit to this mean. The mean of the superimposed sample configurations was then iteratively computed until convergence to the grand mean of the sample (Slice, 2005). A full Procrustes analysis applies translation, rotation, and scaling to find the least-square solution that minimizes the distance between homologous landmarks in different configurations (Dryden & Mardia, 1998). A full Procrustes analysis was used to isolate the rib shape changes by applying scaling to remove any size effects. A partial Procrustes analysis was also conducted in which scaling was not performed and the size of the ribs was preserved, allowing for the quantification of the combined size and shape changes in each rib.

The full GPA matrix equation provided in Eqn 1 was used to isolate the shape difference, E, between the mean configuration and each rib in the sample (Slice, 2005). The number of subjects in the sample used for the GPA is defined as n and the number of landmarks for a particular rib is defined as k. An n × (k × 3) matrix, X₁, contains the homologous landmarks of each subject rib in the sample. This matrix consists of one row for each subject, with the coordinate triplets for each landmark concatenated in a single row. An n × (k × 3) matrix, X₀, contains the homologous landmarks of the mean configuration with identical (k × 3) matrices for every n. Each of the following matrices contain an entry for each subject in the sample, where t is the translation matrix that mean centers each sample configuration, H is a rotation matrix, and CS is the centroid size, an isometric scaling factor. The centroid size is a descriptor for the size of a rib and is calculated as the square root of the sum of the squared rib landmark coordinate values in all dimensions (Eqn 2). To quantify the combined size and shape changes, a partial GPA was also performed in which scaling was not applied. An n × (k × 3) matrix, X, with the translated, rotated, and/or scaled homologous landmark locations of each subject rib in the sample was output using the full GPA (Eqn 3) and partial GPA (Eqn 4).

(1)

(2)

(3)

(4)

The GPA was conducted using in-house software developed using matlab. The GPA was performed for each rib of a given level and laterality on a per-sex basis using subjects from the entire age spectrum (0–100 years). For example, the GPA was applied to analyze the homologous landmarks collected from the right first rib of all males to quantify (i) the size and shape changes (partial GPA) and (ii) the shape changes (full GPA). Thus, the GPA was applied 96 separate times in this study to produce (i) size and shape (partial GPA) and (ii) shape (full GPA) results for each of the 24 ribs in each sex [2 GPA techniques (full and partial) × 24 ribs × 2 sexes].

Landmark regression equations and statistical analysis

The resulting matrix of landmark locations, X, output from the GPA was used to calculate landmark regression equations relating landmark location to age (Eqns 5–7). An n × 4 age matrix, A, is calculated using Eqn 5, where age is an n × 1 matrix of the subjects' ages. The age matrix defines the regression model fit to the data and several regression fits including linear, quadratic, and higher-order polynomial functions were investigated in this study using an optimization software package (tablecurve 2d, Systat Software, Inc., San Jose, CA, USA). The regression model in Eqn 5 was selected because it provided a good fit to the landmark data (higher R² value) and produced smoother rib geometries that captured some local morphology changes. Some of the higher-order polynomial functions captured very small local morphology changes, resulting in rougher geometries, whereas lower-order functions (i.e. linear and quadratic) produced smooth geometries but poorer data fits. The matrix regression coefficients, β, are used to calculate the predicted landmark locations, X_p using Eqn 7, where age is in years and β₁–β₄ are the regression coefficients. A landmark regression equation was computed for each of the 96 GPA outputs, resulting in a total of 96 regression equations that describe the location of the homologous rib landmarks for particular ages and sexes. This produced four regression functions for each rib representing the size and shape variation with age for (i) males and (ii) females and the shape variation with age for (iii) males and (iv) females.

(5)

(6)

(7)

Permutation tests were used to assess the statistical significance of the landmark regression equations describing rib morphology. Due to the large number of variables (landmark regression coefficients), traditional statistical methods are not appropriate. The permutation test evaluates how many random combinations of the regression coefficients (termed ‘random combination models’) are better predictors of landmark location than the regression model (Gunz et al. 2005). The permutation test computes a test statistic, λ', representing the sum of the variance of the regression model. This is compared to the sum of variance, λ, of each random combination model. The number of permutation test loops was set to 100 000, such that 100 000 different random combination models were computed for the sum of variance comparison with the regression model. The null hypothesis of the permutation test is that no relationship exists between subject age and landmark location in the rib of interest. Statistical significance (P < 0.05) is reached if < 5% of the random trials have a sum of variance less than the regression model. A P-value < 0.05 results in rejection of the null hypothesis, indicating statistically significant changes in rib morphology occur with age.

Location and orientation of the individual ribs within the rib cage

The landmark regression equations were evaluated for the following ages to produce the resulting geometries of the 24 ribs for each specified age and sex: 0, 3, 6, 9 months, and 1–100 years in 1-year increments. Since the GPA was conducted on an individual rib basis, a separate analysis was necessary to reconstruct the full rib cage and locate and orient the individual ribs relative to each other. The rib cage from each subject is initially defined in a subject-specific coordinate system with a unique origin. Each subject-specific coordinate system is unique and is different from the coordinate system and origin of the atlas used in the registration algorithm to collect landmarks (Fig. 1a). The steps to locate and orient the individual ribs involved: (i) alignment of the subjects and the atlas to a global coordinate basis, (ii) alignment of each atlas rib and subject rib to a local coordinate basis, (iii) regression of rib translation and rotation parameters to describe the location and orientation of each rib with age relative to the global and local coordinate bases, and (iv) evaluation of the regression functions to translate and rotate the individual ribs to the appropriate 3D location for particular ages and sexes. Evaluation of the sex-specific regression functions for particular ages preserved information from the subject population regarding the location and orientation of the individual ribs within the full rib cage model. Thus, the full rib cage models produced could be used to quantify size and shape variation of the entire rib cage with age and sex.

Figure 1.

(a) Example of the initial difference in coordinate systems for one subject and the atlas. (b) Posterior view of the right and left sixth ribs (R6 and L6) and the right seventh rib (R7) of the atlas. The landmarks selected on the posterior head of the three ribs to define the global coordinate basis are depicted as white points (R6-P, L6-P, and R7-P). The origin was defined as the midpoint between the posterior landmarks on the sixth ribs and is depicted as a black point. Three landmarks located anteriorly, laterally, and posteriorly on R7 that were used to define a local rib coordinate basis are also depicted as white points (R7-A, R7-L, and R7-P). (c) Right side view of the subject from (a) and the atlas after global alignment to the SAE J211 coordinate basis.

Alignment of the subjects and the atlas to a global coordinate basis

A global coordinate basis was defined for each subject and the atlas using three homologous landmarks selected from the posterior heads of the right and left sixth ribs (R6 and L6) and either the right or left seventh rib (R7 or L7). Subjects with collected homologous landmarks for the left and right sixth ribs and a seventh rib met the inclusion criteria for the analysis to locate and orient the ribs. In total, 145 male subjects and 154 female subjects met the inclusion criteria and these were stratified by sex in all analyses to produce sex-specific results. A total of 40 subjects were excluded from the analysis to locate and orient the ribs because in these subjects, homologous landmarks were not collected for all three ribs used for global alignment (left and right sixth ribs and a seventh rib). These 40 subjects had homologous landmarks collected for the majority of the ribs in the rib cage, but registration algorithm insufficiencies prevented homologous landmark collection from select ribs (termed ‘missing ribs’). The ‘missing ribs’ only prevented these 40 subjects from being included in the analysis to locate and orient the ribs, but homologous landmarks that were collected from the ribs of these 40 subjects were incorporated in all other analyses, including the GPA.

An example of the global coordinate basis that uses the R6, L6, and R7 posterior landmarks is illustrated in Fig. 1b. The vector, <L6-P, R6-P>, was used to define one axis of the coordinate basis (i). A second vector, <R7-P, R6-P>, was defined within the global plane created by the three landmarks. The cross product of vectors <L6-P, R6-P> and <R7-P, R6-P> was computed to define the j axis of the global coordinate basis. Finally, the cross product of i and j was computed to define the k axis of the global coordinate basis. The origin of the global coordinate system was defined as the midpoint between the posterior landmarks on the sixth ribs. This global coordinate basis was defined for each subject in the analysis as well as for the atlas. A translation operation was applied to align each subject and the atlas with the origin of the standardized anthropomorphic test device (ATD) coordinate system defined by SAE J211 (Society of Automotive Engineers, 2007). A rotation operation was then applied about the origin for each subject and the atlas to align the ijk axes of the global coordinate basis with the ijk axes of the SAE J211 standard coordinate basis. Following the translation and rotation operation, each subject and the atlas were considered to be aligned with the SAE J211 coordinate system (Fig. 1c).

Following this global alignment, all methods described from this point forward focused on the right side of the rib cage only. To simplify the reporting of the results and ensure that the resulting rib cage models were symmetric, the results of the GPA and landmark regression equations for the right rib cage were mirrored about a median plane to produce the full rib cage. The median plane was defined by three midpoints calculated from homologous landmarks on the (i) posterior left and right first ribs, (ii) posterior left and right sixth ribs, and (iii) anterior left and right sixth ribs. Of note, the same analysis was conducted using the left side of the rib cage and similar results were produced (results not reported).

Alignment of each atlas rib and subject rib to a local coordinate basis

Once the subjects and the atlas were aligned to the SAE J211 coordinate system, rib location and orientation information could be determined. Three landmarks were selected on each right rib of the atlas at anterior, lateral, and posterior locations. For each subject, the homologous landmark locations of the anterior, lateral, and posterior landmarks on each of the 12 right ribs were obtained. These homologous landmarks were defined with respect to the SAE J211 coordinate system, as subject alignment was performed in the previous step.

The anterior, lateral, and posterior landmark locations were analyzed for all subjects to quantify the location and orientation of the ribs relative to each other with age and sex. A local rib coordinate basis (lmn) was calculated for each rib on the atlas and each subject using the anterior, lateral, and posterior landmarks (Fig. 1b). The vector from the posterior to anterior points, <R7-A, R7-P>, was used to define one axis of the coordinate basis (l). A second vector from the posterior to lateral points, <R7-L, R7-P>, was defined within the plane created by the anterior, lateral, and posterior points. The cross product of vectors <R7-A, R7-P> and <R7-L, R7-P> was computed to define the n axis of the coordinate basis. Finally, the cross product of l and n was computed to define the m axis of the coordinate basis.

The local rib coordinate basis was used to calculate a rotation matrix about the posterior landmark (Eqn 8) that aligned the atlas local rib coordinate basis to each subject local rib coordinate basis (e.g. the rotation matrix necessary to align the R7 atlas lmn coordinate basis with the R7 lmn coordinate basis of subject #1 etc.). This rotation matrix was then decomposed into three Euler angles representing rotations about the l, m, and n axes. These Euler angles were calculated with Eqns 9–11 in matlab.

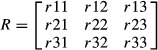(8)

(9)

(10)

(11)

Regression of rib translation and rotation parameters to describe the location and orientation of each rib with age relative to the global and local coordinate bases

The x, y, and z-coordinates of the posterior landmark of each right rib with respect to the origin of the SAE J211 coordinate system were regressed with age using Eqns 5–7. In these equations, age is an n × 1 matrix of the subjects' ages and X is a global n × (1 × 3) landmark data matrix containing the posterior landmark x, y, and z-coordinates. The three Euler angles for each subject that were derived from the decomposition of the rotation matrix previously were regressed with age using Eqns 5–7. In these equations, age is an n × 1 matrix of the subjects' ages and X is a global n × (1 × 3) landmark data matrix containing the three Euler angles (θ_l, θ_m, and θ_n). Separate regression equations were computed for each sex. These regression equations describe, for each sex, how the location and orientation of a particular rib changes with age relative to the atlas configuration.

Evaluation of the regression functions to translate and rotate the individual ribs to the appropriate 3D location for particular ages and sexes

The sex-specific regression equations were evaluated for the following ages: 0, 3, 6, 9 months, and 1–100 years in 1-year increments. To generate a right side rib cage model representing the size and shape variation that occurs with age and sex, the results of the posterior rib landmark and Euler angle regressions were applied to translate and rotate the GPA results for individual ribs to appropriate 3D locations for particular ages and sexes. The rotation of the individual ribs was accomplished by composing a rotation matrix from the results of the three Euler angle regressions using Eqn 12. This rotation matrix, R_p, oriented the ribs in 3D by applying sequential rotations about the l, m, and n axes, respectively. A full rib cage model of the size and shape variation was then produced by mirroring the right side rib cage model about the median plane.

(12)

where

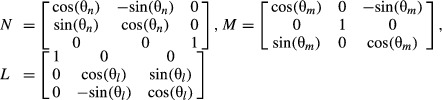To generate a full rib cage model representing just the shape variation that occurs with age and sex, the GPA results for the individual ribs were first scaled using the centroid size of the corresponding rib in the atlas. For example, the first rib shape variation results for every age and sex were scaled to have a centroid size equivalent to the first rib of the atlas. As the atlas was created from a 50th percentile male subject, the centroid size scaling resulted in rib cage models scaled to the 50th percentile male thorax size (Gayzik et al. 2011). For each age and sex, the 12 right ribs were then translated so that the y- and z-coordinates of the posterior landmark location of each rib were equivalent to the location of the homologous posterior landmark in the atlas rib. This ensured that the chest width and height was approximately consistent across all ages. In the x-direction, the 12 right ribs were translated using a normalized version of the x-coordinate of the posterior landmark regression. The x-coordinate from the posterior landmark regression equation was normalized by multiplying by the ratio of the centroid sizes of (i) the atlas rib and (ii) the rib in the size and shape model for a particular age and sex. The normalized x-coordinate of the posterior landmark was used to translate each rib in the anterior-posterior (x) direction within the full rib cage model. The centroid size scaling, translation of each rib to a standard y- and z-coordinate, and translation of each rib in the anterior-posterior direction using a distance scaled by centroid sizes ensured that size effects were not introduced into the rib cage shape models. By applying different translations in the anterior-posterior direction, differences in thoracic kyphosis with age can be quantified. Finally, the results of the regressions of the Euler angles were applied to rotate the GPA results for individual ribs to appropriate 3D locations within the right side rib cage shape model using Eqn 12. The regressions that quantified the rotation of the ribs within the right side of the rib cage are a characterization of the shape variation and do not introduce any size effects into the results. The right side rib cage model was mirrored about the median plane to produce a full rib cage model that represents just the rib cage shape variation for particular ages and sexes.

Results

Study population

The study population consisted of 168 males and 171 females ranging in age from 0 to 97 years (Fig. 2). Height and weight measurements near the CT scan date were collected from 45 and 69% of the subjects, respectively. Height and weight measurements were considered to be near the scan date if measured within 2 weeks of the scan date for ages less than 1, within 1 month of the scan date for ages 1–20, and within 1 year of the scan date for ages 20+. A range of heights and weights were observed in the pediatric and adult study populations (Fig. 2).

Figure 2.

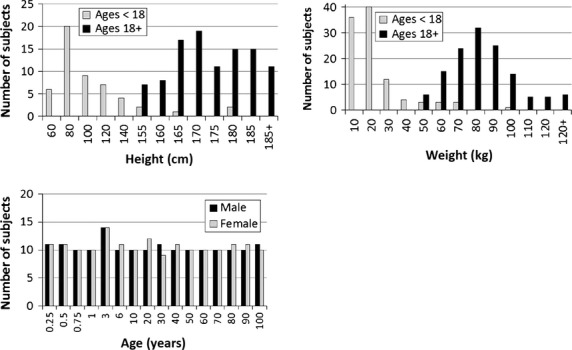
Distribution of height, weight, and age among the study population. In each plot the x-axis bin label corresponds to the upper value of the bin. The subjects are stratified into pediatric and adult age groups (< 18 versus 18+) for the height and weight plots and by sex for the age plot.

Height, weight, and body mass index (BMI) measures in the pediatric population (ages less than 18 years) followed similar trends as pediatric growth charts for 50th percentile males and females (National Center for Health Statistics, 2000). The median height and weight for adult (ages 18+) males was 179 cm (interquartile range, IQR: 173–183 cm) and 83.5 kg (IQR: 74.0–96.1 kg). This median height and weight represent approximately a 70th percentile male as opposed to the 50th percentile male (175 cm, 77.7 kg) that is often used to approximate the average male (Gordon et al. 1989). The median height and weight for adult females was 163 cm (IQR: 157–168 cm) and 68.7 kg (IQR: 59.5–79.6 kg). This median height corresponds to a 50th percentile female (163 cm, 61.3 kg) but the median weight is higher and corresponds to approximately an 80th percentile female (Gordon et al. 1989). The median BMI (in kg m⁻²) for adult males and females was 26.4 and 25.1, respectively (IQR: 24.1–30.7 for males and 22.1–29.8 for females). The correlation between BMI and age in adults was very low (R² = 0.01).

Landmark regression equations and statistical analysis

Landmark regression equations were produced for every rib landmark and the compilation of the regression equations for every landmark in a rib describes how the rib's geometry changes with age and sex. Four regression functions were computed for each of the 24 ribs representing the size and shape variation with age for (i) males and (ii) females and the shape variation for (iii) males and (iv) females. The landmark regressions for the combined size and shape changes in the individual ribs were statistically significant with age in males and females for all 24 ribs (P < 0.0001 for all ribs). The landmark regressions for the isolated shape changes in the individual ribs were statistically significant with age in males and females for all 24 ribs (P < 0.0001 for all male ribs and ribs 1–11 in females; P = 0.0053 and 0.0004 for the left and right 12th female ribs, respectively). The permutation test results indicate that the landmark regression equations are better predictors of rib morphology compared to at least 95% of the random combination models and each of the individual 24 ribs in both sexes undergo significant combined size and shape, as well as isolated shape changes with age. An example of the permutation test results for the shape changes in the right 12th female rib is provided in Fig. 3.

Figure 3.

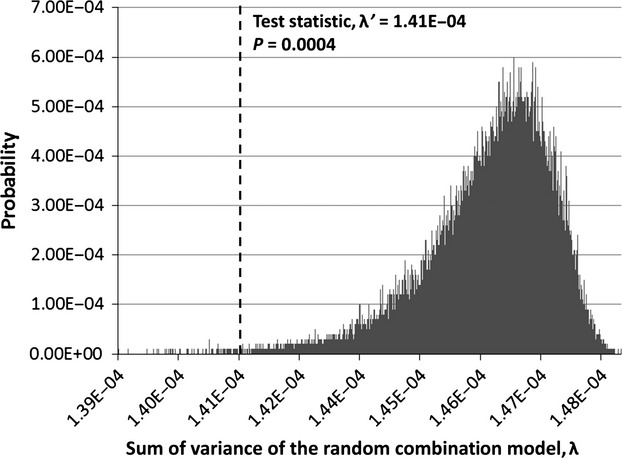
Permutation test results for the shape changes in the right 12th female rib. The dotted line represents the test statistic, λ'. Areas to the left of the test statistic line represent cases where the random combination model had a better (lower) sum of variance, λ, than the regression model. Areas to the right of the test statistic line represent cases where the regression model had a better (lower) sum of variance, λ, than the random combination model. In this example, the sum of the probabilities to the left of the line (P = 0.0004) indicated that only 0.04% of the random combination models had a lower sum of variance than the regression model. Thus, the null hypothesis should be rejected and significant shape changes occur in the right 12th female rib with age.

Rib location and orientation results

Results for the right ninth male rib posterior landmark coordinates and Euler angles are provided in Fig. 4 with individual subjects plotted along with the regression line. Coefficients and R² values for the regression equations for the posterior landmark location and Euler angles are provided in Supporting Information Tables S1 and S2 for the right ribs of males and females (see Eqn 7 for form of the regression equation). The Euler angles about the l-axis have improved R² values compared with all the Euler angles about the n-axis and about half of the Euler angles about the m-axis, which may be due to the sequence of the Euler angle rotations.

Figure 4.

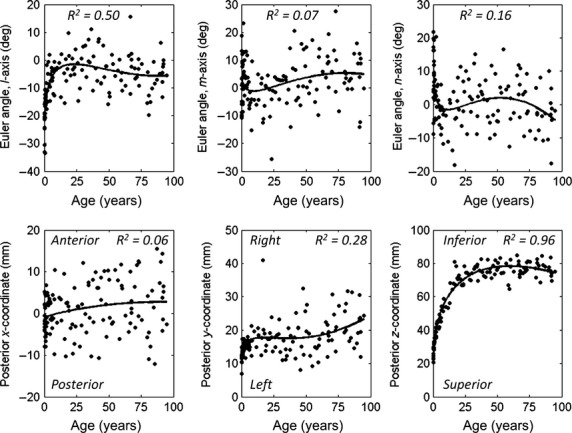
Results for the right ninth male rib (R9M) with individual subjects plotted along with the regressions fit to the data. Euler angles about the l, m, and n-axes (top plots) are regressed with age. Euler angles are relative to the local rib coordinate system of the atlas. The x, y, and z location of the posterior rib landmark relative to the global SAE J211 coordinate system (bottom plots) are regressed with age. Trend lines illustrating the regression are plotted.

In general, the posterior landmark coordinates increased in magnitude from birth through adolescence, indicating the increasing size of the rib cage during development. The x-coordinate regressions indicated an increase in thoracic kyphosis with age, with the posterior rib of upper ribs 1–5 and some of the lower ribs 7–12 moving in the anterior direction relative to the origin at the posterior sixth rib. The y-coordinate regressions indicated an increase in lateral chest width with age. The z-coordinate regressions indicated an increase in superior-inferior chest height with age. The z-coordinate regressions had the highest R² values, indicating that the expansion in chest height is highly correlated with age. Since the x, y, and z-coordinate regressions are computed in reference to the global origin at the sixth thoracic vertebra, the R² values for the x- and z-coordinate regressions (anterior-posterior and superior-inferior directions) were higher for ribs further from the origin (ribs 1–3 and 10–12), whereas the R² values for the y-coordinate regressions (lateral direction) were higher for ribs near the origin (ribs 4–7).

The Euler angles represent the rotation about the l, m, and n-axes of a local rib coordinate system. Euler angles are relative to the orientation of the l, m, and n-axes of the local rib coordinate system defined for the atlas rib. Thus, for a rib oriented with the atlas rib, the Euler angles are all equal to zero. To illustrate the rotational effect of each Euler angle, the Euler angle regressions were evaluated for the right ninth male rib for ages 20 and 90 (Fig. 5). The Euler angle about the l-axis becomes more negative with age (−1.56° at age 20 versus −5.64° at age 90), resulting in rotation of the rib in the superior-medial direction (Fig. 5a). The Euler angle about the m-axis becomes more positive with age (−0.25° at age 20 versus 5.21° at age 90), resulting in rotation of the rib in the superior direction (Fig. 5b). The Euler angle about the n-axis becomes more negative with age (−0.87° at age 20 versus −3.19° at age 90), resulting in rotation of the rib in the medial direction within the local rib plane defined by the anterior, lateral, and posterior landmarks (Fig. 5c). The resulting configurations when applying all three Euler angle rotations to the right ninth male rib for the 20- and 90-year-olds are displayed in Fig. 5d.

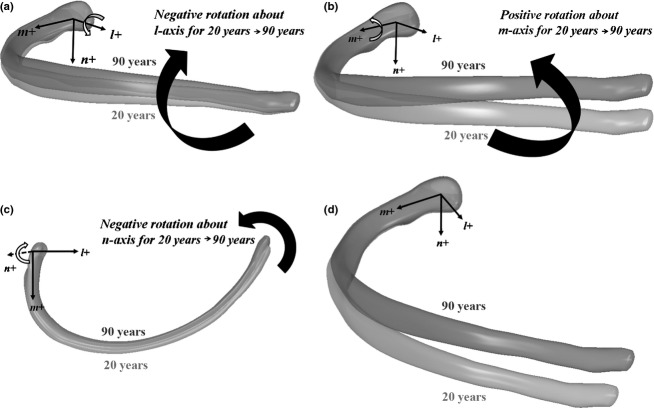
Figure 5.

Euler angle results for the right ninth male rib. (a) Euler angle about the l-axis changes from −1.56° at age 20 to −5.64° at age 90, resulting in rotation of the rib in the superior-medial direction. (b) Euler angle about the m-axis changes from −0.25° at age 20 to 5.21° at age 90, resulting in rotation of the rib in the superior direction. (c) Euler angle about the n-axis changes from −0.87° at age 20 to −3.19° at age 90, resulting in rotation of the rib in the medial direction within the local rib plane defined by the anterior, lateral, and posterior landmarks. (d) Resulting configurations of the 20- and 90-year-olds when applying all three Euler angle rotations to the right ninth male rib.

Rib cage morphometric changes with age and sex

Size and shape morphometric changes

The rib cage models illustrating the size and shape morphological changes for males of select ages ranging from 6 months to 100 years are depicted in Fig. 6. A visible increase in the overall size of the rib cage is evident from 6 months to 20 years of age in males. A slight increase in rib cage size is observed from age 20 to 30, but rib cage size appears fairly constant for ages 30–100. There are also visible shape changes that occur with age, particularly for the angle of the ribs relative to the spine and the kyphosis of the spine. Similar trends were observed in females (not plotted).

Figure 6.

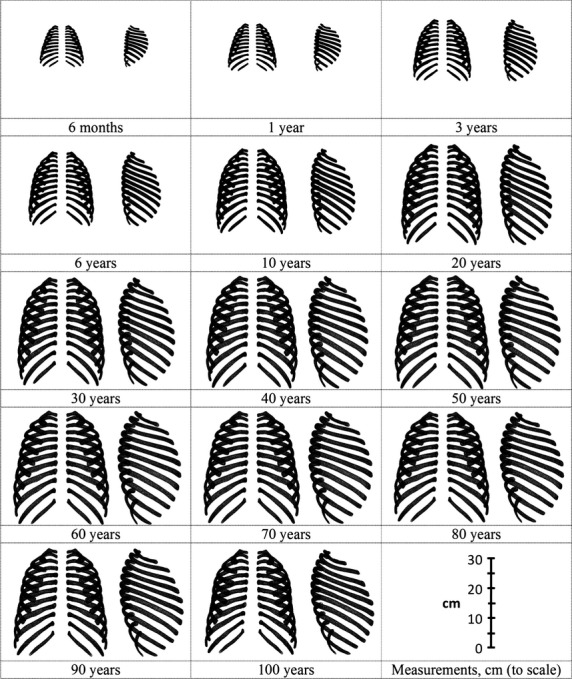
Rib cage models illustrating the size and shape changes in males.

The maximum height of each rib cage model was measured in the superior-inferior direction (Fig. 7). The depth and width of the rib cage models were measured at the level of the posterior head of the third, fifth, seventh, and ninth ribs in the anterior-posterior and lateral directions using techniques adapted from the literature (Bellemare et al. 2003; Bertrand et al. 2008; Sandoz et al. 2013). The average of the anterior-posterior and lateral dimensions from all four rib levels are reported in Fig. 7. The thoracic index was calculated as the ratio of the average anterior-posterior and lateral measurements (Fig. 7). Figure 7 illustrates the increase in the size of the rib cage in all three dimensions from birth until approximately age 30. After age 30, the rib cage dimensions become more constant, with the anterior-posterior and lateral dimensions increasing slightly from age 30 to 60 and then decreasing after age 60. The thoracic index decreased from infancy through early childhood and then began to increase. The thoracic index increases steadily from age 20 to 70 before increasing sharply in the elderly females. The increasing thoracic index in the elderly females may be indicative of increased rounding of the rib cage referred to as ‘barrel chesting’ (Oskvig, 1999). If the thoracic index is calculated differently using the maximum anterior-posterior and lateral dimensions from the entire rib cage, the thoracic index remains fairly constant for ages 20–70, but increases sharply in elderly males and females, indicating increased rounding of the rib cage in both sexes.

Figure 7.

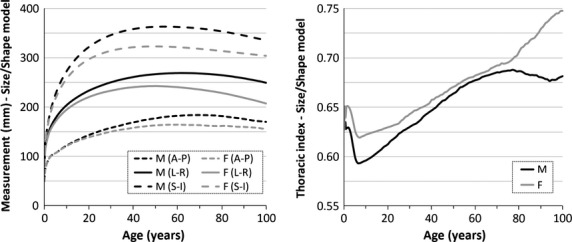
The average anterior-posterior rib cage depth (A-P) and lateral rib cage width (left-right dimension, L-R) from measurements collected at the level of the posterior third, fifth, seventh, and ninth ribs. The superior-inferior rib cage height (S-I) measurements and the thoracic index calculated as the ratio of the A-P and L-R measurements. All measurements were collected from rib cage size and shape models and are plotted for males (M) and females (F) with respect to age.

Shape morphometric changes

In Fig. 8, centerlines of the longitudinal axis of the right ribs from the shape models are overlaid for select ages ranging from 6 months to 90 years. For the shape models, size is controlled for through centroid size scaling techniques. The angle of the ribs relative to the spine in the sagittal plane and the kyphosis of the thoracic spine vary visibly with age.

Figure 8.

Overlaid centerlines of the right rib shape models for select ages. The change in the angle of the rib relative to the thoracic spine in the sagittal plane with age is indicated by the anteriorly located arrows with gray shading. The change in thoracic kyphosis with age is indicated by the posteriorly located arrows.

The x-coordinate of the posterior rib landmark of each rib after normalization using centroid size scaling techniques varies with age, indicating changes in the kyphosis of the thoracic spine as the posterior aspect of the rib is moving anteriorly relative to the global origin near the sixth thoracic vertebra (Figs 8 and 9). The upper rib (first and third ribs) trends indicate decreasing upper thoracic spine kyphosis from birth through adolescence, followed by increased kyphosis after age 20 with a more dramatic increase for females than males. The lower rib (ninth and 11th ribs) trends also show an increase in lower thoracic spine kyphosis with age, especially for males. Less dramatic changes in kyphosis are observed for the fifth and seventh ribs because these ribs are near the origin at the sixth thoracic vertebra.

Figure 9.

The posterior x-coordinate normalized by the centroid size ratio and used to locate the ribs in the shape models for males (upper left) and females (upper right) is plotted versus age. A larger x-coordinate indicates movement of the posterior aspect of the rib in the anterior direction relative to the sixth thoracic vertebra. The change in the Euler angles about the m-axis and l-axis relative to the respective Euler angle for a 6-month-old is plotted versus age for males (middle and lower left) and females (middle and lower right). For these plots, each Euler angle for a 6-month-old was normalized to zero and the change in the Euler angle between the 6-month-old and each specific age is plotted (i.e. the difference in the first rib Euler angle about the m-axis between a 6-month-old male and 40-year-old male is −14.44°). In these plots, the markers are used to plot specific ages: 6 months, 1, 3, 6, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 years. Results are reported for right ribs 1, 3, 5, 7, 9, and 11 (curves labeled as R1, R3, R5, R7, R9, and R11).

The Euler angle about the m-axis is an approximate representation of the angle of the rib relative to the thoracic spine in the sagittal plane (Fig. 5b). The Euler angle about the l-axis was applied first when orienting the ribs and also contributes to the angle of the rib relative to the thoracic spine in the sagittal plane (Fig. 5a). With all three Euler angles applied to orient the ribs, Fig. 8 illustrates the overall change in the angle of the rib relative to the thoracic spine in the sagittal plane from age 6 months to 100 years. Figure 9 illustrates the contribution of the Euler angle about the m-axis and the Euler angle about the l-axis from age 6 months to 100 years. From birth through adolescence, the Euler angle about the m-axis becomes more negative and the Euler angle about the l-axis becomes more positive, indicating the ribs are rotating in the inferior direction within the sagittal plane. Around age 20, the Euler angle about the m-axis becomes more positive and the Euler angle about the l-axis becomes more negative, indicating the ribs are rotating in the superior direction within the sagittal plane. Rotation of the ribs in the superior direction continues until about age 60–70. After age 70, the lower ribs generally maintained similar angles, while the upper ribs (first, third, and fifth) rotated in the inferior direction within the sagittal plane. The trends in rib angles observed for the elderly are possibly due to increased thoracic kyphosis of the upper thoracic spine.

Discussion

Using the GPA, the size and shape variation of the ribs was characterized from high resolution homologous landmark data for males and females to generate functions describing rib morphology. The functions derived in this study capture substantially more information on thoracic skeleton morphology variation with age and sex than is currently available in the literature. These functions quantify normal thoracic anthropometry for both sexes and for the entire age spectrum, which can help clinicians and researchers distinguish deviations from the normal condition. The full 3D changes in rib geometry with age and sex were characterized, which represents an improvement on previous methods of measuring rib cage geometry (e.g. Jit et al. 1980; Kent et al. 2005; Gayzik et al. 2008; Sandoz et al. 2013). Shape variation was characterized separately from the size and shape variation and regression models describing these variations were statistically significant with age.

The size of the rib cage increased in all three dimensions from birth through adolescence, as would be expected during this time of growth and development. Some slight changes in the size of the rib cage with age were also seen in the adult population. The rib cage dimensions increased at different rates with age as indicated by the varying slope of the rib cage dimensions and thoracic index (Fig. 7). The rib cage dimensions and thoracic index were measured from only the ribs in this study, whereas other studies have measured dimensions from the entire chest including the sternum and soft tissue (e.g. Meredith & Knott, 1937; Openshaw et al. 1984). During the first years of life, the ribs are not fully ossified and a larger proportion of the anterior aspect of the rib is cartilaginous (Sandoz et al. 2013). Thus, the anterior-posterior dimension is particularly reduced in comparison to the total chest depth for the pediatric population since it is measured relative to the ossified rib cage. Nonetheless, the measurements in this study are in the range of dimensions collected from the ribs alone or from the internal thoracic cage by other imaging studies of pediatric and adult subjects (e.g. Bellemare et al. 2003; Bertrand et al. 2008; Comeau, 2010; Sandoz et al. 2013).

The angle of the ribs relative to the thoracic spine in the sagittal plane changed with age with the ribs rotating inferiorly from birth through adolescence. This trend is consistent with the reported roundedness of the chest in infancy and decreases in the thoracic index and rib angles that occur with age during pediatric development (Meredith & Knott, 1937; Openshaw et al. 1984). Young adults undergo superior rotation of the ribs in the sagittal plane into their elderly years, which is consistent with the literature (e.g. Oskvig, 1999; Kent et al. 2005; Gayzik et al. 2008). These changes could possibly be influenced by obesity or pulmonary pathologies, or they may be a result of the normal aging process. Gayzik et al. (2008) observed increased roundedness of the rib cage with the ribs becoming more horizontal with the spine in the elderly. Kent et al. (2005) reported a 7° increase in the rib angle from 18 to 89 years, indicating superior rotation of the lower ribs (Kent et al. 2005). Direct comparison with the previous study is not possible due to differences in measurement techniques. However, the Euler angle about the m-axis in the current study exhibited similar trends with the lower ribs (seventh, ninth, and 11th) rotating superiorly an average of 6.79° in males and 4.06° in females from 20 to 90 years. The Euler angle about the l-axis, which also contributes to the rib angle, resulted in the lower ribs rotating superiorly an average of 3.24° in males and 1.45° in females from 20 to 90 years. A combination of the rotations about the l- and m-axes would likely produce a more analogous comparison, but the results of this study do indicate trends of similar magnitude and direction to those of Kent et al. (2005).

The increased roundedness of the rib cage and horizontal angling of the ribs relative to the spine with age influences the biomechanical response of the thorax. With the plane of the rib oriented more horizontally, a loading vector applied in the anterior-posterior direction will result in increased deformation within the plane of the rib and an increased risk for rib fractures (Kent et al. 2005).

Thoracic kyphosis increased with age for adults in this study, which is consistent with the literature (Milne & Williamson, 1983; Puche et al. 1995; Korovessis et al. 1998; Goh et al. 2000; Hammerberg & Wood, 2003; Gayzik et al. 2008; Vafa, 2012). The points of articulation on the ribs were used as an indicator of thoracic kyphosis in this study, which differs from kyphosis measures such as the Cobb angle measured from the vertebral bodies or discs. Lordosis, kyphosis, segmental angulation, sacral inclination, pelvic tilt, and other factors also change with age and may influence thoracic kyphosis and thoracic biomechanics (Korovessis et al. 1998; Hammerberg & Wood, 2003; Vafa, 2012).

Limitations

As with any medical imaging study, the resolution of the CT scan poses a limitation. Efforts were made to select higher resolution clinical CT scans to minimize inaccuracies in the homologous landmarks collected and the majority of the CT scans had the minimum slice thickness available for clinical chest CT scans (0.625 mm). The in-plane CT scan resolution ranged from 0.21 to 0.98 mm with a median of 0.75 mm. Rib morphology was quantified from clinical CT scans in which subjects were instructed to take a deep breath and hold during the entirety of the scan. Thus, rib morphology is quantified in this study at near maximal inspiration. Rib dimensions, the thoracic index, rib angles, and other rib cage morphological characteristics will differ according to the stage of the respiratory cycle (Bellemare et al. 2001, 2003). Adherence of the subjects to the ‘breath hold’ scanning protocol was not verified and is a potential source of inaccuracy for CT scans taken at different stages of the respiratory cycle. The stage of the respiratory cycle at which the CT scan was taken may be less controlled in the pediatric subjects who were too young to understand and follow the scanning protocol. Spinal curvature, rib angles, and rib coverage for thoracic and abdominal organs are also influenced by posture (Beillas et al. 2009; Lafon et al. 2010; Hayes et al. 2013). Due to postural influences on the location and orientation of the ribs, the morphology characterized from supine scans in this study may be different for seated and standing postures. However, the utility of using clinically obtained CT scans to characterize the anatomy from a large number of individuals far outweighs the scanning limitations.

The origin and representativeness of the atlas is a potential limitation because the atlas was used as reference in the homologous landmark collection, GPA, and location and orientation of the individual ribs within the rib cage. Since the atlas was just used as a reference tool, the results of the study are not expected to differ dramatically if a different atlas was used. However, different atlases were not explicitly investigated, which is a limitation because the effects of the particular atlas on the results of the comparative study are unknown.

The choice of the regression model fit to the landmark data affects the resulting functions of morphology. While many different types of regression models were investigated using optimization software, the study is limited in that all possibilities were not exhausted. Some of the regressions had poorer R² values due to biological variability, which is a limitation, as poor correlations could result in inaccuracies in the developed size and shape models. However, qualitative and quantitative comparisons with clinical imaging and published literature on thoracic dimensions, thoracic index, and rib angles showed no indication of misrepresentation of the anatomy in the size and shape models that were developed.

Muscular imbalance due to handedness could possibly alter rib cage geometry, but subject handedness was not known or controlled for. Height and weight were not controlled for in the regression models characterizing rib cage size and shape, which presents a limitation. Age and sex were controlled for in the analysis and thus the increase in height and weight from birth through adolescence and gross size differences between sexes are accounted for. However, size variability within similarly aged subjects of the same sex is not directly controlled for in the size and shape rib cage models produced. Also, the median height and weight of the adult males was larger than the average 50th percentile male. In adult females, the median weight of the subjects was larger than the average 50th percentile female. Thus, the rib cage size and shape models may represent a population of individuals that is slightly larger than average. The shape models address any limitations associated with height and weight by eliminating the effect of size.

Future work and applications

The sternum is an integral part of the thoracic skeleton and characterization of its morphology will be reported in a separate publication. The sternum, as well as the costal cartilage, thoracic spine, and surrounding thoracic musculature and organs will be incorporated into future models of the rib cage. In this study, the shape models were scaled to represent a 50th percentile male height and weight so that comparisons could be made between ages and sexes. In future studies, these shape models could be scaled to represent different percentile males and females so that effects of height and weight can be assessed.

The models of rib cage anatomy developed in this study have applications that include traumatic injury prediction, surgical simulation and planning, and orthotic brace fitting. These models of normal anatomy could improve diagnostic techniques for abnormalities such as scoliosis, kyphosis, lordosis, and congenital thoracic skeleton defects. The external rib cage morphology functions will be used in the future to create age- and sex-specific parametric FE thoracic models. Cortical thickness and bone density changes in the ribs with age and sex will be quantified in future studies and integrated into these parametric models to represent both the structural and material property effects on thoracic response (Stitzel et al. 2003; Kemper et al. 2005, 2007). These models will be validated against experimental testing conditions and used to investigate the biomechanical response and injury tolerance of the aging thorax (Shaw et al. 2009; Lebarbe & Petit, 2012; Vavalle et al. 2013a,b). These models could be used to optimize the performance of seat belts, load limiters, pretensioners, and airbags for the aging population. Age- and sex-specific anatomical models are valuable tools for evaluating vehicle crashworthiness and understanding variations in thoracic injury patterns due to MVCs or falls across populations.

Author contributions

Ashley Weaver collected and analyzed data, participated in the study design, and prepared the manuscript. Samantha Schoell assisted with data analysis and collection and was involved with the study design and manuscript preparation. Dr. Joel Stitzel assisted with study design, acted in an advisory and editorial capacity, and assisted with manuscript preparation.

Supporting Information

Additional Supporting Information may be found in the online version of this article: