Abstract
Animal migrations are spectacular and migratory species have been shown to transmit pathogens that pose risks to human health. Although migration is commonly assumed to enhance pathogen dispersal, empirical work indicates that migration can often have the opposite effect of lowering disease risk.
Key to assessing disease threats to migratory species is the ability to predict how migratory behaviour influences pathogen invasion success and impacts on migratory hosts, thus motivating a mechanistic understanding of migratory host-pathogen interactions.
Here we develop a quantitative framework to examine pathogen transmission in animals that undergo two-way directed migrations between wintering and breeding grounds annually.
Using the case of a pathogen transmitted during the hosts’ breeding season, we show that a more extreme migratory strategy (defined by the time spent away from the breeding site and the total distance migrated) lowers the probability of pathogen invasion. Moreover, if migration substantially lowers the survival probability of infected animals, then populations that spend comparatively less time at the breeding site or that migrate longer distances are less vulnerable to pathogen-induced population declines.
These findings provide theoretical support for two non-exclusive mechanisms proposed to explain how seasonal migration can lower infection risk: (i) escape from habitats where parasite transmission stages have accumulated, and (ii) selective removal of infected hosts during strenuous journeys. Our work further suggests that barriers to long distance movement could increase pathogen prevalence for vulnerable species, an effect already seen in some animal species undergoing anthropogenically induced migratory shifts.
Keywords: long-distance migration, host-parasite interaction, compartment model, pathogen invasion, population dynamics
Introduction
Migration, here defined as directed, seasonal and often long-distance movements of animals to track changes in resources or environmental conditions, is widespread in nature (Dingle 1996; Alerstam et al. 2003). Migratory animals are among the most threatened and most challenging species to conserve, in part because their survival depends on conditions across a network of sites that potentially span large geographical distances, multiple habitat types, and political boundaries (Wilcove and Wikelski 2008; Bowlin et al. 2010). Migratory species can serve as hosts for a number of ecologically relevant infectious diseases, with much recent interest focused on the potential long-distance movement of avian influenza and West Nile virus by birds and Ebola virus, henipaviruses and white nose syndrome by bats (Rappole et al. 2000; Owen et al. 2006; Frick et al. 2010; Plowright et al. 2011; Hayman et al. 2012). Migratory behaviour might also increase pathogen transmission following aggregation and contacts with conspecifics or heterospecifics at breeding, overwintering or migratory stopover sites (Figuerola and Green 2000; Waldenström et al. 2002; Knauss et al 2010).
Although greater pathogen exposure can pose a significant cost of long-distance migration, for many animal species, migration can have the opposite effect of lowering infection risk. Importantly, the bulk of transmission for any given pathogen occurs during a single stage of the annual migratory cycle (see examples in Supplementary Material A1) owing to constraints arising from pathogen biology (e.g., for geographically limited transmission stages) or constraints driven by the host (e.g., hosts only aggregate at high density at certain times of the year). This suggests that migration can act as a mechanism of disease avoidance, or more generally, natural enemy escape (McKinnon et al. 2010). In particular, two hypotheses have been proposed for explaining how migration might lower infection risk (reviewed in Altizer et al. 2011). First, if parasite transmission stages accumulate in the host’s environment over time, migration might allow animals to periodically escape contaminated habitats (e.g., Loehle et al. 1995) through a process termed migratory escape (Bartel et al. 2011). Second, if infected individuals migrate less well and suffer disproportionate mortality during migration, this can reduce infection prevalence through a process termed migratory culling (Bradley and Altizer 2005). Evidence supporting one or both of these mechanisms has been reported from field and laboratory studies of protozoan parasites in monarch butterflies (Bartel et al. 2011; Bradley and Altizer 2005), warble fly and nematode infections in reindeer (Folstad et al. 1991; Kutz et al. 2013), and low pathogenic avian influenza virus infections in migratory waterfowl (van Gils et al. 2007; Weber et al. 2007).
Mathematical models have recently been developed to ask how zoonotic pathogens persist in migratory species and evaluate the consequences of disrupted migration for parasite infection in economically important wildlife. Models of avian influenza transmission showed that environmental persistence of free virus (Breban et al. 2009) and the potential for transmission at stopover sites during the spring or fall migration (Bourouiba et al. 2011) can predict outbreak severity in waterfowl. Other modelling studies showed that spillover infections of sea lice from farmed adult salmon to wild juveniles can overcome a natural barrier to transmission through the migratory separation of adults and juveniles (termed migratory allopatry; Krkošek et al. 2007). However, the need remains for a general theoretical framework for understanding the role of migratory strategy, defined here in terms of time spent at the breeding site (relative to time spent away), and the distance migrated between breeding and non-breeding sites, in influencing pathogen transmission (Bauer and Klaassen 2013). Identifying which migratory strategies are most likely to promote or inhibit the invasion and persistence of infectious diseases is an important step towards conserving rare or economically important species, evaluating spillover threats to livestock and human health, and exploring the evolutionary potential of migration as a mechanism for enemy escape (Altizer et al. 2011; Bowlin et al. 2010).
Here we develop a modelling framework for a host species undergoing a two-way annual migration between a breeding site and wintering site. By specifying how host fecundity and survival change across different points on the migratory cycle, we show that host equilibrium population size depends on two key parameters describing migration strategy: the duration of time spent at the breeding site and the distance migrated between breeding and wintering sites. To investigate infection dynamics, hosts are divided into susceptible (S) and infected (I) classes, and we assume that transmission occurs during the breeding season only. Our key goals were (i) to understand how migratory strategy influences host population size before and after introduction of a pathogen; (ii) to identify those migratory strategies that are most vulnerable to pathogen invasion; and (iii) to investigate host migratory strategies that most strongly limit pathogen impacts, and how this depends on pathogen transmissibility and costs of infection.
Model Development
(A) Population dynamics in the absence of infection
To account for the ecological dynamics of an animal population that undergoes an annual, two-way migration between breeding grounds and wintering sites, we define the population’s migratory strategy by two key parameters: the fraction of the year spent at the breeding grounds (Tb), and the distance from the breeding grounds to the chosen wintering sites (d). The within-year population dynamics by migratory stage are described below.
(i) Breeding site
Let NY(t) represent the population size in year Y at within-year time t, where the start of the annual cycle, t=0, is measured from the start of the breeding season. The interannual dynamics are given by setting the population size at the start of breeding in year Y+1 equal to the number of individuals that successfully completed a migratory cycle in year Y, i.e., NY+1 (0)=NY(1). Environmental conditions at the breeding site vary between two states; a favourable season of length Ts, during which breeding can occur and mortality is relatively low; and an unfavourable season (length 1- Ts) during which breeding is impossible and mortality rates are high. In the favourable season, the population dynamics in year Y are described by
| (1) |
where b0, b1 are the density-independent and dependent components of the per capita birth rate and mb is the per capita mortality rate. If the species leaves the breeding site before the end of the favourable season (i.e. Tb < Ts), the population size prior to migration is found by integrating (1) over time period Tb. During the unfavourable (non-breeding) season, the per capita mortality rate at the breeding site increases to mnb and the dynamics are simply given by
| (2) |
If the species remains at the breeding site during the unfavourable season (i.e. Tb>Ts), the pre-migration population size is obtained by integrating (1) over time Ts and multiplying by the proportion surviving the unfavourable season (obtained by integrating expression 2),
| (3) |
(ii) Migration
During migration, individuals are assumed to experience a constant per capita mortality rate mm, where mm > mb. To account for the fact that there are physiological and/or environmental limits to how far a species can migrate in a given time, we set the species’ migration capacity by fixing its average migration speed, v. Therefore if a wintering site is chosen at distance d from the breeding site, the time taken to complete a one-way migration is Tm = d/v, and the post-migration population size is obtained by multiplying the pre-migration population size by the proportion surviving migration,
| (4) |
(iii) Wintering site
At the wintering site, the per capita mortality rate is mw, and the proportion surviving the winter can be expressed as
| (5) |
where the time spent at the wintering site, Tw, is the fraction of the year remaining following the time spent on the breeding grounds and the two-way migration:
| (6) |
We assume an underlying environmental gradient so that overwintering survival is low if the species winters close to the breeding site, and increases with increasing distance from the breeding site. Thus, the per capita mortality rate at the chosen wintering site, mw, is given by
| (7) |
where the constant k=ln (mnb / mb) is the log-ratio of the mortality rates at the breeding site during the favourable and unfavourable seasons, db is the distance at which wintering site mortality equals mortality at the breeding site during the favourable season, and the shape parameter n determines the rate at which wintering site mortality declines with increasing distance from the breeding site (see Supplementary Material A2 for a visualization of how winter mortality depends on model parameters).
(B) Dynamics in the presence of infection
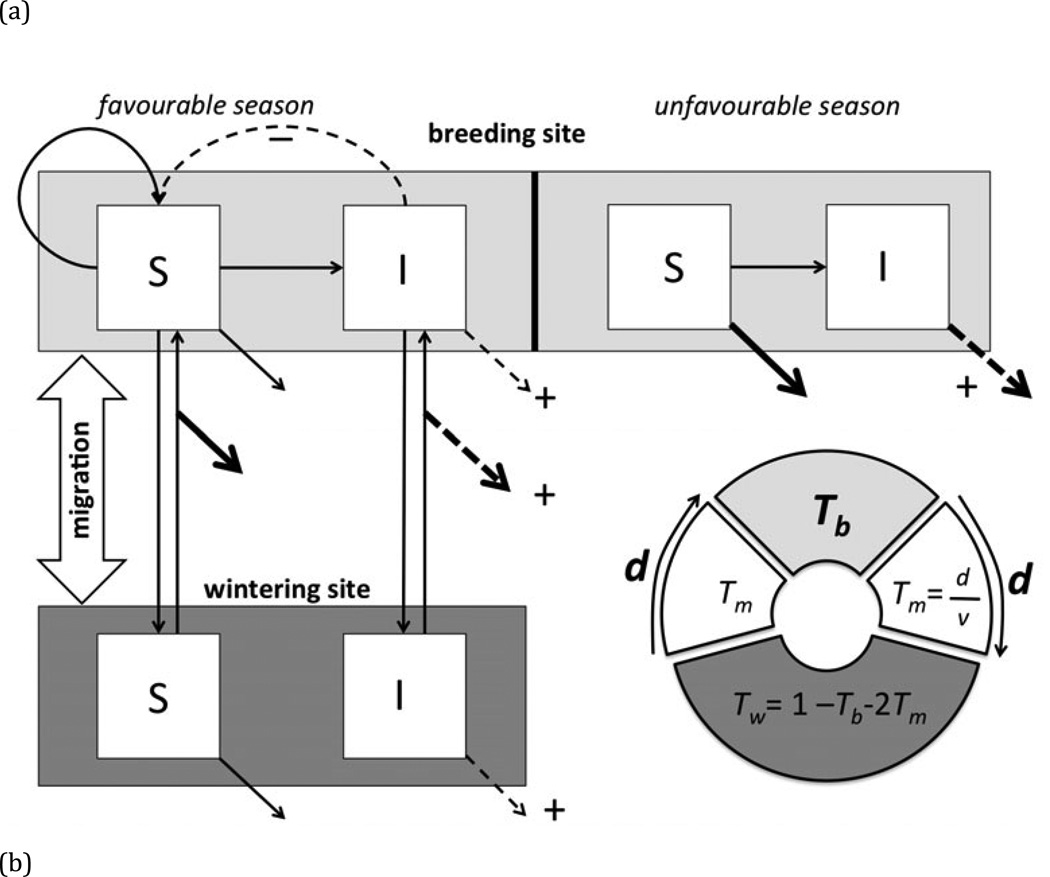
The above framework is amenable to incorporating pathogen transmission under a variety of assumptions about pathogen life history, and at one or more migratory stages (Fig. 1). In this manuscript we restrict our attention to a pathogen transmitted at the breeding site only, following the majority of examples described in Supplementary Material A1. We assume that individuals do not recover from infection, so that the host population at within-year time t in year Y can be subdivided into susceptible and infected individuals with densities SY(t) and IY(t) respectively. Costs of infection to the host are expressed in terms of reductions in fecundity (cf) and/or increases in mortality at each stage of the migration cycle (ci, i = b, nb, m, w). Each of the ci takes values between 0 (representing no cost) and 1 (representing the maximum cost), so that a cost of ci to survival at migratory stage i means that the lifespan of an infected individual is a fraction 1-ci of the lifespan of a susceptible individual experiencing the conditions at stage i. Note that the costs of infection may differ according to migration stage, allowing for disease-induced mortality to be disproportionately high during energetically-demanding migration if the animals are in poor condition or immunosuppressed (Altizer et al. 2011). The dynamics at the breeding site during the favourable season are now given by
| (8a) |
| (8b) |
and during the unfavourable season by
| (9a) |
| (9b) |
where β is the (density-dependent) transmission rate.
Fig. 1.
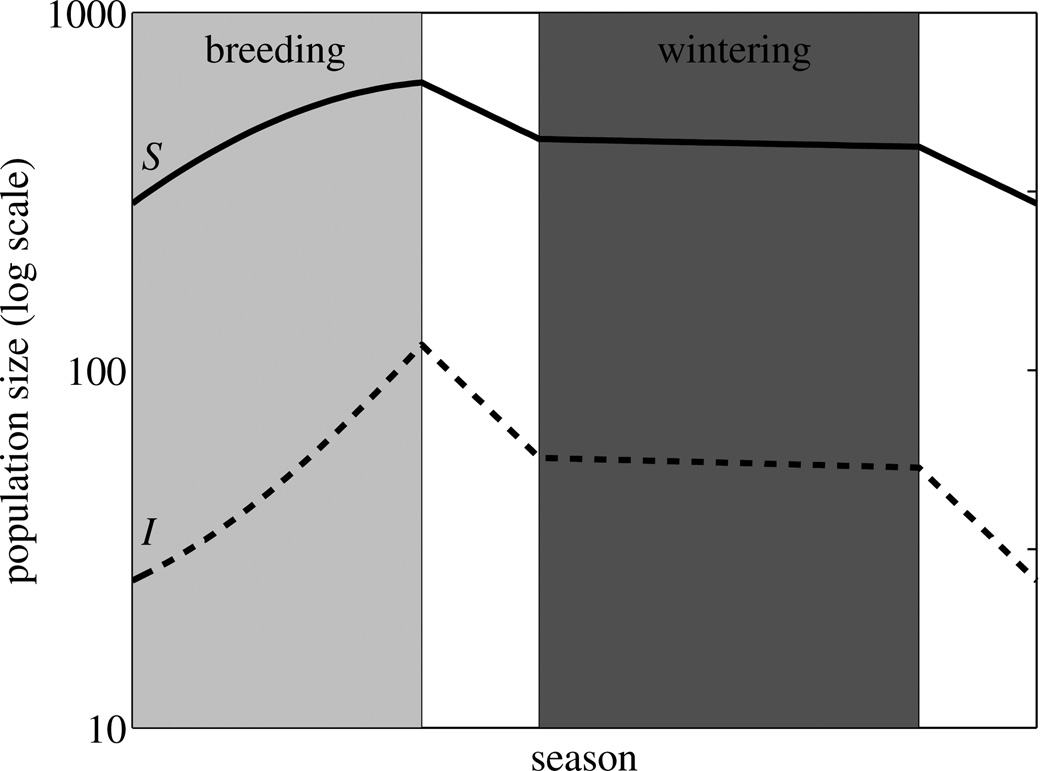
(a) Schematic diagram of model showing Susceptible (S) and Infected (I) individuals of a migratory species at the breeding site (light gray shading), during migration, and at the wintering site (dark gray shading). Pathogen transmission (horizontal arrow) occurs only at the breeding site. Curved arrows represent fecundity, vertical arrows represent movement between the breeding and wintering sites, and diagonal arrows represent mortality at each stage of the migratory cycle. Thicker arrows indicate those portions of the migratory cycle during which mortality is expected to be relatively high, and dashed arrows indicate vital rates that are likely to be influenced by infection, with a plus or minus sign depicting whether infection increases or decreases the corresponding vital rate in infected individuals. The circle depicts the proportions of the annual cycle spent at the breeding site (Tb), on a one-way migration (Tm), and at the wintering site (Tw). The dependence of these times on the two key parameters determining the migratory strategy (time spent at breeding site, Tb, and distance migrated, d, depicted in bold) is shown. (b) Example population dynamics (plotted on a log scale) of susceptible (bold line) and infected (dashed line) individuals employing a migratory strategy of Tb=0.33 yr, and d=2.66 × 103km, and infected with a pathogen with transmission rate β =0.01, and which induces a moderate cost to migratory survival (cm=0.5); the remaining parameter values are listed in Table 1.
For animals that migrate, the proportion of susceptible individuals surviving a one-way migration and overwintering are given by expressions (4) and (5) respectively. Noting that pathogen transmission does not occur during migration or at overwintering sites, the analogous proportions of infected individuals surviving migration and overwintering, respectively, are
| (10) |
and
| (11) |
(C) Parameterization
A combination of techniques including mark-recapture, radio-tagging and stable isotope analysis are yielding ever more detailed information on animal migration routes (Robinson et al. 2009, Wunder 2012). However, low recapture probabilities and financial constraints on the number of radio-tagged animals make it difficult to estimate population demographic rates over the migratory cycle, and consequently very few empirical studies have quantified how mortality varies by migratory stage (but see Klaassen et al. in press). A notable exception is the classic study of Sillett and Holmes (2002), which estimated monthly survival rates of a migratory Nearctic songbird, the Black-throated Blue Warbler (Setophaga caerulescens) throughout its annual migratory cycle. While infectious disease is not considered a primary threat to this species, juvenile mortality at breeding sites has been noted as a result of botfly parasitism, and the species has also tested positive for West Nile Virus (Holmes et al. 2005). We therefore derived our default parameter set (described in full detail in Supplementary Material A3) for the migratory strategy, fecundity and stage- specific survivorship from data on this species, under the assumption that it typifies the life history of other Neotropical migrant passerines. We note that the general trend in mortality rates observed for this species (low mortality at breeding and wintering sites, and high mortality during migration) could apply broadly to other migratory animals undergoing a long-distance migration.
We use the migratory host-pathogen model to investigate the following three questions, with model exploration and results described below: (i) How does a population’s migratory strategy affect host population size before and after the introduction of a pathogen? (ii) Which migratory strategies are most vulnerable to pathogen invasion? (iii) How do pathogen traits influence the ability of migratory strategy to reduce pathogen impacts by maximizing host population size following pathogen introduction?
Results
(i) Migratory strategy and host population dynamics
We calculated the equilibrium host population size at the start of the breeding season (which corresponds to the minimum population size per year and thus could represent a key conservation target for host persistence). This host population size was expressed as a function of the time spent at the breeding site, Tb, and the distance migrated, d, by solving the disease-free model presented in section (A) analytically. We then introduced infected individuals to the population at its disease-free equilibrium and solved the model outlined in section (B) numerically in Matlab (Release 2011), the Mathworks, Inc. until it reached a new equilibrium state. We identified the migratory strategies that maximized the equilibrium host population size in the presence and absence of the pathogen, noting that differences in these optima provide evidence that changing the distance migrated or time spent at the transmission site can lessen the impacts of an introduced pathogen (consistent with the migratory culling and escape hypotheses).
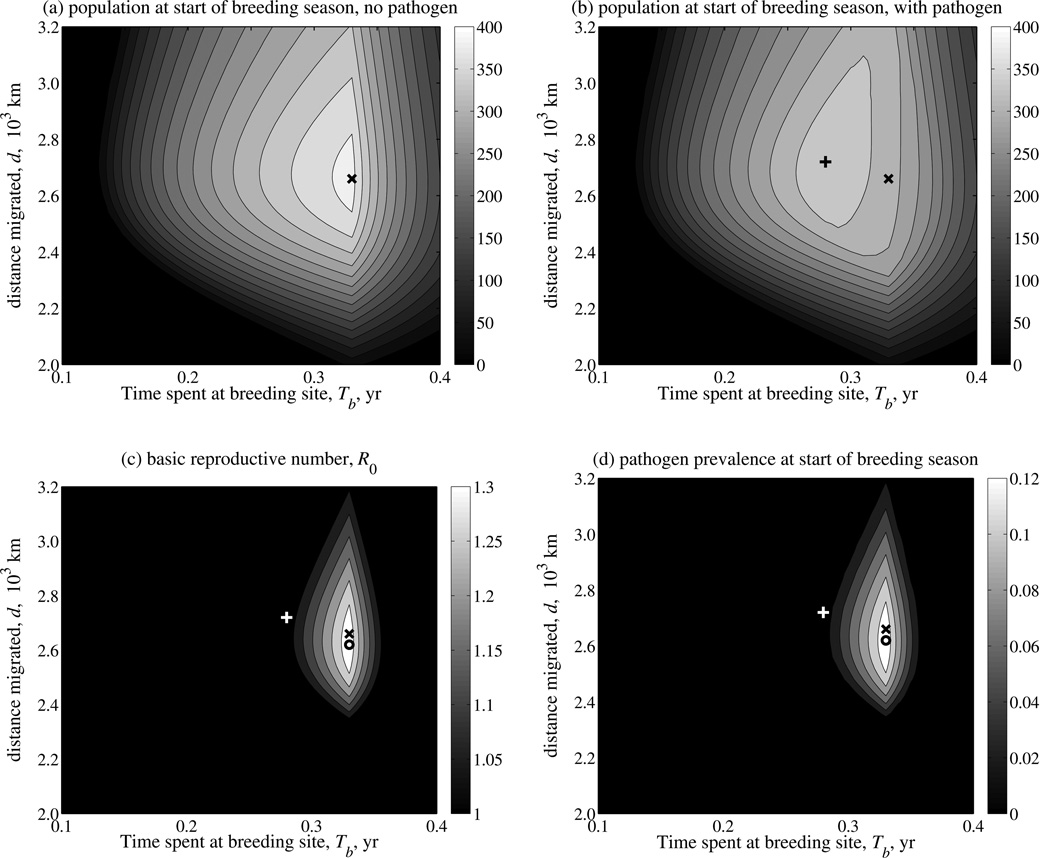
In the absence of the pathogen, the population dynamics settle into an equilibrium annual cycle N(t), where the population size at within-year time step t is the same in all subsequent years (N(t) : NY+1 (t) = NY (t), 0 ≤ t ≤ 1). This cycle is characterized by population increases through recruitment in the breeding season, relatively severe declines due to migratory mortality, and relatively modest declines at the wintering site (Fig. 1b). We derived analytical expressions for the minimum and maximum population size in this equilibrium annual cycle, which occur when the species arrives at the breeding site, and finishes breeding, respectively (see Supplementary Material A4). The dependence of population size on migratory strategy is illustrated by plotting the numbers of individuals returning to the breeding site, N(0), as a function of Tb and d (Fig. 2a). We find that there is a unique strategy that maximizes host population size: staying at the breeding ground for the duration of the favourable season (Tb=Ts) maximizes reproductive output and avoids the onset of high mortality in the unfavourable season. The optimum distance migrated is determined by a balance between increased migratory mortality and reduced overwintering mortality with increasing distance to the wintering site (Fig. 2a).
Fig. 2.
Effect of migratory strategy on host population size (a) before and (b) after introduction of a pathogen, and on pathogen invasion success as characterized by (c) the basic reproductive number, R0, and (d) equilibrium pathogen prevalence. The migratory strategy is characterized by the time spent at the breeding site (Tb, horizontal axis) and distance migrated (d, vertical axis), and the magnitude of each response variable is depicted by contour lines and the gray scale bar. The equilibrium population size, N, and pathogen prevalence, I/N, are measured at the start of the breeding season (t=0). The ‘x’ marks the migratory strategy that maximizes the population size prior to pathogen introduction, the ‘+’ marks the strategy that maximizes population size following pathogen introduction and the ‘o’ marks the strategy that maximizes both R0 and equilibrium pathogen prevalence. Results are illustrated for a pathogen with transmission rate β =0.01, and which induces a moderate cost to migratory survival (cm=0.5); the remaining parameter values are listed in Table 1. The contours in each plot are imputed; the raw values are plotted in Supplementary Material A5.
Following pathogen introduction, the host population either returns to the pre-invasion equilibrium cycle (following pathogen extinction), or a new annual equilibrium cycle is attained following pathogen establishment (an example is shown in Fig. 1b). Importantly, the migratory strategy that maximizes host population size following pathogen introduction differs from the disease-free optimal strategy (Fig. 2b). For this particular pathogen, characterized by breeding-season transmission and a reduced migratory survivorship, we found strong support for populations with early-departing strategies to be larger in size, and weaker support for further-migrating strategies achieving the same. (Fig. 2b).
(ii) Migratory strategy and pathogen invasion
To explore the conditions for pathogen invasion, we derived an expression for the pathogen’s basic reproductive number (the expected number of new infections per infected host when introduced to a wholly susceptible population; Otto and Day 2007a), R0, as a function of the host’s migratory strategy. We identified combinations of Tb and d for which R0 is less than one (and therefore, an introduced pathogen is unable to invade). We similarly examined pathogen persistence by simulating equilibrium pathogen prevalence across a gradient of migratory strategies.
In order to derive an expression for the basic reproductive number of a seasonally-transmitted pathogen in a migratory host, we first consider the simpler case of a pathogen invading a sedentary host population in a constant environment. In the absence of the pathogen, the host attains a disease-free equilibrium density N = N*. If the pathogen has a constant transmission rate β and infected individuals leave the infected class at rate μ, the basic reproductive number is given by R0 = βN* / μ (Otto and Day, 2007a). For a migratory species, the disease-free equilibrium host population size, pathogen transmission rate, and the mortality rate of infected individuals all vary through the annual cycle. We therefore propose that an analogous expression for R0 in a migratory host species is
| (12) |
where the integral is the product of the transmission rate (which potentially varies over the migratory cycle) and equilibrium population size, and m is the annual mortality rate of an infected individual, averaged over the annual cycle (see Supplementary Material A4). We calculated R0 as a function of migratory strategy, and identified the region in which R0 is greater than one, allowing pathogen invasion (Fig. 2c). We find that for many migratory strategies, the pathogen is unable to invade. This occurs when the equilibrium host population is too low to maintain transmission (e.g., for near-residents with Tb close to one, or short-distance migrants with d close to zero, which experience high nonbreeding mortality). Invasion failure can also result from a too-short time window during which transmission is possible (i.e. low Tb), or because the mortality of infected individuals during long-distance migration is too high (i.e. large d). The migratory strategy that maximizes pathogen R0 occurs at a shorter migratory distance than the strategy that maximizes the disease-free host population size, since shorter migrations substantially increase the survival probability of infected individuals (and, therefore, increase the infectious period).
The migratory strategy that maximizes host population size following disease introduction occurs along the contour demarcating the pathogen invasion threshold R0=1. The utility of our heuristic definition of R0 as an invasion threshold was verified by plotting the equilibrium pathogen prevalence (following simulation) at the start of the breeding season as a function of migratory strategy (Fig. 2d). The region in which R0 >1 corresponds with the region where the equilibrium prevalence is non-zero, and pathogen prevalence and R0 are both maximized by the same migratory strategy.
(iii) Pathogen traits and optimal migratory strategy
To examine how pathogen traits determine the migration strategies that optimise host population size (again, measured at the start of the breeding season), we co-varied two key pathogen traits (the transmission rate, β, and the virulence or cost-of-infection during migration, cm) and used simulations over (Tb, d) space to identify which migratory strategy maximized host population size following arrival of a pathogen, and recorded the equilibrium pathogen prevalence at this optimum. Further details of how this optimisation was implemented are provided in Supplementary Material A5. Consistent with the migratory escape and culling hypotheses, the peak response in migratory strategy is to spend less time at the breeding/transmission site, and to undertake a longer-distance migration, than the disease-free optimal strategy (Fig. 3). For our default environmental and demographic parameters (representative of a Neotropical migrant insectivore with a very low overwintering survival probability in the temperate US), the relative magnitude of the response in the optimal distance migrated is much weaker than the response in the time spent at the breeding grounds (Fig. 3a vs. 3b).
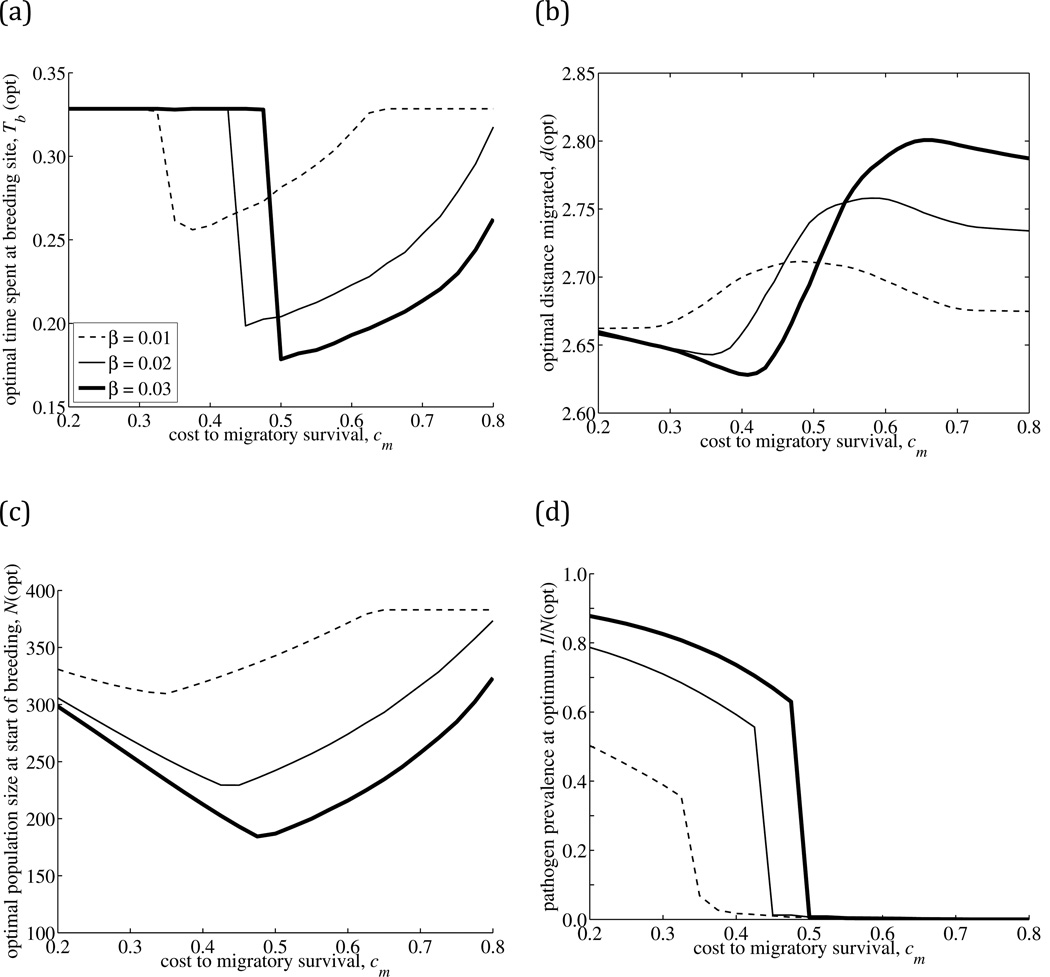
Fig. 3.
The migratory strategy that maximizes population size following pathogen introduction, as a function of two key pathogen traits: the cost-of-infection to migratory survival (cm), and three values of transmission rate (β): low (β =0.01, dashed line), intermediate (β =0.02, thin line) and high (β =0.03, thick line). The response variables for the optimal migratory strategy are (a) time spent at breeding site (Tb), (b) distance migrated (d), (c) equilibrium host population size (N) and (d) equilibrium pathogen prevalence (I/N) measured at the beginning of the breeding season. To account for numerical error in the calculation of the optimum, the lines plotted correspond to the mean values of the top ten strategies for (a) Tb, (c) N and (d) I/N, and a loess regression of d on cm with smoothing parameter 0.3. The range of values of the top ten optimal strategies is shown in Supplementary Material A5. The remaining model parameters are listed in Table 1.
The response of the optimal time spent at the breeding site, Tb(opt), followed a nonlinear pattern (Fig. 3a): when transmission (and hence prevalence) was relatively low, the optimal time spent at the breeding site was high for low costs of infection to migratory survival, decreased with intermediate costs of infection, and increased again when the cost of infection during migration was very high. For higher rates of transmission, greater costs of infection were needed to drive hosts to spend more time away from the breeding grounds, and ultimately resulted in sharper drops in the time spent at breeding grounds in the case where virulence was high (Fig. 3a). An effect of opposite direction but weaker magnitude was seen for the optimal distance migrated, d(opt). When pathogen transmission was low, the optimal distance migrated was relatively low for the case of low virulence, peaked at intermediate virulence, and declined again at high virulence (Fig. 3b). Increasing transmissibility increased both the costs of infection needed to drive hosts to migrate farther, and the magnitude of the peak response (the longest-distance optimal migration strategy for a given transmission rate).
A substantially altered migration strategy following pathogen invasion is only likely to be beneficial if both pathogen prevalence and the costs of infection are relatively high. However, individuals infected with highly virulent pathogens are unlikely to survive an entire migratory cycle to sustain multi-annual epidemics, and substantial changes to migratory strategy are not necessary to reduce prevalence. This explains why peak responses in the optimal migratory strategy occur at intermediate costs. Highly transmissible pathogens are more likely to attain higher prevalence, and therefore the magnitude of the response in migratory strategy needed to reduce prevalence will be larger. The likelihood of multi-annual persistence of highly transmissible pathogens will also increase with pathogen transmissibility, and since high-transmission, high-virulence pathogens are most detrimental to the host, the peak responses in host migratory strategy (i.e., the minimum in the optimal time spent at the breeding ground, and maximum optimal migration distance) occur at higher costs for increasingly transmissible pathogens. The maximum population size attained by the host is a U-shaped function of the cost to migratory survival, and is a decreasing function of transmissibility (Fig. 3c), meaning that migratory populations are most vulnerable to large declines following the arrival of highly transmissible pathogens with intermediate virulence. Equilibrium pathogen prevalence declines slowly with increasing cost to migratory survival, and then experiences a sharp threshold decline towards zero prevalence (Fig. 3d). Increasing transmissibility increases both infection prevalence and the threshold value of migratory cost-of-infection above which the pathogen cannot invade.
Discussion
Our work showed that seasonal migration can sharply lower pathogen prevalence in animal populations, and that the presence of a pathogen can shift the migratory strategy that maximizes host population size. In particular, longer-distance migrations, and earlier departure from transmission grounds (even when this comes at the cost of reduced reproduction), can both be advantageous to the host population following arrival of a pathogen. The migratory strategies that maximize population size in the absence of the pathogen are among the most susceptible to pathogen invasion, and therefore, more drastic changes to host migratory behaviour are required to avoid highly-transmissible pathogens. Changes to migratory behaviour are most likely to be advantageous to population persistence at intermediate pathogen virulence, since highly virulent pathogens are less likely to establish in host populations more generally, and individuals infected by highly-virulent pathogens are unlikely to survive an entire migratory cycle to re-start epidemics. By comparison, the host mortality caused by low-virulence pathogens is likely to be less than the opportunity costs of lost reproduction and/or increased migratory mortality arising through changing migratory strategy.
In our model parameterization based on the life cycle of a Neotropical migrant passerine bird, we found strong evidence for the potential of migratory escape (leaving contaminated habitats early to reduce transmission) and weaker support for migratory culling (longer- distance movement to reduce prevalence) to act as mechanisms of disease avoidance. These modelling insights are consistent with our prior empirical work in monarch butterflies infected by protozoan parasites. Monarchs that breed in temperate locations such as North America undergo a two-way long distance migration to wintering sites in milder climates, whereas monarchs in tropical and sub-tropical locations can form sedentary populations that breed year-round (Ackery and Vane-Wright 1987). Our work on parasitism of monarchs by the debilitating protozoan Ophryocystis elektroscirrha showed that (i) long-distance migratory populations have lower infection prevalence than short-distance migrants and resident populations (Altizer et al. 2000; Altizer and De Roode in press), (ii) infection prevalence within North American migratory monarchs increases over time during the summer breeding season, but then declines during the fall migration and overwintering period (Bartel et al. 2011), and (iii) infected monarchs show lower flight performance (slower speed, shorter distance flights) as compared to healthy butterflies in captive studies (Bradley and Altizer 2005). These observations are consistent with the predictions of migratory escape and culling as mechanisms of disease avoidance. Our modelling study here presents stronger mechanistic support for the migratory escape and culling hypotheses by quantifying how pathogen invasion and prevalence change in response to these two processes (analogous to reductions in Tb and increases in d and cm), and by demonstrating that different migratory strategies maximize host population size before versus after pathogen introduction.
One outstanding question is whether parasites can provide selective pressures to increase the migratory propensity of their hosts. Populations of migratory birds have been demonstrated to show shifts in migratory behaviour over ecological timescales in response to climate change (Bradshaw and Holzapfel 2006) suggesting that adaptive change in migratory behaviour is possible. Moreover, long-distance migration has already been shown to reduce predation risks for ungulates and birds (McKinnon et al. 2010; Hebblewhite and Merrill 2007), with the underlying rationale being that the survival costs of migration are outweighed by the fitness benefits associated with predator release. Our model demonstrates that different migratory strategies optimize population size in the presence vs absence of the pathogen, but since all individuals in the population are assumed to deploy the same migratory strategy, it cannot be used to directly test the adaptive potential of migratory propensity as a mechanism of pathogen avoidance. Further theoretical work is needed to explore the evolution of migration in response to pathogens, for example by conducting an evolutionary invasion analysis (Otto and Day 2007b) to investigate whether rare, longer-distance migratory strategies increase in frequency in a population following emergence of a pathogen.
Our model investigates pathogen transmission in a host population moving between a breeding site and a wintering site annually, but frequently breeding, stopover and wintering habitats are patchily distributed, resulting in seasonal isolation and aggregation of different host subpopulations. The structure and connectivity of a ‘migratory network’ of habitat patches has been demonstrated theoretically to affect how species use patches (Taylor and Norris 2010) and population persistence (Taylor and Hall 2012). It is likely, then, that the network structure of habitat within the migratory range of a host species will affect whether, and how rapidly, an emerging disease spreads through a migratory population. Importantly, avoidance of contaminated sites to escape infection could result in more complex feedbacks between pathogen transmission, movement patterns and population dynamics.
Understanding which combinations of host migratory behaviour and pathogen traits enable pathogens to invade and reach endemic equilibrium is especially important given the enormous changes to the ecology of migratory species in the past century, and the potential of these species to harbour pathogens of public health or conservation concern. Studies suggest that in some species, the propensity to undertake long-distance migration is declining (Wilcove and Wikelski 2008) due loss of habitat in nonbreeding areas (Iwamura et al. 2013), climate warming (La Sorte and Thompson 2007), or urbanization (Partecke and Gwinner 2007). A few recent examples indicate that human activities that disrupt or discourage long-distance animal movements or encourage the formation of sedentary populations can cause the emergence of pathogens harmful to humans, wildlife or domesticated species, as illustrated by the emergence of Hendravirus in urban centers with sedentary fruit bat camps (Plowright et al. 2012), problems with sea lice experienced by juvenile salmon encountering farmed salmon en route to sea (Krosek et al. 2007), and brucellosis infection in non-migratory elk supported by supplemental feeding in the Greater Yellowstone ecosystem (Cross et al. 2010) Our modelling results are consistent with these field observations, and suggest that factors that reduce the migratory propensity of populations are likely to result in increased pathogen prevalence, and may allow the invasion of more highly virulent pathogens, potentially leading to further host population declines and increased human exposure to zoonotic infections.
Supplementary Material
Table 1.
List of model parameters, their definitions, and default values. The migratory and host life history parameters are based on those of the Black-throated Blue Warbler (Setophaga caerulescens); see Supplementary Material A3 for derivation.
| Parameter | Definition | Value |
|---|---|---|
| 1. Migratory strategy | ||
| Tb | proportion of annual cycle spent at breeding site | varied between 0 and 1 |
| Ts | length of favourable season at breeding site | 0.33 yrs (4 months) |
| v | average migration speed (migratory capacity) | 20,800 km/yr |
| d | distance migrated (one-way) | varied between 0 and dmax=0.5 × v |
| Tm | proportion of time spent on one-way migration | d/v |
| Tw | proportion of time spent on wintering grounds | 1-Tb-2Tm |
| 2. Host life history | ||
| b0 | density-independent component of per capita birth rate | 6.2/yr |
| b1 | density-dependent component of per capita birth rate | 0.0062/individual/yr |
| mb | per capita mortality rate at breeding site (breeding season) | 0.12/yr |
| mnb | per capita mortality rate at breeding site (nonbreeding season) | 8.3/yr |
| mm | per capita mortality rate during migration | 2.8/yr |
| db | distance at which winter site mortality=breeding season mortality | 2.6 × 10^3 km |
| n | shape parameter determining how winter mortality drops with distance from breeding site (see Supplementary Material A2) | 5 |
| mw | per capita mortality rate at wintering site | Varies with d, but 0.12/yr when d=db |
| 3. Parasite infection parameters | ||
| β | density-dependent transmission parameter | 0.01–0.05 |
| cf | proportionate cost of infection to per capita fecundity | 0 |
| cb | proportionate cost of infection to breeding season mortality | 0.2 |
| cnb | proportionate cost of infection to nonbreeding season mortality | 0.2 |
| cm | proportionate cost of infection to migratory mortality | 0.2–0.7 |
| cw | proportionate cost of infection to wintering site mortality | 0.2 |
Acknowledgments
We thank Andrew Park, Andy Dobson, Pej Rohani, Andy Davis, Troy Day, members of the Altizer lab and two anonymous referees for discussion and comments on the manuscript. Financial support was provided by the McDonnell Foundation grant 220020193 to RH, NSF DEB grant 0643831 to S.A., a Ruth L. Kirschstein National Research Service Award through the NIH to R.B. The findings and conclusions in this article are those of the authors and do not necessarily represent the views of the U.S. Fish and Wildlife Service.
References
- Ackery, Vane-Wright . Milkweed Butterflies: Their Cladistics and Biology. Cornell University Press; 1984. [Google Scholar]
- Alerstam T, Hedenström A, Åkesson S. Long-distance migration: evolution and determinants. Oikos. 2003;103:247–260. [Google Scholar]
- Altizer SM, Oberhauser KS, Brower LP. Associations between host migration and the prevalence of a protozoan parasite in natural populations of monarch butterflies. Ecological Entomology. 2000;25:125–139. [Google Scholar]
- Altizer S, Bartel R, Han B. Animal migration and infectious disease risk. Science. 2011;331:296–302. doi: 10.1126/science.1194694. [DOI] [PubMed] [Google Scholar]
- Altizer S, De Roode JC. Monarch defense against a debilitating parasite: resistance, immunity and self-medication. In: Oberhauser K, Altizer S, Nail K, editors. To appear in: Monarchs in a Changing World: Biology and Conservation of an Iconic Insect. Cornell University Press; In press. [Google Scholar]
- Bartel RA, Oberhauser KS, De Roode J, Altizer S. Monarch butterfly migration and parasite transmission in eastern North America. Ecology. 2011;92:342–351. doi: 10.1890/10-0489.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer S, Klaassen M. Mechanistic models of animal migration behaviour–their diversity, structure and use. Journal of Animal Ecology. 2013;82:498–508. doi: 10.1111/1365-2656.12054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourouiba L, Teslya A, Wu J. Highly pathogenic avian influenza outbreak mitigated by seasonal low pathogenic strains: insights from dynamic modelling. Journal of Theoretical Biology. 2011;271:181–201. doi: 10.1016/j.jtbi.2010.11.013. [DOI] [PubMed] [Google Scholar]
- Bowlin MS, Bisson I-A, Shamoun-Baranes J, Reichard JD, Sapir N, Marra PP, Kunz TH, Wilcove DS, Hedenström A, Guglielmo CG, Åkesson S, Ramenofsky M, Wikelski M. Grand challenges in migration biology. Integrative and Comparative Biology. 2010;50:261–279. doi: 10.1093/icb/icq013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley CA, Altizer S. Parasites hinder monarch butterfly flight: implications for disease spread in migratory hosts. Ecology Letters. 2005;8:290–300. [Google Scholar]
- Bradshaw WE, Holzapfel CM. Evolutionary response to rapid climate change. Science. 2006;312:1477–1478. doi: 10.1126/science.1127000. [DOI] [PubMed] [Google Scholar]
- Breban R, Drake J, Stallknecht D, Rohani P. The role of environmental transmission in recurrent avian influenza epidemics. PLoS Computational Biology. 2009;5:e1000346. doi: 10.1371/journal.pcbi.1000346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brower LP, Malcolm SB. Animal migrations: endangered phenomena. American Zoologist. 1991;31:265–276. [Google Scholar]
- Cross PC, Cole EK, Dobson AP, Edwards WH, Hamlin KL, Luikart G, Middleton AD, Scurlock BM, White PJ. Probable causes of increasing brucellosis in free-ranging elk of the Greater Yellowstone Ecosystem. Ecological Applications. 2010;20:278–288. doi: 10.1890/08-2062.1. [DOI] [PubMed] [Google Scholar]
- Dingle H. Migration: the biology of life on the move. Oxford, UK: Oxford University Press; 1996. p. 480. [Google Scholar]
- Figuerola J, Green AJ. Haematozoan parasites and migratory behaviour in waterfowl. Evolutionary Ecology. 2000;14:143–153. [Google Scholar]
- Folstad I, Nilssen AC, Halvorsen O, Andersen J. Parasite avoidance: the cause of post-calving migrations in Rangifer? Canadian Journal of Zoology. 1991;69(9):2423–2429. [Google Scholar]
- Frick WF, Pollock JF, Hicks AC, Langwig KE, Reynolds DS, Turner GG, Butchkoski CM, Kunz TH. An emerging disease causes regional population collapse of a common North American bat species. Science. 2010;329:679–682. doi: 10.1126/science.1188594. [DOI] [PubMed] [Google Scholar]
- Hayman DT, Yu M, Crameri G, Wang LF, Suu-Ire R, Wood JL, Cunningham AA. Ebola virus antibodies in fruit bats, Ghana, West Africa. Emerging Infectious Diseases. 2012;18(7):1207. doi: 10.3201/eid1807.111654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hebblewhite M, Merrill EH. Multiscale wolf predation risk for elk: does migration reduce risk? Oecologia. 2007;152:377–387. doi: 10.1007/s00442-007-0661-y. [DOI] [PubMed] [Google Scholar]
- Iwamura T, Possingham HP, Chadès I, Minton C, Murray NJ, Rogers DI, Fuller RA. Migratory connectivity magnifies the consequences of habitat loss from sea-level rise for shorebird populations. Proceedings of the Royal Society B: Biological Sciences. 2013;280(1761) doi: 10.1098/rspb.2013.0325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klaassen RHG, Hake M, Strandberg R, Koks BJ, Trierweiler C, Exo K-M, Barlein F, Alerstam T. When and where does mortality occur in migratory birds ? Direct evidence from long-term satellite tracking of raptors. Journal of Animal Ecology. 2014 doi: 10.1111/1365-2656.12135. in press. [DOI] [PubMed] [Google Scholar]
- Krauss S, Stallknecht DE, Negovetich NJ, Niles LJ, Webby RJ, Webster RG. Coincident ruddy turnstone migration and horseshoe crab spawning creates an ecological ‘hot spot’ for influenza viruses. Proceedings of the Royal Society B: Biological Sciences. 2010;277:3373–3379. doi: 10.1098/rspb.2010.1090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krkošek M, Gottesfel A, Proctor B, Rolston D, Carr-Harrins C, Lewis MA. Effects of host migration, diversity and aquaculture on sea lice threats to Paci.c salmon populations. Proceedings of the Royal Society Biological Sciences Series B. 2007;274:3141–3149. doi: 10.1098/rspb.2007.1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutz, Susan J, Checkley Sylvia, Verocai Guilherme G, Dumond Mathieu, Hoberg Eric P, Peacock Rod, Wu Jessica P, et al. Invasion, establishment, and range expansion of two parasitic nematodes in the Canadian Arctic. Global Change Biology. 2013 doi: 10.1111/gcb.12315. [DOI] [PubMed] [Google Scholar]
- Loehle C. Social barriers to pathogen transmission in wild animal populations. Ecology. 1995;76:326–335. [Google Scholar]
- McKinnon K, Smith PA, Nol E, Martin JL, Doyle FI, Abraham KF, Gilchrist HG, Morrison RIG, Bêty J. Lower predation risk for migratory birds at high latitudes. Science. 2010;327:326–327. doi: 10.1126/science.1183010. [DOI] [PubMed] [Google Scholar]
- Otto SP, Day T. A biologist’s guide to mathematical modeling in ecology and evolution. Princeton, NJ: Princeton University Press; 2007a. Determining the stability of equilibria; pp. 298–301. [Google Scholar]
- Otto SP, Day T. A biologist’s guide to mathematical modeling in ecology and evolution. Princeton, NJ: Princeton University Press; 2007b. Evolutionary invasion analysis; pp. 454–502. [Google Scholar]
- Owen, et al. Migrating birds as dispersal vehicles of West Nile virus. Ecohealth. 2006;3:79–85. [Google Scholar]
- Partecke J, Gwinner E. Increased sedentariness in European blackbirds following urbanization: a consequence of local adaptation? . Ecology. 2007;88(4):882–890. doi: 10.1890/06-1105. [DOI] [PubMed] [Google Scholar]
- Plowright RK, Foley P, Field HE, Dobson AP, Foley JE, Eby P, Daszak P. Urban habituation, ecological connectivity and epidemic dampening: the emergence of Hendra virus from flying foxes (Pteropus spp.) . Proc. R. Soc. B. 2011;22:3703–3712. doi: 10.1098/rspb.2011.0522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rappole JH, Derrickson SR, Hubálek Z. Migratory birds and spread of West Nile virus in the Western hemisphere. Emerging Infectious Diseases. 2000;6:319–328. doi: 10.3201/eid0604.000401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson WD, Bowlin MS, Bisson I, Shamoun-Baranes J, Thorup K, Diehl RH, Kunz TH, Mabey S, Winkler DW. Integrating concepts and technologies to advance the study of bird migration. Frontiers in Ecology and the Environment. 2010;8:354–361. [Google Scholar]
- Sillett TS, Holmes RT. Variation in survivorship of a migratory songbird throughout its annual cycle. Journal of Animal Ecology. 2002;71:296–308. [Google Scholar]
- Sorte FAL, Thompson FR., III Poleward shifts in winter ranges of North American birds. Ecology. 2007;88(7):1803–1812. doi: 10.1890/06-1072.1. [DOI] [PubMed] [Google Scholar]
- Taylor CM, Norris DR. Population dynamics in migratory networks. Theoretical Ecology. 2010;3:65–73. [Google Scholar]
- Taylor CM, Hall RJ. Metapopulation models for seasonally migratory animals. Biology Letters. 2012;8:477–480. doi: 10.1098/rsbl.2011.0916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Gils JA, Munster VJ, Radersma R, Liefhebber D, Fouchier RA, Klaassen M. Hampered foraging and migratory performance in swans infected with low-pathogenic avian influenza A virus. PLoS One. 2007;2(1):e184. doi: 10.1371/journal.pone.0000184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waldenström J, Bensch S, Kiboi S, Hasselquist D. Cross-species infection of blood parasites between resident and migratory songbirds in Africa. Molecular Ecology. 2002;11:1545–1554. doi: 10.1046/j.1365-294x.2002.01523.x. [DOI] [PubMed] [Google Scholar]
- Weber TP, Stilianakis NI. Ecologic immunology of avian influenza (H5N1) in migratory birds. Emerging Infectious Diseases. 2007;13(8):1139. doi: 10.3201/eid1308.070319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcove SD, Wikelski M. Going, going, gone: is animal migration disappearing? PLoS Biology. 2008;6(7):e188. doi: 10.1371/journal.pbio.0060188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wunder MB. Determining geographic patterns of migration and dispersal using stable isotopes in keratins. Journal of Mammalogy. 2012;93:360–367. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.