Two approximations for the geometric model of signal amplification in an electron-multiplying charge-coupled device detector

Abstract

The extraction of information from images acquired under low light conditions represents a common task in diverse disciplines. In single molecule microscopy, for example, techniques for superresolution image reconstruction depend on the accurate estimation of the locations of individual particles from generally low light images. In order to estimate a quantity of interest with high accuracy, however, an appropriate model for the image data is needed. To this end, we previously introduced a data model for an image that is acquired using the electron-multiplying charge-coupled device (EMCCD) detector, a technology of choice for low light imaging due to its ability to amplify weak signals significantly above its readout noise floor. Specifically, we proposed the use of a geometrically multiplied branching process to model the EMCCD detector’s stochastic signal amplification. Geometric multiplication, however, can be computationally expensive and challenging to work with analytically. We therefore describe here two approximations for geometric multiplication that can be used instead. The high gain approximation is appropriate when a high level of signal amplification is used, a scenario which corresponds to the typical usage of an EMCCD detector. It is an accurate approximation that is computationally more efficient, and can be used to perform maximum likelihood estimation on EMCCD image data. In contrast, the Gaussian approximation is applicable at all levels of signal amplification, but is only accurate when the initial signal to be amplified is relatively large. As we demonstrate, it can importantly facilitate the analysis of an information-theoretic quantity called the noise coefficient.

1. INTRODUCTION

The electron-multiplying charge-coupled device (EMCCD) detector is a standard imaging technology in application areas such as single molecule microscopy¹ where relatively weak signals need to be detected from the objects of interest. Just as in the case of a charge-coupled device (CCD) detector, an EMCCD detector accumulates electrons in its pixels in proportion to the number of photons that are detected. Unlike a CCD detector, however, an EMCCD detector contains a multiplication register that can amplify the number of electrons to such an extent that the detector’s readout noise is rendered insignificant compared to the augmented signal. Therefore, whereas the CCD detector is unsuitable for imaging under low light conditions where weak signals are easily overwhelmed by its readout noise, the EMCCD detector is the technology of choice for low light imaging applications.

Signal amplification by the multiplication register of an EMCCD detector is stochastic in nature, and is typically modeled^2–4 as a branching process.⁵ Previously,⁶ we described the amplification using a geometrically multiplied branching process, and by doing so, we obtained a probability distribution for the data in an EMCCD pixel. This probability distribution is useful for purposes such as the derivation⁶ of the Fisher information matrix⁷ corresponding to an EMCCD image, which can in turn be used to calculate the Cramer-Rao lower bound on the variance for estimating a quantity of interest from the image. In our earlier work,⁶ for example, we calculated the Fisher information matrix pertaining to an image of a point source, and the Cramer-Rao lower bound for estimating the positional coordinates of a point source from its image. The point source localization problem^{8, 9} is of practical importance for single molecule microscopy, since applications like superresolution imaging and single particle tracking depend ultimately on the accuracy with which the position of a single molecule can be determined.

While exact, the probability distribution based on the geometrically multiplied branching process is complex, and may be time-consuming to compute and difficult to work with analytically. Computational time is of particular practical importance, since commonly employed data analysis methods such as maximum likelihood estimation require that the probability distribution be repeatedly calculated with different values of the parameters on which it depends. Here, we give two approximations for the geometric multiplication-based probability distribution. The high gain approximation applies when a high level of signal amplification is used, a scenario which corresponds to the typical use of an EMCCD detector at high electron multiplication (EM) gain. Besides being an accurate approximation of the exact probability distribution, it is applicable regardless of the initial signal level in a pixel (i.e., regardless of the number of electrons initially accumulated in a pixel), and requires less time to compute. We have therefore used the high gain approximation to carry out^{4, 6} maximum likelihood estimation on image data. The Gaussian approximation, in contrast, applies at all levels of signal amplification, but only when the initial signal level in a pixel is relatively high. We will use the Gaussian approximation to analytically assess the behavior of an information-theoretic quantity called the noise coefficient,^{4, 6} and to relate the noise coefficient to the well-known excess noise factor^{2, 10, 11} that is found in electron multiplication literature.

As is the case with our earlier work,⁶ the material presented here comprises a subset of the content of our journal article.⁴ In Section 2, geometric multiplication is briefly introduced, and the exact probability distribution that follows from it is given. In Section 3, we show how the high gain approximation of the exact probability distribution is obtained, and demonstrate that it is a good approximation at any initial signal level, but only when the signal amplification level (i.e., the EM gain) is high. In Section 4, we describe how the Gaussian approximation of the exact probability distribution is obtained, and demonstrate its applicability at relatively high initial signal levels. Importantly, we illustrate its usefulness by employing it for the analysis of the noise coefficient.

2. STANDARD GEOMETRIC MULTIPLICATION PROBABILITY DISTRIBUTION

We model electron multiplication in an EMCCD pixel as a branching process⁵ that is geometrically multiplied. Specifically, the branching process is one where an initial Poisson-distributed number of signal electrons are fed into a series of stages, and where in each stage, an input electron generates a total of k electrons, including itself, according to the standard geometric distribution

$$p_k=(1-b)b^{k-1},k=1,2,\dots ,0\le b<1.$$ (1)

It is easily verified that the standard geometric distribution has mean $m=\frac{1}{1-b}$ and variance ${\sigma }^2=\frac{b}{{(1-b)}^2}$. Note that a more general geometric distribution that subsumes the standard geometric distribution was presented in our earlier work.⁶ Also, a Poisson random variable is used to model the number of electrons initially accumulated in a pixel because photon emission by an object of interest, and hence photon detection by a camera, are typically described as Poisson processes.

Using the theory of probability generating functions, a probability distribution was previously derived⁴ for the number of electrons X_N at the output of an N-stage branching process with an initial Poisson-distributed number of electrons and a standard geometric model of multiplication. The probability mass function obtained is given by

$$p_{\mathit{Geom}}(x)=\{\begin{array}{ll}{e}^{-\nu },\hfill & x=0,\hfill \\ e^{-\nu }{\sum }_{j=0}^{x-1}\frac{\left(\begin{array}{c}x-1\\ j\end{array}\right)}{(j+1)!}{\left(1-\frac{1}{m^N}\right)}^{x-1-j}{\left(\frac{\nu }{m^N}\right)}^{j+1},\hfill & x=1,2,\dots ,\hfill \end{array}$$ (2)

where ν > 0 is the mean of the initial Poisson-distributed number of signal electrons, and the term m^N is the average number of electrons at the output of the branching process given a single initial electron. The term m^N is commonly called the mean gain of the branching process, and in the context of EMCCD modeling, it is the EM gain of the EMCCD detector. Note that when modeling the data in an EMCCD pixel, a Gaussian random variable representing the readout noise at the pixel is normally added to the amplified signal X_N (see our earlier work^{4, 6}). This is not done here, however, as it suffices for our current purposes to consider only the amplified signal.

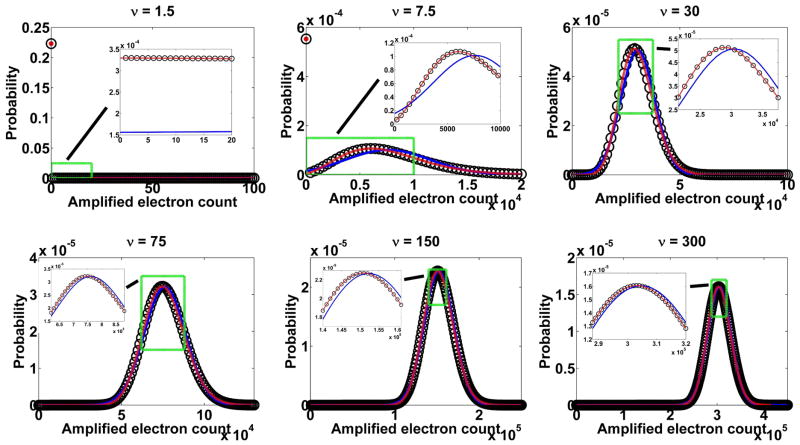
Figure 1 plots, in open circles, the probability mass function p_Geom of Eq. 2 for a relatively high EM gain of m⁵³⁶ = 1015.46, and six different values of the mean initial electron count ν. (Note that the value of N is set to 536 to correspond to the number of multiplication stages in a CCD97 chip (E2V Technologies, Chelmsford, UK), a sensor which is used in many EMCCD cameras.) For small values of ν (1.5 and 7.5), the shape of the function is characterized by a large value at x = 0. This is because the amplified number of electrons will be 0 whenever the initial electron count is 0, an event that is likely given the small ν. However, as ν becomes larger, the shape of the probability mass function starts to resemble that of a Gaussian density function (see Section 4).

Figure 1.

Probability mass function (Eq. 2) of X₅₃₆, the electron count at the output of a 536-stage branching process with a standard geometric (○) model of multiplication and a mean gain of m⁵³⁶ = 1015.46, for six different values of the mean ν of the Poisson-distributed initial electron count. For each value of ν, the probability density functions resulting from the high gain approximation (Eq. 8) (red curve) and the Gaussian approximation (Eq. 11) (blue curve) of the output of the standard geometric multiplication are also shown.

The noise coefficient^{4, 6} is a nonnegative scalar that indicates the amount of information the data in a pixel contains about the quantities of interest (e.g., the positional coordinates of a single molecule) that are to be estimated from an image. The larger its value, the greater the amount of information the data in the pixel contains. Importantly, the noise coefficient can be computed for different data models (e.g., EMCCD, CCD, etc.), and used to compare^{4, 6} the information content of the different models as a function of the initial signal level. In addition to using the probability distribution itself, we will compare the approximations of Sections 3 and 4 with the geometric multiplication-based distribution using their respective noise coefficients. In Section 4, we will also use the Gaussian approximation to analyze the behavior of the noise coefficient. We therefore give here the noise coefficient α_Geom which corresponds to the geometric multiplication-based distribution:

$${\alpha }_{\mathit{Geom}}=\nu ·\left[\sum _{x=1}^{\infty }\frac{e^{-2\nu }}{p_{\mathit{Geom}}(x)}{\left(\sum _{j=0}^{x-1}\left(\begin{array}{c}x-1\\ j\end{array}\right){\left(1-\frac{1}{m^N}\right)}^{x-1-j}{\left(\frac{1}{m^N}\right)}^{j+1}\frac{{\nu }^j}{j!}\right)}^2-1\right].$$ (3)

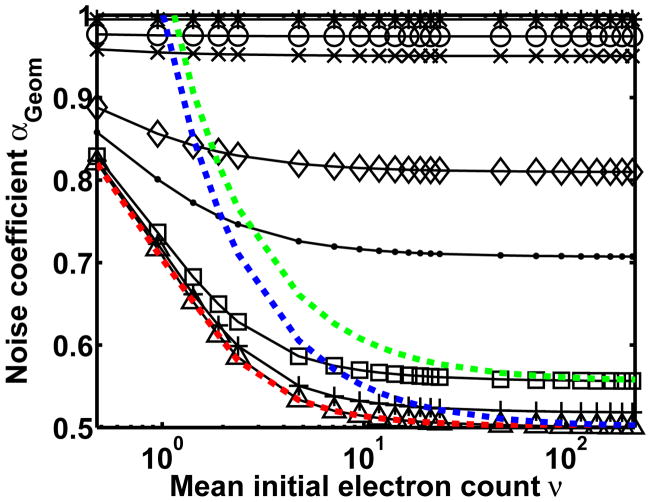
Figure 2 plots the noise coefficient α_Geom of Eq. 3 as a function of the mean ν of the initial signal electron count. It shows curves for different values of the EM gain m^N, ranging from a low value of 1.01 to a high value of 1015.46. For a given value of ν, Fig. 2 shows that multiplication with a higher gain results in a smaller value of α_Geom, indicating that the amount of stochasticity added to the data is proportional to the EM gain, and that the information content of a pixel is inversely proportional to the mean gain. Moreover, for each EM gain value, we see that the value of α_Geom decreases with increasing values of ν, suggesting that the amount of stochasticity added to the data is proportional to the level of the signal to be amplified.

Figure 2.

Noise coefficient α_Geom (Eq. 3), for the scenario of a Poisson-distributed signal that is amplified by multiplication. The noise coefficient is shown as a function of the mean ν of the signal, which ranges in value from 0.48 to 213.79. The signal is amplified through N = 536 stages of standard geometric multiplication, and the different curves correspond to mean gain values of m^N = 1.01 (*), 1.03 (○), 1.06 (×), 1.31 (◇), 1.71 (·), 4.98 (□), 14.49 (+), and 1015.46 (△). The red curve represents the noise coefficient α_H (Eq. 10) of the high gain approximation, while the blue and green curves represent the noise coefficient α_Gauss (Eq. 13) of the Gaussian approximation for mean gains of 1015.46 and 4.98, respectively.

3. HIGH GAIN APPROXIMATION

In this section, we derive the high gain approximation of the geometric multiplication-based probability distribution. The result makes for an accurate approximation that is computationally less expensive, and can be used to carry out the maximum likelihood estimation of quantities of interest.^{4, 6} Note that while we will work with the standard geometric distribution here, a derivation that assumes a more general geometric distribution can be found in our earlier work.⁴

Let (X_n)_n=0,1,… be a branching process with initial electron count X₀ = 1 and multiplication characterized by the standard geometric distribution (see Eq. 1) with mean $m=\frac{1}{1-b}>1$ (i.e., with 0 < b < 1). Then it has been shown⁵ that as the number of multiplication stages n converges to infinity, the sequence of random variables (Y_n = X_n/mⁿ)_n=0,1,… converges, with probability 1 and in mean square, to a random variable Y with an exponential distribution given by

$$p(y)=e^{-y},y>0.$$ (4)

Based on this result, for a large N, the electron count X_N at the output of an N-stage branching process with initial electron count X₀ = 1 and multiplication characterized by the standard geometric distribution with mean $m=\frac{1}{1-b}>1$ (i.e., with 0 < b < 1) can be approximated by the random variable m^N Y, whose probability density function can be verified to be a scaled version of Eq. 4:

$$p(x)=\frac{1}{m^N}{e}^{-\frac{x}{m^N}},x>0.$$ (5)

If instead the branching process has an initial electron count of X₀ = j, j = 1, 2, …, then the distribution of the output electron count X_N can be approximated by the j-fold convolution of p(x) of Eq. 5 with itself. The resulting conditional probability density function can be shown to be, for $m=\frac{1}{1-b}>1$,

$$p(x\mid j)=\frac{e^{-\frac{x}{m^N}}}{m^N(j-1)!}{\left(\frac{x}{m^N}\right)}^{j-1},x>0.$$ (6)

To obtain the approximating probability density function for the case where the initial electron count X₀ is Poisson-distributed with parameter ν > 0, we simply substitute Eq. 6 into the general density function⁴

$$p(x)=\{\begin{array}{ll}{e}^{-\nu },\hfill & x=0,\hfill \\ e^{-\nu }{\sum }_{j=1}^{\infty }\frac{p(x\mid j){\nu }^j}{j!},\hfill & x>0,\hfill \end{array}$$ (7)

which is easily obtained using the law of total probability. The resulting high gain approximation probability density function p_H is given by

$$p_H(x)=\{\begin{array}{ll}{e}^{-\nu },\hfill & x=0,\hfill \\ \frac{e^{-\left(\frac{x}{m^N}+\nu \right)}\sqrt{\nu x/m^N}{I}_1\left(2\sqrt{\nu x/m^N}\right)}{x},\hfill & x>0,m=\frac{1}{1-b},0<b<1,\hfill \end{array}$$ (8)

where I₁ is the first order modified Bessel function of the first kind. Note that in the context of modeling EMCCD signal amplification, Eq. 8 has previously appeared³ in an equivalent form, without the jump at x = 0 and without the modified Bessel function representation. It can also be found in identical form elsewhere.¹²

According to its derivation, the high gain approximation can be expected to apply only in the case of a large EM gain. For illustration, the probability density function of Eq. 8 is shown, for a relatively high EM gain of m⁵³⁶ = 1015.46, as a red curve in each plot of Fig. 1. For each of the six values of the mean initial electron count ν, a close agreement can be seen between this density function and the probability mass function of Eq. 2 (○).

The noise coefficient corresponding to the high gain approximation can be obtained by substituting Eqs. 8 and 6 into the general noise coefficient expression⁴

$$\alpha =\nu ·\left[{\int }_0^{\infty }\frac{1}{p(x)}{\left(e^{-\nu }\sum _{j=1}^{\infty }\frac{p(x\mid j){\nu }^{j-1}}{(j-1)!}\right)}^{2}dx-1\right].$$ (9)

The result, denoted by α_H, is given by

$${\alpha }_H=\nu ·\left[\frac{e^{-\nu }}{4{\nu }^2}{\int }_0^{\infty }\frac{x^2{e}^{-\frac{x^2}{4\nu }}{I}_0^2(x)}{I_1(x)}dx-1\right],$$ (10)

where I₀ is the zeroth order modified Bessel function of the first kind. Note that whereas the EM gain m^N is present in the density function of Eq. 8, it disappears by simple substitution in deriving the noise coefficient of Eq. 10.

As in the case of the probability distribution comparison, a close match can be seen in Fig. 2 between the noise coefficient α_H of Eq. 10 (red curve) and the noise coefficient α_Geom of Eq. 3 computed for the high EM gain of m⁵³⁶ = 1015.46 (△). The figure also demonstrates that the agreement between α_H (which again does not depend on the EM gain m^N) and α_Geom becomes increasingly poor with decreasing EM gain values for α_Geom.

4. GAUSSIAN APPROXIMATION

In this section, we present a Gaussian approximation of the geometric multiplication-based probability distribution. Besides being computationally inexpensive, the expressions associated with the Gaussian approximation allow for relatively simple analytical studies. We will provide examples by analyzing the noise coefficient as a function of the EM gain and the mean initial electron count in a pixel.

Unlike the high gain approximation, the applicability of the Gaussian approximation is not restricted to geometric multiplication. The approximation is based on the general result^{2, 3} that given a large initial electron count, the probability distribution of the output electron count Y of a branching process can be approximated by a Gaussian distribution with the same mean and variance as that of Y. For an N-stage branching process with an initial electron count that is Poisson-distributed with mean ν > 0 and a multiplication model that is characterized by the probability distribution (p_k)_k=0,1,…, the mean and variance of the number of electrons X_N at its output are η_x = m^N ν and ${\sigma }_x^2=\nu \left(\frac{{\sigma }^2{m}^{N-1}(m^N-1)}{m-1}+m^{2N}\right)$, respectively, where m > 0, m ≠ 1 is the mean of (p_k)_k=0,1,…, and σ² ≥ 0 is the variance of (p_k)_k=0,1,…. Therefore, given that the initial electron count is large, the amplified signal can be approximated by a Gaussian random variable X with probability density function

$$p_{\mathit{Gauss}}(x)=\frac{1}{\sqrt{2\pi {\sigma }_x^2}}·e^{-\frac{{(x-{\eta }_x)}^2}{2{\sigma }_x^2}},x\in ℝ.$$ (11)

By substituting $m=\frac{1}{1-b}$ and ${\sigma }^2=\frac{b}{{(1-b)}^2}$ for the standard geometric distribution of Eq. 1 into the expressions for η_x and ${\sigma }_x^2$, the density function of Eq. 11 is plotted, for an EM gain of m⁵³⁶ = 1015.46, as a blue curve in Fig. 1 for each of the six values of the mean initial electron count ν. We see that for small values of ν, the Gaussian density matches poorly with the probability mass function of Eq. 2 (○). However, with increasing values of ν, the Gaussian density starts to coincide more and more with the mass function. This is expected, since the Gaussian approximation is predicated on the initial electron count being large.

The noise coefficient corresponding to the Gaussian density function of Eq. 11 is given by⁴

$${\alpha }_{\mathit{Gauss}}=\nu ·\left[\frac{1}{{\sigma }_x^2}{\left(\frac{\partial {\eta }_x}{\partial \nu }\right)}^2+\frac{1}{2{\sigma }_x^4}{\left(\frac{\partial {\sigma }_x^2}{\partial \nu }\right)}^2\right],$$ (12)

which is based on the well-known expression for the Fisher information of a Gaussian random variable.¹³ Evaluating the derivatives and simplifying, a more explicit expression is obtained:

$${\alpha }_{\mathit{Gauss}}={\left(\frac{{\sigma }^2\left(1-\frac{1}{m^N}\right)}{m(m-1)}+1\right)}^{-1}+\frac{1}{2\nu },m>0,m\ne 1,{\sigma }^2\ge 0.$$ (13)

Substituting $m=\frac{1}{1-b}$ and ${\sigma }^2=\frac{b}{{(1-b)}^2}$ for the standard geometric distribution into Eq. 13, and setting the EM gain to m⁵³⁶ = 1015.46, Fig. 2 shows that, for small values of ν, α_Gauss (blue curve) is in poor agreement with α_Geom of Eq. 3 that has been computed for the same EM gain (△). With increasing values of ν, however, it becomes an increasingly better match of α_Geom. Hence, unlike the high gain approximation which applies for all values of ν, the Gaussian approximation is only appropriate for large value of ν. This is again expected, since the Gaussian approximation assumes a large initial electron count. However, unlike the high gain approximation, the Gaussian approximation can be used for low EM gain values. For example, Fig. 2 shows that for a low EM gain of m⁵³⁶ = 4.98, α_Gauss (green curve) similarly becomes an increasingly better match of α_Geom (□) with increasing values of ν.

We next demonstrate how the Gaussian approximation can be useful for analytical studies. To give a simple example, it can be seen directly from Eq. 13 that the noise coefficient is dependent on the inverse of ν, indicating that multiplication is more beneficial when low initial signal levels are expected. This is consistent with what is observed for the α_Geom curves in Fig. 2.

Interestingly, the expression $\frac{{\sigma }^2(1-1/m^N)}{m(m-1)}+1$ in Eq. 13 is easily verifiable to be the excess noise factor for the case of a Poisson-distributed initial electron count. In electron multiplication literature,^{2, 10, 11} the excess noise factor is defined as the ratio of the variance of the output electron count of a multiplication process to the variance of the initial electron count, normalized by the square of the EM gain. It is thus a measure of the increase in the stochasticity of the data due to the signal amplification.

By letting the EM gain m^N converge to infinity in Eq. 13, and substituting $m=\frac{1}{1-b}$ and ${\sigma }^2=\frac{b}{{(1-b)}^2}$ for standard geometric multiplication, Eq. 13 becomes

$${\alpha }_{\mathit{Gauss}}=\frac{1}{2}+\frac{1}{2\nu }.$$ (14)

Therefore, in the limit that the EM gain converges to infinity, standard geometric multiplication yields an excess noise factor (i.e., the inverse of the first summand in Eq. 14) of 2, indicating a twofold increase in the stochasticity of the data due to the high gain signal amplification. This result is interestingly consistent with what has been reported^{10, 14} for the Bernoulli model of multiplication, which is commonly used to describe electron multiplication in an EMCCD detector.

If we further let the mean initial electron count ν converge to infinity in Eq. 14, we obtain α_Gauss = 0.5. This importantly suggests that when standard geometric multiplication with a high gain is unnecessarily used to amplify an already large initial signal, the information content of the amplified signal will be no less than half of the information content corresponding to the ideal best-case scenario where the noise coefficient has the value 1.^{4, 6} The best-case scenario is the hypothetical scenario where the original signal in a pixel can be read out from the detector without being corrupted by noise of any kind. This result is consistent with the α_Geom curves in Fig. 2, which suggest that α_Geom converges to 0.5 as the EM gain and ν are increased.