Cellular Communication and Heterogeneity in Pancreatic Islet Insulin Secretion Dynamics

Abstract

Coordinated pulses of electrical activity and insulin secretion are a hallmark of the islet of Langerhans. These coordinated behaviors are lost when β-cells are dissociated, which also leads to increased insulin secretion at low glucose. Islets without gap junctions exhibit asynchronous electrical activity similar to dispersed cells, but their secretion at low glucose is still clamped off, putatively by a juxtacrine mechanism. Mice lacking β-cell gap junctions have near-normal average insulin levels, but are glucose intolerant due to reduced first-phase and pulsatile insulin secretion, illustrating the importance of temporal dynamics. We review the quantitative data on islet synchronization and the current mathematical models that have been developed to explain these behaviors and generate greater understanding of the underlying mechanisms.

The Unique Properties of the Pancreatic Islet Are Important for Blood Glucose Homeostasis

The islet of Langerhans (see Glossary) is a pancreatic micro-organ comprised of a majority of β-cells, which play a central role in blood glucose homeostasis through dose-dependent and regulated insulin secretion [1]. There are several important properties of insulin secretion that are unique to the intact islet: 1) near-zero insulin secretion at glucose levels < 3 mM; 2) a steep sigmoidal secretory response to glucose; 3) a peaked first phase of insulin secretion; 4) coordinated secretory pulses during second phase insulin secretion; and 5) increased insulin secretion at glucose levels >11 mM. All of these behaviors are lost upon dispersion of the islet into individual β-cells, which exhibit significant heterogeneities [2, 3].

In normal physiology of humans and rodents, a first peaked phase of insulin secretion (~5-10 min) is followed by a sustained second phase during which pulses of insulin are secreted with a 3-8 minute period [4, 5]. The full implications of the two secretory phases and insulin pulsatility is poorly understood, but increasing evidence points to major roles in blood glucose homeostasis [6-10]. First phase insulin secretion and insulin pulsatility are both reduced and eventually lost as Type 2 diabetes (T2D) progresses [11], and these losses correlate with long-term complications of diabetes. Pulsatile insulin secretion leads to enhanced suppression of hepatic glucose production [10], and therapeutic insulin pulses have been postulated as an improved diabetes treatment [6, 7]. Insulin pulsatility depends on oscillations in membrane potential, intracellular free calcium ([Ca²⁺]_i) [12], and cAMP [13], and are recapitulated in isolated islets. Cell interactions between β-cells play a key role in islet function, since dissociated β-cells exhibit different insulin secretion profiles than do those within intact islets [14, 15]. Functional coordination among β-cells was first observed by electrophysiology [16] with further evidence from measurements of [Ca²⁺]_i [17], interstitial K⁺ [18, 19], and insulin secretion [20].

Despite a preponderance of evidence regarding its multicellular nature, many of the current paradigms underlying islet biology are based on single cell studies and concepts, which includes many mathematical models. We are now beginning to understand quantitatively how these properties of islet behavior arise from multicellular interactions, and how cellular heterogeneity forms an important basis for islet behavior. Here, we will describe key experimental data that reveal various aspects of cellular communication between β-cells in the islet and present mathematical models that have been used to describe and predict islet function, with an emphasis on models based on its specific multi-cellular structure

β-cell Heterogeneity and Gap Junctions

All of the coordinated events described above are lost upon dispersion of the islet into individual β-cells, which exhibit significant heterogeneities [2, 3]. Dispersed β-cells show heterogeneous glucose transport [21], insulin biosynthesis [2], glucose sensitivity of metabolism [22], [Ca²⁺] response and dynamics [23], and insulin secretion [24-26], but most manifestations of these cellular heterogeneities are lost within the intact islet. Deletion of the glucose sensor, glucokinase (GK), in ~30% of β-cells leads to a heterogeneous distribution of metabolic responses within the islet [27]. However, the overall islet electrical activity and insulin secretion profiles from these islets was unchanged from wild-type islets, which shows the importance of cell coupling in creating a homogeneous response from the heterogeneous population of β-cells. Recently, incretin action was shown to play a role in maintaining coordinated islet activity during lipotoxicity in mice and humans, although the molecular determinants of this effect remain to be defined [28, 29].

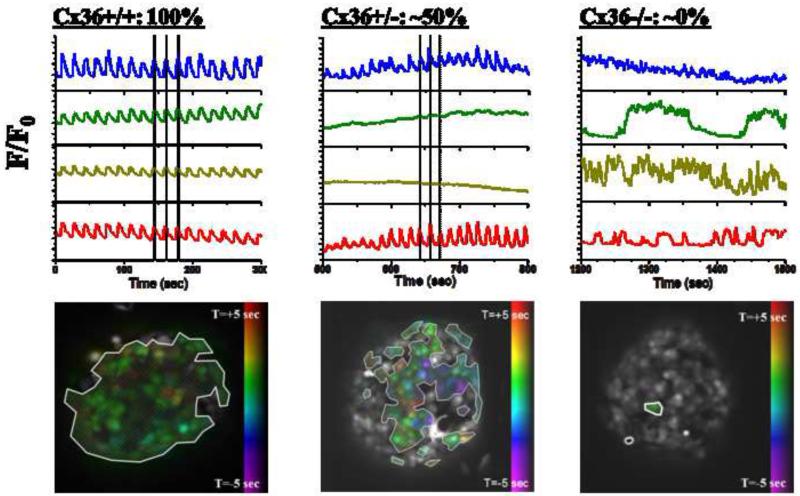
Gap junctions are intercellular channels that allow the direct transfer of ions and second messengers between adjacent cells. β-cell gap junctions were initially detected by EM [30] and functionally characterized by dye coupling [31] and electrophysiology [32]. After twenty years of research (reviewed in [33]), the biophysical properties of β-cell gap junctions pointed to connexin 36 (Cx36) as the pore forming unit in the islet [34], and this was quickly confirmed using mice lacking the Cx36 gene (Cx36^−/−), whose islets do not show synchronous oscillations in [Ca²⁺]_i and insulin release [35]. β-cells within Cx36^−/− islets exhibit random [Ca²⁺]_i oscillations similar to those measured in dispersed β-cells from either normal or Cx36^−/− islets (Fig. 1) [36, 37], and [Ca²⁺]_i waves are also lost in the Cx36^−/− islets [37].

Figure 1. Experimental dependence of [Ca²⁺]_i dynamics of gap junction coupling.

Representative oscillations of [Ca²⁺]_i in 4 cells of an islet, together with phase map of [Ca²⁺]_i oscillations, where colored cells show oscillations that are synchronized with other colored cells, whereas uncolored (grey) cells show poorly synchronized oscillations or absence of oscillations. Oscillations and phase map are displayed for a wild-type islet with normal gap junction coupling (left, Cx36, 100%); an islet from a mouse with a heterozygous knockout of Cx36 which has ~50% gap junction conductance (middle, Cx36+/−, 50%); and an islet from a mouse with a homozygous knockout of Cx36 which has ~0% gap junction conductance (right, Cx36−/−, 50%). Note the transition between regular, near-fully synchronized oscillations, and heterogeneous irregular an uncoordinated oscillations as Cx36 is reduced. Figure adapted from [37].

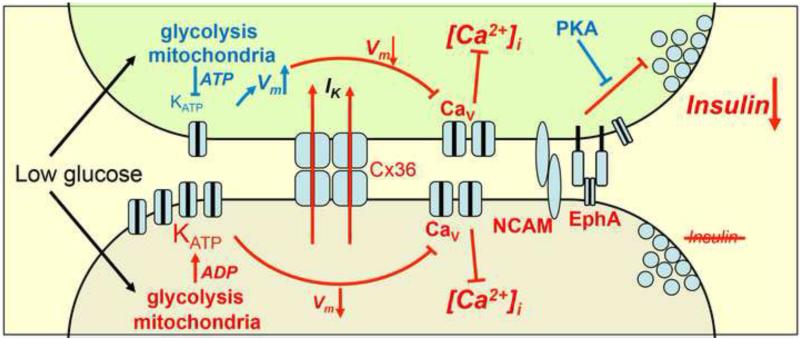
Together, these data strongly suggest that the synchronized electrical activity of the islet arises from gap junction coupling by Cx36 subunits, so it was expected that Cx36 also regulates the release of insulin in the same fashion. It has long been recognized that intact islets secrete more insulin in response to elevated glucose than do dispersed β-cells, and that at low glucose levels, the insulin released from dispersed β-cells is much greater than that from intact islets [38]. The first data on Cx36^−/− islets suggested that gap junctions may explain the differences in secretion between islets and dispersed cells, as insulin levels at non-stimulatory glucose concentrations (~3 mM) were significantly higher out of perfused pancreata from Cx36^−/− mice, than from wild-type mice [35]. This observation was consistent with the model that β-cells with the lowest glucose thresholds depolarize and undergo [Ca²⁺]_i fluctuations [36, 39]. However, measurements on isolated islets gave similar insulin secretion profiles for Cx36^−/− and wild-type islets, even though dispersed β-cells from either set of islets showed significantly increased insulin release. These findings suggest that another cellular interaction mechanism beyond gap junctions is required for normal islet function [40]. Several possible non-gap junction communication mechanisms have been hypothesized between β-cells in the islet, including paracrine signaling by NO [41] and/or ATP [42]. The EphA-ephrin-A juxtacrine signaling system has also been shown to be necessary for normal glucose-stimulated insulin secretion [43], and its putative role in down-regulating insulin secretion at low glucose levels is consistent with the observed data from Cx36^−/− islets (Fig. 2). Regardless of the exact molecules involved, the multiple regulatory mechanisms within the islet complicate mathematical modeling of its function (see modeling section below).

Figure 2. Schematic of cellular interactions that regulate insulin release.

Two representative heterogeneous cells in an islet that have different threshold for glucose activation of Ca²⁺-signaling which may arise for many reasons but here is indicated as different K_ATP activation. At basal glucose levels, one cell (upper, green shaded) is more excitable and in isolation would depolarize and fire action potentials, whereas the other cell (lower, grey shaded) is less excitable and would remain quiescent. Cx36 gap junction coupling mediates a hyperpolarizing current (I_K) to the more excitable cell, preventing transient depolarization, voltage-gated calcium channel activation, and suppressing [Ca²⁺]_i elevations and Ca²⁺-triggering of insulin secretion in the more excitable cell. In the absence of Cx36 the more excitable cell can depolarize and elevate [Ca²⁺]_i. Distally, other juxtacrine mechanisms, putatively including EphA forward signaling and NCAM signaling, also suppress insulin granule trafficking and/or exocytosis to additionally suppress insulin secretion. cAMP acting via PKA overcomes the effect of other suppressive juxtacrine mechanisms, but only when gap junction coupling is also inhibited will the more excitable cell show elevated Ca²⁺-triggering and elevated basal insulin secretion, as in isolated cells.

Even though gap junctions are not the only relevant cellular communication mechanism in the islet, deletion of β-cell gap junctions does lead to pathological effects that mimic key phenotypic aspects of T2D. As described above, insulin secretion in vivo or from islets exhibits a biphasic response to increasing glucose: a peaked first phase followed by a sustained second phase with characteristic oscillations of insulin release. A significant decrease in the peak amplitude of first phase insulin secretion is observed both in vivo and in isolated islets from Cx36^−/− mice, although the total insulin output is unchanged [9]. These data suggest that the sharp peak of first phase secretion is dependent on the coordinated synchronous pulses of insulin coming from the islet. Disruption of this coordination within an islet would be expected to produce release over a longer time span, thus reducing the peak level despite a similar total amount of insulin. However, it remains unclear how the loss of pulsatility within islets affects the integrated behavior of all of the islets in the pancreas in vivo. In an analogous fashion, the second phase insulin oscillations are also greatly reduced in Cx36^−/− mice, which again suggest a role for the islet’s coordinated electrical activity in these oscillations. These findings are similar to those seen in T2D, where first phase insulin secretion and second phase oscillations are reduced and eventually lost as the disease progresses [11], although it is not clear whether lost β-cell coupling is a cause or symptom of T2D. More striking is the fact that the Cx36^−/− mice are glucose intolerant [9], which demonstrates the regulation of glucose homeostasis by Cx36. Parallel to the loss of the first and second phase dynamics, glucose intolerance similar to what is measured in Cx36^−/− mice is also observed in pre-diabetic and diabetic phenotypes [44]. It is important to note that the total insulin released in the Cx36^−/− animals is similar to that of wild-type counterparts, rather it is the temporal dynamics that have changed significantly. Thus understanding the dynamics of islet function is critical not only for understanding at the cellular level, but also at the level of whole animal physiology.

Although it is not the focus of this article, it should be mentioned that Cx36 has also been implicated in β-cell survival, and that it may play a role in protecting β-cells from cytotoxic factors, including those involved with the inception of type 1 diabetes (T1D) [45]. Further, Cx36 has been identified as a possible regulator of β-cell differentiation and maturation [46, 47]. Because Cx36 plays such a critical role in islet dynamics and function, it is not surprising that it would support islet development and fitness as well. Cx36 and its specific roles in the islet was recently reviewed in depth [33].

Heterogeneity and Excitability in the Islet

The known heterogeneity of dispersed β-cells has led to a model where β-cells with elevated excitability, from differences in glucose metabolism or channel activity for instance, will trigger first, and eventually bring along the cells with lower excitability [3, 23]. However, it is difficult to observe local excitability within intact islets under normal conditions due to gap junction coordination of [Ca²⁺]_i [36, 37]. To test whether locally elevated excitability arising from random heterogeneity between β-cells controls activity throughout the islet, it is necessary to introduce a defined local heterogeneity. This has been done in two ways: by introducing a variegated transgene that creates a heterogeneous population of β-cells in the islet, or by fabricating a non-uniform stimulation pattern to the islet.

Creating defined local heterogeneity via a variegated transgene

The first approach is to create two distinct populations of β-cells within the islet based on mosaic expression of a dominant-negative Kir6.2[AAA] transgene, in which the pore-forming subunit of the K_ATP becomes nonfunctional [48]. In β-cells, glucose metabolism is coupled to electrical activity by the K_ATP channels. Therefore a loss of K_ATP channel function is expected to eliminate metabolic control of the downstream Ca²⁺ influx and insulin secretion, leading to glucose-independent hyper-excitability on a cell-by-cell basis. In fact, this is exactly what is seen in dispersed β-cells (GFP-positive/AAA mutation cells) from these islets, where β-cells presented [Ca²⁺]_i transients at all glucose levels, even at very low levels (2mM). Intact islets from the Kir6.2[AAA] mice displayed a mosaic GFP pattern where 70% of β-cells expressed the mutated gene, and the remaining cells showed normal K_ATP channel function. Based on observed β-cell heterogeneities, it was hypothesized that cells within the islet may create a uniform membrane potential by ‘sharing’ K_ATP channels through gap junctions [49, 50]. In agreement with the islet syncytium hypothesis, all of the β-cells in the Kir6.2[AAA] islets showed coordinated synchronous [Ca²⁺]_i oscillations at stimulatory glucose levels. Perhaps more importantly, none of the β-cells in the islet gave elevated [Ca²⁺]_i transients at nonstimulatory glucose concentrations [51]. These results indicate that even a small percentage of functional β-cells are sufficient to polarize the entire islet, and strongly supports the electrical syncytium model of the islet. The functional consequence of this effect is to prevent any highly excitable β-cells in an islet from accidentally secreting insulin at low glucose levels. The islet does this through gap junction coupling that clamps the membrane potential of all neighboring cells to what appears to be an average value [3, 51]. In this fashion, gap junctional coupling averages the stimulatory glucose level over the entire islet, thus limiting the effect of heterogeneities in individual cell excitability [36, 51].

Creating defined local heterogeneity by fabricating a glucose gradient across the islet

The second approach was developed using a novel two-sided microfluidic device which created a glucose gradient across the islet, which could be measured by fluorescent glucose and NAD(P)H intensities [52]. These measurements confirmed previous studies, which showed that β-cells are not metabolically coupled in the islet [27]. However, this work showed a surprising sharp line of demarcation between β-cells with fully active [Ca²⁺]_i oscillation and those clamped at basal [Ca²⁺]_i, without any gradient of β-cells with intermediate [Ca²⁺]_i levels between them. These data showed that β-cells within an islet are largely controlled by their own glucose sensing, and that they are not sufficiently coupled to allow an initiated [Ca²⁺]_i response to propagate into regions where the glucose concentration is below the oscillation threshold (~7 mM glucose). Still, the cells are effectively coupled to coordinate the [Ca²⁺]_i response within regions above this threshold. Thus, the islet response must be understood in terms of both the local glucose environment that each cell experiences, and the overall electrical syncytium. It appears that the initiation and coordination of the [Ca²⁺]_i response are controlled by two different mechanisms, which is likely a balance between gap junction coupling and the K_ATP channels that maintain each cell’s membrane polarization. These data are consistent with the expected control of individual β-cells by K_ATP channels. The microfluidic device creates a gradient of glucose stimulation across the islet, so cells in the middle are expected to have varying fractions of open and closed K_ATP channels. Because the neighbor of the last oscillating cell is exposed to only slightly lower glucose than the oscillating cell, it likely has only a small number of open K_ATP channels, yet it still resists the coupling force to depolarize. Of course, this cell is also coupled to other cells that are experiencing even less glucose, therefore providing additional resistance to depolarization. While many aspects of islet behavior in this device can be accurately described by mathematical models [53, 54], predicting the existence and precise location of the sharp line of oscillation activation remains elusive.

Quantitative Modeling of Islet Dynamics

Quantitative mathematical models are important to understand the unique and complex multicellular dynamics of the islet, such that observed measurements can be related to putative underlying mechanisms. Many models have been developed that have generated quantitative predictions regarding the balance of underlying β-cell behavior and interactions that give insight into the overall islet response. Most islet models have described the dynamics of electrical activity using Hodgkin-Huxley model equations and the known activation kinetics of the main constituent ionic currents and their regulation, as measured in β-cells [55-59]. However additional models have used more reductionist methods to specifically describe aspects of cellular coupling and architecture on islet function within a static framework [37].

A large number of islet models have approximated the islet as a single cellular unit to describe oscillatory dynamics of multiple signaling components, including membrane polarization and [Ca²⁺]_i [59, 60], as well as glycolysis and mitochondrial metabolism [56], including how a broad range of observed slow, fast or mixed (compound) oscillations can be generated from the dynamics of underlying metabolic and electrical signaling pathways [61]. The oscillatory dynamics of cAMP, and the complex interaction between cAMP and [Ca²⁺]_i [62], as well as with protein kinase A (PKA) [63] have also been modelled. Further extensions have examined putative means by which islets themselves are coordinated throughout the pancreas, through cholinergic pacemaker action [64] or entrainment by glucose oscillations [65, 66]. It is important to note that approximating the islet as a single unit assumes all components of the signaling pathways underlying electrical activity and insulin release are perfectly coupled. As described above, this is not precisely correct, and as such, these models do not allow us to understand how β-cells within the intact islet behave differently from isolated β-cells. To examine this, multicellular models of the islet are required.

Multi-cellular models of islet dynamics

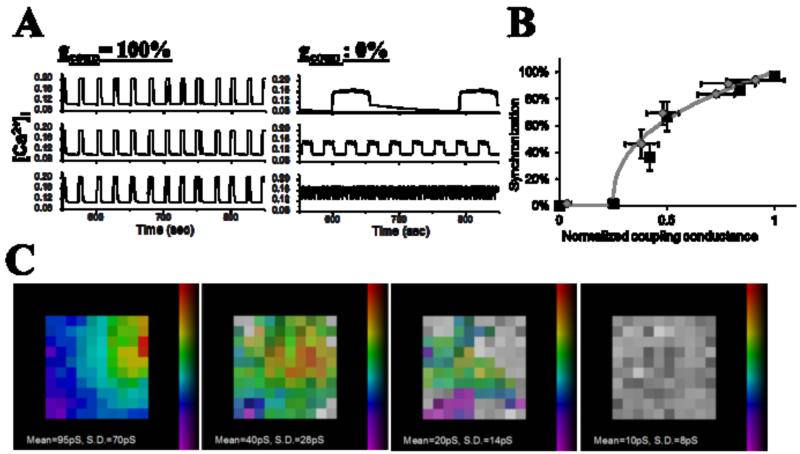
Isolated β-cells show heterogeneous responses in many factors, as well as showing noisy and irregular electrical dynamics. The finite number of channels expressed in a single β-cell has been modelled to lead to stochastic channel opening/closing, thus affecting the regularity of membrane potential bursting and [Ca²⁺] oscillations [50, 67]. Variability in the number of specific channels between β-cells (or their underling regulation) has been modelled to generate variable oscillation patterns and responses [68]. When multiple noisy and heterogeneous β-cells are then electrically coupled, the, stochastic and heterogeneous behavior is eliminated and uniform behavior occurs, due to the averaging effect of gap junctions [37, 69]. The overall islet behavior however is dependent on the constituent β-cells and their coupling. The oscillation period within an islet is dependent on the heterogeneous oscillation patterns in constituent cells, where a mix of slow (~mins) or fast (~sec) oscillators couple to generate robust intermediate (~20s) synchronized oscillations [70]. The proportion of heterogeneous coupled β-cells that are synchronized and contribute to the overall islet dynamics could also be described as a function of coupling conductance (Figs. 1 & 3) [37]. A specific prediction was that at ~25% of the wild-type coupling conductance the islet transitions between coordinated behavior and fully desynchronized independent behavior. Developing experimental methods to block gap junctions with well-defined range of efficacies will be required to test this prediction. As a result of the heterogeneous electrical coupling required in this model, in accordance with experimental measurements [34], a highly coupled ‘backbone’ of cells is suggested to preferentially mediate the coordination of electrical dynamics. This has been suggested from recent experimental results showing a subset of robustly synchronized cells within the islet [71], and the dependence of electrical dynamics on coupling strength, size and dimension can be related to the topology of a partially coupled electrical network [37]. Thus, the link between the level of coupling, synchronized [Ca²⁺]_i dynamics and resultant insulin dynamics (particularly the modulation of first phase pulse and second phase oscillations) can be well predicted.

Figure 3. Modelled multicellular islet [Ca²⁺]_i.

A: Representative oscillations of [Ca²⁺]_i in 3 heterogeneous cells of a modelled multicellular islet, in the presence of full electrical coupling (left) and absence of electrical coupling (right).

B: Dependence of the synchronization of [Ca²⁺]_i oscillations measured experimentally (grey diamonds) and form modelled islet (black squares) as a function of electrical coupling, normalized to that of wild-type islet or modeled islet showing wild-type behavior.

C: representative phase maps of modelled islets as the level of electrical coupling is progressively decreased. Presence of color indicates cell is synchronized, absence of color (grey) indicates cell is desynchronized with the rest of the islet. Figure adapted from [37].

Multicellular models of coupling by other pathways

Oscillations in other factors such as glycolysis, mitochondrial metabolism and ATP-production, and cAMP are also synchronized across the islet, but the mechanism(s) underlying this synchronization are poorly understood. In modelling the interactions of metabolic and electrical activity, diffusion of metabolic intermediates between cells was necessary to synchronize metabolic oscillations [72]. Experimental data discussed above suggests that β-cells are not sufficiently metabolically coupled, to overcome metabolic heterogeneity. However, weak metabolic coupling may still be sufficient to synchronize metabolic oscillations, particularly if their frequencies are similar. An alternative explanation is that they are simply phase-locked to the coordinated [Ca²⁺] oscillations [72]. Further testing if and how other factors in β-cell function are coupled will require further predictive models and quantitative experimental measurements.

The importance of spatiotemporal dynamics

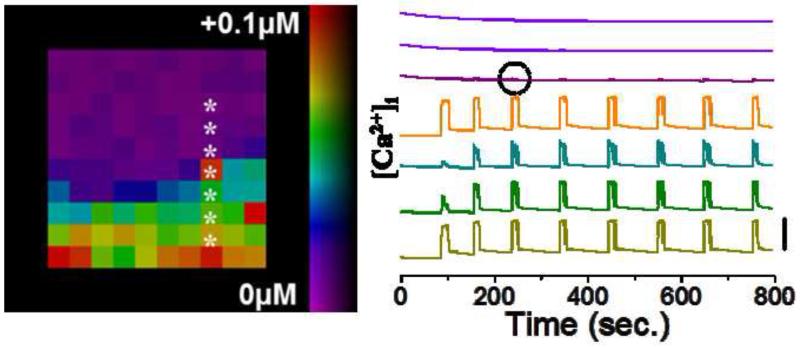
Multi-cellular modelling has also allowed examination of emergent spatiotemporal dynamics, such as propagating calcium waves that mediate the synchronization of [Ca²⁺]_i dynamics [73]. Calcium waves show a significant dependence on β-cell heterogeneity [53], where heterogeneity in β-cell activity and β-cell coupling was necessary to reproduce measured calcium wave velocities [37]. The inclusion of such heterogeneity was further required to lead to a sharp halting of calcium wave propagation in the presence of a gradient of glucose (figure 4) [54]. As described above, while the presence of β-cell heterogeneity cannot be directly measured in intact islets, model results suggest calcium waves are one manifestation of cellular heterogeneities. This predicted that calcium waves originate from more excitable regions of the islet that arise from the random distribution of heterogeneous β-cell excitability [37]. The ability to generate such testable predictions based on key aspects of islet behavior is a good example of the predictive power of quantitative islet models.

Figure 4. Modelling [Ca²⁺]_i upon glucose gradient.

Map of [Ca²⁺]_i elevation upon a gradient of glucose metabolism, with [Ca²⁺]_i time courses from indicated cells. Time courses are offset for clarity, with vertical bar indicating change of 0.1μM. Small amount of excitation bleed through is circled which is experimentally measured. Otherwise, a sharp transition between an area of coordinated excitability and quiescent behavior can be seen. Figure adapted from [54].

Describing defined local heterogeneity and model improvements

The coupled behaviors resulting from an imposition of defined heterogeneity, including a glucose gradient or Kir6.2[AAA] expression, have been less well described with predicative mathematical models. Specifically, that electrical coupling experimentally mediates a suppression of electrical activity rather than synchronizing dynamics is not well described. For example, when modelling a glucose gradient, the wave propagation halts sharply but the transition point between synchronized activity and silent activity is not at the correct position: calcium waves propagate too far across the islet [54]. It should be noted that mathematical models can describe the suppression of electrical activity that physiologically occurs at basal (~5mM) glucose, which sharpens the glucose-dose response [39]. However in mathematical models where perturbations exceed the physiological level of heterogeneity, coupling appears to propagate a depolarizing effect instead of mediating a repolarizing effect. These discrepancies may result from models having been developed to describe glucose-stimulated electrical activity rather than conditions that involve quiescent behavior and large heterogeneities across the islet. Therefore, the electrical coupling modelled between β-cells or the electrical activity within β-cells is not fully descriptive when inhibitory behavior occurs following defined perturbations. This suggests that we do not yet have a complete understanding of the suppressive effects that can occur in the islet.

To better model gap junction electrical coupling, modelling an electrochemical gradient between cells rather than purely an electrical gradient, can account for different ionic concentrations in active and quiescent cells. In a simple 2-cell description of a Kir6.2[AAA] islet (i.e. 1 normal cell, 1 mutant cell), this generated near-normal glucose-dependent activity [74]. An alternative approach includes Ca²⁺ feedback to inhibit ATP production and open K_ATP channels in normal cells of the Kir6.2[AAA] islet [75]. This describes experimental measurements but predicts Kir6.2[AAA] expressing β-cells would have much lower ATP/ADP levels; where higher NAD(P)H has been measured in those cells [51]. Interestingly this required strong diffusion of Ca²⁺ between cells which implies the importance of ionic concentrations in mediating the action of gap junctions; in a similar manner to inclusion of an electrochemical gradient. Finally, the currents that are important to describe a synchronization of oscillatory dynamics may also not be sufficient when inhibitory behavior occurs (Fig. 4). Recently a more comprehensive, albeit single cell model including 11 currents (compared to 4-5 that are required to model synchronized oscillatory dynamics) has been developed [57, 58]. Examining whether this model can describe the above experimental data with simple electrical coupling should help determine what is missing from current models and give a better understanding for the multicellular regulation of the islet.

Concluding remarks and future perspectives

In summary, cellular coupling within the islet, principally via Cx36 gap junction channels, result in a marked suppression of insulin release at low glucose, generate a steep sigmoidal secretory response to elevated glucose, enhance the peak first phase of insulin secretion and coordinate the second phase pulses of insulin secretion. The synchronization of electrical activity and overcoming of β-cell heterogeneity and noise by gap junction channels are well understood, with the heterogeneity of cellular excitability; electrical coupling; the architecture of coupling occurs well described by mathematical models. Understanding how factors such as metabolism and cAMP are coupled remains to be determined. The coupling of suppressive effects which occurs when excitable and non-excitable cells interact is also less well understood, although newer mathematical models and experiments should yield better understanding for these multicellular properties of the islet.

Highlights.

• Insulin secretion form the islet of Langerhans is pulsatile.

• The pulsatile dynamics are necessary for normal physiology.

• Gap junctions underlie synchronous electrical activity leading to insulin pulses.

• Mathematical models can explain some, but not all synchronous islet behaviors.

Glossary

Connexin 36 (Cx36)

belongs to a family of structurally related transmembrane proteins that assemble to form gap junctions between cells. These are four-pass transmembrane proteins with two extracellular loops and both the C and N terminus in the cytoplasm.

EphA-(ephrin-A)

are a subfamily of receptor tyrosine kinases that are activated in response to binding ephrin ligands. Both Eph receptors and their ephrin ligands are membrane-bound proteins that require direct cell-cell interactions for receptor activation.

Kir6. 2

is the pore-forming subunit of the ATP-sensitive K+ channel, an integral membrane protein that allows potassium to flow into a cell. Kir6. 2 is found associated with the sulfonylurea receptor. Mutations in this gene are associated with congenital hyperinsulinism.

Hodgkin–Huxley model

is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is based on a set of equations that approximate the electrical characteristics of excitable cells.

Islets of Langerhans

the islets of Langerhans are clusters of hormone-producing cells of different types that make up the endocrine part of the pancreas. Each islet contains 1,000 to 10,000 β-cells and there are about 1 million islets in the human pancreas.

Insulin oscillation

The insulin concentration in blood rises after meals and gradually returns to basal levels, during the next 1-2 hours. However, the level of postprandial insulin level is not stable but oscillates with a period of 3-6 min. While the amplitude of these oscillations increases after a meal, the periodicity remains constant. Insulin oscillations are generated in part by pulsatile release of the hormone, which is driven by oscillation of the calcium concentration in the β-cells. Pulsatile secretion requires exquisite synchronization between β-cells. Insulin oscillations become synchronized by electrical coupling between closely located β-cells, that are connected by gap junctions. Beta cells lacking gap junctions exhibit variable periodicity in insulin oscillations.

Insulin secretion

Insulin release from β-cells takes place in a rapid, 1st phase release followed by a 2nd, slow phase, sustained release, of newly formed vesicles. During the 1st phase, glucose enters the β-cells through the glucose transporter, GLUT2. Glucose gets metabolized leading to an increase in the intracellular ATP:ADP ratio that in turn closes the ATP-sensitive SUR1/Kir6.2 potassium channel. The increased potassium concentration leads to depolarization of the cell membrane, whereby voltage-gated calcium ion (Ca2+) channels open allowing calcium to move into the cell. The increased intracellular calcium activates phospholipase C and downstream signaling pathways that further raise the calcium, ultimately causing the release of previously synthesized insulin stored in secretory vesicles.