A Molecular Dynamics Simulation Study of the Association of 1,1’-Binaphthyl-2,2’-diyl hydrogenphosphate Enantiomers with a Chiral Molecular Micelle

Abstract

Molecular dynamics (MD) simulations were used to investigate the binding of 1,1’-binaphthyl-2,2’-diyl hydrogenphosphate (BNP) enantiomers to the molecular micelle poly-(sodium undecyl-(L,L)-leucine-valine) (poly(SULV)). Poly(SULV) is used as a chiral selector in capillary electrophoresis separations. Four poly(SULV) binding pockets were identified and either (R)-BNP or (S)-BNP were docked into each pocket. MD simulations were then used to identify the preferred BNP binding site. Within the preferred site, both enantiomers formed hydrogen bonds with poly(SULV) and penetrated into the poly(SULV) core. Comparisons of BNP enantiomer binding to the preferred poly(SULV) pocket showed that (S)-BNP formed stronger hydrogen bonds, moved deeper into the binding site, and had a lower poly(SULV) binding free energy than the (R) enantiomer. Finally, MD simulation results were in agreement with capillary electrophoresis and NMR experiments. Each technique showed (S)-BNP interacted more strongly with poly(SULV) than (R)-BNP and that the site of chiral recognition was near the poly(SULV) leucine chiral center.

Introduction

Chiral molecular micelles are macromolecules used as chiral pseudostationary phases in capillary electrophoresis (CE). The goal of this project was to identify the fundamental factors responsible for chiral recognition by these macromolecules in CE separations. Efficient chiral separations with CE and other chromatographic techniques are needed because the chirality of a molecule often affects its physiological activity. Thus, the Food and Drug Administration mandates analysis and proof of enantiomeric purity for drugs that exist in enantiomeric form [1]. Demand for optically pure compounds also exists in the agrochemical and food industries since many agrochemicals and food additives are also chiral. Molecular micelles (MM) are made up of surfactant monomer chains connected by covalent bonds in the macromolecule’s hydrocarbon core. In the MM investigated here, each surfactant monomer was terminated with a chiral dipeptide leucine-valine headgroup.

Chiral separations are based upon differential interactions between analyte enantiomers and a chiral separation medium. However, differences in the free energies of binding between analyte (R) and (S) enantiomers and the chiral compounds in the separation media are often small, making the enantiomers in racemic compounds difficult to separate [2–5]. Chiral versions of thin layer chromatography, gas chromatography, supercritical fluid chromatography, HPLC, and capillary electrophoresis have been developed and used in chiral separation applications [6,7]. In most chiral CE-based techniques, enantiomers are separated based upon their differential interactions with a psuedostationary phase as both are pulled through a capillary by an electric field [2]. The high separation efficiency often achieved in CE allows chiral separations to be done in short period of time, thus making capillary electrophoresis a popular chiral separation technique [8].

Many CE pseudostationary phases have been developed, including chiral cyclodextrins, micelles, peptides, and polymers [9,10]. Wang and Warner in 1994 and Dobashi, et al. in 1995 were the first researchers to use chiral amino acid terminated molecular micelles as the pseudostationary phase in chiral CE [11,12]. Since these first applications of amino acid-based MM in chiral CE separations, extensive work has been done to investigate how the physical properties of the MM and the positions of the stereocenters in the amino acid headgroup affect interactions with chiral analytes [13–15]. The specific intermolecular interactions leading to chiral discrimination in CE separations with amino acid-based MM have also been investigated, including the roles played by hydrophobic and steric factors [16–19], electrostatic interactions, and hydrogen bonding [20–22].

Despite these efforts, there is still much to be learned about the fundamental chiral recognition mechanism in CE separations. This project, therefore, is part of an ongoing effort to use MD simulations to investigate the intermolecular interactions leading to chiral discrimination in CE separations with dipeptide-based MM. The long-term goal of these studies is to combine MD simulation and experimental results to develop quantitative structure-property relationships that can then be used to evaluate and compare the effectiveness of different chiral selectors in CE separations.

MD simulation efforts to date have focused on investigating the effect of MM amino acid order on chiral recognition by carrying out MD simulations with the molecular micelles poly-(sodium undecyl-(L,L)-leucine-valine) (poly(SULV)) and poly-(sodium undecyl-(L,L)-valine-leucine) (poly(SUVL)) in aqueous solution [23,24]. These specific MM were chosen because including non-polar amino acids such as alanine, valine, and leucine in the headgroups of dipeptide-terminated MM allows chiral analytes interacting with the MM headgroups to experience hydrophobic as well as hydrophilic and hydrogen-bonding interactions [14,15]. Furthermore, a CE study of sixteen different dipeptide-terminated MM by Billiot et al. found that chiral resolution was generally higher when the larger of the two amino acids was in the N-terminal position and identified poly(SULV) as an effective chiral selector [15]. A subsequent study by Shamsi, et al. showed that poly(SULV) was also a versatile chiral selector based upon the successful enantioseparation of 58 out of 75 racemic compounds using this MM [25]. Chiral resolution in CE separations using poly(SUVL) as the chiral selector, in contrast, has been found to be relatively poor [14]. Therefore, in the MD simulation study investigating the effect of amino acid order, we chose to compare the structures of a relatively effective (poly(SULV)) and a relatively ineffective (poly(SUVL)) MM.

MD simulation structures reported for poly(SULV) and poly(SUVL) were found to be in good agreement with experiment, based upon comparisons of radial distribution functions and micelle radii from MD simulations to NMR NOESY spectra and hydrodynamic radii calculated from NMR-derived diffusion coefficients [23]. A subsequent MD simulation study focused on the effect of dipeptide headgroup amino acid order on MM structure. Overall, it was found that poly(SULV) adopted a more open MM structure than poly(SUVL), based upon the observation that poly(SULV) provided water molecules greater access to its dipeptide headgroup and MM hydrocarbon core regions. Poly(SULV) was also found to have a larger solvent accessible surface area and a more conformationally flexible dipeptide headgroup than poly(SUVL) [24].

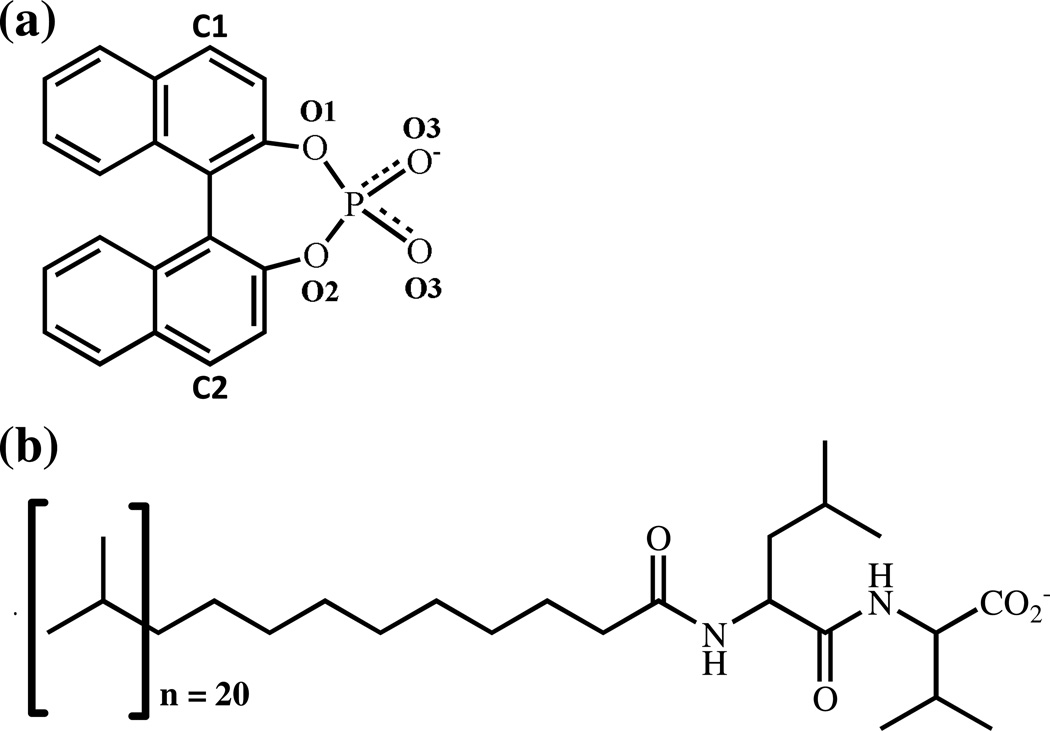
In this study, MD simulations were used to investigate the binding of (R) and (S) enantiomers of 1,1’-binaphthyl-2,2’-diyl hydrogenphosphate (BNP) to poly(SULV) molecular micelles. The molecular structures of BNP and poly(SULV) are shown in Figure 1. BNP and other 1,1’-binaphthyl compounds are used in chiral syntheses and as chiral selectors in HPLC [26–28]. Separation of BNP enantiomers with amino acid-based MM was first reported by Shamsi, et al. [29]. BNP enantiomers have also been shown to experience strong chiral interactions with poly(SULV), based upon the finding that relatively low concentrations of the MM were needed to separate BNP enantiomers [25]. NMR spectroscopy [2–5,30], fluorescence anisotropy [2,31–33], and CE techniques [2,31,34,35] have also been used to characterize the interactions between BNP enantiomers and MM. These studies have shown that (S)-BNP experiences stronger chiral interactions with poly(SULV) than the (R)-enantiomer [2,3]. In addition, chiral interactions between BNP enantiomers and poly(SULV) have been found to occur predominately at or near the N-terminal leucine chiral center in the dipeptide headgroup [2,3] and BNP enantiomers have been shown to penetrate deeper into the cores of MM than into cores of micelles formed by corresponding unpolymerized surfactants [35]. A study by Rizvi, et al. also examined how changes in MM concentration, pH, MM polymerization conditions, and the background electrolyte affected chiral selectivity in BNP separations using leucine and isoleucine-terminated MM [36]. This MD simulation study was undertaken to gain further insight into the association of BNP enantiomers with poly(SULV). Previous work on this system will also allow for comparisons between MD simulation predictions and experimental work.

Figure 1.

Molecular structures of (a) 1,1’-binaphthyl-2,2’-diyl hydrogenphosphate (BNP) and (b) poly-(sodium undecyl-(L,L)-leucine-valine). The BNP oxygen atom labels are used in the hydrogen bond analyses presented in Table I.

In this MD simulation study, poly(SULV) binding pockets or sites were first identified and characterized with respect to the intermolecular interactions (hydrophobic, hydrophilic, H-bond, etc.) that could occur when a chiral molecule bound to the MM in each respective pocket. (R)-BNP or (S)-BNP enantiomers were then separately docked into each pocket, MD simulations were carried out and the distances between the center of the MM and BNP phosphorus atom were monitored. The intermolecular interactions experienced by the BNP enantiomers in each different poly(SULV) binding pocket were investigated by monitoring changes in each BNP enantiomers’ root mean squared deviation (rmsd) and solvent accessible surface area with simulation time. Intermolecular hydrogen bonds formed between the BNP enantiomers and the MM surfactant chains were also studied, the binding free energies for (R)-BNP and (S)-BNP in each poly(SULV) pocket were calculated, and comparisons were made between the MD simulation results and experiment. Taken together, the MD simulations allowed the preferred MM binding pocket to be identified and provided insight into why (S)-BNP experiences stronger chiral interactions with poly(SULV) than the (R)-BNP enantiomer.

Experimental Details

BNP:poly(SULV) complexes were generated using the MOE package (MOE 2011.10) [37]. The initial MM structures were representative structures generated from a 15.0 ns MD simulation [23, 24]. These representative structures were chosen by first calculating the average structure over all the structures collected during the MD simulations. The root mean squared deviation (RMSD) of each MD simulation structure with respect to the average was then calculated. Representative structures were selected as those with the lowest RMSD with respect to the average [38]. The MM structure chosen in this manner is the MD simulation frame that represents the most likely conformation of the molecular micelle. In other words, when a ligand molecule binds to the molecular micelle, it is most likely to encounter the poly(SULV) receptor in a conformation very close to this structure. Therefore, instead of using different structures to sample the different properties of the MM, we used the best representative molecular micelle structure to perform the ensemble-average approach.

The BNP enantiomers were built using the MOE-builder and energy minimized individually in the MMFF94x force field. The active sites of each MM were identified with Site Finder module of MOE. The Site Finder module utilizes alpha-shape and discrete-flow methods developed by Edelsbrunner, et al. [39, 40]. The Site Finder module scores and visualizes individual sites by populating them with dummy atoms which serve as probes denoting zones of tight atom packing available for ligand docking. The collection of these dummy atoms, also called alpha spheres, are classified as either "hydrophobic" or "hydrophilic" depending upon whether the sphere is in a good hydrogen bonding environment in the receptor. In the MM, multiple sites were identified and the stereo and the electrostatic properties were defined by the number of the hydrophobic and hydrophilic alpha spheres. The docking procedure followed used the standard protocol implemented in MOE 2011.10 [37]. The MM was set as receptor and the atoms in one of the binding pockets previously identified were selected as the target binding site. Other general parameters were: Placement: Triangle Matcher; Rescoring 1: London dG. Following the MOE 2011.10 standard docking protocol, during the docking process the MM was set as structurally rigid while the BNP was set as completely flexible. During each binding procedure, the London dG scoring function implemented in MOE was employed to estimate the free energy of binding of the ligand from a given pose. A total of 30 top-score docking poses were constructed and the best scoring MM-BNP complexes in the specific site were selected for the further MD simulation study [41].

After the ligand docking procedure was performed, MD simulations on the BNP:MM intermolecular complexes were performed using AMBER 12 [42] and the parm99 [43] force field. The specific Amber 12 parameters used in the MD simulations are given in the Supplemental Information. Each MD simulation contained the MM poly(SULV), either (R)-BNP or (S)-BNP, twenty Na⁺ counterions, and from 8360 to 8689 water residues. The TIP3P water model was used in all MD simulations. The complexes were first energy minimized. A 20 ps MD simulation was then carried out to heat to 300 K followed by a 1 ns simulation to equilibrate the system to 1 atm and 300 K. Finally, a 15.0 ns production run was carried out for each complex to collect statistical data. In the production run, the time step was 2.0 fs and structures were saved every 0.2 ps. The MD simulations were also done using cubic periodic boundary conditions (PBC). The cutoff used in the PBC ensured that the edge lengths were well above twice the cutoff distance for the van der Waals interactions (10 Å) [44]. Analyses of the MD simulation trajectories were done with the ptraj and cpptraj utilities in AMBER 12 [42].

The binding free energies were calculated using the mm-PBSA method [45]. Binding free energies were computed by taking the difference between the mm-PBSA free energy of the complex (R/S-BNP-MM) and that of the ligand (R/S-BNP) and receptor (MM): ΔG_bind = G_complex − G_receptor − G_ligand, where G = G_solute+ G_solvent. The G_solute term for each system can be obtained by G_solute= E −T·S. S represents the entropy contribution to ligand binding. E was the MM energy averaged over all the snapshots acquired between 0.50 ns and 15.0 ns and includes contributions from the electrostatic and van der Waals interactions for the complex, receptor, and ligand. All MM calculations (AMBER 12) were performed with a non-bonded cutoff of 99 Å and a dielectric constant of 1 in the absence of any solvent or counterions. The receptor and ligand geometries were taken from those of the complex, and thus there is no internal energy (i.e., bonds, angles, and dihedrals) contribution to the net MM average. The G_solvent term can be obtained by G_solvent = G_es + G_nes. G_es is the electrostatic contribution which is obtained by the PB method, and G_nes (PBSUR) is the non electrostatic contribution and is proportional to the solvent-accessible surface area of the molecule.

Results and Discussion

Distance and RMSD Analyses

The MOE docking analysis described above identified six regions or pockets in poly(SULV) where ligand molecule binding could occur. However, when the BNP enantiomers were docked into three of these pockets, it was observed that the ligand molecules occupied the same region of the molecular micelle. For example, when BNP enantiomers were simultaneously docked into pockets one and two, the distance between the ligand P atoms was only 2.23 Å. In contrast, the distance between the carbon atoms labeled C1 and C2 in Figure 1 (a) was 7.12 Å. When ligands were simultaneously docked into pockets one and five, the distance between the P atoms was only 4.92 Å. Again this distance is small compared to overall size of the BNP molecule. Therefore, it was concluded that pockets one, two, and five placed the ligand into the same MM binding site. Pockets two and five were thus discarded and a single MD simulation was carried out with the ligand docked into pocket one.

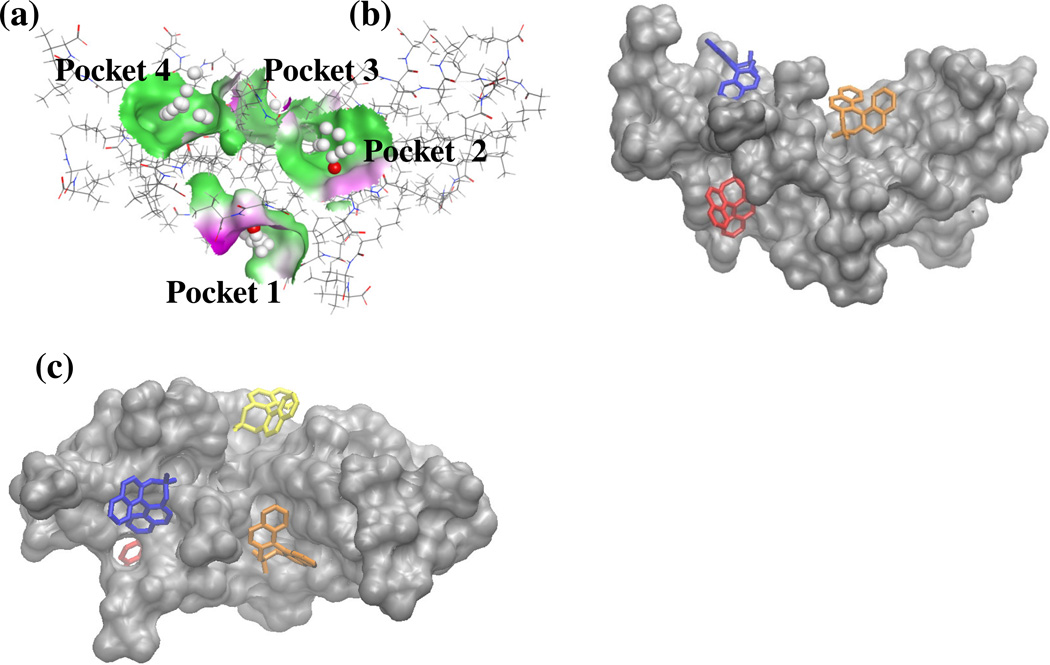
Figure 2 shows the four distinct MM binding sites that placed the enantiomers in different regions of the MM. These binding sites or pocket are referred to from here forward as pockets one-four. As described previously, the MM was initially constructed by connecting twenty surfactant monomers together with covalent bonds at the end of each surfactant's hydrocarbon chain. These chains were then labeled sequentially one through twenty. Table I lists the poly(SULV) monomer chains that were closest to (R) or (S)-BNP molecules when the enantiomers were docked into each of the four respective pockets. MOE was also used to characterize the local environment experienced by a ligand molecule in each binding pocket. The structure in Figure 2(a) generated with MOE uses grey spheres to indicate a hydrophobic region within the bonding pocket and red spheres to indicate regions where hydrogen bonding or hydrophilic contacts between the MM and a ligand molecule could occur. Note that there are both hydrophobic and hydrophilic regions within pockets one-three. Pocket four in contrast provides ligand molecules with a primarily hydrophobic environment. Figures 2(b) and 2(c) show (S)-BNP molecules docked into each of the four respective MM binding pockets. Two orientations of the MM are shown in Figure 2 so that all four pockets can be visualized.

Figure 2.

(a) Poly(SULV) binding pocket analysis from MOE. Grey and red spheres indicate hydrophobic and hydrophilic interactions, respectively. The solid colors represent the lipophilicity of receptor pocket. Green and red correspond to hydrophobic and hydrophilic regions, respectively. (b) (S)-BNP molecules docked into each of the four poly(SULV) binding pockets. Docked (S)-BNP molecules are red, orange, yellow, and blue for pockets one, two, three, and four, respectively. (c) Alternative view of (b) showing (S)-BNP docked into pocket 3.

Table I.

Molecular micelle chains closest to docked ligand molecules in pockets one through four. Results are the same for both (R)-BNP and (S)-BNP.

Poly(SULV) binding pocket	MM chains closest to the docked ligand
1	2, 9, and 12
2	6, 13, and 18
3	8, 10, and 11
4	4, 5, and 7

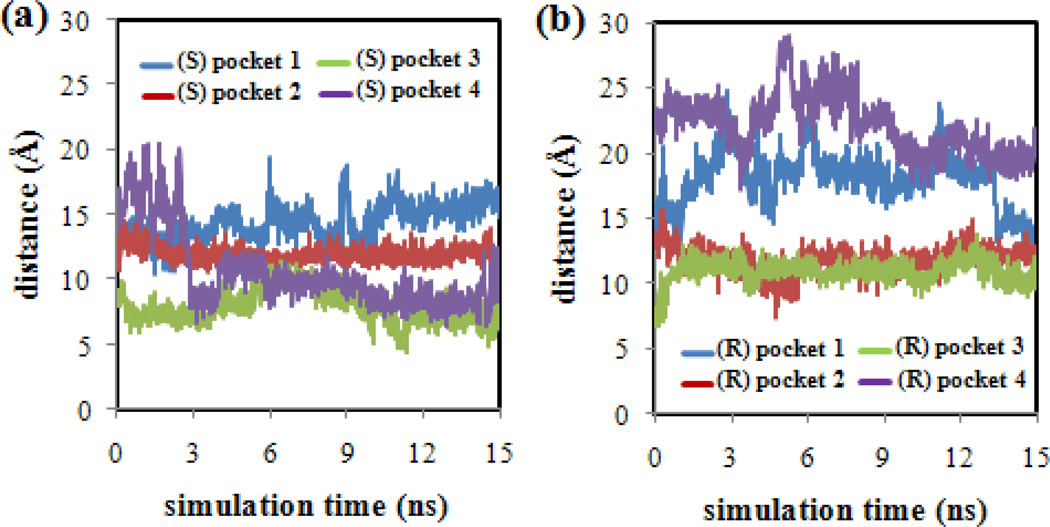
In order to confirm that the BNP enantiomers did not drift into the bulk water phase during the MD simulations, the distances between the center of the MM (taken as the C atom at the end of the hydrocarbon tail of poly(SULV) chain number 10) and the (R)-BNP or (S)-BNP phosphorus atom were measured. This analysis was performed for each of the MD simulations in which the BNP enantiomers were docked into MM pockets one-four, respectively. The results of this analysis are shown in Figure 3. Note that in each MD simulation, the BNP enantiomers remained within ~20 Å of the MM center. For the (S)-BNP results in Figure 3(a), pocket one showed generally larger separations between the (S)-BNP and MM atoms. Pockets two, three, and four, in contrast, showed generally smaller separations between the (S)-BNP and MM center. In the (R)-BNP analysis shown in Figure 3(b), the ligand was generally farther from the micelle center in pockets one and four and closer in pockets two and three. The poly(SULV) structure shown in Figure 2 shows that the MM adopts an elongated or elliptical shape. Measurements of the major and minor elliptical axes yielded distances of ~46 Å and ~21 Å, respectively. Since the plots in Figures 3(a) and 3(b) show that each BNP enantiomer remained within ~20 Å of the MM center in each of the four pockets, it can be concluded that BNP molecules remained associated with the MM throughout each of the MD simulations. Finally, it should be noted that the distance measurements reported in Figure 3 only serve as a validation method, in the sense that they confirm that throughout the MD simulations the BNP enantiomers remained close to the MM and did not drift away into the bulk water phase. These distance measurements, however, cannot be used to determine if the BNP enantiomers remained in their original binding pockets or if they penetrated into the micelle core. Measurements of the solvent accessible surface areas described below will be used to assess the later behavior.

Figure 3.

Distances between the center of the poly(SULV) MM and the phosphorus atom of (a) (S)-BNP and (b) (R)-BNP in binding pockets one-four.

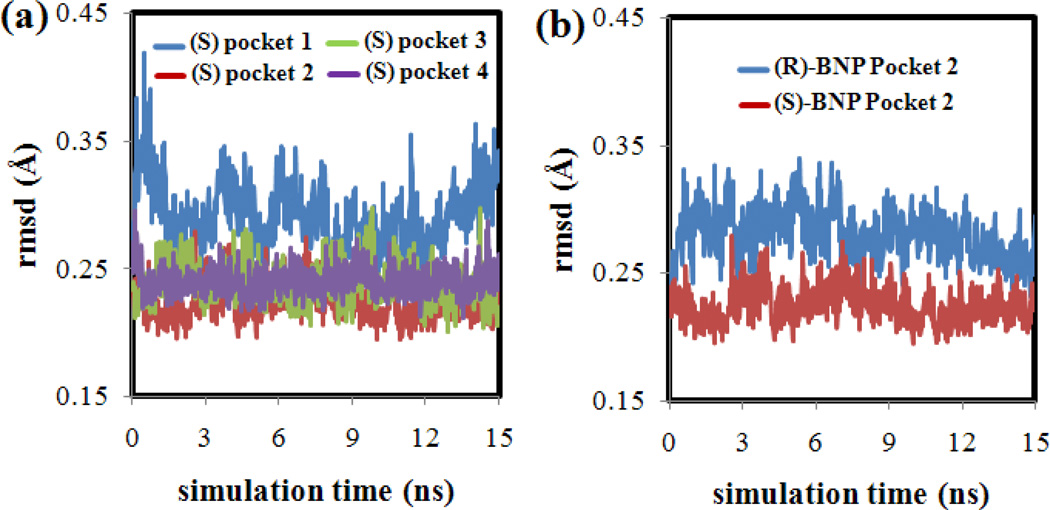
Furthermore, Figure 4(a) plots (S)-BNP root mean squared deviation (rmsd) values versus simulation time for each of the four binding pockets. All BNP atoms were included in the rmsd calculation. This plot shows that the (S)-BNP rmsd values were smallest throughout the MD simulation when the enantiomer was bound to pocket two. The overall small rmsd values indicate that in pocket two the (S)-BNP molecule remained in a similar orientation throughout the MD simulation. Similar results were found in the (R)-BNP:MM MD simulations. As shown in Figure 4(b), when (R)-BNP was bound to pocket two, the enantiomer also showed small rmsd values indicating that the (R) enantiomer also remained in a similar orientation throughout the MD simulation.

Figure 4.

(a) RMSD plots for (S)-BNP docked into each of the four poly(SULV) pockets. (b) comparison RMSD plot for (R)-BNP and (S)-BNP in poly(SULV) pocket 2.

Hydrogen Bonding

It would be expected that intermolecular hydrogen bonds between BNP enantiomers and MM atoms near the chiral centers of the dipeptide headgroup would play an important role in chiral discrimination within this system. The hydrogen bond donor and acceptor atoms and the percent occupancy of each intermolecular hydrogen bond detected in the MD simulations are given in Table II. Hydrogen bonds were identified using the ptraj utility in Amber 12 [42]. In the H-bond analysis, the distance cutoff between the heavy atoms participating in the hydrogen-bond was set at 3.5 Å and the angle cutoff between donor and H-bond acceptor atoms was set to ± 30°. The percent occupancies in Table II were determined by calculating the percent of the total simulation frames that H-bonds between BNP and MM atoms were present, based upon above H-bond criteria. The BNP atom labels used to index the hydrogen bonds are shown in Figure 1(a). No intermolecular (S)-BNP:MM or (R)-BNP:MM hydrogen bonds were detected during the MD simulations in which the enantiomers were docked into MM pockets three or four. The absence of intermolecular hydrogen bonding interactions makes it unlikely that either pocket three or four is the preferred poly(SULV) chiral recognition site.

Table II.

(S)-BNP and (R)-BNP:poly(SULV) hydrogen bond analyses. See Figure 1 for BNP atom labels.

(S)-BNP in Pocket 1
Acceptor	Donor	%-occupancy
Chain 9: Leu NH	(S)-BNP O3	0.37%
Chain 9: Val NH	(S)-BNP O3	0.23%
Chain 2: Leu NH	(S)-BNP O3	0.12%
(S)-BNP in Pocket 2
Acceptor	Donor	%-occupancy
Chain 6: Leu NH	(S)-BNP O3	11.88%
Chain 6: Val NH	(S)-BNP O3	3.11%
Chain 6: Leu NH	(S)-BNP O1	1.09%
(R)-BNP in Pocket 1
Acceptor	Donor	%-occupancy
Chain 9: Val NH	(R)-BNP O3	0.07%
Chain 9: Leu NH	(R)-BNP O3	0.01%
Chain 2: Val NH	(R)-BNP O3	0.01%
(R)-BNP in Pocket 2
Acceptor	Donor	%-occupancy
Chain 6: Val NH	(S)-BNP O3	0.13%
Chain 6: Leu NH	(S)-BNP O3	0.04%

The most significant hydrogen-bonding detected in the MD simulations occurred when (S)-BNP was bound to the MM in pocket two. Table II shows an intermolecular H-bond with an occupancy of 11.88% between a donor oxygen on the phosphate group of (S)-BNP and the MM leucine NH atom on poly(SULV) chain six. Two other H-bonds with lower occupancies (3.11% and 1.09%) also formed between (S)-BNP phosphate oxygen atoms and, respectively, the MM valine and leucine NH atoms of chain six. These results suggest that MM pocket two is the preferred binding and preferred chiral recognition site for BNP enantiomers because the strongest intermolecular H-bonding occurs in this pocket.

Relatively weak hydrogen-bonding was detected between (S)-BNP and the MM in pocket one. However, further analysis showed that the MM H-bond donor atom on chain nine and the (S)-BNP acceptor atom were only close to one another at the very beginning of the MD simulation and that poly(SULV) chain nine and (S)-BNP drifted away from one another as the MD simulation proceeded. This behavior is shown in Figure 5(a) where the distance between the (S)-BNP:MM hydrogen bond donor and acceptor atoms is plotted. Note that the separation between the atoms is relatively small at the beginning of the MD simulation, but increases steadily to ~ 15 Å by the end. Therefore, the (S)-BNP hydrogen bond detected in pocket one had both a relatively low %occupancy and only formed at the very beginning of the MD simulation. This observation suggests that relatively few hydrogen bonds form between the (S)-BNP phosphate group and atoms at or near the MM chiral centers in pocket one and therefore, relatively weak chiral interactions between the MM and (S)-BNP likely occur when the ligand molecule binds in this pocket.

Figure 5.

(a) Distances between hydrogen bond donor and acceptor atoms for (S)-BNP docked into poly(SULV) pocket one. (b) Distances between hydrogen bond donor and acceptor atoms for (R)-BNP and (S)-BNP docked into poly(SULV) pocket two.

Table II also presents the results of hydrogen bond analyses for the (R)-BNP:MM MD simulations. It should be noted first that no intermolecular hydrogen bonds were detected between (R)-BNP and the MM when the ligand molecule was docked in pockets three or four. Three hydrogen bonds were detected between (R)-BNP and the NH atoms of the MM dipeptide headgroup in pocket one. These H-bonds, though, had percent occupancies well below 1%. Two additional hydrogen bonds with less than 1% occupancy were detected in pocket two between valine and leucine NH atoms on chain six of poly(SULV) and (R)-BNP phosphate oxygen atoms. The hydrogen bonds detected for (R)-BNP, however, had a considerably lower percent occupancy than those detected for the (S) enantiomer. For example, the strongest (S)-BNP H-bond to the MM had an occupancy of 11.88%, while the occupancy of the strongest (R) enantiomer H-bond to the same poly(SULV) chain was only 0.13%.

This observation is also illustrated in Figure 5(b) where the distances between the pocket two hydrogen bond donor and acceptor atoms for both BNP enantiomers are plotted versus simulation time. In the (S)-BNP MD simulation, the donor and acceptor atoms are initially over 10 Å apart. The atoms approached one another during the first 0.50 ns of the MD simulation and for the remainder of the simulation the separation oscillated between approximately 2 and 7 Å. The (R)-BNP plot in Figure 5(b) also shows that the distance between the (R)-BNP phosphate oxygen and MM NH atoms oscillated between smaller and larger separations. However, the time that the (R)-BNP:MM H-bond donor and acceptor atoms spend close together is much less than was observed for (S)-BNP. Therefore, hydrogen bond analyses suggest that both (R) and (S)-BNP experience the strongest intermolecular hydrogen bonding interactions with the MM in pocket two. However, when the two enantiomers are compared to one another, the (S)-BNP enantiomer was found to form H-bonds with a significantly greater percent occupancy than the (R) enantiomer. As discussed in more detail below, this result is consistent with (R)-BNP eluting before (S)-BNP in CE separations with poly(SULV) as the chiral selector [2].

In order to further contrast the binding of (R) and (S)-BNP enantiomers to poly(SULV), representative structures were extracted at 10.0 ns of the MD simulation. Figures 6(a) and 6(b) show structures for, respectively (S)-BNP and (R)-BNP bound to poly(SULV) pocket two. In the Figure 6 structures, generated with MOE [38], green represents a non-polar region of the binding pocket, while red represents a polar region. The blue dotted line in Figure 6(a) represents a hydrogen bond detected by MOE between an (S)-BNP phosphate oxygen and the leucine NH atom on poly(SULV) chain six. This result is in good agreement with the MD simulation results which showed that this H-bond had a percent occupancy of 11.88%. Note that no such H-bond was detected in the Figure 6(b) structure. Furthermore, Figure 6(a) shows that when (S)-BNP binds to the MM in pocket two, the ligand penetrates well into the MM binding pocket. In contrast in Figure 6(b), the (R)-BNP enantiomer remains on the exterior of the pocket near the MM surface. It would be expected that favorable hydrophobic interactions between the BNP aromatic rings and non-polar regions of the MM surfactant chains would be more likely to occur when a ligand penetrates into its MM binding pocket. The dark blue dotted lines in Figure 6(a) in fact depict three arene-H interactions detected by MOE between the (S)-BNP aromatic rings and poly(SULV) H atoms. Again, no such interactions were detected in the (R)-BNP:MM complex shown in Figure 6(b).

Figure 6.

Representative structures showing the (a) (S)-BNP:poly(SULV) and (b) (R)-BNP:poly(SULV) intermolecular complexes. The structures were extracted at 10.0 ns of the MD simulation. In both structures, the BNP molecules are docked into poly(SULV) pocket two.

Solvent Accessible Surface Areas

In order to gain further insight into the local environment surrounding the BNP enantiomers in each poly(SULV) pocket and the hydrophobic interactions between the enantiomers and MM, the solvent accessible surface areas (SASA) of the BNP enantiomers were monitored as a function of simulation time. Analyses of the intermolecular hydrogen-bonds formed between water molecules and the MM and BNP H-bond donor/acceptor atoms were also carried out. The hydrogen bond analyses showed no water molecules stayed in the binding sites long enough to be included as a permanent part of the molecular micelle receptor. The results of these hydrogen bonding analyses are presented in Tables I and II of the Supporting Information. A plot of SASA versus simulation time for (S)-BNP in pockets one through four is shown in Figure 7(a). The horizontal line at ~ 420 Ų corresponds to the change in SASA vs. simulation time during a MD simulation containing only (S)-BNP and water, but no MM. Figure 7(a) shows that the (S)-BNP SASA is considerably less than the free solution value of ~ 420 Ų in each of the four binding pockets. However, the decrease in SASA upon MM binding is most pronounced when (S)-BNP is in pocket two. Therefore, the SASA analysis indicates that the (S)-BNP molecule penetrates most deeply into the MM core when bound to this pocket. Penetration into the MM likely allows favorable hydrophobic interactions to occur between the ligand molecule and poly(SULV). In contrast, if the (S)-BNP binds to a pocket in a more solvent accessible region of the MM, fewer hydrophobic and potentially stereoselective interactions would likely occur. The SASA results, therefore, also support the conclusion that pocket two is the preferred MM binding site.

Figure 7.

(a) Plots of (S)-BNP SASA versus simulation time for (S)-BNP docked into poly(SULV) binding pockets one-four and in free solution. (b) Comparison of pocket two SASA for (R)-BNP and (S)-BNP.

Furthermore, a comparison of the solvent accessible surface areas for (R)-BNP and (S)-BNP during MD simulations in which each enantiomer was bound to pocket two of poly(SULV) are shown in Figure 7(b). Throughout the MD simulation, the (R)-BNP SASA is approximately 100 Ų higher than the corresponding (S)-BNP value. The surface areas for both enantiomers are also less than the free solution value of ~ 420 Ų. This result indicates that when (S)-BNP binds to pocket two, it is able to penetrate deeper than (R)-BNP into the binding pocket or MM core. As discussed above, this effect likely allows more hydrophobic interactions between this enantiomer and the MM non-polar hydrocarbon chains and amino acid side chains to occur. Therefore, the representative structures in Figure 6 and the SASA analyses both show that the (S) enantiomer lies deeper within pocket two of poly(SULV) than the R enantiomer. Deeper penetration into the pocket in turn likely increases the ability of the ligand molecule to interact hydrophobically with the non-polar regions of the MM.

Free Energy Calculations

In summary, the MD simulation results presented above point to MM pocket two as the preferred BNP binding site and suggest that overall (S)-BNP interacts with the MM more favorably than the (R) enantiomer. These conclusions are also supported by the results of binding free energy calculations shown in Table III. Here binding free energy is defined as the free energy of the intermolecular complex minus the sum of the free energies of the poly(SULV) molecular micelle and BNP ligand. Table III also presents the fractional population, f_i, of each binding site, based upon the binding free energies. Populations were calculated from the binding energies with the Boltzmann relation in equation (1),

$$f_i=\frac{e^{-G_i/k_B·T}}{\sum _i{e}^{-G_i/k_B·T}}$$ (1)

where G_i is the binding free energy of the i^th pocket, k_B is Boltzmann’s constant, T is Kelvin temperature, and the summation goes over the four MM binding sites. For (S)-BNP it was found that the most negative or most favorable binding free energy was associated with pocket two. In addition, the pocket two binding free energy was sufficiently lower than the energies of the other pockets that the fractional population of pocket two was near one. Similar results were obtained for (R)-BNP, where again pocket two had the most negative binding free energy and a much higher fractional population than the other three pockets. Finally, Table III also shows that the (S)-BNP binding free energy of -78.12 J·mol⁻¹ is lower or more favorable than the respective (R) enantiomer value of -60.33 kJ·mol⁻¹. Therefore, the free energy calculations show that the (S) enantiomer experiences more favorable interactions with poly(SULV) and thus binds more strongly to the MM than the R enantiomer.

Table III.

Binding Free Energies for (S) and (R)-BNP in poly(SULV) pockets one-four.

(S)-BNP
Binding	Pocket Binding Free Energy (kJ·mol−1)	Fractional Population
Pocket 1	−52.84	3.6×10−5
Pocket 2	−78.12	≈1
Pocket 3	−59.50	5.4×10−4
Pocket 4	−52.95	3.8×10−5
(R)-BNP
Binding	Pocket Binding Free Energy (kJ·mol−1)	Fractional Population
Pocket 1	−48.97	9.3×10−3
Pocket 2	−60.33	0.91
Pocket 3	−50.10	1.5×10−2
Pocket 4	−53.96	0.069

The MD simulation prediction that (S)-BNP interacts more strongly with poly(SULV) than (R)-BNP is supported by results from both CE and NMR spectroscopy experiments. In CE, (S)-BNP was observed to elute after (R)-BNP in separations performed with poly(SULV) as the chiral selector [2]. This result showed that in solution, as in the MD simulations, (S)-BNP experienced stronger interactions with the MM. Furthermore, NMR diffusion measurements have also been used to investigate the relative binding affinities of (R)-BNP and (S)-BNP for poly(SULV) in aqueous solution. In these experiments, solutions were prepared containing poly(SULV) and one of the BNP enantiomers. Pulsed field gradient NMR experiments were then used to measure the diffusion coefficients of the MM and BNP enantiomers. The free solution BNP diffusion coefficient was also measured. From these values, the fraction of BNP molecules bound to the MM and the BNP:MM association constant, K, were calculated [3]. This analysis showed that (S)-BNP had a poly(SULV) association constant of 125±3, while the corresponding K value for (R)-BNP was 73.8±3.5 [3]. Therefore, the NMR results also demonstrate that (S)-BNP exhibits stronger interactions with the MM than (R)-BNP and provide experimental verification of the MD simulation work presented.

Another point of comparison between the MD simulations and experimental results is with respect to the identification of the poly(SULV) amino acid (N-terminal leucine or C-terminal valine) that is the site of primary chiral recognition for the (S)-BNP enantiomer. Both CE and NMR experiments have shown that when (S)-BNP binds to poly(SULV), the primary site of chiral interaction is the N-terminal leucine amino acid in the dipeptide headgroup [2–4]. In the CE studies, Valle, et al. synthesized poly(SULV) molecules with all possible optical configurations of the leucine and valine chiral centers (D,D; D,L; L,D; and L,L). A racemic mixture of BNP, spiked with either the (R) or (S) enantiomer to allow for the identification of elution order, was then separated using poly(SULV) molecules with each of the four dipeptide optical configurations listed above. The site of primary chiral recognition was identified as the N-terminal leucine amino acid by monitoring how the elution order of the BNP enantiomers was affected by changes in the optical configurations of the poly(SULV) headgroup chiral centers [2]. In the NMR experiments, two-dimensional NOESY spectra of (S)-BNP:poly(SULV) mixtures were collected. These spectra showed more intense intermolecular cross peaks between the protons on the (S)-BNP aromatic rings and the leucine Hα protons and less intense intermolecular cross peaks between the same BNP protons and the valine Hα. Since NOESY cross peak volumes are expected to be higher when hydrogen atoms are closer to one another, this result suggested that (S)-BNP was on average closer to the leucine chiral center and thus the leucine amino acid was the primary site of chiral recognition [2–4].

The results of the MD simulation pocket two hydrogen bond analyses were consistent with the experimental finding that the site of (S)-BNP chiral recognition is at or near the leucine chiral center. Table II shows that three intermolecular hydrogen bonds between (S)-BNP and poly(SULV) were detected. Two of these three hydrogen bonds along with the H-bond with the highest occupancy of 11.88 % were between an (S)-BNP oxygen atom and the poly(SULV) leucine NH hydrogen bond donor atom. Therefore, the MD simulations show that when hydrogen bonds form between (S)-BNP and MM dipeptide headgroup atoms, those H-bonds are more likely to form with the leucine rather than the valine NH atoms. This result is consistent CE and NMR which have shown that (S)-BNP interacts primarily with the N-terminal leucine chiral center of the poly(SULV) headgroup.

Conclusions

Molecular dynamics simulations were used to characterize the interactions between enantiomers of BNP and the chiral molecular micelle poly(SULV). Four poly(SULV) binding pockets were identified and MD simulations were carried out with either (R)-BNP or (S)-BNP molecules docked into each site. Pocket two, near MM chains six, thirteen, and eighteen was found to be the preferred binding site for both BNP enantiomers. In pocket two, both enantiomers experienced the strongest intermolecular hydrogen bonding and penetrated most deeply into the MM core. Furthermore, as confirmed by experiment, the MD simulations showed that (S)-BNP interacted more favorably with poly(SULV) than the (R) enantiomer.

Highlights.

Molecular micelle-chiral ligand Intermolecular interactions were studied.

Ligand enantiomers bound preferentially to one molecular micelle binding pocket.

The ligand (S) enantiomer had a lower micelle binding energy than the (R) enantiomer.

The (S) enantiomer penetrated deeper than the (R) enantiomer into the micelle core.

Molecular dynamics results agreed with NMR and capillary electrophoresis experiments.